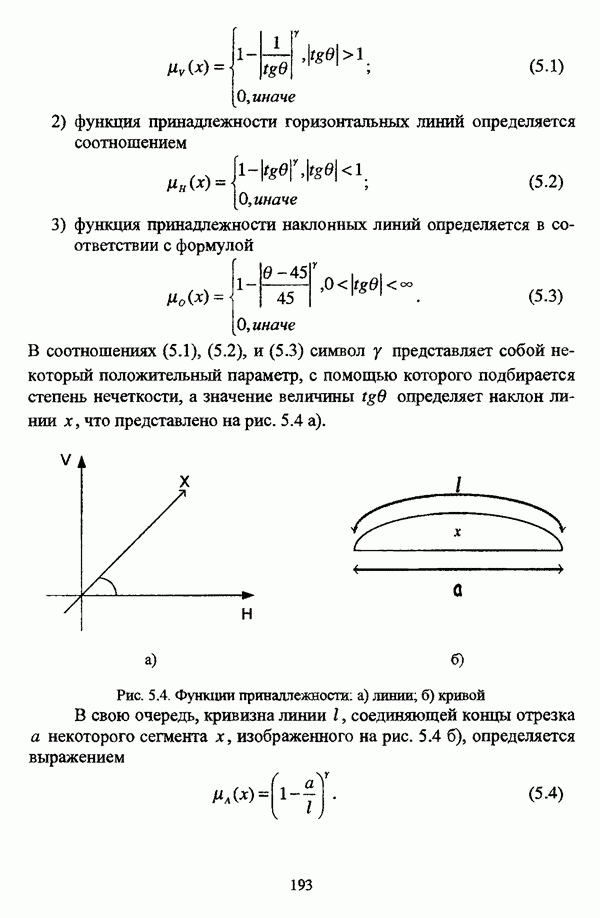
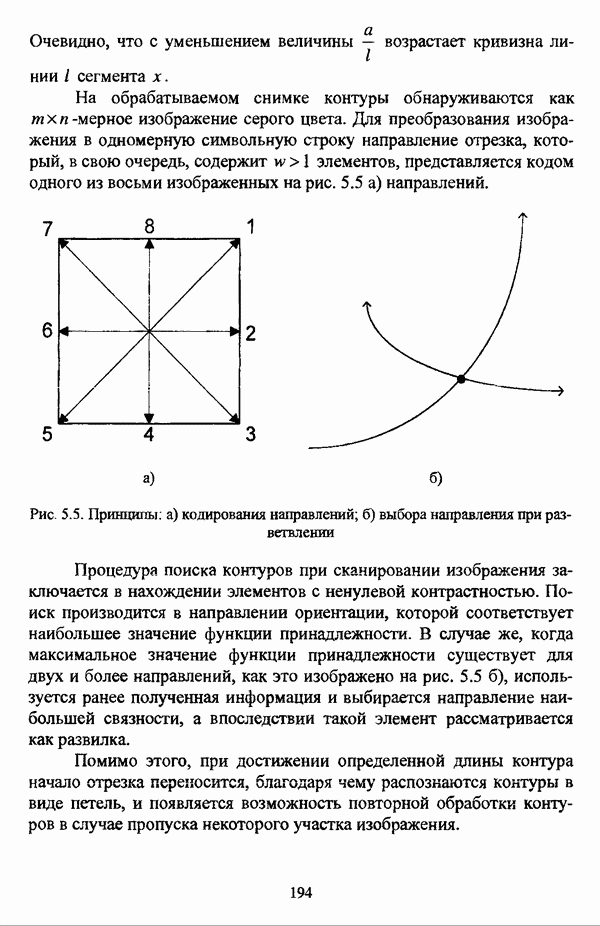
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.3.2. Результаты вычислительных экспериментов
Для проведения сравнения были отобраны оптимизационные процедуры Беждека — Данна, Педрича и Уиндхема, иерархический вариант алгоритма Тамуры - Хигути — Танаки и алгоритм классификации на нечетких графах Берштейна — Дзюбы. Для всех оптимизационных процедур эксперименты проводились при числе классов, равном двум, трем и четырем, для процедуры классификации на нечетких графах Берштейна — Дзюбы эксперименты проводились при числе классов, равном двум и трем. При проведении вычислительных экспериментов с оптимизационными процедурами в качестве матрицы первоначального разбиения в каждом эксперименте для определенного числа классов использовалась одна и та же, сгенерированная случайным образом с соблюдением условия нечеткого разбиения Распини  матрица
матрица  При обработке данных алгоритмом Беждека — Данна значение показателя нечеткости у полагалось равным двум.
При обработке данных алгоритмом Беждека — Данна значение показателя нечеткости у полагалось равным двум.
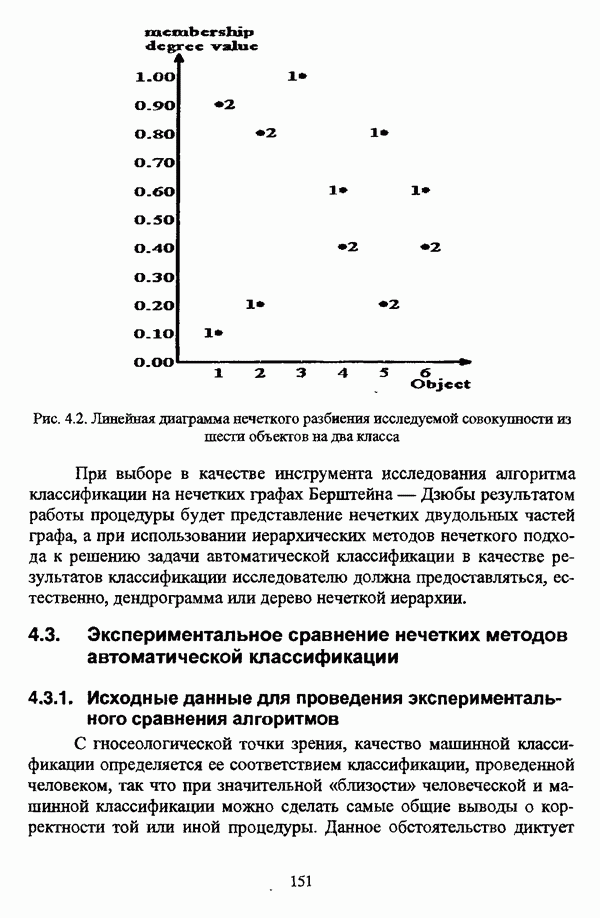
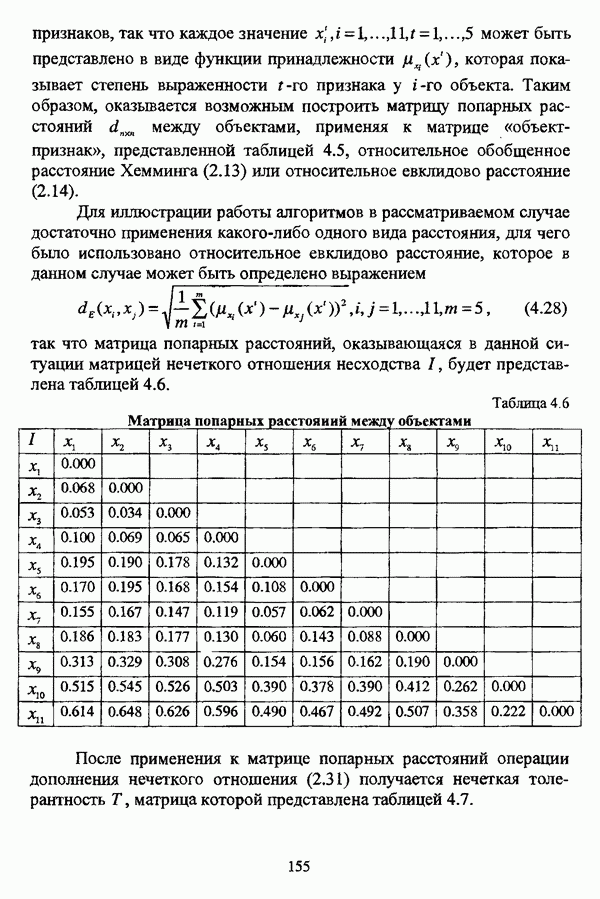
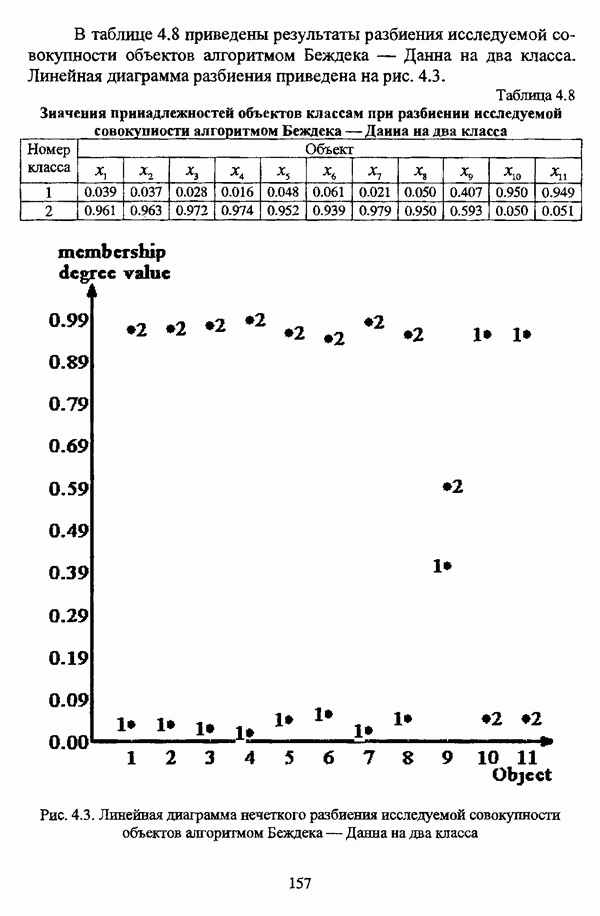
В таблице 4.8 приведены результаты разбиения исследуемой совокупности объектов алгоритмом Беждека — Данна на два класса. Линейная диаграмма разбиения приведена на рис. 4.3.
Таблица 4.8. Значения принадлежностей объектов классам при разбиении исследуемой совокупности алгоритмом Беждека—Данна на два класса

(см. скан)
Рис. 4.3. Линейная диаграмма нечеткого разбиения исследуемой совокупности объектов алгоритмом Беждека — Данна на два класса
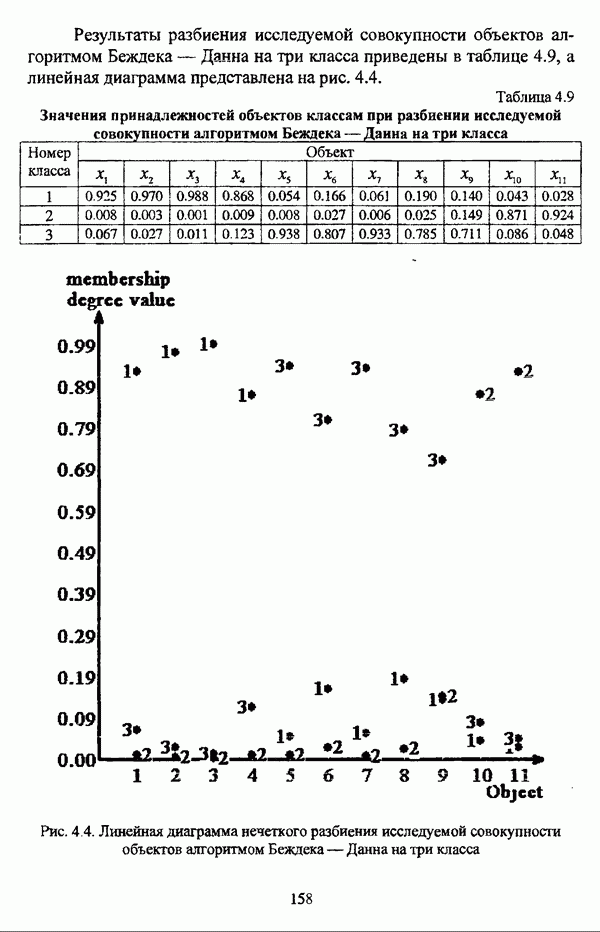
Результаты разбиения исследуемой совокупности объектов алгоритмом Беждека — Данна на три класса приведены в таблице 4.9, а линейная диаграмма представлена на рис. 4.4.
Таблица 4.9
Значения принадлежностей объектов классам при разбиении исследуемой совокупности алгоритмом Беждека — Данна на три класса

(см. скан)
Рис. 4.4. Линейная диаграмма нечеткого разбиения исследуемой совокупности объектов алгоритмом Беждека — Данна на три класса
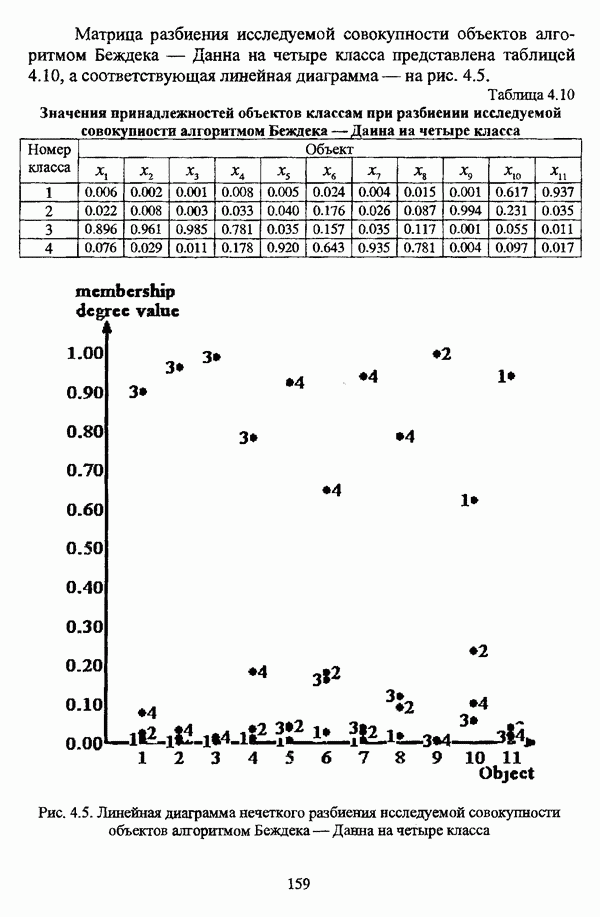
Матрица разбиения исследуемой совокупности объектов алгоритмом Беждека — Данна на четыре класса представлена таблицей 4.10, а соответствующая линейная диаграмма — на рис. 4.5.
Таблица 4.10
Значения принадлежностей объектов классам при разбиении исследуемой совокупности алгоритмом Беждека—Данна на четыре класса

(см. скан)
Рис. 4.5. Линейная диаграмма нечеткого разбиения исследуемой совокупности объектов алгоритмом Беждека — Данна на четыре класса
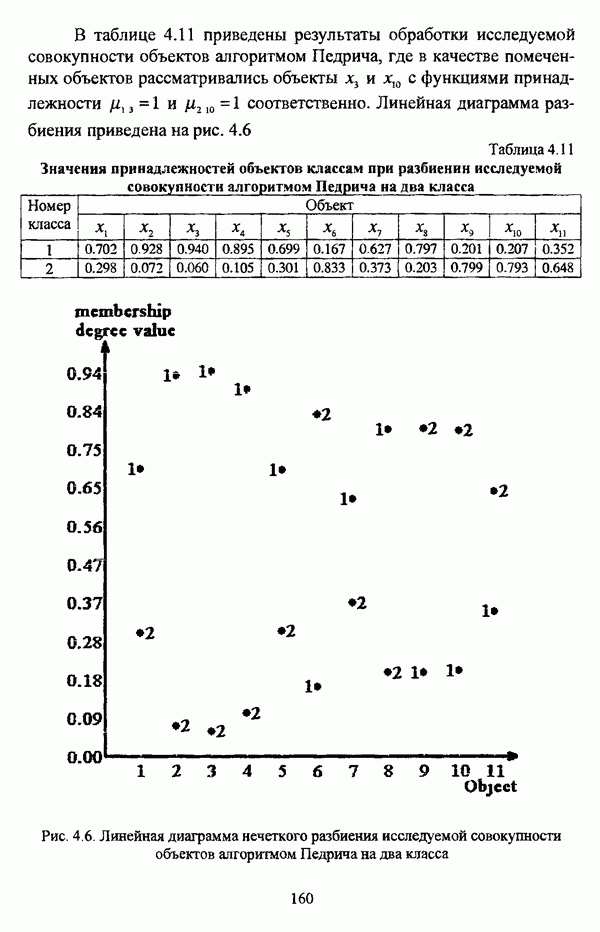
В таблице 4.11 приведены результаты обработки исследуемой совокупности объектов алгоритмом Педрича, где в качестве помеченных объектов рассматривались объекты  с функциями принадлежности
с функциями принадлежности  соответственно. Линейная диаграмма разбиения приведена на рис. 4.6
соответственно. Линейная диаграмма разбиения приведена на рис. 4.6
Таблица 4.11
Значения принадлежностей объектов классам при разбиении исследуемой совокупности алгоритмом Педрича на два класса

(см. скан)
Рис. 4.6. Линейная диаграмма нечеткого разбиения исследуемой совокупности объектов алгоритмом Педрича на два класса
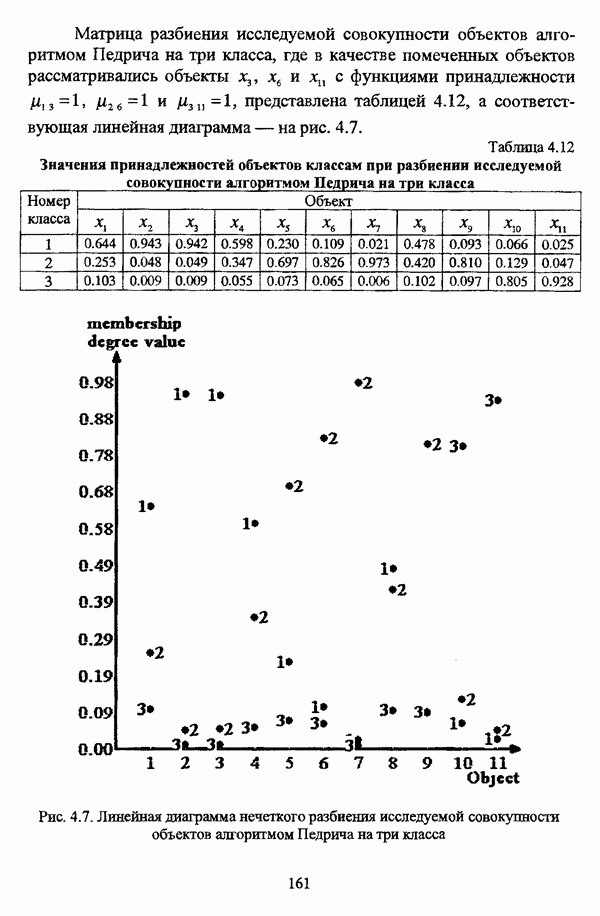
Матрица разбиения исследуемой совокупности объектов алгоритмом Педрича на три класса, где в качестве помеченных объектов рассматривались объекты  с функциями принадлежности
с функциями принадлежности  представлена таблицей 4.12, а соответствующая линейная диаграмма — на рис. 4.7.
представлена таблицей 4.12, а соответствующая линейная диаграмма — на рис. 4.7.
Таблица 4.12
Значения принадлежностей объектов классам при разбиении исследуемой совокупности алгоритмом Педрича на три класса

(см. скан)
Рис. 4.7. Линейная диаграмма нечеткого разбиения исследуемой совокупности объектов алгоритмом Педрича на три класса
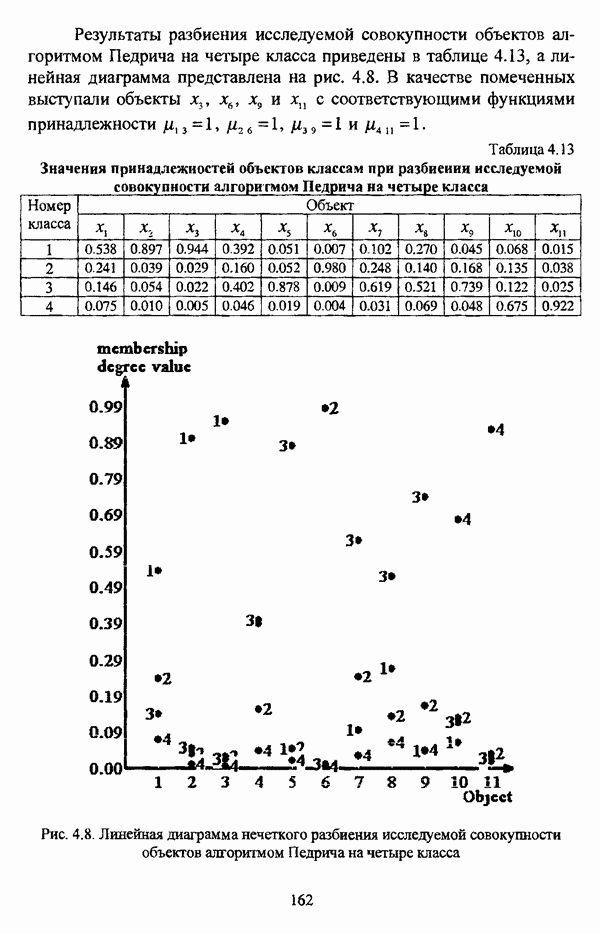
Результаты разбиения исследуемой совокупности объектов алгоритмом Педрича на четыре класса приведены в таблице 4.13, а линейная диаграмма представлена на рис, 4.8. В качестве помеченных выступали объекты  с соответствующими функциями принадлежности
с соответствующими функциями принадлежности 
Таблица 4.13
Значения принадлежностей объектов классам при разбиении исследуемой совокупности алгоритмом Педрича на четыре класса

(см. скан)
Рис. 4.8. Линейная диаграмма нечеткого разбиения исследуемой совокупности объектов алгоритмом Педрича на четыре класса
При обработке данных алгоритмом Беждека — Данна объекты  всегда попадают в один класс с высоким значением принадлежности: при разбиении на два и четыре класса они образуют ядро группы с номером 1, при разбиении на три класса — ядро группы номер 2, Объект
всегда попадают в один класс с высоким значением принадлежности: при разбиении на два и четыре класса они образуют ядро группы с номером 1, при разбиении на три класса — ядро группы номер 2, Объект  занимает промежуточное положение между хорошо выделяющимися группами
занимает промежуточное положение между хорошо выделяющимися группами  что особенно заметно при разбиении на два класса, а при разбиении на четыре класса объект
что особенно заметно при разбиении на два класса, а при разбиении на четыре класса объект  выделяется в класс номер 2.
выделяется в класс номер 2.
Результаты обработки данных алгоритмом Педрича отличаются от результатов, полученных при помощи алгоритма Беждека — Данна, не только значениями принадлежности объектов классам, но и распределением объектов по классам: к примеру, при разбиении на два класса ядра групп выглядят как  и
и  При разбиении на три и четыре класса результаты работы обоих алгоритмов также довольно существенно отличаются друг от друга, что объясняется зависимостью результатов разбиения от элементов множества помеченных объектов при использовании алгоритма Педрича.
При разбиении на три и четыре класса результаты работы обоих алгоритмов также довольно существенно отличаются друг от друга, что объясняется зависимостью результатов разбиения от элементов множества помеченных объектов при использовании алгоритма Педрича.
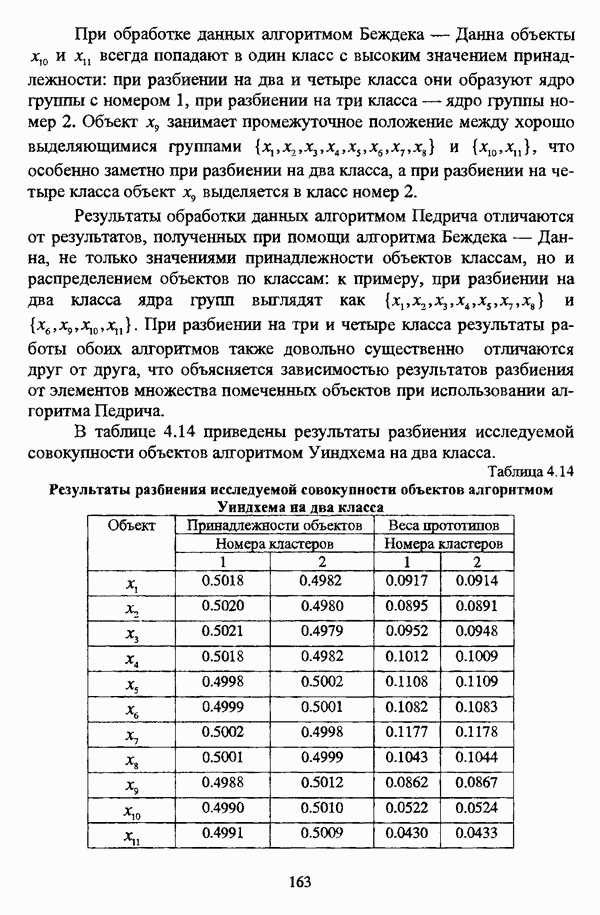
В таблице 4.14 приведены результаты разбиения исследуемой совокупности объектов алгоритмом Уиндхема на два класса.
Таблица 4.14. Результаты разбиения исследуемой совокупности объектов алгоритмом Уиндхема на два класса

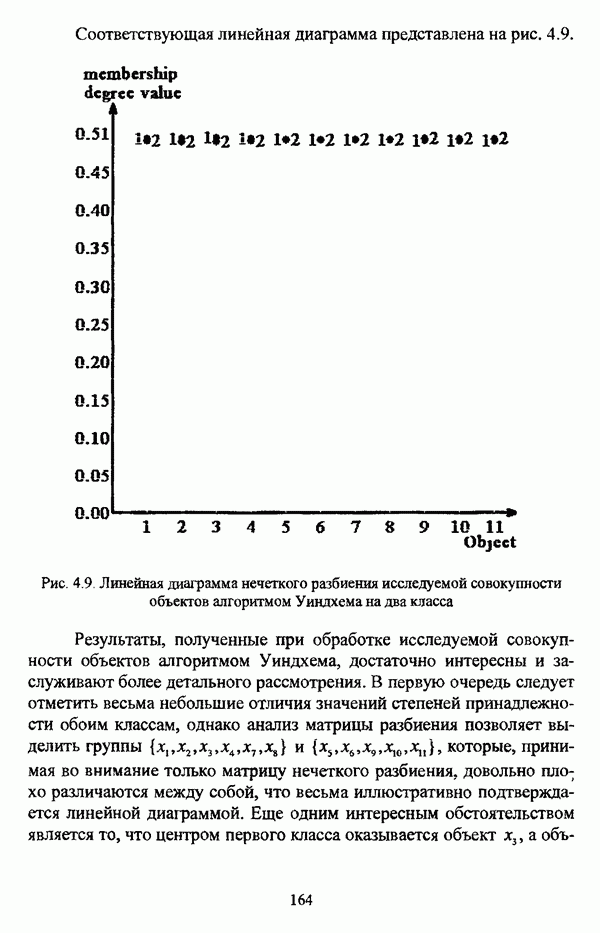
Соответствующая линейная диаграмма представлена на рис. 4.9.
(см. скан)
Рис. 4.9, Линейная диаграмма нечеткого разбиения исследуемой совокупности объектов алгоритмом Уиндхема на два класса
Результаты, полученные при обработке исследуемой совокупности объектов алгоритмом Уиндхема, достаточно интересны и заслуживают более детального рассмотрения. В первую очередь следует отметить весьма небольшие отличия значений степеней принадлежности обоим классам, однако анализ матрицы разбиения позволяет выделить группы и  которые, принимая во внимание только матрицу нечеткого разбиения, довольно плохо различаются между собой, что весьма иллюстративно подтверждается линейной диаграммой. Еще одним интересным обстоятельством является то, что центром первого класса оказывается объект х, а объект
которые, принимая во внимание только матрицу нечеткого разбиения, довольно плохо различаются между собой, что весьма иллюстративно подтверждается линейной диаграммой. Еще одним интересным обстоятельством является то, что центром первого класса оказывается объект х, а объект
 может быть выделен как центр второго класса. Эти результаты, если не принимать во внимание значения степеней принадлежности объектов классам, почти полностью совпадают с результатами, полученными при обработке данных алгоритмом Педрича: исключение составляет объект
может быть выделен как центр второго класса. Эти результаты, если не принимать во внимание значения степеней принадлежности объектов классам, почти полностью совпадают с результатами, полученными при обработке данных алгоритмом Педрича: исключение составляет объект  перемещенный при обработке данных алгоритмом Уиндхема во вторую группу. В то же время анализ результатов обработки данных, полученных при помощи алгоритма Беждека
перемещенный при обработке данных алгоритмом Уиндхема во вторую группу. В то же время анализ результатов обработки данных, полученных при помощи алгоритма Беждека  Данна, позволяет выделить центрами соответствующих групп объекты
Данна, позволяет выделить центрами соответствующих групп объекты 
Весьма интересны также результаты, представленные матрицей весов прототипов классов. Отчетливо выделяется группа  для элементов которой имеет место
для элементов которой имеет место  Если данную группу интерпретировать как «ядро» всей исследуемой совокупности, то, очевидно, центром исследуемого множества объектов следует считать объект
Если данную группу интерпретировать как «ядро» всей исследуемой совокупности, то, очевидно, центром исследуемого множества объектов следует считать объект  Вместе с тем, для объектов
Вместе с тем, для объектов  значение «степени прототипности»
значение «степени прототипности» 
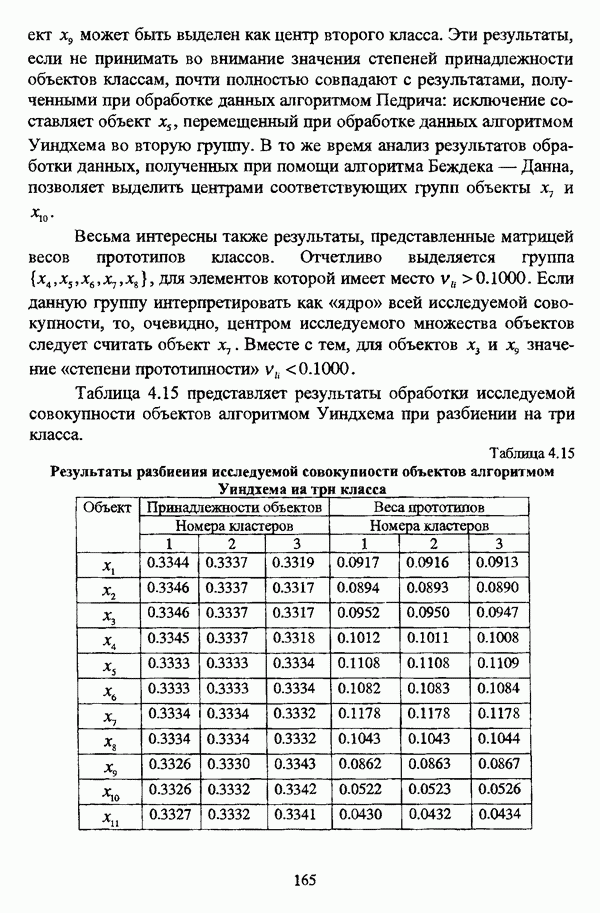
Таблица 4.15 представляет результаты обработки исследуемой совокупности объектов алгоритмом Уиндхема при разбиении на три класса.
Таблица 4.15. Результаты разбиения исследуемой совокупности объектов алгоритмом Уиндхема на три класса

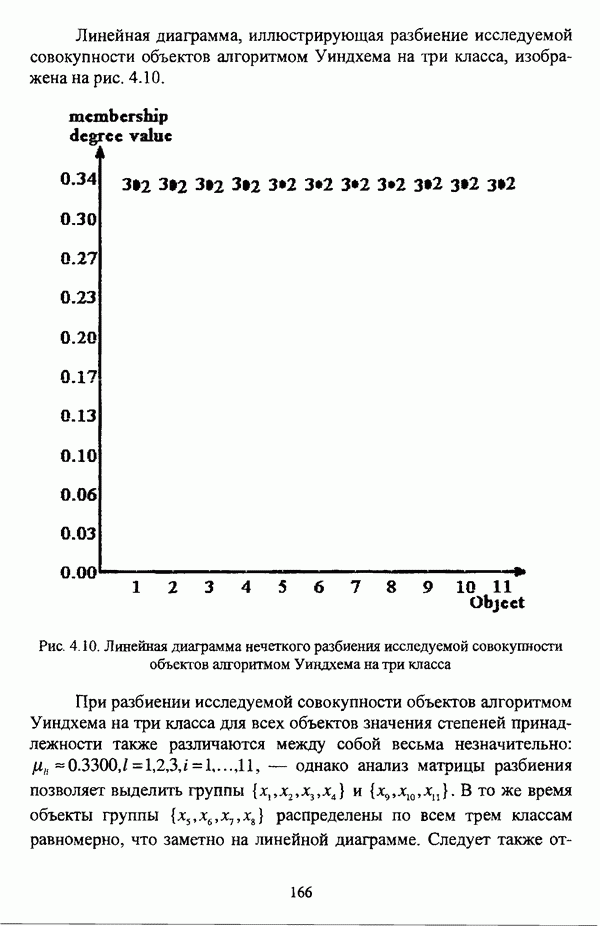
Линейная диаграмма, иллюстрирующая разбиение исследуемой совокупности объектов алгоритмом Уиндхема на три класса, изображена на рис. 4.10.
(см. скан)
Рис. 4.10. Линейная диаграмма нечеткого разбиения исследуемой совокупности объектов алгоритмом Уиндхема на три класса
При разбиении исследуемой совокупности объектов алгоритмом Уиндхема на три класса для всех объектов значения степеней принадлежности также различаются между собой весьма незначительно:  однако анализ матрицы разбиения позволяет выделить группы
однако анализ матрицы разбиения позволяет выделить группы  . В то же время объекты группы
. В то же время объекты группы  распределены по всем трем классам равномерно, что заметно на линейной диаграмме. Следует также отметить
распределены по всем трем классам равномерно, что заметно на линейной диаграмме. Следует также отметить
то обстоятельство, что значения степеней принадлежности объектов  всем трем классам совпадают, что, с одной стороны, позволяет любой из этих объектов в равной мере рассматривать в качестве центра первой группы, с другой стороны, однако для объекта
всем трем классам совпадают, что, с одной стороны, позволяет любой из этих объектов в равной мере рассматривать в качестве центра первой группы, с другой стороны, однако для объекта  «степень прототипности» выше, чем для объекта
«степень прототипности» выше, чем для объекта  так что центром первого класса вновь оказывается объект
так что центром первого класса вновь оказывается объект  . В свою очередь, объект
. В свою очередь, объект  отчетливо выделяется в качестве центра третьего класса, тогда как при обработке данных как алгоритмом Беждека — Данна, так и при их обработке алгоритмом Педрича объект
отчетливо выделяется в качестве центра третьего класса, тогда как при обработке данных как алгоритмом Беждека — Данна, так и при их обработке алгоритмом Педрича объект  явно относится к другой группе, чем объекты
явно относится к другой группе, чем объекты 
Анализ матрицы весов прототипов в данном случае оказывается малопригодным для интерпретации полученных результатов, поскольку, аналогично разбиению на два класса, выделяется группа для элементов которой имеет место  однако только объект
однако только объект  может быть отнесен к первой группе в силу значения степени принадлежности.
может быть отнесен к первой группе в силу значения степени принадлежности.
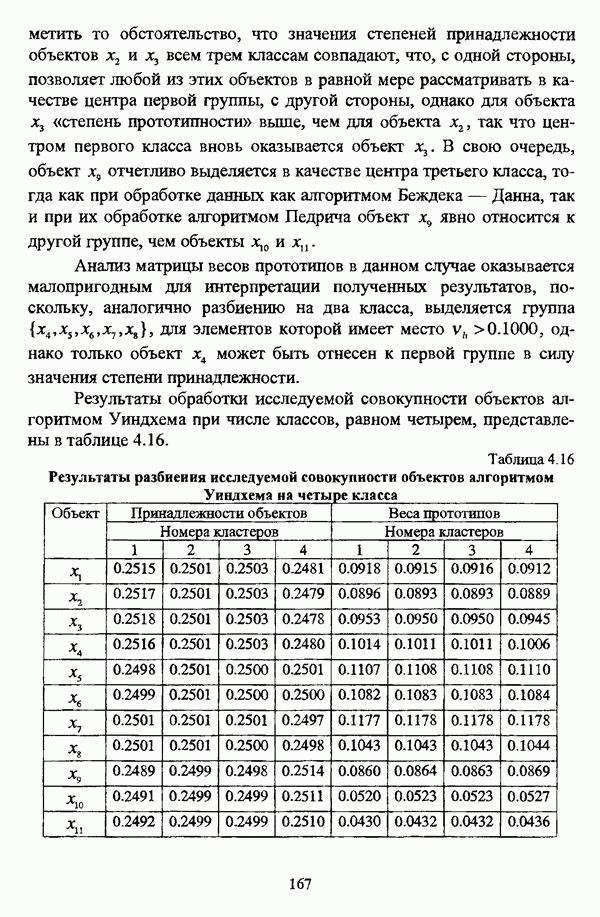
Результаты обработки исследуемой совокупности объектов алгоритмом Уиндхема при числе классов, равном четырем, представлены в таблице 4.16.
Таблица 4.16. Результаты разбиения исследуемой совокупности объектов алгоритмом Уиндхема на четыре класса

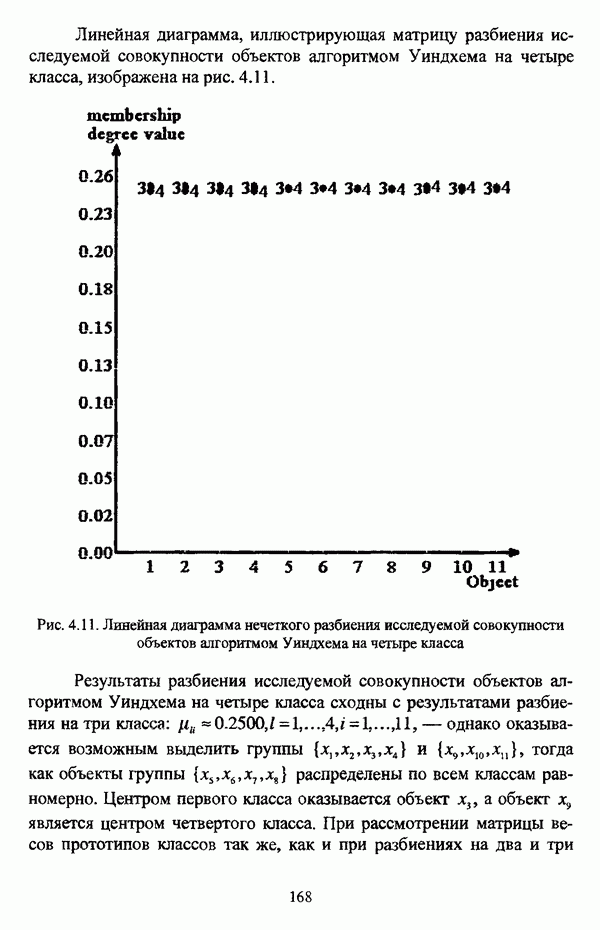
Линейная диаграмма, иллюстрирующая матрицу разбиения исследуемой совокупности объектов алгоритмом Уиндхема на четыре класса, изображена на рис. 4.11.
(см. скан)
Рис. 4.11. Линейная диаграмма нечеткого разбиения исследуемой совокупности объектов алгоритмом Уиндхема на четыре класса
Результаты разбиения исследуемой совокупности объектов алгоритмом Уиндхема на четыре класса сходны с результатами разбиения на три класса:  — однако оказывается возможным выделить группы
— однако оказывается возможным выделить группы  тогда как объекты группы
тогда как объекты группы  распределены по всем классам равномерно. Центром первого класса оказывается объект
распределены по всем классам равномерно. Центром первого класса оказывается объект  а объект
а объект  является центром четвертого класса. При рассмотрении матрицы весов прототипов классов так же, как и при разбиениях на два и три
является центром четвертого класса. При рассмотрении матрицы весов прототипов классов так же, как и при разбиениях на два и три
класса, выделяется группа объектов  Для которых
Для которых 
Таким образом, при обработке рассматриваемых исходных данных алгоритмом Уиндхема наиболее просто интерпретируются результаты разбиения на два класса.
Следует указать, что при обработке данных Е. Андерсона алгоритмом Уиндхема отчетливо выделяется класс SETOSA, тогда как классы VERSICOLOR и VIRGINICA «сливаются»  что также демонстрировалось Дж. Беждеком при обработке данных Е. Андерсона классическим методом с-средних, методом нечетких с-средних и методами расщепления смесей [53]. Результаты обработки данных Е. Андерсона методом нечетких с-средних при различных значениях показателя нечеткости классификации у также подробно рассматриваются в работе В. Педрича [144, с. 138-139].
что также демонстрировалось Дж. Беждеком при обработке данных Е. Андерсона классическим методом с-средних, методом нечетких с-средних и методами расщепления смесей [53]. Результаты обработки данных Е. Андерсона методом нечетких с-средних при различных значениях показателя нечеткости классификации у также подробно рассматриваются в работе В. Педрича [144, с. 138-139].
В таблице 4.17 представлены значения коэффициента разбиения  и энтропии разбиения
и энтропии разбиения  при разбиении исследуемой совокупности объектов нечеткими оптимизационными кластер-процедурами на два, три и четыре класса.
при разбиении исследуемой совокупности объектов нечеткими оптимизационными кластер-процедурами на два, три и четыре класса.
Таблица 4.17
Значения показателей качества разбиения при обработке исследуемой совокупности объектов различными оптимизационными алгоритмами

При рассмотрении значений коэффициента разбиения  для различного числа классов уместно указать, что при обработке данных алгоритмом Педрича значения коэффициента разбиения
для различного числа классов уместно указать, что при обработке данных алгоритмом Педрича значения коэффициента разбиения  для
для  практически совпадают, тогда как при их обработке методом нечетких с-средних наблюдается существенный «скачок»
практически совпадают, тогда как при их обработке методом нечетких с-средних наблюдается существенный «скачок»
значений  Сравнивая «скачки» значений обоих показателей разбиения при переходе от к
Сравнивая «скачки» значений обоих показателей разбиения при переходе от к  и при переходе от
и при переходе от  можно сделать вывод, что, хотя
можно сделать вывод, что, хотя  вполне может соответствовать «реальному» числу классов,
вполне может соответствовать «реальному» числу классов,  является более «приемлемым» числом классов в нечетком разбиении, чем
является более «приемлемым» числом классов в нечетком разбиении, чем  что, в свою очередь, соответствует числу классов в экспертном разбиении.
что, в свою очередь, соответствует числу классов в экспертном разбиении.
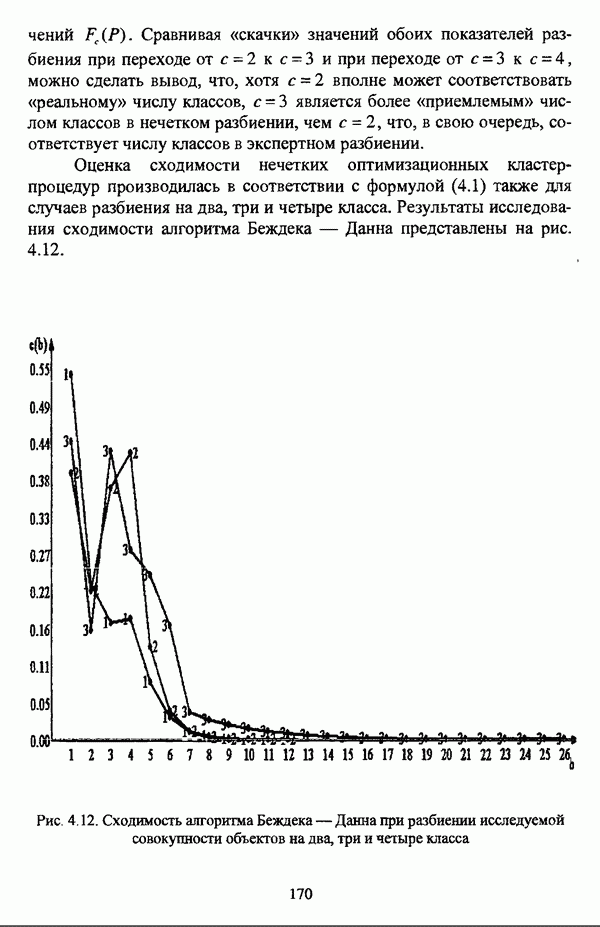
Оценка сходимости нечетких оптимизационных кластер-процедур производилась в соответствии с формулой (4.1) также для случаев разбиения на два, три и четыре класса. Результаты исследования сходимости алгоритма Беждека — Данна представлены на рис. 4.12.

Рис. 4.12. Сходимость алгоритма Беждека — Данна при разбиении исследуемой совокупности объектов на два, три и четыре класса
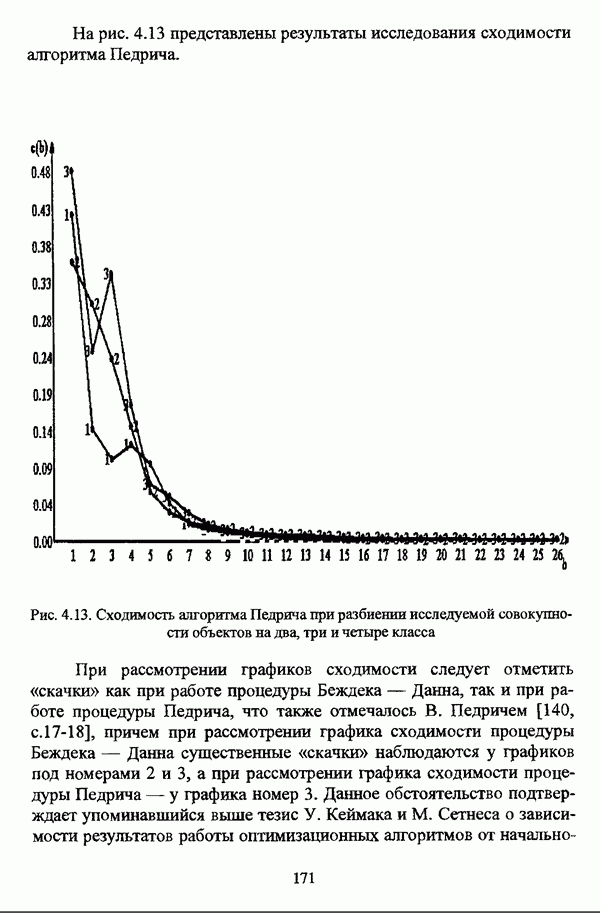
На рис. 4.13 представлены результаты исследования сходимости алгоритма Педрича.

Рис. 4.13. Сходимость алгоритма Педрича при разбиении исследуемой совокупности объектов на два, три и четыре класса
При рассмотрении графиков сходимости следует отметить «скачки» как при работе процедуры Беждека — Данна, так и при работе процедуры Педрича, что также отмечалось В. Педричем [140, с. 17-18], причем при рассмотрении графика сходимости процедуры Беждека — Данна существенные «скачки» наблюдаются у графиков под номерами 2 и 3, а при рассмотрении графика сходимости процедуры Педрича — у графика номер 3. Данное обстоятельство подтверждает упоминавшийся выше тезис У. Кеймака и М. Сетнеса о зависимости результатов работы оптимизационных алгоритмов от начального
разбиения и целесообразности проведения ряда экспериментов с различными начальными разбиениями.
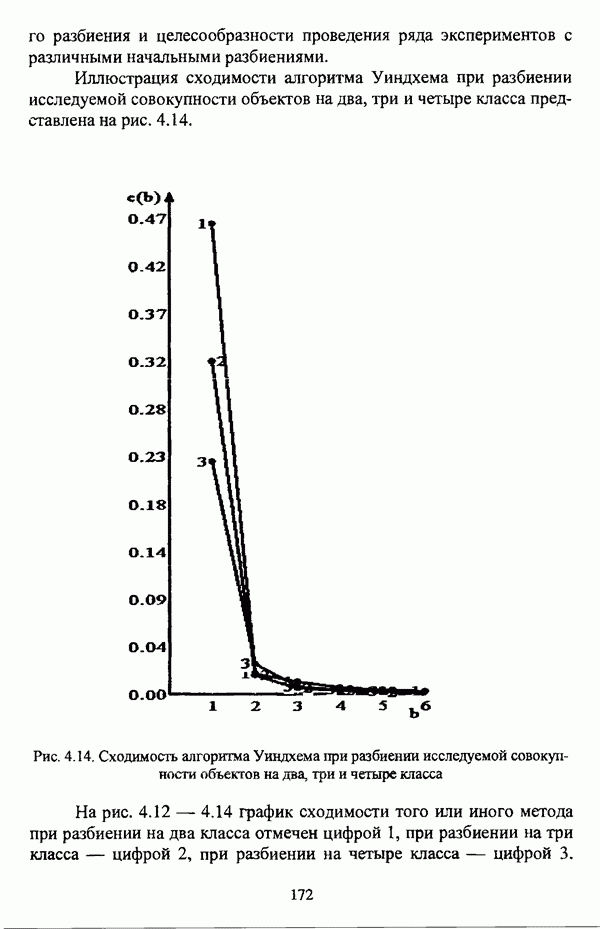
Иллюстрация сходимости алгоритма Уиндхема при разбиении исследуемой совокупности объектов на два, три и четыре класса представлена на рис. 4.14.

Рис. 4.14. Сходимость алгоритма Уиндхема при разбиении исследуемой совокупности объектов на два, три и четыре класса
На рис. 4.12-4.14 график сходимости того или иного метода при разбиении на два класса отмечен цифрой 1, при разбиении на три класса — цифрой 2, при разбиении на четыре класса — цифрой 3.
Рассмотрение представленных результатов работы нечетких оптимизационных методов кластеризации показывают, что наиболее быстрым является алгоритм Уиндхема. Касательно сходимости оптимизационных процедур следует также отметить, что с целью уменьшения числа итераций в тех случаях, когда решаемая задача не требует высокой точности вычислений, удовлетворительные результаты могут быть получены при значении порога в, приблизительно равном 0.01.
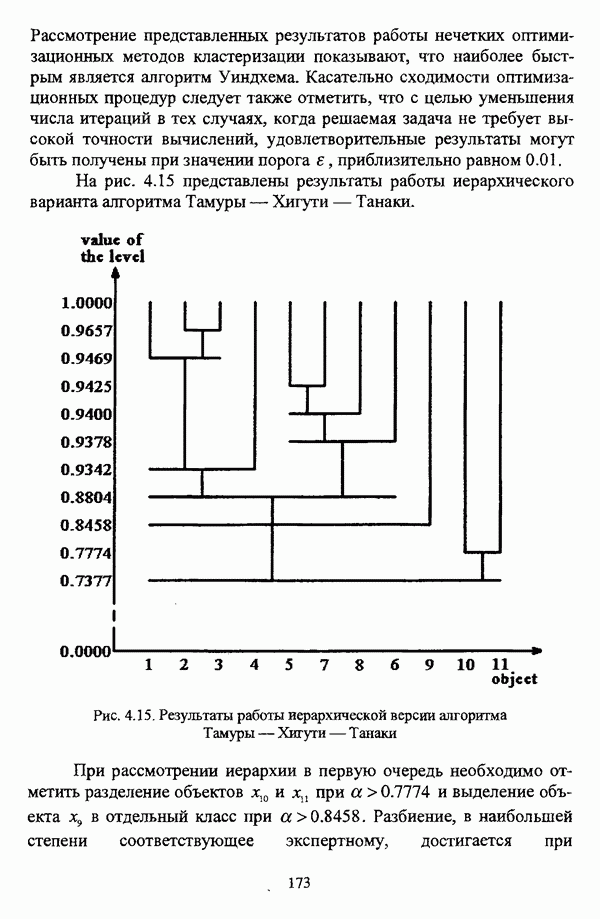
На рис. 4.15 представлены результаты работы иерархического варианта алгоритма Тамуры — Хигути — Танаки.

Рис. 4.15. Результаты работы иерархической версии алгоритма Тамуры—Хигути—Танаки
При рассмотрении иерархии в первую очередь необходимо отметить разделение объектов  при
при  и выделение объекта
и выделение объекта  в отдельный класс при а
в отдельный класс при а  Разбиение, в наибольшей степени соответствующее экспертному, достигается при
Разбиение, в наибольшей степени соответствующее экспертному, достигается при
 и выглядит следующим образом: первый класс представляет собой множество объектов
и выглядит следующим образом: первый класс представляет собой множество объектов  второй класс представляет собой множество объектов
второй класс представляет собой множество объектов  объект
объект  представляет собой третий класс, а объекты
представляет собой третий класс, а объекты  — соответственно четвертый и пятый классы, так что при объединении третьего, четвертого и пятого классов результаты полностью совпадут с экспертным разбиением. Данное обстоятельство указывает на то, что операция (max-min)-транзитивного замыкания в некоторой степени искажает геометрическую структуру исследуемой совокупности объектов, что накладывает ограничения на использование алгоритма Тамуры — Хигути — Танаки при классификации объектов.
— соответственно четвертый и пятый классы, так что при объединении третьего, четвертого и пятого классов результаты полностью совпадут с экспертным разбиением. Данное обстоятельство указывает на то, что операция (max-min)-транзитивного замыкания в некоторой степени искажает геометрическую структуру исследуемой совокупности объектов, что накладывает ограничения на использование алгоритма Тамуры — Хигути — Танаки при классификации объектов.
На рис. 4.16 изображен исходный граф, иллюстрирующий классифицируемую с помощью алгоритма Берштейна — Дзюбы совокупность объектов.

Рис. 4.16. Граф сходства исследуемой совокупности объектов
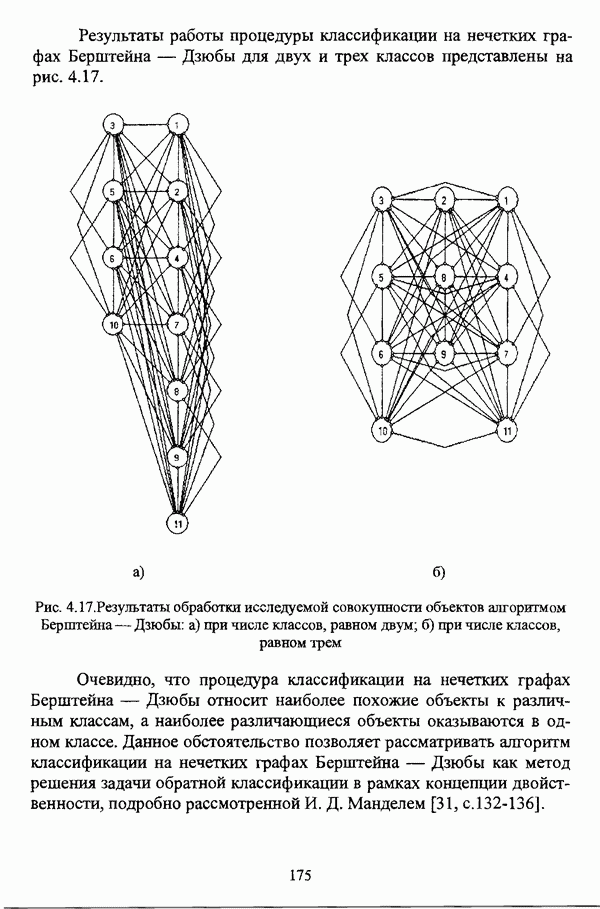
Результаты работы процедуры классификации на нечетких графах Берштейна — Дзюбы для двух и трех классов представлены на рис. 4.17.

Рис. 4.17. Результаты обработки исследуемой совокупности объектов алгоритмом Берштейна—Дзюбы: а) при числе классов, равном двум; б) при числе классов, равном трем
Очевидно, что процедура классификации на нечетких графах Берштейна — Дзюбы относит наиболее похожие объекты к различным классам, а наиболее различающиеся объекты оказываются в одном классе. Данное обстоятельство позволяет рассматривать алгоритм классификации на нечетких графах Берштейна — Дзюбы как метод решения задачи обратной классификации в рамках концепции двойственности, подробно рассмотренной И. Д. Манделем [31, с. 132-136].
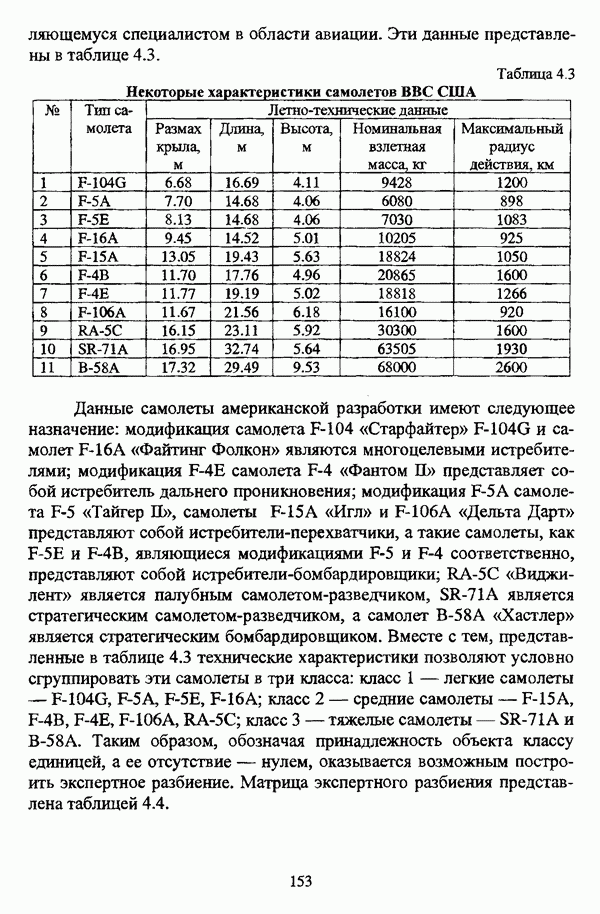
Представленные результаты работы различных нечетких кластер-процедур имеют иллюстративный характер, и, безусловно, не могут служить основанием для предпочтения каких-либо одних кластер-процедур перед другими.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
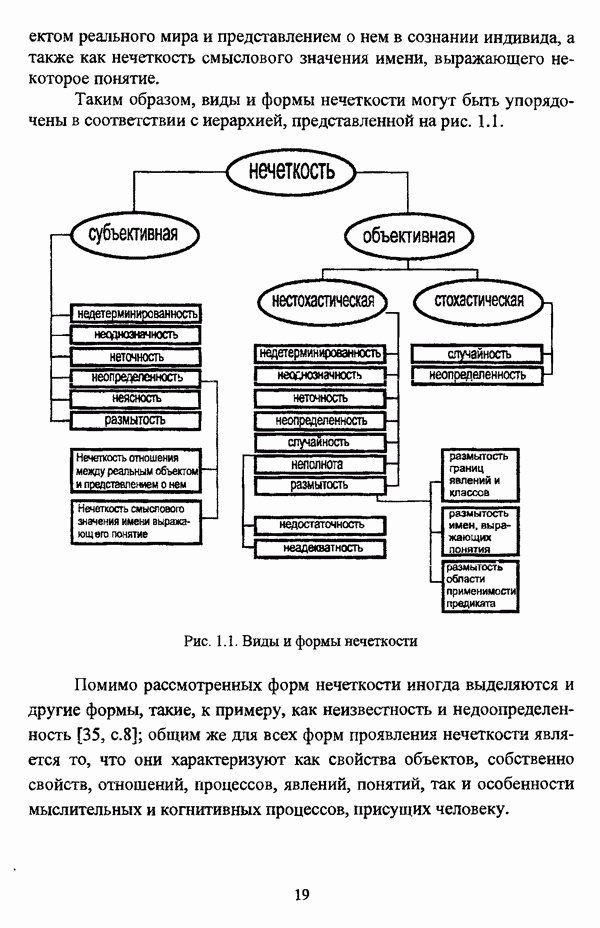
- ГЛАВА 1. ПРОБЛЕМА НЕОПРЕДЕЛЕННОСТИ В ЗАДАЧАХ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 1.1. Понятие однородности и проблема классификации объектов
- 1.1.2. Общая постановка задачи автоматической классификации и основные направления ее решения
- 1.2. Подход к решению задачи автоматической классификации с позиции теории нечетких множеств
- 1.2.2. Гносеологические аспекты подхода к решению задач классификации с позиции теории нечетких множеств
- Резюме
- ГЛАВА 2. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ НЕЧЕТКИХ МНОЖЕСТВ
- 2.1. Нечеткие множества
- 2.1.2. Основные операции над нечеткими множествами
- 2.2. Нечеткие отношения
- 2.2.2. Основные операции над нечеткими отношениями
- Резюме
- ГЛАВА 3. МЕТОДЫ НЕЧЕТКОГО ПОДХОДА К РЕШЕНИЮ ЗАДАЧ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 3.1.2. Описание алгоритмов
- 3.2. Оптимизационные методы
- 3.2.2. Описание алгоритмов
- 3.2.2.2. Алгоритм Уиндхема
- 3.2.2.3. Алгоритм Рубенса
- 3.2.2.4. Алгоритм Беждека — Данна
- 3.2.2.5. Алгоритм Педрича
- 3.2.2.6. Алгоритм Даве — Сена
- 3.2.2.7. Другие алгоритмы оптимизационного подхода
- 3.3. Иерархические методы
- 3.3.2. Описание алгоритмов
- 3.3.2.2. Алгоритм Думитреску (FDH algorithm)
- 3.3.2.3. Другие алгоритмы иерархического подхода
- Резюме
- ГЛАВА 4. СРАВНИТЕЛЬНЫЙ АНАЛИЗ НЕЧЕТКИХ МЕТОДОВ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 4.1.2. Виды исходных данных и общая схема проведения сравнительного анализа
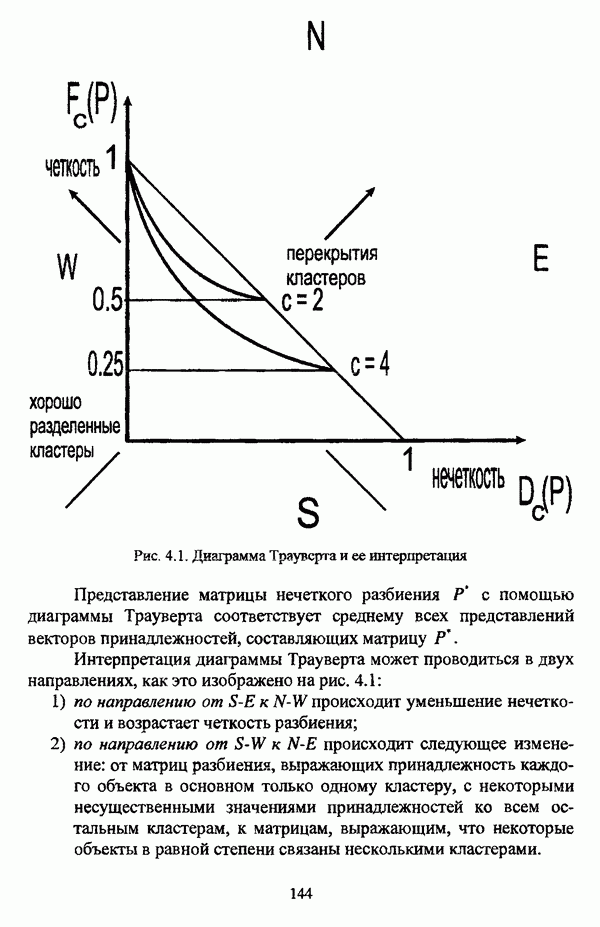
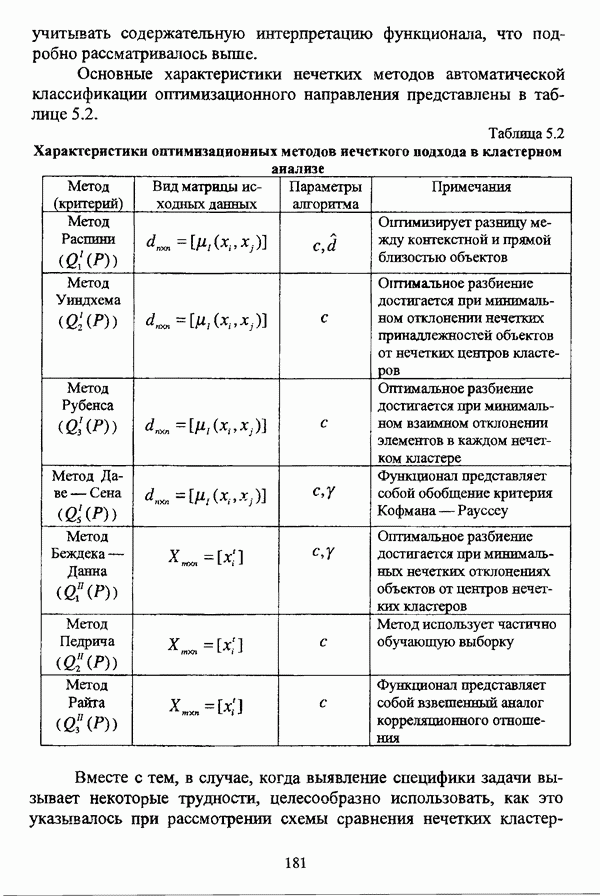
- 4.2. Оценка и представление результатов обработки данных нечеткими методами автоматической классификации
- 4.2.2. Представление и интерпретация результатов нечеткой классификации
- 4.3. Экспериментальное сравнение нечетких методов автоматической классификации
- 4.3.2. Результаты вычислительных экспериментов
- Резюме
- ГЛАВА 5. МЕТОДОЛОГИЧЕСКИЕ АСПЕКТЫ НЕЧЕТКОГО ПОДХОДА К РЕШЕНИЮ ЗАДАЧИ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
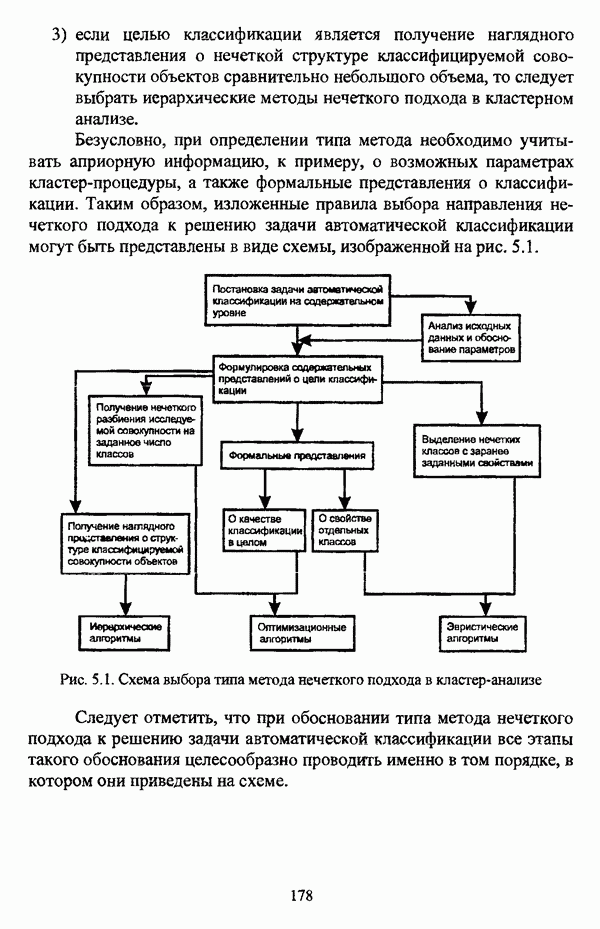
- 5.1.2. Выбор алгоритма нечеткого подхода к решению задачи автоматической классификации и обоснование параметров
- 5.2. Прикладные аспекты нечеткой классификации
- 5.2.2. Нечеткие методы автоматической классификации и другие нечеткие методы распознавания образов
- Резюме
- ЗАКЛЮЧЕНИЕ
- Основные обозначения
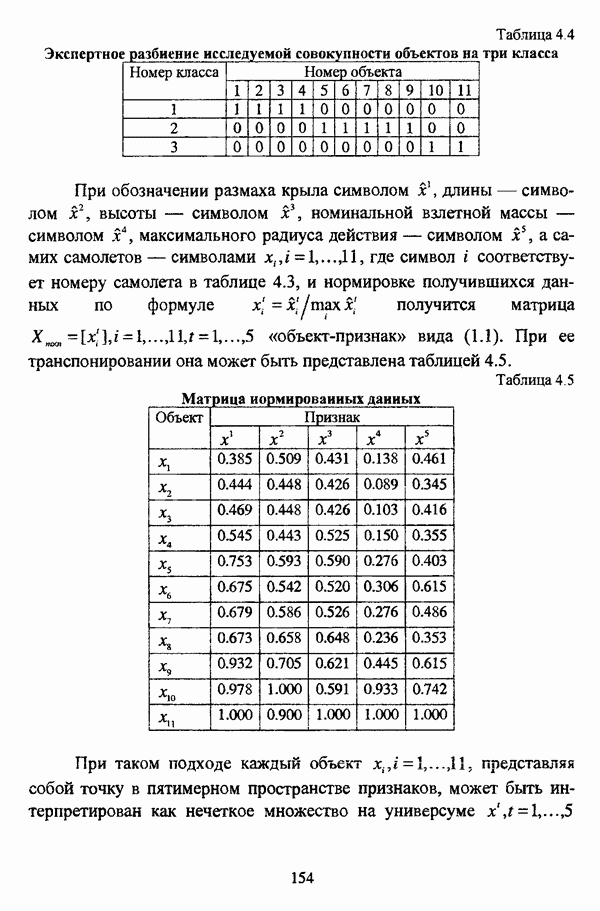
- Список литературы