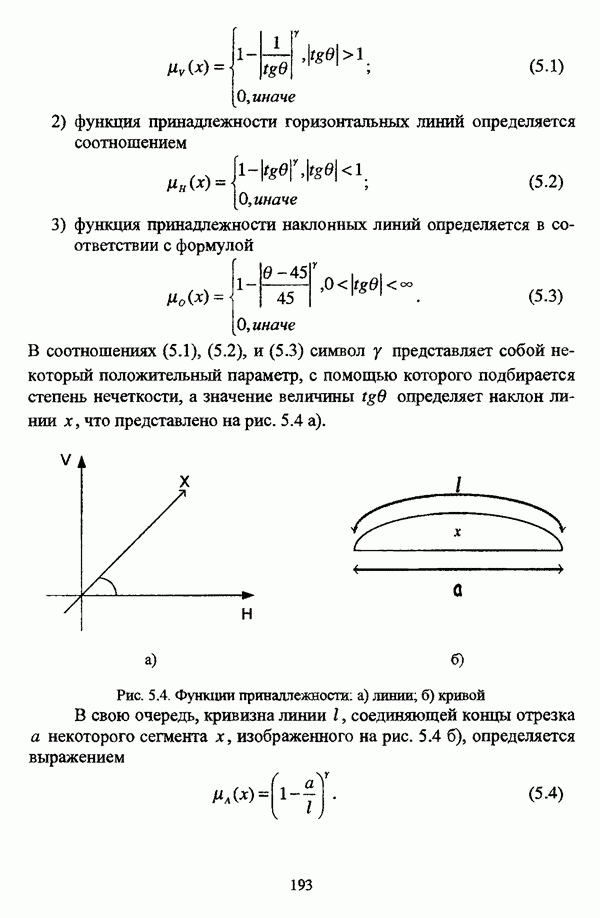
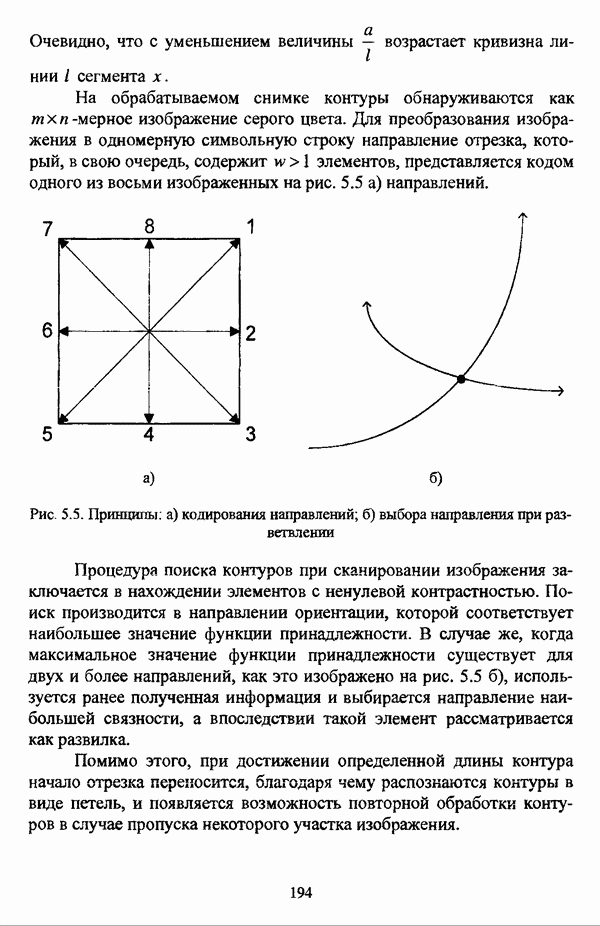
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Резюме
Понятие нечеткого множества вводится путем расширения двухэлементного множества принадлежностей  элементов универсума X его подмножеству А до интервала [0,1], так что нечеткое множество
элементов универсума X его подмножеству А до интервала [0,1], так что нечеткое множество  определяется как совокупность упорядоченных пар, составленных из элементов
определяется как совокупность упорядоченных пар, составленных из элементов  универсума
универсума  и соответствующих степеней принадлежности функции
и соответствующих степеней принадлежности функции  принимающих значения в интервале [0,1]. Поскольку функция принадлежности полностью описывает нечеткое множество, то око может задаваться непосредственно в виде функции принадлежности
принимающих значения в интервале [0,1]. Поскольку функция принадлежности полностью описывает нечеткое множество, то око может задаваться непосредственно в виде функции принадлежности  Понятие нечеткого множества может различным образом обобщаться, и одним из обобщений является понятие нечеткого множества типа
Понятие нечеткого множества может различным образом обобщаться, и одним из обобщений является понятие нечеткого множества типа  .
.
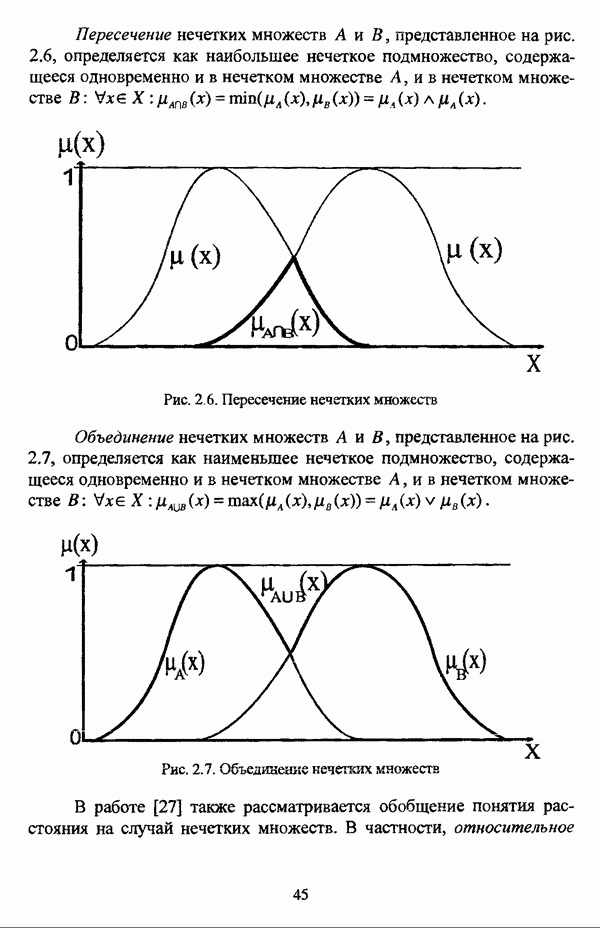
Над нечеткими множествами определяются такие основные операции, как включение, равенство, дополнение, пересечение, объединение и некоторые другие, не имеющие аналогов в случае обычных множеств, а также понятие расстояния между нечеткими множествами. Бинарным нечетким отношением R между множествами X и Y называется функция  [0,1]; в случае, когда множества X и Y совпадают, нечеткое отношение
[0,1]; в случае, когда множества X и Y совпадают, нечеткое отношение  называется бинарным нечетким отношением R на множестве
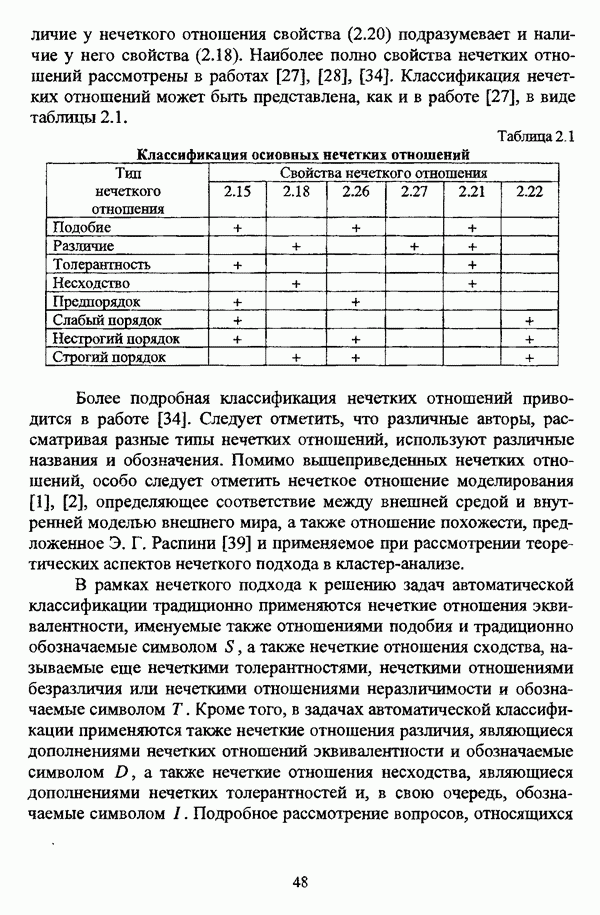
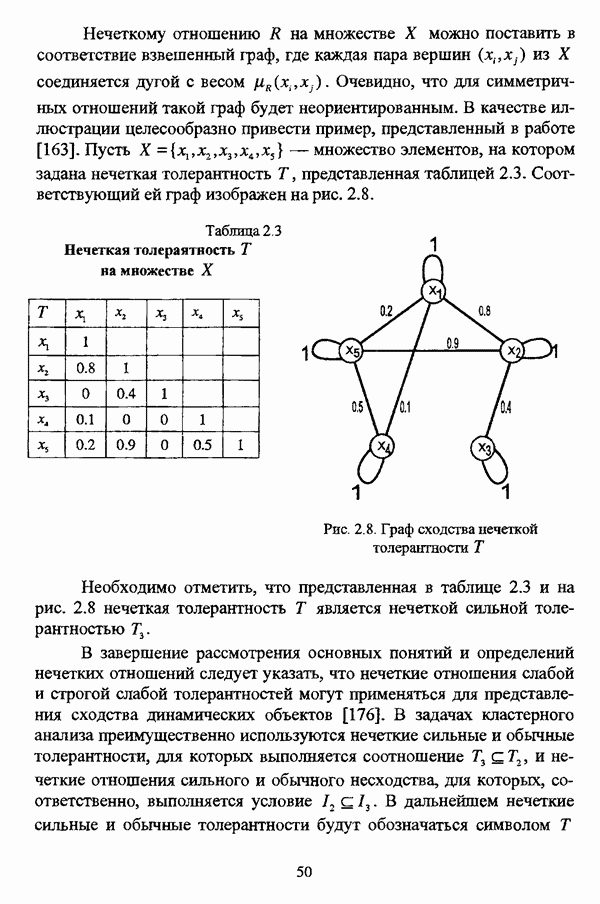
называется бинарным нечетким отношением R на множестве  Иначе, нечеткое отношение может определяться как нечеткое множество на декартовом произведении базовых множеств, так что для нечетких отношений сохраняются многие результаты, полученные для нечетких множеств, В зависимости от свойств, которыми они обладают, выделяют различные типы нечетких отношений, такие как отношения подобия, различия, толерантности, несходства, предпорядка, слабого порядка, строгого порядка, нестрогого порядка и некоторые другие. Любому нечеткому отношению R на множестве X можно поставить в соответствие взвешенный граф, где каждая пара вершин
Иначе, нечеткое отношение может определяться как нечеткое множество на декартовом произведении базовых множеств, так что для нечетких отношений сохраняются многие результаты, полученные для нечетких множеств, В зависимости от свойств, которыми они обладают, выделяют различные типы нечетких отношений, такие как отношения подобия, различия, толерантности, несходства, предпорядка, слабого порядка, строгого порядка, нестрогого порядка и некоторые другие. Любому нечеткому отношению R на множестве X можно поставить в соответствие взвешенный граф, где каждая пара вершин  из X соединяется дугой с весом
из X соединяется дугой с весом  Над нечеткими отношениями также определяются различные операции, как свойственные четким отношениям, так и не имеющие аналога в четком случае.
Над нечеткими отношениями также определяются различные операции, как свойственные четким отношениям, так и не имеющие аналога в четком случае.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ПРОБЛЕМА НЕОПРЕДЕЛЕННОСТИ В ЗАДАЧАХ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 1.1. Понятие однородности и проблема классификации объектов
- 1.1.2. Общая постановка задачи автоматической классификации и основные направления ее решения
- 1.2. Подход к решению задачи автоматической классификации с позиции теории нечетких множеств
- 1.2.2. Гносеологические аспекты подхода к решению задач классификации с позиции теории нечетких множеств
- Резюме
- ГЛАВА 2. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ НЕЧЕТКИХ МНОЖЕСТВ
- 2.1. Нечеткие множества
- 2.1.2. Основные операции над нечеткими множествами
- 2.2. Нечеткие отношения
- 2.2.2. Основные операции над нечеткими отношениями
- Резюме
- ГЛАВА 3. МЕТОДЫ НЕЧЕТКОГО ПОДХОДА К РЕШЕНИЮ ЗАДАЧ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 3.1.2. Описание алгоритмов
- 3.2. Оптимизационные методы
- 3.2.2. Описание алгоритмов
- 3.2.2.2. Алгоритм Уиндхема
- 3.2.2.3. Алгоритм Рубенса
- 3.2.2.4. Алгоритм Беждека — Данна
- 3.2.2.5. Алгоритм Педрича
- 3.2.2.6. Алгоритм Даве — Сена
- 3.2.2.7. Другие алгоритмы оптимизационного подхода
- 3.3. Иерархические методы
- 3.3.2. Описание алгоритмов
- 3.3.2.2. Алгоритм Думитреску (FDH algorithm)
- 3.3.2.3. Другие алгоритмы иерархического подхода
- Резюме
- ГЛАВА 4. СРАВНИТЕЛЬНЫЙ АНАЛИЗ НЕЧЕТКИХ МЕТОДОВ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 4.1.2. Виды исходных данных и общая схема проведения сравнительного анализа
- 4.2. Оценка и представление результатов обработки данных нечеткими методами автоматической классификации
- 4.2.2. Представление и интерпретация результатов нечеткой классификации
- 4.3. Экспериментальное сравнение нечетких методов автоматической классификации
- 4.3.2. Результаты вычислительных экспериментов
- Резюме
- ГЛАВА 5. МЕТОДОЛОГИЧЕСКИЕ АСПЕКТЫ НЕЧЕТКОГО ПОДХОДА К РЕШЕНИЮ ЗАДАЧИ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 5.1.2. Выбор алгоритма нечеткого подхода к решению задачи автоматической классификации и обоснование параметров
- 5.2. Прикладные аспекты нечеткой классификации
- 5.2.2. Нечеткие методы автоматической классификации и другие нечеткие методы распознавания образов
- Резюме
- ЗАКЛЮЧЕНИЕ
- Основные обозначения
- Список литературы