| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
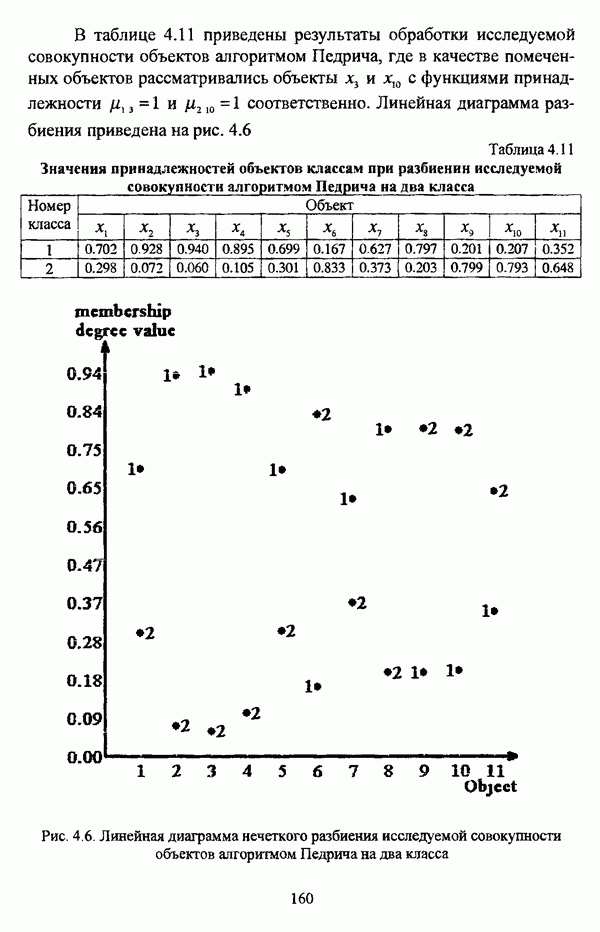
2.1.2. Основные операции над нечеткими множествами
Пусть А и В — два нечетких множества, определенные на универсуме X. Для определения основных операций над нечеткими множествами целесообразно использование традиционной формы записи, преимущественно используемой в литературе по нечетким множествам.
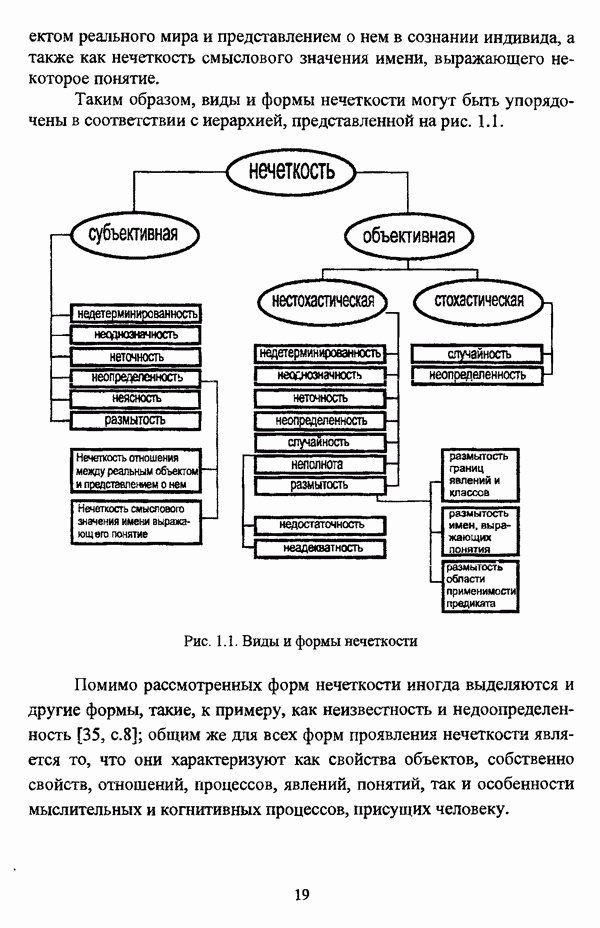
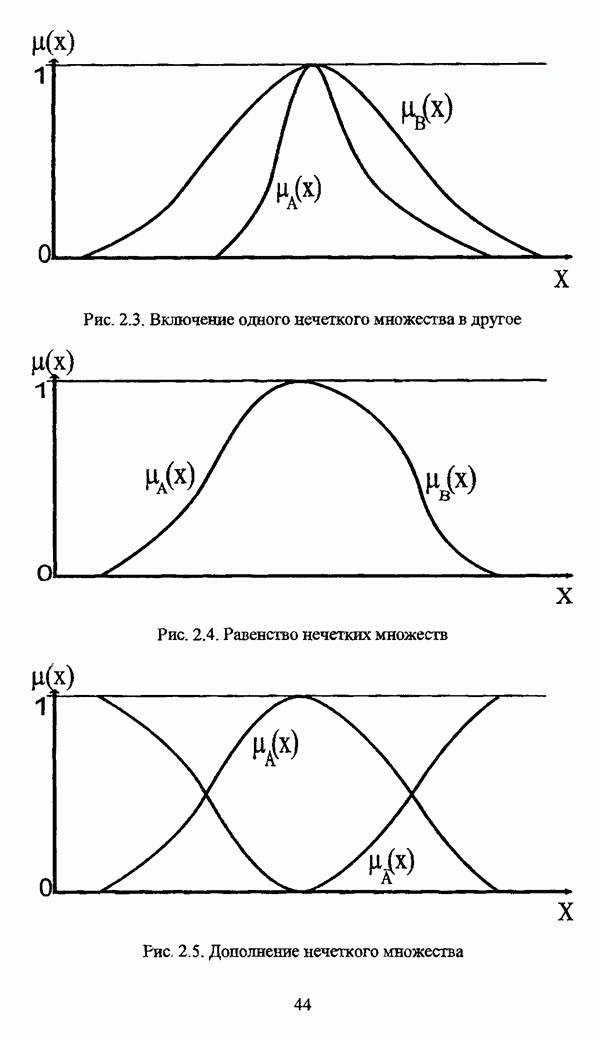
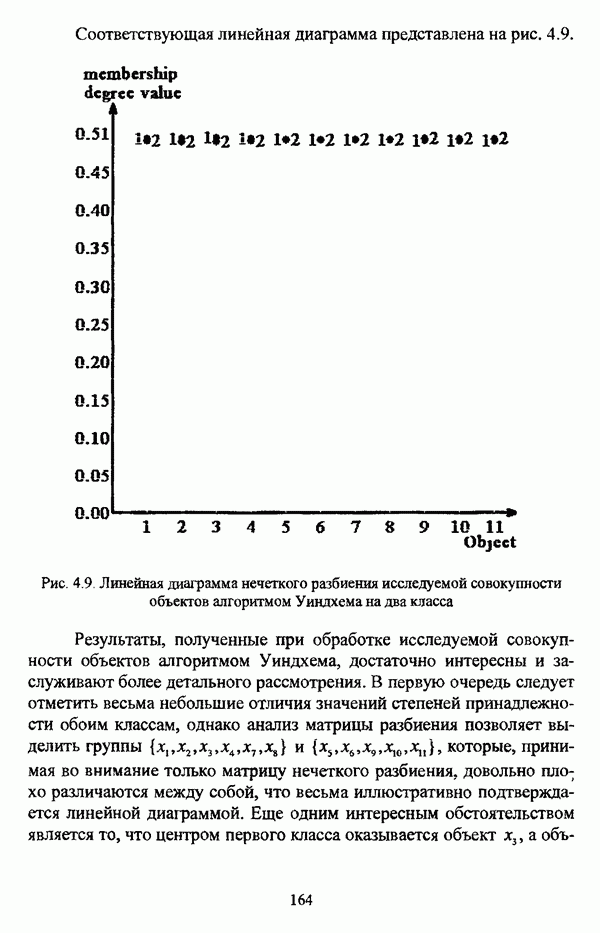
Включение нечеткого множества А в нечеткое множество В, которое представлено на рис. 2.3, определяется условием 
Равенство нечеткого множества А нечеткому множеству В, которое представлено на рис. 2.4, определяется условием 
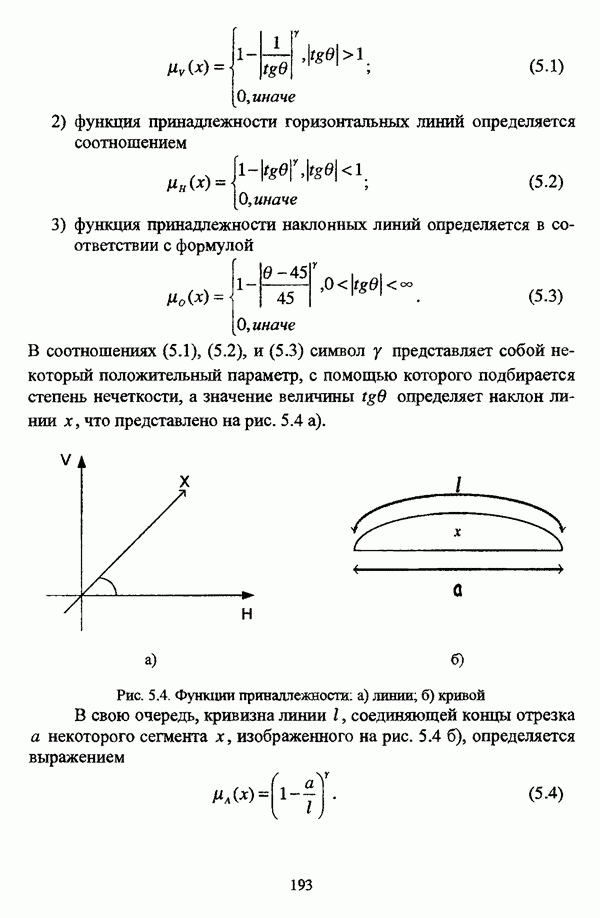
Дополнение нечеткого множества А, представленное на рис. 2.5, определяется условием 
В теории нечетких множеств для обозначения операции взятия минимума используется символ а, а для обозначения операции взятия максимума — символ 

Рис. 2.3. Включение одного нечеткого множества в другое

Рис. 2.4. Равенство нечетких множеств

Рис. 2.5. Дополнение нечеткого множества
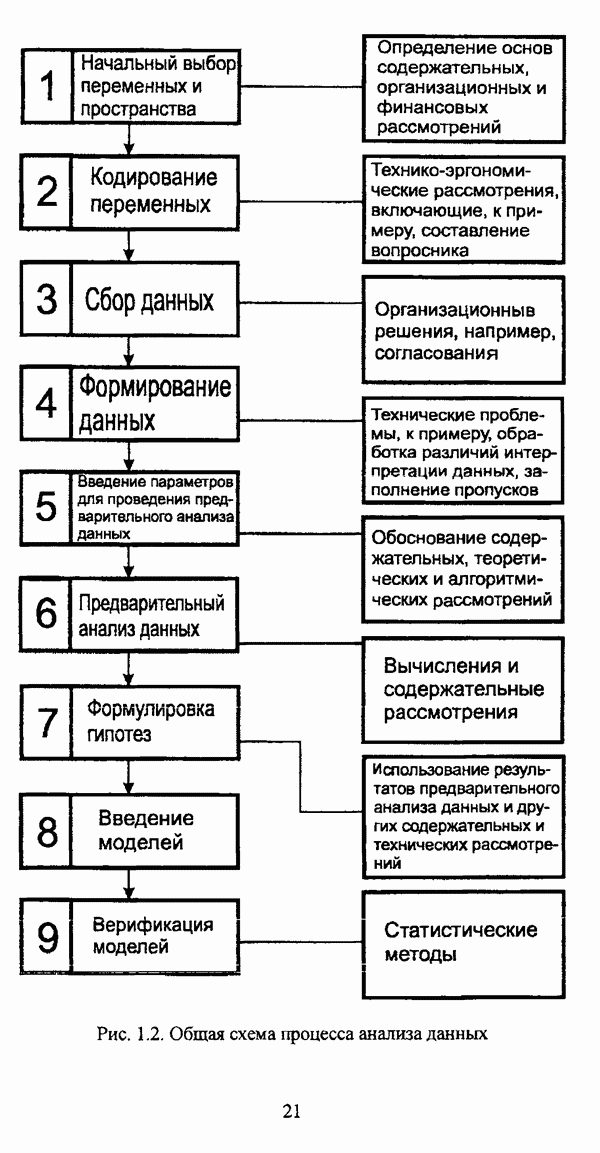
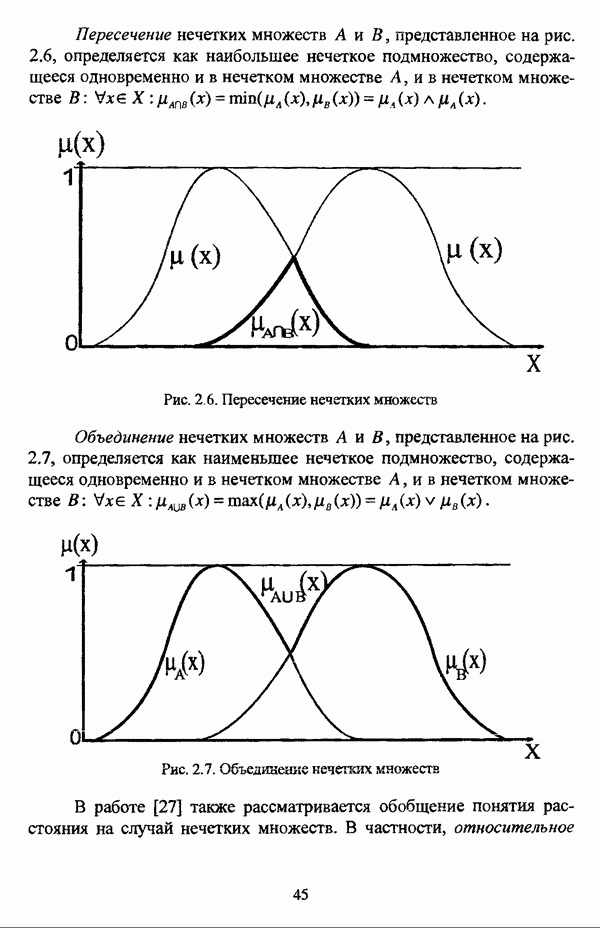
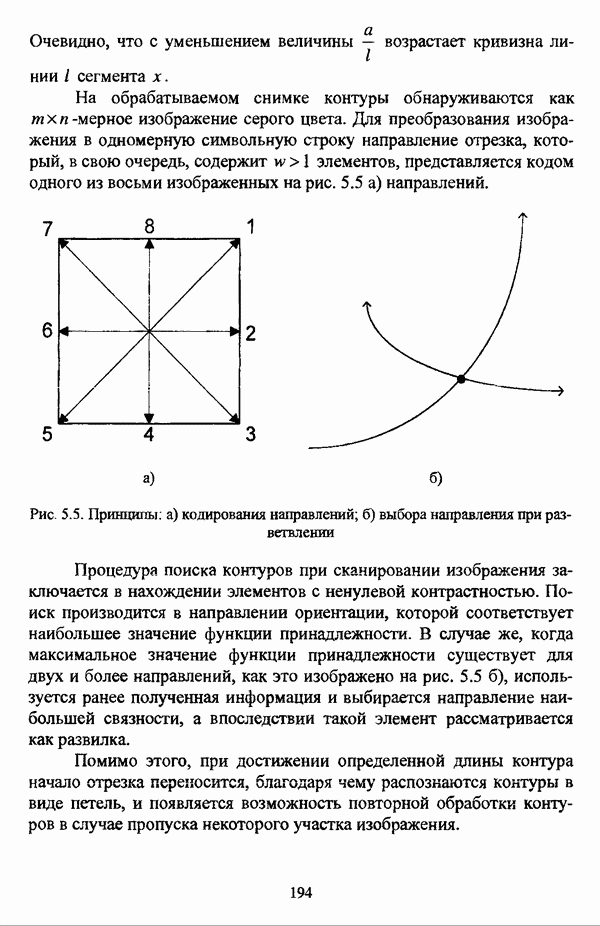
Пересечение нечетких множеств А и В, представленное на рис. 2.6, определяется как наибольшее нечеткое подмножество, содержащееся одновременно и в нечетком множестве А, и в нечетком множестве 

Рис. 2.6. Пересечение нечетких множеств
Объединение нечетких множеств А и В, представленное на рис.
2.7, определяется как наименьшее нечеткое подмножество, содержащееся одновременно и в нечетком множестве А, и в нечетком множестве 

Рис. 2.7. Объединение нечетких множеств
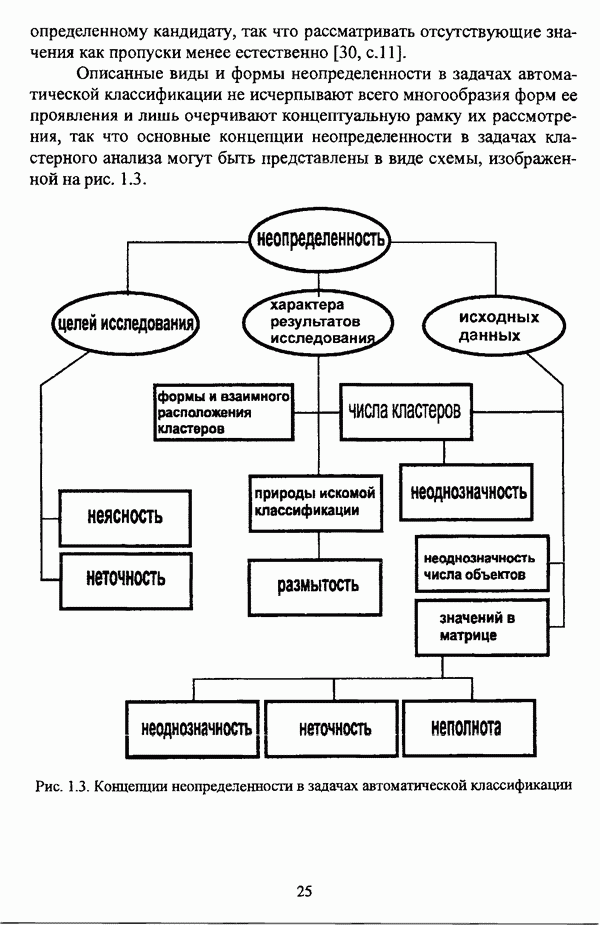
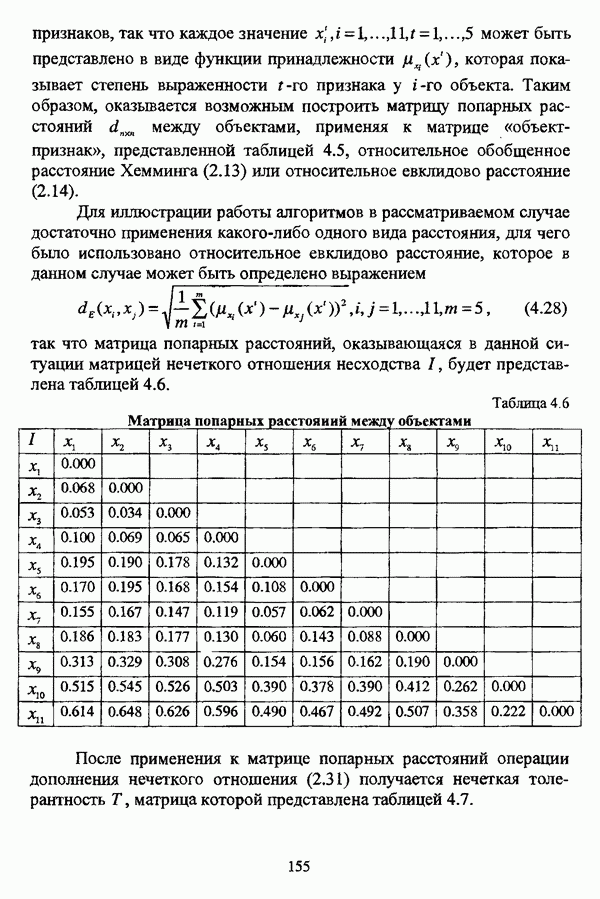
В работе [27] также рассматривается обобщение понятия расстояния на случай нечетких множеств. В частности, относительное
обобщенное расстояние Хемминга между нечеткими множествами А и В определяется по формуле

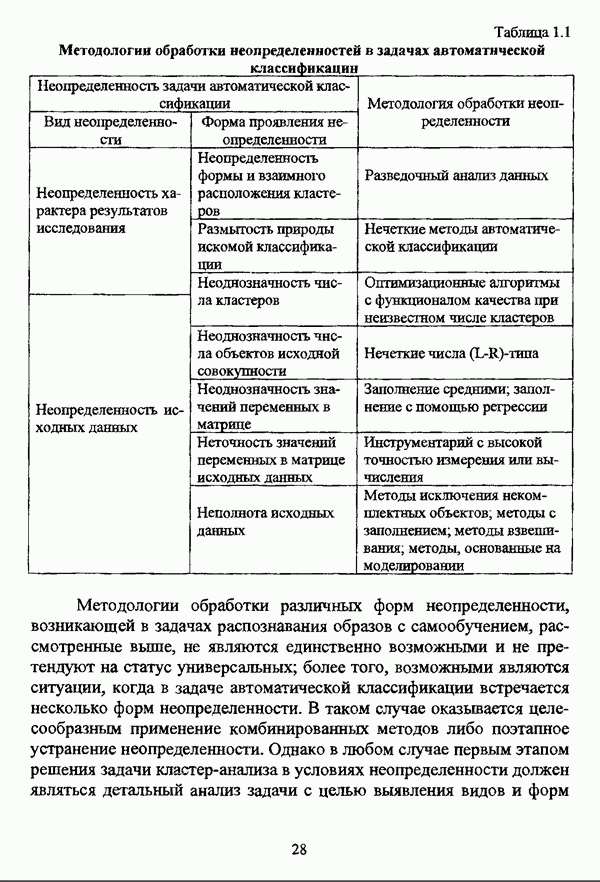
где  так что очевидно, что
так что очевидно, что  Относительное евклидово расстояние между нечеткими множествами А и 5 определяется по формуле
Относительное евклидово расстояние между нечеткими множествами А и 5 определяется по формуле

где  так что
так что 
Более полный обзор операций над нечеткими множествами содержится в [27], [34].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ПРОБЛЕМА НЕОПРЕДЕЛЕННОСТИ В ЗАДАЧАХ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 1.1. Понятие однородности и проблема классификации объектов
- 1.1.2. Общая постановка задачи автоматической классификации и основные направления ее решения
- 1.2. Подход к решению задачи автоматической классификации с позиции теории нечетких множеств
- 1.2.2. Гносеологические аспекты подхода к решению задач классификации с позиции теории нечетких множеств
- Резюме
- ГЛАВА 2. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ НЕЧЕТКИХ МНОЖЕСТВ
- 2.1. Нечеткие множества
- 2.1.2. Основные операции над нечеткими множествами
- 2.2. Нечеткие отношения
- 2.2.2. Основные операции над нечеткими отношениями
- Резюме
- ГЛАВА 3. МЕТОДЫ НЕЧЕТКОГО ПОДХОДА К РЕШЕНИЮ ЗАДАЧ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 3.1.2. Описание алгоритмов
- 3.2. Оптимизационные методы
- 3.2.2. Описание алгоритмов
- 3.2.2.2. Алгоритм Уиндхема
- 3.2.2.3. Алгоритм Рубенса
- 3.2.2.4. Алгоритм Беждека — Данна
- 3.2.2.5. Алгоритм Педрича
- 3.2.2.6. Алгоритм Даве — Сена
- 3.2.2.7. Другие алгоритмы оптимизационного подхода
- 3.3. Иерархические методы
- 3.3.2. Описание алгоритмов
- 3.3.2.2. Алгоритм Думитреску (FDH algorithm)
- 3.3.2.3. Другие алгоритмы иерархического подхода
- Резюме
- ГЛАВА 4. СРАВНИТЕЛЬНЫЙ АНАЛИЗ НЕЧЕТКИХ МЕТОДОВ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 4.1.2. Виды исходных данных и общая схема проведения сравнительного анализа
- 4.2. Оценка и представление результатов обработки данных нечеткими методами автоматической классификации
- 4.2.2. Представление и интерпретация результатов нечеткой классификации
- 4.3. Экспериментальное сравнение нечетких методов автоматической классификации
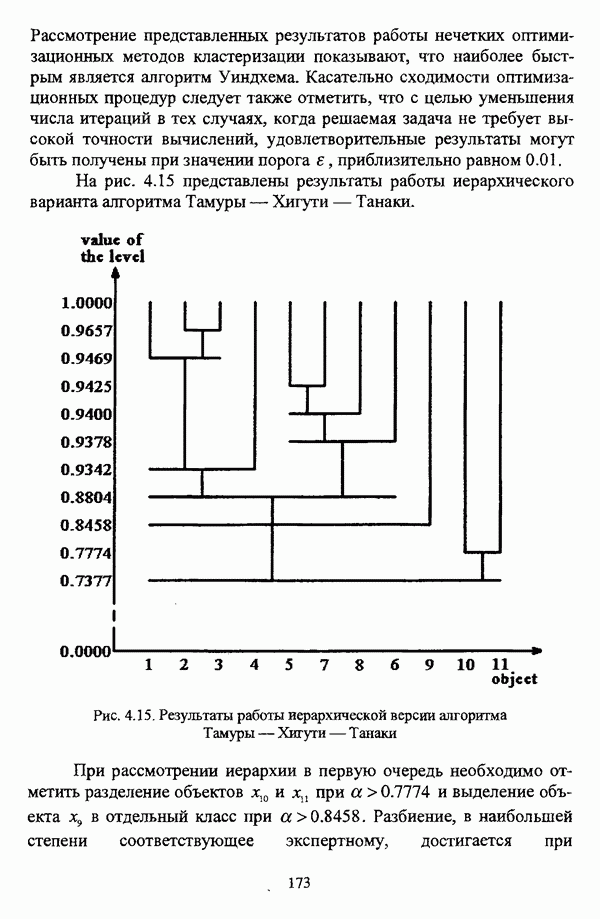
- 4.3.2. Результаты вычислительных экспериментов
- Резюме
- ГЛАВА 5. МЕТОДОЛОГИЧЕСКИЕ АСПЕКТЫ НЕЧЕТКОГО ПОДХОДА К РЕШЕНИЮ ЗАДАЧИ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 5.1.2. Выбор алгоритма нечеткого подхода к решению задачи автоматической классификации и обоснование параметров
- 5.2. Прикладные аспекты нечеткой классификации
- 5.2.2. Нечеткие методы автоматической классификации и другие нечеткие методы распознавания образов
- Резюме
- ЗАКЛЮЧЕНИЕ
- Основные обозначения
- Список литературы