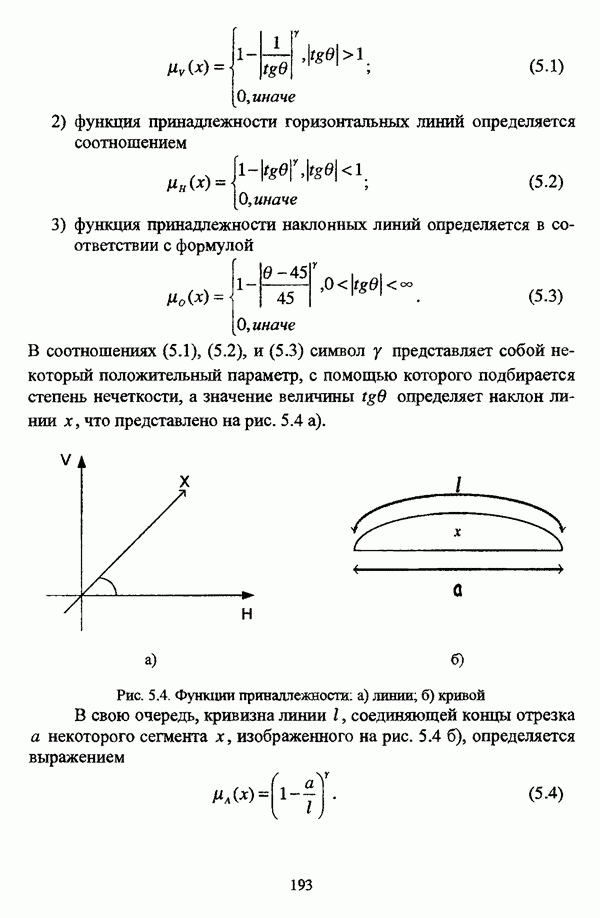
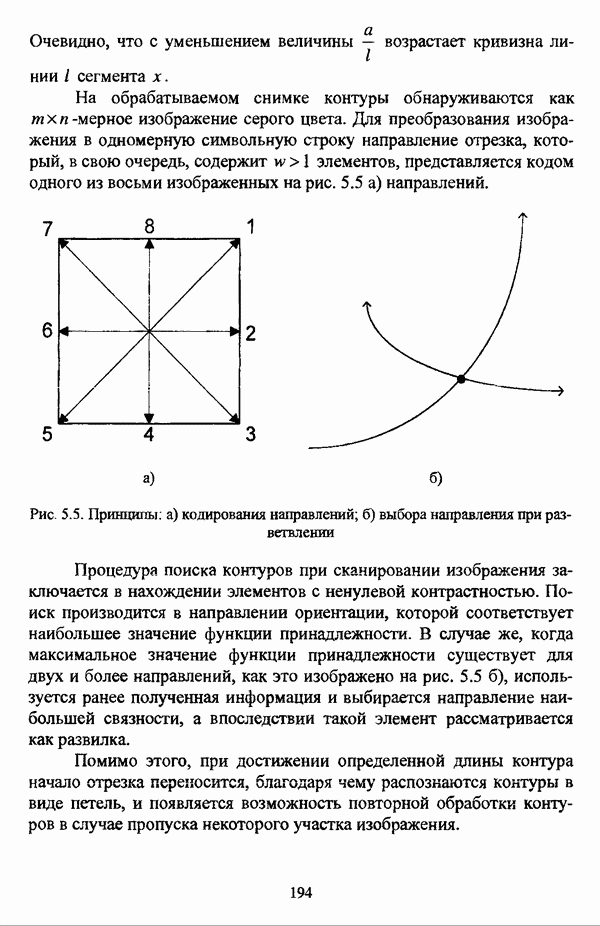
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.2. Нечеткие отношения
2.2.1. Определение нечеткого отношения; свойства и классификация нечетких отношений
Бинарным нечетким отношением R между множествами X и Y будет называться функция  где
где  — функция принадлежности отношения
— функция принадлежности отношения  — базовые множества; [0,1] — отрезок вещественной прямой от 0 до 1. В случае, когда множества X и Y в силу связи между объектами совпадают, нечеткое отношение
— базовые множества; [0,1] — отрезок вещественной прямой от 0 до 1. В случае, когда множества X и Y в силу связи между объектами совпадают, нечеткое отношение  где X — базовое множество, или, иначе говоря, универсум, называется нечетким отношением на множестве
где X — базовое множество, или, иначе говоря, универсум, называется нечетким отношением на множестве  Другими словами, бинарное нечеткое отношение является нечетким множеством на декартовом произведении базовых множеств. В дальнейшем, за некоторыми исключениями, которые будут оговариваться особо, рассматриваются нечеткие отношения на множестве X. Поскольку нечеткое отношение может определяться как нечеткое множество на декартовом произведении базовых множеств, так что нечеткое отношение R на множестве X может задаваться непосредственно в виде функции принадлежности
Другими словами, бинарное нечеткое отношение является нечетким множеством на декартовом произведении базовых множеств. В дальнейшем, за некоторыми исключениями, которые будут оговариваться особо, рассматриваются нечеткие отношения на множестве X. Поскольку нечеткое отношение может определяться как нечеткое множество на декартовом произведении базовых множеств, так что нечеткое отношение R на множестве X может задаваться непосредственно в виде функции принадлежности  для нечетких отношений сохраняются многие результаты, полученные для нечетких множеств. В частности, понятие нечеткого отношения
для нечетких отношений сохраняются многие результаты, полученные для нечетких множеств. В частности, понятие нечеткого отношения
также может обобщаться, и одним из обобщений понятия нечеткого отношения является понятие нечеткого отношения типа  .
.
В зависимости от свойств, которыми они обладают, выделяют различные типы нечетких отношений. Среди всех рассматриваемых в специальной литературе свойств нечетких отношений, полагая, что S — некоторое произвольное бинарное нечеткое отношение на множестве  следует особо отметить следующие свойства:
следует особо отметить следующие свойства:
рефлексивность:

слабая рефлексивность:

сильная рефлексивность:

антирефлексивность:

слабая антирефлексивность:

сильная антирефлексивность:

симметричность:

антисимметричность:

асимметричность:

полнота сильная:

полнота слабая:

(max-min)-транзитивность:

(min-max)-транзитивность:

Очевидно, к примеру, что если нечеткое отношение обладает свойством (2.17), то оно обладает и свойством (2.15), так же, как наличие
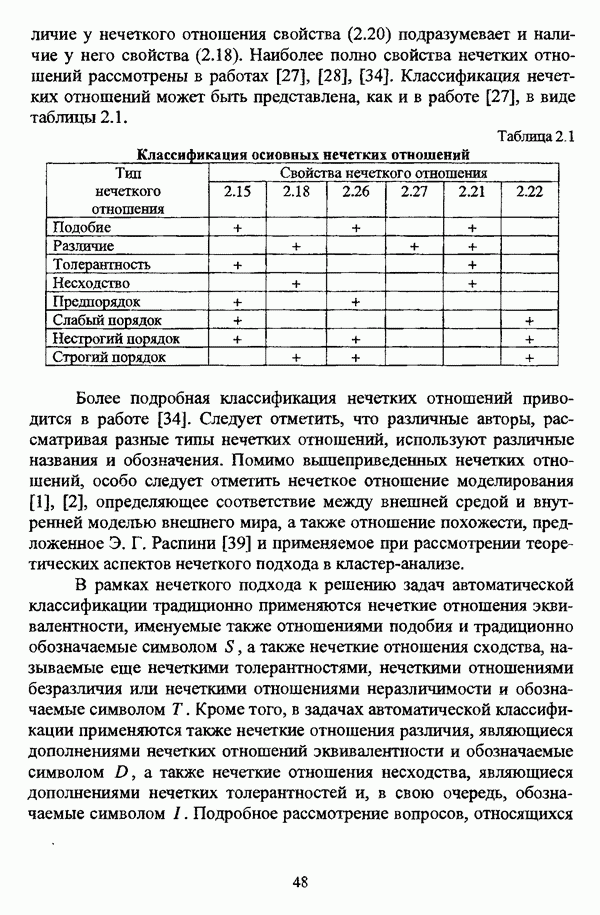
у нечеткого отношения свойства (2.20) подразумевает и наличие у него свойства (2.18). Наиболее полно свойства нечетких отношений рассмотрены в работах [27], [28], [34]. Классификация нечетких отношений может быть представлена, как и в работе [27], в виде таблицы 2.1.
Таблица 2.1. Классификация основных нечетких отношений (см. скан)
Более подробная классификация нечетких отношений приводится в работе [34]. Следует отметить, что различные авторы, рассматривая разные типы нечетких отношений, используют различные названия и обозначения. Помимо вышеприведенных нечетких отношений, особо следует отметить нечеткое отношение моделирования [1], [2], определяющее соответствие между внешней средой и внутренней моделью внешнего мира, а также отношение похожести, предложенное Э. Г. Распини [39] и применяемое при рассмотрении теоретических аспектов нечеткого подхода в кластер-анализе.
В рамках нечеткого подхода к решению задач автоматической классификации традиционно применяются нечеткие отношения эквивалентности, именуемые также отношениями подобия и традиционно обозначаемые символом S, а также нечеткие отношения сходства, называемые еще нечеткими толерантностями, нечеткими отношениями безразличия или нечеткими отношениями неразличимости и обозначаемые символом Т. Кроме того, в задачах автоматической классификации применяются также нечеткие отношения различия, являющиеся дополнениями нечетких отношений эквивалентности и обозначаемые символом Z), а также нечеткие отношения несходства, являющиеся дополнениями нечетких толерантностей и, в свою очередь, обозначаемые символом  Подробное рассмотрение вопросов, относящихся
Подробное рассмотрение вопросов, относящихся
к применению нечетких отношений в задачах классификации, содержится в работе [190].
В работах [174], [175], [16] были предложены нечеткие отношения сильной, слабой и строгой слабой толерантностей, а в работе [177] были рассмотрены их дополнения, именуемые соответственно нечеткими отношениями сильного, слабого и строгого слабого несходства. Строгая слабая толерантность отличается от слабой толерантности выполнением строгого неравенства в условии (2.16):

а строгое слабое несходство отличается от слабого несходства, соответственно, выполнением строгого неравенства в условии (2.19):

Основные свойства, по которым выделяют различные нечеткие толерантности, а также нечеткие отношения несходства, представлены таблицей 2.2.
Таблица 2.2. Нечеткие толерантности и нечеткие отношения несходства, применяемые в кластер-анализе (см. скан)
Нечеткому отношению R на множестве X можно поставить в соответствие взвешенный граф, где каждая пара вершин  из X соединяется дугой с весом
из X соединяется дугой с весом  Очевидно, что
Очевидно, что  симметричных отношений такой граф будет неориентированным. В качестве иллюстрации целесообразно привести пример, представленный в работе [163]. Пусть
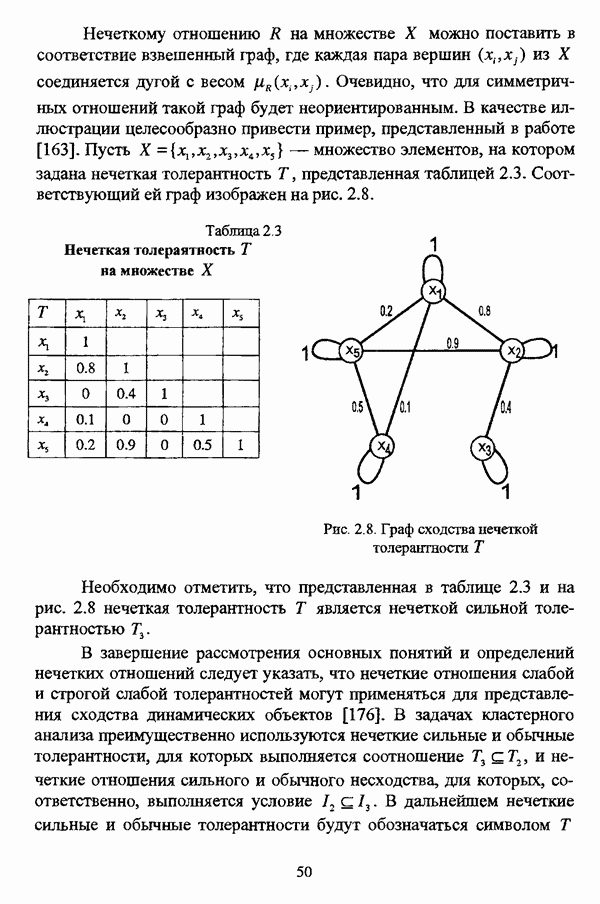
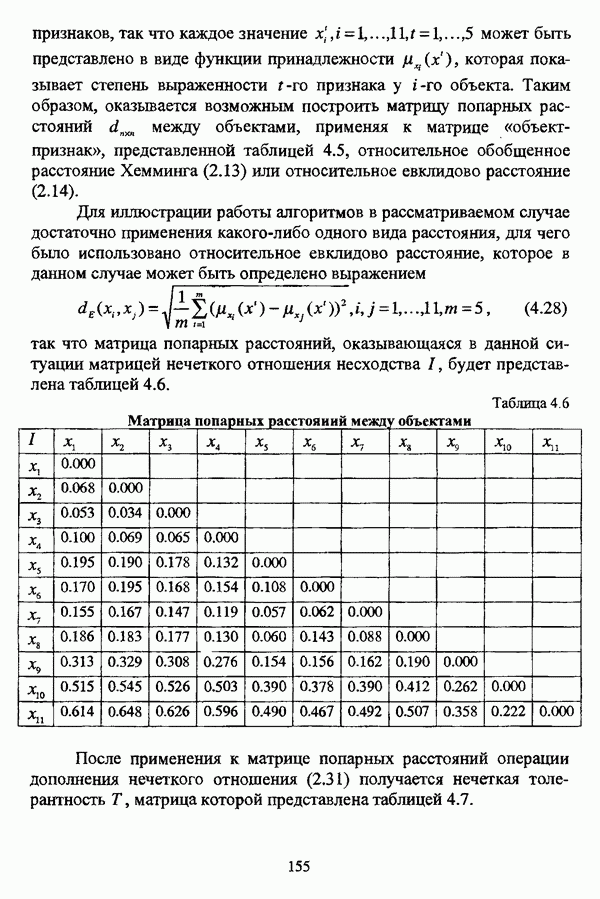
симметричных отношений такой граф будет неориентированным. В качестве иллюстрации целесообразно привести пример, представленный в работе [163]. Пусть  множество элементов, на котором задана нечеткая толерантность Г, представленная таблицей 2.3. Соответствующий ей граф изображен на рис. 2.8.
множество элементов, на котором задана нечеткая толерантность Г, представленная таблицей 2.3. Соответствующий ей граф изображен на рис. 2.8.
Таблица 2.3
Нечеткая толерантность Т на множестве X


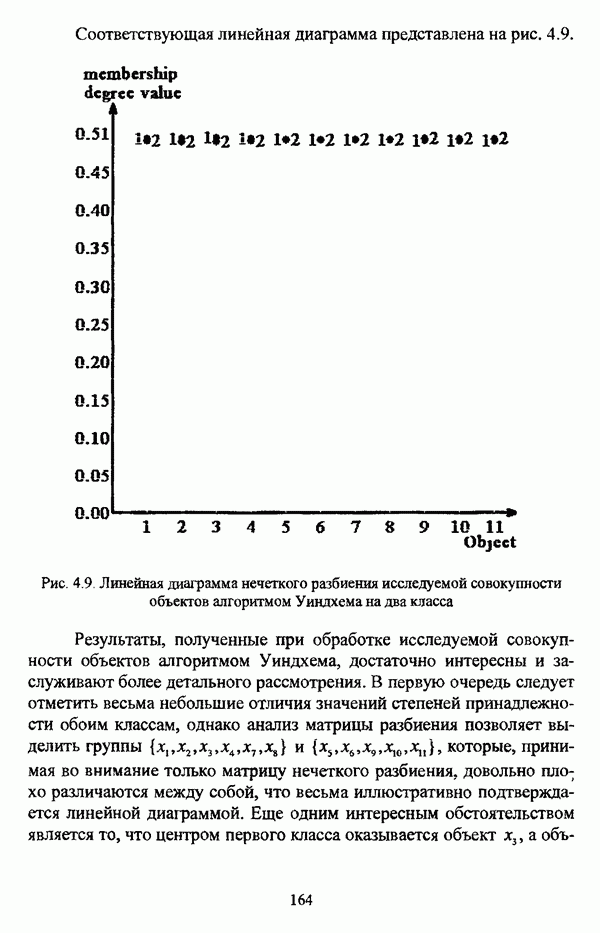
Рис. 2.8. Граф сходства нечеткой толерантности Т
Необходимо отметить, что представленная в таблице 2.3 и на рис. 2.8 нечеткая толерантность Т является нечеткой сильной толерантностью 
В завершение рассмотрения основных понятий и определений нечетких отношений следует указать, что нечеткие отношения слабой и строгой слабой толерантностей могут применяться для представления сходства динамических объектов [176]. В задачах кластерного анализа преимущественно используются нечеткие сильные и обычные толерантности, для которых выполняется соотношение  и нечеткие отношения сильного и обычного несходства, для которых, соответственно, выполняется условие
и нечеткие отношения сильного и обычного несходства, для которых, соответственно, выполняется условие  . В дальнейшем нечеткие сильные и обычные толерантности будут обозначаться символом Т
. В дальнейшем нечеткие сильные и обычные толерантности будут обозначаться символом Т
без индекса, а нечеткие отношения сильного и обычного несходства — соответственно, символом  без индекса.
без индекса.
Свойства и содержательная интерпретация нечетких эквивалентностей и нечетких толерантностей, а также их дополнений подробно рассматриваются в работах [12], [27], [28], [34], [67], [68], [193].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ПРОБЛЕМА НЕОПРЕДЕЛЕННОСТИ В ЗАДАЧАХ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 1.1. Понятие однородности и проблема классификации объектов
- 1.1.2. Общая постановка задачи автоматической классификации и основные направления ее решения
- 1.2. Подход к решению задачи автоматической классификации с позиции теории нечетких множеств
- 1.2.2. Гносеологические аспекты подхода к решению задач классификации с позиции теории нечетких множеств
- Резюме
- ГЛАВА 2. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ НЕЧЕТКИХ МНОЖЕСТВ
- 2.1. Нечеткие множества
- 2.1.2. Основные операции над нечеткими множествами
- 2.2. Нечеткие отношения
- 2.2.2. Основные операции над нечеткими отношениями
- Резюме
- ГЛАВА 3. МЕТОДЫ НЕЧЕТКОГО ПОДХОДА К РЕШЕНИЮ ЗАДАЧ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 3.1.2. Описание алгоритмов
- 3.2. Оптимизационные методы
- 3.2.2. Описание алгоритмов
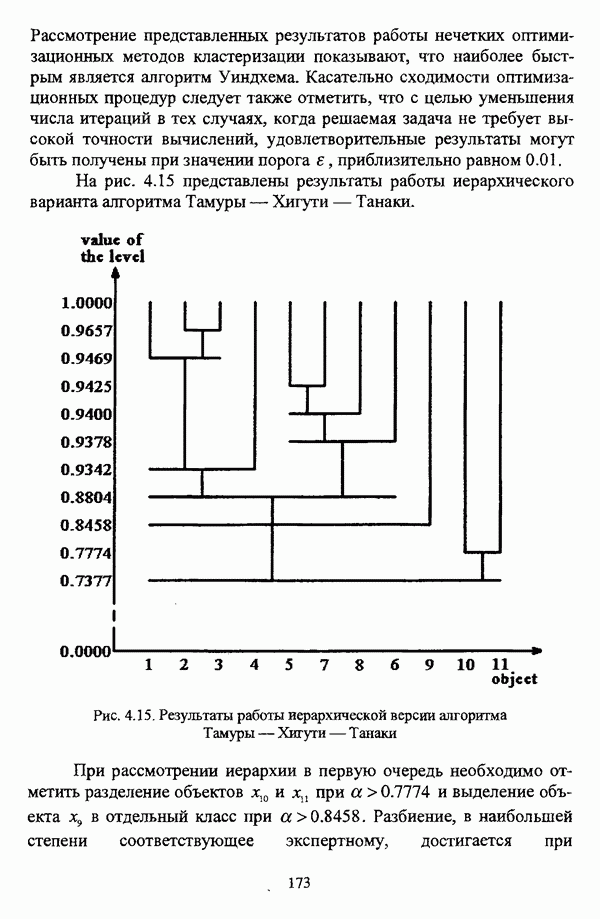
- 3.2.2.2. Алгоритм Уиндхема
- 3.2.2.3. Алгоритм Рубенса
- 3.2.2.4. Алгоритм Беждека — Данна
- 3.2.2.5. Алгоритм Педрича
- 3.2.2.6. Алгоритм Даве — Сена
- 3.2.2.7. Другие алгоритмы оптимизационного подхода
- 3.3. Иерархические методы
- 3.3.2. Описание алгоритмов
- 3.3.2.2. Алгоритм Думитреску (FDH algorithm)
- 3.3.2.3. Другие алгоритмы иерархического подхода
- Резюме
- ГЛАВА 4. СРАВНИТЕЛЬНЫЙ АНАЛИЗ НЕЧЕТКИХ МЕТОДОВ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 4.1.2. Виды исходных данных и общая схема проведения сравнительного анализа
- 4.2. Оценка и представление результатов обработки данных нечеткими методами автоматической классификации
- 4.2.2. Представление и интерпретация результатов нечеткой классификации
- 4.3. Экспериментальное сравнение нечетких методов автоматической классификации
- 4.3.2. Результаты вычислительных экспериментов
- Резюме
- ГЛАВА 5. МЕТОДОЛОГИЧЕСКИЕ АСПЕКТЫ НЕЧЕТКОГО ПОДХОДА К РЕШЕНИЮ ЗАДАЧИ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 5.1.2. Выбор алгоритма нечеткого подхода к решению задачи автоматической классификации и обоснование параметров
- 5.2. Прикладные аспекты нечеткой классификации
- 5.2.2. Нечеткие методы автоматической классификации и другие нечеткие методы распознавания образов
- Резюме
- ЗАКЛЮЧЕНИЕ
- Основные обозначения
- Список литературы