ГЛАВА 3. МЕТОДЫ НЕЧЕТКОГО ПОДХОДА К РЕШЕНИЮ ЗАДАЧ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ

3.1. Эвристические методы

3.1.1. Особенности эвристических методов решения

нечеткой модификации задачи автоматической классификации

Эвристические алгоритмы, как правило, непосредственно опираются на постановку задачи выделения в исследуемой совокупности объектов структура которой характеризуется нечеткостью, групп объектов являющихся нечеткими множествами с соответствующими функциями принадлежности или, для краткости,

В основе такой постановки, как правило, лежат содержательные представления исследователя о нечеткости структуры исследуемой совокупности и условиях объединения объектов в классы. Число нечетких эвристических кластер-процедур немногочисленно, и, пожалуй, единственной особенностью, общей для всех этих алгоритмов, является то обстоятельство, что в качестве входных данных в них используется матрица вида «объект-объект»; исключением является только алгоритм, предложенный И. Гитманом и М. Д. Левиным [90], где исходные данные задаются в виде матрицы «объект-признак» (1.1). Таким образом, основные определения и особенности каждого алгоритма целесообразно рассматривать по ходу его описания в каждом отдельном случае, а перед этим ограничиться краткой характеристикой каждого из представленных ниже алгоритмов.

Наиболее интересной особенностью алгоритма классификации, предложенного И. Гитманом и М. Д. Левиным [90], является то обстоятельство, что группировка объектов производится с использованием как значений функции принадлежности нечеткого множества объектов, подлежащих классификации, так и некоторой заданной метрики, что позволяет выделять классы объектов достаточно сложной формы при отсутствии априорной информации о числе классов. Вместе с тем, необходимо указать, что в данной процедуре понятие нечеткого множества, вообще говоря, используется лишь как вспомогательное,

так что задача автоматической классификации решается, по сути, в детерминистском смысле, что нашло свое отражение в полном отказе от использования понятия нечеткого множества в более поздней версии алгоритма [91]. Подобные соображения приводятся также в работе И. И. Елисеевой и В. О. Рукавишникова [22, с. 53].

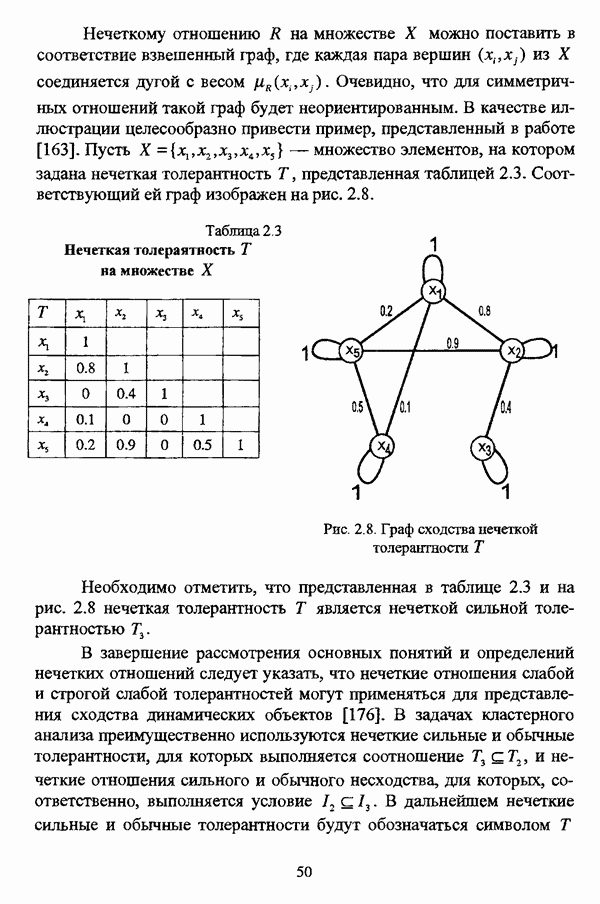
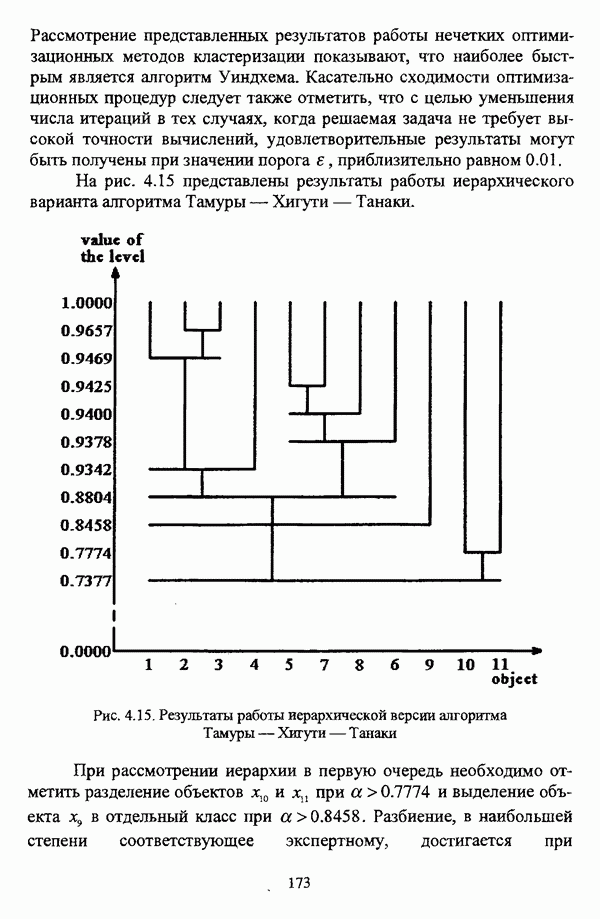
Метод классификации, предложенный С. Тамурой, С. Хигути и К. Танакой в работе [163], использует операцию (max-min)-транзитивного замыкания (2.40) нечеткой толерантности Т, описывающей исходные данные в виде матрицы близости , а процедура, соответствующая данному методу, оказывается весьма простой с вычислительной точки зрения и строит иерархию четких разбиений по -уровням транзитовного замыкания Т. Таким образом, для выбора некоторого единственного разбиения требуется априорная информация о числе классов. Если некоторое разбиение выбрано, то соответствующее значение а будет представлять собой порог сходства элементов, объединяемых в кластеры, что является довольно существенным обстоятельством при содержательной интерпретации полученного результата. Детальное рассмотрение некоторых результатов, представленных в исследовании [163], было произведено также Дж. Данном в работах [82], [86].

А. Кутюрье и Б. Фьолео в работе [71] предложили достаточно простой с вычислительной точки зрения алгоритм, строящий покрытие исследуемой совокупности объектов нечеткими кластерами. Нечеткие множества определенные на универсуме с функциями принадлежности образуют покрытие если для каждого объекта выполняется условие -1 Таким образом, для данного метода оказывается характерной возможность пересечения нечетких кластеров, что позволяет углубить анализ результатов нечеткой классификации. Однако следует отметить, что в предложенном в работе [71] методе понятие нечеткого кластера достаточно точно определено, так что не любое нечеткое множество, определенное на множестве объектов рассматривается как нечеткий кластер.

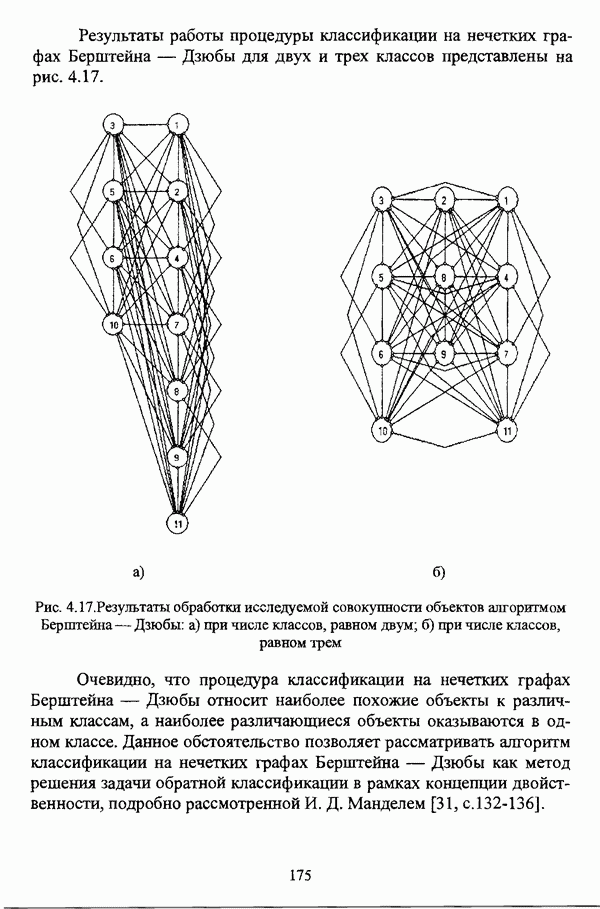
В алгоритме классификации, предложенном Л. С. Берштейном и Т. А. Дзюбой [11], исходные данные представляются в виде нечеткого графа, и алгоритм представляет собой процедуру разбиения множества

объектов являющихся вершинами нечеткого графа, на два класса путем выделения в графе такой двудольной структуры, при которой введенная в качестве критерия оптимизации разбиения степень двудольности является максимальной. В силу этого обстоятельства данную процедуру можно отнести к алгоритмам эвристического направления лишь с некоторой долей условности, поскольку, как отмечает И. Д. Мандель, «проблематика разрезания графа в смысле некоторых оптимизационных требований является специфическим направлением теории графов» [31, с. 75].

Нечеткие кластер-процедуры эвристического направления, помимо решения собственно задач классификации, имеют большое значение на этапе предварительного анализа данных, когда неизвестны число кластеров, их структура и взаимное расположение. К примеру, в работе [22] алгоритм Гитмана-Левина рассматривается как процедура, предваряющая работу нечеткой оптимизационной кластер-процедуры, предложенной Э. Г. Распини [150], с целью определения числа и центров классов, а также построения первоначального разбиения.