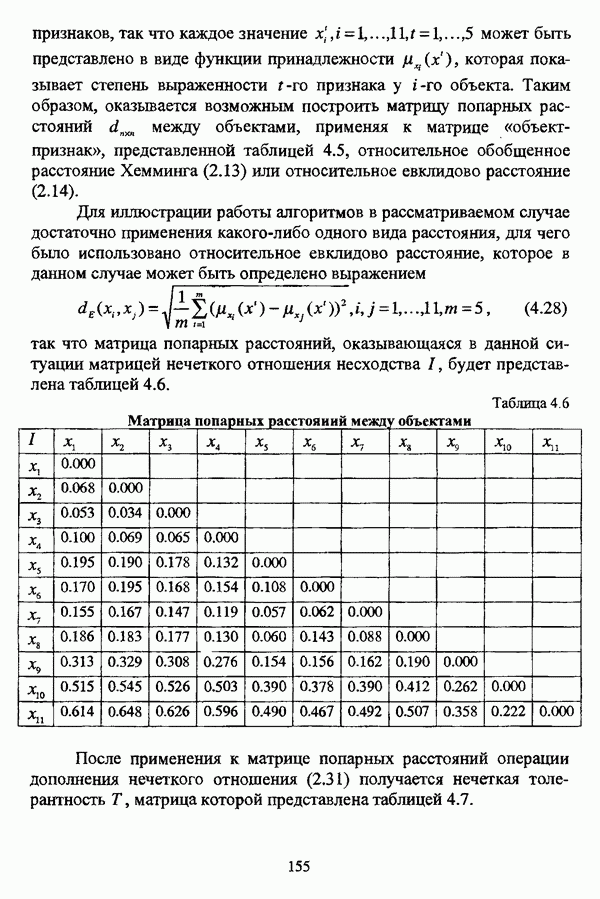
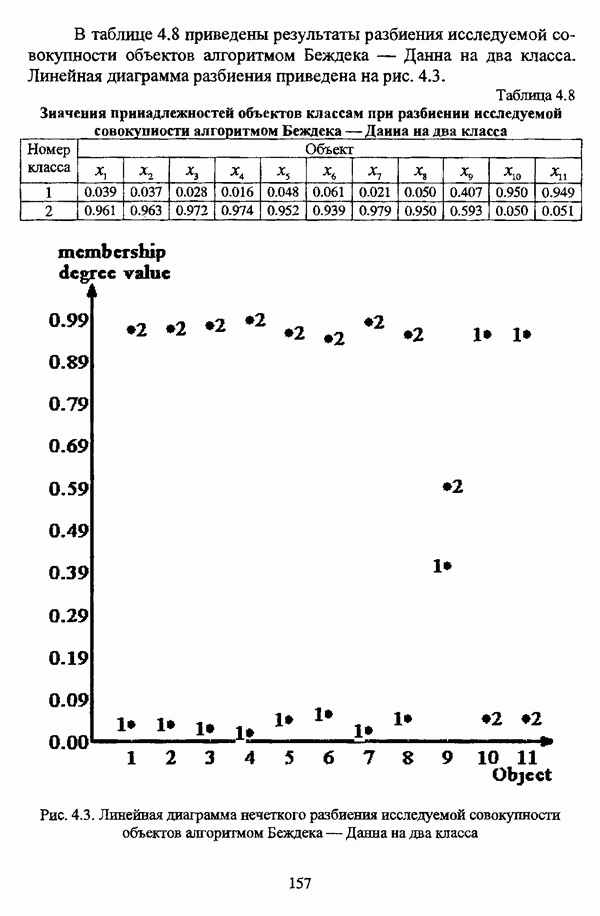
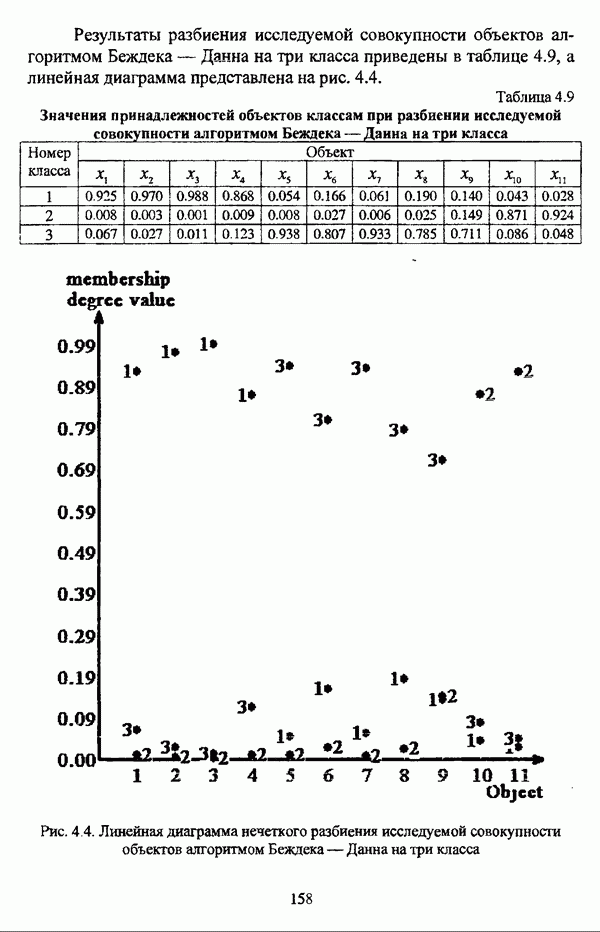
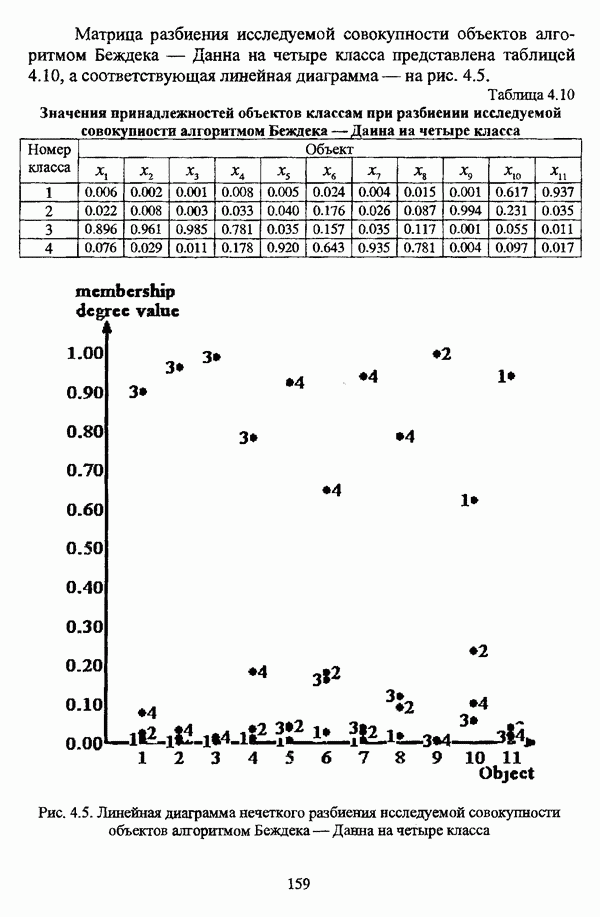
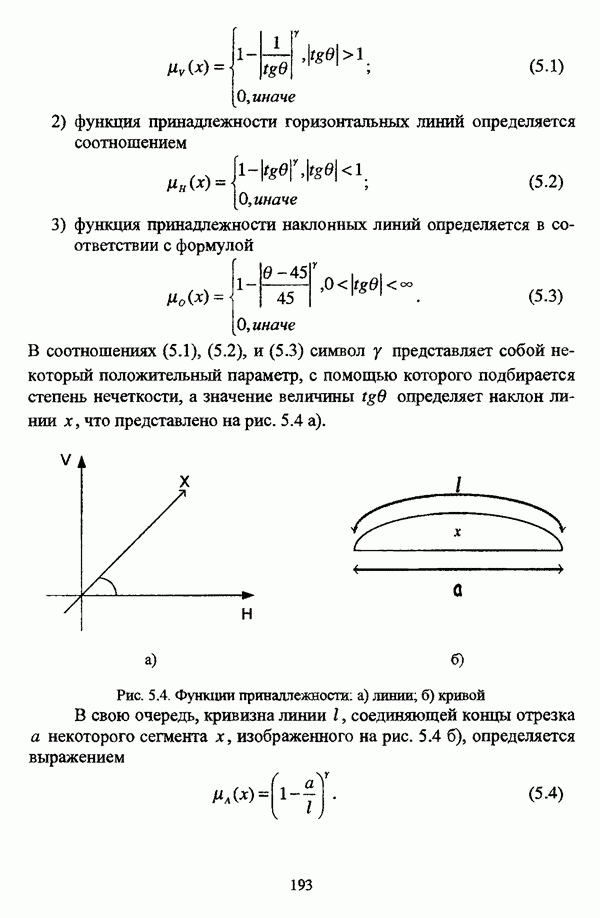
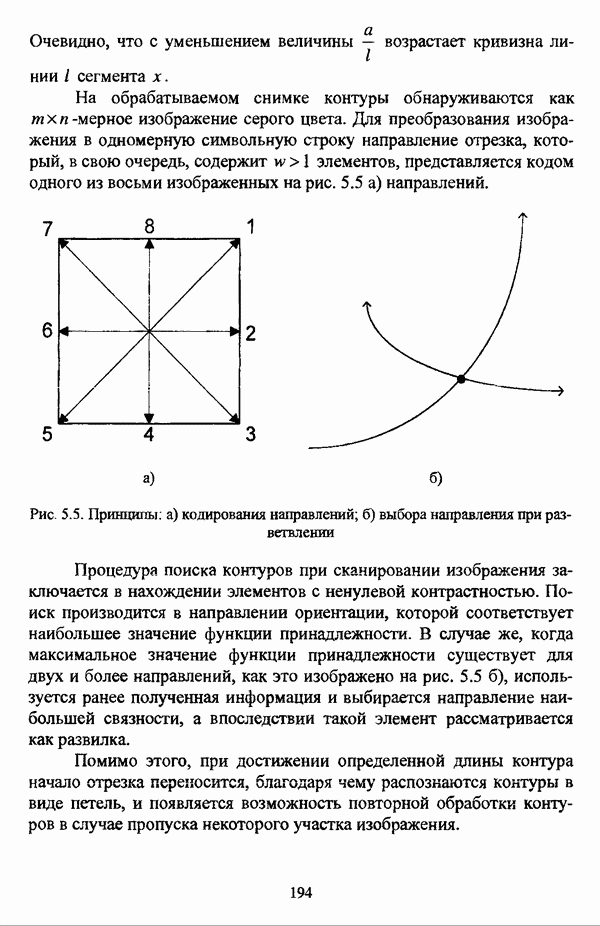
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.1.2. Общая постановка задачи автоматической классификации и основные направления ее решения
Рассмотрим формы представления исходных данных в задачах классификации в условиях отсутствия обучающих выборок. Пусть  — множество
— множество  объектов, каждый из которых характеризуется
объектов, каждый из которых характеризуется  признаками, так что каждый объект рассматривается как точка в
признаками, так что каждый объект рассматривается как точка в  -мерном признаковом пространстве. Тогда исходные данные могут быть представлены матрицей
-мерном признаковом пространстве. Тогда исходные данные могут быть представлены матрицей

именуемой также матрицей «объект-свойство» [37, с. 143], где  представляет собой значение
представляет собой значение  признака на
признака на  объекте. Таким образом,
объекте. Таким образом,  столбец этой матрицы
столбец этой матрицы  полностью характеризует объект
полностью характеризует объект  и будет интерпретироваться как точка в
и будет интерпретироваться как точка в  -мерном признаковом пространстве
-мерном признаковом пространстве  .
.
Если же известны взаимные расстояния между объектами множества  то исходные данные могут быть представлены в форме матрицы взаимных расстояний объектов
то исходные данные могут быть представлены в форме матрицы взаимных расстояний объектов  или, что то же самое, точек
или, что то же самое, точек 

где величина  представляет отдаленность объектов
представляет отдаленность объектов  и друг от друга. Как вариант такой формы представления исходных данных может быть использована матрица
и друг от друга. Как вариант такой формы представления исходных данных может быть использована матрица

где величина  напротив, характеризует близость объектов
напротив, характеризует близость объектов  друг к другу. Очевидно, что чем более сходны объекты
друг к другу. Очевидно, что чем более сходны объекты  тем ближе расположены соответствующие точки в признаковом пространстве; таким образом, из неравенства
тем ближе расположены соответствующие точки в признаковом пространстве; таким образом, из неравенства  должно следовать выполнение неравенства
должно следовать выполнение неравенства  Поскольку переход от матрицы
Поскольку переход от матрицы  к матрице
к матрице  и наоборот, как правило, оказывается элементарным, то в дальнейших рассмотрениях вместо обозначений метрики
и наоборот, как правило, оказывается элементарным, то в дальнейших рассмотрениях вместо обозначений метрики  или меры сходства
или меры сходства  будет использоваться одно общее обозначение функции близости или отдаленности
будет использоваться одно общее обозначение функции близости или отдаленности  а вместо матриц
а вместо матриц  — соответственно матрица
— соответственно матрица

но при необходимости будет осуществляться возвращение к рассмотрению величины расстояния  или величины близости
или величины близости  и матриц
и матриц  соответственно, что будет оговариваться особо. В специальной литературе матрица рпхл любого типа носит название матрицы «объект-объект» [37, с. 143].
соответственно, что будет оговариваться особо. В специальной литературе матрица рпхл любого типа носит название матрицы «объект-объект» [37, с. 143].
В наиболее общем виде проблема классификации объектов в условиях отсутствия обучающих выборок состоит в разбиении на заранее известное либо нет число однородных, в определенном смысле, классов всего исходного множества объектов  представленного в виде матрицы «объект-свойство» или матрицы «объект-объект».
представленного в виде матрицы «объект-свойство» или матрицы «объект-объект».
Следует сразу оговорить, что при такой постановке задачи исходные данные могут иметь и вероятностную природу, однако поскольку объектом рассмотрения является кластерный анализ, то следует придерживаться взгляда о геометрической природе исходных данных.
Необходимо также отметить, что аналогичным образом интерпретируется исходная информация в задаче классификации совокупности признаков, характеризующих множество объектов, представленных в виде матрицы «объект-свойство». Разница заключается в том, что каждый объект множества  представлен соответствующим столбцом матрицы
представлен соответствующим столбцом матрицы  тогда как признак будет задаваться соответствующей строкой матрицы
тогда как признак будет задаваться соответствующей строкой матрицы  . Поскольку постановка задачи и основная методологическая схема исследования и для задачи классификации объектов, и для задачи классификации признаков являются общими [37, с. 144-145], то дальнейшее рассмотрение проблемы классификации будет проводиться применительно к объектам, а в случае задачи классификации признаков этот момент будет оговариваться особо.
. Поскольку постановка задачи и основная методологическая схема исследования и для задачи классификации объектов, и для задачи классификации признаков являются общими [37, с. 144-145], то дальнейшее рассмотрение проблемы классификации будет проводиться применительно к объектам, а в случае задачи классификации признаков этот момент будет оговариваться особо.
При интерпретации объектов как точек в соответствующем пространстве признаков возникает следующая задача: разделить совокупность точек  в пространстве
в пространстве  на однородные классы таким образом, чтобы точки, принадлежащие одному классу, находились бы относительно близко друг от друга, а сами классы различались бы между собой. Полученные в результате разбиения группы именуются кластерами, классами, образами или таксонами, а методы их обнаружения соответственно называются кластерным анализом, автоматической классификацией, распознаванием образов с самообучением или численной таксономией. Следует указать, что термин «кластер» (cluster), имеющий английское происхождение, понимается в математике как группа элементов, характеризуемых некоторым общим свойством, а термин «таксон» (taxon), используемый в биологии и также заимствованный из английского языка, в задаче кластерного анализа понимается как систематизированная группа любой категории.
на однородные классы таким образом, чтобы точки, принадлежащие одному классу, находились бы относительно близко друг от друга, а сами классы различались бы между собой. Полученные в результате разбиения группы именуются кластерами, классами, образами или таксонами, а методы их обнаружения соответственно называются кластерным анализом, автоматической классификацией, распознаванием образов с самообучением или численной таксономией. Следует указать, что термин «кластер» (cluster), имеющий английское происхождение, понимается в математике как группа элементов, характеризуемых некоторым общим свойством, а термин «таксон» (taxon), используемый в биологии и также заимствованный из английского языка, в задаче кластерного анализа понимается как систематизированная группа любой категории.
При такой постановке задачи оказывается необходимым формальное определение понятий однородности и близости объектов.
Матрица  однозначно задает геометрическую структуру множества объектов X однако координаты соответствующих точек оказываются неизвестными. Если же исходные данные заданы матрицей
однозначно задает геометрическую структуру множества объектов X однако координаты соответствующих точек оказываются неизвестными. Если же исходные данные заданы матрицей  то точки
то точки  представляют собой, как указывалось выше, векторы-столбцы геометрических координат наблюдений в
представляют собой, как указывалось выше, векторы-столбцы геометрических координат наблюдений в  -мерном признаковом пространстве
-мерном признаковом пространстве  Задавая
Задавая
способ вычисления величины  характеризующей отдаленность или близость объектов
характеризующей отдаленность или близость объектов  исходного множества
исходного множества  однородность можно определить следующим образом: близкие в смысле функции
однородность можно определить следующим образом: близкие в смысле функции  объекты считаются однородными и попадают в один класс. Близость объектов исходного множества, в свою очередь, определяется сопоставлением значения функции
объекты считаются однородными и попадают в один класс. Близость объектов исходного множества, в свою очередь, определяется сопоставлением значения функции  для каждой пары объектов с некоторым пороговым значением. Способ же вычисления величины
для каждой пары объектов с некоторым пороговым значением. Способ же вычисления величины  можно задать только в случае, когда известны все координаты точек
можно задать только в случае, когда известны все координаты точек  Если же способ вычисления
Если же способ вычисления  задан, то возможен переход от матрицы
задан, то возможен переход от матрицы  к матрице
к матрице  Обратный переход от матрицы рпхл к матрице Хтхя осуществляется с помощью аппарата многомерного метрического шкалирования. Проблема выбора метрики или меры близости детально рассматривается С. А. Айвазяном [37, с. 147-153] и И. Д. Манделем [31, с. 26-35].
Обратный переход от матрицы рпхл к матрице Хтхя осуществляется с помощью аппарата многомерного метрического шкалирования. Проблема выбора метрики или меры близости детально рассматривается С. А. Айвазяном [37, с. 147-153] и И. Д. Манделем [31, с. 26-35].
Если алгоритм разбиения множества объектов задан, то проблема выбора функции  , выступает на первый план, поскольку от этого полностью зависит разбиение множества объектов на классы. Выбор меры близости или расстояния определяется, во-первых, конечной целью проводимого исследования, природой исходных данных, а также некоторыми предположениями, к примеру о форме кластеров и их взаимном расположении. Таким образом, способ вычисления величины
, выступает на первый план, поскольку от этого полностью зависит разбиение множества объектов на классы. Выбор меры близости или расстояния определяется, во-первых, конечной целью проводимого исследования, природой исходных данных, а также некоторыми предположениями, к примеру о форме кластеров и их взаимном расположении. Таким образом, способ вычисления величины  должен быть адекватен геометрической структуре исходного множества объектов; в этой связи С. А. Айвазян совершенно справедливо подчеркивал, что «выбор метрики (или меры близости) является узловым моментом исследования» [37, с. 147].
должен быть адекватен геометрической структуре исходного множества объектов; в этой связи С. А. Айвазян совершенно справедливо подчеркивал, что «выбор метрики (или меры близости) является узловым моментом исследования» [37, с. 147].
Для анализа структуры множества объектов, а также при разработке различных алгоритмов автоматической классификации иногда оказывается необходимым рассматривать близость не только отдельных объектов, но и целых классов, для чего также используются различные расстояния и меры близости, что более подробно рассматривается С. А. Айвазяном в работе [37, с. 153-156].
Если в процессе исследования имеются некоторые предположения о свойствах кластеров или принципах объединения объектов в классы, то оказывается вполне естественным формально определить понятие кластера и построить процедуру, выделяющую из исходного
множества объектов группы, удовлетворяющие данному определению. Подобный подход является основой эвристического направления решения задачи кластерного анализа, а алгоритмы разбиения исходного множества объектов на кластеры с заранее заданными свойствами, соответствующие группе методов этого направления, носят общее название эвристических алгоритмов.
Если же целью исследования является не разбиение исходного множества объектов на классы, а выявление стратификационной структуры исходного множества, то применяются методы, объединенные в иерархическое направление кластер-анализа. Группа иерархических методов объединяет агломеративные и дивизимные алгоритмы кнастер-анализа. Для алгоритмов, соответствующих методам агломеративного подхода иерархического направления, предполагается вначале, что каждый объект представляет собой отдельный класс, после чего элементы и их группы объединяются, пока в результате последовательного объединения не получится исходное множество. Алгоритмы же дивизимной группы методов, напротив, исходят из предположения об исходном множестве как одном классе, который постепенно делится на все более мелкие, вплоть до отдельных элементов, группы объектов. Результаты работы иерархических алгоритмов обычно представляются в виде дендрограммы или графа иерархии.
Очевидно, что одно и то же множество объектов можно разбить на кластеры различными способами или при использовании одного метода можно получить целую группу различных разбиений. В таком случае имеет смысл определить качество разбиений с целью выбора наилучшего разбиения, то есть сформулировать количественный критерий, в соответствии с которым можно было бы предпочесть одно разбиение другому. Для формулировки представлений о качестве классификации в постановку задачи вводится функционал качества разбиения, задающий способ сопоставления с каждым разбиением Р числа  которое оценивает в некоторой шкале степень оптимальности разбиения Р. То разбиение
которое оценивает в некоторой шкале степень оптимальности разбиения Р. То разбиение  на котором выбранный функционал достигает экстремального значения, считается наиболее предпочтительным. Данное направление в кластерном анализе называется оптимизационным и вводит задачу автоматической классификации в сугубо математическое русло, так что в математической постановке задача автоматической классификации сводится к поиску оптимального разбиения Р и формулируется в виде
на котором выбранный функционал достигает экстремального значения, считается наиболее предпочтительным. Данное направление в кластерном анализе называется оптимизационным и вводит задачу автоматической классификации в сугубо математическое русло, так что в математической постановке задача автоматической классификации сводится к поиску оптимального разбиения Р и формулируется в виде

где П — множество всех возможных разбиений исходного множества объектов  Математические методы и реализующие их кластер-процедуры, доставляющие экстремум выбранному функционалу, соответственно называют оптимизационными.
Математические методы и реализующие их кластер-процедуры, доставляющие экстремум выбранному функционалу, соответственно называют оптимизационными.
В продолжение рассмотрения оптимизационных методов решения задачи автоматической классификации следует указать на то обстоятельство, что, как отмечал С. А. Айвазян, «в статистической практике выбор функционала качества разбиения  обычно осуществляется весьма произвольно, опирается скорее на эмпирические и профессионально-интуитивные соображения, чем на какую-либо точную формализованную схему... Однако ряд распространенных в статистической практике функционалов качества удается постфактум обосновать и осмыслить в рамках строгих математических моделей» [37, с. 181].
обычно осуществляется весьма произвольно, опирается скорее на эмпирические и профессионально-интуитивные соображения, чем на какую-либо точную формализованную схему... Однако ряд распространенных в статистической практике функционалов качества удается постфактум обосновать и осмыслить в рамках строгих математических моделей» [37, с. 181].
Если классификация, которую требуется найти, описывается матрицей определенной структуры, к примеру, матрицей отношения эквивалентности, то задача заключается в оценке параметров искомой структуры так, чтобы искомая структура минимально отличалась бы от исходной структуры. Иными словами, отношение, отвечающее исходным данным, необходимо аппроксимировать отношением, которое отвечает представлению о наилучшей классификации, так что это направление решения задач кластер-анализа именуется аппроксимационным; в этом случае проблема сводится к следующей оптимизационной задаче:

где  В этом равенстве J обозначает отношение, которое требуется найти, X — матрица исходных данных, В — оператор перехода от X к
В этом равенстве J обозначает отношение, которое требуется найти, X — матрица исходных данных, В — оператор перехода от X к  обозначает некоторую норму. На практике применяют методы аппроксимации как матрицы «объект-свойство», так и матрицы «объект-объект».
обозначает некоторую норму. На практике применяют методы аппроксимации как матрицы «объект-свойство», так и матрицы «объект-объект».
Рассмотренные выше группы методов решения задач кластер-анализа не являются строгими и не исчерпывают всего богатства методов классификации объектов в условиях отсутствия обучающих выборок; многие алгоритмы находятся на стыке вышеизложенных направлений. Проблема же классификации собственно алгоритмов кластер-анализа была обозначена около тридцати лет назад и остается актуальной по настоящее время 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ПРОБЛЕМА НЕОПРЕДЕЛЕННОСТИ В ЗАДАЧАХ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 1.1. Понятие однородности и проблема классификации объектов
- 1.1.2. Общая постановка задачи автоматической классификации и основные направления ее решения
- 1.2. Подход к решению задачи автоматической классификации с позиции теории нечетких множеств
- 1.2.2. Гносеологические аспекты подхода к решению задач классификации с позиции теории нечетких множеств
- Резюме
- ГЛАВА 2. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ НЕЧЕТКИХ МНОЖЕСТВ
- 2.1. Нечеткие множества
- 2.1.2. Основные операции над нечеткими множествами
- 2.2. Нечеткие отношения
- 2.2.2. Основные операции над нечеткими отношениями
- Резюме
- ГЛАВА 3. МЕТОДЫ НЕЧЕТКОГО ПОДХОДА К РЕШЕНИЮ ЗАДАЧ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 3.1.2. Описание алгоритмов
- 3.2. Оптимизационные методы
- 3.2.2. Описание алгоритмов
- 3.2.2.2. Алгоритм Уиндхема
- 3.2.2.3. Алгоритм Рубенса
- 3.2.2.4. Алгоритм Беждека — Данна
- 3.2.2.5. Алгоритм Педрича
- 3.2.2.6. Алгоритм Даве — Сена
- 3.2.2.7. Другие алгоритмы оптимизационного подхода
- 3.3. Иерархические методы
- 3.3.2. Описание алгоритмов
- 3.3.2.2. Алгоритм Думитреску (FDH algorithm)
- 3.3.2.3. Другие алгоритмы иерархического подхода
- Резюме
- ГЛАВА 4. СРАВНИТЕЛЬНЫЙ АНАЛИЗ НЕЧЕТКИХ МЕТОДОВ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 4.1.2. Виды исходных данных и общая схема проведения сравнительного анализа
- 4.2. Оценка и представление результатов обработки данных нечеткими методами автоматической классификации
- 4.2.2. Представление и интерпретация результатов нечеткой классификации
- 4.3. Экспериментальное сравнение нечетких методов автоматической классификации
- 4.3.2. Результаты вычислительных экспериментов
- Резюме
- ГЛАВА 5. МЕТОДОЛОГИЧЕСКИЕ АСПЕКТЫ НЕЧЕТКОГО ПОДХОДА К РЕШЕНИЮ ЗАДАЧИ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 5.1.2. Выбор алгоритма нечеткого подхода к решению задачи автоматической классификации и обоснование параметров
- 5.2. Прикладные аспекты нечеткой классификации
- 5.2.2. Нечеткие методы автоматической классификации и другие нечеткие методы распознавания образов
- Резюме
- ЗАКЛЮЧЕНИЕ
- Основные обозначения
- Список литературы