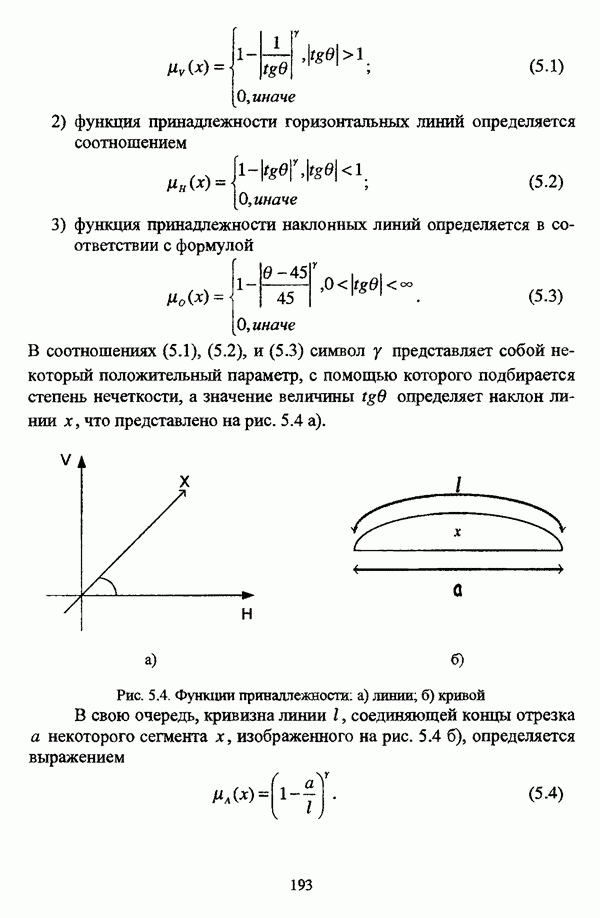
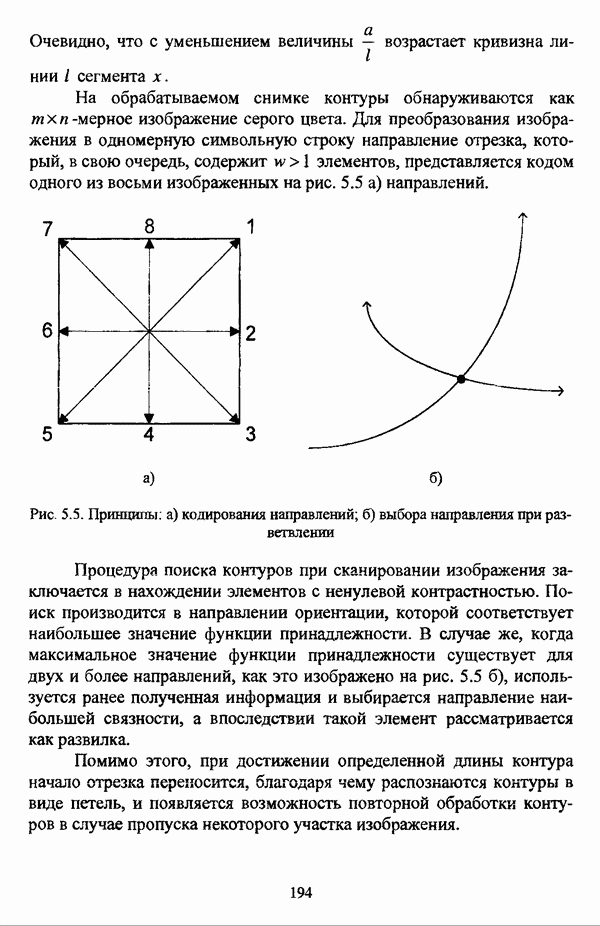
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.1.2. Виды исходных данных и общая схема проведения сравнительного анализа
В зависимости от характера проводимого исследования следует различать несколько видов исходных данных для сравнения работы нечетких кластер-процедур. Проблема экспериментального сравнения алгоритмов кластерного анализа достаточно подробно рассматривалась И. Д. Манделем [31, с. 107-117], который выделял несколько подходов к ее решению.
Первый подход заключается в использовании реальных данных с неизвестной структурой и сравнении результатов работы различных алгоритмов между собой, а если в распоряжении исследователя имеется экспертное разбиение, то эти результаты сравниваются и с ним. Касательно данного подхода И. Д. Мандель отмечал, что «этот способ малоубедителен для общих выводов, но очень полезен в конкретном исследовании, где близость результатов почти всегда говорит о структурированности в данных» [31, с. 107].
Второй подход состоит в использовании для тестирования алгоритмов реальных данных с известной структурой, на которых уже были опробованы различные алгоритмы классификации и которые могут послужить хорошим тестом для новых кластер-процедур. Примером подобных данных может послужить матрица четырехмерных данных по 150 ирисам Е. Андерсона [45]. Вместе с тем, число подобных наборов данных незначительно, кроме того, как подчеркивал И. Д. Мандель, «данные такого типа, безусловно, весьма привлекательны, но и они не могут убедительно ответить на вопрос о качестве алгоритмов в общем случае, так как успешное разбиение на конкретной выборке не гарантирует успеха на другой» [31, с. 108].
Третий подход заключается в подборе искусственных данных с хорошо известной и определенной структурой, в которых кластеры могут быть выделены визуально, так что подобные массивы данных, как правило, являются двумерными. Этот подход предоставляет широкие возможности для сопоставления и осмысления человеческого и машинного способов классификации. Однако субъективизм человека при формировании данных является довольно сильным ограничением для применения такого подхода, так как «трудно установить устойчивые характеристики алгоритмов, связанные со случайным разбросом. К тому же, двумерная ситуация не является универсальной» [31, с. 108].
Четвертый подход предполагает использование для экспериментального сравнения алгоритмов автоматической классификации генерируемых ЭВМ искусственных данных с заданной структурой, которые в процессе исследования будут искажаться контролируемым образом. Подобный способ является весьма предпочтительным и для проверки хорошо известных алгоритмов, поскольку позволяет моделировать данные самой разнообразной структуры и проводить управляемые искажения любого типа [31, с. 108].
В рамках конкретного прикладного исследования производится классификация реальных данных, так что целью сравнения работы различных алгоритмов является, как правило, определение действительной структуры исследуемой совокупности для последующего детального рассмотрения. Таким образом, сравнительный анализ работы различных алгоритмов должен проводиться в зависимости от цели предпринимаемого исследования. Если целью сравнения является определение числа нечетких кластеров, то следует сравнить результаты работы одной или нескольких оптимизационных нечетких кластер-процедур при различном числе кластеров. В свою очередь, при обращении к оптимизационному подходу для отыскания истинной структуры данных следует использовать несколько различных функционалов. Поскольку в случаях использования разных функционалов классификации будут различаться, тогда если при использовании нескольких функционалов окажется, что, как указывал И. Д. Мандель, «...классификации похожи, то скорее всего выявлена реальная структура» [31, с. 38]. Для выявления взаимосвязи между свойствами отдельных кластеров и разбиением в целом целесообразно сравнить между собой результаты работы оптимизационных и эвристических кластер-процедур, примером чего может послужить сравнение результатов работы алгоритма Беждека — Данна с результатами работы алгоритма Кутюрье — Фьолео при различных параметрах [71]. Если же необходимо определить характер взаимосвязи между стратификационной и кластерной структурами исследуемой совокупности объектов, то целесообразно сравнить результаты работы оптимизационных и иерархических кластер-процедур. К примеру, если исходные данные представлены в виде матрицы «объект-свойство», то для выявления подобной взаимосвязи следует сравнить результаты работы алгоритма Беждека — Данна и алгоритма Думитреску, а если исходные данные представлены в виде матрицы «объект- объект», то можно сравнить результаты работы, к примеру, алгоритма Уиндхема и алгоритма Ватады — Танаки — Асаи. Если же в процессе исследования возникает задача выявления взаимосвязи между стратификационной структурой исследуемой совокупности объектов и свойствами нечетких классов, то следует сравнить результаты работы нечетких иерархических и нечетких эвристических алгоритмов автоматической классификации. При необходимости детального исследования свойств нечетких кластеров целесообразно применить к исходным данным несколько эвристических нечетких кластер-процедур и сравнить между собой
результаты их работы. Наконец, если целью исследования является получение наиболее полного представления о стратификационной структуре исследуемой совокупности, следует сравнить между собой результаты работы нескольких иерархических кластер-процедур.
Безусловно, предложенная схема, в силу предельной общности, не является окончательной и никоим образом не претендует на универсальность. Вместе с тем, следование предложенной установке позволит, более эффективно проводить сравнение алгоритмов как в процессе теоретического исследования, так и в процессе конкретного прикладного исследования.
Великолепным примером применения сравнения различных оптимизационных процедур для выявления характера и оценки кластерной структуры исследуемой совокупности объектов, может послужить методология, предложенная В. Педричем [144], сущность которой состоит в следующем.
При обработке исследуемой совокупности объектов  несколькими оптимизационными процедурами, в каждом случае получается матрица разбиения
несколькими оптимизационными процедурами, в каждом случае получается матрица разбиения  где К — число методов, которыми обрабатывалось множество объектов. Таким образом, оказывается возможным построить последовательность матриц
где К — число методов, которыми обрабатывалось множество объектов. Таким образом, оказывается возможным построить последовательность матриц  i-й столбец любой из них выражает степени принадлежности
i-й столбец любой из них выражает степени принадлежности  объекта каждому из с нечетких кластеров. Для выявления взаимосвязи между кластерами, полученными при использовании нескольких методов, необходимо сопоставить соответствующие строки матриц
объекта каждому из с нечетких кластеров. Для выявления взаимосвязи между кластерами, полученными при использовании нескольких методов, необходимо сопоставить соответствующие строки матриц  Субоптимальная процедура, предложенная В. Педричем [144, с. 137-142] для решения этой проблемы, может быть представлена в виде следующей последовательности шагов:
Субоптимальная процедура, предложенная В. Педричем [144, с. 137-142] для решения этой проблемы, может быть представлена в виде следующей последовательности шагов:
1 Полагается 
2 Сравнивается  строка матрицы разбиения
строка матрицы разбиения  со строками матрицы разбиения
со строками матрицы разбиения  и отыскивается индекс
и отыскивается индекс  такой, что некоторое расстояние, к примеру, Хемминга, между I-й строкой матрицы
такой, что некоторое расстояние, к примеру, Хемминга, между I-й строкой матрицы  строкой матрицы
строкой матрицы  достигает минимума;
достигает минимума;
3 Предыдущий шаг выполняется для всех  что позволяет построить функцию
что позволяет построить функцию  выражающую соответствие между строками матриц разбиения
выражающую соответствие между строками матриц разбиения 
4. Вычисляются средние значения функций принадлежности соответствующих кластеров, так что строится средняя матрица разбиения;
5. Если  то полагается
то полагается  и осуществляется переход на шаг 2, производится замещение матрицы разбиения Р вычисленной средней матрицей разбиения; при
и осуществляется переход на шаг 2, производится замещение матрицы разбиения Р вычисленной средней матрицей разбиения; при  процесс останавливается.
процесс останавливается.
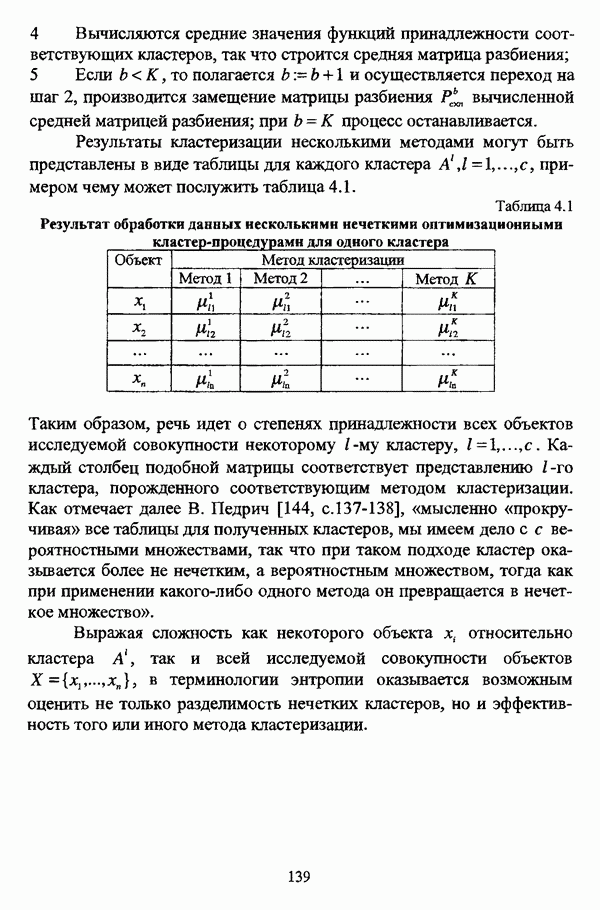
Результаты кластеризации несколькими методами могут быть представлены в виде таблицы для каждого кластера  примером чему может послужить таблица 4.1.
примером чему может послужить таблица 4.1.
Таблица 4.1. Результат обработки данных несколькими нечеткими оптимизационными

 -процедурами для одного
-процедурами для одного 
Таким образом, речь идет о степенях принадлежности всех объектов исследуемой совокупности некоторому  кластеру, Каждый столбец подобной матрицы соответствует представлению
кластеру, Каждый столбец подобной матрицы соответствует представлению  кластера, порожденного соответствующим методом кластеризации. Как отмечает далее В. Педрич
кластера, порожденного соответствующим методом кластеризации. Как отмечает далее В. Педрич  «мысленно «прокручивая» все таблицы для полученных кластеров, мы имеем дело с с вероятностными множествами, так что при таком подходе кластер оказывается более не нечетким, а вероятностным множеством, тогда как при применении какого-либо одного метода он превращается в нечеткое множество».
«мысленно «прокручивая» все таблицы для полученных кластеров, мы имеем дело с с вероятностными множествами, так что при таком подходе кластер оказывается более не нечетким, а вероятностным множеством, тогда как при применении какого-либо одного метода он превращается в нечеткое множество».
Выражая сложность как некоторого объекта  относительно кластера
относительно кластера  так и всей исследуемой совокупности объектов
так и всей исследуемой совокупности объектов  в терминологии энтропии оказывается возможным оценить не только разделимость нечетких кластеров, но и эффективность того или иного метода кластеризации.
в терминологии энтропии оказывается возможным оценить не только разделимость нечетких кластеров, но и эффективность того или иного метода кластеризации.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ПРОБЛЕМА НЕОПРЕДЕЛЕННОСТИ В ЗАДАЧАХ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 1.1. Понятие однородности и проблема классификации объектов
- 1.1.2. Общая постановка задачи автоматической классификации и основные направления ее решения
- 1.2. Подход к решению задачи автоматической классификации с позиции теории нечетких множеств
- 1.2.2. Гносеологические аспекты подхода к решению задач классификации с позиции теории нечетких множеств
- Резюме
- ГЛАВА 2. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ НЕЧЕТКИХ МНОЖЕСТВ
- 2.1. Нечеткие множества
- 2.1.2. Основные операции над нечеткими множествами
- 2.2. Нечеткие отношения
- 2.2.2. Основные операции над нечеткими отношениями
- Резюме
- ГЛАВА 3. МЕТОДЫ НЕЧЕТКОГО ПОДХОДА К РЕШЕНИЮ ЗАДАЧ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 3.1.2. Описание алгоритмов
- 3.2. Оптимизационные методы
- 3.2.2. Описание алгоритмов
- 3.2.2.2. Алгоритм Уиндхема
- 3.2.2.3. Алгоритм Рубенса
- 3.2.2.4. Алгоритм Беждека — Данна
- 3.2.2.5. Алгоритм Педрича
- 3.2.2.6. Алгоритм Даве — Сена
- 3.2.2.7. Другие алгоритмы оптимизационного подхода
- 3.3. Иерархические методы
- 3.3.2. Описание алгоритмов
- 3.3.2.2. Алгоритм Думитреску (FDH algorithm)
- 3.3.2.3. Другие алгоритмы иерархического подхода
- Резюме
- ГЛАВА 4. СРАВНИТЕЛЬНЫЙ АНАЛИЗ НЕЧЕТКИХ МЕТОДОВ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 4.1.2. Виды исходных данных и общая схема проведения сравнительного анализа
- 4.2. Оценка и представление результатов обработки данных нечеткими методами автоматической классификации
- 4.2.2. Представление и интерпретация результатов нечеткой классификации
- 4.3. Экспериментальное сравнение нечетких методов автоматической классификации
- 4.3.2. Результаты вычислительных экспериментов
- Резюме
- ГЛАВА 5. МЕТОДОЛОГИЧЕСКИЕ АСПЕКТЫ НЕЧЕТКОГО ПОДХОДА К РЕШЕНИЮ ЗАДАЧИ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 5.1.2. Выбор алгоритма нечеткого подхода к решению задачи автоматической классификации и обоснование параметров
- 5.2. Прикладные аспекты нечеткой классификации
- 5.2.2. Нечеткие методы автоматической классификации и другие нечеткие методы распознавания образов
- Резюме
- ЗАКЛЮЧЕНИЕ
- Основные обозначения
- Список литературы