55. Обобщение понятия нечеткого подмножества

Сначала рассмотрим частные примеры.

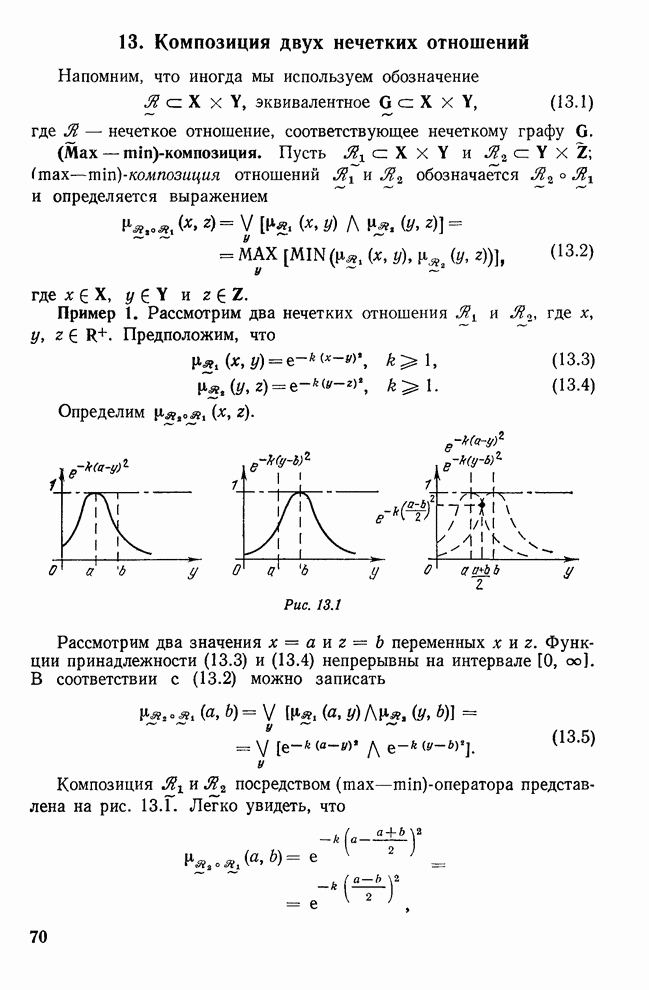
Пример 1. Предположим, что

,                      (55.1)

.                (55.2)

Предположим, также, что  имеет структуру булевой решетки (т. е. дистрибутивной и с дополнением), подобную той, которая представлена на рис. 55.1.

Рис. 55.1.

Для операций  и  результаты для  можно видеть на матрицах (55.3) и (55.4).

	(55.3)
	(55.4)

Исследуем свойства . Положим

,                   (55.5)

,                    (55.6)

,       (55.7)

.       (55.8)

Положим

,             (55.9)

.                        (55.10)

Поскольку  имеет структуру булевой решетки, то для операций  и  выполняются следующие свойства: ассоциативность, коммутативность, идемпотентность, поглощение, дистрибутивность  относительно  и наоборот, существование единственного дополнения для каждого элемента .

Теперь исследуем свойства . Легко видеть, что  ассоциативна, поскольку ассоциативна . Аналогично  ассоциативна в силу ассоциативности . Таким же образом исключительно легко доказать коммутативность, идемпотентность и поглощение.

Докажем дистрибутивность и существование дополнений.

         (55.11)

Положим

.                    (55.12)

Убедимся, что

,                   (55.13)

аналогично

.                  (55.14)

Таким образом,  так же, как и , обладает структурой булевой решетки, и эта структура изображена на рис. 55.2.

На рисунке  обозначает

Рис. 55.2.

Пример 2. Пусть опять

, где ,                (55.15)

.                (55.16)

Пусть теперь структура  представляет собой решетку, состоящую из единственной цепи (рис. 55.3). Решетка дистрибутивна, но без дополнений (т. е., скорее, это векторная решетка). Для операций  и  имеем

	(55.17)
	(55.18)

Рис. 55.3.

Структура множества  обладает следующими свойствами: ассоциативностью, коммутативностью, идемпотентностью, поглощением, дистрибутивностью относительно  и .

Легко проверить, что  обладает теми же свойствами, а структура  - также векторная решетка (рис. 55.4).

На рисунке  обозначает

Рис. 55.4.

Пример 3. Пусть

,                     (55.19)

.                (55.20)

Структура  представляет собой нижнюю полурешетку (см. рис. 55.5), и поэтому можно определить только . Имеем

(55.21)

Рис. 55.5.

В  выполняются следующие свойства операции : ассоциативность для , коммутативность для , идемпотентность для ; таким образом,  имеет структуру нижней полурешетки (см. рис. 55.6).

Рис. 55.6.

Если в этом примере изменить структуру , а именно, поменять местами верх и низ на рис. 55.5, то для  получим верхнюю полурешетку.

Пример 4. Пусть

,                     (55.22)

.                (55.23)

Структура , показанная на рис. 55.7, не полурешетка. В ней для некоторых упорядоченных пар уже не существует ни нижней, ни верхней границы. Структуру  можно определить для отношения доминирования; эта структура изображена на рис. 55.8.

Рис. 55.7.

Рис. 55.8.

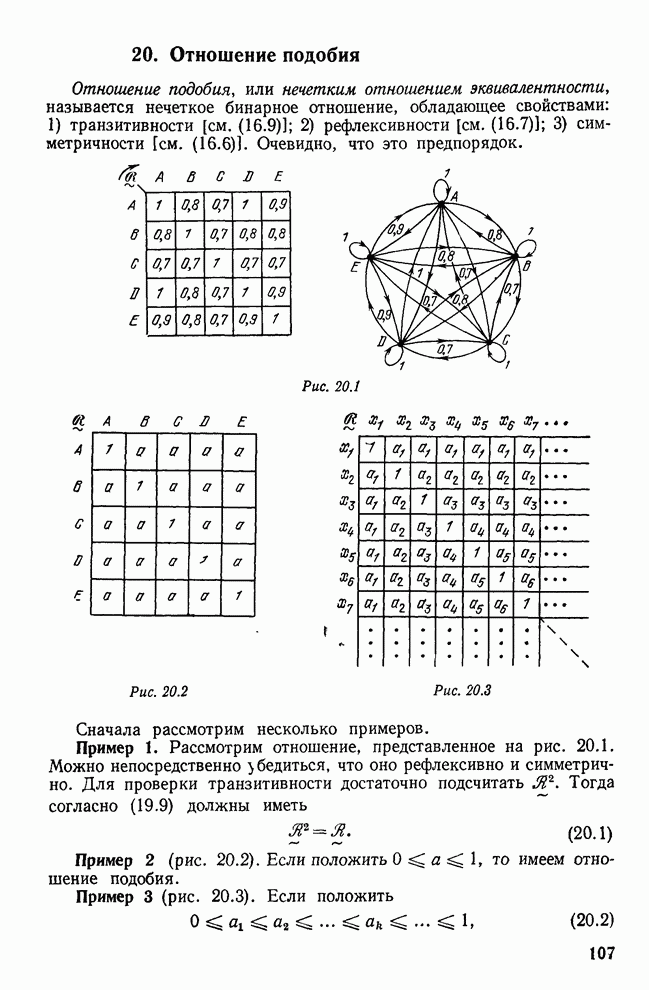
Замечание. Обычно граф, представляющий отношение, называют конфигурацией. Таким образом, решетку можно рассматривать как конфигурацию, то же самое можно сказать о полурешетке и в конце концов, следовательно, о любом графе, представляющем отношение. Однако, как мы видели, решетка также представляет структуру для операций  и , а полурешетка - структуру для одной из операций  или . Графы, соответствующие диаграммам Хассе на рис. 55.7 и 55.8, представляют собой конфигурации, а не структуры по крайней мере для  или (и) .

Случай, когда  имеет конфигурацию предпорядка. Если структура  имеет конфигурацию обычного предпорядка (в смысле обычной теории графов), то мы знаем, что в этом предпорядке можно определить множество классов эквивалентности и тогда эти классы сами с собой образуют (частичный или полный) порядок. Именно так мы будем поступать в случае, когда  имеет конфигурацию обычного предпорядка.

Рассмотрим пример. Пусть

,                  (55.24)

.                (55.25)

Предположим, что  имеет структуру предпорядка, подобную той, которая изображена в виде обычного графа на рис. 55.9. На рис. 55.10 мы выделили четыре класса эквивалентности этого предпорядка, на рис. 55.11 показан порядок на этих классах, на рис. 55.12 - максимальные цепи этого порядка.

Рис. 55.9.

Рис. 55.10.

Рис. 55.11.

Рис. 55.12.

Отметим, что классы образуют верхнюю полурешетку.

Изучая состав классов эквивалентности на рис. 55.10, замечаем, что

, , , .                 (55.26)

Для упрощения записи каждому классу эквивалентности поставим в соответствие по одному представителю

, , , ,                (55.26')

которые и будем использовать для представления классов.

Верхнюю полурешетку  можно представить с помощью следующего отношения:

(55.27)

На рис. 55.13 изображена верхняя полурешетка , где  - представитель класса.

Рис. 55.13.

В этой верхней полурешетке имеется 16 классов эквивалентности. Выпишем для примера класс :

.                        (55.28)

Очевидно, что 64 элемента  разбиваются на классы эквивалентности следующим образом:

                       (55.29)

Таким образом,  - обычный предпорядок, содержащий 16 классов эквивалентности.

Случай, когда  имеет структуру кольца. Пусть

, ,

	(55.30)
	(55.31)

Если положим

,                      (55.32)

,                     (55.33)

где  и , то

,             (55.34)

.             (55.35)

Для  мы получаем структуру кольца, представленную в явном виде в (55.36) и (55.37), где запись типа  использована для обозначения :

	(55.36)
	(55.37)

Замечание. Интересно сравнить кольцо (55.30) и (55.31) с булевым кольцом (55.3) и (55.4). Используем обозначения (55.30) и (55.31) для (55.3) и (55.4) и сравним их на рис. 55.14. Кольцо из примера (55.30) и (55.31) - это (см. левый рисунок) кольцо с операциями сложения и умножения по модулю 4 (чтобы убедиться в этом, достаточно положить , ,  и ), а правый рисунок иллюстрирует построение булева кольца на множестве .

Рис. 55.14.

Это замечание можно уточнить, напомнив, что булево кольцо - это только одна из многих кольцевых структур.

Перенесение свойств. После всего, что мы изложили в данном параграфе, легко доказать, что

 - обычный предпорядок  - обычный предпорядок,                    (55.38)

 - обычный порядок  - обычный порядок,            (55.39)

 - нижняя полурешетка  - нижняя полурешетка,              (55.40)

 - верхняя полурешетка  - верхняя полурешетка,                       (55.41)

 - решетка  - решетка,                    (55.42)

 - кольцо  - кольцо.             (55.43)

Эти свойства следует добавить к тем, которые уже были определены в (53.16)-(53.18), помня, что любой ассоциативный для  закон  индуцирует ассоциативный закон  для ; аналогично, если закон  коммутативный, то коммутативен и закон , если закон идемпотентный, то и закон  идемпотентный.

Другие свойства. Формулы (52.33)-(52.39) позволяют определить другие свойства. Рассмотрим случай, когда

.               (55.44)

Можно легко доказать несколько свойств.

Если  и  имеют конфигурации обычного предпорядка, то  имеет такую же конфигурацию; аналогичные результаты получаем, рассматривая конфигурации порядка, полурешетки, решетки или кольца. Эти же свойства обнаруживаются и в связи с операциями взятия произведения и возведения в степень.

Рассмотрим пример.

Пример. Пусть

,                        (55.46)

,              (55.47)

где  имеет структуру нижней полурешетки, которая отражена на рис. 55.15, и  - структуру решетки (рис. 55.16).

Рис. 55.15.

Рис. 55.16.

Произведение

              (55.48)

обладает структурой нижней полурешетки (рис. 55.17).

Рис. 55.17.

Теперь положим

.                   (55.49)

Тогда множество  с элементами

,                 (55.50)

где ; ; ; , состоит из  элементов и имеет структуру нижней полурешетки.

Другой пример: нечеткие подмножества высших порядков. Пусть

,                      (55.51)

,              (55.52)

.                (55.53)

Исследуем представление . Сначала имеем

      (55.54)

Сохраняя произвольный порядок элементов в , для упрощения записи положим

.              (55.55)

Легко видеть, что множество  содержит  элементов, из которых выпишем только один:

. (55.56)

Если  - решетки, то  - тоже решетка.

Здесь мы видим, как появляется понятие нечеткого подмножества порядка 2. Можно пойти еще дальше и определить нечеткие подмножества порядка  .

Не нужно путать

 с ,                  (55.57)

т. е. с нечеткостью другого типа.

Относительное обобщенное расстояние Хемминга для случая, когда  - решетка, и для более общего случая - ориентированного графа. Перед тем как определить это понятие, еще более общее, чем то, которое изучалось в § 5, напомним, что понимают под расстоянием между двумя вершинами в неориентированном выпуклом обычном графе.

Расстоянием между двумя вершинами неориентированного графа называется длина кратчайшей неориентированной цепи (число звеньев кратчайшей цепи). Определенное таким образом расстояние между  и  обозначим через .

Проверим, что аксиомы (5.49)-(5.51) действительно удовлетворяются. Пусть  - множество вершин рассматриваемого неориентированного графа, нужно проверить, что

,                     (55.58)

,                 (55.59)

,                  (55.60)

и, кроме того, что

.                      (55.61)

Легко убедиться в том, что эти условия действительно выполняются и, значит, расстояние между вершинами определено корректно.

На рис. 55.18 мы изобразили неориентированный связный обычный граф. На рис. 55.19 приведена матрица расстояний  в этом графе.

Рис. 55.18.

Рис. 55.19.

Рассмотрим случай, когда мы имеем дело с множеством , нечеткие подмножества которого принимают свои значения в , причем  - упорядоченное множество. Для этого упорядоченного множества построим диаграмму Хассе, которая определит неориентированный обычный граф; в этом неориентированном обычном графе измерим расстояния  между вершинами, как это было определено выше.

Пусть

                  (55.62)

- множества с элементами, функции принадлежности которых принимают свои значения в упорядоченном множестве . Диаграмма Хассе для  представлена на рис. 55.20. Матрица расстояний  в этом неориентированном обычном графе приведена на рис. 55.21.

Рис. 55.20.

Рис. 55.21.

Теперь предположим, что мы рассматриваем для нечетких подмножества  и  множества :

                     (55.63)

и

                   (55.64)

Сначала подсчитаем расстояния  между «значениями» или «вершинами графа» для каждого элемента . Эти расстояния можно взять из матрицы на рис. 55.21. Имеем

                  (55.65)

Эти расстояния можно записать в одну строку

                       (55.66)

Теперь напомним, что понимается под диаметром связного неориентированного обычного графа - это максимальный кратчайший путь между любыми двумя вершинами. Например, для графа на рис. 55.18 диаметр равен 4 (см. правый столбец на рис. 55.19, расположенный под словом max). Следовательно, для графа на рис. 55.20 диаметр тоже равен 4. Теперь разделим каждое расстояние в (55.66) на 4 и получим

               (55.67)

Таким образом, мы приходим к случаю, когда числа принадлежат  и могут трактоваться как значения функции принадлежности.

Теперь определим относительное обобщенное расстояние Хемминга между  и

.                       (55.68)

Понятие относительного обобщенного расстояния Хемминга между двумя нечеткими подмножествами одного и того же универсального множества, в свою очередь, можно обобщить дальше, если допустить, что каждый элемент , , можно оценить по некоторому критерию, который может быть ему присущ или нет. Тогда можно использовать следующий общий алгоритм.

Общий алгоритм. 1. Представляем каждый критерий в виде матрицы кратчайших путей в неориентированном обычном графе.

2. Рассматриваем два нечетких подмножества:

             (55.69)

и

                        (55.70)

где  и  - оценки расположения по критерию , которому будет соответствовать диаметр ;  и  - оценки расположения по критерию , которому будет соответствовать диаметр , …;  и  - оценки расположения по критерию , которому будет соответствовать диаметр .

3. Подсчитываем расстояния , , …,  и делим каждое расстояние на его диаметр; таким образом,

                (55.71)

4. Определяем относительное обобщенное расстояние Хемминга:

.                       (55.72)

Рассмотрим довольно искусственный пример.

Пример (см. рис. 55.22). Пусть

                 (55.73)

                 (55.74)

Рис. 55.22.

Тогда имеем

расстояния                      (55.75)

диаметры                                     (55.76)

относительные расстояния                                  (55.77)

и относительное обобщенное расстояние Хемминга

.                  (55.78)

Неоднородное нечеткое подмножество. Предположим, что  принимает свои значения в , . Тогда множество нечетких подмножеств можно записать в виде

,                     (55.79)

где ,  - обычные одноточечные подмножества .

Любой элемент вида (55.79) будет называться неоднородным нечетким подмножеством. Примерами неоднородных нечетких подмножеств одного и того же универсального множества могут служить подмножества (55.73) и (55.74).

Если

,                 (55.83)

то

.                (55.84)

Мы снова приходим к понятию нечеткого подмножества, которое рассматривалось до сих пор.

Замечание. Очевидно, что в обобщении можно пойти дальше, считая некоторые  и  зависимыми.

Например, обычное подмножество  может принимать свои значения в , а не  в  и  в . Это позволяет ввести очень интересное расширение понятия нечеткого подмножества, которое можно описать как состоящее из взаимозависимых нечетких подмножеств. Предворяя рассмотрение этого вопроса в последующих томах, читатель может сам придумать много видов интересных расширений.