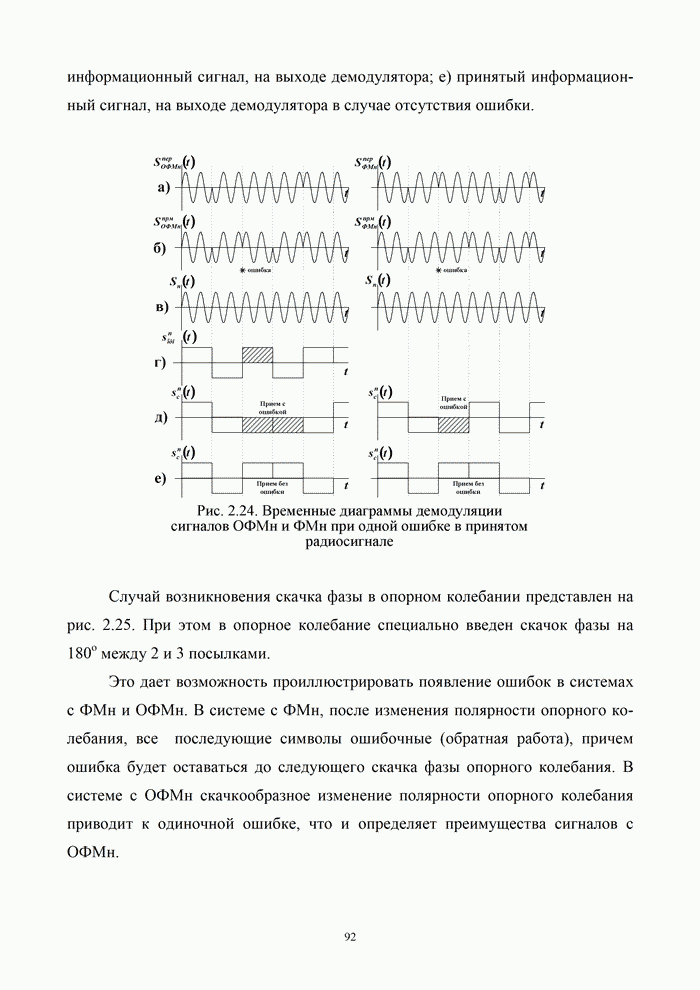
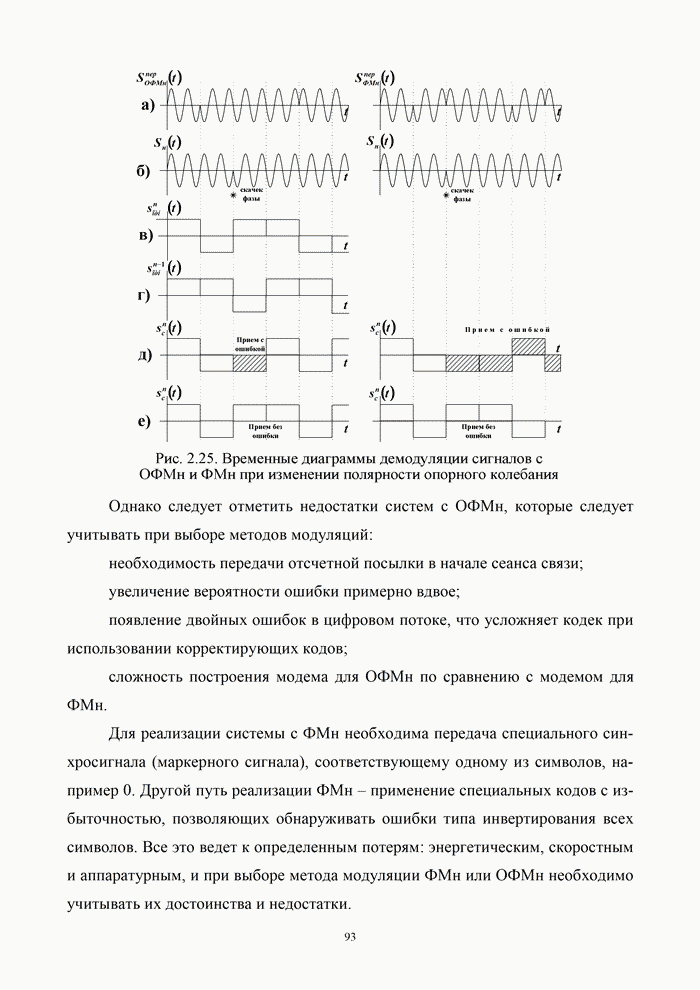
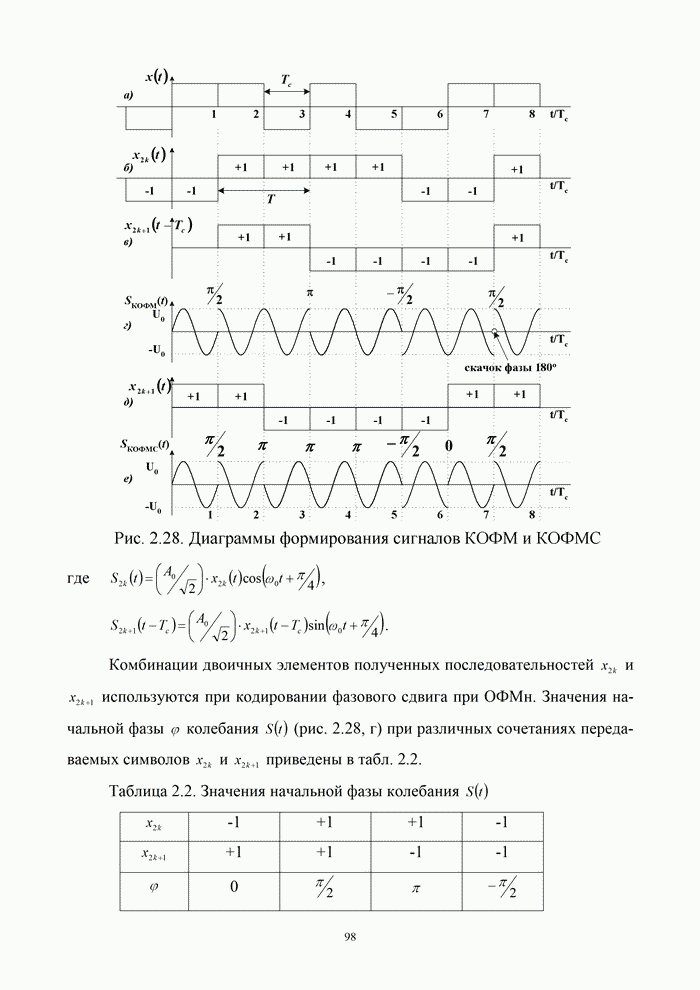
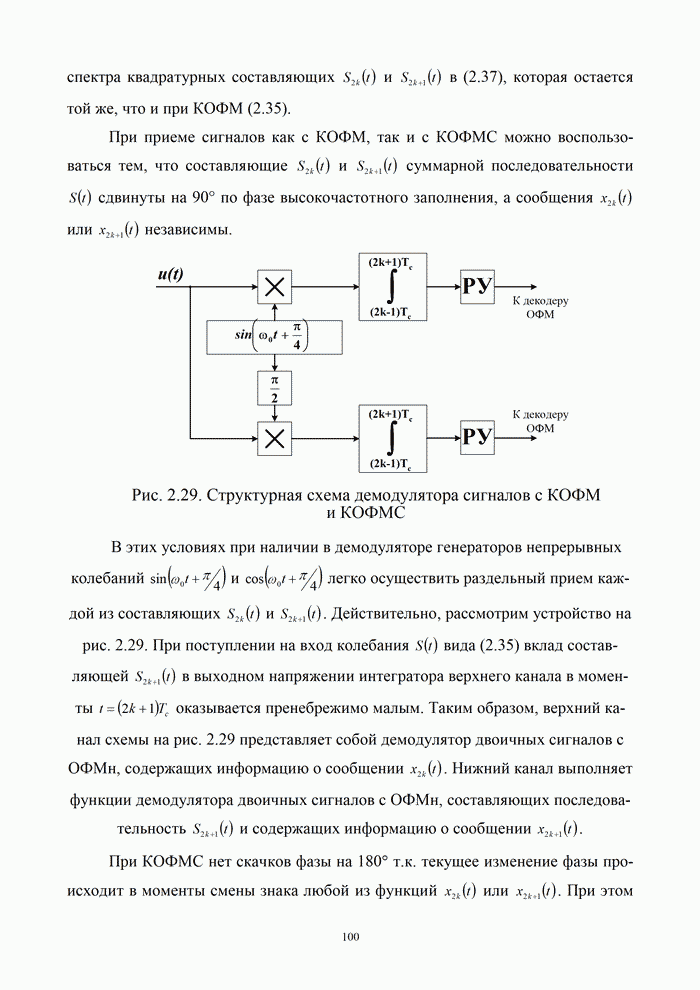
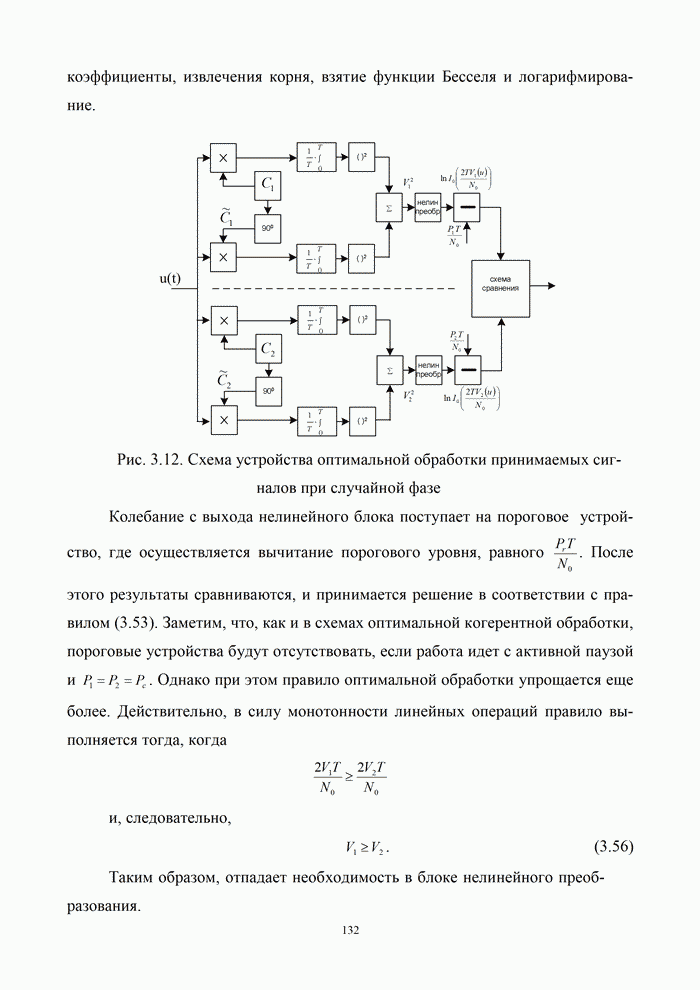
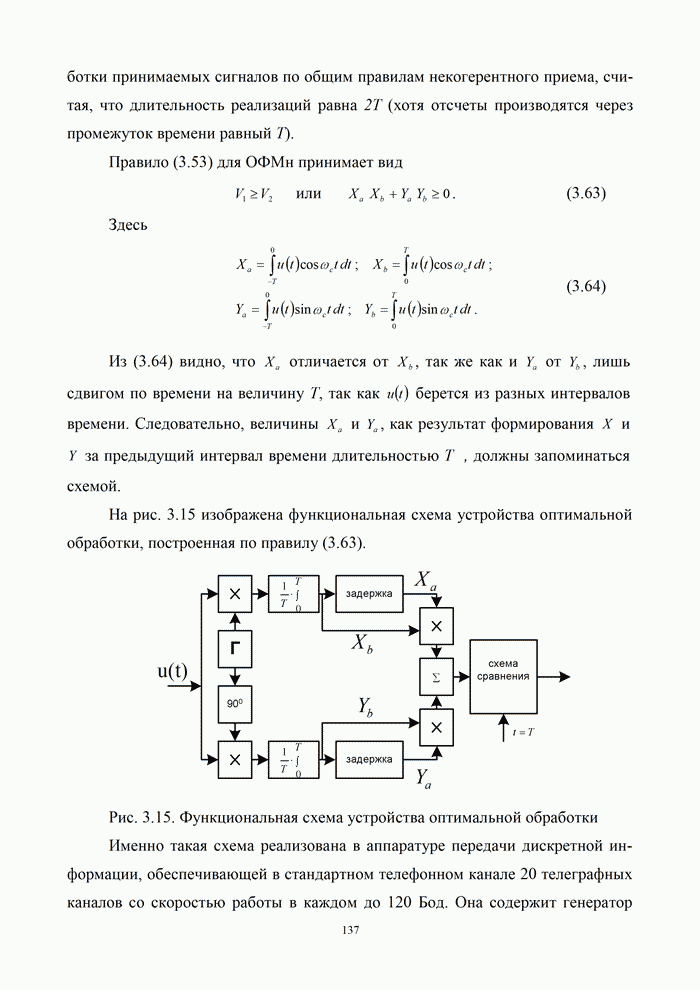
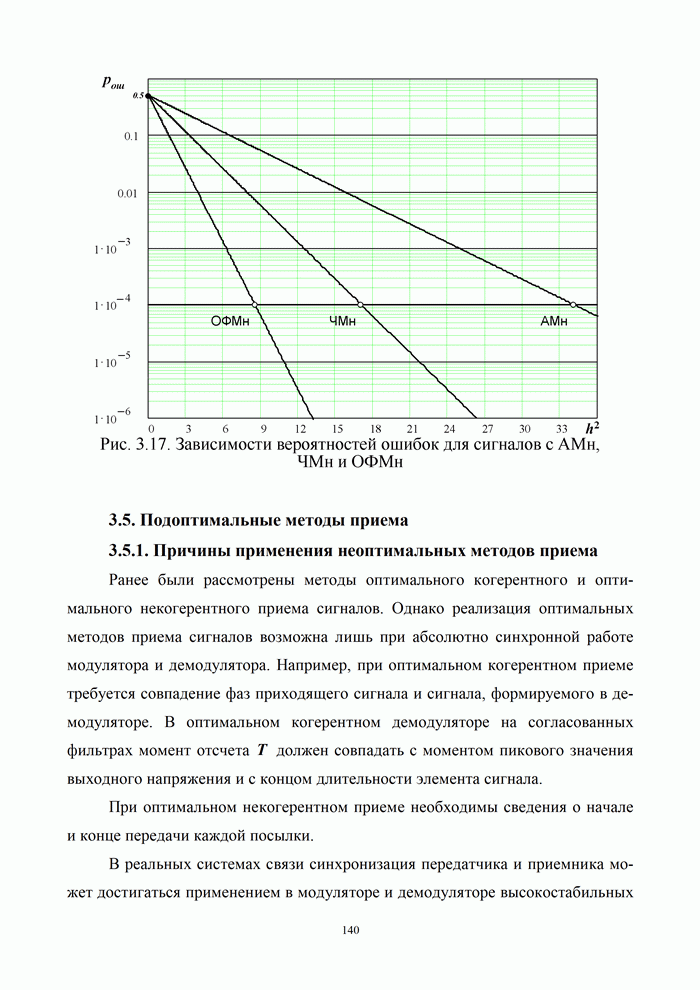
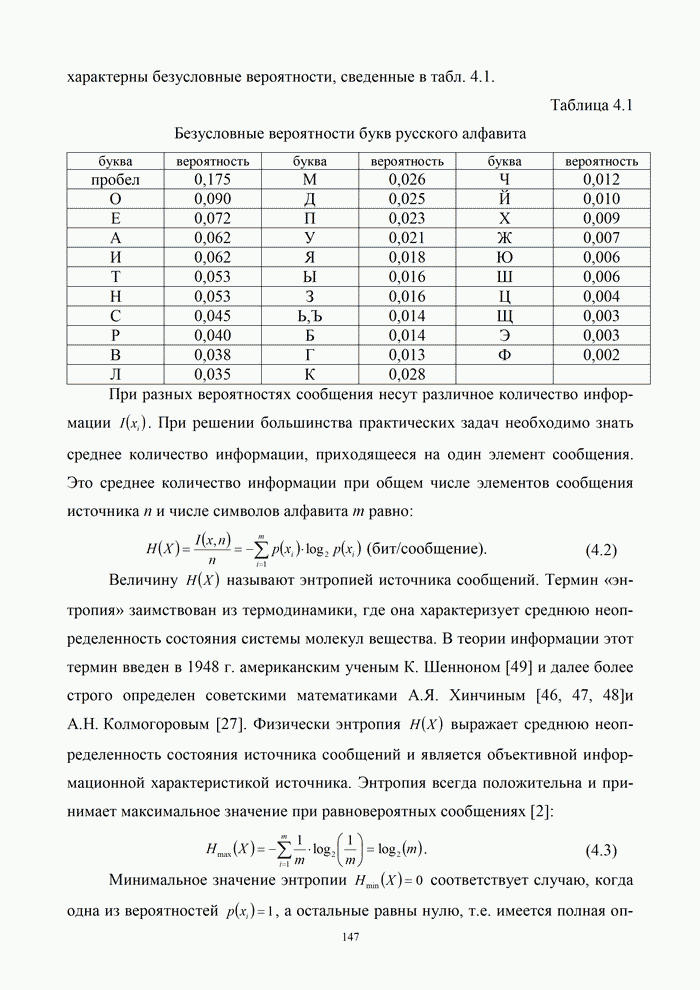
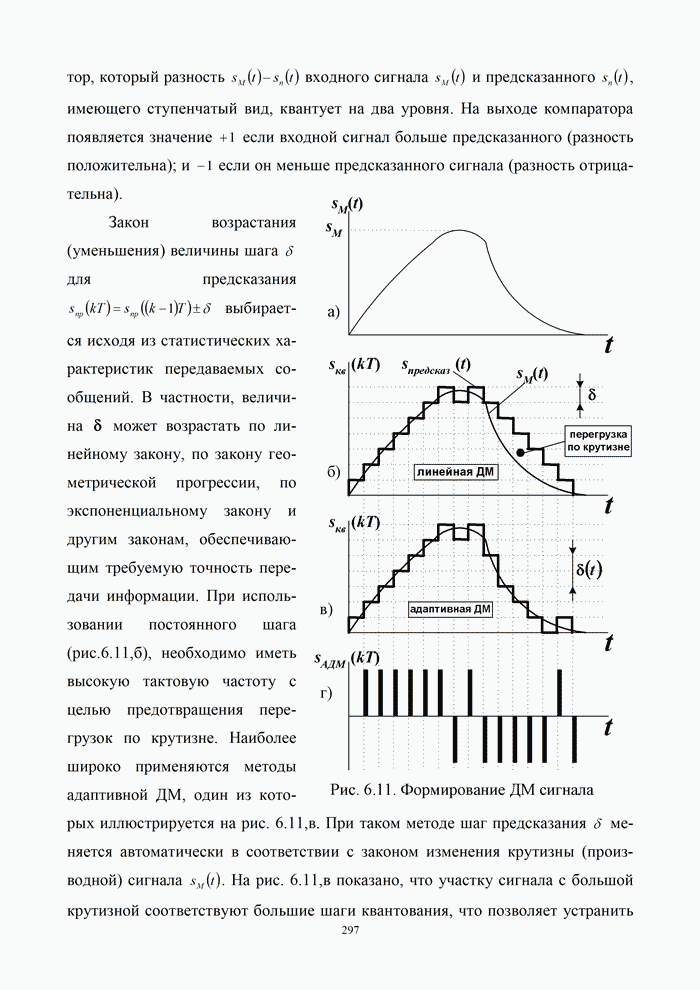
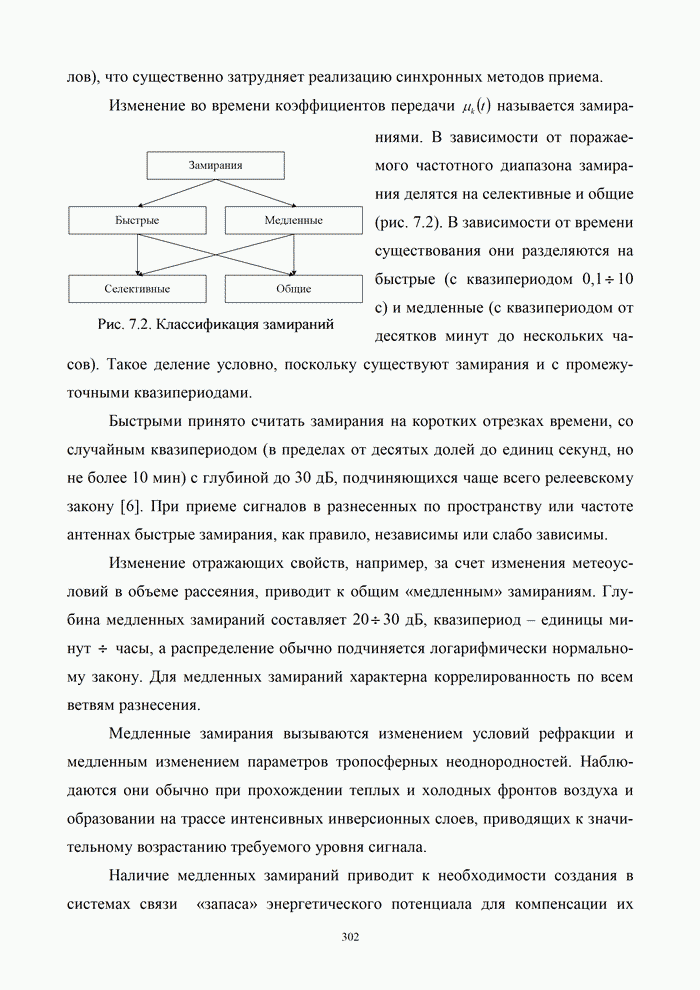
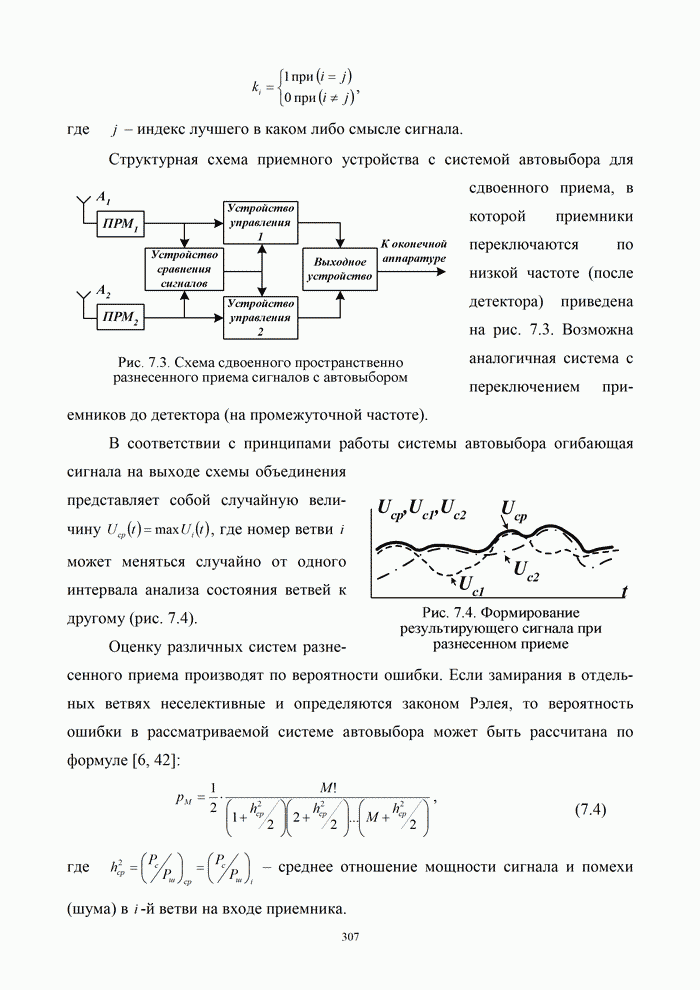
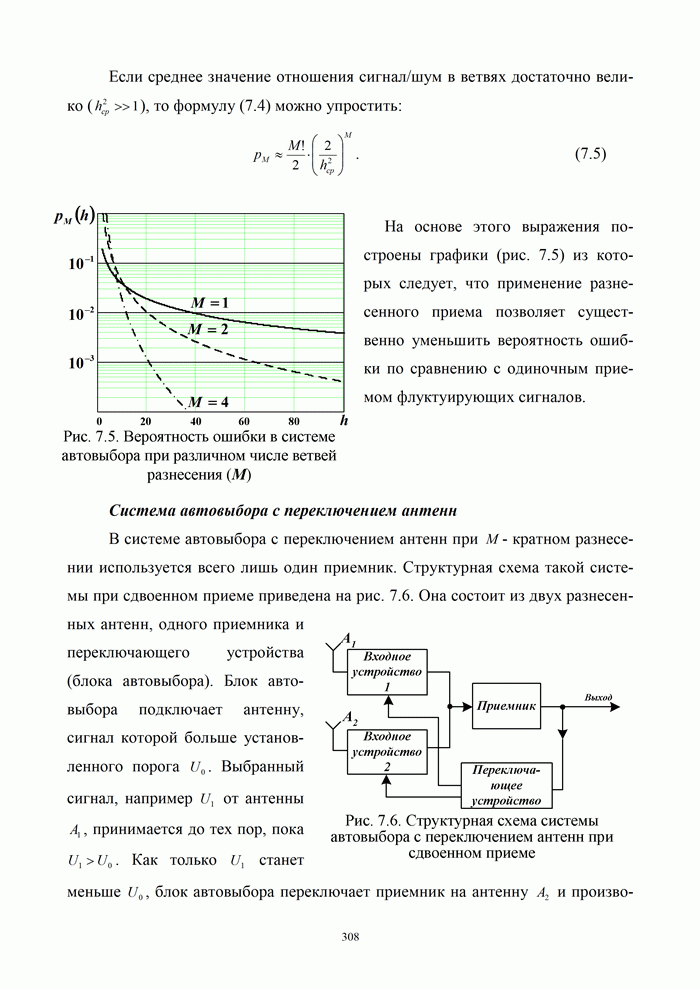
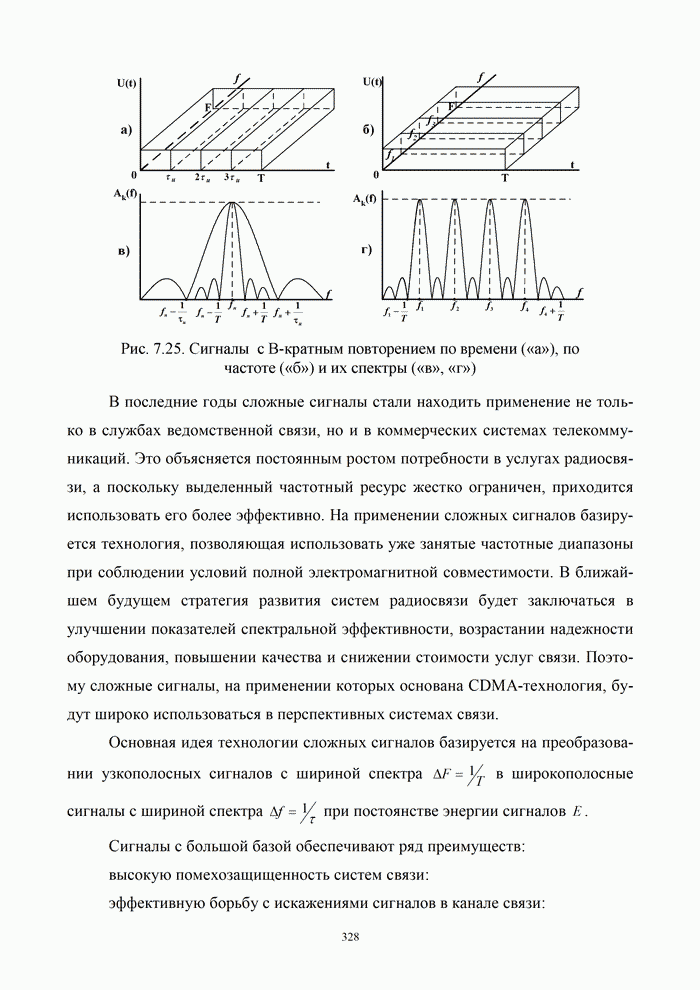
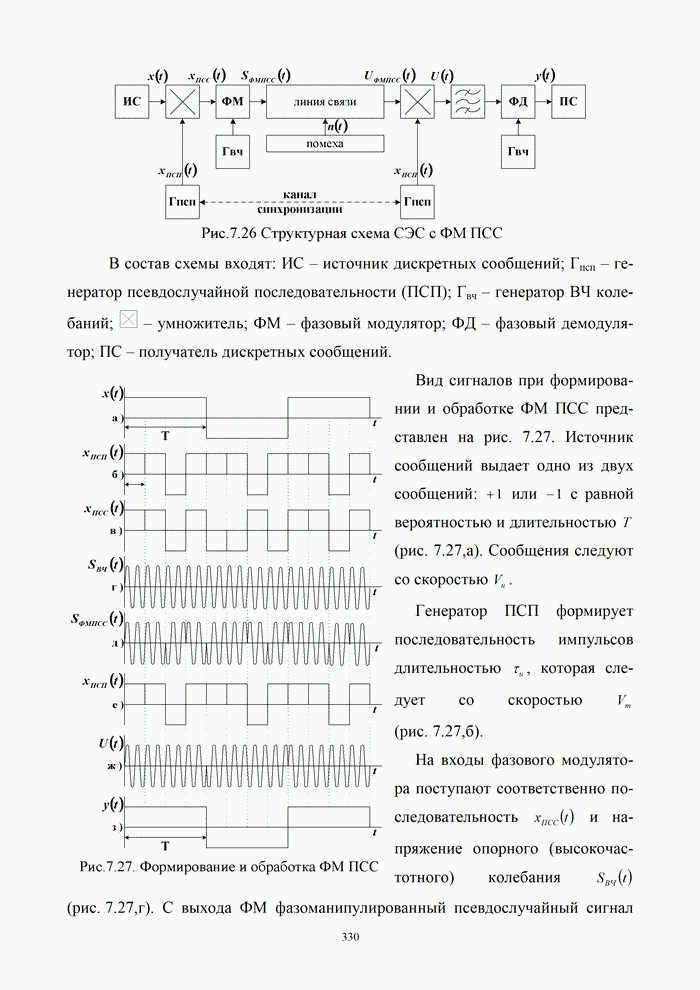
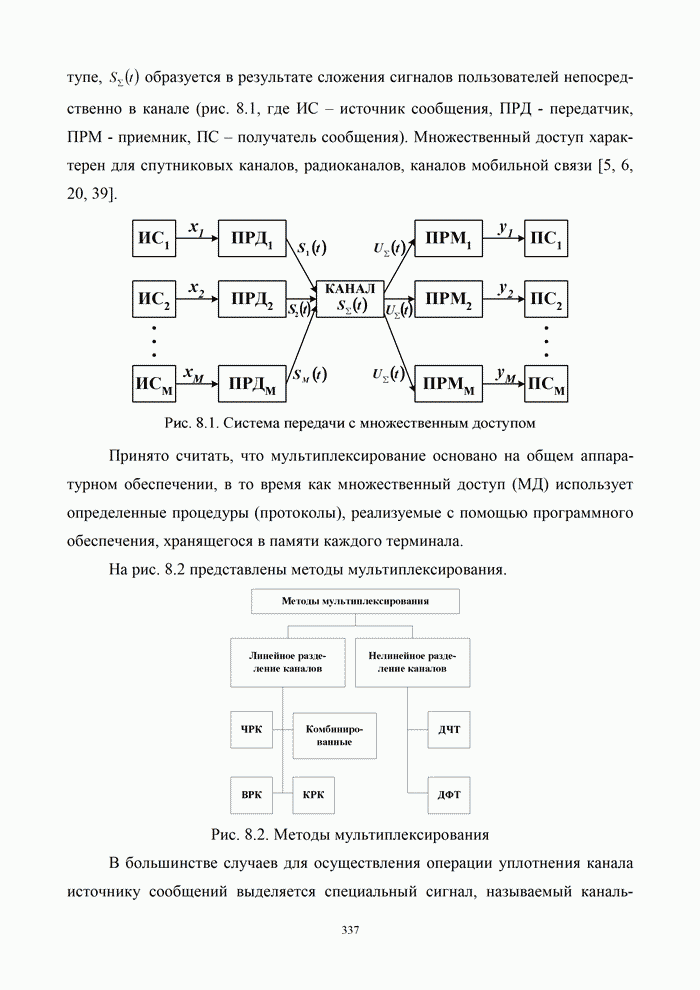
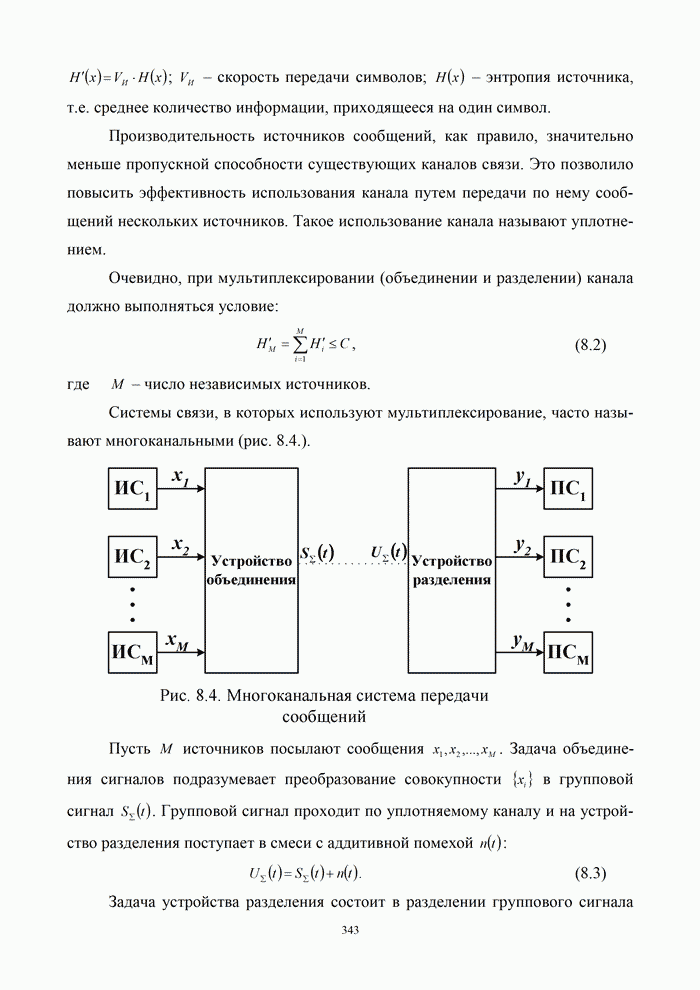
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
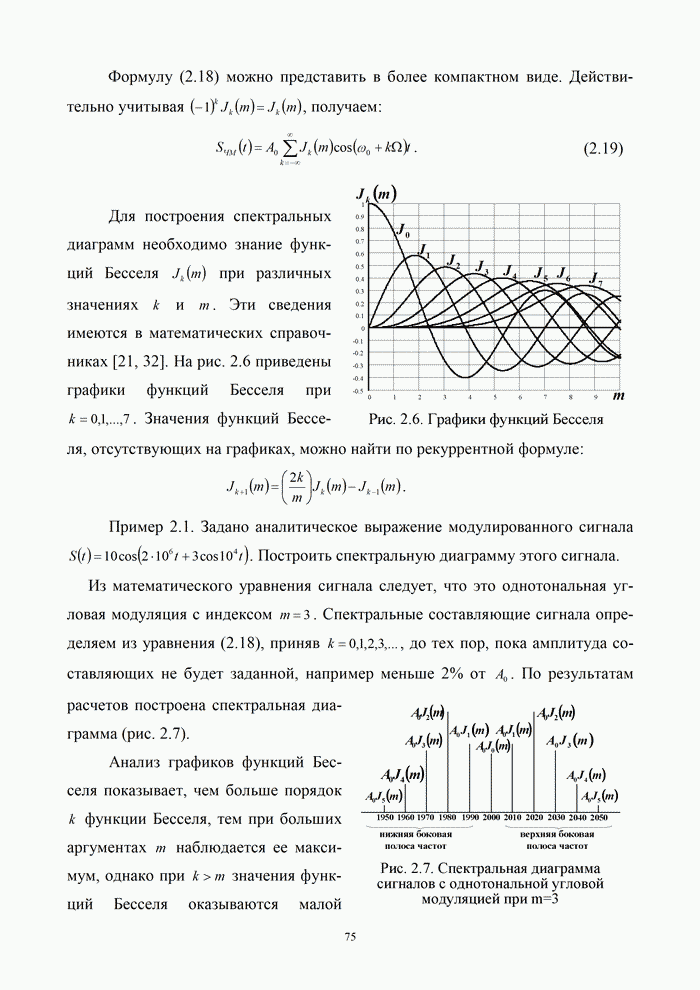
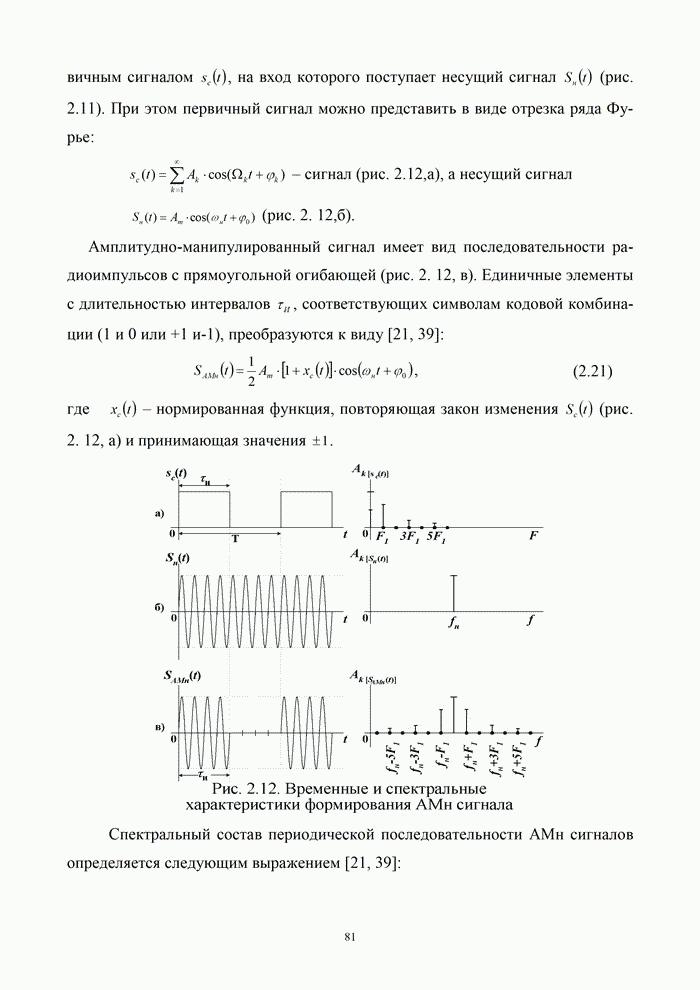
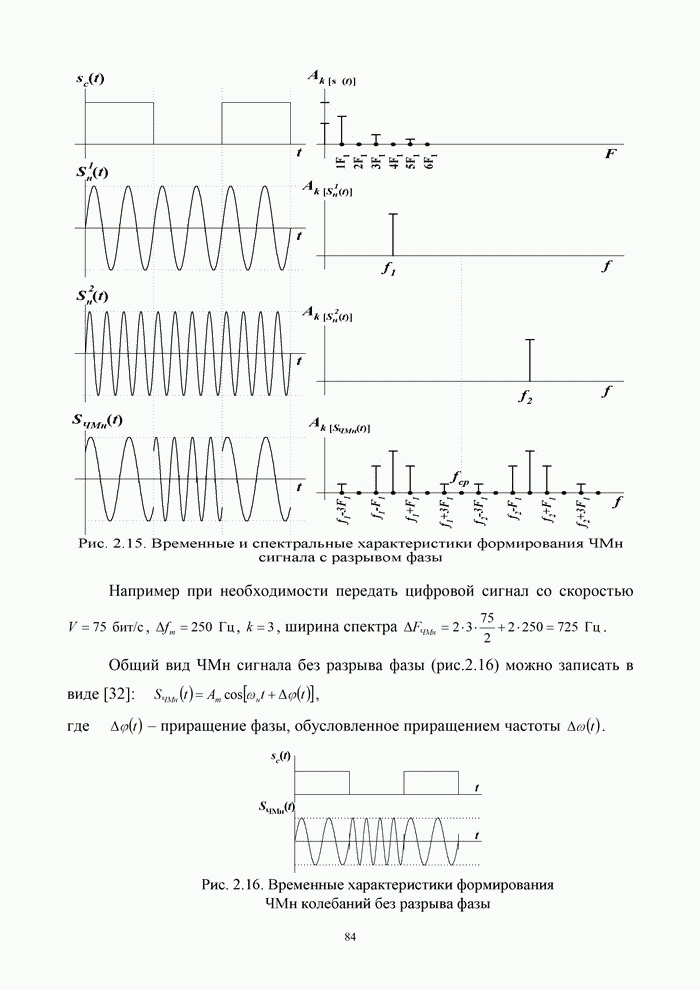
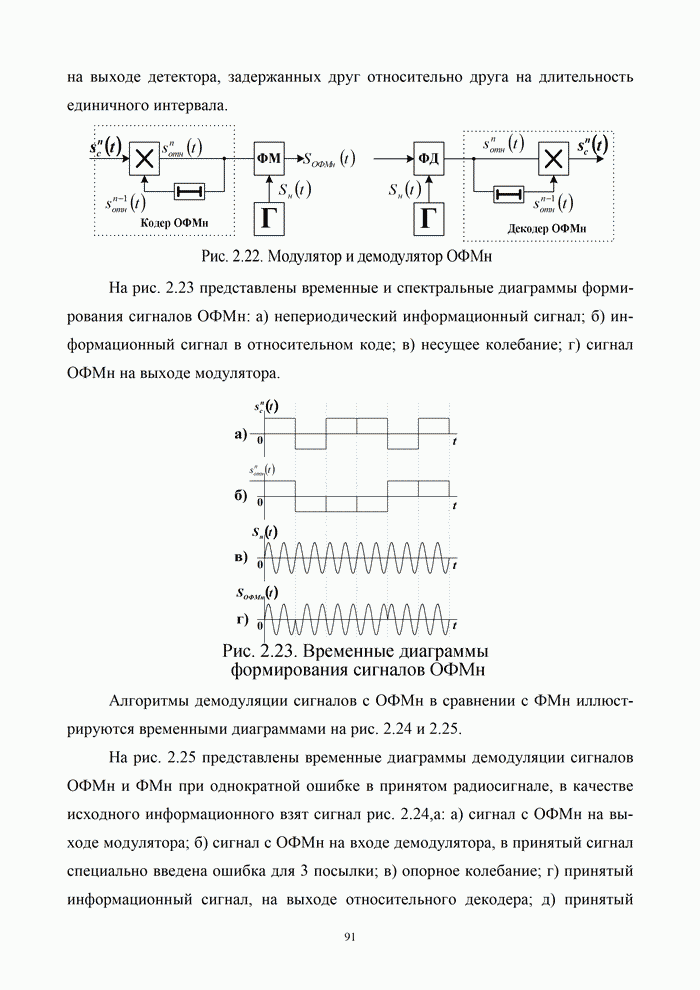
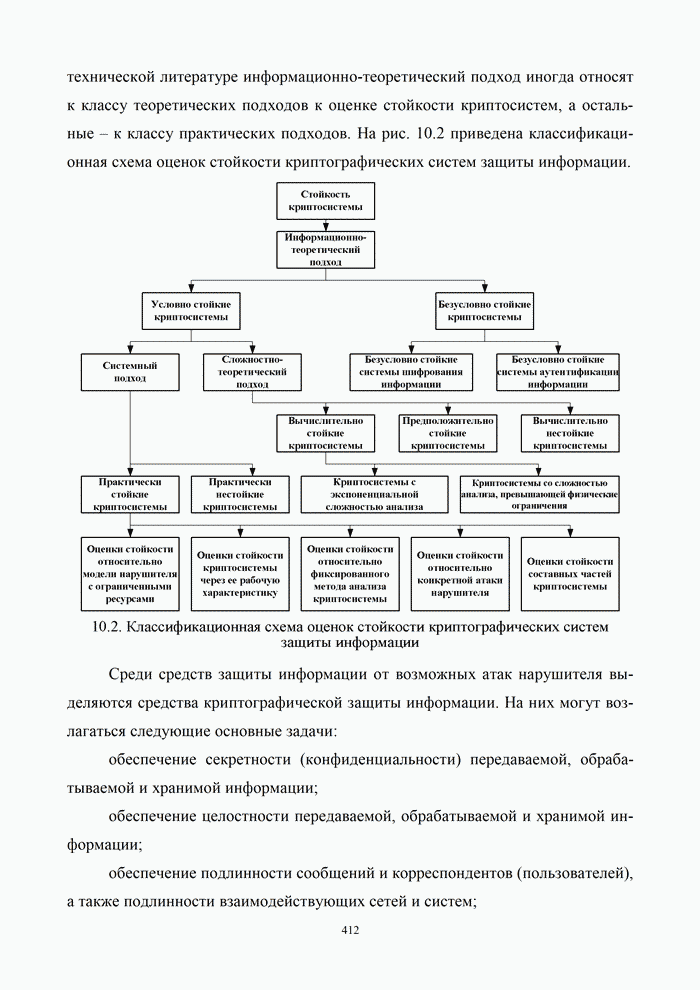
9.1.3. Эффективность аналоговых и цифровых систем
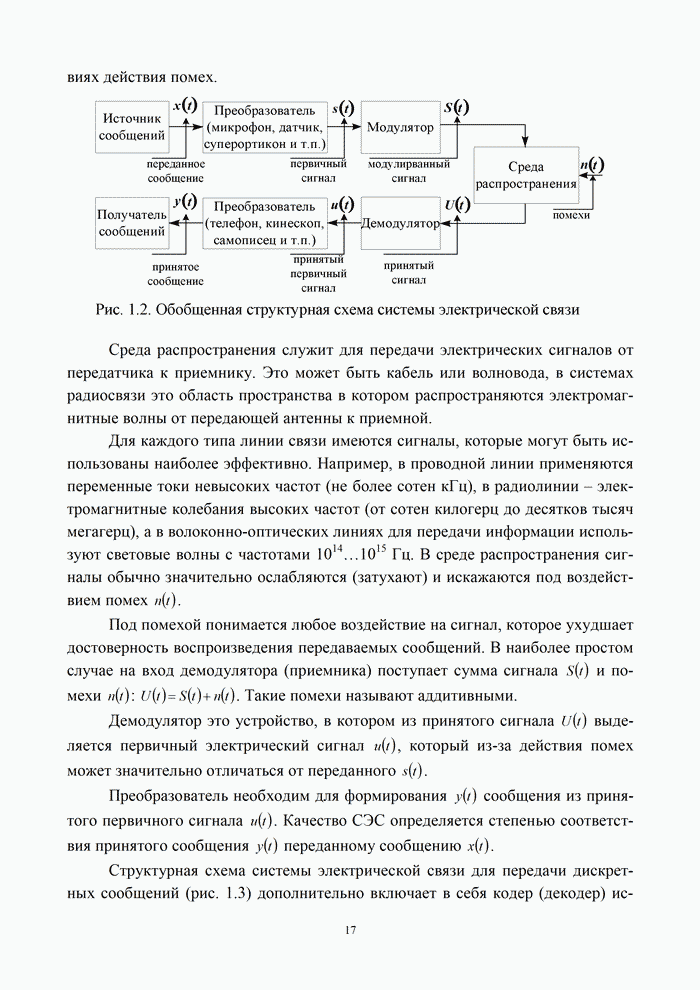
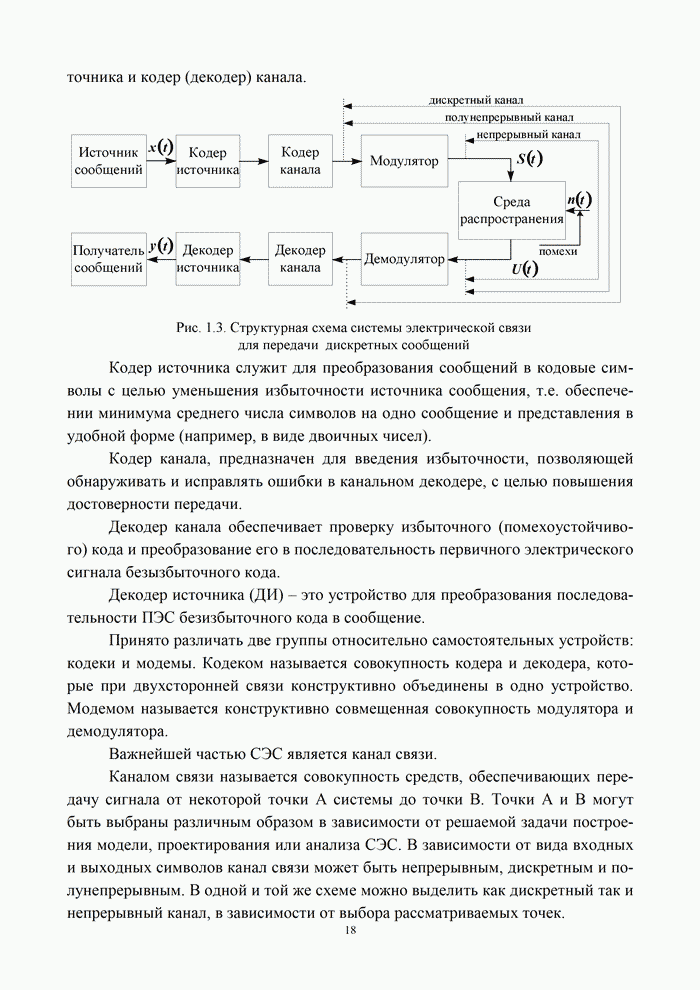
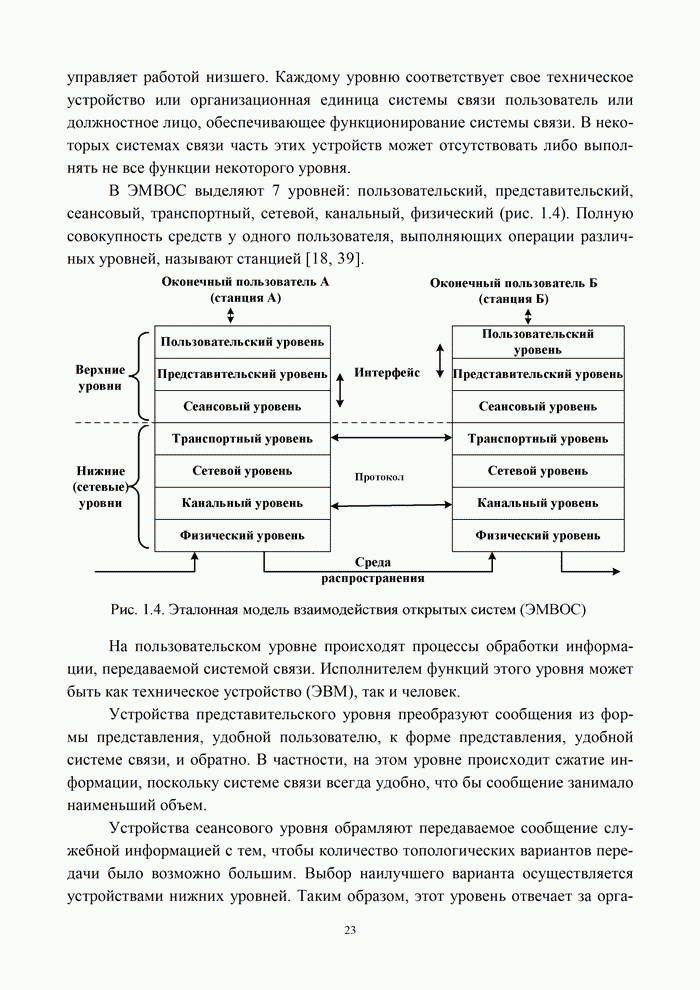
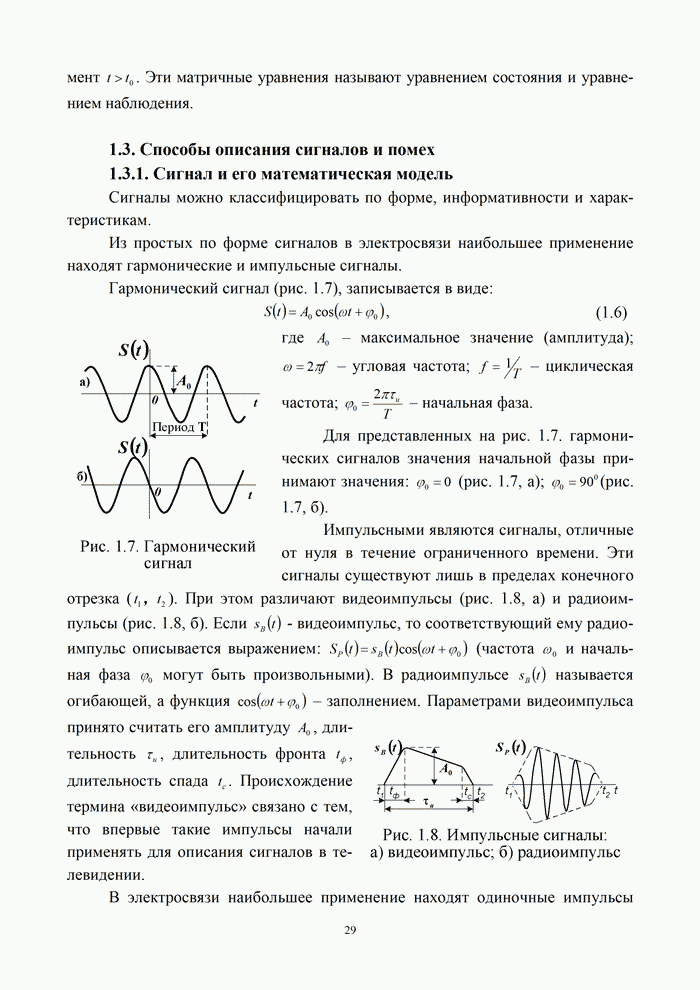
В системах передачи дискретных сообщений сигнал формируется с помощью кодирования и модуляции. При этом кодирование осуществляется обычно в два этапа: кодирование источника с целью сокращения его избыточности и кодирование канала с целью уменьшения вероятности ошибки за счет введения избыточности кода. При этом выражение (9.1) для информационной эффективности системы передачи дискретных сообщений можно представить в виде произведения [5, 20]:
|
|
(9.9) |
где ![]() – эффективность кодера источника;
– эффективность кодера источника; ![]() – эффективность кодера канала;
– эффективность кодера канала; ![]() – эффективность модема, зависящая от
вида модуляции и способа обработки сигнала в канале.
– эффективность модема, зависящая от
вида модуляции и способа обработки сигнала в канале.
Средняя
скорость передачи информации в системе при использовании многопозиционных
сигналов длительностью ![]() равна
равна ![]() (бит/с), где
(бит/с), где ![]() – скорость помехоустойчивого кода.
Тогда энергетическая эффективность [5, 20, 21, 32]
– скорость помехоустойчивого кода.
Тогда энергетическая эффективность [5, 20, 21, 32]
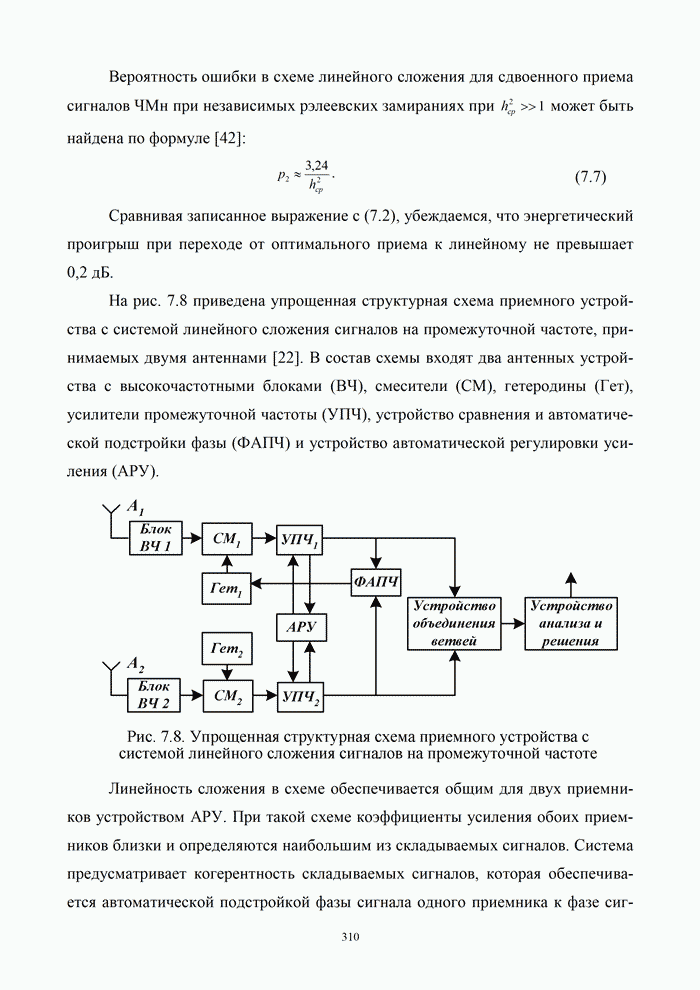
|
|
(9.10) |
частотная эффективность может быть найдена по формуле
|
|
(9.11) |
где ![]() – энергия сигнала;
– энергия сигнала; ![]() – энергия, затрачиваемая
на передачу одного бита информации.
– энергия, затрачиваемая
на передачу одного бита информации.
Значения
![]() можно
определить по известным формулам или графикам, рассчитанным для вероятности
ошибки
можно
определить по известным формулам или графикам, рассчитанным для вероятности
ошибки ![]() .
.
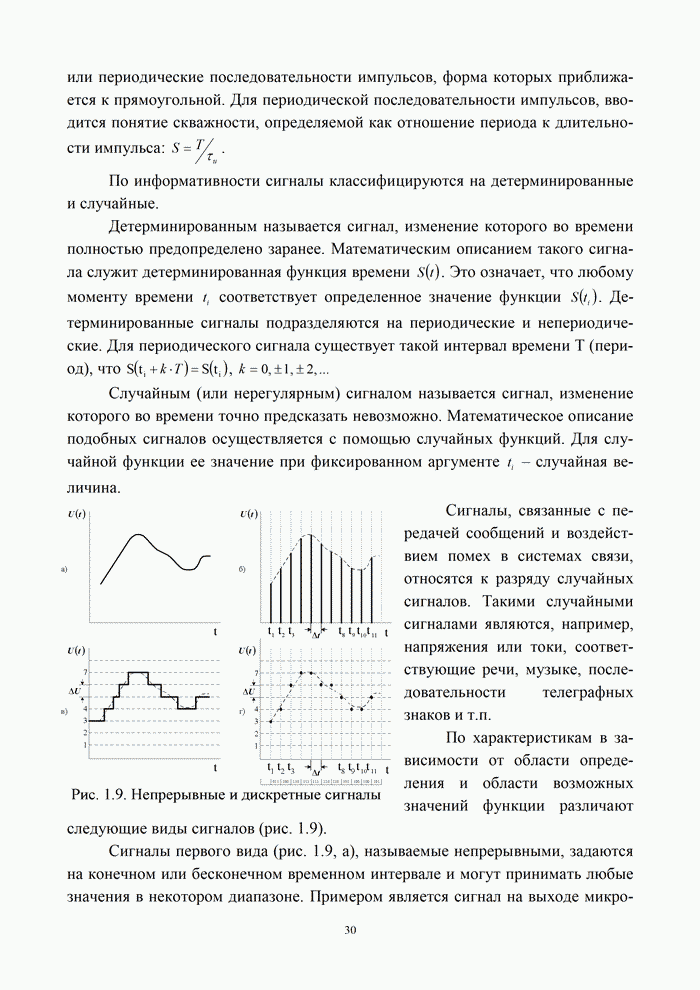
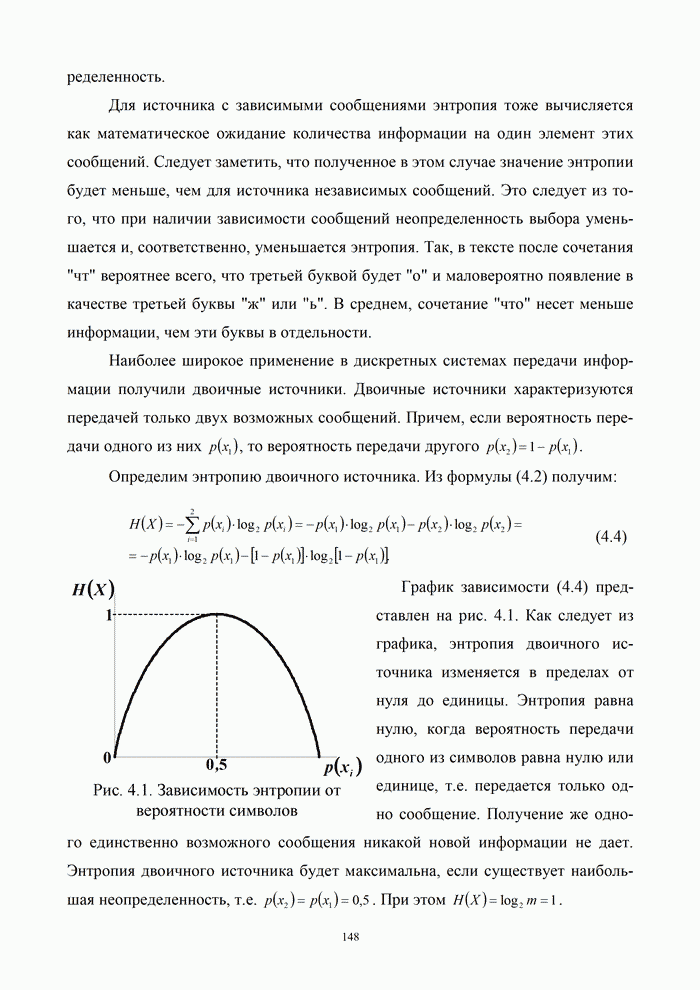
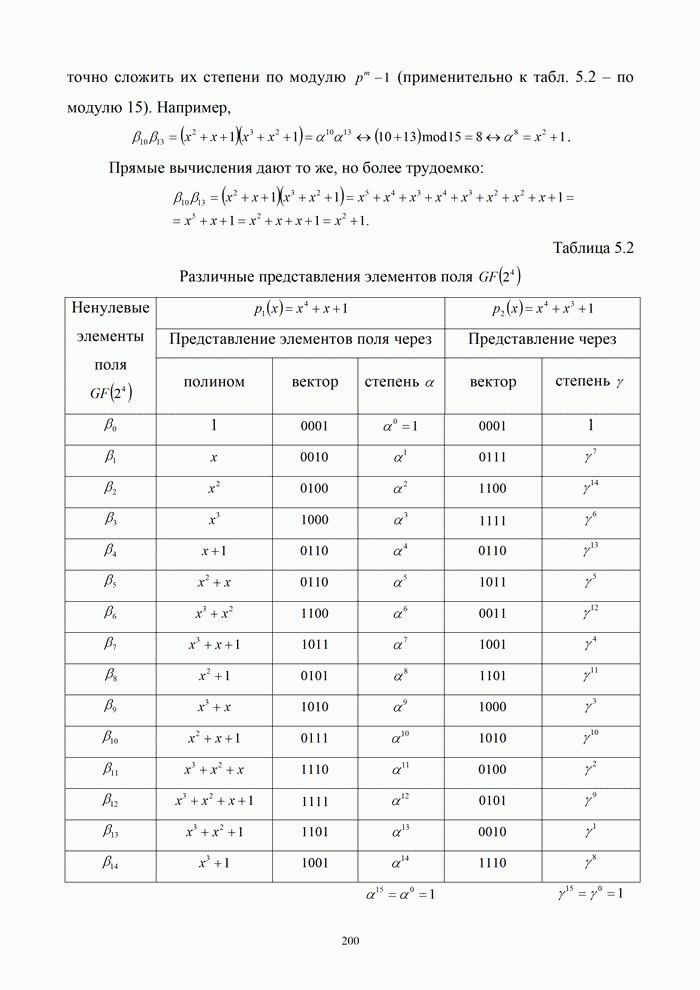
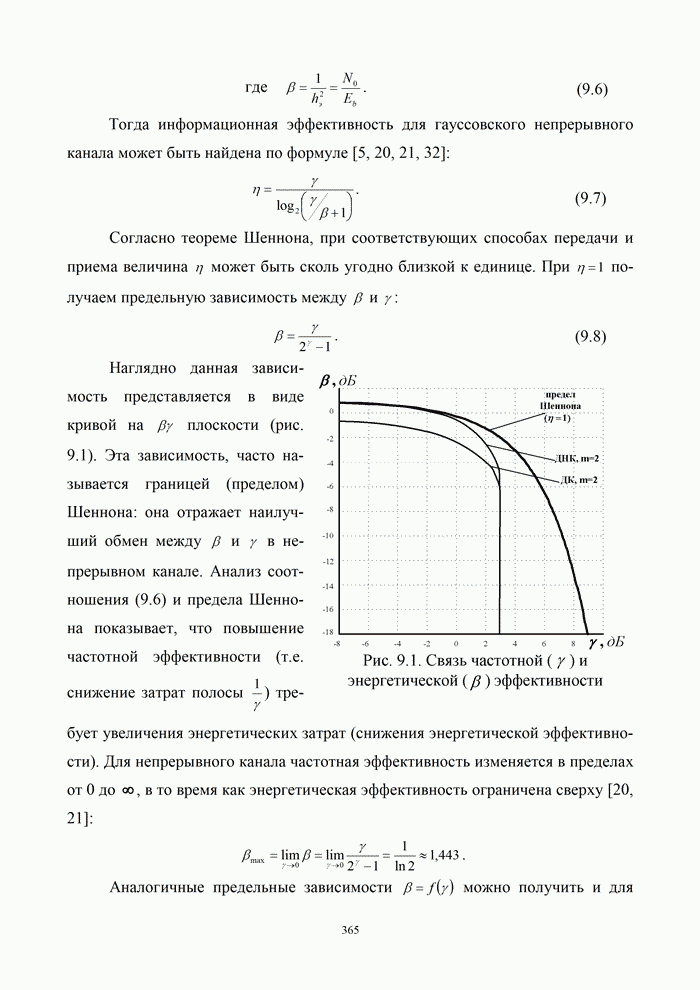
На
рис. 9.1 приведены предельные кривые ![]() для симметричных
двоичных дискретных и дискретно-непрерывных каналов.
При этом выходом ДНК считается согласованный фильтр в
оптимальной схеме приема дискретных сообщений при примитивном кодировании (
для симметричных
двоичных дискретных и дискретно-непрерывных каналов.
При этом выходом ДНК считается согласованный фильтр в
оптимальной схеме приема дискретных сообщений при примитивном кодировании (![]() ).
).
Для
двухпозиционных систем ![]() предельное значение полосы пропускания
канала равно частоте манипуляции. В этом случае частотная эффективность (предел
Найквиста) будет иметь наибольшее значение, равное
предельное значение полосы пропускания
канала равно частоте манипуляции. В этом случае частотная эффективность (предел
Найквиста) будет иметь наибольшее значение, равное ![]() . Было показано, что в
двоичных симметричных каналах с различными видами модуляции максимум
энергетической эффективности наступает при
. Было показано, что в
двоичных симметричных каналах с различными видами модуляции максимум
энергетической эффективности наступает при ![]() , однако удельная скорость передачи при
этом стремится к нулю. Предельные значения показателей эффективности
достигаются при
, однако удельная скорость передачи при
этом стремится к нулю. Предельные значения показателей эффективности
достигаются при ![]() и
при малой вероятности ошибки. Для определения
и
при малой вероятности ошибки. Для определения ![]() и
и ![]() могут использоваться приближенные
формулы:
могут использоваться приближенные
формулы:
|
|
(9.12) |
где ![]() – размерность
сигнала, в
– размерность
сигнала, в ![]() -позиционной
системе. В табл.9.1 приведены значения
-позиционной
системе. В табл.9.1 приведены значения ![]() и формулы для приближенных расчетов
и формулы для приближенных расчетов ![]() некоторых ансамблей
сигналов.
некоторых ансамблей
сигналов.
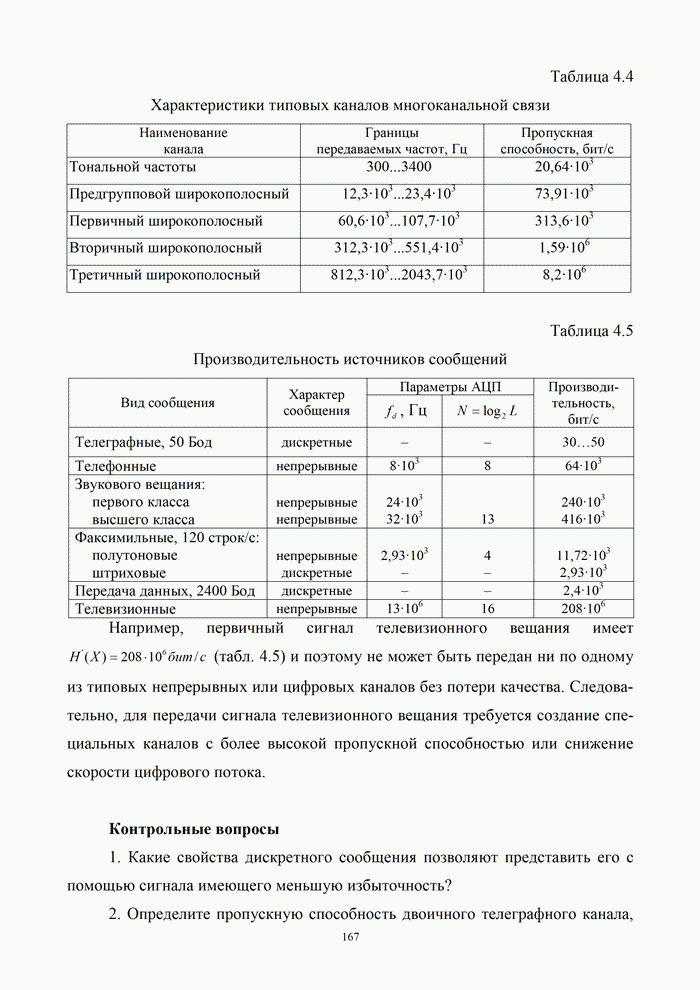
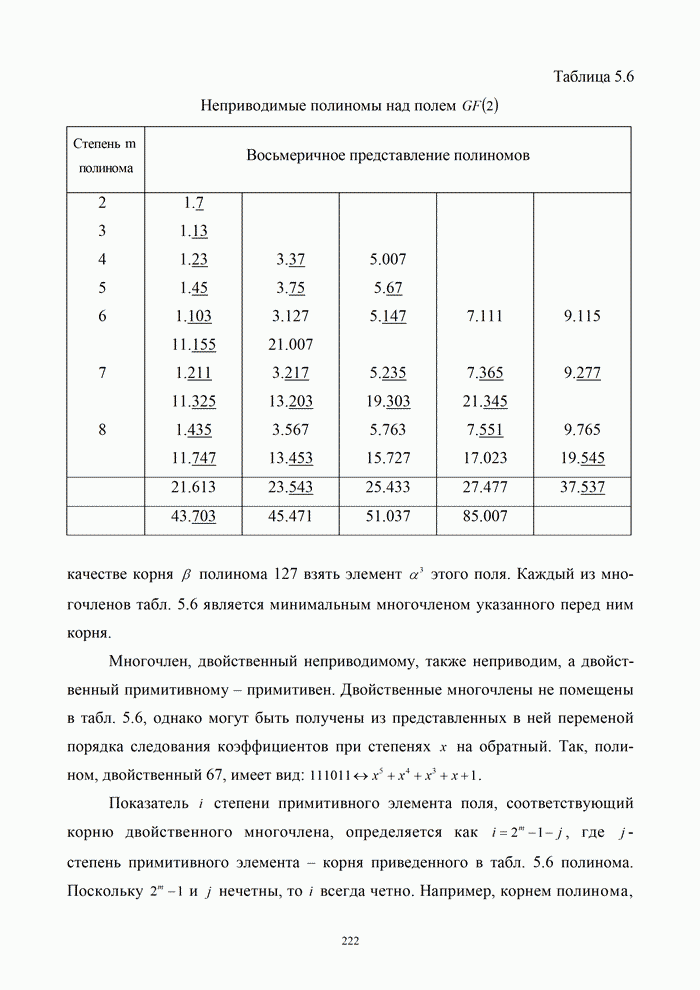
Таблица 9.1. Формулы для приближенных расчетов частотной эффективности некоторых ансамблей сигналов
|
Ансамбль сигналов |
Ортогональный |
Биортогональный |
Симплексный |
|
|
|
|
|
|
|
|
|
|
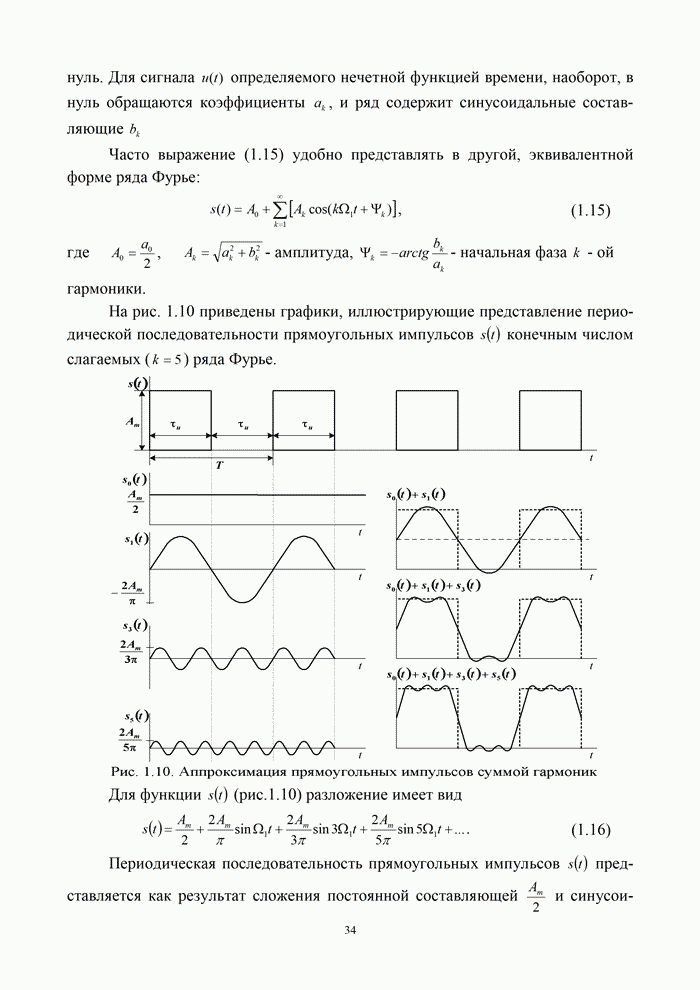
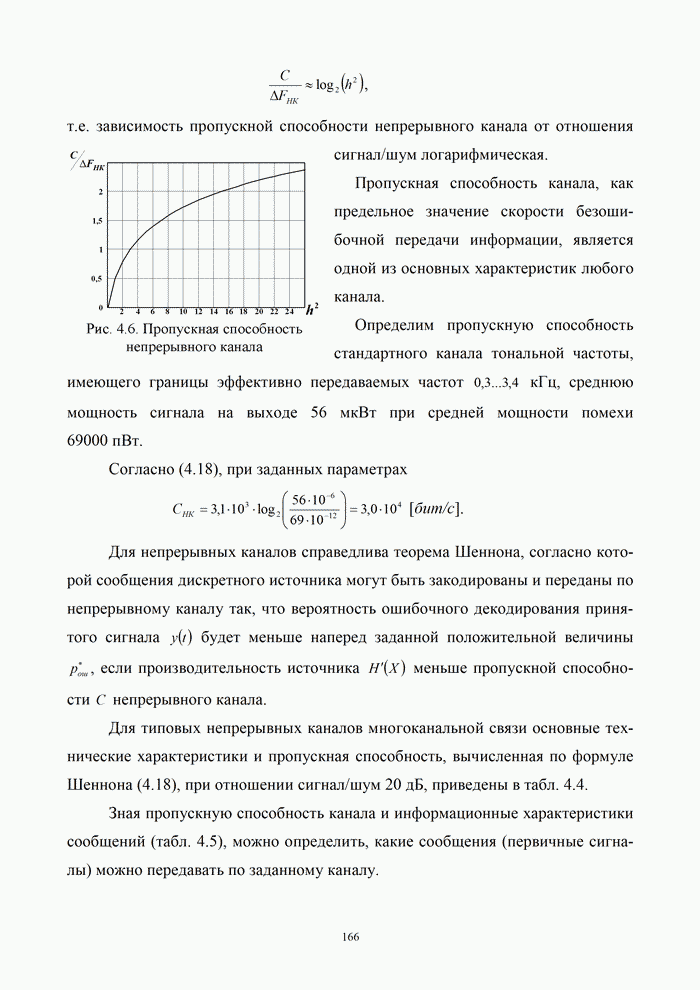
В
реальных системах вероятность ошибки всегда имеет ненулевое значение и ![]() . В этих случаях при заданном
значении
. В этих случаях при заданном
значении ![]() можно
определить отдельно
можно
определить отдельно ![]() и
и ![]() и построить кривые
и построить кривые ![]() .
.
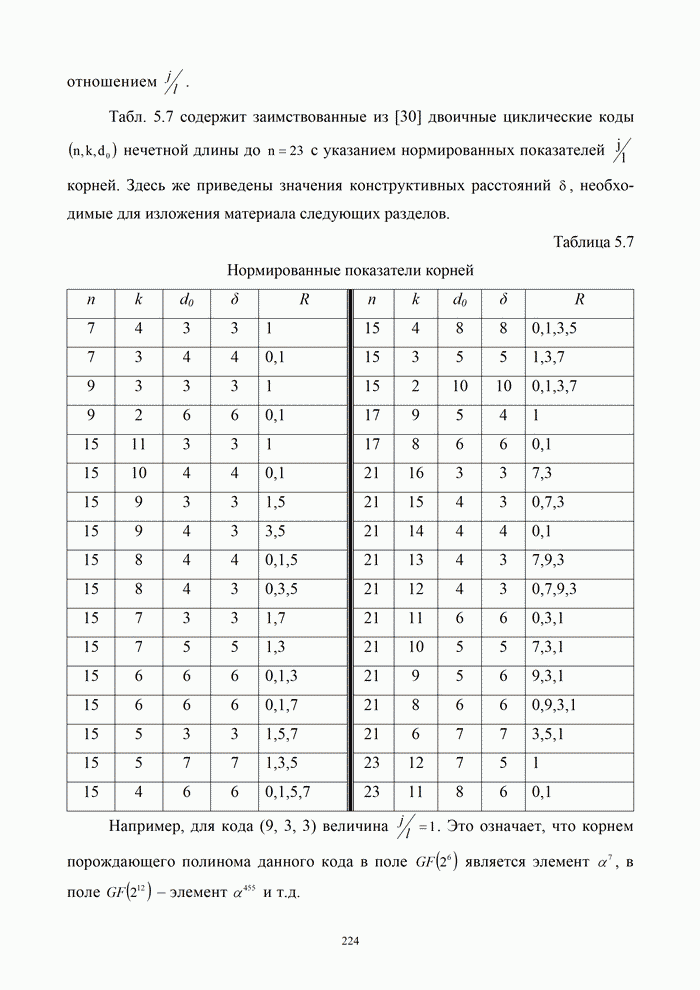
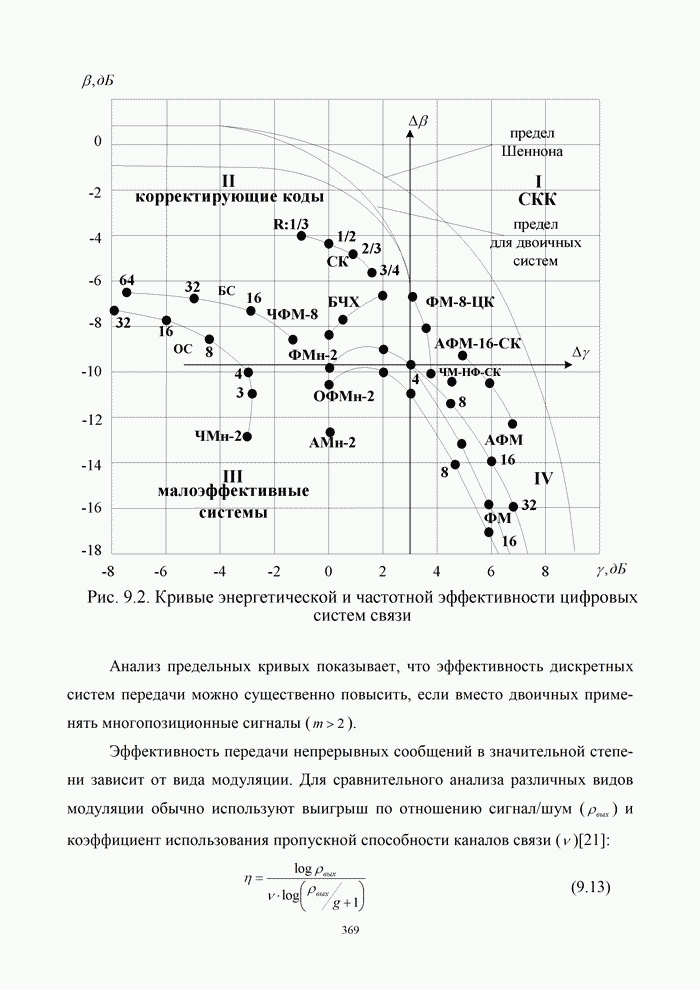
В
координатах ![]() и
и
![]() каждому
варианту реальной системы будет соответствовать точка на плоскости (рис. 9.2) [5, 20, 21, 32]. Все эти точки
располагаются ниже предельной кривой Шеннона и ниже предельной кривой соответствующего
канала. Ход этих кривых зависит от вида модуляции, метода кодирования и способа
обработки сигналов. Около графиков на рис. 9.2 указано число позиций
дискретного сигнала
каждому
варианту реальной системы будет соответствовать точка на плоскости (рис. 9.2) [5, 20, 21, 32]. Все эти точки
располагаются ниже предельной кривой Шеннона и ниже предельной кривой соответствующего
канала. Ход этих кривых зависит от вида модуляции, метода кодирования и способа
обработки сигналов. Около графиков на рис. 9.2 указано число позиций
дискретного сигнала ![]() . Кривые рассчитаны на основании формул оценки
помехоустойчивости различных методов модуляции (раздел 3) для оптимального приема
сигналов при вероятности ошибки на бит
. Кривые рассчитаны на основании формул оценки
помехоустойчивости различных методов модуляции (раздел 3) для оптимального приема
сигналов при вероятности ошибки на бит ![]() . При этом занимаемая полоса частот для ЧМн
. При этом занимаемая полоса частот для ЧМн ![]() , а для ФМн (АМн)
, а для ФМн (АМн)![]() .
.
Анализ
рис. 9.2 показывает, что в системах с ЧМн при увеличении числа позиций ![]() энергетическая эффективность
энергетическая эффективность
![]() увеличивается, а частотная эффективность
увеличивается, а частотная эффективность
![]() уменьшается. В системах с ФМн и ОФМн, наоборот, с увеличением
уменьшается. В системах с ФМн и ОФМн, наоборот, с увеличением ![]() коэффициент
коэффициент ![]() уменьшается, а
уменьшается, а ![]() – увеличивается. Таким образом, условия
обмена
– увеличивается. Таким образом, условия
обмена ![]() на
на ![]() за счет
изменения числа позиций сигналов в системах связи с ЧМн и ФМн различны.
за счет
изменения числа позиций сигналов в системах связи с ЧМн и ФМн различны.
Представленные на рис. 9.2 результаты позволяют определить системы, удовлетворяющие заданным требованиям по энергетической и частотной эффективности, и установить, насколько эти показатели близки к предельным.
После
выбора системы по показателям ![]() и
и ![]() , информационная эффективность вычисляется
с использованием формулы (9.7).
, информационная эффективность вычисляется
с использованием формулы (9.7).
Например,
для сигналов АМн-2 показатель информационной эффективности составляет ![]() , а для ЧМн-2
, а для ЧМн-2 ![]() ; для ФМн-2
; для ФМн-2 ![]() , а для ФМн-4
, а для ФМн-4 ![]() .
.

Анализ
предельных кривых показывает, что эффективность дискретных систем передачи
можно существенно повысить, если вместо двоичных применять многопозиционные сигналы
(![]() ).
).
Эффективность
передачи непрерывных сообщений в значительной степени зависит от вида
модуляции. Для сравнительного анализа различных видов модуляции обычно
используют выигрыш по отношению сигнал/шум (![]() ) и коэффициент использования пропускной
способности каналов связи (
) и коэффициент использования пропускной
способности каналов связи (![]() )[21]:
)[21]:
|
|
(9.13) |
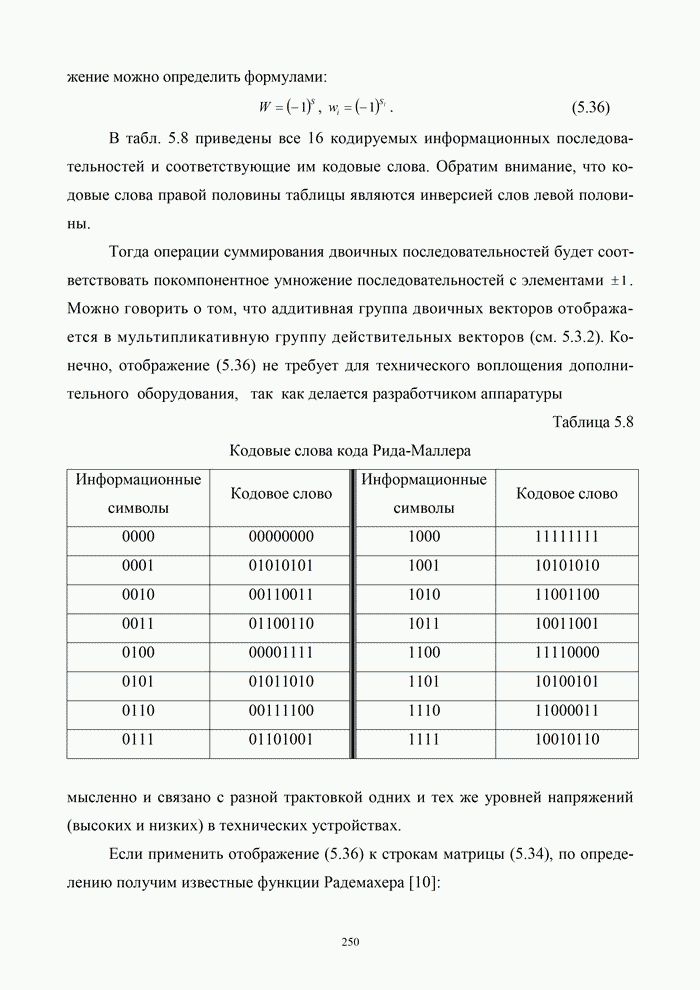
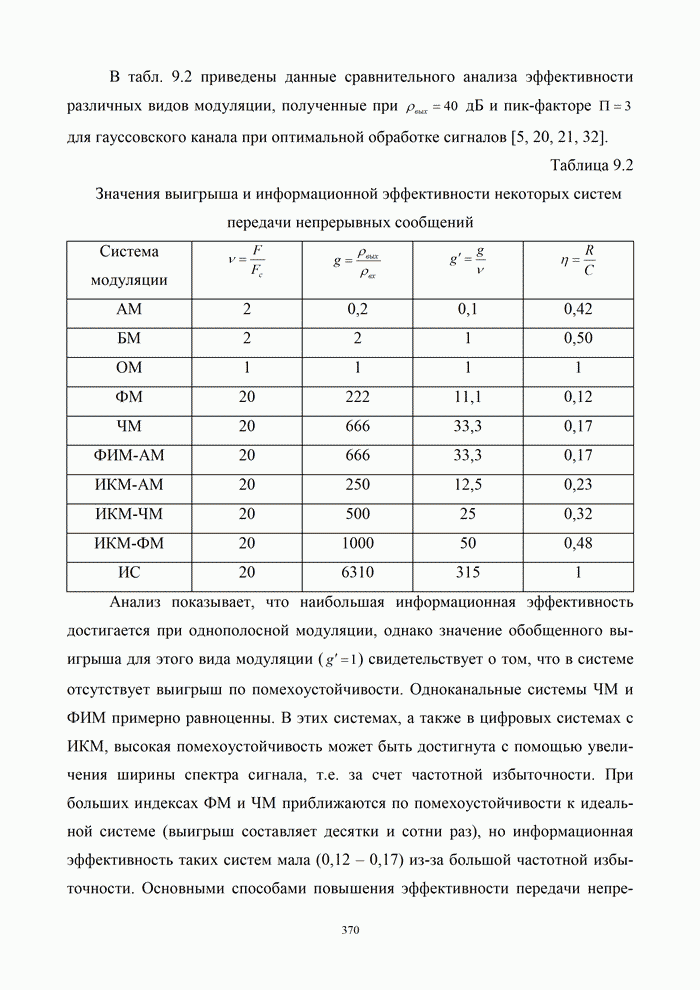
В
табл. 9.2 приведены данные сравнительного анализа эффективности различных видов
модуляции, полученные при ![]() дБ и пик-факторе
дБ и пик-факторе ![]() для гауссовского канала при
оптимальной обработке сигналов [5, 20, 21, 32].
для гауссовского канала при
оптимальной обработке сигналов [5, 20, 21, 32].
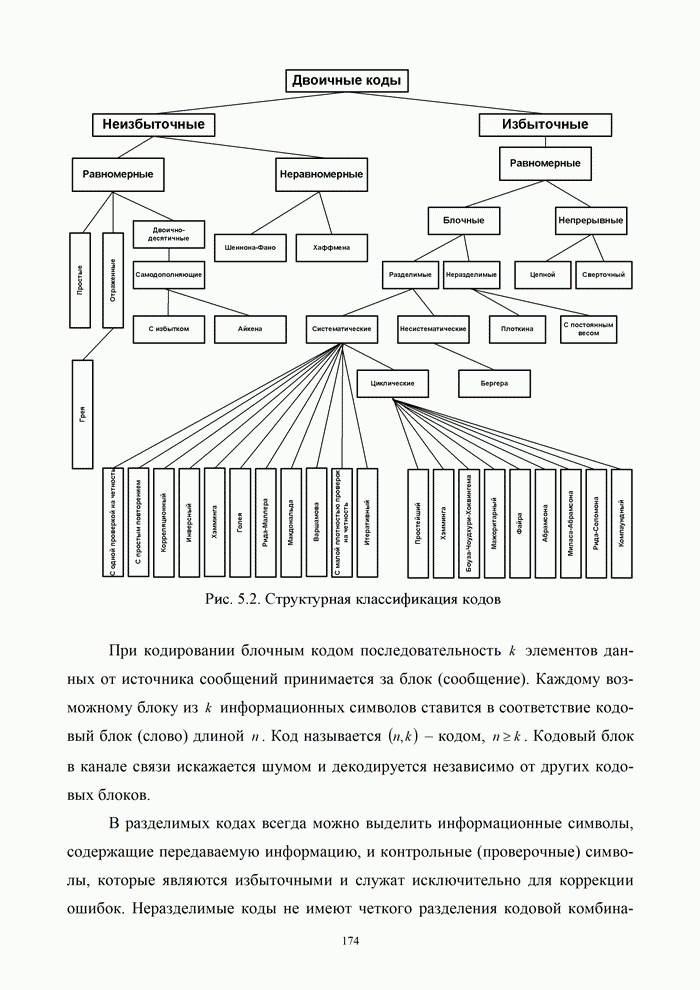
Таблица 9.2. Значения выигрыша и информационной эффективности некоторых систем передачи непрерывных сообщений
|
Система модуляции |
|
|
|
|
|
AM |
2 |
0,2 |
0,1 |
0,42 |
|
БМ |
2 |
2 |
1 |
0,50 |
|
ОМ |
1 |
1 |
1 |
1 |
|
ФМ |
20 |
222 |
11,1 |
0,12 |
|
ЧМ |
20 |
666 |
33,3 |
0,17 |
|
ФИМ-АМ |
20 |
666 |
33,3 |
0,17 |
|
ИКМ-АМ |
20 |
250 |
12,5 |
0,23 |
|
ИКМ-ЧМ |
20 |
500 |
25 |
0,32 |
|
ИКМ-ФМ |
20 |
1000 |
50 |
0,48 |
|
ИС |
20 |
6310 |
315 |
1 |
Анализ
показывает, что наибольшая информационная эффективность достигается при однополосной
модуляции, однако значение обобщенного выигрыша для этого вида модуляции (![]() ) свидетельствует о
том, что в системе отсутствует выигрыш по помехоустойчивости. Одноканальные
системы ЧМ и ФИМ примерно равноценны. В этих системах, а также в цифровых
системах с ИКМ, высокая помехоустойчивость может быть достигнута с помощью увеличения
ширины спектра сигнала, т.е. за счет частотной избыточности. При больших
индексах ФМ и ЧМ приближаются по помехоустойчивости к идеальной системе
(выигрыш составляет десятки и сотни раз), но информационная эффективность таких
систем мала (0,12 – 0,17) из-за большой частотной избыточности. Основными
способами повышения эффективности передачи непрерывных сообщений являются
устранение избыточности, статистическое уплотнение и применение цифровых видов
модуляции.
) свидетельствует о
том, что в системе отсутствует выигрыш по помехоустойчивости. Одноканальные
системы ЧМ и ФИМ примерно равноценны. В этих системах, а также в цифровых
системах с ИКМ, высокая помехоустойчивость может быть достигнута с помощью увеличения
ширины спектра сигнала, т.е. за счет частотной избыточности. При больших
индексах ФМ и ЧМ приближаются по помехоустойчивости к идеальной системе
(выигрыш составляет десятки и сотни раз), но информационная эффективность таких
систем мала (0,12 – 0,17) из-за большой частотной избыточности. Основными
способами повышения эффективности передачи непрерывных сообщений являются
устранение избыточности, статистическое уплотнение и применение цифровых видов
модуляции.
Аналоговые
системы ОМ, AM и узкополосная ЧМ
обеспечивают высокую частотную эффективность при сравнительно низкой
энергетической эффективности. Применение этих систем целесообразно в каналах с
хорошей энергетикой (при больших значениях ![]() ) или в тех случаях, когда требуемое значение
) или в тех случаях, когда требуемое значение ![]() мало. Цифровые системы обеспечивают
высокую
мало. Цифровые системы обеспечивают
высокую ![]() -эффективность при достаточно
хорошей
-эффективность при достаточно
хорошей ![]() -эффективности. В каналах с ограниченной
энергетикой (при малых значениях
-эффективности. В каналах с ограниченной
энергетикой (при малых значениях ![]() ) преимущества цифровых систем особенно
заметны. При высоком качестве передачи, когда требуемые значения
) преимущества цифровых систем особенно
заметны. При высоком качестве передачи, когда требуемые значения ![]() велики,
широкополосная ЧМ и цифровые системы обеспечивают примерно одинаковую эффективность.
велики,
широкополосная ЧМ и цифровые системы обеспечивают примерно одинаковую эффективность.
В многоканальных системах эффективность связи снижается за счет несовершенства системы разделения сигналов.
Расчеты
показывают, что наиболее эффективным является метод временного разделения каналов;
менее эффективен метод частотного разделения. При временном разделении пропускная
способность не зависит от числа каналов, т.к. в каждый момент времени передается
только один сигнал. При ЧРК пропускная способность канала с ограниченной
средней мощностью сигнала также не зависит от числа каналов. При разделении по
форме между ![]() парциальными
каналами делится только мощность, полоса частот и время передачи используются
одновременно всеми сигналами. В этом случае информационная эффективность уменьшается с увеличением
парциальными
каналами делится только мощность, полоса частот и время передачи используются
одновременно всеми сигналами. В этом случае информационная эффективность уменьшается с увеличением ![]() , причем амплитудное ограничение сигнала
слабо влияет на эту зависимость.
, причем амплитудное ограничение сигнала
слабо влияет на эту зависимость.
Показатели частотной, энергетической и информационной эффективности для систем с множественным доступом определяются на основании суммарной скорости передачи СЭС, зависящей от методов формирования и обработки информационных сигналов в парциальных каналах и методов доступа.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Список сокращений
- Основные обозначения
- ВВЕДЕНИЕ
- Глава 1. Сообщения, сигналы и помехи, их математические модели
- 1.1. Основные понятия и определения
- 1.1.1. Сообщение, сигнал, модуляция
- 1.1.2. Основные параметры сигналов
- 1.2. Системы связи. Каналы связи
- 1.2.1. Структура канала электросвязи
- 1.2.2. Линия и сеть связи
- 1.2.3. Помехи и искажения в канале
- 1.2.4. Эталонная модель взаимодействия открытых систем
- 1.2.5. Модели каналов связи и их математическое описание
- 1.3. Способы описания сигналов и помех
- 1.3.1. Сигнал и его математическая модель
- 1.3.2. Энергетические характеристики детерминированного сигнала
- 1.4.2. Представление сигналов и помех рядом Фурье
- 1.4.3. Применение преобразования Фурье для непериодических сигналов
- 1.5. Теорема Котельникова
- 1.6. Пространство сигналов
- 1.6.1. Линейное пространство
- 1.6.2. Представление сигнала в многомерном пространстве
- 1.7. Сигналы как случайные процессы
- 1.7.1. Характеристики случайного процесса
- 1.7.2. Флуктуационный шум
- 1.8. Комплексное представление сигналов и помех
- 1.8.1. Понятие аналитического сигнала
- 1.8.2. Огибающая, мгновенная фаза и мгновенная частота узкополосного случайного процесса
- Контрольные вопросы
- Глава 2. Методы формирования и преобразования сигналов
- 2.1. Модуляция сигналов
- 2.1.1. Амплитудная модуляция гармонической несущей
- 2.1.2. Балансная и однополосная модуляция гармонической несущей
- 2.2. Методы угловой модуляции
- 2.2.1. Принципы частотной и фазовой (угловой) модуляции
- 2.2.2. Спектр сигналов угловой модуляции
- 2.3. Формирование и детектирование модулированных сигналов
- 2.3.1. Формирование и детектирование сигналов амплитудной и однополосной амплитудной модуляции
- 2.3.2. Формирование и детектирование сигналов угловой модуляции
- 2.4. Манипуляция сигналов
- 2.4.1. Временные и спектральные характеристики амплитудно-манипулированных сигналов
- 2.4.2. Временные и спектральные характеристики частотно-манипулированных сигналов
- 2.4.3. Фазовая (относительно-фазовая) манипуляция сигналов
- 2.5. Системы связи с многопозиционной относительной фазовой манипуляцией
- 2.5.1. Принцип формирования сигнала с многократной относительной фазовой манипуляцией
- 2.5.2. Квадратурная относительно-фазовая манипуляция (КОФМ)
- 2.5.3. Принцип частотной модуляции с непрерывной фазой
- Контрольные вопросы
- Глава 3. Помехоустойчивость приема дискретных сообщений
- 3.1. Критерии качества и правила приема дискретных сообщений
- 3.1.1. Понятие о помехоустойчивости систем электрической связи
- 3.1.2. Задача оптимального приема
- 3.1.3. Вычисление вероятностей ошибок
- 3.2. Оптимальная демодуляция при когерентном приеме сигналов
- 3.2.1. Оптимальные алгоритмы приема при полностью известных сигналах
- 3.2.2. Реализация алгоритмов оптимального когерентного приема
- 3.3. Помехоустойчивость приема сигналов с известными параметрами
- 3.4. Прием сигналов с неопределенной фазой
- 3.4.1. Оптимальный некогерентный прием дискретных сигналов
- 3.4.2. Помехоустойчивость оптимального некогерентного приема
- 3.5. Подоптимальные методы приема
- 3.5.1. Причины применения неоптимальных методов приема
- 3.5.2. Квазиоптимальные методы приема
- Контрольные вопросы
- Глава 4. Теория передачи информации
- 4.1. Информационные характеристики источника сообщений
- 4.1.1. Количественное определение информации
- 4.1.2. Энтропия и производительность дискретного источника сообщений
- 4.2. Пропускная способность дискретного канала
- 4.2.1. Количество информации переданной по дискретному каналу
- 4.2.2. Пропускная способность дискретного канала
- 4.2.3. Пропускная способность симметричного дискретного канала без памяти
- 4.3. Методы сжатия дискретных сообщений
- 4.3.1. Условия существования оптимального неравномерного кода
- 4.3.2. Прямая и обратная теоремы кодирования источника неравномерными кодами
- 4.3.3. Показатели эффективности сжатия
- 4.3.4. Кодирование источника дискретных сообщений методом Шеннона-Фано
- 4.3.5. Кодирование источника дискретных сообщений методом Хаффмена
- 4.4. Пропускная способность непрерывного канала
- 4.4.1. Постановка задачи передачи дискретных сообщений в непрерывном канале
- 4.4.2. Количество информации, переданной по непрерывному каналу
- 4.4.3. Пропускная способность непрерывного канала
- Контрольные вопросы
- Глава 5. Теория кодирования сообщений
- 5.1. Помехоустойчивое кодирование: блочные и непрерывные коды
- 5.1.1. Постановка задачи помехоустойчивого кодирования
- 5.1.2. Классификация кодов
- 5.1.3. Основные характеристики и свойства блочных кодов
- 5.2. Эффективность помехоустойчивого кодирования
- 5.2.1. Эффективность кода в режиме исправления ошибок
- 5.2.2. Эффективность кода в режиме обнаружения ошибок
- 5.2.3. Эффективность помехоустойчивых кодов
- 5.3. Математические основы теории помехоустойчивого кодирования
- 5.3.1. Краткие сведения из теории чисел
- 5.3.2. Группы
- 5.3.3. Кольца и поля
- 5.3.4. Векторное пространство
- 5.3.5. Конечные поля
- 5.4. Линейные блочные коды
- 5.4.1. Система передачи дискретных сообщений
- 5.4.2. Параметры линейного кода
- 5.4.3. Полиномиальные циклические коды
- 5.4.4. Циклические коды и корни полиномов
- 5.4.5. Спектральное описание циклических кодов
- 5.4.6. Простейшие блочные линейные коды
- 5.5. Коды Боуза-Чоудхури-Хоквингема
- 5.5.1. Методы задания кодов БЧХ
- 5.5.2. Принципы декодирования кодов БЧХ
- 5.5.3. Методы реализации этапов декодирования кодов БЧХ
- 5.6. Коды Рида-Соломона
- 5.6.1. Основные определения
- 5.6.2. Обнаружение и исправление пакетов ошибок
- 5.7. Коды Рида-Маллера
- 5.7.1. Задание и декодирование кодов Рида-Маллера
- 5.7.2. Симплексные коды и m-последовательности
- 5.7.3. Связь между блочными кодами
- 5.8. Сверточные коды
- 5.8.1. Основные параметры
- 5.8.2. Способы задания сверточного кода
- 5.8.3. Алгоритм декодирования Витерби
- 5.9. Помехоустойчивость систем передачи дискретных сообщений
- 5.9.1. Две процедуры приема сигналов
- 5.9.2. Помехоустойчивость систем передачи информации при оптимальной процедуре приема
- 5.9.3. Помехоустойчивость систем передачи информации при посимвольном приеме сигналов
- Контрольные вопросы
- Глава 6. Сигналы с импульсной модуляцией
- 6.1. Методы импульсной модуляции
- 6.1.1. Импульсные методы передачи непрерывных сигналов
- 6.1.2. Спектральные характеристики импульсных методов модуляции
- 6.2. Помехоустойчивость непрерывных каналов связи с импульсной модуляцией
- 6.2.1. Помехоустойчивость систем передачи с импульсными методами модуляции
- 6.3. Цифровые методы передачи непрерывных сообщений
- 6.3.1. Передача сигналов с импульсно-кодовой модуляцией
- 6.3.2. Передача сигналов с дельта модуляцией
- 6.3.3. Квантование сигналов в системах с ИКМ и ДМ
- Контрольные вопросы
- Глава 7. Методы приема сигналов в сложных условиях
- 7.1. Прием сигналов в каналах с замираниями
- 7.1.1. Сущность замираний и их классификация
- 7.1.2. Принципы разнесенного приема сигналов
- 7.2. Методы борьбы с замираниями сигналов
- 7.2.1. Методы борьбы с замираниями в аналоговых системах связи
- 7.2.2. Методы борьбы с замираниями в цифровых системах связи
- 7.3. Методы борьбы с межсимвольной интерференцией
- 7.3.1. Причины возникновения и сущность межсимвольной интерференции
- 7.3.2. Обработка сигналов в каналах с межсимвольной интерференцией
- 7.3.3. Помехоустойчивость в каналах с межсимвольной интерференцией
- 7.4. Прием дискретных сообщений в каналах с сосредоточенными по спектру и импульсными помехами
- 7.4.1. Общая характеристика сосредоточенных по спектру и импульсных помех
- 7.4.2. Борьба с сосредоточенными и импульсными помехами
- 7.5. Компенсация помех и искажений в канале
- 7.5.1. Принцип работы радиолинии с ФМ ПСС (ФМ ШПС)
- 7.5.2. Помехоустойчивость радиолинии с ФМ ПСС
- 7.5.3. Принципы работы радиолиний с ППРЧ
- 7.5.4. Помехоустойчивость радиолиний с ППРЧ
- Контрольные вопросы
- Глава 8. Многоканальная связь и распределение информации
- 8.1. Методы распределения ресурса общего канала
- 8.1.1. Классификация систем передачи информации, использующих единый ресурс
- 8.1.2. Постановка задачи объединения и разделения сигналов
- 8.1.3. Энергетическая и спектральная цена уплотнения
- 8.2. Частотное разделение каналов
- 8.2.1. Принцип частотного объединения и разделения каналов
- 8.2.2. Групповой сигнал, его структура и характеристики
- 8.3. Временное разделение каналов
- 8.3.1. Принцип временного разделения каналов
- 8.3.2. Характеристики группового сигнала систем с ВРК
- 8.4. Разделение сигналов по форме
- Контрольные вопросы
- Глава 9. Эффективность систем связи
- 9.1. Оценка эффективности систем связи
- 9.1.1. Подходы к оценке эффективности
- 9.1.2. Критерии эффективности
- 9.1.3. Эффективность аналоговых и цифровых систем
- 9.2. Выбор сигналов и помехоустойчивых кодов
- 9.2.1. Многопозиционные сигналы
- 9.2.2. Корректирующие коды
- 9.3. Оптимизация систем связи
- 9.3.1. Согласование методов модуляции и кодирования
- 9.3.2. Классификация сигнально – кодовых конструкций
- 9.4. Характеристики основных типов СКК
- 9.4.1. Согласование канала кодом Грея
- 9.4.2. Согласование на основе разбиения ансамбля на вложенные подансамбли
- 9.5. Алгоритмы цифровой обработки сигналов
- 9.5.1. Дискретные сигналы и их спектры
- 9.5.2. Алгоритмы дискретного и быстрого преобразований Фурье
- Контрольные вопросы
- Глава 10. Теоретико-информационные основы криптозащиты сообщений в телекоммуникационных системах
- 10.1. Классификация криптографических систем
- 10.1.2. Классификация криптографических систем защиты информации
- 10.1.3. Оценка стойкости криптосистем
- 10.2. Функции, используемые в криптографических системах
- 10.2.1. Общее описание функций, используемых в криптографических системах
- 10.2.2. Однонаправленные функции
- 10.2.3. Криптографические хэш-функции
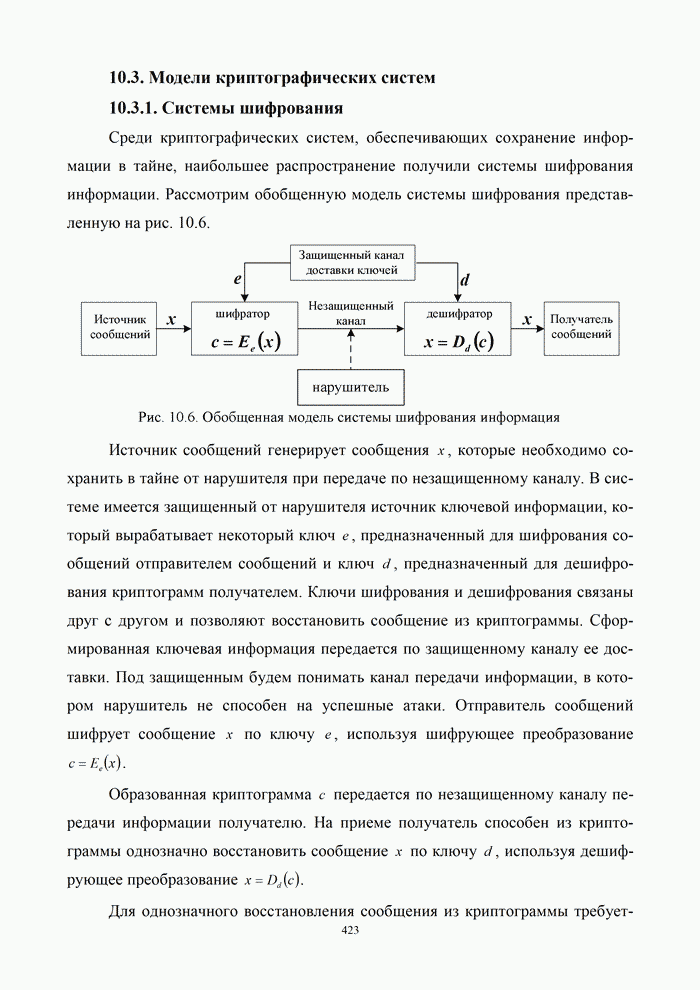
- 10.3. Модели криптографических систем
- 10.3.1. Системы шифрования
- 10.3.2. Традиционные симметричные криптосистемы
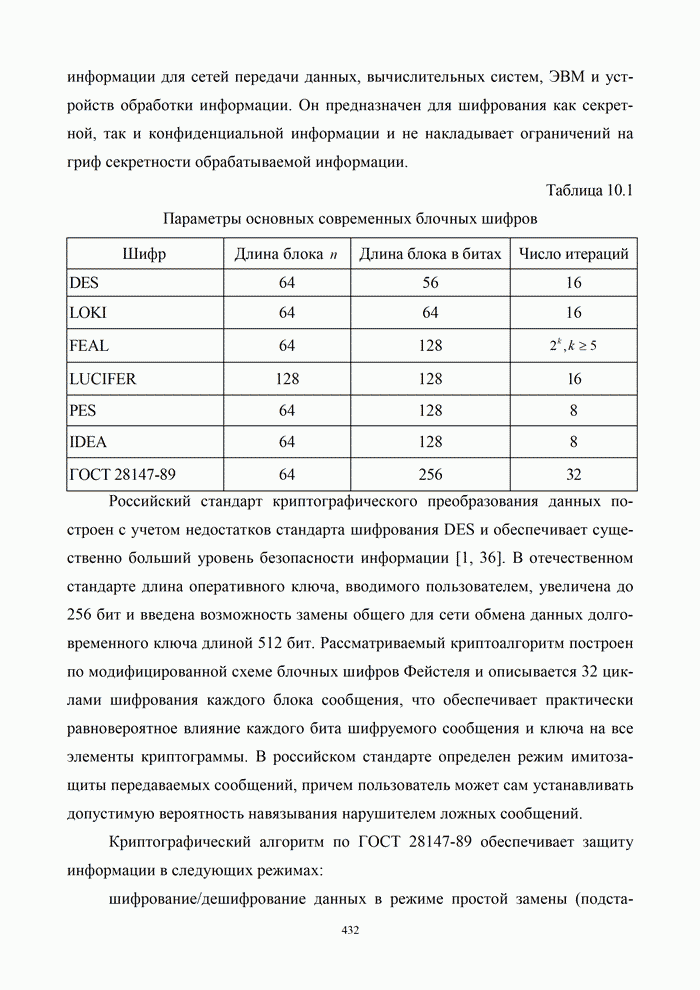
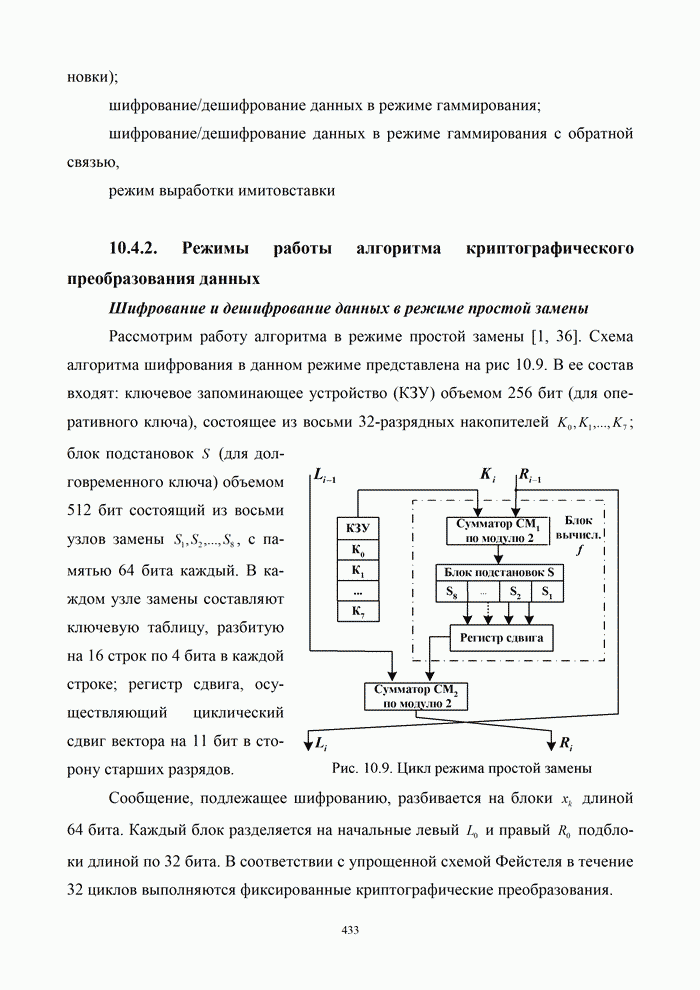
- 10.4. Алгоритмы криптографической защиты
- 10.4.1. Алгоритм криптографической защиты информации согласно ГОСТ 28147-89
- Контрольные вопросы
- Заключение
- Список литературы








































































































































































































































































































































































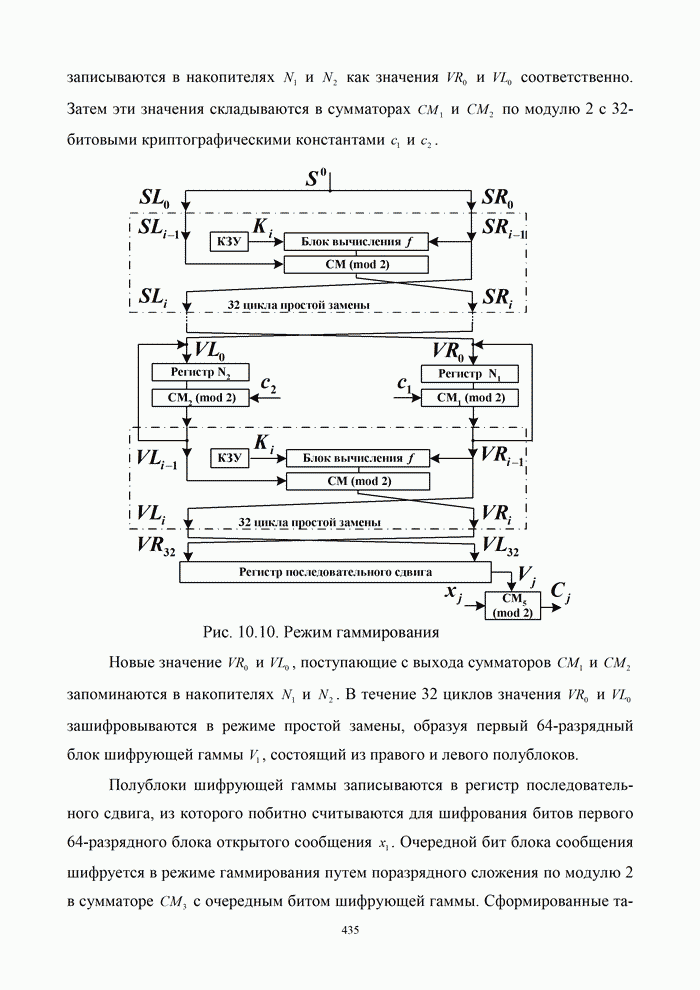











 ,
,
 ;
;

