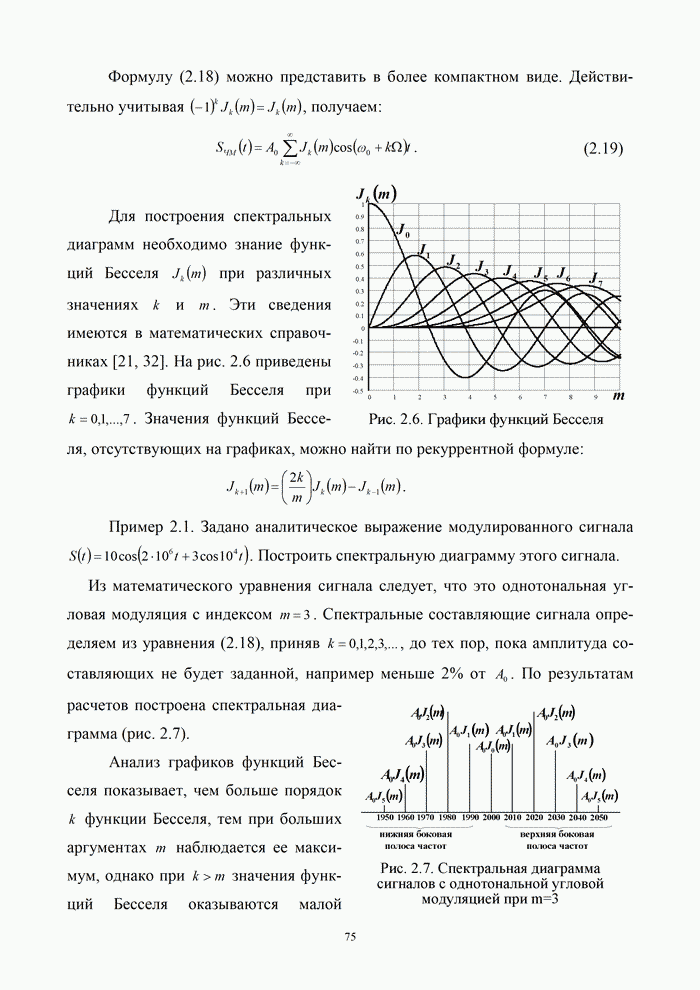
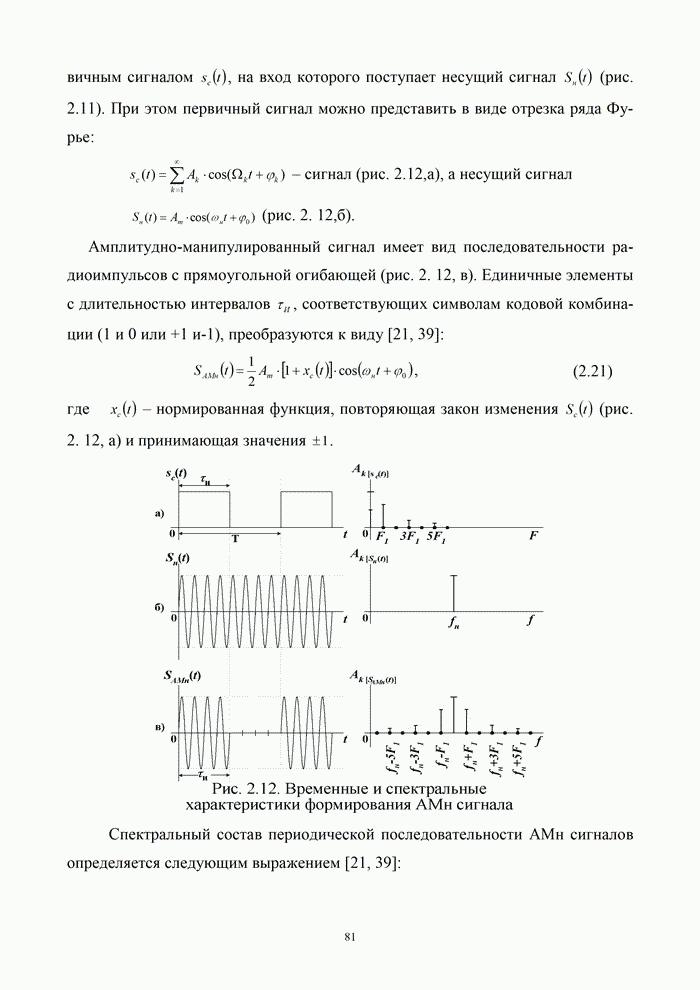
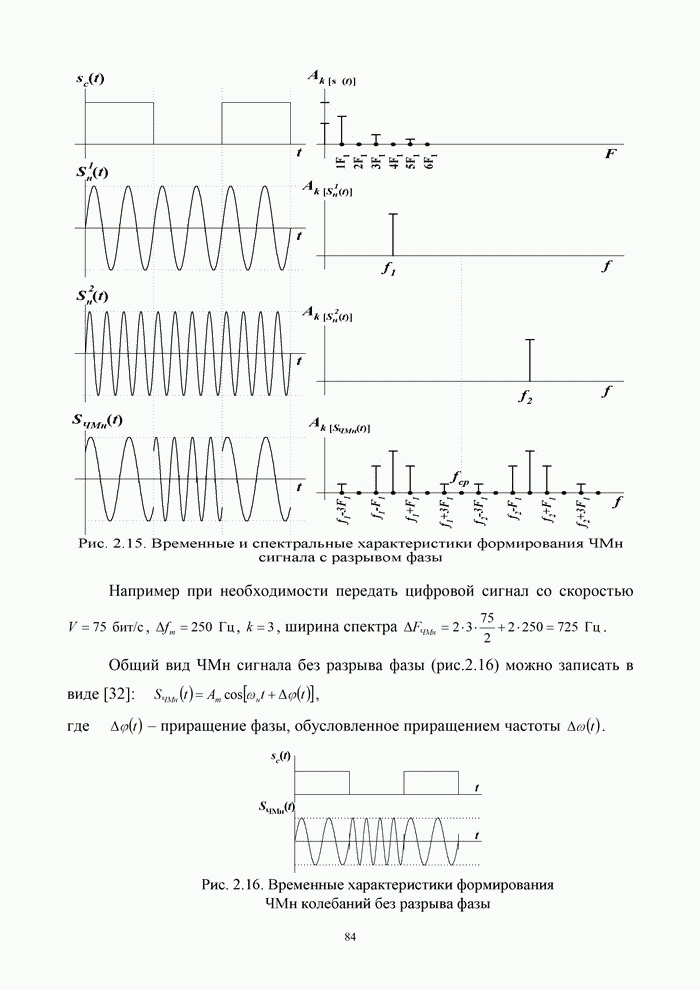
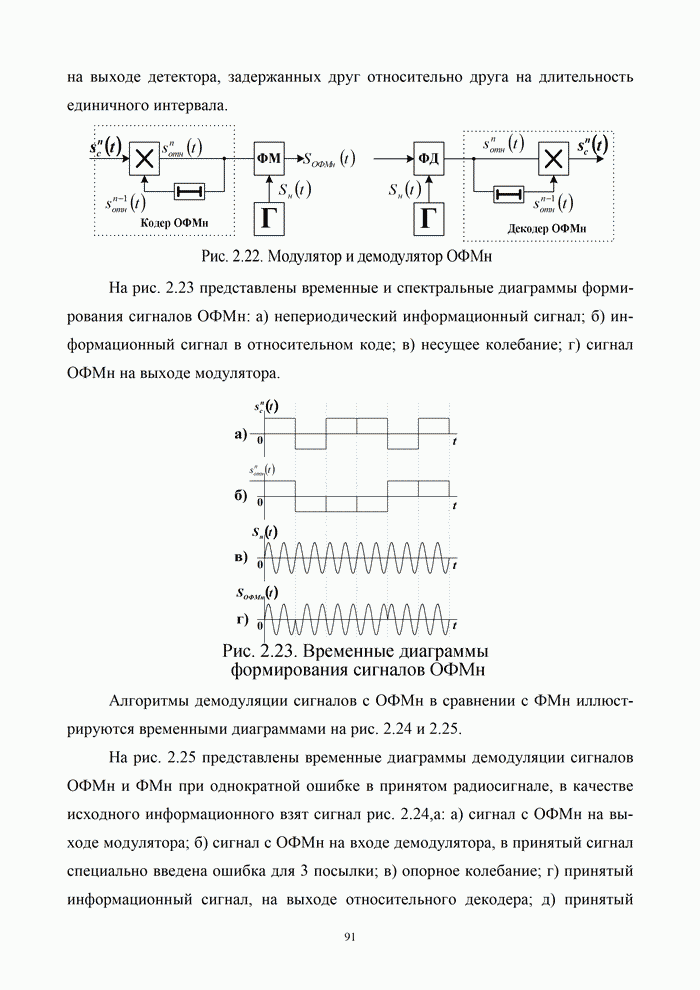
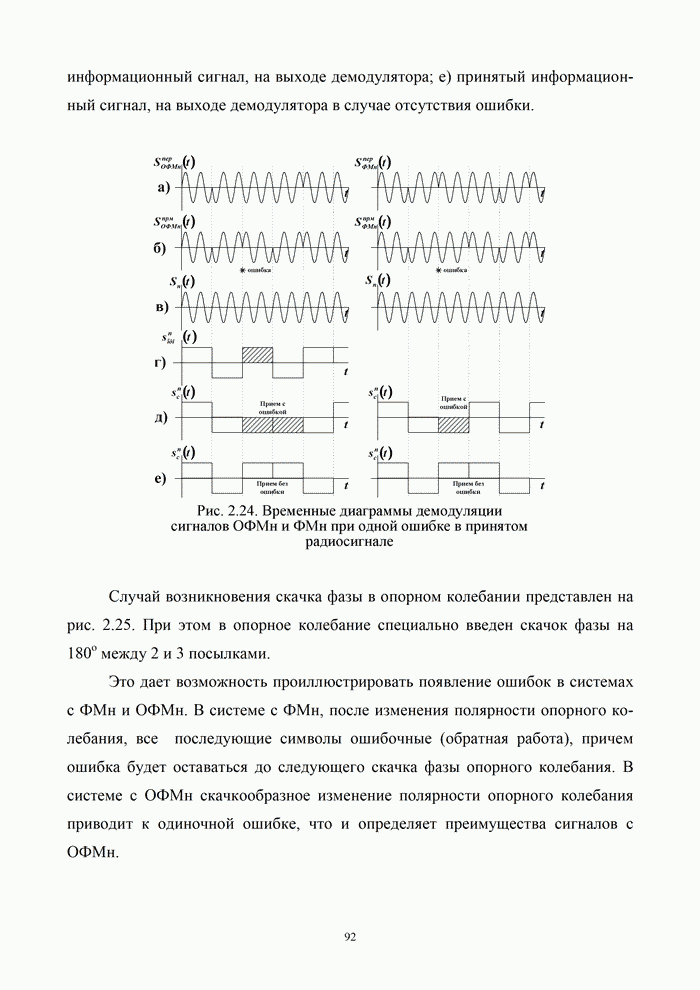
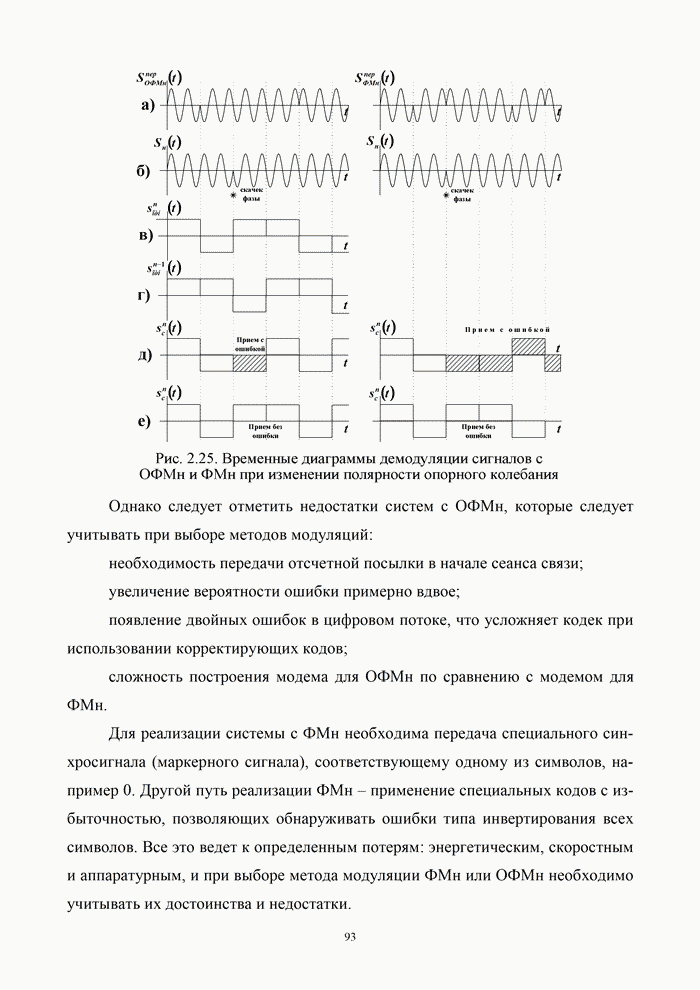
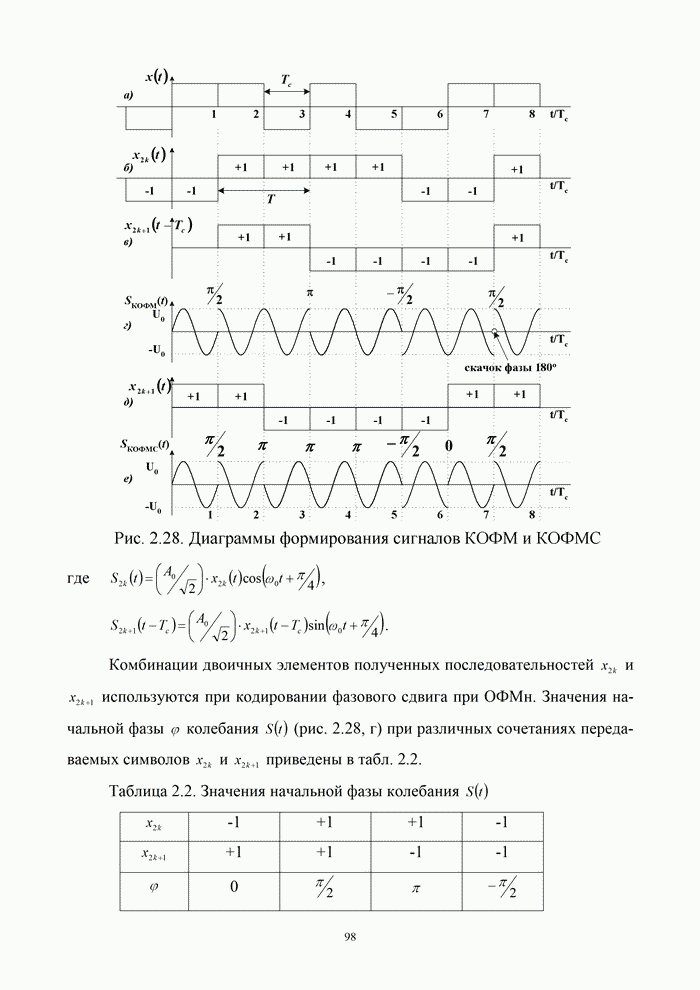
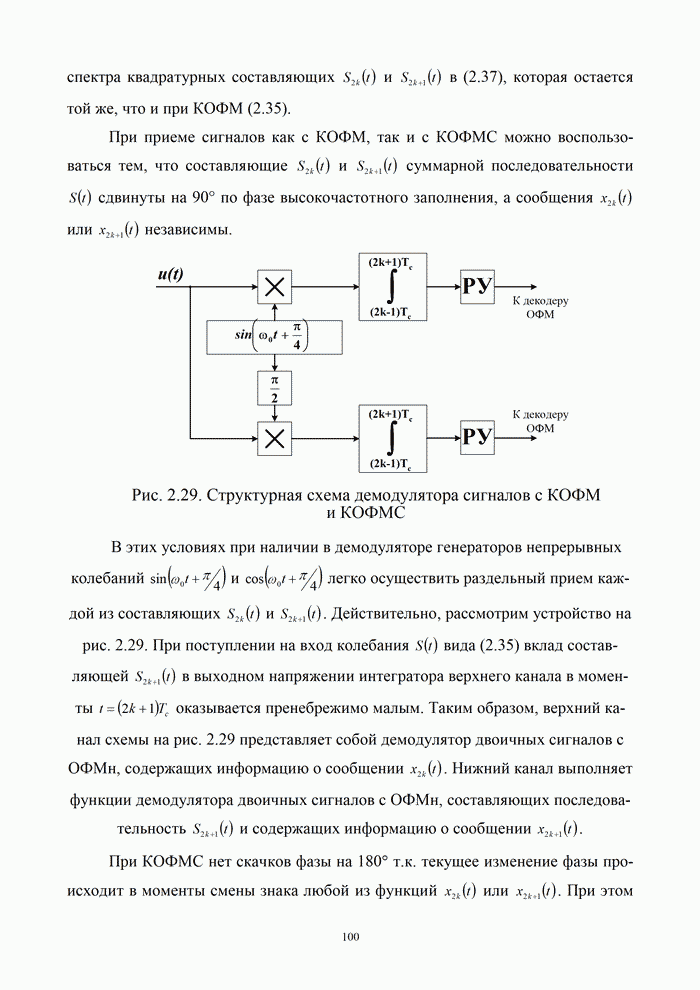
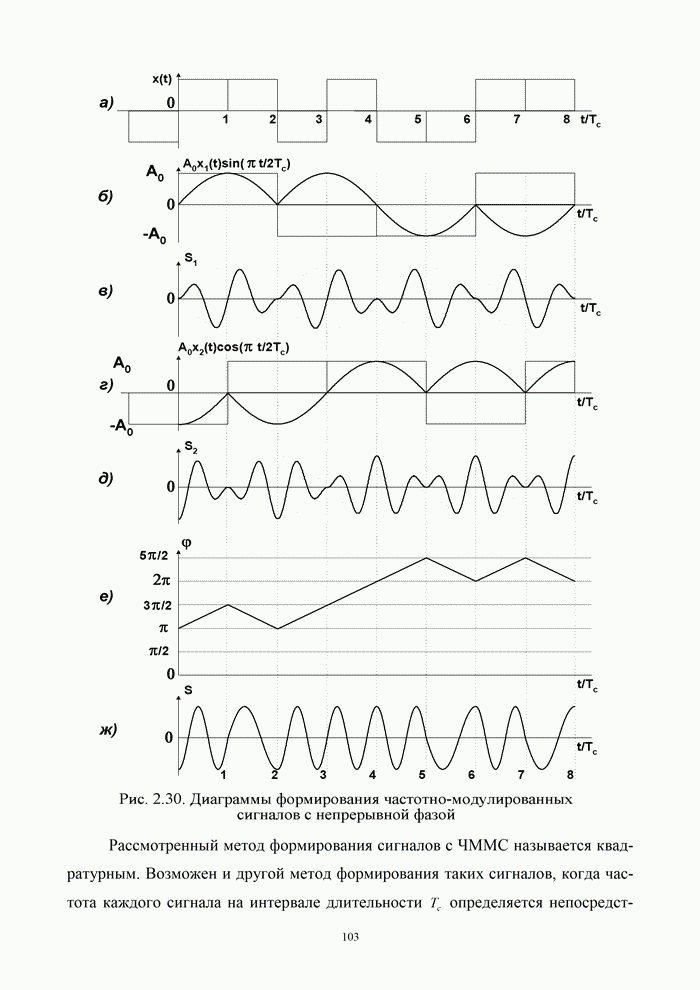
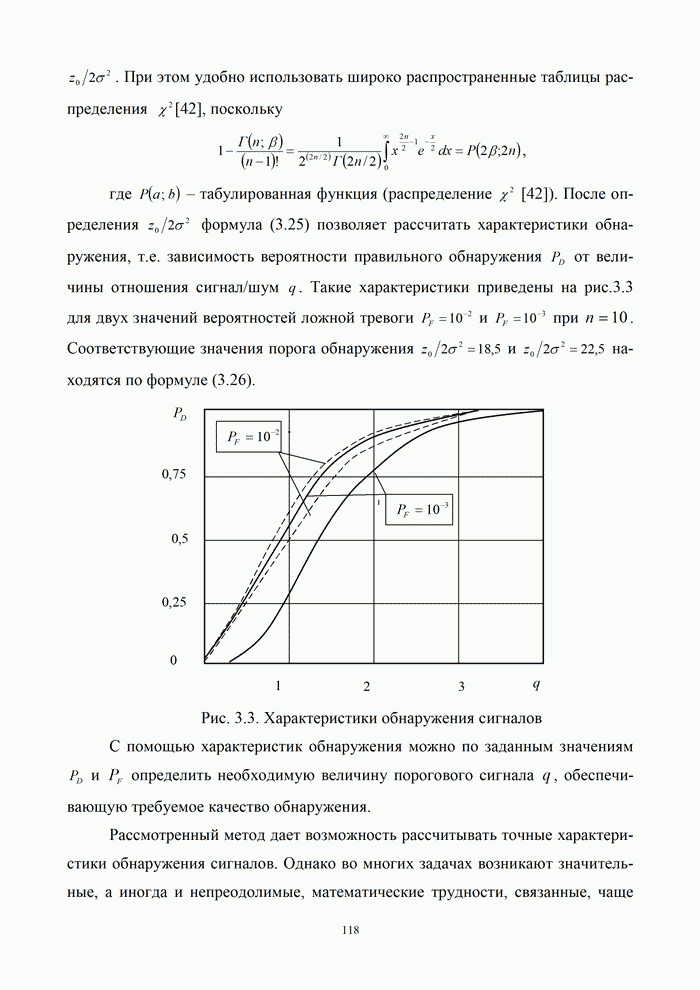
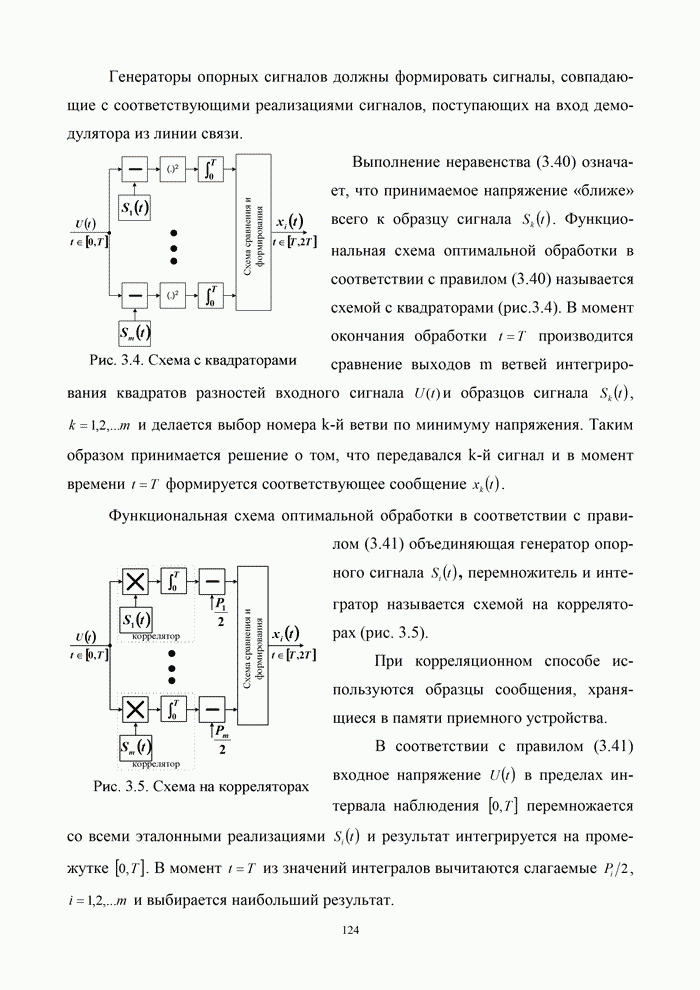
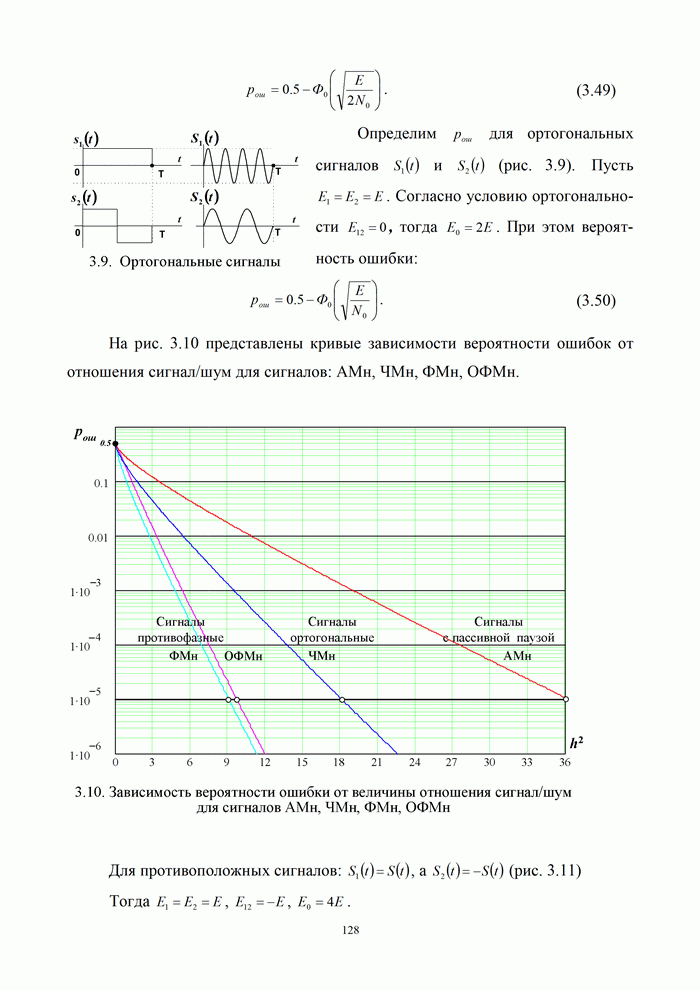
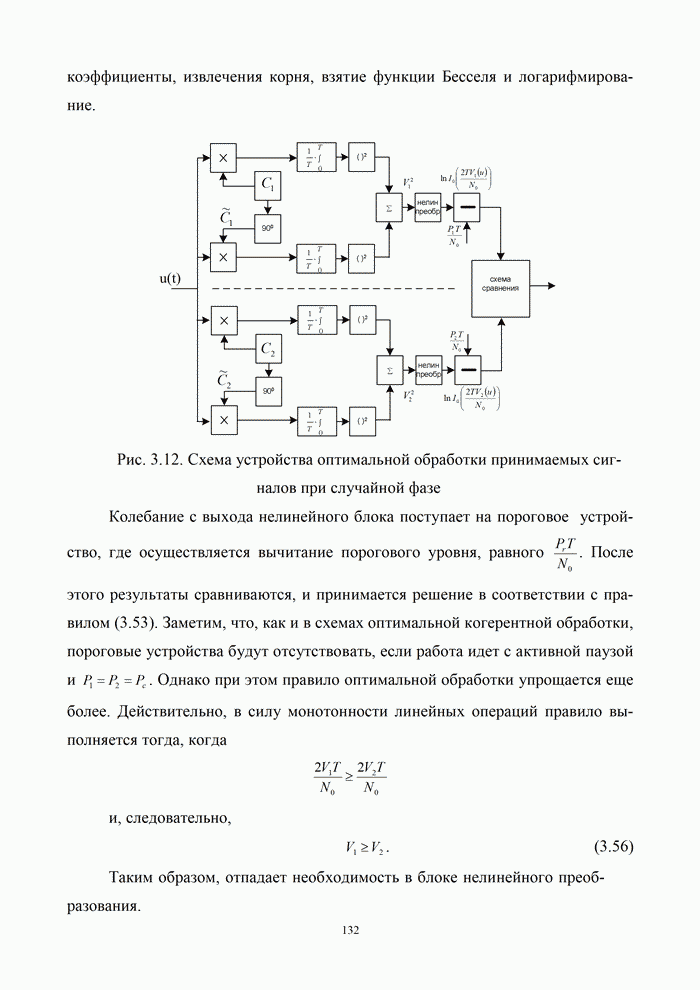
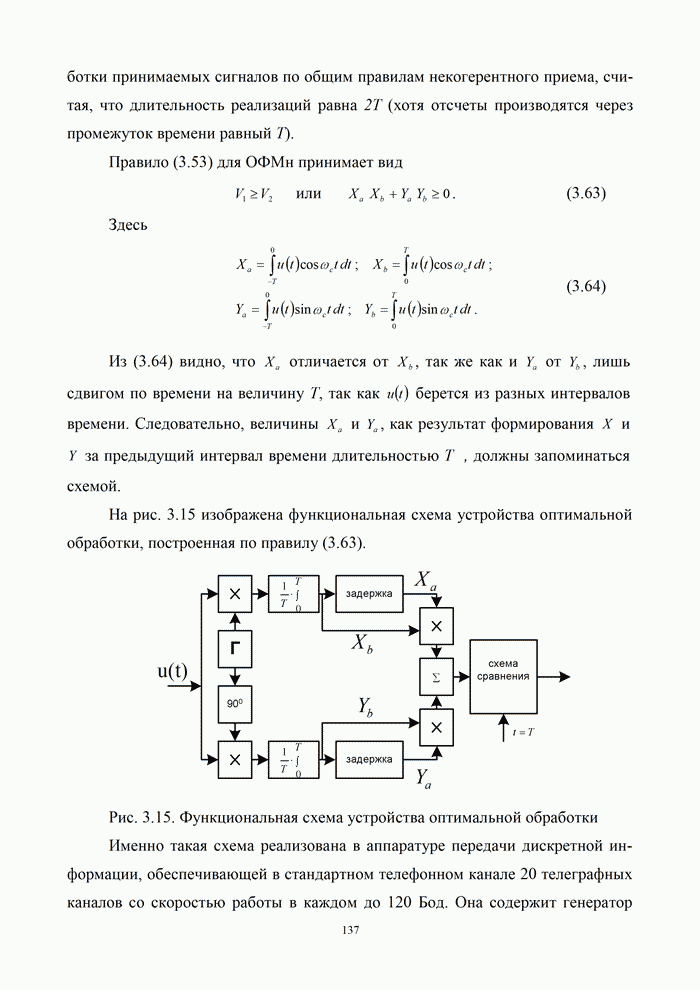
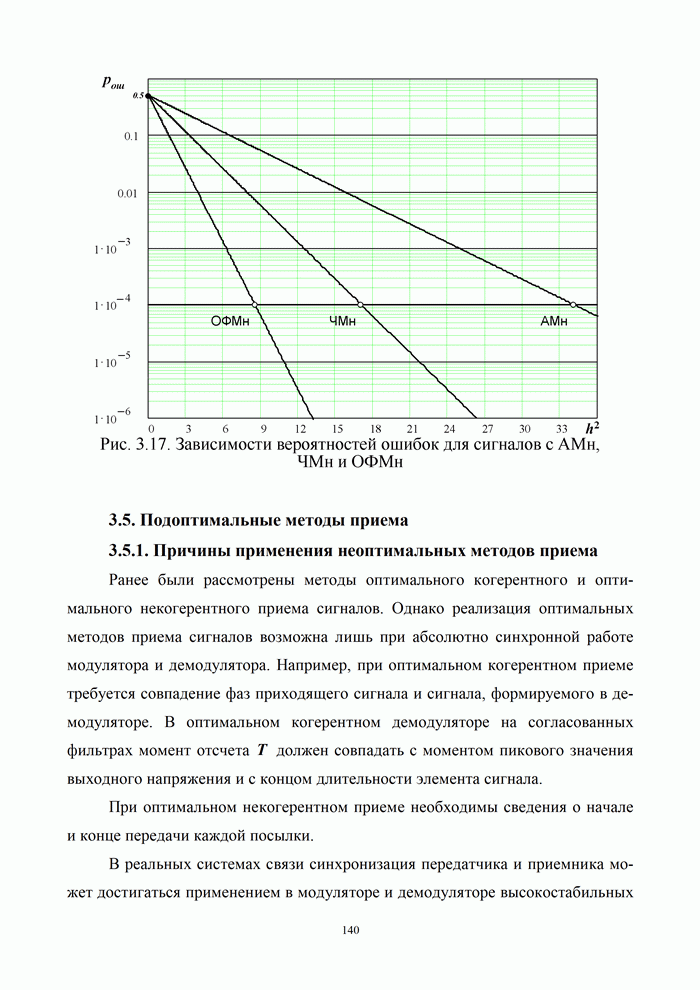
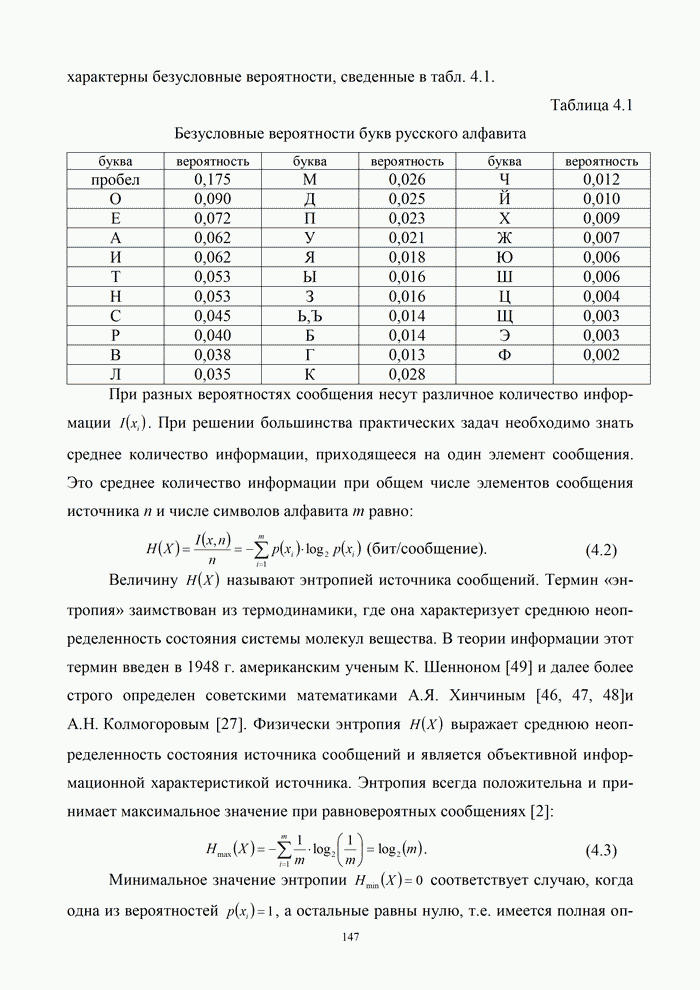
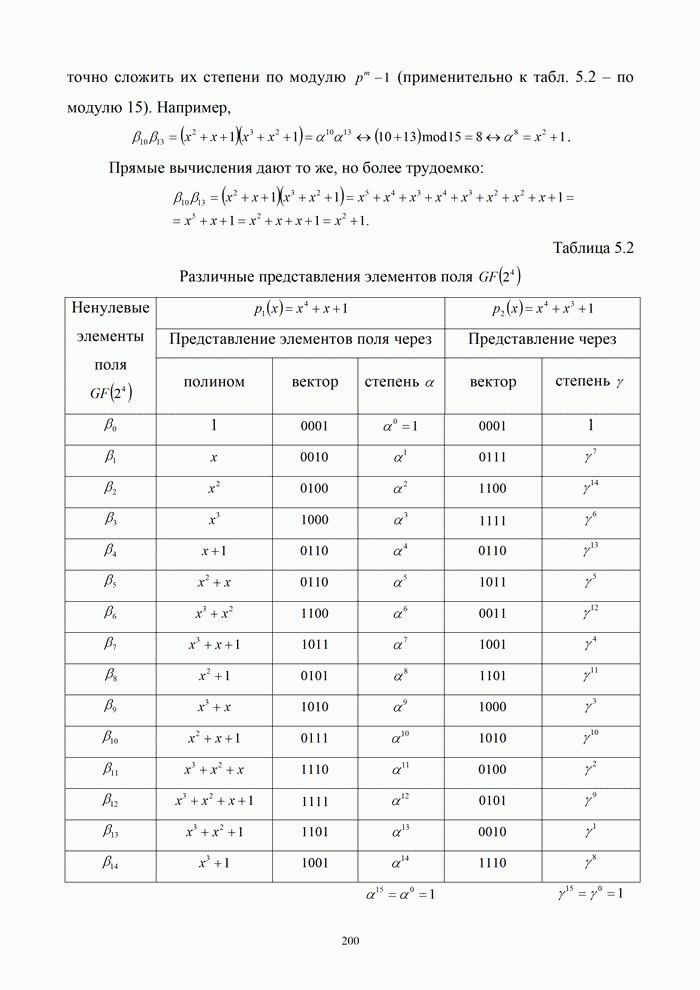
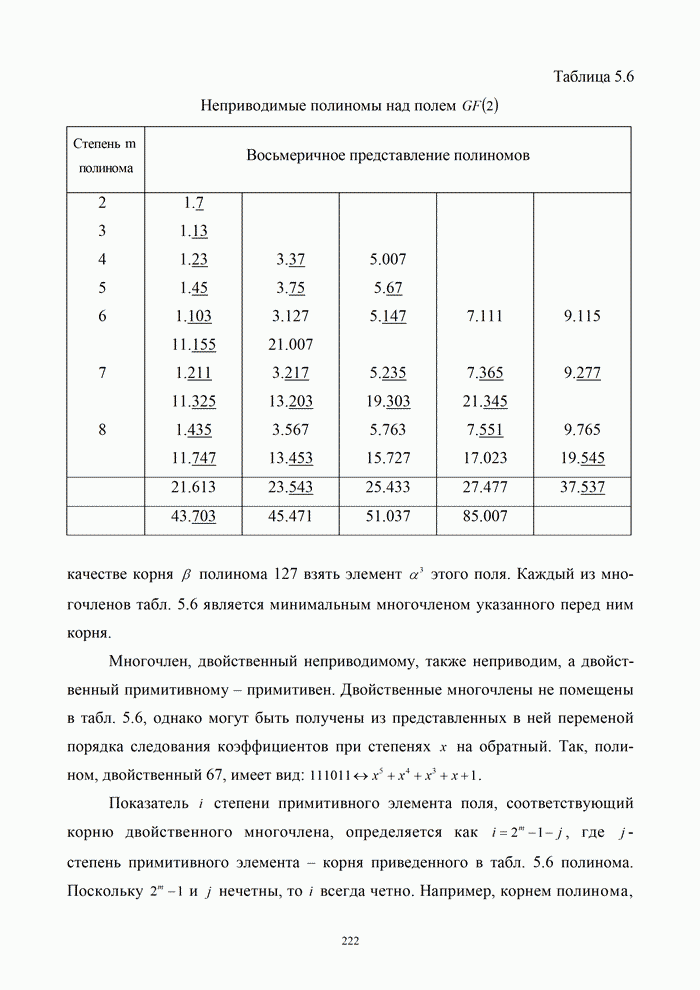
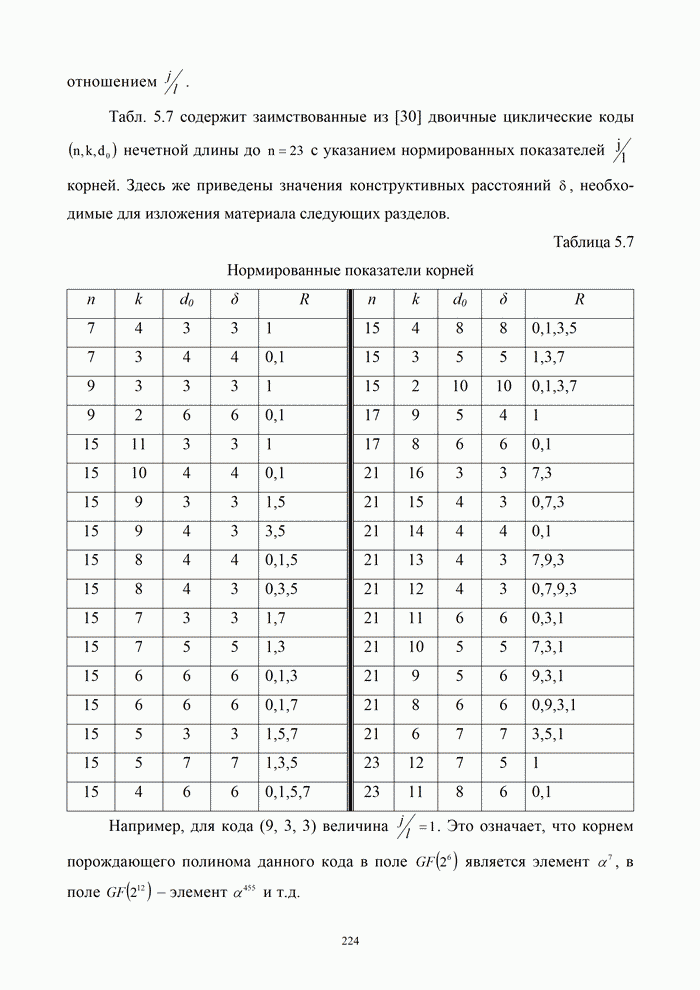
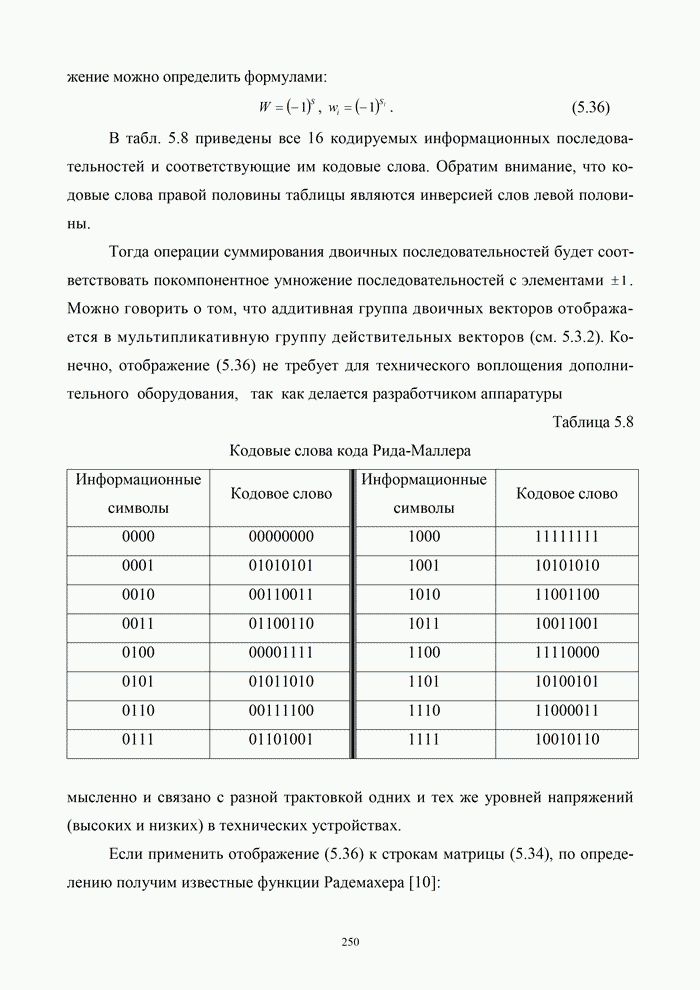
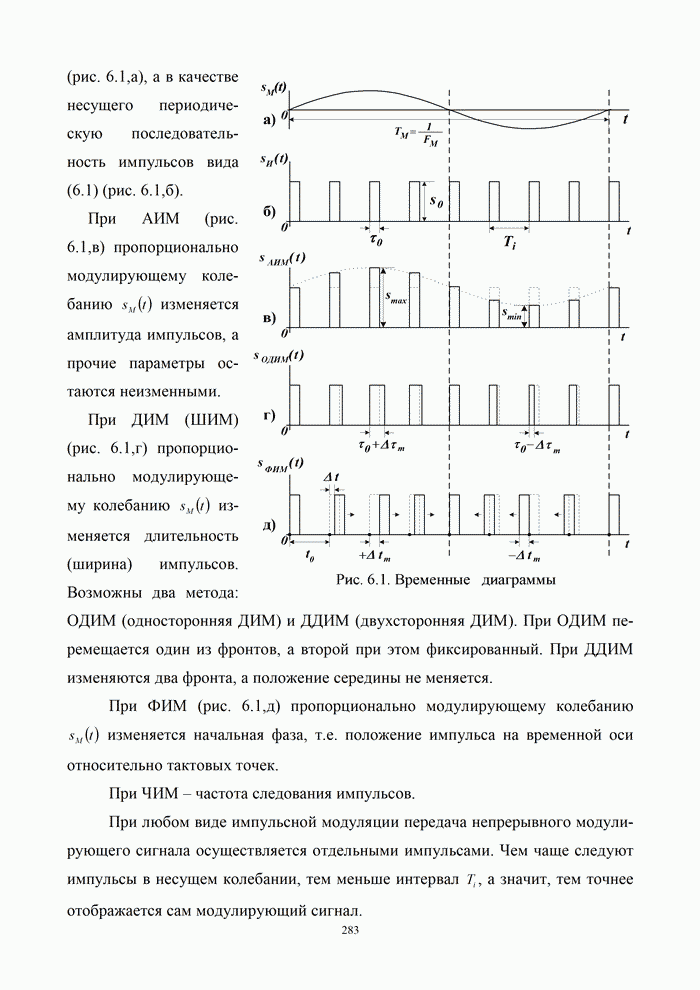
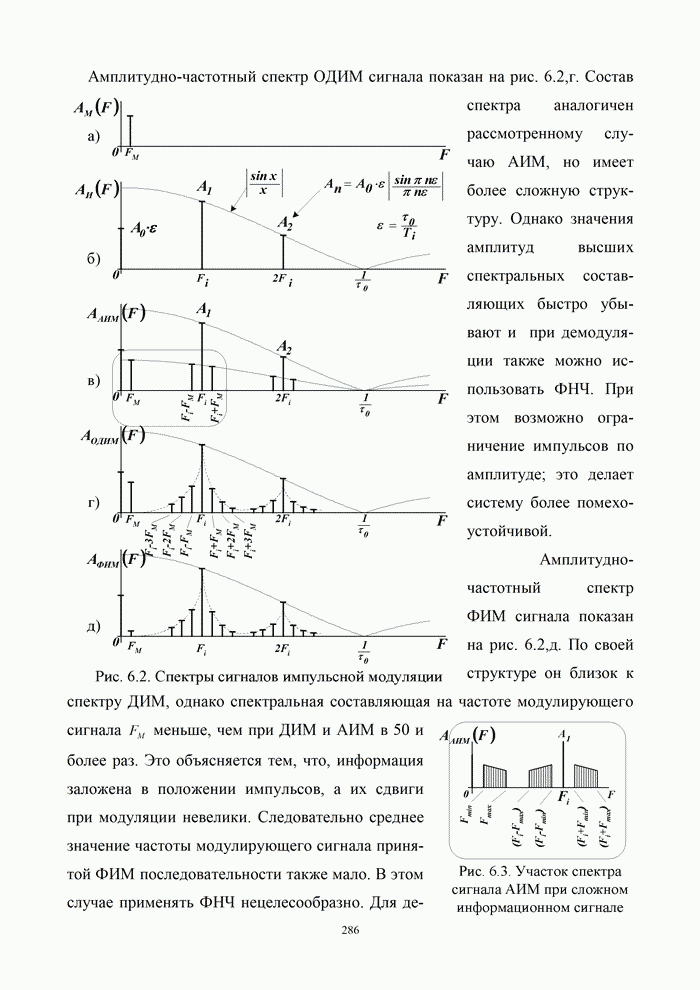
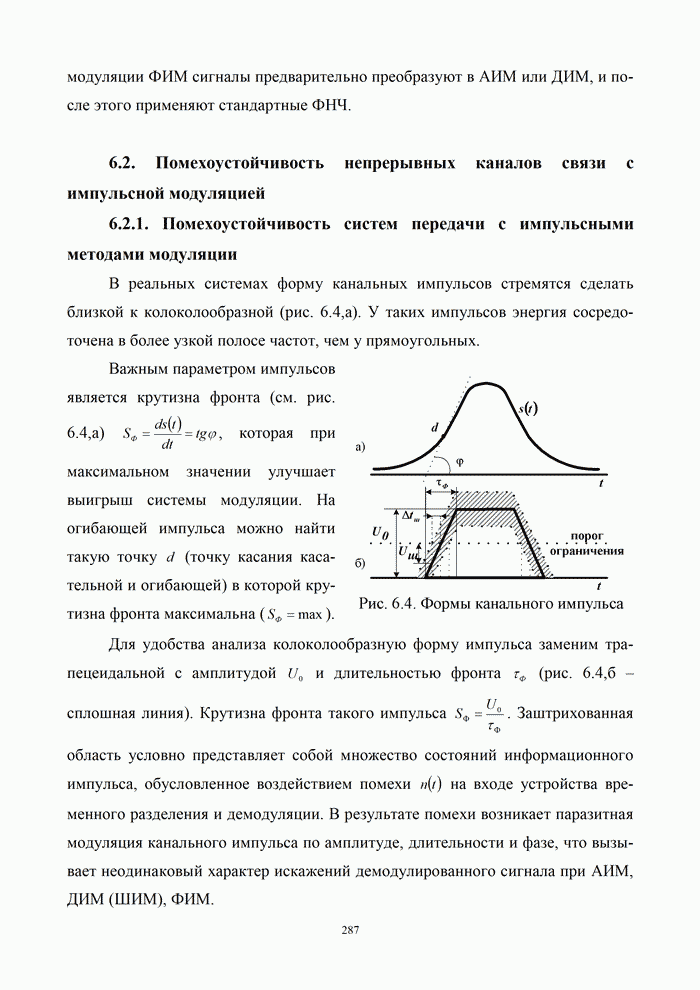
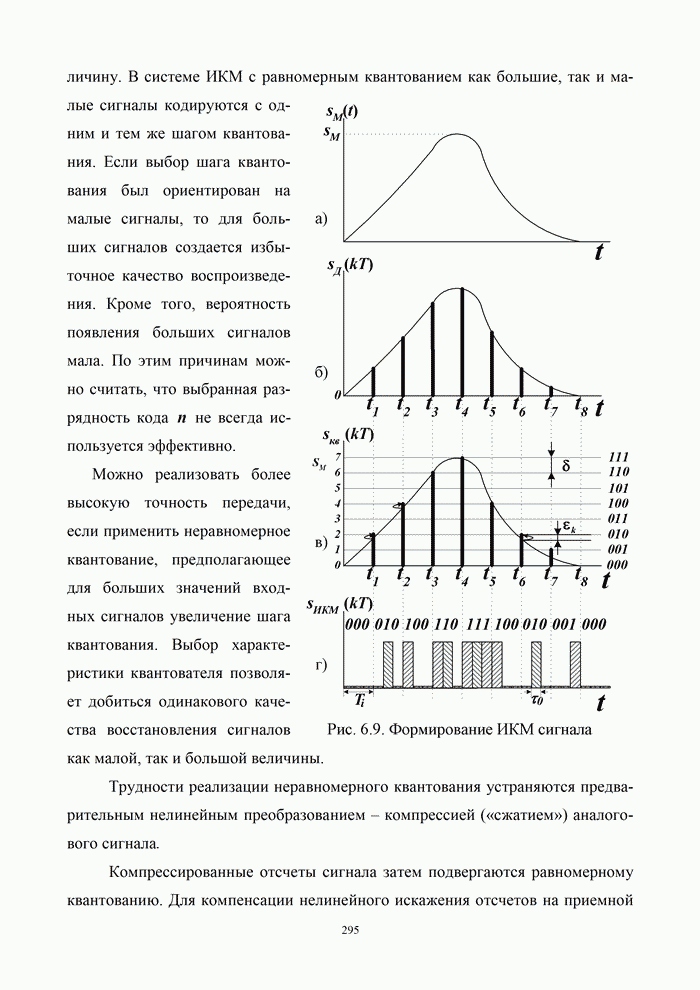
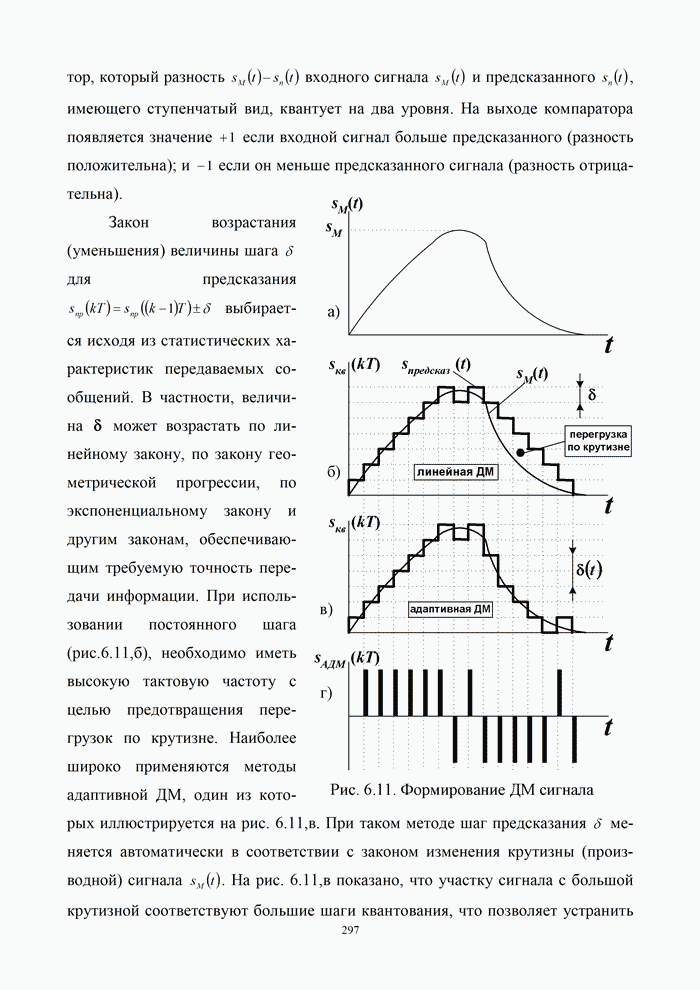
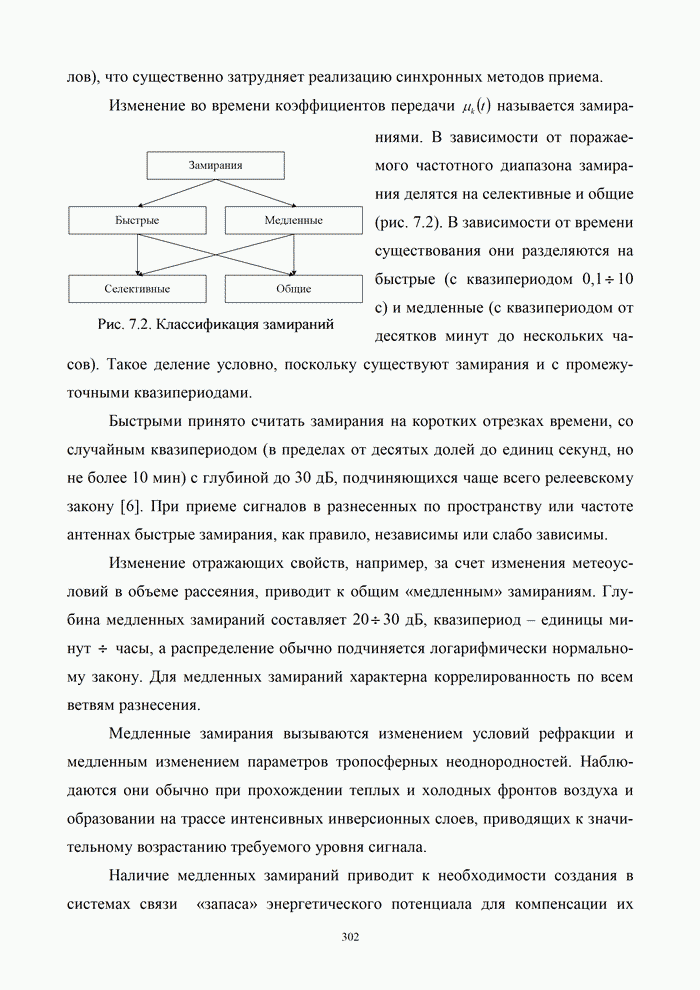
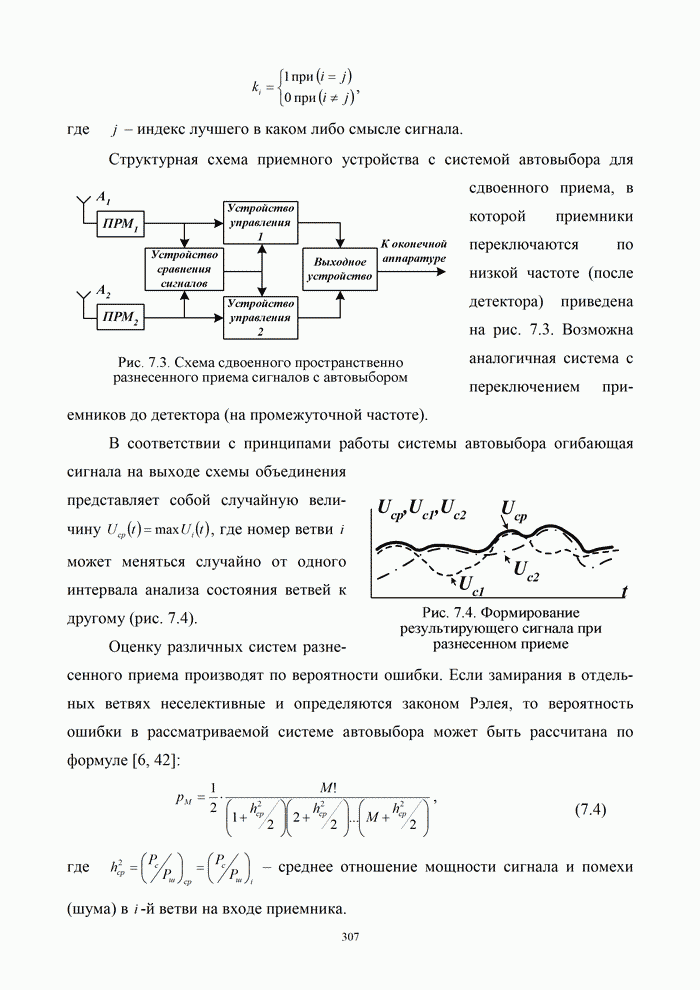
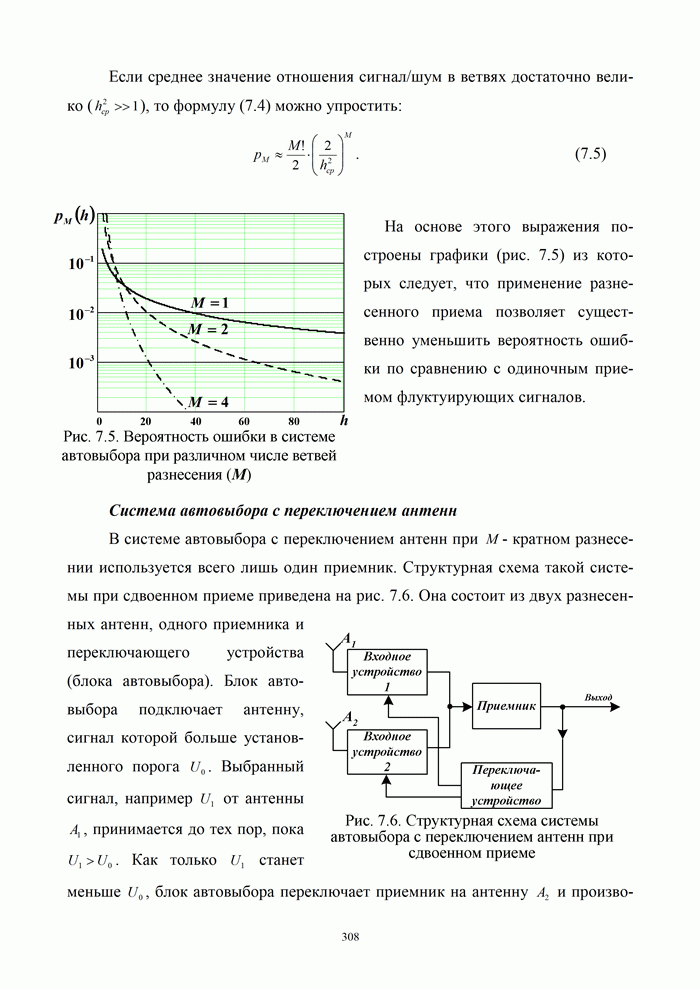
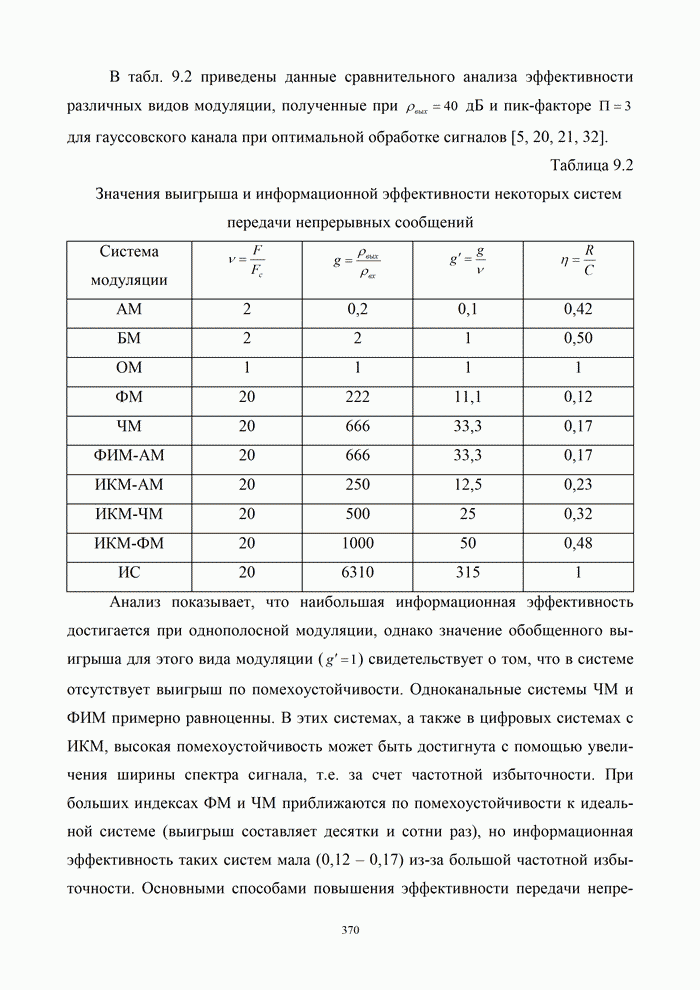
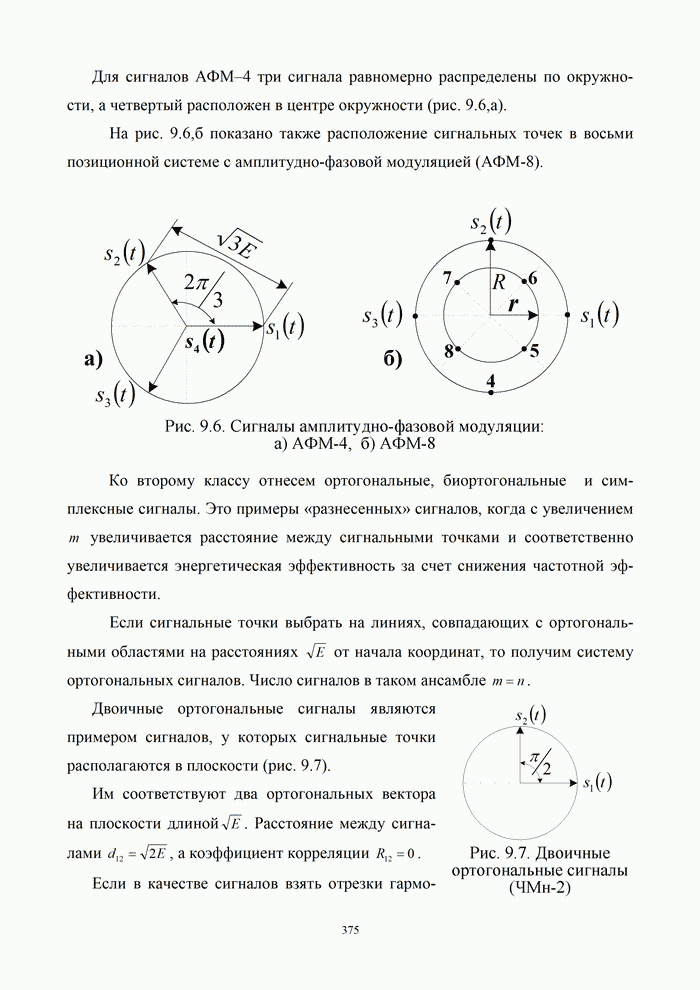
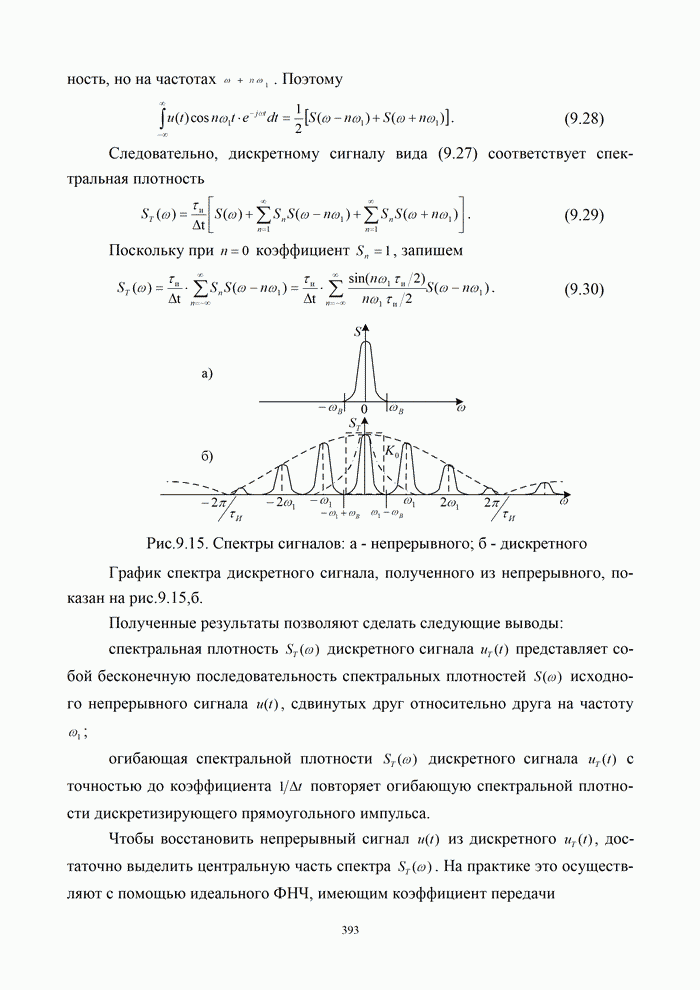
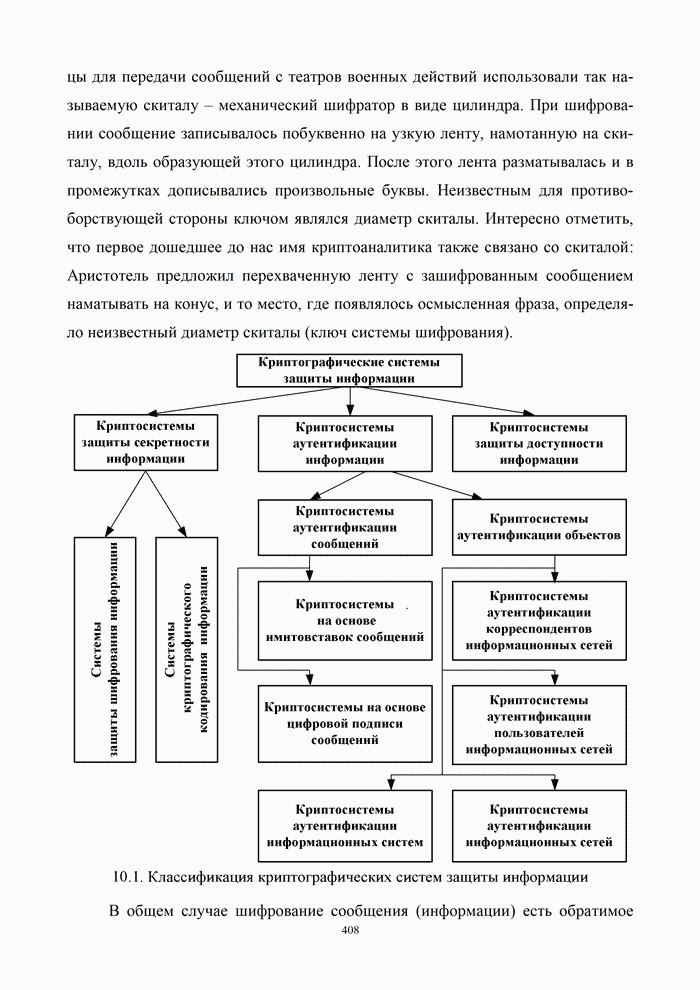
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.1.1. Постановка задачи помехоустойчивого кодирования
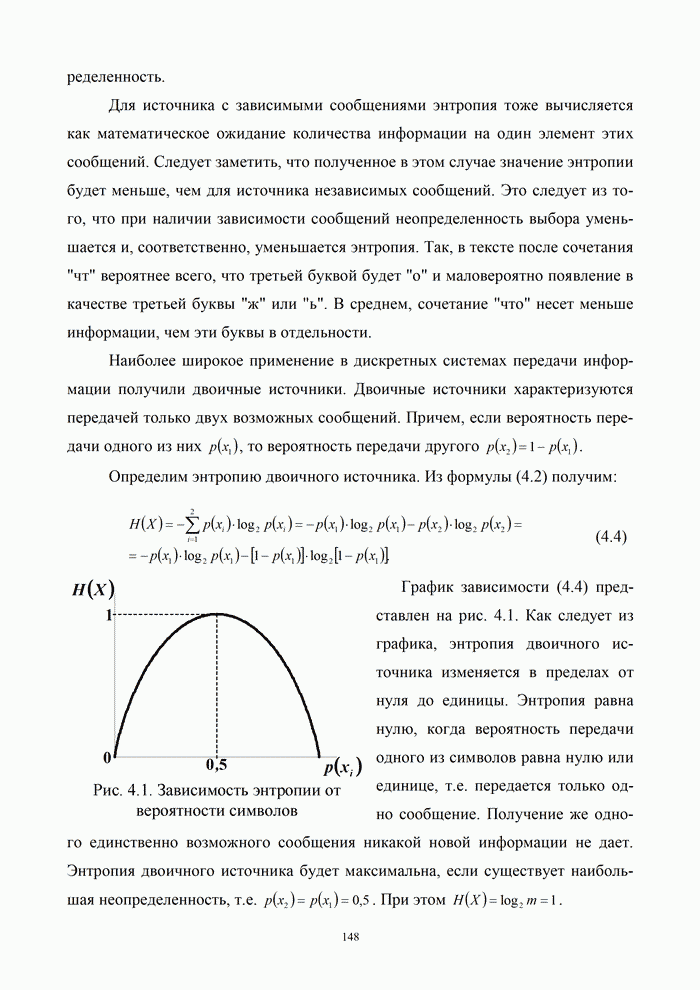
Кодирование называется процесс преобразования сообщений в комбинации из дискретных сигналов. Основными задачами, решаемыми кодированием в процессе передачи сообщений, являются:
- согласование источника сообщений с каналом по объемам алфавитов;
- повышение скорости передачи информации по каналу за счет устранения избыточности в последовательности сообщений;
- повышение помехоустойчивости передачи информации.
Первые две задачи решаются в кодере источника сообщений. Третья задача решается в кодере канала.
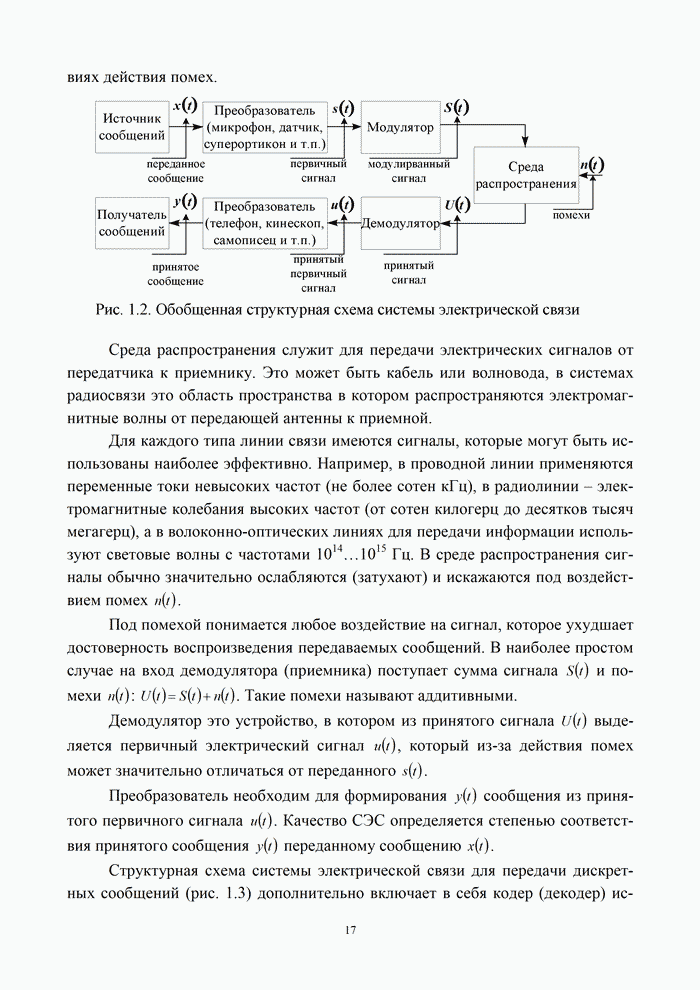
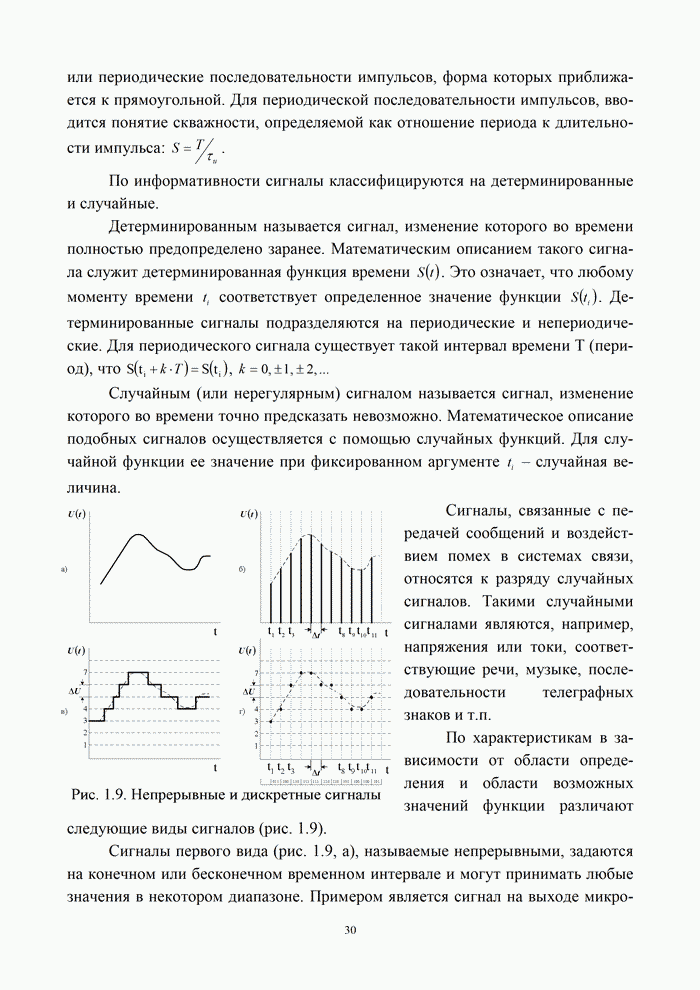
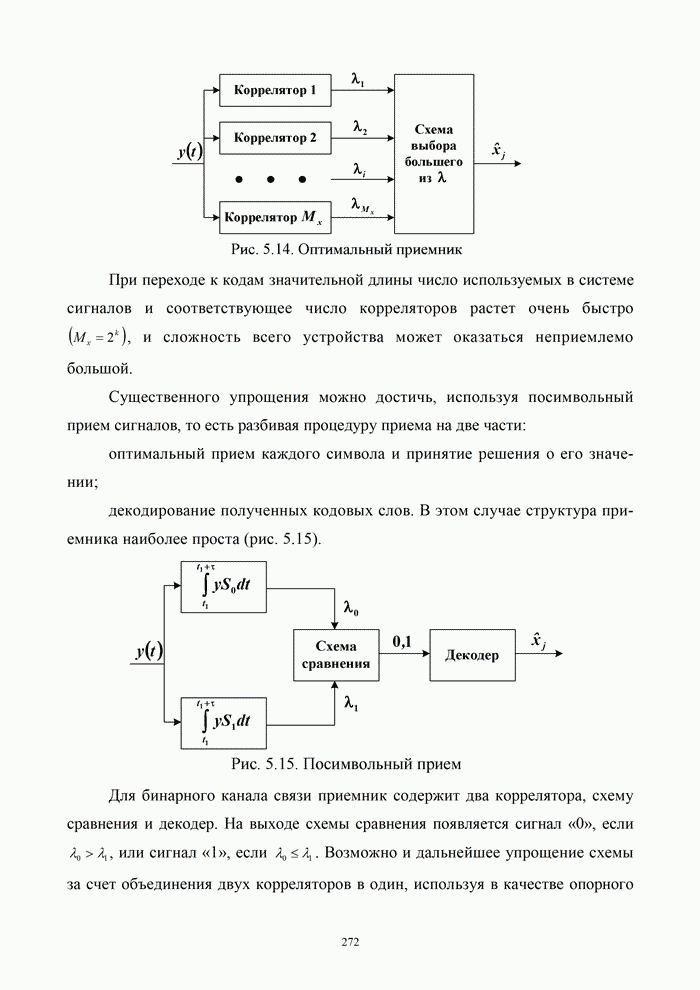
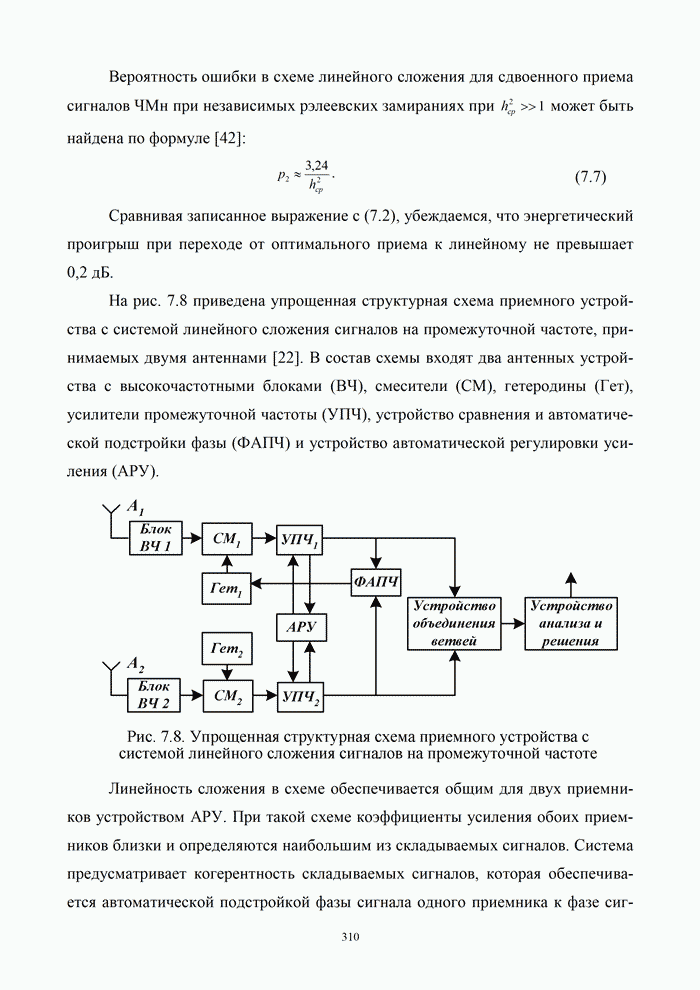
Для постановки задачи помехоустойчивого кодирования обратимся к структурной схеме канала электрической связи (рис. 5.1).
В общем случае в системе электрической связи можно передавать самые различные по физической природе сообщения: цифровые данные, полученные от ЭВМ, речь, тексты телеграмм, команды управления, результаты измерений различных физических величин. Естественно, что все эти сообщения предварительно должны быть преобразованы в электрические колебания, сохраняющие все свойства исходных сообщений, а затем унифицированы, т.е. представлены в форме, удобной для последующей передачи.
Множество
возможных дискретных сообщений источника ![]() , должно при этом обладать следующими
свойствами:
, должно при этом обладать следующими
свойствами:
- оно должно быть конечным;
- все сообщения равновероятны.
Тем самым обеспечивается максимальная энтропия источника (т.е. кодирование источника выполнено наилучшим образом).
Под источником информации на рис. 5.1 понимается устройство, в котором выполнены все названные ранее операции.

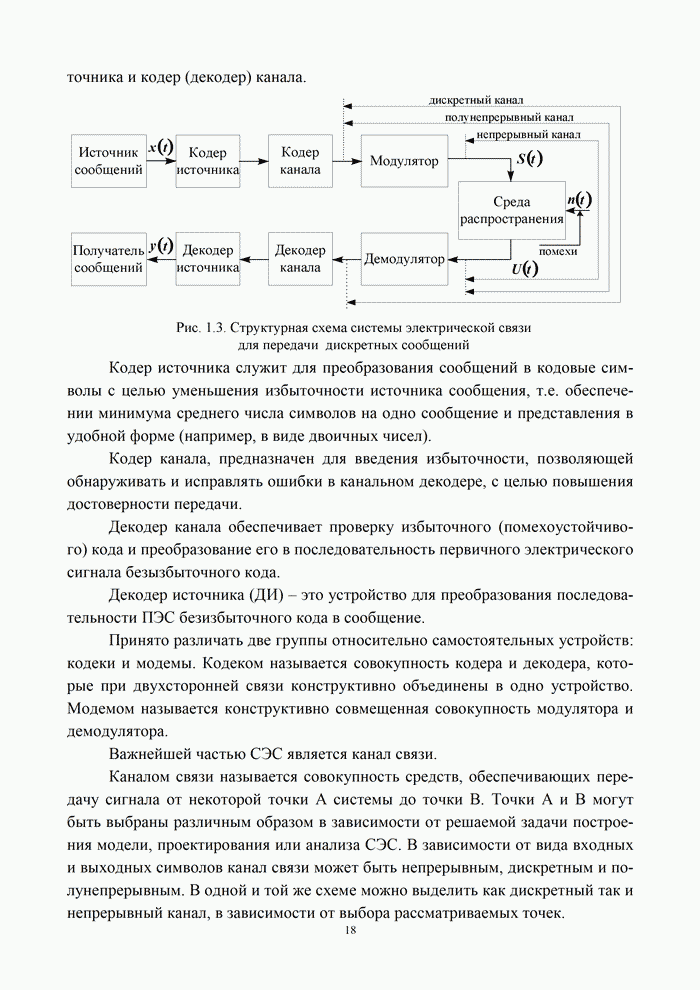
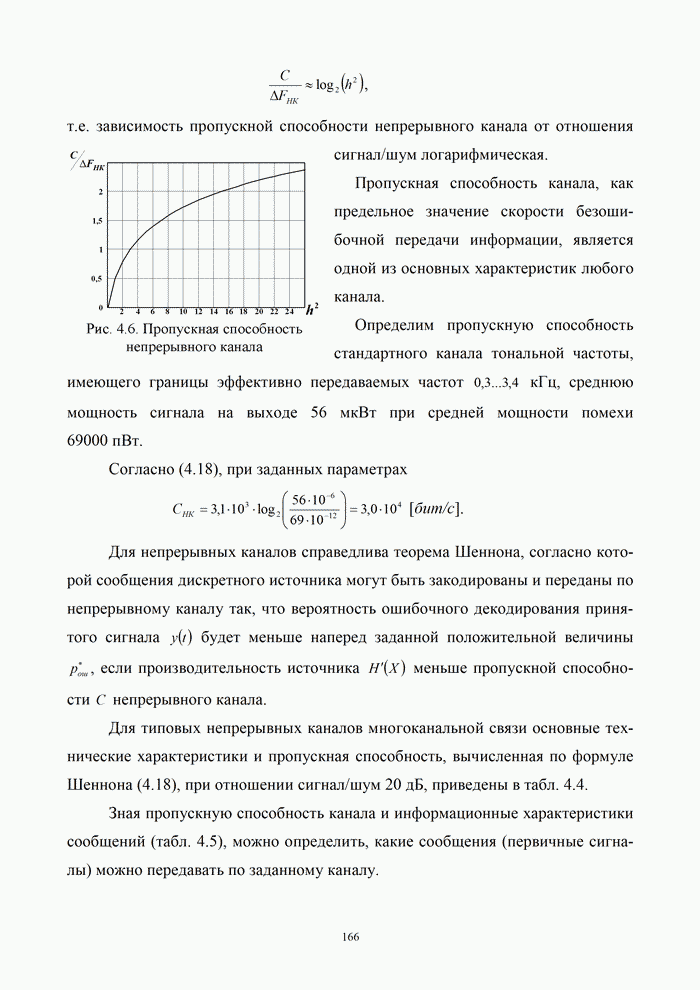
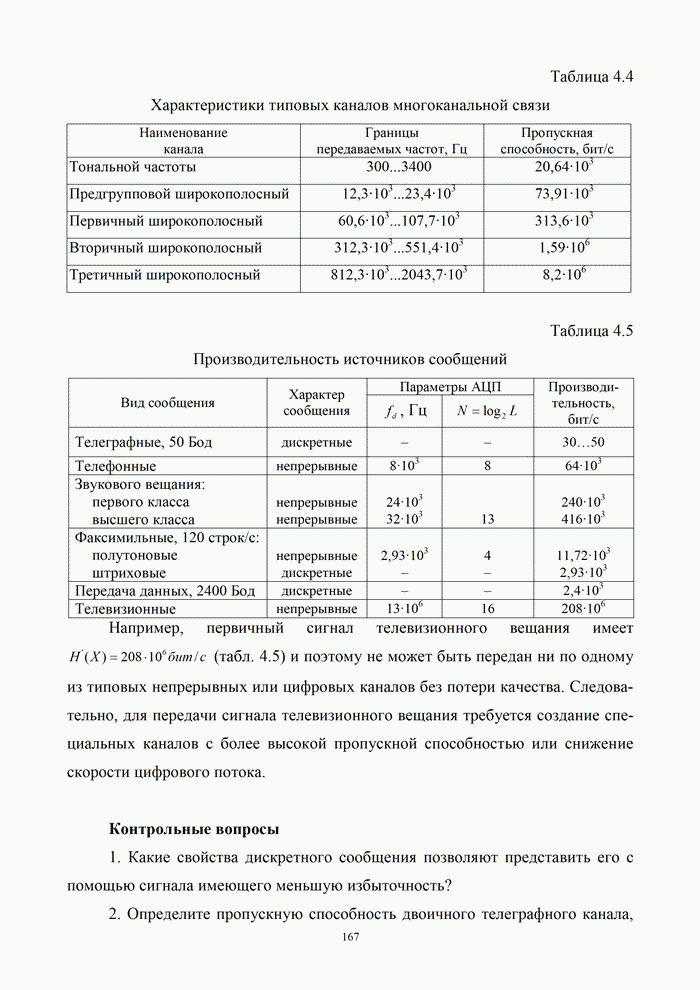
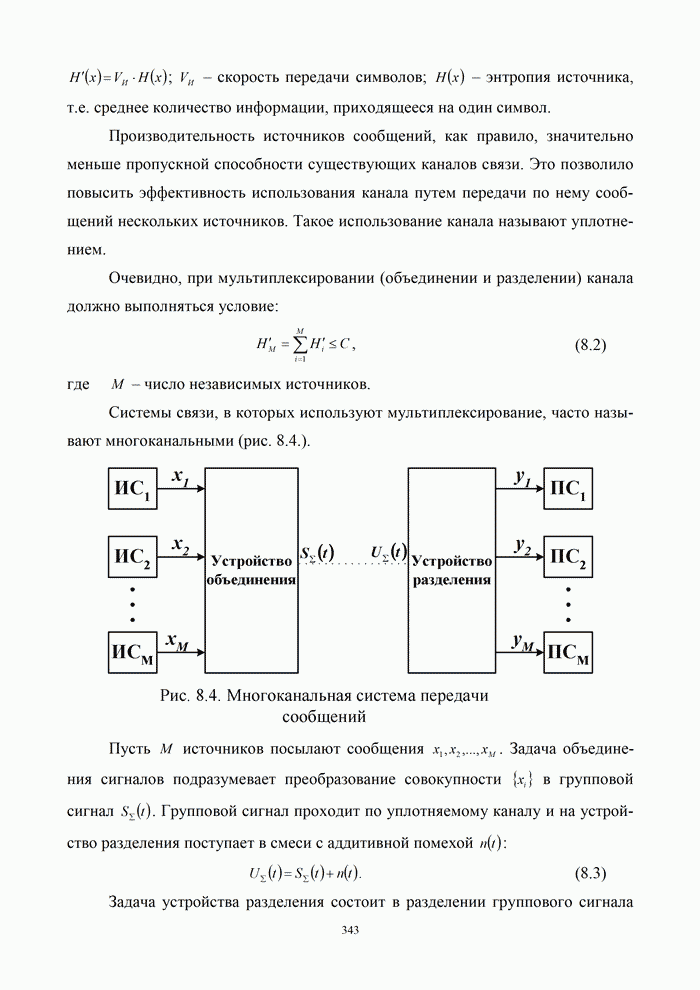
Для более экономного использования линии связи, а также для уменьшения влияния различных помех и искажений передаваемая от источника информация может быть в дальнейшем преобразована с помощью кодирующего устройства. Это преобразование, как правило, состоит из ряда операций, включающих учет статистики поступающей информации для устранения избыточности (статистическое кодирование) реализуемое в кодере источника, а также введение дополнительных элементов для уменьшения влияния помех и искажений (помехоустойчивое кодирование) – кодер канала.
В результате ряда преобразований на выходе кодирующего устройства образуется последовательность элементов, которая с помощью модулятора преобразуется в форму, удобную для передачи по линии связи. Среда распространения – это среда, по которой происходит передача сигналов от передатчика (модулятора) к приемнику (демодулятору).
На вход демодулятора, кроме сигналов, прошедших среду, попадают также различные помехи. Демодулятор выделяет из смеси сигнала и помех последовательность, которая должна соответствовать последовательности на выходе кодирующего устройства. Однако из-за действия помех, влияния среды, погрешностей различных преобразований полное соответствие получить невозможно. Поэтому такая последовательность вводится в декодирующее устройство, которое выполняет операции по ее преобразованию в последовательность, соответствующую переданной. Полнота этого соответствия зависит от ряда факторов: корректирующих возможностей кодированной последовательности, уровня сигнала и помех, а также их статистики, свойств декодирующего устройства. Сформированная в результате декодирования последовательность поступает к получателю информации. Естественно, что при проектировании систем передачи информации всегда стремятся обеспечить такие условия работы, чтобы отличие информации, получаемой от источника, от информации, передаваемой получателю, было невелико и не превышало некоторой допустимой величины. В данном случае основным показателем качества передачи является достоверность передачи информации – степень соответствия принятого сообщения переданному [2, 21].
Основной
принцип построения линейных кодов – отыскание процедур, которые позволяют
получать все разрешенные кодовые комбинации ![]() путем конечного числа несложных линейных
преобразований исходных разрешенных комбинаций
путем конечного числа несложных линейных
преобразований исходных разрешенных комбинаций ![]() , а при декодировании для обнаружения и исправления
ошибок получать информацию об ошибках по результатам конечного числа относительно
простых преобразований над символами получаемых кодовых комбинаций
, а при декодировании для обнаружения и исправления
ошибок получать информацию об ошибках по результатам конечного числа относительно
простых преобразований над символами получаемых кодовых комбинаций ![]() [23].
[23].
Основная
задача оптимального построения корректирующего кода заключается в том, что из всех
возможных кодовых комбинаций ![]() применяется лишь некоторая часть.
Используемые при передаче кодовые комбинации
применяется лишь некоторая часть.
Используемые при передаче кодовые комбинации ![]() обычно называются разрешенными, а
остальные – запрещенными. Следовательно, если под действием помехи передаваемая
кодовая комбинация переходит в запрещенную, то такую ошибку можно обнаружить.
обычно называются разрешенными, а
остальные – запрещенными. Следовательно, если под действием помехи передаваемая
кодовая комбинация переходит в запрещенную, то такую ошибку можно обнаружить.
Чтобы получаемый код обладал наилучшей корректирующей способностью и минимальной вероятностью некорректируемых ошибок, необходимо выполнить следующие пять условий:
- множество
кодовых слов
 должно
быть конечным;
должно
быть конечным;
- любому
сообщению из множества
 источника соответствует кодовое слово из
множества
источника соответствует кодовое слово из
множества  ;
;
- множество
 , должно
иметь большую размерность, чем
, должно
иметь большую размерность, чем  ;
;
- в
качестве кодового слова соответствующего сообщению используется не все
множество возможных кодовых слов
 , а лишь некоторая его часть
, а лишь некоторая его часть  – множество
разрешенных кодовых слов;
– множество
разрешенных кодовых слов;
- в
канал должны передаваться только разрешенные кодовые слова из множества
 .
.
Правило,
по которому сообщению из множества ![]() ставится в соответствие кодовое слово из
множества
ставится в соответствие кодовое слово из
множества ![]() ,
называется алгоритмом кодирования или кодом, корректирующим ошибки.
,
называется алгоритмом кодирования или кодом, корректирующим ошибки.
Рассмотрим
следующий пример. Пусть множество ![]() составляет 2 сообщения: 0 и 1, а множество
составляет 2 сообщения: 0 и 1, а множество
![]() составляет
8 кодовых слов: 000, 001, 010, 100, 011, 101, 110, 111.
составляет
8 кодовых слов: 000, 001, 010, 100, 011, 101, 110, 111.
В
качестве разрешенных (множество ![]() ) выбраны только 2 кодовые комбинации: 000
и 111.
) выбраны только 2 кодовые комбинации: 000
и 111.
При равновероятной передаче
сообщений по каналам с независимыми ошибками, когда вероятность появления
ошибок с увеличением кратности уменьшается, для минимизации средней вероятности
ошибочного декодирования необходимо в первую очередь исправлять однократные
ошибки как наиболее часто встречающиеся, затем двукратные и т.д. При этом
декодер из множества кодовых комбинаций ![]() выделяет кодовые комбинации
выделяет кодовые комбинации ![]() , которые отличаются от
, которые отличаются от ![]() в меньшем числе символов.
Соответственно декодер принимает решение оптимальное по критерию максимума
правдоподобия [5, 23].
в меньшем числе символов.
Соответственно декодер принимает решение оптимальное по критерию максимума
правдоподобия [5, 23].
Правило,
по которому кодовому слову из множества ![]() ставится в соответствие сообщение из
множества
ставится в соответствие сообщение из
множества ![]() ,
называется алгоритмом декодирования.
,
называется алгоритмом декодирования.
Избыточный код дает возможность обнаружить, в каких принятых символах имеются ошибочные символы. Кроме того, при разумном выборе кода вероятность не обнаруживаемой ошибки (т.е. ошибки, которая переводит разрешенную кодовую комбинацию в другую разрешенную кодовую комбинацию) может быть весьма малой.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Список сокращений
- Основные обозначения
- ВВЕДЕНИЕ
- Глава 1. Сообщения, сигналы и помехи, их математические модели
- 1.1. Основные понятия и определения
- 1.1.1. Сообщение, сигнал, модуляция
- 1.1.2. Основные параметры сигналов
- 1.2. Системы связи. Каналы связи
- 1.2.1. Структура канала электросвязи
- 1.2.2. Линия и сеть связи
- 1.2.3. Помехи и искажения в канале
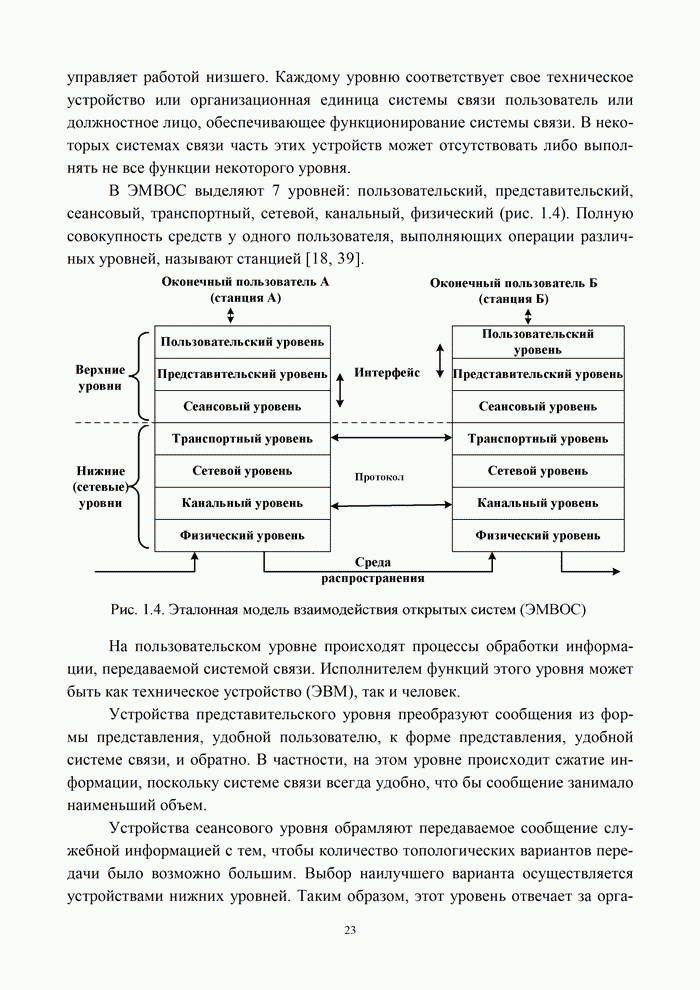
- 1.2.4. Эталонная модель взаимодействия открытых систем
- 1.2.5. Модели каналов связи и их математическое описание
- 1.3. Способы описания сигналов и помех
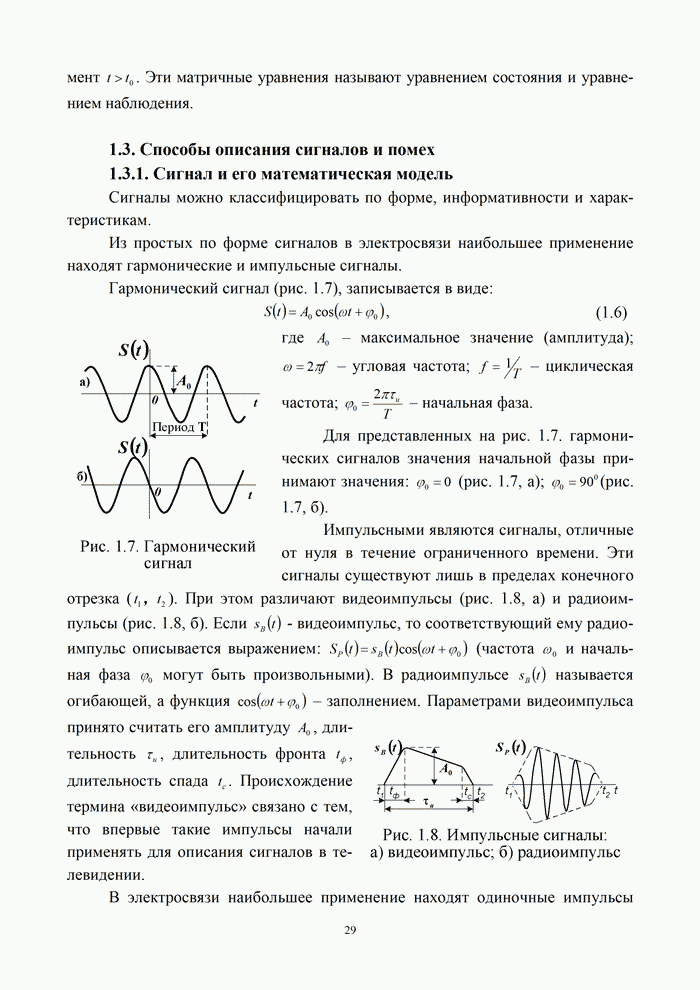
- 1.3.1. Сигнал и его математическая модель
- 1.3.2. Энергетические характеристики детерминированного сигнала
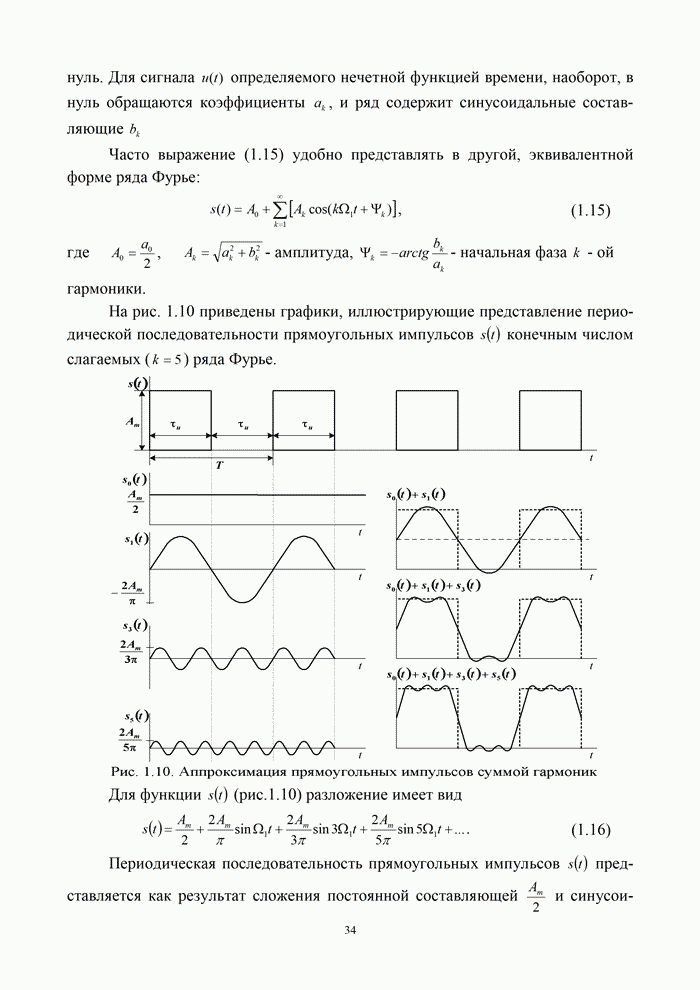
- 1.4.2. Представление сигналов и помех рядом Фурье
- 1.4.3. Применение преобразования Фурье для непериодических сигналов
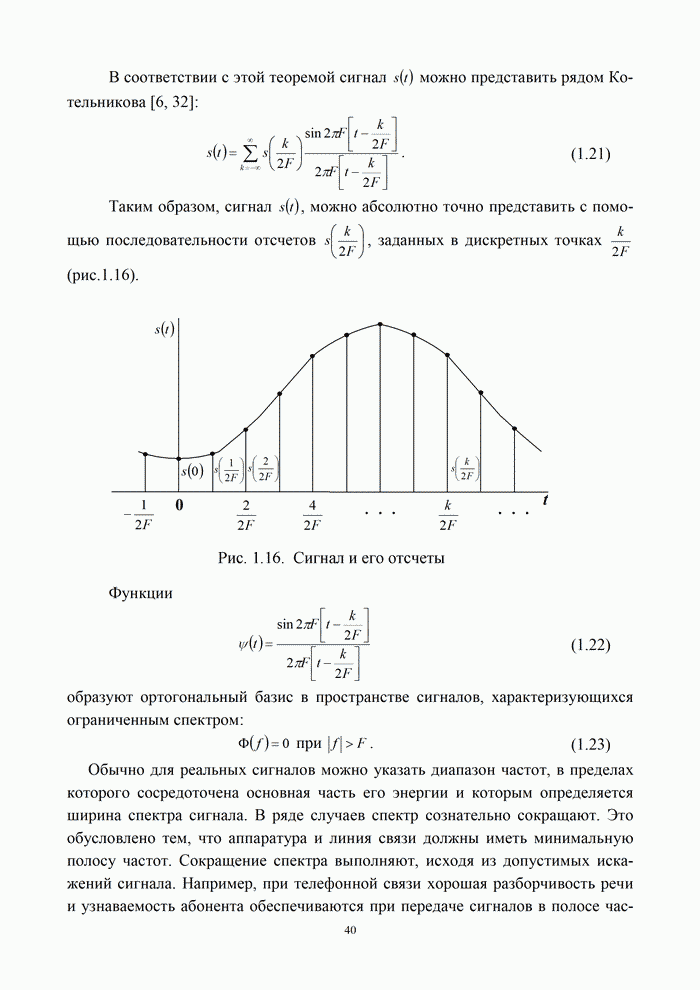
- 1.5. Теорема Котельникова
- 1.6. Пространство сигналов
- 1.6.1. Линейное пространство
- 1.6.2. Представление сигнала в многомерном пространстве
- 1.7. Сигналы как случайные процессы
- 1.7.1. Характеристики случайного процесса
- 1.7.2. Флуктуационный шум
- 1.8. Комплексное представление сигналов и помех
- 1.8.1. Понятие аналитического сигнала
- 1.8.2. Огибающая, мгновенная фаза и мгновенная частота узкополосного случайного процесса
- Контрольные вопросы
- Глава 2. Методы формирования и преобразования сигналов
- 2.1. Модуляция сигналов
- 2.1.1. Амплитудная модуляция гармонической несущей
- 2.1.2. Балансная и однополосная модуляция гармонической несущей
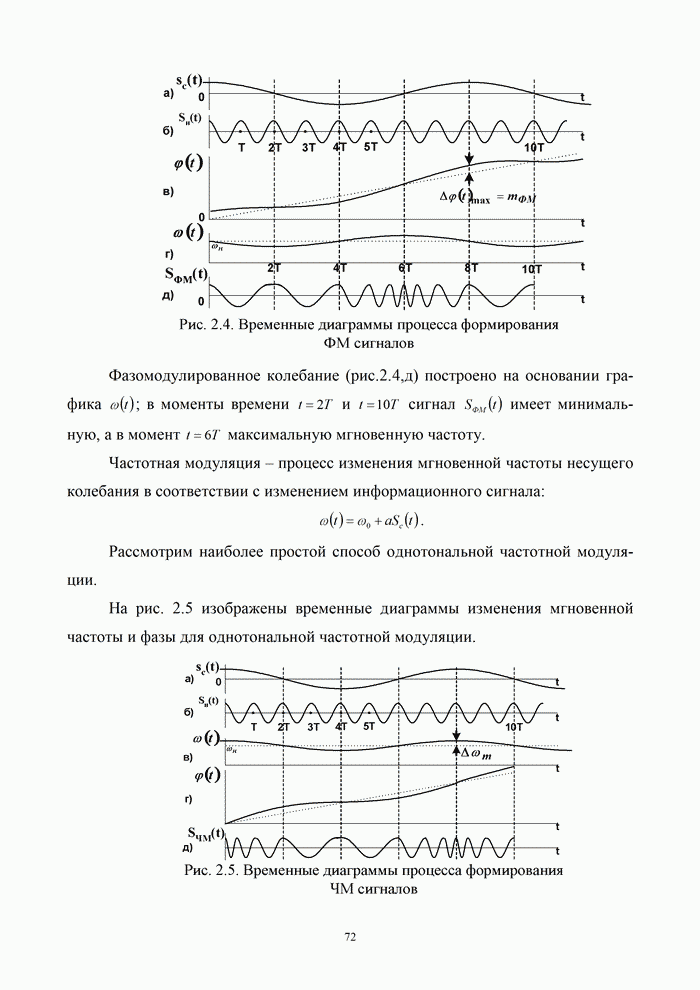
- 2.2. Методы угловой модуляции
- 2.2.1. Принципы частотной и фазовой (угловой) модуляции
- 2.2.2. Спектр сигналов угловой модуляции
- 2.3. Формирование и детектирование модулированных сигналов
- 2.3.1. Формирование и детектирование сигналов амплитудной и однополосной амплитудной модуляции
- 2.3.2. Формирование и детектирование сигналов угловой модуляции
- 2.4. Манипуляция сигналов
- 2.4.1. Временные и спектральные характеристики амплитудно-манипулированных сигналов
- 2.4.2. Временные и спектральные характеристики частотно-манипулированных сигналов
- 2.4.3. Фазовая (относительно-фазовая) манипуляция сигналов
- 2.5. Системы связи с многопозиционной относительной фазовой манипуляцией
- 2.5.1. Принцип формирования сигнала с многократной относительной фазовой манипуляцией
- 2.5.2. Квадратурная относительно-фазовая манипуляция (КОФМ)
- 2.5.3. Принцип частотной модуляции с непрерывной фазой
- Контрольные вопросы
- Глава 3. Помехоустойчивость приема дискретных сообщений
- 3.1. Критерии качества и правила приема дискретных сообщений
- 3.1.1. Понятие о помехоустойчивости систем электрической связи
- 3.1.2. Задача оптимального приема
- 3.1.3. Вычисление вероятностей ошибок
- 3.2. Оптимальная демодуляция при когерентном приеме сигналов
- 3.2.1. Оптимальные алгоритмы приема при полностью известных сигналах
- 3.2.2. Реализация алгоритмов оптимального когерентного приема
- 3.3. Помехоустойчивость приема сигналов с известными параметрами
- 3.4. Прием сигналов с неопределенной фазой
- 3.4.1. Оптимальный некогерентный прием дискретных сигналов
- 3.4.2. Помехоустойчивость оптимального некогерентного приема
- 3.5. Подоптимальные методы приема
- 3.5.1. Причины применения неоптимальных методов приема
- 3.5.2. Квазиоптимальные методы приема
- Контрольные вопросы
- Глава 4. Теория передачи информации
- 4.1. Информационные характеристики источника сообщений
- 4.1.1. Количественное определение информации
- 4.1.2. Энтропия и производительность дискретного источника сообщений
- 4.2. Пропускная способность дискретного канала
- 4.2.1. Количество информации переданной по дискретному каналу
- 4.2.2. Пропускная способность дискретного канала
- 4.2.3. Пропускная способность симметричного дискретного канала без памяти
- 4.3. Методы сжатия дискретных сообщений
- 4.3.1. Условия существования оптимального неравномерного кода
- 4.3.2. Прямая и обратная теоремы кодирования источника неравномерными кодами
- 4.3.3. Показатели эффективности сжатия
- 4.3.4. Кодирование источника дискретных сообщений методом Шеннона-Фано
- 4.3.5. Кодирование источника дискретных сообщений методом Хаффмена
- 4.4. Пропускная способность непрерывного канала
- 4.4.1. Постановка задачи передачи дискретных сообщений в непрерывном канале
- 4.4.2. Количество информации, переданной по непрерывному каналу
- 4.4.3. Пропускная способность непрерывного канала
- Контрольные вопросы
- Глава 5. Теория кодирования сообщений
- 5.1. Помехоустойчивое кодирование: блочные и непрерывные коды
- 5.1.1. Постановка задачи помехоустойчивого кодирования
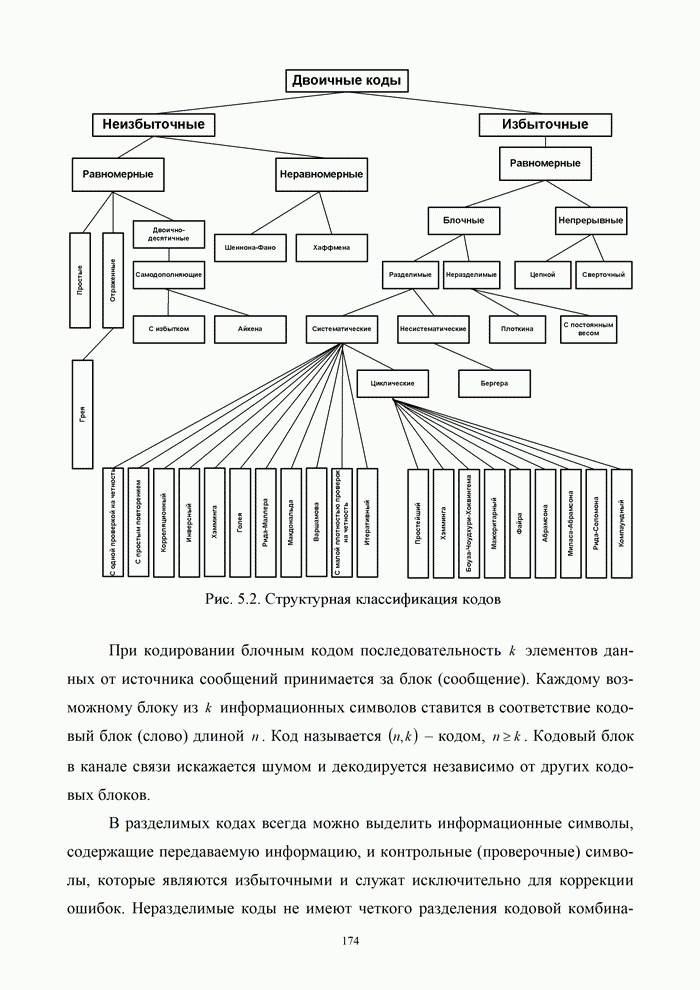
- 5.1.2. Классификация кодов
- 5.1.3. Основные характеристики и свойства блочных кодов
- 5.2. Эффективность помехоустойчивого кодирования
- 5.2.1. Эффективность кода в режиме исправления ошибок
- 5.2.2. Эффективность кода в режиме обнаружения ошибок
- 5.2.3. Эффективность помехоустойчивых кодов
- 5.3. Математические основы теории помехоустойчивого кодирования
- 5.3.1. Краткие сведения из теории чисел
- 5.3.2. Группы
- 5.3.3. Кольца и поля
- 5.3.4. Векторное пространство
- 5.3.5. Конечные поля
- 5.4. Линейные блочные коды
- 5.4.1. Система передачи дискретных сообщений
- 5.4.2. Параметры линейного кода
- 5.4.3. Полиномиальные циклические коды
- 5.4.4. Циклические коды и корни полиномов
- 5.4.5. Спектральное описание циклических кодов
- 5.4.6. Простейшие блочные линейные коды
- 5.5. Коды Боуза-Чоудхури-Хоквингема
- 5.5.1. Методы задания кодов БЧХ
- 5.5.2. Принципы декодирования кодов БЧХ
- 5.5.3. Методы реализации этапов декодирования кодов БЧХ
- 5.6. Коды Рида-Соломона
- 5.6.1. Основные определения
- 5.6.2. Обнаружение и исправление пакетов ошибок
- 5.7. Коды Рида-Маллера
- 5.7.1. Задание и декодирование кодов Рида-Маллера
- 5.7.2. Симплексные коды и m-последовательности
- 5.7.3. Связь между блочными кодами
- 5.8. Сверточные коды
- 5.8.1. Основные параметры
- 5.8.2. Способы задания сверточного кода
- 5.8.3. Алгоритм декодирования Витерби
- 5.9. Помехоустойчивость систем передачи дискретных сообщений
- 5.9.1. Две процедуры приема сигналов
- 5.9.2. Помехоустойчивость систем передачи информации при оптимальной процедуре приема
- 5.9.3. Помехоустойчивость систем передачи информации при посимвольном приеме сигналов
- Контрольные вопросы
- Глава 6. Сигналы с импульсной модуляцией
- 6.1. Методы импульсной модуляции
- 6.1.1. Импульсные методы передачи непрерывных сигналов
- 6.1.2. Спектральные характеристики импульсных методов модуляции
- 6.2. Помехоустойчивость непрерывных каналов связи с импульсной модуляцией
- 6.2.1. Помехоустойчивость систем передачи с импульсными методами модуляции
- 6.3. Цифровые методы передачи непрерывных сообщений
- 6.3.1. Передача сигналов с импульсно-кодовой модуляцией
- 6.3.2. Передача сигналов с дельта модуляцией
- 6.3.3. Квантование сигналов в системах с ИКМ и ДМ
- Контрольные вопросы
- Глава 7. Методы приема сигналов в сложных условиях
- 7.1. Прием сигналов в каналах с замираниями
- 7.1.1. Сущность замираний и их классификация
- 7.1.2. Принципы разнесенного приема сигналов
- 7.2. Методы борьбы с замираниями сигналов
- 7.2.1. Методы борьбы с замираниями в аналоговых системах связи
- 7.2.2. Методы борьбы с замираниями в цифровых системах связи
- 7.3. Методы борьбы с межсимвольной интерференцией
- 7.3.1. Причины возникновения и сущность межсимвольной интерференции
- 7.3.2. Обработка сигналов в каналах с межсимвольной интерференцией
- 7.3.3. Помехоустойчивость в каналах с межсимвольной интерференцией
- 7.4. Прием дискретных сообщений в каналах с сосредоточенными по спектру и импульсными помехами
- 7.4.1. Общая характеристика сосредоточенных по спектру и импульсных помех
- 7.4.2. Борьба с сосредоточенными и импульсными помехами
- 7.5. Компенсация помех и искажений в канале
- 7.5.1. Принцип работы радиолинии с ФМ ПСС (ФМ ШПС)
- 7.5.2. Помехоустойчивость радиолинии с ФМ ПСС
- 7.5.3. Принципы работы радиолиний с ППРЧ
- 7.5.4. Помехоустойчивость радиолиний с ППРЧ
- Контрольные вопросы
- Глава 8. Многоканальная связь и распределение информации
- 8.1. Методы распределения ресурса общего канала
- 8.1.1. Классификация систем передачи информации, использующих единый ресурс
- 8.1.2. Постановка задачи объединения и разделения сигналов
- 8.1.3. Энергетическая и спектральная цена уплотнения
- 8.2. Частотное разделение каналов
- 8.2.1. Принцип частотного объединения и разделения каналов
- 8.2.2. Групповой сигнал, его структура и характеристики
- 8.3. Временное разделение каналов
- 8.3.1. Принцип временного разделения каналов
- 8.3.2. Характеристики группового сигнала систем с ВРК
- 8.4. Разделение сигналов по форме
- Контрольные вопросы
- Глава 9. Эффективность систем связи
- 9.1. Оценка эффективности систем связи
- 9.1.1. Подходы к оценке эффективности
- 9.1.2. Критерии эффективности
- 9.1.3. Эффективность аналоговых и цифровых систем
- 9.2. Выбор сигналов и помехоустойчивых кодов
- 9.2.1. Многопозиционные сигналы
- 9.2.2. Корректирующие коды
- 9.3. Оптимизация систем связи
- 9.3.1. Согласование методов модуляции и кодирования
- 9.3.2. Классификация сигнально – кодовых конструкций
- 9.4. Характеристики основных типов СКК
- 9.4.1. Согласование канала кодом Грея
- 9.4.2. Согласование на основе разбиения ансамбля на вложенные подансамбли
- 9.5. Алгоритмы цифровой обработки сигналов
- 9.5.1. Дискретные сигналы и их спектры
- 9.5.2. Алгоритмы дискретного и быстрого преобразований Фурье
- Контрольные вопросы
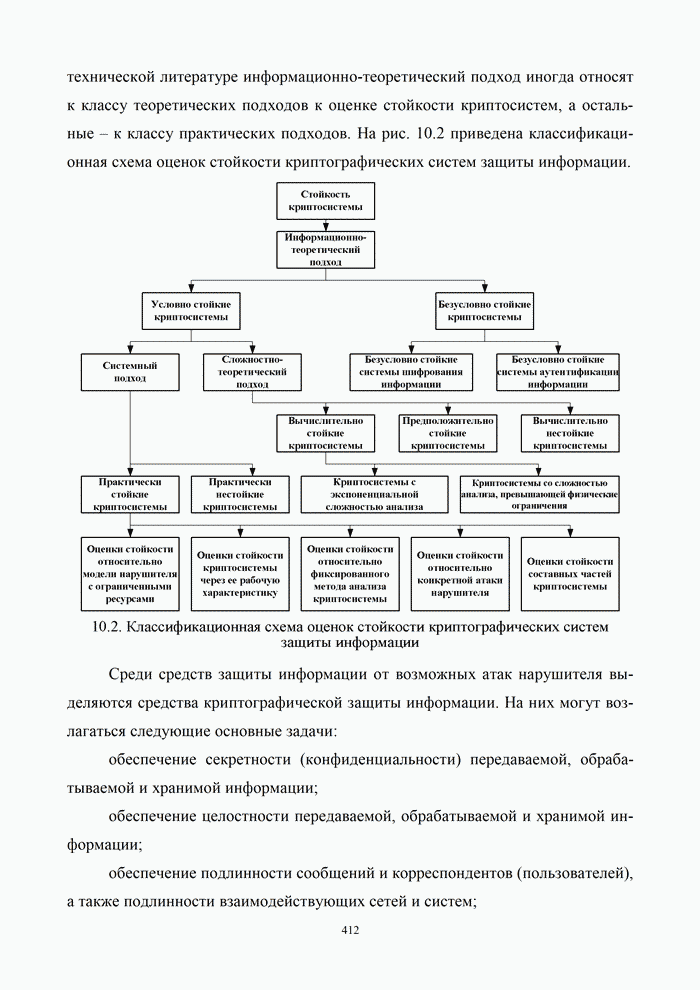
- Глава 10. Теоретико-информационные основы криптозащиты сообщений в телекоммуникационных системах
- 10.1. Классификация криптографических систем
- 10.1.2. Классификация криптографических систем защиты информации
- 10.1.3. Оценка стойкости криптосистем
- 10.2. Функции, используемые в криптографических системах
- 10.2.1. Общее описание функций, используемых в криптографических системах
- 10.2.2. Однонаправленные функции
- 10.2.3. Криптографические хэш-функции
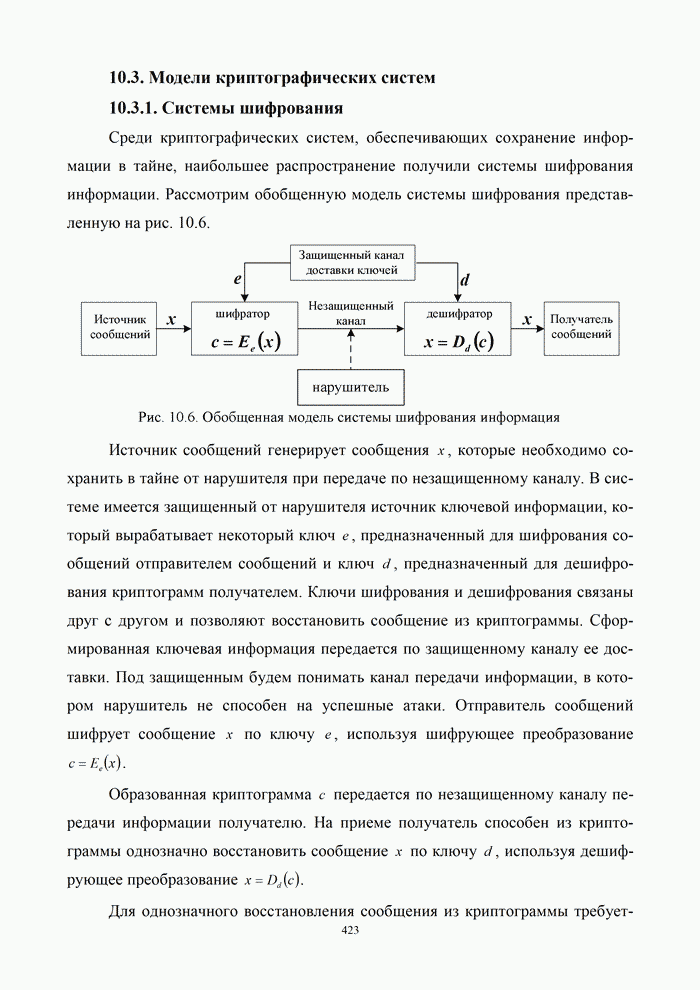
- 10.3. Модели криптографических систем
- 10.3.1. Системы шифрования
- 10.3.2. Традиционные симметричные криптосистемы
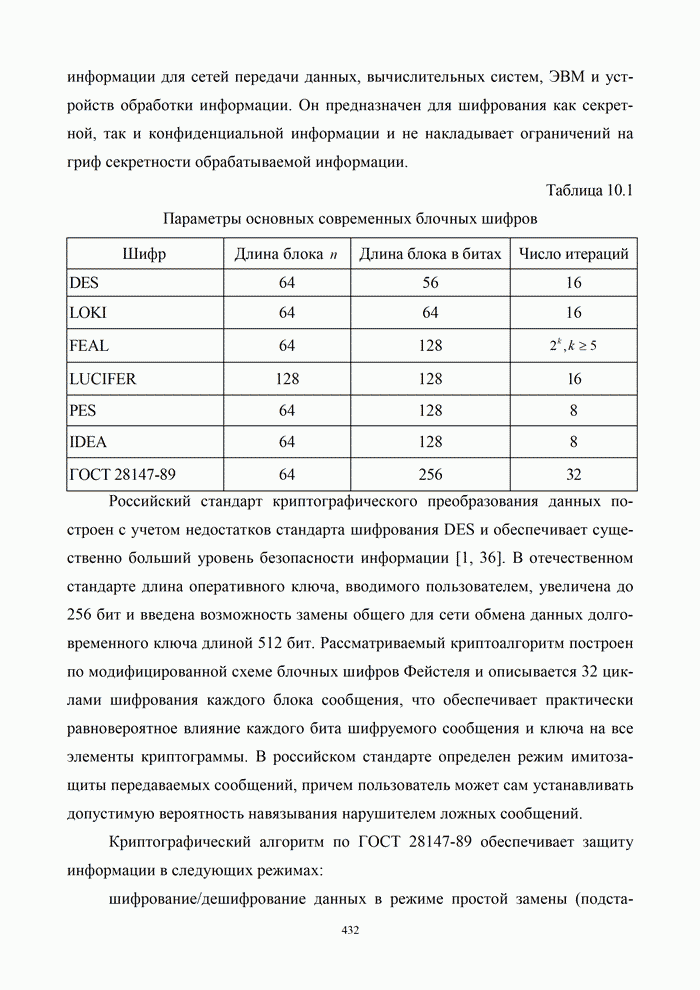
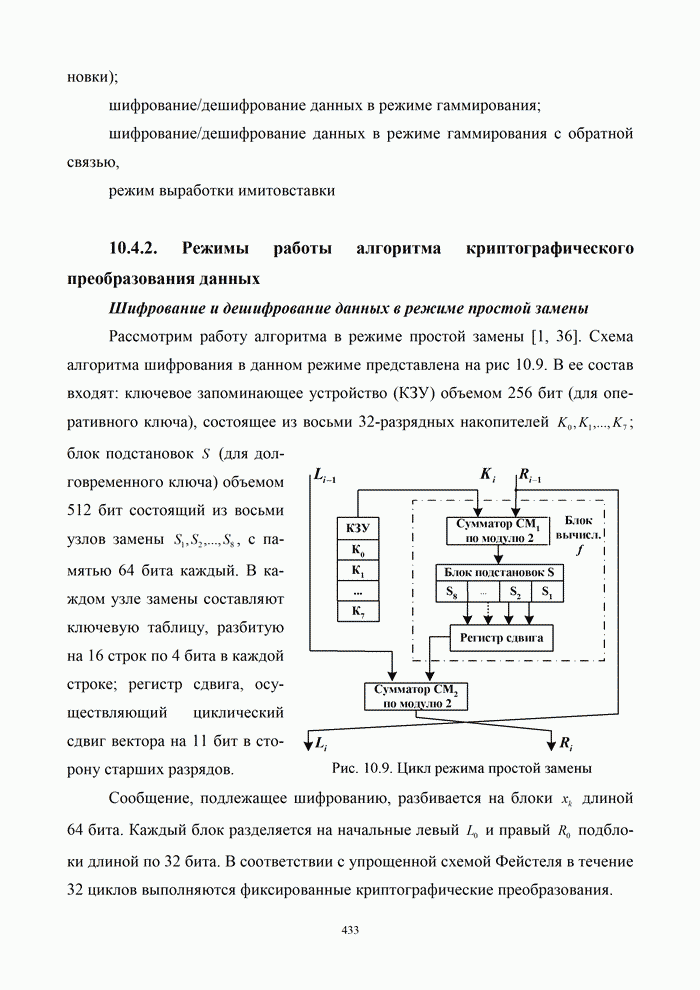
- 10.4. Алгоритмы криптографической защиты
- 10.4.1. Алгоритм криптографической защиты информации согласно ГОСТ 28147-89
- Контрольные вопросы
- Заключение
- Список литературы