| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
9.5.2. Алгоритмы дискретного и быстрого преобразований Фурье
Как и при анализе аналоговых сигналов, дискретные сигналы можно представить во временной и частотной областях. В настоящее время обработку дискретных сигналов чаще всего проводят в частотной области, что диктуется значительными сокращениями объема цифровой аппаратуры и времени обработки.
Пусть дискретной
обработке подвергается аналоговый импульсный сигнал ![]() длительностью
длительностью ![]() , имеющий
спектральную плотность
, имеющий
спектральную плотность ![]() (рис. 9.16, а, б). Теоретически можно
предположить, что дискретизация сигнала производится периодической
последовательностью дельта-функций
(рис. 9.16, а, б). Теоретически можно
предположить, что дискретизация сигнала производится периодической
последовательностью дельта-функций
|
|
(9.35) |
где ![]() — требуемое число отсчетов,
отвечающих теореме Котельникова.
— требуемое число отсчетов,
отвечающих теореме Котельникова.
Подставив в (9.32)
пределы суммирования от 0 до ![]() , и заменив здесь и далее для упрощения
и уменьшения объема формул
, и заменив здесь и далее для упрощения
и уменьшения объема формул ![]() , запишем выражение для дискретного
сигнала (рис. 9.16, е)
, запишем выражение для дискретного
сигнала (рис. 9.16, е)
|
|
(9.36) |
На основании формулы (9.36)
можно сделать вывод, что спектр данного дискретного сигнала имеет периодическую
структуру с периодом по оси частот ![]() (рис. . 9.16, г). Мысленно продолжим
дискретный сигнал периодически с интервалом
(рис. . 9.16, г). Мысленно продолжим
дискретный сигнал периодически с интервалом ![]() (рис. . 9.16, д).
(рис. . 9.16, д).![]()

Рис. 9.16. Графики к выводу ДПФ:
а,б - аналоговый сигнал и его спектр; в,г - дискретный сигнал и его спектр; д - периодическая последовательность дискретного сигнала; е - ДПФ сигнала
![]() ,
, ![]() .
.
По аналогии с представлением периодических непрерывных сигналов
![]() , где
, где  - комплексная амплитуда
- комплексная амплитуда ![]() -й гармоники. Дискретную
функцию
-й гармоники. Дискретную
функцию ![]() можно
разложить в комплексный ряд Фурье:
можно
разложить в комплексный ряд Фурье:
|
|
(9.37) |
где ![]() - частота дискретизации сигнала.
- частота дискретизации сигнала.
Коэффициенты этого ряда
|
|
(9.38) |
Для определения
коэффициентов проделаем следующее. Подставим формулу (9.36) в (9.38) и заменим
параметр ![]() .
Введем безразмерную переменную
.
Введем безразмерную переменную ![]() и запишем
и запишем
 .
.
Используя фильтрующее свойство дельта – функции, находим
|
|
(9.39) |
Это называется дискретным
преобразованием Фурье (ДПФ). Дискретное преобразование Фурье по существу
представляет собой алгоритм вычисления гармонических составляющих спектра ![]() по заданным дискретным
отсчетам
по заданным дискретным
отсчетам ![]() аналогового
сигнала
аналогового
сигнала ![]() ,
что значительно сокращает время обработки. Характерный вид модулей
коэффициентов
,
что значительно сокращает время обработки. Характерный вид модулей
коэффициентов ![]() показан
на рис. 9.16,е.
показан
на рис. 9.16,е.
Следует отметить ряд свойств ДПФ, которые вытекают из определения (9.39).
1. Дискретное преобразование Фурье обладает свойством линейности: линейной комбинации дискретных сигналов соответствует линейная комбинация их ДПФ.
2. Коэффициент ![]() представляет собой
среднее значение (постоянную составляющую) всех дискретных отсчетов сигнала
представляет собой
среднее значение (постоянную составляющую) всех дискретных отсчетов сигнала
![]() .
.
3. Число различных
коэффициентов ![]() равно
числу отсчетов
равно
числу отсчетов ![]() за
длительность сигнала
за
длительность сигнала ![]() ; при
; при ![]() коэффициент
коэффициент ![]() .
.
Пример 9.2. Определить
коэффициенты ДПФ дискретизированного прямоугольного импульса единичной
амплитуды, заданного четырьмя отсчетами ![]() .
.
Решение. Используя
основную формулу (9.39), вычислим пять первых коэффициентов ДПФ: ![]() ;
;
![]() ;
; ![]()
![]() ;
; ![]() .
.
При изучении теории ДПФ
возникает очевидный вопрос: можно ли по известным коэффициентам ДПФ вычислить
отсчетные значения ![]() непрерывного
сигнала? По аналогии с периодическими сигналами представим заданную
периодическую последовательность отсчетов комплексным рядом Фурье. Заменив в
(7.25)
непрерывного
сигнала? По аналогии с периодическими сигналами представим заданную
периодическую последовательность отсчетов комплексным рядом Фурье. Заменив в
(7.25) ![]() ,
, ![]() и, учитывая, что
суммируется конечное число членов ряда, запишем
и, учитывая, что
суммируется конечное число членов ряда, запишем
|
|
(9.40) |
Данное соотношение определяет алгоритм обратного дискретного преобразования Фурье (ОДПФ). Формулы (9.39) и (9.40) являются аналогами прямого и обратного преобразований Фурье для непрерывных сигналов.
Выражение (9.39)
показывает, что для определения одного коэффициента ДПФ сигнальной
последовательности из N отсчетов, необходимо выполнить около N
операций умножения на комплексное число и столько же сложений, а для нахождения
всех коэффициентов объем вычислений составит ![]() . В частности, при
. В частности, при ![]() надо осуществить более
миллиона
надо осуществить более
миллиона ![]() умножений
и сложений. Если длины обрабатываемых массивов превышают тысячу единиц, то
дискретная спектральная обработка сигналов в реальном масштабе времени требует высокопроизводительных
вычислительных комплексов.
умножений
и сложений. Если длины обрабатываемых массивов превышают тысячу единиц, то
дискретная спектральная обработка сигналов в реальном масштабе времени требует высокопроизводительных
вычислительных комплексов.

Рис.9.17. Разбиение последовательности
![]() на две
подпоследовательности: а - входная; б - с четными номерами; в
- с нечетными номерами
на две
подпоследовательности: а - входная; б - с четными номерами; в
- с нечетными номерами
Многократно сократить
число операций позволяет быстрое преобразование Фурье (БПФ), обеспечивающее
вычисление коэффициентов ДПФ за меньшее число операций. В основу БПФ положен
принцип разбиения заданной последовательности отсчетов дискретного сигнала на несколько
промежуточных последовательностей. Для этого число отсчетов N
разделяется на множители (например, ![]() ). Затем определяются спектры этих промежуточных
последовательностей и через них находится спектр всего сигнала. В зависимости
от состава, числа и порядка следования указанных множеств можно создать
различные алгоритмы БПФ. В цифровой технике удобно обрабатывать сигнальные
последовательности со значениями N, являющимся степенью числа два (4, 8, 16 и
так далее). Это позволяет многократно делить входную последовательность
отсчетов на подпоследовательности.
). Затем определяются спектры этих промежуточных
последовательностей и через них находится спектр всего сигнала. В зависимости
от состава, числа и порядка следования указанных множеств можно создать
различные алгоритмы БПФ. В цифровой технике удобно обрабатывать сигнальные
последовательности со значениями N, являющимся степенью числа два (4, 8, 16 и
так далее). Это позволяет многократно делить входную последовательность
отсчетов на подпоследовательности.
Пусть требуется вычислить
ДПФ дискретного сигнала ![]() , имеющего четное число отсчетов (рис. 9.17,
а), причем
, имеющего четное число отсчетов (рис. 9.17,
а), причем ![]() ;
;
![]() - целое число.
- целое число.
Представим входную последовательность
в виде двух подпоследовательностей с четными и нечетными номерами и половинным
числом членов в каждой (рис. 9.17, б,в): ![]() ;
; ![]() ;
;![]() .
.
Коэффициенты ДПФ для последовательностей с четными и нечетными номерами запишем отдельно:

|
|
(9.41) |
Коэффициенты ![]() результирующего ДПФ
входной последовательности можно выразить через параметры
результирующего ДПФ
входной последовательности можно выразить через параметры ![]() и
и ![]() двух вновь введенных подпоследовательностей.
Анализ (9.41) показывает, что в диапазоне номеров
отсчетов от 0 до
двух вновь введенных подпоследовательностей.
Анализ (9.41) показывает, что в диапазоне номеров
отсчетов от 0 до ![]() ,
ДПФ входной последовательности определяется соотношением:
,
ДПФ входной последовательности определяется соотношением:
|
|
(9.42) |
Так как ДПФ четной и
нечетной последовательностей являются периодическими, с периодом ![]() , то
, то ![]() ;
; ![]() .
.
Запишем экспоненциальный
множитель в формуле (9.42) при ![]() , т.е. для ДПФ
, т.е. для ДПФ ![]() , в виде:
, в виде:
![]()
С учетом двух последних
выражений находим коэффициенты ДПФ входной последовательности для отсчетов с
номерами от ![]() до
до![]() :
:
|
|
(9.43) |
Соотношения (9.42) и (9.43)
полностью определяют алгоритмы вычисления коэффициентов с помощью БПФ. Отметим,
что экспоненциальные фазовые множители ![]() в этих алгоритмах учитывают влияние
сдвига нечетной подпоследовательности относительно четной.
в этих алгоритмах учитывают влияние
сдвига нечетной подпоследовательности относительно четной.
Чтобы еще уменьшить число
вычислений, четную и нечетную подпоследовательности также разбивают каждую на
две промежуточные части. Разбиение продолжают вплоть до получения простейших
двухэлементных последовательностей. Определив ДПФ данных простейших пар
отсчетов, можно вычислить ДПФ четырехэлементных, восьмиэлементных и так далее
подпоследовательностей. При объединении ДПФ четной и нечетной
подпоследовательностей используют алгоритмы (9.42) и (9.43), подставляя в них
соответствующие значения номеров ![]() и
и ![]() .
.
Нетрудно заметить, что
вычисления по формулам (9.41) не потребуют операций умножения, в (9.41) имеются
только сложение и вычитание комплексных чисел. Учитываться же должны лишь
операции умножения в алгоритмах (9.42) и (9.43) для различных ![]() при разбиениях
массива отчетов на мелкие подпоследовательности. Число этих операций при первом
разбиении составляло
при разбиениях
массива отчетов на мелкие подпоследовательности. Число этих операций при первом
разбиении составляло ![]() . Такое же число
. Такое же число ![]() операций требуется выполнить
при каждом следующем разбиении. Таким образом, вдвое увеличивается число
подпоследовательностей и вдвое сокращается наибольшее число
операций требуется выполнить
при каждом следующем разбиении. Таким образом, вдвое увеличивается число
подпоследовательностей и вдвое сокращается наибольшее число ![]() в формулах (7.30), (7.31).
в формулах (7.30), (7.31).
Вычисление коэффициентов ДПФ
последовательности из N отсчетов по алгоритмам БПФ требует примерно ![]() операций умножения.
Алгоритмы БПФ сокращают число операций по сравнению с алгоритмами ДПФ в
операций умножения.
Алгоритмы БПФ сокращают число операций по сравнению с алгоритмами ДПФ в ![]() раз. Например, при
количестве отсчетов
раз. Например, при
количестве отсчетов ![]() , имеем
, имеем ![]() и сокращение числа операций составляет
и сокращение числа операций составляет ![]() . При очень больших
массивах отсчетов входного сигнала выигрыш в скорости обработки может достигать
нескольких тысяч.
. При очень больших
массивах отсчетов входного сигнала выигрыш в скорости обработки может достигать
нескольких тысяч.
Таким образом, в алгоритмах
БПФ выполняются операции сложения и вычитания с умножением одного из
компонентов на экспоненциальный множитель ![]() . Эту базовую для БПФ операцию очень
удобно представлять сигнальным графом, называемым в цифровой технике
«бабочкой».
. Эту базовую для БПФ операцию очень
удобно представлять сигнальным графом, называемым в цифровой технике
«бабочкой».
БПФ по рассмотренному методу (его называют методом прореживания отсчетов
во времени) осуществляют, как правило, в следующем порядке. Сначала для
получения желательного при обработке сигнала порядка следования отсчетов ![]() ,
,![]() , выполняется двоично-инверсная
перестановка элементов исходной последовательности
, выполняется двоично-инверсная
перестановка элементов исходной последовательности ![]() ,
, ![]() . Для этого записывают порядковые номера элементов
. Для этого записывают порядковые номера элементов ![]() в двоичном коде и инвертируют порядок
следования разрядов. Новый порядок следования элементов
в двоичном коде и инвертируют порядок
следования разрядов. Новый порядок следования элементов ![]() определяется номерами,
полученными после инверсии разрядов.
определяется номерами,
полученными после инверсии разрядов.
Пример при N=4
|
u(l) |
|
u(k) |
|
|
0→ |
00→ |
00→ |
0→ |
|
1→ |
01→ |
10→ |
2→ |
|
2→ |
10→ |
01→ |
1→ |
|
3→ |
11→ |
11→ |
3→ |
Новый порядок следования элементов: ![]() . После этого поступают так. На
первом этапе вычислений определяют двух точечные ДПФ "новой"
последовательности
. После этого поступают так. На
первом этапе вычислений определяют двух точечные ДПФ "новой"
последовательности ![]() ,
объединяя попарно элементы этой последовательности. На втором этапе из двух
точечных ДПФ получают четырех точечные ДПФ, пользуясь основной базовой
операцией данного метода (см. ниже). Затем четырех точечные ДПФ объединяют в восьми
точечные и т.д.
,
объединяя попарно элементы этой последовательности. На втором этапе из двух
точечных ДПФ получают четырех точечные ДПФ, пользуясь основной базовой
операцией данного метода (см. ниже). Затем четырех точечные ДПФ объединяют в восьми
точечные и т.д.
Базовые операции ![]() и
и ![]() показывают, как два входных числа А и
В объединяются для получения двух выходных чисел X и Y. Для метода прореживания во времени базовая операция изображается
«бабочкой», представленной на рис. 9.18. Надпись
показывают, как два входных числа А и
В объединяются для получения двух выходных чисел X и Y. Для метода прореживания во времени базовая операция изображается
«бабочкой», представленной на рис. 9.18. Надпись ![]() у стрелки, идущей вверх, означает умножение
у стрелки, идущей вверх, означает умножение ![]() на величину В.
на величину В.

Рис. 9.18. Операция «бабочка», используемая
при реализации алгоритма БПФ
При вычислении двух точечного ДПФ ![]() и выходные числа X и Y определяются без операции умножения
и выходные числа X и Y определяются без операции умножения ![]() ,
, ![]() .
.
Пример 9.3. Построим граф вычисления БДНФ с прореживанием во времени для N=4 (рис. 9.19).

Рис. 9.19. Граф для вычисления БПФ при N=4
Учитывая, что![]() ,
, ![]() , получаем согласно
приведенному графу
, получаем согласно
приведенному графу
![]()
![]()
![]()
![]()
На рис. 9.20 показан граф вычисления БДПФ с прореживанием во времени для N=8.

Рис. 9.20. Граф для вычисления БПФ при N=8
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Список сокращений
- Основные обозначения
- ВВЕДЕНИЕ
- Глава 1. Сообщения, сигналы и помехи, их математические модели
- 1.1. Основные понятия и определения
- 1.1.1. Сообщение, сигнал, модуляция
- 1.1.2. Основные параметры сигналов
- 1.2. Системы связи. Каналы связи
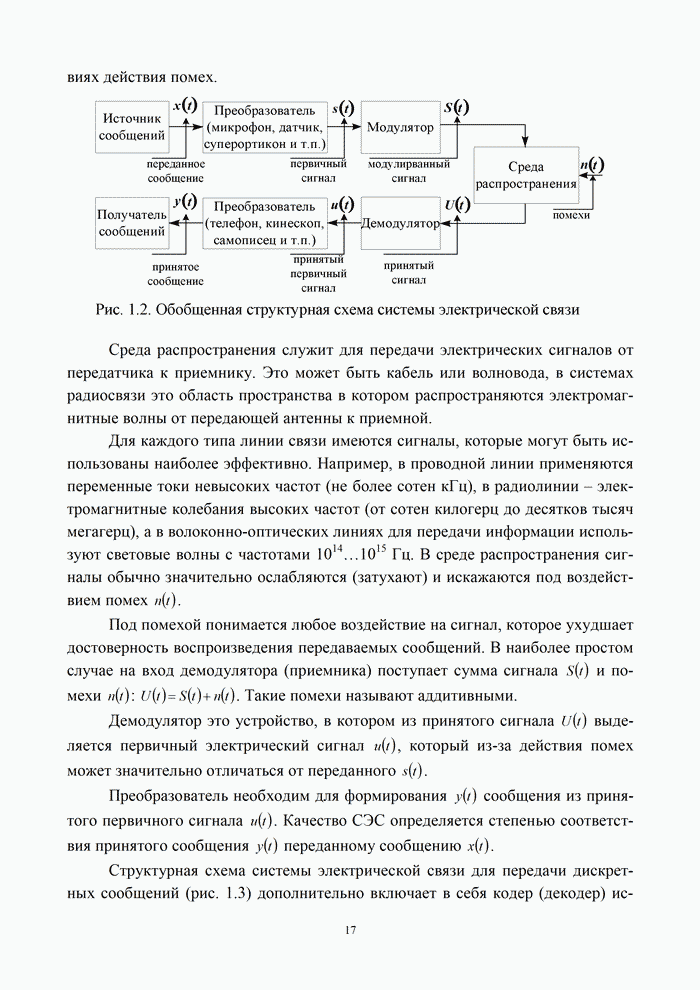
- 1.2.1. Структура канала электросвязи
- 1.2.2. Линия и сеть связи
- 1.2.3. Помехи и искажения в канале
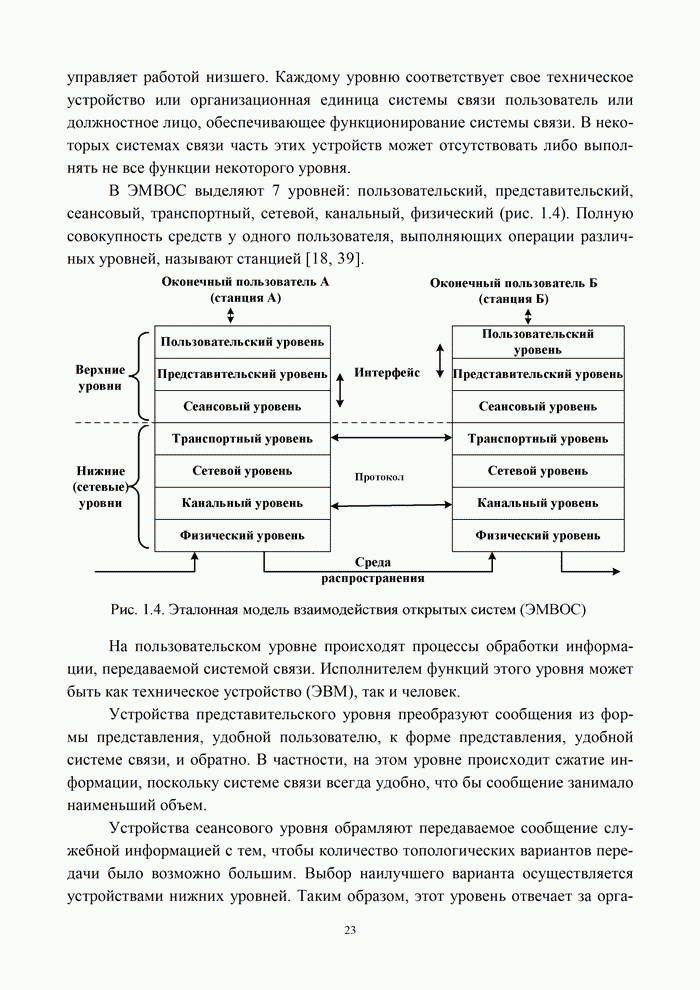
- 1.2.4. Эталонная модель взаимодействия открытых систем
- 1.2.5. Модели каналов связи и их математическое описание
- 1.3. Способы описания сигналов и помех
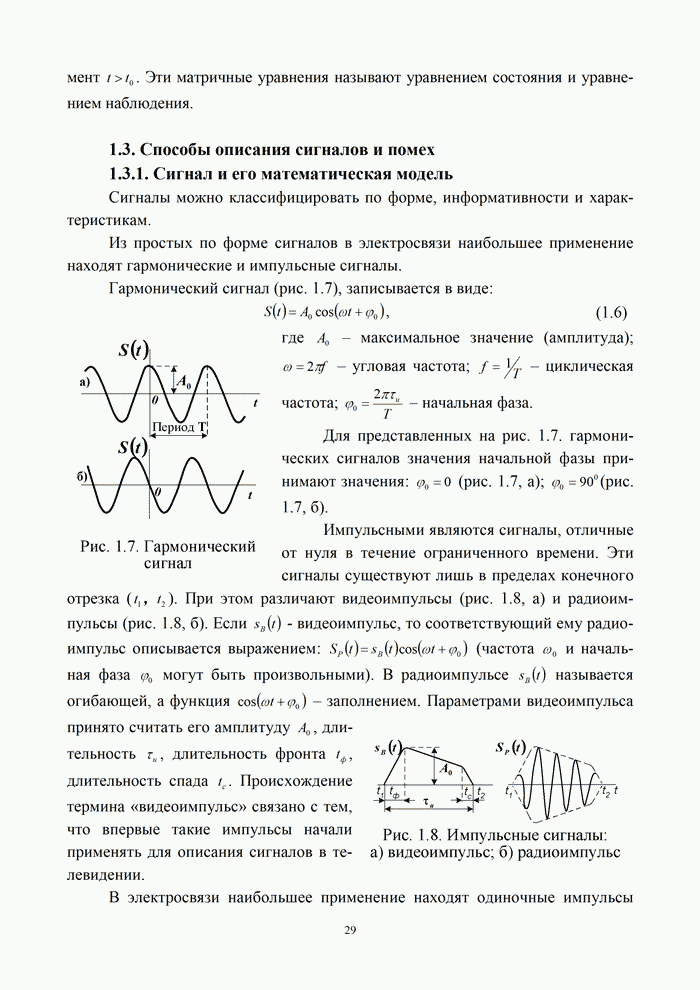
- 1.3.1. Сигнал и его математическая модель
- 1.3.2. Энергетические характеристики детерминированного сигнала
- 1.4.2. Представление сигналов и помех рядом Фурье
- 1.4.3. Применение преобразования Фурье для непериодических сигналов
- 1.5. Теорема Котельникова
- 1.6. Пространство сигналов
- 1.6.1. Линейное пространство
- 1.6.2. Представление сигнала в многомерном пространстве
- 1.7. Сигналы как случайные процессы
- 1.7.1. Характеристики случайного процесса
- 1.7.2. Флуктуационный шум
- 1.8. Комплексное представление сигналов и помех
- 1.8.1. Понятие аналитического сигнала
- 1.8.2. Огибающая, мгновенная фаза и мгновенная частота узкополосного случайного процесса
- Контрольные вопросы
- Глава 2. Методы формирования и преобразования сигналов
- 2.1. Модуляция сигналов
- 2.1.1. Амплитудная модуляция гармонической несущей
- 2.1.2. Балансная и однополосная модуляция гармонической несущей
- 2.2. Методы угловой модуляции
- 2.2.1. Принципы частотной и фазовой (угловой) модуляции
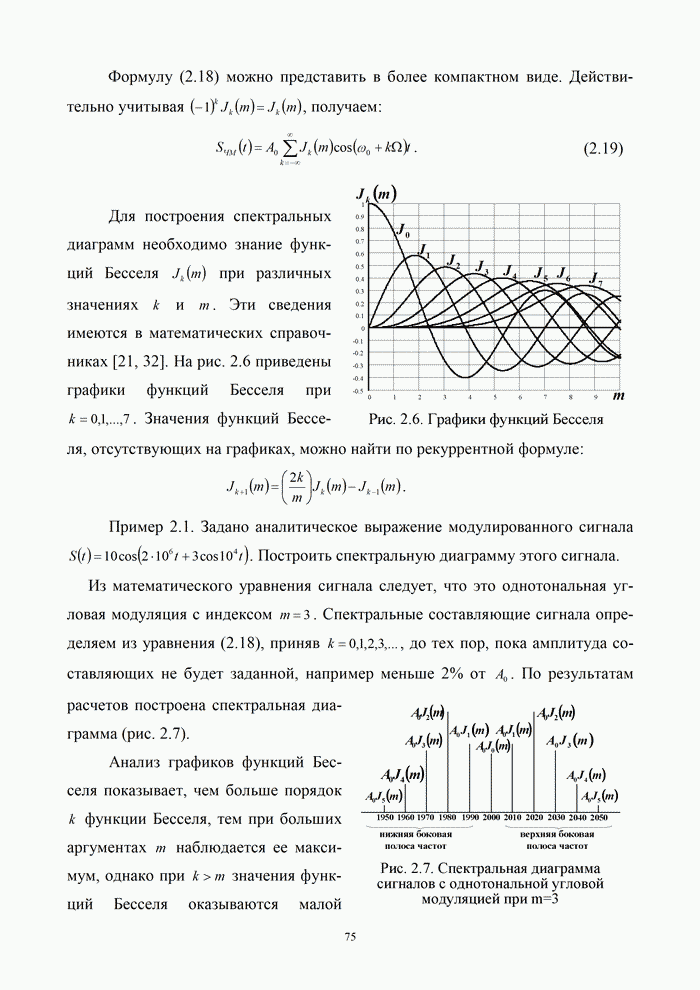
- 2.2.2. Спектр сигналов угловой модуляции
- 2.3. Формирование и детектирование модулированных сигналов
- 2.3.1. Формирование и детектирование сигналов амплитудной и однополосной амплитудной модуляции
- 2.3.2. Формирование и детектирование сигналов угловой модуляции
- 2.4. Манипуляция сигналов
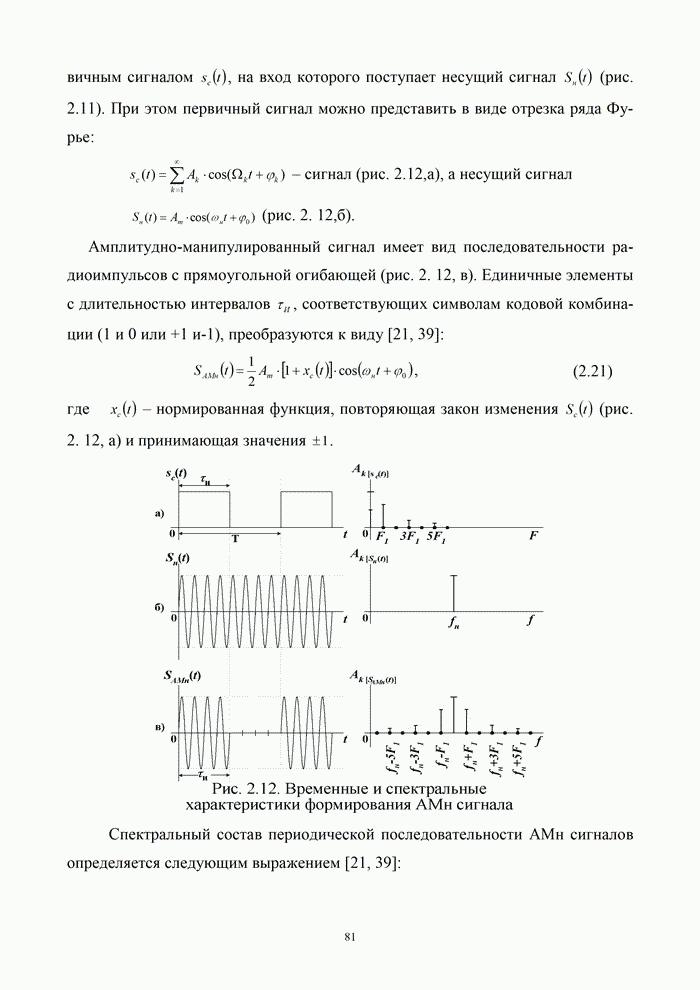
- 2.4.1. Временные и спектральные характеристики амплитудно-манипулированных сигналов
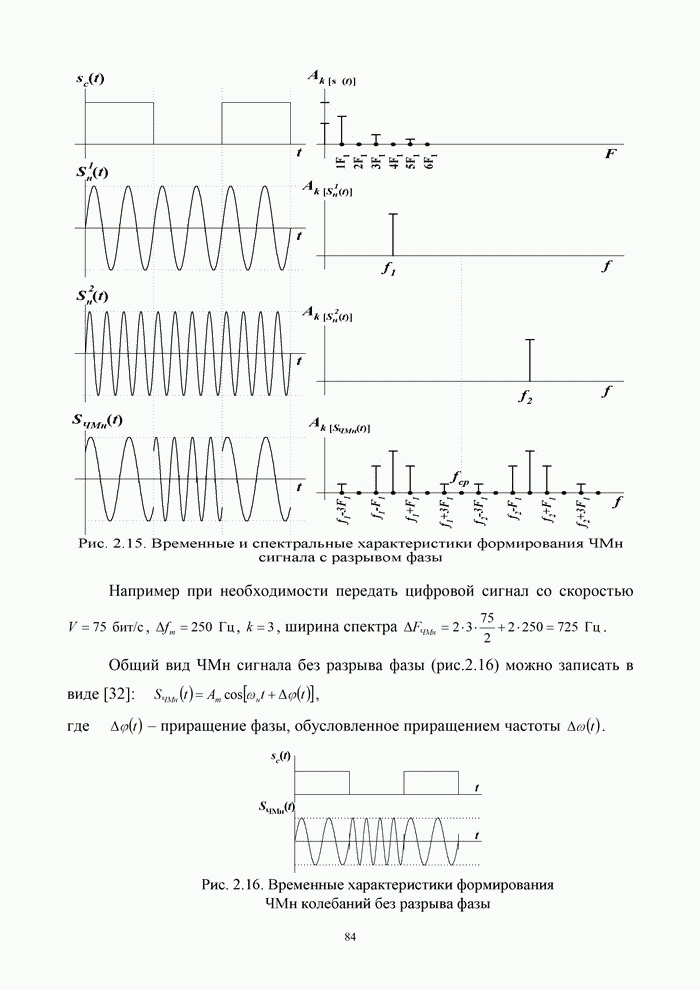
- 2.4.2. Временные и спектральные характеристики частотно-манипулированных сигналов
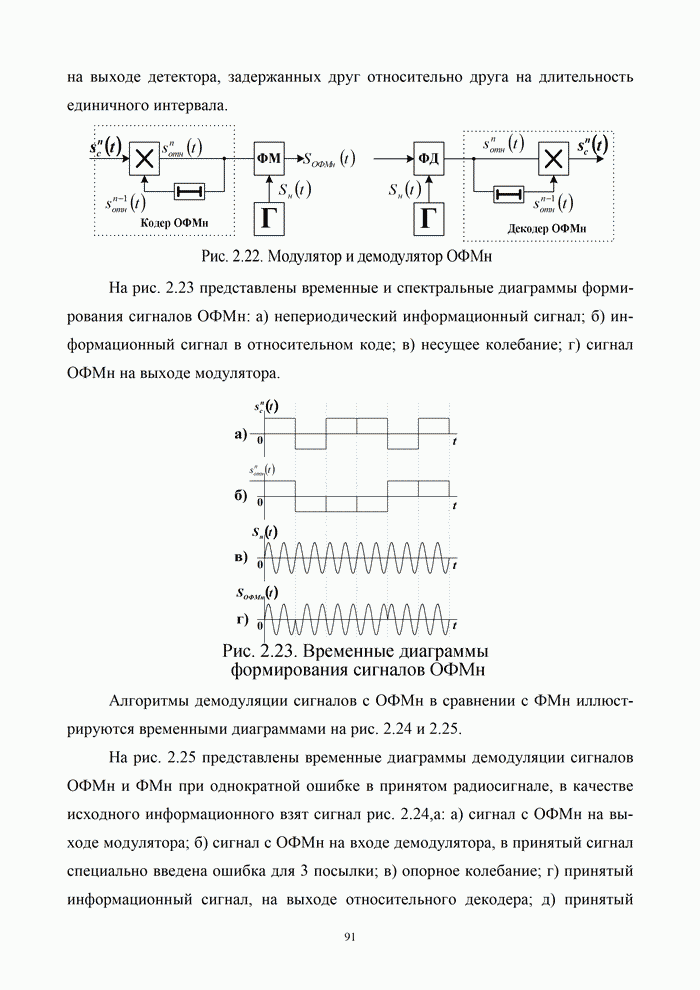
- 2.4.3. Фазовая (относительно-фазовая) манипуляция сигналов
- 2.5. Системы связи с многопозиционной относительной фазовой манипуляцией
- 2.5.1. Принцип формирования сигнала с многократной относительной фазовой манипуляцией
- 2.5.2. Квадратурная относительно-фазовая манипуляция (КОФМ)
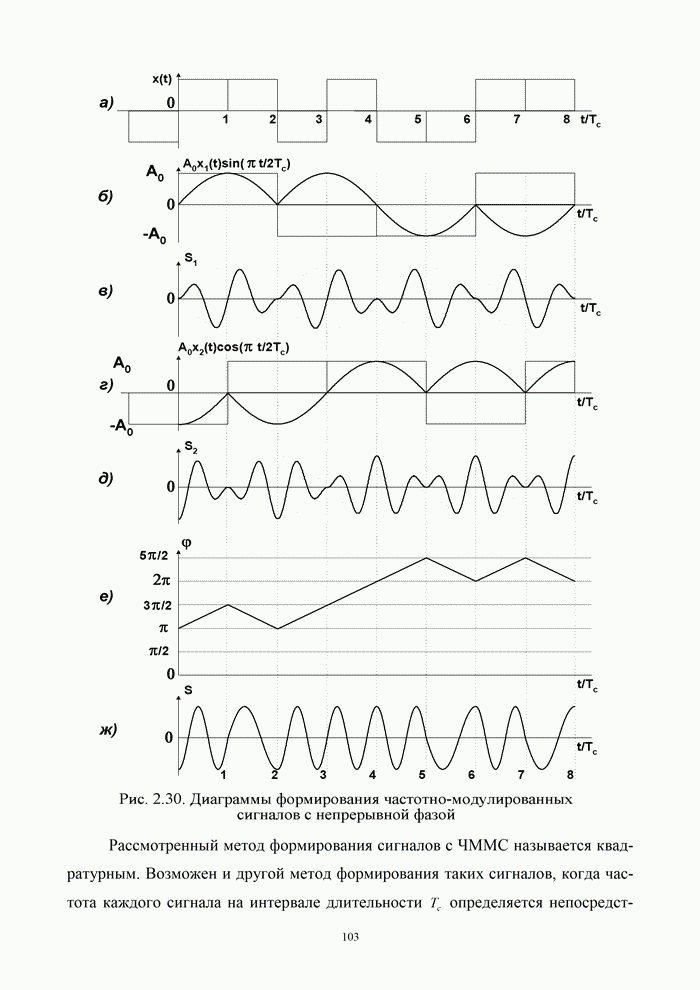
- 2.5.3. Принцип частотной модуляции с непрерывной фазой
- Контрольные вопросы
- Глава 3. Помехоустойчивость приема дискретных сообщений
- 3.1. Критерии качества и правила приема дискретных сообщений
- 3.1.1. Понятие о помехоустойчивости систем электрической связи
- 3.1.2. Задача оптимального приема
- 3.1.3. Вычисление вероятностей ошибок
- 3.2. Оптимальная демодуляция при когерентном приеме сигналов
- 3.2.1. Оптимальные алгоритмы приема при полностью известных сигналах
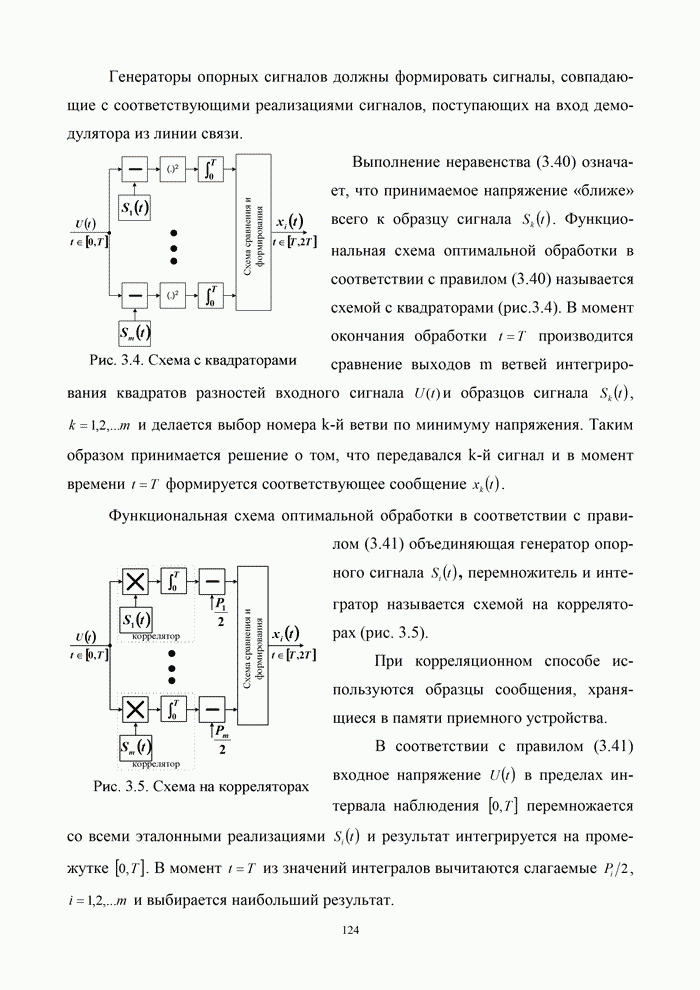
- 3.2.2. Реализация алгоритмов оптимального когерентного приема
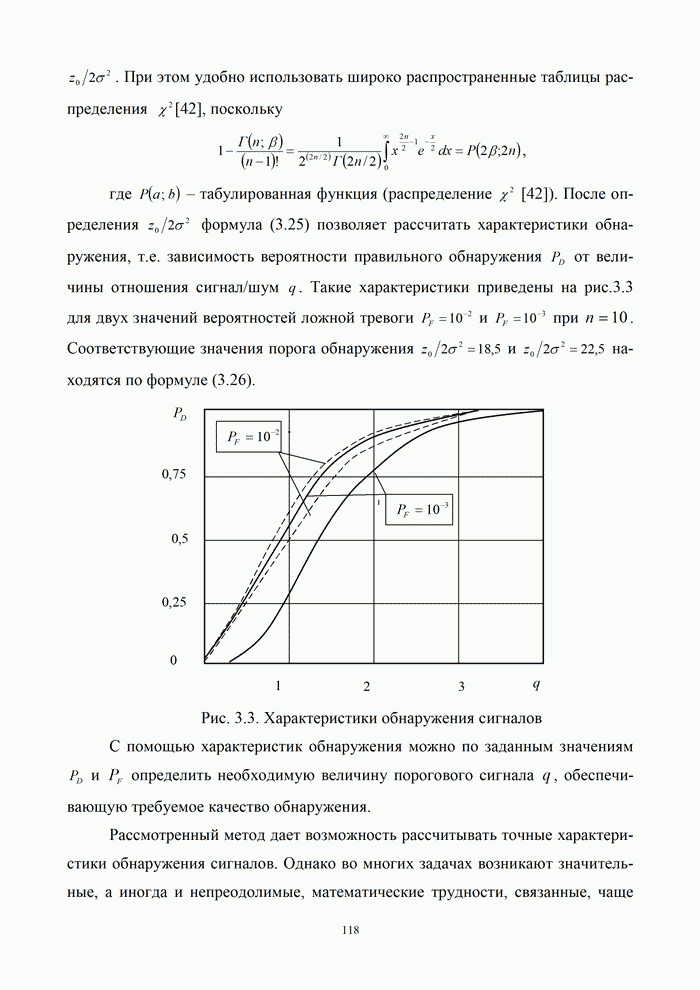
- 3.3. Помехоустойчивость приема сигналов с известными параметрами
- 3.4. Прием сигналов с неопределенной фазой
- 3.4.1. Оптимальный некогерентный прием дискретных сигналов
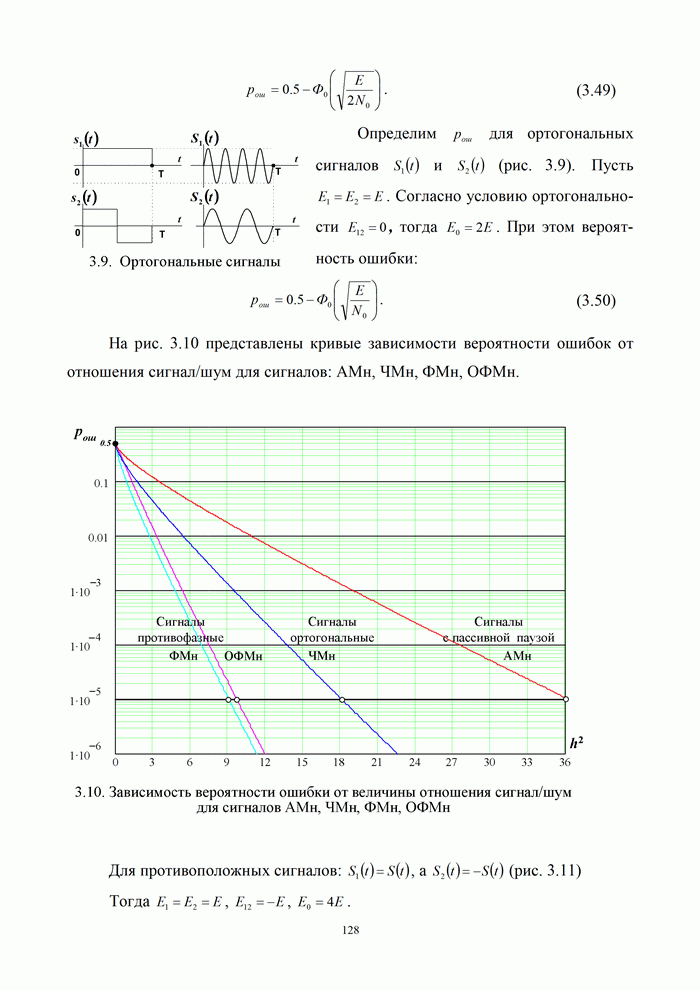
- 3.4.2. Помехоустойчивость оптимального некогерентного приема
- 3.5. Подоптимальные методы приема
- 3.5.1. Причины применения неоптимальных методов приема
- 3.5.2. Квазиоптимальные методы приема
- Контрольные вопросы
- Глава 4. Теория передачи информации
- 4.1. Информационные характеристики источника сообщений
- 4.1.1. Количественное определение информации
- 4.1.2. Энтропия и производительность дискретного источника сообщений
- 4.2. Пропускная способность дискретного канала
- 4.2.1. Количество информации переданной по дискретному каналу
- 4.2.2. Пропускная способность дискретного канала
- 4.2.3. Пропускная способность симметричного дискретного канала без памяти
- 4.3. Методы сжатия дискретных сообщений
- 4.3.1. Условия существования оптимального неравномерного кода
- 4.3.2. Прямая и обратная теоремы кодирования источника неравномерными кодами
- 4.3.3. Показатели эффективности сжатия
- 4.3.4. Кодирование источника дискретных сообщений методом Шеннона-Фано
- 4.3.5. Кодирование источника дискретных сообщений методом Хаффмена
- 4.4. Пропускная способность непрерывного канала
- 4.4.1. Постановка задачи передачи дискретных сообщений в непрерывном канале
- 4.4.2. Количество информации, переданной по непрерывному каналу
- 4.4.3. Пропускная способность непрерывного канала
- Контрольные вопросы
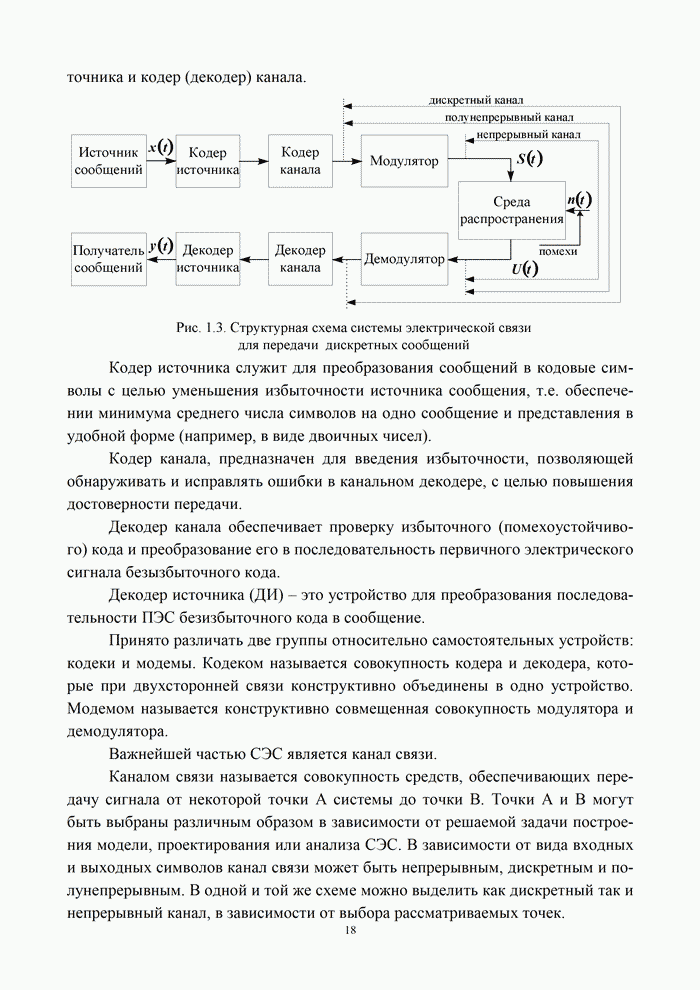
- Глава 5. Теория кодирования сообщений
- 5.1. Помехоустойчивое кодирование: блочные и непрерывные коды
- 5.1.1. Постановка задачи помехоустойчивого кодирования
- 5.1.2. Классификация кодов
- 5.1.3. Основные характеристики и свойства блочных кодов
- 5.2. Эффективность помехоустойчивого кодирования
- 5.2.1. Эффективность кода в режиме исправления ошибок
- 5.2.2. Эффективность кода в режиме обнаружения ошибок
- 5.2.3. Эффективность помехоустойчивых кодов
- 5.3. Математические основы теории помехоустойчивого кодирования
- 5.3.1. Краткие сведения из теории чисел
- 5.3.2. Группы
- 5.3.3. Кольца и поля
- 5.3.4. Векторное пространство
- 5.3.5. Конечные поля
- 5.4. Линейные блочные коды
- 5.4.1. Система передачи дискретных сообщений
- 5.4.2. Параметры линейного кода
- 5.4.3. Полиномиальные циклические коды
- 5.4.4. Циклические коды и корни полиномов
- 5.4.5. Спектральное описание циклических кодов
- 5.4.6. Простейшие блочные линейные коды
- 5.5. Коды Боуза-Чоудхури-Хоквингема
- 5.5.1. Методы задания кодов БЧХ
- 5.5.2. Принципы декодирования кодов БЧХ
- 5.5.3. Методы реализации этапов декодирования кодов БЧХ
- 5.6. Коды Рида-Соломона
- 5.6.1. Основные определения
- 5.6.2. Обнаружение и исправление пакетов ошибок
- 5.7. Коды Рида-Маллера
- 5.7.1. Задание и декодирование кодов Рида-Маллера
- 5.7.2. Симплексные коды и m-последовательности
- 5.7.3. Связь между блочными кодами
- 5.8. Сверточные коды
- 5.8.1. Основные параметры
- 5.8.2. Способы задания сверточного кода
- 5.8.3. Алгоритм декодирования Витерби
- 5.9. Помехоустойчивость систем передачи дискретных сообщений
- 5.9.1. Две процедуры приема сигналов
- 5.9.2. Помехоустойчивость систем передачи информации при оптимальной процедуре приема
- 5.9.3. Помехоустойчивость систем передачи информации при посимвольном приеме сигналов
- Контрольные вопросы
- Глава 6. Сигналы с импульсной модуляцией
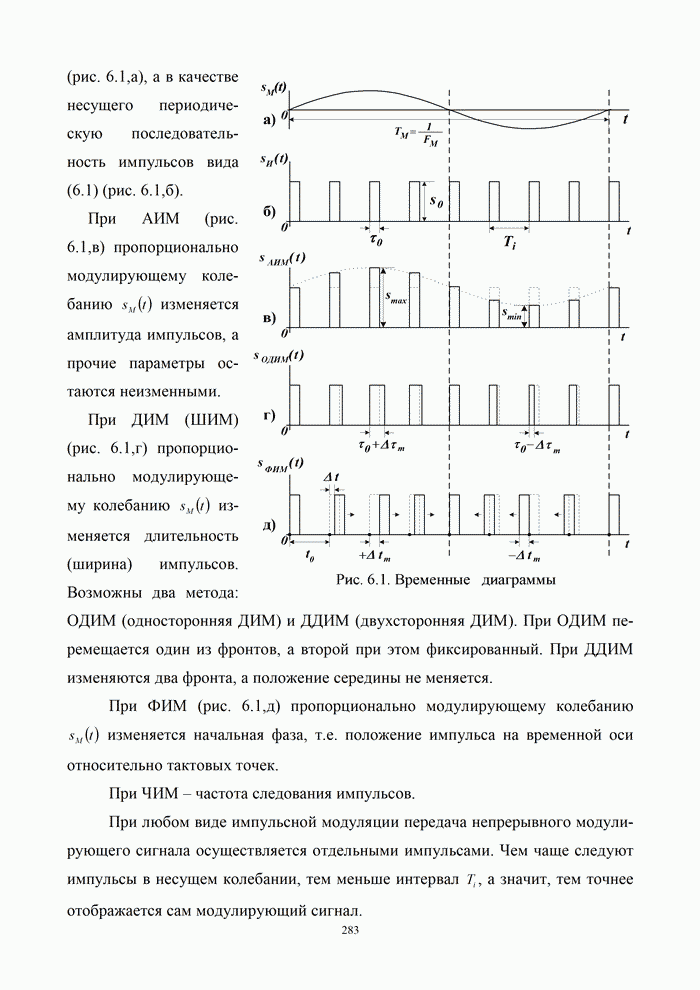
- 6.1. Методы импульсной модуляции
- 6.1.1. Импульсные методы передачи непрерывных сигналов
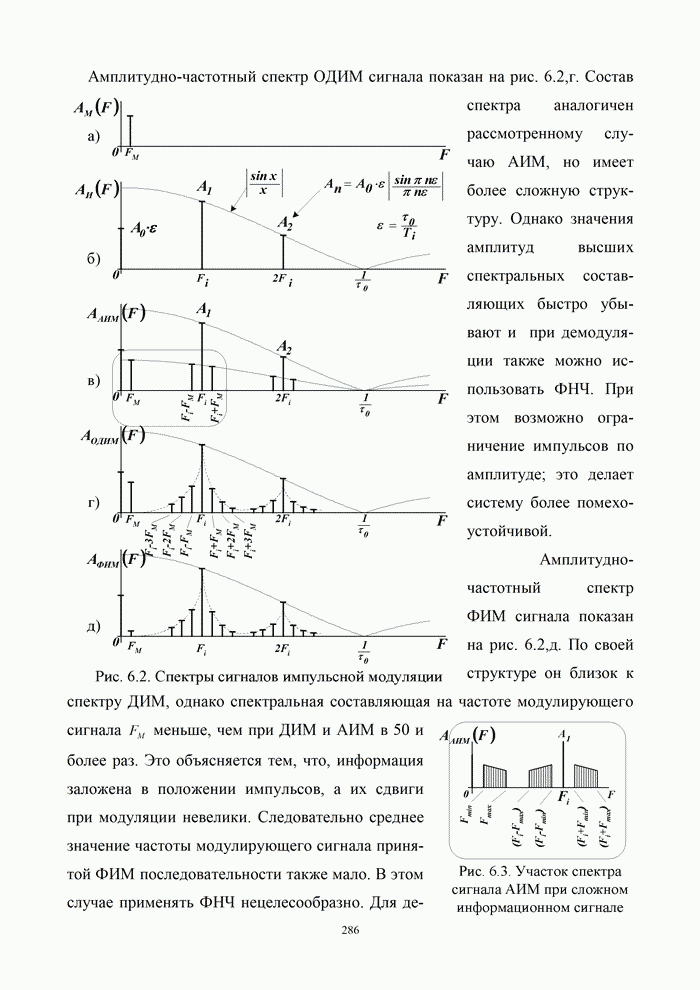
- 6.1.2. Спектральные характеристики импульсных методов модуляции
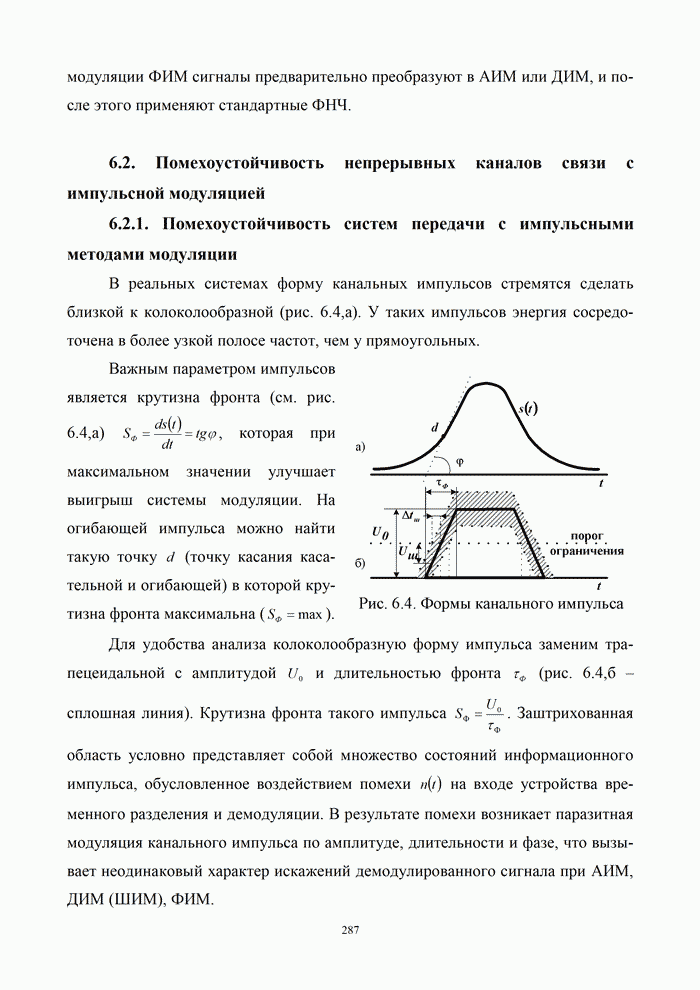
- 6.2. Помехоустойчивость непрерывных каналов связи с импульсной модуляцией
- 6.2.1. Помехоустойчивость систем передачи с импульсными методами модуляции
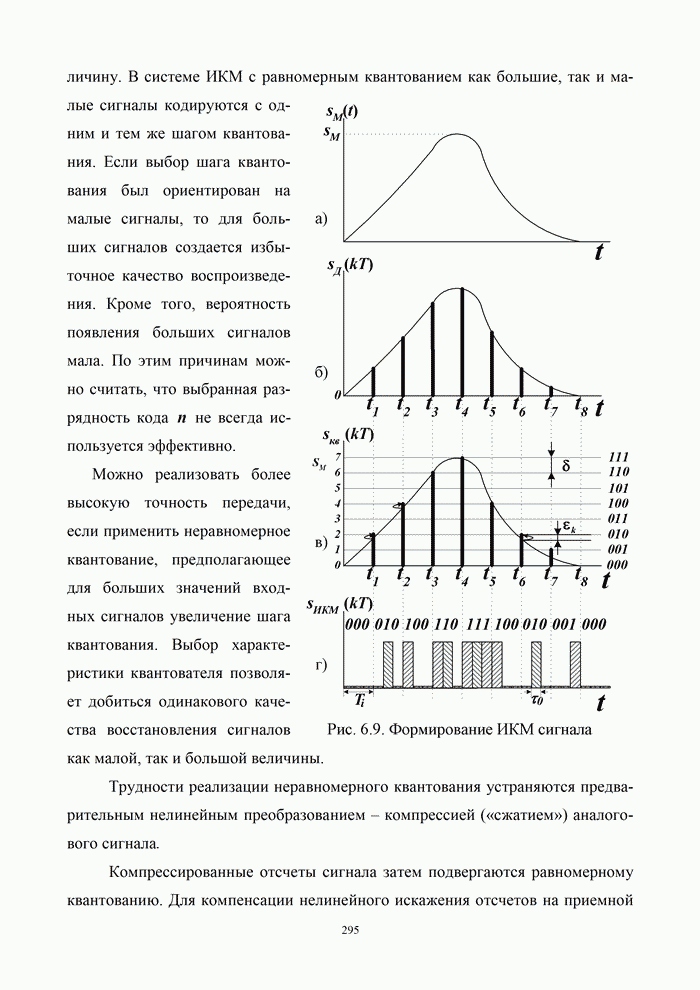
- 6.3. Цифровые методы передачи непрерывных сообщений
- 6.3.1. Передача сигналов с импульсно-кодовой модуляцией
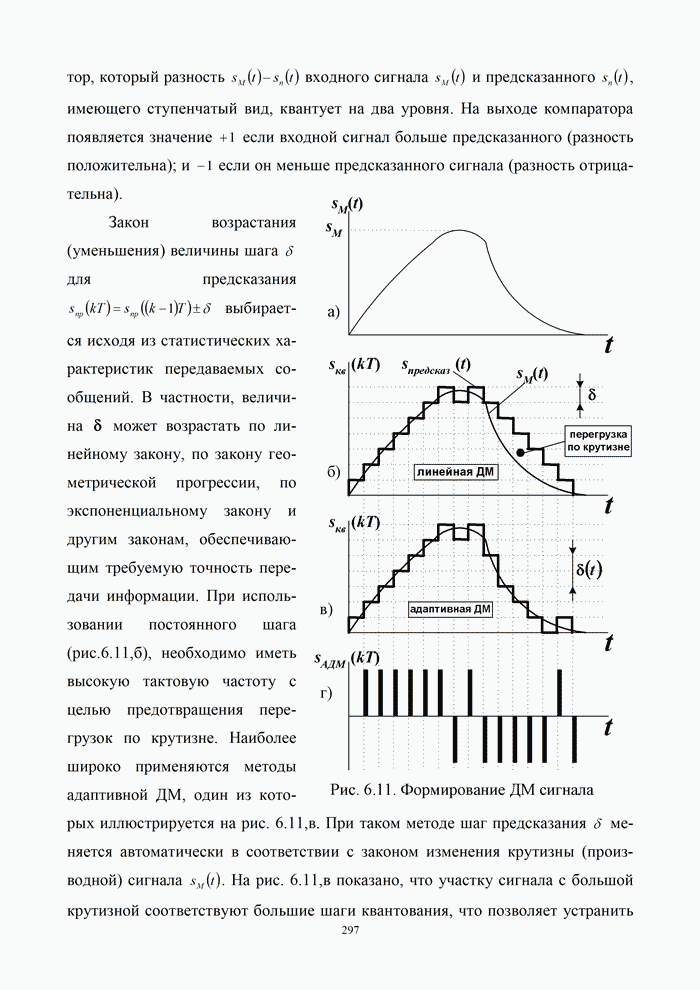
- 6.3.2. Передача сигналов с дельта модуляцией
- 6.3.3. Квантование сигналов в системах с ИКМ и ДМ
- Контрольные вопросы
- Глава 7. Методы приема сигналов в сложных условиях
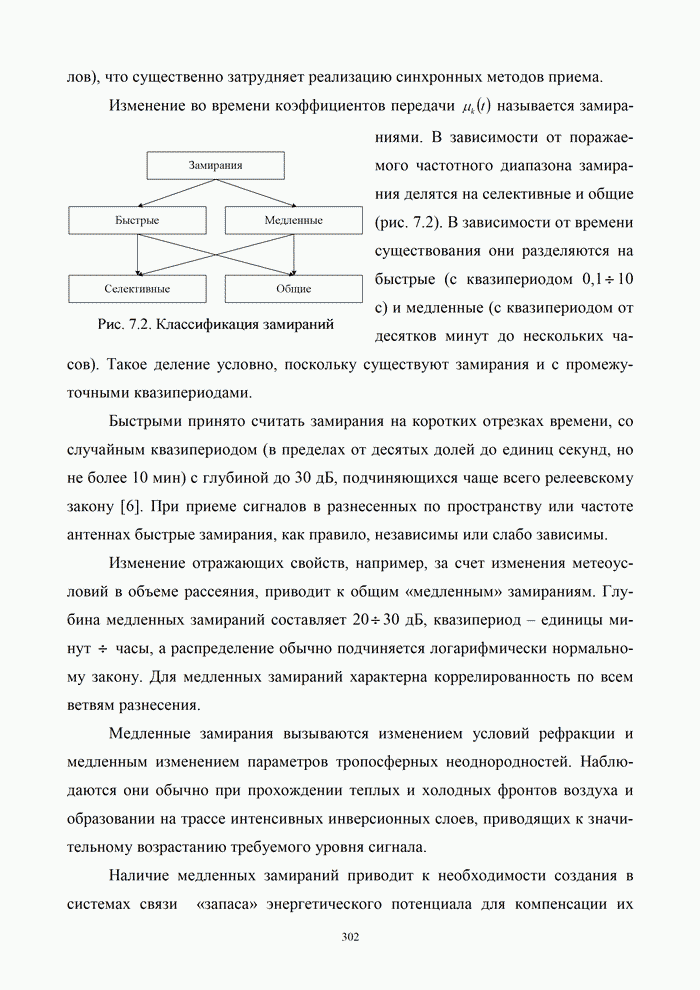
- 7.1. Прием сигналов в каналах с замираниями
- 7.1.1. Сущность замираний и их классификация
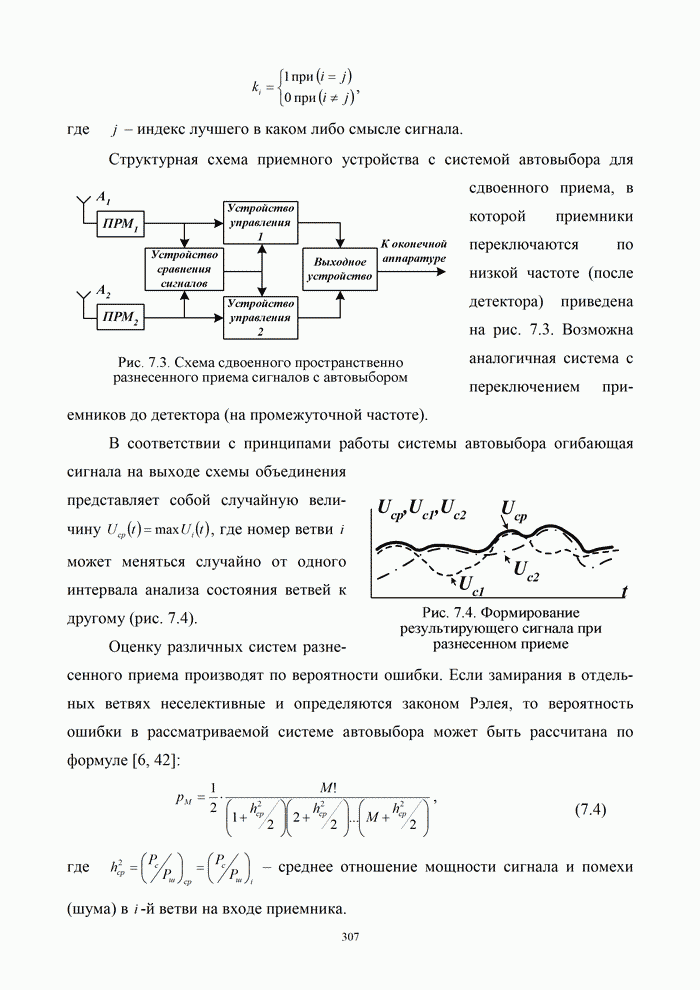
- 7.1.2. Принципы разнесенного приема сигналов
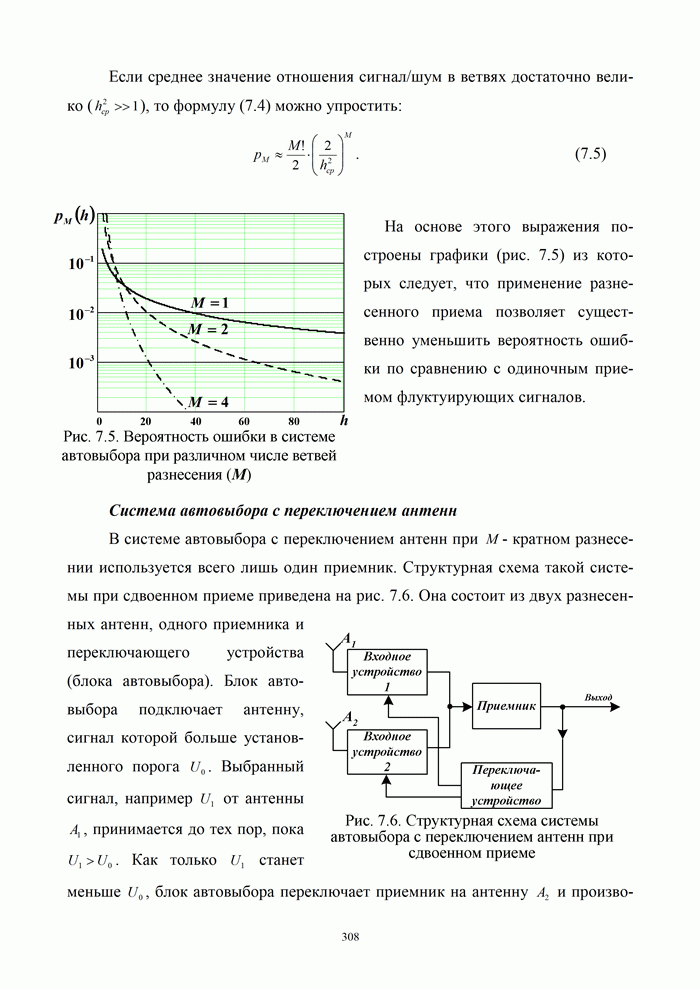
- 7.2. Методы борьбы с замираниями сигналов
- 7.2.1. Методы борьбы с замираниями в аналоговых системах связи
- 7.2.2. Методы борьбы с замираниями в цифровых системах связи
- 7.3. Методы борьбы с межсимвольной интерференцией
- 7.3.1. Причины возникновения и сущность межсимвольной интерференции
- 7.3.2. Обработка сигналов в каналах с межсимвольной интерференцией
- 7.3.3. Помехоустойчивость в каналах с межсимвольной интерференцией
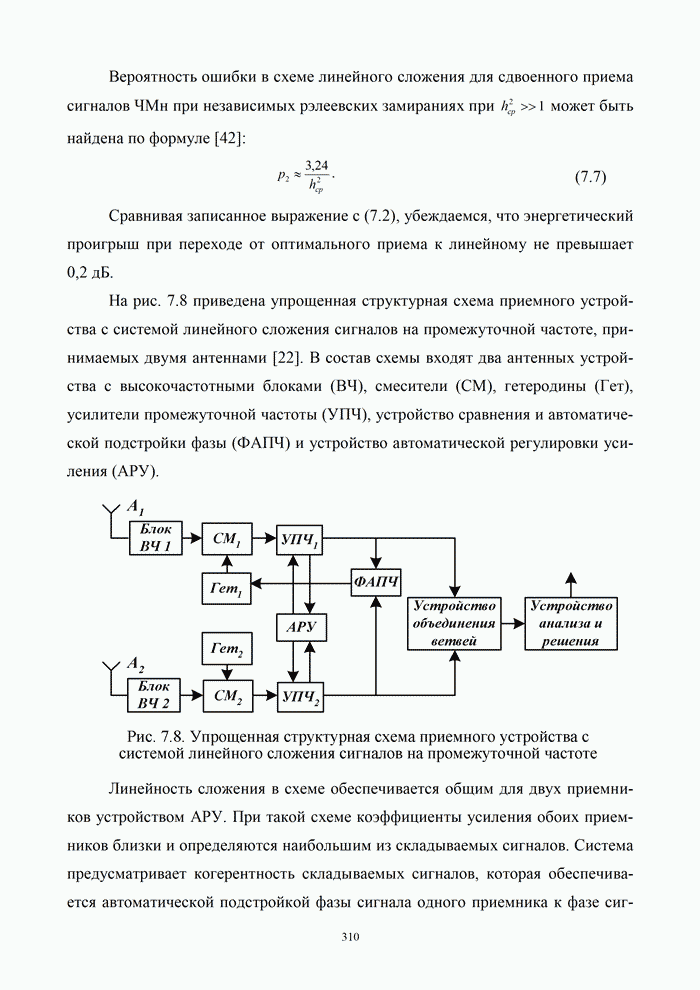
- 7.4. Прием дискретных сообщений в каналах с сосредоточенными по спектру и импульсными помехами
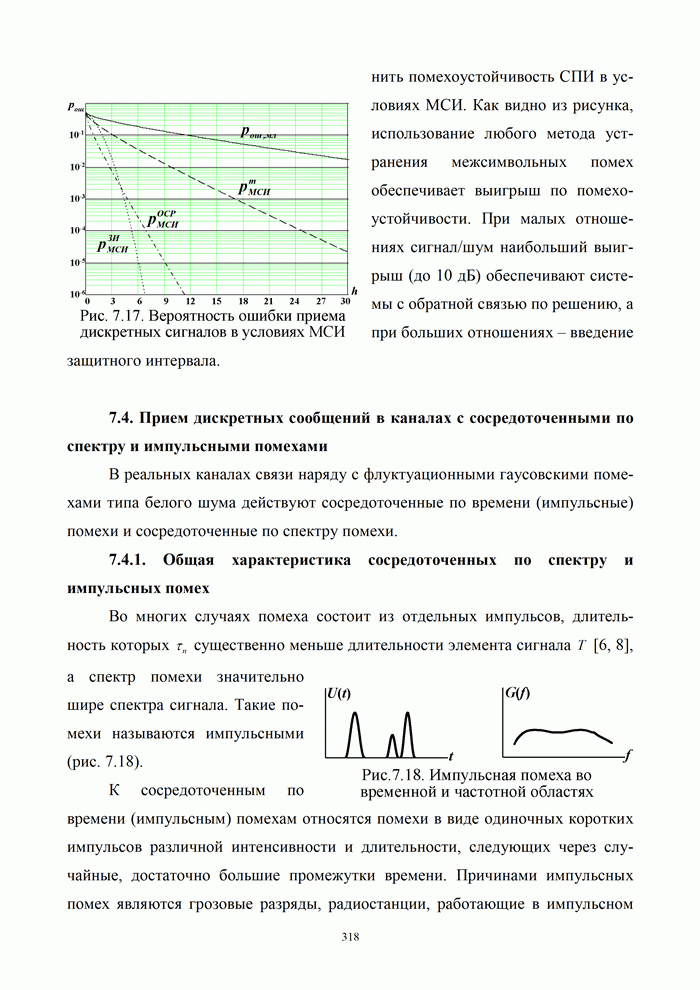
- 7.4.1. Общая характеристика сосредоточенных по спектру и импульсных помех
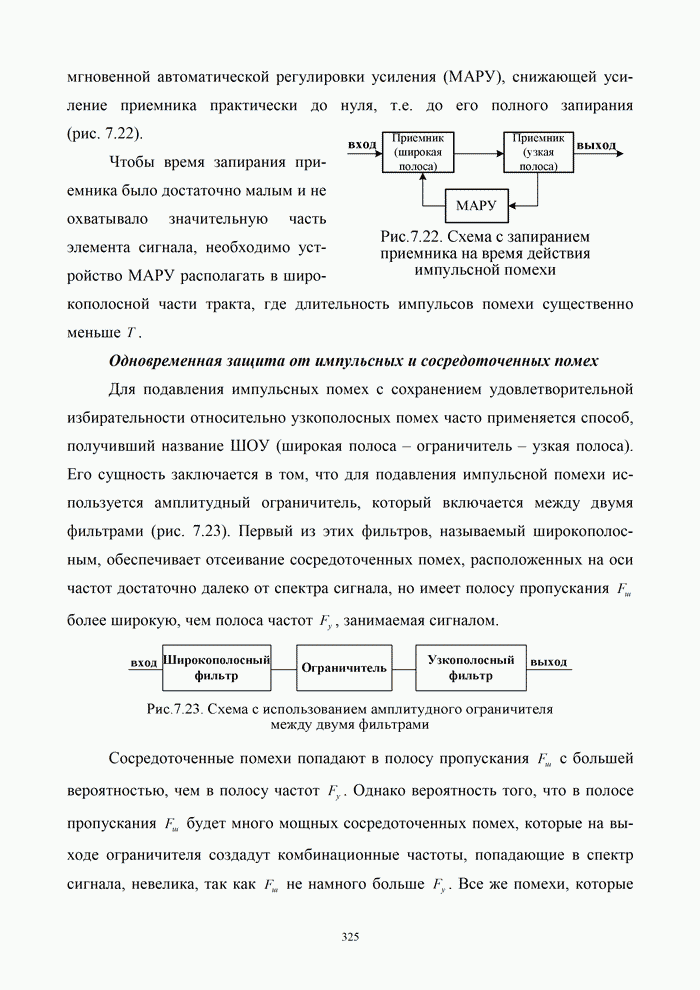
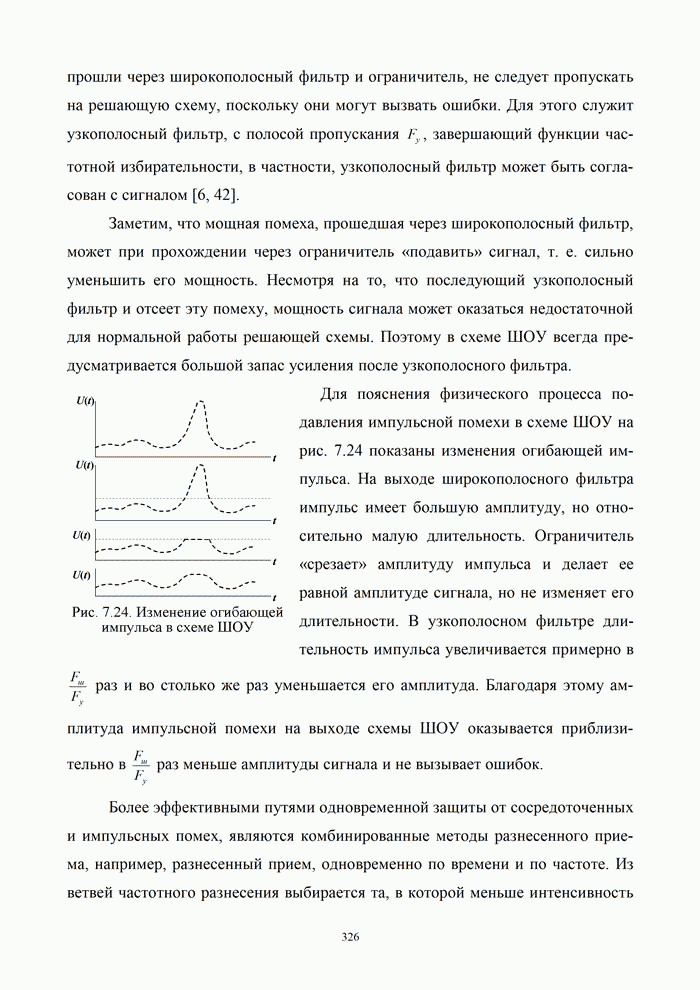
- 7.4.2. Борьба с сосредоточенными и импульсными помехами
- 7.5. Компенсация помех и искажений в канале
- 7.5.1. Принцип работы радиолинии с ФМ ПСС (ФМ ШПС)
- 7.5.2. Помехоустойчивость радиолинии с ФМ ПСС
- 7.5.3. Принципы работы радиолиний с ППРЧ
- 7.5.4. Помехоустойчивость радиолиний с ППРЧ
- Контрольные вопросы
- Глава 8. Многоканальная связь и распределение информации
- 8.1. Методы распределения ресурса общего канала
- 8.1.1. Классификация систем передачи информации, использующих единый ресурс
- 8.1.2. Постановка задачи объединения и разделения сигналов
- 8.1.3. Энергетическая и спектральная цена уплотнения
- 8.2. Частотное разделение каналов
- 8.2.1. Принцип частотного объединения и разделения каналов
- 8.2.2. Групповой сигнал, его структура и характеристики
- 8.3. Временное разделение каналов
- 8.3.1. Принцип временного разделения каналов
- 8.3.2. Характеристики группового сигнала систем с ВРК
- 8.4. Разделение сигналов по форме
- Контрольные вопросы
- Глава 9. Эффективность систем связи
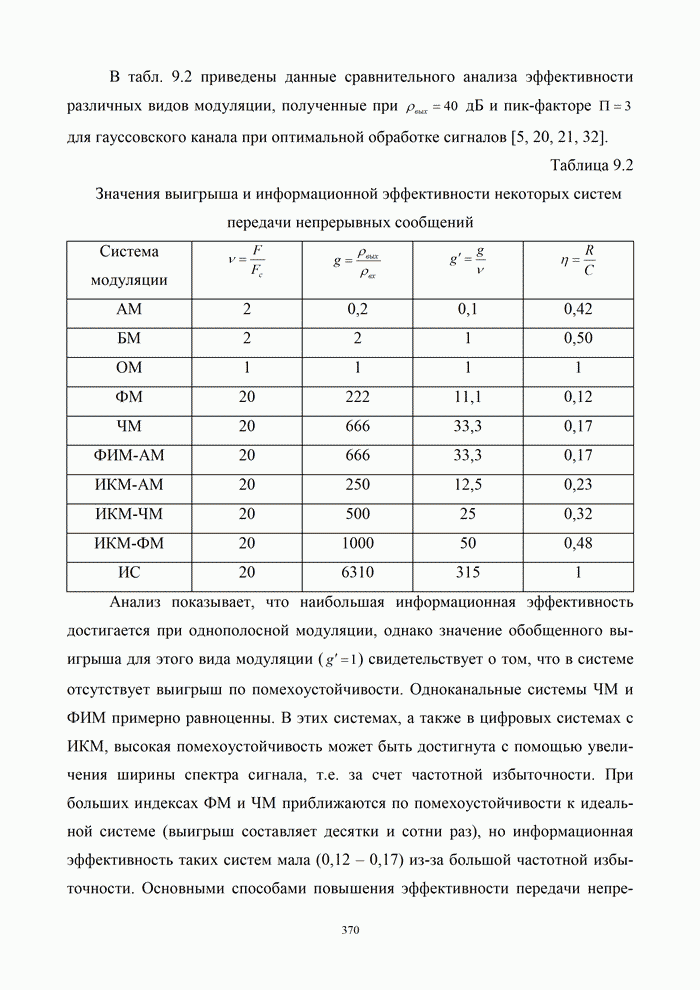
- 9.1. Оценка эффективности систем связи
- 9.1.1. Подходы к оценке эффективности
- 9.1.2. Критерии эффективности
- 9.1.3. Эффективность аналоговых и цифровых систем
- 9.2. Выбор сигналов и помехоустойчивых кодов
- 9.2.1. Многопозиционные сигналы
- 9.2.2. Корректирующие коды
- 9.3. Оптимизация систем связи
- 9.3.1. Согласование методов модуляции и кодирования
- 9.3.2. Классификация сигнально – кодовых конструкций
- 9.4. Характеристики основных типов СКК
- 9.4.1. Согласование канала кодом Грея
- 9.4.2. Согласование на основе разбиения ансамбля на вложенные подансамбли
- 9.5. Алгоритмы цифровой обработки сигналов
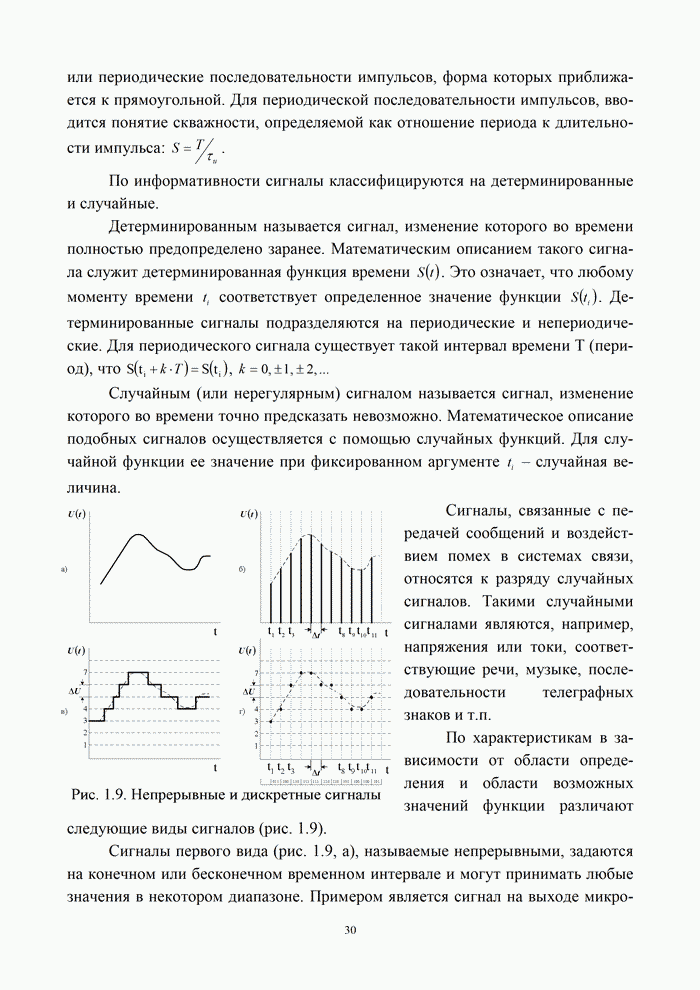
- 9.5.1. Дискретные сигналы и их спектры
- 9.5.2. Алгоритмы дискретного и быстрого преобразований Фурье
- Контрольные вопросы
- Глава 10. Теоретико-информационные основы криптозащиты сообщений в телекоммуникационных системах
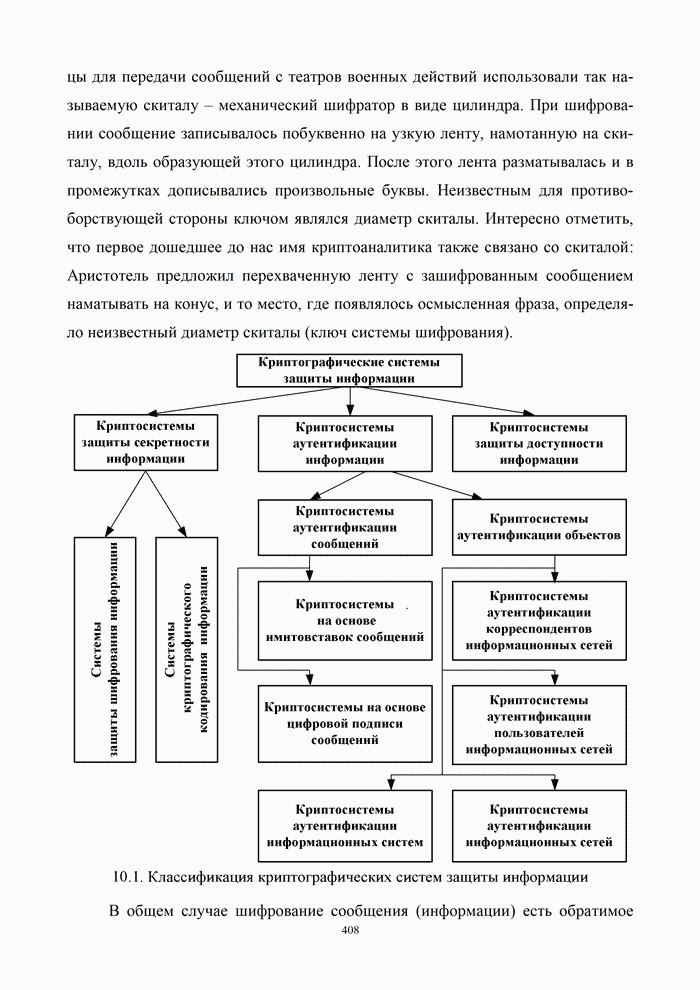
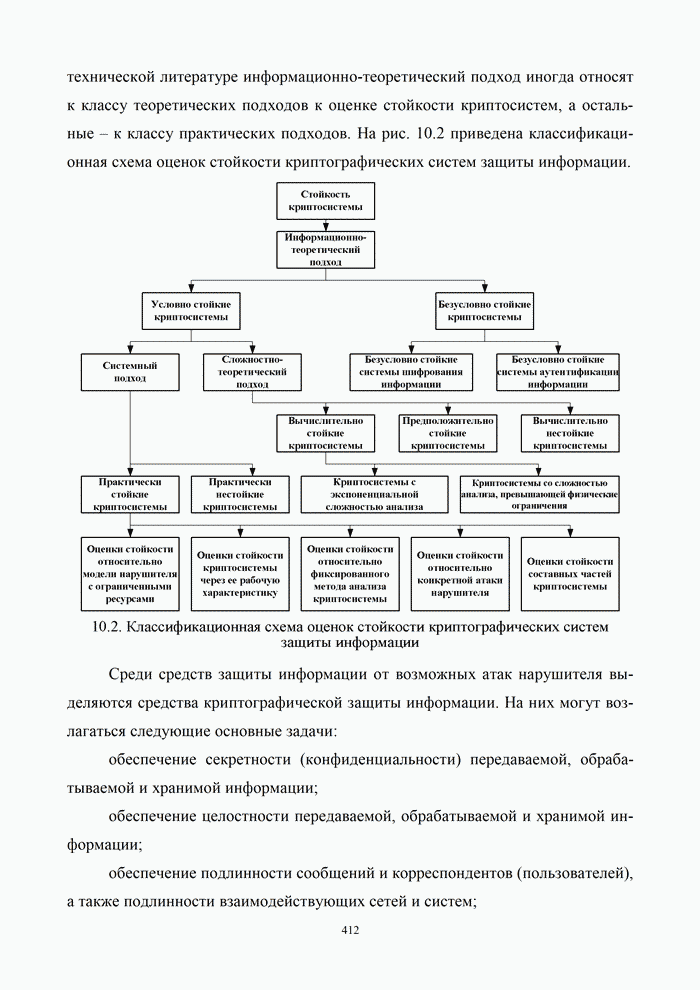
- 10.1. Классификация криптографических систем
- 10.1.2. Классификация криптографических систем защиты информации
- 10.1.3. Оценка стойкости криптосистем
- 10.2. Функции, используемые в криптографических системах
- 10.2.1. Общее описание функций, используемых в криптографических системах
- 10.2.2. Однонаправленные функции
- 10.2.3. Криптографические хэш-функции
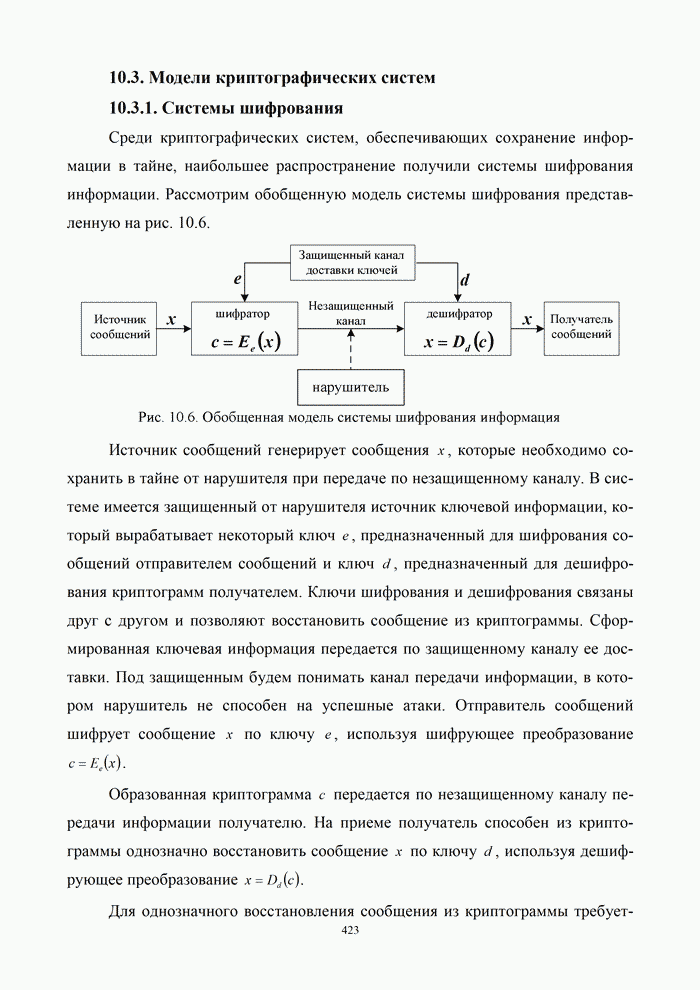
- 10.3. Модели криптографических систем
- 10.3.1. Системы шифрования
- 10.3.2. Традиционные симметричные криптосистемы
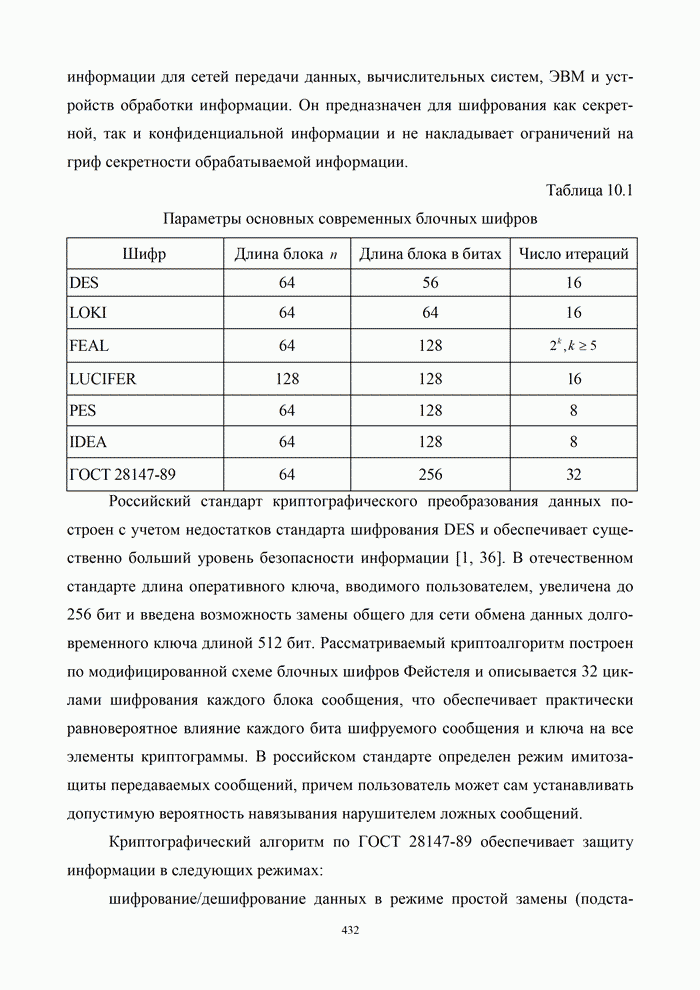
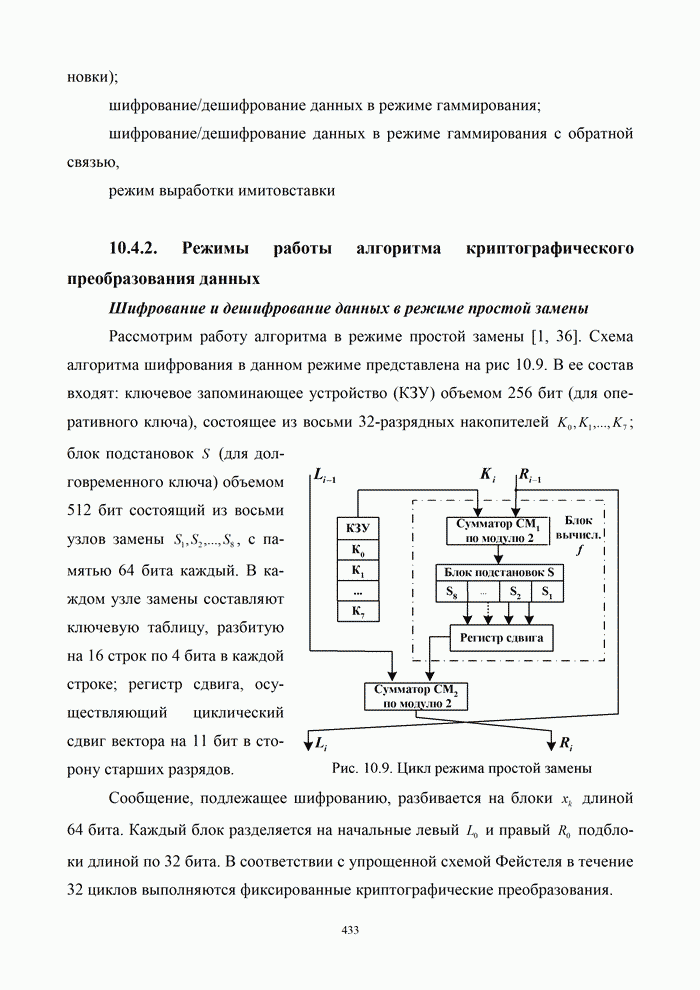
- 10.4. Алгоритмы криптографической защиты
- 10.4.1. Алгоритм криптографической защиты информации согласно ГОСТ 28147-89
- Контрольные вопросы
- Заключение
- Список литературы



















































































































































































































































































































































































 ,
,
 .
.
 .
.
