| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
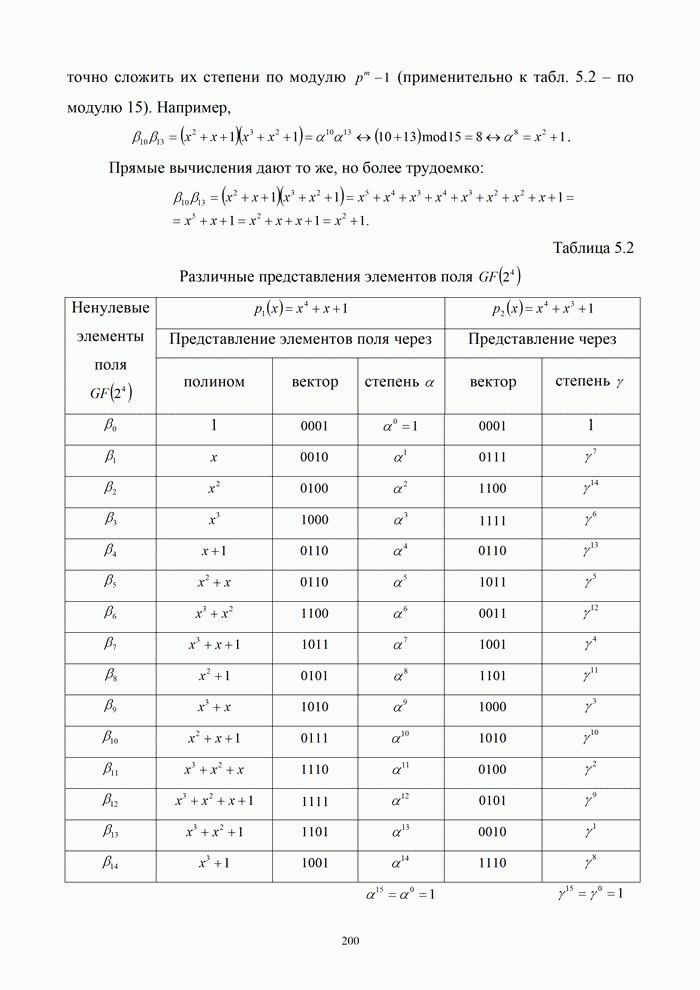
5.8.2. Способы задания сверточного кода
Для получения слова систематического кода
надо по известным информационным символам найти проверочные и расположить их на
заданных позициях элементарного блока. Для простоты положим ![]() , т. е. будем кодировать
одну последовательность информационных символов
, т. е. будем кодировать
одну последовательность информационных символов ![]() , которая представляется
многочленом
, которая представляется
многочленом
|
|
|
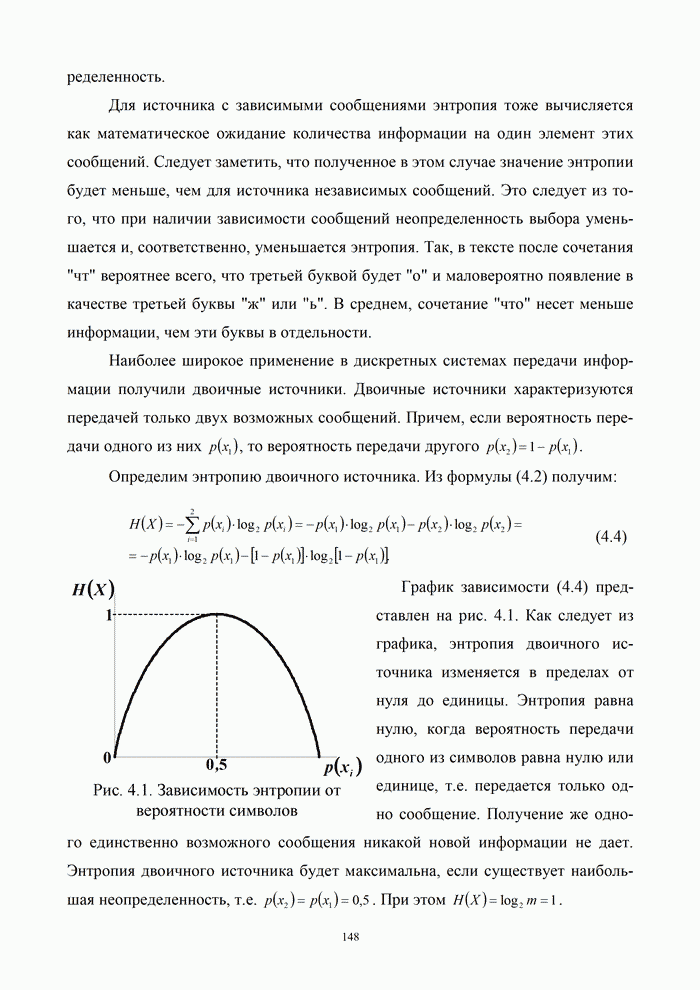
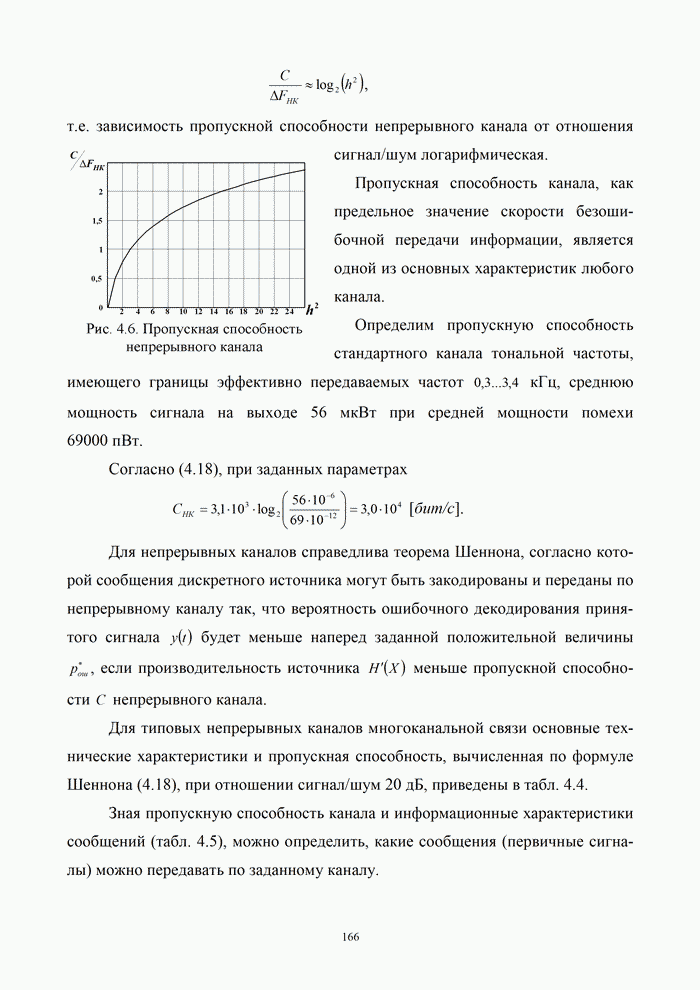
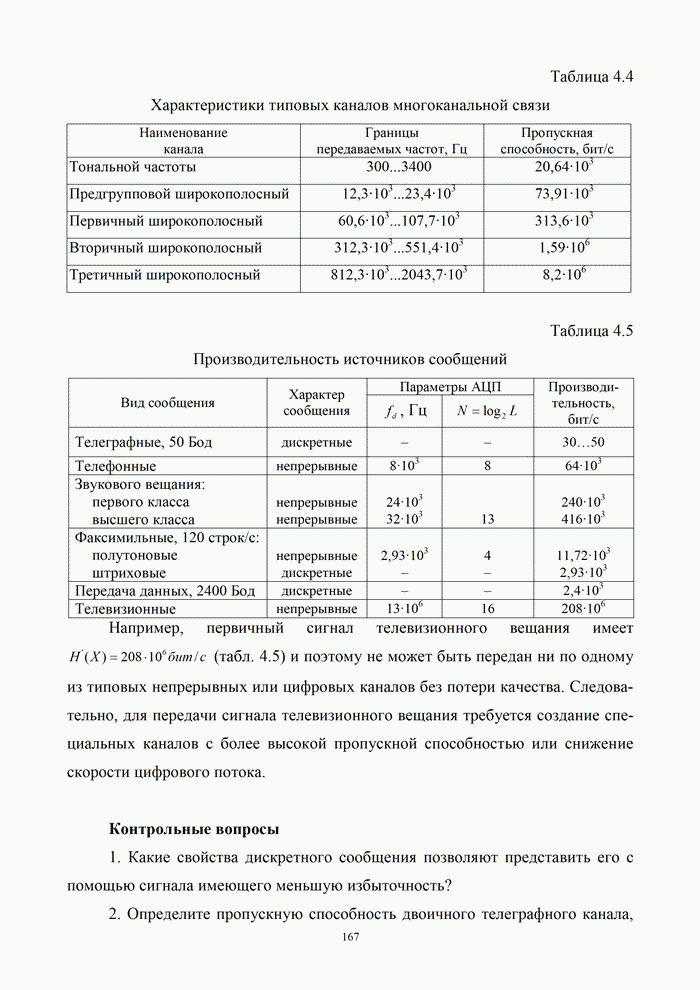
Требуется найти последовательности проверочных символов, которые также можно описать многочленами:
|
|
|
|
|
|
|
…………………………….. |
|
|
|
|
Укажем некоторые способы задания сверточных кодов, которые во многом напоминают способы задания блочных.
1. Проверочные символы
определяются по известным информационным с помощью ![]() рекуррентных соотношений:
рекуррентных соотношений:
|
|
|
|
|
|
|
…………… |
|
|
|
|
где ![]() ,
, ![]() , ... ,
, ... ,![]() – известные двоичные
коэффициенты; суммирование проводится по модулю 2.
– известные двоичные
коэффициенты; суммирование проводится по модулю 2.
2. Последовательность
проверочных символов ![]() находится с помощью
порождающего многочлена
находится с помощью
порождающего многочлена
|
|
|
по формуле
|
|
(5.39) |
Отсюда следует, что проверочный символ ![]() является сверткой
информационной последовательности и коэффициентов порождающего многочлена
является сверткой
информационной последовательности и коэффициентов порождающего многочлена
|
|
(5.40) |
Как уже указывалось, соотношение (5.40) дало
название этому классу кодов. Для задания всех проверочных
последовательностей требуется ![]() порождающий многочлен.
Максимальная степень многочлена определяет число кадров, хранимых в
кодере, т.е. длину кодового ограничения.
порождающий многочлен.
Максимальная степень многочлена определяет число кадров, хранимых в
кодере, т.е. длину кодового ограничения.
Если кодируется ![]() информационных последовательностей
информационных последовательностей ![]() , то систематический
сверточный код со скоростью
, то систематический
сверточный код со скоростью ![]() задается с помощью
задается с помощью ![]() порождающих многочленов, а
несистематический – с помощью
порождающих многочленов, а
несистематический – с помощью ![]() многочленов. Порождающие многочлены
хороших сверточных кодов приведены, например, в работе [3].
многочленов. Порождающие многочлены
хороших сверточных кодов приведены, например, в работе [3].
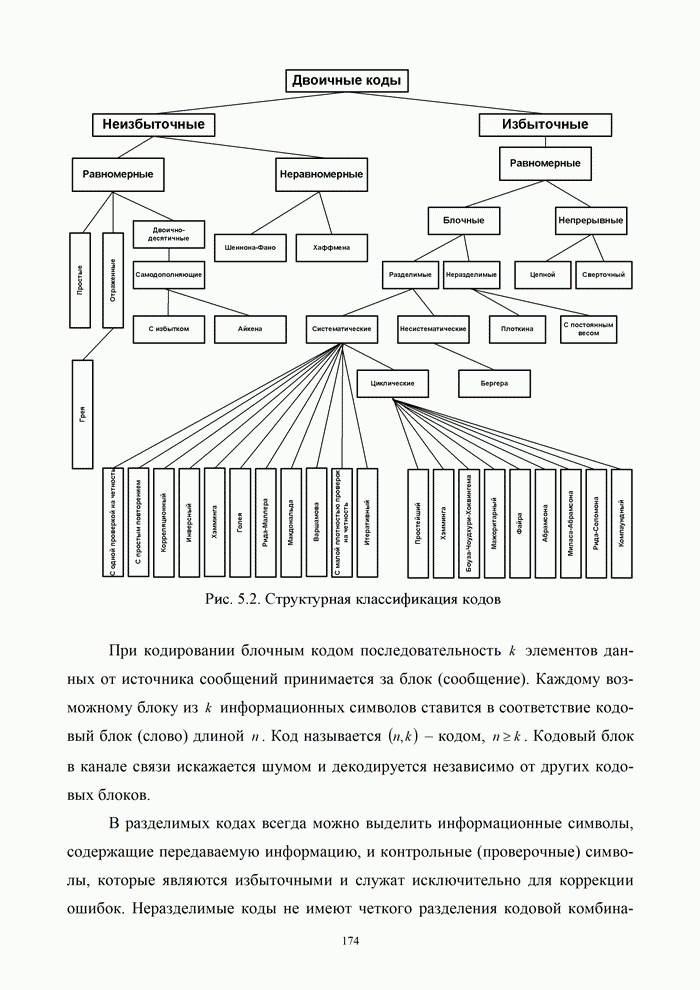
3. Сверточный код задается с помощью графа и кодовой решетки. Кодовое слово изображается последовательным соединением ребер графа, структура которого похожа на ветвящееся дерево. Поэтому сверточные коды относятся к классу древовидных.
4. Для сверточного кода могут быть построены порождающая и проверочная матрицы. По сравнению с теми же матрицами блочного кода эти матрицы (как кодируемая и принятая последовательности) полубесконечны.
Пример 5.15. Пусть требуется применить простейший систематический сверточный код с параметрами: ![]() ,
, ![]() , кодовым ограничением
, кодовым ограничением ![]() , скоростью
, скоростью ![]() бит на один символ. Кодовое слово
является полубесконечной последовательностью
символов
бит на один символ. Кодовое слово
является полубесконечной последовательностью
символов ![]() , состоящей из элементарных блоков
, состоящей из элементарных блоков ![]() .
Рассмотрим способы задания этого кода.
.
Рассмотрим способы задания этого кода.
1. Проверочный символ определяется через информационные линейным рекуррентным соотношением
|
|
(5.41) |
Видно, что значение проверочного символа зависит от значений информационных символов, входящих в текущий и предыдущий кадры. Предыдущий информационный символ должен быть запомнен в кодере, для чего необходим один двоичный элемент памяти.
2. Порождающий многочлен этого
кода ![]() . С
помощью заданного
многочлена
. С
помощью заданного
многочлена ![]() найдем проверочные символы для
следующей информационной последовательности
найдем проверочные символы для
следующей информационной последовательности ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,..., которая описывается многочленом
,..., которая описывается многочленом ![]() .
.
Используя (5.39), получим ![]()
![]() , что
соответствует
, что
соответствует ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
3. Графические способы задания поясним по схеме кодера, для построения
которого следует пользоваться заданием сверточного кода с помощью соотношения (5.41)
или порождающего многочлена ![]() .
.
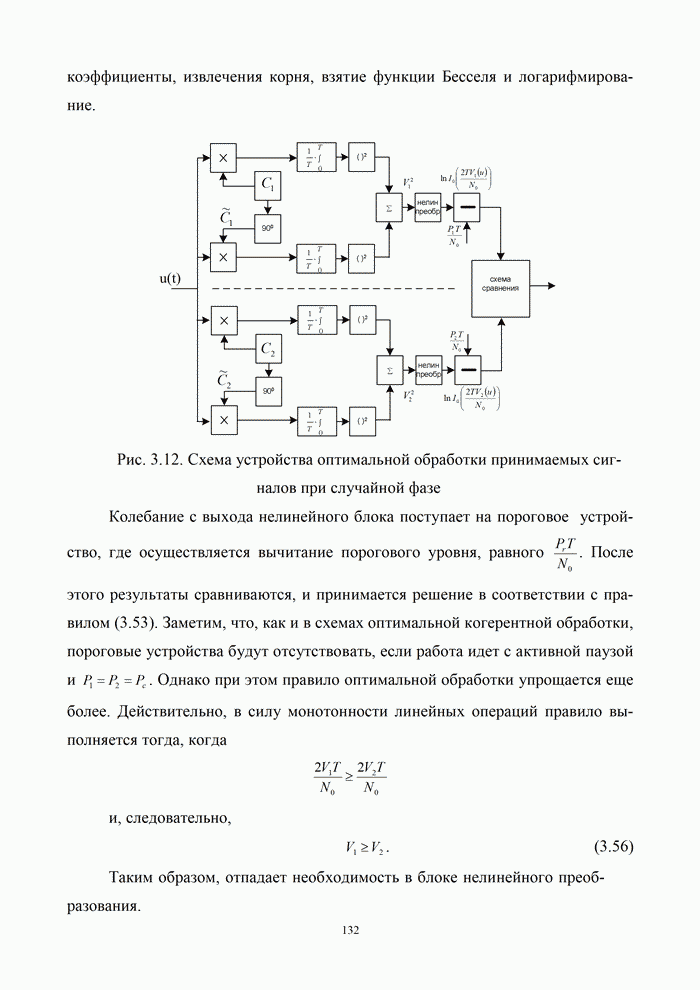
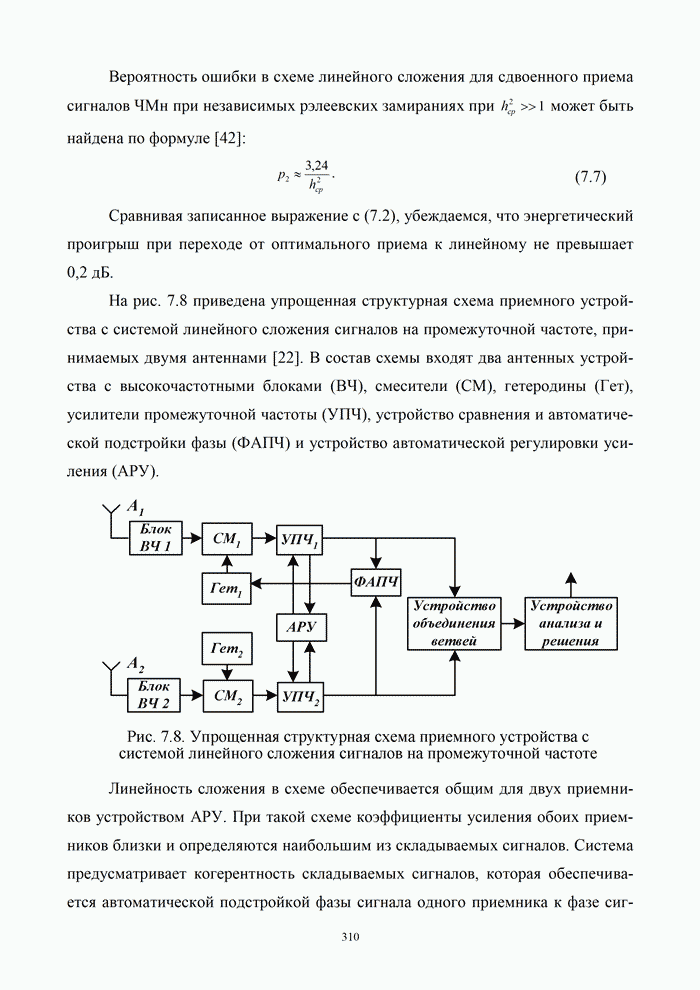
Схема кодирующего устройства приведена на
рис. 5.8. Кодер представляет собой линейную систему (со сложением по модулю 2),
отклик которой на входную единицу равен (11),
что соответствует коэффициентам многочлена ![]() . При подаче на вход информационной
последовательности выходная последовательность образуется в соответствии с (5.41).
Слово систематического сверточного кода формируется с помощью электронного
ключа
. При подаче на вход информационной
последовательности выходная последовательность образуется в соответствии с (5.41).
Слово систематического сверточного кода формируется с помощью электронного
ключа ![]() , который поочередно подключает шины информационных и
проверочных символов к выходу. Такт
работы ключа в два раза меньше такта поступления и сдвига информационных
символов.
, который поочередно подключает шины информационных и
проверочных символов к выходу. Такт
работы ключа в два раза меньше такта поступления и сдвига информационных
символов.

Схема
на рис. 5.8 позволяет пояснить задание сверточного кода с помощью решетки. Решеткой
называется граф, узлы которого находятся в полубесконечной прямоугольной
координатной сетке и связаны ребрами. Число узлов
в каждом столбце конечно, а конфигурация ребер, соединяющих узлы каждого столбца с узлами следующего столбца, одинакова
для всех столбцов. Каждый столбец отображает набор возможных состояний
кодера. Поэтому ребра показывают изменение
состояния кодера при подаче на вход новою информационного символа. Маркировка ребер соответствует
последовательности кодовых символов, передаваемых в канал связи, т.е. комбинации
элементарного блока из ![]() символов.
символов.

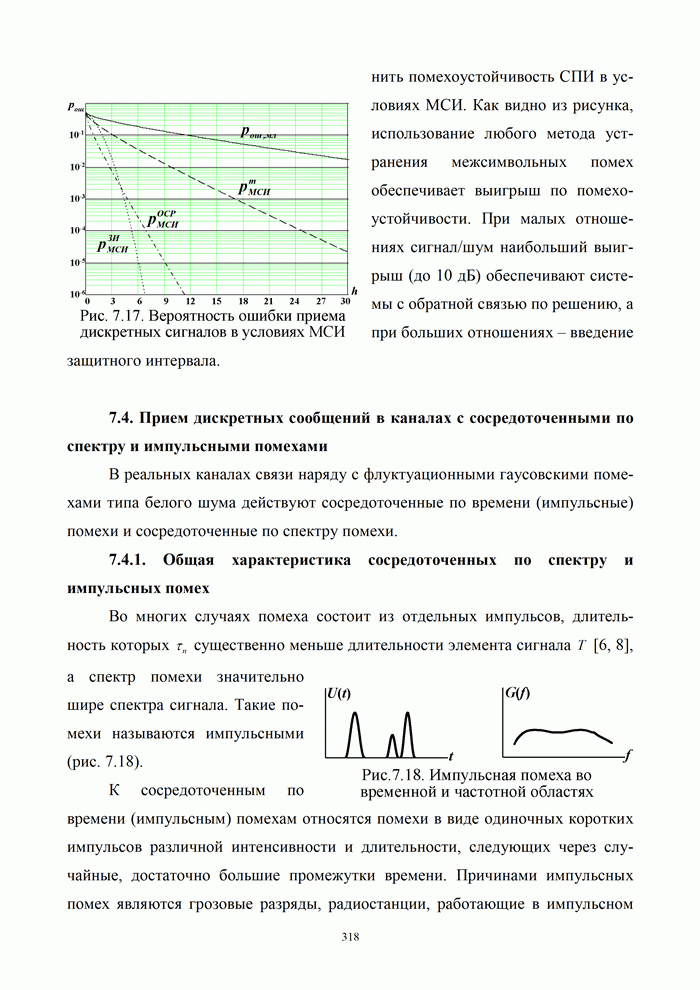
Для рассматриваемого примера кодовая решетка
изображена на рис. 5.9 в предположении, что верхнее ребро, исходящее из каждого
узла, соответствует поступающему информационному символу ![]() , а нижнее
, а нижнее ![]() . Поэтому на первых двух
фрагментах решетки верхние ребра помечены наборами
. Поэтому на первых двух
фрагментах решетки верхние ребра помечены наборами ![]() и
и ![]() ,
а нижние –
,
а нижние – ![]() и
и ![]() . Для получения маркированной решетки
требуется определить согласно (5.41)
значения проверочных символов. Результаты вычислений отражены на правых фрагментах
решетки.
. Для получения маркированной решетки
требуется определить согласно (5.41)
значения проверочных символов. Результаты вычислений отражены на правых фрагментах
решетки.
Решетка описывает код в том смысле, что каждой последовательности информационных символов соответствует свой путь по решетке, а маркировка ребер, составляющих этот путь, дает кодовое слово. Так, ранее рассмотренной последовательности 01011 соответствует путь и кодовое слово 00 11 01 11 10, в котором последовательность проверочных символов совпадает с получаемой согласно (5.40).
Кодовая решетка удобна для наглядного пояснения принципов декодирования сверточных кодов. Напомним, что в двоичном симметричном канале оптимальной оценкой переданного кодового слова является слово, ближайшее к принятой комбинации, т.е. путь по кодовой решетке, отстоящий от этой последовательности на минимальное расстояние Хэмминга. Поиск такого пути и составляет сущность алгоритма декодирования Витерби, который рассматривается в следующем параграфе.
Пример 5.16. Пусть дан
несистематический сверточный код с параметрами ![]() ,
, ![]() , скоростью
, скоростью ![]() , кодовым ограничением
, кодовым ограничением
![]() . Он
задается многочленами
. Он
задается многочленами ![]() и
и ![]() .
.
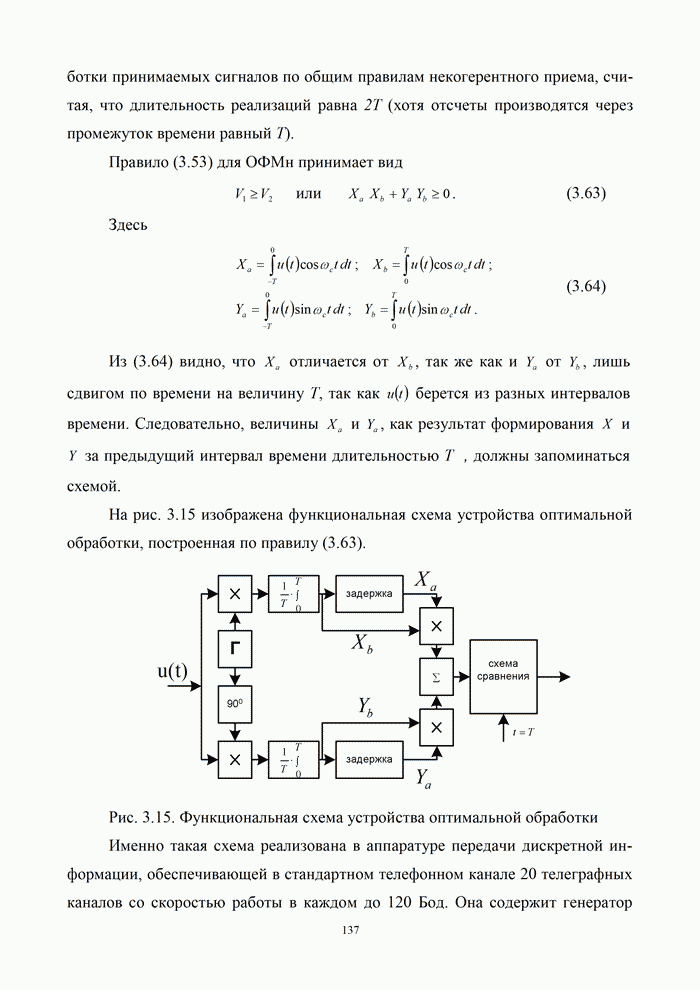
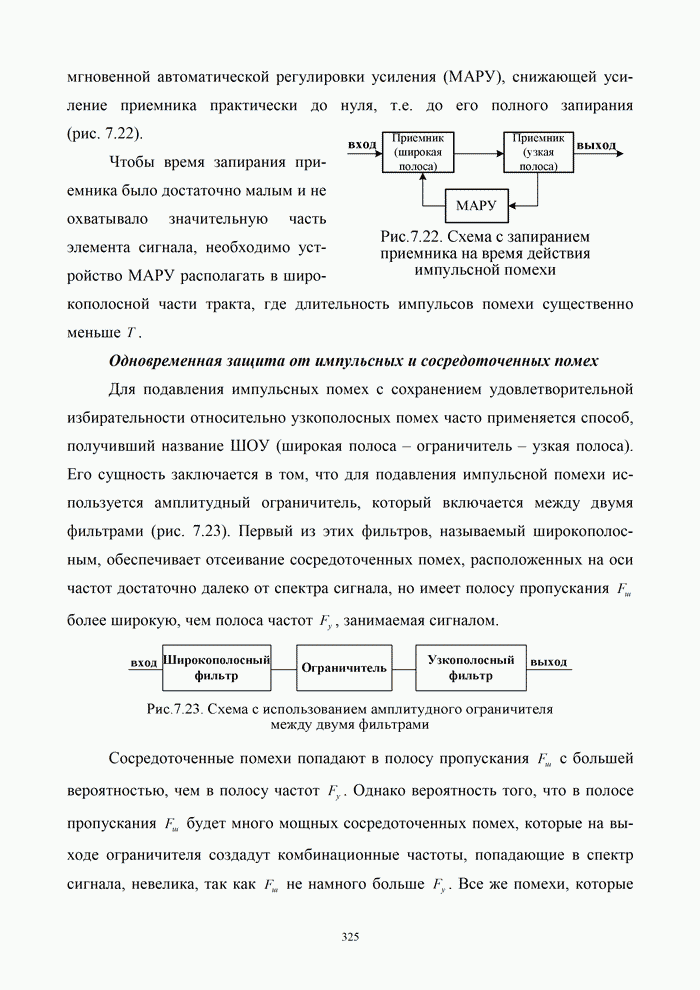
Схема кодера приведена на рис.5.10. В отличие
от примера 5.14 кодовое слово состоит из элементарных блоков, не содержащих информационные
символы. Первые символы каждого блока ![]() являются сверткой
информационной последовательности и
многочлена
являются сверткой
информационной последовательности и
многочлена ![]() , а вторые
, а вторые ![]() -
сверткой той же последовательности и многочлена
-
сверткой той же последовательности и многочлена ![]() .
Заметим, что если один из
многочленов приравнять 1, то получим систематический сверточный код.
.
Заметим, что если один из
многочленов приравнять 1, то получим систематический сверточный код.

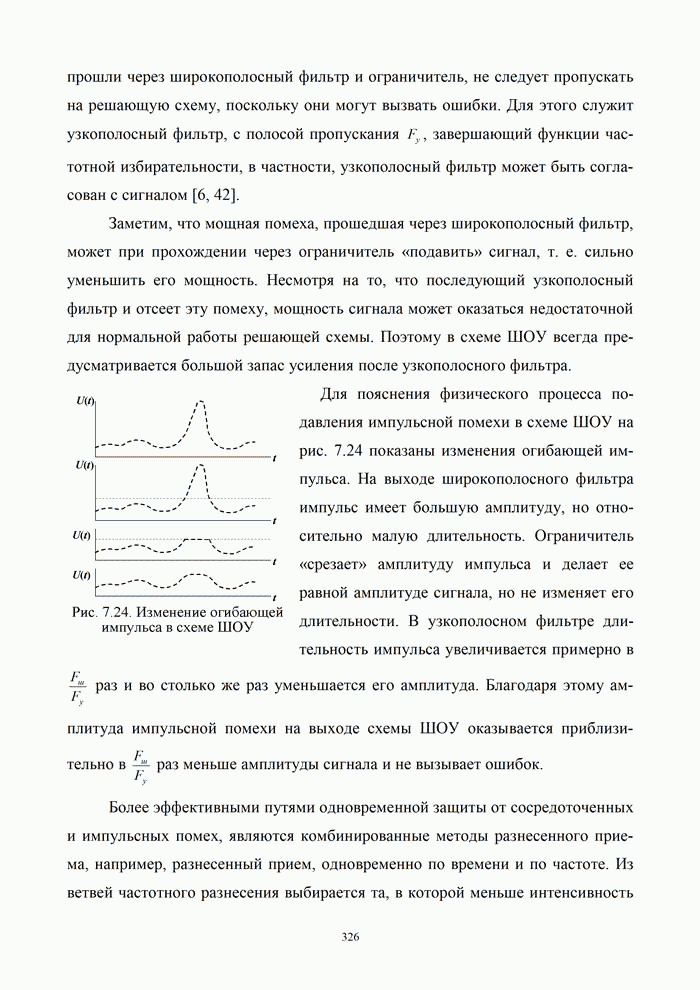
Кодовая решетка, построенная по правилам примера 5.14, показана на рис. 5.11.

Кодер имеет 2-разрядный сдвигающий регистр с четырьмя состояниями,
следовательно, столбцы решетки содержат по четыре узла, помеченных содержимым
регистра. Поэтому левый символ в обозначении узла равен последнему
информационному
символу, поступившему в регистр. Порядок обозначения узлов выбран так, что при ![]() регистр переходит в
следующее состояние
по верхнему ребру, а при
регистр переходит в
следующее состояние
по верхнему ребру, а при ![]() – по нижнему.
Маркировка ребер совпадает с комбинацией элементарного блока, посылаемого в
канал. По-прежнему информационной
последовательности соответствует путь на кодовой решетке и кодовое
слово. Если входные символы 0 1 1 0 , то по решетке находим кодовое слово 00 11 01 01.
– по нижнему.
Маркировка ребер совпадает с комбинацией элементарного блока, посылаемого в
канал. По-прежнему информационной
последовательности соответствует путь на кодовой решетке и кодовое
слово. Если входные символы 0 1 1 0 , то по решетке находим кодовое слово 00 11 01 01.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Список сокращений
- Основные обозначения
- ВВЕДЕНИЕ
- Глава 1. Сообщения, сигналы и помехи, их математические модели
- 1.1. Основные понятия и определения
- 1.1.1. Сообщение, сигнал, модуляция
- 1.1.2. Основные параметры сигналов
- 1.2. Системы связи. Каналы связи
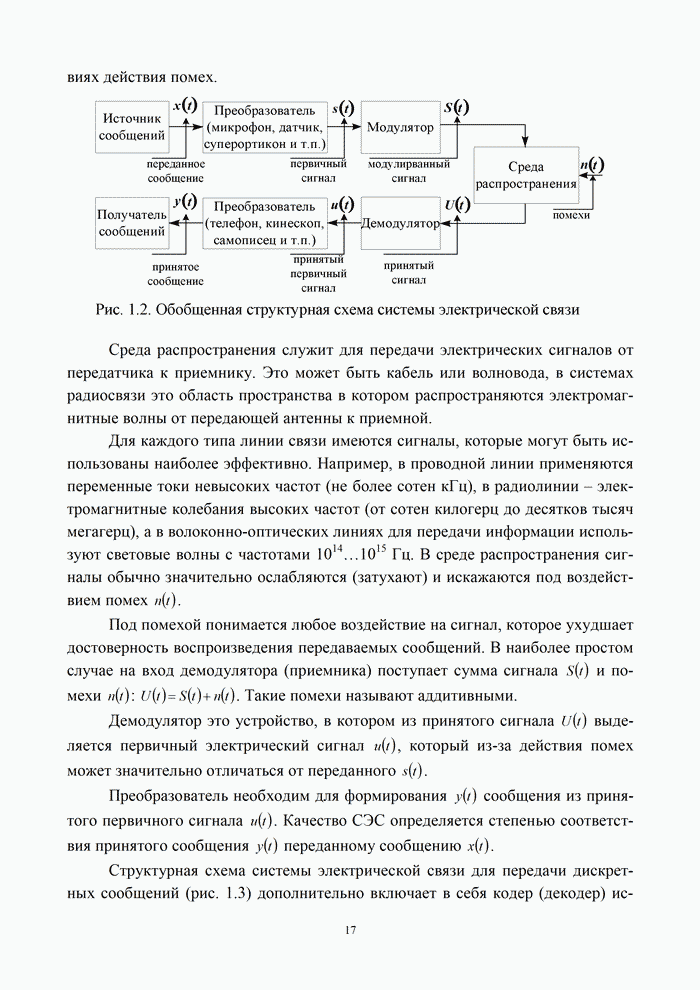
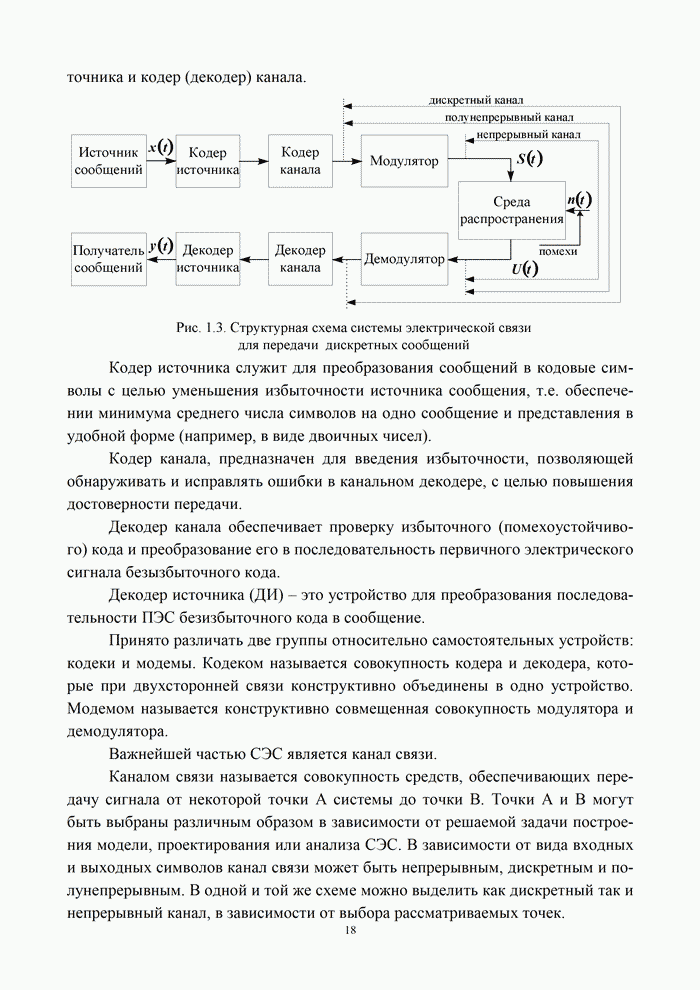
- 1.2.1. Структура канала электросвязи
- 1.2.2. Линия и сеть связи
- 1.2.3. Помехи и искажения в канале
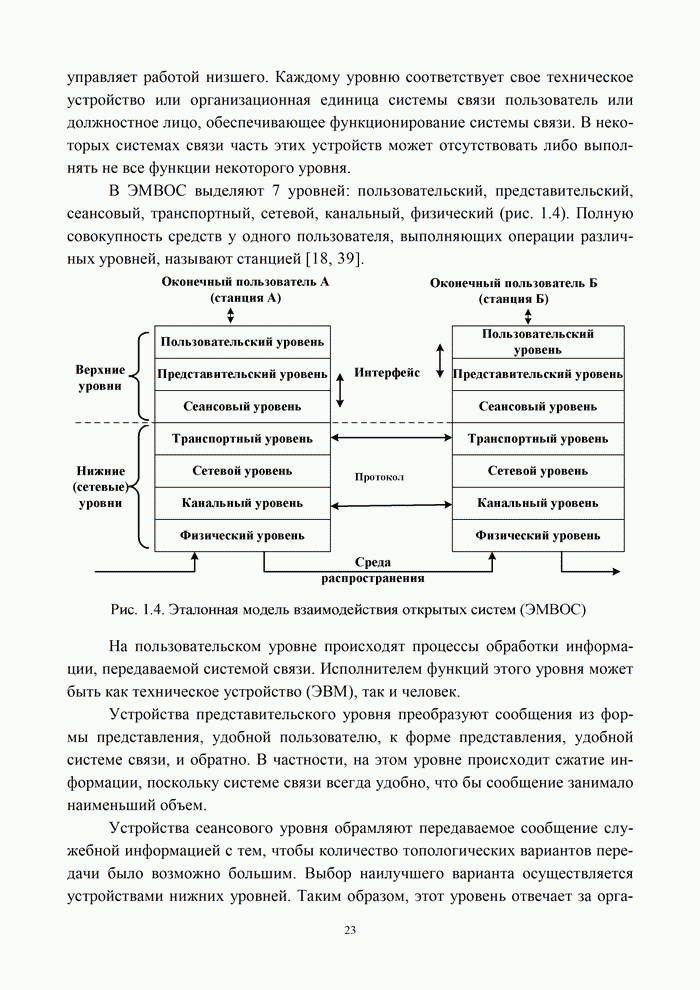
- 1.2.4. Эталонная модель взаимодействия открытых систем
- 1.2.5. Модели каналов связи и их математическое описание
- 1.3. Способы описания сигналов и помех
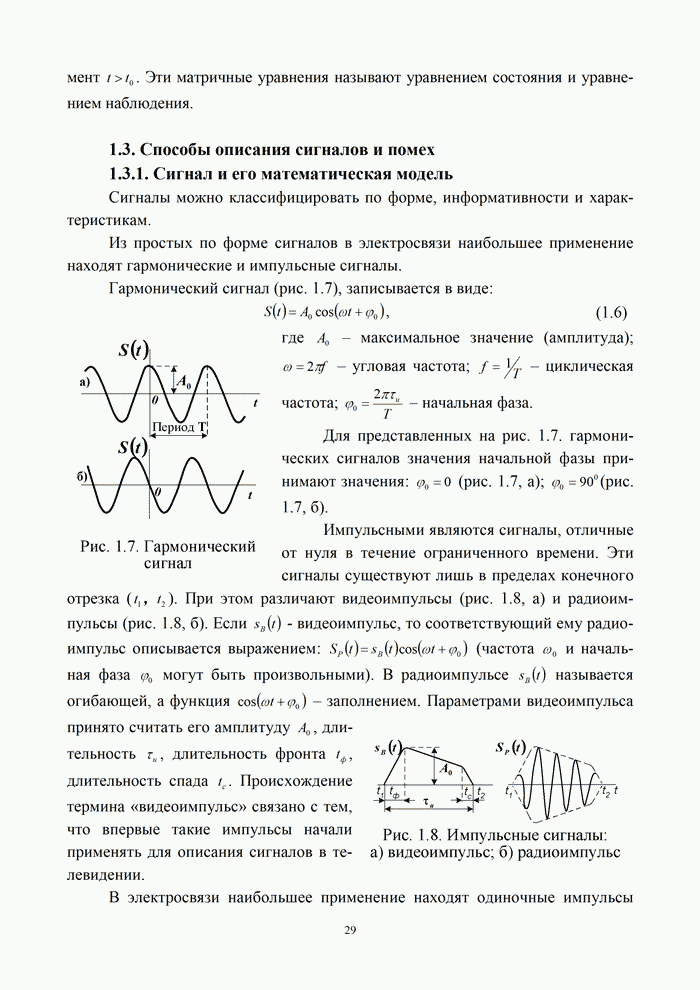
- 1.3.1. Сигнал и его математическая модель
- 1.3.2. Энергетические характеристики детерминированного сигнала
- 1.4.2. Представление сигналов и помех рядом Фурье
- 1.4.3. Применение преобразования Фурье для непериодических сигналов
- 1.5. Теорема Котельникова
- 1.6. Пространство сигналов
- 1.6.1. Линейное пространство
- 1.6.2. Представление сигнала в многомерном пространстве
- 1.7. Сигналы как случайные процессы
- 1.7.1. Характеристики случайного процесса
- 1.7.2. Флуктуационный шум
- 1.8. Комплексное представление сигналов и помех
- 1.8.1. Понятие аналитического сигнала
- 1.8.2. Огибающая, мгновенная фаза и мгновенная частота узкополосного случайного процесса
- Контрольные вопросы
- Глава 2. Методы формирования и преобразования сигналов
- 2.1. Модуляция сигналов
- 2.1.1. Амплитудная модуляция гармонической несущей
- 2.1.2. Балансная и однополосная модуляция гармонической несущей
- 2.2. Методы угловой модуляции
- 2.2.1. Принципы частотной и фазовой (угловой) модуляции
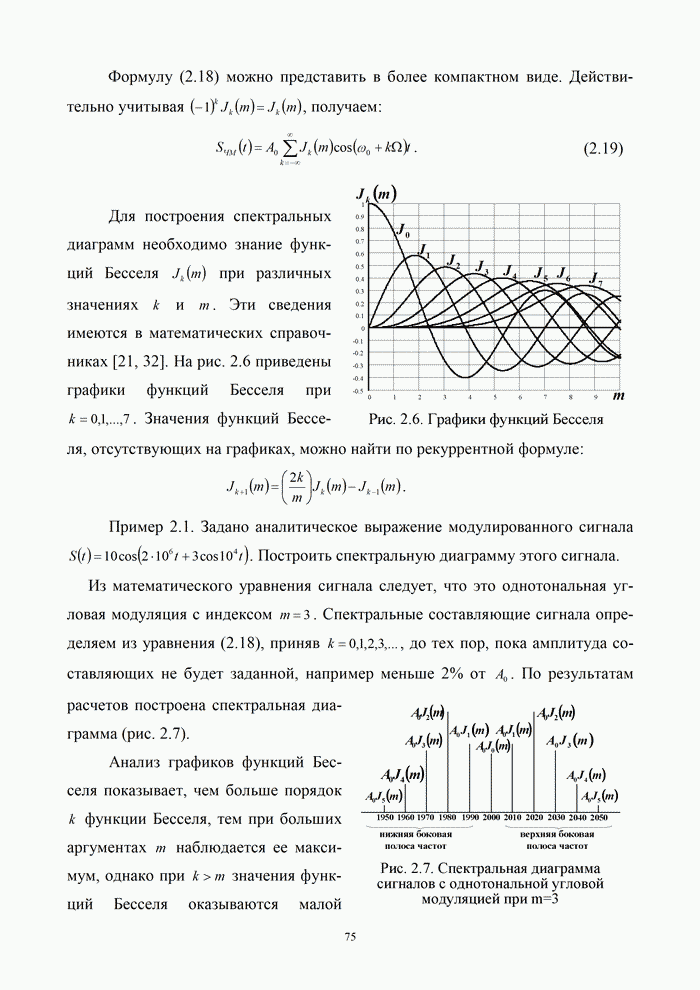
- 2.2.2. Спектр сигналов угловой модуляции
- 2.3. Формирование и детектирование модулированных сигналов
- 2.3.1. Формирование и детектирование сигналов амплитудной и однополосной амплитудной модуляции
- 2.3.2. Формирование и детектирование сигналов угловой модуляции
- 2.4. Манипуляция сигналов
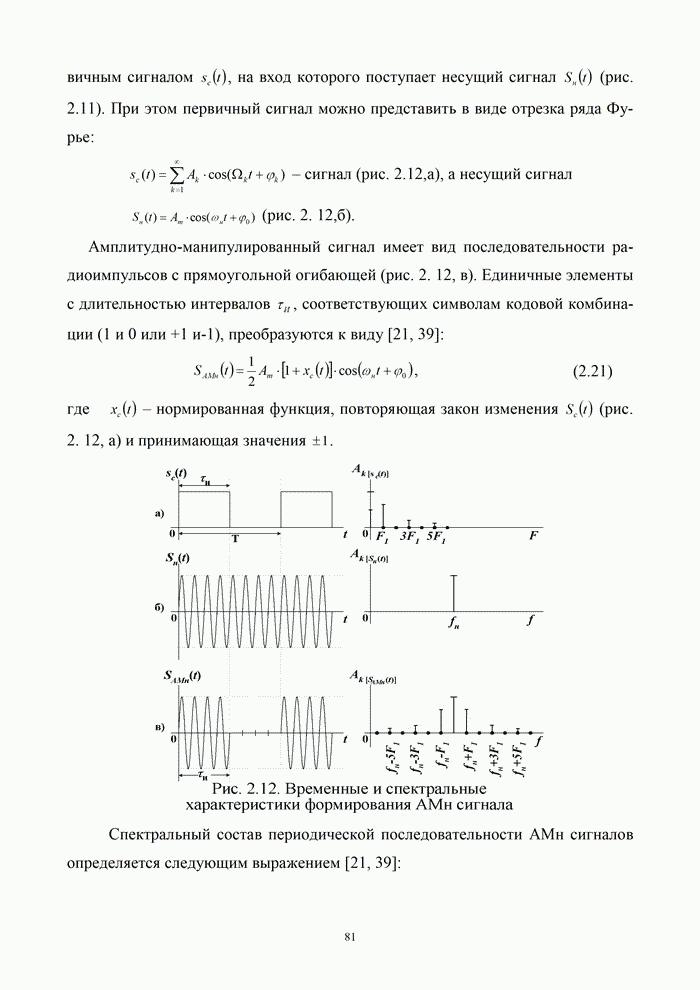
- 2.4.1. Временные и спектральные характеристики амплитудно-манипулированных сигналов
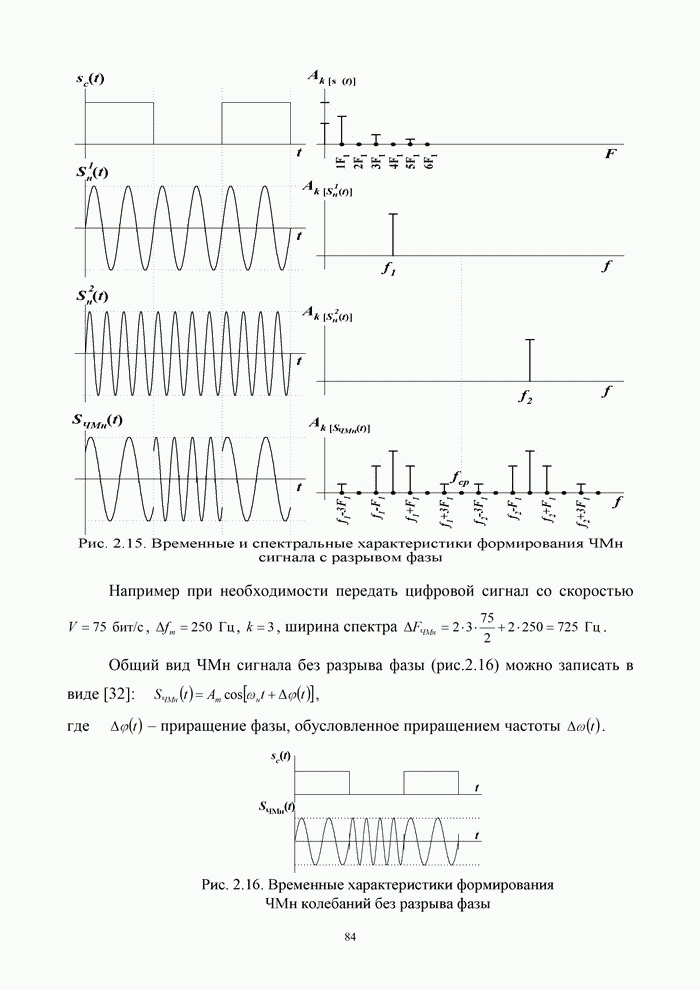
- 2.4.2. Временные и спектральные характеристики частотно-манипулированных сигналов
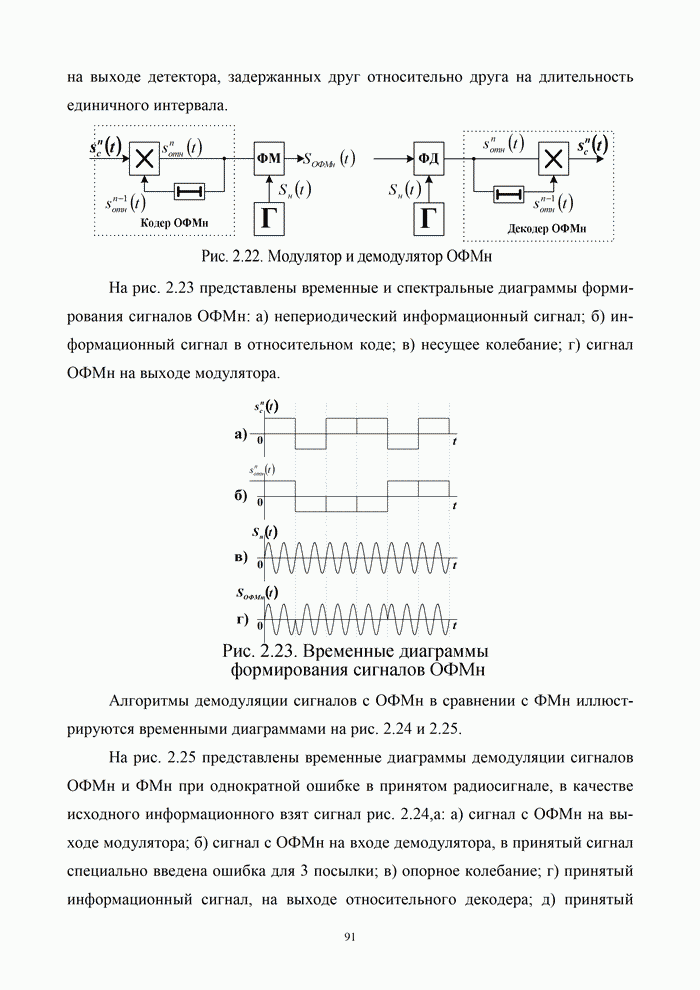
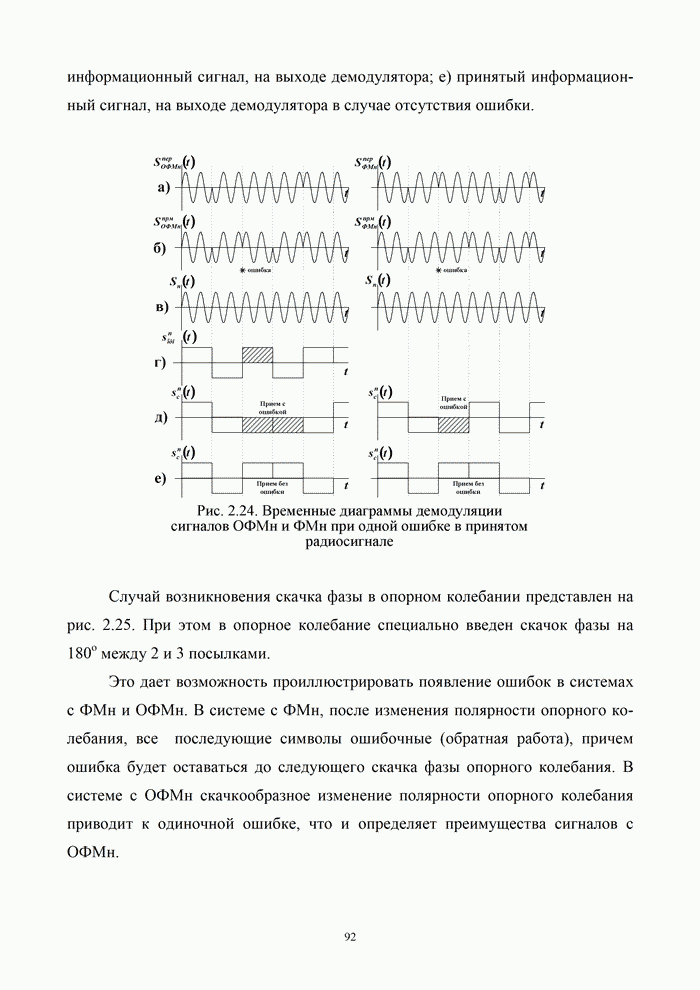
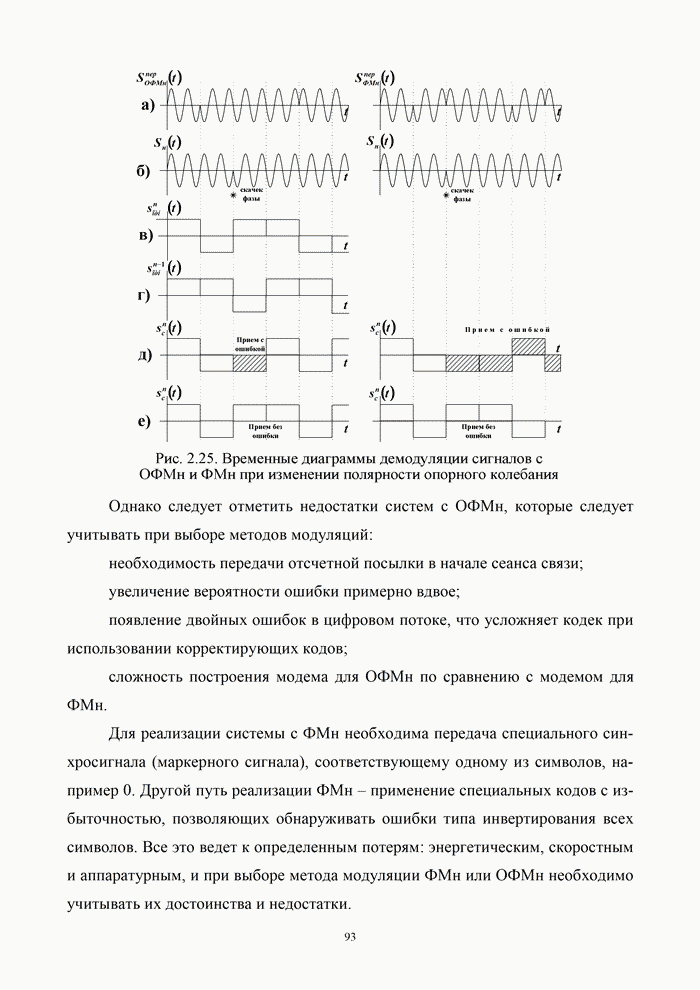
- 2.4.3. Фазовая (относительно-фазовая) манипуляция сигналов
- 2.5. Системы связи с многопозиционной относительной фазовой манипуляцией
- 2.5.1. Принцип формирования сигнала с многократной относительной фазовой манипуляцией
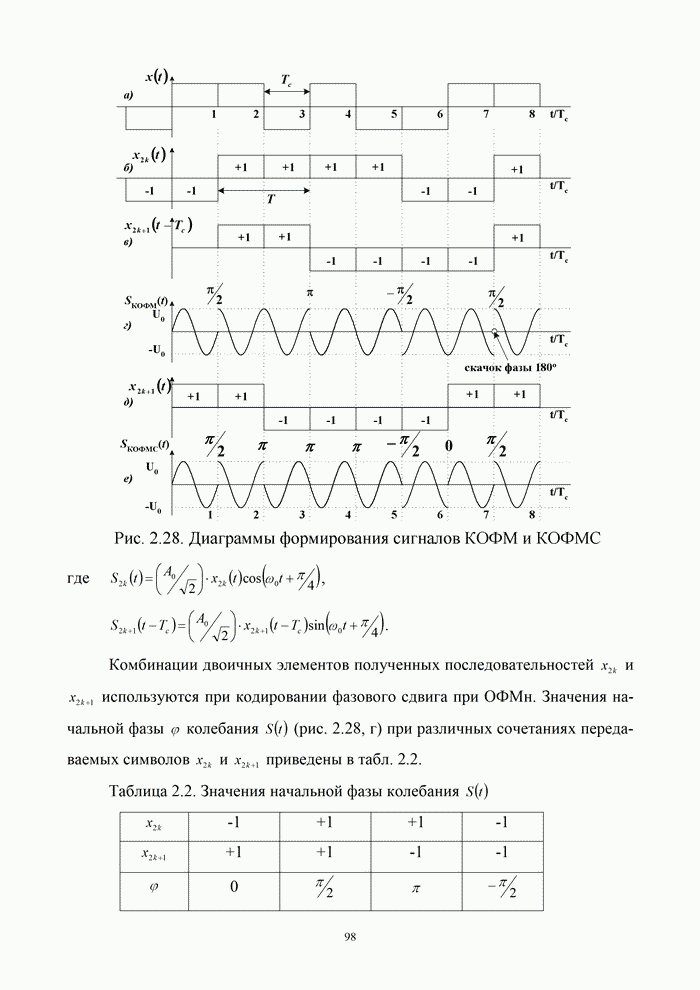
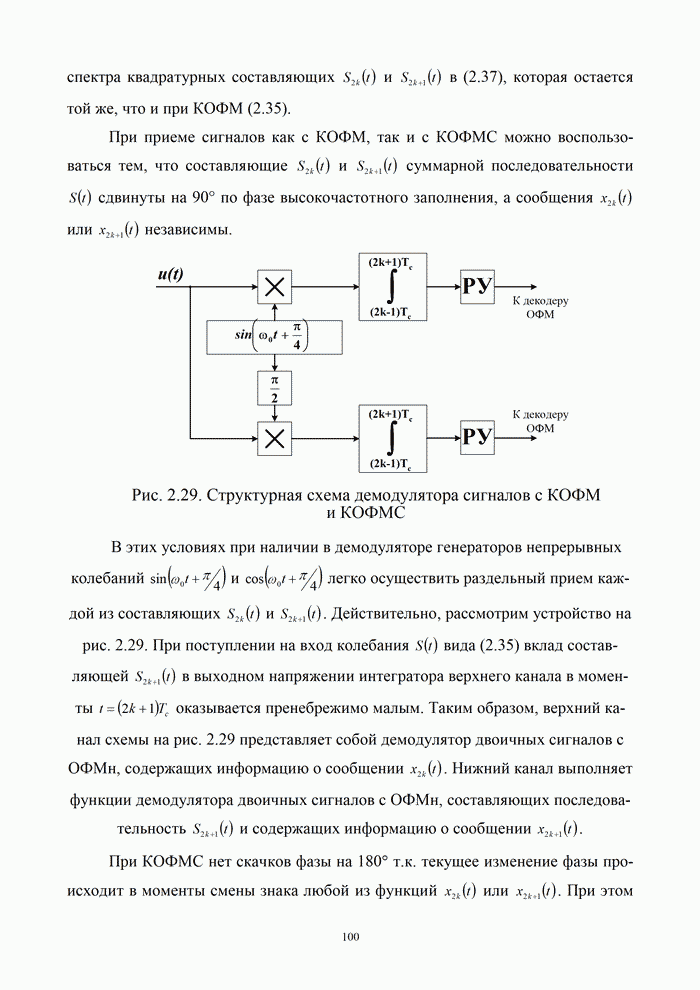
- 2.5.2. Квадратурная относительно-фазовая манипуляция (КОФМ)
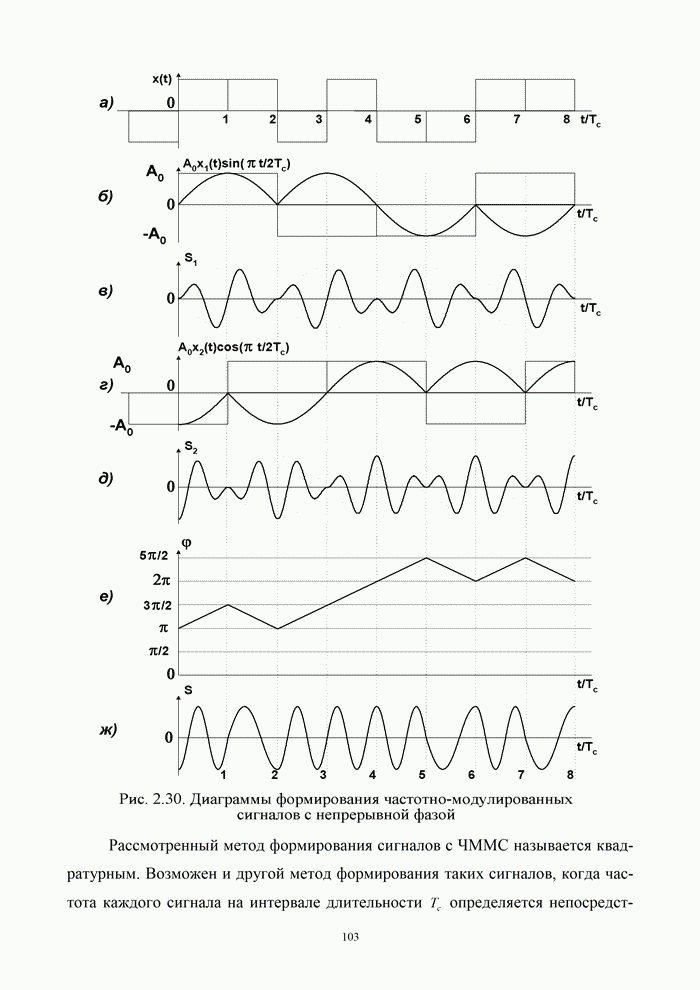
- 2.5.3. Принцип частотной модуляции с непрерывной фазой
- Контрольные вопросы
- Глава 3. Помехоустойчивость приема дискретных сообщений
- 3.1. Критерии качества и правила приема дискретных сообщений
- 3.1.1. Понятие о помехоустойчивости систем электрической связи
- 3.1.2. Задача оптимального приема
- 3.1.3. Вычисление вероятностей ошибок
- 3.2. Оптимальная демодуляция при когерентном приеме сигналов
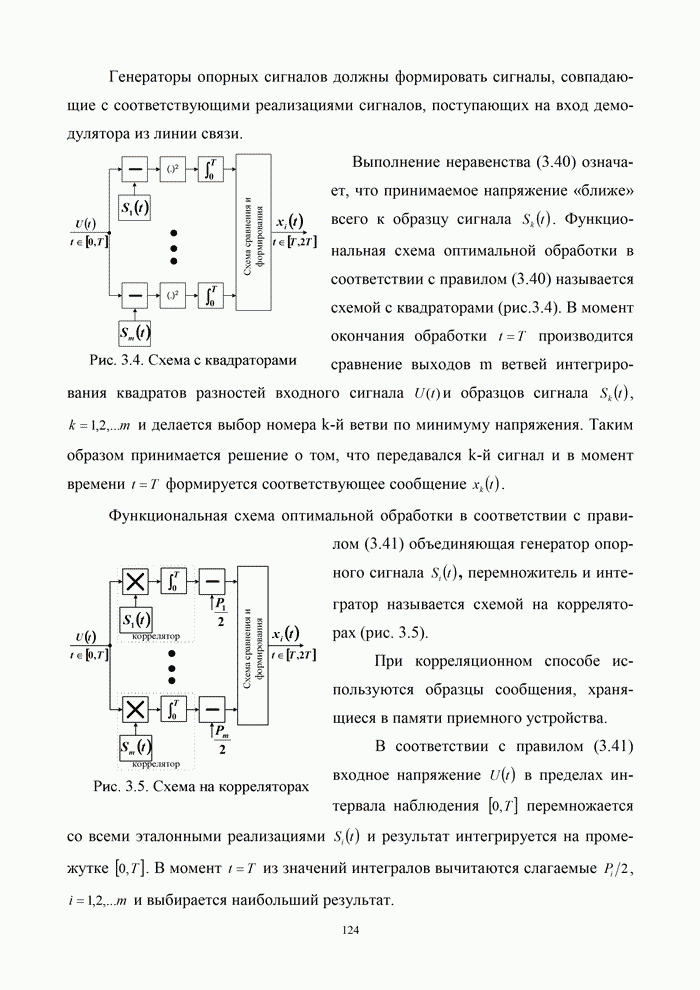
- 3.2.1. Оптимальные алгоритмы приема при полностью известных сигналах
- 3.2.2. Реализация алгоритмов оптимального когерентного приема
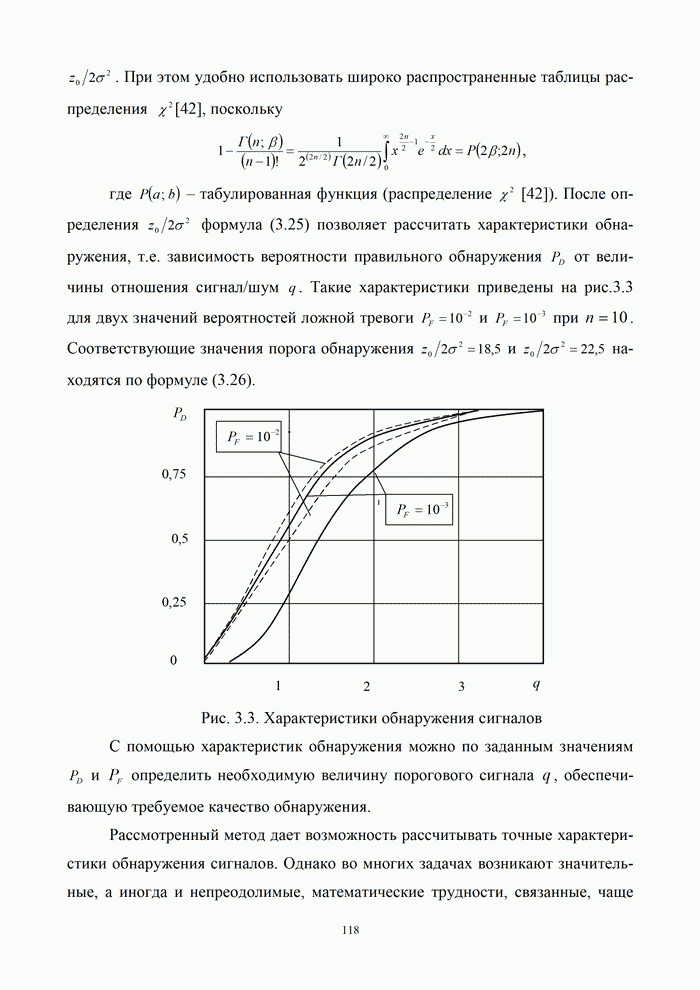
- 3.3. Помехоустойчивость приема сигналов с известными параметрами
- 3.4. Прием сигналов с неопределенной фазой
- 3.4.1. Оптимальный некогерентный прием дискретных сигналов
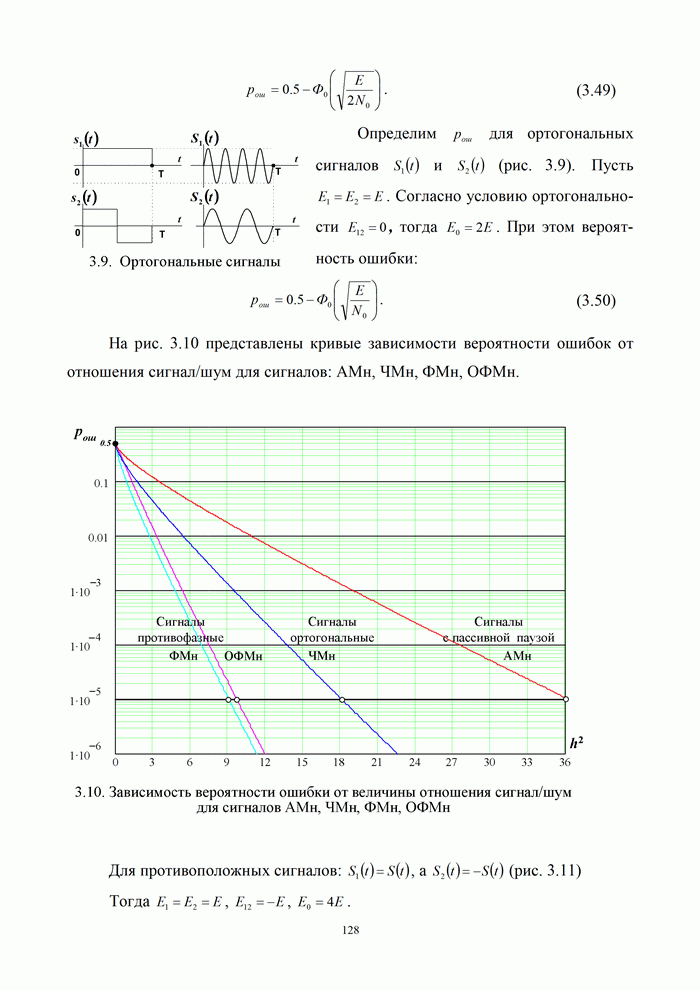
- 3.4.2. Помехоустойчивость оптимального некогерентного приема
- 3.5. Подоптимальные методы приема
- 3.5.1. Причины применения неоптимальных методов приема
- 3.5.2. Квазиоптимальные методы приема
- Контрольные вопросы
- Глава 4. Теория передачи информации
- 4.1. Информационные характеристики источника сообщений
- 4.1.1. Количественное определение информации
- 4.1.2. Энтропия и производительность дискретного источника сообщений
- 4.2. Пропускная способность дискретного канала
- 4.2.1. Количество информации переданной по дискретному каналу
- 4.2.2. Пропускная способность дискретного канала
- 4.2.3. Пропускная способность симметричного дискретного канала без памяти
- 4.3. Методы сжатия дискретных сообщений
- 4.3.1. Условия существования оптимального неравномерного кода
- 4.3.2. Прямая и обратная теоремы кодирования источника неравномерными кодами
- 4.3.3. Показатели эффективности сжатия
- 4.3.4. Кодирование источника дискретных сообщений методом Шеннона-Фано
- 4.3.5. Кодирование источника дискретных сообщений методом Хаффмена
- 4.4. Пропускная способность непрерывного канала
- 4.4.1. Постановка задачи передачи дискретных сообщений в непрерывном канале
- 4.4.2. Количество информации, переданной по непрерывному каналу
- 4.4.3. Пропускная способность непрерывного канала
- Контрольные вопросы
- Глава 5. Теория кодирования сообщений
- 5.1. Помехоустойчивое кодирование: блочные и непрерывные коды
- 5.1.1. Постановка задачи помехоустойчивого кодирования
- 5.1.2. Классификация кодов
- 5.1.3. Основные характеристики и свойства блочных кодов
- 5.2. Эффективность помехоустойчивого кодирования
- 5.2.1. Эффективность кода в режиме исправления ошибок
- 5.2.2. Эффективность кода в режиме обнаружения ошибок
- 5.2.3. Эффективность помехоустойчивых кодов
- 5.3. Математические основы теории помехоустойчивого кодирования
- 5.3.1. Краткие сведения из теории чисел
- 5.3.2. Группы
- 5.3.3. Кольца и поля
- 5.3.4. Векторное пространство
- 5.3.5. Конечные поля
- 5.4. Линейные блочные коды
- 5.4.1. Система передачи дискретных сообщений
- 5.4.2. Параметры линейного кода
- 5.4.3. Полиномиальные циклические коды
- 5.4.4. Циклические коды и корни полиномов
- 5.4.5. Спектральное описание циклических кодов
- 5.4.6. Простейшие блочные линейные коды
- 5.5. Коды Боуза-Чоудхури-Хоквингема
- 5.5.1. Методы задания кодов БЧХ
- 5.5.2. Принципы декодирования кодов БЧХ
- 5.5.3. Методы реализации этапов декодирования кодов БЧХ
- 5.6. Коды Рида-Соломона
- 5.6.1. Основные определения
- 5.6.2. Обнаружение и исправление пакетов ошибок
- 5.7. Коды Рида-Маллера
- 5.7.1. Задание и декодирование кодов Рида-Маллера
- 5.7.2. Симплексные коды и m-последовательности
- 5.7.3. Связь между блочными кодами
- 5.8. Сверточные коды
- 5.8.1. Основные параметры
- 5.8.2. Способы задания сверточного кода
- 5.8.3. Алгоритм декодирования Витерби
- 5.9. Помехоустойчивость систем передачи дискретных сообщений
- 5.9.1. Две процедуры приема сигналов
- 5.9.2. Помехоустойчивость систем передачи информации при оптимальной процедуре приема
- 5.9.3. Помехоустойчивость систем передачи информации при посимвольном приеме сигналов
- Контрольные вопросы
- Глава 6. Сигналы с импульсной модуляцией
- 6.1. Методы импульсной модуляции
- 6.1.1. Импульсные методы передачи непрерывных сигналов
- 6.1.2. Спектральные характеристики импульсных методов модуляции
- 6.2. Помехоустойчивость непрерывных каналов связи с импульсной модуляцией
- 6.2.1. Помехоустойчивость систем передачи с импульсными методами модуляции
- 6.3. Цифровые методы передачи непрерывных сообщений
- 6.3.1. Передача сигналов с импульсно-кодовой модуляцией
- 6.3.2. Передача сигналов с дельта модуляцией
- 6.3.3. Квантование сигналов в системах с ИКМ и ДМ
- Контрольные вопросы
- Глава 7. Методы приема сигналов в сложных условиях
- 7.1. Прием сигналов в каналах с замираниями
- 7.1.1. Сущность замираний и их классификация
- 7.1.2. Принципы разнесенного приема сигналов
- 7.2. Методы борьбы с замираниями сигналов
- 7.2.1. Методы борьбы с замираниями в аналоговых системах связи
- 7.2.2. Методы борьбы с замираниями в цифровых системах связи
- 7.3. Методы борьбы с межсимвольной интерференцией
- 7.3.1. Причины возникновения и сущность межсимвольной интерференции
- 7.3.2. Обработка сигналов в каналах с межсимвольной интерференцией
- 7.3.3. Помехоустойчивость в каналах с межсимвольной интерференцией
- 7.4. Прием дискретных сообщений в каналах с сосредоточенными по спектру и импульсными помехами
- 7.4.1. Общая характеристика сосредоточенных по спектру и импульсных помех
- 7.4.2. Борьба с сосредоточенными и импульсными помехами
- 7.5. Компенсация помех и искажений в канале
- 7.5.1. Принцип работы радиолинии с ФМ ПСС (ФМ ШПС)
- 7.5.2. Помехоустойчивость радиолинии с ФМ ПСС
- 7.5.3. Принципы работы радиолиний с ППРЧ
- 7.5.4. Помехоустойчивость радиолиний с ППРЧ
- Контрольные вопросы
- Глава 8. Многоканальная связь и распределение информации
- 8.1. Методы распределения ресурса общего канала
- 8.1.1. Классификация систем передачи информации, использующих единый ресурс
- 8.1.2. Постановка задачи объединения и разделения сигналов
- 8.1.3. Энергетическая и спектральная цена уплотнения
- 8.2. Частотное разделение каналов
- 8.2.1. Принцип частотного объединения и разделения каналов
- 8.2.2. Групповой сигнал, его структура и характеристики
- 8.3. Временное разделение каналов
- 8.3.1. Принцип временного разделения каналов
- 8.3.2. Характеристики группового сигнала систем с ВРК
- 8.4. Разделение сигналов по форме
- Контрольные вопросы
- Глава 9. Эффективность систем связи
- 9.1. Оценка эффективности систем связи
- 9.1.1. Подходы к оценке эффективности
- 9.1.2. Критерии эффективности
- 9.1.3. Эффективность аналоговых и цифровых систем
- 9.2. Выбор сигналов и помехоустойчивых кодов
- 9.2.1. Многопозиционные сигналы
- 9.2.2. Корректирующие коды
- 9.3. Оптимизация систем связи
- 9.3.1. Согласование методов модуляции и кодирования
- 9.3.2. Классификация сигнально – кодовых конструкций
- 9.4. Характеристики основных типов СКК
- 9.4.1. Согласование канала кодом Грея
- 9.4.2. Согласование на основе разбиения ансамбля на вложенные подансамбли
- 9.5. Алгоритмы цифровой обработки сигналов
- 9.5.1. Дискретные сигналы и их спектры
- 9.5.2. Алгоритмы дискретного и быстрого преобразований Фурье
- Контрольные вопросы
- Глава 10. Теоретико-информационные основы криптозащиты сообщений в телекоммуникационных системах
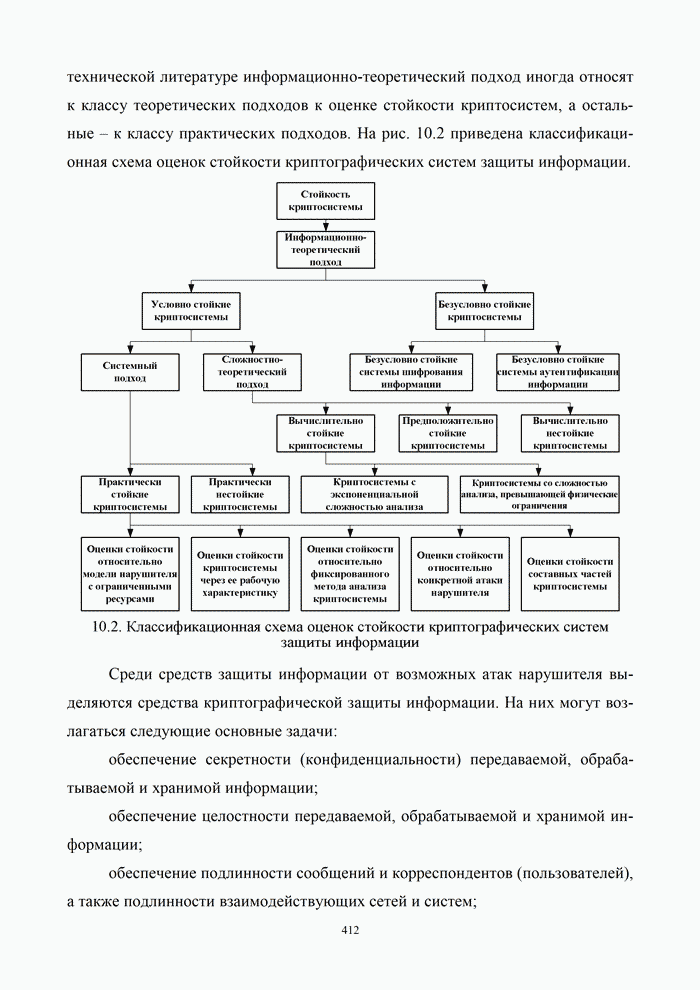
- 10.1. Классификация криптографических систем
- 10.1.2. Классификация криптографических систем защиты информации
- 10.1.3. Оценка стойкости криптосистем
- 10.2. Функции, используемые в криптографических системах
- 10.2.1. Общее описание функций, используемых в криптографических системах
- 10.2.2. Однонаправленные функции
- 10.2.3. Криптографические хэш-функции
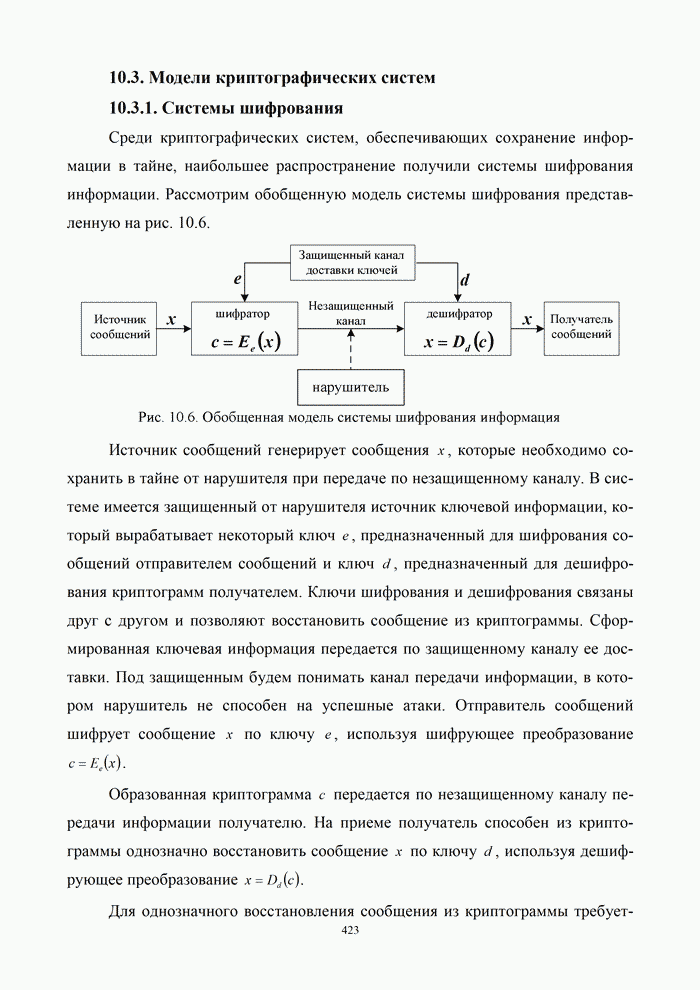
- 10.3. Модели криптографических систем
- 10.3.1. Системы шифрования
- 10.3.2. Традиционные симметричные криптосистемы
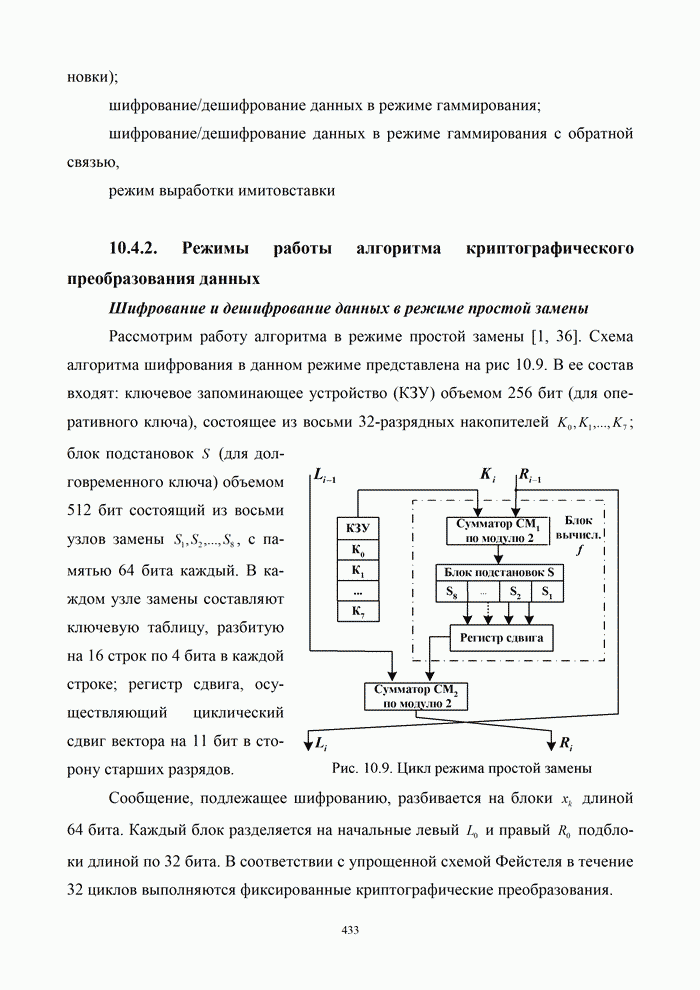
- 10.4. Алгоритмы криптографической защиты
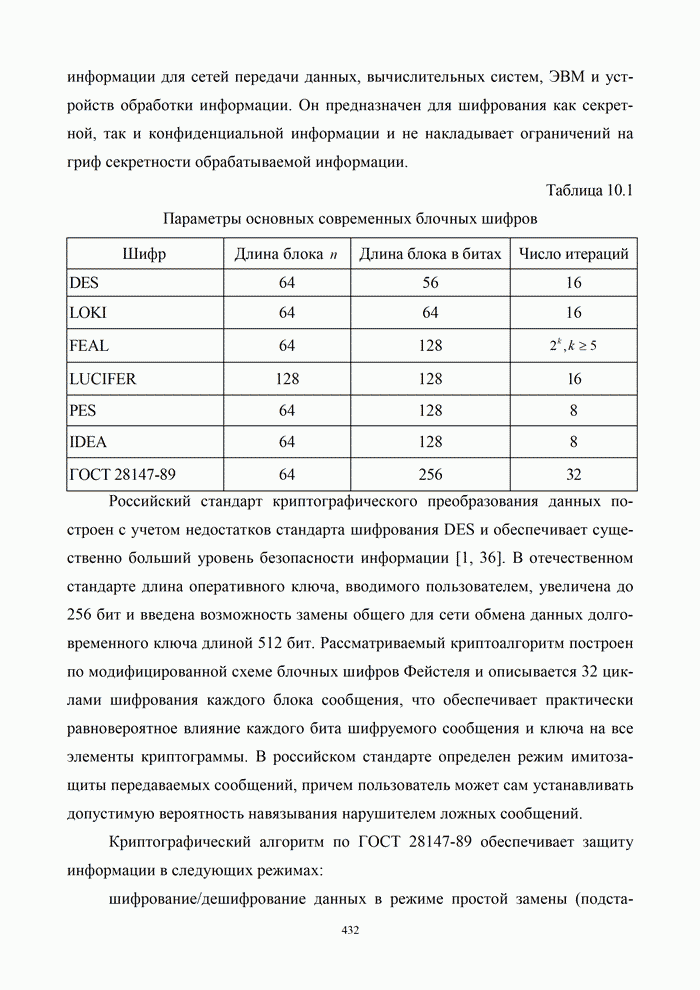
- 10.4.1. Алгоритм криптографической защиты информации согласно ГОСТ 28147-89
- Контрольные вопросы
- Заключение
- Список литературы