| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.4. Прием сигналов с неопределенной фазой
Когерентный
прием дискретных сигналов основан на точном знании фазы возможных реализаций
переданного сигнала на входе демодулятора. Однако при передаче сигналов по
каналам радиосвязи фаза принимаемого сигнала обычно является случайной
величиной, принимающей значения в пределах
от 0 до ![]() .
.
3.4.1. Оптимальный некогерентный прием дискретных сигналов
Способ когерентной обработки сигналов относится к идеализированным условиям, когда неизвестно, какая из заданных реализаций была передана. Форма реализаций, момент прихода и мощность достоверно известны.
Изменение параметров канала связи ![]() , изменение режима передающего
устройства и ряд других факторов приводят к тому, что некоторые параметры
реализаций сигнала делаются случайными и могут быть оценены с некоторой погрешностью.
Такая ситуация особенно характерна для радиоканалов. Получение алгоритмов
оптимальной обработки сигналов со случайными параметрами — проблема значительно
более сложная. При ее решении пользуются двумя приемами.
, изменение режима передающего
устройства и ряд других факторов приводят к тому, что некоторые параметры
реализаций сигнала делаются случайными и могут быть оценены с некоторой погрешностью.
Такая ситуация особенно характерна для радиоканалов. Получение алгоритмов
оптимальной обработки сигналов со случайными параметрами — проблема значительно
более сложная. При ее решении пользуются двумя приемами.
Первый прием характерен для ситуации, когда некоторый
случайный параметр ![]() меняется
медленно и за время действия одной реализации его можно считать неизменным.
Тогда правило обработки, и схема приемника сохраняются, а параметр для каждого
следующего решения экстраполируется по множеству его предыдущих значений.
Обычно это удается выполнить с помощью введения автоматических регулировок.
Так, например, при неизвестной амплитуде сигнала вводится автоматическая
регулировка порогового уровня.
меняется
медленно и за время действия одной реализации его можно считать неизменным.
Тогда правило обработки, и схема приемника сохраняются, а параметр для каждого
следующего решения экстраполируется по множеству его предыдущих значений.
Обычно это удается выполнить с помощью введения автоматических регулировок.
Так, например, при неизвестной амплитуде сигнала вводится автоматическая
регулировка порогового уровня.
Второй прием применяется в условиях, если параметр ![]() меняется
быстро и за время действия реализации Т он может значительно изменяться.
Для получения правила оптимальной обработки в этих условиях составляют функцию
правдоподобия
меняется
быстро и за время действия реализации Т он может значительно изменяться.
Для получения правила оптимальной обработки в этих условиях составляют функцию
правдоподобия ![]() ,
как это делалось ранее. Поскольку функция правдоподобия оказывается зависящей
от параметра
,
как это делалось ранее. Поскольку функция правдоподобия оказывается зависящей
от параметра ![]() ,
ее усредняют. Для усреднения необходимо знать плотность распределения
вероятностей
,
ее усредняют. Для усреднения необходимо знать плотность распределения
вероятностей ![]()
![]() случайного
параметра
случайного
параметра ![]() . Тогда правило оптимальной обработки
принимает вид
. Тогда правило оптимальной обработки
принимает вид
![]() ,
,
где величина порога ![]() зависит от выбранного
критерия.
зависит от выбранного
критерия.
Оптимальный прием сигнала в условиях, когда начальная фаза сигнала является величиной случайной, называют оптимальным некогерентным приемом.
Обычно предполагают, что в пределах периода начальная фаза имеет равновероятное распределение, так что плотность распределения постоянна и равна
![]() .
.
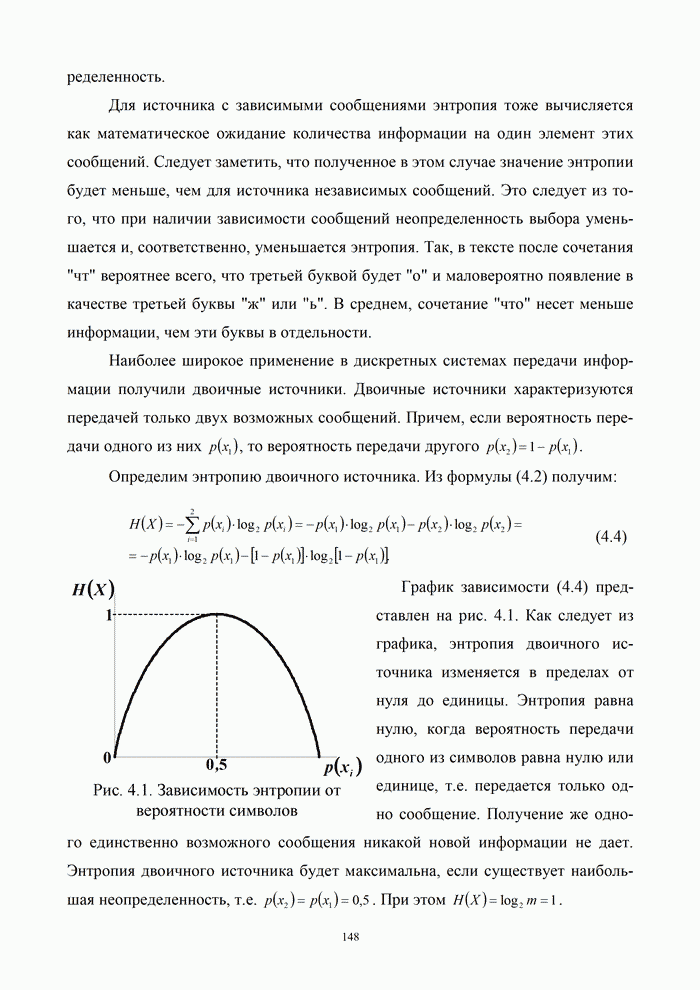
При этом правило оптимальной обработки имеет вид:
 , (3.53)
, (3.53)
![]() — модифицированная функция Бесселя нулевого порядка;
— модифицированная функция Бесселя нулевого порядка; ![]() — огибающая некоторого процесса
— огибающая некоторого процесса ![]() , зависящего от
принимаемого сигнала.
, зависящего от
принимаемого сигнала.
Если неравенство (3.53) выполняется, то
принимается решение пользу реализации ![]() .
.
Прежде чем перейти к правилам обработки сигнала,
остановимся несколько подробнее на смысле функции ![]() . Рассмотрим реализацию сигнала на входе приемника:
. Рассмотрим реализацию сигнала на входе приемника:
![]() .
.
Если в ее спектре все составляющие сдвинуты по фазе на — 90°,
то получится реализация ![]() , ортогональная с
, ортогональная с ![]() и однозначно ней связанная, которую называют сопряженной реализацией
с
и однозначно ней связанная, которую называют сопряженной реализацией
с ![]() .
.
Образуем взаимокорреляционные функции принимаемого сигала
с ![]() и
и ![]() :
:
 (3.54)
(3.54)
Тогда
![]() . (3.55)
. (3.55)
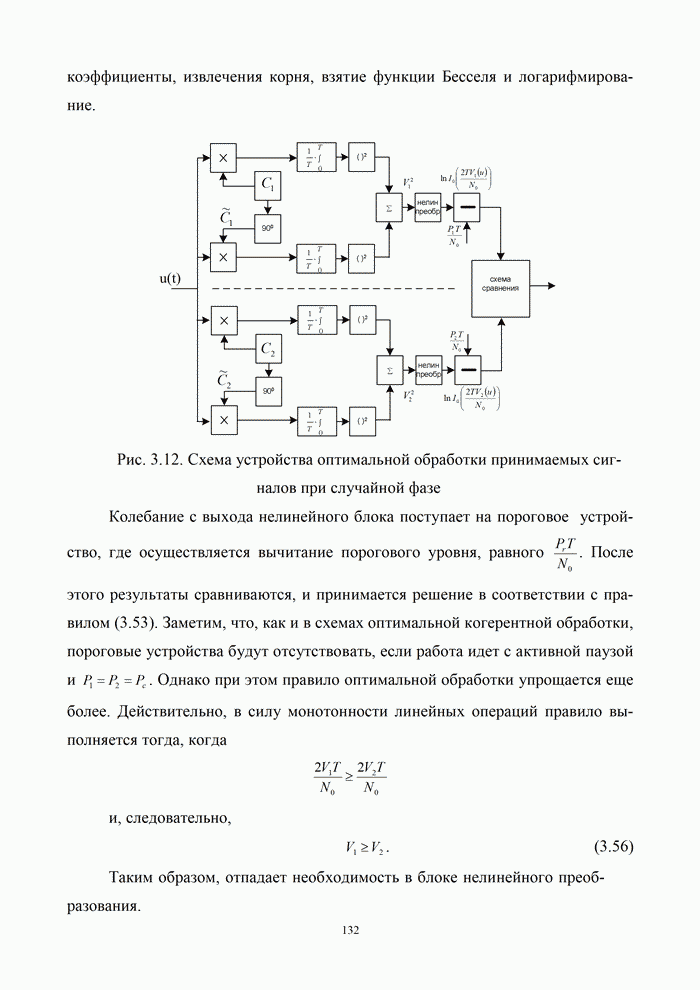
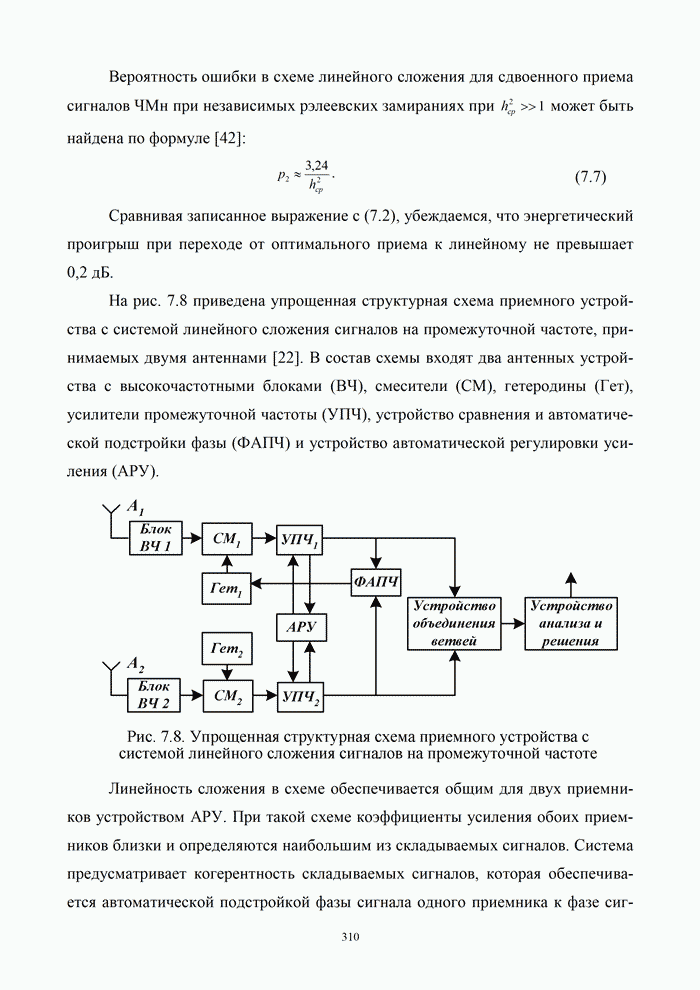
На рис. 3.12 приведена функциональная схема устройства
оптимальной обработки принимаемых сигналов при случайной фазе. Она содержит
генераторы реализаций ![]() и
и ![]() , от которых формируются сопряженные с ними
реализации
, от которых формируются сопряженные с ними
реализации ![]() и
и
![]() . Затем путем
перемножения, интегрирования, возведения в квадрат и суммирования формируются
. Затем путем
перемножения, интегрирования, возведения в квадрат и суммирования формируются ![]() . Результаты
суммирования поступают в блок нелинейного преобразования, который осуществляет
умножение на коэффициенты, извлечения корня, взятие функции Бесселя и
логарифмирование.
. Результаты
суммирования поступают в блок нелинейного преобразования, который осуществляет
умножение на коэффициенты, извлечения корня, взятие функции Бесселя и
логарифмирование.

Рис. 3.12. Схема устройства оптимальной обработки принимаемых сигналов при случайной фазе
Колебание с выхода нелинейного блока поступает на пороговое
устройство, где осуществляется вычитание порогового уровня, равного ![]() . После этого
результаты сравниваются, и принимается решение в соответствии с правилом (3.53).
Заметим, что, как и в схемах оптимальной когерентной обработки, пороговые
устройства будут отсутствовать, если работа идет с активной паузой и
. После этого
результаты сравниваются, и принимается решение в соответствии с правилом (3.53).
Заметим, что, как и в схемах оптимальной когерентной обработки, пороговые
устройства будут отсутствовать, если работа идет с активной паузой и ![]() . Однако при этом
правило оптимальной обработки упрощается еще более. Действительно, в силу
монотонности линейных операций правило выполняется тогда, когда
. Однако при этом
правило оптимальной обработки упрощается еще более. Действительно, в силу
монотонности линейных операций правило выполняется тогда, когда
![]()
и, следовательно,
![]() . (3.56)
. (3.56)
Таким образом, отпадает необходимость в блоке нелинейного преобразования.
Более просто выглядит схема устройства
оптимальной обработки, если удается создать согласованные с реализациями ![]() и
и ![]() фильтры. На рис. 3.13 приведена такая схема с пороговыми
устройствами.
фильтры. На рис. 3.13 приведена такая схема с пороговыми
устройствами.

Рис. 3.13. Схема с пороговыми устройствами
В случае ![]() пороговые устройства отсутствуют,
и детекторная характеристика может быть любой. Важно лишь, чтобы эти
характеристики для обоих детекторов были одинаковыми и монотонно нарастающими.
В этом случае входной сигнал
пороговые устройства отсутствуют,
и детекторная характеристика может быть любой. Важно лишь, чтобы эти
характеристики для обоих детекторов были одинаковыми и монотонно нарастающими.
В этом случае входной сигнал ![]() поступает на согласованные
фильтры, отклики фильтров детектируются и в момент отсчета результаты
сравниваются. Решение принимается в пользу той реализации, у которой огибающая
на выходе согласованного фильтра оказалась больше.
поступает на согласованные
фильтры, отклики фильтров детектируются и в момент отсчета результаты
сравниваются. Решение принимается в пользу той реализации, у которой огибающая
на выходе согласованного фильтра оказалась больше.
Вероятность ошибки при оптимальном некогерентном приеме, естественно, больше, чем при когерентном:
![]() . (3.57)
. (3.57)
Рассмотрим примеры некогерентного приема двоичных радиосигналов, т. е. таких сигналов, которые могут быть представлены отрезками гармонических колебаний. При этом будем считать, что значение начальной фазы сигнала, действующего на входе приемника, неизвестно.
Амплитудная манипуляция
Для AМн, как уже отмечалось, реализации сигналов записывают следующим образом:
![]() ;
;
![]() ,
,
где ![]() — случайная величина, а
— случайная величина, а ![]() .
.
Правило оптимальности обработки (8.34) принимает вид
![]()
 . (3.58)
. (3.58)
Если неравенство (3.58) выполняется, то решение принимается в
пользу реализации ![]() .
.
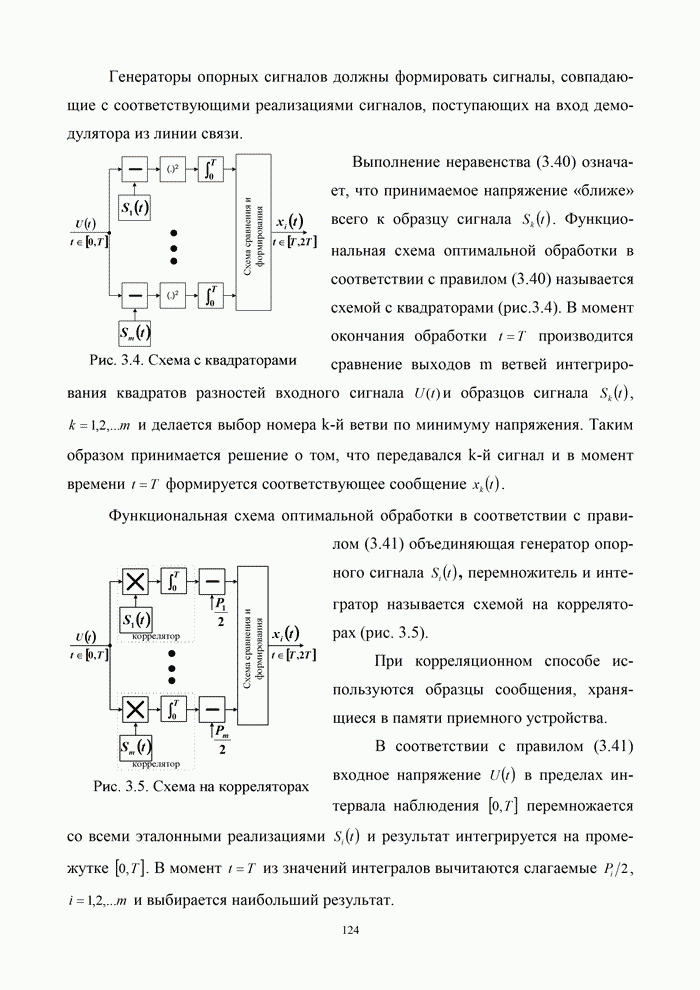
Правило (3.58) может быть реализовано в виде корреляционного приемника или в виде приемника на согласованных фильтрах. Структурные схемы таких устройств изображены в верхней части схем рис. 3.12 и 3.13, отделенной пунктирной линией.
Таким образом, после выделения огибающей и
нелинейного ее преобразования производится сравнение результатов с пороговым
уровнем. Если результат нелинейного преобразования превышает порог, то
принимается решение о том, что передавалась реализация ![]() . Заметим,
что пороговый уровень определяется мощностью сигнала и спектральной плотностью
мощности шума. И то и другое может быть оценено в реальных условиях лишь с
определенной точностью и к тому же имеет тенденцию к изменению во времени.
. Заметим,
что пороговый уровень определяется мощностью сигнала и спектральной плотностью
мощности шума. И то и другое может быть оценено в реальных условиях лишь с
определенной точностью и к тому же имеет тенденцию к изменению во времени.
На рис. 3.14 изображены условные плотности распределения огибающих при передаче ![]() и
и ![]() . Они подчиняются обобщенному закону Рэлея при передаче
. Они подчиняются обобщенному закону Рэлея при передаче ![]() или
просто закону Рэлея, если передается
или
просто закону Рэлея, если передается ![]() и фактически речь идет о законе распределения огибающей
белого шума.
и фактически речь идет о законе распределения огибающей
белого шума.

Рис. 3.14 Условные плотности распределения огибающих при передаче ![]() и
и ![]()
Пороговый уровень на практике выбирают по точке пересечения кривых распределения, для которой
![]() .
.
Это достаточно близко к теоретическому значению уровня,
вытекающему из правила (3.58), а при ![]() такой выбор порога является оптимальным.
такой выбор порога является оптимальным.
Вероятность ошибки определяется как сумма
площадей, ограниченных осью абсцисс, кривой 1 (для ![]() ) и кривой 2 (для
) и кривой 2 (для
![]() ). На рис. 3.14
эти площади заштрихованы. Приближенно можно пользоваться и формулой (3.57).
). На рис. 3.14
эти площади заштрихованы. Приближенно можно пользоваться и формулой (3.57).
Частотная манипуляция
При ЧМн реализации сигнала записываются в виде:
![]() (3.59)
(3.59)
где ![]() и
и ![]() — случайные фазы, a
— случайные фазы, a ![]() .
.
Рассматриваемый случай отличается от AМн тем, что работа осуществляется с активной паузой. Что касается реализации оптимальных фильтров или устройств выделения огибающей V корреляционным способом, то они такие же, как при AМн.
Структурные схемы оптимальной обработки принимаемых сигналов с неизвестной
начальной фазой при ЧМн полностью совпадают со схемами, изображенными на рис. 3.12
и 3.13. Генераторы Г1 и Г2 (см. рис. 3.12)
генерируют косинусоиды с нулевыми начальными
фазами и с частотами соответственно ![]() и
и ![]() . В схеме, приведенной на рис. 3.13,
оптимальные фильтры должны быть согласны с такими реализациями. Принцип работы
подобных схем описан выше. Отметим лишь один существенный момент. В системах с
активной паузой различие форм реализаций существенно влияет на вероятность
ошибки. Минимум вероятности ошибки имел место при противоположных реализациях,
когда
. В схеме, приведенной на рис. 3.13,
оптимальные фильтры должны быть согласны с такими реализациями. Принцип работы
подобных схем описан выше. Отметим лишь один существенный момент. В системах с
активной паузой различие форм реализаций существенно влияет на вероятность
ошибки. Минимум вероятности ошибки имел место при противоположных реализациях,
когда ![]() .
При частотной телеграфии создать противоположные реализации невозможно, однако
можно добиться их ортогональности, если выбрать
.
При частотной телеграфии создать противоположные реализации невозможно, однако
можно добиться их ортогональности, если выбрать
![]() ,
,
или
![]() , (3.60)
, (3.60)
где k = 1,2,3,...; ![]() — скорость работы в бодах, равная числу
символов, передаваемых по каналу связи в одну секунду.
— скорость работы в бодах, равная числу
символов, передаваемых по каналу связи в одну секунду.
Относительно-фазовая манипуляция
Естественно, что фазовую телеграфию, обеспечивающую минимум вероятности ошибки, трудно осуществить при случайной фазе, так как значение фазы реализации сигнала несет информацию передаваемом сообщении. При ОФМн информация заключена в значении фазы, а в ее изменении при переходе от одной реализации к другой. Для того чтобы принять решение о том, какой из символов передавался, необходимо анализировать принимаемый сигнал не в течение времени Т, равного длительности одной реализации, а за промежуток времени, в два раза больший. Возможны два взаимно исключающих случая.
1. За промежуток времени
(![]() ) начальная
фаза реализаций принимаемого сигнала не изменилась и, следовательно, можно
записать:
) начальная
фаза реализаций принимаемого сигнала не изменилась и, следовательно, можно
записать:
![]() , (3.61)
, (3.61)
где ![]() —
случайная фаза.
—
случайная фаза.
2. В момент времени ![]() произошла смена фазы
и, следовательно, для принимаемых реализаций сигнала справедливо условие
произошла смена фазы
и, следовательно, для принимаемых реализаций сигнала справедливо условие
 (3.62)
(3.62)
Отсюда
следует, что ОФМн можно представить, как некоторый вид работы с активной
паузой, когда реализации сигнала ![]() и
и ![]() описываются выражениями (3.61) и (3.62). Таким образом, можно синтезировать устройство обработки
принимаемых сигналов по общим правилам некогерентного приема, считая, что
длительность реализаций равна 2Т (хотя отсчеты производятся через промежуток
времени равный Т).
описываются выражениями (3.61) и (3.62). Таким образом, можно синтезировать устройство обработки
принимаемых сигналов по общим правилам некогерентного приема, считая, что
длительность реализаций равна 2Т (хотя отсчеты производятся через промежуток
времени равный Т).
Правило (3.53) для ОФМн принимает вид
![]() или
или ![]() . (3.63)
. (3.63)
Здесь
 (3.64)
(3.64)
Из (3.64) видно, что ![]() отличается от
отличается от ![]() , так же как и
, так же как и ![]() от
от ![]() , лишь сдвигом по
времени на величину Т, так как
, лишь сдвигом по
времени на величину Т, так как ![]() берется из разных интервалов
времени. Следовательно, величины
берется из разных интервалов
времени. Следовательно, величины ![]() и
и ![]() , как результат формирования
, как результат формирования ![]() и
и ![]() за предыдущий
интервал времени длительностью Т
за предыдущий
интервал времени длительностью Т![]() , должны запоминаться схемой.
, должны запоминаться схемой.
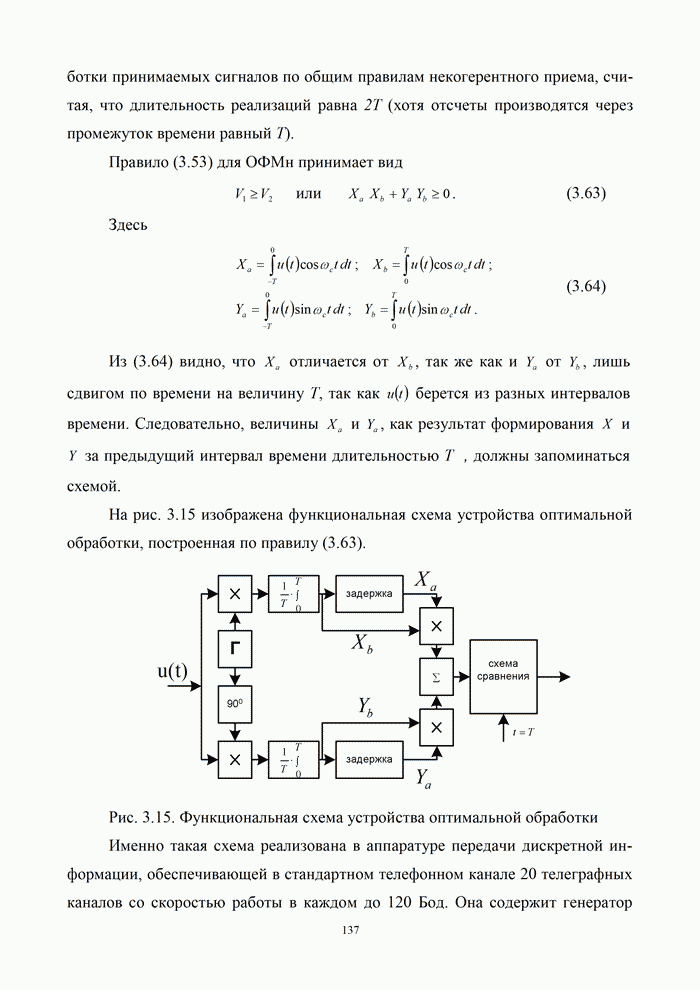
На рис. 3.15 изображена функциональная схема устройства оптимальной обработки, построенная по правилу (3.63).

Рис. 3.15. Функциональная схема устройства оптимальной обработки
Именно такая схема реализована в аппаратуре
передачи дискретной информации, обеспечивающей в стандартном телефонном канале 20
телеграфных каналов со скоростью работы в каждом до 120 Бод. Она содержит
генератор колебания косинусоидальной формы, фазовращатель на угол 90°,
позволяющий получить синусоидальные колебания, сдвинутые друг относительно
друга на 90°, два высокочастотных перемножителя, две линии задержки для
формирования ![]() и
и
![]() , сумматор
и устройства определения знака результата суммирования. Отсчет производится
через интервалы времени, равные Т. Если результат суммирования больше
нуля, то принимается решение, что передавалась реализация
, сумматор
и устройства определения знака результата суммирования. Отсчет производится
через интервалы времени, равные Т. Если результат суммирования больше
нуля, то принимается решение, что передавалась реализация ![]() , в противном случае решение принимается в пользу
, в противном случае решение принимается в пользу ![]() .
.
Следует отметить, что в данной аппаратуре задержка сигналов осуществляется с помощью запоминающих устройств.
Правило (3.63) может быть реализовано с помощью согласованного фильтра. На рис.3.16 приведена функциональная схема такого устройства.

Рис.3.16 Схема реализации с помощью согласованного фильтра
Согласованный фильтр строится на реализацию сигнала длительностью Т косинусоидальной формы. Текущий отклик фильтра и отклик с выхода линии задержки перемножаются и интегрируются на интервале [0, Т].
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Список сокращений
- Основные обозначения
- ВВЕДЕНИЕ
- Глава 1. Сообщения, сигналы и помехи, их математические модели
- 1.1. Основные понятия и определения
- 1.1.1. Сообщение, сигнал, модуляция
- 1.1.2. Основные параметры сигналов
- 1.2. Системы связи. Каналы связи
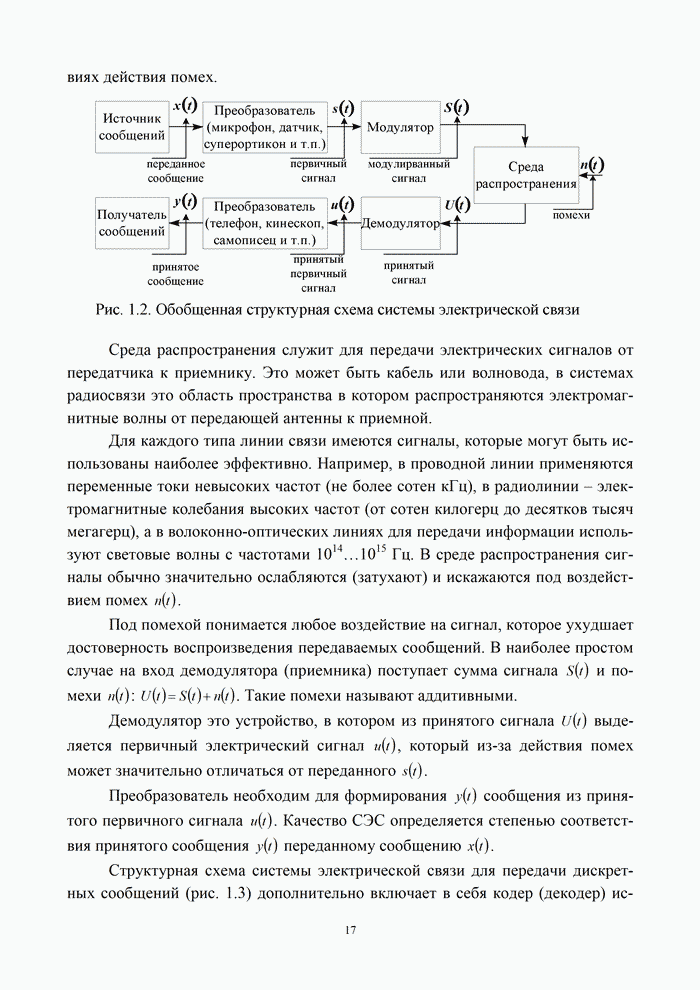
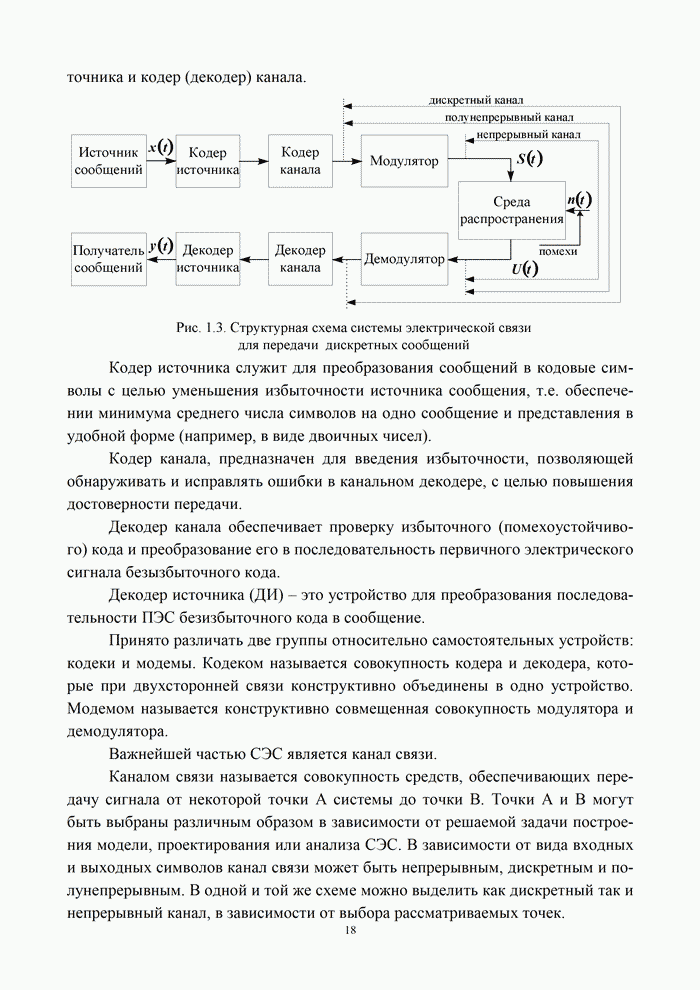
- 1.2.1. Структура канала электросвязи
- 1.2.2. Линия и сеть связи
- 1.2.3. Помехи и искажения в канале
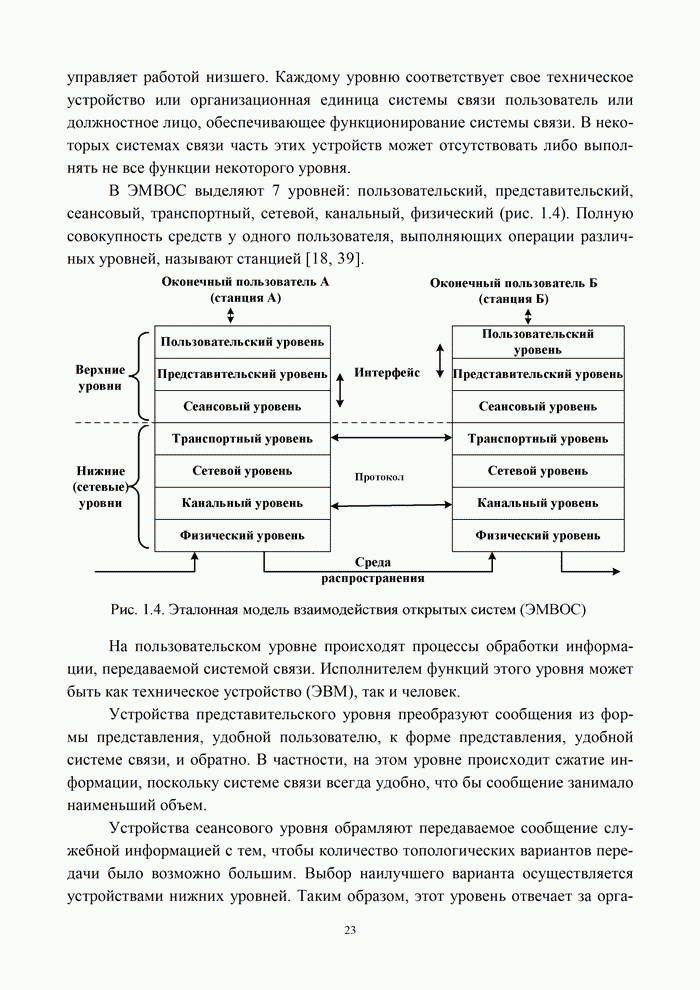
- 1.2.4. Эталонная модель взаимодействия открытых систем
- 1.2.5. Модели каналов связи и их математическое описание
- 1.3. Способы описания сигналов и помех
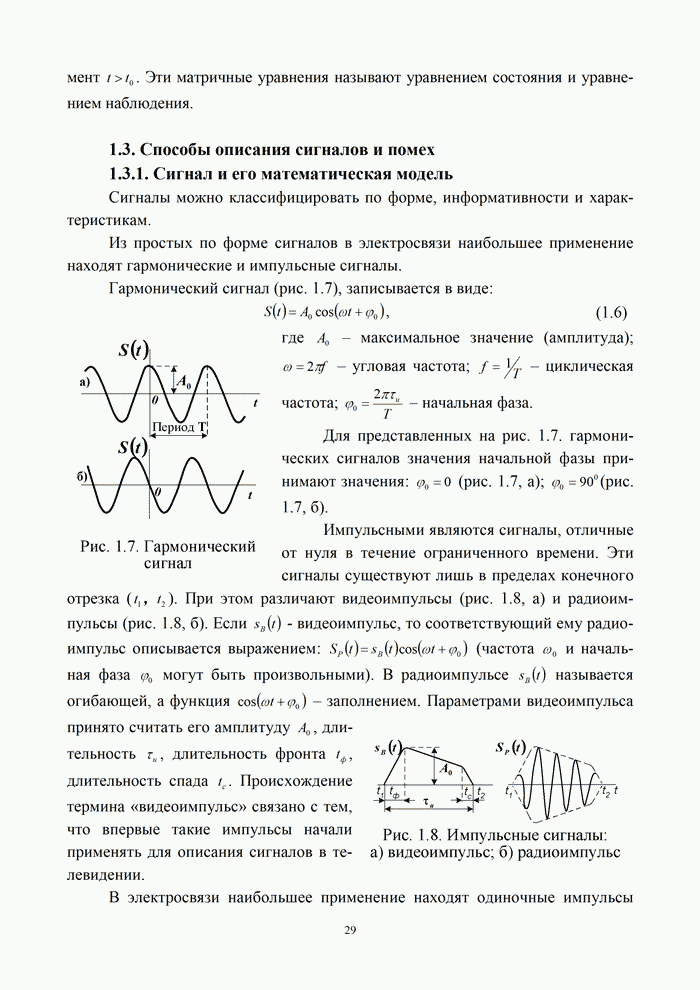
- 1.3.1. Сигнал и его математическая модель
- 1.3.2. Энергетические характеристики детерминированного сигнала
- 1.4.2. Представление сигналов и помех рядом Фурье
- 1.4.3. Применение преобразования Фурье для непериодических сигналов
- 1.5. Теорема Котельникова
- 1.6. Пространство сигналов
- 1.6.1. Линейное пространство
- 1.6.2. Представление сигнала в многомерном пространстве
- 1.7. Сигналы как случайные процессы
- 1.7.1. Характеристики случайного процесса
- 1.7.2. Флуктуационный шум
- 1.8. Комплексное представление сигналов и помех
- 1.8.1. Понятие аналитического сигнала
- 1.8.2. Огибающая, мгновенная фаза и мгновенная частота узкополосного случайного процесса
- Контрольные вопросы
- Глава 2. Методы формирования и преобразования сигналов
- 2.1. Модуляция сигналов
- 2.1.1. Амплитудная модуляция гармонической несущей
- 2.1.2. Балансная и однополосная модуляция гармонической несущей
- 2.2. Методы угловой модуляции
- 2.2.1. Принципы частотной и фазовой (угловой) модуляции
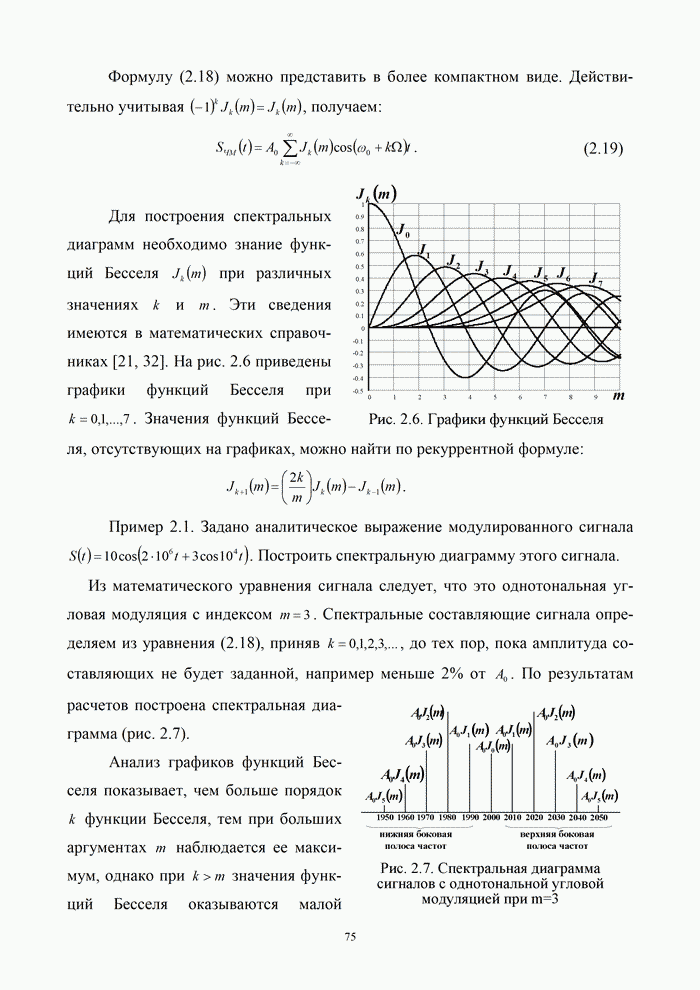
- 2.2.2. Спектр сигналов угловой модуляции
- 2.3. Формирование и детектирование модулированных сигналов
- 2.3.1. Формирование и детектирование сигналов амплитудной и однополосной амплитудной модуляции
- 2.3.2. Формирование и детектирование сигналов угловой модуляции
- 2.4. Манипуляция сигналов
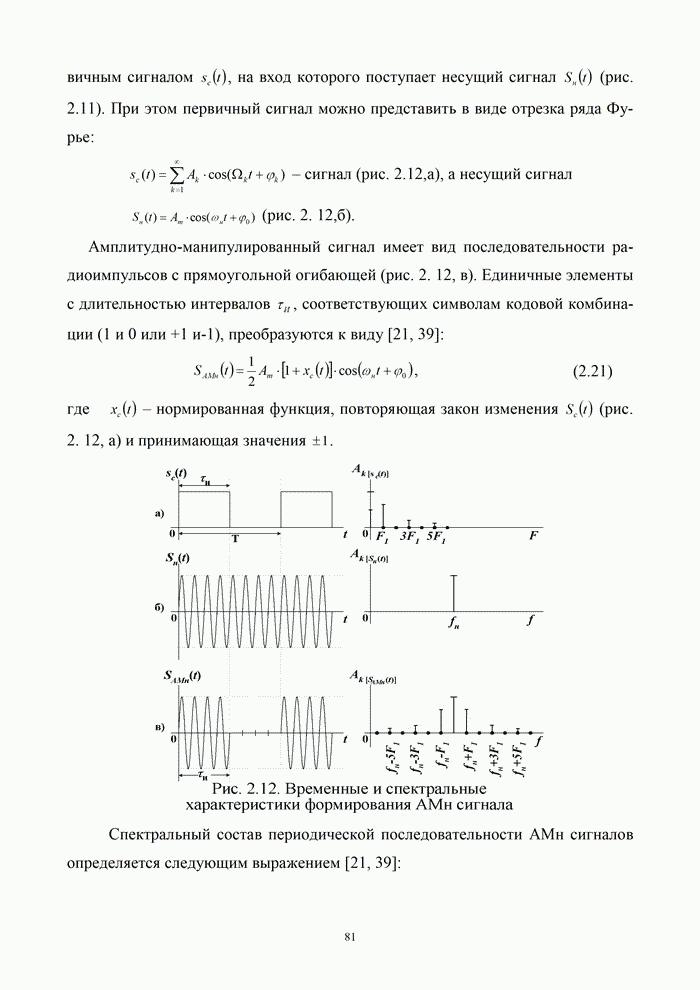
- 2.4.1. Временные и спектральные характеристики амплитудно-манипулированных сигналов
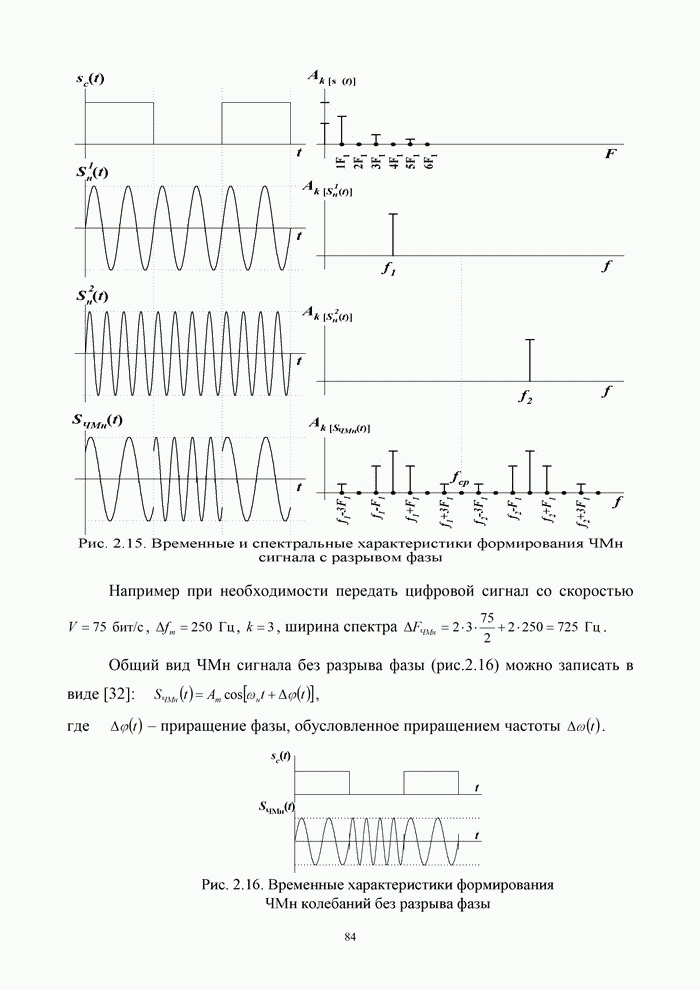
- 2.4.2. Временные и спектральные характеристики частотно-манипулированных сигналов
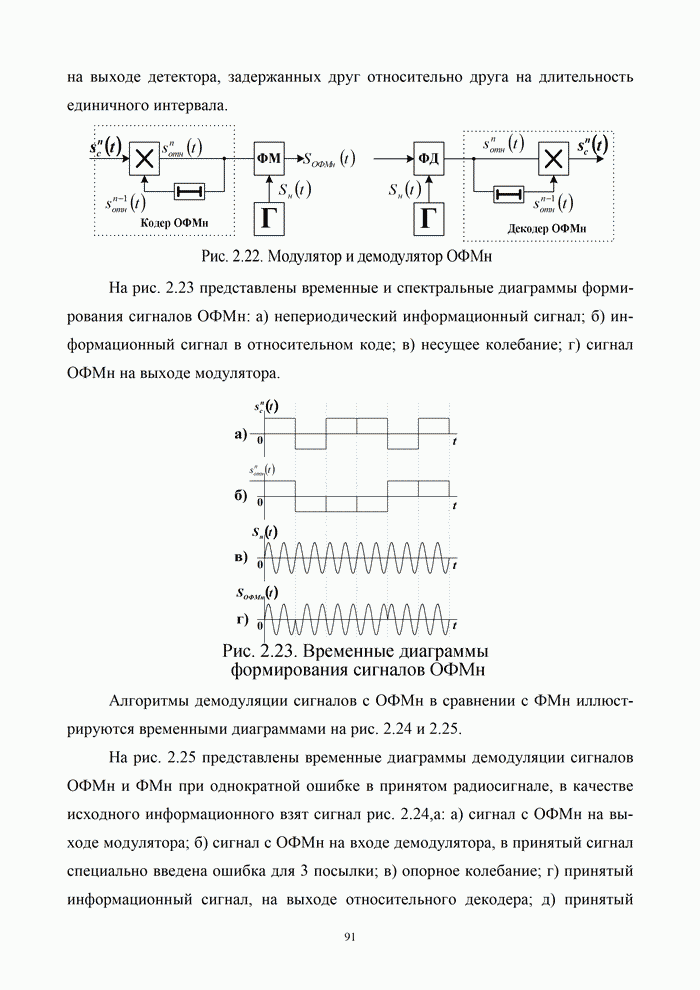
- 2.4.3. Фазовая (относительно-фазовая) манипуляция сигналов
- 2.5. Системы связи с многопозиционной относительной фазовой манипуляцией
- 2.5.1. Принцип формирования сигнала с многократной относительной фазовой манипуляцией
- 2.5.2. Квадратурная относительно-фазовая манипуляция (КОФМ)
- 2.5.3. Принцип частотной модуляции с непрерывной фазой
- Контрольные вопросы
- Глава 3. Помехоустойчивость приема дискретных сообщений
- 3.1. Критерии качества и правила приема дискретных сообщений
- 3.1.1. Понятие о помехоустойчивости систем электрической связи
- 3.1.2. Задача оптимального приема
- 3.1.3. Вычисление вероятностей ошибок
- 3.2. Оптимальная демодуляция при когерентном приеме сигналов
- 3.2.1. Оптимальные алгоритмы приема при полностью известных сигналах
- 3.2.2. Реализация алгоритмов оптимального когерентного приема
- 3.3. Помехоустойчивость приема сигналов с известными параметрами
- 3.4. Прием сигналов с неопределенной фазой
- 3.4.1. Оптимальный некогерентный прием дискретных сигналов
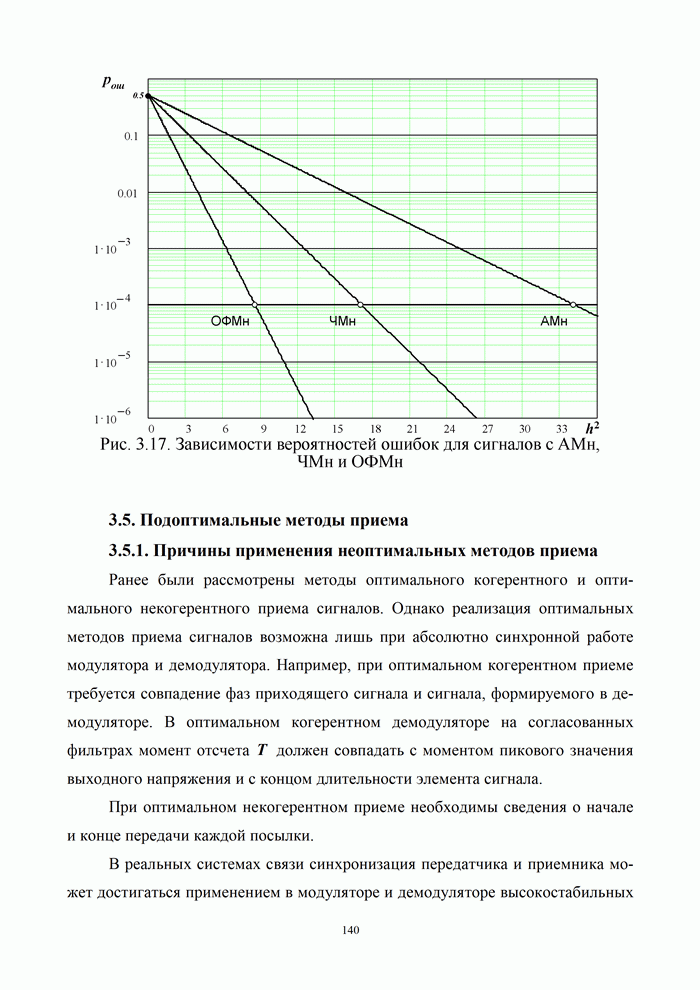
- 3.4.2. Помехоустойчивость оптимального некогерентного приема
- 3.5. Подоптимальные методы приема
- 3.5.1. Причины применения неоптимальных методов приема
- 3.5.2. Квазиоптимальные методы приема
- Контрольные вопросы
- Глава 4. Теория передачи информации
- 4.1. Информационные характеристики источника сообщений
- 4.1.1. Количественное определение информации
- 4.1.2. Энтропия и производительность дискретного источника сообщений
- 4.2. Пропускная способность дискретного канала
- 4.2.1. Количество информации переданной по дискретному каналу
- 4.2.2. Пропускная способность дискретного канала
- 4.2.3. Пропускная способность симметричного дискретного канала без памяти
- 4.3. Методы сжатия дискретных сообщений
- 4.3.1. Условия существования оптимального неравномерного кода
- 4.3.2. Прямая и обратная теоремы кодирования источника неравномерными кодами
- 4.3.3. Показатели эффективности сжатия
- 4.3.4. Кодирование источника дискретных сообщений методом Шеннона-Фано
- 4.3.5. Кодирование источника дискретных сообщений методом Хаффмена
- 4.4. Пропускная способность непрерывного канала
- 4.4.1. Постановка задачи передачи дискретных сообщений в непрерывном канале
- 4.4.2. Количество информации, переданной по непрерывному каналу
- 4.4.3. Пропускная способность непрерывного канала
- Контрольные вопросы
- Глава 5. Теория кодирования сообщений
- 5.1. Помехоустойчивое кодирование: блочные и непрерывные коды
- 5.1.1. Постановка задачи помехоустойчивого кодирования
- 5.1.2. Классификация кодов
- 5.1.3. Основные характеристики и свойства блочных кодов
- 5.2. Эффективность помехоустойчивого кодирования
- 5.2.1. Эффективность кода в режиме исправления ошибок
- 5.2.2. Эффективность кода в режиме обнаружения ошибок
- 5.2.3. Эффективность помехоустойчивых кодов
- 5.3. Математические основы теории помехоустойчивого кодирования
- 5.3.1. Краткие сведения из теории чисел
- 5.3.2. Группы
- 5.3.3. Кольца и поля
- 5.3.4. Векторное пространство
- 5.3.5. Конечные поля
- 5.4. Линейные блочные коды
- 5.4.1. Система передачи дискретных сообщений
- 5.4.2. Параметры линейного кода
- 5.4.3. Полиномиальные циклические коды
- 5.4.4. Циклические коды и корни полиномов
- 5.4.5. Спектральное описание циклических кодов
- 5.4.6. Простейшие блочные линейные коды
- 5.5. Коды Боуза-Чоудхури-Хоквингема
- 5.5.1. Методы задания кодов БЧХ
- 5.5.2. Принципы декодирования кодов БЧХ
- 5.5.3. Методы реализации этапов декодирования кодов БЧХ
- 5.6. Коды Рида-Соломона
- 5.6.1. Основные определения
- 5.6.2. Обнаружение и исправление пакетов ошибок
- 5.7. Коды Рида-Маллера
- 5.7.1. Задание и декодирование кодов Рида-Маллера
- 5.7.2. Симплексные коды и m-последовательности
- 5.7.3. Связь между блочными кодами
- 5.8. Сверточные коды
- 5.8.1. Основные параметры
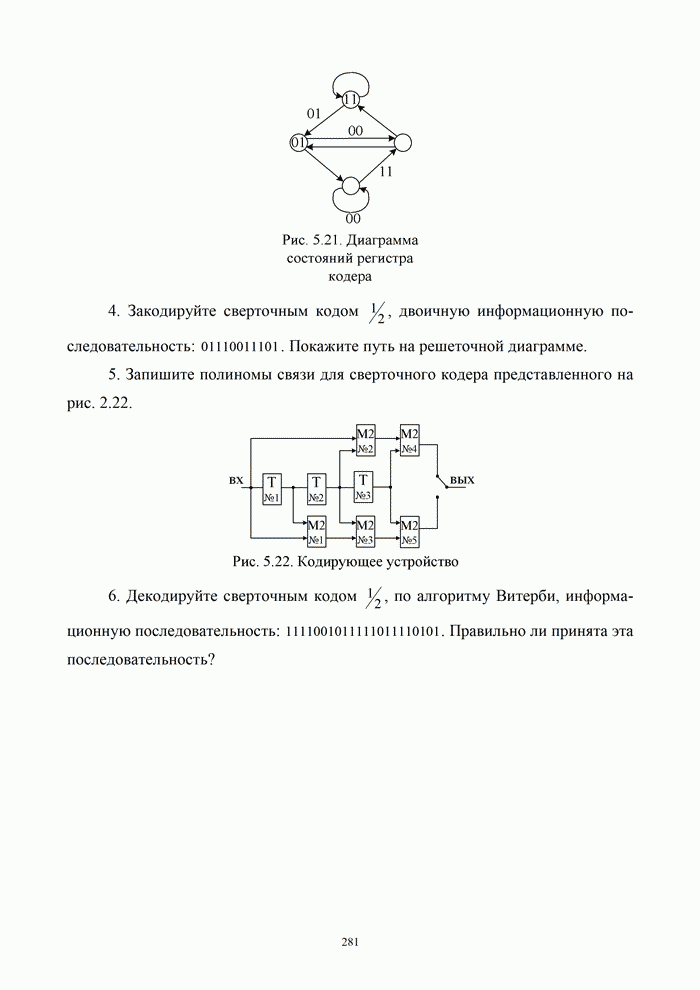
- 5.8.2. Способы задания сверточного кода
- 5.8.3. Алгоритм декодирования Витерби
- 5.9. Помехоустойчивость систем передачи дискретных сообщений
- 5.9.1. Две процедуры приема сигналов
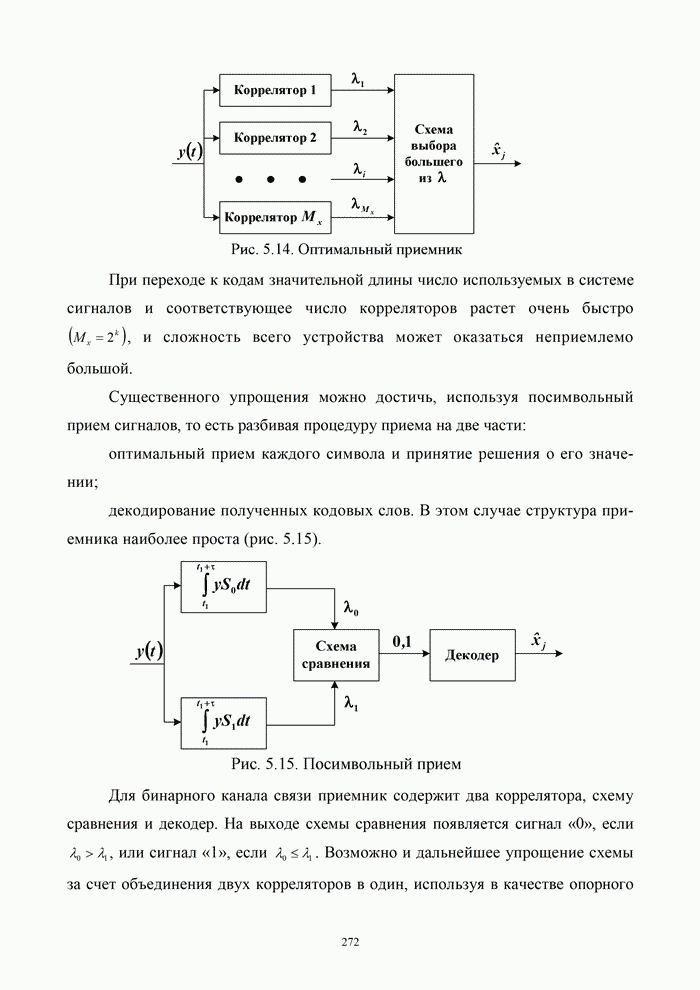
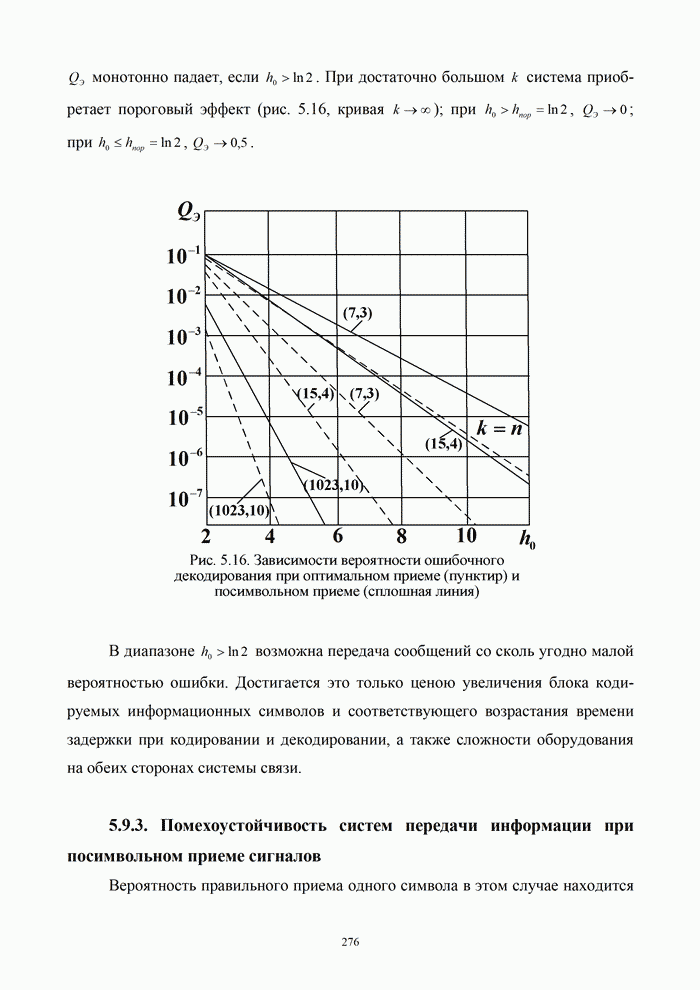
- 5.9.2. Помехоустойчивость систем передачи информации при оптимальной процедуре приема
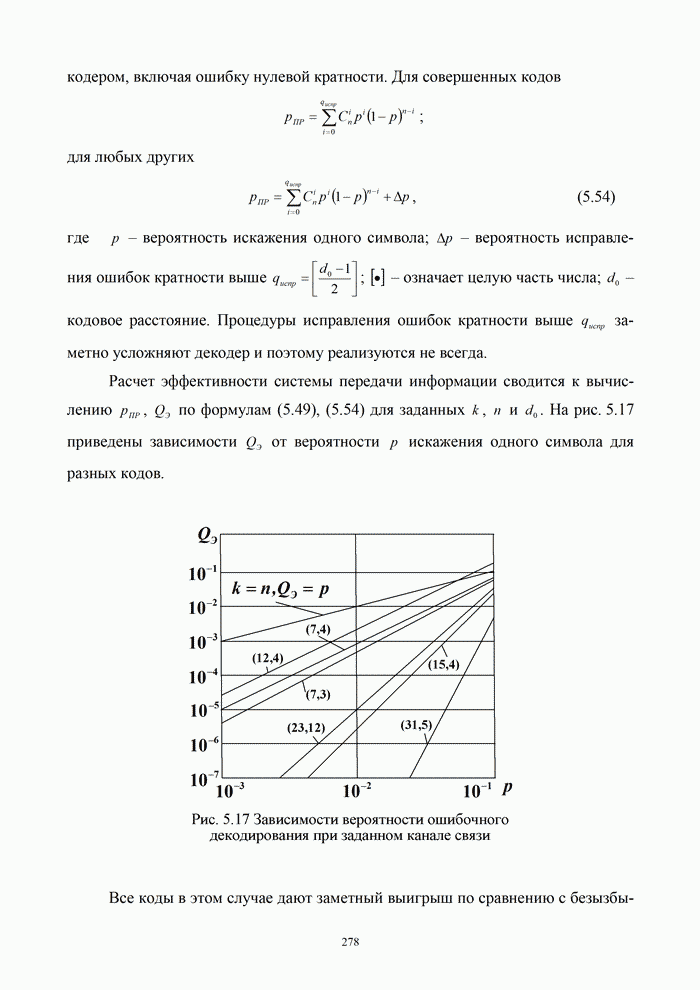
- 5.9.3. Помехоустойчивость систем передачи информации при посимвольном приеме сигналов
- Контрольные вопросы
- Глава 6. Сигналы с импульсной модуляцией
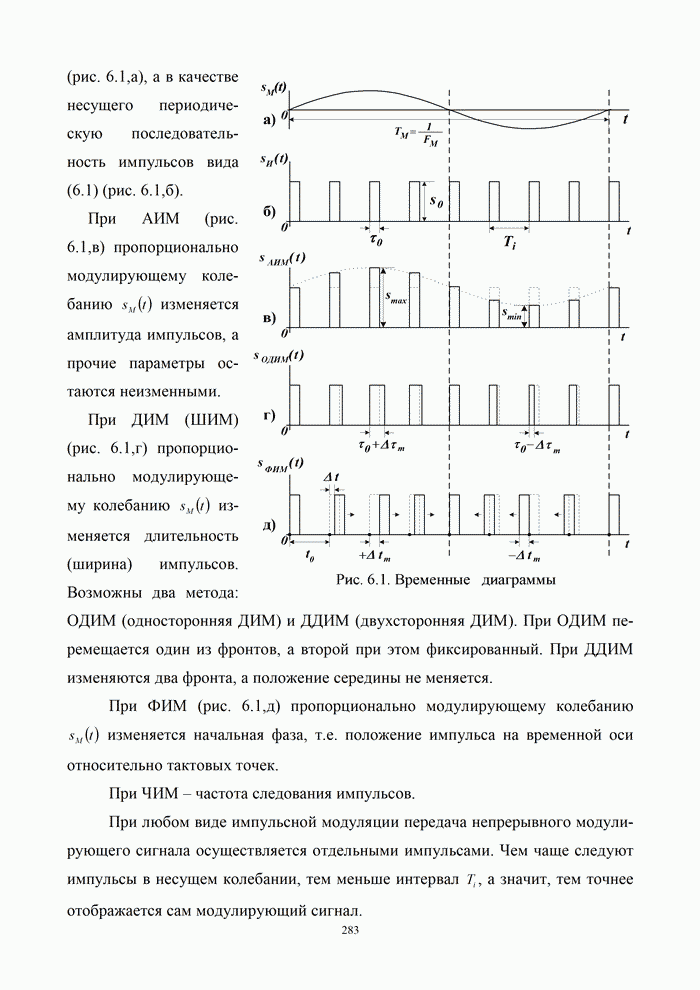
- 6.1. Методы импульсной модуляции
- 6.1.1. Импульсные методы передачи непрерывных сигналов
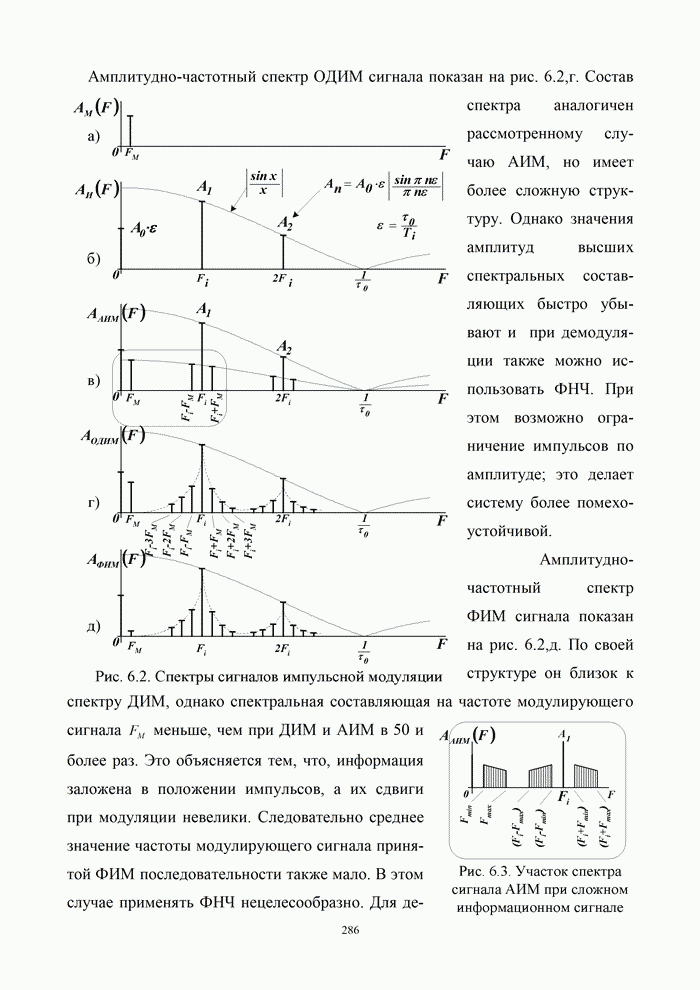
- 6.1.2. Спектральные характеристики импульсных методов модуляции
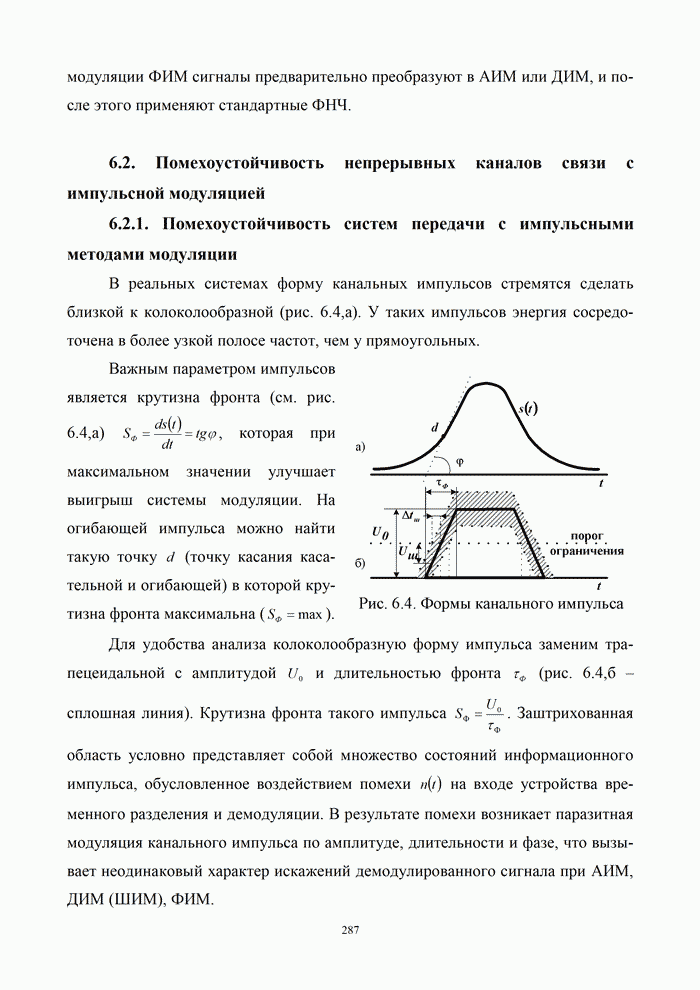
- 6.2. Помехоустойчивость непрерывных каналов связи с импульсной модуляцией
- 6.2.1. Помехоустойчивость систем передачи с импульсными методами модуляции
- 6.3. Цифровые методы передачи непрерывных сообщений
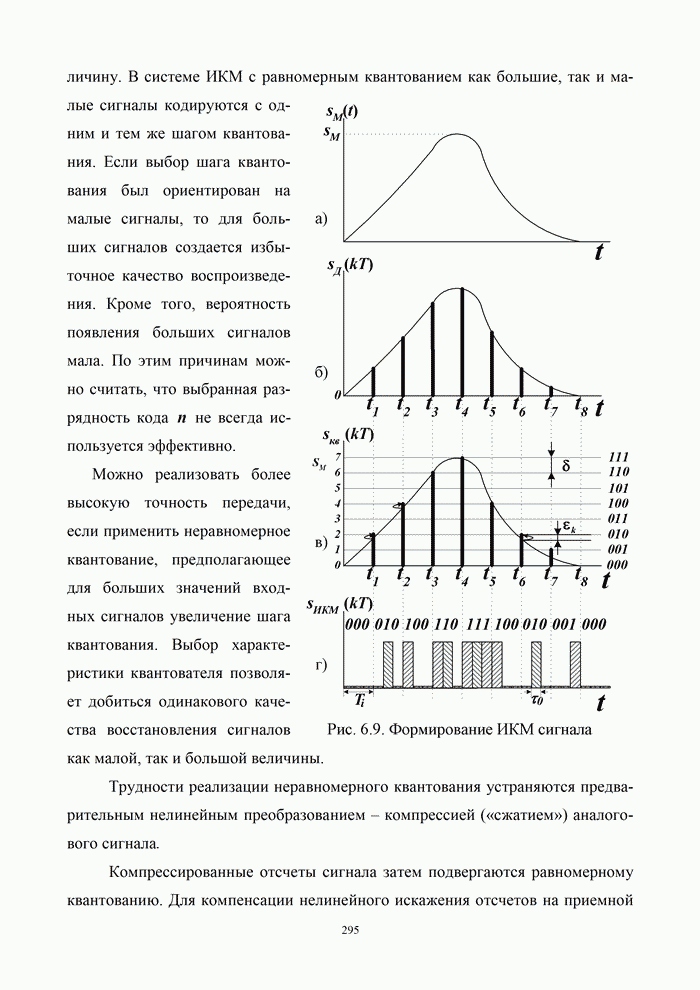
- 6.3.1. Передача сигналов с импульсно-кодовой модуляцией
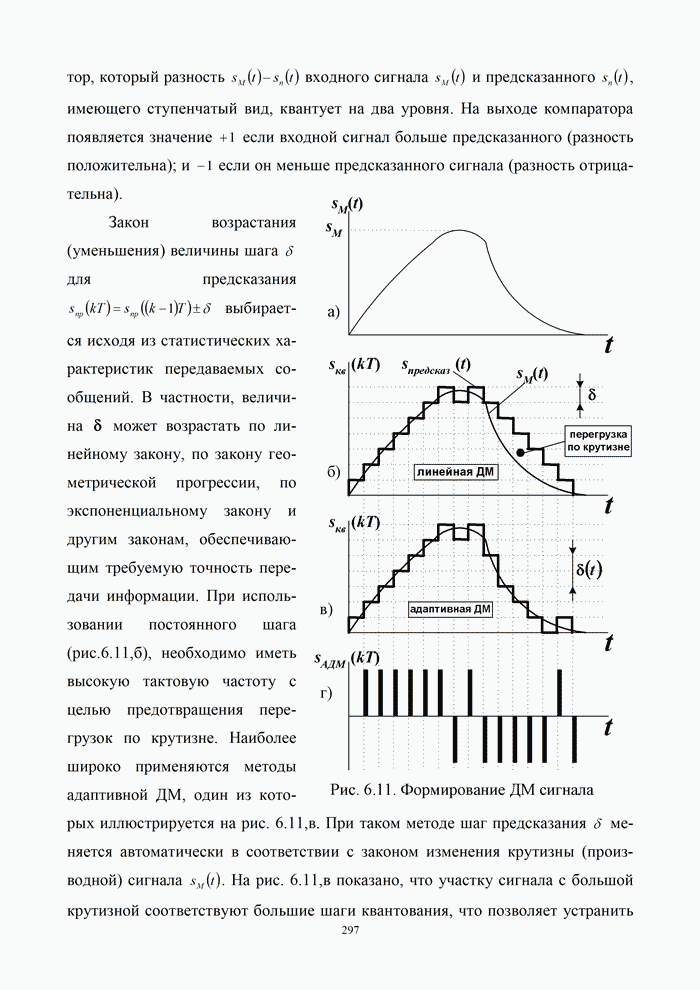
- 6.3.2. Передача сигналов с дельта модуляцией
- 6.3.3. Квантование сигналов в системах с ИКМ и ДМ
- Контрольные вопросы
- Глава 7. Методы приема сигналов в сложных условиях
- 7.1. Прием сигналов в каналах с замираниями
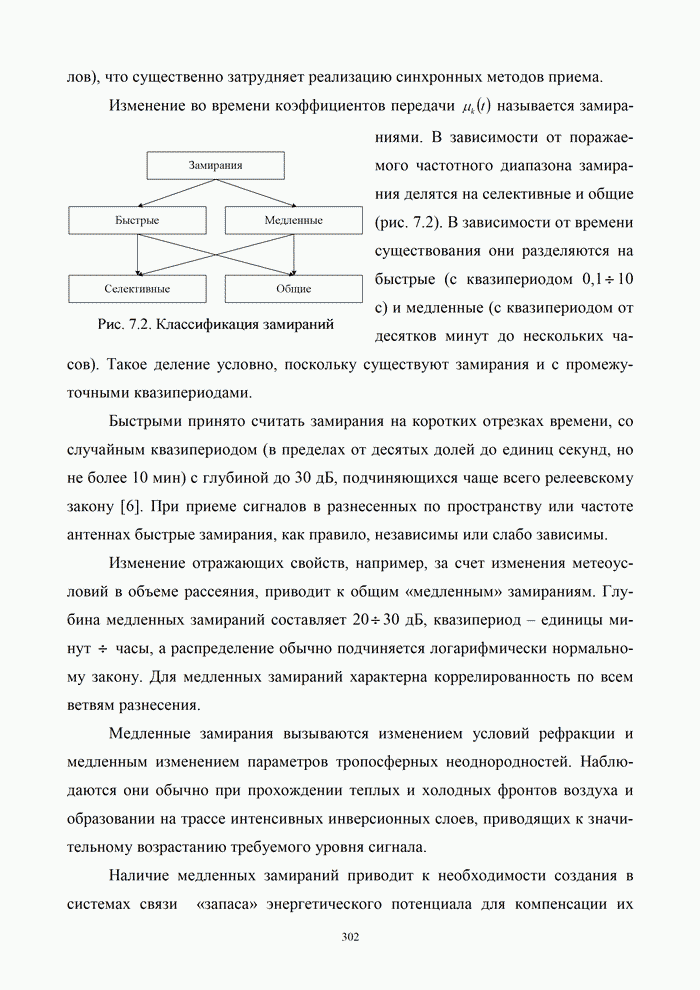
- 7.1.1. Сущность замираний и их классификация
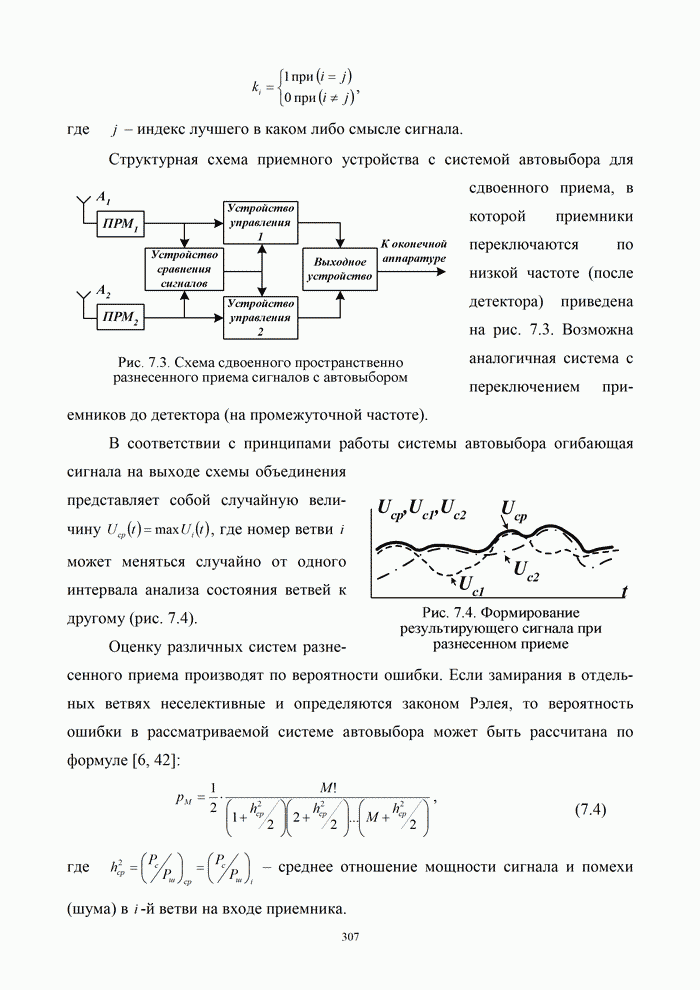
- 7.1.2. Принципы разнесенного приема сигналов
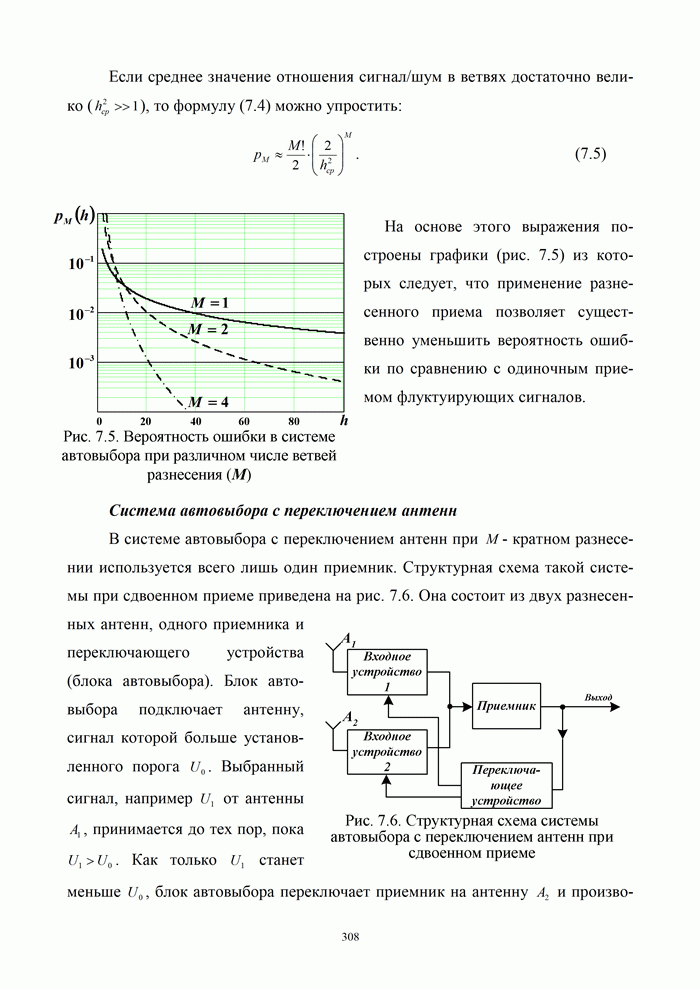
- 7.2. Методы борьбы с замираниями сигналов
- 7.2.1. Методы борьбы с замираниями в аналоговых системах связи
- 7.2.2. Методы борьбы с замираниями в цифровых системах связи
- 7.3. Методы борьбы с межсимвольной интерференцией
- 7.3.1. Причины возникновения и сущность межсимвольной интерференции
- 7.3.2. Обработка сигналов в каналах с межсимвольной интерференцией
- 7.3.3. Помехоустойчивость в каналах с межсимвольной интерференцией
- 7.4. Прием дискретных сообщений в каналах с сосредоточенными по спектру и импульсными помехами
- 7.4.1. Общая характеристика сосредоточенных по спектру и импульсных помех
- 7.4.2. Борьба с сосредоточенными и импульсными помехами
- 7.5. Компенсация помех и искажений в канале
- 7.5.1. Принцип работы радиолинии с ФМ ПСС (ФМ ШПС)
- 7.5.2. Помехоустойчивость радиолинии с ФМ ПСС
- 7.5.3. Принципы работы радиолиний с ППРЧ
- 7.5.4. Помехоустойчивость радиолиний с ППРЧ
- Контрольные вопросы
- Глава 8. Многоканальная связь и распределение информации
- 8.1. Методы распределения ресурса общего канала
- 8.1.1. Классификация систем передачи информации, использующих единый ресурс
- 8.1.2. Постановка задачи объединения и разделения сигналов
- 8.1.3. Энергетическая и спектральная цена уплотнения
- 8.2. Частотное разделение каналов
- 8.2.1. Принцип частотного объединения и разделения каналов
- 8.2.2. Групповой сигнал, его структура и характеристики
- 8.3. Временное разделение каналов
- 8.3.1. Принцип временного разделения каналов
- 8.3.2. Характеристики группового сигнала систем с ВРК
- 8.4. Разделение сигналов по форме
- Контрольные вопросы
- Глава 9. Эффективность систем связи
- 9.1. Оценка эффективности систем связи
- 9.1.1. Подходы к оценке эффективности
- 9.1.2. Критерии эффективности
- 9.1.3. Эффективность аналоговых и цифровых систем
- 9.2. Выбор сигналов и помехоустойчивых кодов
- 9.2.1. Многопозиционные сигналы
- 9.2.2. Корректирующие коды
- 9.3. Оптимизация систем связи
- 9.3.1. Согласование методов модуляции и кодирования
- 9.3.2. Классификация сигнально – кодовых конструкций
- 9.4. Характеристики основных типов СКК
- 9.4.1. Согласование канала кодом Грея
- 9.4.2. Согласование на основе разбиения ансамбля на вложенные подансамбли
- 9.5. Алгоритмы цифровой обработки сигналов
- 9.5.1. Дискретные сигналы и их спектры
- 9.5.2. Алгоритмы дискретного и быстрого преобразований Фурье
- Контрольные вопросы
- Глава 10. Теоретико-информационные основы криптозащиты сообщений в телекоммуникационных системах
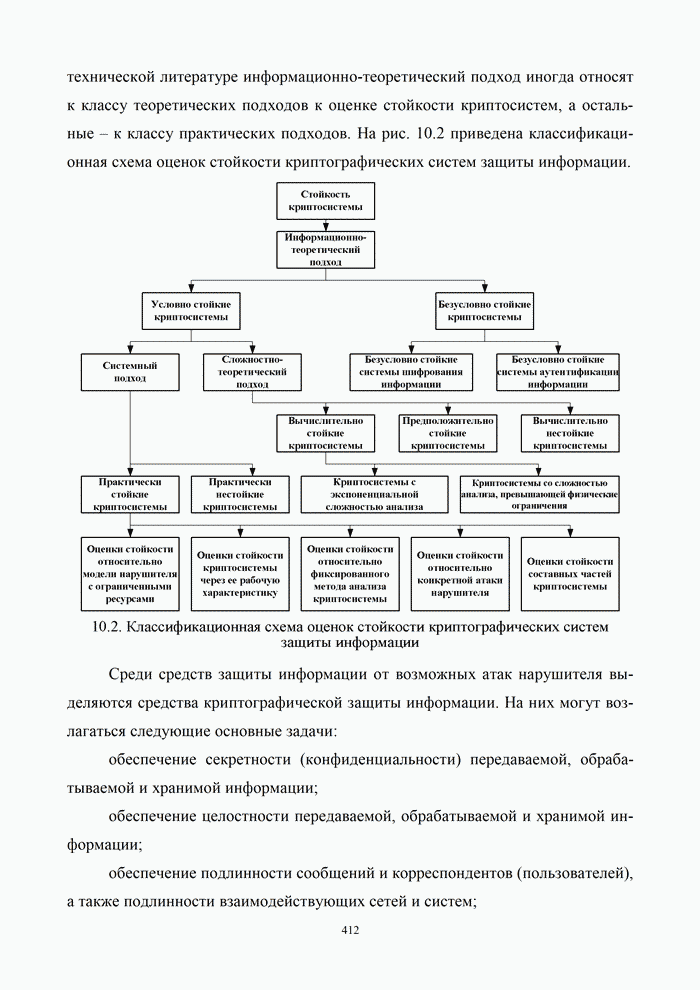
- 10.1. Классификация криптографических систем
- 10.1.2. Классификация криптографических систем защиты информации
- 10.1.3. Оценка стойкости криптосистем
- 10.2. Функции, используемые в криптографических системах
- 10.2.1. Общее описание функций, используемых в криптографических системах
- 10.2.2. Однонаправленные функции
- 10.2.3. Криптографические хэш-функции
- 10.3. Модели криптографических систем
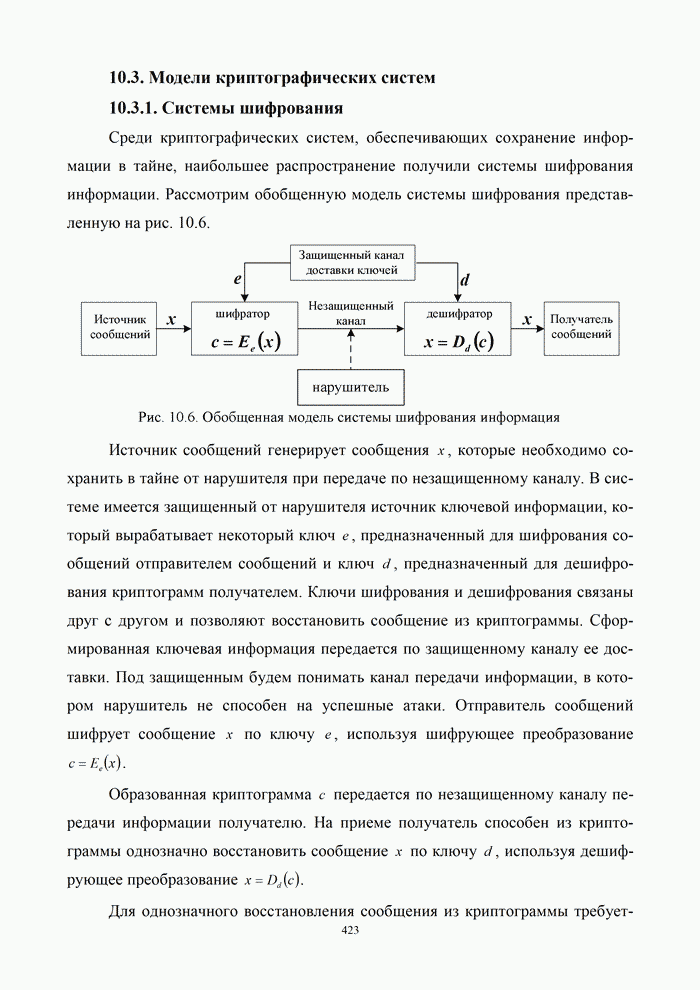
- 10.3.1. Системы шифрования
- 10.3.2. Традиционные симметричные криптосистемы
- 10.4. Алгоритмы криптографической защиты
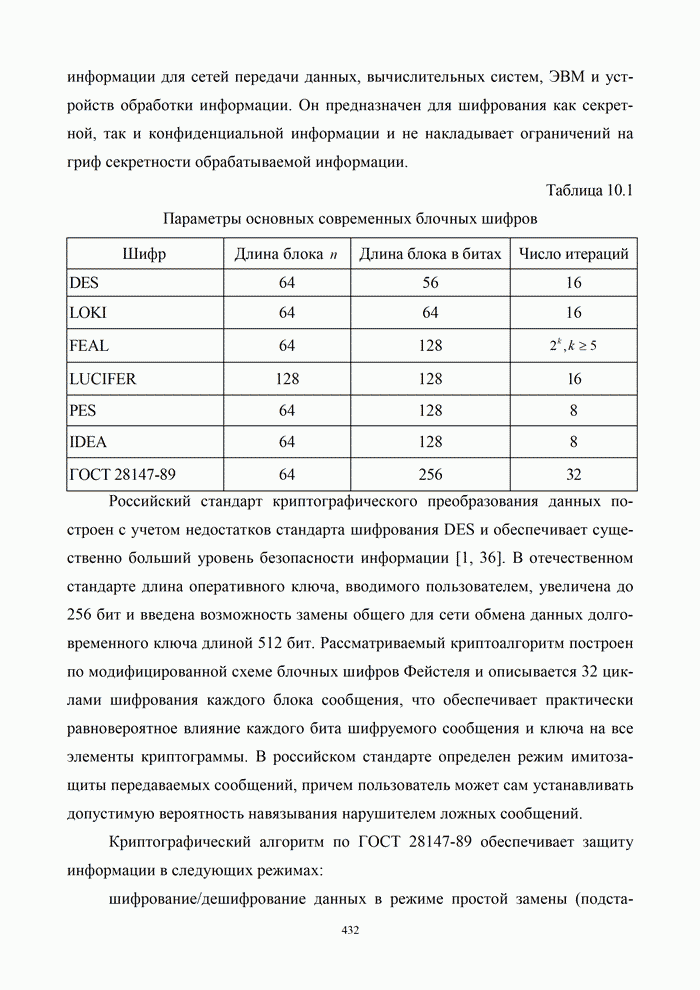
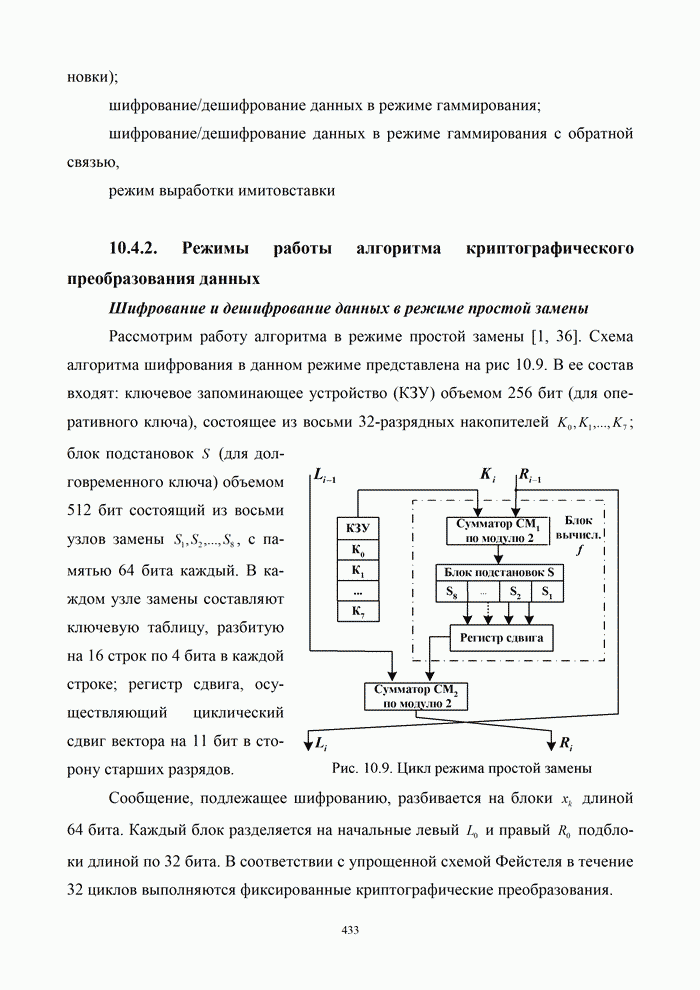
- 10.4.1. Алгоритм криптографической защиты информации согласно ГОСТ 28147-89
- Контрольные вопросы
- Заключение
- Список литературы