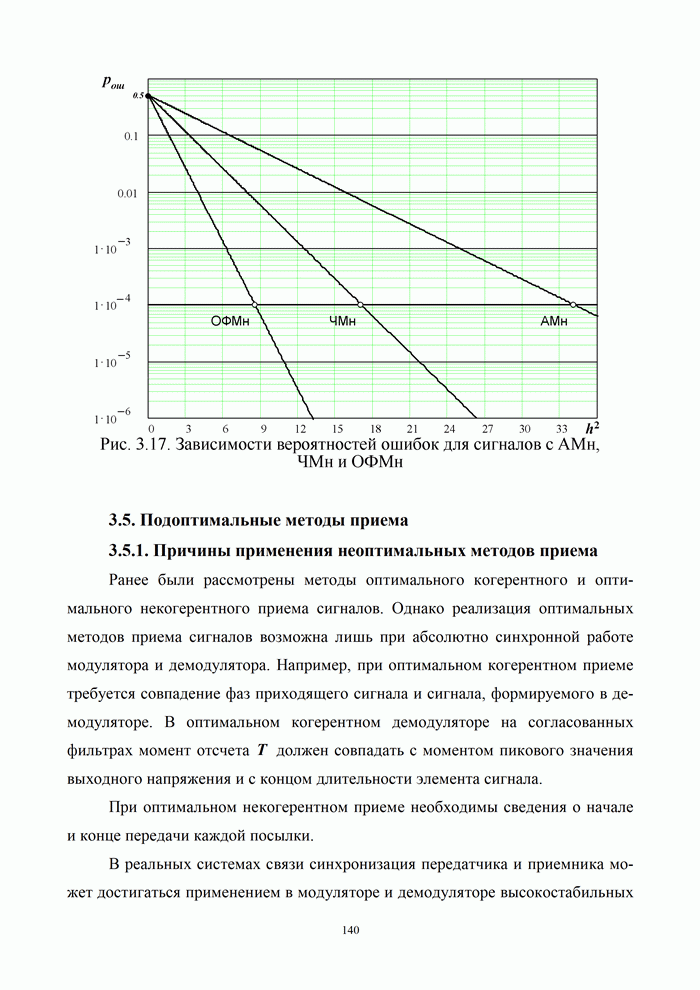
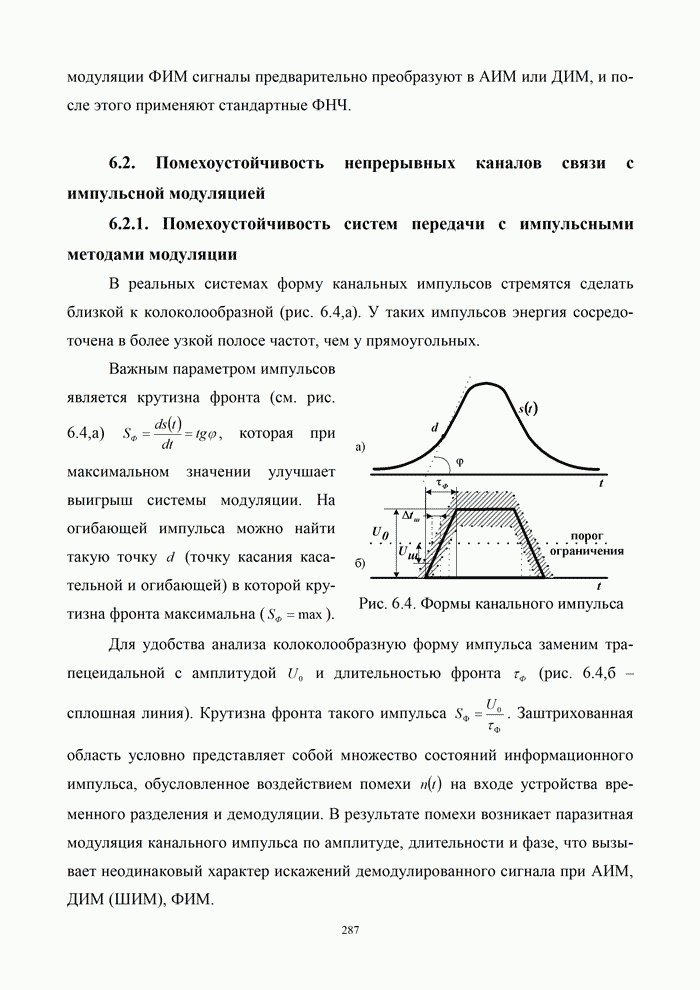
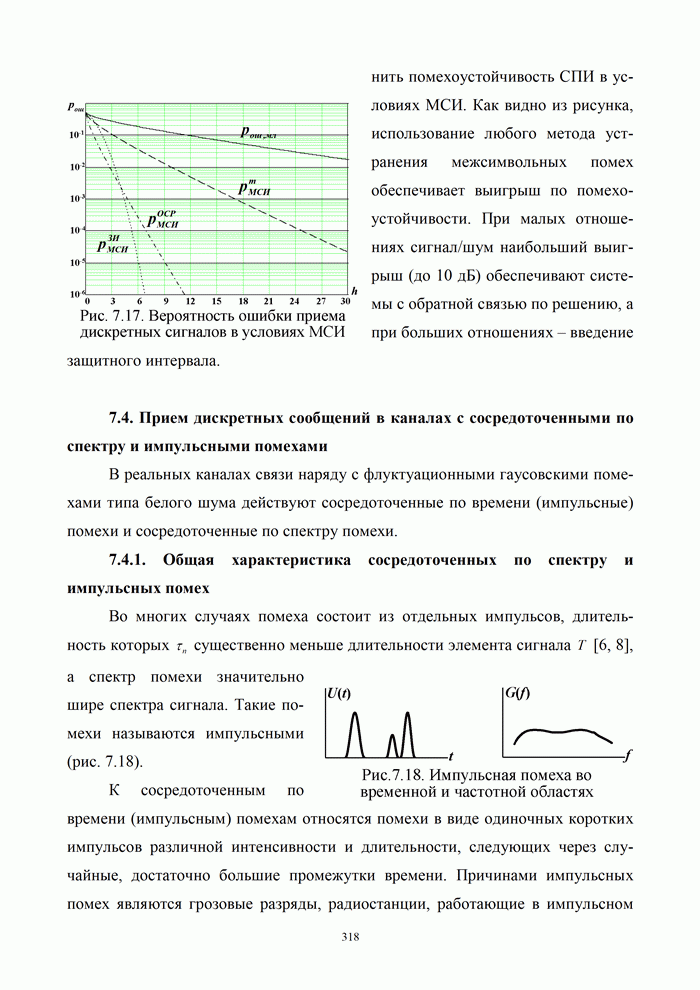
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.3.5. Конечные поля
Определение конечного поля
Ранее в 1.3.2 дано определение поля ![]() как коммутативного
кольца с единицей, в котором каждый ненулевой элемент имеет
мультипликативный обратный элемент. В теории помехоустойчивых
кодов весьма важное значение имеют поля, образованные конечным множеством
элементов – так называемые конечные поля Галуа (Galois Field), обозначаемые
как коммутативного
кольца с единицей, в котором каждый ненулевой элемент имеет
мультипликативный обратный элемент. В теории помехоустойчивых
кодов весьма важное значение имеют поля, образованные конечным множеством
элементов – так называемые конечные поля Галуа (Galois Field), обозначаемые ![]() . В связи с этим дадим их развернутое определение.
. В связи с этим дадим их развернутое определение.
Конечным полем ![]() называется конечное
множество элементов, замкнутое по отношению к двум заданным в нем операциям
комбинирования элементов. Под замкнутостью
понимается тот факт, что результаты операций не выходят за пределы конечного
множества введенных элементов. Для конечных полей выполняются следующие
аксиомы.
называется конечное
множество элементов, замкнутое по отношению к двум заданным в нем операциям
комбинирования элементов. Под замкнутостью
понимается тот факт, что результаты операций не выходят за пределы конечного
множества введенных элементов. Для конечных полей выполняются следующие
аксиомы.
- GF.1. Из
введенных операций над элементами поля одна называется сложением
и обозначается как
 , а другая - умножением и обозначается как
, а другая - умножением и обозначается как
 .
.
- GF.2. Для
любого элемента
 существует
обратный элемент по сложению
существует
обратный элемент по сложению  и обратный элемент по умножению
и обратный элемент по умножению  (если
(если  ) такие, что
) такие, что  и
и  . Наличие обратных
элементов позволяет наряду с операциями сложения и умножения выполнять также вычитание и
деление:
. Наличие обратных
элементов позволяет наряду с операциями сложения и умножения выполнять также вычитание и
деление:  ,
,  . Поэтому иногда просто говорят, что в поле определены все четыре арифметические операции
(кроме деления на 0).
. Поэтому иногда просто говорят, что в поле определены все четыре арифметические операции
(кроме деления на 0).
- GF.3. Поле
всегда содержит мультипликативную единицу 1 и аддитивную единицу
0, такие что
 ,
и
,
и  для
любого элемента поля.
для
любого элемента поля.
- GF.4. Для введенных операций выполняются обычные правила ассоциативности
 ,
,  , коммутативности
, коммутативности  ,
,  и дистрибутивности
и дистрибутивности  .
.
- GF.5. Результатом сложения или умножения двух элементов поля является третий элемент из того же конечного множества.
Аксиомы GF.1 – GF.5 являются общими для полей как с конечным, так и с бесконечным числом элементов. Специфику же конечного поля определяет аксиома GF.5, где ключевыми являются слова «из того же конечного множества».
Требование конечности множества определяет
ряд ограничений как на количество элементов поля ![]() , так и на понятия «сложение» и
«умножение».
, так и на понятия «сложение» и
«умножение».
Конечные поля существуют не при любом числе
элементов, а только в том случае, если их количество –
простое число ![]() или
его степень
или
его степень ![]() ,
где
,
где ![]() – целое. В первом случае
поле
– целое. В первом случае
поле ![]() называется
простым, а во втором – расширением
называется
простым, а во втором – расширением ![]() простого
поля.
простого
поля.
Очевидно, операции комбинирования элементов
конечного поля не могут быть обычными сложением и умножением. Выполнение аксиомы GF.5 для простого конечного поля обеспечивается
совершением арифметических операций по модулю числа ![]() , которое носит название характеристики
конечного поля. Можно убедиться, что в кольце вычетов по модулю
, которое носит название характеристики
конечного поля. Можно убедиться, что в кольце вычетов по модулю ![]() (см. 5.3.1) каждый
ненулевой элемент имеет обратный элемент тогда и только тогда, когда
(см. 5.3.1) каждый
ненулевой элемент имеет обратный элемент тогда и только тогда, когда ![]() – простое число [25,
26, 33]. Следовательно, кольцо вычетов по модулю простого числа
– простое число [25,
26, 33]. Следовательно, кольцо вычетов по модулю простого числа ![]() является простым полем
является простым полем ![]() . Элементами этого
поля являются целые числа
. Элементами этого
поля являются целые числа ![]() . Операции сложения и умножения в таком поле производятся по модулю
. Операции сложения и умножения в таком поле производятся по модулю ![]() . Пример простейшего
двоичного поля
. Пример простейшего
двоичного поля ![]() приведен
в 5.3.3.
приведен
в 5.3.3.
Элементами ![]() расширенного поля
расширенного поля ![]() могут быть, например, все многочлены степени
могут быть, например, все многочлены степени ![]() или меньше, коэффициенты которых лежат в
простом поле
или меньше, коэффициенты которых лежат в
простом поле ![]() . Число
. Число
![]() называется порядком
расширенного поля и определяет количество различных многочленов.
называется порядком
расширенного поля и определяет количество различных многочленов.
Правила сложения и умножения полиномов –
элементов расширенного конечного поля получаются из обычных правил сложения и
умножения полиномов
с последующим приведением результата по модулю некоторого специального
многочлена ![]() степени
степени
![]() . Такое
приведение эквивалентно делению многочлена
результата на
. Такое
приведение эквивалентно делению многочлена
результата на ![]() и
использованию только остатка.
и
использованию только остатка.
Очевидно, любые результаты вычислений в поле после приведения по
модулю ![]() должны
оставаться обратимыми – только в этом случае наша система образует поле. Для этого используемый полином
должны
оставаться обратимыми – только в этом случае наша система образует поле. Для этого используемый полином ![]() должен быть неприводимым в поле
должен быть неприводимым в поле ![]() ,
т.е. его нельзя разложить на множители, используя только многочлены с коэффициентами из
,
т.е. его нельзя разложить на множители, используя только многочлены с коэффициентами из ![]() . Это означает также,
что
. Это означает также,
что ![]() не
имеет корней в поле
не
имеет корней в поле ![]() .
Аналогом неприводимого полинома является
простое число в поле вещественных чисел.
.
Аналогом неприводимого полинома является
простое число в поле вещественных чисел.
К сожалению, регулярных методов поиска неприводимых полиномов не существует, они обычно определяются перебором. К настоящему времени имеются подробные таблицы неприводимых полиномов [30, 33].
Особым свойством конечных полей является связь между собой всех ненулевых элементов ![]() и возможность выражения каждого из них
через один элемент
и возможность выражения каждого из них
через один элемент ![]() , называемый примитивным, как некоторую
целую степень этого элемента. Множество
, называемый примитивным, как некоторую
целую степень этого элемента. Множество ![]() ненулевых элементов
расширения
ненулевых элементов
расширения ![]() образует циклическую мультипликативную группу (см. 5.3.2), т.е. элементы находятся между собой в
соотношении
образует циклическую мультипликативную группу (см. 5.3.2), т.е. элементы находятся между собой в
соотношении ![]() .
Примитивных элементов в
.
Примитивных элементов в ![]() может быть несколько.
может быть несколько.
Построение конечного поля
Построим конечное поле ![]() и его расширение
и его расширение ![]() . Пусть элементами
. Пусть элементами
![]() являются 0
и 1, а элементами
являются 0
и 1, а элементами ![]() – 16 всевозможных полиномов
степени 3 и менее с коэффициентами из
– 16 всевозможных полиномов
степени 3 и менее с коэффициентами из ![]() :
:
|
|
|
Теперь необходимо определить операции над элементами таким образом, чтобы их результаты не давали новых элементов, кроме уже введенных.
В поле ![]() обычные
операции умножения (на 0 и 1) и деления (на 1) не выводят результат
за пределы множества 0; 1. Однако при сложении и вычитании
элементов это требование может уже не выполняться:
обычные
операции умножения (на 0 и 1) и деления (на 1) не выводят результат
за пределы множества 0; 1. Однако при сложении и вычитании
элементов это требование может уже не выполняться: ![]() ;
; ![]() и т.
д. Свойства конечного поля будут, очевидно, соблюдаться, если
в качестве операции сложения использовать суммирование по модулю 2
и т.
д. Свойства конечного поля будут, очевидно, соблюдаться, если
в качестве операции сложения использовать суммирование по модулю 2 ![]() :
:
|
|
(5.9) |
причем операции сложения
и вычитания в поле ![]() совпадают.
Этим мы будем пользоваться в дальнейшем,
заменяя, например, полином вида
совпадают.
Этим мы будем пользоваться в дальнейшем,
заменяя, например, полином вида ![]() на
на
![]() в
тех случаях, когда полиномы заданы над полем характеристики 2. Если, однако, характеристика поля
в
тех случаях, когда полиномы заданы над полем характеристики 2. Если, однако, характеристика поля ![]() , такая замена
неправомерна, и полиномы каждого
вида нужно рассматривать самостоятельно.
, такая замена
неправомерна, и полиномы каждого
вида нужно рассматривать самостоятельно.
В поле ![]() операцией,
которая может вывести результат за пределы поля,
является умножение многочленов. Обычное перемножение может дать полином степени больше 3, не принадлежащий
множеству элементов
операцией,
которая может вывести результат за пределы поля,
является умножение многочленов. Обычное перемножение может дать полином степени больше 3, не принадлежащий
множеству элементов ![]() . Действительно, используя представление
полиномов через векторы их коэффициентов [26], а также учитывая (5.9),
получим
. Действительно, используя представление
полиномов через векторы их коэффициентов [26], а также учитывая (5.9),
получим
|
|
|
Поэтому введем дополнительное условие, чтобы ![]() удовлетворял некоторому уравнению степени
удовлетворял некоторому уравнению степени ![]() , например,
, например, ![]() или
или ![]() . Тогда
. Тогда ![]() ;
; ![]() ;
; ![]() и т.д., а
и т.д., а ![]() , т.е. не выходит за пределы поля
, т.е. не выходит за пределы поля ![]() .
.
Нетрудно видеть, что результат проделанного
преобразования полинома ![]() эквивалентен вычислению остатка от
его деления на полином
эквивалентен вычислению остатка от
его деления на полином ![]() , т.е. приведению произведения многочленов по модулю
, т.е. приведению произведения многочленов по модулю ![]() :
:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Или ![]() . Делением на
полиномы первой степени
. Делением на
полиномы первой степени ![]() и
и ![]() , и второй степени
, и второй степени ![]() ,
, ![]() и
и![]() можно убедиться, что
рассматриваемый многочлен
можно убедиться, что
рассматриваемый многочлен ![]() неприводим над
неприводим над ![]() , а следовательно, не имеет в нем корней. В противном случае
, а следовательно, не имеет в нем корней. В противном случае ![]() раскладывался
бы на сомножители
раскладывался
бы на сомножители ![]() и
и ![]() , ибо корнями в поле
, ибо корнями в поле ![]() могут
быть только 0 или 1.
могут
быть только 0 или 1.
Для нахождения примитивных элементов поля, как и неприводимых полиномов,
приходится прибегать к таблицам. В нашем примере поля ![]() ,
задаваемого многочленом
,
задаваемого многочленом ![]() ,
примитивным элементом является
,
примитивным элементом является ![]() . Последовательно
применяя равенства
. Последовательно
применяя равенства ![]() и
и
![]() (или, что эквивалентно,
(или, что эквивалентно, ![]() ), получим упорядоченное по степеням примитивного
элемента
), получим упорядоченное по степеням примитивного
элемента ![]() множество
элементов
множество
элементов ![]() ,
составляющее конечное поле
,
составляющее конечное поле ![]() .
.
В табл. 5.2 даны различные представления
элементов ![]() поля
поля
![]() , заданного полиномом
, заданного полиномом ![]() , а
также полиномом
, а
также полиномом ![]() .
.
Представление элементов поля по степеням примитивного элемента ![]() удобно, в частности, при умножении элементов друг
на друга. Для этого достаточно сложить
их степени по модулю
удобно, в частности, при умножении элементов друг
на друга. Для этого достаточно сложить
их степени по модулю ![]() (применительно к табл. 5.2 – по модулю 15). Например,
(применительно к табл. 5.2 – по модулю 15). Например,
|
|
|
Прямые вычисления дают то же, но более трудоемко:
|
|
Таблица 5.2. Различные представления элементов поля ![]()
|
Ненулевые элементы поля |
|
|
||||
|
Представление элементов поля через |
Представление через |
|||||
|
полином |
вектор |
степень |
вектор |
степень |
||
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ненулевые элементы ![]() расположены
в порядке нарастания степени примитивного элемента и образуют циклическую группу
порядка 15. При этом
расположены
в порядке нарастания степени примитивного элемента и образуют циклическую группу
порядка 15. При этом ![]() ,
, ![]() ,
, ![]() , … ,
, … , ![]() и т.д.
и т.д.
Нетрудно убедиться, что примитивным в поле ![]() является
не только один элемент
является
не только один элемент ![]() , но и
, но и ![]() ,
, ![]() ,
, ![]() и ряд других (предлагается их отыскать
самостоятельно), а
и ряд других (предлагается их отыскать
самостоятельно), а ![]() и
и ![]() таковыми
не являются.
таковыми
не являются.
Основные свойства конечных полей и полиномов
Связь между элементами конечного поля
Все ненулевые элементы ![]() конечного поля
конечного поля ![]() являются
степенями одного примитивного элемента:
являются
степенями одного примитивного элемента:
|
|
|
Порядок элемента поля
Порядком ![]() элемента
элемента ![]() конечного поля называется
наименьшее значение
конечного поля называется
наименьшее значение ![]() , для которого
, для которого ![]() . Пусть
. Пусть ![]() . Поскольку ненулевые элементы
. Поскольку ненулевые элементы ![]() образуют
циклическую группу, порядок элемента
образуют
циклическую группу, порядок элемента ![]() может быть определен из равенства
может быть определен из равенства
|
|
|
где ![]() – наибольший общий
делитель. Порядки элементов
– наибольший общий
делитель. Порядки элементов ![]() лежат в пределах
от 1 (элемент
лежат в пределах
от 1 (элемент ![]() ) до
) до ![]() (примитивные элементы), но
(примитивные элементы), но ![]() всегда
кратно порядку элемента.
всегда
кратно порядку элемента.
Возведение многочлена над полем ![]() в
степень
в
степень ![]()
Если ![]() – произвольный многочлен, коэффициенты
которого лежат в
– произвольный многочлен, коэффициенты
которого лежат в ![]() , то
, то ![]() .
Справедливость этого утверждения вытекает из того, что все по парные
или многократные произведения в
.
Справедливость этого утверждения вытекает из того, что все по парные
или многократные произведения в ![]() появляются с коэффициентами,
которые делятся на
появляются с коэффициентами,
которые делятся на ![]() ,
и значит, равны 0 в
,
и значит, равны 0 в ![]() .
.
Так для многочлена над полем характеристики ![]() справедливо
справедливо ![]() , в чем можно убедиться
на примере:
, в чем можно убедиться
на примере:
|
|
|
Корни полиномов
Ключевым при построении кодов и их
декодировании является вопрос о корнях полиномов, соответствующих
кодовым комбинациям. Напомним, что из теории полиномов над полем вещественных чисел (не
конечных!) известно, что полином степени ![]() всегда имеет
всегда имеет ![]() корней, только не все
они обязательно лежат в поле вещественных
чисел (на вещественной оси). Часть корней может находиться в поле
комплексных чисел как некотором расширении
поля вещественных чисел.
корней, только не все
они обязательно лежат в поле вещественных
чисел (на вещественной оси). Часть корней может находиться в поле
комплексных чисел как некотором расширении
поля вещественных чисел.
Известная аналогия этому имеется и в конечных
полях. Любой многочлен степени ![]() , в том числе и неприводимый над
полем
, в том числе и неприводимый над
полем ![]() (не имеющий корней среди элементов этого поля), всегда имеет
(не имеющий корней среди элементов этого поля), всегда имеет ![]() корней в
расширении
корней в
расширении ![]() ,
и этими корнями является часть
элементов поля
,
и этими корнями является часть
элементов поля ![]() . Как элементы конечного
поля, корни находятся между собой в определенном соотношении. Если
. Как элементы конечного
поля, корни находятся между собой в определенном соотношении. Если ![]() – неприводимый полином с коэффициентами
из
– неприводимый полином с коэффициентами
из ![]() и
и ![]() – его корень, то
– его корень, то ![]() также являются его корнями. В поле
также являются его корнями. В поле ![]() корнями неприводимого
полинома степени
корнями неприводимого
полинома степени ![]() будут
будут
![]() .
.
Полиномы ![]()
Для дальнейшего обсуждения процедур кодирования и декодирования полезно иметь в виду следующие свойства многочлена
вида ![]() .
Для любого элемента
.
Для любого элемента ![]() как циклической
группы справедливо равенство
как циклической
группы справедливо равенство ![]() .
Это означает, что любой из элементов
.
Это означает, что любой из элементов ![]() является корнем
уравнения
является корнем
уравнения ![]() или,
что то же самое, корнем полинома
или,
что то же самое, корнем полинома ![]() или
или ![]() .
Нулевой элемент
.
Нулевой элемент ![]() – корень полинома
– корень полинома ![]() , а каждый из
ненулевых элементов поля
, а каждый из
ненулевых элементов поля ![]() –
один из корней полинома
–
один из корней полинома ![]() . Таким образом,
. Таким образом,
|
|
(5.10) |
Пусть ![]() – порядок элемента поля
– порядок элемента поля ![]() , т.е.
, т.е. ![]() . Следовательно,
. Следовательно, ![]() – корень
полинома
– корень
полинома ![]() .
Если
.
Если ![]() является
также и корнем неприводимого многочлена
является
также и корнем неприводимого многочлена ![]() , то
, то ![]() делится
без остатка на
делится
без остатка на ![]() .
.
В более общем случае минимальное значение ![]() , для которого
произвольный многочлен
, для которого
произвольный многочлен ![]() без кратных корней делит
без кратных корней делит ![]() ,
совпадает с наименьшим общим кратным (НОК) порядков корней
,
совпадает с наименьшим общим кратным (НОК) порядков корней ![]() .
.
Многочлен ![]() делится на
делится на ![]() только
в том случае, если
только
в том случае, если ![]() делится
на
делится
на ![]() . Действительно,
если корни
. Действительно,
если корни ![]() являются также корнями
являются также корнями ![]() , то
, то
![]() должно
делиться на
должно
делиться на ![]() .
.
Циклотомические классы
Каждый из корней ![]() полинома
полинома ![]() в
поле
в
поле ![]() есть
степень примитивного элемента
есть
степень примитивного элемента ![]() . Показатели степеней, соответствующие
корням
. Показатели степеней, соответствующие
корням
|
|
|
образуют
циклотомический класс чисел ![]() по модулю
по модулю ![]() , а
весь набор показателей степеней примитивного элемента в поле
, а
весь набор показателей степеней примитивного элемента в поле ![]() распадается
на не перекрывающиеся циклотомические классы
распадается
на не перекрывающиеся циклотомические классы ![]() . Индекс
. Индекс ![]() равен наименьшему из чисел в
классе и называется представителем класса по модулю
равен наименьшему из чисел в
классе и называется представителем класса по модулю ![]() .
.
С другой стороны, как отмечалось в 5.3.5, каждый из ![]() ненулевых
элементов
ненулевых
элементов ![]() поля
поля
![]() является
одним из корней полинома
является
одним из корней полинома ![]() , который, в свою очередь,
раскладывается на произведение неприводимых полиномов
, который, в свою очередь,
раскладывается на произведение неприводимых полиномов ![]() меньшей степени.
Каждый из циклотомических классов содержит набор показателей степеней
примитивного элемента, соответствующих корням одного из полиномов
меньшей степени.
Каждый из циклотомических классов содержит набор показателей степеней
примитивного элемента, соответствующих корням одного из полиномов ![]() .
.
Убедимся в этом на примере полинома ![]() над
полем
над
полем ![]() . Поскольку
сложение и вычитание по модулю 2 здесь неразличимы, то записи
. Поскольку
сложение и вычитание по модулю 2 здесь неразличимы, то записи ![]() и
и ![]() эквивалентны.
Разложение
эквивалентны.
Разложение ![]() на неприводимые полиномы
на неприводимые полиномы
![]() выглядит
следующим образом [30]:
выглядит
следующим образом [30]:
|
|
В табл. 5.3 приведено распределение элементов
поля ![]() ,
представленных степенями примитивного элемента
,
представленных степенями примитивного элемента ![]() , по циклотомическим
классам
, по циклотомическим
классам ![]() с
указанием соответствующих им неприводимых полиномов
с
указанием соответствующих им неприводимых полиномов ![]() .
.
Класс ![]() содержит
один элемент,
содержит
один элемент, ![]() – два
элемента, а классы
– два
элемента, а классы ![]() ,
, ![]() и
и ![]() – по четыре элемента. Это значит, что неприводимый
над полем
– по четыре элемента. Это значит, что неприводимый
над полем ![]() полином,
имеющий в качестве корня элемент
полином,
имеющий в качестве корня элемент ![]() поля
поля ![]() , должен
быть полиномом
первой степени, т.е.
, должен
быть полиномом
первой степени, т.е. ![]() . Корни
. Корни ![]() и
и ![]() принадлежат неприводимому полиному 2-й степени, который определяется по известному правилу:
принадлежат неприводимому полиному 2-й степени, который определяется по известному правилу:
|
|
|
Остальные ненулевые элементы поля ![]() являются корнями неприводимых
полиномов
являются корнями неприводимых
полиномов ![]() ,
, ![]() ,
, ![]() четвертой степени, вычисляемых аналогичным образом.
четвертой степени, вычисляемых аналогичным образом.
Имея в виду связь между корнями одного полинома, часто об его корнях говорят в единственном числе: «неприводимый полином имеет корень...», понимая под корнем один элемент поля, соответствующий, как правило, младшему из чисел циклотомического ряда, называемому его представителем.
Таблица 5.3. Распределение элементов поля ![]() по
циклотомическим классам
по
циклотомическим классам
|
Корни |
Циклотомические классы |
Полиномы |
|||
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Минимальные многочлены
Рассмотренное распределение элементов конечного поля по циклотомическим классам позволяет лучше понять следующее
важное в теории кодирования понятие. Минимальным многочленом или минимальной
функцией элемента ![]() поля
поля ![]() называется многочлен
называется многочлен ![]() с коэффициентами из
с коэффициентами из ![]() наименьшей степени, для которого
наименьшей степени, для которого ![]() является корнем, т.е.
является корнем, т.е.
![]() .
Обсудим его основные свойства.
.
Обсудим его основные свойства.
Прежде всего, очевидно, что минимальный многочлен должен быть неприводимым, иначе он раскладывался бы на полиномы меньшей степени.
Любой другой полином, имеющий тот же корень ![]() , что и минимальный, делится
на
, что и минимальный, делится
на ![]() . На
. На ![]() делится
и полином
делится
и полином ![]() , т.к. корнями последнего
в соответствии с (5.10) будут все ненулевые
элементы поля
, т.к. корнями последнего
в соответствии с (5.10) будут все ненулевые
элементы поля ![]() .
Степень
минимального многочлена определяется количеством компонентов циклотомического класса, которому
соответствует его корень (табл. 5.3). Действительно, минимальный
многочлен, показатели корней которого принадлежат циклотомическому классу
.
Степень
минимального многочлена определяется количеством компонентов циклотомического класса, которому
соответствует его корень (табл. 5.3). Действительно, минимальный
многочлен, показатели корней которого принадлежат циклотомическому классу ![]() , может быть записан в
виде
, может быть записан в
виде
|
|
(5.11) |
Для ![]() (см. 5.3.5):
(см. 5.3.5):
|
|
|
Аналогично для ![]() :
:
|
|
|
С учетом (5.10) справедливо равенство
|
|
|
где ![]() пробегает все
множество классов по модулю
пробегает все
множество классов по модулю ![]() , т.е. многочлен
, т.е. многочлен ![]() раскладывается на произведение минимальных многочленов элементов, показатели которых принадлежат
каждому из циклотомических классов
по модулю
раскладывается на произведение минимальных многочленов элементов, показатели которых принадлежат
каждому из циклотомических классов
по модулю ![]() .
.
Минимальные многочлены элементов ![]() и
и ![]() равны. В частности, в поле
равны. В частности, в поле ![]() равны
минимальные многочлены элементов
равны
минимальные многочлены элементов ![]() и
и ![]() . В этом можно убедиться,
обратив внимание на тот факт, что элементы
. В этом можно убедиться,
обратив внимание на тот факт, что элементы ![]() и
и ![]() всегда соответствуют одному
циклотомическому классу (табл. 5.3), а следовательно, принадлежат набору корней
одного неприводимого полинома. Более того, между собой равны минимальные
многочлены всех элементов, соответствующих
одному циклотомическому классу, т.к. любые два соседние из таких элементов
находятся в соотношении
всегда соответствуют одному
циклотомическому классу (табл. 5.3), а следовательно, принадлежат набору корней
одного неприводимого полинома. Более того, между собой равны минимальные
многочлены всех элементов, соответствующих
одному циклотомическому классу, т.к. любые два соседние из таких элементов
находятся в соотношении ![]() и
и ![]() .
.
И еще об одном свойстве минимального многочлена, имеющем отношение к нахождению примитивных элементов поля.
Минимальный многочлен, корнем которого является примитивный элемент поля,
называется примитивным многочленом. Его степень всегда равна ![]() . Для практических приложений важно иметь в виду следующее. В тех
случаях, когда неприводимый многочлен
. Для практических приложений важно иметь в виду следующее. В тех
случаях, когда неприводимый многочлен
![]() , задающий
операции в поле, является также и примитивным многочленом, примитивным элементом поля будет элемент
, задающий
операции в поле, является также и примитивным многочленом, примитивным элементом поля будет элемент ![]() .
.
Таблицы неприводимых многочленов [33] обычно
содержат сведения о том, какие из многочленов являются
примитивными, что позволяет избежать возможных затруднений в
определении примитивных элементов поля. В табл. 5.4 приведены
примитивные многочлены над ![]() для
для ![]() от 1 до 20 [3,
30].
от 1 до 20 [3,
30].
Помимо представленных в таблице примитивными являются также полиномы, векторы коэффициентов которых написаны в обратном порядке. Такие полиномы называются двойственными, или взаимными исходным.
Таблица 5.4. Примитивные
многочлены до степени ![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Это пары ![]() и
и ![]() ;
; ![]() и
и ![]() и т.д. Использовавшийся
ранее при построении
и т.д. Использовавшийся
ранее при построении ![]() полином
полином
![]() примитивен,
на основании чего в качестве примитивного элемента поля был взят
примитивен,
на основании чего в качестве примитивного элемента поля был взят
![]() .
.
Изоморфизм конечных полей
Расширение конечного поля ![]() может быть задано
разными полиномами одинаковых степеней
может быть задано
разными полиномами одинаковых степеней ![]() . В каком соотношении
находятся эти поля? Прежде всего, очевидно, ненулевыми элементами любого поля
порядка
. В каком соотношении
находятся эти поля? Прежде всего, очевидно, ненулевыми элементами любого поля
порядка ![]() является тот же полный набор всевозможных
многочленов степени
является тот же полный набор всевозможных
многочленов степени ![]() и ниже, отличающийся для разных полиномов
и ниже, отличающийся для разных полиномов ![]() лишь порядком
следования элементов
лишь порядком
следования элементов ![]() по степеням примитивного элемента.
по степеням примитивного элемента.
В теории конечных полей доказывается, что все
поля ![]() одного
порядка
одного
порядка ![]() изоморфны («подобны
по форме»), т.е. между
изоморфны («подобны
по форме»), т.е. между ![]() и
и ![]() существует взаимнооднозначное
отображение
существует взаимнооднозначное
отображение ![]() друг
на друга, сохраняющее операции сложения и умножения. Это означает,
что для любых двух
элементов
друг
на друга, сохраняющее операции сложения и умножения. Это означает,
что для любых двух
элементов ![]() и
и
![]() из
из ![]() справедливы соотношения
справедливы соотношения
|
|
(5.12) |
|
|
(5.13) |
Нетрудно убедиться, что между полями,
построенными на основе неприводимых полиномов ![]() и
и ![]() (табл.
5.2), существует взаимнооднозначное отображение:
(табл.
5.2), существует взаимнооднозначное отображение: ![]() . Простой подстановкой можно убедиться,
что при таком отображении сохраняются операции сложения и умножения (5.12) и (5.13). Например, для сложения
. Простой подстановкой можно убедиться,
что при таком отображении сохраняются операции сложения и умножения (5.12) и (5.13). Например, для сложения
|
|
|
|
|
|
Аналогично для умножения
|
|
|
|
|
|
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Список сокращений
- Основные обозначения
- ВВЕДЕНИЕ
- Глава 1. Сообщения, сигналы и помехи, их математические модели
- 1.1. Основные понятия и определения
- 1.1.1. Сообщение, сигнал, модуляция
- 1.1.2. Основные параметры сигналов
- 1.2. Системы связи. Каналы связи
- 1.2.1. Структура канала электросвязи
- 1.2.2. Линия и сеть связи
- 1.2.3. Помехи и искажения в канале
- 1.2.4. Эталонная модель взаимодействия открытых систем
- 1.2.5. Модели каналов связи и их математическое описание
- 1.3. Способы описания сигналов и помех
- 1.3.1. Сигнал и его математическая модель
- 1.3.2. Энергетические характеристики детерминированного сигнала
- 1.4.2. Представление сигналов и помех рядом Фурье
- 1.4.3. Применение преобразования Фурье для непериодических сигналов
- 1.5. Теорема Котельникова
- 1.6. Пространство сигналов
- 1.6.1. Линейное пространство
- 1.6.2. Представление сигнала в многомерном пространстве
- 1.7. Сигналы как случайные процессы
- 1.7.1. Характеристики случайного процесса
- 1.7.2. Флуктуационный шум
- 1.8. Комплексное представление сигналов и помех
- 1.8.1. Понятие аналитического сигнала
- 1.8.2. Огибающая, мгновенная фаза и мгновенная частота узкополосного случайного процесса
- Контрольные вопросы
- Глава 2. Методы формирования и преобразования сигналов
- 2.1. Модуляция сигналов
- 2.1.1. Амплитудная модуляция гармонической несущей
- 2.1.2. Балансная и однополосная модуляция гармонической несущей
- 2.2. Методы угловой модуляции
- 2.2.1. Принципы частотной и фазовой (угловой) модуляции
- 2.2.2. Спектр сигналов угловой модуляции
- 2.3. Формирование и детектирование модулированных сигналов
- 2.3.1. Формирование и детектирование сигналов амплитудной и однополосной амплитудной модуляции
- 2.3.2. Формирование и детектирование сигналов угловой модуляции
- 2.4. Манипуляция сигналов
- 2.4.1. Временные и спектральные характеристики амплитудно-манипулированных сигналов
- 2.4.2. Временные и спектральные характеристики частотно-манипулированных сигналов
- 2.4.3. Фазовая (относительно-фазовая) манипуляция сигналов
- 2.5. Системы связи с многопозиционной относительной фазовой манипуляцией
- 2.5.1. Принцип формирования сигнала с многократной относительной фазовой манипуляцией
- 2.5.2. Квадратурная относительно-фазовая манипуляция (КОФМ)
- 2.5.3. Принцип частотной модуляции с непрерывной фазой
- Контрольные вопросы
- Глава 3. Помехоустойчивость приема дискретных сообщений
- 3.1. Критерии качества и правила приема дискретных сообщений
- 3.1.1. Понятие о помехоустойчивости систем электрической связи
- 3.1.2. Задача оптимального приема
- 3.1.3. Вычисление вероятностей ошибок
- 3.2. Оптимальная демодуляция при когерентном приеме сигналов
- 3.2.1. Оптимальные алгоритмы приема при полностью известных сигналах
- 3.2.2. Реализация алгоритмов оптимального когерентного приема
- 3.3. Помехоустойчивость приема сигналов с известными параметрами
- 3.4. Прием сигналов с неопределенной фазой
- 3.4.1. Оптимальный некогерентный прием дискретных сигналов
- 3.4.2. Помехоустойчивость оптимального некогерентного приема
- 3.5. Подоптимальные методы приема
- 3.5.1. Причины применения неоптимальных методов приема
- 3.5.2. Квазиоптимальные методы приема
- Контрольные вопросы
- Глава 4. Теория передачи информации
- 4.1. Информационные характеристики источника сообщений
- 4.1.1. Количественное определение информации
- 4.1.2. Энтропия и производительность дискретного источника сообщений
- 4.2. Пропускная способность дискретного канала
- 4.2.1. Количество информации переданной по дискретному каналу
- 4.2.2. Пропускная способность дискретного канала
- 4.2.3. Пропускная способность симметричного дискретного канала без памяти
- 4.3. Методы сжатия дискретных сообщений
- 4.3.1. Условия существования оптимального неравномерного кода
- 4.3.2. Прямая и обратная теоремы кодирования источника неравномерными кодами
- 4.3.3. Показатели эффективности сжатия
- 4.3.4. Кодирование источника дискретных сообщений методом Шеннона-Фано
- 4.3.5. Кодирование источника дискретных сообщений методом Хаффмена
- 4.4. Пропускная способность непрерывного канала
- 4.4.1. Постановка задачи передачи дискретных сообщений в непрерывном канале
- 4.4.2. Количество информации, переданной по непрерывному каналу
- 4.4.3. Пропускная способность непрерывного канала
- Контрольные вопросы
- Глава 5. Теория кодирования сообщений
- 5.1. Помехоустойчивое кодирование: блочные и непрерывные коды
- 5.1.1. Постановка задачи помехоустойчивого кодирования
- 5.1.2. Классификация кодов
- 5.1.3. Основные характеристики и свойства блочных кодов
- 5.2. Эффективность помехоустойчивого кодирования
- 5.2.1. Эффективность кода в режиме исправления ошибок
- 5.2.2. Эффективность кода в режиме обнаружения ошибок
- 5.2.3. Эффективность помехоустойчивых кодов
- 5.3. Математические основы теории помехоустойчивого кодирования
- 5.3.1. Краткие сведения из теории чисел
- 5.3.2. Группы
- 5.3.3. Кольца и поля
- 5.3.4. Векторное пространство
- 5.3.5. Конечные поля
- 5.4. Линейные блочные коды
- 5.4.1. Система передачи дискретных сообщений
- 5.4.2. Параметры линейного кода
- 5.4.3. Полиномиальные циклические коды
- 5.4.4. Циклические коды и корни полиномов
- 5.4.5. Спектральное описание циклических кодов
- 5.4.6. Простейшие блочные линейные коды
- 5.5. Коды Боуза-Чоудхури-Хоквингема
- 5.5.1. Методы задания кодов БЧХ
- 5.5.2. Принципы декодирования кодов БЧХ
- 5.5.3. Методы реализации этапов декодирования кодов БЧХ
- 5.6. Коды Рида-Соломона
- 5.6.1. Основные определения
- 5.6.2. Обнаружение и исправление пакетов ошибок
- 5.7. Коды Рида-Маллера
- 5.7.1. Задание и декодирование кодов Рида-Маллера
- 5.7.2. Симплексные коды и m-последовательности
- 5.7.3. Связь между блочными кодами
- 5.8. Сверточные коды
- 5.8.1. Основные параметры
- 5.8.2. Способы задания сверточного кода
- 5.8.3. Алгоритм декодирования Витерби
- 5.9. Помехоустойчивость систем передачи дискретных сообщений
- 5.9.1. Две процедуры приема сигналов
- 5.9.2. Помехоустойчивость систем передачи информации при оптимальной процедуре приема
- 5.9.3. Помехоустойчивость систем передачи информации при посимвольном приеме сигналов
- Контрольные вопросы
- Глава 6. Сигналы с импульсной модуляцией
- 6.1. Методы импульсной модуляции
- 6.1.1. Импульсные методы передачи непрерывных сигналов
- 6.1.2. Спектральные характеристики импульсных методов модуляции
- 6.2. Помехоустойчивость непрерывных каналов связи с импульсной модуляцией
- 6.2.1. Помехоустойчивость систем передачи с импульсными методами модуляции
- 6.3. Цифровые методы передачи непрерывных сообщений
- 6.3.1. Передача сигналов с импульсно-кодовой модуляцией
- 6.3.2. Передача сигналов с дельта модуляцией
- 6.3.3. Квантование сигналов в системах с ИКМ и ДМ
- Контрольные вопросы
- Глава 7. Методы приема сигналов в сложных условиях
- 7.1. Прием сигналов в каналах с замираниями
- 7.1.1. Сущность замираний и их классификация
- 7.1.2. Принципы разнесенного приема сигналов
- 7.2. Методы борьбы с замираниями сигналов
- 7.2.1. Методы борьбы с замираниями в аналоговых системах связи
- 7.2.2. Методы борьбы с замираниями в цифровых системах связи
- 7.3. Методы борьбы с межсимвольной интерференцией
- 7.3.1. Причины возникновения и сущность межсимвольной интерференции
- 7.3.2. Обработка сигналов в каналах с межсимвольной интерференцией
- 7.3.3. Помехоустойчивость в каналах с межсимвольной интерференцией
- 7.4. Прием дискретных сообщений в каналах с сосредоточенными по спектру и импульсными помехами
- 7.4.1. Общая характеристика сосредоточенных по спектру и импульсных помех
- 7.4.2. Борьба с сосредоточенными и импульсными помехами
- 7.5. Компенсация помех и искажений в канале
- 7.5.1. Принцип работы радиолинии с ФМ ПСС (ФМ ШПС)
- 7.5.2. Помехоустойчивость радиолинии с ФМ ПСС
- 7.5.3. Принципы работы радиолиний с ППРЧ
- 7.5.4. Помехоустойчивость радиолиний с ППРЧ
- Контрольные вопросы
- Глава 8. Многоканальная связь и распределение информации
- 8.1. Методы распределения ресурса общего канала
- 8.1.1. Классификация систем передачи информации, использующих единый ресурс
- 8.1.2. Постановка задачи объединения и разделения сигналов
- 8.1.3. Энергетическая и спектральная цена уплотнения
- 8.2. Частотное разделение каналов
- 8.2.1. Принцип частотного объединения и разделения каналов
- 8.2.2. Групповой сигнал, его структура и характеристики
- 8.3. Временное разделение каналов
- 8.3.1. Принцип временного разделения каналов
- 8.3.2. Характеристики группового сигнала систем с ВРК
- 8.4. Разделение сигналов по форме
- Контрольные вопросы
- Глава 9. Эффективность систем связи
- 9.1. Оценка эффективности систем связи
- 9.1.1. Подходы к оценке эффективности
- 9.1.2. Критерии эффективности
- 9.1.3. Эффективность аналоговых и цифровых систем
- 9.2. Выбор сигналов и помехоустойчивых кодов
- 9.2.1. Многопозиционные сигналы
- 9.2.2. Корректирующие коды
- 9.3. Оптимизация систем связи
- 9.3.1. Согласование методов модуляции и кодирования
- 9.3.2. Классификация сигнально – кодовых конструкций
- 9.4. Характеристики основных типов СКК
- 9.4.1. Согласование канала кодом Грея
- 9.4.2. Согласование на основе разбиения ансамбля на вложенные подансамбли
- 9.5. Алгоритмы цифровой обработки сигналов
- 9.5.1. Дискретные сигналы и их спектры
- 9.5.2. Алгоритмы дискретного и быстрого преобразований Фурье
- Контрольные вопросы
- Глава 10. Теоретико-информационные основы криптозащиты сообщений в телекоммуникационных системах
- 10.1. Классификация криптографических систем
- 10.1.2. Классификация криптографических систем защиты информации
- 10.1.3. Оценка стойкости криптосистем
- 10.2. Функции, используемые в криптографических системах
- 10.2.1. Общее описание функций, используемых в криптографических системах
- 10.2.2. Однонаправленные функции
- 10.2.3. Криптографические хэш-функции
- 10.3. Модели криптографических систем
- 10.3.1. Системы шифрования
- 10.3.2. Традиционные симметричные криптосистемы
- 10.4. Алгоритмы криптографической защиты
- 10.4.1. Алгоритм криптографической защиты информации согласно ГОСТ 28147-89
- Контрольные вопросы
- Заключение
- Список литературы