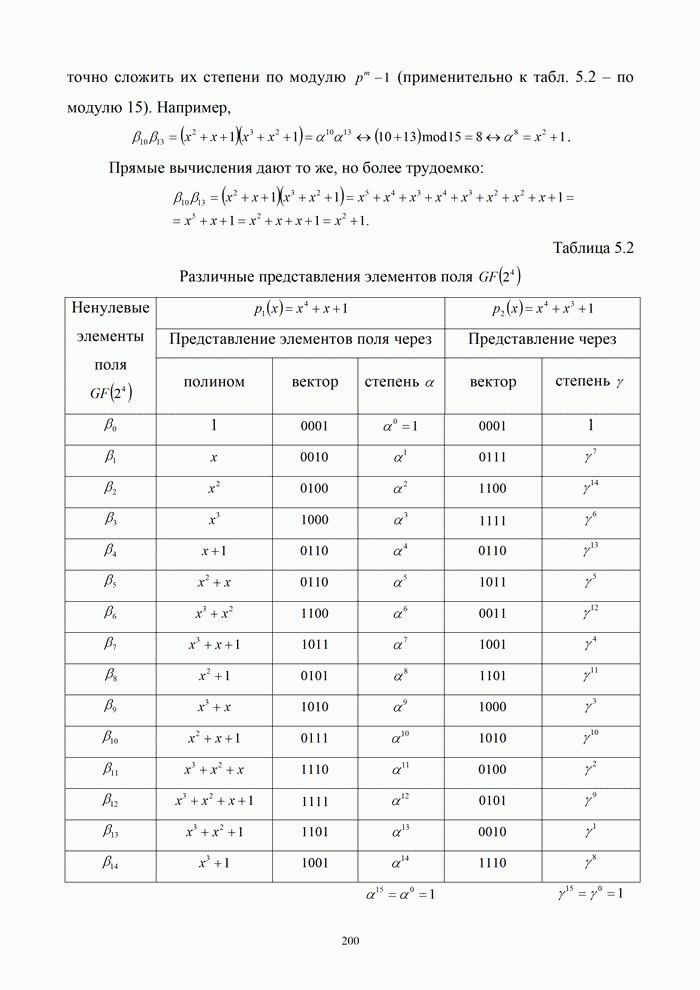
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
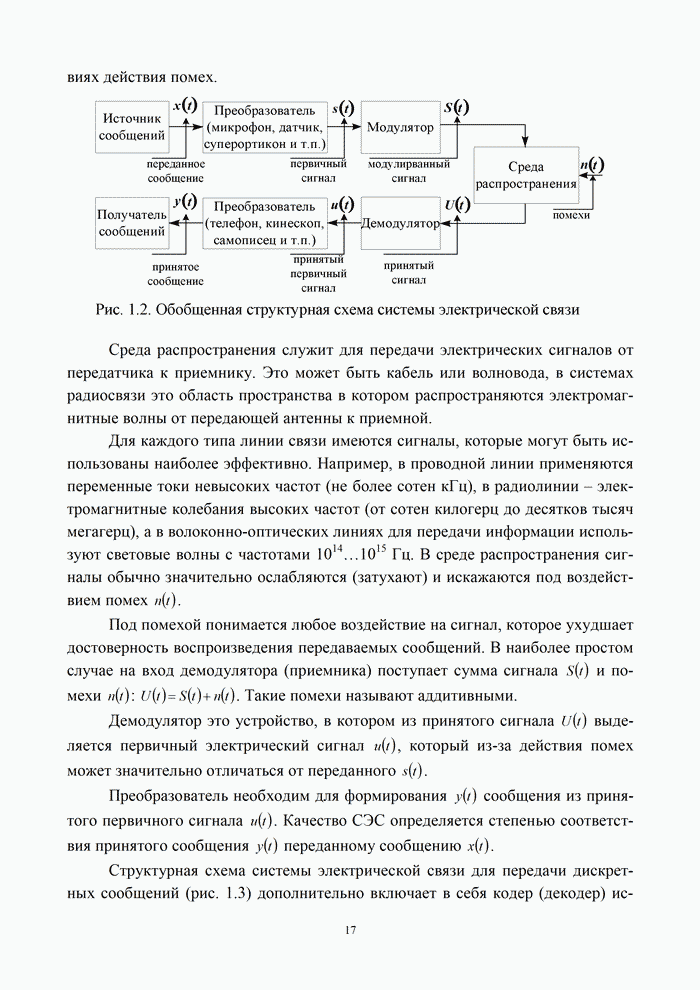
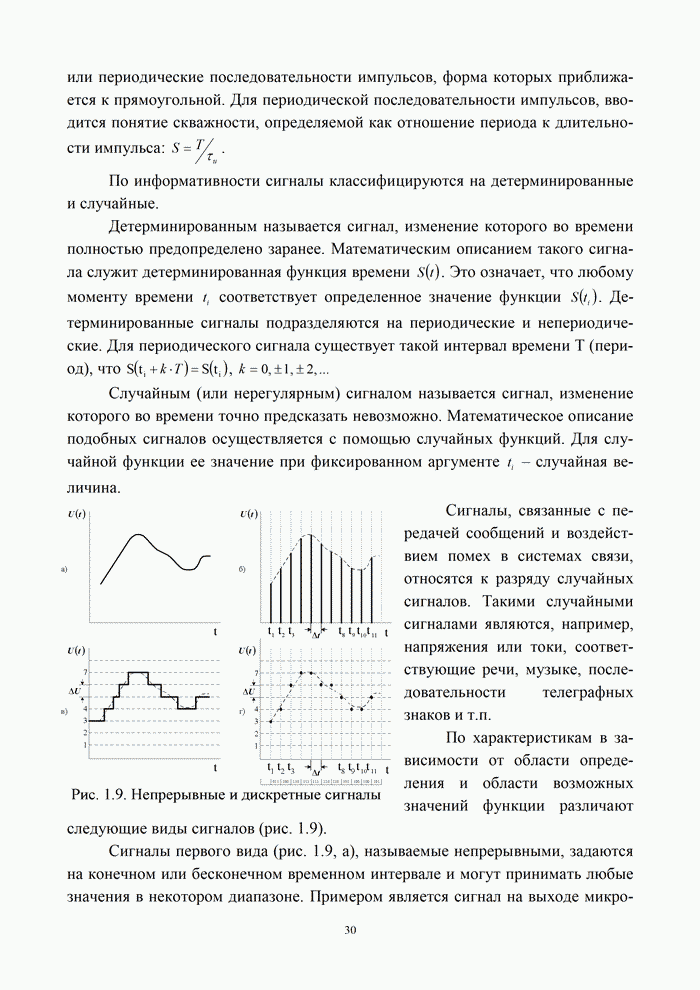
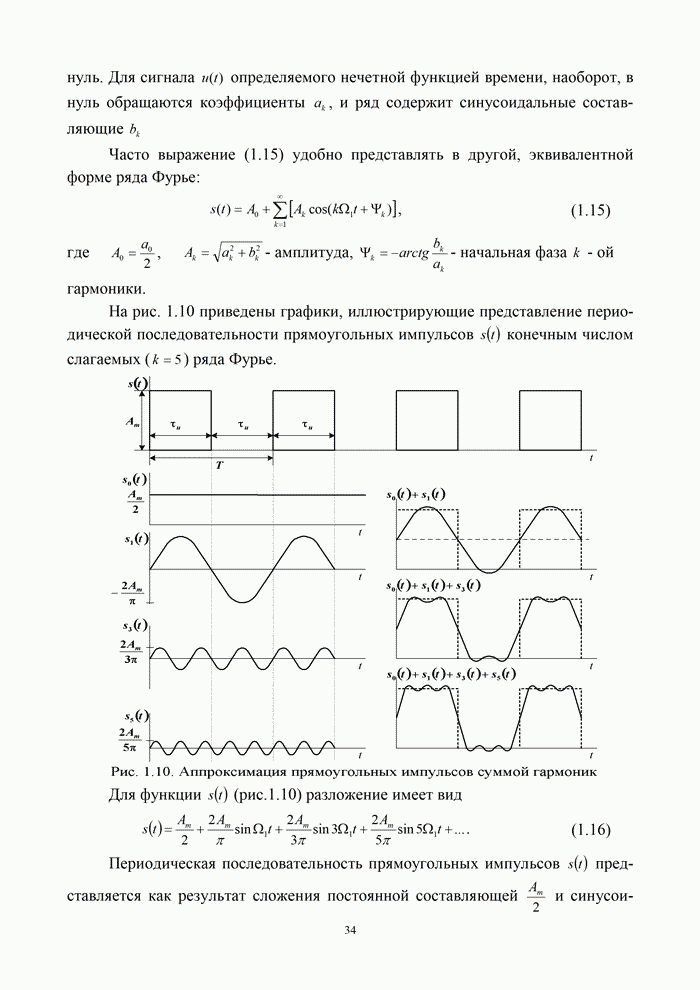
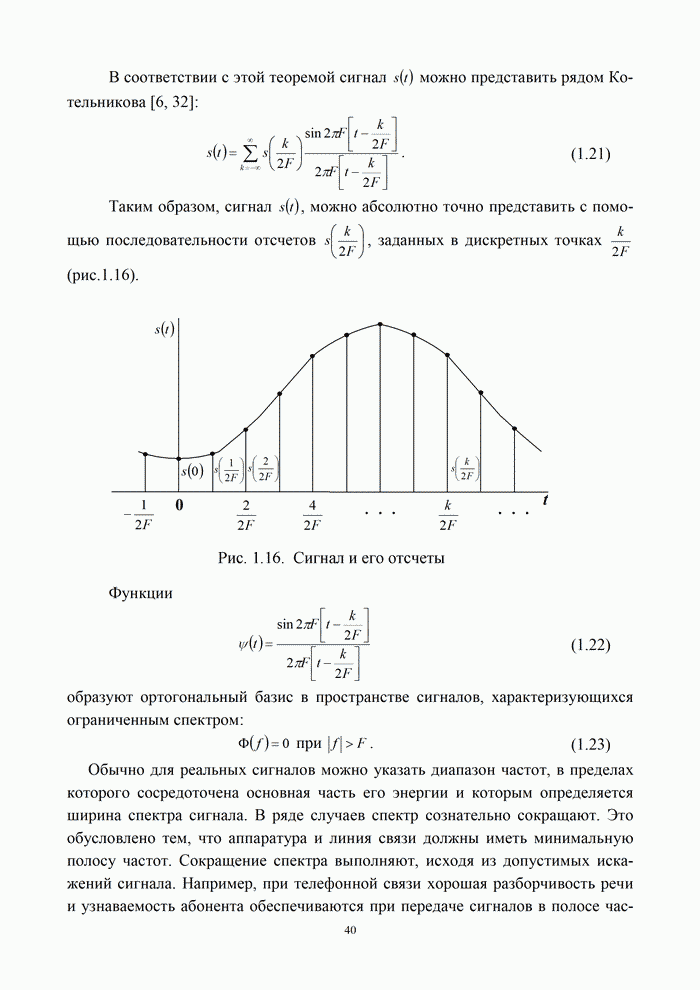
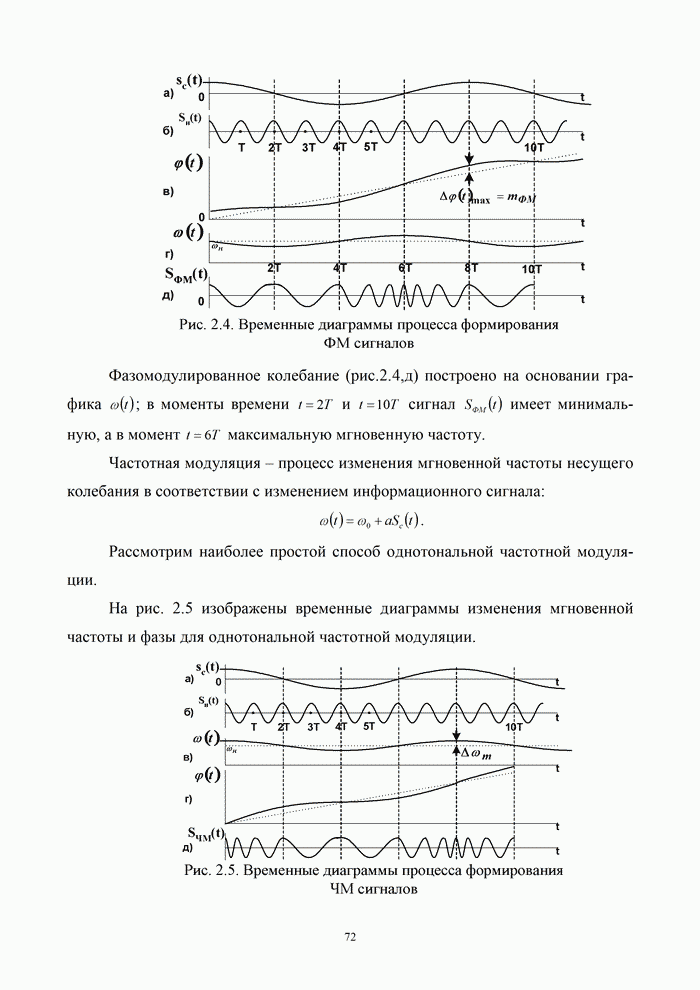
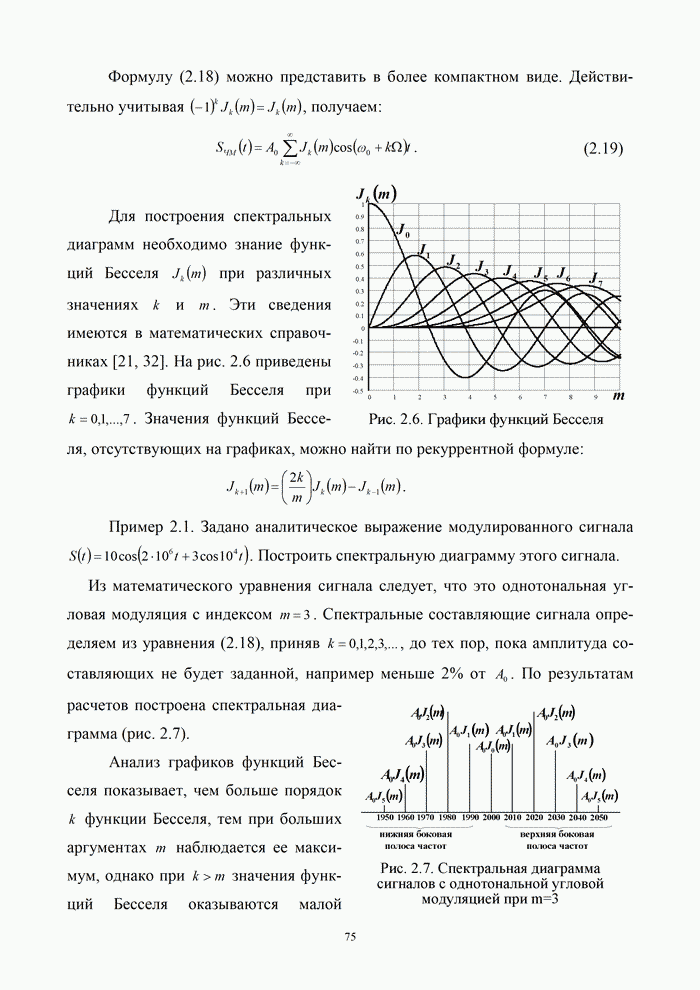
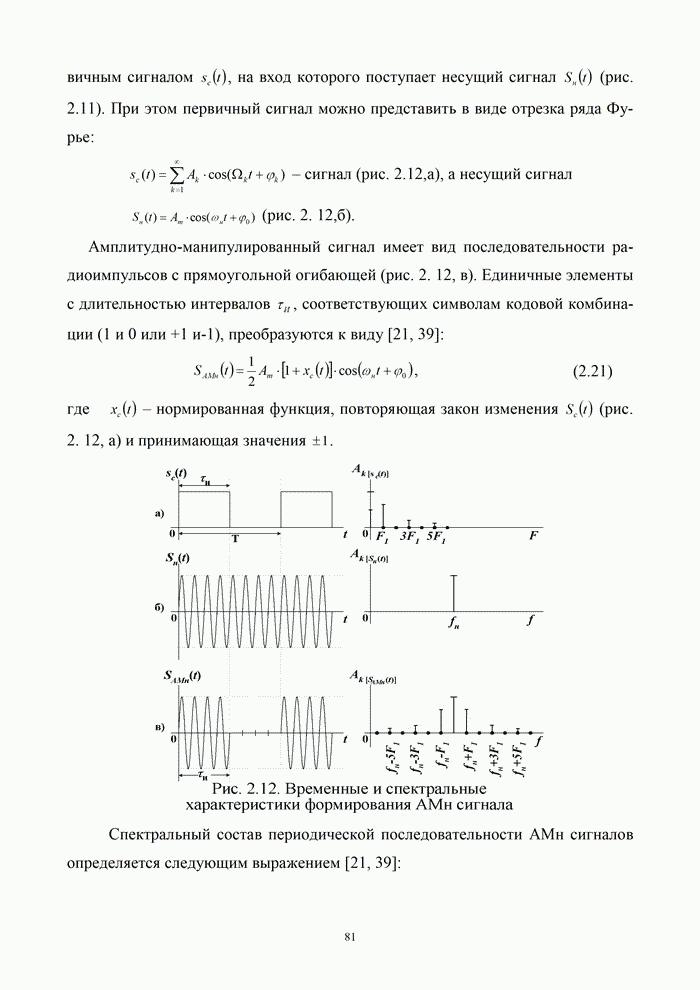
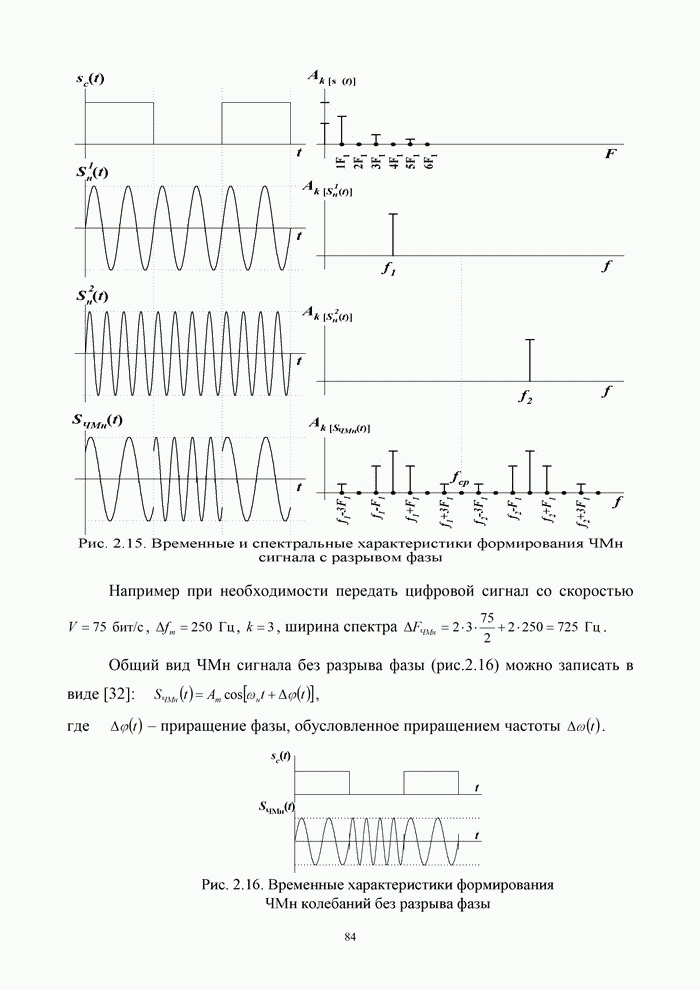
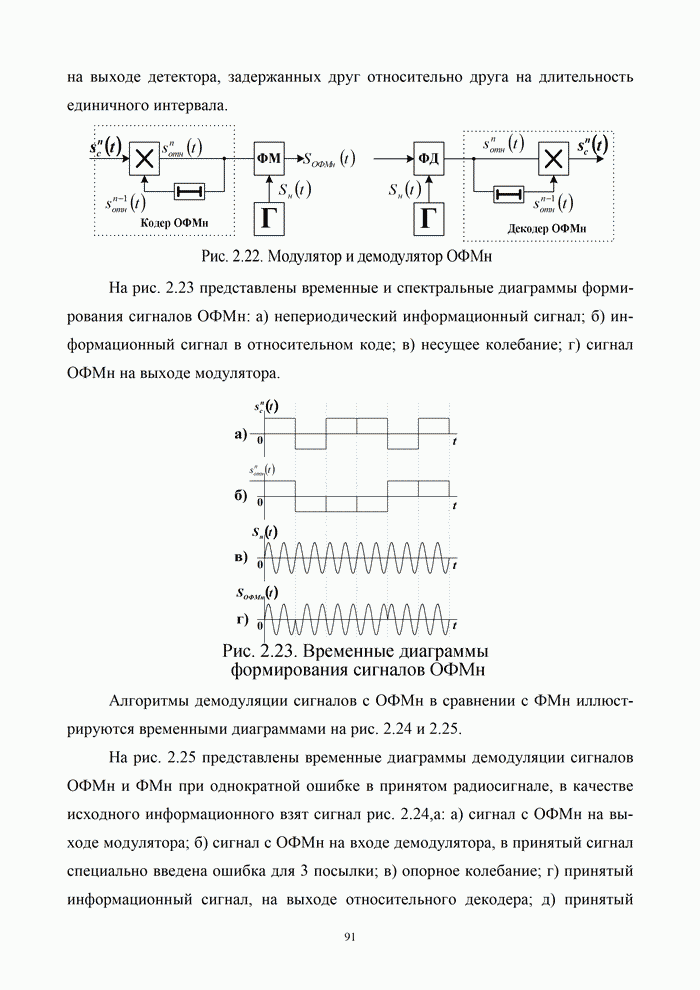
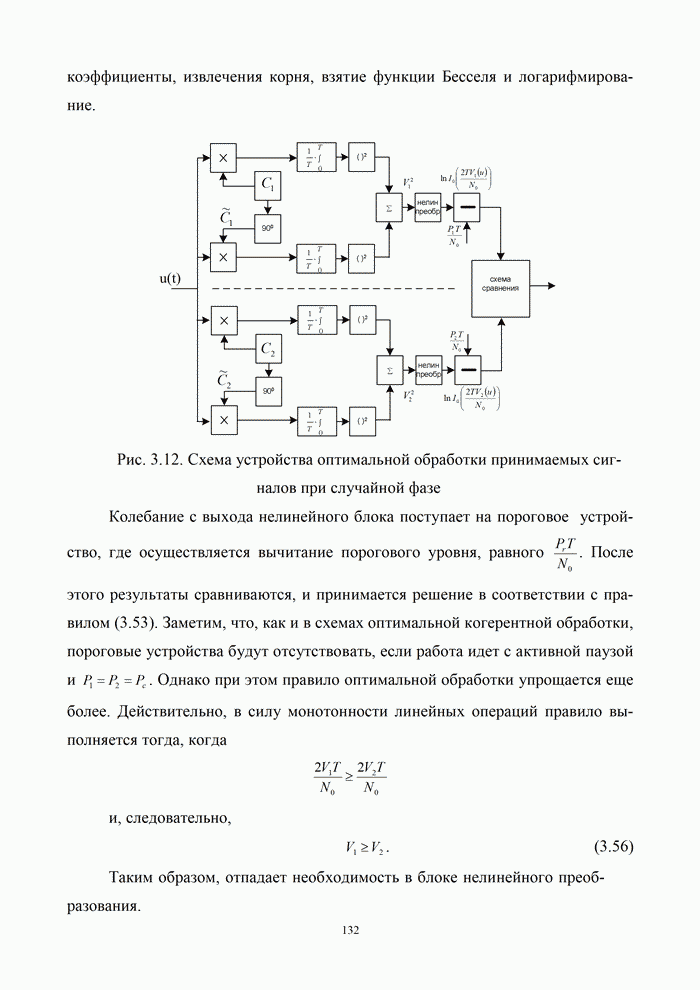
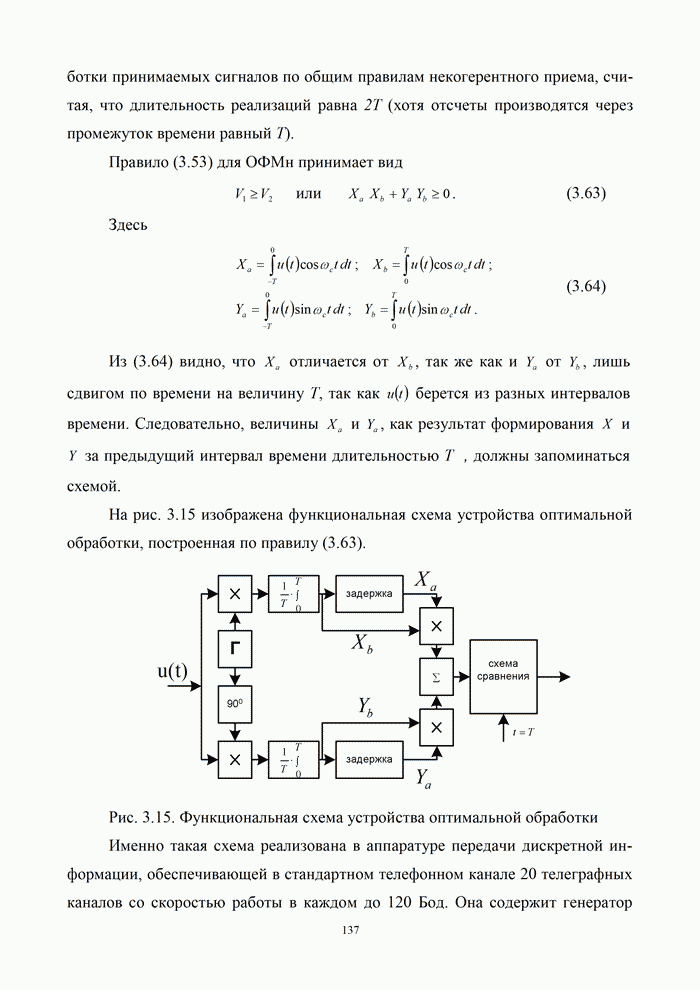
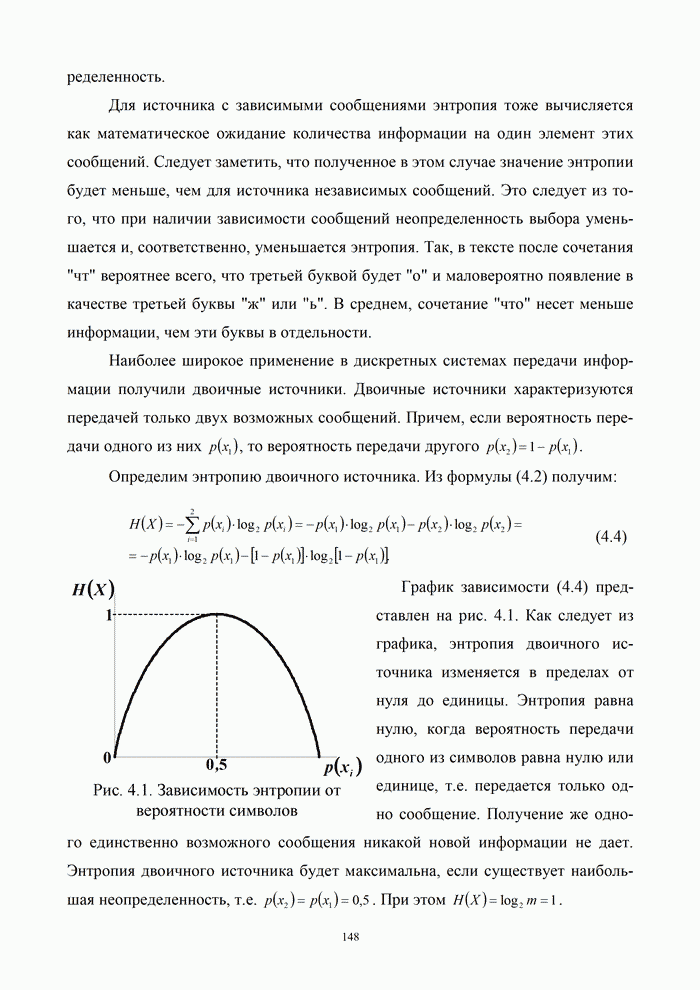
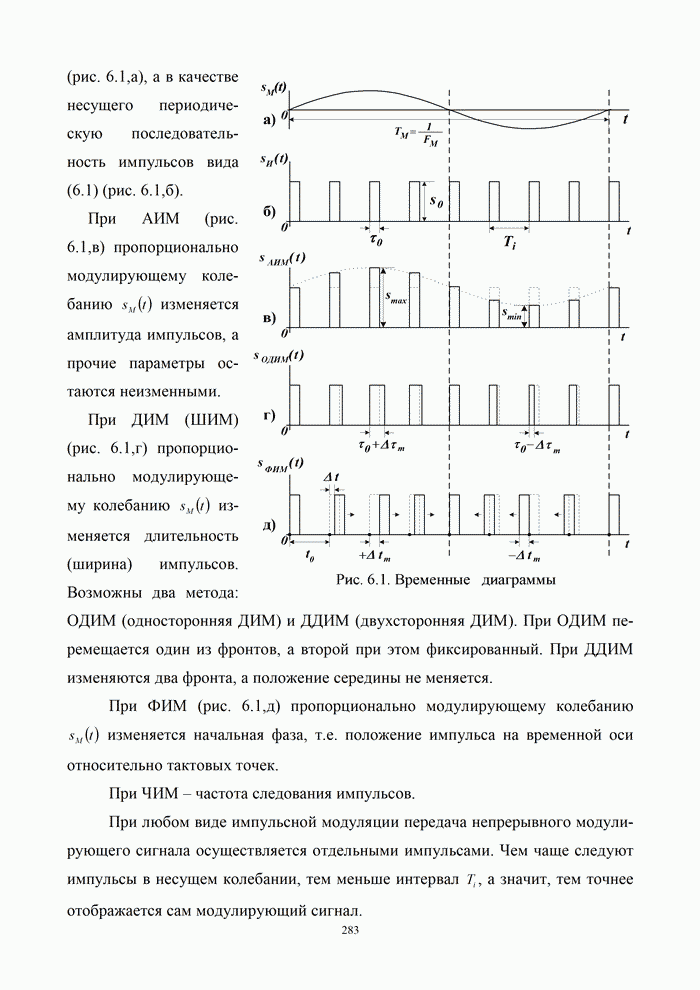
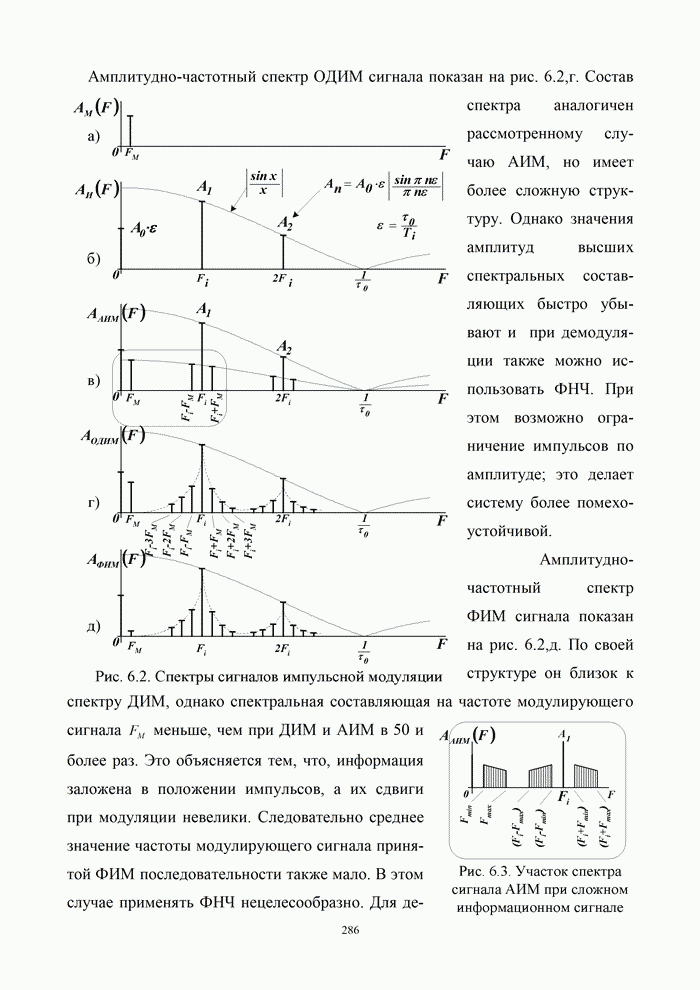
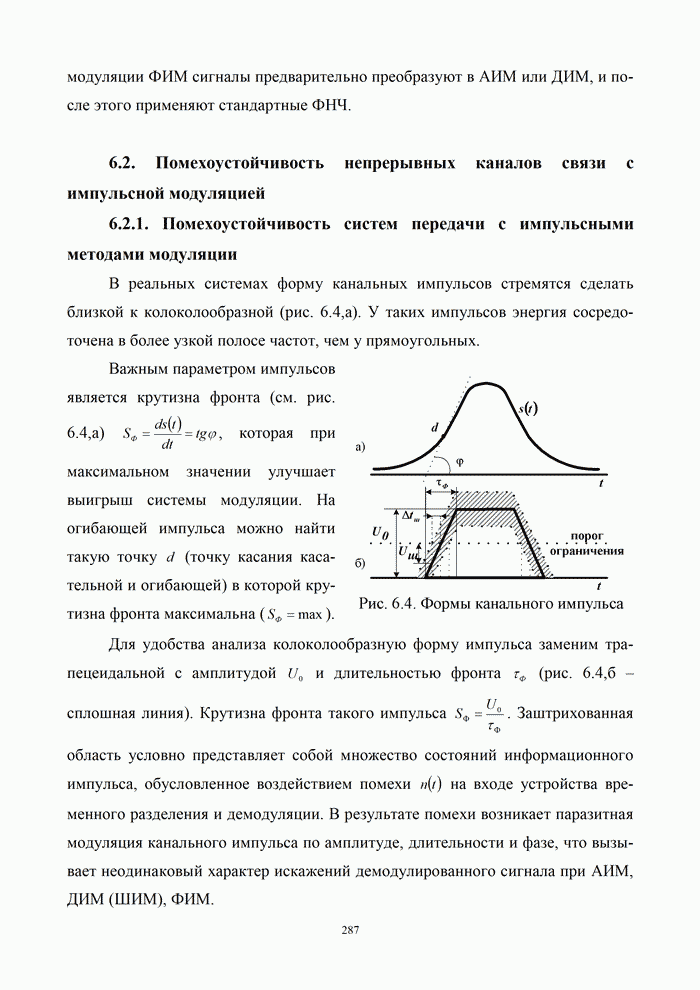
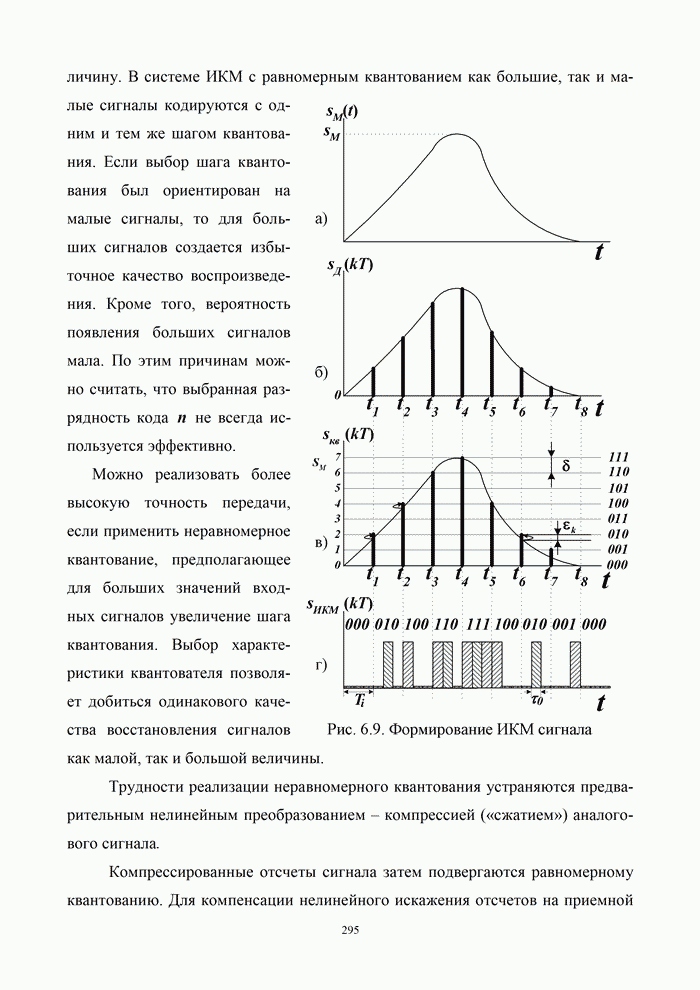
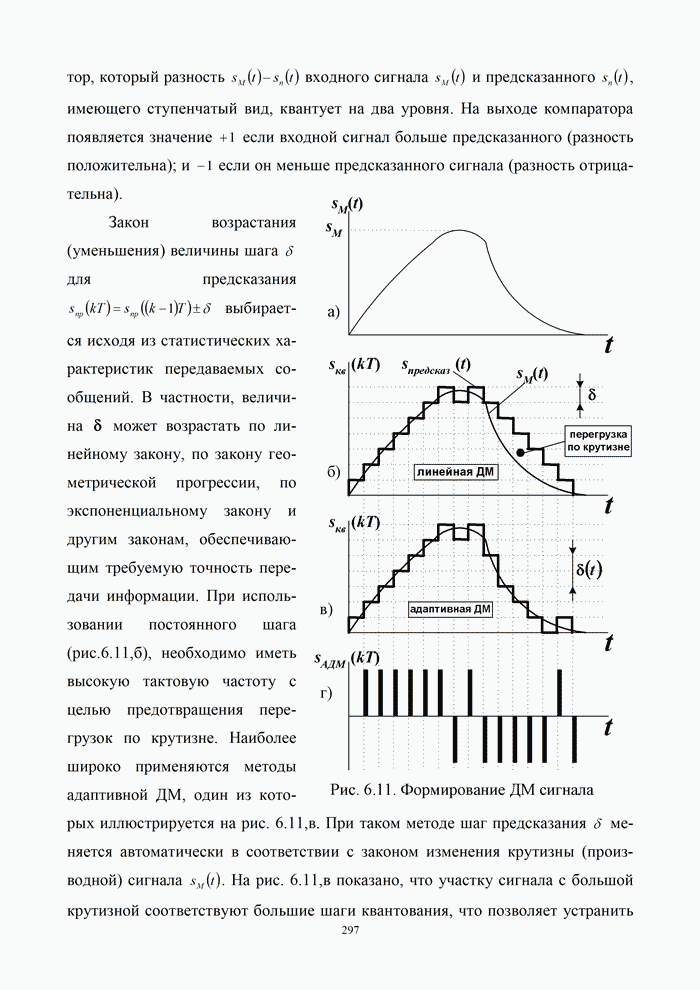
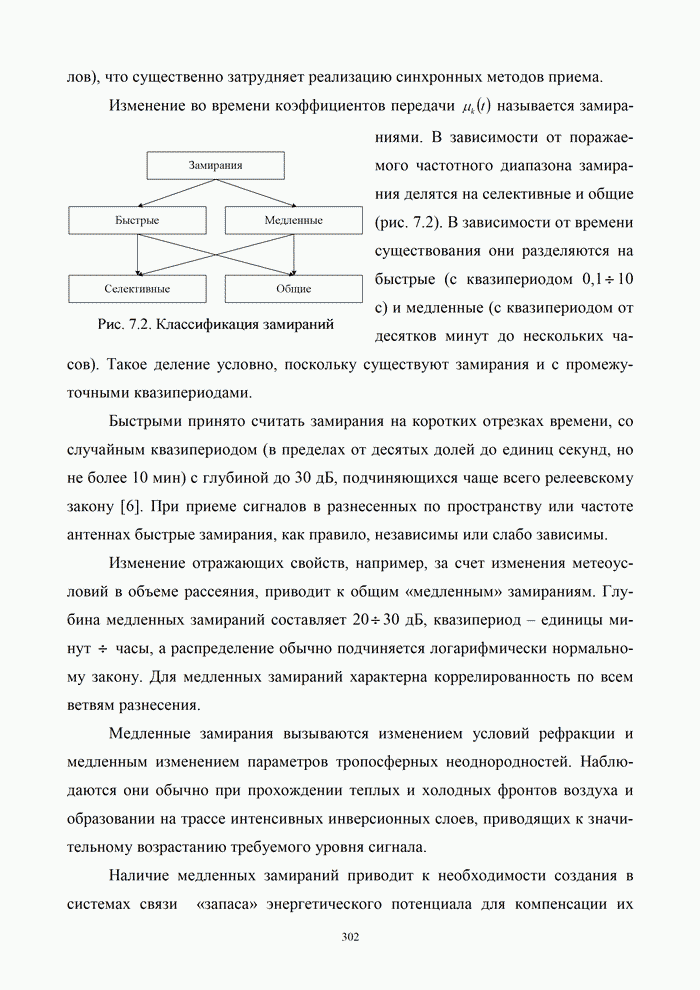
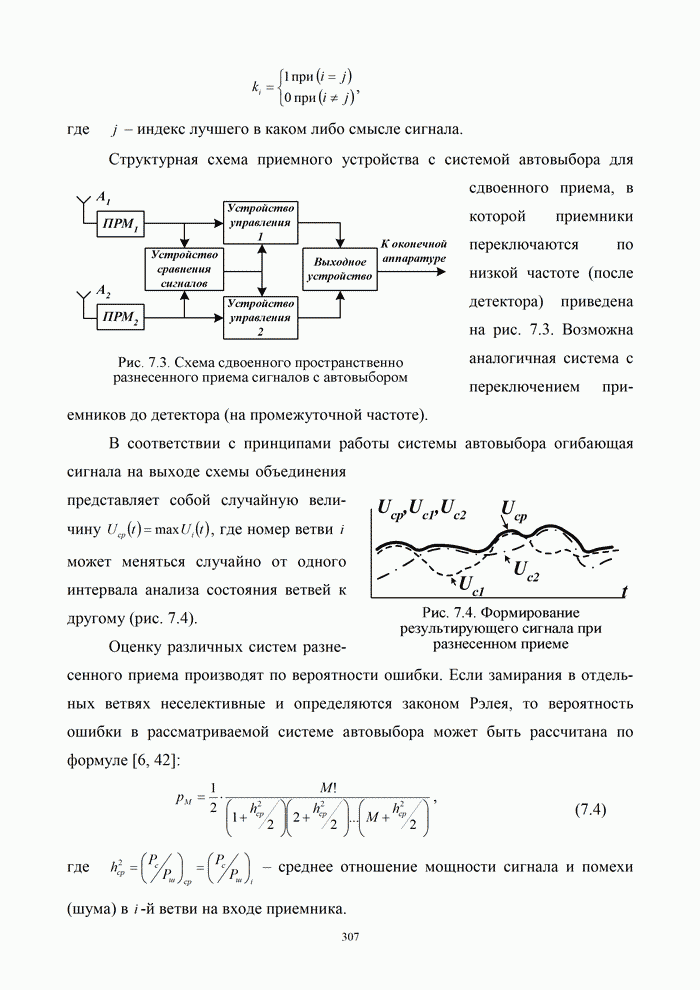
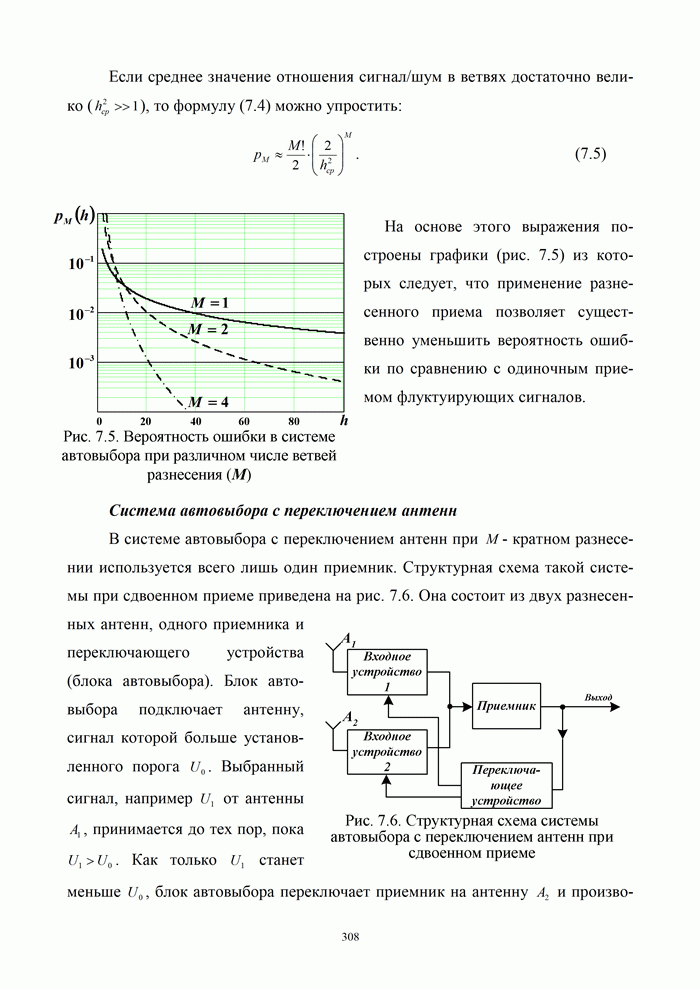
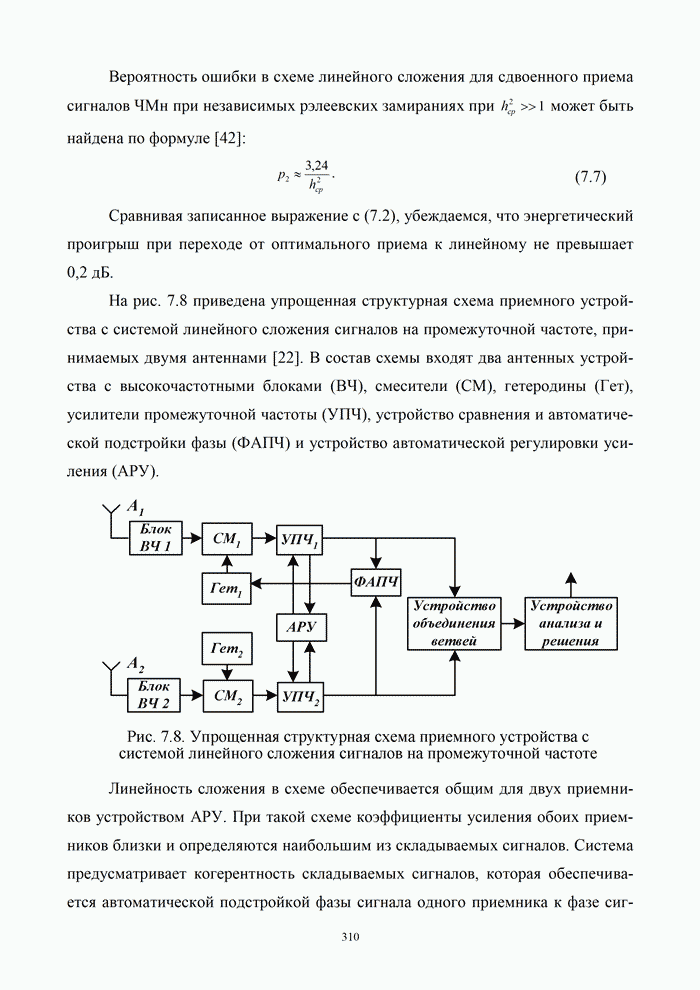
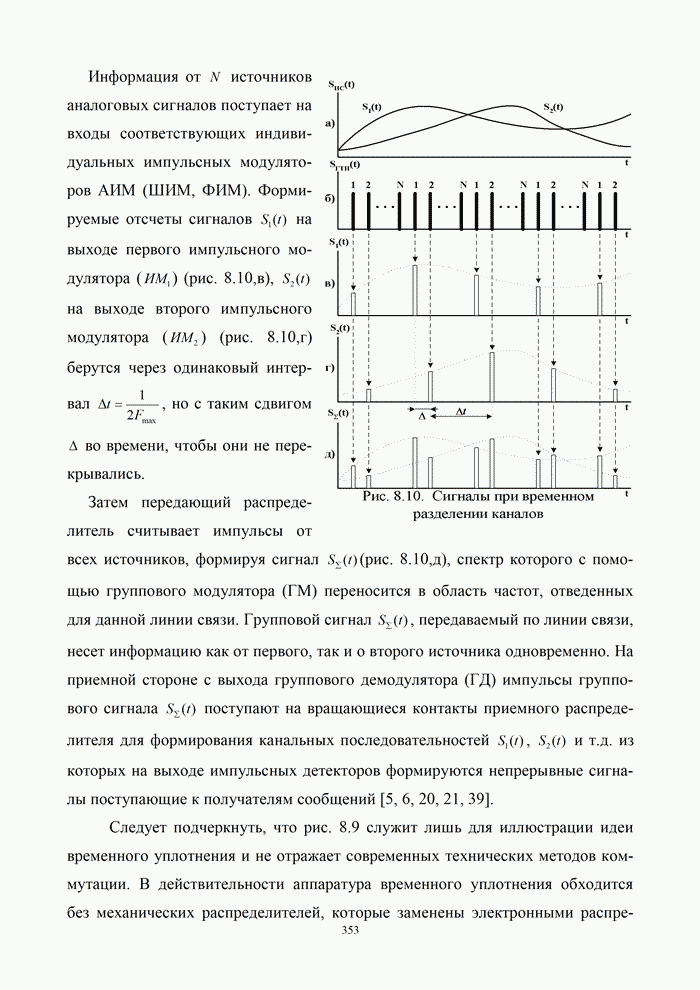
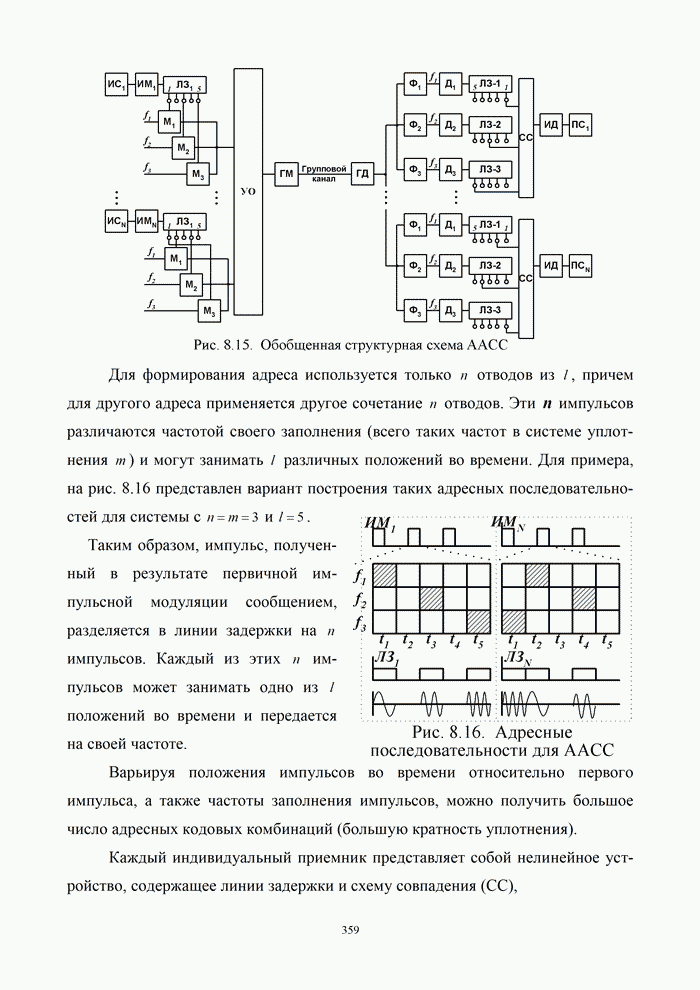
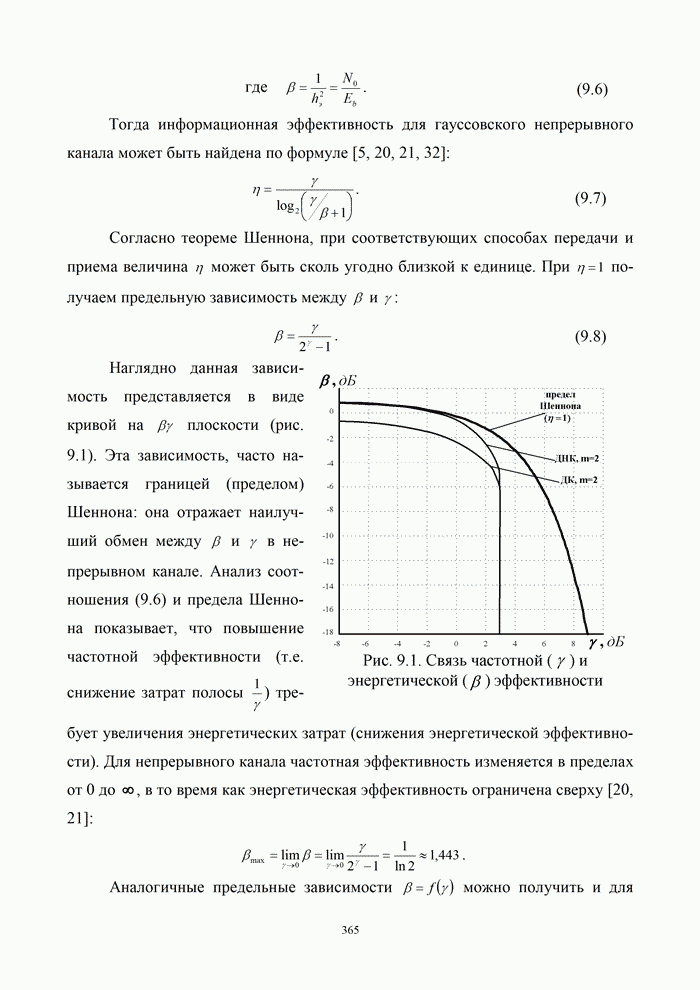
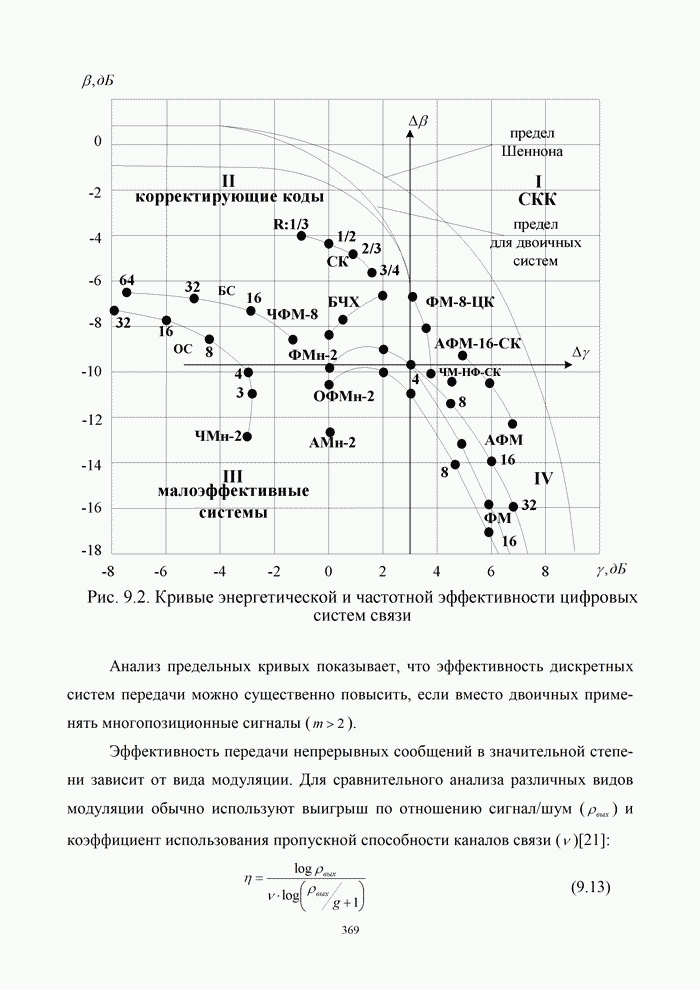
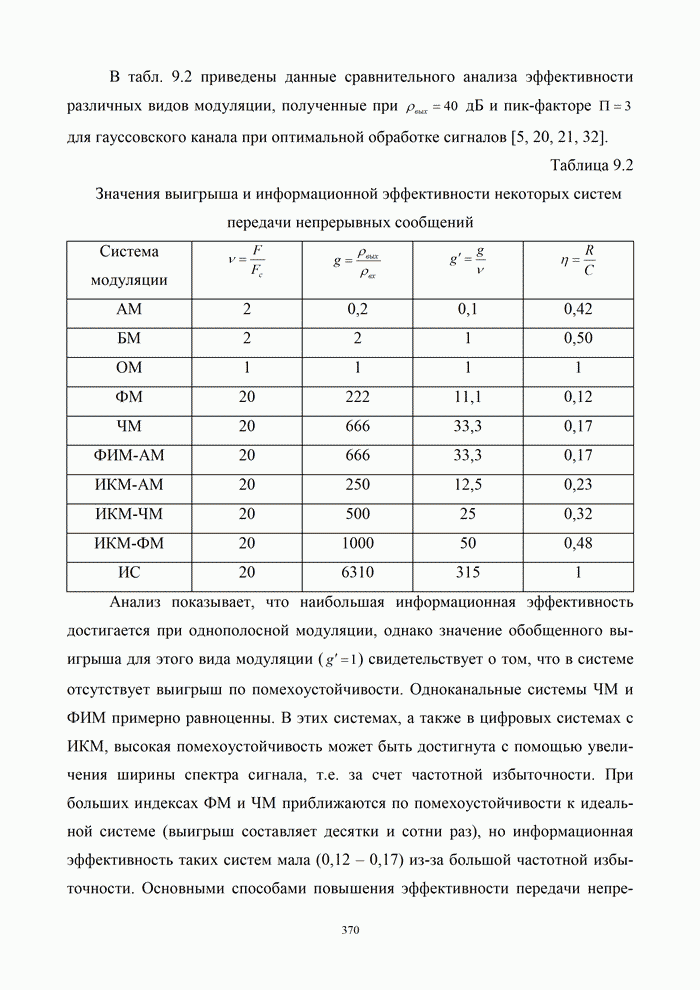
5.9.3. Помехоустойчивость систем передачи информации при посимвольном приеме сигналов
Вероятность правильного приема одного символа
в этом случае находится с помощью формулы (5.48) при ![]() . При использовании для
передачи сигналов фазовой манипуляции (ФМн), характеризуемой коэффициентом
корреляции между сигналами
. При использовании для
передачи сигналов фазовой манипуляции (ФМн), характеризуемой коэффициентом
корреляции между сигналами ![]() ,
,
|
|
(5.50) |
где ![]() – энергия одного
символа. После замены
– энергия одного
символа. После замены ![]() ,
, ![]() выражения для вероятности правильного (
выражения для вероятности правильного (![]() ) и ошибочного (
) и ошибочного (![]() ) приема символа при
ФМн преобразуются к следующему виду:
) приема символа при
ФМн преобразуются к следующему виду:
|
|
(5.51) |
Аналогично при использовании частотной (ЧМн) или амплитудной (АМн) манипуляций:
|
|
(5.52) |
|
|
(5.53) |
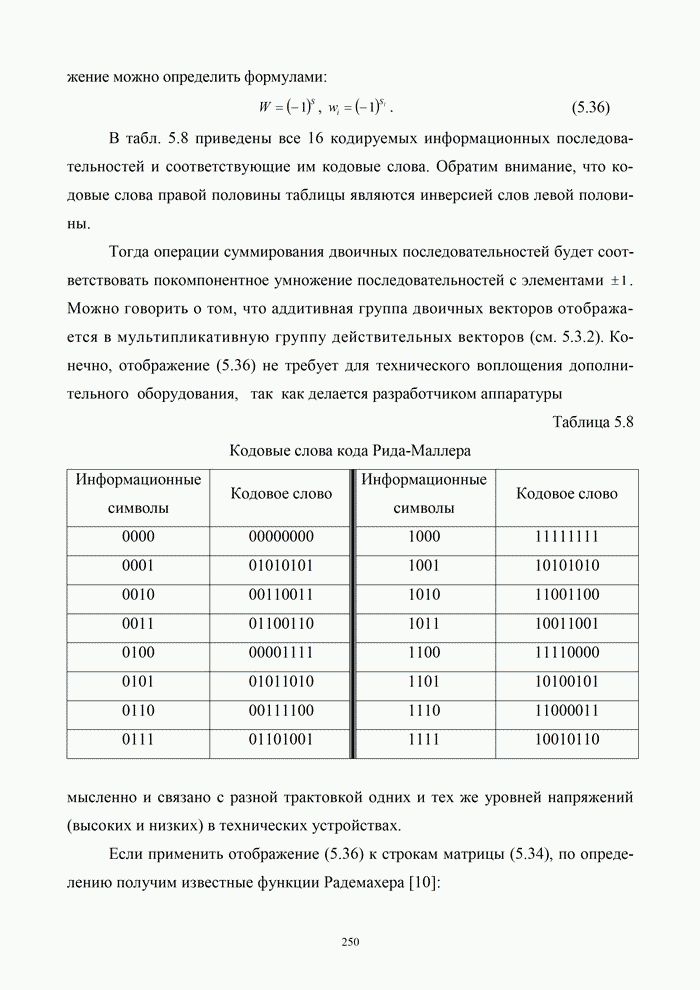
По результатам оценки каждого символа декодер выносит решение о всем принятом сигнале. Эффективность работы системы передачи информации целесообразно оценить раздельно для следующих двух вариантов организации системы передачи информации.
Случай заданного канала связи
Пусть параметры двоичного симметричного
канала связи (длительность символа ![]() и вероятность его искажения
и вероятность его искажения ![]() ) являются
неизменными, а при смене кода (изменении
) являются
неизменными, а при смене кода (изменении ![]() ) меняется скорость передачи.
Следовательно, такой источник сообщений должен быть управляемым [10] в
отношении своей производительности.
) меняется скорость передачи.
Следовательно, такой источник сообщений должен быть управляемым [10] в
отношении своей производительности.
Вероятность правильного принятия решения декодером по всей комбинации символов равна сумме вероятностей появления ошибок, исправляемых декодером, включая ошибку нулевой кратности. Для совершенных кодов
|
|
|
для любых других
|
|
(5.54) |
где ![]() – вероятность
искажения одного символа;
– вероятность
искажения одного символа; ![]() – вероятность исправления ошибок кратности
выше
– вероятность исправления ошибок кратности
выше ![]() ;
; ![]() – означает целую
часть числа;
– означает целую
часть числа; ![]() –
кодовое расстояние. Процедуры исправления ошибок кратности выше
–
кодовое расстояние. Процедуры исправления ошибок кратности выше ![]() заметно усложняют
декодер и поэтому реализуются не всегда.
заметно усложняют
декодер и поэтому реализуются не всегда.
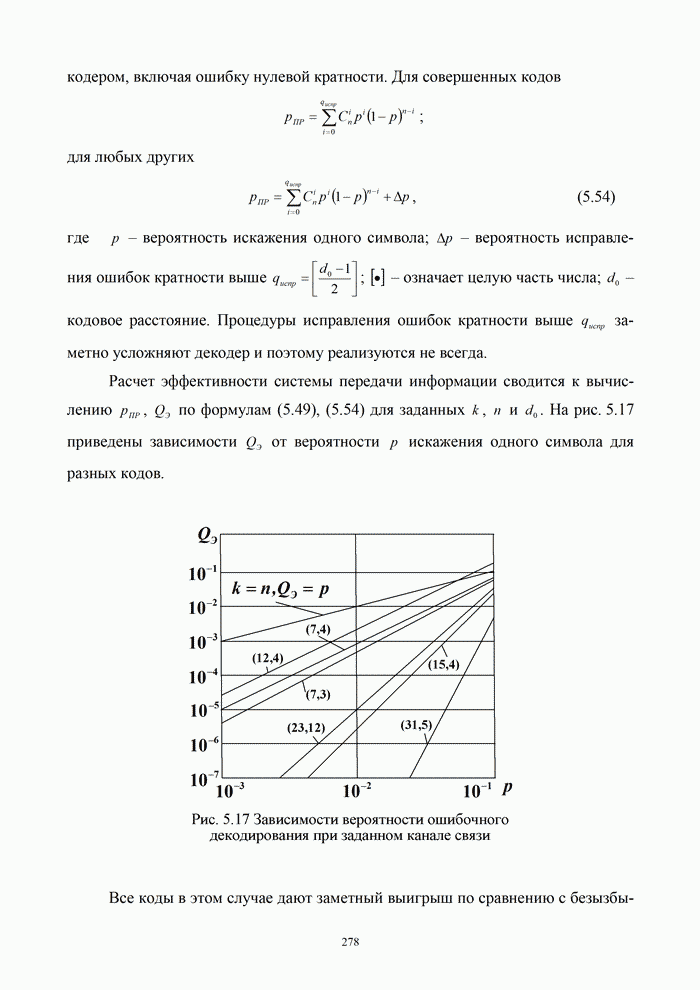
Расчет эффективности системы передачи
информации сводится к вычислению ![]() ,
, ![]() по формулам (5.49), (5.54) для
заданных
по формулам (5.49), (5.54) для
заданных ![]() ,
, ![]() и
и ![]() . На рис. 5.17 приведены
зависимости
. На рис. 5.17 приведены
зависимости ![]() от
вероятности
от
вероятности ![]() искажения
одного символа для разных кодов.
искажения
одного символа для разных кодов.

Все коды в этом случае дают заметный выигрыш по сравнению с безызбыточной передачей. Коды (7,3) и (7,4) близки по эффективности. Остальные коды располагаются в порядке возрастания кодового расстояния и числа избыточных символов.
Модель заданного канала связи хорошо соответствует случаю организации обмена информацией между блоками одного устройства, например, вычислительного комплекса. Из приведенных кривых следует, в частности, что применение кода (15.7) выгоднее трехкратного дублирования семи информационных символов. В этом случае выше и скорость передачи (15 тактов вместо 21), и помехоустойчивость.
Случай заданной производительности источника
Пусть источник сообщений характеризуется
производительностью ![]() .
.
Применяя для передачи тот или иной код ![]() , необходимо
обеспечивать скорость передачи информации по каналу связи, соответствующую
производительности
, необходимо
обеспечивать скорость передачи информации по каналу связи, соответствующую
производительности ![]() ,
где
,
где ![]() –
длительность одного символа.
–
длительность одного символа.
Разные коды имеет разное отношение ![]() . Следовательно, со
сменой кода в общем случае должна меняться длительность символа, а значит, и
полоса пропускания канала связи, и энергия на один символ
. Следовательно, со
сменой кода в общем случае должна меняться длительность символа, а значит, и
полоса пропускания канала связи, и энергия на один символ ![]() , что следует учесть в формулах
(5.51), (5.52), (5.53). Так, при ФМ вероятность ошибочного опознания символа
, что следует учесть в формулах
(5.51), (5.52), (5.53). Так, при ФМ вероятность ошибочного опознания символа
|
|
(5.55) |
Задаваясь значениями ![]() для параметров конкретного
кода
для параметров конкретного
кода ![]() ,
, ![]() и
и ![]() , по формуле (5.55) вычисляют
вероятности
, по формуле (5.55) вычисляют
вероятности ![]() (
(![]() или
или
![]() )
искажения одного символа в блоке посимвольного приема, а затем по (5.54) и (5.49)
находят
)
искажения одного символа в блоке посимвольного приема, а затем по (5.54) и (5.49)
находят ![]() и
и ![]() .
.
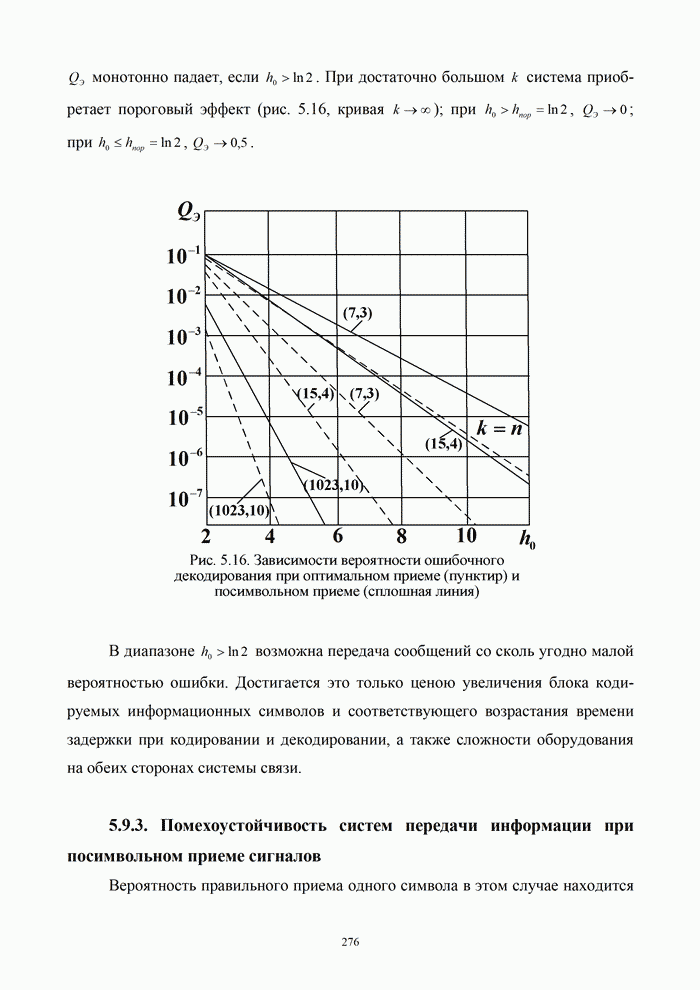
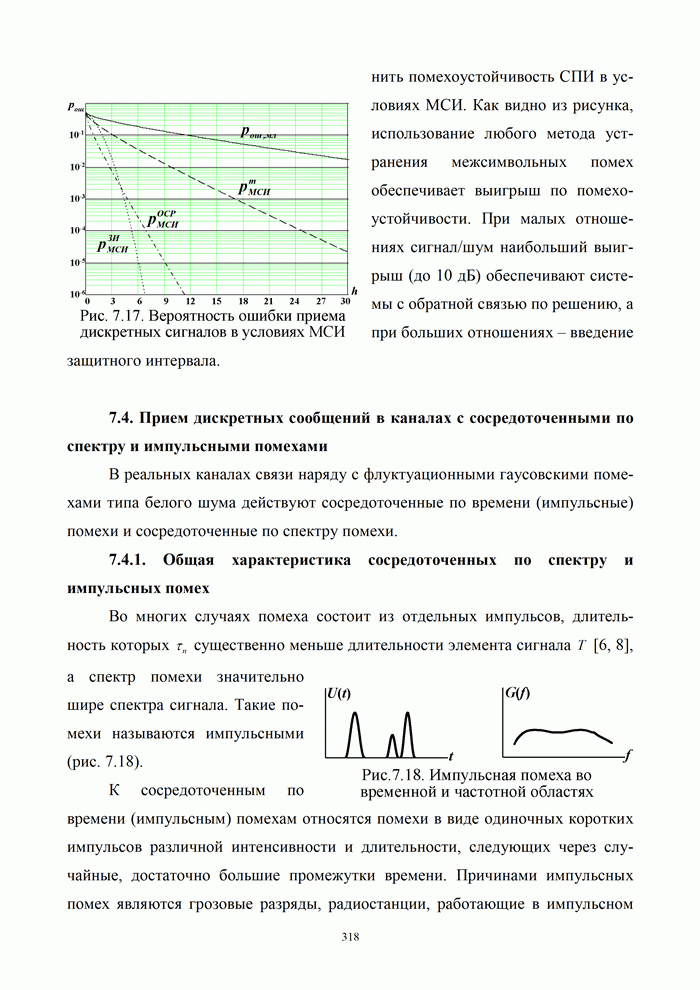
На рис. 5.16 пунктиром нанесены кривые для симплексных кодов (7,3), (15,4), (31,5), (1023,10), совершенных кодов Хэмминга (3,1) и (7,4) и Голея (23,12), БЧХ-кода (15,7) при использовании ФМн и посимвольной процедуре приема.
Сопоставление кривых посимвольного приема с
соответствующими (сплошными) кривыми оптимальной процедуры, а также
безызбыточной передачи ![]() показывает следующее.
показывает следующее.
1. Применение помехоустойчивых кодов в
системах с постоянной производительностью источника менее эффективно, чем при
заданном канале связи (рис. 5.17). Это объясняется тем обстоятельством, что в
данном случае переход к коду с большим кодовым расстоянием, а следовательно,
большим числом избыточных символов, сопровождается уменьшением энергии ![]() каждого символа.
каждого символа.
2. Посимвольный прием симплексных кодов по
сравнению с оптимальной процедурой дает проигрыш 2...4 дБ в отношении
сигнал/шум или 2...3 порядка в величине ![]() .
.
3. При малом числе информационных разрядов
ряд кодов дает большую вероятность ошибки, чем в отсутствии избыточности ![]() . Таковы коды (3,1), (7,3);
код (15,4) приносит выигрыш лишь при
. Таковы коды (3,1), (7,3);
код (15,4) приносит выигрыш лишь при ![]() .
.
4. Совершенные коды при посимвольном приеме дают лучшие результаты, чем симплексные. Так, код (7,4) лучше кодов (7,3) и (15,4).
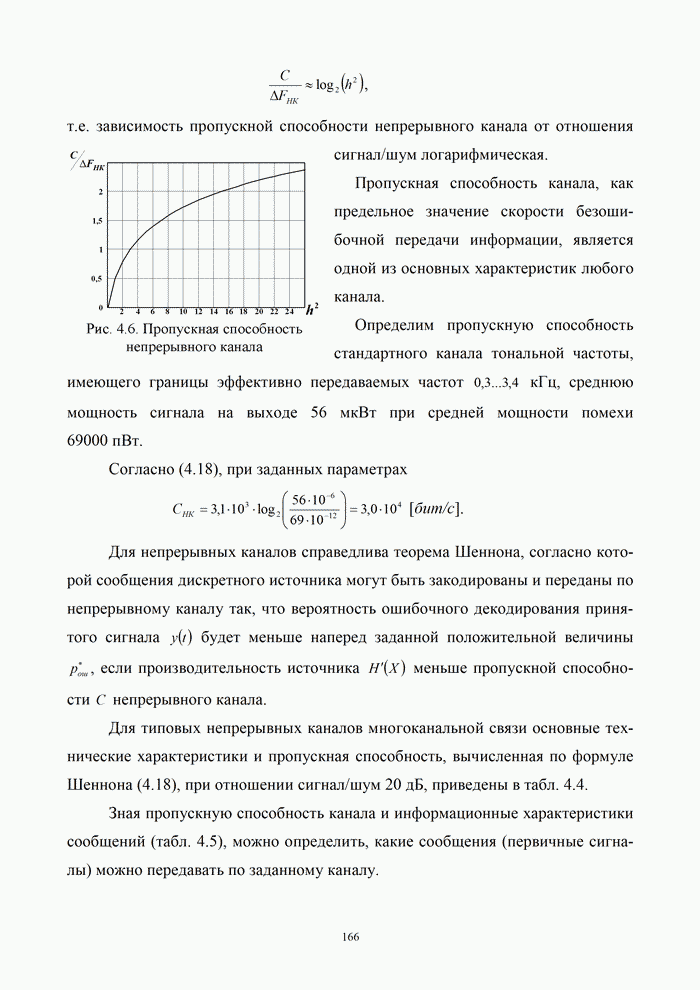
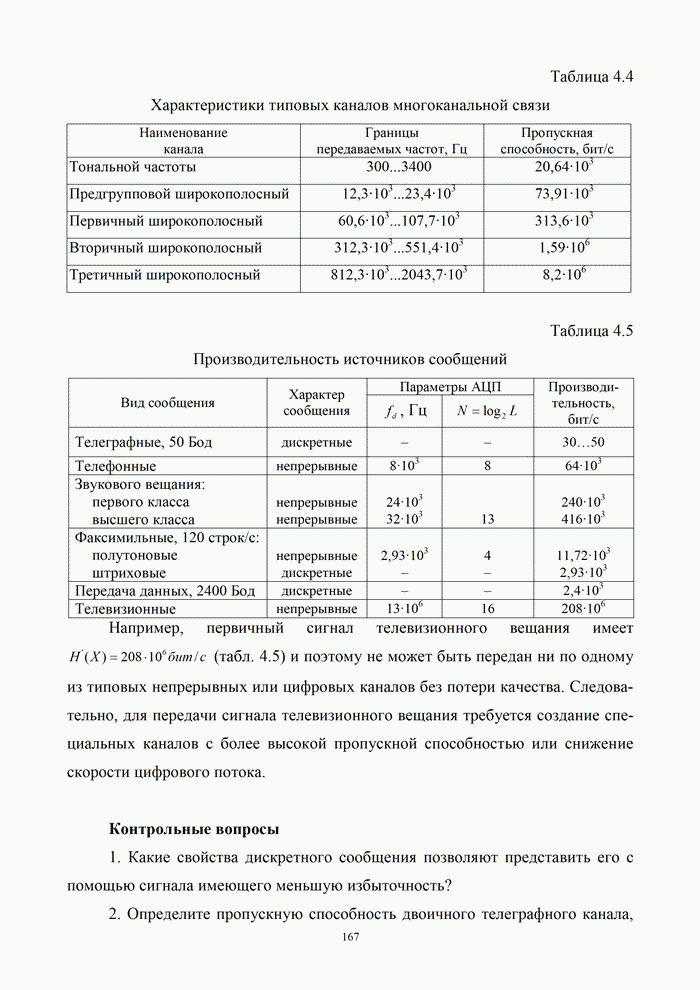
Следует отметить, что при безызбыточном
кодировании кодовое расстояние ![]() , а следовательно, посимвольный прием
принципиально равноценен оптимальной процедуре.
, а следовательно, посимвольный прием
принципиально равноценен оптимальной процедуре.
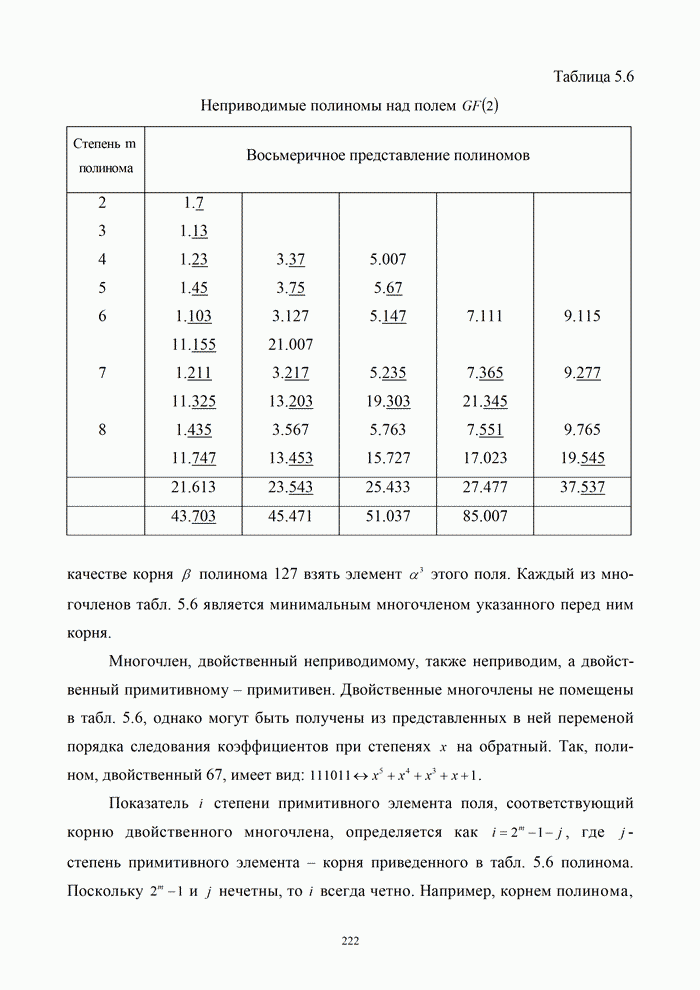
Более подробно с вопросами помехоустойчивости систем передачи информации, использующих кодирование, можно познакомиться по работам [25].
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Список сокращений
- Основные обозначения
- ВВЕДЕНИЕ
- Глава 1. Сообщения, сигналы и помехи, их математические модели
- 1.1. Основные понятия и определения
- 1.1.1. Сообщение, сигнал, модуляция
- 1.1.2. Основные параметры сигналов
- 1.2. Системы связи. Каналы связи
- 1.2.1. Структура канала электросвязи
- 1.2.2. Линия и сеть связи
- 1.2.3. Помехи и искажения в канале
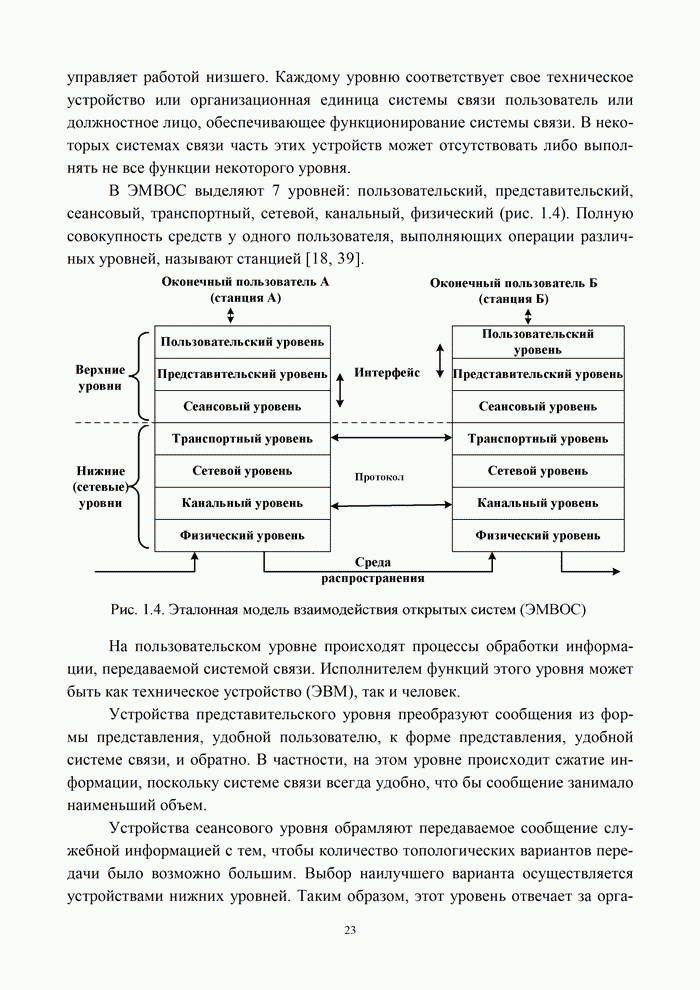
- 1.2.4. Эталонная модель взаимодействия открытых систем
- 1.2.5. Модели каналов связи и их математическое описание
- 1.3. Способы описания сигналов и помех
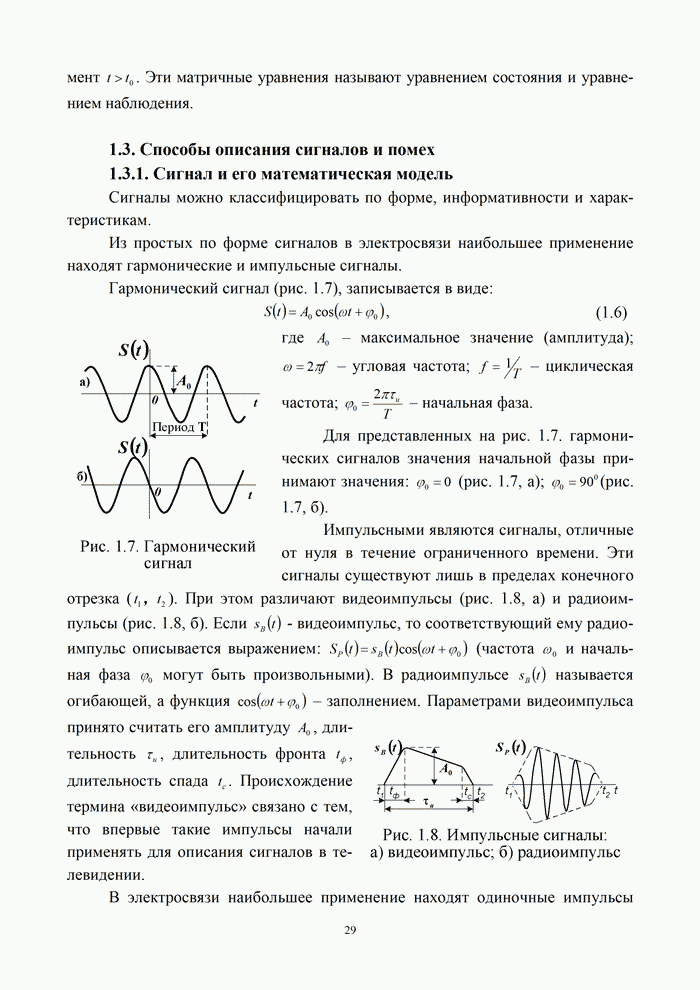
- 1.3.1. Сигнал и его математическая модель
- 1.3.2. Энергетические характеристики детерминированного сигнала
- 1.4.2. Представление сигналов и помех рядом Фурье
- 1.4.3. Применение преобразования Фурье для непериодических сигналов
- 1.5. Теорема Котельникова
- 1.6. Пространство сигналов
- 1.6.1. Линейное пространство
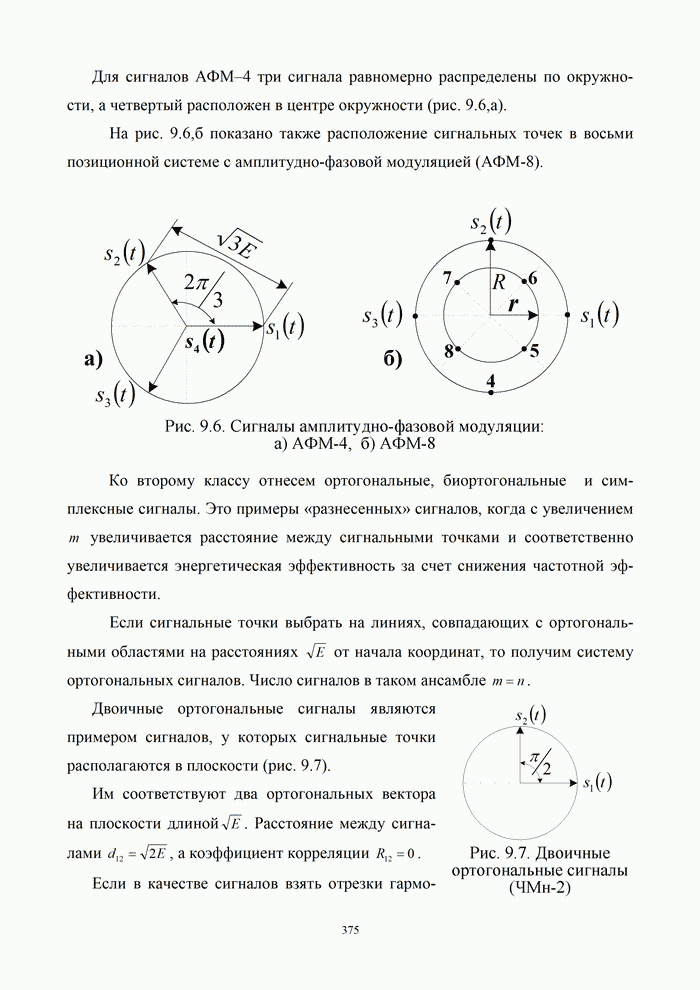
- 1.6.2. Представление сигнала в многомерном пространстве
- 1.7. Сигналы как случайные процессы
- 1.7.1. Характеристики случайного процесса
- 1.7.2. Флуктуационный шум
- 1.8. Комплексное представление сигналов и помех
- 1.8.1. Понятие аналитического сигнала
- 1.8.2. Огибающая, мгновенная фаза и мгновенная частота узкополосного случайного процесса
- Контрольные вопросы
- Глава 2. Методы формирования и преобразования сигналов
- 2.1. Модуляция сигналов
- 2.1.1. Амплитудная модуляция гармонической несущей
- 2.1.2. Балансная и однополосная модуляция гармонической несущей
- 2.2. Методы угловой модуляции
- 2.2.1. Принципы частотной и фазовой (угловой) модуляции
- 2.2.2. Спектр сигналов угловой модуляции
- 2.3. Формирование и детектирование модулированных сигналов
- 2.3.1. Формирование и детектирование сигналов амплитудной и однополосной амплитудной модуляции
- 2.3.2. Формирование и детектирование сигналов угловой модуляции
- 2.4. Манипуляция сигналов
- 2.4.1. Временные и спектральные характеристики амплитудно-манипулированных сигналов
- 2.4.2. Временные и спектральные характеристики частотно-манипулированных сигналов
- 2.4.3. Фазовая (относительно-фазовая) манипуляция сигналов
- 2.5. Системы связи с многопозиционной относительной фазовой манипуляцией
- 2.5.1. Принцип формирования сигнала с многократной относительной фазовой манипуляцией
- 2.5.2. Квадратурная относительно-фазовая манипуляция (КОФМ)
- 2.5.3. Принцип частотной модуляции с непрерывной фазой
- Контрольные вопросы
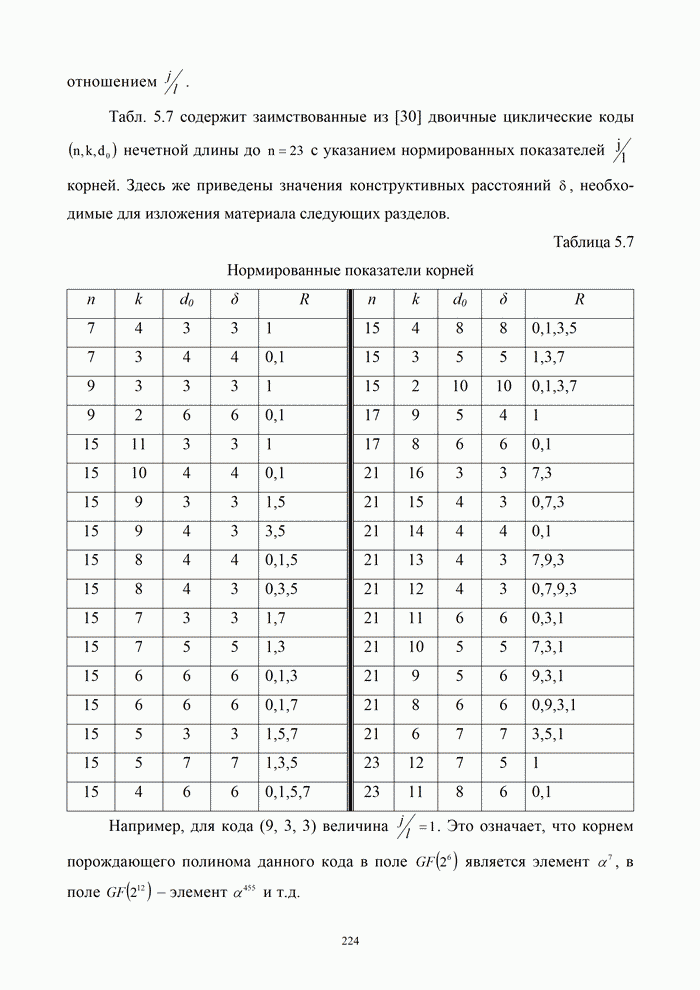
- Глава 3. Помехоустойчивость приема дискретных сообщений
- 3.1. Критерии качества и правила приема дискретных сообщений
- 3.1.1. Понятие о помехоустойчивости систем электрической связи
- 3.1.2. Задача оптимального приема
- 3.1.3. Вычисление вероятностей ошибок
- 3.2. Оптимальная демодуляция при когерентном приеме сигналов
- 3.2.1. Оптимальные алгоритмы приема при полностью известных сигналах
- 3.2.2. Реализация алгоритмов оптимального когерентного приема
- 3.3. Помехоустойчивость приема сигналов с известными параметрами
- 3.4. Прием сигналов с неопределенной фазой
- 3.4.1. Оптимальный некогерентный прием дискретных сигналов
- 3.4.2. Помехоустойчивость оптимального некогерентного приема
- 3.5. Подоптимальные методы приема
- 3.5.1. Причины применения неоптимальных методов приема
- 3.5.2. Квазиоптимальные методы приема
- Контрольные вопросы
- Глава 4. Теория передачи информации
- 4.1. Информационные характеристики источника сообщений
- 4.1.1. Количественное определение информации
- 4.1.2. Энтропия и производительность дискретного источника сообщений
- 4.2. Пропускная способность дискретного канала
- 4.2.1. Количество информации переданной по дискретному каналу
- 4.2.2. Пропускная способность дискретного канала
- 4.2.3. Пропускная способность симметричного дискретного канала без памяти
- 4.3. Методы сжатия дискретных сообщений
- 4.3.1. Условия существования оптимального неравномерного кода
- 4.3.2. Прямая и обратная теоремы кодирования источника неравномерными кодами
- 4.3.3. Показатели эффективности сжатия
- 4.3.4. Кодирование источника дискретных сообщений методом Шеннона-Фано
- 4.3.5. Кодирование источника дискретных сообщений методом Хаффмена
- 4.4. Пропускная способность непрерывного канала
- 4.4.1. Постановка задачи передачи дискретных сообщений в непрерывном канале
- 4.4.2. Количество информации, переданной по непрерывному каналу
- 4.4.3. Пропускная способность непрерывного канала
- Контрольные вопросы
- Глава 5. Теория кодирования сообщений
- 5.1. Помехоустойчивое кодирование: блочные и непрерывные коды
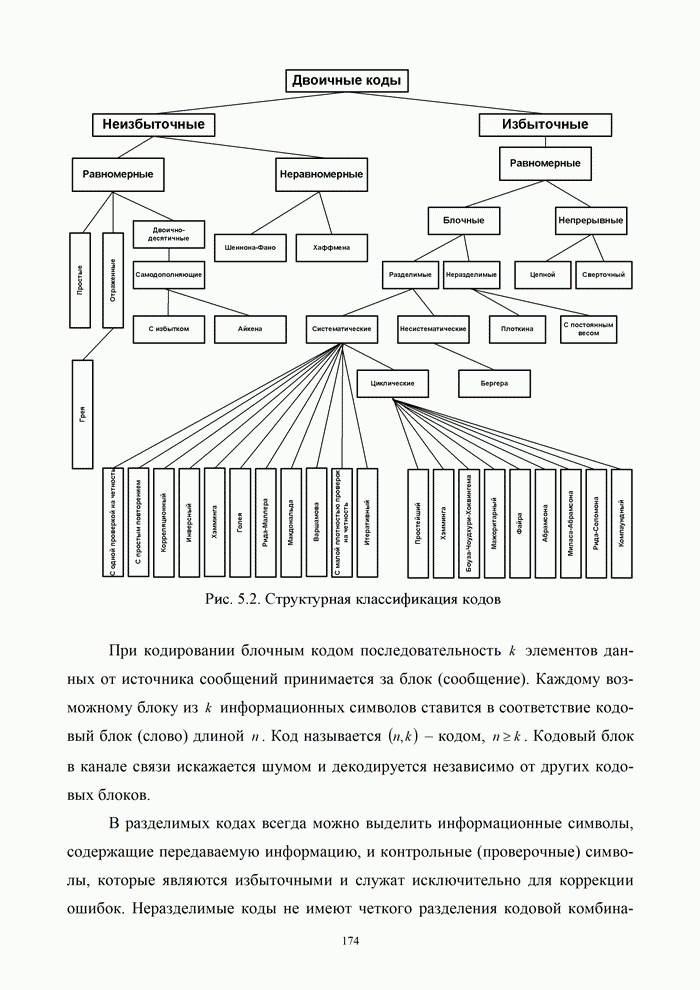
- 5.1.1. Постановка задачи помехоустойчивого кодирования
- 5.1.2. Классификация кодов
- 5.1.3. Основные характеристики и свойства блочных кодов
- 5.2. Эффективность помехоустойчивого кодирования
- 5.2.1. Эффективность кода в режиме исправления ошибок
- 5.2.2. Эффективность кода в режиме обнаружения ошибок
- 5.2.3. Эффективность помехоустойчивых кодов
- 5.3. Математические основы теории помехоустойчивого кодирования
- 5.3.1. Краткие сведения из теории чисел
- 5.3.2. Группы
- 5.3.3. Кольца и поля
- 5.3.4. Векторное пространство
- 5.3.5. Конечные поля
- 5.4. Линейные блочные коды
- 5.4.1. Система передачи дискретных сообщений
- 5.4.2. Параметры линейного кода
- 5.4.3. Полиномиальные циклические коды
- 5.4.4. Циклические коды и корни полиномов
- 5.4.5. Спектральное описание циклических кодов
- 5.4.6. Простейшие блочные линейные коды
- 5.5. Коды Боуза-Чоудхури-Хоквингема
- 5.5.1. Методы задания кодов БЧХ
- 5.5.2. Принципы декодирования кодов БЧХ
- 5.5.3. Методы реализации этапов декодирования кодов БЧХ
- 5.6. Коды Рида-Соломона
- 5.6.1. Основные определения
- 5.6.2. Обнаружение и исправление пакетов ошибок
- 5.7. Коды Рида-Маллера
- 5.7.1. Задание и декодирование кодов Рида-Маллера
- 5.7.2. Симплексные коды и m-последовательности
- 5.7.3. Связь между блочными кодами
- 5.8. Сверточные коды
- 5.8.1. Основные параметры
- 5.8.2. Способы задания сверточного кода
- 5.8.3. Алгоритм декодирования Витерби
- 5.9. Помехоустойчивость систем передачи дискретных сообщений
- 5.9.1. Две процедуры приема сигналов
- 5.9.2. Помехоустойчивость систем передачи информации при оптимальной процедуре приема
- 5.9.3. Помехоустойчивость систем передачи информации при посимвольном приеме сигналов
- Контрольные вопросы
- Глава 6. Сигналы с импульсной модуляцией
- 6.1. Методы импульсной модуляции
- 6.1.1. Импульсные методы передачи непрерывных сигналов
- 6.1.2. Спектральные характеристики импульсных методов модуляции
- 6.2. Помехоустойчивость непрерывных каналов связи с импульсной модуляцией
- 6.2.1. Помехоустойчивость систем передачи с импульсными методами модуляции
- 6.3. Цифровые методы передачи непрерывных сообщений
- 6.3.1. Передача сигналов с импульсно-кодовой модуляцией
- 6.3.2. Передача сигналов с дельта модуляцией
- 6.3.3. Квантование сигналов в системах с ИКМ и ДМ
- Контрольные вопросы
- Глава 7. Методы приема сигналов в сложных условиях
- 7.1. Прием сигналов в каналах с замираниями
- 7.1.1. Сущность замираний и их классификация
- 7.1.2. Принципы разнесенного приема сигналов
- 7.2. Методы борьбы с замираниями сигналов
- 7.2.1. Методы борьбы с замираниями в аналоговых системах связи
- 7.2.2. Методы борьбы с замираниями в цифровых системах связи
- 7.3. Методы борьбы с межсимвольной интерференцией
- 7.3.1. Причины возникновения и сущность межсимвольной интерференции
- 7.3.2. Обработка сигналов в каналах с межсимвольной интерференцией
- 7.3.3. Помехоустойчивость в каналах с межсимвольной интерференцией
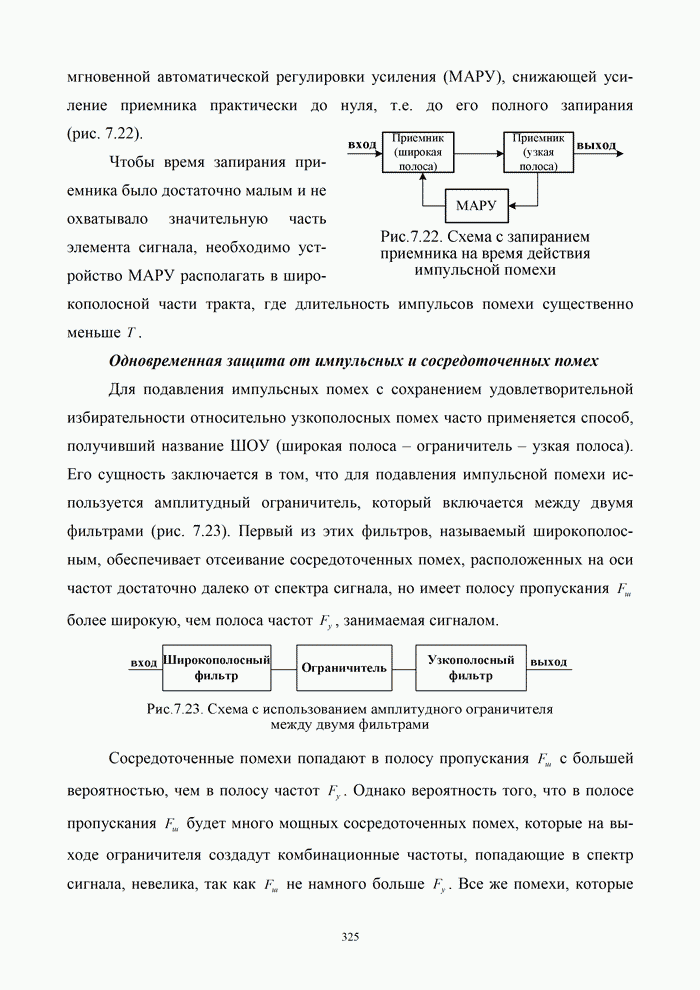
- 7.4. Прием дискретных сообщений в каналах с сосредоточенными по спектру и импульсными помехами
- 7.4.1. Общая характеристика сосредоточенных по спектру и импульсных помех
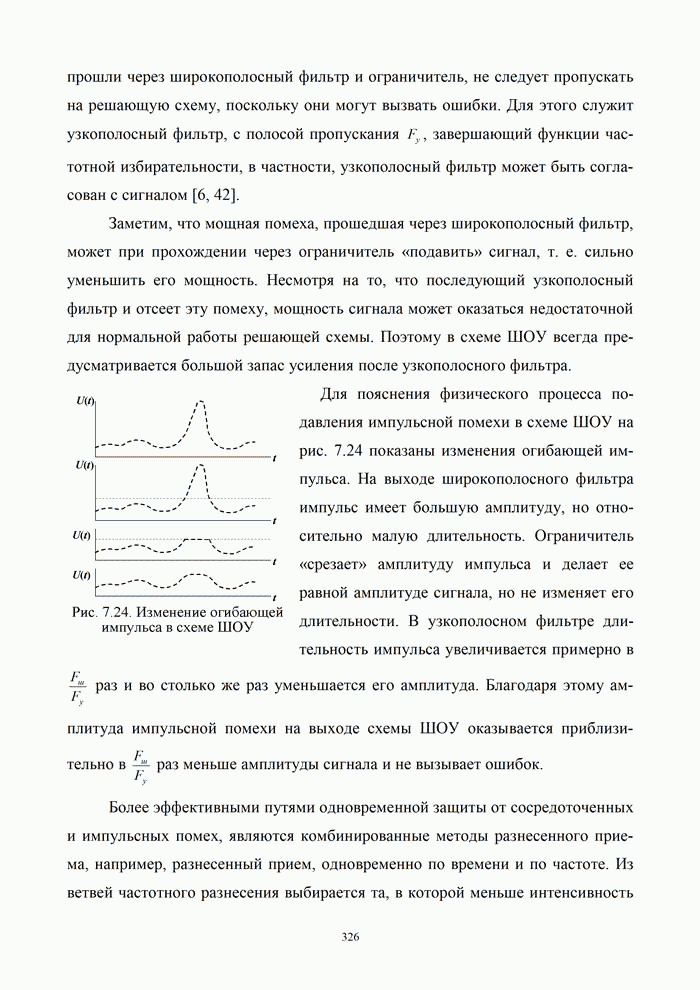
- 7.4.2. Борьба с сосредоточенными и импульсными помехами
- 7.5. Компенсация помех и искажений в канале
- 7.5.1. Принцип работы радиолинии с ФМ ПСС (ФМ ШПС)
- 7.5.2. Помехоустойчивость радиолинии с ФМ ПСС
- 7.5.3. Принципы работы радиолиний с ППРЧ
- 7.5.4. Помехоустойчивость радиолиний с ППРЧ
- Контрольные вопросы
- Глава 8. Многоканальная связь и распределение информации
- 8.1. Методы распределения ресурса общего канала
- 8.1.1. Классификация систем передачи информации, использующих единый ресурс
- 8.1.2. Постановка задачи объединения и разделения сигналов
- 8.1.3. Энергетическая и спектральная цена уплотнения
- 8.2. Частотное разделение каналов
- 8.2.1. Принцип частотного объединения и разделения каналов
- 8.2.2. Групповой сигнал, его структура и характеристики
- 8.3. Временное разделение каналов
- 8.3.1. Принцип временного разделения каналов
- 8.3.2. Характеристики группового сигнала систем с ВРК
- 8.4. Разделение сигналов по форме
- Контрольные вопросы
- Глава 9. Эффективность систем связи
- 9.1. Оценка эффективности систем связи
- 9.1.1. Подходы к оценке эффективности
- 9.1.2. Критерии эффективности
- 9.1.3. Эффективность аналоговых и цифровых систем
- 9.2. Выбор сигналов и помехоустойчивых кодов
- 9.2.1. Многопозиционные сигналы
- 9.2.2. Корректирующие коды
- 9.3. Оптимизация систем связи
- 9.3.1. Согласование методов модуляции и кодирования
- 9.3.2. Классификация сигнально – кодовых конструкций
- 9.4. Характеристики основных типов СКК
- 9.4.1. Согласование канала кодом Грея
- 9.4.2. Согласование на основе разбиения ансамбля на вложенные подансамбли
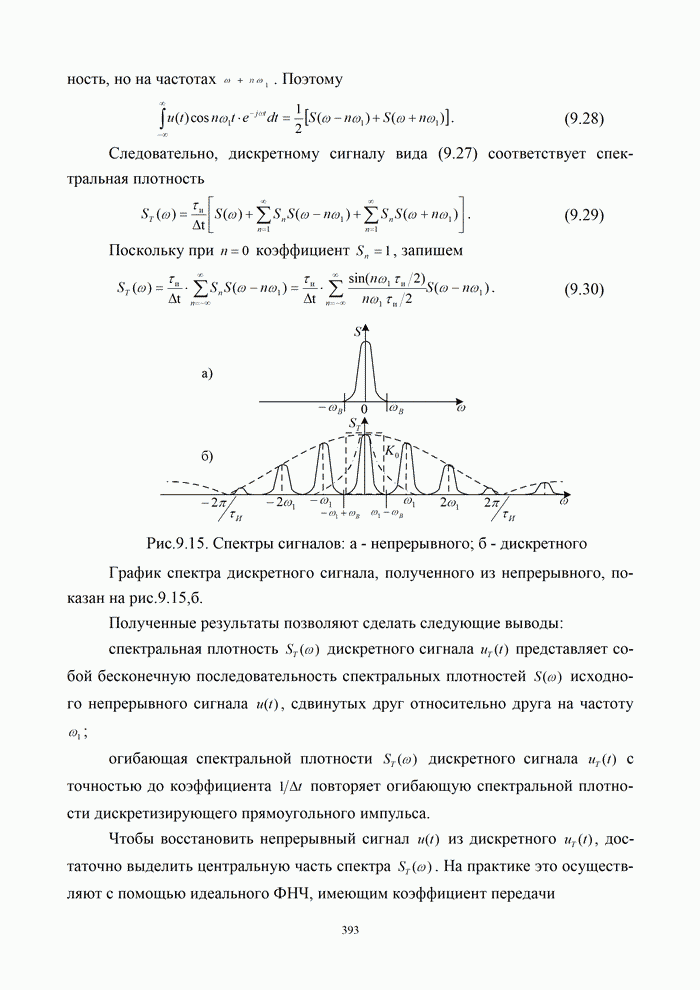
- 9.5. Алгоритмы цифровой обработки сигналов
- 9.5.1. Дискретные сигналы и их спектры
- 9.5.2. Алгоритмы дискретного и быстрого преобразований Фурье
- Контрольные вопросы
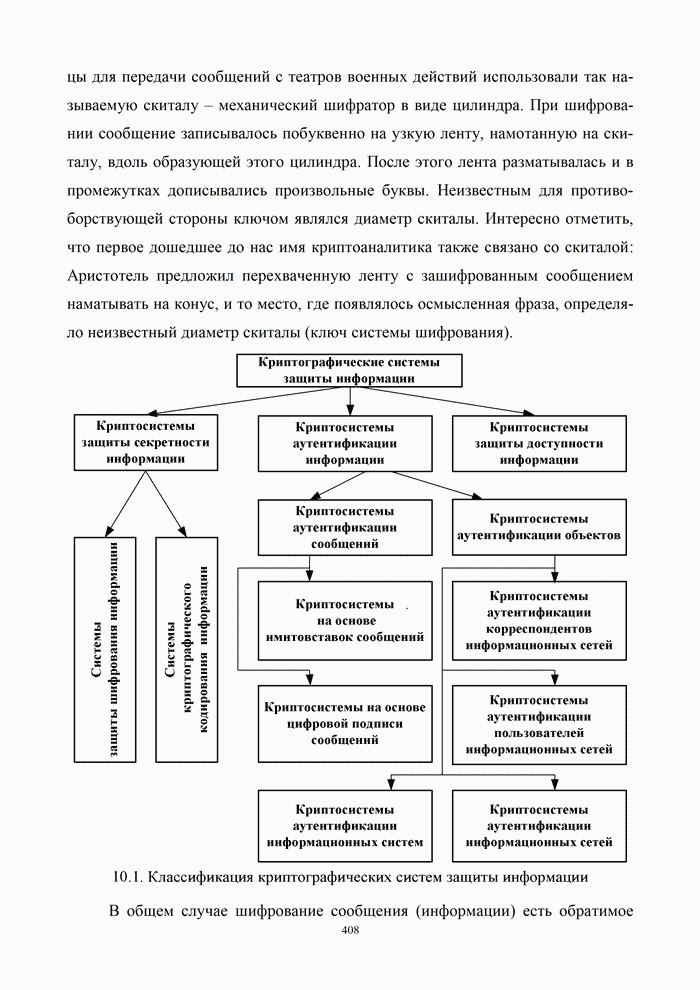
- Глава 10. Теоретико-информационные основы криптозащиты сообщений в телекоммуникационных системах
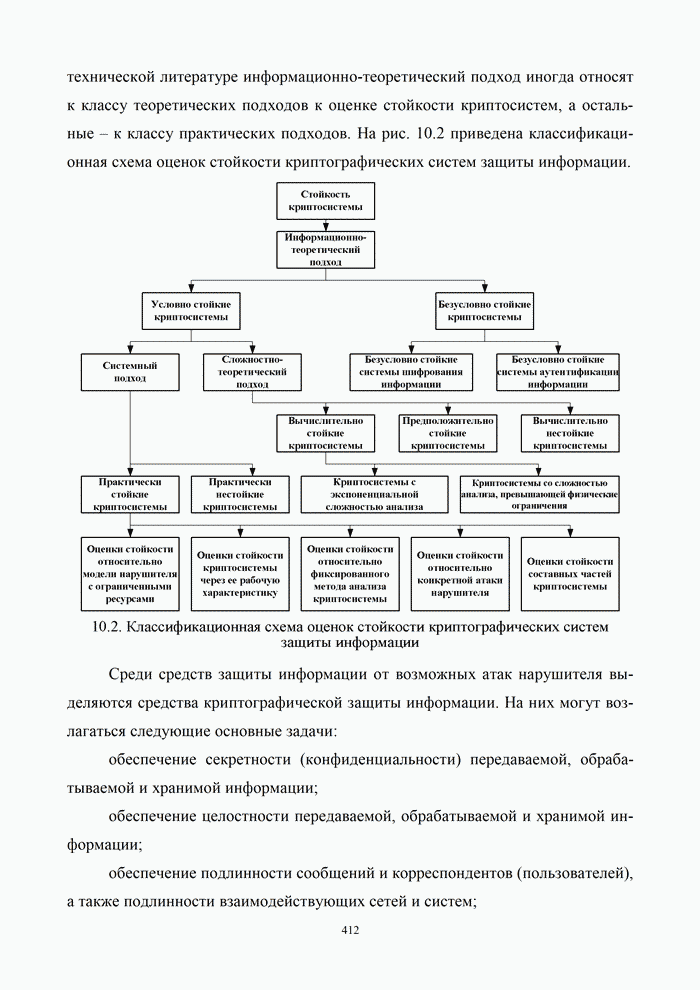
- 10.1. Классификация криптографических систем
- 10.1.2. Классификация криптографических систем защиты информации
- 10.1.3. Оценка стойкости криптосистем
- 10.2. Функции, используемые в криптографических системах
- 10.2.1. Общее описание функций, используемых в криптографических системах
- 10.2.2. Однонаправленные функции
- 10.2.3. Криптографические хэш-функции
- 10.3. Модели криптографических систем
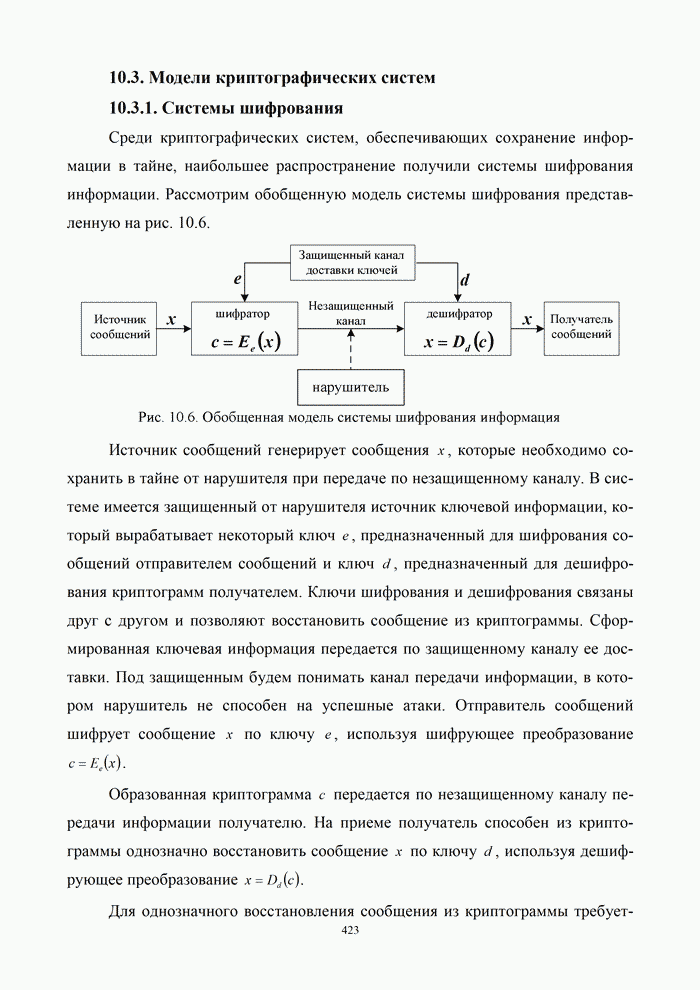
- 10.3.1. Системы шифрования
- 10.3.2. Традиционные симметричные криптосистемы
- 10.4. Алгоритмы криптографической защиты
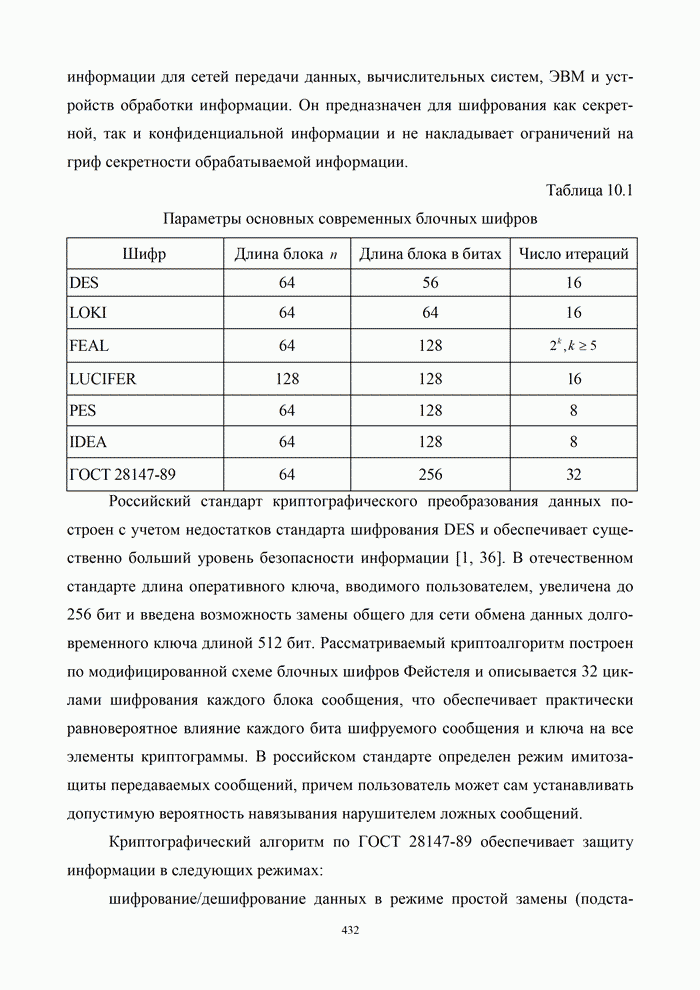
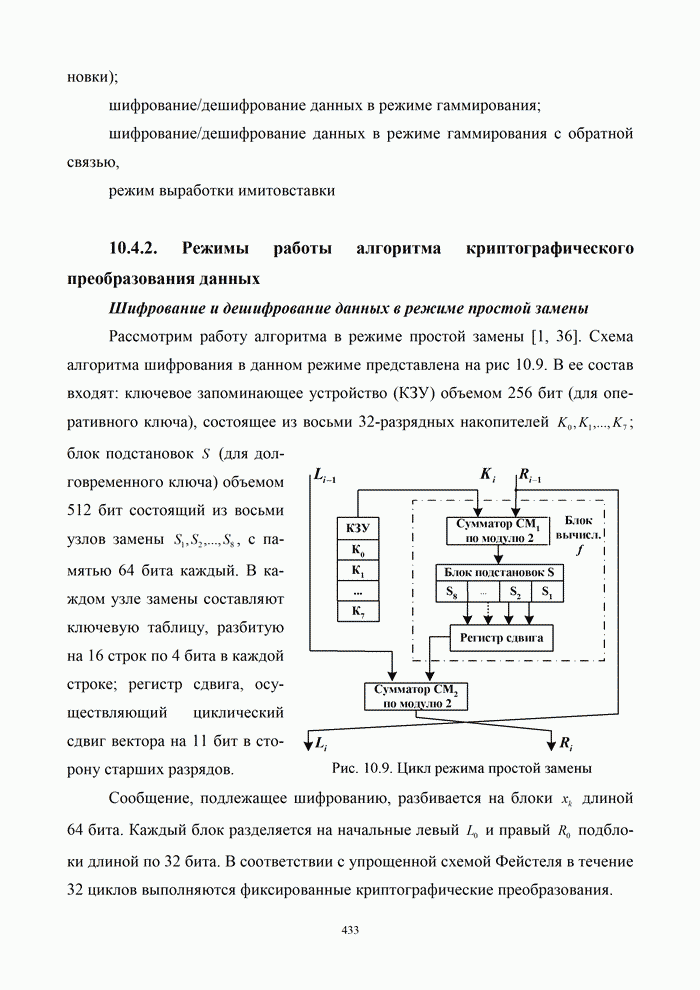
- 10.4.1. Алгоритм криптографической защиты информации согласно ГОСТ 28147-89
- Контрольные вопросы
- Заключение
- Список литературы

















































































































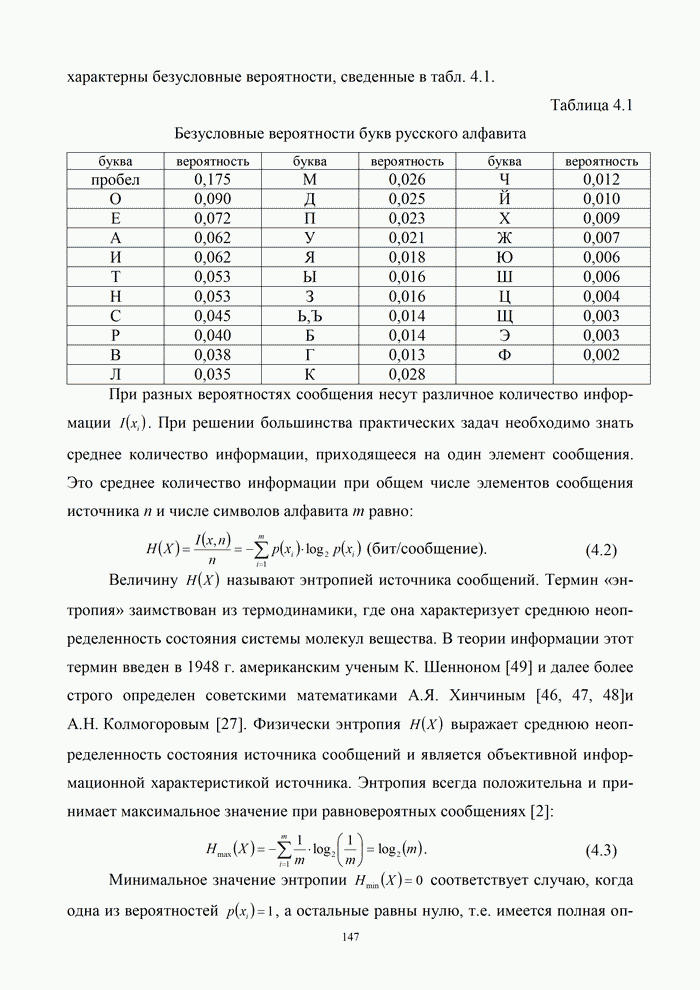


































































































































































































































































 ,
,
 ;
;  .
.
 ;
;  .
.
 ;
;  .
.
 .
.
