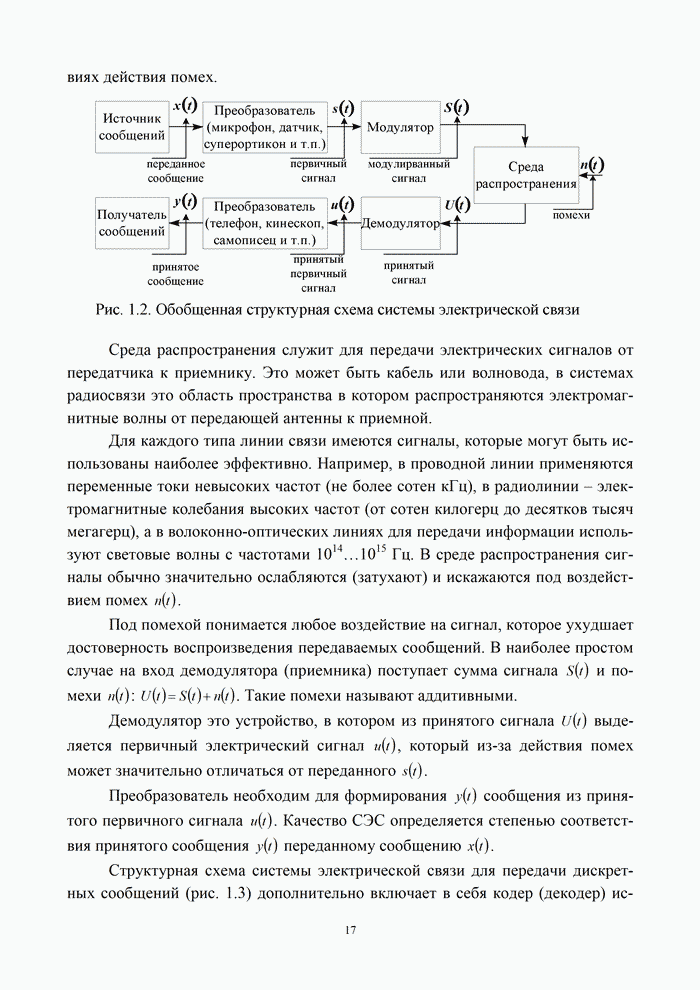
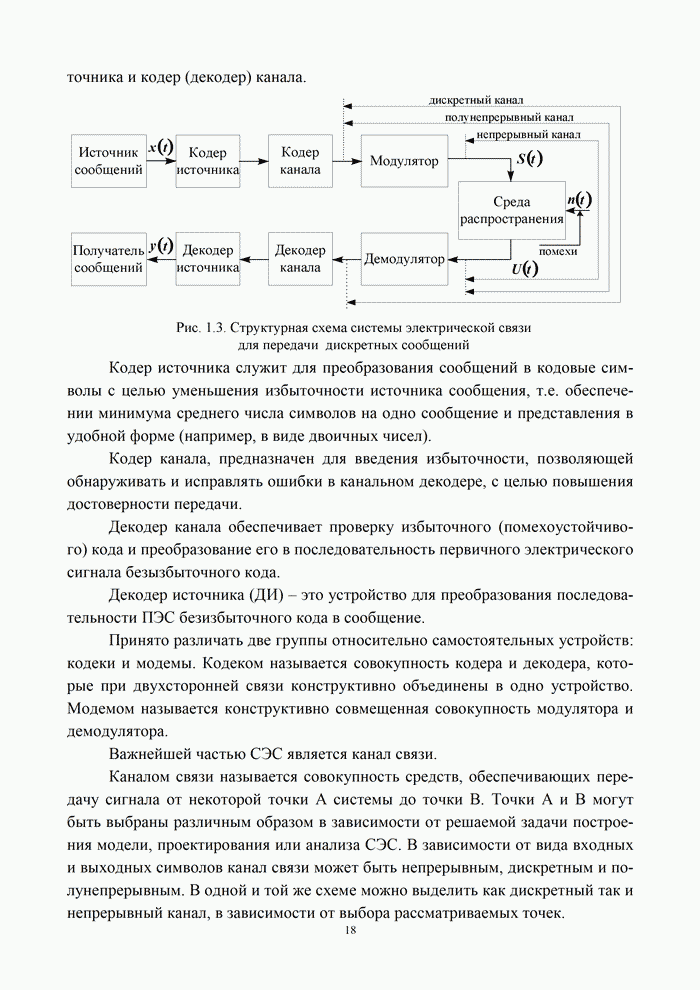
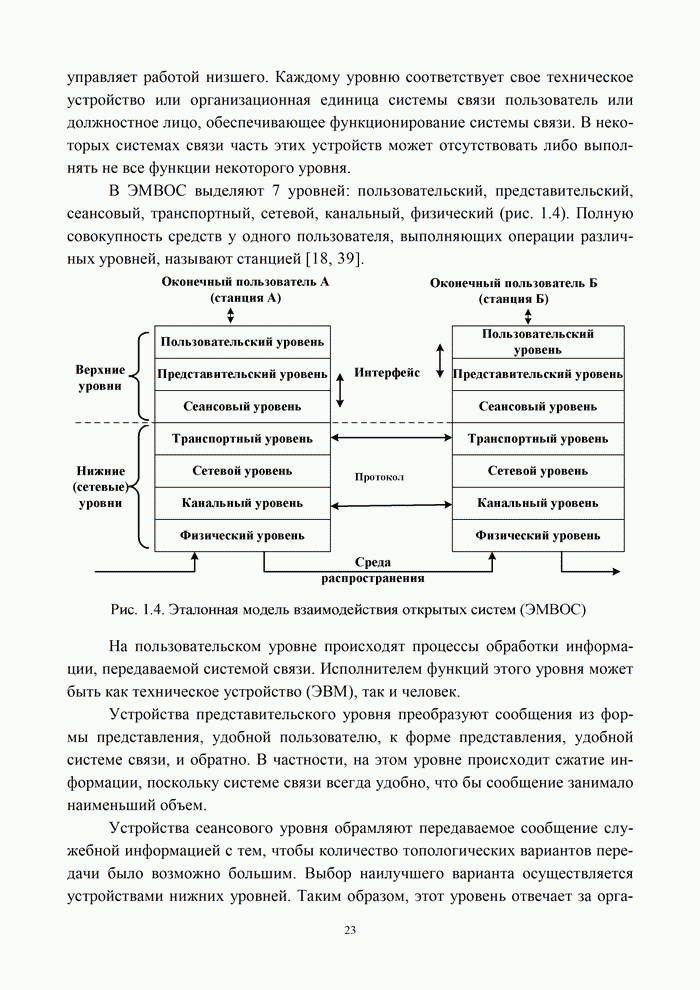
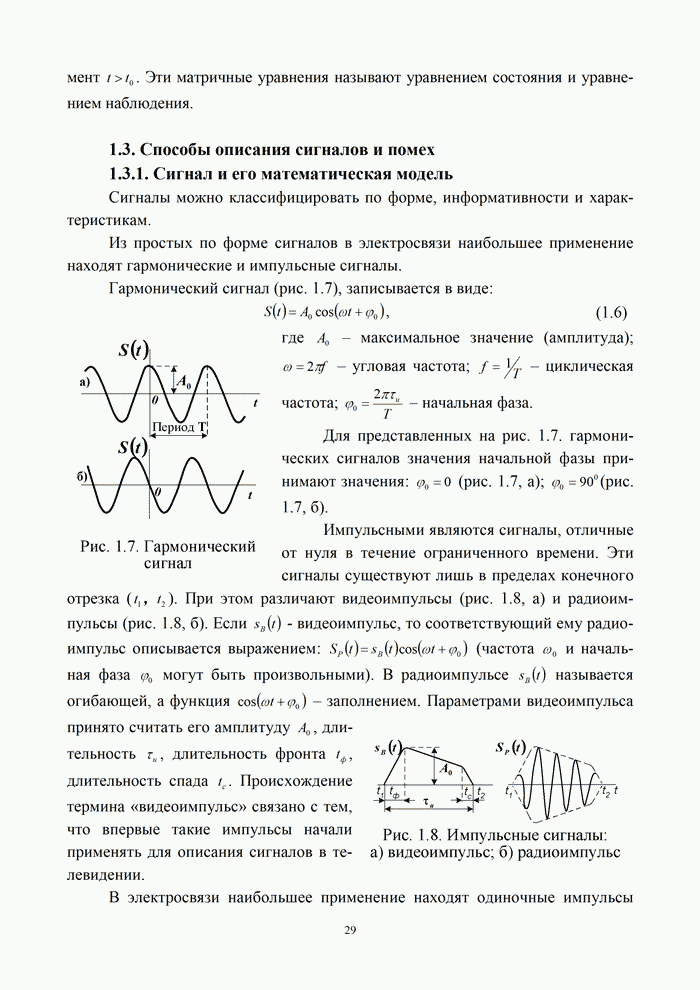
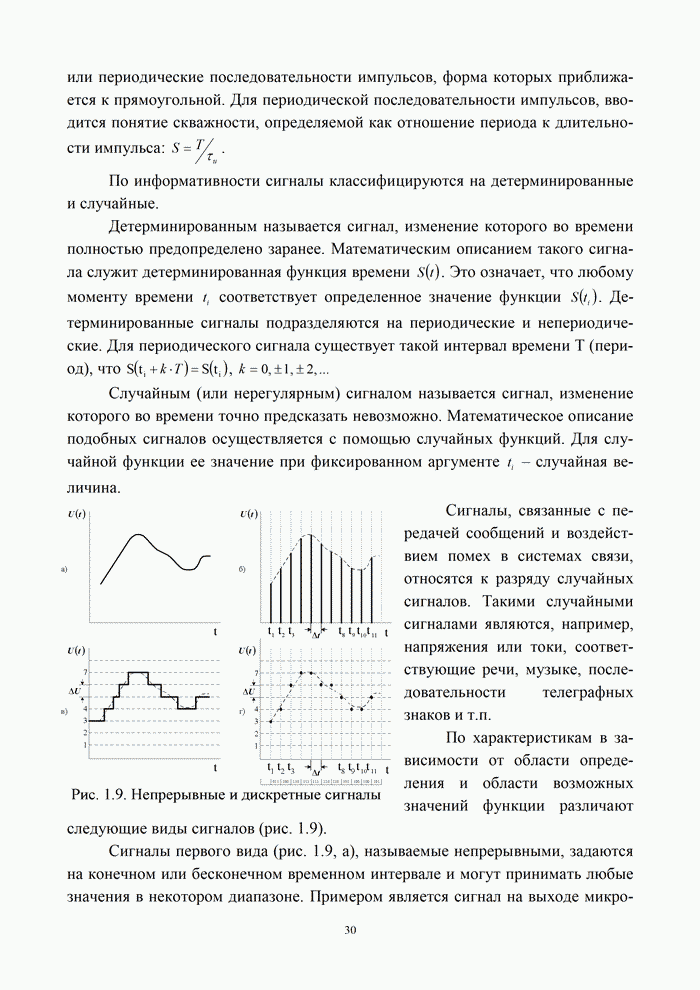
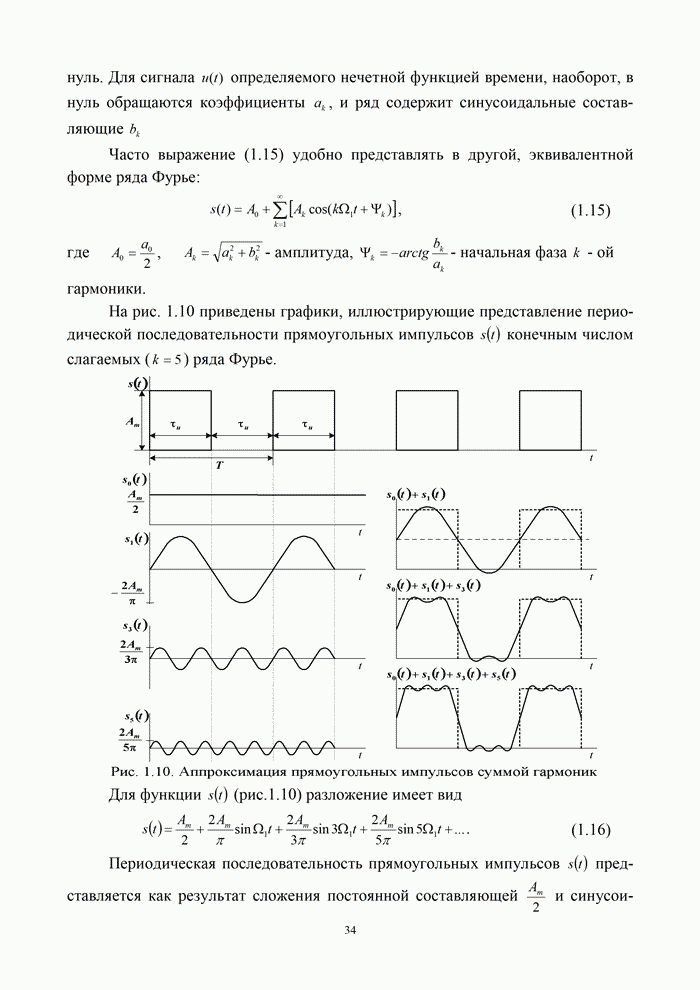
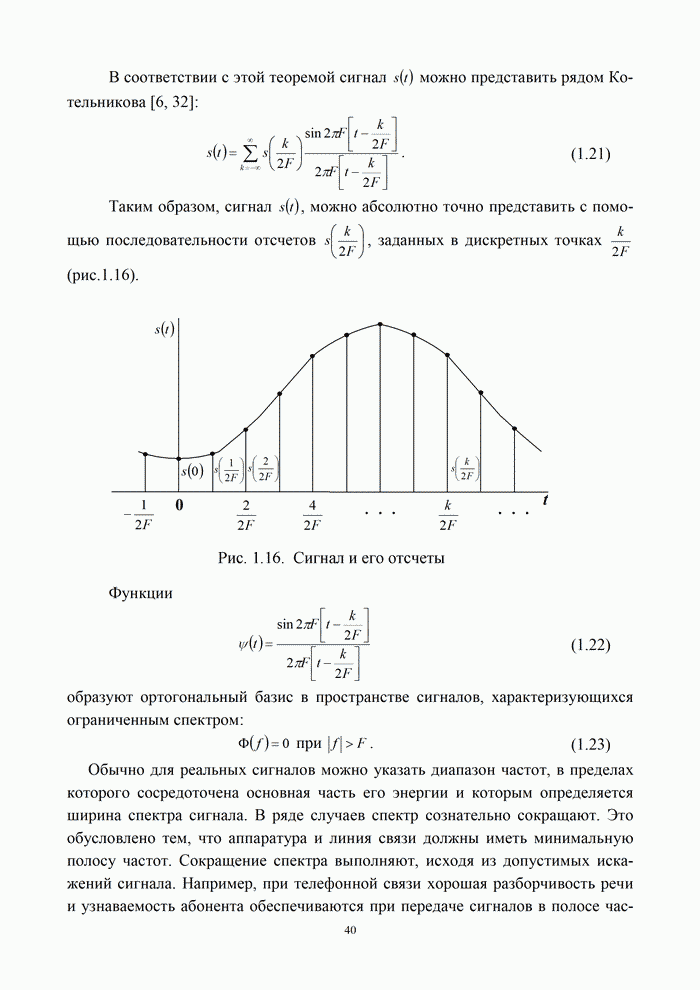
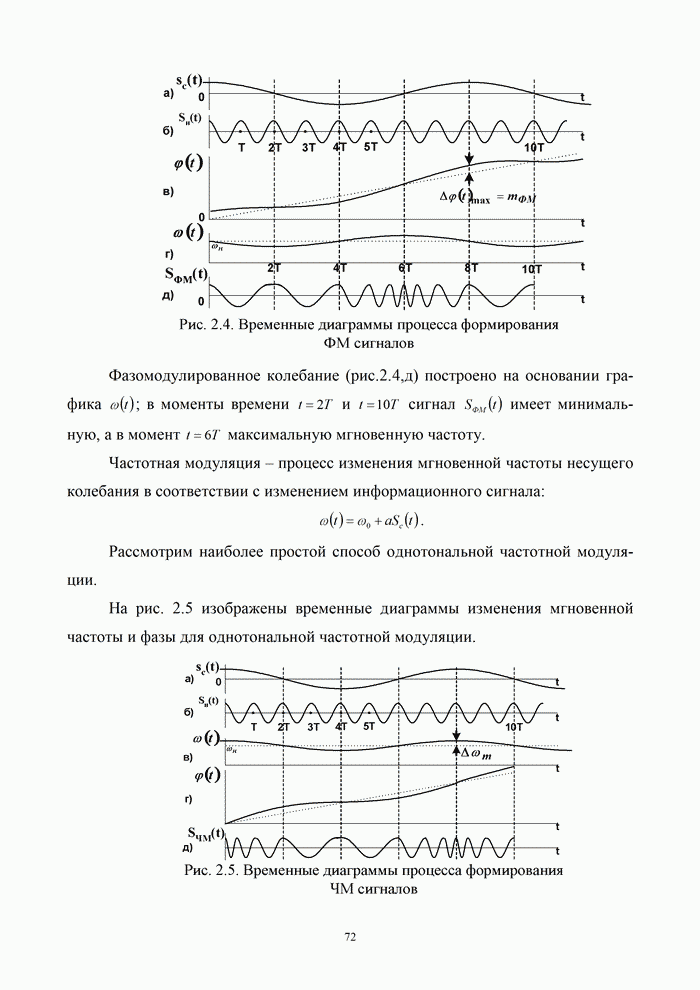
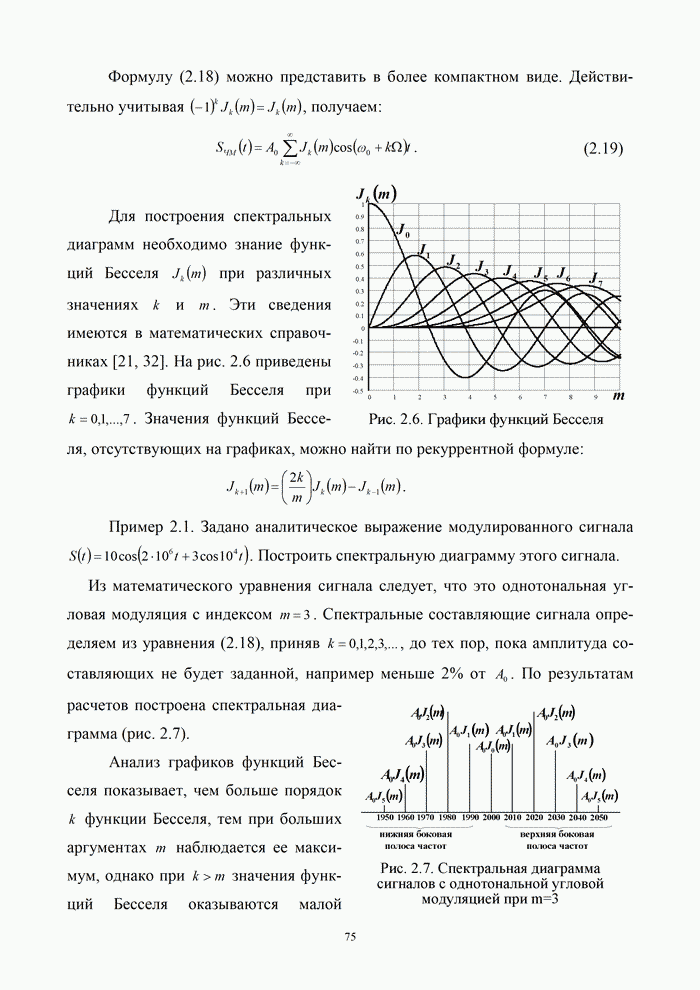
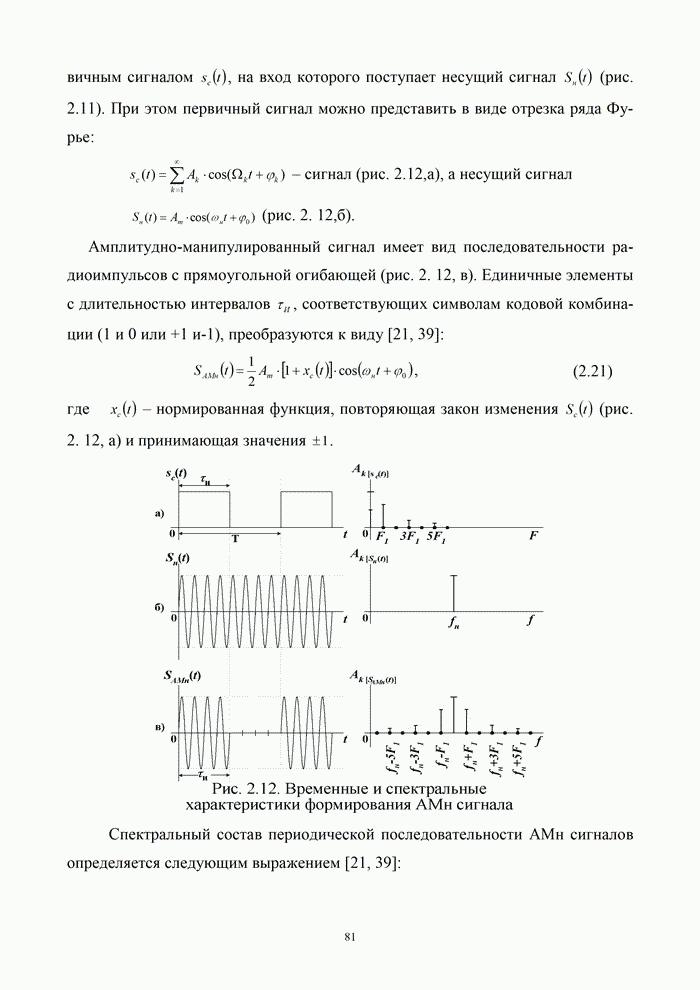
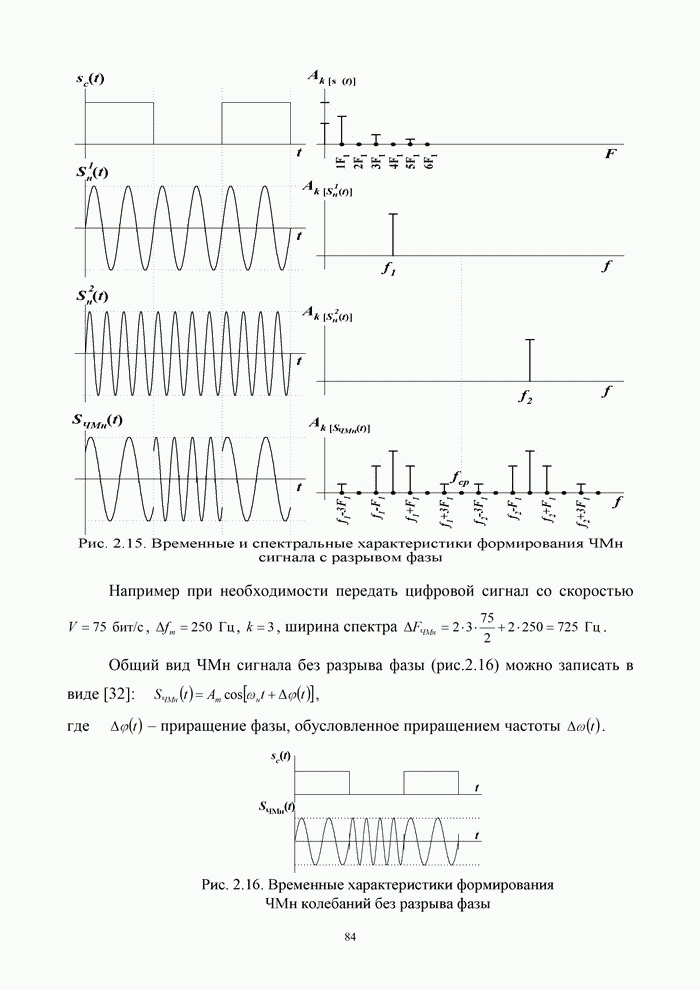
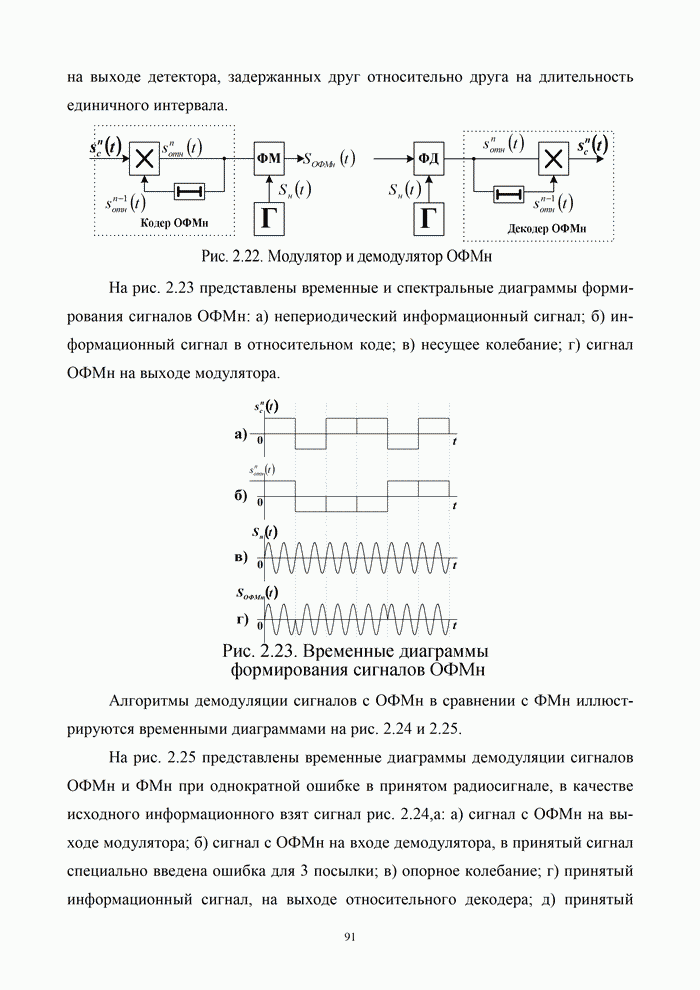
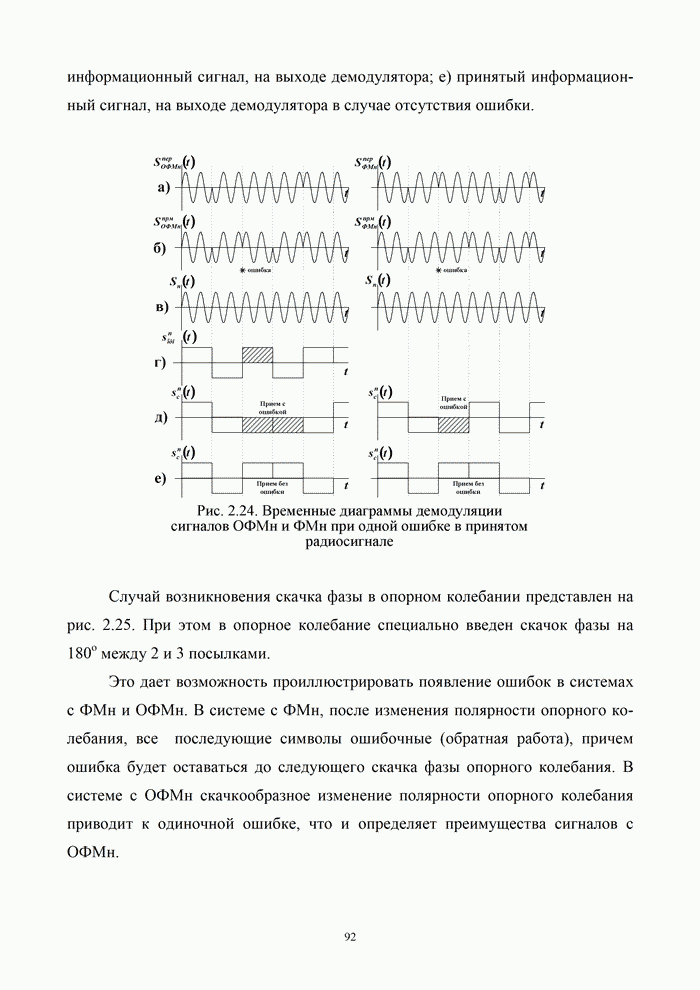
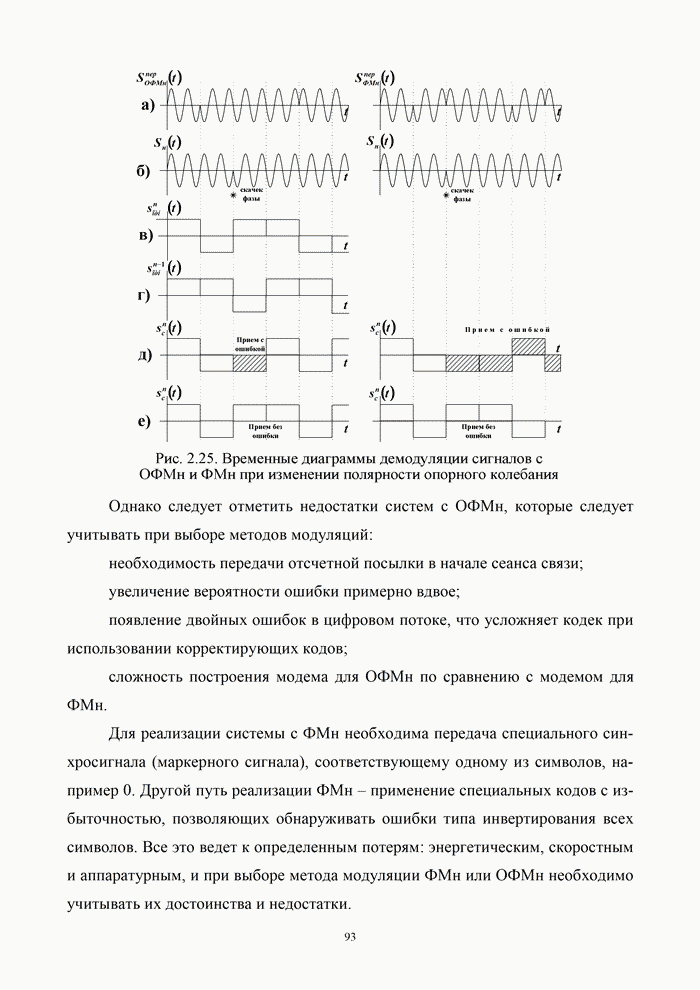
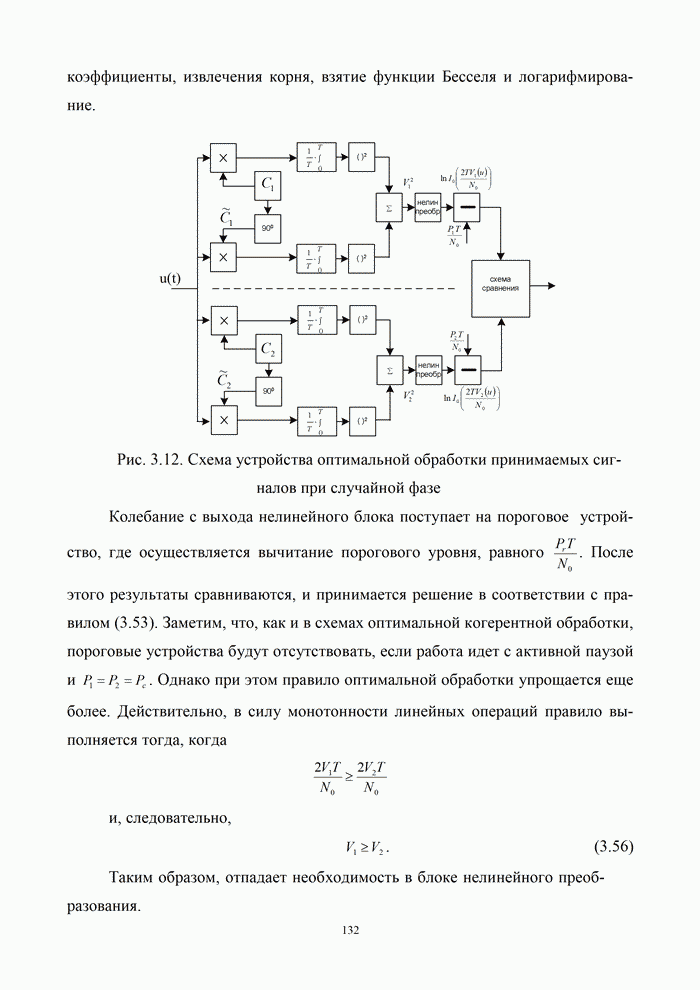
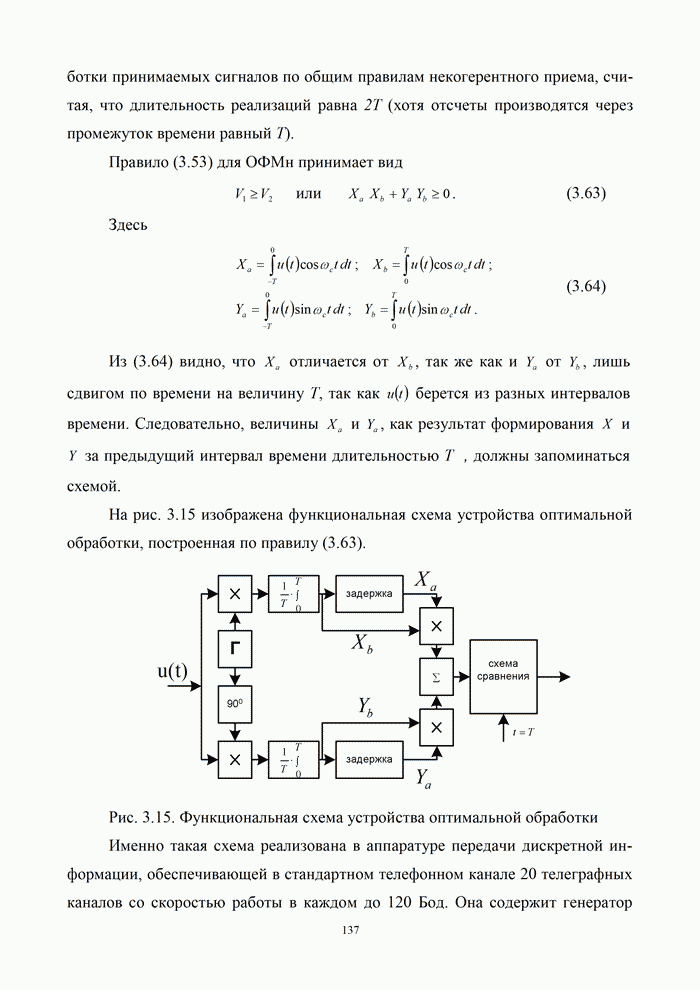
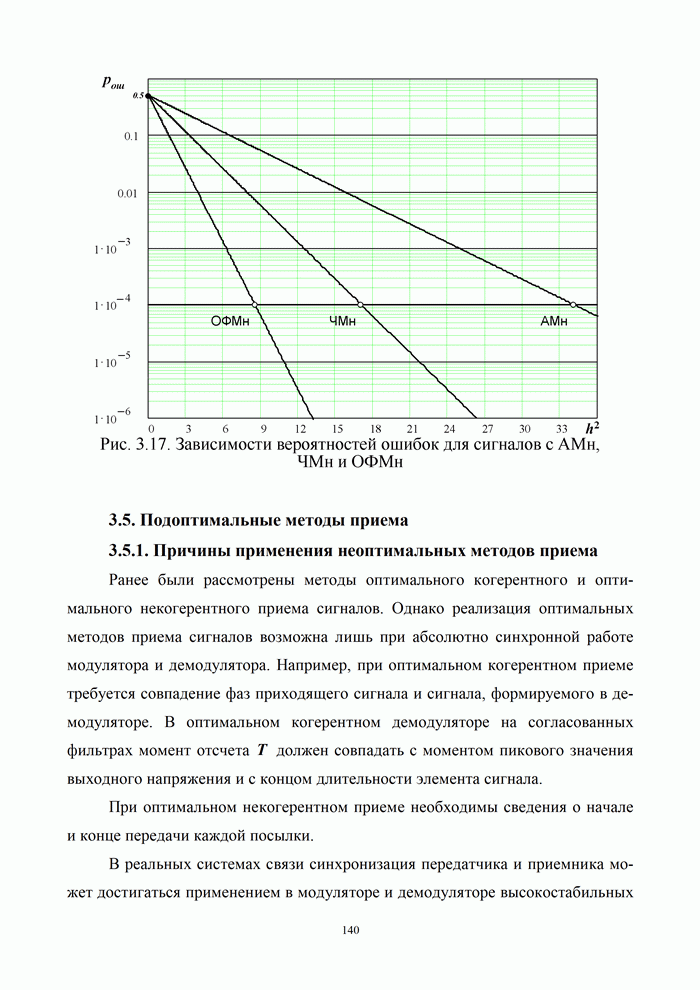
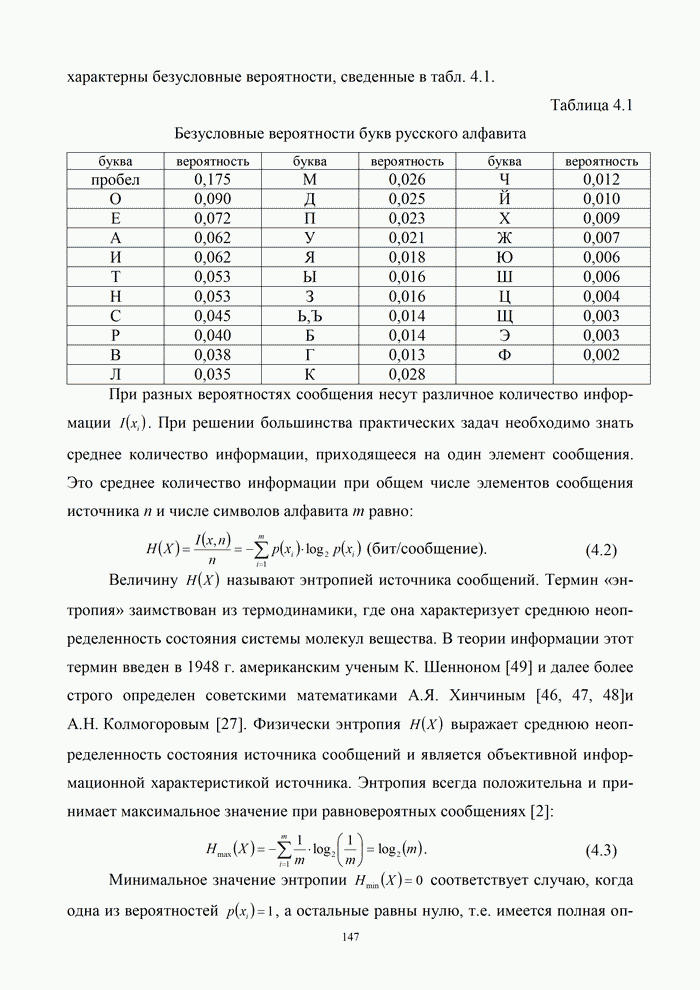
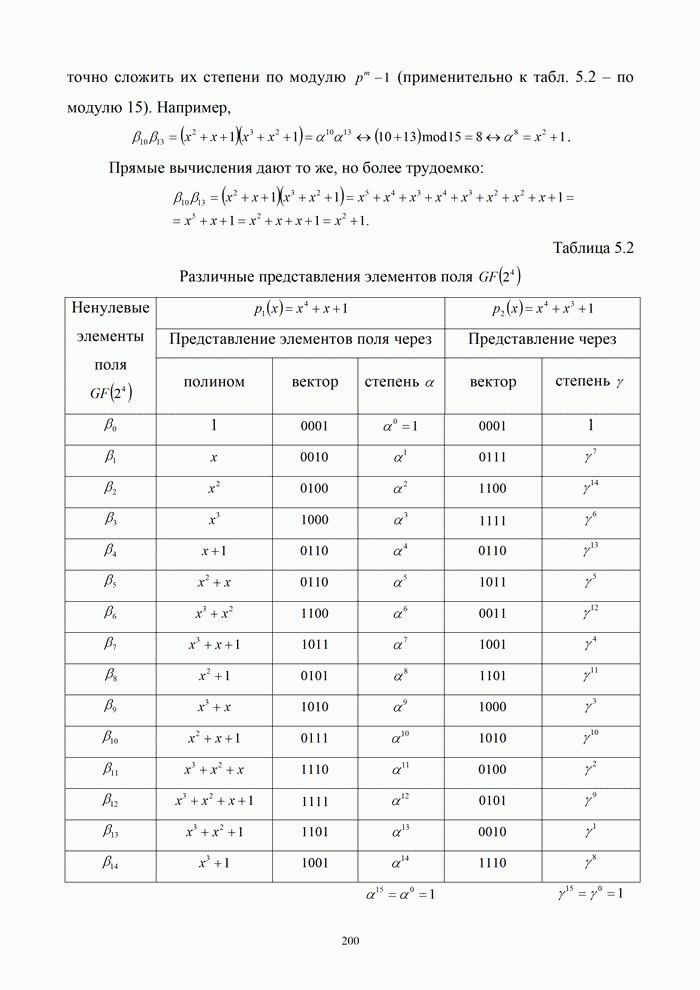
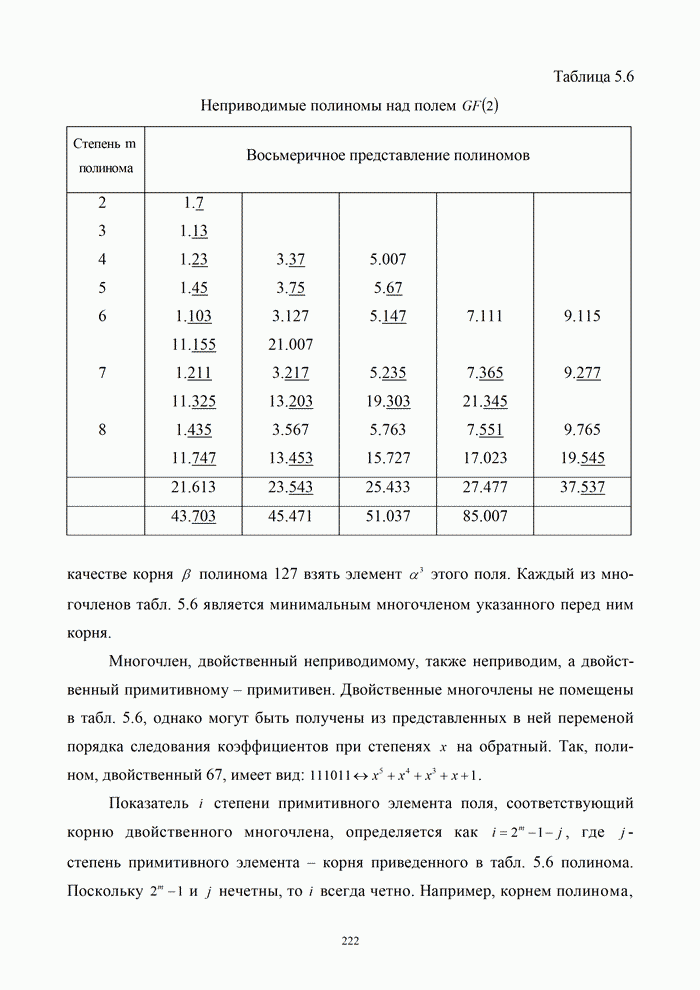
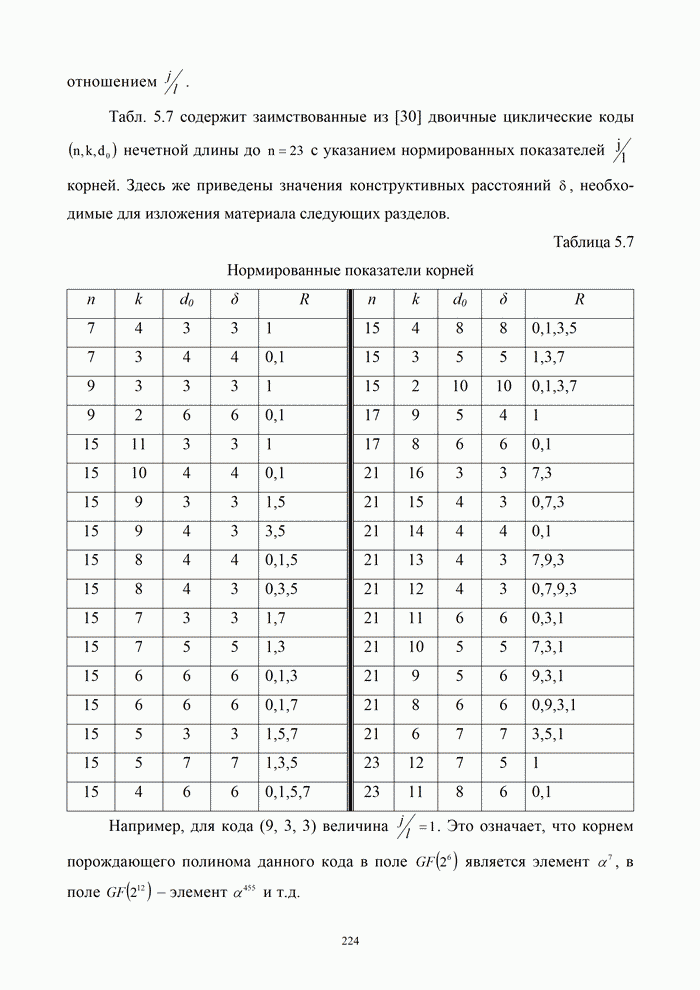
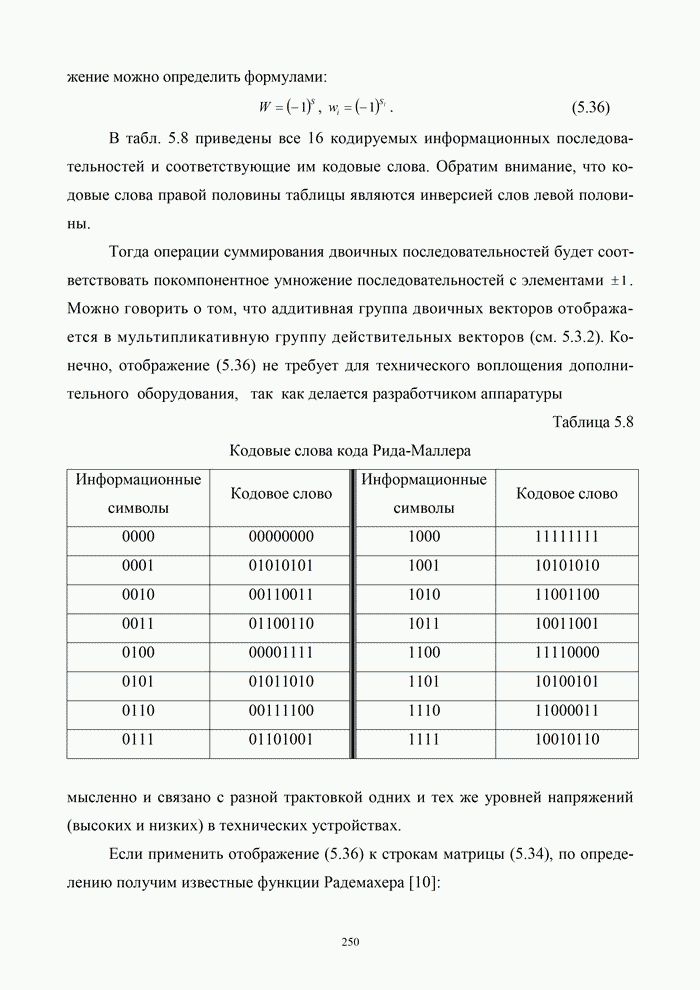
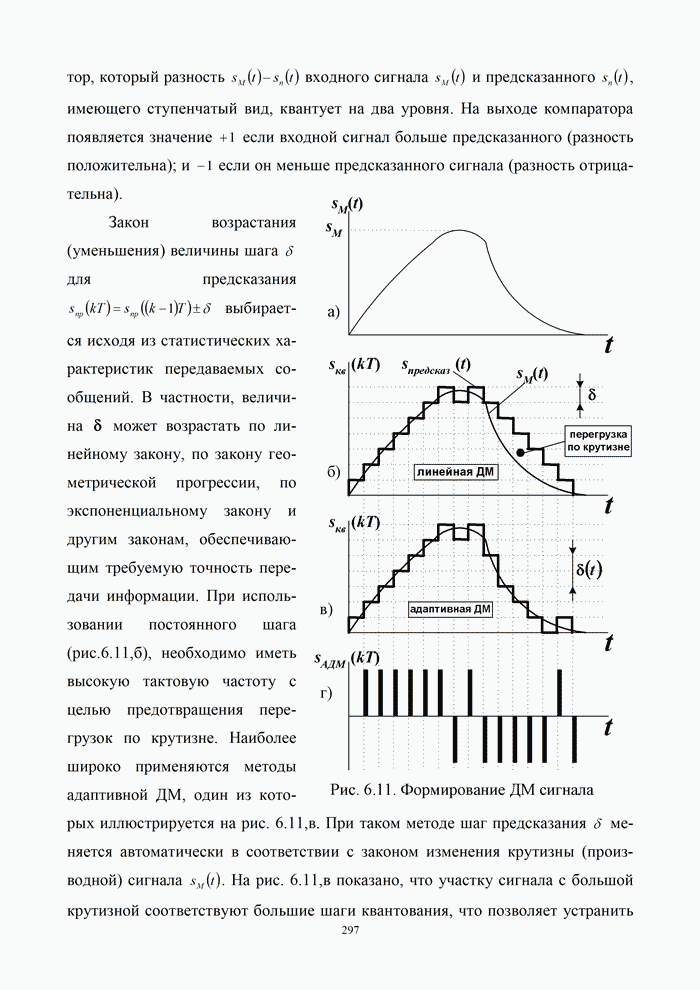
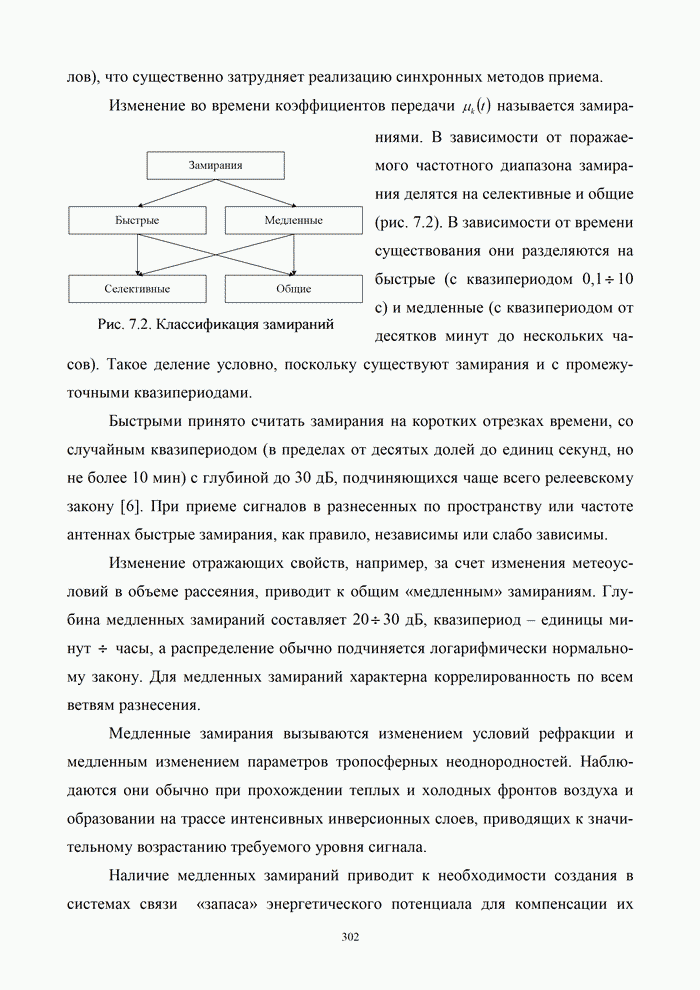
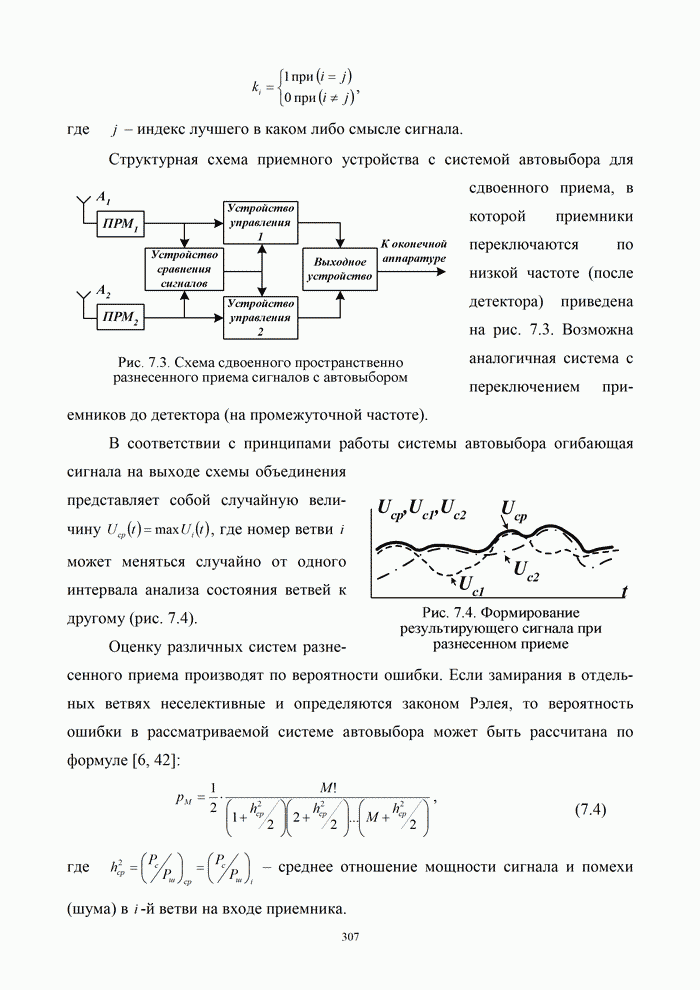
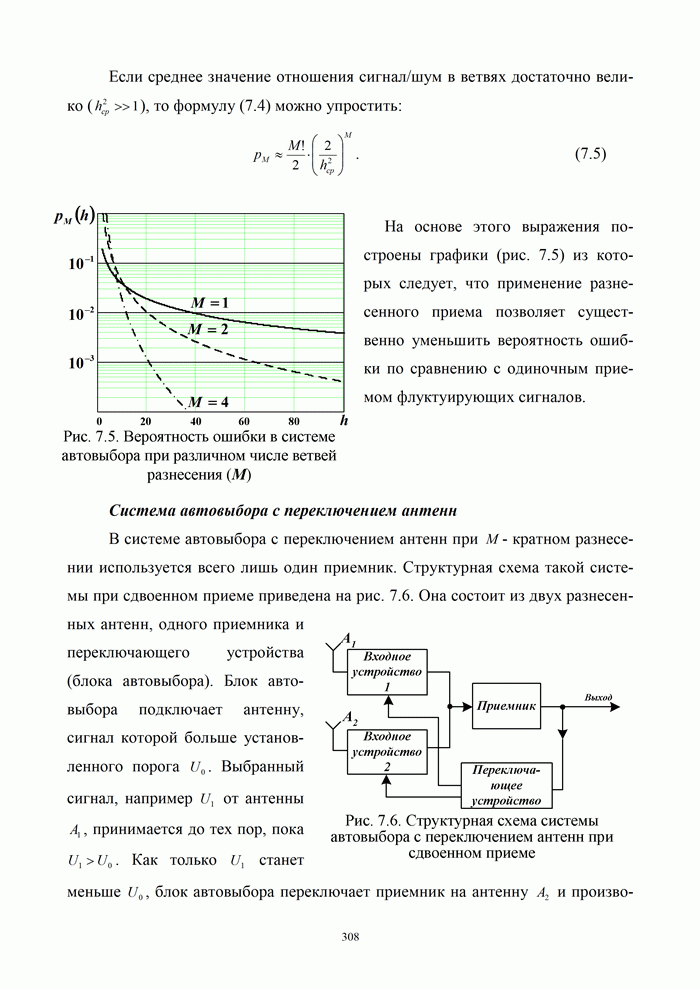
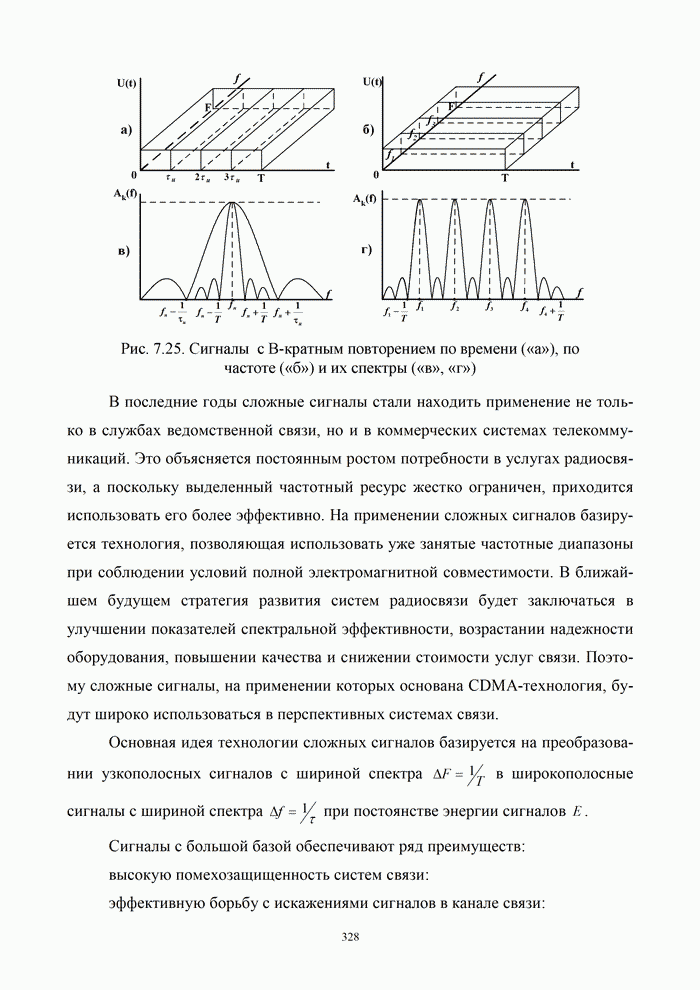
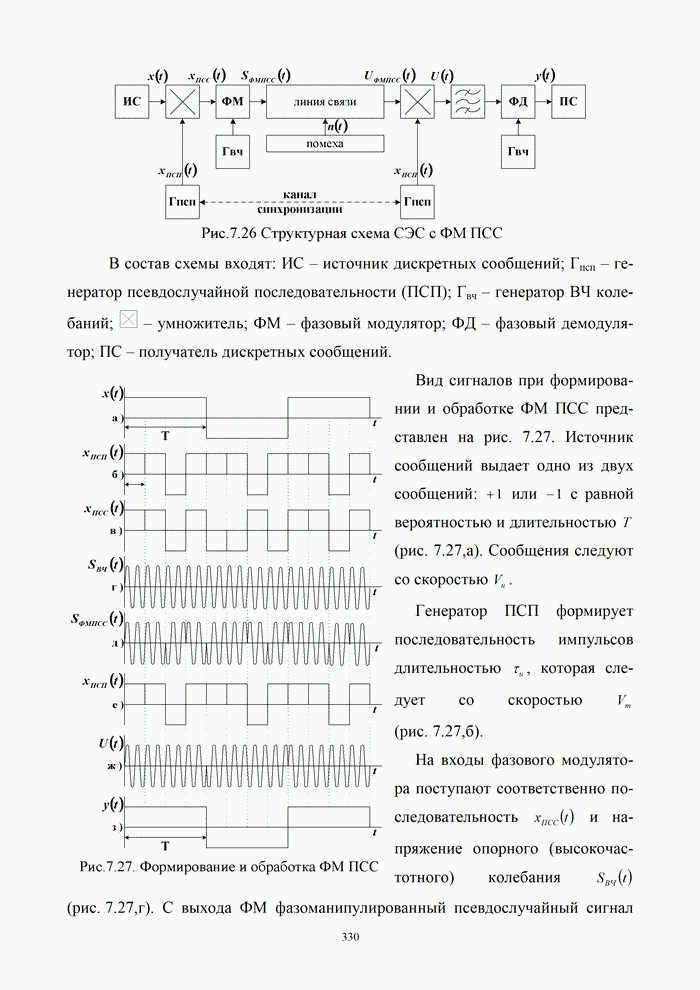
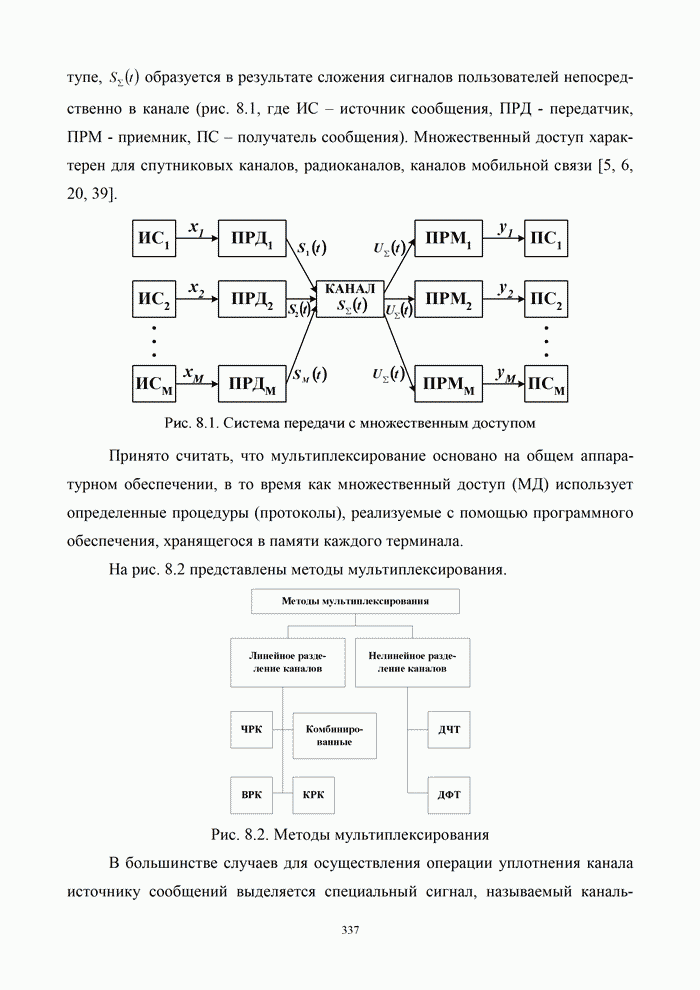
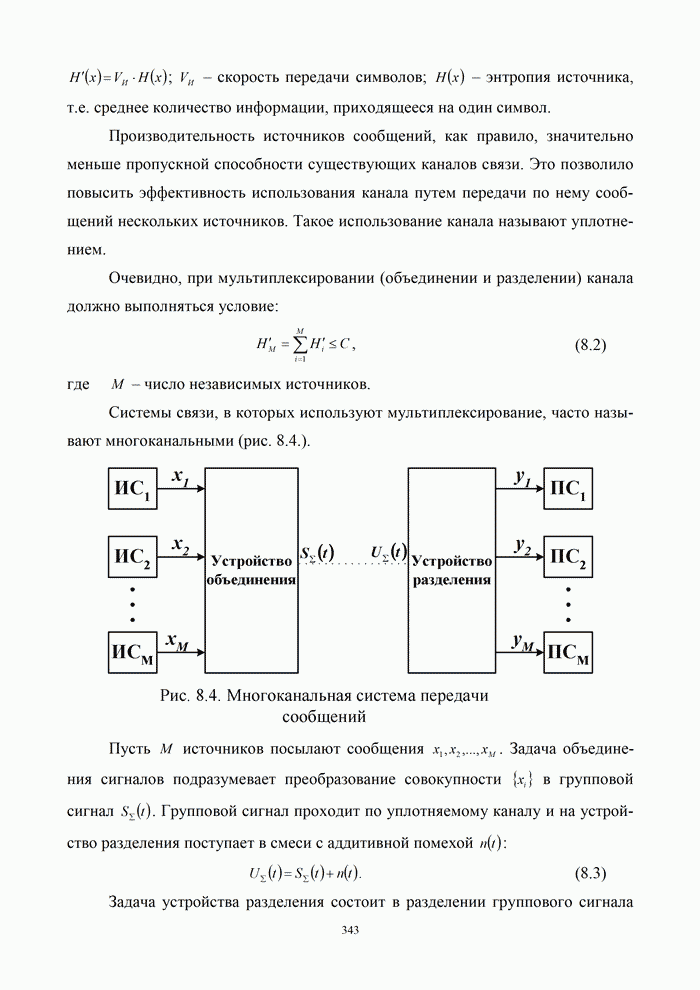
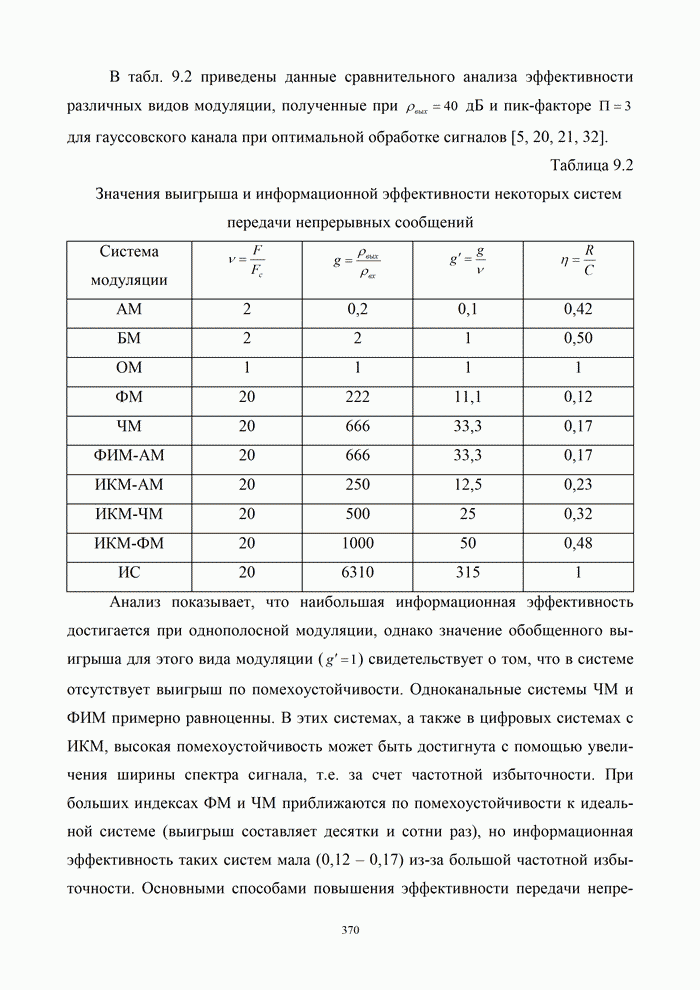
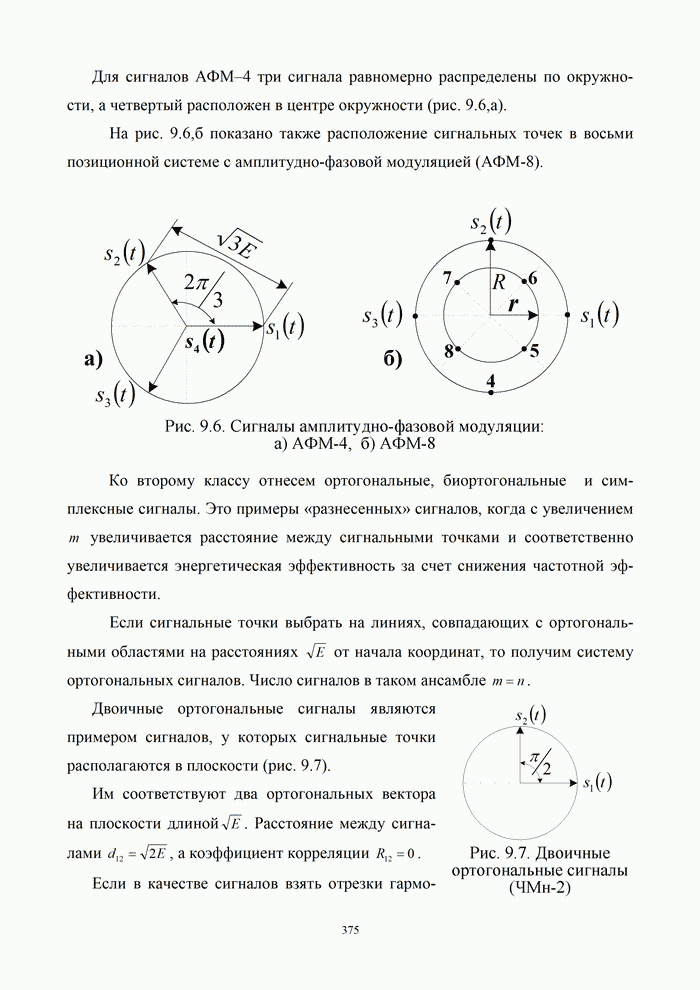
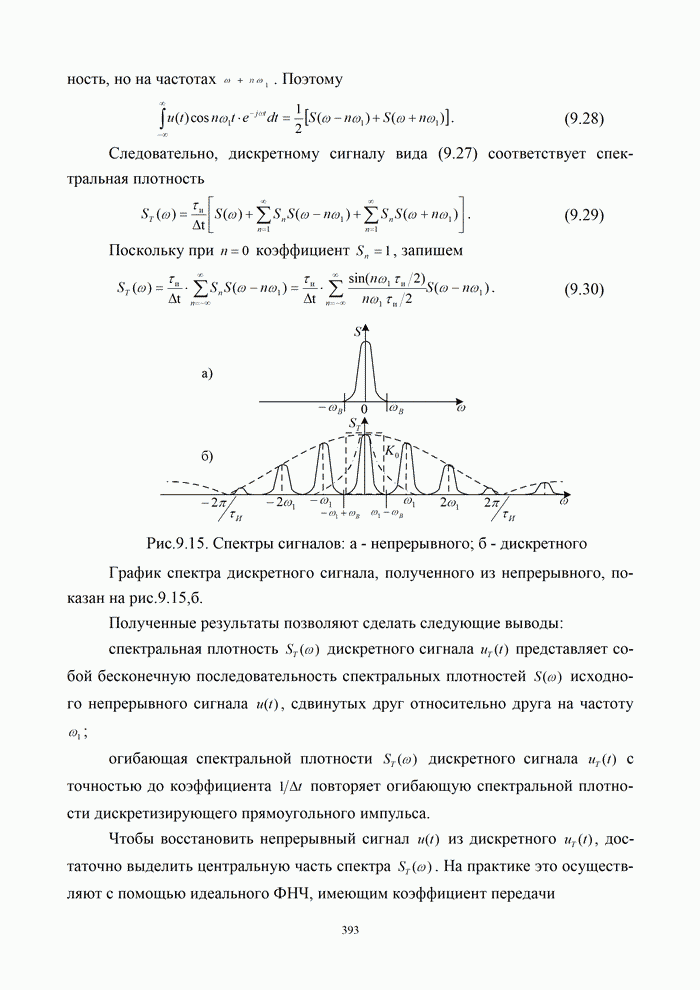
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.5.2. Квадратурная относительно-фазовая манипуляция (КОФМ)
Формирование
модулируемого цифрового сигнала удобно пояснить на основе квадратурного представления
сигналов. Смысл его заключается в представлении гармонического колебания с
произвольной фазой линейной комбинацией синусоидального и косинусоидального
колебания, что вытекает из тригонометрического равенства: ![]() .
.
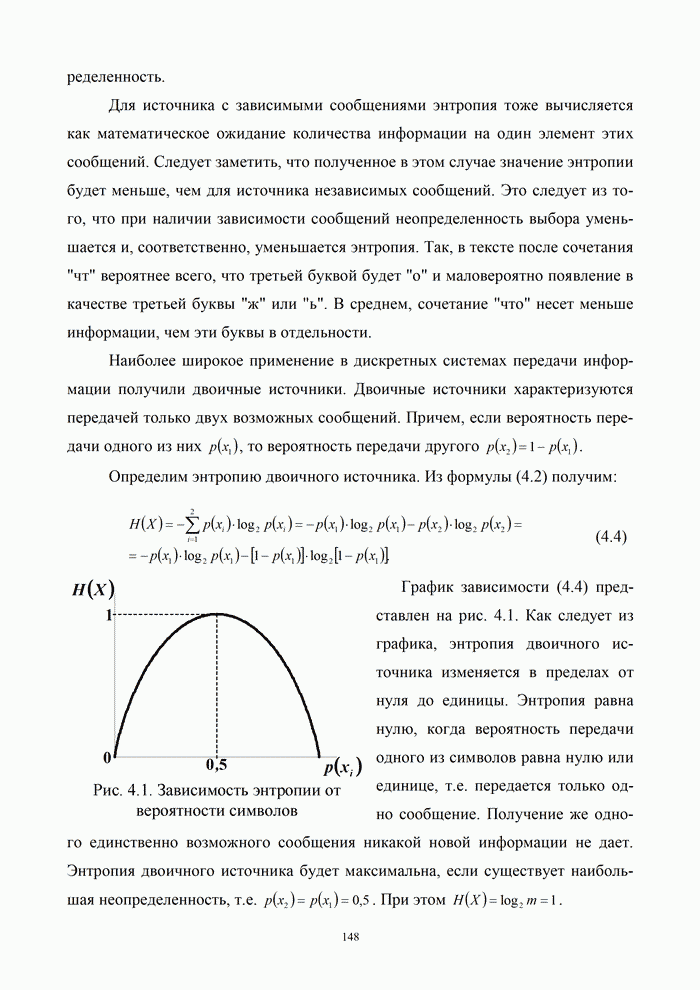
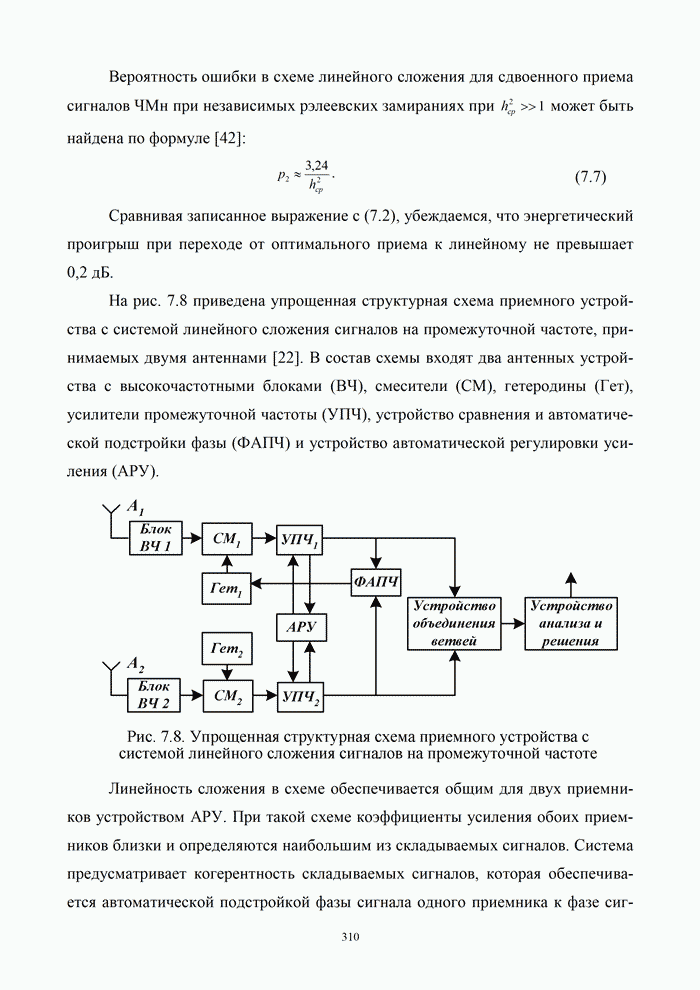
Модулятор может быть выполнен по схеме, представленной на рис.2.27,а. Преобразователь кода (Пр) преобразует входной сигнал в два параллельных сигнала каждый из которых модулирует по фазе на 180o синфазную и квадратурную составляющие.

Манипуляция
осуществляется в двух каналах на несущих, которые имеют относительный угловой
сдвиг 90°
(![]() и
и ![]() – базисные функции
разложения), т.е. находящихся в квадратуре (откуда и название метода
модуляции). Именно в силу специфики формирования последовательности сигналов
метод ОФМн при
– базисные функции
разложения), т.е. находящихся в квадратуре (откуда и название метода
модуляции). Именно в силу специфики формирования последовательности сигналов
метод ОФМн при ![]() часто
называют квадратурной ОФМн (КОФМ).
часто
называют квадратурной ОФМн (КОФМ).
Сигнальные
векторы ![]() получаются
суммированием базисных векторов при умножении их на определенные коэффициенты.
Если длина сигнального вектора равна
получаются
суммированием базисных векторов при умножении их на определенные коэффициенты.
Если длина сигнального вектора равна ![]() , то коэффициенты равны
, то коэффициенты равны ![]() .
.
Таким образом, в качестве манипулирующих сигналов используют сигналы, отличающиеся по структуре от исходных передаваемых двоичных сигналов, для формирования которых используется специальное кодирующее устройство - кодер модулятора.
Рассмотрим
подробнее один из возможных методов формирования сигналов с двукратной ОФМн-4
манипуляцией (m=4) по квадратурной схеме (рис. 2.27, а), на примере
сигнала ФМн-4 при которой формируются четыре элементарных сигнала ![]() , каждый из
которых характеризуется своей фазой
, каждый из
которых характеризуется своей фазой ![]() [5]:
[5]:
|
|
(2.32) |
Метод ОФМн можно рассматривать как обычную фазовую манипуляцию на 180° при условии предварительного перекодирования исходного сообщения:
|
|
(2.33) |
Поэтому для простоты будем считать, что в сообщениях, представленных
функциями ![]() и
и
![]() в (2.33),
перекодирование произведено, и для передачи исходного сообщения необходимо лишь
осуществить ФМн высокочастотных колебаний на 180°.
в (2.33),
перекодирование произведено, и для передачи исходного сообщения необходимо лишь
осуществить ФМн высокочастотных колебаний на 180°.
Исходная
последовательность двоичных информационных символов разделяется на
последовательности четных ![]() , и нечетных символов
, и нечетных символов ![]() с длительностью элементов
с длительностью элементов ![]() . Так, например,
исходная последовательность двоичных элементов длительностью
. Так, например,
исходная последовательность двоичных элементов длительностью ![]() с помощью кодера
модулятора преобразуется в совокупность 2-х
с помощью кодера
модулятора преобразуется в совокупность 2-х ![]() или 3-х
или 3-х ![]() последовательностей двоичных элементов
длительностью
последовательностей двоичных элементов
длительностью ![]() или
или
![]() соответственно.
Тогда передаваемое сообщение
соответственно.
Тогда передаваемое сообщение ![]() (рис.2.28,а), можно представить
в виде суммы четных
(рис.2.28,а), можно представить
в виде суммы четных ![]() (рис.2.28,б),
и нечетных
(рис.2.28,б),
и нечетных ![]() (рис.
2.28,в) составляющих:
(рис.
2.28,в) составляющих:
|
|
(2.34) |
|
Для экономии полосы
занимаемых частот осуществим раздельно фазовую модуляцию сообщениями ![]() и
и
![]() двух квадратурных составляющих
одного и того же колебания
двух квадратурных составляющих
одного и того же колебания ![]() . При этом
последовательность передаваемых сигналов
. При этом
последовательность передаваемых сигналов ![]() представляется в виде [5, 13, 15]:
представляется в виде [5, 13, 15]:
|
|
(2.35) |

где ![]() ,
,
![]() .
.
Комбинации
двоичных элементов полученных последовательностей ![]() и
и ![]() используются при кодировании фазового
сдвига при ОФМн. Значения начальной фазы
используются при кодировании фазового
сдвига при ОФМн. Значения начальной фазы ![]() колебания
колебания ![]() (рис. 2.28, г) при различных сочетаниях
передаваемых символов
(рис. 2.28, г) при различных сочетаниях
передаваемых символов ![]() и
и ![]() приведены в табл. 2.2.
приведены в табл. 2.2.
Таблица 2.2. Значения начальной фазы колебания ![]()
|
|
-1 |
+1 |
+1 |
-1 |
|
|
+1 |
+1 |
-1 |
-1 |
|
|
0 |
|
|
|
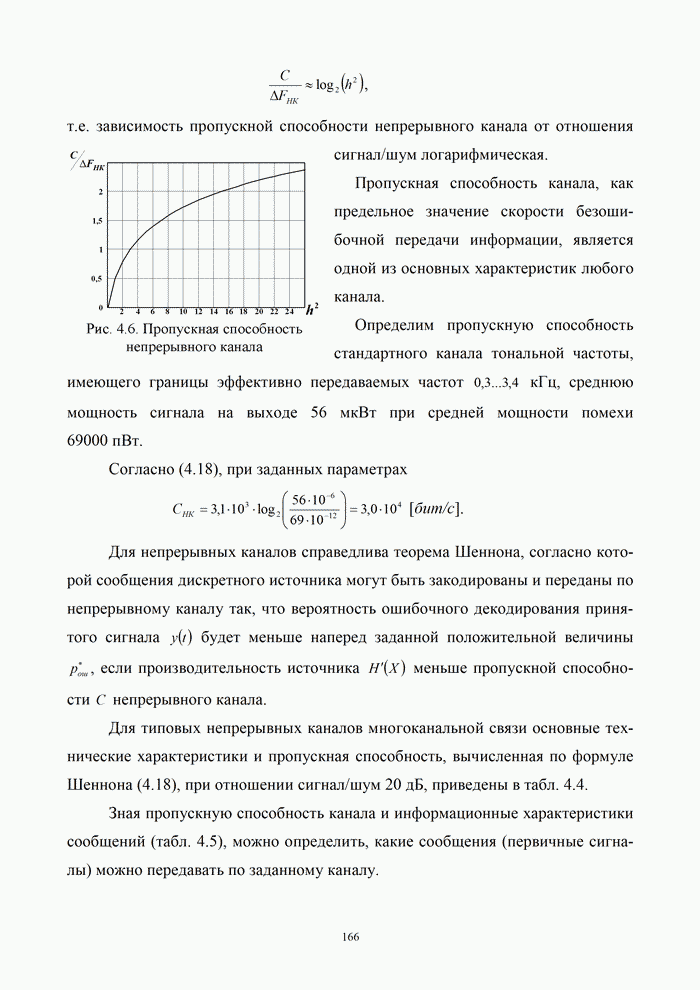
При
одновременной смене символов в обоих каналах модулятора в сигнале КОФМ
происходят скачки начальной фазы на 180° (как, например, в момент ![]() на (рис. 2.28, г).
При прохождении последовательности таких сигналов через узкополосные фильтры в
моменты скачков фазы колебания на 180° возникает глубокая паразитная
амплитудная модуляция огибающей сигнала (в ней появляются провалы огибающей до
нуля). Это приводит к увеличению пик–фактора сигнала и, как следствие, к
дополнительным искажениям при нелинейных режимах усиления, может увеличить
энергию боковых полос и увеличить помехи в соседних каналах.
на (рис. 2.28, г).
При прохождении последовательности таких сигналов через узкополосные фильтры в
моменты скачков фазы колебания на 180° возникает глубокая паразитная
амплитудная модуляция огибающей сигнала (в ней появляются провалы огибающей до
нуля). Это приводит к увеличению пик–фактора сигнала и, как следствие, к
дополнительным искажениям при нелинейных режимах усиления, может увеличить
энергию боковых полос и увеличить помехи в соседних каналах.
Для снижения
уровня такой паразитной амплитудной модуляции при ![]() разработана модификация метода КОФМн,
называемая квадратурной относительной фазовой модуляцией со сдвигом (КОФМС). В
этом случае колебание
разработана модификация метода КОФМн,
называемая квадратурной относительной фазовой модуляцией со сдвигом (КОФМС). В
этом случае колебание ![]() , и отличие от (2.35),
формируется в виде [5, 13]:
, и отличие от (2.35),
формируется в виде [5, 13]:
|
|
(2.36) |
|
где |
(2.37) |
Как следует
из соотношений (2.33) и
(2.37), знак любой из функций ![]() или
или ![]() может меняться лишь в те
моменты, когда значение другой функции сохраняется неизменным. Такой сдвиг по
времени моментов возможной смены знака модулирующих последовательностей
приводит к существенному отличию результирующего колебания
может меняться лишь в те
моменты, когда значение другой функции сохраняется неизменным. Такой сдвиг по
времени моментов возможной смены знака модулирующих последовательностей
приводит к существенному отличию результирующего колебания ![]() (рис. 2.28, е) при КОФМС по
сравнению с КОФМ.
(рис. 2.28, е) при КОФМС по
сравнению с КОФМ.
Заметим, что
скачки начальной фазы ![]() колебания
колебания ![]() возможны лишь на
возможны лишь на ![]() (рис. 2.28, е) что снижает
паразитную амплитудную модуляцию при прохождении сигнала через полосовые цепи. Длительность
радиосигнала
(рис. 2.28, е) что снижает
паразитную амплитудную модуляцию при прохождении сигнала через полосовые цепи. Длительность
радиосигнала ![]() КОФМС
равна длительности исходного информационного символа
КОФМС
равна длительности исходного информационного символа ![]() , т.е. вдвое меньше, чем при
КОФМ. Однако это не приводит к расширению спектра последовательности
, т.е. вдвое меньше, чем при
КОФМ. Однако это не приводит к расширению спектра последовательности ![]() по сравнению с
использованием КОФМ. Последнее объясняется тем, что ширина спектра колебания
по сравнению с
использованием КОФМ. Последнее объясняется тем, что ширина спектра колебания ![]() определяется шириной
спектра квадратурных составляющих
определяется шириной
спектра квадратурных составляющих ![]() и
и ![]() в (2.37), которая остается той же,
что и при КОФМ (2.35).
в (2.37), которая остается той же,
что и при КОФМ (2.35).
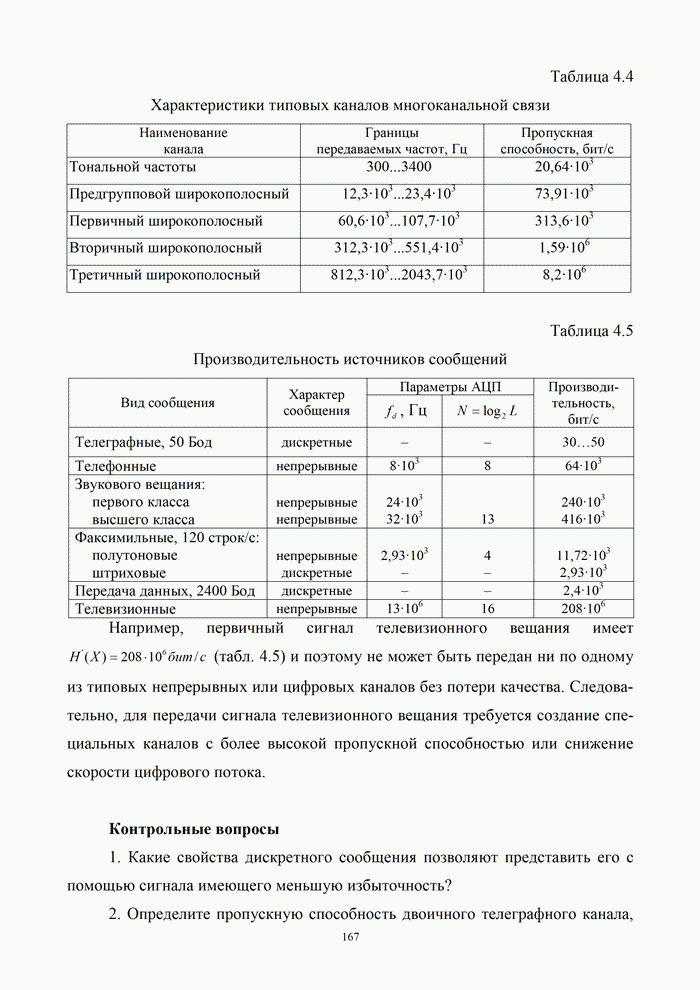
При приеме
сигналов как с КОФМ, так и с КОФМС можно воспользоваться тем, что составляющие ![]() и
и ![]() суммарной последовательности
суммарной последовательности ![]() сдвинуты на 90° по
фазе высокочастотного заполнения, а сообщения
сдвинуты на 90° по
фазе высокочастотного заполнения, а сообщения ![]() или
или ![]() независимы.
независимы.

В
этих условиях при наличии в демодуляторе генераторов непрерывных колебаний ![]() и
и ![]() легко осуществить раздельный
прием каждой из составляющих
легко осуществить раздельный
прием каждой из составляющих ![]() и
и ![]() . Действительно, рассмотрим устройство на
рис. 2.29. При поступлении на вход колебания
. Действительно, рассмотрим устройство на
рис. 2.29. При поступлении на вход колебания ![]() вида (2.35) вклад составляющей
вида (2.35) вклад составляющей ![]() в выходном напряжении
интегратора верхнего канала в моменты
в выходном напряжении
интегратора верхнего канала в моменты ![]() оказывается пренебрежимо малым. Таким
образом, верхний канал схемы на рис. 2.29 представляет собой демодулятор
двоичных сигналов с ОФМн, содержащих информацию о сообщении
оказывается пренебрежимо малым. Таким
образом, верхний канал схемы на рис. 2.29 представляет собой демодулятор
двоичных сигналов с ОФМн, содержащих информацию о сообщении ![]() . Нижний канал выполняет
функции демодулятора двоичных сигналов с ОФМн, составляющих последовательность
. Нижний канал выполняет
функции демодулятора двоичных сигналов с ОФМн, составляющих последовательность ![]() и содержащих
информацию о сообщении
и содержащих
информацию о сообщении ![]() .
.
При КОФМС нет
скачков фазы на 180° т.к. текущее изменение фазы происходит в моменты
смены знака любой из функций ![]() или
или ![]() . При этом значение другой функции
сохраняется неизменным, что позволяет избежать глубокой паразитной модуляции
огибающей.
. При этом значение другой функции
сохраняется неизменным, что позволяет избежать глубокой паразитной модуляции
огибающей.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Список сокращений
- Основные обозначения
- ВВЕДЕНИЕ
- Глава 1. Сообщения, сигналы и помехи, их математические модели
- 1.1. Основные понятия и определения
- 1.1.1. Сообщение, сигнал, модуляция
- 1.1.2. Основные параметры сигналов
- 1.2. Системы связи. Каналы связи
- 1.2.1. Структура канала электросвязи
- 1.2.2. Линия и сеть связи
- 1.2.3. Помехи и искажения в канале
- 1.2.4. Эталонная модель взаимодействия открытых систем
- 1.2.5. Модели каналов связи и их математическое описание
- 1.3. Способы описания сигналов и помех
- 1.3.1. Сигнал и его математическая модель
- 1.3.2. Энергетические характеристики детерминированного сигнала
- 1.4.2. Представление сигналов и помех рядом Фурье
- 1.4.3. Применение преобразования Фурье для непериодических сигналов
- 1.5. Теорема Котельникова
- 1.6. Пространство сигналов
- 1.6.1. Линейное пространство
- 1.6.2. Представление сигнала в многомерном пространстве
- 1.7. Сигналы как случайные процессы
- 1.7.1. Характеристики случайного процесса
- 1.7.2. Флуктуационный шум
- 1.8. Комплексное представление сигналов и помех
- 1.8.1. Понятие аналитического сигнала
- 1.8.2. Огибающая, мгновенная фаза и мгновенная частота узкополосного случайного процесса
- Контрольные вопросы
- Глава 2. Методы формирования и преобразования сигналов
- 2.1. Модуляция сигналов
- 2.1.1. Амплитудная модуляция гармонической несущей
- 2.1.2. Балансная и однополосная модуляция гармонической несущей
- 2.2. Методы угловой модуляции
- 2.2.1. Принципы частотной и фазовой (угловой) модуляции
- 2.2.2. Спектр сигналов угловой модуляции
- 2.3. Формирование и детектирование модулированных сигналов
- 2.3.1. Формирование и детектирование сигналов амплитудной и однополосной амплитудной модуляции
- 2.3.2. Формирование и детектирование сигналов угловой модуляции
- 2.4. Манипуляция сигналов
- 2.4.1. Временные и спектральные характеристики амплитудно-манипулированных сигналов
- 2.4.2. Временные и спектральные характеристики частотно-манипулированных сигналов
- 2.4.3. Фазовая (относительно-фазовая) манипуляция сигналов
- 2.5. Системы связи с многопозиционной относительной фазовой манипуляцией
- 2.5.1. Принцип формирования сигнала с многократной относительной фазовой манипуляцией
- 2.5.2. Квадратурная относительно-фазовая манипуляция (КОФМ)
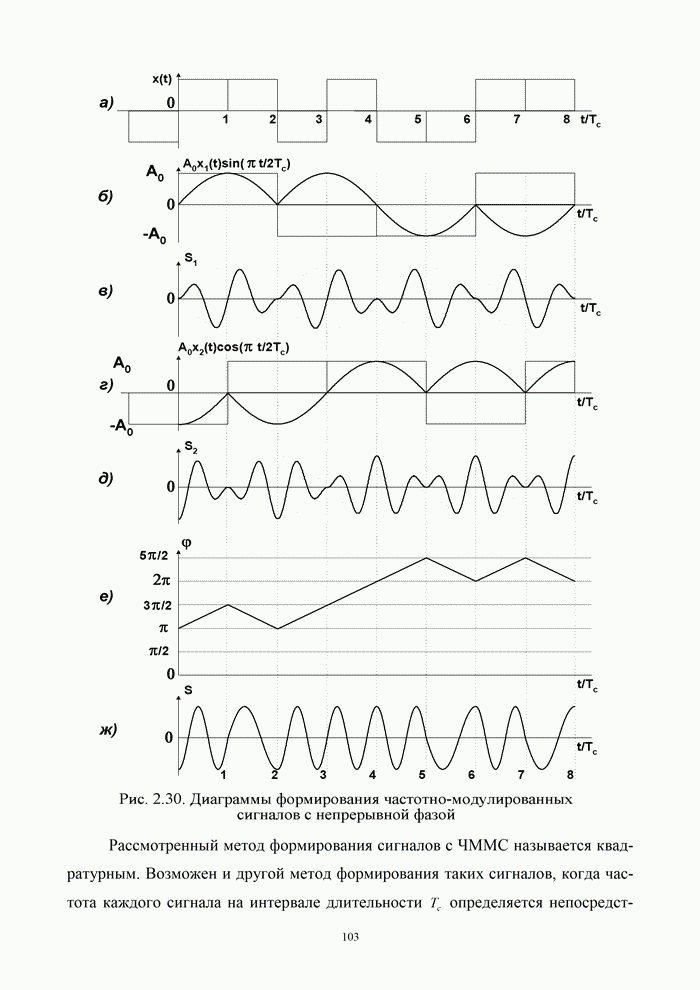
- 2.5.3. Принцип частотной модуляции с непрерывной фазой
- Контрольные вопросы
- Глава 3. Помехоустойчивость приема дискретных сообщений
- 3.1. Критерии качества и правила приема дискретных сообщений
- 3.1.1. Понятие о помехоустойчивости систем электрической связи
- 3.1.2. Задача оптимального приема
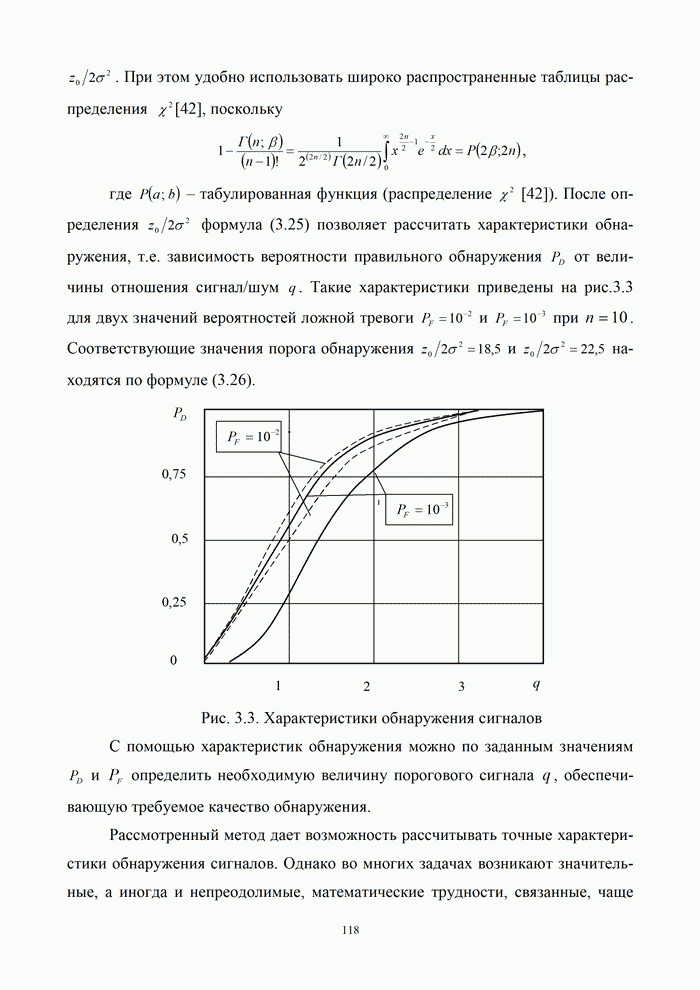
- 3.1.3. Вычисление вероятностей ошибок
- 3.2. Оптимальная демодуляция при когерентном приеме сигналов
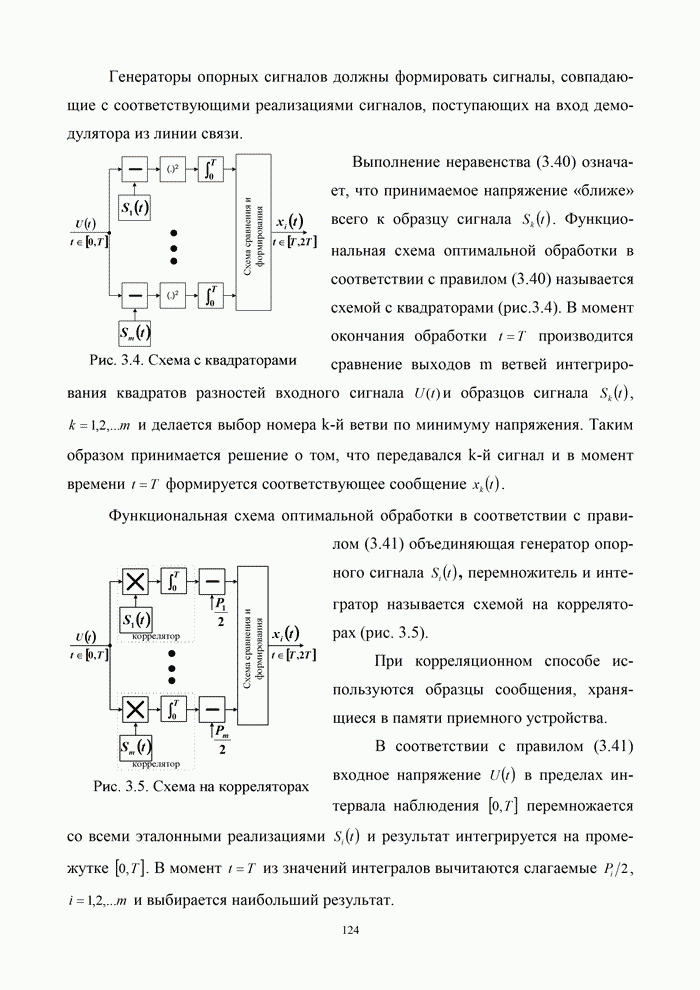
- 3.2.1. Оптимальные алгоритмы приема при полностью известных сигналах
- 3.2.2. Реализация алгоритмов оптимального когерентного приема
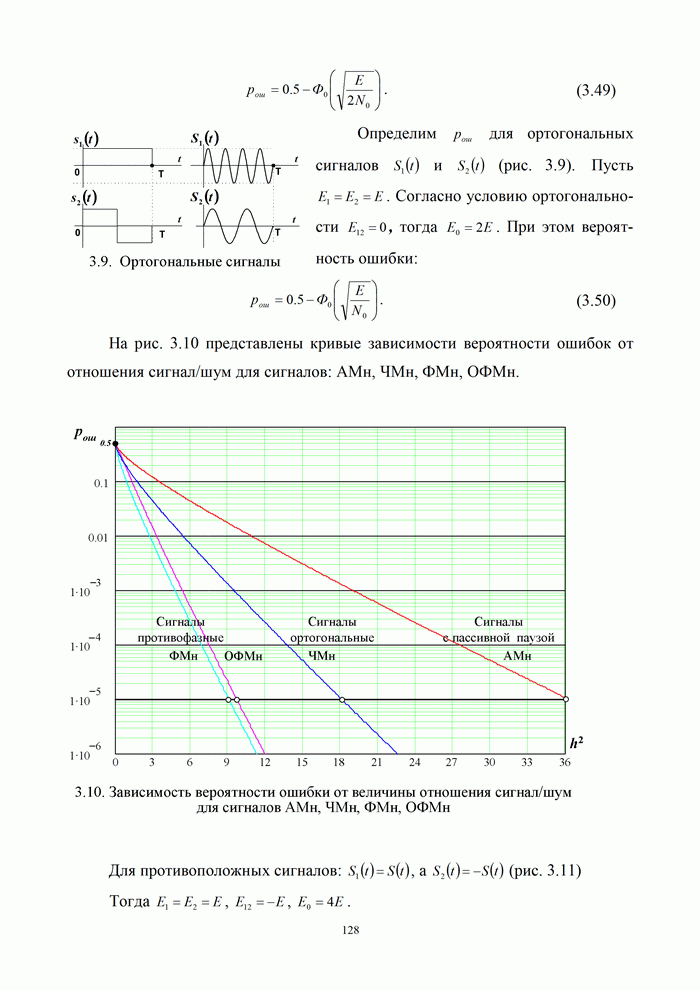
- 3.3. Помехоустойчивость приема сигналов с известными параметрами
- 3.4. Прием сигналов с неопределенной фазой
- 3.4.1. Оптимальный некогерентный прием дискретных сигналов
- 3.4.2. Помехоустойчивость оптимального некогерентного приема
- 3.5. Подоптимальные методы приема
- 3.5.1. Причины применения неоптимальных методов приема
- 3.5.2. Квазиоптимальные методы приема
- Контрольные вопросы
- Глава 4. Теория передачи информации
- 4.1. Информационные характеристики источника сообщений
- 4.1.1. Количественное определение информации
- 4.1.2. Энтропия и производительность дискретного источника сообщений
- 4.2. Пропускная способность дискретного канала
- 4.2.1. Количество информации переданной по дискретному каналу
- 4.2.2. Пропускная способность дискретного канала
- 4.2.3. Пропускная способность симметричного дискретного канала без памяти
- 4.3. Методы сжатия дискретных сообщений
- 4.3.1. Условия существования оптимального неравномерного кода
- 4.3.2. Прямая и обратная теоремы кодирования источника неравномерными кодами
- 4.3.3. Показатели эффективности сжатия
- 4.3.4. Кодирование источника дискретных сообщений методом Шеннона-Фано
- 4.3.5. Кодирование источника дискретных сообщений методом Хаффмена
- 4.4. Пропускная способность непрерывного канала
- 4.4.1. Постановка задачи передачи дискретных сообщений в непрерывном канале
- 4.4.2. Количество информации, переданной по непрерывному каналу
- 4.4.3. Пропускная способность непрерывного канала
- Контрольные вопросы
- Глава 5. Теория кодирования сообщений
- 5.1. Помехоустойчивое кодирование: блочные и непрерывные коды
- 5.1.1. Постановка задачи помехоустойчивого кодирования
- 5.1.2. Классификация кодов
- 5.1.3. Основные характеристики и свойства блочных кодов
- 5.2. Эффективность помехоустойчивого кодирования
- 5.2.1. Эффективность кода в режиме исправления ошибок
- 5.2.2. Эффективность кода в режиме обнаружения ошибок
- 5.2.3. Эффективность помехоустойчивых кодов
- 5.3. Математические основы теории помехоустойчивого кодирования
- 5.3.1. Краткие сведения из теории чисел
- 5.3.2. Группы
- 5.3.3. Кольца и поля
- 5.3.4. Векторное пространство
- 5.3.5. Конечные поля
- 5.4. Линейные блочные коды
- 5.4.1. Система передачи дискретных сообщений
- 5.4.2. Параметры линейного кода
- 5.4.3. Полиномиальные циклические коды
- 5.4.4. Циклические коды и корни полиномов
- 5.4.5. Спектральное описание циклических кодов
- 5.4.6. Простейшие блочные линейные коды
- 5.5. Коды Боуза-Чоудхури-Хоквингема
- 5.5.1. Методы задания кодов БЧХ
- 5.5.2. Принципы декодирования кодов БЧХ
- 5.5.3. Методы реализации этапов декодирования кодов БЧХ
- 5.6. Коды Рида-Соломона
- 5.6.1. Основные определения
- 5.6.2. Обнаружение и исправление пакетов ошибок
- 5.7. Коды Рида-Маллера
- 5.7.1. Задание и декодирование кодов Рида-Маллера
- 5.7.2. Симплексные коды и m-последовательности
- 5.7.3. Связь между блочными кодами
- 5.8. Сверточные коды
- 5.8.1. Основные параметры
- 5.8.2. Способы задания сверточного кода
- 5.8.3. Алгоритм декодирования Витерби
- 5.9. Помехоустойчивость систем передачи дискретных сообщений
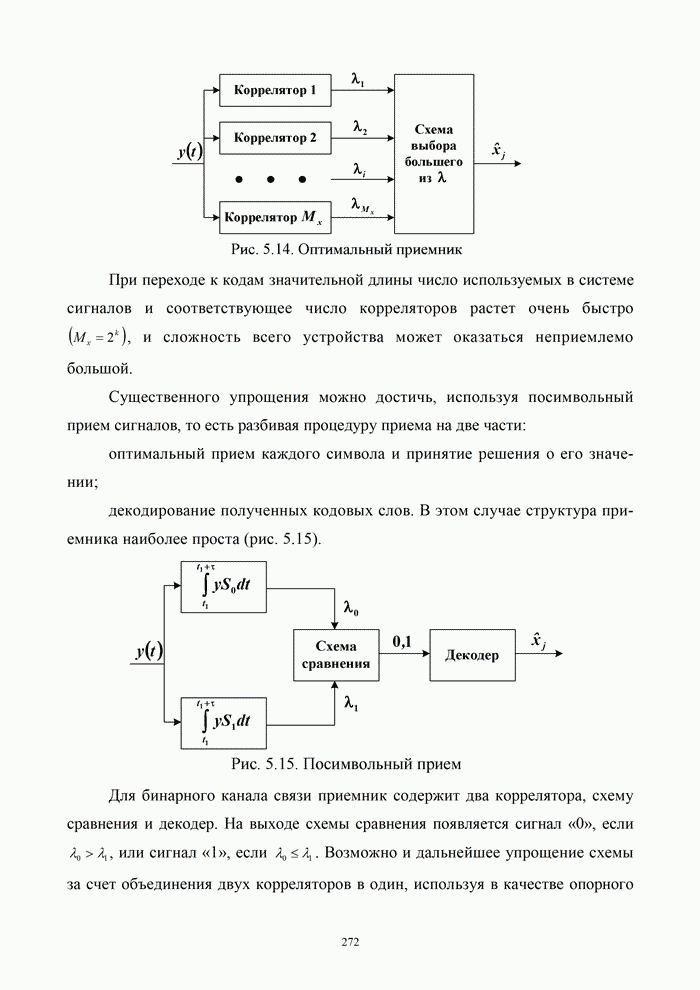
- 5.9.1. Две процедуры приема сигналов
- 5.9.2. Помехоустойчивость систем передачи информации при оптимальной процедуре приема
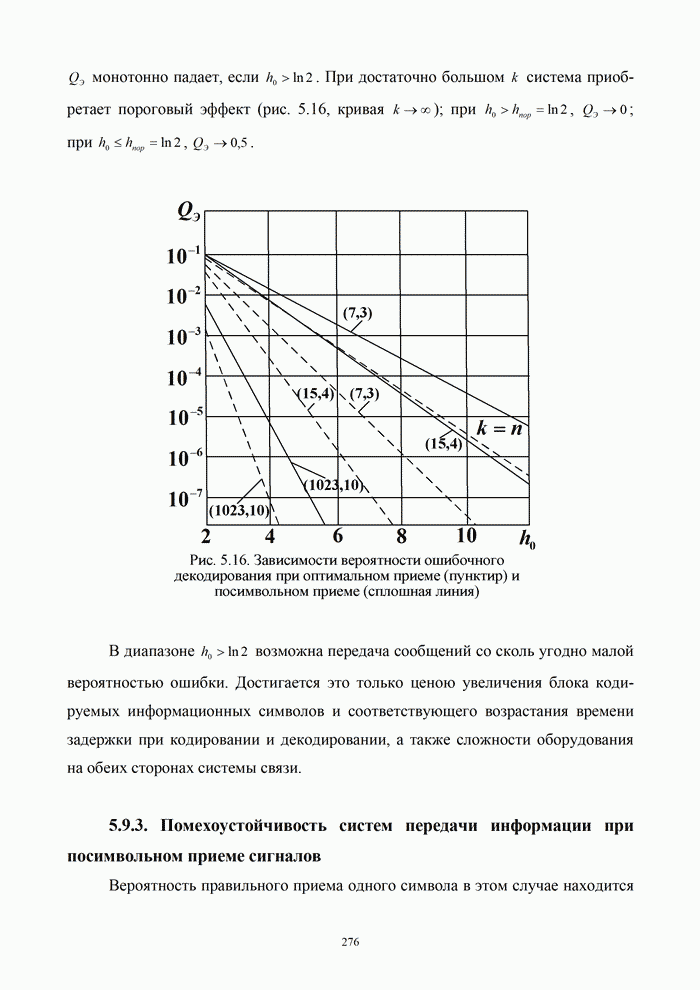
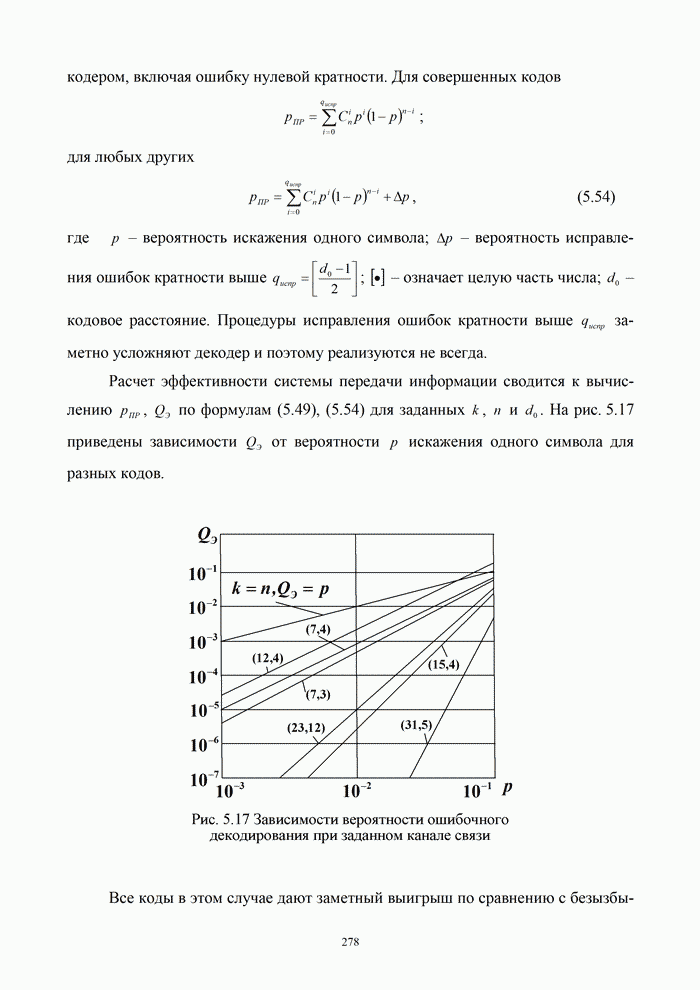
- 5.9.3. Помехоустойчивость систем передачи информации при посимвольном приеме сигналов
- Контрольные вопросы
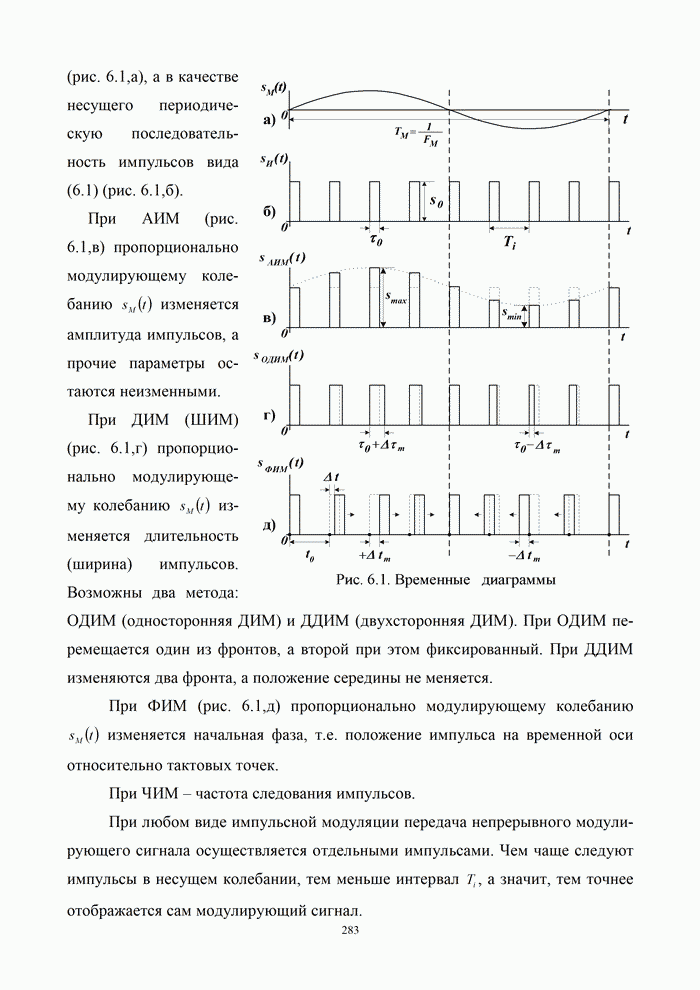
- Глава 6. Сигналы с импульсной модуляцией
- 6.1. Методы импульсной модуляции
- 6.1.1. Импульсные методы передачи непрерывных сигналов
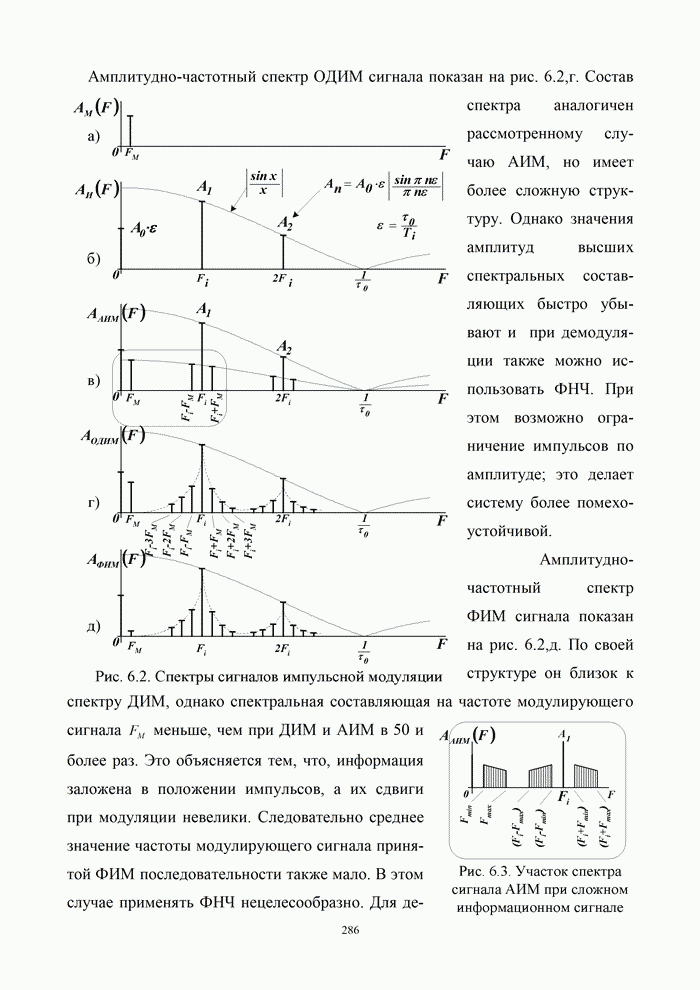
- 6.1.2. Спектральные характеристики импульсных методов модуляции
- 6.2. Помехоустойчивость непрерывных каналов связи с импульсной модуляцией
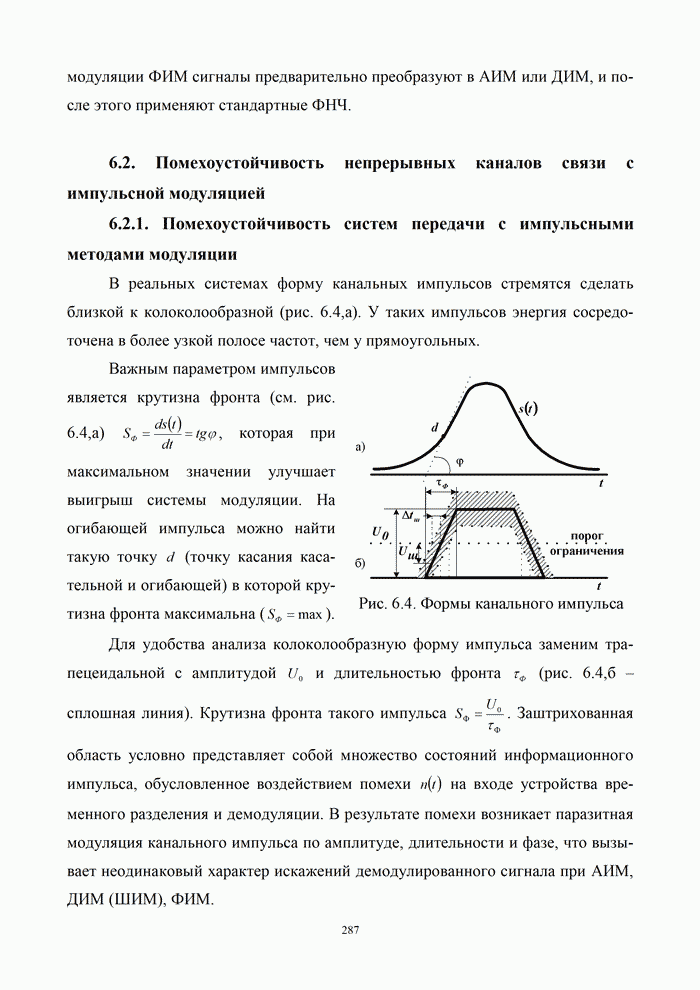
- 6.2.1. Помехоустойчивость систем передачи с импульсными методами модуляции
- 6.3. Цифровые методы передачи непрерывных сообщений
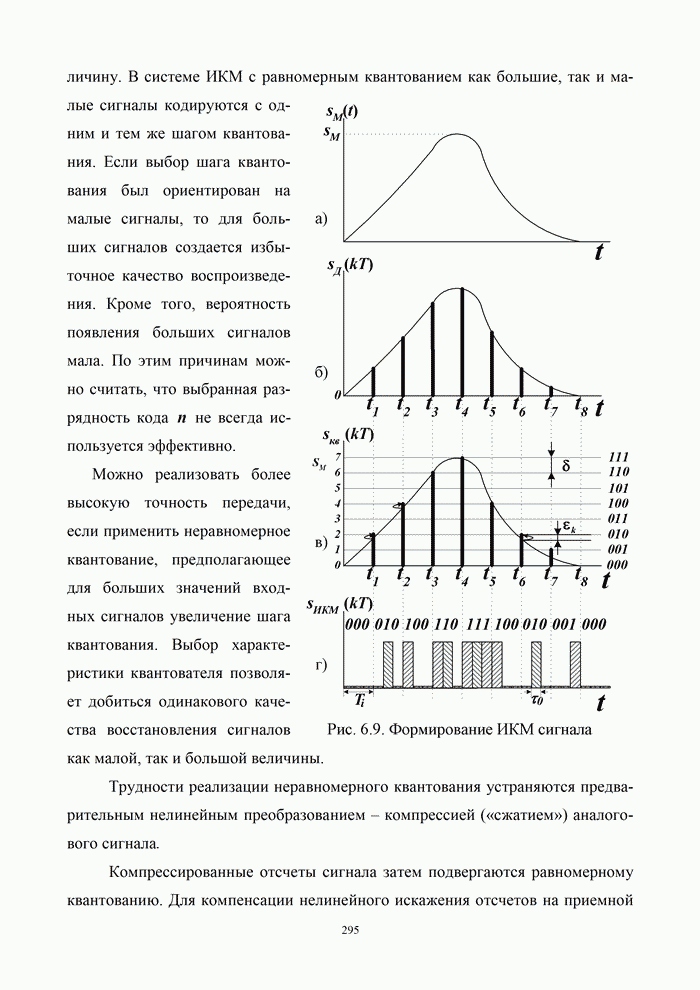
- 6.3.1. Передача сигналов с импульсно-кодовой модуляцией
- 6.3.2. Передача сигналов с дельта модуляцией
- 6.3.3. Квантование сигналов в системах с ИКМ и ДМ
- Контрольные вопросы
- Глава 7. Методы приема сигналов в сложных условиях
- 7.1. Прием сигналов в каналах с замираниями
- 7.1.1. Сущность замираний и их классификация
- 7.1.2. Принципы разнесенного приема сигналов
- 7.2. Методы борьбы с замираниями сигналов
- 7.2.1. Методы борьбы с замираниями в аналоговых системах связи
- 7.2.2. Методы борьбы с замираниями в цифровых системах связи
- 7.3. Методы борьбы с межсимвольной интерференцией
- 7.3.1. Причины возникновения и сущность межсимвольной интерференции
- 7.3.2. Обработка сигналов в каналах с межсимвольной интерференцией
- 7.3.3. Помехоустойчивость в каналах с межсимвольной интерференцией
- 7.4. Прием дискретных сообщений в каналах с сосредоточенными по спектру и импульсными помехами
- 7.4.1. Общая характеристика сосредоточенных по спектру и импульсных помех
- 7.4.2. Борьба с сосредоточенными и импульсными помехами
- 7.5. Компенсация помех и искажений в канале
- 7.5.1. Принцип работы радиолинии с ФМ ПСС (ФМ ШПС)
- 7.5.2. Помехоустойчивость радиолинии с ФМ ПСС
- 7.5.3. Принципы работы радиолиний с ППРЧ
- 7.5.4. Помехоустойчивость радиолиний с ППРЧ
- Контрольные вопросы
- Глава 8. Многоканальная связь и распределение информации
- 8.1. Методы распределения ресурса общего канала
- 8.1.1. Классификация систем передачи информации, использующих единый ресурс
- 8.1.2. Постановка задачи объединения и разделения сигналов
- 8.1.3. Энергетическая и спектральная цена уплотнения
- 8.2. Частотное разделение каналов
- 8.2.1. Принцип частотного объединения и разделения каналов
- 8.2.2. Групповой сигнал, его структура и характеристики
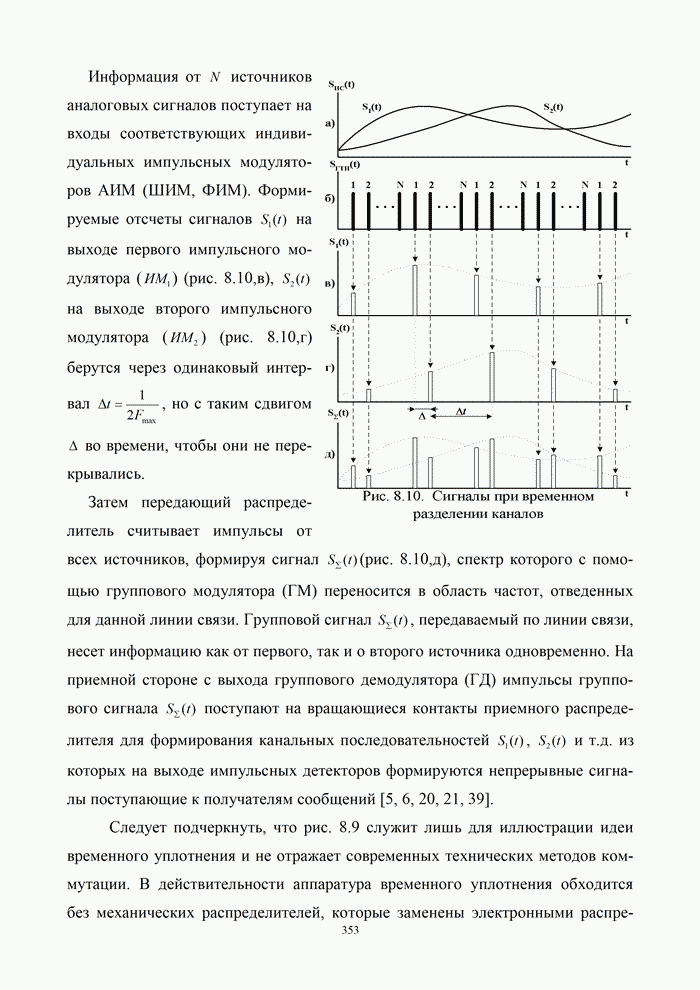
- 8.3. Временное разделение каналов
- 8.3.1. Принцип временного разделения каналов
- 8.3.2. Характеристики группового сигнала систем с ВРК
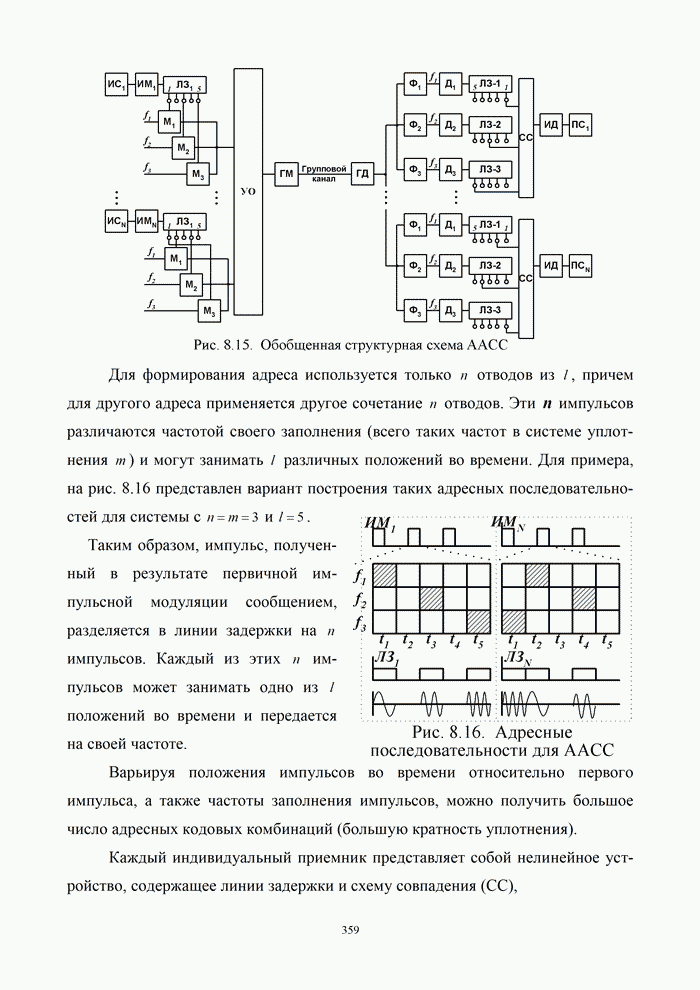
- 8.4. Разделение сигналов по форме
- Контрольные вопросы
- Глава 9. Эффективность систем связи
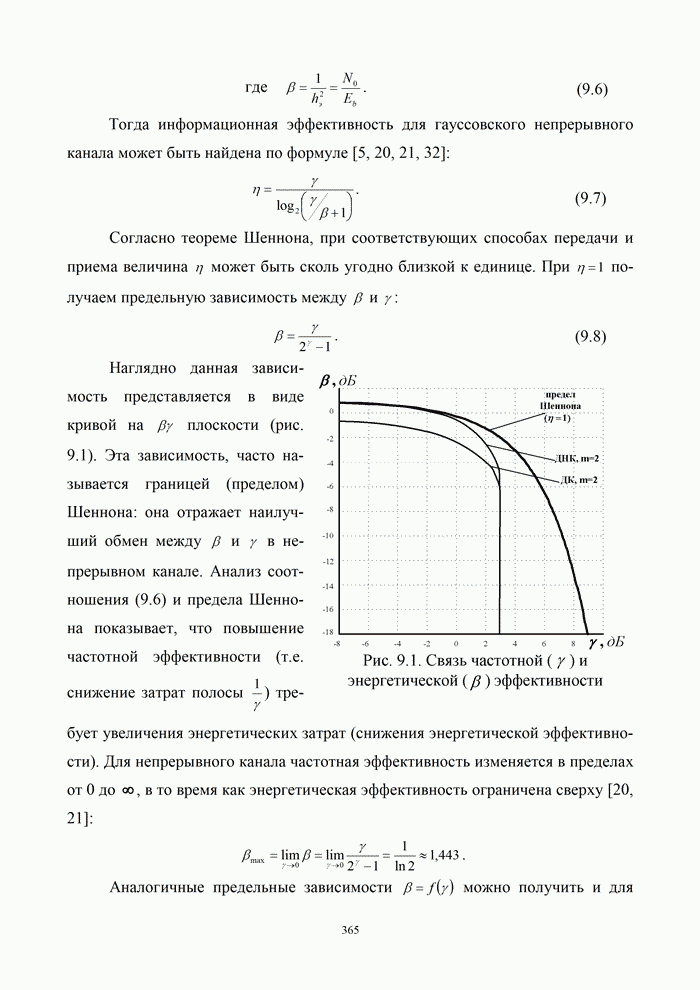
- 9.1. Оценка эффективности систем связи
- 9.1.1. Подходы к оценке эффективности
- 9.1.2. Критерии эффективности
- 9.1.3. Эффективность аналоговых и цифровых систем
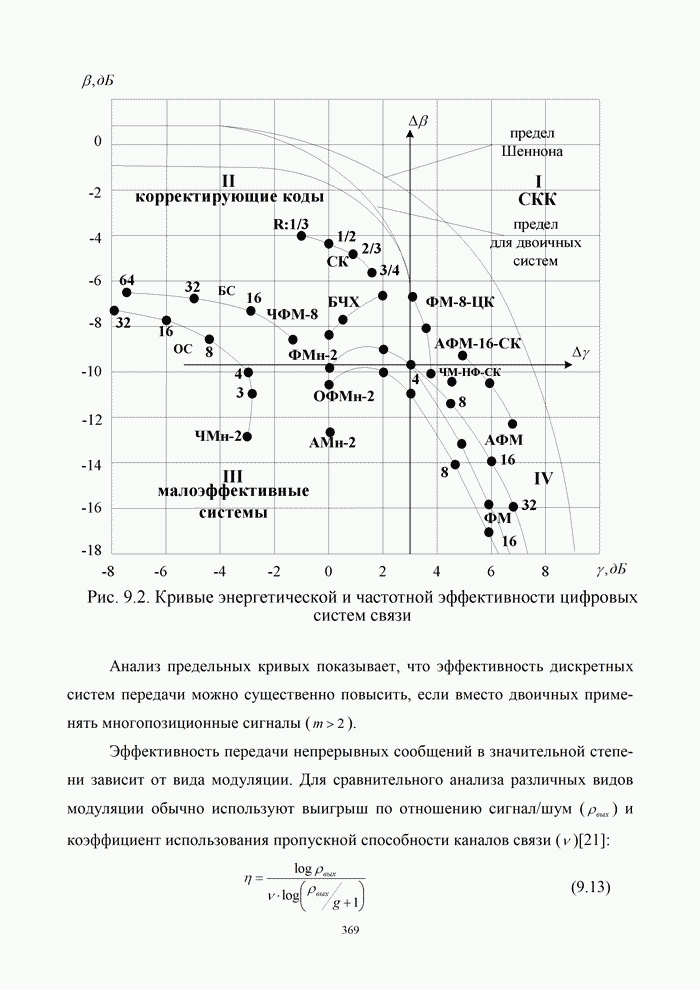
- 9.2. Выбор сигналов и помехоустойчивых кодов
- 9.2.1. Многопозиционные сигналы
- 9.2.2. Корректирующие коды
- 9.3. Оптимизация систем связи
- 9.3.1. Согласование методов модуляции и кодирования
- 9.3.2. Классификация сигнально – кодовых конструкций
- 9.4. Характеристики основных типов СКК
- 9.4.1. Согласование канала кодом Грея
- 9.4.2. Согласование на основе разбиения ансамбля на вложенные подансамбли
- 9.5. Алгоритмы цифровой обработки сигналов
- 9.5.1. Дискретные сигналы и их спектры
- 9.5.2. Алгоритмы дискретного и быстрого преобразований Фурье
- Контрольные вопросы
- Глава 10. Теоретико-информационные основы криптозащиты сообщений в телекоммуникационных системах
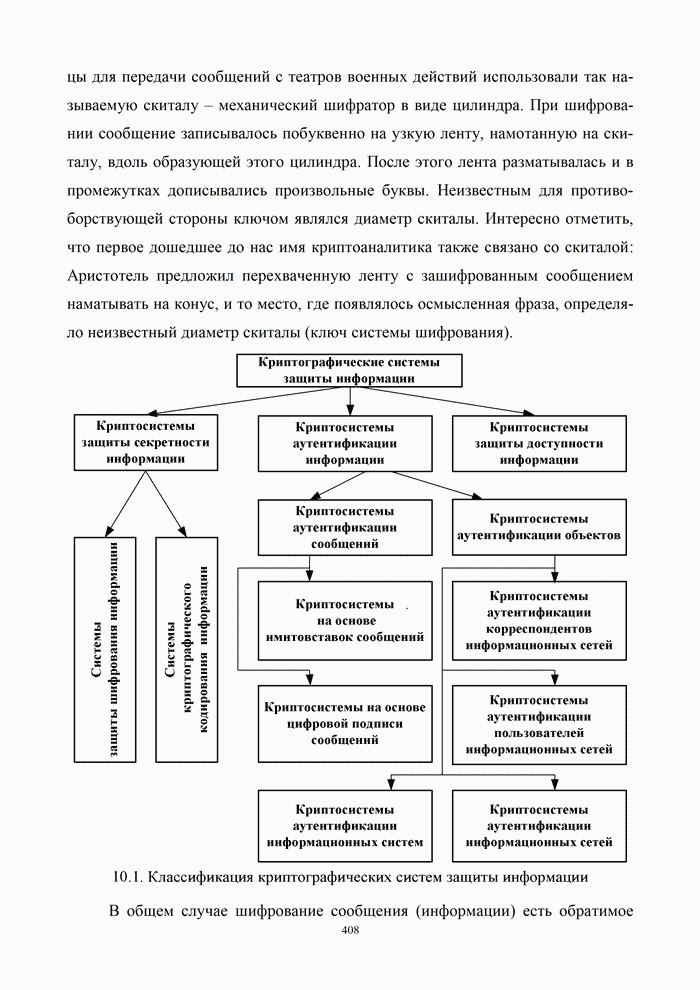
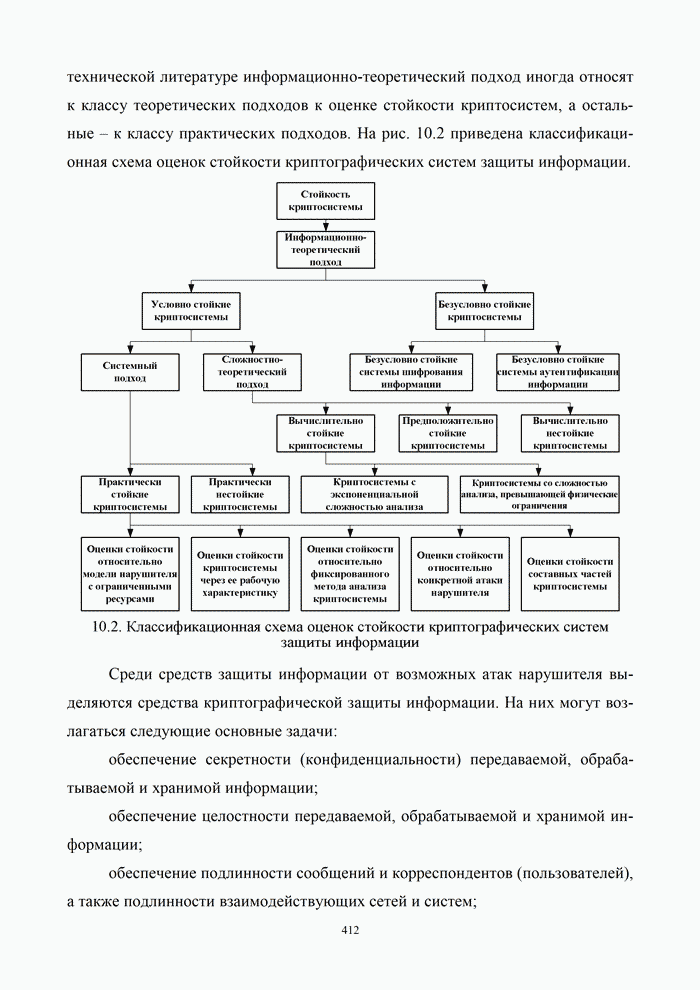
- 10.1. Классификация криптографических систем
- 10.1.2. Классификация криптографических систем защиты информации
- 10.1.3. Оценка стойкости криптосистем
- 10.2. Функции, используемые в криптографических системах
- 10.2.1. Общее описание функций, используемых в криптографических системах
- 10.2.2. Однонаправленные функции
- 10.2.3. Криптографические хэш-функции
- 10.3. Модели криптографических систем
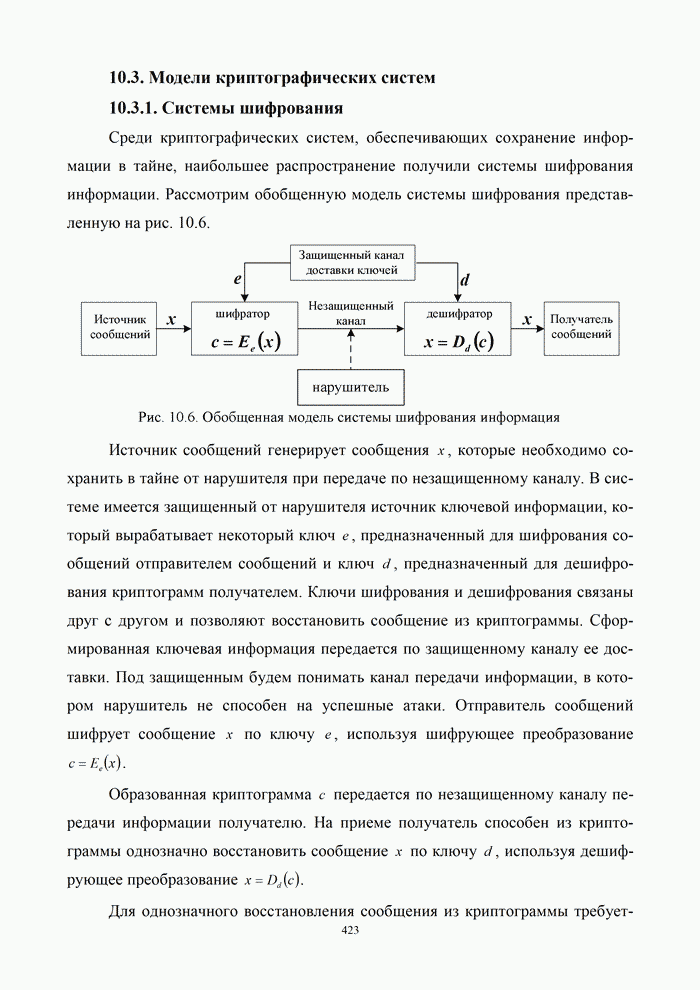
- 10.3.1. Системы шифрования
- 10.3.2. Традиционные симметричные криптосистемы
- 10.4. Алгоритмы криптографической защиты
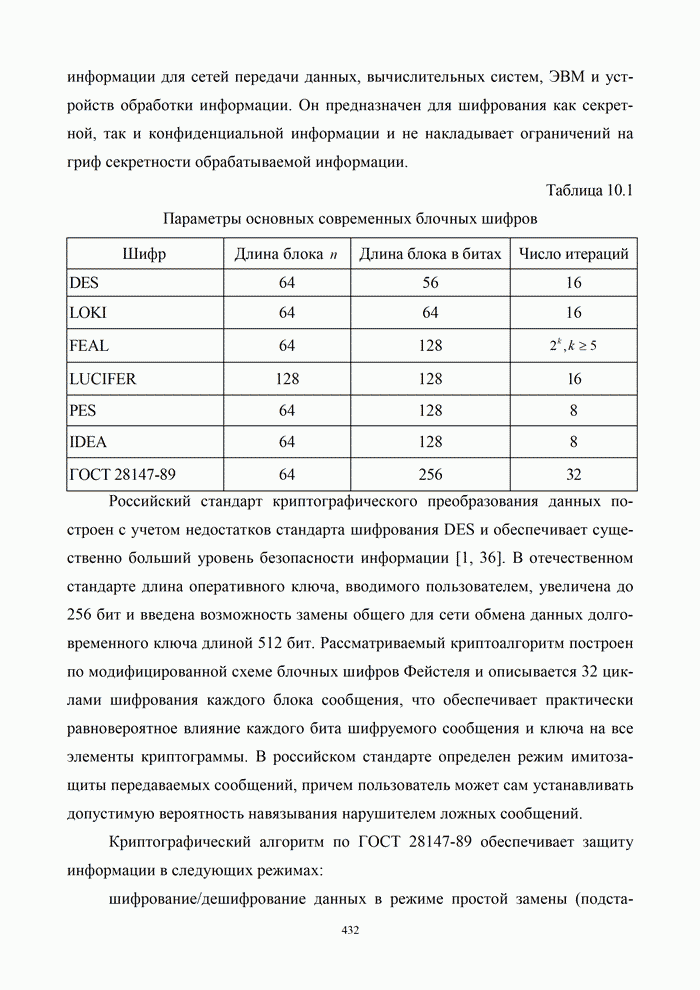
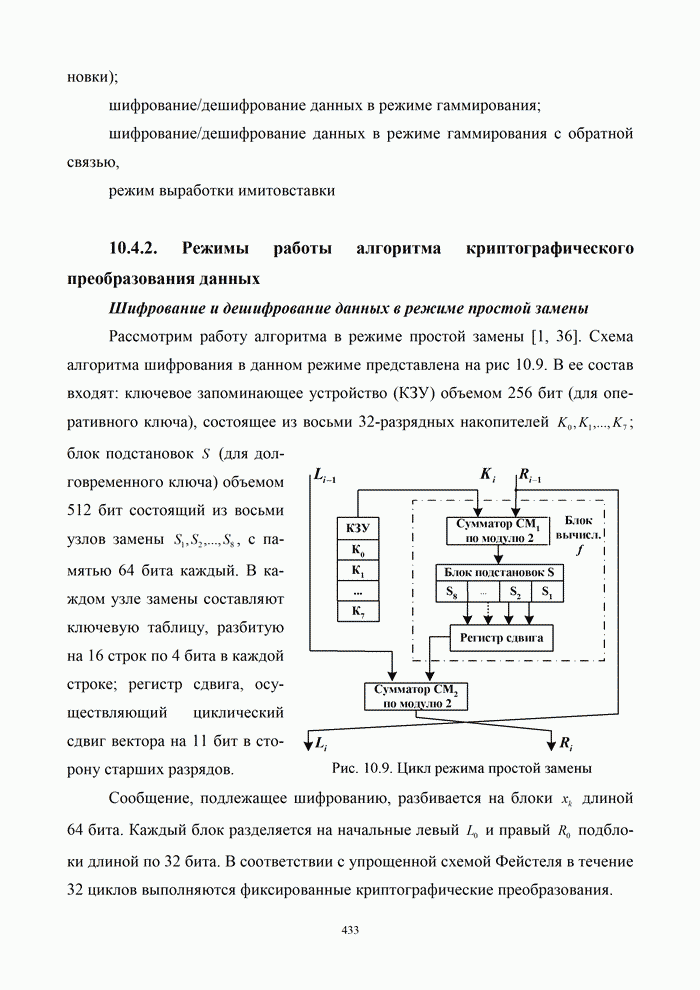
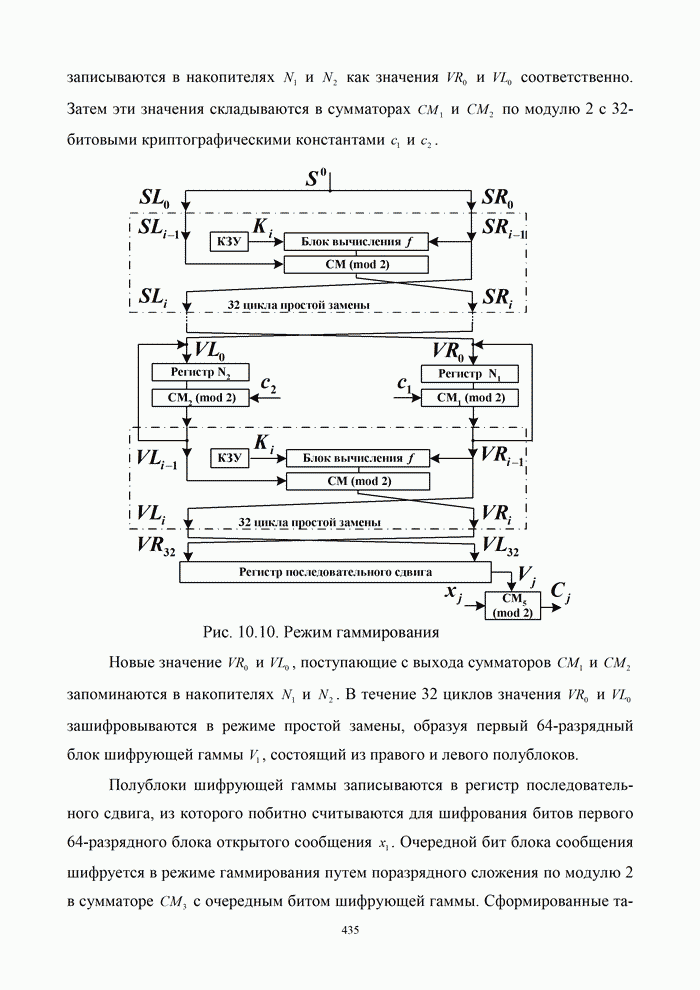
- 10.4.1. Алгоритм криптографической защиты информации согласно ГОСТ 28147-89
- Контрольные вопросы
- Заключение
- Список литературы