| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
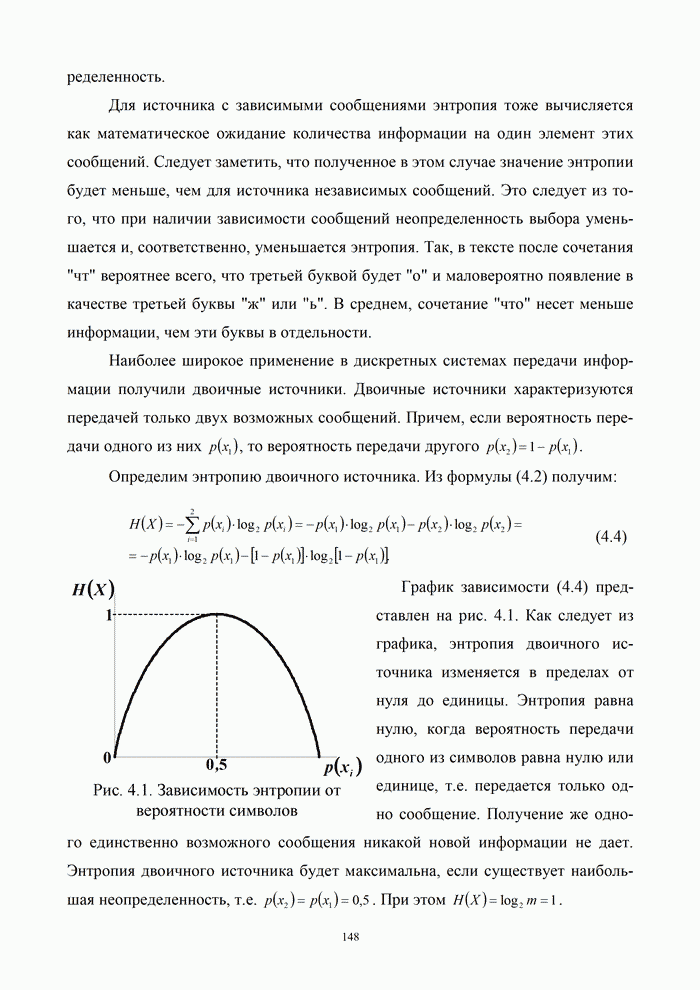
9.2. Выбор сигналов и помехоустойчивых кодов
Эффективность систем передачи дискретных сообщений можно существенно повысить путем применения многопозиционных сигналов и корректирующих кодов.
9.2.1. Многопозиционные сигналы
Ансамбль сигналов ![]() , где
, где ![]() , на отрезке
, на отрезке ![]() можно представить в виде [5, 21, 32]:
можно представить в виде [5, 21, 32]:
|
|
(9.14) |
Здесь ![]() -число отсчетов на интервале
-число отсчетов на интервале ![]() , а
, а ![]() – система базисных
ортонормированных функций:
– система базисных
ортонормированных функций:
|
|
(9.15) |
Геометрически каждому
сигналу ансамбля ![]() соответствует
точка (или вектор) в
соответствует
точка (или вектор) в ![]() -мерном пространстве с координатами (
-мерном пространстве с координатами (![]() ). В соответствии с
формулой (1.8), энергия сигнала
). В соответствии с
формулой (1.8), энергия сигнала
|
|
(9.16) |
а расстояние (1.42) между сигналами
|
|
(9.17) |
где
|
|
(9.18) |
коэффициент взаимной корреляции рассматриваемых сигналов.
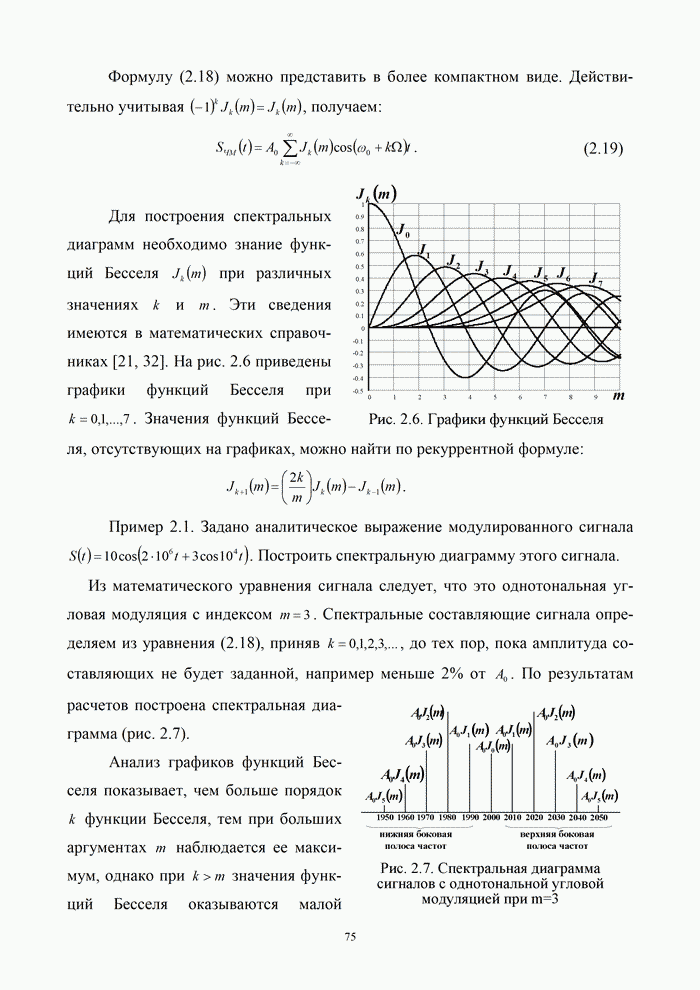
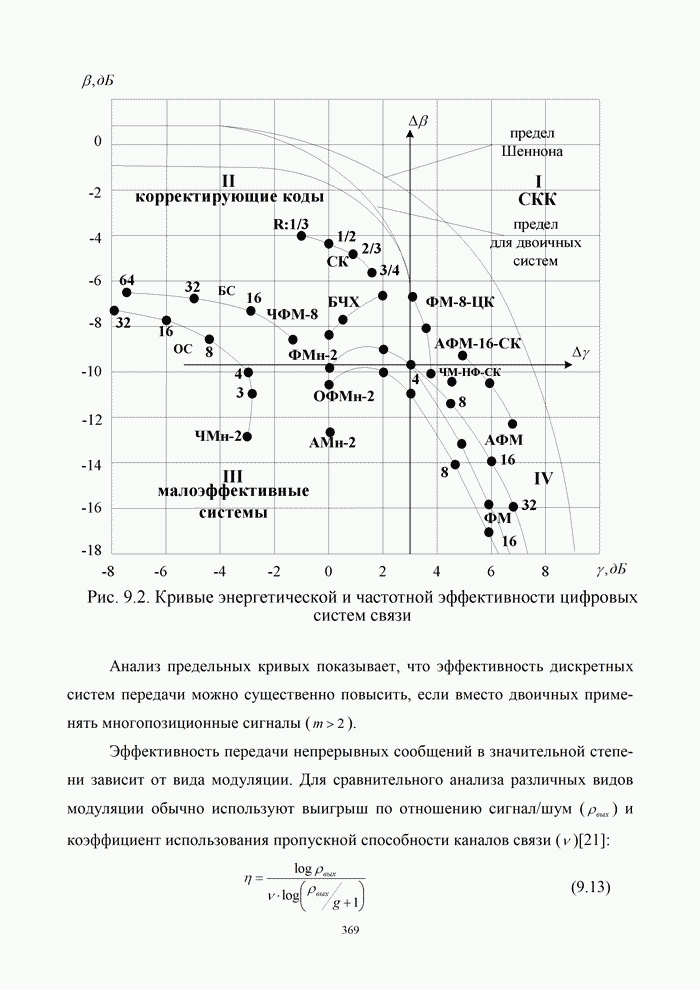
На рис. 9.2 приведены ![]() -диаграммы для
некоторых ансамблей многопозиционных сигналов. Центральное место на рис. 9.2
занимают кривые для систем с сигналами ФМн-4, которые относятся к классу многопозиционных
при
-диаграммы для
некоторых ансамблей многопозиционных сигналов. Центральное место на рис. 9.2
занимают кривые для систем с сигналами ФМн-4, которые относятся к классу многопозиционных
при ![]() . В
цифровых сетях система ФМн-4 является наиболее распространенной и принята в
качестве стандарта, поэтому при сравнительной оценке эффективности систем она
принята за эталон. Если начало координат перенести в точку, соответствующую ФМн-4,
то в новой системе координат по вертикальной оси будет отсчитываться
энергетический выигрыш
. В
цифровых сетях система ФМн-4 является наиболее распространенной и принята в
качестве стандарта, поэтому при сравнительной оценке эффективности систем она
принята за эталон. Если начало координат перенести в точку, соответствующую ФМн-4,
то в новой системе координат по вертикальной оси будет отсчитываться
энергетический выигрыш ![]() рассматриваемых систем по сравнению с
ФМн-4, а по горизонтальной оси – выигрыш
рассматриваемых систем по сравнению с
ФМн-4, а по горизонтальной оси – выигрыш ![]() по удельной скорости. В этой системе
координат все возможные системы связи можно условно разделить на четыре группы,
соответствующие четырем квадрантам на плоскости.
по удельной скорости. В этой системе
координат все возможные системы связи можно условно разделить на четыре группы,
соответствующие четырем квадрантам на плоскости.
Малоэффективные
системы (III квадрант),
имеющие относительно ФМн-4 проигрыш по ![]() и
и ![]() , например,
АМн-2, ЧМн-2. Системы с высокой энергетической эффективностью (II квадрант),
обеспечивающие выигрыш по
, например,
АМн-2, ЧМн-2. Системы с высокой энергетической эффективностью (II квадрант),
обеспечивающие выигрыш по ![]() и проигрыш
по
и проигрыш
по ![]() (системы с корректирующими кодами). Системы с высокой
частотной эффективностью (IV квадрант), обеспечивающие выигрыш по
(системы с корректирующими кодами). Системы с высокой
частотной эффективностью (IV квадрант), обеспечивающие выигрыш по ![]() и проигрыш по
и проигрыш по ![]() (системы
с многопозиционными ФМн и АФМ сигналами). Высокоэффективные системы (I
квадрант), позволяющие получить одновременно выигрыш по обоим показателям
(системы
с многопозиционными ФМн и АФМ сигналами). Высокоэффективные системы (I
квадрант), позволяющие получить одновременно выигрыш по обоим показателям ![]() и
и ![]() на основе применения сложных сигнально-кодовых
конструкций).
на основе применения сложных сигнально-кодовых
конструкций).

Можно выделить также два
класса многопозиционных сигналов. К первому отнесем так называемые «плотные» сигналы,
когда с ростом объема ансамбля ![]() при фиксированной размерности
при фиксированной размерности ![]() расстояние между
сигнальными точками уменьшается, а удельная скорость
расстояние между
сигнальными точками уменьшается, а удельная скорость ![]() возрастает при соответствующем
снижении энергетической эффективности
возрастает при соответствующем
снижении энергетической эффективности ![]() . Примерами таких сигналов служат многопозиционные ФМн и АФМ.
. Примерами таких сигналов служат многопозиционные ФМн и АФМ.
Примером сигналов, у
которых сигнальные векторы располагаются на прямой, являются двоичные противоположные
сигналы ФМн-2 (рис. 9.3). Им соответствует два симметрично расположенных
относительно начала координат вектора длиной ![]() . Расстояние между сигналами
. Расстояние между сигналами ![]() , а коэффициент
корреляции
, а коэффициент
корреляции ![]() .
.

К этому же классу
относятся и широко используемые сигналы с фазовой манипуляцией и числом позиций
![]() (рис. 9.4).
Сигналы ФМн-4 имеют одинаковые энергии, а сигнальные точки располагаются на
одинаковом расстоянии от начала координат. На амплитудно-фазовой плоскости они
образуют квадратную сеть. Сигналы этого ансамбля отличаются только начальными фазами.
Расстояние между ближайшими сигнальными точками равно
(рис. 9.4).
Сигналы ФМн-4 имеют одинаковые энергии, а сигнальные точки располагаются на
одинаковом расстоянии от начала координат. На амплитудно-фазовой плоскости они
образуют квадратную сеть. Сигналы этого ансамбля отличаются только начальными фазами.
Расстояние между ближайшими сигнальными точками равно ![]() , а между противоположными
сигналами
, а между противоположными
сигналами ![]() .
.
Многопозиционные сигналы с ФМн-8 образуют круговую сеть с равномерным распределением точек по окружности (рис. 9.5).

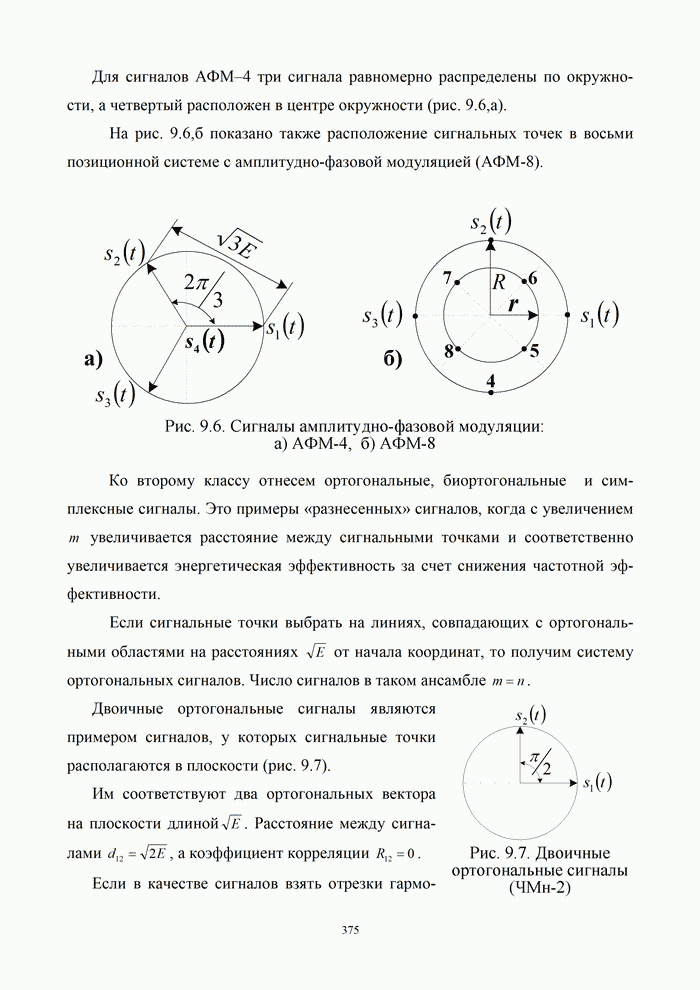
Для сигналов АФМ–4 три сигнала равномерно распределены по окружности, а четвертый расположен в центре окружности (рис. 9.6,а).
На рис. 9.6,б показано также расположение сигнальных точек в восьми позиционной системе с амплитудно-фазовой модуляцией (АФМ-8).

Ко
второму классу отнесем ортогональные, биортогональные и симплексные сигналы. Это
примеры «разнесенных» сигналов, когда с увеличением ![]() увеличивается расстояние
между сигнальными точками и соответственно увеличивается энергетическая
эффективность за счет снижения частотной эффективности.
увеличивается расстояние
между сигнальными точками и соответственно увеличивается энергетическая
эффективность за счет снижения частотной эффективности.

Если сигнальные точки
выбрать на линиях, совпадающих с ортогональными областями на расстояниях ![]() от начала координат,
то получим систему ортогональных сигналов. Число сигналов в таком ансамбле
от начала координат,
то получим систему ортогональных сигналов. Число сигналов в таком ансамбле ![]() .
.
Двоичные ортогональные сигналы являются примером сигналов, у которых сигнальные точки располагаются в плоскости (рис. 9.7).
Им соответствуют два
ортогональных вектора на плоскости длиной![]() . Расстояние между сигналами
. Расстояние между сигналами ![]() , а коэффициент корреляции
, а коэффициент корреляции
![]() .
.
Если в качестве сигналов взять
отрезки гармонических колебаний разных частот ![]() , удовлетворяющих условию ортогональности,
то получим сигналы многочастотной модуляции (МЧМ). Ортогональные сигналы
образуют эквидистантную систему; расстояния между любыми двумя сигнальными
точками одинаковы:
, удовлетворяющих условию ортогональности,
то получим сигналы многочастотной модуляции (МЧМ). Ортогональные сигналы
образуют эквидистантную систему; расстояния между любыми двумя сигнальными
точками одинаковы: ![]() .
Перспективным вариантом ЧМн сигналов являются частотно-манипулированные сигналы
с непрерывной фазой.
.
Перспективным вариантом ЧМн сигналов являются частотно-манипулированные сигналы
с непрерывной фазой.
Биортогональные сигналы
образуются путем добавления к каждому ортогональному сигналу противоположного. При
этом общее число сигналов удваивается: ![]() .
.

Симплексные сигналы
отстоят друг от друга на одинаковом расстоянии. В ![]() -мерном пространстве они образуют
правильный симплекс с числом вершин
-мерном пространстве они образуют
правильный симплекс с числом вершин ![]() . В двумерном пространстве сигнальные
точки лежат в вершинах равностороннего треугольника (рис. 9.8). Расстояние
между сигнальными точками симплексного ансамбля
. В двумерном пространстве сигнальные
точки лежат в вершинах равностороннего треугольника (рис. 9.8). Расстояние
между сигнальными точками симплексного ансамбля ![]() . При
. При ![]() симплексные сигналы совпадают с
противоположными. Для ансамблей с большим объемом (
симплексные сигналы совпадают с
противоположными. Для ансамблей с большим объемом (![]() ) симплексные сигналы по своим
свойствам и в частности по помехоустойчивости близки к ортогональным
) симплексные сигналы по своим
свойствам и в частности по помехоустойчивости близки к ортогональным ![]() .
.
Построение ансамблей
многопозиционных сигналов можно осуществить и на основе двоичных
последовательностей: для этого можно использовать элементарную матрицу Уолша–Адамара
(![]() ).
Формирование матриц высшего порядка подчинено следующему правилу: матрица
младшего порядка трижды повторяется в позитивной и один раз в негативной форме.
При достижении размерности матрицы
).
Формирование матриц высшего порядка подчинено следующему правилу: матрица
младшего порядка трижды повторяется в позитивной и один раз в негативной форме.
При достижении размерности матрицы ![]() , она уже представляет собой ансамбль многопозиционных
ортогональных сигналов с
, она уже представляет собой ансамбль многопозиционных
ортогональных сигналов с ![]() [5, 21]:
[5, 21]:
|
|
(9.19) |
Каждая строка этой
матрицы (последовательность двоичных символов) образует один сигнал; нетрудно убедиться
в том, что строки (столбцы) этой матрицы взаимно ортогональны. Дополняя матрицу
![]() инверсиями
строк, можно получить матрицу
инверсиями
строк, можно получить матрицу ![]() , представляющую ансамбль
, представляющую ансамбль ![]() биортогональных сигналов:
биортогональных сигналов:
|
|
(9.20) |
Ансамбли с большим числом
сигналов строятся аналогично. В асинхронно-адресных системах широко
используются ансамбли «почти ортогональных» сигналов, которые также формируются
на основе двоичных последовательностей. Это известные рекуррентные псевдослучайные
![]() и
и ![]() -последовательности.
-последовательности.
Приведенные на рис. 9.2 кривые
позволяют количественно оценить обменный выигрыш (проигрыш) различных систем.
Так, применение многопозиционных АФМ сигналов с ![]() позволяет получить частотный выигрыш в
2 раза (
позволяет получить частотный выигрыш в
2 раза (![]() дБ)
в обмен на снижение энергетического выигрыша
дБ)
в обмен на снижение энергетического выигрыша ![]() более чем на 4 дБ. Получить
энергетический выигрыш в обмен на снижение удельной скорости можно с помощью ортогональных
и биортогональных сигналов.
более чем на 4 дБ. Получить
энергетический выигрыш в обмен на снижение удельной скорости можно с помощью ортогональных
и биортогональных сигналов.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Список сокращений
- Основные обозначения
- ВВЕДЕНИЕ
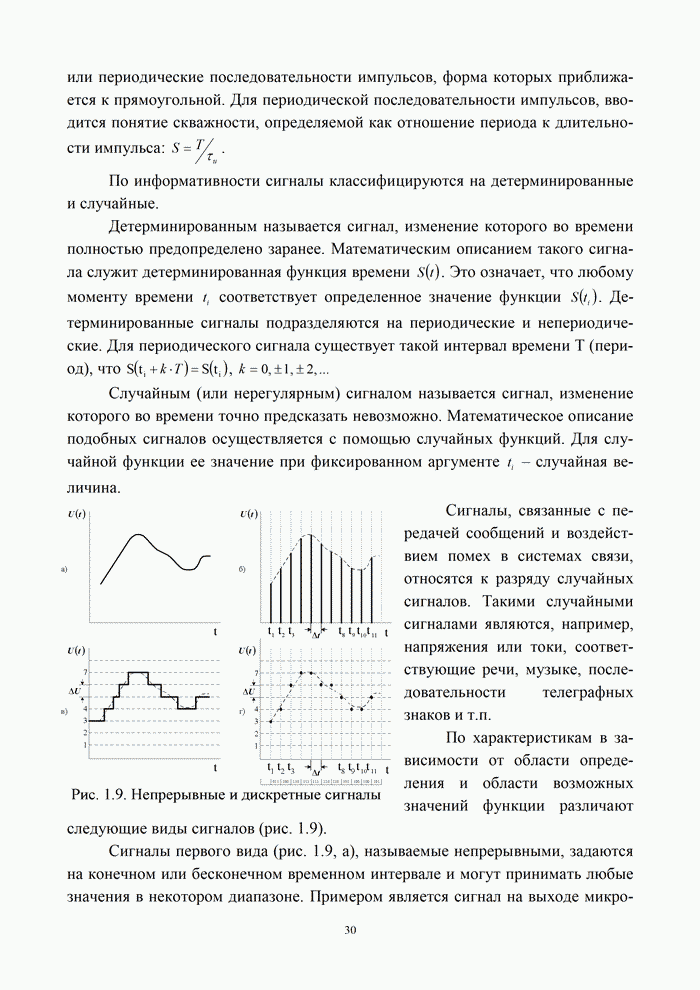
- Глава 1. Сообщения, сигналы и помехи, их математические модели
- 1.1. Основные понятия и определения
- 1.1.1. Сообщение, сигнал, модуляция
- 1.1.2. Основные параметры сигналов
- 1.2. Системы связи. Каналы связи
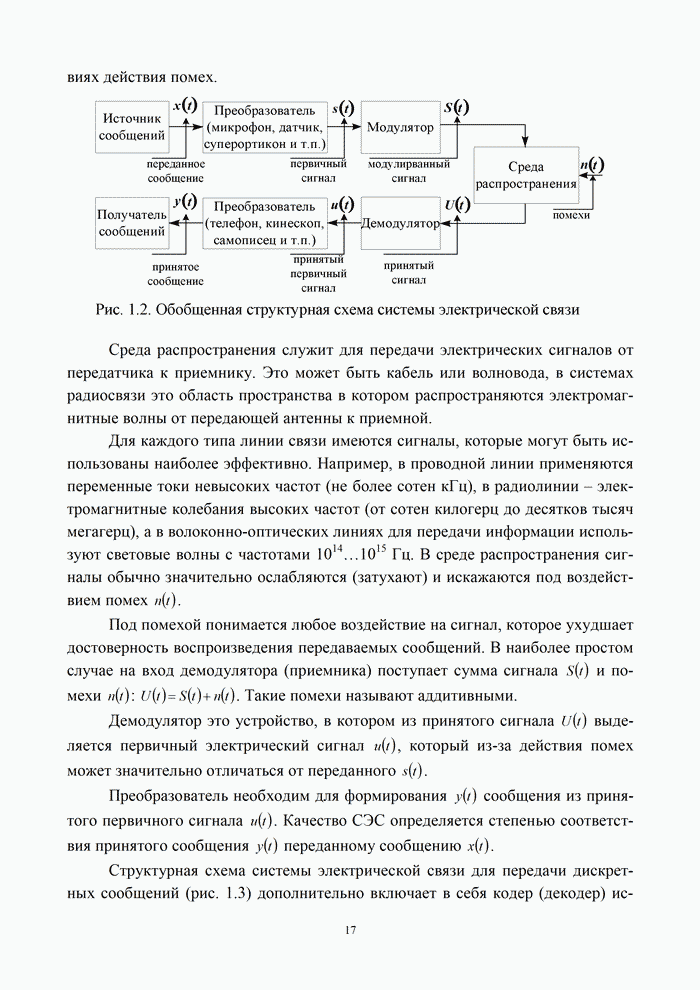
- 1.2.1. Структура канала электросвязи
- 1.2.2. Линия и сеть связи
- 1.2.3. Помехи и искажения в канале
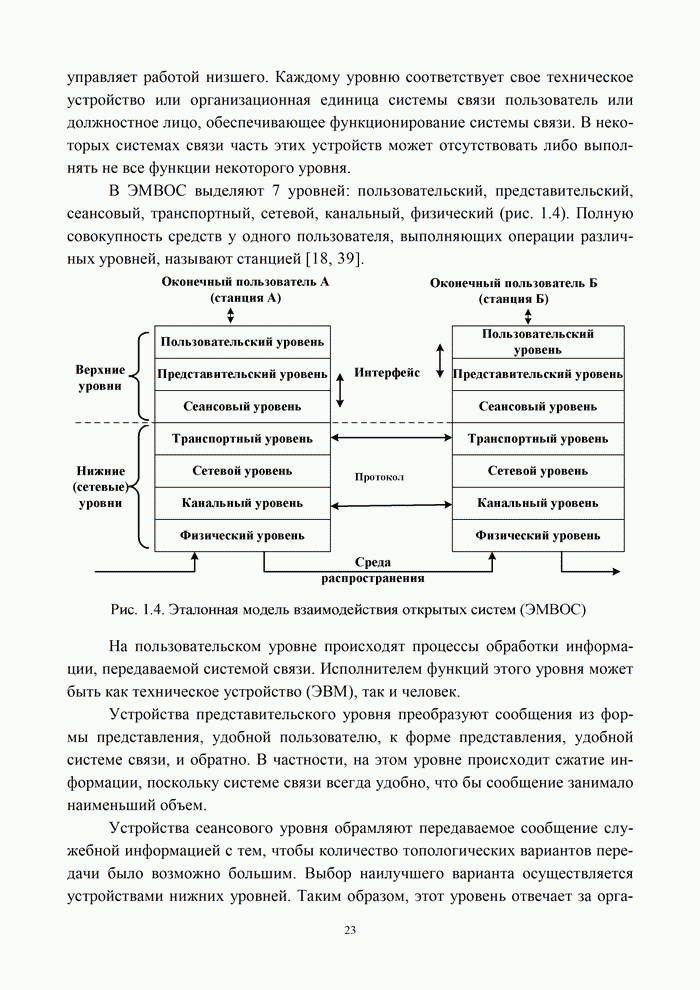
- 1.2.4. Эталонная модель взаимодействия открытых систем
- 1.2.5. Модели каналов связи и их математическое описание
- 1.3. Способы описания сигналов и помех
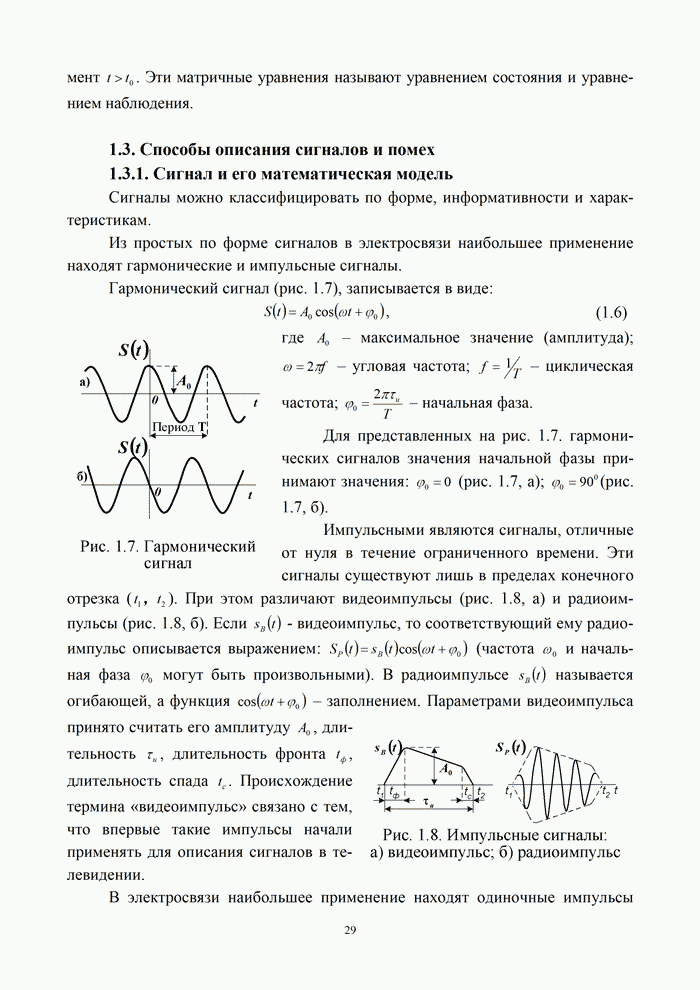
- 1.3.1. Сигнал и его математическая модель
- 1.3.2. Энергетические характеристики детерминированного сигнала
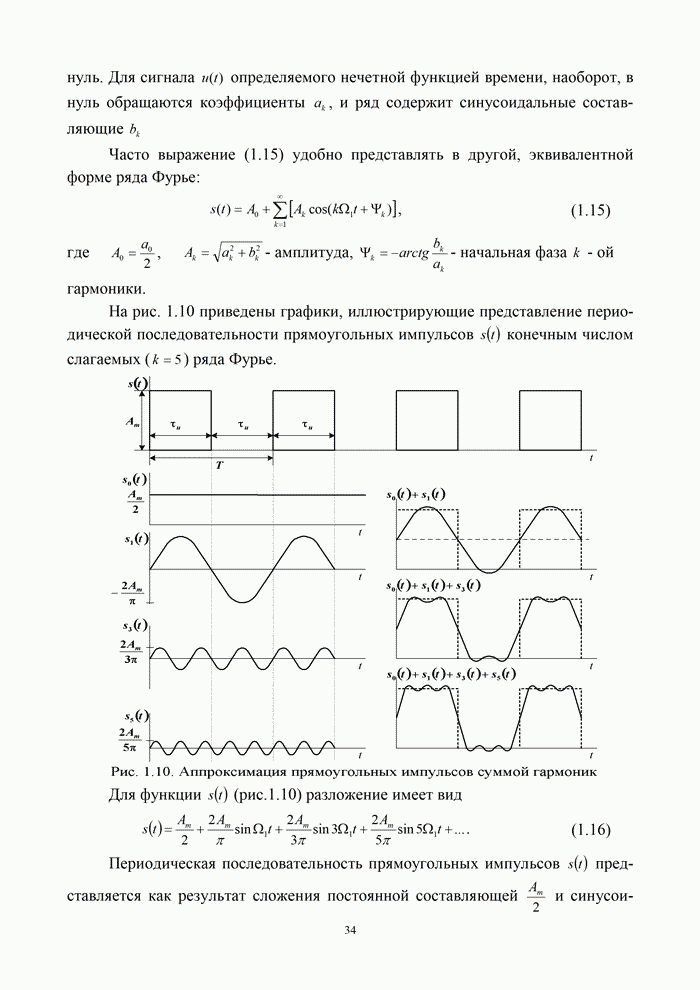
- 1.4.2. Представление сигналов и помех рядом Фурье
- 1.4.3. Применение преобразования Фурье для непериодических сигналов
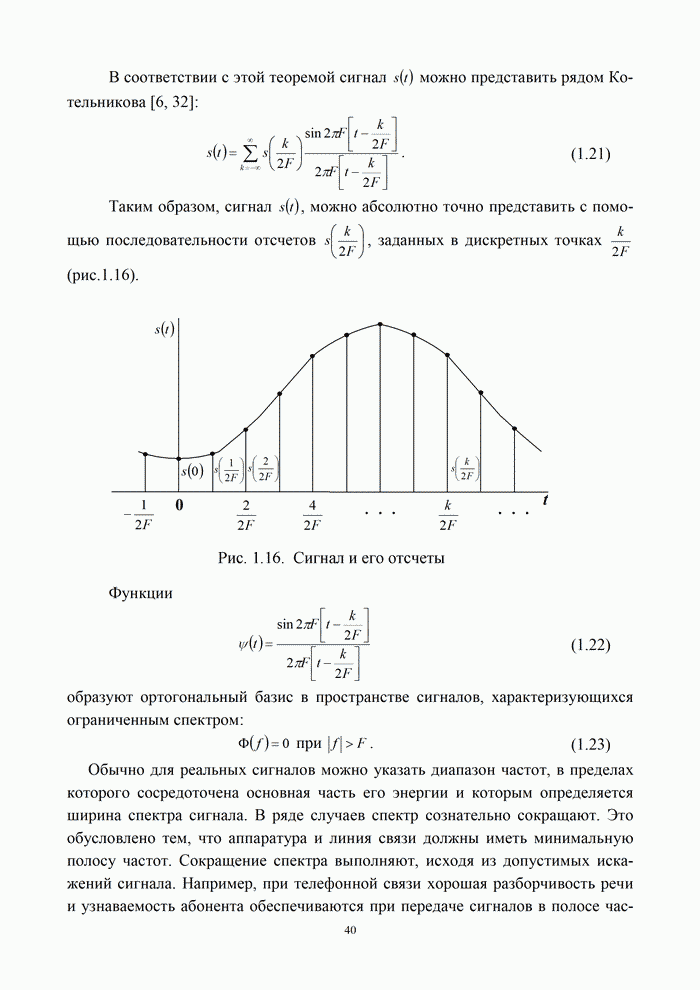
- 1.5. Теорема Котельникова
- 1.6. Пространство сигналов
- 1.6.1. Линейное пространство
- 1.6.2. Представление сигнала в многомерном пространстве
- 1.7. Сигналы как случайные процессы
- 1.7.1. Характеристики случайного процесса
- 1.7.2. Флуктуационный шум
- 1.8. Комплексное представление сигналов и помех
- 1.8.1. Понятие аналитического сигнала
- 1.8.2. Огибающая, мгновенная фаза и мгновенная частота узкополосного случайного процесса
- Контрольные вопросы
- Глава 2. Методы формирования и преобразования сигналов
- 2.1. Модуляция сигналов
- 2.1.1. Амплитудная модуляция гармонической несущей
- 2.1.2. Балансная и однополосная модуляция гармонической несущей
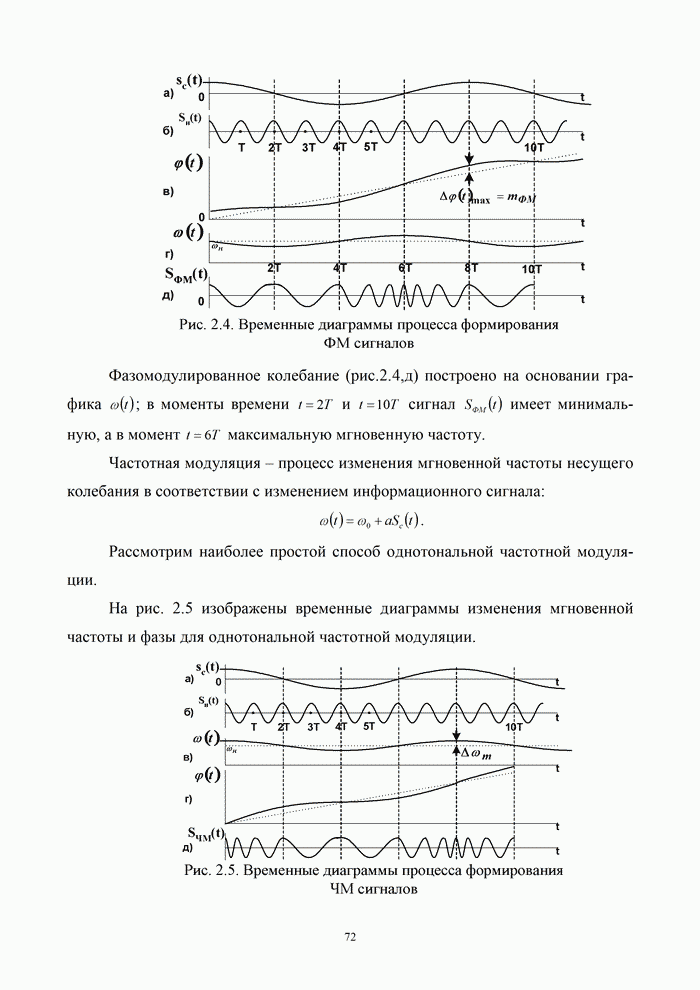
- 2.2. Методы угловой модуляции
- 2.2.1. Принципы частотной и фазовой (угловой) модуляции
- 2.2.2. Спектр сигналов угловой модуляции
- 2.3. Формирование и детектирование модулированных сигналов
- 2.3.1. Формирование и детектирование сигналов амплитудной и однополосной амплитудной модуляции
- 2.3.2. Формирование и детектирование сигналов угловой модуляции
- 2.4. Манипуляция сигналов
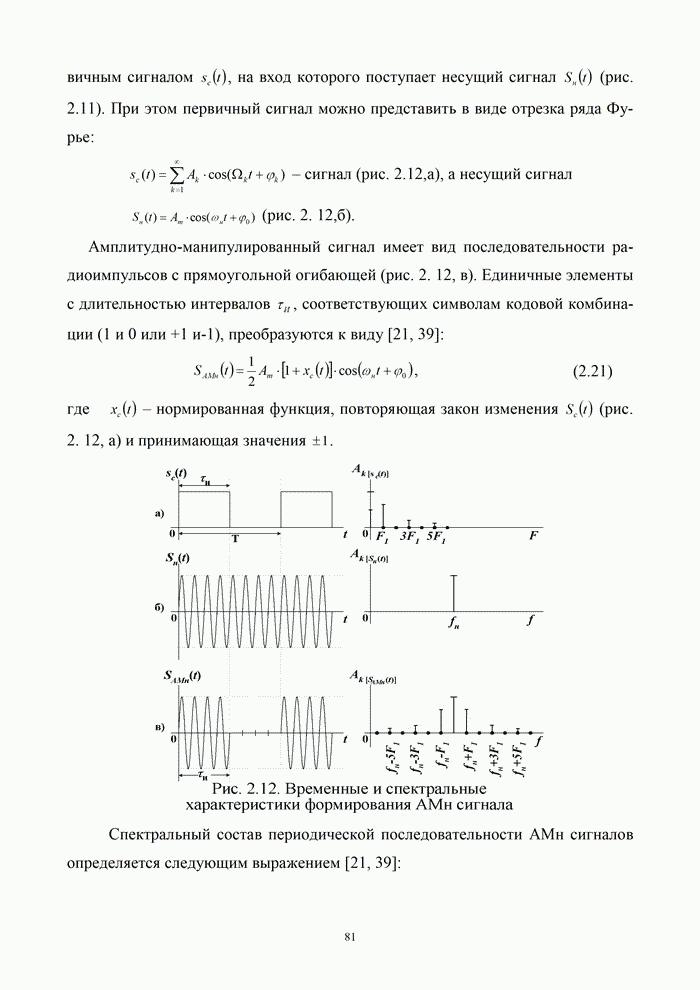
- 2.4.1. Временные и спектральные характеристики амплитудно-манипулированных сигналов
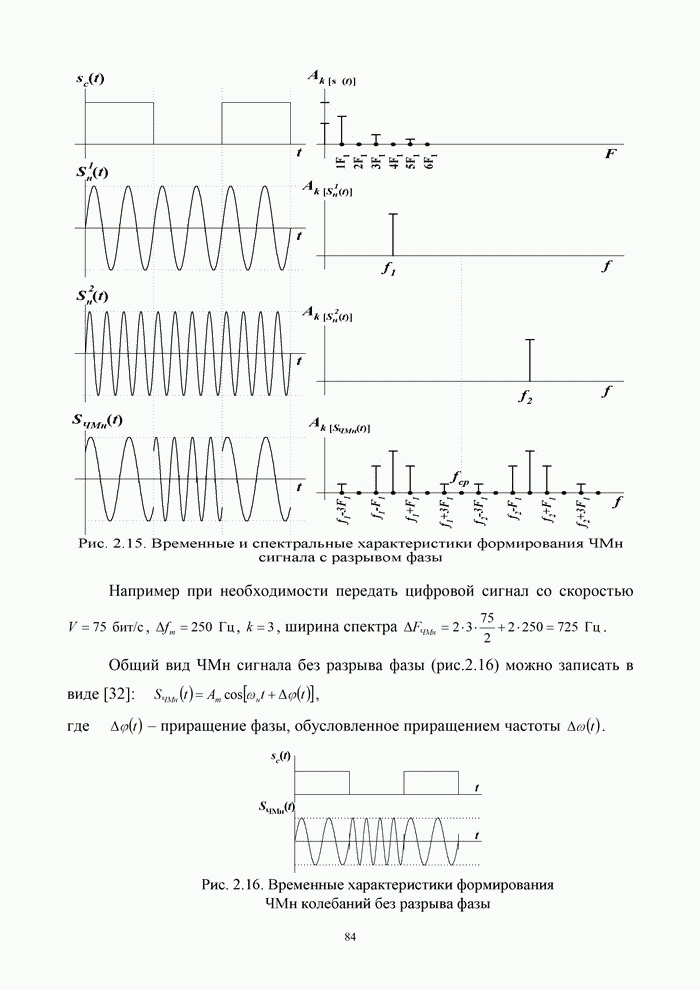
- 2.4.2. Временные и спектральные характеристики частотно-манипулированных сигналов
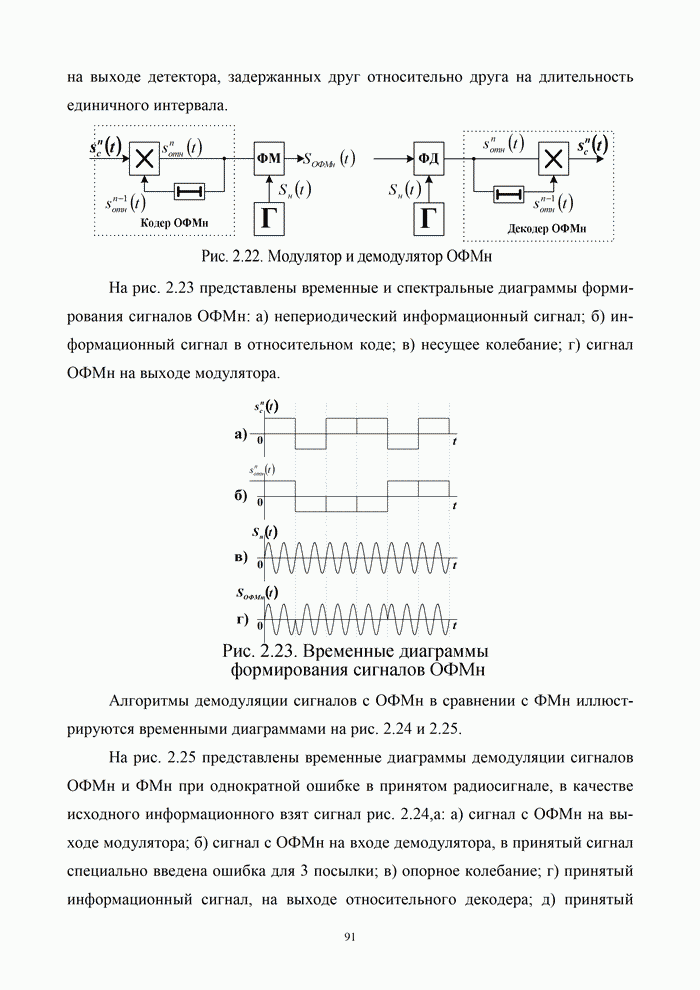
- 2.4.3. Фазовая (относительно-фазовая) манипуляция сигналов
- 2.5. Системы связи с многопозиционной относительной фазовой манипуляцией
- 2.5.1. Принцип формирования сигнала с многократной относительной фазовой манипуляцией
- 2.5.2. Квадратурная относительно-фазовая манипуляция (КОФМ)
- 2.5.3. Принцип частотной модуляции с непрерывной фазой
- Контрольные вопросы
- Глава 3. Помехоустойчивость приема дискретных сообщений
- 3.1. Критерии качества и правила приема дискретных сообщений
- 3.1.1. Понятие о помехоустойчивости систем электрической связи
- 3.1.2. Задача оптимального приема
- 3.1.3. Вычисление вероятностей ошибок
- 3.2. Оптимальная демодуляция при когерентном приеме сигналов
- 3.2.1. Оптимальные алгоритмы приема при полностью известных сигналах
- 3.2.2. Реализация алгоритмов оптимального когерентного приема
- 3.3. Помехоустойчивость приема сигналов с известными параметрами
- 3.4. Прием сигналов с неопределенной фазой
- 3.4.1. Оптимальный некогерентный прием дискретных сигналов
- 3.4.2. Помехоустойчивость оптимального некогерентного приема
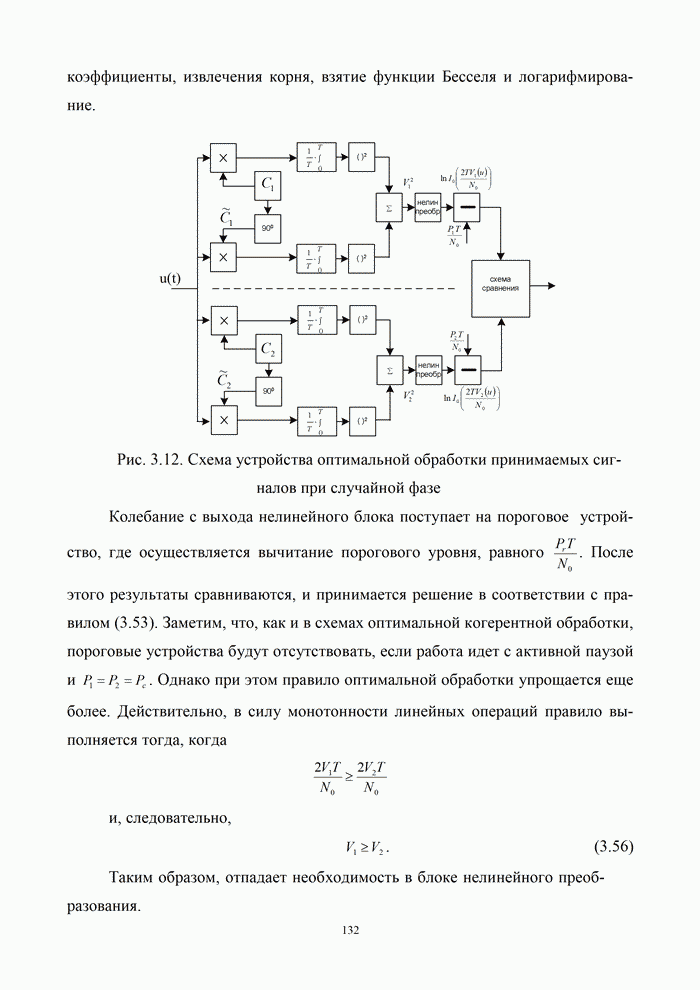
- 3.5. Подоптимальные методы приема
- 3.5.1. Причины применения неоптимальных методов приема
- 3.5.2. Квазиоптимальные методы приема
- Контрольные вопросы
- Глава 4. Теория передачи информации
- 4.1. Информационные характеристики источника сообщений
- 4.1.1. Количественное определение информации
- 4.1.2. Энтропия и производительность дискретного источника сообщений
- 4.2. Пропускная способность дискретного канала
- 4.2.1. Количество информации переданной по дискретному каналу
- 4.2.2. Пропускная способность дискретного канала
- 4.2.3. Пропускная способность симметричного дискретного канала без памяти
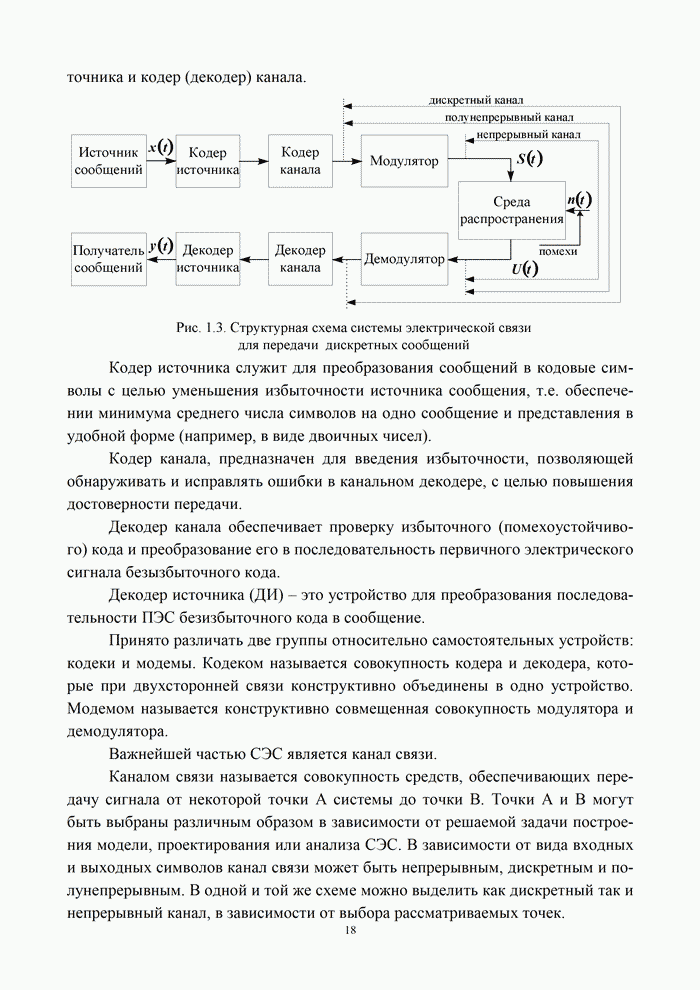
- 4.3. Методы сжатия дискретных сообщений
- 4.3.1. Условия существования оптимального неравномерного кода
- 4.3.2. Прямая и обратная теоремы кодирования источника неравномерными кодами
- 4.3.3. Показатели эффективности сжатия
- 4.3.4. Кодирование источника дискретных сообщений методом Шеннона-Фано
- 4.3.5. Кодирование источника дискретных сообщений методом Хаффмена
- 4.4. Пропускная способность непрерывного канала
- 4.4.1. Постановка задачи передачи дискретных сообщений в непрерывном канале
- 4.4.2. Количество информации, переданной по непрерывному каналу
- 4.4.3. Пропускная способность непрерывного канала
- Контрольные вопросы
- Глава 5. Теория кодирования сообщений
- 5.1. Помехоустойчивое кодирование: блочные и непрерывные коды
- 5.1.1. Постановка задачи помехоустойчивого кодирования
- 5.1.2. Классификация кодов
- 5.1.3. Основные характеристики и свойства блочных кодов
- 5.2. Эффективность помехоустойчивого кодирования
- 5.2.1. Эффективность кода в режиме исправления ошибок
- 5.2.2. Эффективность кода в режиме обнаружения ошибок
- 5.2.3. Эффективность помехоустойчивых кодов
- 5.3. Математические основы теории помехоустойчивого кодирования
- 5.3.1. Краткие сведения из теории чисел
- 5.3.2. Группы
- 5.3.3. Кольца и поля
- 5.3.4. Векторное пространство
- 5.3.5. Конечные поля
- 5.4. Линейные блочные коды
- 5.4.1. Система передачи дискретных сообщений
- 5.4.2. Параметры линейного кода
- 5.4.3. Полиномиальные циклические коды
- 5.4.4. Циклические коды и корни полиномов
- 5.4.5. Спектральное описание циклических кодов
- 5.4.6. Простейшие блочные линейные коды
- 5.5. Коды Боуза-Чоудхури-Хоквингема
- 5.5.1. Методы задания кодов БЧХ
- 5.5.2. Принципы декодирования кодов БЧХ
- 5.5.3. Методы реализации этапов декодирования кодов БЧХ
- 5.6. Коды Рида-Соломона
- 5.6.1. Основные определения
- 5.6.2. Обнаружение и исправление пакетов ошибок
- 5.7. Коды Рида-Маллера
- 5.7.1. Задание и декодирование кодов Рида-Маллера
- 5.7.2. Симплексные коды и m-последовательности
- 5.7.3. Связь между блочными кодами
- 5.8. Сверточные коды
- 5.8.1. Основные параметры
- 5.8.2. Способы задания сверточного кода
- 5.8.3. Алгоритм декодирования Витерби
- 5.9. Помехоустойчивость систем передачи дискретных сообщений
- 5.9.1. Две процедуры приема сигналов
- 5.9.2. Помехоустойчивость систем передачи информации при оптимальной процедуре приема
- 5.9.3. Помехоустойчивость систем передачи информации при посимвольном приеме сигналов
- Контрольные вопросы
- Глава 6. Сигналы с импульсной модуляцией
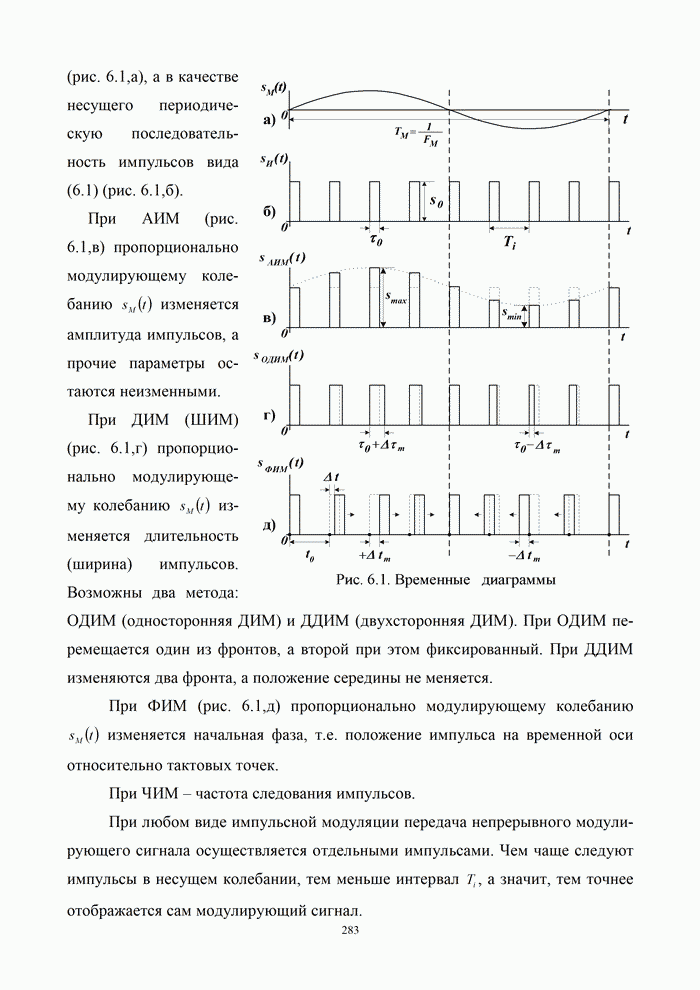
- 6.1. Методы импульсной модуляции
- 6.1.1. Импульсные методы передачи непрерывных сигналов
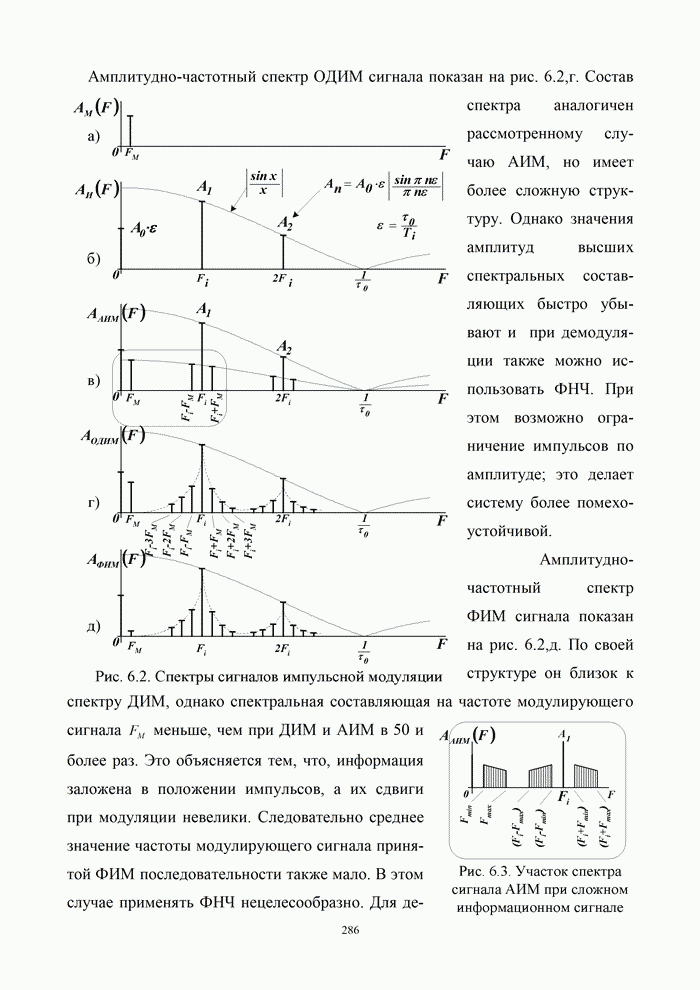
- 6.1.2. Спектральные характеристики импульсных методов модуляции
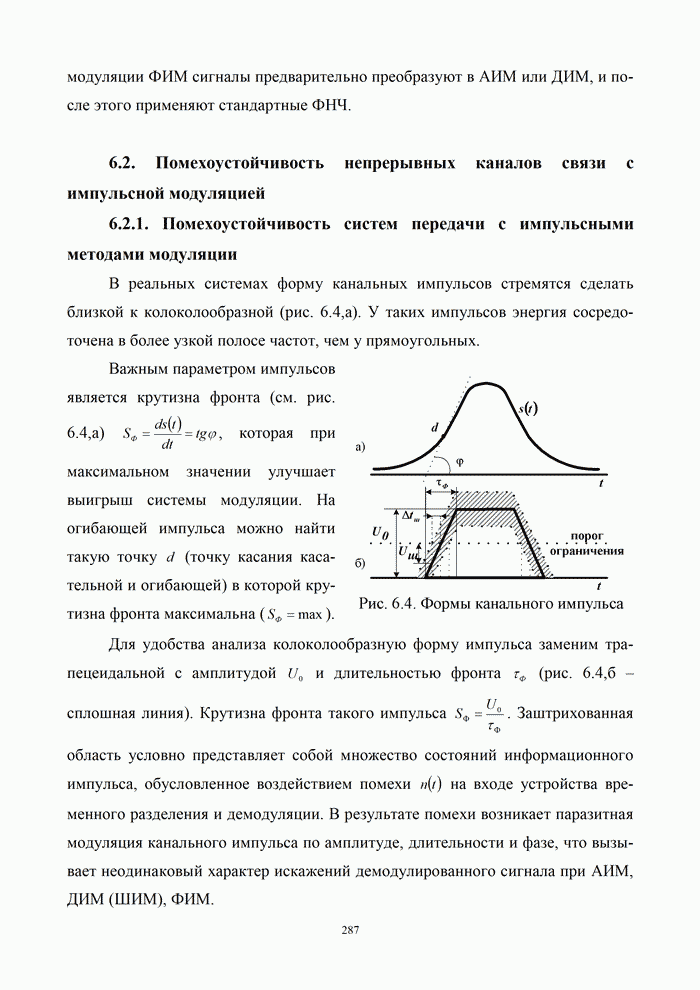
- 6.2. Помехоустойчивость непрерывных каналов связи с импульсной модуляцией
- 6.2.1. Помехоустойчивость систем передачи с импульсными методами модуляции
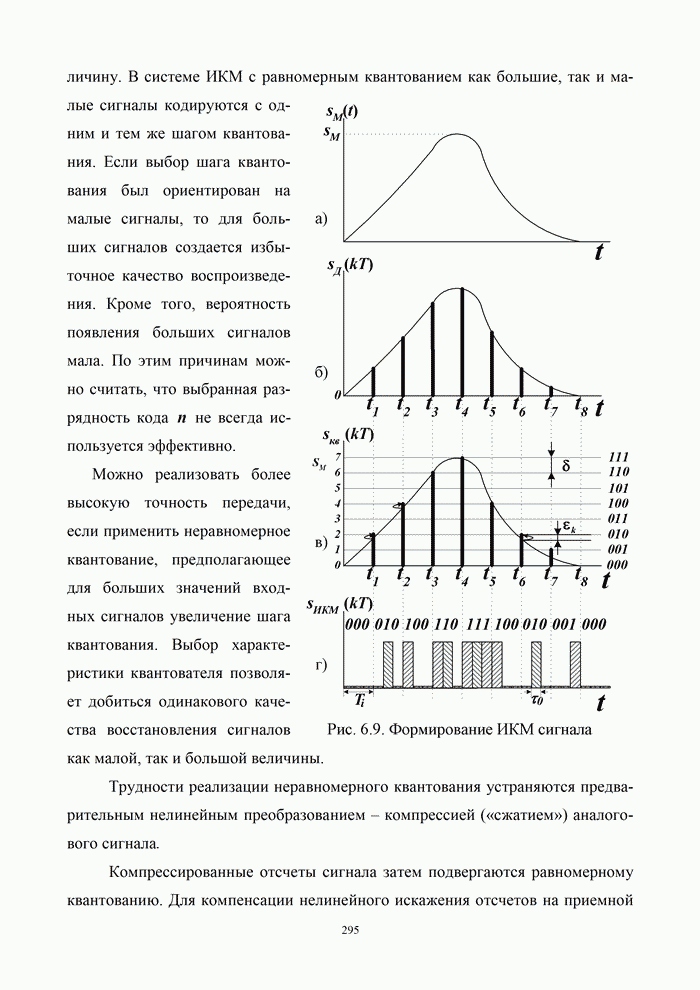
- 6.3. Цифровые методы передачи непрерывных сообщений
- 6.3.1. Передача сигналов с импульсно-кодовой модуляцией
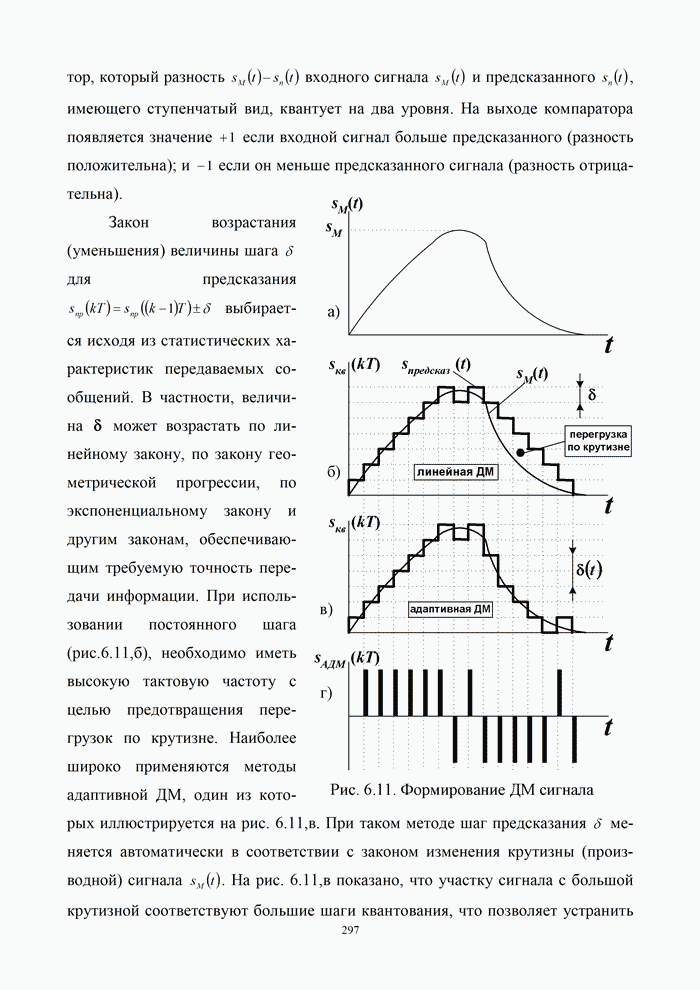
- 6.3.2. Передача сигналов с дельта модуляцией
- 6.3.3. Квантование сигналов в системах с ИКМ и ДМ
- Контрольные вопросы
- Глава 7. Методы приема сигналов в сложных условиях
- 7.1. Прием сигналов в каналах с замираниями
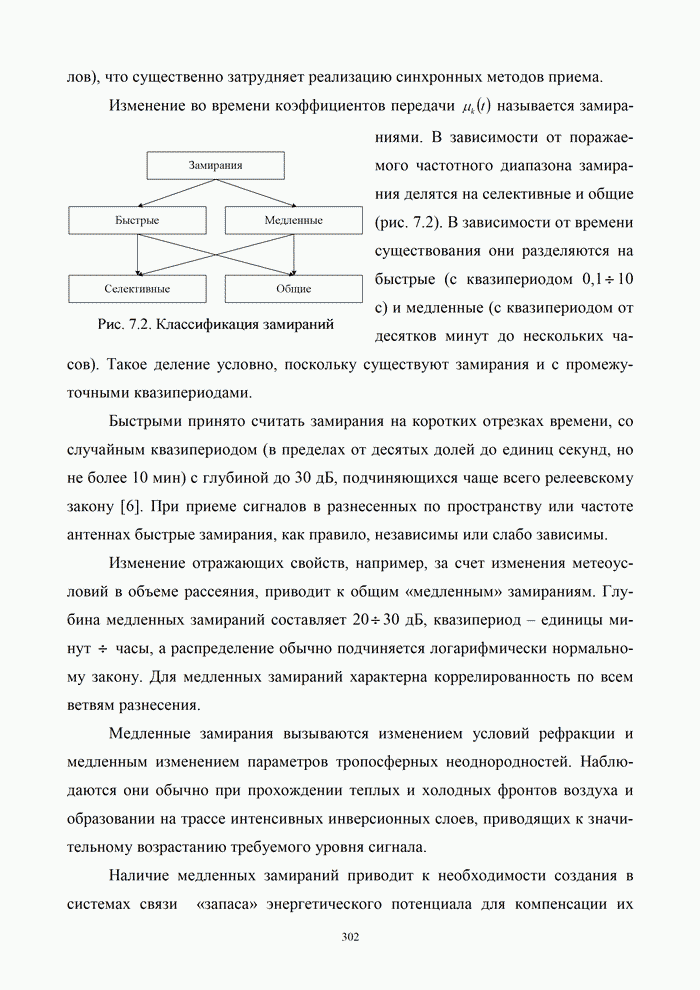
- 7.1.1. Сущность замираний и их классификация
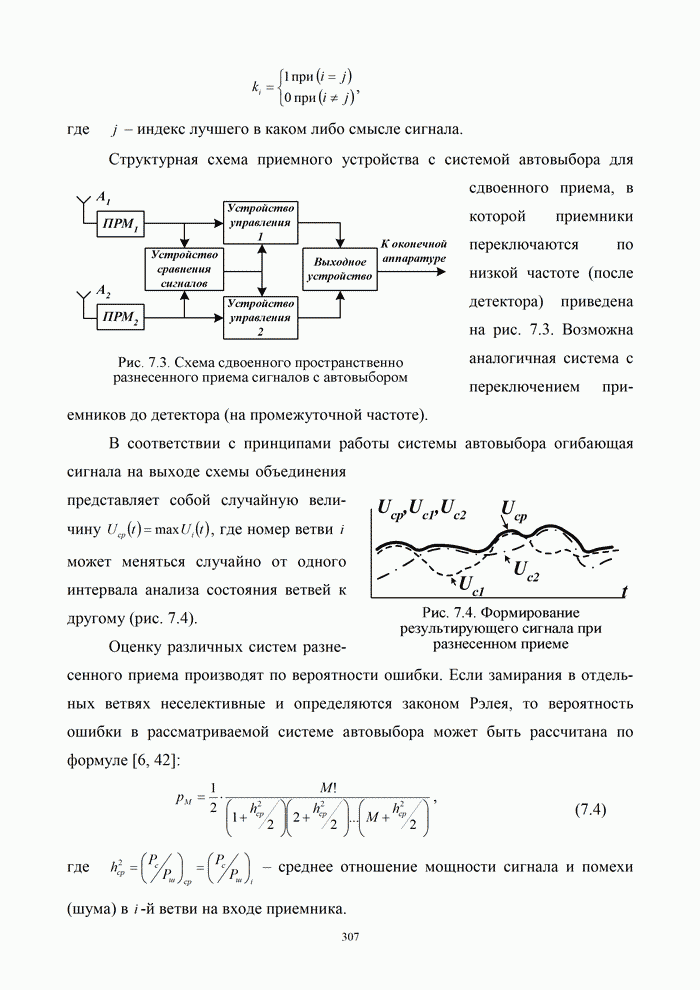
- 7.1.2. Принципы разнесенного приема сигналов
- 7.2. Методы борьбы с замираниями сигналов
- 7.2.1. Методы борьбы с замираниями в аналоговых системах связи
- 7.2.2. Методы борьбы с замираниями в цифровых системах связи
- 7.3. Методы борьбы с межсимвольной интерференцией
- 7.3.1. Причины возникновения и сущность межсимвольной интерференции
- 7.3.2. Обработка сигналов в каналах с межсимвольной интерференцией
- 7.3.3. Помехоустойчивость в каналах с межсимвольной интерференцией
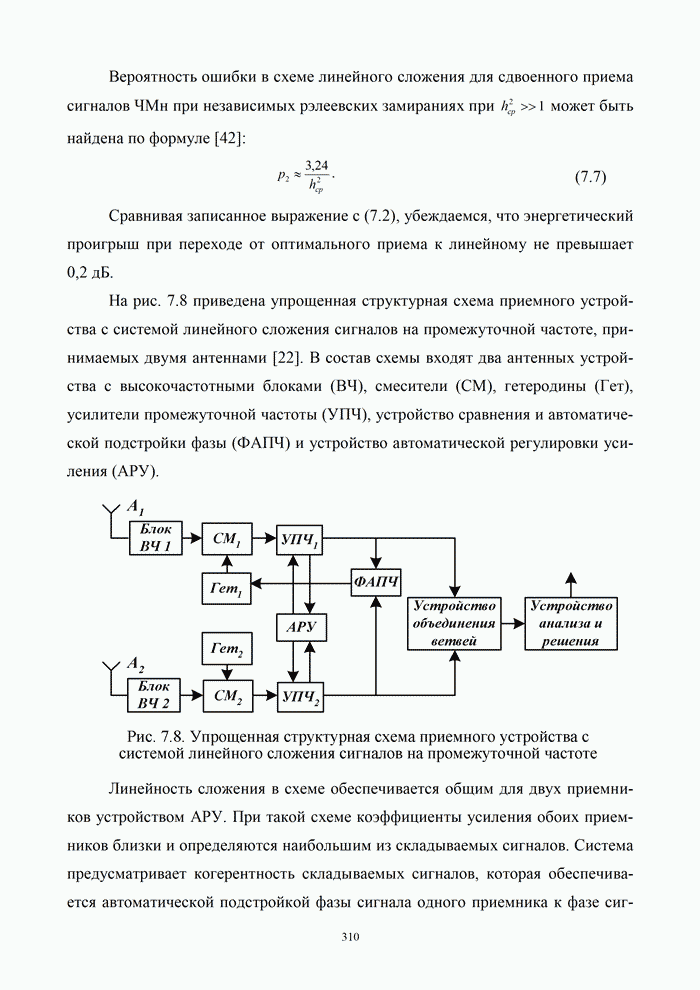
- 7.4. Прием дискретных сообщений в каналах с сосредоточенными по спектру и импульсными помехами
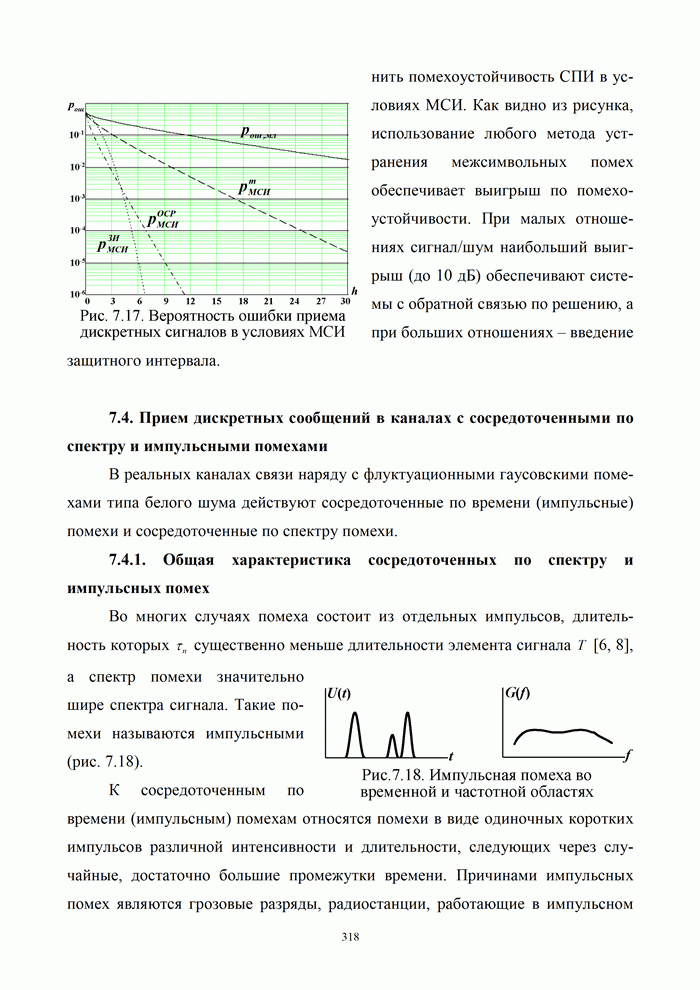
- 7.4.1. Общая характеристика сосредоточенных по спектру и импульсных помех
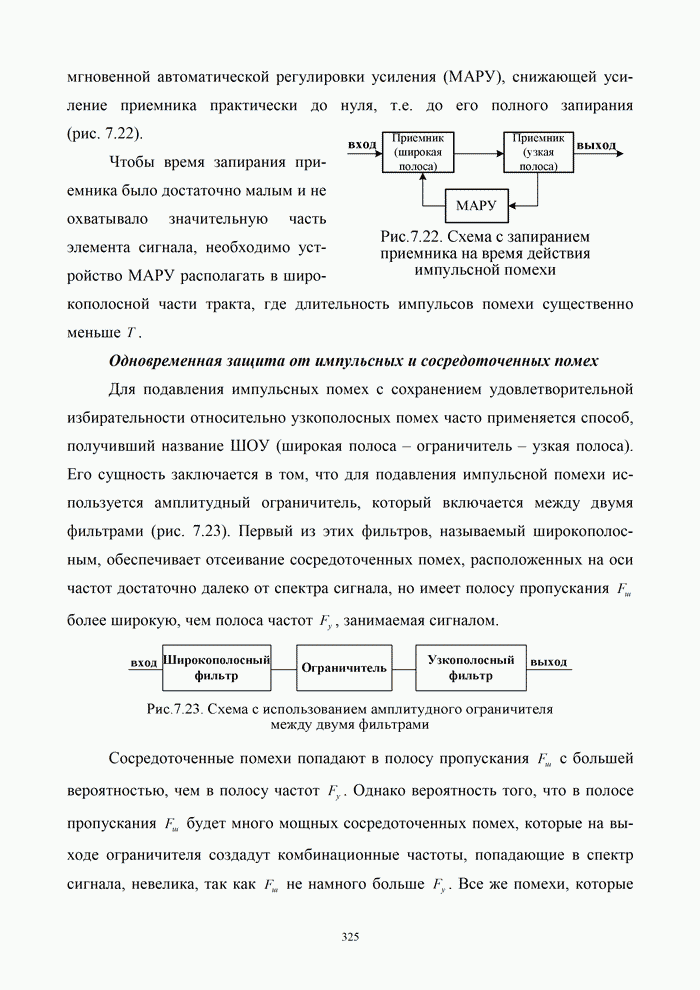
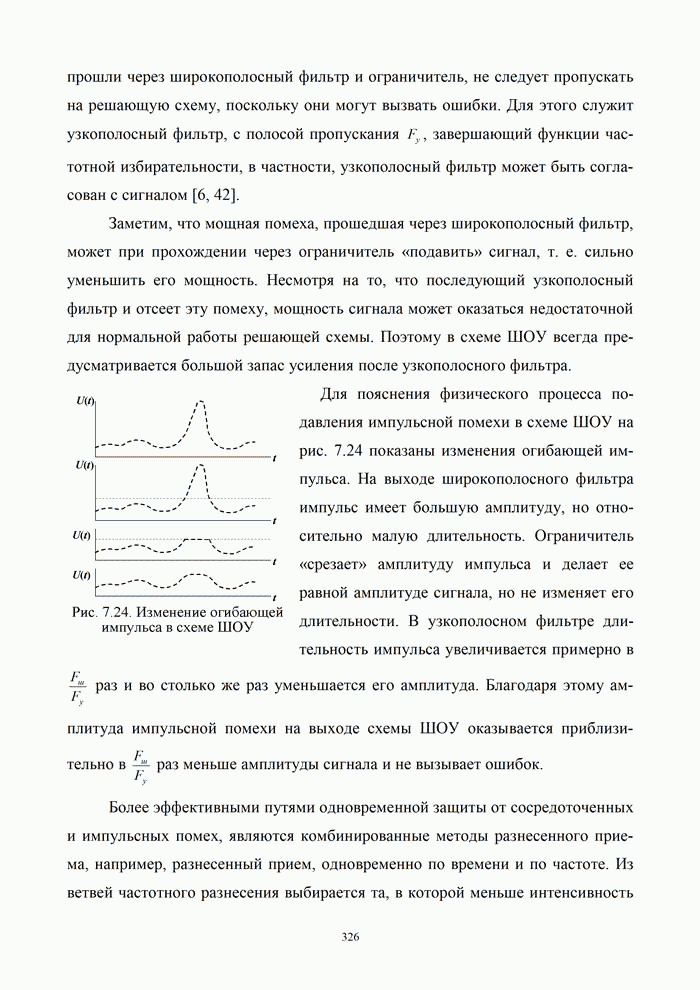
- 7.4.2. Борьба с сосредоточенными и импульсными помехами
- 7.5. Компенсация помех и искажений в канале
- 7.5.1. Принцип работы радиолинии с ФМ ПСС (ФМ ШПС)
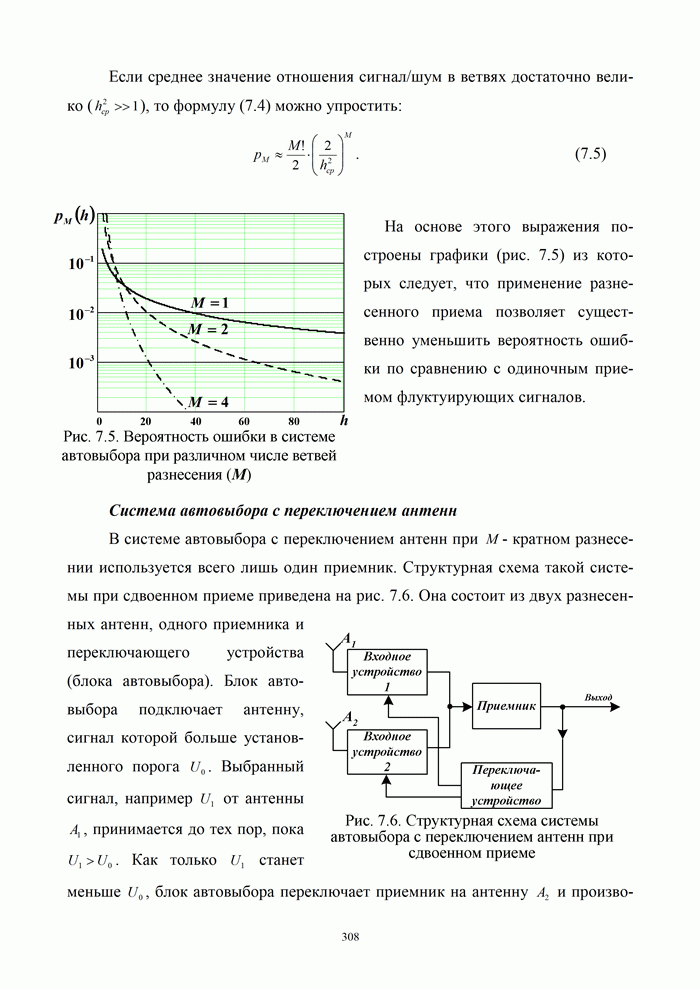
- 7.5.2. Помехоустойчивость радиолинии с ФМ ПСС
- 7.5.3. Принципы работы радиолиний с ППРЧ
- 7.5.4. Помехоустойчивость радиолиний с ППРЧ
- Контрольные вопросы
- Глава 8. Многоканальная связь и распределение информации
- 8.1. Методы распределения ресурса общего канала
- 8.1.1. Классификация систем передачи информации, использующих единый ресурс
- 8.1.2. Постановка задачи объединения и разделения сигналов
- 8.1.3. Энергетическая и спектральная цена уплотнения
- 8.2. Частотное разделение каналов
- 8.2.1. Принцип частотного объединения и разделения каналов
- 8.2.2. Групповой сигнал, его структура и характеристики
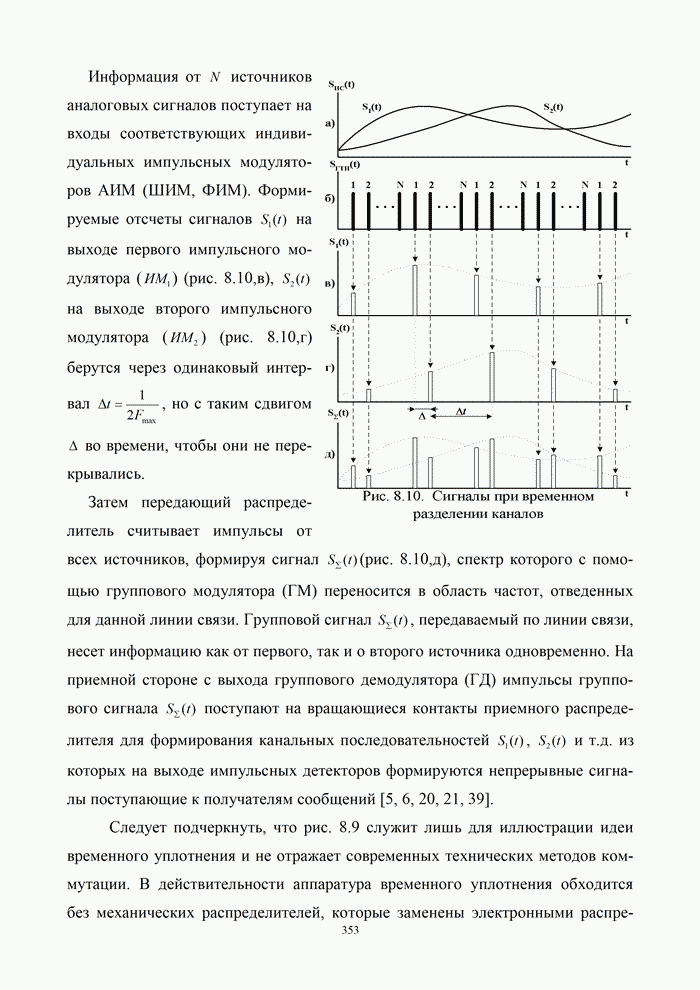
- 8.3. Временное разделение каналов
- 8.3.1. Принцип временного разделения каналов
- 8.3.2. Характеристики группового сигнала систем с ВРК
- 8.4. Разделение сигналов по форме
- Контрольные вопросы
- Глава 9. Эффективность систем связи
- 9.1. Оценка эффективности систем связи
- 9.1.1. Подходы к оценке эффективности
- 9.1.2. Критерии эффективности
- 9.1.3. Эффективность аналоговых и цифровых систем
- 9.2. Выбор сигналов и помехоустойчивых кодов
- 9.2.1. Многопозиционные сигналы
- 9.2.2. Корректирующие коды
- 9.3. Оптимизация систем связи
- 9.3.1. Согласование методов модуляции и кодирования
- 9.3.2. Классификация сигнально – кодовых конструкций
- 9.4. Характеристики основных типов СКК
- 9.4.1. Согласование канала кодом Грея
- 9.4.2. Согласование на основе разбиения ансамбля на вложенные подансамбли
- 9.5. Алгоритмы цифровой обработки сигналов
- 9.5.1. Дискретные сигналы и их спектры
- 9.5.2. Алгоритмы дискретного и быстрого преобразований Фурье
- Контрольные вопросы
- Глава 10. Теоретико-информационные основы криптозащиты сообщений в телекоммуникационных системах
- 10.1. Классификация криптографических систем
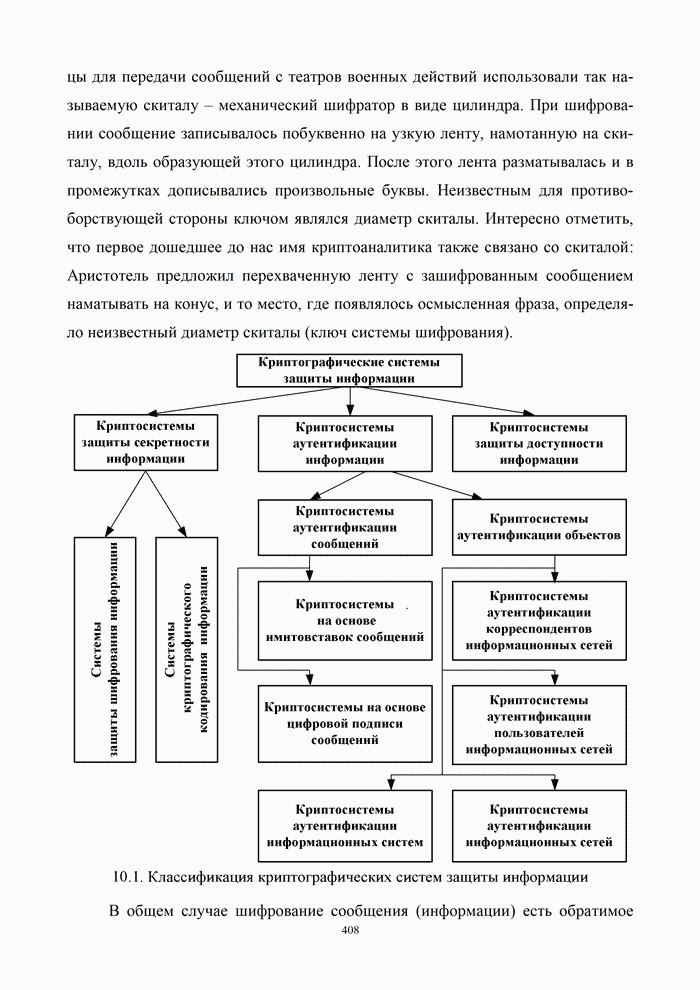
- 10.1.2. Классификация криптографических систем защиты информации
- 10.1.3. Оценка стойкости криптосистем
- 10.2. Функции, используемые в криптографических системах
- 10.2.1. Общее описание функций, используемых в криптографических системах
- 10.2.2. Однонаправленные функции
- 10.2.3. Криптографические хэш-функции
- 10.3. Модели криптографических систем
- 10.3.1. Системы шифрования
- 10.3.2. Традиционные симметричные криптосистемы
- 10.4. Алгоритмы криптографической защиты
- 10.4.1. Алгоритм криптографической защиты информации согласно ГОСТ 28147-89
- Контрольные вопросы
- Заключение
- Список литературы



















































































































































































































































































































































































 .
.
 ,
,
 ,
,
 .
.
 .
.
