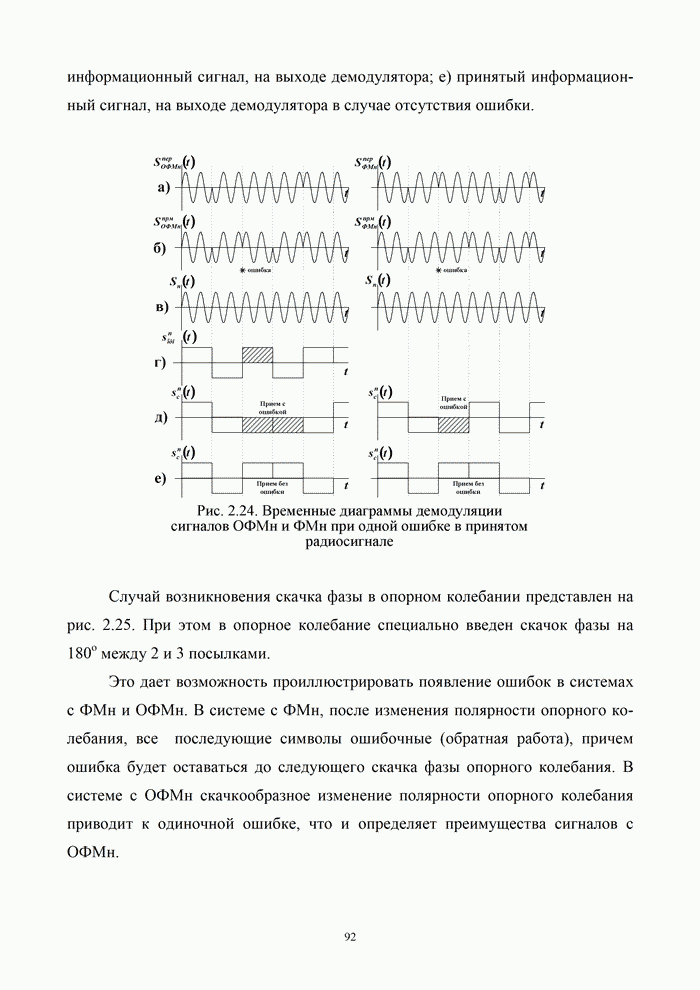
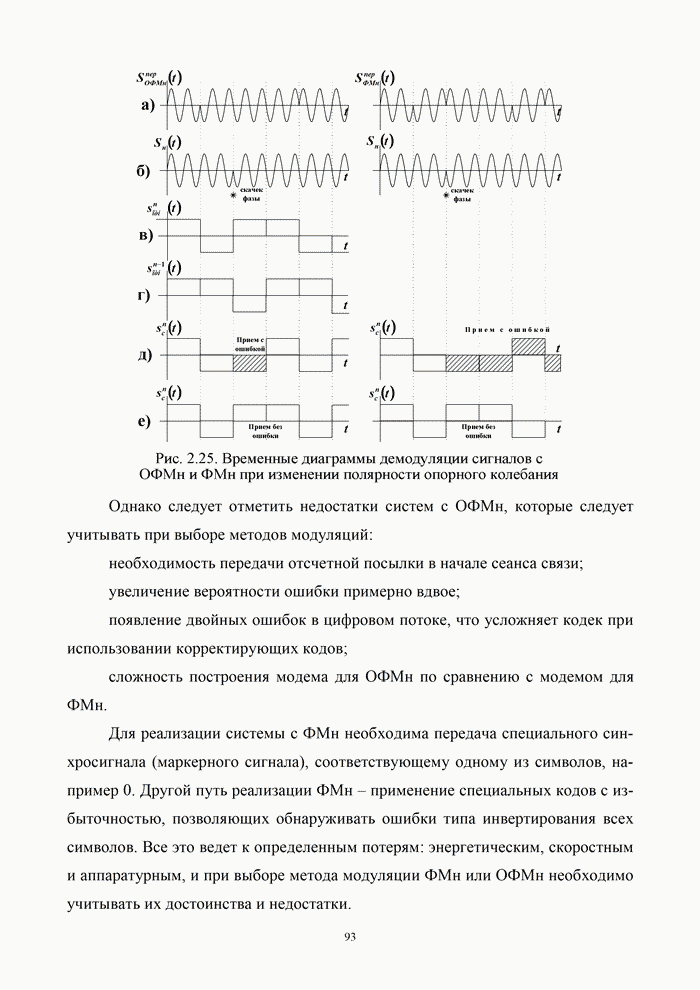
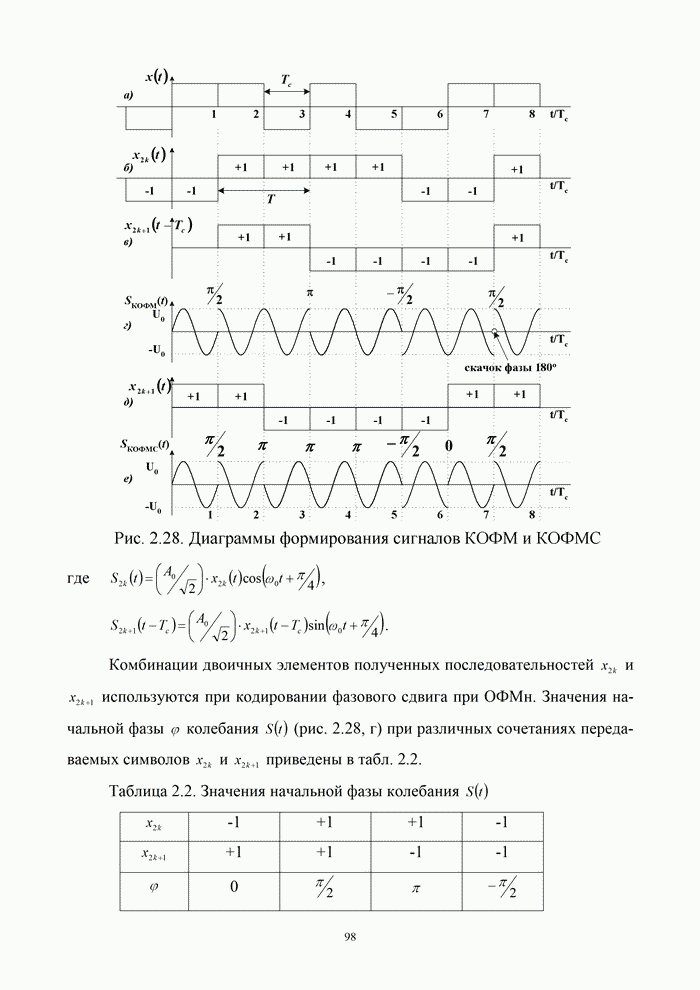
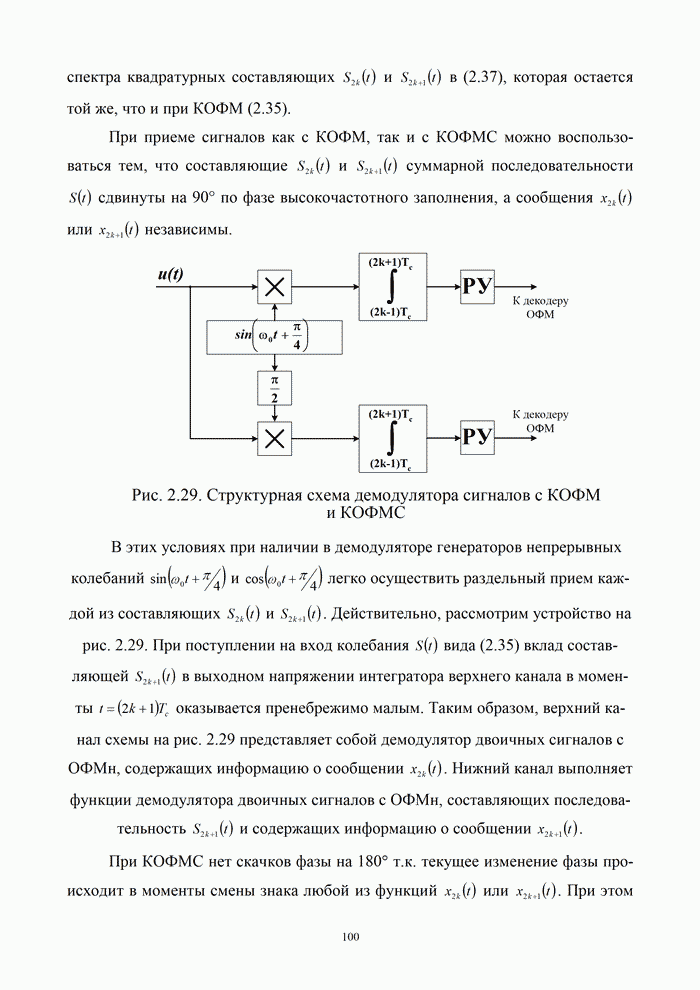
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
5.5.3. Методы реализации этапов декодирования кодов БЧХ
Изложенные в 5.5.2 основные идеи декодирования кодов БЧХ позволяют представить процесс декодирования в виде совокупности следующих трех основных этапов.
Этап 1. Вычисление синдрома ![]() по принятой комбинации символов
по принятой комбинации символов ![]() .
.
Этап 2. Нахождение коэффициентов многочлена
локаторов ошибок ![]() .
.
Этап 3. Вычисление корней многочлена ![]() ,
определение взаимных с ним величин – локаторов ошибок и исправление ошибочных
символов в принятой комбинации
,
определение взаимных с ним величин – локаторов ошибок и исправление ошибочных
символов в принятой комбинации ![]() (для недвоичных кодов БЧХ
требуется найти, помимо локаторов, оценки компонентов
(для недвоичных кодов БЧХ
требуется найти, помимо локаторов, оценки компонентов ![]() вектора ошибки).
вектора ошибки).
Каждый из перечисленных этапов процесса декодирования кодов БЧХ может быть реализован разными способами, существенно отличающимися друг от друга по сложности реализации. Рассмотрим основные из этих способов и проиллюстрируем их примером.
Этап 1. Отыскание синдрома ![]() кода БЧХ по принятой последовательности
символов
кода БЧХ по принятой последовательности
символов ![]() может
осуществляться путем деления многочлена
может
осуществляться путем деления многочлена ![]() на минимальные
многочлены
на минимальные
многочлены ![]() ,
задающие порождающий многочлен
,
задающие порождающий многочлен ![]() двоичного кода БЧХ (5.25).
Действительно:
двоичного кода БЧХ (5.25).
Действительно:
|
|
|
|
|
|
|
………………………….. |
|
|
|
|
где ![]() – остаток от деления
многочлена
– остаток от деления
многочлена ![]() на минимальный многочлен
на минимальный многочлен ![]() .
.
Подставив в ![]() -е уравнение корень
-е уравнение корень ![]() минимального многочлена
минимального многочлена ![]() ,
имеем
,
имеем
|
|
(5.30) |
поскольку
![]() . Учитывая (5.27),
получим, что
. Учитывая (5.27),
получим, что ![]() -й
компонент синдрома
-й
компонент синдрома ![]() .
.
Таким образом, первый этап декодирования кодов БЧХ может быть сведен к вычислению остатков ![]() от деления многочлена
от деления многочлена ![]() на минимальные
многочлены
на минимальные
многочлены ![]() элементов
элементов ![]() и
подстановке этих элементов в многочлены остатка
и
подстановке этих элементов в многочлены остатка ![]() .
.
Сопоставляя выражение (5.30) с (5.23), описывающим
прямое преобразование Фурье, можно сделать вывод о том, что компонент ![]() синдрома есть
синдрома есть ![]() -й коэффициент ДПФ принятой последовательности
символов
-й коэффициент ДПФ принятой последовательности
символов ![]() .
Учтем также, что
.
Учтем также, что ![]() -й коэффициент ДПФ этой
последовательности есть сумма
-й коэффициент ДПФ этой
последовательности есть сумма ![]() -х коэффициентов ДПФ кодового слова
-х коэффициентов ДПФ кодового слова ![]() и вектора ошибки
и вектора ошибки ![]() , поэтому
, поэтому
|
|
|
Поскольку по определению кода БЧХ ![]() для
для
![]() , то
компонент синдрома
, то
компонент синдрома ![]() ,
, ![]() .
.
Таким образом, блок компонентов синдрома как
бы образует в частотной области окно, через которое можно наблюдать ![]() из
из
![]() частотных
составляющих спектра вектора ошибки. Заметим, что для двоичных
кодов БЧХ из этих
частотных
составляющих спектра вектора ошибки. Заметим, что для двоичных
кодов БЧХ из этих ![]() компонентов
компонентов ![]() компоненты
с нечетными номерами
компоненты
с нечетными номерами ![]() вычисляются в соответствии
с (5.30), а с четными – по формуле с
вычисляются в соответствии
с (5.30), а с четными – по формуле с ![]() . Справедливость
этой формулы следует из правила возведения многочлена над
. Справедливость
этой формулы следует из правила возведения многочлена над ![]() в степень
в степень ![]() (см. 5.3.5).
(см. 5.3.5).
Этап 2. Вычисления коэффициентов полинома локаторов ошибок кодов
БЧХ, ориентированных на исправление ![]() ошибок,
оказываются наиболее трудоемкими.
Разработаны различные алгоритмы решения этой задачи, отличающиеся скоростью реализации.
ошибок,
оказываются наиболее трудоемкими.
Разработаны различные алгоритмы решения этой задачи, отличающиеся скоростью реализации.
При больших значениях кратности ошибок, особенно интересных на практике, более эффективным оказывается метод, предложенный Берлекэмпом [3, 26]. Суть метода состоит в сведении задачи отыскания коэффициентов о,- многочлена локаторов ошибок к задаче нахождения коэффициентов авторегрессионного фильтра (регистра сдвига минимальной длины с линейной обратной связью), генерирующего известную последовательность компонентов синдрома. Следует указать также на возможность решения ключевого уравнения при помощи алгоритма Евклида [3], являющегося рекуррентным и по сложности реализации близким к алгоритму Берлекэмпа.
Этап 3. На данном этапе необходимо отыскать корни ![]() многочлена локаторов ошибок
многочлена локаторов ошибок ![]() , коэффициенты
которого найдены на предыдущем этапе. Эти
корни являются обратными локаторам
, коэффициенты
которого найдены на предыдущем этапе. Эти
корни являются обратными локаторам ![]() , т.е.
, т.е. ![]() (см. 5.4). По вычисленным таким образом
локаторам
(см. 5.4). По вычисленным таким образом
локаторам ![]() для двоичных кодов БЧХ
остается
лишь исправить (проинвертировать) ошибочные символы, номер
для двоичных кодов БЧХ
остается
лишь исправить (проинвертировать) ошибочные символы, номер ![]() которых соответствует локатору
которых соответствует локатору ![]() . При декодировании недвоичных кодов БЧХ
необходимо найти оценку компонентов
. При декодировании недвоичных кодов БЧХ
необходимо найти оценку компонентов ![]() вектора ошибки и лишь затем произвести
исправление, формируя оценки символов переданного кодового слова
вектора ошибки и лишь затем произвести
исправление, формируя оценки символов переданного кодового слова ![]() .
.
Поиск элементов ![]() поля
поля ![]() , удовлетворяющих условию
, удовлетворяющих условию ![]() , состоит в переборе всех
элементов поля. Именно этот способ реализован в процедуре Ченя [30], широко используемой для решения задач третьего
этапа декодирования кодов БЧХ.
Сущность процедуры состоит в том, что при известных коэффициентах
, состоит в переборе всех
элементов поля. Именно этот способ реализован в процедуре Ченя [30], широко используемой для решения задач третьего
этапа декодирования кодов БЧХ.
Сущность процедуры состоит в том, что при известных коэффициентах ![]() декодер вычисляет значения
декодер вычисляет значения ![]() ,
, ![]() и т.д. (здесь
и т.д. (здесь ![]() – примитивный элемент поля
– примитивный элемент поля ![]() ).
).
Если для некоторого ![]() значение
значение ![]() , то это означает, что
, то это означает, что ![]() является корнем многочлена локаторов ошибки, а элемент
является корнем многочлена локаторов ошибки, а элемент ![]() является
локатором, указывающим на ошибочную
позицию в кодовой последовательности, которую следует исправить.
является
локатором, указывающим на ошибочную
позицию в кодовой последовательности, которую следует исправить.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Список сокращений
- Основные обозначения
- ВВЕДЕНИЕ
- Глава 1. Сообщения, сигналы и помехи, их математические модели
- 1.1. Основные понятия и определения
- 1.1.1. Сообщение, сигнал, модуляция
- 1.1.2. Основные параметры сигналов
- 1.2. Системы связи. Каналы связи
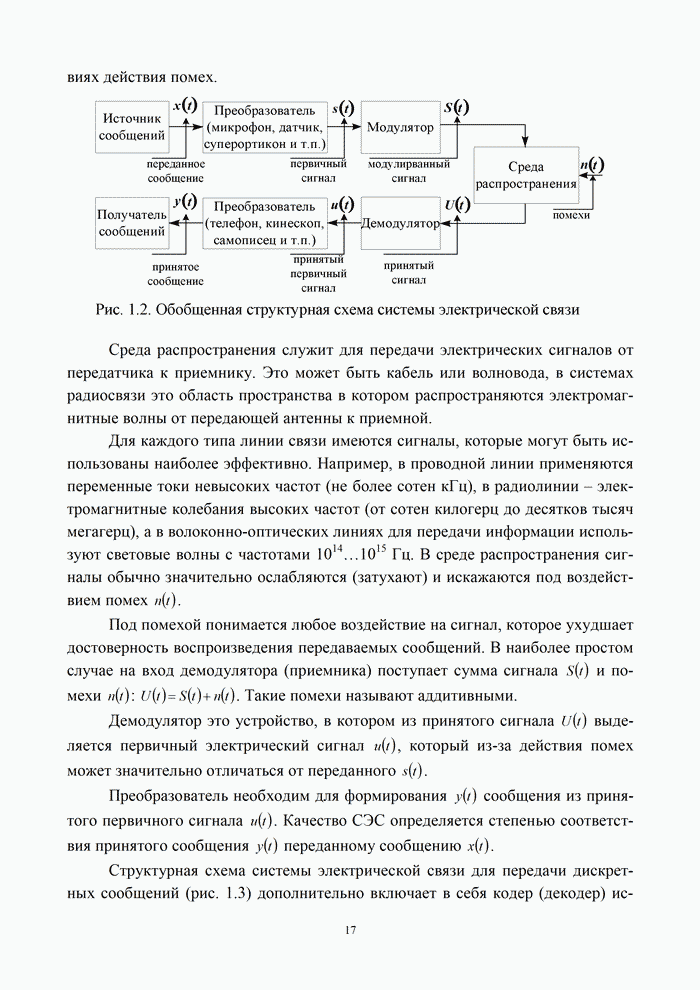
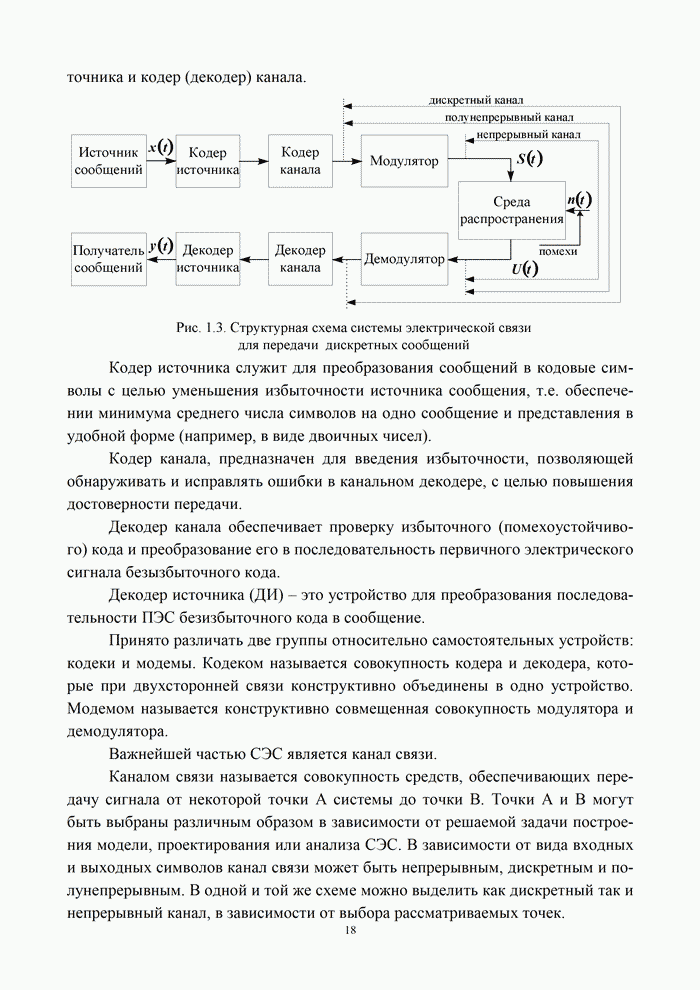
- 1.2.1. Структура канала электросвязи
- 1.2.2. Линия и сеть связи
- 1.2.3. Помехи и искажения в канале
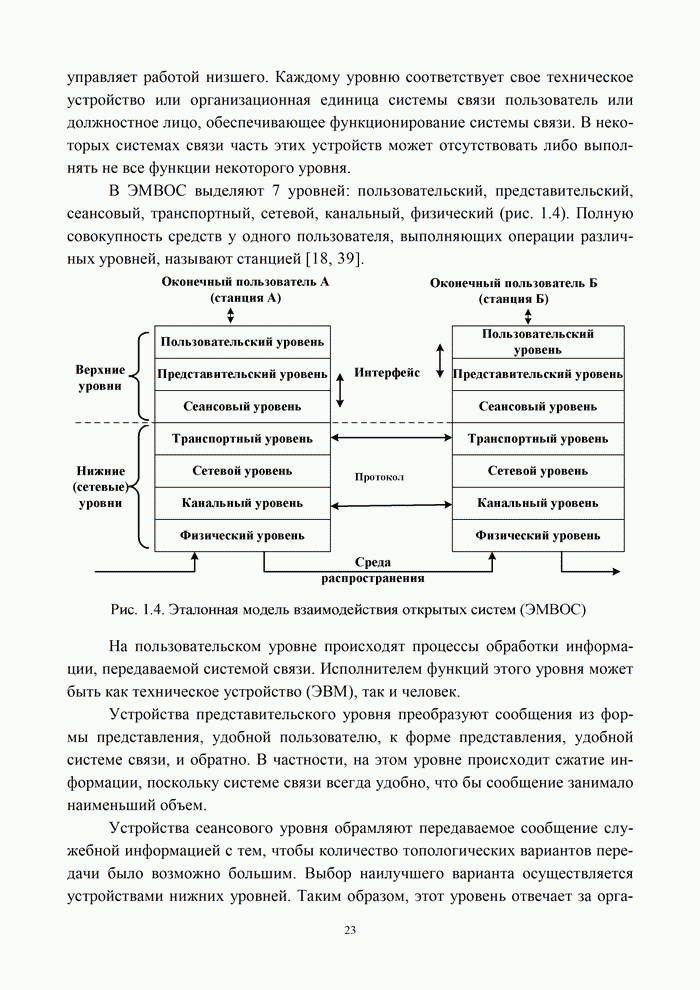
- 1.2.4. Эталонная модель взаимодействия открытых систем
- 1.2.5. Модели каналов связи и их математическое описание
- 1.3. Способы описания сигналов и помех
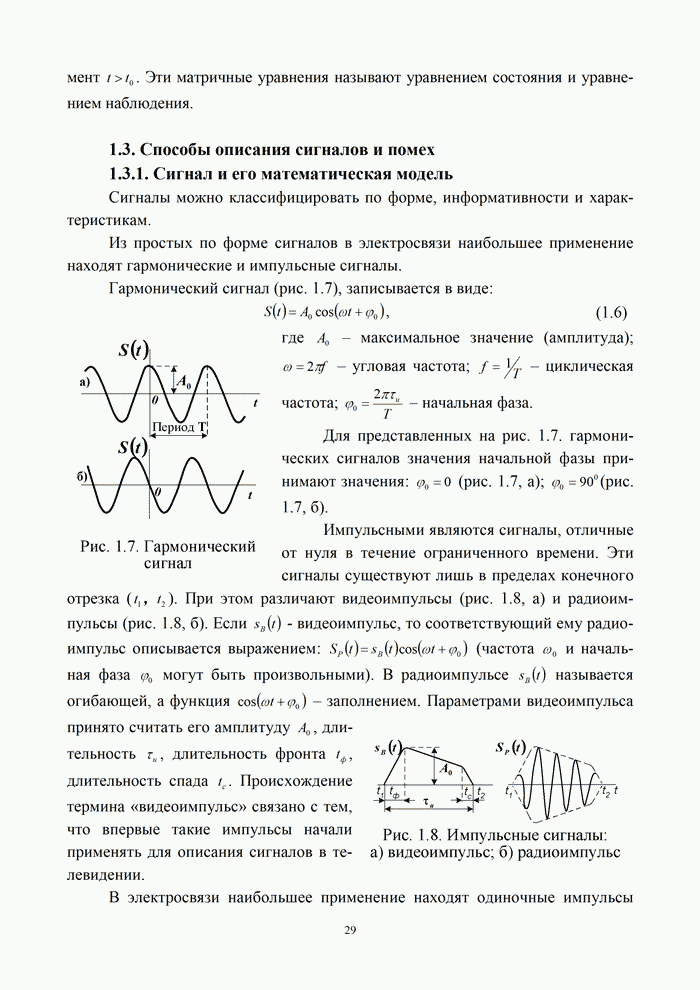
- 1.3.1. Сигнал и его математическая модель
- 1.3.2. Энергетические характеристики детерминированного сигнала
- 1.4.2. Представление сигналов и помех рядом Фурье
- 1.4.3. Применение преобразования Фурье для непериодических сигналов
- 1.5. Теорема Котельникова
- 1.6. Пространство сигналов
- 1.6.1. Линейное пространство
- 1.6.2. Представление сигнала в многомерном пространстве
- 1.7. Сигналы как случайные процессы
- 1.7.1. Характеристики случайного процесса
- 1.7.2. Флуктуационный шум
- 1.8. Комплексное представление сигналов и помех
- 1.8.1. Понятие аналитического сигнала
- 1.8.2. Огибающая, мгновенная фаза и мгновенная частота узкополосного случайного процесса
- Контрольные вопросы
- Глава 2. Методы формирования и преобразования сигналов
- 2.1. Модуляция сигналов
- 2.1.1. Амплитудная модуляция гармонической несущей
- 2.1.2. Балансная и однополосная модуляция гармонической несущей
- 2.2. Методы угловой модуляции
- 2.2.1. Принципы частотной и фазовой (угловой) модуляции
- 2.2.2. Спектр сигналов угловой модуляции
- 2.3. Формирование и детектирование модулированных сигналов
- 2.3.1. Формирование и детектирование сигналов амплитудной и однополосной амплитудной модуляции
- 2.3.2. Формирование и детектирование сигналов угловой модуляции
- 2.4. Манипуляция сигналов
- 2.4.1. Временные и спектральные характеристики амплитудно-манипулированных сигналов
- 2.4.2. Временные и спектральные характеристики частотно-манипулированных сигналов
- 2.4.3. Фазовая (относительно-фазовая) манипуляция сигналов
- 2.5. Системы связи с многопозиционной относительной фазовой манипуляцией
- 2.5.1. Принцип формирования сигнала с многократной относительной фазовой манипуляцией
- 2.5.2. Квадратурная относительно-фазовая манипуляция (КОФМ)
- 2.5.3. Принцип частотной модуляции с непрерывной фазой
- Контрольные вопросы
- Глава 3. Помехоустойчивость приема дискретных сообщений
- 3.1. Критерии качества и правила приема дискретных сообщений
- 3.1.1. Понятие о помехоустойчивости систем электрической связи
- 3.1.2. Задача оптимального приема
- 3.1.3. Вычисление вероятностей ошибок
- 3.2. Оптимальная демодуляция при когерентном приеме сигналов
- 3.2.1. Оптимальные алгоритмы приема при полностью известных сигналах
- 3.2.2. Реализация алгоритмов оптимального когерентного приема
- 3.3. Помехоустойчивость приема сигналов с известными параметрами
- 3.4. Прием сигналов с неопределенной фазой
- 3.4.1. Оптимальный некогерентный прием дискретных сигналов
- 3.4.2. Помехоустойчивость оптимального некогерентного приема
- 3.5. Подоптимальные методы приема
- 3.5.1. Причины применения неоптимальных методов приема
- 3.5.2. Квазиоптимальные методы приема
- Контрольные вопросы
- Глава 4. Теория передачи информации
- 4.1. Информационные характеристики источника сообщений
- 4.1.1. Количественное определение информации
- 4.1.2. Энтропия и производительность дискретного источника сообщений
- 4.2. Пропускная способность дискретного канала
- 4.2.1. Количество информации переданной по дискретному каналу
- 4.2.2. Пропускная способность дискретного канала
- 4.2.3. Пропускная способность симметричного дискретного канала без памяти
- 4.3. Методы сжатия дискретных сообщений
- 4.3.1. Условия существования оптимального неравномерного кода
- 4.3.2. Прямая и обратная теоремы кодирования источника неравномерными кодами
- 4.3.3. Показатели эффективности сжатия
- 4.3.4. Кодирование источника дискретных сообщений методом Шеннона-Фано
- 4.3.5. Кодирование источника дискретных сообщений методом Хаффмена
- 4.4. Пропускная способность непрерывного канала
- 4.4.1. Постановка задачи передачи дискретных сообщений в непрерывном канале
- 4.4.2. Количество информации, переданной по непрерывному каналу
- 4.4.3. Пропускная способность непрерывного канала
- Контрольные вопросы
- Глава 5. Теория кодирования сообщений
- 5.1. Помехоустойчивое кодирование: блочные и непрерывные коды
- 5.1.1. Постановка задачи помехоустойчивого кодирования
- 5.1.2. Классификация кодов
- 5.1.3. Основные характеристики и свойства блочных кодов
- 5.2. Эффективность помехоустойчивого кодирования
- 5.2.1. Эффективность кода в режиме исправления ошибок
- 5.2.2. Эффективность кода в режиме обнаружения ошибок
- 5.2.3. Эффективность помехоустойчивых кодов
- 5.3. Математические основы теории помехоустойчивого кодирования
- 5.3.1. Краткие сведения из теории чисел
- 5.3.2. Группы
- 5.3.3. Кольца и поля
- 5.3.4. Векторное пространство
- 5.3.5. Конечные поля
- 5.4. Линейные блочные коды
- 5.4.1. Система передачи дискретных сообщений
- 5.4.2. Параметры линейного кода
- 5.4.3. Полиномиальные циклические коды
- 5.4.4. Циклические коды и корни полиномов
- 5.4.5. Спектральное описание циклических кодов
- 5.4.6. Простейшие блочные линейные коды
- 5.5. Коды Боуза-Чоудхури-Хоквингема
- 5.5.1. Методы задания кодов БЧХ
- 5.5.2. Принципы декодирования кодов БЧХ
- 5.5.3. Методы реализации этапов декодирования кодов БЧХ
- 5.6. Коды Рида-Соломона
- 5.6.1. Основные определения
- 5.6.2. Обнаружение и исправление пакетов ошибок
- 5.7. Коды Рида-Маллера
- 5.7.1. Задание и декодирование кодов Рида-Маллера
- 5.7.2. Симплексные коды и m-последовательности
- 5.7.3. Связь между блочными кодами
- 5.8. Сверточные коды
- 5.8.1. Основные параметры
- 5.8.2. Способы задания сверточного кода
- 5.8.3. Алгоритм декодирования Витерби
- 5.9. Помехоустойчивость систем передачи дискретных сообщений
- 5.9.1. Две процедуры приема сигналов
- 5.9.2. Помехоустойчивость систем передачи информации при оптимальной процедуре приема
- 5.9.3. Помехоустойчивость систем передачи информации при посимвольном приеме сигналов
- Контрольные вопросы
- Глава 6. Сигналы с импульсной модуляцией
- 6.1. Методы импульсной модуляции
- 6.1.1. Импульсные методы передачи непрерывных сигналов
- 6.1.2. Спектральные характеристики импульсных методов модуляции
- 6.2. Помехоустойчивость непрерывных каналов связи с импульсной модуляцией
- 6.2.1. Помехоустойчивость систем передачи с импульсными методами модуляции
- 6.3. Цифровые методы передачи непрерывных сообщений
- 6.3.1. Передача сигналов с импульсно-кодовой модуляцией
- 6.3.2. Передача сигналов с дельта модуляцией
- 6.3.3. Квантование сигналов в системах с ИКМ и ДМ
- Контрольные вопросы
- Глава 7. Методы приема сигналов в сложных условиях
- 7.1. Прием сигналов в каналах с замираниями
- 7.1.1. Сущность замираний и их классификация
- 7.1.2. Принципы разнесенного приема сигналов
- 7.2. Методы борьбы с замираниями сигналов
- 7.2.1. Методы борьбы с замираниями в аналоговых системах связи
- 7.2.2. Методы борьбы с замираниями в цифровых системах связи
- 7.3. Методы борьбы с межсимвольной интерференцией
- 7.3.1. Причины возникновения и сущность межсимвольной интерференции
- 7.3.2. Обработка сигналов в каналах с межсимвольной интерференцией
- 7.3.3. Помехоустойчивость в каналах с межсимвольной интерференцией
- 7.4. Прием дискретных сообщений в каналах с сосредоточенными по спектру и импульсными помехами
- 7.4.1. Общая характеристика сосредоточенных по спектру и импульсных помех
- 7.4.2. Борьба с сосредоточенными и импульсными помехами
- 7.5. Компенсация помех и искажений в канале
- 7.5.1. Принцип работы радиолинии с ФМ ПСС (ФМ ШПС)
- 7.5.2. Помехоустойчивость радиолинии с ФМ ПСС
- 7.5.3. Принципы работы радиолиний с ППРЧ
- 7.5.4. Помехоустойчивость радиолиний с ППРЧ
- Контрольные вопросы
- Глава 8. Многоканальная связь и распределение информации
- 8.1. Методы распределения ресурса общего канала
- 8.1.1. Классификация систем передачи информации, использующих единый ресурс
- 8.1.2. Постановка задачи объединения и разделения сигналов
- 8.1.3. Энергетическая и спектральная цена уплотнения
- 8.2. Частотное разделение каналов
- 8.2.1. Принцип частотного объединения и разделения каналов
- 8.2.2. Групповой сигнал, его структура и характеристики
- 8.3. Временное разделение каналов
- 8.3.1. Принцип временного разделения каналов
- 8.3.2. Характеристики группового сигнала систем с ВРК
- 8.4. Разделение сигналов по форме
- Контрольные вопросы
- Глава 9. Эффективность систем связи
- 9.1. Оценка эффективности систем связи
- 9.1.1. Подходы к оценке эффективности
- 9.1.2. Критерии эффективности
- 9.1.3. Эффективность аналоговых и цифровых систем
- 9.2. Выбор сигналов и помехоустойчивых кодов
- 9.2.1. Многопозиционные сигналы
- 9.2.2. Корректирующие коды
- 9.3. Оптимизация систем связи
- 9.3.1. Согласование методов модуляции и кодирования
- 9.3.2. Классификация сигнально – кодовых конструкций
- 9.4. Характеристики основных типов СКК
- 9.4.1. Согласование канала кодом Грея
- 9.4.2. Согласование на основе разбиения ансамбля на вложенные подансамбли
- 9.5. Алгоритмы цифровой обработки сигналов
- 9.5.1. Дискретные сигналы и их спектры
- 9.5.2. Алгоритмы дискретного и быстрого преобразований Фурье
- Контрольные вопросы
- Глава 10. Теоретико-информационные основы криптозащиты сообщений в телекоммуникационных системах
- 10.1. Классификация криптографических систем
- 10.1.2. Классификация криптографических систем защиты информации
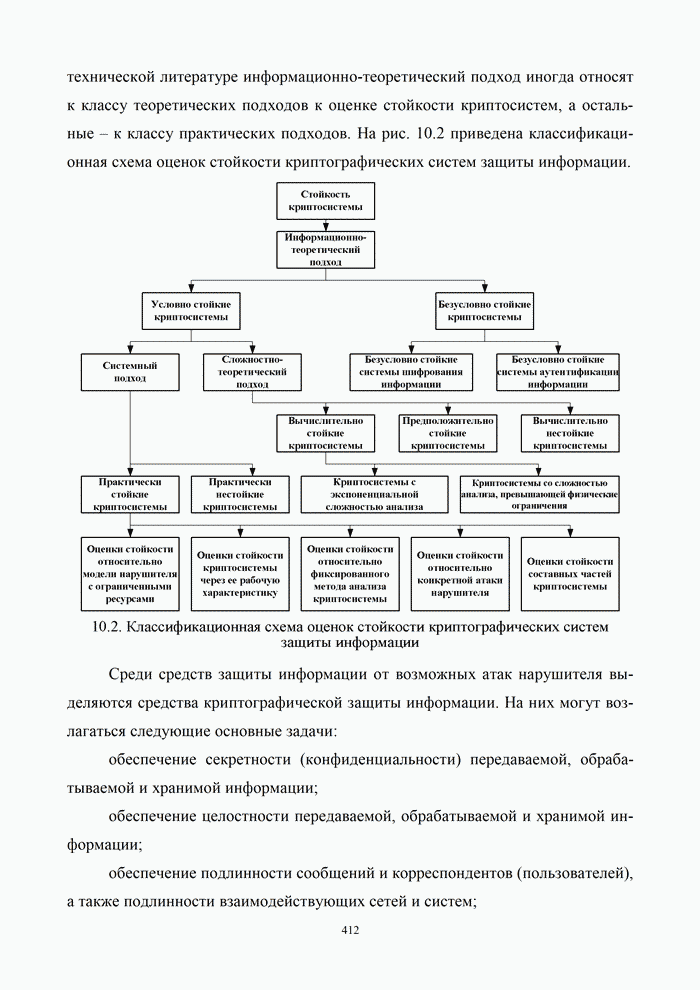
- 10.1.3. Оценка стойкости криптосистем
- 10.2. Функции, используемые в криптографических системах
- 10.2.1. Общее описание функций, используемых в криптографических системах
- 10.2.2. Однонаправленные функции
- 10.2.3. Криптографические хэш-функции
- 10.3. Модели криптографических систем
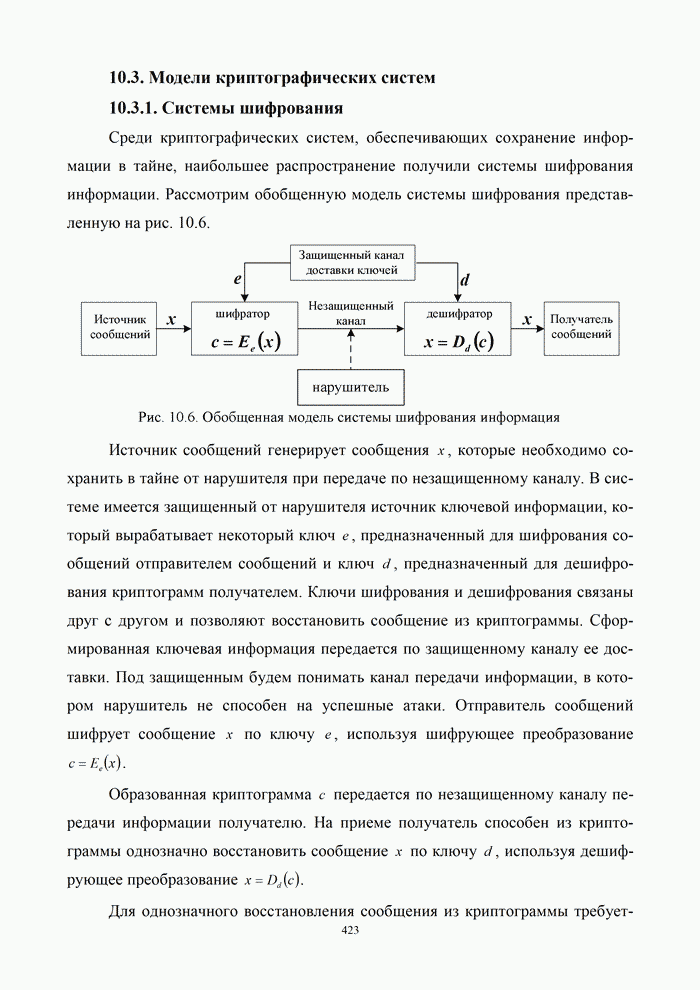
- 10.3.1. Системы шифрования
- 10.3.2. Традиционные симметричные криптосистемы
- 10.4. Алгоритмы криптографической защиты
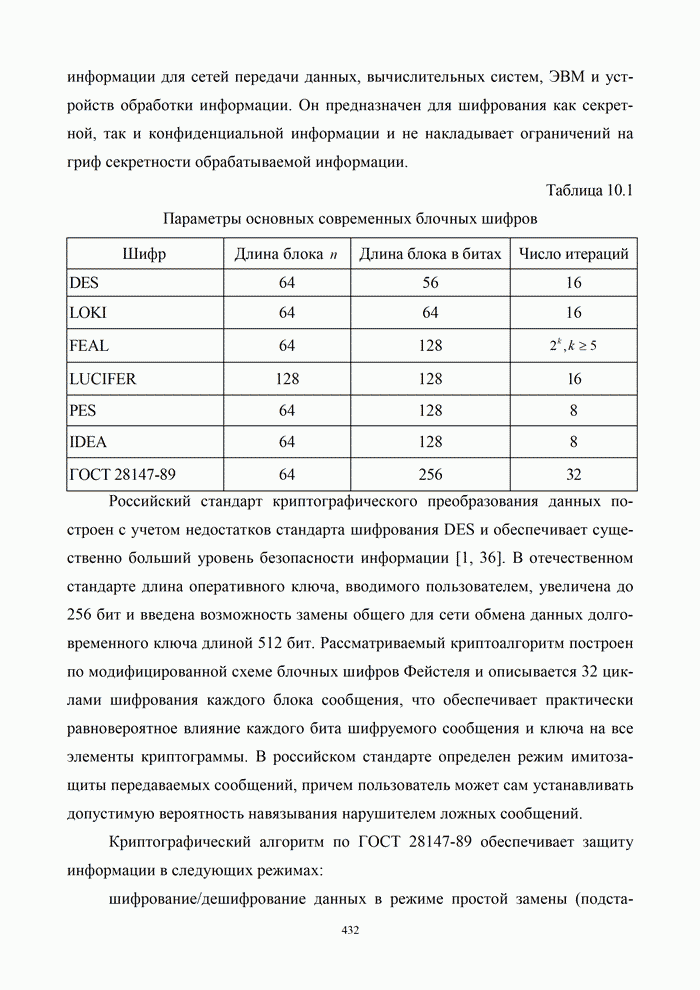
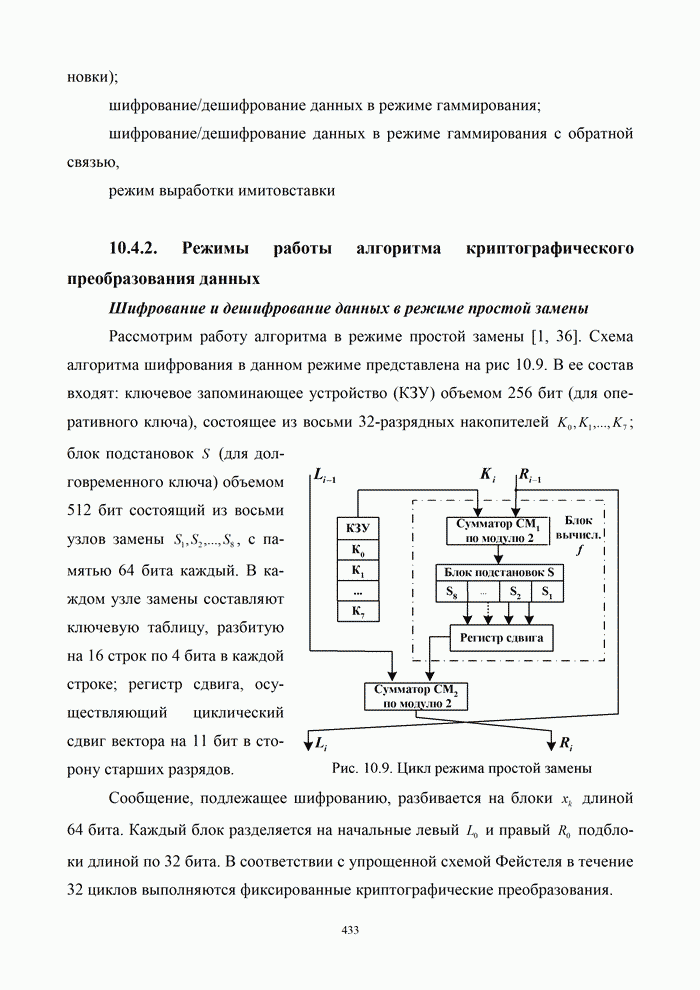
- 10.4.1. Алгоритм криптографической защиты информации согласно ГОСТ 28147-89
- Контрольные вопросы
- Заключение
- Список литературы