| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
4.4.2. Количество информации, переданной по непрерывному каналу
Рассмотрим непрерывный
источник с дискретным временем, в котором амплитуды импульсов статистически
независимы друг от друга. Предположим, что в канале действует аддитивная помеха
![]() с широким
спектром, не зависящая от очередных и предыдущих импульсов. Тогда на выходе
получим последовательность импульсов с амплитудами
с широким
спектром, не зависящая от очередных и предыдущих импульсов. Тогда на выходе
получим последовательность импульсов с амплитудами ![]() , статистически не зависящими
друг от друга.
, статистически не зависящими
друг от друга.

Свойства источника
непрерывного сигнала будут определяться ПРВ ![]() ,
, ![]() входных (информационных) случайных
величин
входных (информационных) случайных
величин ![]() , а
воздействие помехи будет определяться условными ПРВ
, а
воздействие помехи будет определяться условными ПРВ ![]() выходных СВ
выходных СВ ![]() при заданных входных СВ
при заданных входных СВ
![]() (рис. 4.5).
(рис. 4.5).
Разделим области определения величин ![]() и
и ![]() на малые отрезки длиной
на малые отрезки длиной ![]() и
и ![]() . Вероятность
. Вероятность ![]() того,
что значение
того,
что значение ![]() лежит
на некотором отрезке
лежит
на некотором отрезке ![]() , приблизительно равна
, приблизительно равна ![]() . Аналогично,
. Аналогично, ![]() , а
совместная вероятность этих двух событий будет
, а
совместная вероятность этих двух событий будет
![]() . При такой дискретизации
количество информации, переданное по
каналу и рассчитанное на один импульс,
приближенно находится по формуле:
. При такой дискретизации
количество информации, переданное по
каналу и рассчитанное на один импульс,
приближенно находится по формуле:
|
|
|
Устремив ![]() и
и ![]() к нулю, перейдем к
непрерывному каналу. При этом двойная сумма преобразуется в
двойной интеграл, а количество передаваемой информации
к нулю, перейдем к
непрерывному каналу. При этом двойная сумма преобразуется в
двойной интеграл, а количество передаваемой информации
|
|
(4.10) |
Отметим следующие свойства количества информации, передаваемой в непрерывном канале:
![]() , причем
, причем ![]() тогда и только тогда, когда вход и выход канала статистически
независимы, т.е.
тогда и только тогда, когда вход и выход канала статистически
независимы, т.е. ![]() ;
;
![]() – свойство симметрии;
– свойство симметрии;
![]() , если помехи в канале
отсутствуют, т.е.
, если помехи в канале
отсутствуют, т.е. ![]() ,
, ![]() .
.
Можно показать, что энтропия источника неограниченно возрастает, когда его алфавит переходит от дискретного к непрерывному. Для этого разделим область определения непрерывного сигнала ![]() на отрезки
на отрезки ![]() (рис. 4.5), и превратим сигнал в
дискретный, положив вероятность появления
(рис. 4.5), и превратим сигнал в
дискретный, положив вероятность появления ![]() , равной
, равной
![]() . Энтропия
такого дискретного сигнала
. Энтропия
такого дискретного сигнала
|
|
|
Устремим теперь ![]() к нулю для перехода к энтропии
непрерывного сигнала [6]:
к нулю для перехода к энтропии
непрерывного сигнала [6]:
|
|
|
Первое слагаемое
|
|
|
представляет
собой так называемую дифференциальную энтропию сигнала (или
дифференциальную энтропию распределения ![]() ). Второе слагаемое
стремится к бесконечности совершенно независимо от природы и распределения вероятностей сигнала.
Таким образом, при
переходе от дискретных значений
). Второе слагаемое
стремится к бесконечности совершенно независимо от природы и распределения вероятностей сигнала.
Таким образом, при
переходе от дискретных значений ![]() к непрерывным энтропия сигнала неограниченно возрастает.
к непрерывным энтропия сигнала неограниченно возрастает.
По аналогии с дискретным каналом количество информации, переданной по непрерывному каналу можно представить в следующей форме:
|
|
(4.11) |
где ![]() – условная дифференциальная энтропия
сигнала
– условная дифференциальная энтропия
сигнала ![]() при
известном сигнале
при
известном сигнале ![]() .
.
Второе равенство следует
из второго свойства количества передаваемой информации (симметрии). Полученное
выражение по форме напоминает (4.7), а дифференциальная энтропия играет здесь
роль обычной энтропии дискретных сигналов. Однако свойства дифференциальной
энтропии существенно отличаются от свойств обычной энтропии. Так, например, ![]() и
и ![]() могут быть отрицательными.
могут быть отрицательными.
Дифференциальная энтропия
![]() уже не представляет собой среднее количество информации,
выдаваемое источником сигнала (для непрерывного сигнала оно бесконечно).
Аналогично
уже не представляет собой среднее количество информации,
выдаваемое источником сигнала (для непрерывного сигнала оно бесконечно).
Аналогично ![]() не представляет собой количество информации, потерянной в
канале, поскольку эта величина тоже бесконечна. Поэтому дифференциальную
энтропию следует понимать лишь формально, как некоторую
вспомогательную величину полезную
при расчетах.
не представляет собой количество информации, потерянной в
канале, поскольку эта величина тоже бесконечна. Поэтому дифференциальную
энтропию следует понимать лишь формально, как некоторую
вспомогательную величину полезную
при расчетах.
Если
помеха аддитивная ![]() , то нетрудно
показать, что
, то нетрудно
показать, что
|
|
(4.12) |
где
![]() – ПРВ помехи;
– ПРВ помехи;
![]() – дифференциальная энтропия
помехи.
– дифференциальная энтропия
помехи.
Подставляя (4.12) в (4.11), находим
|
|
(4.13) |
Найдем дифференциальную энтропию гауссовской
помехи с нулевым средним и дисперсией ![]() при отсутствии корреляции
между значениями помехи. Согласно (4.12),
при отсутствии корреляции
между значениями помехи. Согласно (4.12),
|
|
Учитывая
![]() и
и ![]() , получим:
, получим:
|
|
(4.14) |
Дифференциальная энтропия
принятого сигнала ![]() с
гауссовским нормальным законом распределения вероятности [6]:
с
гауссовским нормальным законом распределения вероятности [6]:
|
|
(4.15) |
где ![]() ;
; ![]() – дисперсия сигнала. Подставляя (4.14) и (4.15) в (4.13) получим
выражение для определения количества информации, переданной по непрерывному
каналу:
– дисперсия сигнала. Подставляя (4.14) и (4.15) в (4.13) получим
выражение для определения количества информации, переданной по непрерывному
каналу:
|
|
(4.16) |
Полученное выражение
показывает, что пропускная способность гауссовского канала с дискретным
временем определяется отношением дисперсии сигнала к дисперсии помехи. Нередко
величину ![]() называют
отношением сигнал/шум. Чем больше это отношение, тем выше пропускная
способность. Последнее вполне естественно, так как если дисперсия сигнала
меньше дисперсии помехи или сравнима с ней, то по принятому сигналу трудно
судить с определенностью, какое значение сигнала было подано на вход канала.
называют
отношением сигнал/шум. Чем больше это отношение, тем выше пропускная
способность. Последнее вполне естественно, так как если дисперсия сигнала
меньше дисперсии помехи или сравнима с ней, то по принятому сигналу трудно
судить с определенностью, какое значение сигнала было подано на вход канала.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Список сокращений
- Основные обозначения
- ВВЕДЕНИЕ
- Глава 1. Сообщения, сигналы и помехи, их математические модели
- 1.1. Основные понятия и определения
- 1.1.1. Сообщение, сигнал, модуляция
- 1.1.2. Основные параметры сигналов
- 1.2. Системы связи. Каналы связи
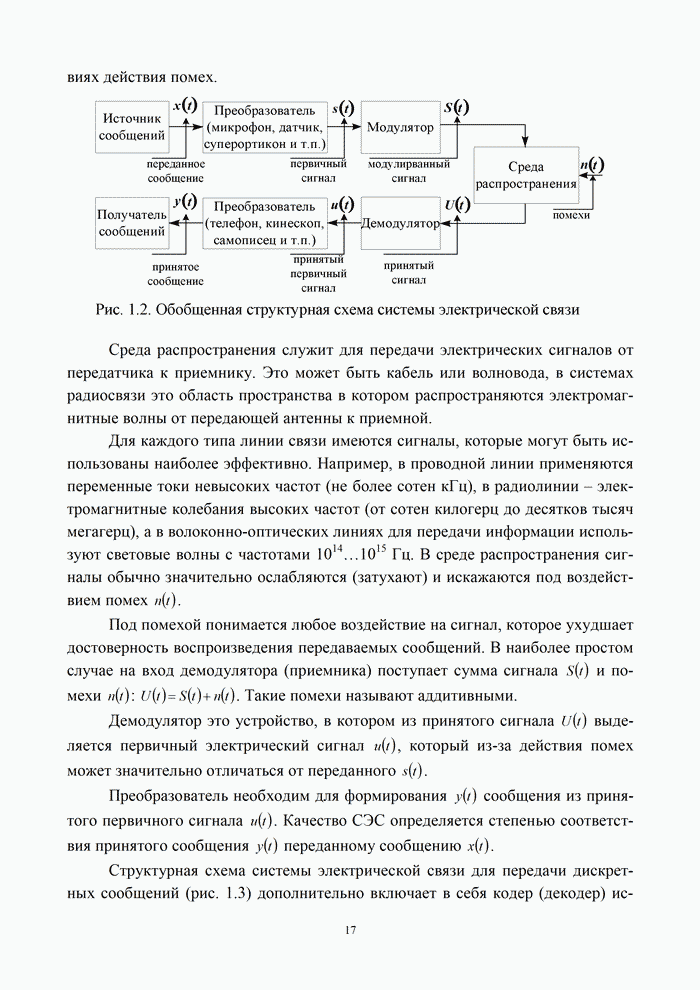
- 1.2.1. Структура канала электросвязи
- 1.2.2. Линия и сеть связи
- 1.2.3. Помехи и искажения в канале
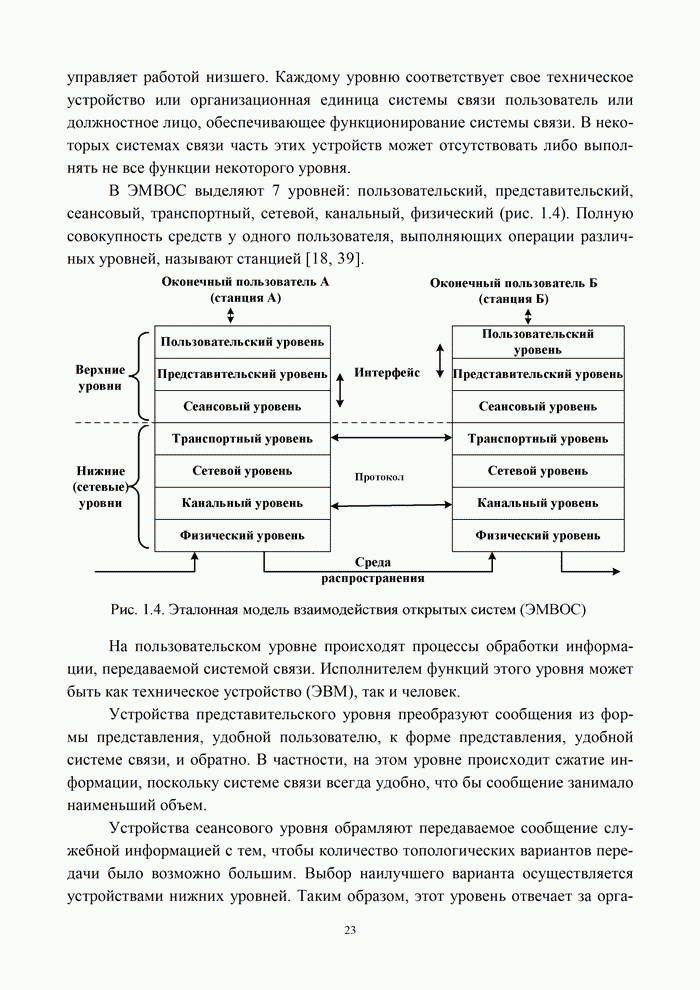
- 1.2.4. Эталонная модель взаимодействия открытых систем
- 1.2.5. Модели каналов связи и их математическое описание
- 1.3. Способы описания сигналов и помех
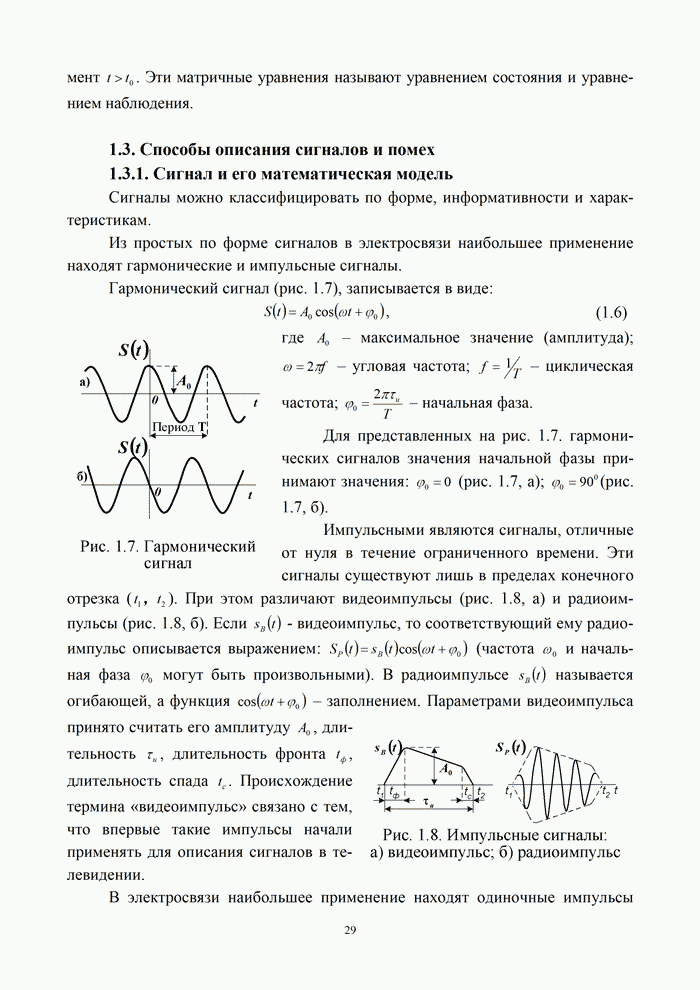
- 1.3.1. Сигнал и его математическая модель
- 1.3.2. Энергетические характеристики детерминированного сигнала
- 1.4.2. Представление сигналов и помех рядом Фурье
- 1.4.3. Применение преобразования Фурье для непериодических сигналов
- 1.5. Теорема Котельникова
- 1.6. Пространство сигналов
- 1.6.1. Линейное пространство
- 1.6.2. Представление сигнала в многомерном пространстве
- 1.7. Сигналы как случайные процессы
- 1.7.1. Характеристики случайного процесса
- 1.7.2. Флуктуационный шум
- 1.8. Комплексное представление сигналов и помех
- 1.8.1. Понятие аналитического сигнала
- 1.8.2. Огибающая, мгновенная фаза и мгновенная частота узкополосного случайного процесса
- Контрольные вопросы
- Глава 2. Методы формирования и преобразования сигналов
- 2.1. Модуляция сигналов
- 2.1.1. Амплитудная модуляция гармонической несущей
- 2.1.2. Балансная и однополосная модуляция гармонической несущей
- 2.2. Методы угловой модуляции
- 2.2.1. Принципы частотной и фазовой (угловой) модуляции
- 2.2.2. Спектр сигналов угловой модуляции
- 2.3. Формирование и детектирование модулированных сигналов
- 2.3.1. Формирование и детектирование сигналов амплитудной и однополосной амплитудной модуляции
- 2.3.2. Формирование и детектирование сигналов угловой модуляции
- 2.4. Манипуляция сигналов
- 2.4.1. Временные и спектральные характеристики амплитудно-манипулированных сигналов
- 2.4.2. Временные и спектральные характеристики частотно-манипулированных сигналов
- 2.4.3. Фазовая (относительно-фазовая) манипуляция сигналов
- 2.5. Системы связи с многопозиционной относительной фазовой манипуляцией
- 2.5.1. Принцип формирования сигнала с многократной относительной фазовой манипуляцией
- 2.5.2. Квадратурная относительно-фазовая манипуляция (КОФМ)
- 2.5.3. Принцип частотной модуляции с непрерывной фазой
- Контрольные вопросы
- Глава 3. Помехоустойчивость приема дискретных сообщений
- 3.1. Критерии качества и правила приема дискретных сообщений
- 3.1.1. Понятие о помехоустойчивости систем электрической связи
- 3.1.2. Задача оптимального приема
- 3.1.3. Вычисление вероятностей ошибок
- 3.2. Оптимальная демодуляция при когерентном приеме сигналов
- 3.2.1. Оптимальные алгоритмы приема при полностью известных сигналах
- 3.2.2. Реализация алгоритмов оптимального когерентного приема
- 3.3. Помехоустойчивость приема сигналов с известными параметрами
- 3.4. Прием сигналов с неопределенной фазой
- 3.4.1. Оптимальный некогерентный прием дискретных сигналов
- 3.4.2. Помехоустойчивость оптимального некогерентного приема
- 3.5. Подоптимальные методы приема
- 3.5.1. Причины применения неоптимальных методов приема
- 3.5.2. Квазиоптимальные методы приема
- Контрольные вопросы
- Глава 4. Теория передачи информации
- 4.1. Информационные характеристики источника сообщений
- 4.1.1. Количественное определение информации
- 4.1.2. Энтропия и производительность дискретного источника сообщений
- 4.2. Пропускная способность дискретного канала
- 4.2.1. Количество информации переданной по дискретному каналу
- 4.2.2. Пропускная способность дискретного канала
- 4.2.3. Пропускная способность симметричного дискретного канала без памяти
- 4.3. Методы сжатия дискретных сообщений
- 4.3.1. Условия существования оптимального неравномерного кода
- 4.3.2. Прямая и обратная теоремы кодирования источника неравномерными кодами
- 4.3.3. Показатели эффективности сжатия
- 4.3.4. Кодирование источника дискретных сообщений методом Шеннона-Фано
- 4.3.5. Кодирование источника дискретных сообщений методом Хаффмена
- 4.4. Пропускная способность непрерывного канала
- 4.4.1. Постановка задачи передачи дискретных сообщений в непрерывном канале
- 4.4.2. Количество информации, переданной по непрерывному каналу
- 4.4.3. Пропускная способность непрерывного канала
- Контрольные вопросы
- Глава 5. Теория кодирования сообщений
- 5.1. Помехоустойчивое кодирование: блочные и непрерывные коды
- 5.1.1. Постановка задачи помехоустойчивого кодирования
- 5.1.2. Классификация кодов
- 5.1.3. Основные характеристики и свойства блочных кодов
- 5.2. Эффективность помехоустойчивого кодирования
- 5.2.1. Эффективность кода в режиме исправления ошибок
- 5.2.2. Эффективность кода в режиме обнаружения ошибок
- 5.2.3. Эффективность помехоустойчивых кодов
- 5.3. Математические основы теории помехоустойчивого кодирования
- 5.3.1. Краткие сведения из теории чисел
- 5.3.2. Группы
- 5.3.3. Кольца и поля
- 5.3.4. Векторное пространство
- 5.3.5. Конечные поля
- 5.4. Линейные блочные коды
- 5.4.1. Система передачи дискретных сообщений
- 5.4.2. Параметры линейного кода
- 5.4.3. Полиномиальные циклические коды
- 5.4.4. Циклические коды и корни полиномов
- 5.4.5. Спектральное описание циклических кодов
- 5.4.6. Простейшие блочные линейные коды
- 5.5. Коды Боуза-Чоудхури-Хоквингема
- 5.5.1. Методы задания кодов БЧХ
- 5.5.2. Принципы декодирования кодов БЧХ
- 5.5.3. Методы реализации этапов декодирования кодов БЧХ
- 5.6. Коды Рида-Соломона
- 5.6.1. Основные определения
- 5.6.2. Обнаружение и исправление пакетов ошибок
- 5.7. Коды Рида-Маллера
- 5.7.1. Задание и декодирование кодов Рида-Маллера
- 5.7.2. Симплексные коды и m-последовательности
- 5.7.3. Связь между блочными кодами
- 5.8. Сверточные коды
- 5.8.1. Основные параметры
- 5.8.2. Способы задания сверточного кода
- 5.8.3. Алгоритм декодирования Витерби
- 5.9. Помехоустойчивость систем передачи дискретных сообщений
- 5.9.1. Две процедуры приема сигналов
- 5.9.2. Помехоустойчивость систем передачи информации при оптимальной процедуре приема
- 5.9.3. Помехоустойчивость систем передачи информации при посимвольном приеме сигналов
- Контрольные вопросы
- Глава 6. Сигналы с импульсной модуляцией
- 6.1. Методы импульсной модуляции
- 6.1.1. Импульсные методы передачи непрерывных сигналов
- 6.1.2. Спектральные характеристики импульсных методов модуляции
- 6.2. Помехоустойчивость непрерывных каналов связи с импульсной модуляцией
- 6.2.1. Помехоустойчивость систем передачи с импульсными методами модуляции
- 6.3. Цифровые методы передачи непрерывных сообщений
- 6.3.1. Передача сигналов с импульсно-кодовой модуляцией
- 6.3.2. Передача сигналов с дельта модуляцией
- 6.3.3. Квантование сигналов в системах с ИКМ и ДМ
- Контрольные вопросы
- Глава 7. Методы приема сигналов в сложных условиях
- 7.1. Прием сигналов в каналах с замираниями
- 7.1.1. Сущность замираний и их классификация
- 7.1.2. Принципы разнесенного приема сигналов
- 7.2. Методы борьбы с замираниями сигналов
- 7.2.1. Методы борьбы с замираниями в аналоговых системах связи
- 7.2.2. Методы борьбы с замираниями в цифровых системах связи
- 7.3. Методы борьбы с межсимвольной интерференцией
- 7.3.1. Причины возникновения и сущность межсимвольной интерференции
- 7.3.2. Обработка сигналов в каналах с межсимвольной интерференцией
- 7.3.3. Помехоустойчивость в каналах с межсимвольной интерференцией
- 7.4. Прием дискретных сообщений в каналах с сосредоточенными по спектру и импульсными помехами
- 7.4.1. Общая характеристика сосредоточенных по спектру и импульсных помех
- 7.4.2. Борьба с сосредоточенными и импульсными помехами
- 7.5. Компенсация помех и искажений в канале
- 7.5.1. Принцип работы радиолинии с ФМ ПСС (ФМ ШПС)
- 7.5.2. Помехоустойчивость радиолинии с ФМ ПСС
- 7.5.3. Принципы работы радиолиний с ППРЧ
- 7.5.4. Помехоустойчивость радиолиний с ППРЧ
- Контрольные вопросы
- Глава 8. Многоканальная связь и распределение информации
- 8.1. Методы распределения ресурса общего канала
- 8.1.1. Классификация систем передачи информации, использующих единый ресурс
- 8.1.2. Постановка задачи объединения и разделения сигналов
- 8.1.3. Энергетическая и спектральная цена уплотнения
- 8.2. Частотное разделение каналов
- 8.2.1. Принцип частотного объединения и разделения каналов
- 8.2.2. Групповой сигнал, его структура и характеристики
- 8.3. Временное разделение каналов
- 8.3.1. Принцип временного разделения каналов
- 8.3.2. Характеристики группового сигнала систем с ВРК
- 8.4. Разделение сигналов по форме
- Контрольные вопросы
- Глава 9. Эффективность систем связи
- 9.1. Оценка эффективности систем связи
- 9.1.1. Подходы к оценке эффективности
- 9.1.2. Критерии эффективности
- 9.1.3. Эффективность аналоговых и цифровых систем
- 9.2. Выбор сигналов и помехоустойчивых кодов
- 9.2.1. Многопозиционные сигналы
- 9.2.2. Корректирующие коды
- 9.3. Оптимизация систем связи
- 9.3.1. Согласование методов модуляции и кодирования
- 9.3.2. Классификация сигнально – кодовых конструкций
- 9.4. Характеристики основных типов СКК
- 9.4.1. Согласование канала кодом Грея
- 9.4.2. Согласование на основе разбиения ансамбля на вложенные подансамбли
- 9.5. Алгоритмы цифровой обработки сигналов
- 9.5.1. Дискретные сигналы и их спектры
- 9.5.2. Алгоритмы дискретного и быстрого преобразований Фурье
- Контрольные вопросы
- Глава 10. Теоретико-информационные основы криптозащиты сообщений в телекоммуникационных системах
- 10.1. Классификация криптографических систем
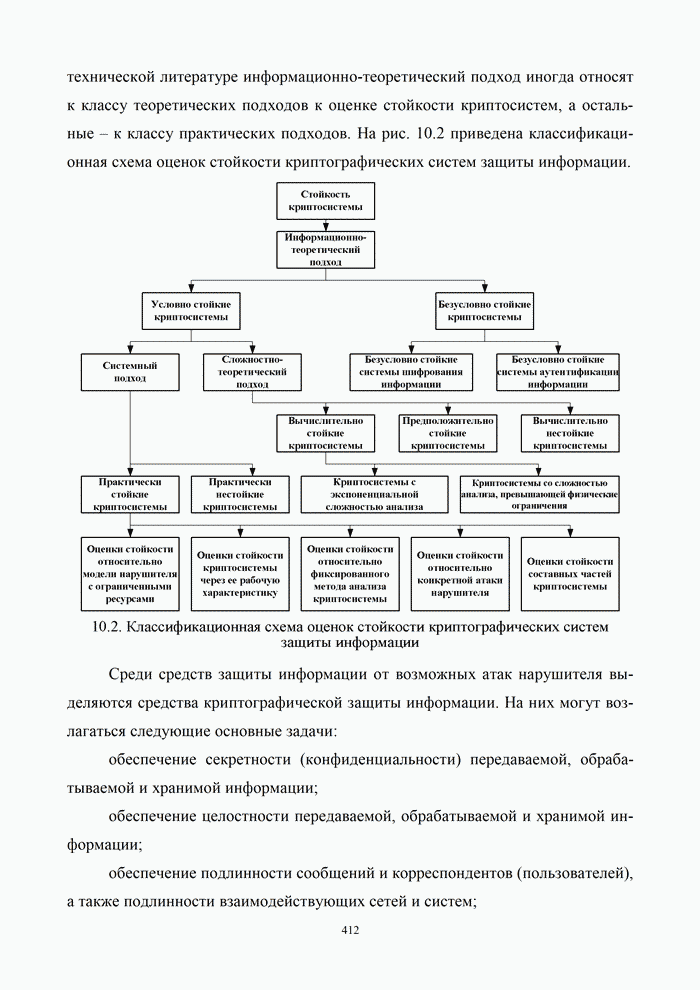
- 10.1.2. Классификация криптографических систем защиты информации
- 10.1.3. Оценка стойкости криптосистем
- 10.2. Функции, используемые в криптографических системах
- 10.2.1. Общее описание функций, используемых в криптографических системах
- 10.2.2. Однонаправленные функции
- 10.2.3. Криптографические хэш-функции
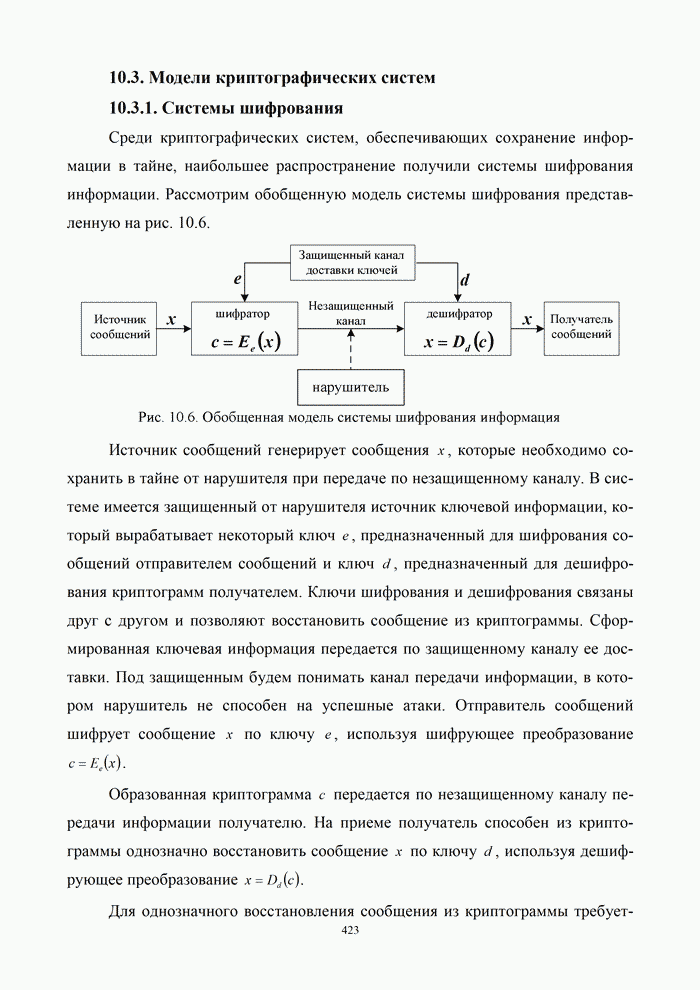
- 10.3. Модели криптографических систем
- 10.3.1. Системы шифрования
- 10.3.2. Традиционные симметричные криптосистемы
- 10.4. Алгоритмы криптографической защиты
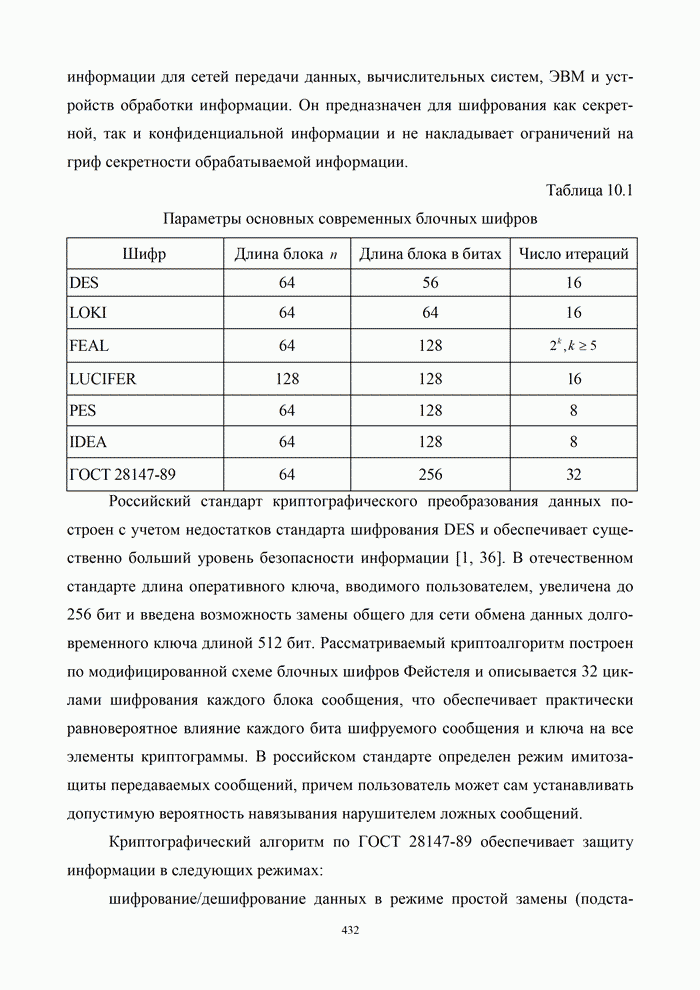
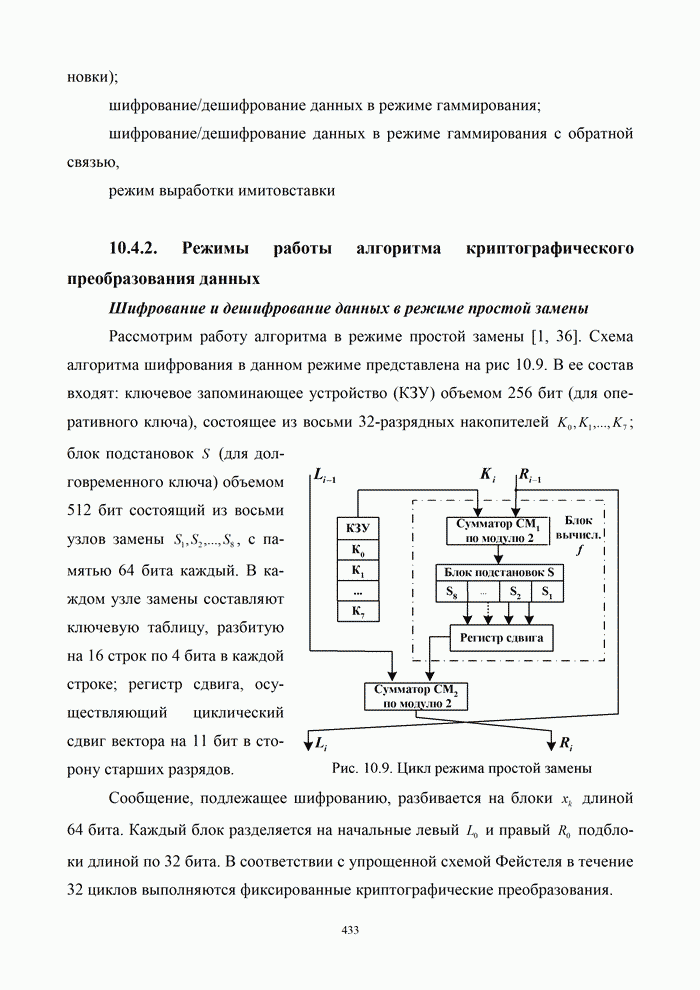
- 10.4.1. Алгоритм криптографической защиты информации согласно ГОСТ 28147-89
- Контрольные вопросы
- Заключение
- Список литературы



















































































































































































































































































































































































 .
.

 .
.
 .
.
