| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
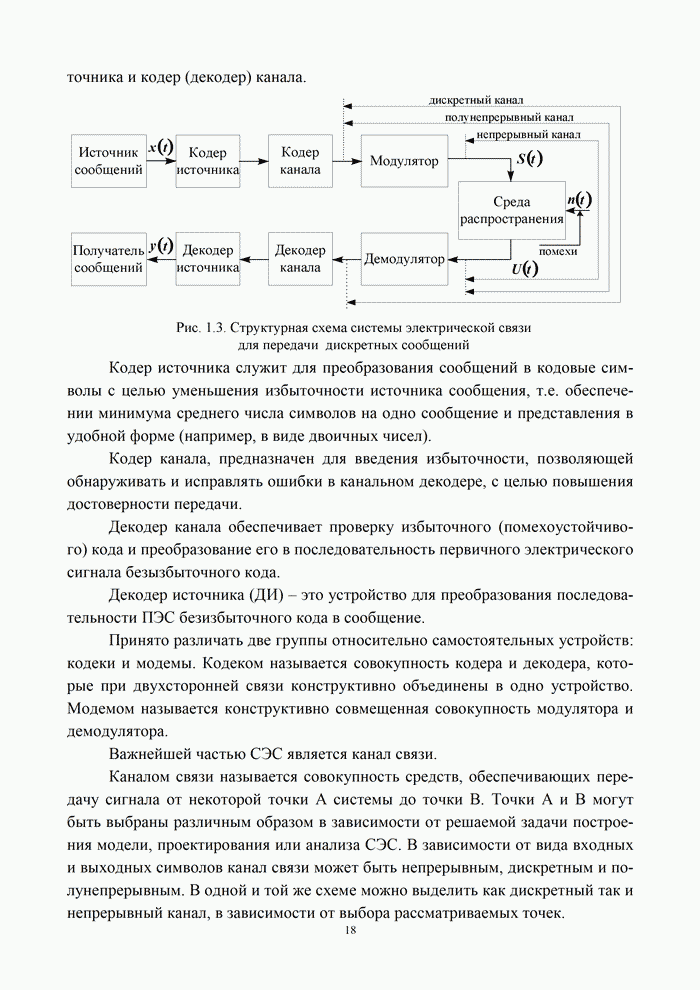
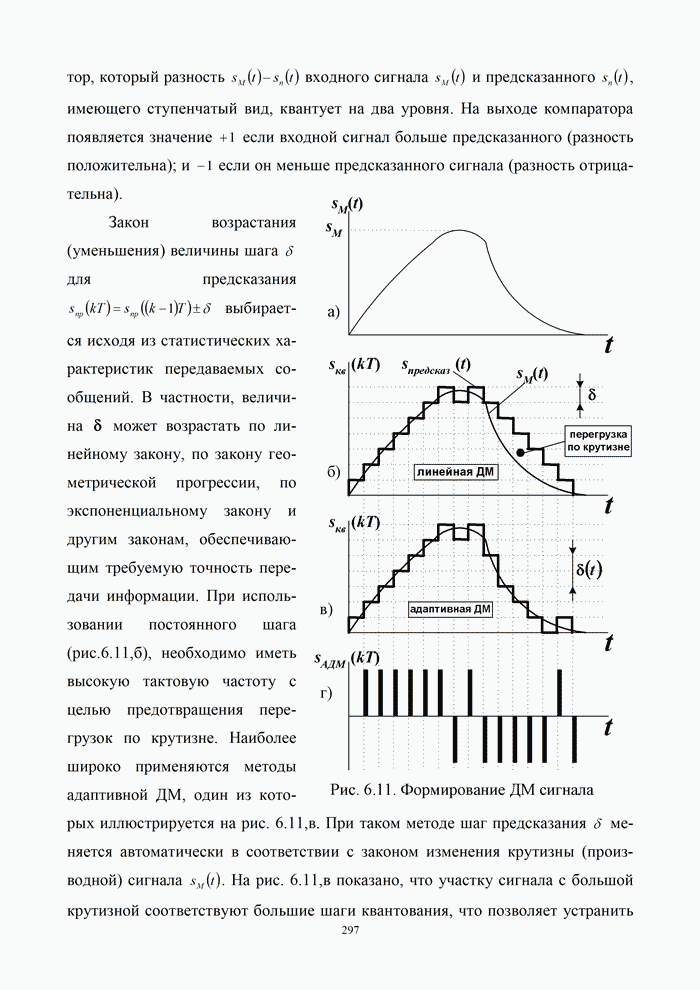
1.3. Способы описания сигналов и помех
1.3.1. Сигнал и его математическая модель
Сигналы можно классифицировать по форме, информативности и характеристикам.
Из простых по форме сигналов в электросвязи наибольшее применение находят гармонические и импульсные сигналы.
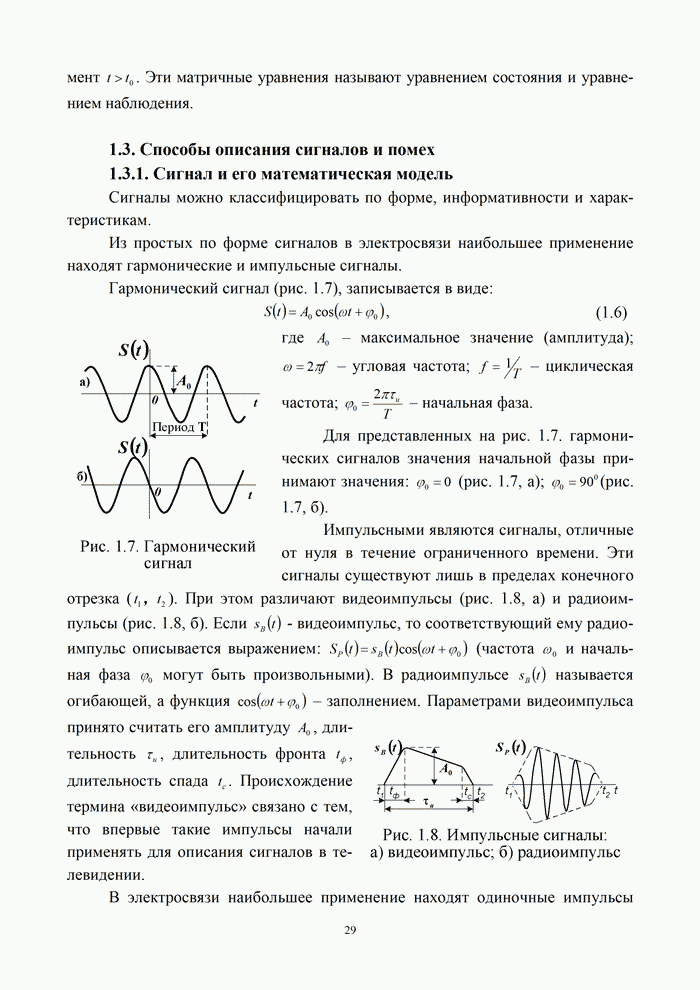
Гармонический сигнал (рис. 1.7), записывается в виде:
|
|
(1.6) |
где ![]() – максимальное значение
(амплитуда);
– максимальное значение
(амплитуда); ![]() – угловая частота;
– угловая частота; ![]() – циклическая
частота;
– циклическая
частота; ![]() –
начальная фаза.
–
начальная фаза.


Для представленных на рис.
1.7. гармонических сигналов значения начальной фазы принимают значения: ![]() (рис. 1.7, а);
(рис. 1.7, а); ![]() (рис. 1.7, б).
(рис. 1.7, б).
Импульсными являются
сигналы, отличные от нуля в течение ограниченного времени. Эти сигналы
существуют лишь в пределах конечного отрезка (![]() ,
, ![]() ). При этом различают
видеоимпульсы (рис. 1.8, а) и радиоимпульсы (рис. 1.8, б). Если
). При этом различают
видеоимпульсы (рис. 1.8, а) и радиоимпульсы (рис. 1.8, б). Если ![]() - видеоимпульс, то
соответствующий ему радиоимпульс описывается выражением:
- видеоимпульс, то
соответствующий ему радиоимпульс описывается выражением: ![]() (частота
(частота ![]() и начальная фаза
и начальная фаза ![]() могут быть
произвольными). В радиоимпульсе
могут быть
произвольными). В радиоимпульсе ![]() называется огибающей, а функция
называется огибающей, а функция ![]() – заполнением.
Параметрами видеоимпульса принято считать его амплитуду
– заполнением.
Параметрами видеоимпульса принято считать его амплитуду ![]() , длительность
, длительность ![]() , длительность фронта
, длительность фронта ![]() , длительность спада
, длительность спада ![]() . Происхождение термина
«видеоимпульс» связано с тем, что впервые такие импульсы начали применять для
описания сигналов в телевидении.
. Происхождение термина
«видеоимпульс» связано с тем, что впервые такие импульсы начали применять для
описания сигналов в телевидении.
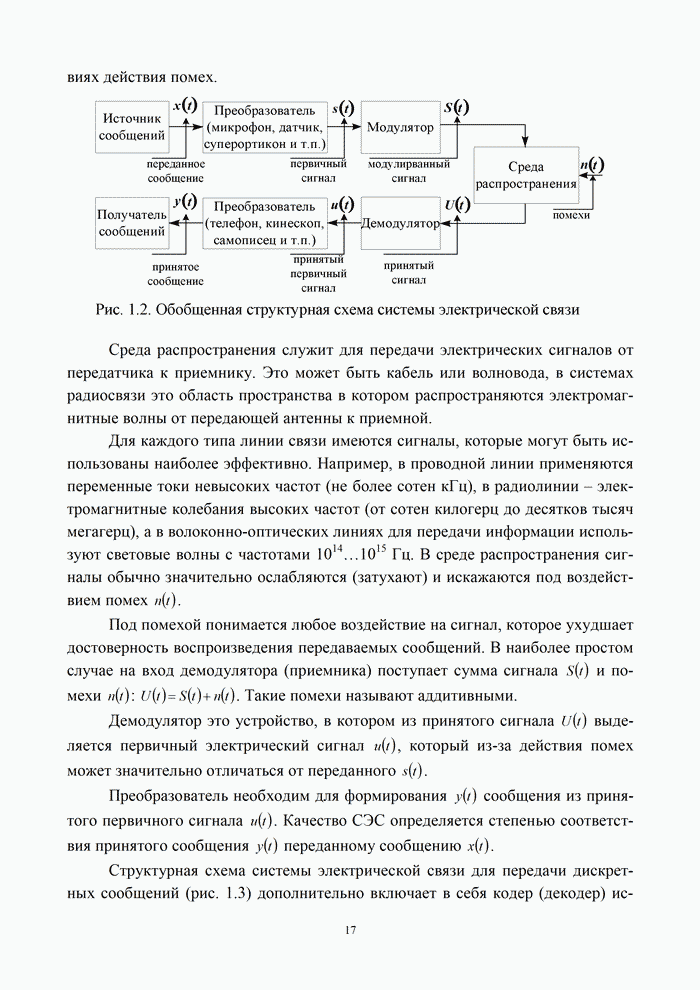
В электросвязи наибольшее
применение находят одиночные импульсы или периодические последовательности
импульсов, форма которых приближается к прямоугольной. Для периодической
последовательности импульсов, вводится понятие скважности, определяемой как
отношение периода к длительности импульса: ![]() .
.
По информативности сигналы классифицируются на детерминированные и случайные.
Детерминированным
называется сигнал, изменение которого во времени полностью предопределено
заранее. Математическим описанием такого сигнала служит детерминированная
функция времени ![]() .
Это означает, что любому моменту времени
.
Это означает, что любому моменту времени ![]() соответствует определенное значение
функции
соответствует определенное значение
функции ![]() . Детерминированные
сигналы подразделяются на периодические и непериодические. Для периодического
сигнала существует такой интервал времени Т (период), что
. Детерминированные
сигналы подразделяются на периодические и непериодические. Для периодического
сигнала существует такой интервал времени Т (период), что ![]() ,
, ![]()
Случайным (или
нерегулярным) сигналом называется сигнал, изменение которого во времени точно
предсказать невозможно. Математическое описание подобных сигналов
осуществляется с помощью случайных функций. Для случайной функции ее значение
при фиксированном аргументе ![]() – случайная величина.
– случайная величина.
 Сигналы, связанные с
передачей сообщений и воздействием помех в системах связи, относятся к разряду
случайных сигналов. Такими случайными сигналами являются, например, напряжения
или токи, соответствующие речи, музыке, последовательности телеграфных знаков и
т.п.
Сигналы, связанные с
передачей сообщений и воздействием помех в системах связи, относятся к разряду
случайных сигналов. Такими случайными сигналами являются, например, напряжения
или токи, соответствующие речи, музыке, последовательности телеграфных знаков и
т.п.
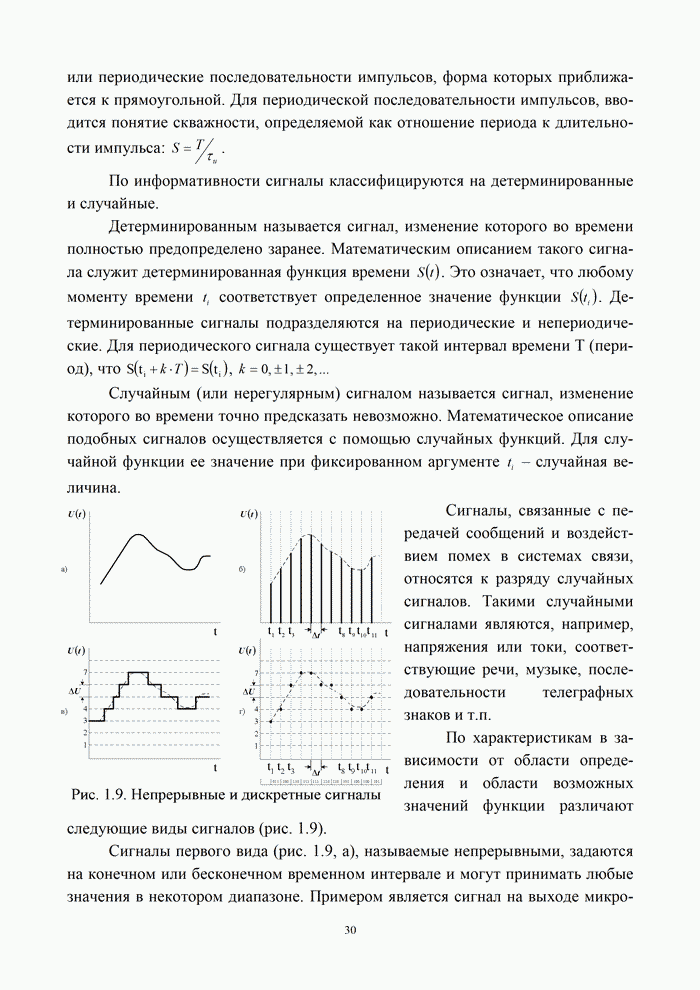
По характеристикам в зависимости от области определения и области возможных значений функции различают следующие виды сигналов (рис. 1.9).
Сигналы первого вида (рис. 1.9, а), называемые непрерывными, задаются на конечном или бесконечном временном интервале и могут принимать любые значения в некотором диапазоне. Примером является сигнал на выходе микрофона. Такие сигналы часто называются аналоговыми.
Сигналы второго вида - непрерывные
по уровню и дискретные по времени (рис. 1.9, б). Дискретизация по времени обычно
выполняется путем взятия отсчетов непрерывной по времени функции ![]() в определенные
дискретные моменты времени
в определенные
дискретные моменты времени ![]() . В результате непрерывную функцию
. В результате непрерывную функцию ![]() заменяют совокупностью
мгновенных значений
заменяют совокупностью
мгновенных значений ![]() .
Дискретизация по времени лежит в основе всех видов импульсной модуляции.
.
Дискретизация по времени лежит в основе всех видов импульсной модуляции.
Сигналы третьего вида - дискретные
(квантованные) по уровню и непрерывные по времени (рис. 1.9, в). Дискретизация
значений непрерывной функции ![]() по уровню называется амплитудным
квантованием. В результате квантования непрерывный сигнал заменяется
ступенчатой функцией. Шаг квантования
по уровню называется амплитудным
квантованием. В результате квантования непрерывный сигнал заменяется
ступенчатой функцией. Шаг квантования ![]() (расстояние между двумя соседними
разрешенными уровнями) может быть как постоянным, так и переменным. Его обычно
выбирают из условий обеспечения требуемой точности восстановления непрерывного
сигнала из квантованного.
(расстояние между двумя соседними
разрешенными уровнями) может быть как постоянным, так и переменным. Его обычно
выбирают из условий обеспечения требуемой точности восстановления непрерывного
сигнала из квантованного.
Сигналы четвертого вида, называемые дискретными (рис. 1.9, г), задаются в определенные дискретные моменты и принимают определенные дискретные значения. Их можно получить, например, из непрерывных сигналов, осуществляя операции дискретизации по времени и квантования по уровню. Такие сигналы легко представить в цифровой форме, т.е. в виде чисел с конечным числом разрядов. По этой причине их называют цифровыми.
Достоинством цифровых сигналов является возможность применения кодирования для повышения помехоустойчивости.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Список сокращений
- Основные обозначения
- ВВЕДЕНИЕ
- Глава 1. Сообщения, сигналы и помехи, их математические модели
- 1.1. Основные понятия и определения
- 1.1.1. Сообщение, сигнал, модуляция
- 1.1.2. Основные параметры сигналов
- 1.2. Системы связи. Каналы связи
- 1.2.1. Структура канала электросвязи
- 1.2.2. Линия и сеть связи
- 1.2.3. Помехи и искажения в канале
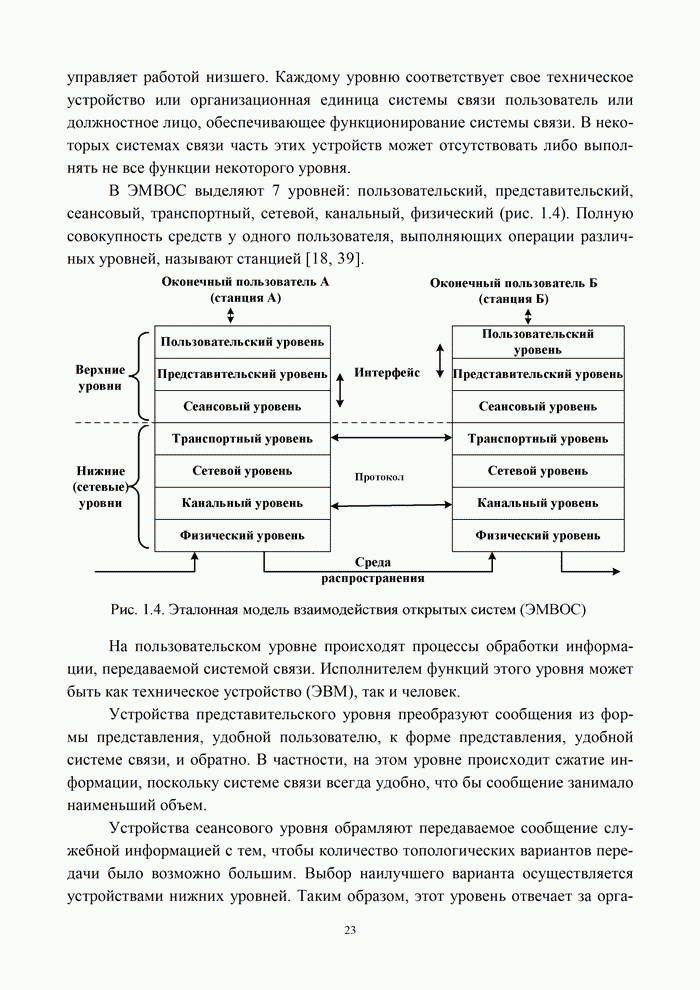
- 1.2.4. Эталонная модель взаимодействия открытых систем
- 1.2.5. Модели каналов связи и их математическое описание
- 1.3. Способы описания сигналов и помех
- 1.3.1. Сигнал и его математическая модель
- 1.3.2. Энергетические характеристики детерминированного сигнала
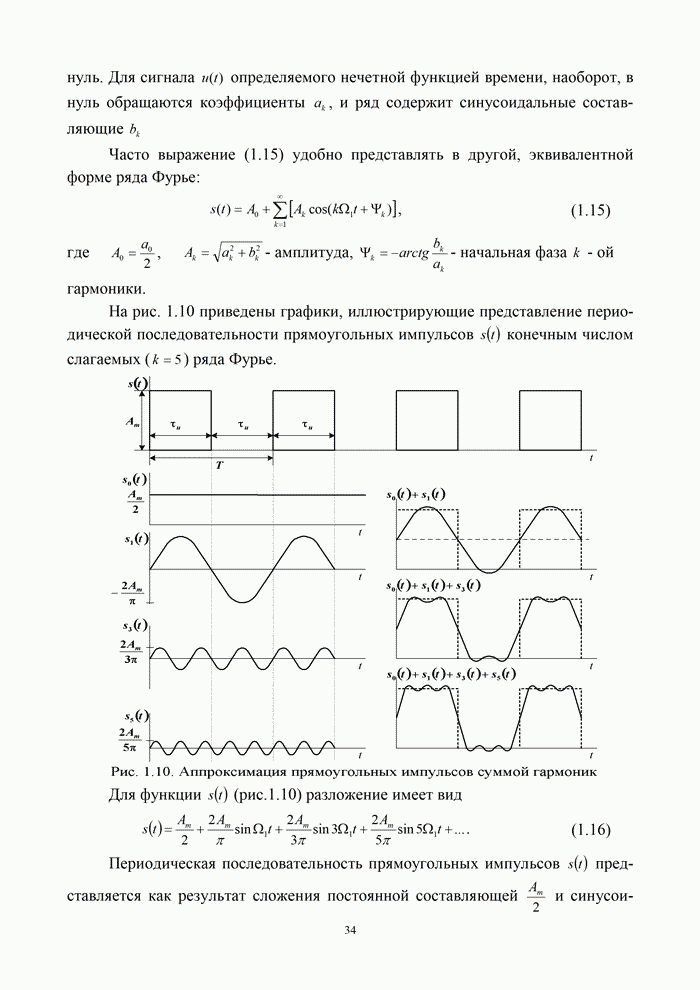
- 1.4.2. Представление сигналов и помех рядом Фурье
- 1.4.3. Применение преобразования Фурье для непериодических сигналов
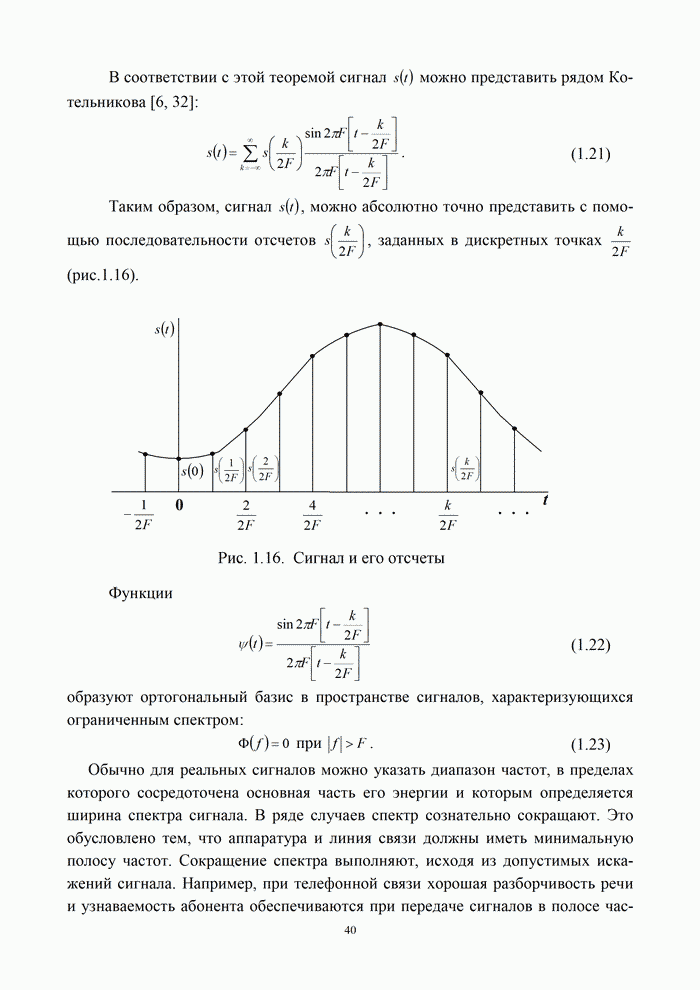
- 1.5. Теорема Котельникова
- 1.6. Пространство сигналов
- 1.6.1. Линейное пространство
- 1.6.2. Представление сигнала в многомерном пространстве
- 1.7. Сигналы как случайные процессы
- 1.7.1. Характеристики случайного процесса
- 1.7.2. Флуктуационный шум
- 1.8. Комплексное представление сигналов и помех
- 1.8.1. Понятие аналитического сигнала
- 1.8.2. Огибающая, мгновенная фаза и мгновенная частота узкополосного случайного процесса
- Контрольные вопросы
- Глава 2. Методы формирования и преобразования сигналов
- 2.1. Модуляция сигналов
- 2.1.1. Амплитудная модуляция гармонической несущей
- 2.1.2. Балансная и однополосная модуляция гармонической несущей
- 2.2. Методы угловой модуляции
- 2.2.1. Принципы частотной и фазовой (угловой) модуляции
- 2.2.2. Спектр сигналов угловой модуляции
- 2.3. Формирование и детектирование модулированных сигналов
- 2.3.1. Формирование и детектирование сигналов амплитудной и однополосной амплитудной модуляции
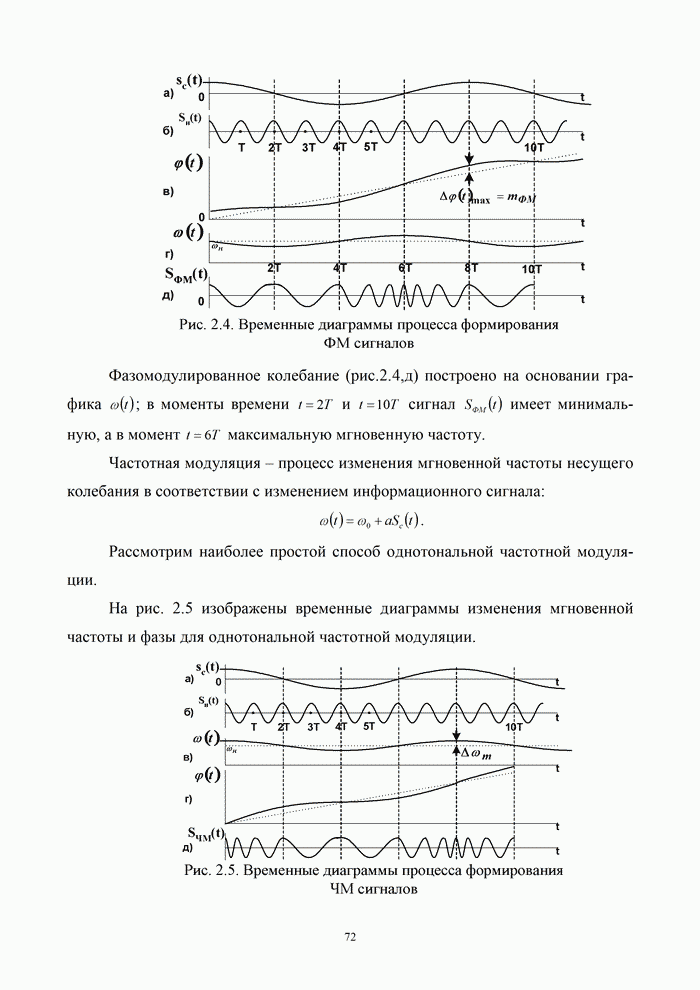
- 2.3.2. Формирование и детектирование сигналов угловой модуляции
- 2.4. Манипуляция сигналов
- 2.4.1. Временные и спектральные характеристики амплитудно-манипулированных сигналов
- 2.4.2. Временные и спектральные характеристики частотно-манипулированных сигналов
- 2.4.3. Фазовая (относительно-фазовая) манипуляция сигналов
- 2.5. Системы связи с многопозиционной относительной фазовой манипуляцией
- 2.5.1. Принцип формирования сигнала с многократной относительной фазовой манипуляцией
- 2.5.2. Квадратурная относительно-фазовая манипуляция (КОФМ)
- 2.5.3. Принцип частотной модуляции с непрерывной фазой
- Контрольные вопросы
- Глава 3. Помехоустойчивость приема дискретных сообщений
- 3.1. Критерии качества и правила приема дискретных сообщений
- 3.1.1. Понятие о помехоустойчивости систем электрической связи
- 3.1.2. Задача оптимального приема
- 3.1.3. Вычисление вероятностей ошибок
- 3.2. Оптимальная демодуляция при когерентном приеме сигналов
- 3.2.1. Оптимальные алгоритмы приема при полностью известных сигналах
- 3.2.2. Реализация алгоритмов оптимального когерентного приема
- 3.3. Помехоустойчивость приема сигналов с известными параметрами
- 3.4. Прием сигналов с неопределенной фазой
- 3.4.1. Оптимальный некогерентный прием дискретных сигналов
- 3.4.2. Помехоустойчивость оптимального некогерентного приема
- 3.5. Подоптимальные методы приема
- 3.5.1. Причины применения неоптимальных методов приема
- 3.5.2. Квазиоптимальные методы приема
- Контрольные вопросы
- Глава 4. Теория передачи информации
- 4.1. Информационные характеристики источника сообщений
- 4.1.1. Количественное определение информации
- 4.1.2. Энтропия и производительность дискретного источника сообщений
- 4.2. Пропускная способность дискретного канала
- 4.2.1. Количество информации переданной по дискретному каналу
- 4.2.2. Пропускная способность дискретного канала
- 4.2.3. Пропускная способность симметричного дискретного канала без памяти
- 4.3. Методы сжатия дискретных сообщений
- 4.3.1. Условия существования оптимального неравномерного кода
- 4.3.2. Прямая и обратная теоремы кодирования источника неравномерными кодами
- 4.3.3. Показатели эффективности сжатия
- 4.3.4. Кодирование источника дискретных сообщений методом Шеннона-Фано
- 4.3.5. Кодирование источника дискретных сообщений методом Хаффмена
- 4.4. Пропускная способность непрерывного канала
- 4.4.1. Постановка задачи передачи дискретных сообщений в непрерывном канале
- 4.4.2. Количество информации, переданной по непрерывному каналу
- 4.4.3. Пропускная способность непрерывного канала
- Контрольные вопросы
- Глава 5. Теория кодирования сообщений
- 5.1. Помехоустойчивое кодирование: блочные и непрерывные коды
- 5.1.1. Постановка задачи помехоустойчивого кодирования
- 5.1.2. Классификация кодов
- 5.1.3. Основные характеристики и свойства блочных кодов
- 5.2. Эффективность помехоустойчивого кодирования
- 5.2.1. Эффективность кода в режиме исправления ошибок
- 5.2.2. Эффективность кода в режиме обнаружения ошибок
- 5.2.3. Эффективность помехоустойчивых кодов
- 5.3. Математические основы теории помехоустойчивого кодирования
- 5.3.1. Краткие сведения из теории чисел
- 5.3.2. Группы
- 5.3.3. Кольца и поля
- 5.3.4. Векторное пространство
- 5.3.5. Конечные поля
- 5.4. Линейные блочные коды
- 5.4.1. Система передачи дискретных сообщений
- 5.4.2. Параметры линейного кода
- 5.4.3. Полиномиальные циклические коды
- 5.4.4. Циклические коды и корни полиномов
- 5.4.5. Спектральное описание циклических кодов
- 5.4.6. Простейшие блочные линейные коды
- 5.5. Коды Боуза-Чоудхури-Хоквингема
- 5.5.1. Методы задания кодов БЧХ
- 5.5.2. Принципы декодирования кодов БЧХ
- 5.5.3. Методы реализации этапов декодирования кодов БЧХ
- 5.6. Коды Рида-Соломона
- 5.6.1. Основные определения
- 5.6.2. Обнаружение и исправление пакетов ошибок
- 5.7. Коды Рида-Маллера
- 5.7.1. Задание и декодирование кодов Рида-Маллера
- 5.7.2. Симплексные коды и m-последовательности
- 5.7.3. Связь между блочными кодами
- 5.8. Сверточные коды
- 5.8.1. Основные параметры
- 5.8.2. Способы задания сверточного кода
- 5.8.3. Алгоритм декодирования Витерби
- 5.9. Помехоустойчивость систем передачи дискретных сообщений
- 5.9.1. Две процедуры приема сигналов
- 5.9.2. Помехоустойчивость систем передачи информации при оптимальной процедуре приема
- 5.9.3. Помехоустойчивость систем передачи информации при посимвольном приеме сигналов
- Контрольные вопросы
- Глава 6. Сигналы с импульсной модуляцией
- 6.1. Методы импульсной модуляции
- 6.1.1. Импульсные методы передачи непрерывных сигналов
- 6.1.2. Спектральные характеристики импульсных методов модуляции
- 6.2. Помехоустойчивость непрерывных каналов связи с импульсной модуляцией
- 6.2.1. Помехоустойчивость систем передачи с импульсными методами модуляции
- 6.3. Цифровые методы передачи непрерывных сообщений
- 6.3.1. Передача сигналов с импульсно-кодовой модуляцией
- 6.3.2. Передача сигналов с дельта модуляцией
- 6.3.3. Квантование сигналов в системах с ИКМ и ДМ
- Контрольные вопросы
- Глава 7. Методы приема сигналов в сложных условиях
- 7.1. Прием сигналов в каналах с замираниями
- 7.1.1. Сущность замираний и их классификация
- 7.1.2. Принципы разнесенного приема сигналов
- 7.2. Методы борьбы с замираниями сигналов
- 7.2.1. Методы борьбы с замираниями в аналоговых системах связи
- 7.2.2. Методы борьбы с замираниями в цифровых системах связи
- 7.3. Методы борьбы с межсимвольной интерференцией
- 7.3.1. Причины возникновения и сущность межсимвольной интерференции
- 7.3.2. Обработка сигналов в каналах с межсимвольной интерференцией
- 7.3.3. Помехоустойчивость в каналах с межсимвольной интерференцией
- 7.4. Прием дискретных сообщений в каналах с сосредоточенными по спектру и импульсными помехами
- 7.4.1. Общая характеристика сосредоточенных по спектру и импульсных помех
- 7.4.2. Борьба с сосредоточенными и импульсными помехами
- 7.5. Компенсация помех и искажений в канале
- 7.5.1. Принцип работы радиолинии с ФМ ПСС (ФМ ШПС)
- 7.5.2. Помехоустойчивость радиолинии с ФМ ПСС
- 7.5.3. Принципы работы радиолиний с ППРЧ
- 7.5.4. Помехоустойчивость радиолиний с ППРЧ
- Контрольные вопросы
- Глава 8. Многоканальная связь и распределение информации
- 8.1. Методы распределения ресурса общего канала
- 8.1.1. Классификация систем передачи информации, использующих единый ресурс
- 8.1.2. Постановка задачи объединения и разделения сигналов
- 8.1.3. Энергетическая и спектральная цена уплотнения
- 8.2. Частотное разделение каналов
- 8.2.1. Принцип частотного объединения и разделения каналов
- 8.2.2. Групповой сигнал, его структура и характеристики
- 8.3. Временное разделение каналов
- 8.3.1. Принцип временного разделения каналов
- 8.3.2. Характеристики группового сигнала систем с ВРК
- 8.4. Разделение сигналов по форме
- Контрольные вопросы
- Глава 9. Эффективность систем связи
- 9.1. Оценка эффективности систем связи
- 9.1.1. Подходы к оценке эффективности
- 9.1.2. Критерии эффективности
- 9.1.3. Эффективность аналоговых и цифровых систем
- 9.2. Выбор сигналов и помехоустойчивых кодов
- 9.2.1. Многопозиционные сигналы
- 9.2.2. Корректирующие коды
- 9.3. Оптимизация систем связи
- 9.3.1. Согласование методов модуляции и кодирования
- 9.3.2. Классификация сигнально – кодовых конструкций
- 9.4. Характеристики основных типов СКК
- 9.4.1. Согласование канала кодом Грея
- 9.4.2. Согласование на основе разбиения ансамбля на вложенные подансамбли
- 9.5. Алгоритмы цифровой обработки сигналов
- 9.5.1. Дискретные сигналы и их спектры
- 9.5.2. Алгоритмы дискретного и быстрого преобразований Фурье
- Контрольные вопросы
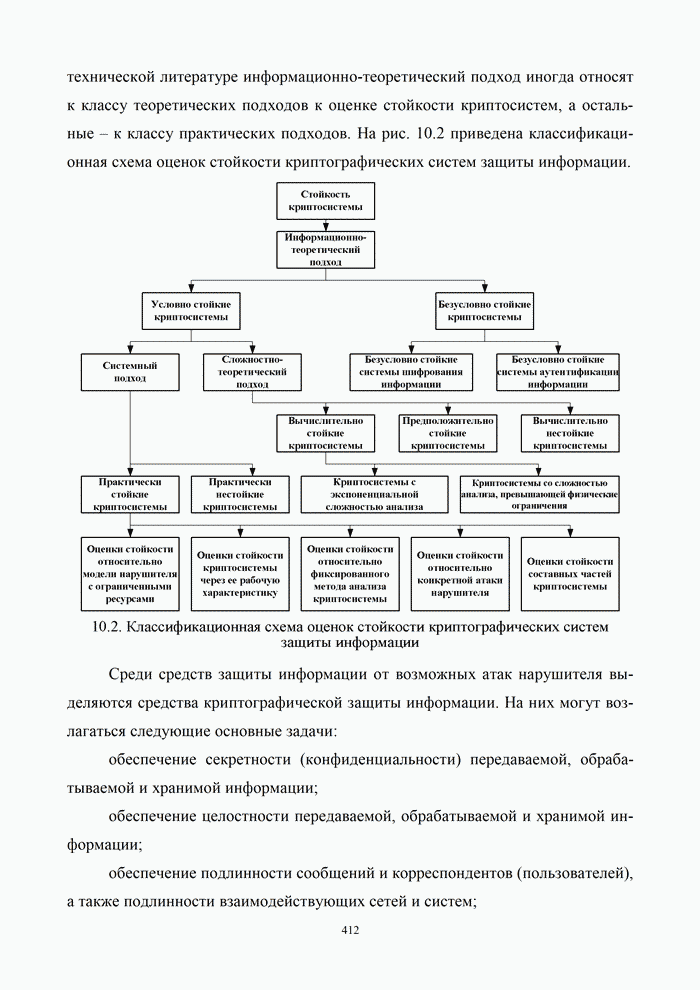
- Глава 10. Теоретико-информационные основы криптозащиты сообщений в телекоммуникационных системах
- 10.1. Классификация криптографических систем
- 10.1.2. Классификация криптографических систем защиты информации
- 10.1.3. Оценка стойкости криптосистем
- 10.2. Функции, используемые в криптографических системах
- 10.2.1. Общее описание функций, используемых в криптографических системах
- 10.2.2. Однонаправленные функции
- 10.2.3. Криптографические хэш-функции
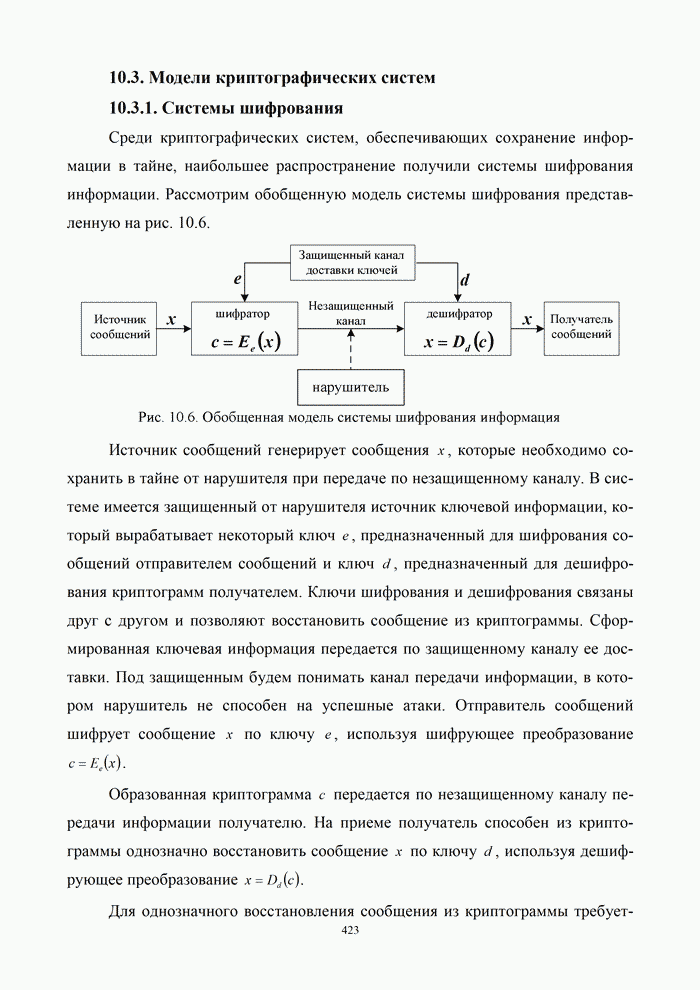
- 10.3. Модели криптографических систем
- 10.3.1. Системы шифрования
- 10.3.2. Традиционные симметричные криптосистемы
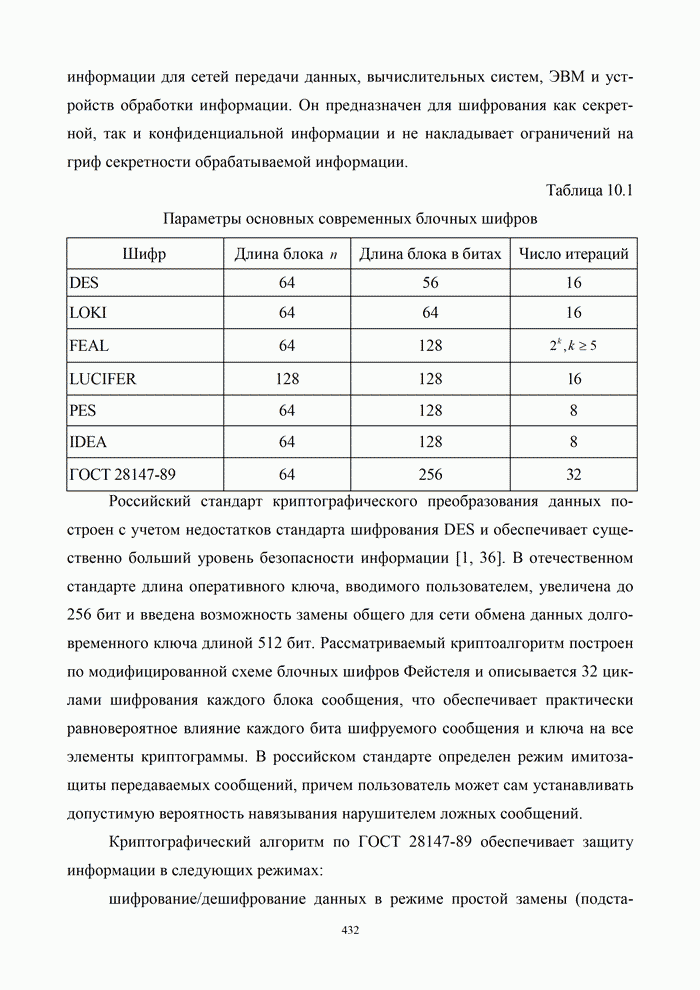
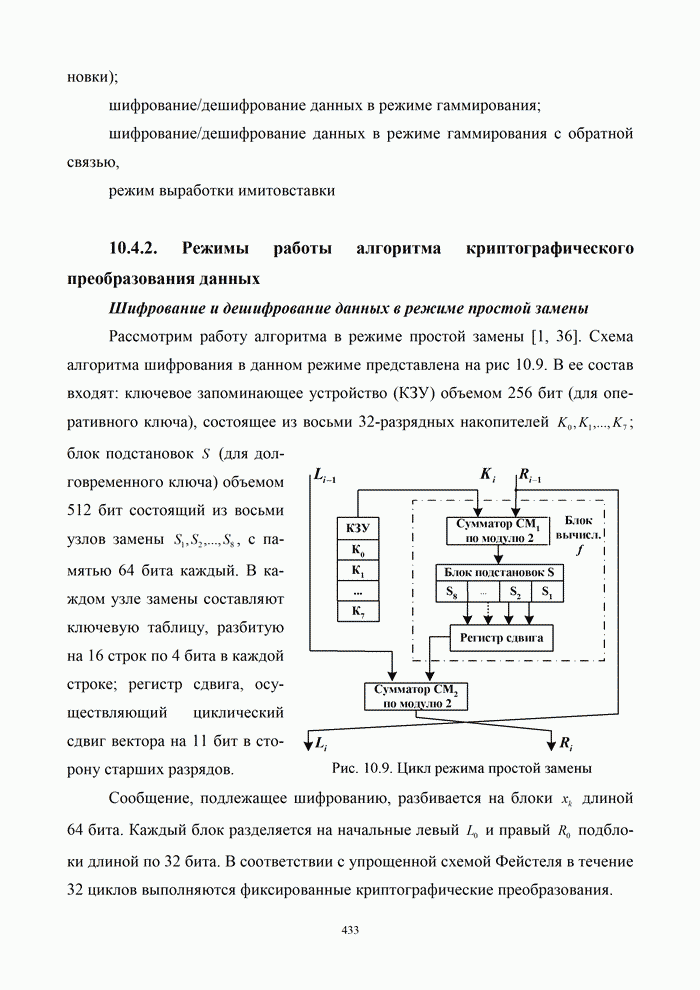
- 10.4. Алгоритмы криптографической защиты
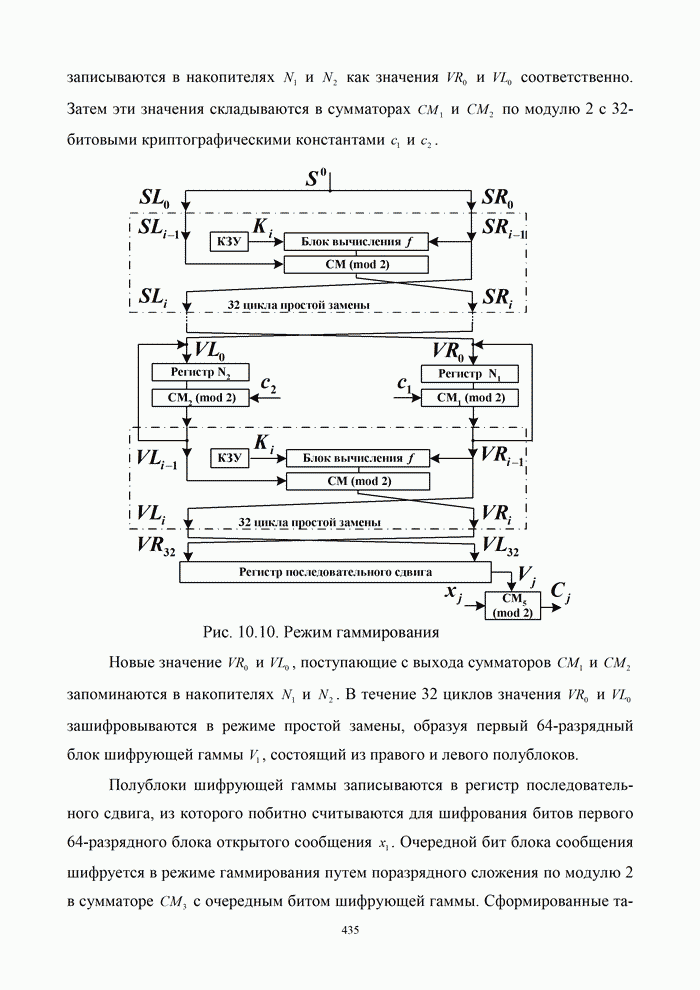
- 10.4.1. Алгоритм криптографической защиты информации согласно ГОСТ 28147-89
- Контрольные вопросы
- Заключение
- Список литературы