| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
10.2.2. Однонаправленные функции
Особую роль в криптографии играют однонаправленные функции, которые в общем случае не являются биективными.
Однонаправленной
называется такая функция ![]() , для которой легко определить значение
функции
, для которой легко определить значение
функции ![]() ,
но практически невозможно отыскать для заданного
,
но практически невозможно отыскать для заданного ![]() такое
такое ![]() , что
, что ![]() .
.
Для построения криптографических систем защиты информации чаще используются однонаправленные функции, для которых обратное преобразование существует и однозначно, но вычислительно нереализуемо. Они называются вычислительно необратимыми функциями.
В
качестве примера однонаправленной функции ![]() рассмотрим широко известную функцию
дискретного возведения в степень:
рассмотрим широко известную функцию
дискретного возведения в степень: ![]() , где
, где ![]() – целое число от 1 до
– целое число от 1 до ![]() включительно, а
вычисление производится по модулю
включительно, а
вычисление производится по модулю ![]() , где
, где ![]() – очень большое простое число;
– очень большое простое число; ![]() – целое число (
– целое число (![]() ).
).
Напомним, что простым числом называется целое число, которое не делится ни на какие числа, кроме себя самого и единицы.
Пример
10.1. Для примера возьмем небольшое простое число ![]() ; тогда для осуществления
преобразований можно выбрать примитивный элемент
; тогда для осуществления
преобразований можно выбрать примитивный элемент ![]() , так как
, так как ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Функция
![]() вычисляется
сравнительно просто, а обратная к ней функция
вычисляется
сравнительно просто, а обратная к ней функция ![]() является вычислительно сложной
практически для всех (
является вычислительно сложной
практически для всех (![]() ) при условии, что не только
) при условии, что не только ![]() велико, но и (
велико, но и (![]() ) имеет большой простой
множитель (лучше всего, если это будет другое простое число, умноженное на 2).
В связи с этим такую задачу называют задачей нахождения дискретного логарифма
или задачей дискретного логарифмирования.
) имеет большой простой
множитель (лучше всего, если это будет другое простое число, умноженное на 2).
В связи с этим такую задачу называют задачей нахождения дискретного логарифма
или задачей дискретного логарифмирования.
Задача
дискретного логарифмирования состоит в том, что для известных целых ![]() ,
, ![]() ,
, ![]() необходимо найти целое число
необходимо найти целое число ![]() . Однако алгоритм
вычисления дискретного логарифма за приемлемое время пока не найден. Поэтому
модульная экспонента считается однонаправленной функцией.
. Однако алгоритм
вычисления дискретного логарифма за приемлемое время пока не найден. Поэтому
модульная экспонента считается однонаправленной функцией.
По
современным оценкам теории чисел при целых числах ![]() и
и ![]() решение задачи дискретного
логарифмирования потребует около
решение задачи дискретного
логарифмирования потребует около ![]() операций, что имеет в
операций, что имеет в ![]() раз большую
вычислительную сложность, чем задача разложения на множители. При увеличении
длины чисел разница в оценках сложности задач возрастает.
раз большую
вычислительную сложность, чем задача разложения на множители. При увеличении
длины чисел разница в оценках сложности задач возрастает.
Следует отметить, что пока не удалось доказать, что не существует эффективного алгоритма вычисления дискретного логарифма за приемлемое время. Исходя из этого, модульная экспонента отнесена к однонаправленным функциям условно, что, однако, не мешает с успехом применять ее на практике.
Одним из первых применений однонаправленных функций было решение задачи обеспечения безопасности и использования пароля, по которому осуществляется доступ пользователя к ресурсам и услугам в автоматизированных системах.
Открытое
значение ![]() вместе
с именем пользователя может быть помещено в список паролей доступа, хранящихся в
ЭВМ. Законный пользователь для получения доступа в автоматизированную систему
предъявляет свое число
вместе
с именем пользователя может быть помещено в список паролей доступа, хранящихся в
ЭВМ. Законный пользователь для получения доступа в автоматизированную систему
предъявляет свое число ![]() . ЭВМ вычисляет по этому числу значение
однонаправленной функции
. ЭВМ вычисляет по этому числу значение
однонаправленной функции ![]() и сравнивает с хранящимся значением
и сравнивает с хранящимся значением ![]() . При совпадении этих
значений пользователь становится идентифицированным и получает требуемый
доступ.
. При совпадении этих
значений пользователь становится идентифицированным и получает требуемый
доступ.
Кроме однонаправленных функций, не имеющих вычислительно простого обратного отображения даже для законных пользователей, знающих секретную ключевую информацию, в криптографии широко используются однонаправленные функции, для которых знание секретного ключа дает возможность законному пользователю вычислительно просто находить обратное отображение. Они получили название однонаправленных функций с потайным ходом, иногда их называют однонаправленными функциями с лазейкой.
Однонаправленные функции с потайным ходом
Быстрое развитие криптографии в последние два десятилетия во многом стало возможным благодаря открытию американскими учеными В. Диффи и М. Хэлманом однонаправленных функций с потайным ходом и их использованием для различных криптосистем защиты информации [1, 31].
Однонаправленная
функция с потайным ходом есть однонаправленная функция ![]() с дополнительным свойством,
таким, что, зная информацию z потайного хода для каждого
с дополнительным свойством,
таким, что, зная информацию z потайного хода для каждого ![]() вычислительно просто
определить
вычислительно просто
определить ![]() ,
удовлетворяющее уравнению
,
удовлетворяющее уравнению ![]() .
.
Для
нарушителя, не знающего информации ![]() потайного хода, нахождение отображения
потайного хода, нахождение отображения ![]() может быть сделано
вычислительно нереализуемым. Поэтому информация
может быть сделано
вычислительно нереализуемым. Поэтому информация ![]() может служить секретным ключом для
пользователя функций с потайным ходом.
может служить секретным ключом для
пользователя функций с потайным ходом.
Однонаправленные функции с потайным ходом относятся к вычислительно необратимым функциям.
Функция вычислительно необратима, если при попытке формирования алгоритма нахождения обратного отображения к ней противник наталкивается на непреодолимую вычислительную проблему.
Оценивая стойкость криптосистем, построенных на основе известных однонаправленных функций с потайным ходом, отметим, что ни одна из них не является безусловно стойкой. Это объясняется тем, что нарушитель с теоретически бесконечными вычислительными ресурсами способен вычислять обратное отображение к таким функциям.
На основе однонаправленных функций с потайным ходом можно построить криптосистемы аутентификации информации в условиях взаимного недоверия корреспондентов, системы шифрования информации, в которых отправители сообщений могут пользоваться несекретными ключами шифрования, криптосистемы обмена секретной ключевой информации по открытым каналам связи, а также многие другие криптосистемы.
К настоящему времени предложено большое количество однонаправленных функций с потайным ходом, построенных на основе известных вычислительно сложных математических задач. Наиболее часто для построения однонаправленных функций с потайным ходом используется сложность решения следующих теоретико-числовых задач:
отыскание дискретного логарифма элемента в большом конечном поле или группе (криптосистема открытого распространения ключей Диффи-Хэллмана, криптосистема шифрования и криптосистема цифровой подписи сообщений Эль-Гамаля, криптосистема цифровой подписи сообщений Шнорра и другие криптосистемы) [1, 31, 36];
разложение больших чисел на простые множители (криптосистема шифрования и криптосистема цифровой подписи сообщений РША, криптосистема цифровой подписи сообщений Рабина и другие криптосистемы) [1, 19];
задача об укладке целочисленного ранца (класс ранцевых систем шифрования информации Меркля-Хэллмана) [1, 36];
декодирование неизвестных получателю кодов Гоппы (класс систем шифрования информации Мак-Эллиса) [1].
Рассмотрим конкретные однонаправленные функции с потайным ходом, послужившие основой для широко используемых на практике криптографических систем защиты информация.
Однонаправленная функция РША с потайным ходом
В 1978 году была предложена первая однонаправленная функция с потайным ходом, положенная в основу широко используемой на практике несимметричной криптографической системы РША. Первые буквы фамилий ее авторов (Р. Ривеста, А. Шамира и Л. Адлемара) образовали общепринятое название предложенной ими функции и криптосистемы. Для описания однонаправленной функции РША с потайным ходом требуются некоторые сведения из элементарной теория чисел [1, 19, 31].
Однонаправленная
функция РША с потайным ходом определяется как дискретное возведение значения ![]() в степень ключа
в степень ключа ![]() :
: ![]() , где
, где ![]() – информация
потайного хода;
– информация
потайного хода; ![]() и
и
![]() являются
большими простыми числами;
являются
большими простыми числами; ![]() – положительное целое число, не
превосходящее
– положительное целое число, не
превосходящее ![]() ;
а значение
;
а значение ![]() –
положительное целое число, не превосходящее
–
положительное целое число, не превосходящее ![]() – функции Эйлера, для которого наибольший
общий делитель
– функции Эйлера, для которого наибольший
общий делитель ![]() .
.
Пусть
![]() имеет
обратную функцию вида
имеет
обратную функцию вида ![]() , где значение
, где значение ![]() есть единственное
положительное целое, меньшее
есть единственное
положительное целое, меньшее ![]() и удовлетворяющее условию
и удовлетворяющее условию ![]() .
.
Исследования
однонаправленной функции РША с потайным ходом показали, что практически все
попытки противостоящей стороны получить информацию о потайном ходе эквивалентны
разложению ![]() на
множители. Поэтому в последние десятилетия интенсивно исследовались методы разложения
составного числа на множители. В математике такая задача называется задачей
факторизацией составного числа и в течение столетий она привлекала внимание
многих ученых. Известный наилучший алгоритм факторизации составного числа имеет
субэкспоненциальную вычислительную сложность.
на
множители. Поэтому в последние десятилетия интенсивно исследовались методы разложения
составного числа на множители. В математике такая задача называется задачей
факторизацией составного числа и в течение столетий она привлекала внимание
многих ученых. Известный наилучший алгоритм факторизации составного числа имеет
субэкспоненциальную вычислительную сложность.
За
последние годы в области разработки эффективных методов факторизации достигнуты
существенные успехи, поэтому для обеспечения требуемой безопасности применения
однонаправленной функции РША с потайным ходом должны использоваться числа ![]() и
и ![]() ‚ размерностью многие
сотни и даже тысячи бит.
‚ размерностью многие
сотни и даже тысячи бит.
Однонаправленная функция Эль-Гамаля c потайным ходом
Ранее
была рассмотрена однонаправленная функция на основе вычисления дискретных
логарифмов в алгебраической группе. Поле Галуа ![]() , где
, где ![]() – простое число, является более сложной
алгебраической структурой по сравнению с группой, над его элементами можно
выполнять операции сложения и умножения, а в группе - только сложение или
только умножение. Например, рассмотренная ранее однонаправленная функция Диффи
и Хеллмана, послужившая основой криптосистемы открытого распространения ключей,
использует операцию умножения над элементами группы [1, 31, 36].
– простое число, является более сложной
алгебраической структурой по сравнению с группой, над его элементами можно
выполнять операции сложения и умножения, а в группе - только сложение или
только умножение. Например, рассмотренная ранее однонаправленная функция Диффи
и Хеллмана, послужившая основой криптосистемы открытого распространения ключей,
использует операцию умножения над элементами группы [1, 31, 36].
Задача
вычисления дискретных логарифмов в алгебраическом поле формулируется следующим
образом. При заданных простом числе ![]() , порождающем поле
, порождающем поле ![]() , и примитивном элементе
, и примитивном элементе ![]() (
(![]() ) по элементу
) по элементу ![]() поля отыскать
элемент
поля отыскать
элемент ![]() (
(![]() ) такой, что
выполняется тождество
) такой, что
выполняется тождество ![]() .
.
Число
![]() является
ключом формирования цифровой подписи сообщений отправителя и должно храниться
отправителем сообщений в секрете, а значение у сообщается всем как открытый
ключ проверки цифровой подписи сообщений отправителя.
является
ключом формирования цифровой подписи сообщений отправителя и должно храниться
отправителем сообщений в секрете, а значение у сообщается всем как открытый
ключ проверки цифровой подписи сообщений отправителя.
На основе однонаправленной функции Эль-Гамаля с потайным ходом, как для функции РША, можно построить несимметричную систему шифрования информации.
Безопасность использования однонаправленной функции Эль-Гамаля с потайным ходом основана на вычислительной сложности задачи дискретного логарифмирования в алгебраическом поле большой размерности. Объем вычислений для ее решения выше, чем при факторизации составного числа.
Однонаправленная функция с потайным ходом на основе алгебраических уравнений по модулю 2
Значение
однонаправленной функции ![]() с потайным ходом зависит от аргументов
с потайным ходом зависит от аргументов ![]() и
и ![]() :
:
|
|
|
где ![]() – вектор сообщения,
состоящий из двух частей
– вектор сообщения,
состоящий из двух частей ![]() и
и ![]() длиной по
длиной по ![]() бит каждая:
бит каждая: ![]() ;
; ![]() – вектор ключа, который
определяется совокупностью подвекторов:
– вектор ключа, который
определяется совокупностью подвекторов: ![]() .
.
Над
вектором ![]() циклически
выполняются
циклически
выполняются ![]() раз
операции вида:
раз
операции вида:
|
|
|
где ![]() – некоторое
фиксированное нелинейное преобразование, а знак
– некоторое
фиксированное нелинейное преобразование, а знак ![]() означает сложение по модулю два.
означает сложение по модулю два.
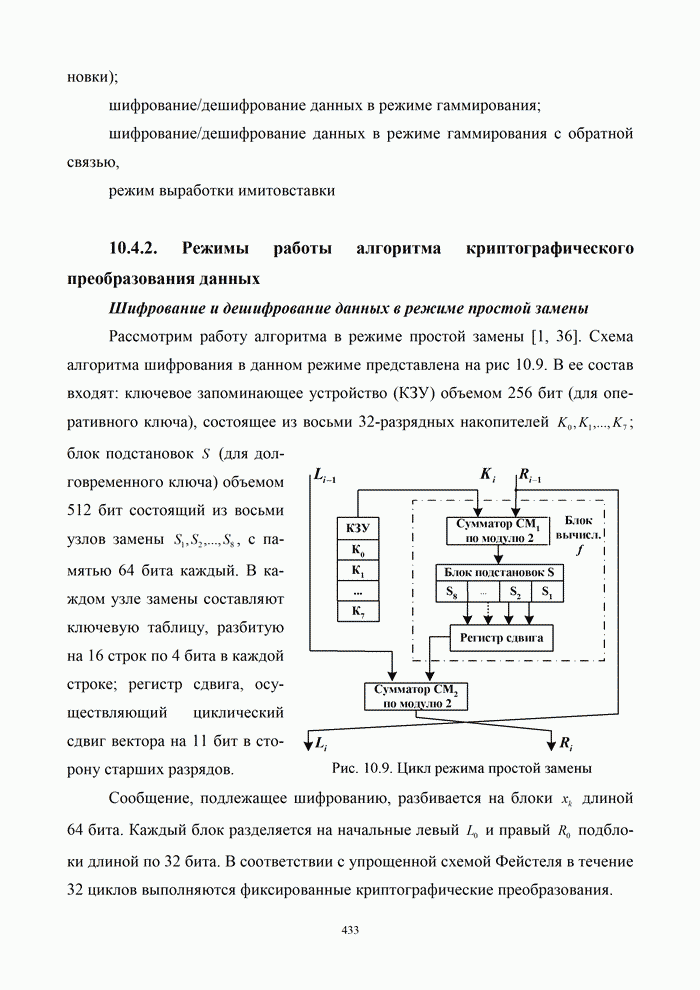
Рассмотренный принцип построения однонаправленной функции с потайным ходом используется при построении широкого класса блочных систем шифрования (класс блочных шифров Фейстеля) к которому принадлежат известный американский алгоритм шифрования данных DES и отечественный алгоритм шифрования согласно ГОСТ 28147–89 [1, 31, 36].
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Список сокращений
- Основные обозначения
- ВВЕДЕНИЕ
- Глава 1. Сообщения, сигналы и помехи, их математические модели
- 1.1. Основные понятия и определения
- 1.1.1. Сообщение, сигнал, модуляция
- 1.1.2. Основные параметры сигналов
- 1.2. Системы связи. Каналы связи
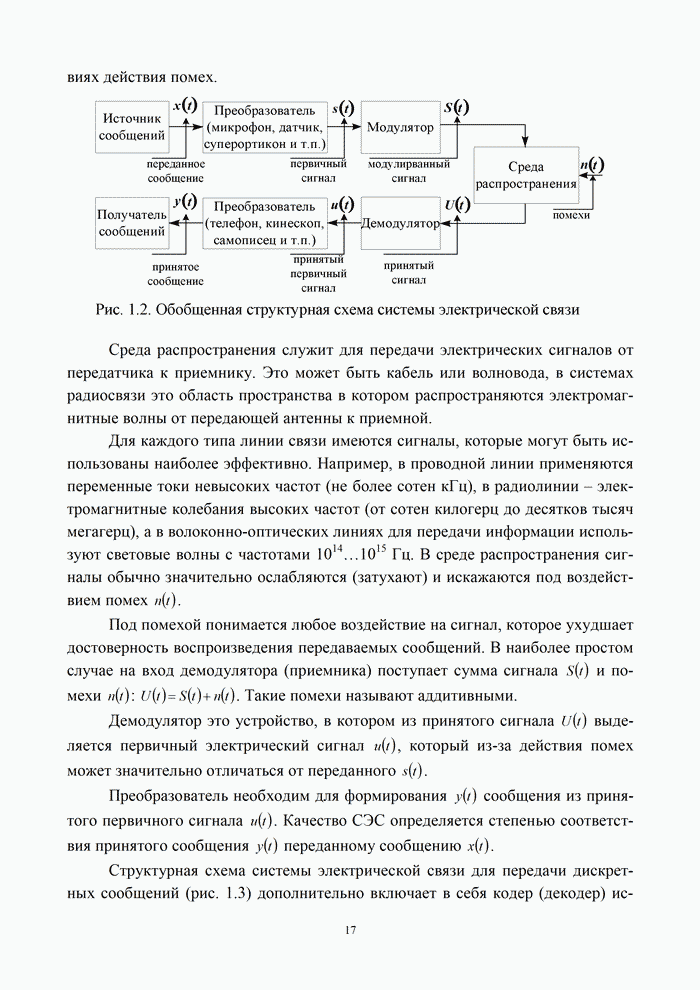
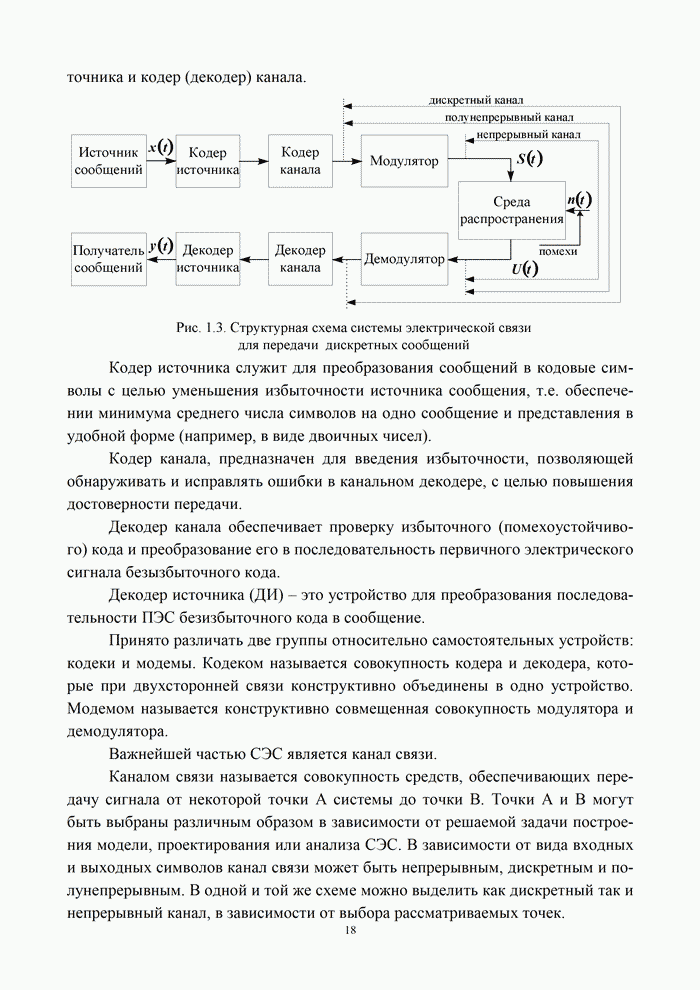
- 1.2.1. Структура канала электросвязи
- 1.2.2. Линия и сеть связи
- 1.2.3. Помехи и искажения в канале
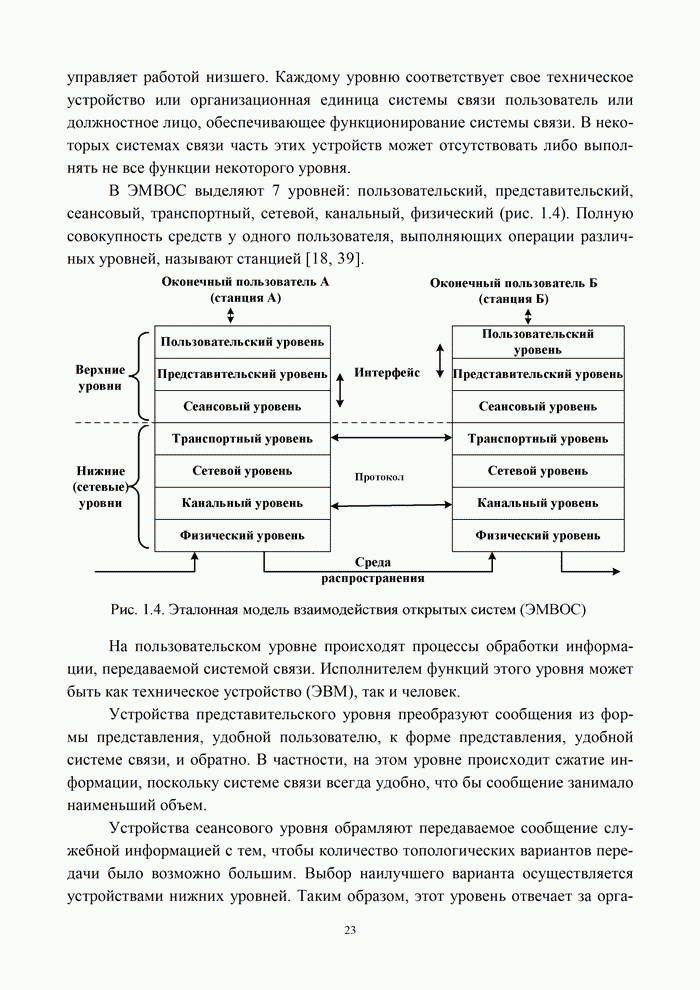
- 1.2.4. Эталонная модель взаимодействия открытых систем
- 1.2.5. Модели каналов связи и их математическое описание
- 1.3. Способы описания сигналов и помех
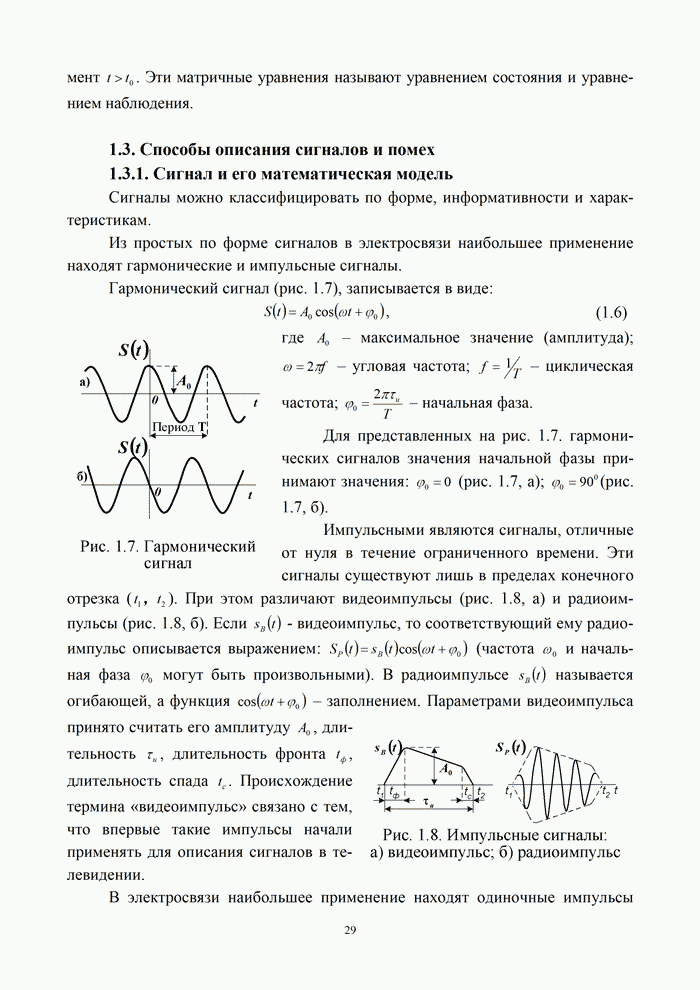
- 1.3.1. Сигнал и его математическая модель
- 1.3.2. Энергетические характеристики детерминированного сигнала
- 1.4.2. Представление сигналов и помех рядом Фурье
- 1.4.3. Применение преобразования Фурье для непериодических сигналов
- 1.5. Теорема Котельникова
- 1.6. Пространство сигналов
- 1.6.1. Линейное пространство
- 1.6.2. Представление сигнала в многомерном пространстве
- 1.7. Сигналы как случайные процессы
- 1.7.1. Характеристики случайного процесса
- 1.7.2. Флуктуационный шум
- 1.8. Комплексное представление сигналов и помех
- 1.8.1. Понятие аналитического сигнала
- 1.8.2. Огибающая, мгновенная фаза и мгновенная частота узкополосного случайного процесса
- Контрольные вопросы
- Глава 2. Методы формирования и преобразования сигналов
- 2.1. Модуляция сигналов
- 2.1.1. Амплитудная модуляция гармонической несущей
- 2.1.2. Балансная и однополосная модуляция гармонической несущей
- 2.2. Методы угловой модуляции
- 2.2.1. Принципы частотной и фазовой (угловой) модуляции
- 2.2.2. Спектр сигналов угловой модуляции
- 2.3. Формирование и детектирование модулированных сигналов
- 2.3.1. Формирование и детектирование сигналов амплитудной и однополосной амплитудной модуляции
- 2.3.2. Формирование и детектирование сигналов угловой модуляции
- 2.4. Манипуляция сигналов
- 2.4.1. Временные и спектральные характеристики амплитудно-манипулированных сигналов
- 2.4.2. Временные и спектральные характеристики частотно-манипулированных сигналов
- 2.4.3. Фазовая (относительно-фазовая) манипуляция сигналов
- 2.5. Системы связи с многопозиционной относительной фазовой манипуляцией
- 2.5.1. Принцип формирования сигнала с многократной относительной фазовой манипуляцией
- 2.5.2. Квадратурная относительно-фазовая манипуляция (КОФМ)
- 2.5.3. Принцип частотной модуляции с непрерывной фазой
- Контрольные вопросы
- Глава 3. Помехоустойчивость приема дискретных сообщений
- 3.1. Критерии качества и правила приема дискретных сообщений
- 3.1.1. Понятие о помехоустойчивости систем электрической связи
- 3.1.2. Задача оптимального приема
- 3.1.3. Вычисление вероятностей ошибок
- 3.2. Оптимальная демодуляция при когерентном приеме сигналов
- 3.2.1. Оптимальные алгоритмы приема при полностью известных сигналах
- 3.2.2. Реализация алгоритмов оптимального когерентного приема
- 3.3. Помехоустойчивость приема сигналов с известными параметрами
- 3.4. Прием сигналов с неопределенной фазой
- 3.4.1. Оптимальный некогерентный прием дискретных сигналов
- 3.4.2. Помехоустойчивость оптимального некогерентного приема
- 3.5. Подоптимальные методы приема
- 3.5.1. Причины применения неоптимальных методов приема
- 3.5.2. Квазиоптимальные методы приема
- Контрольные вопросы
- Глава 4. Теория передачи информации
- 4.1. Информационные характеристики источника сообщений
- 4.1.1. Количественное определение информации
- 4.1.2. Энтропия и производительность дискретного источника сообщений
- 4.2. Пропускная способность дискретного канала
- 4.2.1. Количество информации переданной по дискретному каналу
- 4.2.2. Пропускная способность дискретного канала
- 4.2.3. Пропускная способность симметричного дискретного канала без памяти
- 4.3. Методы сжатия дискретных сообщений
- 4.3.1. Условия существования оптимального неравномерного кода
- 4.3.2. Прямая и обратная теоремы кодирования источника неравномерными кодами
- 4.3.3. Показатели эффективности сжатия
- 4.3.4. Кодирование источника дискретных сообщений методом Шеннона-Фано
- 4.3.5. Кодирование источника дискретных сообщений методом Хаффмена
- 4.4. Пропускная способность непрерывного канала
- 4.4.1. Постановка задачи передачи дискретных сообщений в непрерывном канале
- 4.4.2. Количество информации, переданной по непрерывному каналу
- 4.4.3. Пропускная способность непрерывного канала
- Контрольные вопросы
- Глава 5. Теория кодирования сообщений
- 5.1. Помехоустойчивое кодирование: блочные и непрерывные коды
- 5.1.1. Постановка задачи помехоустойчивого кодирования
- 5.1.2. Классификация кодов
- 5.1.3. Основные характеристики и свойства блочных кодов
- 5.2. Эффективность помехоустойчивого кодирования
- 5.2.1. Эффективность кода в режиме исправления ошибок
- 5.2.2. Эффективность кода в режиме обнаружения ошибок
- 5.2.3. Эффективность помехоустойчивых кодов
- 5.3. Математические основы теории помехоустойчивого кодирования
- 5.3.1. Краткие сведения из теории чисел
- 5.3.2. Группы
- 5.3.3. Кольца и поля
- 5.3.4. Векторное пространство
- 5.3.5. Конечные поля
- 5.4. Линейные блочные коды
- 5.4.1. Система передачи дискретных сообщений
- 5.4.2. Параметры линейного кода
- 5.4.3. Полиномиальные циклические коды
- 5.4.4. Циклические коды и корни полиномов
- 5.4.5. Спектральное описание циклических кодов
- 5.4.6. Простейшие блочные линейные коды
- 5.5. Коды Боуза-Чоудхури-Хоквингема
- 5.5.1. Методы задания кодов БЧХ
- 5.5.2. Принципы декодирования кодов БЧХ
- 5.5.3. Методы реализации этапов декодирования кодов БЧХ
- 5.6. Коды Рида-Соломона
- 5.6.1. Основные определения
- 5.6.2. Обнаружение и исправление пакетов ошибок
- 5.7. Коды Рида-Маллера
- 5.7.1. Задание и декодирование кодов Рида-Маллера
- 5.7.2. Симплексные коды и m-последовательности
- 5.7.3. Связь между блочными кодами
- 5.8. Сверточные коды
- 5.8.1. Основные параметры
- 5.8.2. Способы задания сверточного кода
- 5.8.3. Алгоритм декодирования Витерби
- 5.9. Помехоустойчивость систем передачи дискретных сообщений
- 5.9.1. Две процедуры приема сигналов
- 5.9.2. Помехоустойчивость систем передачи информации при оптимальной процедуре приема
- 5.9.3. Помехоустойчивость систем передачи информации при посимвольном приеме сигналов
- Контрольные вопросы
- Глава 6. Сигналы с импульсной модуляцией
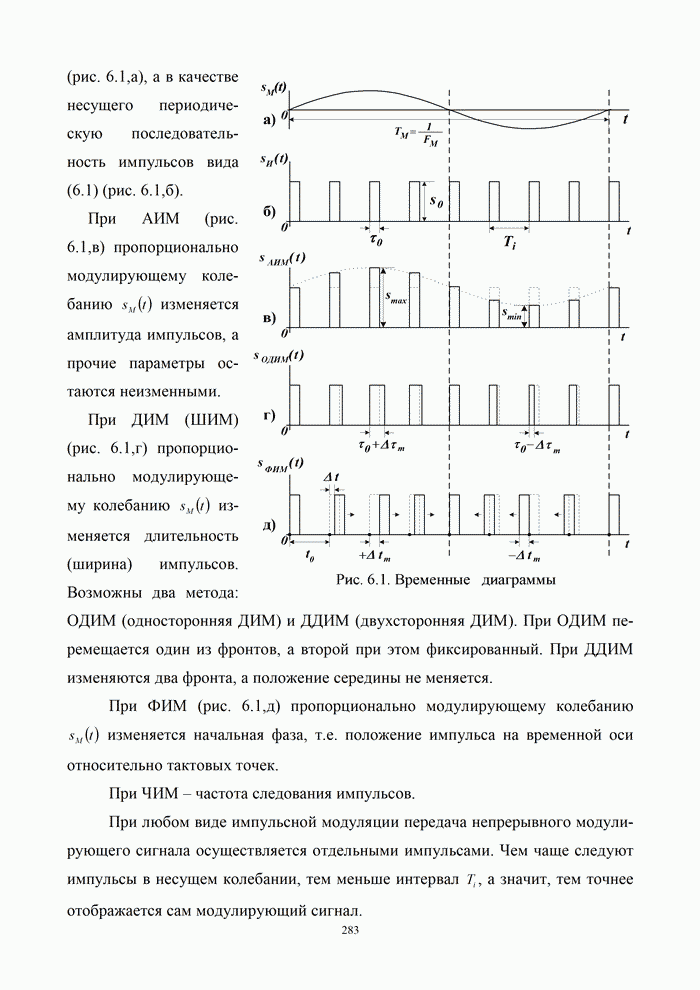
- 6.1. Методы импульсной модуляции
- 6.1.1. Импульсные методы передачи непрерывных сигналов
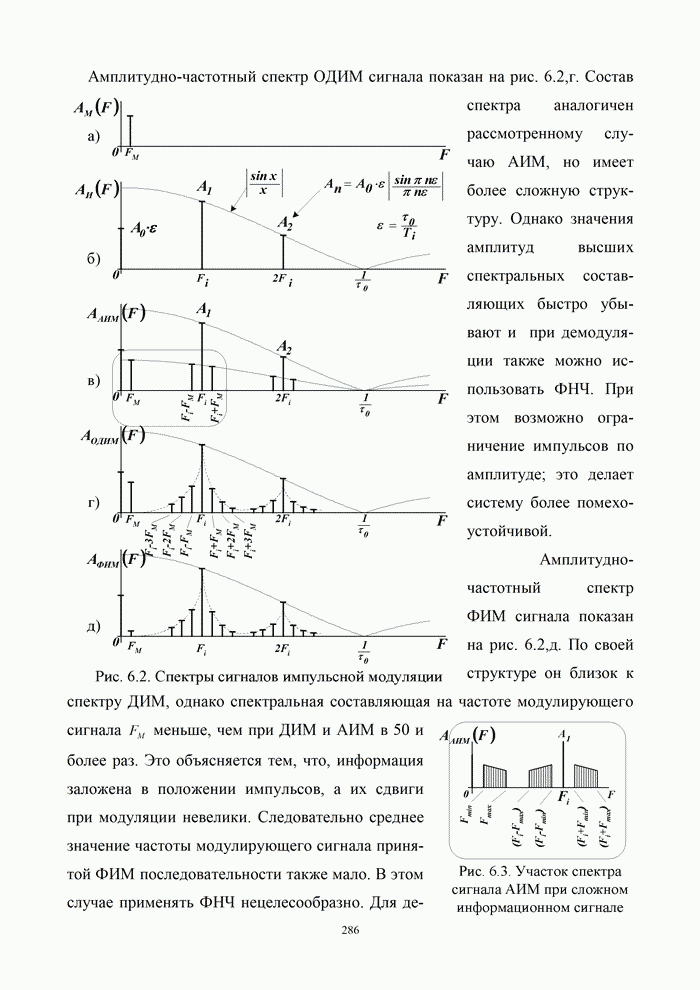
- 6.1.2. Спектральные характеристики импульсных методов модуляции
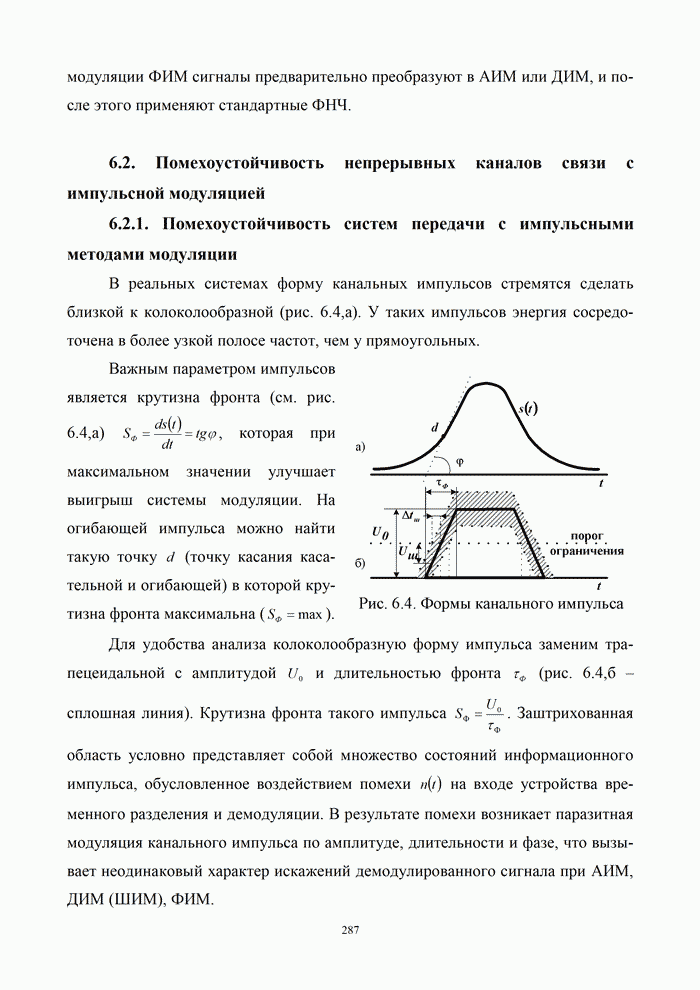
- 6.2. Помехоустойчивость непрерывных каналов связи с импульсной модуляцией
- 6.2.1. Помехоустойчивость систем передачи с импульсными методами модуляции
- 6.3. Цифровые методы передачи непрерывных сообщений
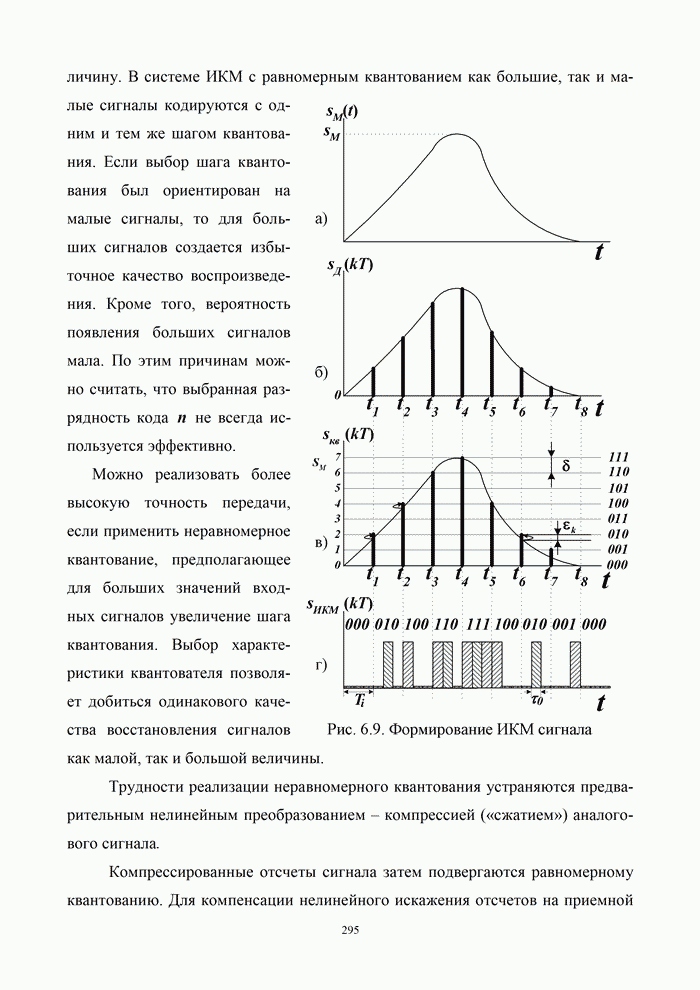
- 6.3.1. Передача сигналов с импульсно-кодовой модуляцией
- 6.3.2. Передача сигналов с дельта модуляцией
- 6.3.3. Квантование сигналов в системах с ИКМ и ДМ
- Контрольные вопросы
- Глава 7. Методы приема сигналов в сложных условиях
- 7.1. Прием сигналов в каналах с замираниями
- 7.1.1. Сущность замираний и их классификация
- 7.1.2. Принципы разнесенного приема сигналов
- 7.2. Методы борьбы с замираниями сигналов
- 7.2.1. Методы борьбы с замираниями в аналоговых системах связи
- 7.2.2. Методы борьбы с замираниями в цифровых системах связи
- 7.3. Методы борьбы с межсимвольной интерференцией
- 7.3.1. Причины возникновения и сущность межсимвольной интерференции
- 7.3.2. Обработка сигналов в каналах с межсимвольной интерференцией
- 7.3.3. Помехоустойчивость в каналах с межсимвольной интерференцией
- 7.4. Прием дискретных сообщений в каналах с сосредоточенными по спектру и импульсными помехами
- 7.4.1. Общая характеристика сосредоточенных по спектру и импульсных помех
- 7.4.2. Борьба с сосредоточенными и импульсными помехами
- 7.5. Компенсация помех и искажений в канале
- 7.5.1. Принцип работы радиолинии с ФМ ПСС (ФМ ШПС)
- 7.5.2. Помехоустойчивость радиолинии с ФМ ПСС
- 7.5.3. Принципы работы радиолиний с ППРЧ
- 7.5.4. Помехоустойчивость радиолиний с ППРЧ
- Контрольные вопросы
- Глава 8. Многоканальная связь и распределение информации
- 8.1. Методы распределения ресурса общего канала
- 8.1.1. Классификация систем передачи информации, использующих единый ресурс
- 8.1.2. Постановка задачи объединения и разделения сигналов
- 8.1.3. Энергетическая и спектральная цена уплотнения
- 8.2. Частотное разделение каналов
- 8.2.1. Принцип частотного объединения и разделения каналов
- 8.2.2. Групповой сигнал, его структура и характеристики
- 8.3. Временное разделение каналов
- 8.3.1. Принцип временного разделения каналов
- 8.3.2. Характеристики группового сигнала систем с ВРК
- 8.4. Разделение сигналов по форме
- Контрольные вопросы
- Глава 9. Эффективность систем связи
- 9.1. Оценка эффективности систем связи
- 9.1.1. Подходы к оценке эффективности
- 9.1.2. Критерии эффективности
- 9.1.3. Эффективность аналоговых и цифровых систем
- 9.2. Выбор сигналов и помехоустойчивых кодов
- 9.2.1. Многопозиционные сигналы
- 9.2.2. Корректирующие коды
- 9.3. Оптимизация систем связи
- 9.3.1. Согласование методов модуляции и кодирования
- 9.3.2. Классификация сигнально – кодовых конструкций
- 9.4. Характеристики основных типов СКК
- 9.4.1. Согласование канала кодом Грея
- 9.4.2. Согласование на основе разбиения ансамбля на вложенные подансамбли
- 9.5. Алгоритмы цифровой обработки сигналов
- 9.5.1. Дискретные сигналы и их спектры
- 9.5.2. Алгоритмы дискретного и быстрого преобразований Фурье
- Контрольные вопросы
- Глава 10. Теоретико-информационные основы криптозащиты сообщений в телекоммуникационных системах
- 10.1. Классификация криптографических систем
- 10.1.2. Классификация криптографических систем защиты информации
- 10.1.3. Оценка стойкости криптосистем
- 10.2. Функции, используемые в криптографических системах
- 10.2.1. Общее описание функций, используемых в криптографических системах
- 10.2.2. Однонаправленные функции
- 10.2.3. Криптографические хэш-функции
- 10.3. Модели криптографических систем
- 10.3.1. Системы шифрования
- 10.3.2. Традиционные симметричные криптосистемы
- 10.4. Алгоритмы криптографической защиты
- 10.4.1. Алгоритм криптографической защиты информации согласно ГОСТ 28147-89
- Контрольные вопросы
- Заключение
- Список литературы