| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
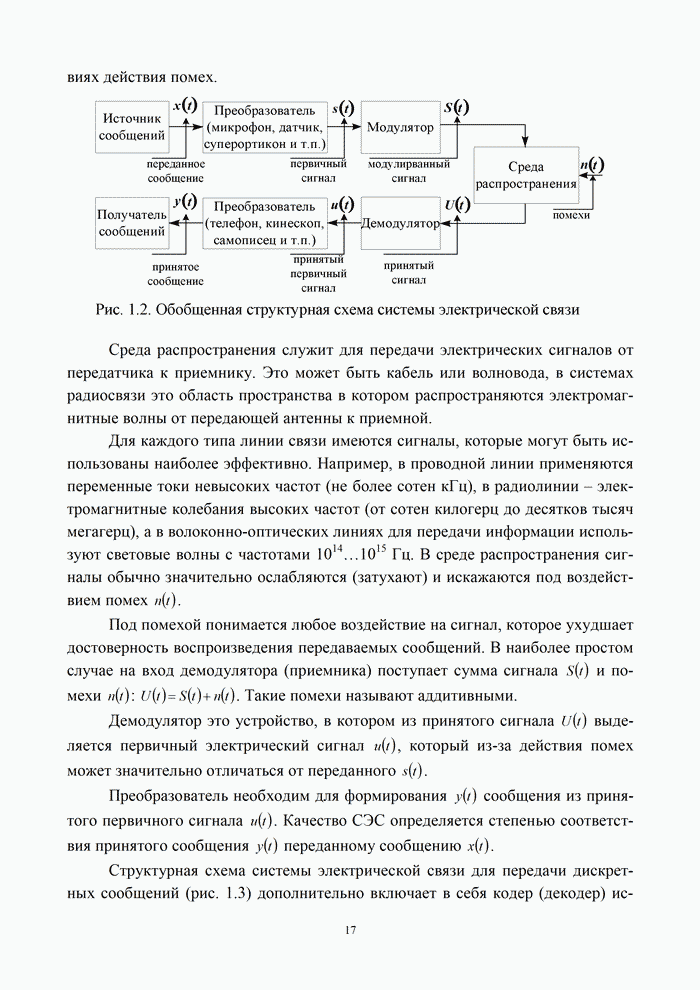
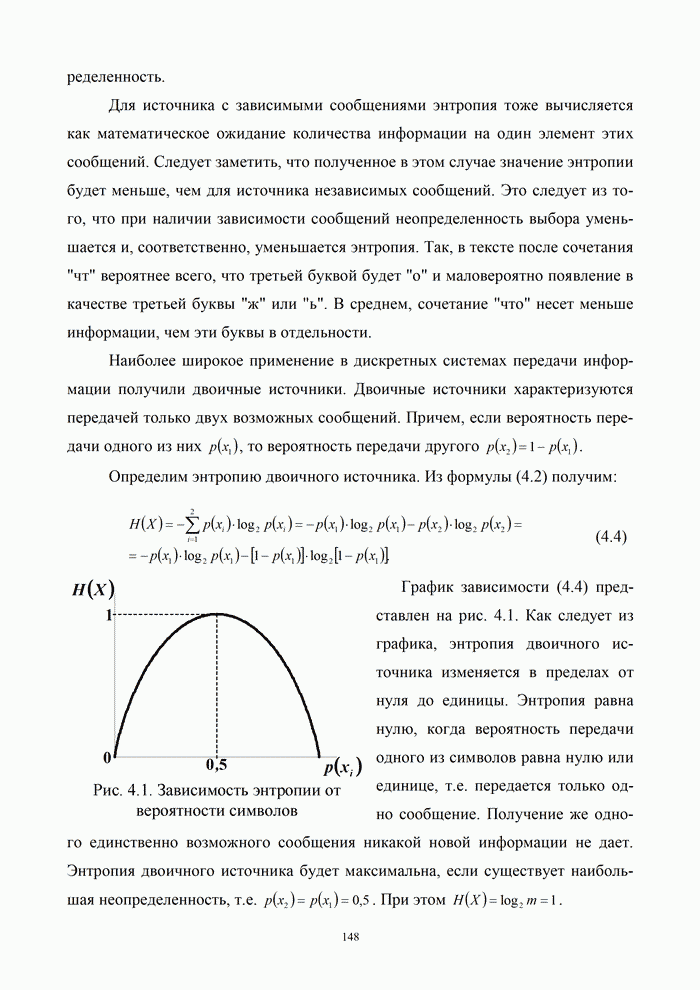
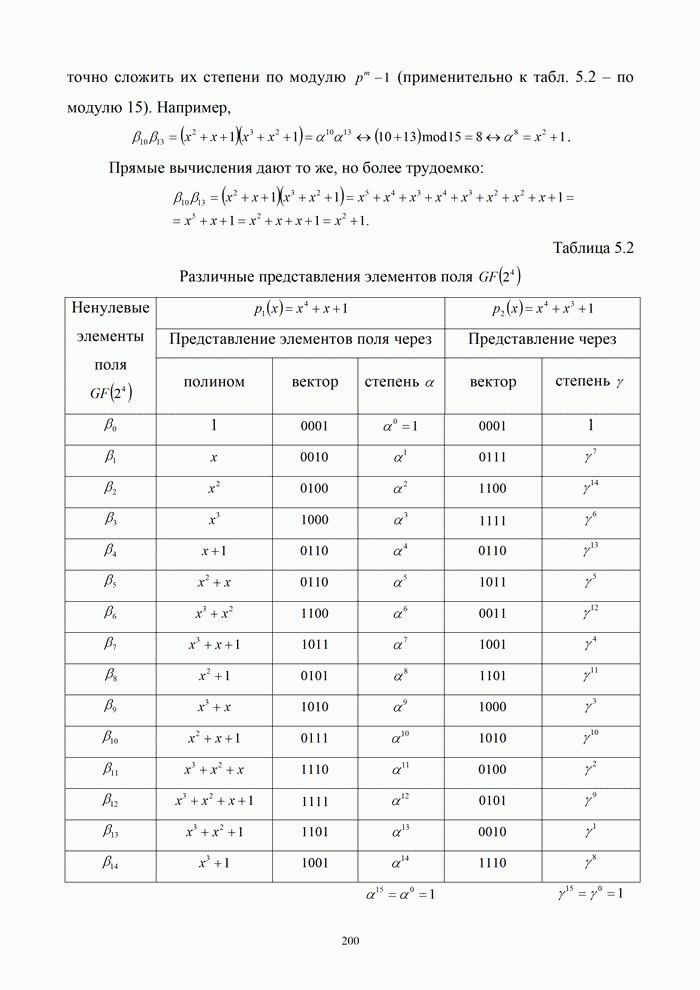
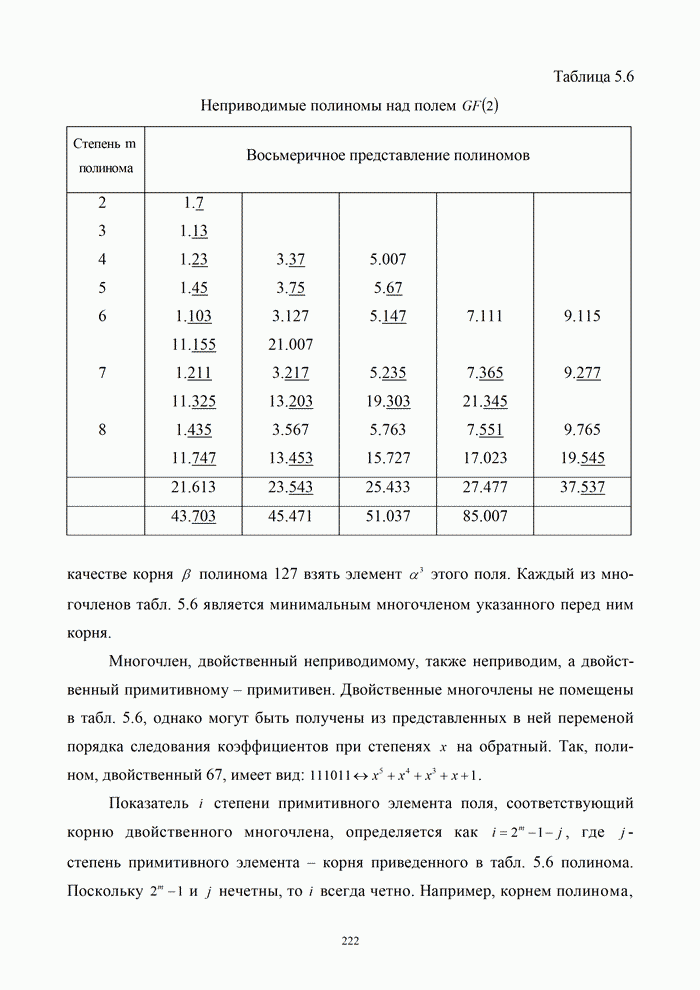
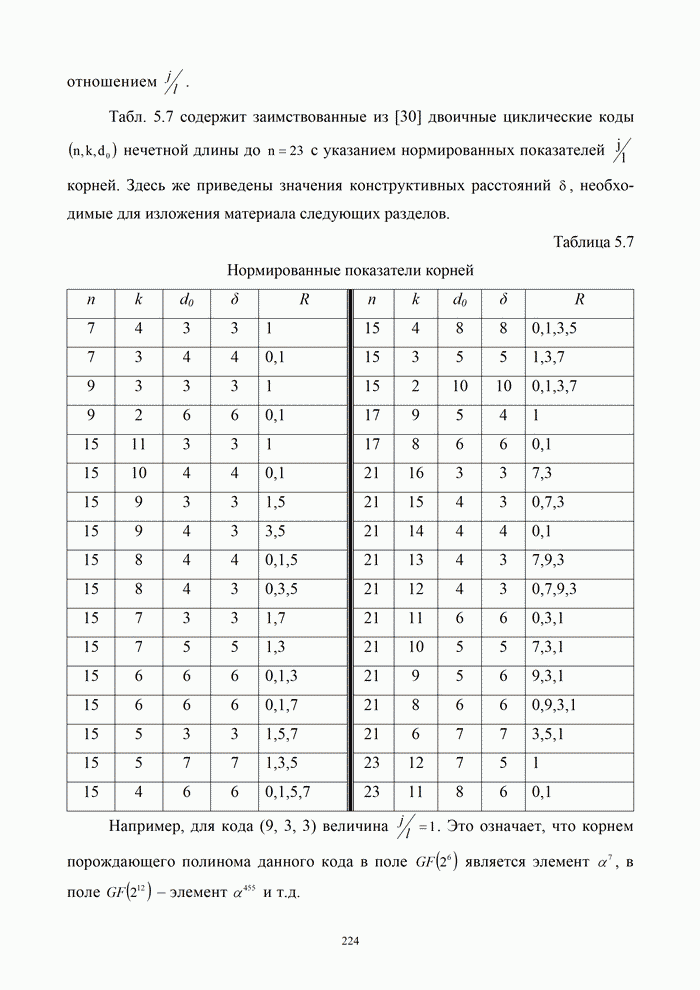
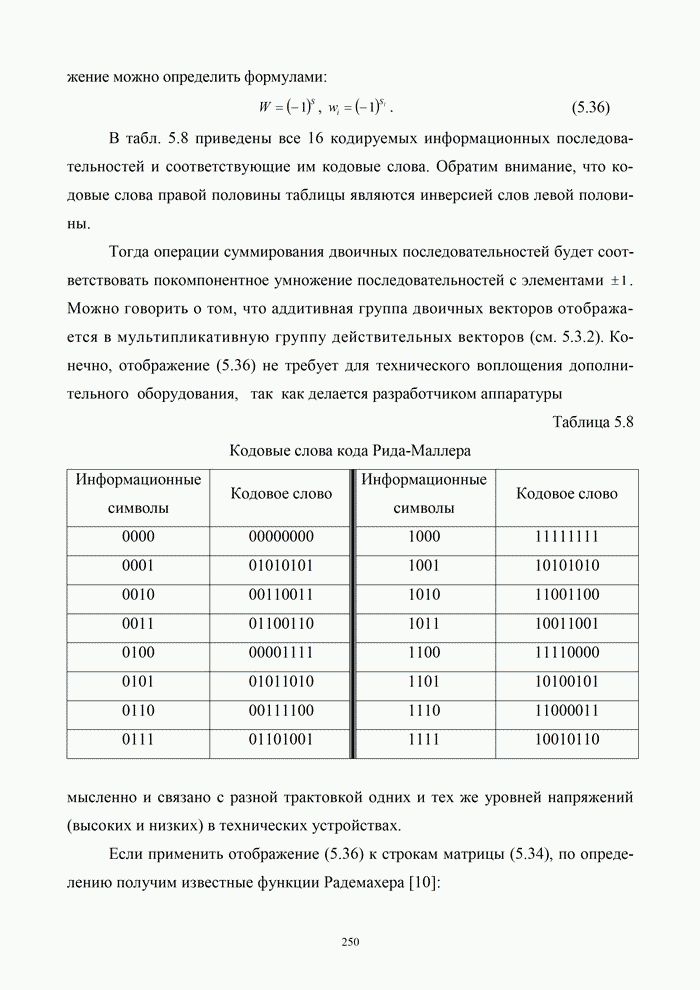
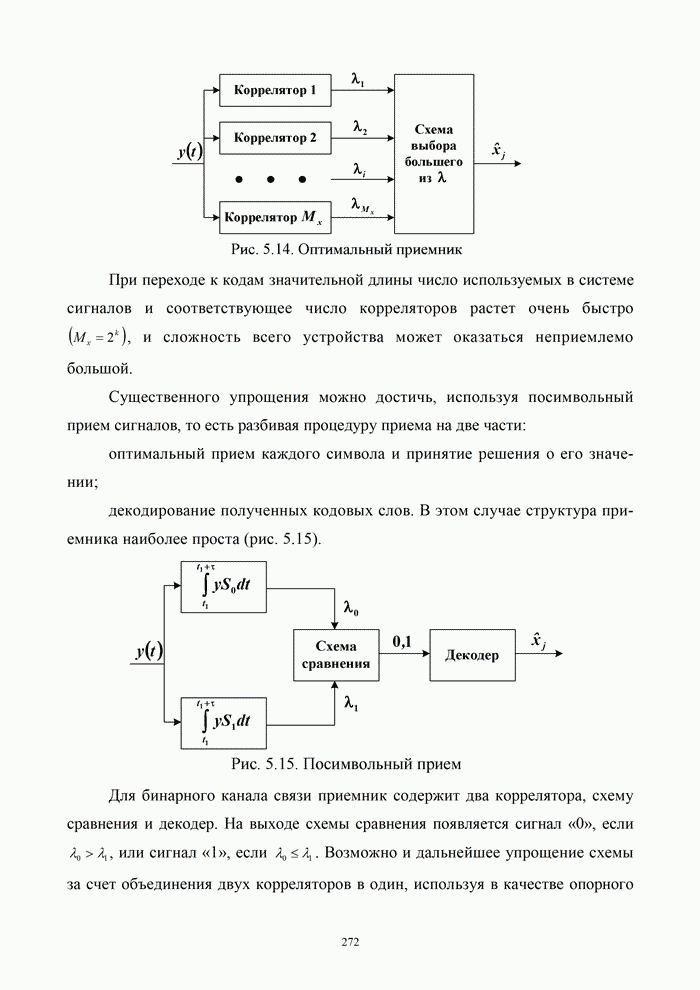
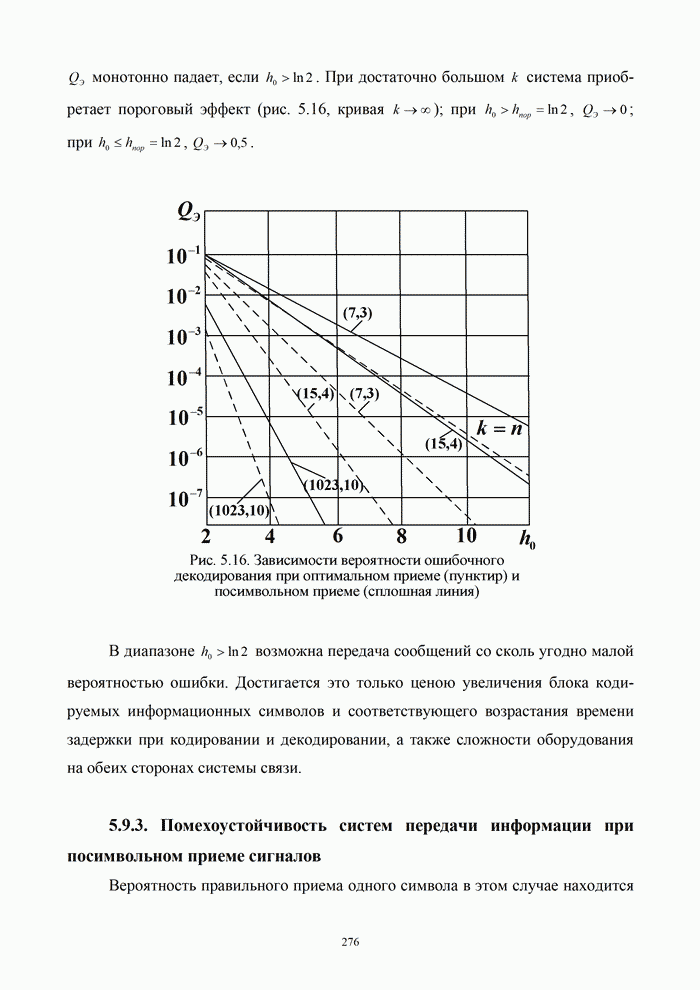
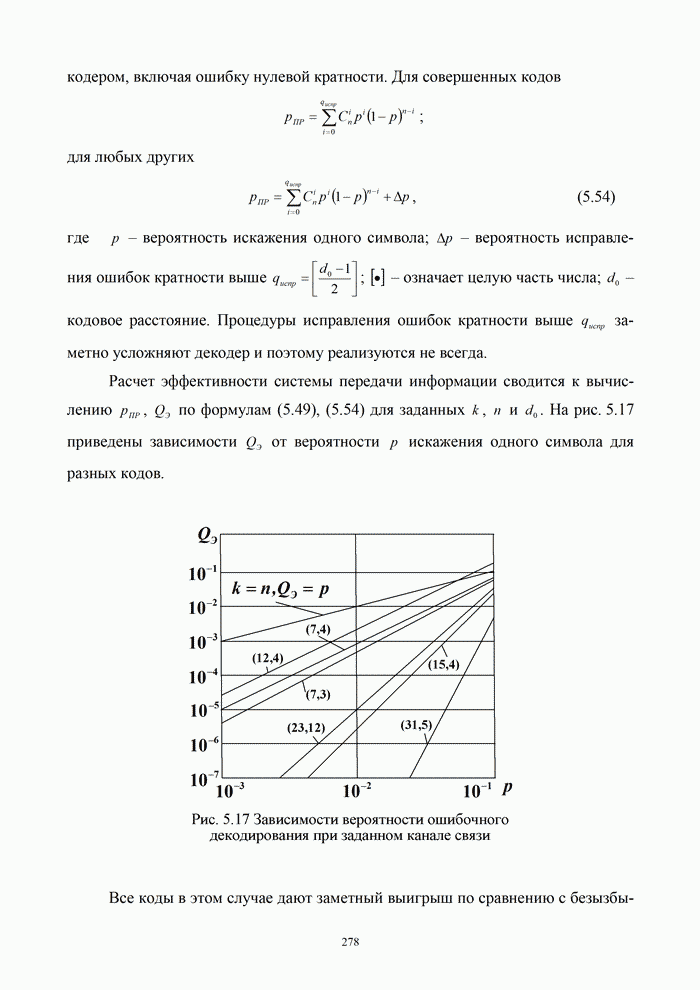
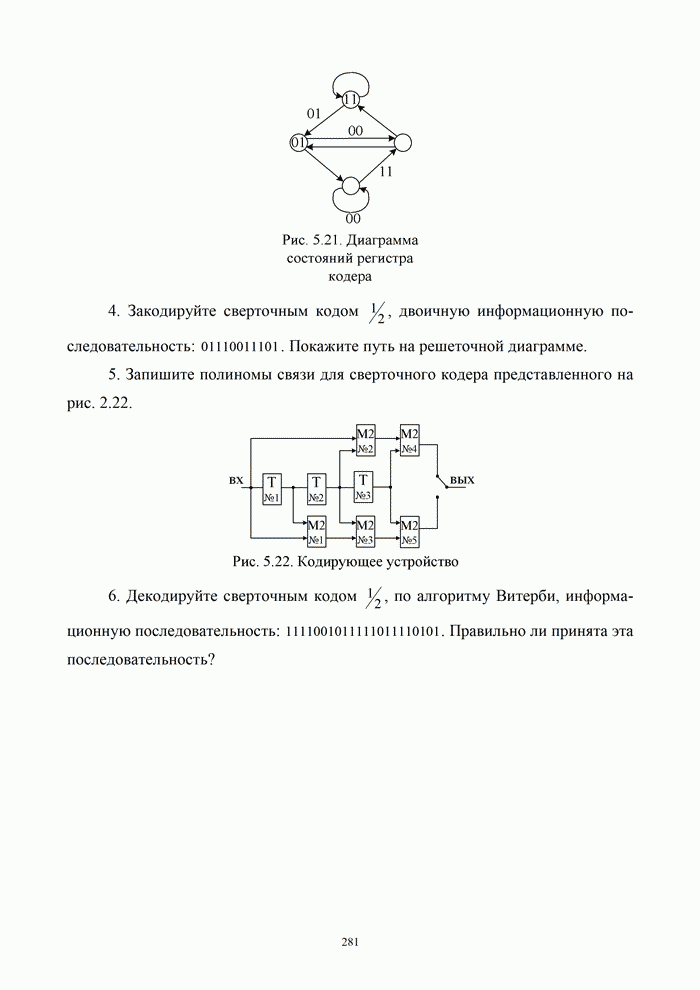
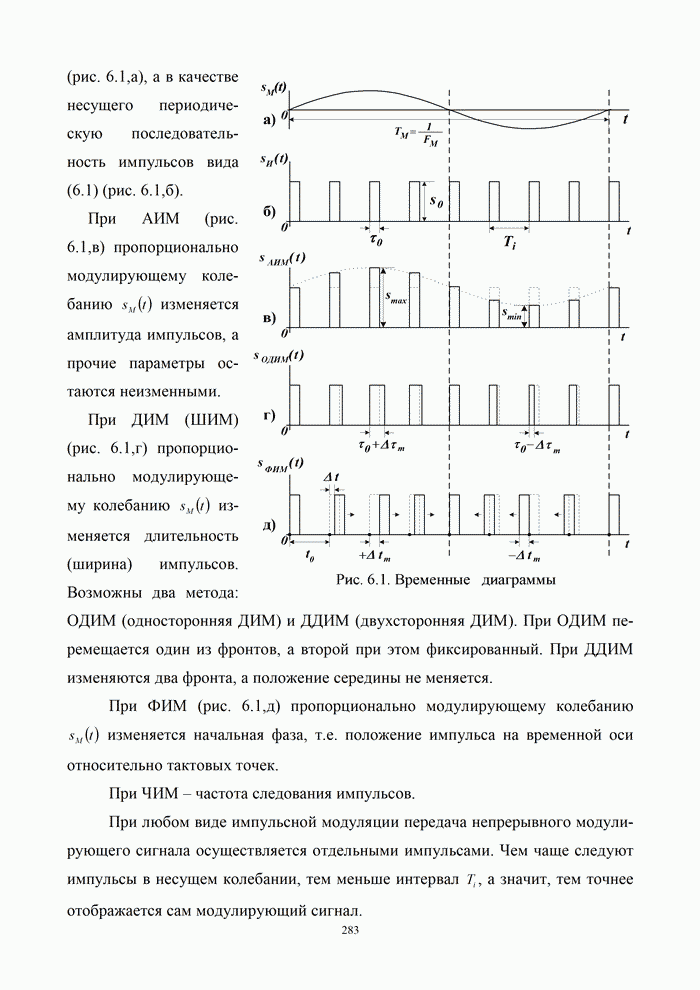
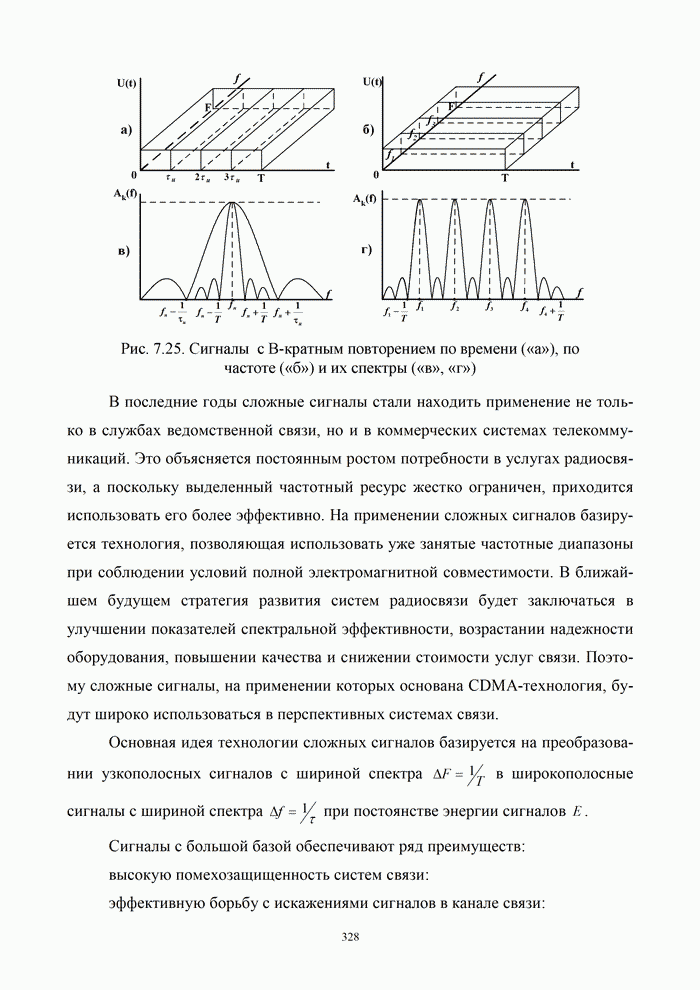
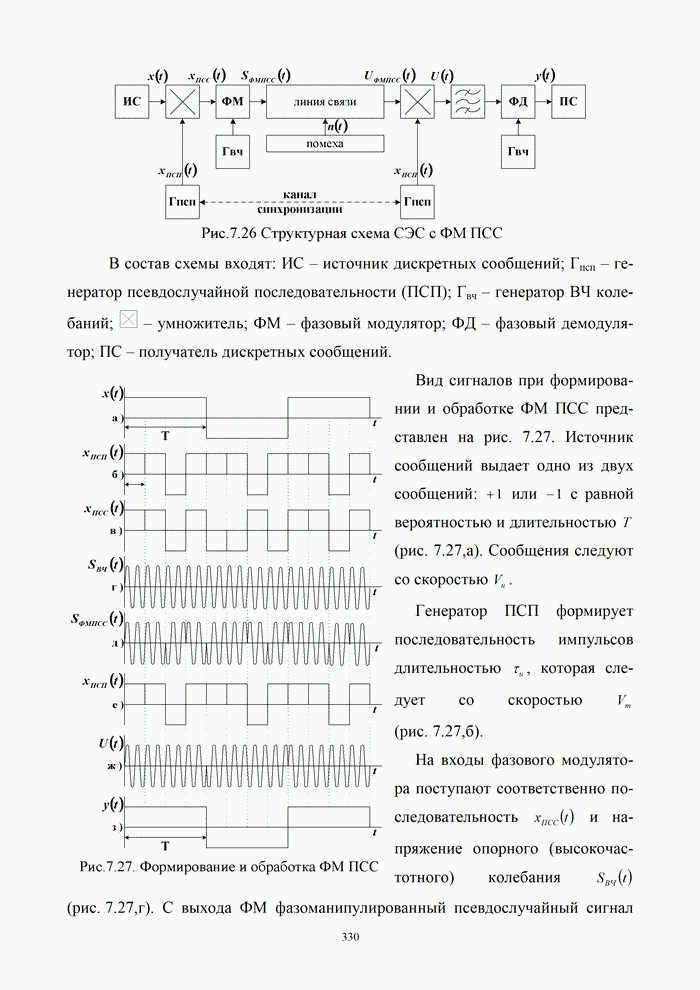
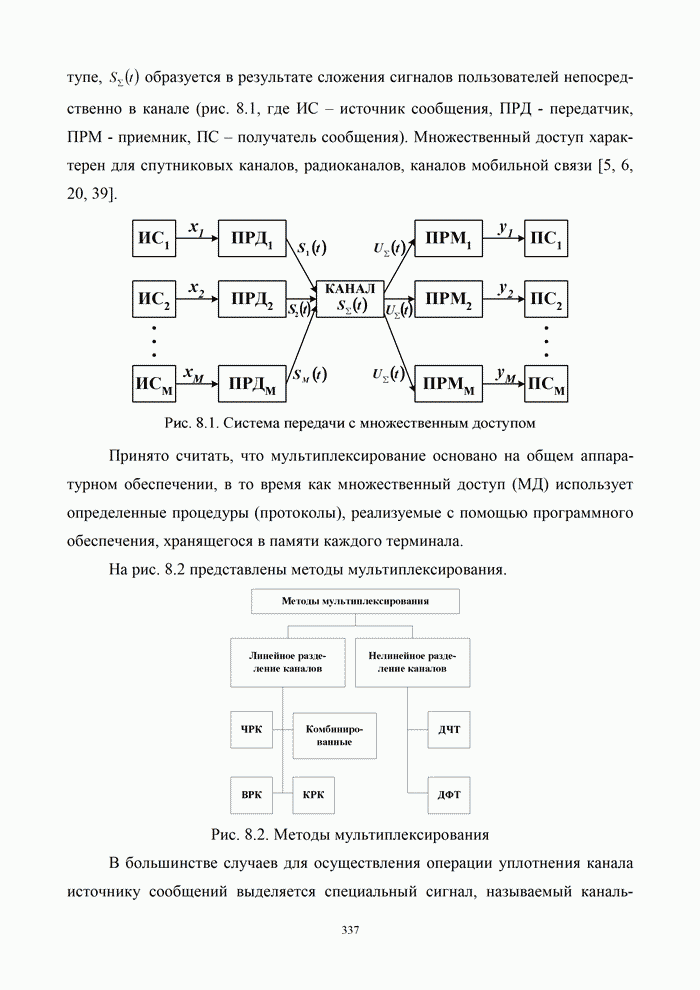
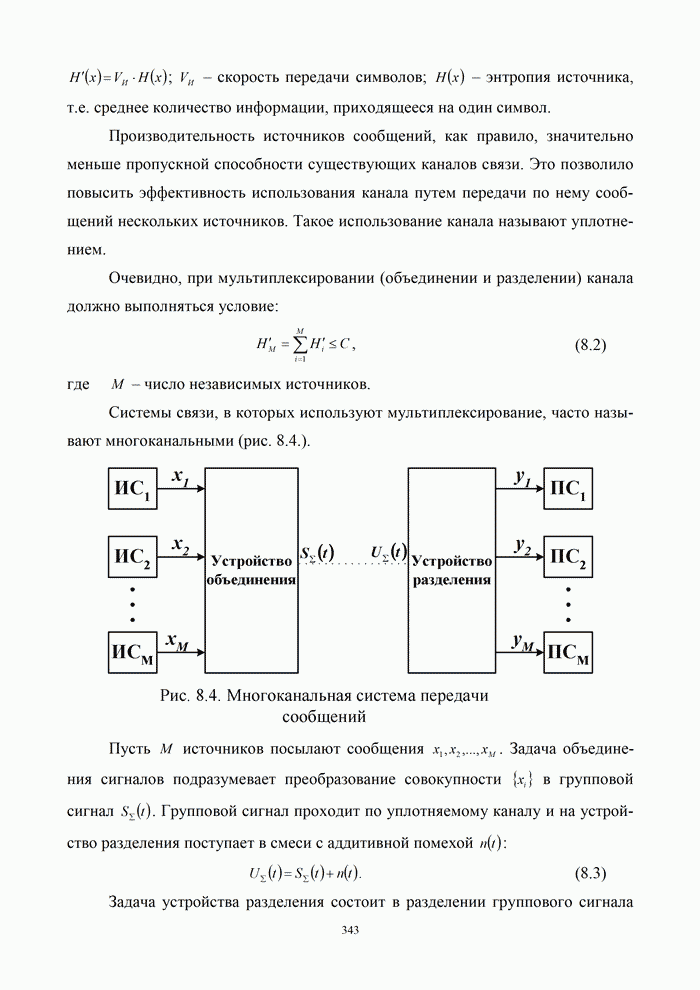
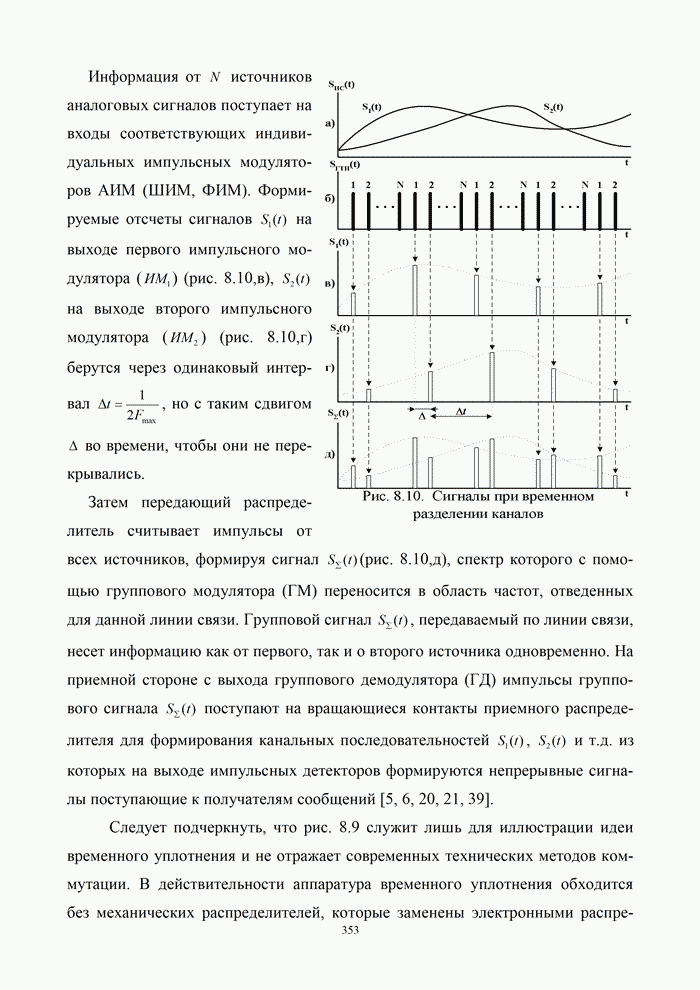
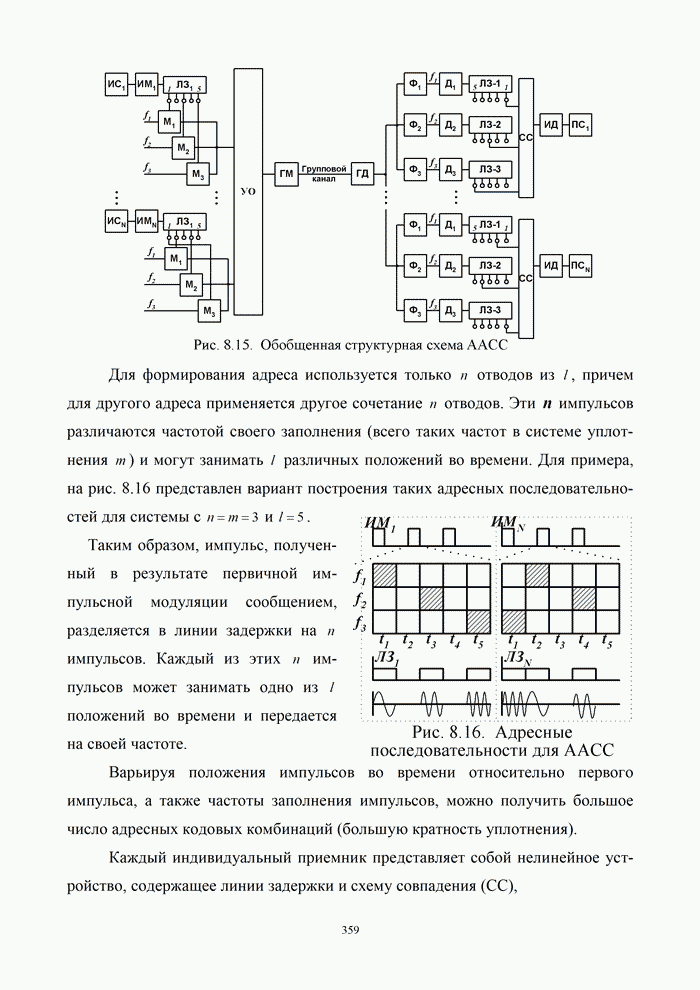
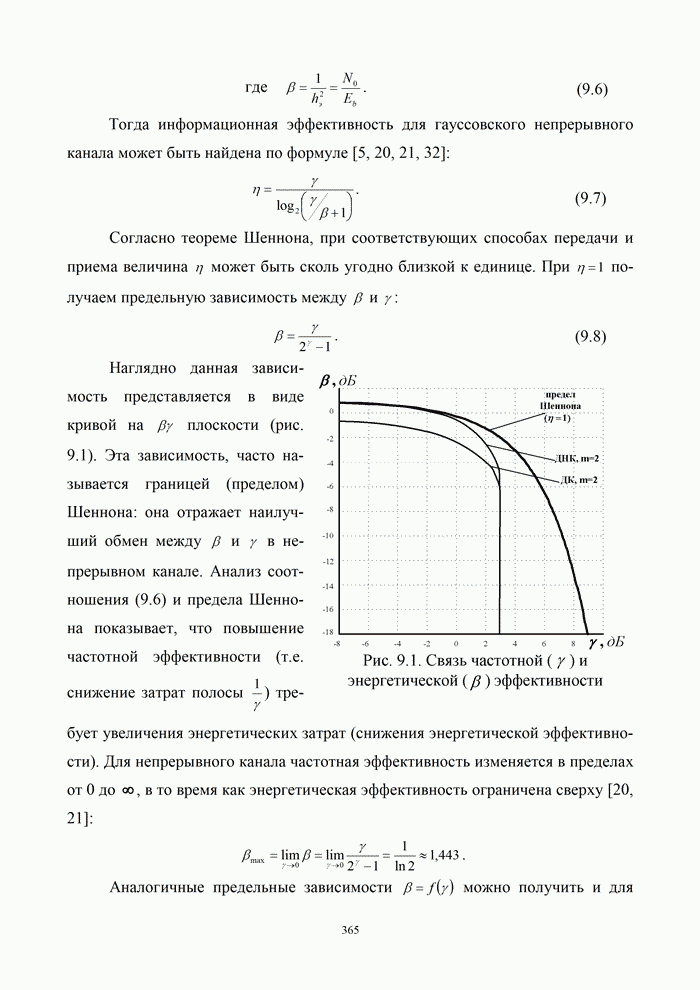
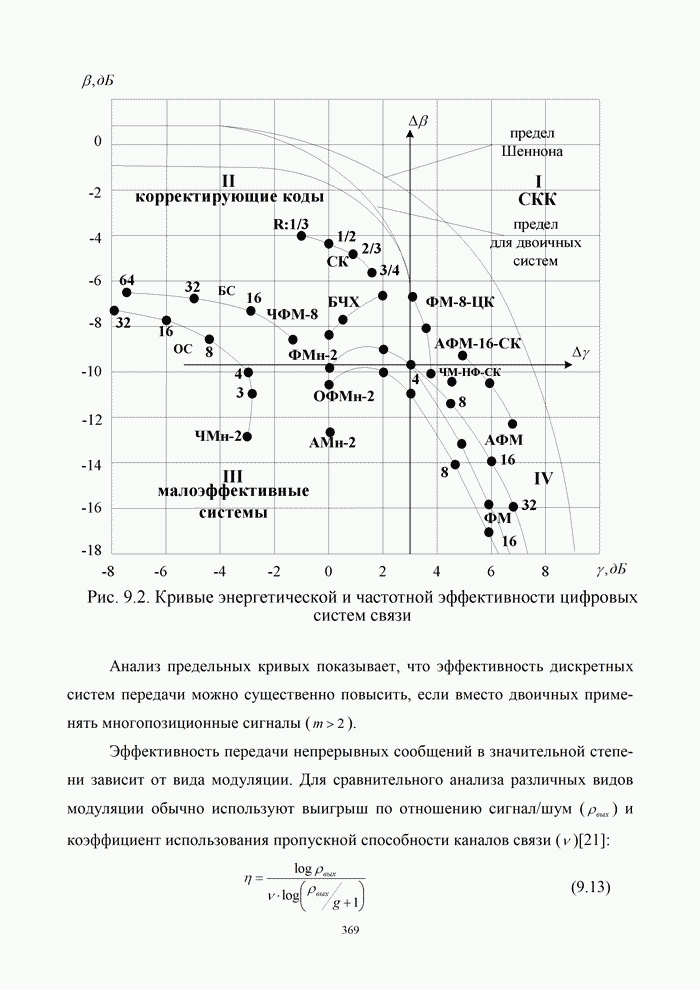
1.8. Комплексное представление сигналов и помех
Ранее было изучено представление детерминированных сигналов рядами ортогональных функций. Такая модель оказывается особенно полезной при анализе прохождения сигналов через линейные радиотехнический устройства.
Вместе с тем при анализе нелинейных преобразований сигналов и, в частности, модуляции и демодуляции, требуется иной подход. Этот подход основывается на понятии аналитического сигнала.
1.8.1. Понятие аналитического сигнала
Многие формулы гармонического анализа записываются значительно проще и некоторые задачи решаются легче, если использовать в качестве элементарных функций не обычные действительные синусоиды, а экспоненциальные функции мнимого аргумента. Действительно, по формуле Эйлера [6, 21]:
|
|
(1.50) |
Этой записи можно дать геометрическую трактовку, пользуясь представлением комплексных чисел в виде точек или векторов на плоскости.
Выражение ![]() представляет в данном
случае вектор единичной длины, проведенный под углом
представляет в данном
случае вектор единичной длины, проведенный под углом ![]() к действительной оси (рис.1.22).
При изменении времени
к действительной оси (рис.1.22).
При изменении времени ![]() этот вектор, единичной длины, меняет
положение, вращаясь в положительном направлении с угловой скоростью
этот вектор, единичной длины, меняет
положение, вращаясь в положительном направлении с угловой скоростью ![]() .
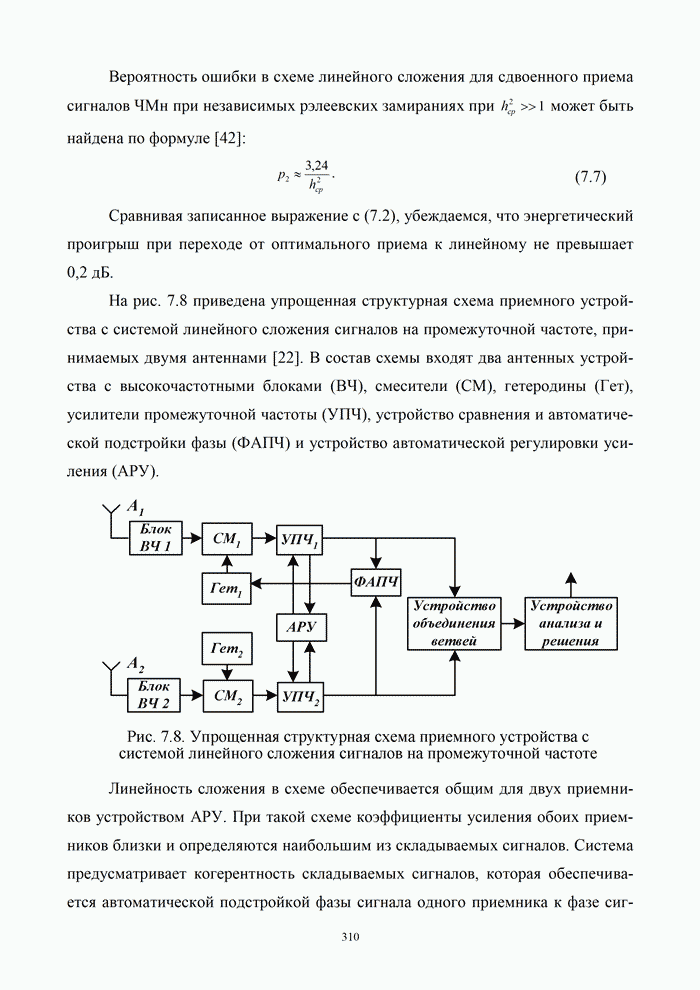
.


Изобразить синусоиду в
форме (1.50), это значит представить ее суммой двух векторов, длина каждого из которых
равна ![]() , расположенных
в любой момент времени симметрично относительно действительной оси и
вращающихся в разных направлениях с угловыми скоростями
, расположенных
в любой момент времени симметрично относительно действительной оси и
вращающихся в разных направлениях с угловыми скоростями ![]() и
и ![]() (рис.1.23).
(рис.1.23).
В момент ![]() они занимают
положения под углами
они занимают
положения под углами ![]() и
и ![]() относительно действительной оси.
Геометрическая сумма векторов всегда совпадает по направлению с действительной
осью и представляет действительную функцию времени
относительно действительной оси.
Геометрическая сумма векторов всегда совпадает по направлению с действительной
осью и представляет действительную функцию времени ![]() .
.
При представлении косинусоиды
в виде ![]() можно
ограничиться одним вращающимся в положительном направлении вектором и
представить косинусоиду его проекцией на действительную ось.
можно
ограничиться одним вращающимся в положительном направлении вектором и
представить косинусоиду его проекцией на действительную ось.
В этом случае нет необходимости
вводить отрицательные частоты. Длина вектора представляет амплитуду косинусоиды,
а угол, образуемый им в данный момент с действительной осью, - полную фазу ![]() .
.
Проекция этого вектора на
мнимую ось равна ![]() ,
т.е. представляет ту же косинусоиду, сдвинутую по фазе на
,
т.е. представляет ту же косинусоиду, сдвинутую по фазе на ![]() (рис. 1.24).
(рис. 1.24).
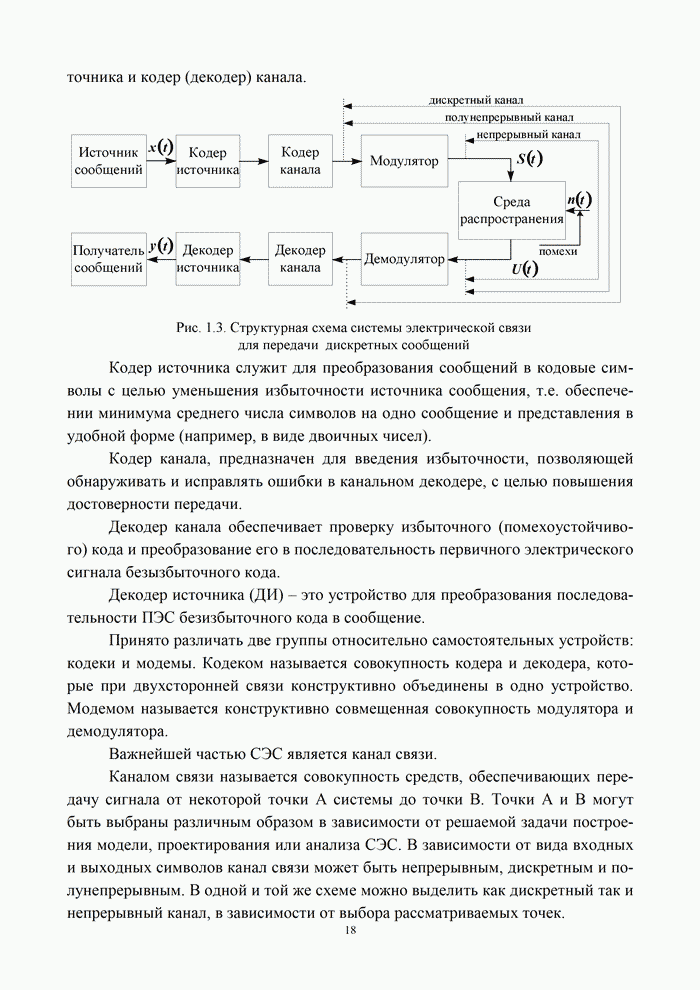
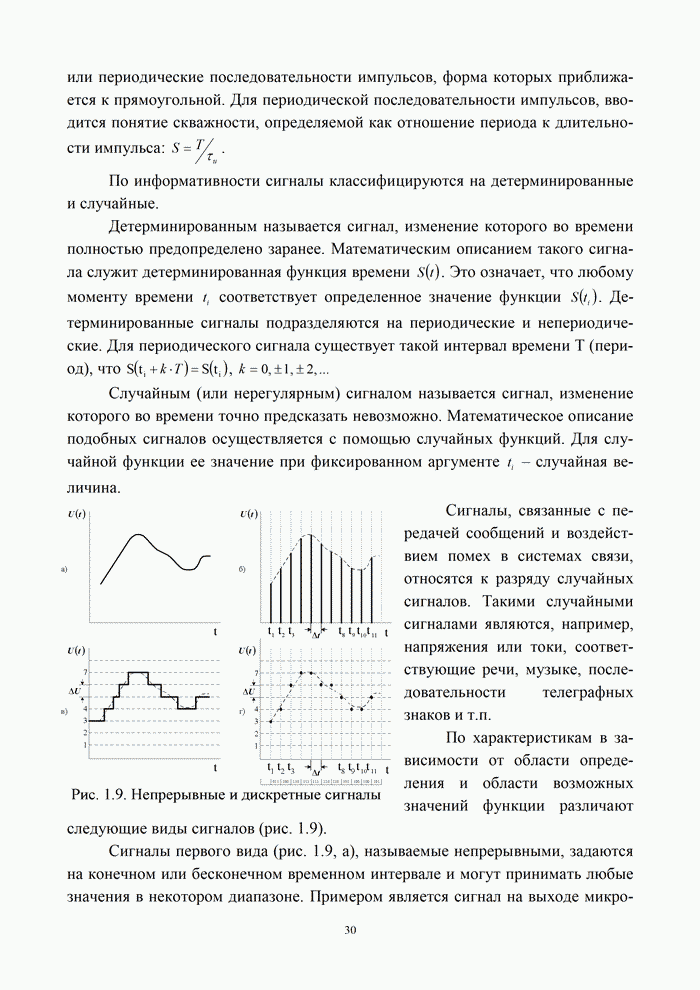
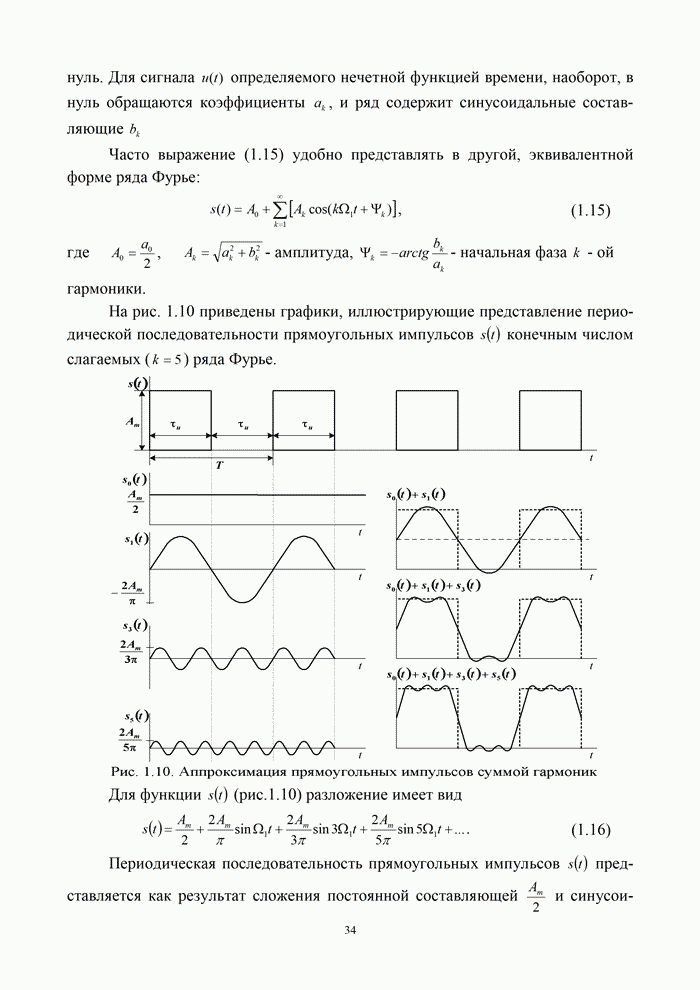
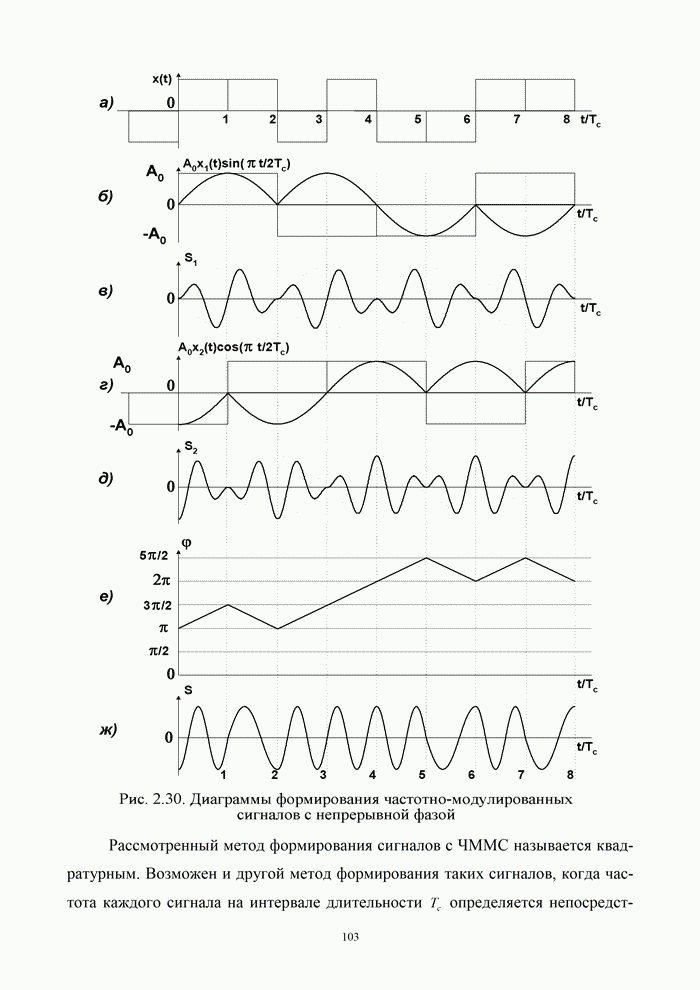
Многие сигналы в системах электросвязи можно представлять в виде:
|
|
(1.51) |
 т.е. как «квазигармоническую» функцию
с переменными «амплитудой» и «начальной фазой». Такой сигнал можно интерпретировать
геометрически как проекцию на действительную ось вращающегося вектора, но при
этом изменяющего свою длину и угловую скорость. Для описания свойств сигнала представленного
в форме (1.51) вводят понятие комплексного аналитического сигнала.
т.е. как «квазигармоническую» функцию
с переменными «амплитудой» и «начальной фазой». Такой сигнал можно интерпретировать
геометрически как проекцию на действительную ось вращающегося вектора, но при
этом изменяющего свою длину и угловую скорость. Для описания свойств сигнала представленного
в форме (1.51) вводят понятие комплексного аналитического сигнала.
Рассмотрим отрезок
сигнала на некотором интервале времени ![]() .
.
Его можно представить на этом интервале рядом Фурье в экспоненциальной форме [6, 21]:
|
|
(1.52) |
Пользуясь геометрическим
представлением синусоиды, можно представить сигнал ![]() в виде суммы вращающихся
векторов, каждый из которых имеет вид:
в виде суммы вращающихся
векторов, каждый из которых имеет вид:
|
|
|
Векторы с индексами ![]() вращаются в положительном
направлении, а с
вращаются в положительном
направлении, а с ![]() в
отрицательном. Пара таких векторов с индексами
в
отрицательном. Пара таких векторов с индексами ![]() и
и ![]() образует одну действительную косинусоиду.
образует одну действительную косинусоиду.
Поэтому предполагая среднее состояние сигнала нулевым (![]() )косинусоида может быть представлена проекцией на
действительную ось одного вектора, вращающегося, например, в положительном
направлении. Вместо (1.68) можно взять проекцию (т.е. действительную часть)
суммы векторов, вращающихся только в положительном направлении, увеличив их величину
вдвое:
)косинусоида может быть представлена проекцией на
действительную ось одного вектора, вращающегося, например, в положительном
направлении. Вместо (1.68) можно взять проекцию (т.е. действительную часть)
суммы векторов, вращающихся только в положительном направлении, увеличив их величину
вдвое:
|
|
(1.53) |
Ряд в правой части (1.53)
представляет собой комплексную функцию времени, которую обозначим ![]() и будем называть
комплексным или аналитическим сигналом:
и будем называть
комплексным или аналитическим сигналом:
|
|
(1.54) |
 Его геометрическим
представлением является вектор, образующийся при суммировании элементарных
векторов
Его геометрическим
представлением является вектор, образующийся при суммировании элементарных
векторов ![]() .
Так как элементарные векторы вращаются с разными угловыми скоростями
.
Так как элементарные векторы вращаются с разными угловыми скоростями ![]() , то их взаимная
конфигурация со временем изменяется. Поэтому их векторная сумма (рис. 1.25) представляет
собой вектор с переменной длиной, вращающийся с переменной угловой скоростью.
, то их взаимная
конфигурация со временем изменяется. Поэтому их векторная сумма (рис. 1.25) представляет
собой вектор с переменной длиной, вращающийся с переменной угловой скоростью.
Исходный сигнал (1.51) является действительной частью аналитического сигнала.
Учитывая выражение (1.19) для комплексных коэффициентов ряда Фурье
получим:
|
|
(1.55) |
что является обычным разложением сигнала в ряд Фурье в тригонометрической форме.
Мнимая часть
аналитического сигнала представляет собой некоторую функцию времени, однозначно
определяемую исходным сигналом ![]() .
.
Ее обозначают ![]() и называют сигналом,
сопряженным по Гильберту с
и называют сигналом,
сопряженным по Гильберту с ![]() [6, 20]:
[6, 20]:
|
|
(1.56) |
Отсюда видно, что
сопряженный сигнал можно получить из исходного, повернув начальные фазы всех
его составляющих на ![]() или,
другими словами, заменив в ряде Фурье (1.71)
или,
другими словами, заменив в ряде Фурье (1.71) ![]() на
на ![]() , а
, а ![]() на
на ![]() .
.
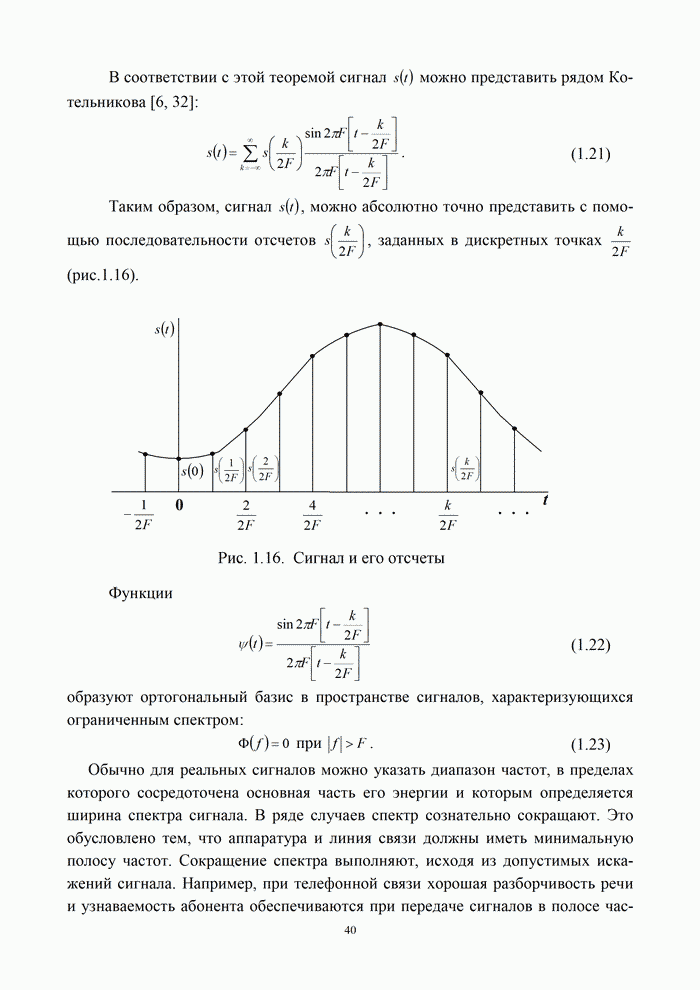
В соответствии с (1.54), (1.55) и (1.56) аналитический сигнал может быть выражен через реальный и сопряженный сигналы следующим образом:
|
|
(1.57) |
 Исходя из этого,
аналитический сигнал в момент времени t может быть представлен точкой на комплексной
плоскости, если по оси абсцисс откладывать значения реального сигнала
Исходя из этого,
аналитический сигнал в момент времени t может быть представлен точкой на комплексной
плоскости, если по оси абсцисс откладывать значения реального сигнала ![]() , а по оси ординат
- сопряженного с ним сигнала
, а по оси ординат
- сопряженного с ним сигнала ![]() (рис. 1.26).
(рис. 1.26).
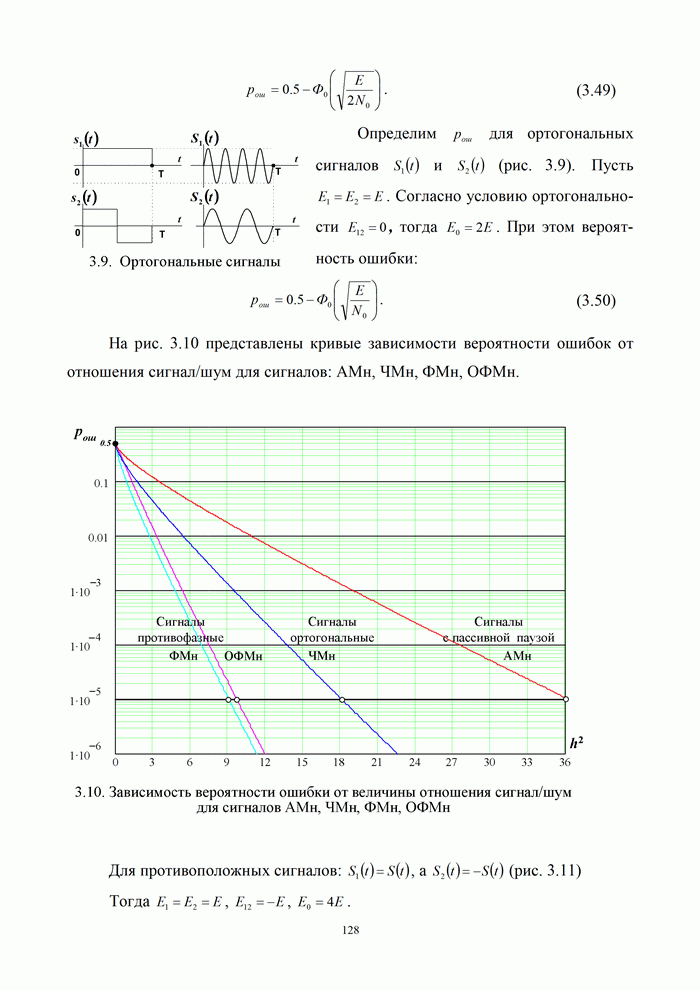
В качестве примера рассмотрим гармоническое колебание:
|
|
(1.58) |
Такой сигнал представляется только одним членом ряда Фурье, так как
|
|
(1.59) |
|
|
(1.60) |
|
|
(1.61) |
Справедливость (1.60) и
(1.61) вытекает из ортогональности функций ![]() и
и ![]() .
.
В соответствии с (1.56), (1.60), (1.61) сопряженный сигнал:
|
|
(1.62) |
Тогда аналитический сигнал
![]() ,
соответствующий реальному сигналу (9), можно записать следующим образом:
,
соответствующий реальному сигналу (9), можно записать следующим образом:
|
|
(1.63) |
Точки, отображающие реальный и сопряженный сигналы (рис.1.28), совершают в данном случае гармонические колебания по оси абсцисс и ординат относительно точки 0 по законам, соответственно, косинуса и синуса.
Длина вектора,
соединяющего начало координат на рис.1.28 с точкой ![]() , отображающей аналитический
сигнал [6, 32],
, отображающей аналитический
сигнал [6, 32],
|
|
(1.64) |
Угол между вектором ![]() и осью абсцисс
и осью абсцисс
|
|
(1.65) |
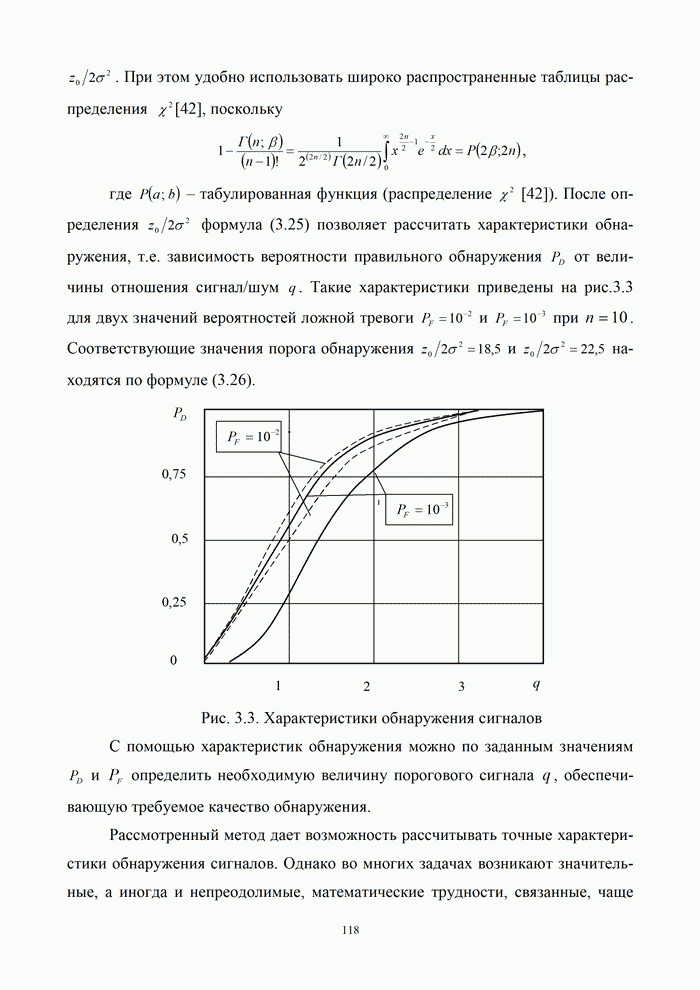
В рассматриваемом случае для верхней полуплоскости получаем:
|
|
(1.66) |
Таким образом, с течением
времени точка, отображающая аналитический сигнал ![]() , соответствующий гармоническому
колебанию (1.58), равномерно вращается по окружности с радиусом
, соответствующий гармоническому
колебанию (1.58), равномерно вращается по окружности с радиусом ![]() с угловой
скоростью
с угловой
скоростью ![]() . Параметры
. Параметры
![]() и
и ![]() в данном случае
определяют амплитуду и фазу синусоидального сигнала.
в данном случае
определяют амплитуду и фазу синусоидального сигнала.
Для других сигналов,
отличных от гармонических, точка ![]() перемещается на комплексной плоскости по
более сложной траектории, отличающейся от круговой.
перемещается на комплексной плоскости по
более сложной траектории, отличающейся от круговой.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Список сокращений
- Основные обозначения
- ВВЕДЕНИЕ
- Глава 1. Сообщения, сигналы и помехи, их математические модели
- 1.1. Основные понятия и определения
- 1.1.1. Сообщение, сигнал, модуляция
- 1.1.2. Основные параметры сигналов
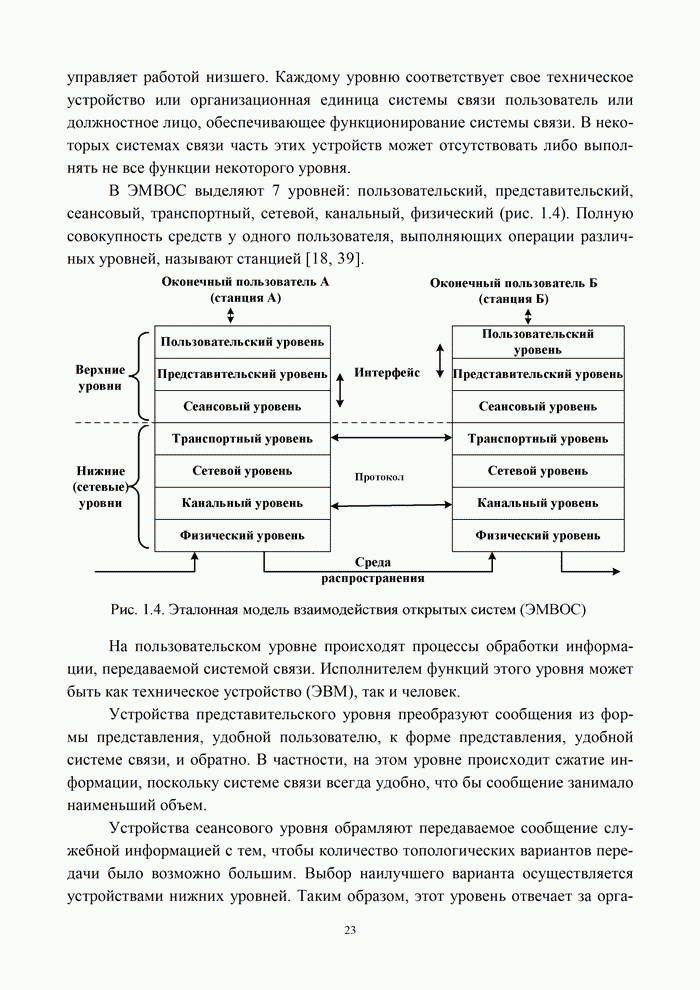
- 1.2. Системы связи. Каналы связи
- 1.2.1. Структура канала электросвязи
- 1.2.2. Линия и сеть связи
- 1.2.3. Помехи и искажения в канале
- 1.2.4. Эталонная модель взаимодействия открытых систем
- 1.2.5. Модели каналов связи и их математическое описание
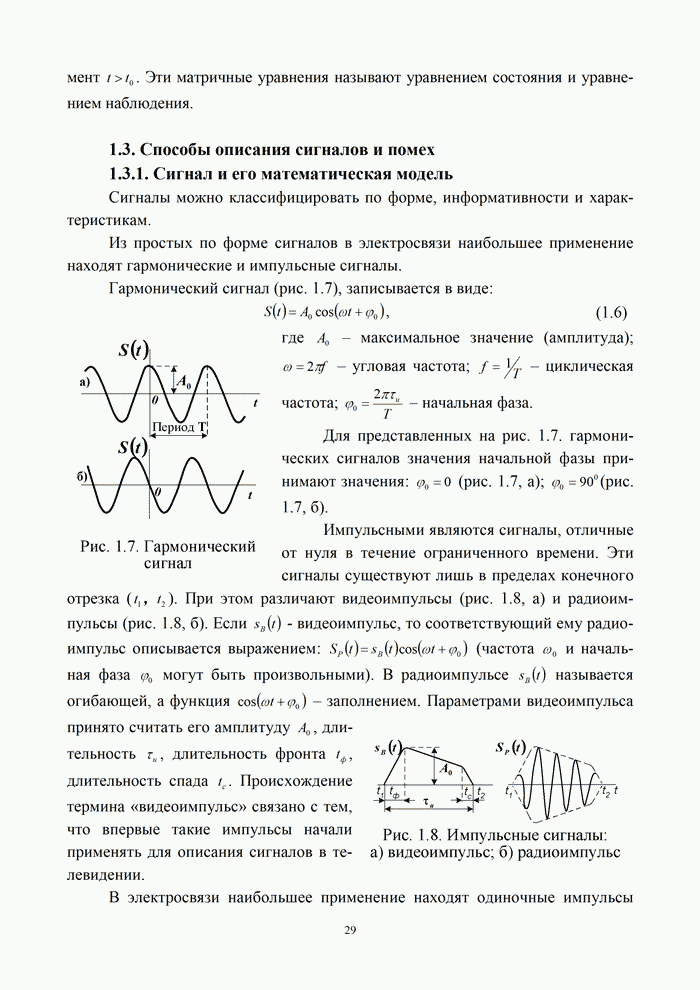
- 1.3. Способы описания сигналов и помех
- 1.3.1. Сигнал и его математическая модель
- 1.3.2. Энергетические характеристики детерминированного сигнала
- 1.4.2. Представление сигналов и помех рядом Фурье
- 1.4.3. Применение преобразования Фурье для непериодических сигналов
- 1.5. Теорема Котельникова
- 1.6. Пространство сигналов
- 1.6.1. Линейное пространство
- 1.6.2. Представление сигнала в многомерном пространстве
- 1.7. Сигналы как случайные процессы
- 1.7.1. Характеристики случайного процесса
- 1.7.2. Флуктуационный шум
- 1.8. Комплексное представление сигналов и помех
- 1.8.1. Понятие аналитического сигнала
- 1.8.2. Огибающая, мгновенная фаза и мгновенная частота узкополосного случайного процесса
- Контрольные вопросы
- Глава 2. Методы формирования и преобразования сигналов
- 2.1. Модуляция сигналов
- 2.1.1. Амплитудная модуляция гармонической несущей
- 2.1.2. Балансная и однополосная модуляция гармонической несущей
- 2.2. Методы угловой модуляции
- 2.2.1. Принципы частотной и фазовой (угловой) модуляции
- 2.2.2. Спектр сигналов угловой модуляции
- 2.3. Формирование и детектирование модулированных сигналов
- 2.3.1. Формирование и детектирование сигналов амплитудной и однополосной амплитудной модуляции
- 2.3.2. Формирование и детектирование сигналов угловой модуляции
- 2.4. Манипуляция сигналов
- 2.4.1. Временные и спектральные характеристики амплитудно-манипулированных сигналов
- 2.4.2. Временные и спектральные характеристики частотно-манипулированных сигналов
- 2.4.3. Фазовая (относительно-фазовая) манипуляция сигналов
- 2.5. Системы связи с многопозиционной относительной фазовой манипуляцией
- 2.5.1. Принцип формирования сигнала с многократной относительной фазовой манипуляцией
- 2.5.2. Квадратурная относительно-фазовая манипуляция (КОФМ)
- 2.5.3. Принцип частотной модуляции с непрерывной фазой
- Контрольные вопросы
- Глава 3. Помехоустойчивость приема дискретных сообщений
- 3.1. Критерии качества и правила приема дискретных сообщений
- 3.1.1. Понятие о помехоустойчивости систем электрической связи
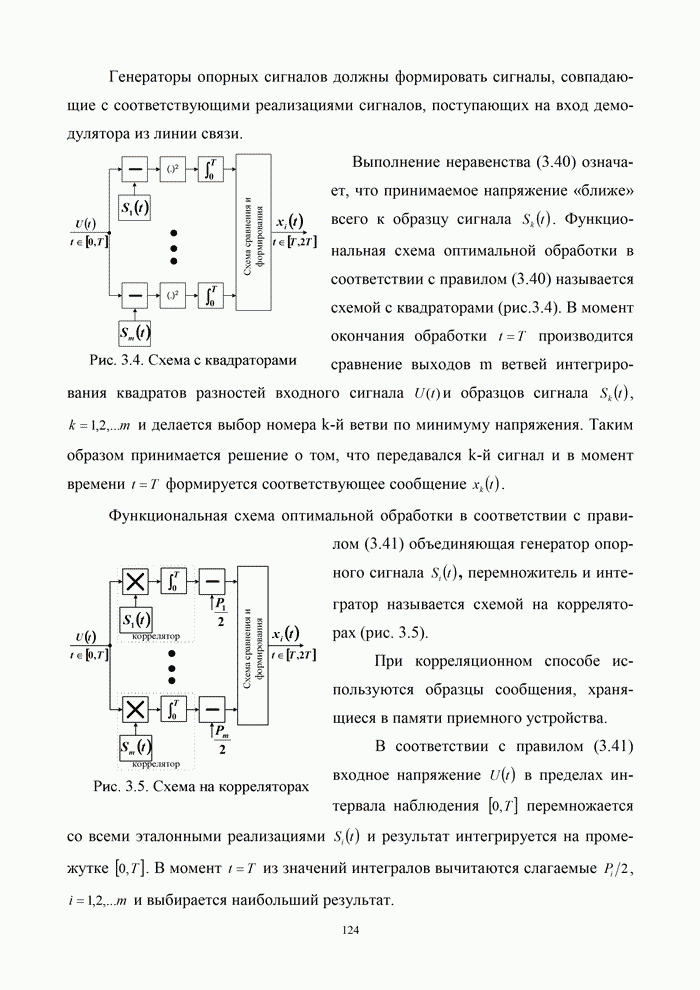
- 3.1.2. Задача оптимального приема
- 3.1.3. Вычисление вероятностей ошибок
- 3.2. Оптимальная демодуляция при когерентном приеме сигналов
- 3.2.1. Оптимальные алгоритмы приема при полностью известных сигналах
- 3.2.2. Реализация алгоритмов оптимального когерентного приема
- 3.3. Помехоустойчивость приема сигналов с известными параметрами
- 3.4. Прием сигналов с неопределенной фазой
- 3.4.1. Оптимальный некогерентный прием дискретных сигналов
- 3.4.2. Помехоустойчивость оптимального некогерентного приема
- 3.5. Подоптимальные методы приема
- 3.5.1. Причины применения неоптимальных методов приема
- 3.5.2. Квазиоптимальные методы приема
- Контрольные вопросы
- Глава 4. Теория передачи информации
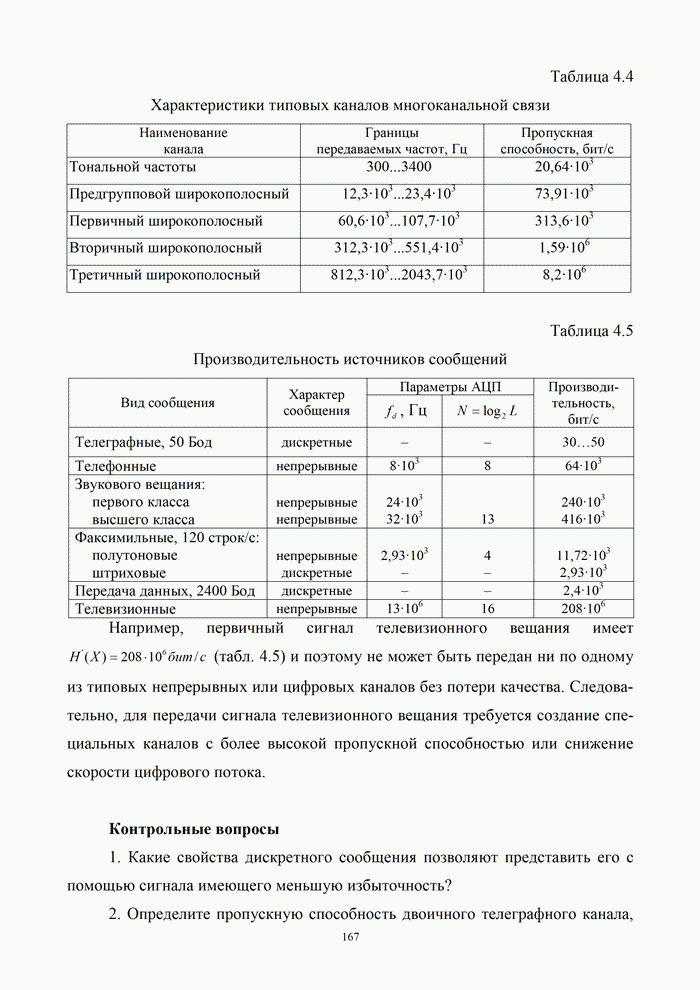
- 4.1. Информационные характеристики источника сообщений
- 4.1.1. Количественное определение информации
- 4.1.2. Энтропия и производительность дискретного источника сообщений
- 4.2. Пропускная способность дискретного канала
- 4.2.1. Количество информации переданной по дискретному каналу
- 4.2.2. Пропускная способность дискретного канала
- 4.2.3. Пропускная способность симметричного дискретного канала без памяти
- 4.3. Методы сжатия дискретных сообщений
- 4.3.1. Условия существования оптимального неравномерного кода
- 4.3.2. Прямая и обратная теоремы кодирования источника неравномерными кодами
- 4.3.3. Показатели эффективности сжатия
- 4.3.4. Кодирование источника дискретных сообщений методом Шеннона-Фано
- 4.3.5. Кодирование источника дискретных сообщений методом Хаффмена
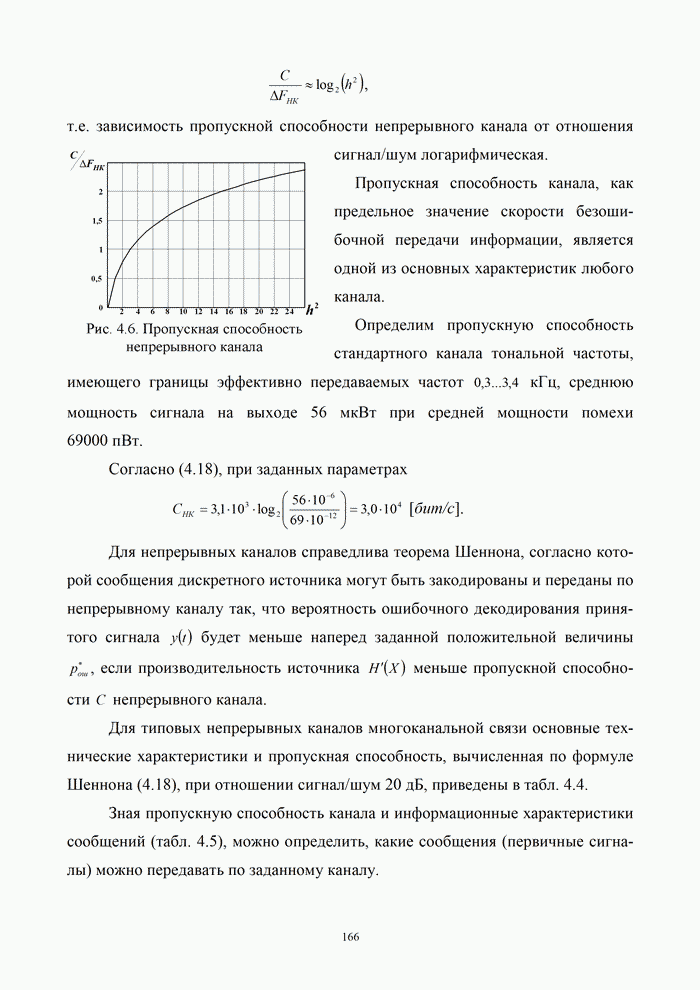
- 4.4. Пропускная способность непрерывного канала
- 4.4.1. Постановка задачи передачи дискретных сообщений в непрерывном канале
- 4.4.2. Количество информации, переданной по непрерывному каналу
- 4.4.3. Пропускная способность непрерывного канала
- Контрольные вопросы
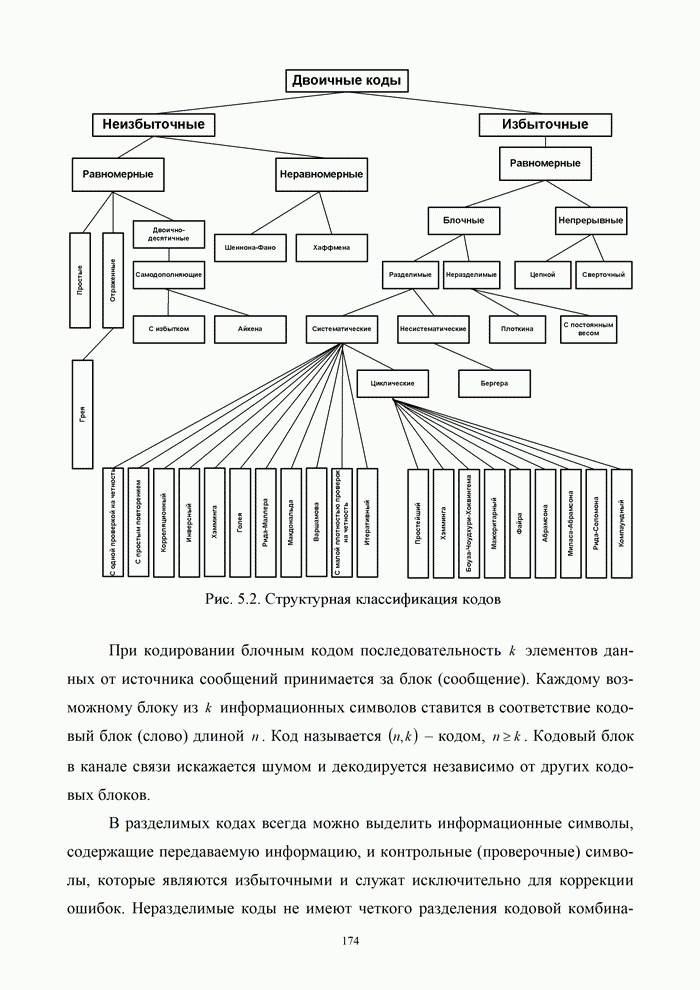
- Глава 5. Теория кодирования сообщений
- 5.1. Помехоустойчивое кодирование: блочные и непрерывные коды
- 5.1.1. Постановка задачи помехоустойчивого кодирования
- 5.1.2. Классификация кодов
- 5.1.3. Основные характеристики и свойства блочных кодов
- 5.2. Эффективность помехоустойчивого кодирования
- 5.2.1. Эффективность кода в режиме исправления ошибок
- 5.2.2. Эффективность кода в режиме обнаружения ошибок
- 5.2.3. Эффективность помехоустойчивых кодов
- 5.3. Математические основы теории помехоустойчивого кодирования
- 5.3.1. Краткие сведения из теории чисел
- 5.3.2. Группы
- 5.3.3. Кольца и поля
- 5.3.4. Векторное пространство
- 5.3.5. Конечные поля
- 5.4. Линейные блочные коды
- 5.4.1. Система передачи дискретных сообщений
- 5.4.2. Параметры линейного кода
- 5.4.3. Полиномиальные циклические коды
- 5.4.4. Циклические коды и корни полиномов
- 5.4.5. Спектральное описание циклических кодов
- 5.4.6. Простейшие блочные линейные коды
- 5.5. Коды Боуза-Чоудхури-Хоквингема
- 5.5.1. Методы задания кодов БЧХ
- 5.5.2. Принципы декодирования кодов БЧХ
- 5.5.3. Методы реализации этапов декодирования кодов БЧХ
- 5.6. Коды Рида-Соломона
- 5.6.1. Основные определения
- 5.6.2. Обнаружение и исправление пакетов ошибок
- 5.7. Коды Рида-Маллера
- 5.7.1. Задание и декодирование кодов Рида-Маллера
- 5.7.2. Симплексные коды и m-последовательности
- 5.7.3. Связь между блочными кодами
- 5.8. Сверточные коды
- 5.8.1. Основные параметры
- 5.8.2. Способы задания сверточного кода
- 5.8.3. Алгоритм декодирования Витерби
- 5.9. Помехоустойчивость систем передачи дискретных сообщений
- 5.9.1. Две процедуры приема сигналов
- 5.9.2. Помехоустойчивость систем передачи информации при оптимальной процедуре приема
- 5.9.3. Помехоустойчивость систем передачи информации при посимвольном приеме сигналов
- Контрольные вопросы
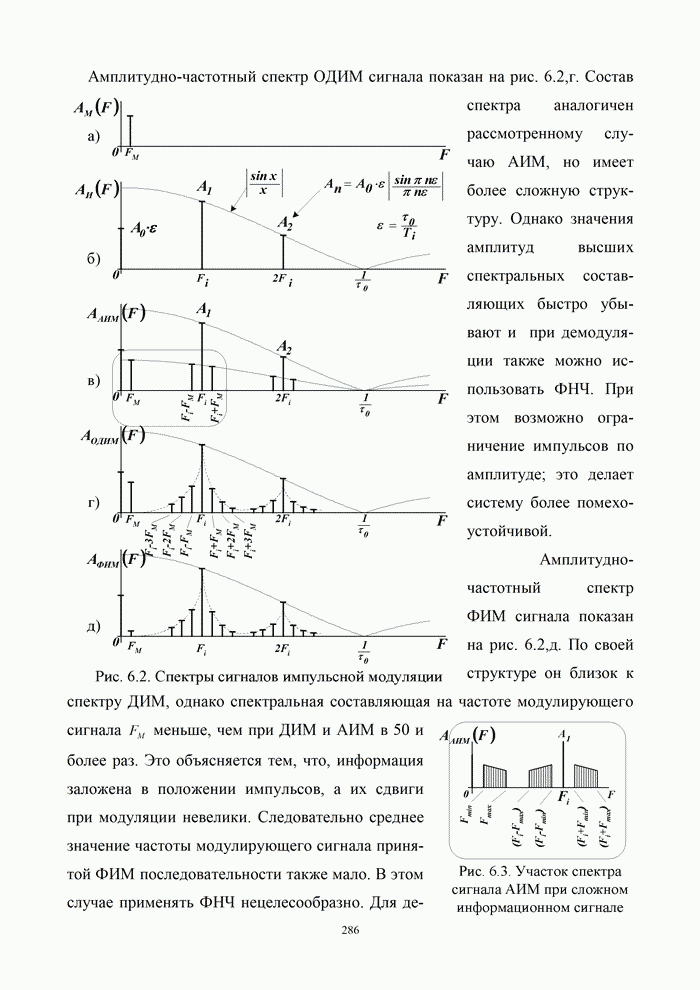
- Глава 6. Сигналы с импульсной модуляцией
- 6.1. Методы импульсной модуляции
- 6.1.1. Импульсные методы передачи непрерывных сигналов
- 6.1.2. Спектральные характеристики импульсных методов модуляции
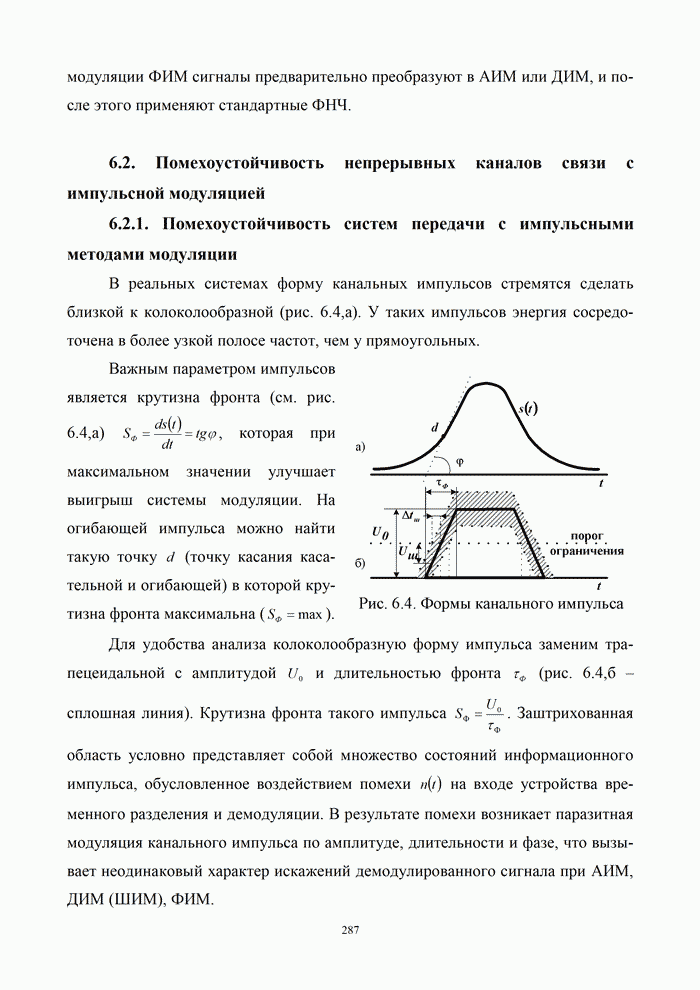
- 6.2. Помехоустойчивость непрерывных каналов связи с импульсной модуляцией
- 6.2.1. Помехоустойчивость систем передачи с импульсными методами модуляции
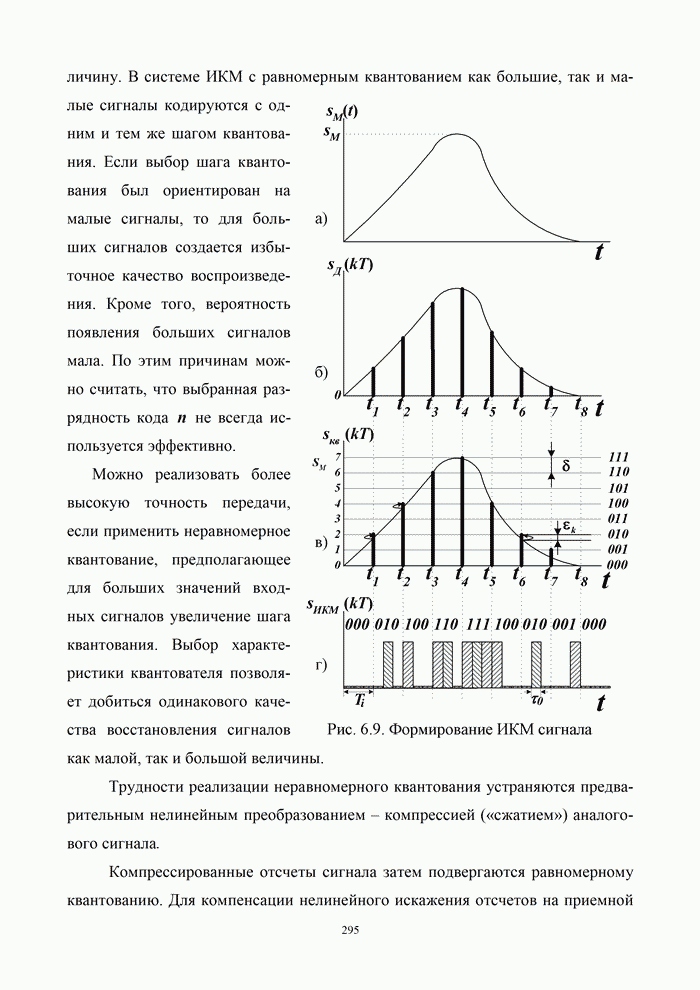
- 6.3. Цифровые методы передачи непрерывных сообщений
- 6.3.1. Передача сигналов с импульсно-кодовой модуляцией
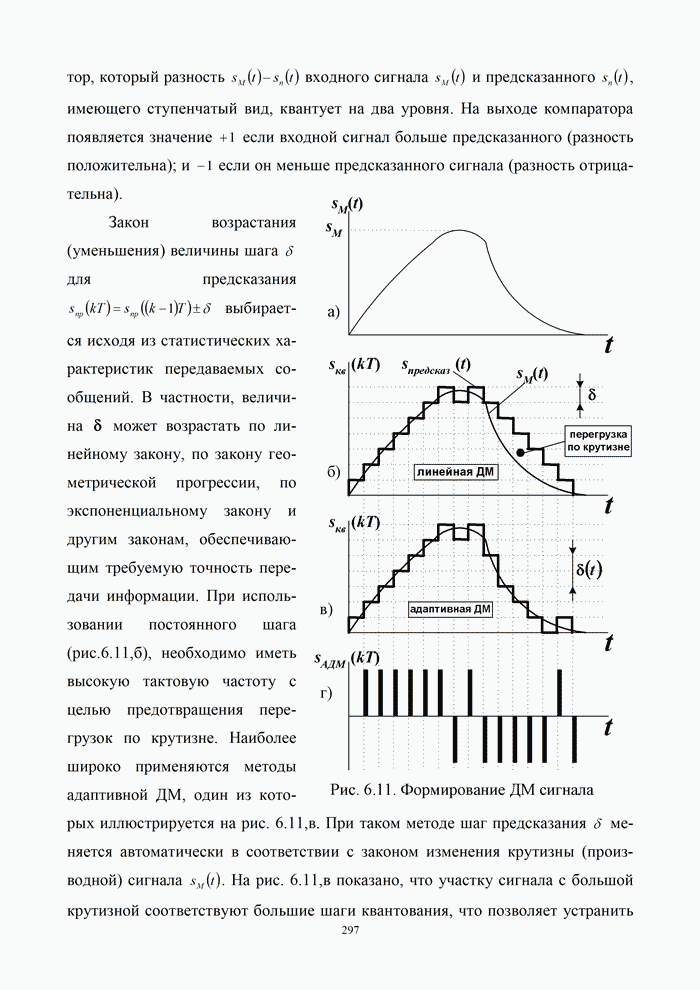
- 6.3.2. Передача сигналов с дельта модуляцией
- 6.3.3. Квантование сигналов в системах с ИКМ и ДМ
- Контрольные вопросы
- Глава 7. Методы приема сигналов в сложных условиях
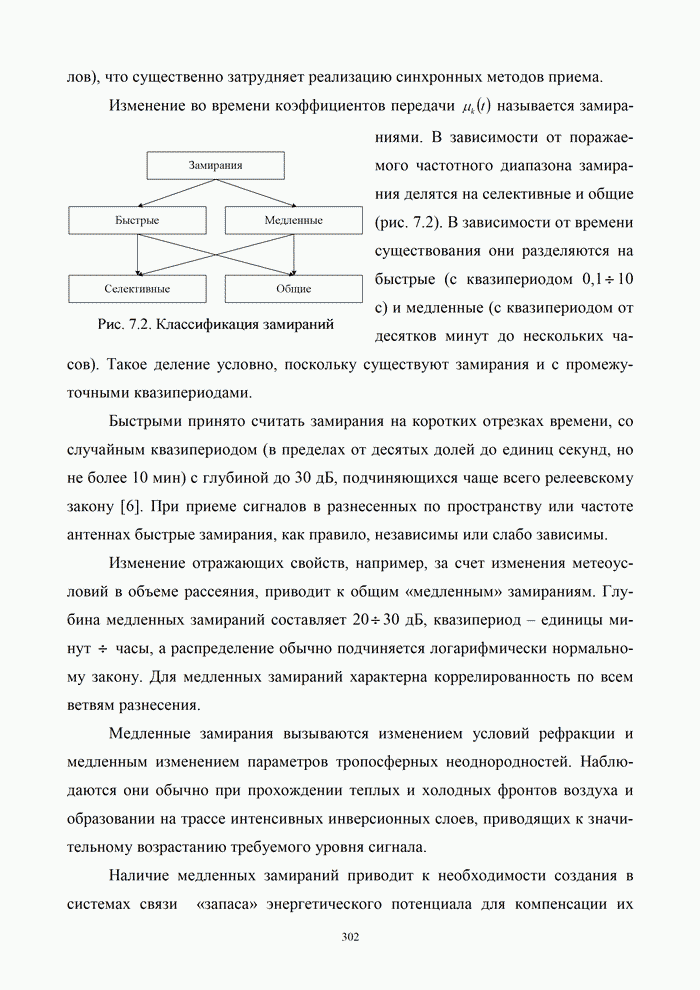
- 7.1. Прием сигналов в каналах с замираниями
- 7.1.1. Сущность замираний и их классификация
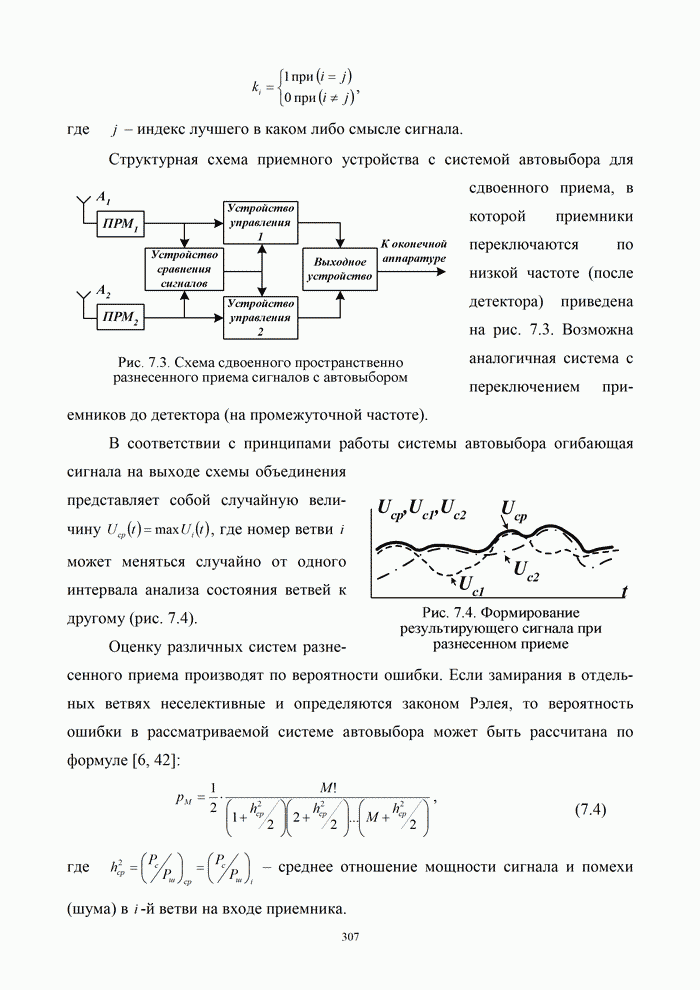
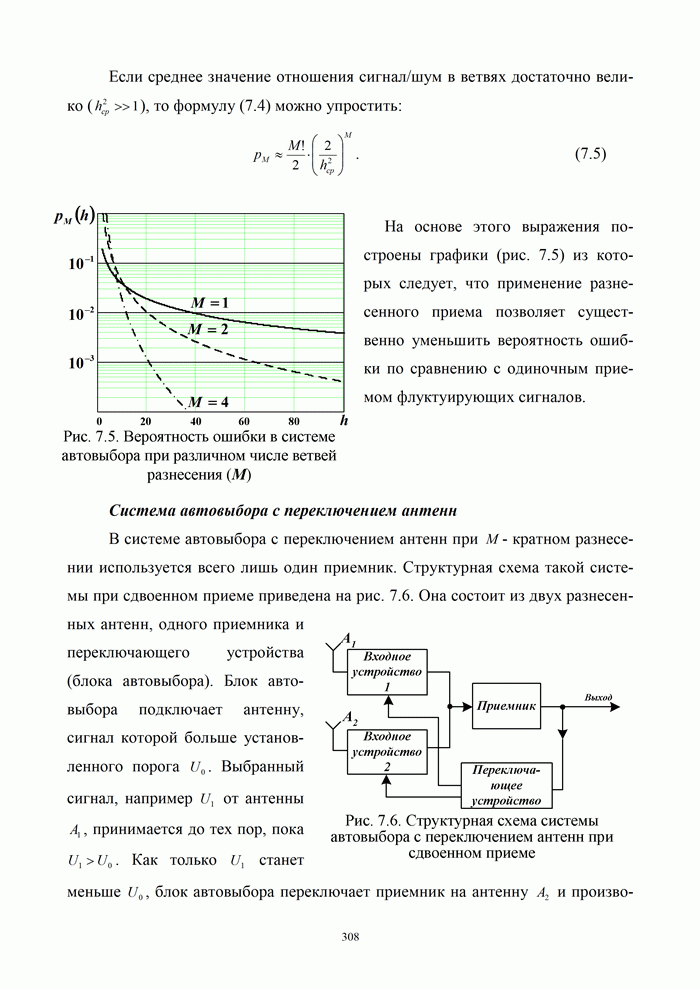
- 7.1.2. Принципы разнесенного приема сигналов
- 7.2. Методы борьбы с замираниями сигналов
- 7.2.1. Методы борьбы с замираниями в аналоговых системах связи
- 7.2.2. Методы борьбы с замираниями в цифровых системах связи
- 7.3. Методы борьбы с межсимвольной интерференцией
- 7.3.1. Причины возникновения и сущность межсимвольной интерференции
- 7.3.2. Обработка сигналов в каналах с межсимвольной интерференцией
- 7.3.3. Помехоустойчивость в каналах с межсимвольной интерференцией
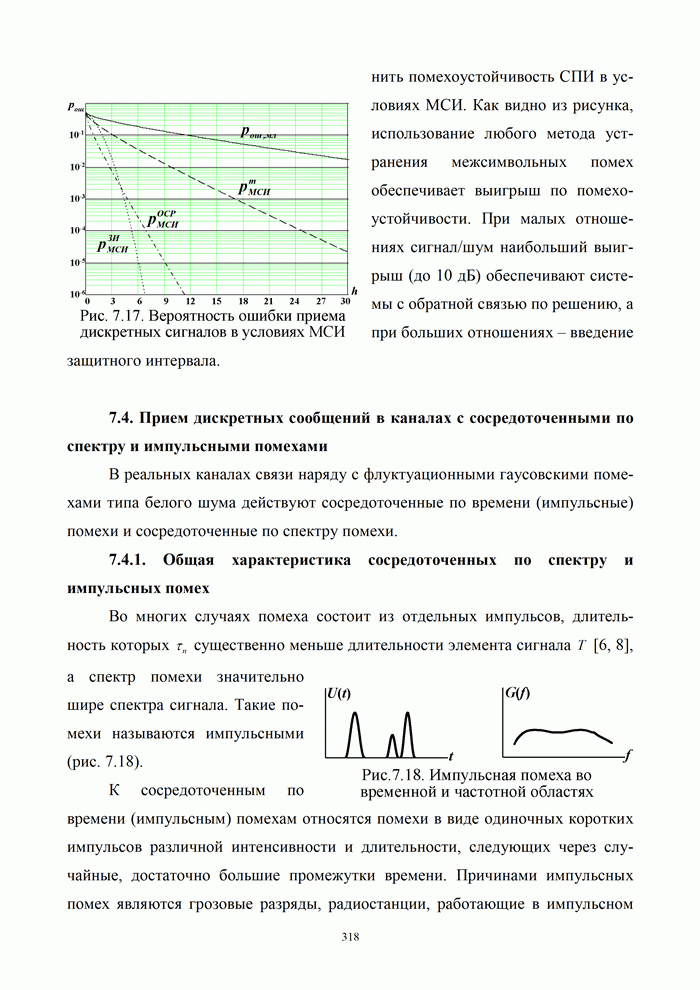
- 7.4. Прием дискретных сообщений в каналах с сосредоточенными по спектру и импульсными помехами
- 7.4.1. Общая характеристика сосредоточенных по спектру и импульсных помех
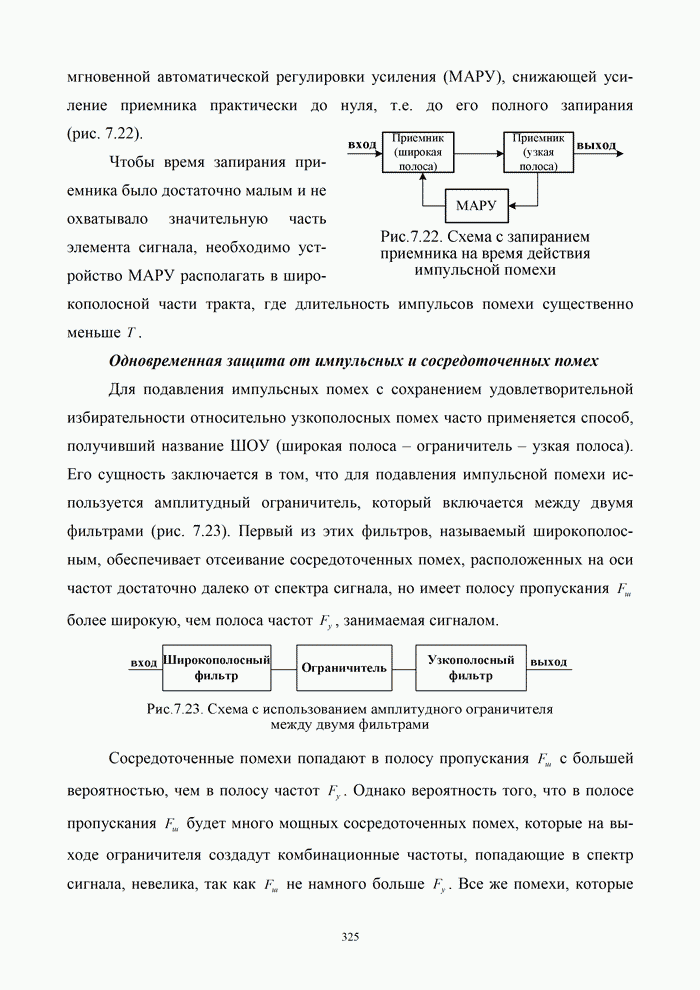
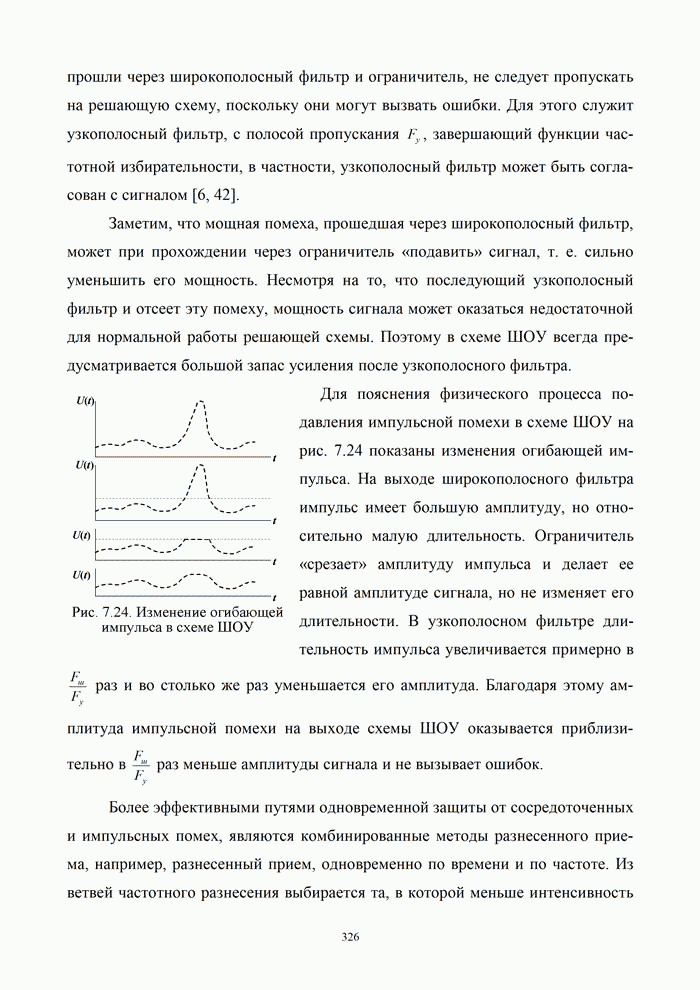
- 7.4.2. Борьба с сосредоточенными и импульсными помехами
- 7.5. Компенсация помех и искажений в канале
- 7.5.1. Принцип работы радиолинии с ФМ ПСС (ФМ ШПС)
- 7.5.2. Помехоустойчивость радиолинии с ФМ ПСС
- 7.5.3. Принципы работы радиолиний с ППРЧ
- 7.5.4. Помехоустойчивость радиолиний с ППРЧ
- Контрольные вопросы
- Глава 8. Многоканальная связь и распределение информации
- 8.1. Методы распределения ресурса общего канала
- 8.1.1. Классификация систем передачи информации, использующих единый ресурс
- 8.1.2. Постановка задачи объединения и разделения сигналов
- 8.1.3. Энергетическая и спектральная цена уплотнения
- 8.2. Частотное разделение каналов
- 8.2.1. Принцип частотного объединения и разделения каналов
- 8.2.2. Групповой сигнал, его структура и характеристики
- 8.3. Временное разделение каналов
- 8.3.1. Принцип временного разделения каналов
- 8.3.2. Характеристики группового сигнала систем с ВРК
- 8.4. Разделение сигналов по форме
- Контрольные вопросы
- Глава 9. Эффективность систем связи
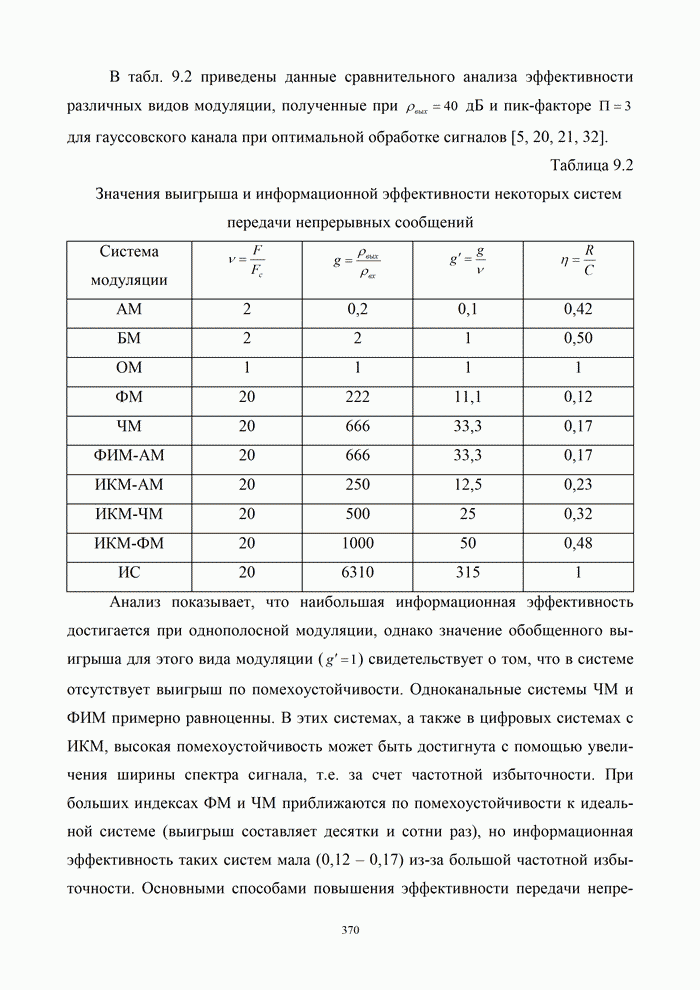
- 9.1. Оценка эффективности систем связи
- 9.1.1. Подходы к оценке эффективности
- 9.1.2. Критерии эффективности
- 9.1.3. Эффективность аналоговых и цифровых систем
- 9.2. Выбор сигналов и помехоустойчивых кодов
- 9.2.1. Многопозиционные сигналы
- 9.2.2. Корректирующие коды
- 9.3. Оптимизация систем связи
- 9.3.1. Согласование методов модуляции и кодирования
- 9.3.2. Классификация сигнально – кодовых конструкций
- 9.4. Характеристики основных типов СКК
- 9.4.1. Согласование канала кодом Грея
- 9.4.2. Согласование на основе разбиения ансамбля на вложенные подансамбли
- 9.5. Алгоритмы цифровой обработки сигналов
- 9.5.1. Дискретные сигналы и их спектры
- 9.5.2. Алгоритмы дискретного и быстрого преобразований Фурье
- Контрольные вопросы
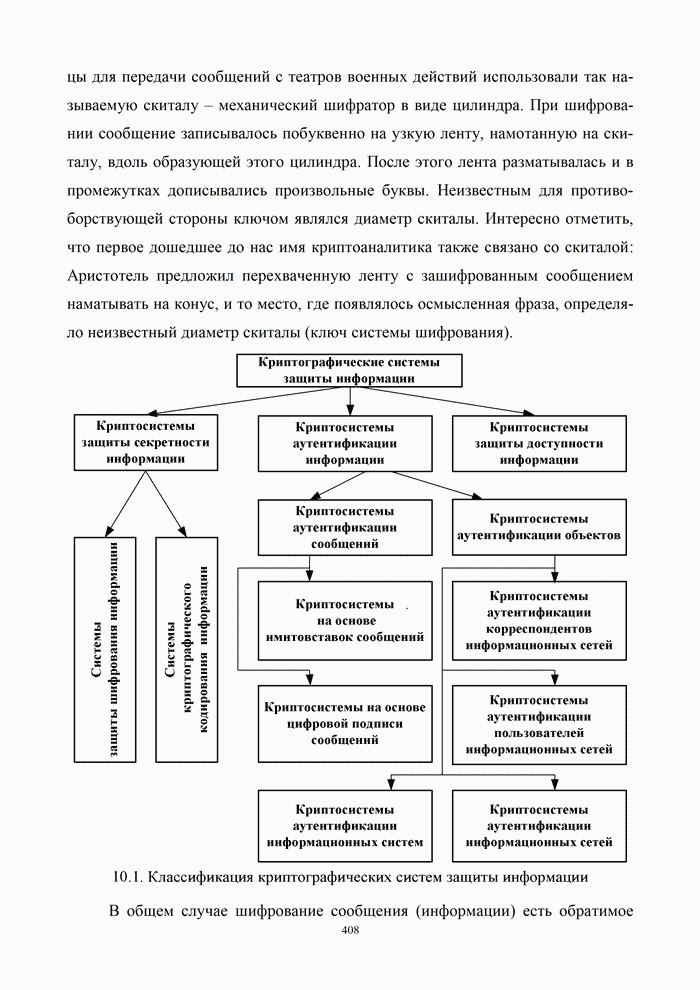
- Глава 10. Теоретико-информационные основы криптозащиты сообщений в телекоммуникационных системах
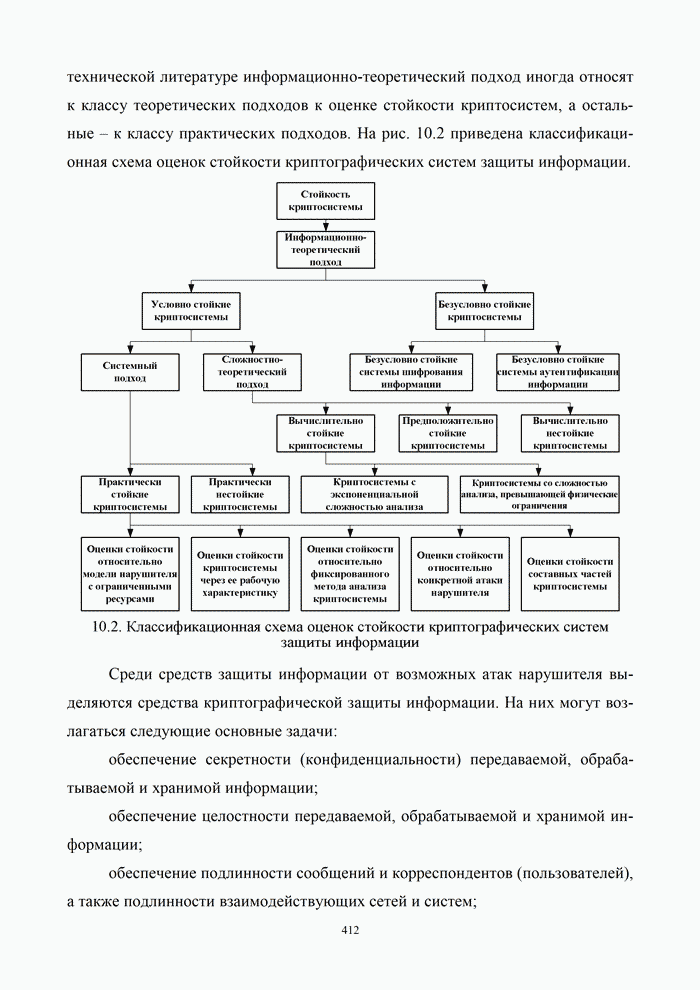
- 10.1. Классификация криптографических систем
- 10.1.2. Классификация криптографических систем защиты информации
- 10.1.3. Оценка стойкости криптосистем
- 10.2. Функции, используемые в криптографических системах
- 10.2.1. Общее описание функций, используемых в криптографических системах
- 10.2.2. Однонаправленные функции
- 10.2.3. Криптографические хэш-функции
- 10.3. Модели криптографических систем
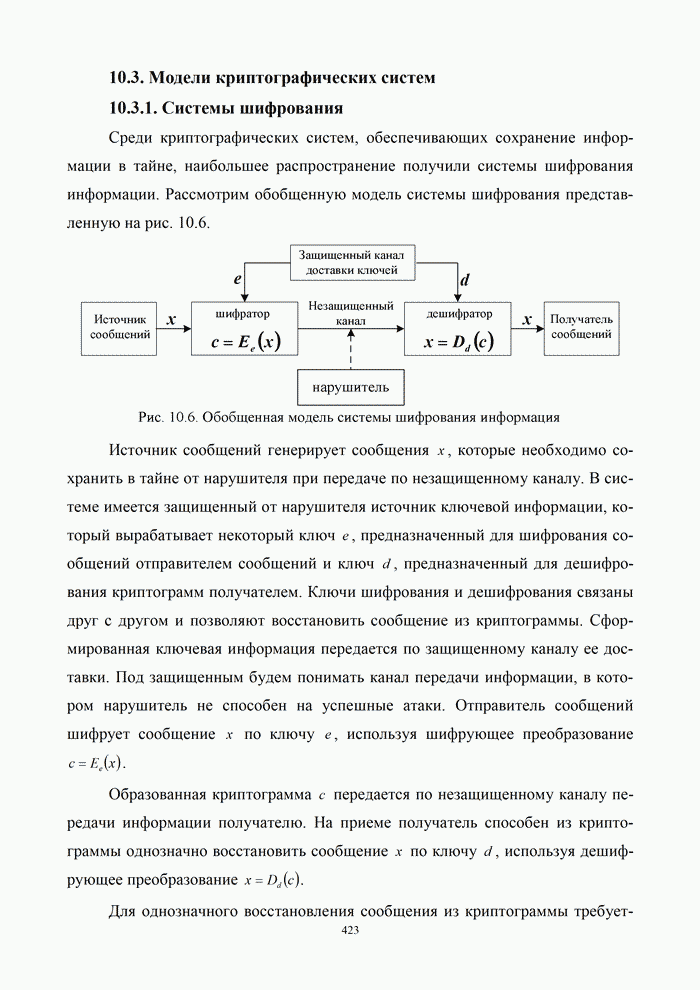
- 10.3.1. Системы шифрования
- 10.3.2. Традиционные симметричные криптосистемы
- 10.4. Алгоритмы криптографической защиты
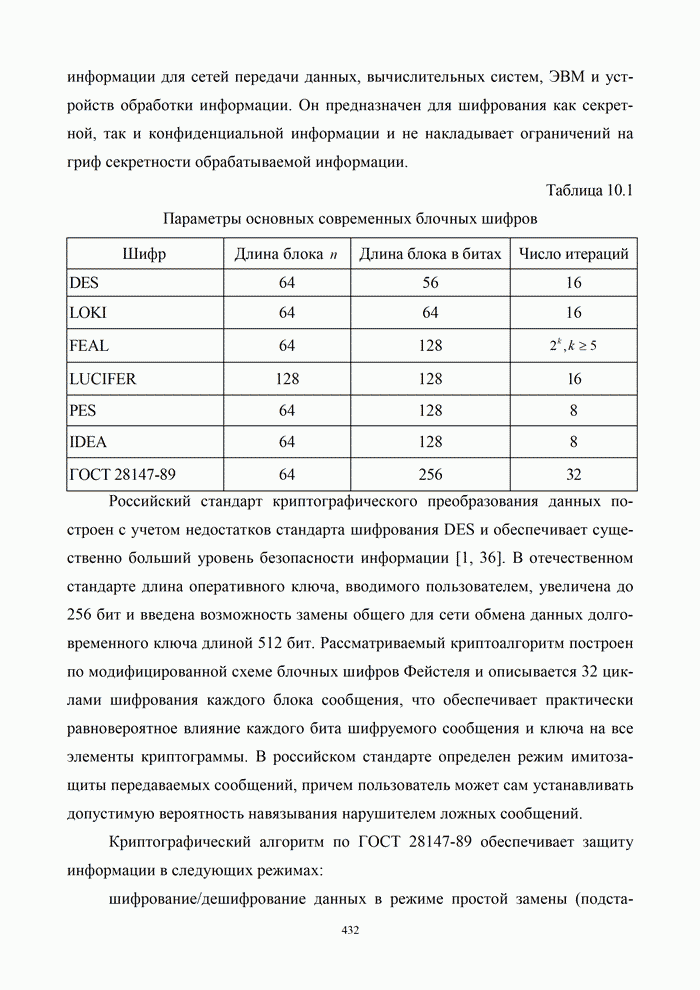
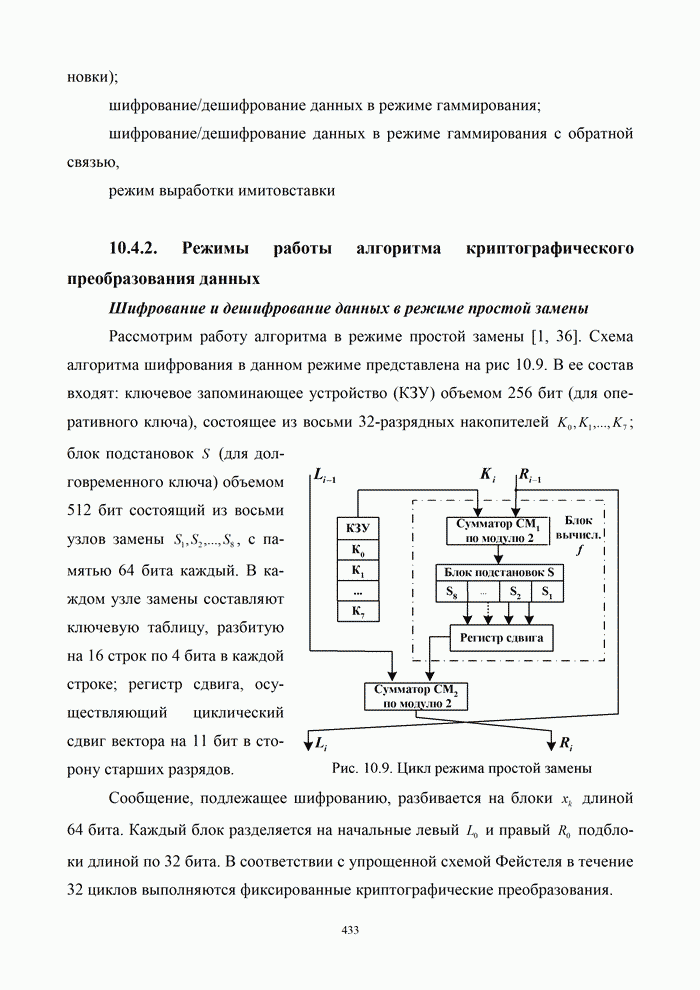
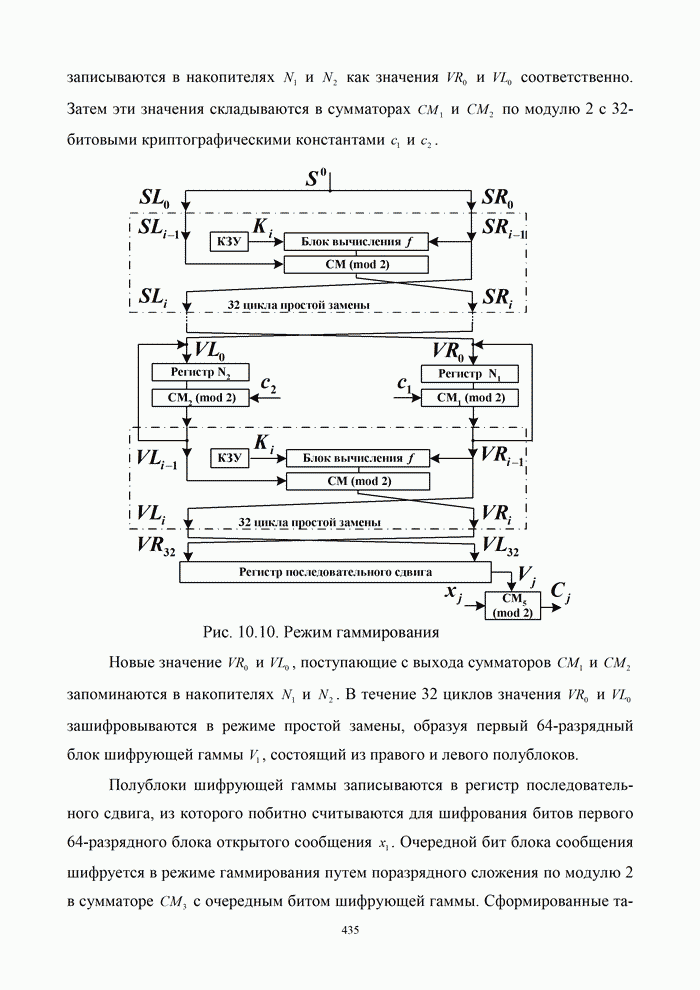
- 10.4.1. Алгоритм криптографической защиты информации согласно ГОСТ 28147-89
- Контрольные вопросы
- Заключение
- Список литературы
























































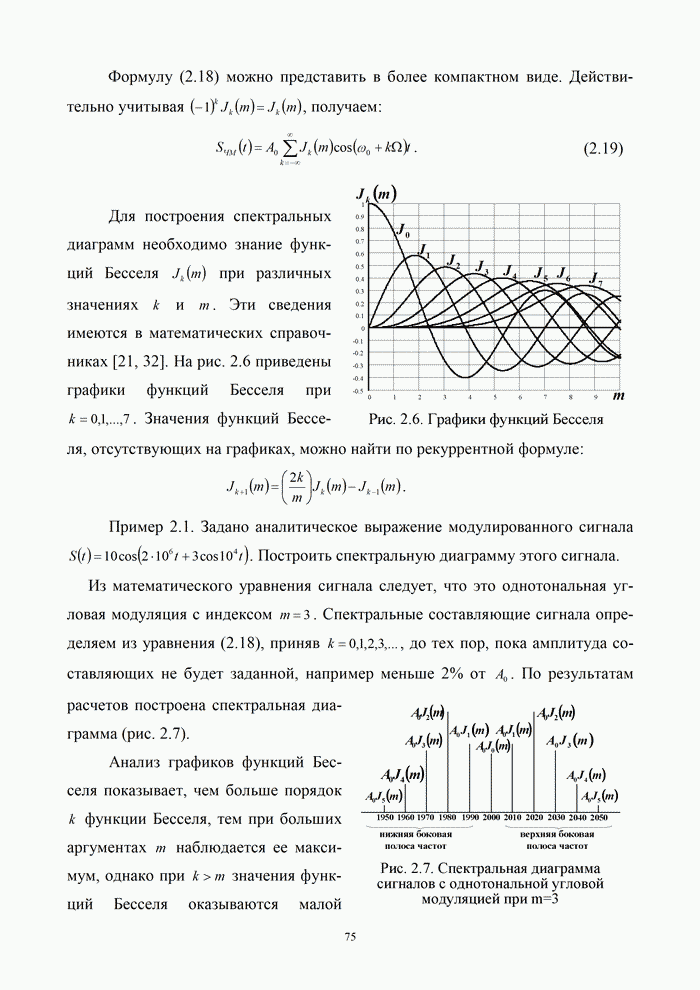





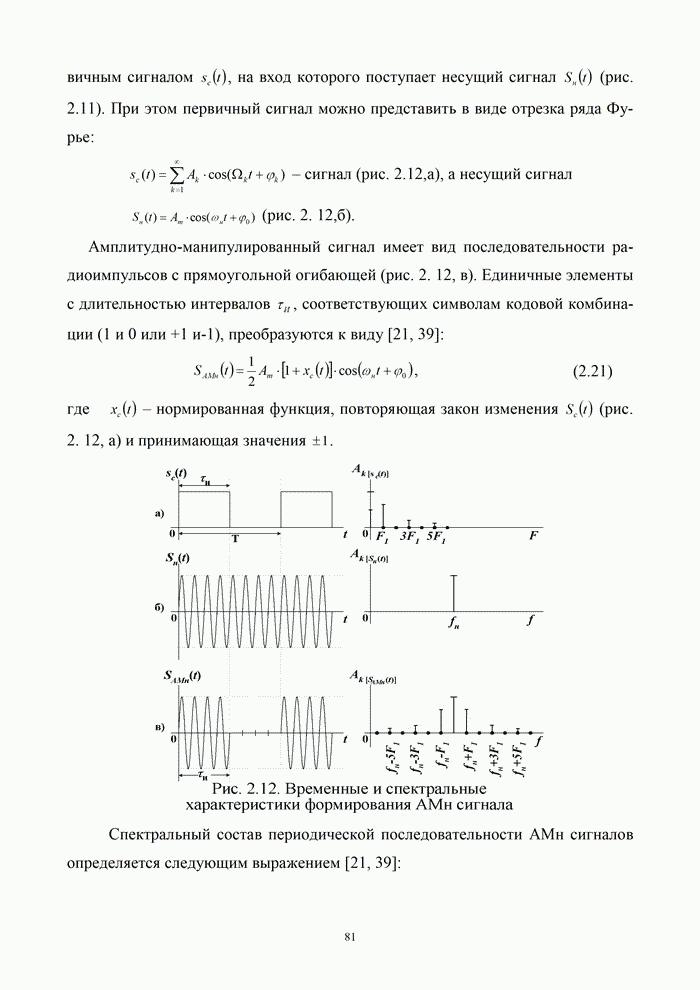


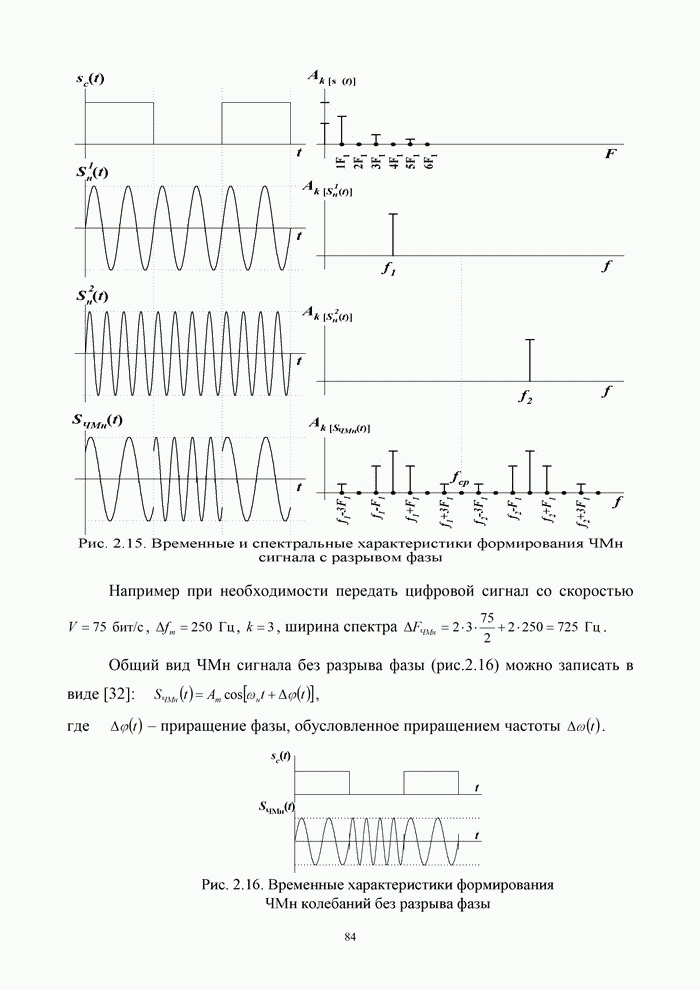






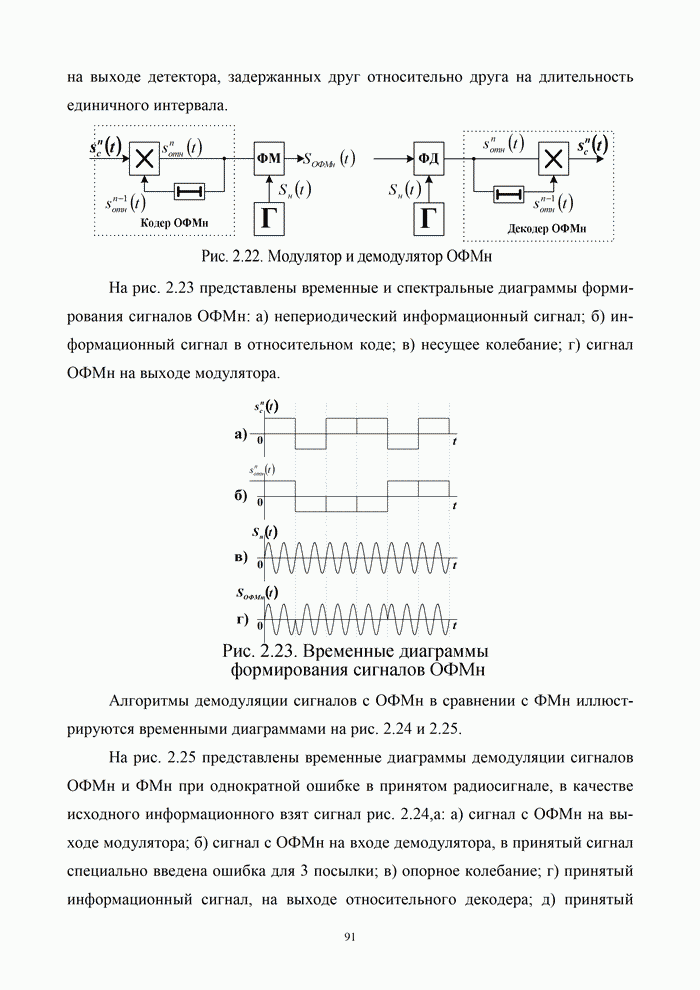














































































































































































































































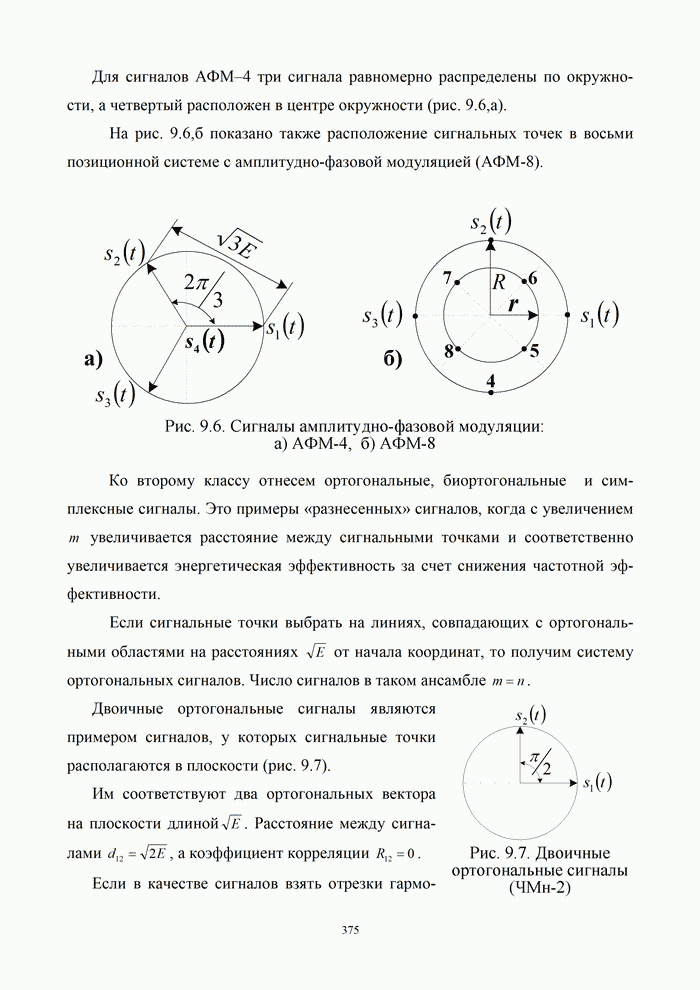

















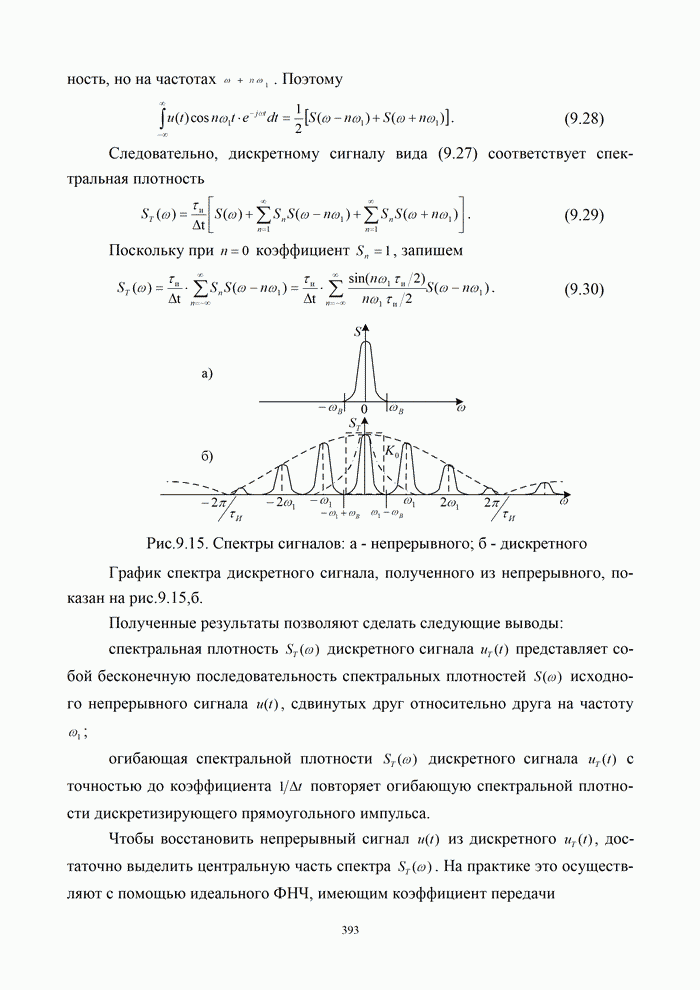

















































 .
.
