| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.7. Коды Рида-Маллера
5.7.1. Задание и декодирование кодов Рида-Маллера
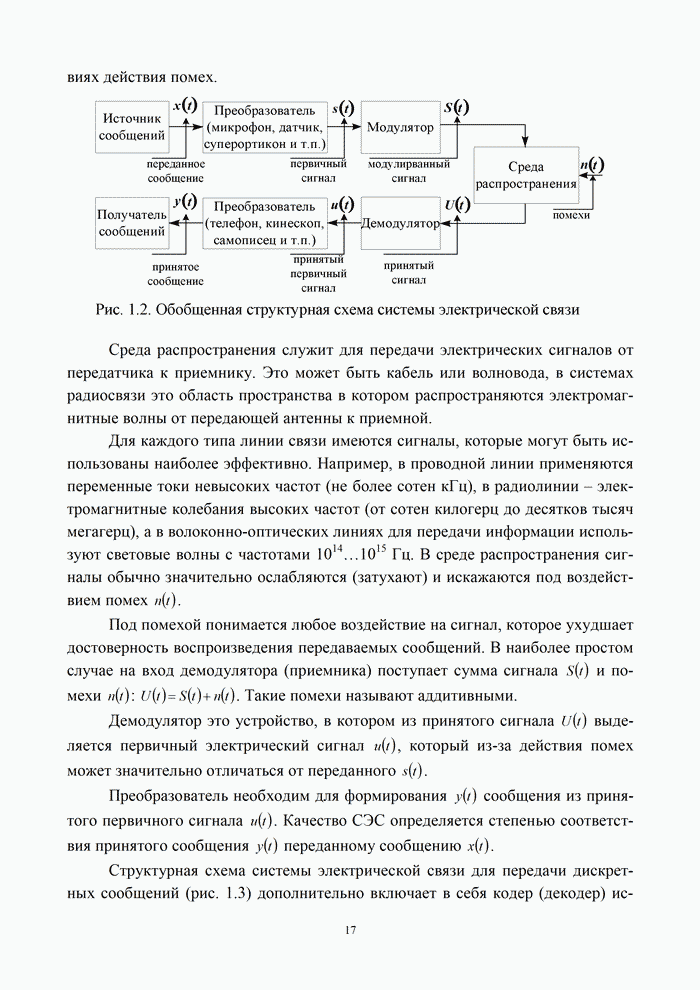
Коды Рида-Маллера относятся к линейным
двоичным кодам, имеющим большие кодовые расстояния и исправляющим благодаря
этому много ошибок. Они пригодны для каналов с малым отношением сигнал/помеха.
Этот класс кодов интересен и потому, что с
ним связаны многие другие сигналы, применяемые
в радиотехнических системах: ортогональные и биортогональные сигналы,
симплексные коды, ![]() -последовательности
и коды Хэмминга.
-последовательности
и коды Хэмминга.
Будем рассматривать простейшие коды Рида-Маллера, слова которых являются линейными комбинациями некоторых двоичных функций обладающих полезными для практики свойствами. Сразу укажем, что эти функции выбраны такими, что их отображение в поле действительных чисел дает систему ортогональных функций. Это свойство используется при декодировании.
Данное ограничение означает, что в базис кода не входят произведения двоичных функций, т.е. рассматривается код Рида-Маллера 1-го порядка. Некоторые сведения о кодах Рида-Маллера более высоких порядков имеются в [30].
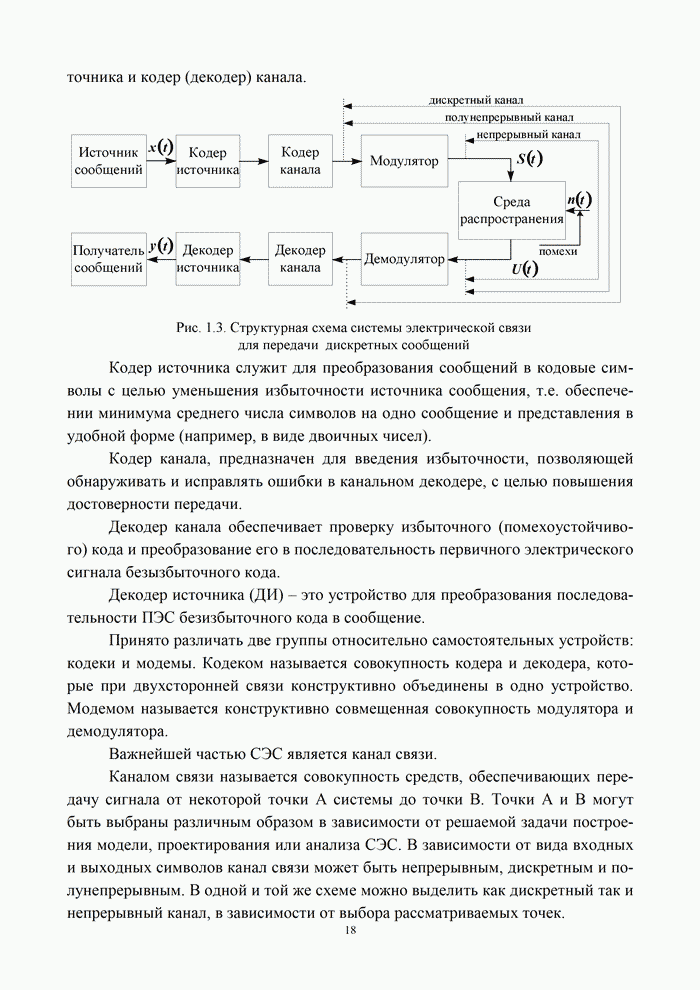
Кодовое слово длины ![]() обычно рассматривается как
булева функция (или ее инверсия), заданная в
обычно рассматривается как
булева функция (или ее инверсия), заданная в ![]() точках, т.е. на наборах из
точках, т.е. на наборах из ![]() двоичных элементов. Можно многими способами нумеровать
позиции кодового слова
двоичных элементов. Можно многими способами нумеровать
позиции кодового слова ![]() -разрядными двоичными векторами. Ясно,
что, как в случае кодов Хэмминга, такая перестановка не влияет на
помехоустойчивость получаемых кодов. Будем
нумеровать позиции кодового слова числами в двоичной системе счисления
-разрядными двоичными векторами. Ясно,
что, как в случае кодов Хэмминга, такая перестановка не влияет на
помехоустойчивость получаемых кодов. Будем
нумеровать позиции кодового слова числами в двоичной системе счисления ![]() , где
, где
![]() для
для ![]() . Ввиду линейности кодов
Рида-Маллера каждый символ кодового слова
. Ввиду линейности кодов
Рида-Маллера каждый символ кодового слова ![]() представим линейной комбинацией
представим линейной комбинацией
|
|
|
или ее инверсией
|
|
|
где ![]() –
известные информационные символы.
–
известные информационные символы.
В соответствии с определением порождающей
матрицы (5.16) и правилом покомпонентного сложения векторов элементы ![]() являются столбцами матрицы
являются столбцами матрицы ![]() . Для
. Для ![]() порождающая матрица
размера
порождающая матрица
размера ![]() на
на ![]() имеет вид:
имеет вид:
|
|
|
Столбцы матрицы ![]() без верхней строки
представляют собой последовательность чисел, записанных в двоичной системе
счисления (младшие разряды внизу). Таким образом, столбцы матрицы можно рассматривать как
последовательность состояний двоичного суммирующего счетчика:
без верхней строки
представляют собой последовательность чисел, записанных в двоичной системе
счисления (младшие разряды внизу). Таким образом, столбцы матрицы можно рассматривать как
последовательность состояний двоичного суммирующего счетчика:
|
|
(5.34) |
где 1
– последовательность из единиц; ![]() – последовательность состояний последнего
(старшего) разряда счетчика;
– последовательность состояний последнего
(старшего) разряда счетчика; ![]() – последовательность состояний
первого (младшего) разряда. Отметим, что перестановка столбцов и строк порождающей
матрицы приводит к эквивалентным кодам.
– последовательность состояний
первого (младшего) разряда. Отметим, что перестановка столбцов и строк порождающей
матрицы приводит к эквивалентным кодам.
Кодовое слово есть линейная комбинация
базисных векторов (строк матрицы ![]() ):
):
|
|
(5.35) |
Вид матрицы (5.34) указывает простой способ формирования
базисных векторов и получения кодового слова.
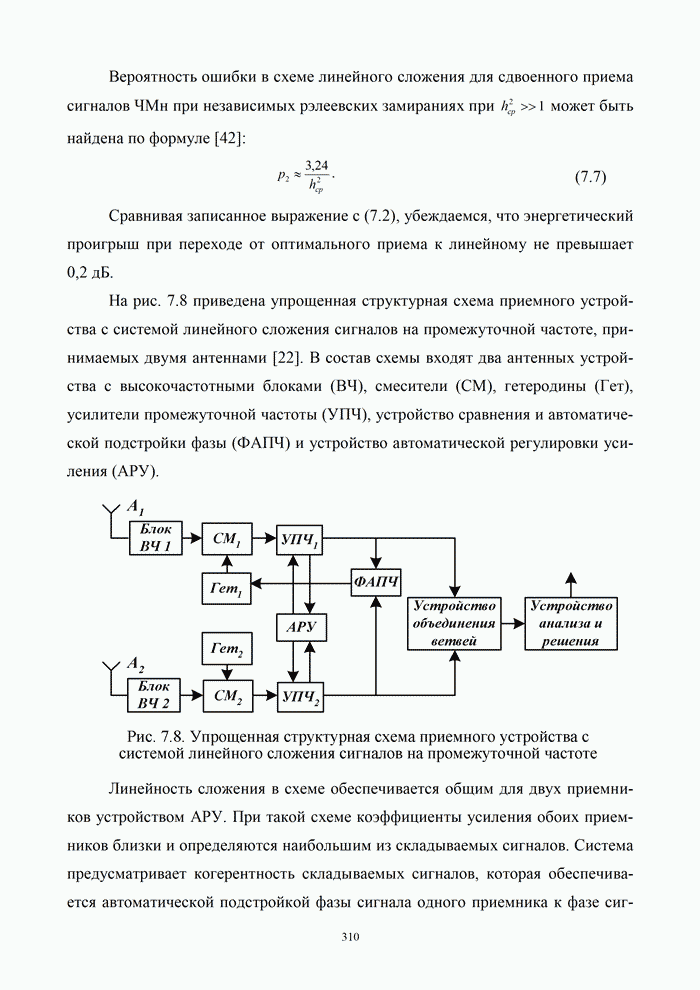
Схема кодирующего устройства для ![]() (рис.
5.5) содержит трехразрядный двоичный счетчик, вырабатывающий функции
(рис.
5.5) содержит трехразрядный двоичный счетчик, вырабатывающий функции ![]() , и комбинационную схему, реализующую
булеву функцию (5.35). Естественно, длительность информационных символов, подаваемых в этот кодер, предполагается равной
длительности кодового слова, т.е. в
данной случае 8 длительностям символов канала.
, и комбинационную схему, реализующую
булеву функцию (5.35). Естественно, длительность информационных символов, подаваемых в этот кодер, предполагается равной
длительности кодового слова, т.е. в
данной случае 8 длительностям символов канала.

Двоичный вектор ![]() с
компонентами
с
компонентами ![]() может быть отображен в
вектор
может быть отображен в
вектор ![]() с
действительными компонентами
с
действительными компонентами ![]() . Для этого надо «0» в
двоичном векторе заменить на (+1), а «1» – на (–1). Такое отображение можно определить формулами:
. Для этого надо «0» в
двоичном векторе заменить на (+1), а «1» – на (–1). Такое отображение можно определить формулами:
|
|
(5.36) |
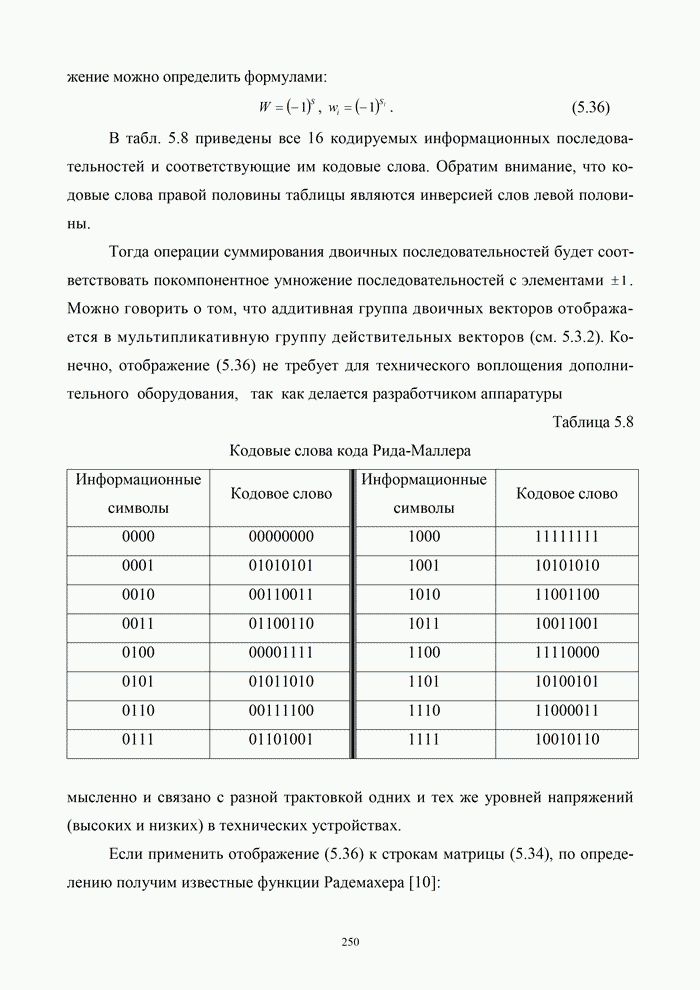
В табл. 5.8 приведены все 16 кодируемых информационных последовательностей и соответствующие им кодовые слова. Обратим внимание, что кодовые слова правой половины таблицы являются инверсией слов левой половины.
Тогда операции суммирования двоичных
последовательностей будет соответствовать покомпонентное умножение
последовательностей с элементами ![]() . Можно говорить о том, что аддитивная
группа двоичных векторов отображается в мультипликативную группу
действительных векторов (см. 5.3.2). Конечно, отображение (5.36) не требует для технического
воплощения дополнительного оборудования, так
как делается разработчиком аппаратуры
. Можно говорить о том, что аддитивная
группа двоичных векторов отображается в мультипликативную группу
действительных векторов (см. 5.3.2). Конечно, отображение (5.36) не требует для технического
воплощения дополнительного оборудования, так
как делается разработчиком аппаратуры
Таблица 5.8. Кодовые слова кода Рида-Маллера
|
Информационные символы |
Кодовое слово |
Информационные символы |
Кодовое слово |
|
0000 |
00000000 |
1000 |
11111111 |
|
0001 |
01010101 |
1001 |
10101010 |
|
0010 |
00110011 |
1010 |
11001100 |
|
0011 |
01100110 |
1011 |
10011001 |
|
0100 |
00001111 |
1100 |
11110000 |
|
0101 |
01011010 |
1101 |
10100101 |
|
0110 |
00111100 |
1110 |
11000011 |
|
0111 |
01101001 |
1111 |
10010110 |
мысленно и связано с разной трактовкой одних и тех же уровней напряжений (высоких и низких) в технических устройствах.
Если применить отображение (5.36) к строкам матрицы (5.34), по определению получим известные функции Радемахера [10]:
|
|
|
Известно, что всевозможные произведения функций Радемахера образуют
полную ортогональную систему функций, которые называются функциями Уолша, и им
соответствуют слова кода Рида-Маллера. Ортогональность функций означает, что для двух произвольных функций Уолша ![]() и
и ![]() ,
, ![]() скалярное произведение
скалярное произведение
|
|
|
т.е.
число позиций, на которых символы последовательностей совпадают, равно
числу позиций, на которых последовательности отличаются, и равно поэтому ![]() . Из определения
расстояния Хэмминга (см. 5.4.1) заключаем, что кодовое расстояние кода Рида-Маллера равно
. Из определения
расстояния Хэмминга (см. 5.4.1) заключаем, что кодовое расстояние кода Рида-Маллера равно ![]() . Отметим, что для пар слов, являющихся инверсией друг друга,
расстояние равно
. Отметим, что для пар слов, являющихся инверсией друг друга,
расстояние равно ![]() .
.
Таким образом, коды Рида-Маллера имеют длину
![]() ,
, ![]() информационный
символ, кодовое расстояние
информационный
символ, кодовое расстояние ![]() . Отображение
двоичных кодовых слов в область
действительных чисел
. Отображение
двоичных кодовых слов в область
действительных чисел ![]() дает множество функций Уолша, включающее
дает множество функций Уолша, включающее ![]() функций Уолша
функций Уолша ![]() ,
, ![]() , и
, и ![]() противоположных функций
противоположных функций ![]() ,
,
![]() .
Множество сигналов, составленных из
функций Уолша и противоположных им, называется системой биортогональных сигналов.
Если в систему не включать противоположные сигналы, то получим систему ортогональных
сигналов, которые используются в качестве адресов абонентов в системах
множественного доступа с кодовым разделением
каналов. Применение ортогональных сигналов в качестве канальных позволяет разделять их в таких системах без взаимных помех [20].
.
Множество сигналов, составленных из
функций Уолша и противоположных им, называется системой биортогональных сигналов.
Если в систему не включать противоположные сигналы, то получим систему ортогональных
сигналов, которые используются в качестве адресов абонентов в системах
множественного доступа с кодовым разделением
каналов. Применение ортогональных сигналов в качестве канальных позволяет разделять их в таких системах без взаимных помех [20].
Для кодов Рида-Маллера разработаны
достаточно эффективные алгоритмы порогового (мажоритарного) декодирования, изложенные в [30].
Здесь рассмотрим декодирование кодов
Рида-Маллера по принципу максимума правдоподобия. Для симметричного
канала это совпадает с декодированием по минимуму
расстояния между векторами, при котором в качестве оценки переданного вектора ![]() берется слово,
ближайшее к принятому вектору
берется слово,
ближайшее к принятому вектору ![]() .
.
Имея в виду преобразование (5.36), рассмотрим коэффициент
корреляции ![]() между
принятым вектором
между
принятым вектором ![]() и
функцией Уолша
и
функцией Уолша ![]() .
При
.
При ![]()
|
|
|
где ![]() и
и ![]() принимают значения
принимают значения ![]() .
.
Поскольку при совпадении знаков ![]() и
и ![]() их
произведение равно 1, а при несовпадении – (–1), то
их
произведение равно 1, а при несовпадении – (–1), то
|
|
|
где ![]() и
и ![]() – соответственно числа
совпадающих и несовпадающих символов в
– соответственно числа
совпадающих и несовпадающих символов в ![]() и
и ![]() , а
, а ![]() . При
. При ![]() , очевидно, получим
, очевидно, получим
|
|
|
Таким образом, оптимальный алгоритм декодирования предполагает следующие этапы:
1. Вычисление ![]() коэффициентов корреляции
коэффициентов корреляции ![]() между
между ![]() и функциями Уолша
и функциями Уолша ![]() ,
, ![]() .
.
2. Поиск максимального по абсолютной
величине коэффициента ![]() .
.
3. Принятие решения по правилу: ![]() , если
, если ![]() , и
, и ![]() , если
, если ![]() .
.
Следовательно, данная процедура представляет
собой многоканальный корреляционный прием. Ее сложность пропорциональна числу ![]() операций сложения и
вычитания. Разработаны быстрые алгоритмы декодирования кодов Рида-Маллера, по
своей сути аналогичные алгоритмам быстрого преобразования Фурье [30].
операций сложения и
вычитания. Разработаны быстрые алгоритмы декодирования кодов Рида-Маллера, по
своей сути аналогичные алгоритмам быстрого преобразования Фурье [30].
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Список сокращений
- Основные обозначения
- ВВЕДЕНИЕ
- Глава 1. Сообщения, сигналы и помехи, их математические модели
- 1.1. Основные понятия и определения
- 1.1.1. Сообщение, сигнал, модуляция
- 1.1.2. Основные параметры сигналов
- 1.2. Системы связи. Каналы связи
- 1.2.1. Структура канала электросвязи
- 1.2.2. Линия и сеть связи
- 1.2.3. Помехи и искажения в канале
- 1.2.4. Эталонная модель взаимодействия открытых систем
- 1.2.5. Модели каналов связи и их математическое описание
- 1.3. Способы описания сигналов и помех
- 1.3.1. Сигнал и его математическая модель
- 1.3.2. Энергетические характеристики детерминированного сигнала
- 1.4.2. Представление сигналов и помех рядом Фурье
- 1.4.3. Применение преобразования Фурье для непериодических сигналов
- 1.5. Теорема Котельникова
- 1.6. Пространство сигналов
- 1.6.1. Линейное пространство
- 1.6.2. Представление сигнала в многомерном пространстве
- 1.7. Сигналы как случайные процессы
- 1.7.1. Характеристики случайного процесса
- 1.7.2. Флуктуационный шум
- 1.8. Комплексное представление сигналов и помех
- 1.8.1. Понятие аналитического сигнала
- 1.8.2. Огибающая, мгновенная фаза и мгновенная частота узкополосного случайного процесса
- Контрольные вопросы
- Глава 2. Методы формирования и преобразования сигналов
- 2.1. Модуляция сигналов
- 2.1.1. Амплитудная модуляция гармонической несущей
- 2.1.2. Балансная и однополосная модуляция гармонической несущей
- 2.2. Методы угловой модуляции
- 2.2.1. Принципы частотной и фазовой (угловой) модуляции
- 2.2.2. Спектр сигналов угловой модуляции
- 2.3. Формирование и детектирование модулированных сигналов
- 2.3.1. Формирование и детектирование сигналов амплитудной и однополосной амплитудной модуляции
- 2.3.2. Формирование и детектирование сигналов угловой модуляции
- 2.4. Манипуляция сигналов
- 2.4.1. Временные и спектральные характеристики амплитудно-манипулированных сигналов
- 2.4.2. Временные и спектральные характеристики частотно-манипулированных сигналов
- 2.4.3. Фазовая (относительно-фазовая) манипуляция сигналов
- 2.5. Системы связи с многопозиционной относительной фазовой манипуляцией
- 2.5.1. Принцип формирования сигнала с многократной относительной фазовой манипуляцией
- 2.5.2. Квадратурная относительно-фазовая манипуляция (КОФМ)
- 2.5.3. Принцип частотной модуляции с непрерывной фазой
- Контрольные вопросы
- Глава 3. Помехоустойчивость приема дискретных сообщений
- 3.1. Критерии качества и правила приема дискретных сообщений
- 3.1.1. Понятие о помехоустойчивости систем электрической связи
- 3.1.2. Задача оптимального приема
- 3.1.3. Вычисление вероятностей ошибок
- 3.2. Оптимальная демодуляция при когерентном приеме сигналов
- 3.2.1. Оптимальные алгоритмы приема при полностью известных сигналах
- 3.2.2. Реализация алгоритмов оптимального когерентного приема
- 3.3. Помехоустойчивость приема сигналов с известными параметрами
- 3.4. Прием сигналов с неопределенной фазой
- 3.4.1. Оптимальный некогерентный прием дискретных сигналов
- 3.4.2. Помехоустойчивость оптимального некогерентного приема
- 3.5. Подоптимальные методы приема
- 3.5.1. Причины применения неоптимальных методов приема
- 3.5.2. Квазиоптимальные методы приема
- Контрольные вопросы
- Глава 4. Теория передачи информации
- 4.1. Информационные характеристики источника сообщений
- 4.1.1. Количественное определение информации
- 4.1.2. Энтропия и производительность дискретного источника сообщений
- 4.2. Пропускная способность дискретного канала
- 4.2.1. Количество информации переданной по дискретному каналу
- 4.2.2. Пропускная способность дискретного канала
- 4.2.3. Пропускная способность симметричного дискретного канала без памяти
- 4.3. Методы сжатия дискретных сообщений
- 4.3.1. Условия существования оптимального неравномерного кода
- 4.3.2. Прямая и обратная теоремы кодирования источника неравномерными кодами
- 4.3.3. Показатели эффективности сжатия
- 4.3.4. Кодирование источника дискретных сообщений методом Шеннона-Фано
- 4.3.5. Кодирование источника дискретных сообщений методом Хаффмена
- 4.4. Пропускная способность непрерывного канала
- 4.4.1. Постановка задачи передачи дискретных сообщений в непрерывном канале
- 4.4.2. Количество информации, переданной по непрерывному каналу
- 4.4.3. Пропускная способность непрерывного канала
- Контрольные вопросы
- Глава 5. Теория кодирования сообщений
- 5.1. Помехоустойчивое кодирование: блочные и непрерывные коды
- 5.1.1. Постановка задачи помехоустойчивого кодирования
- 5.1.2. Классификация кодов
- 5.1.3. Основные характеристики и свойства блочных кодов
- 5.2. Эффективность помехоустойчивого кодирования
- 5.2.1. Эффективность кода в режиме исправления ошибок
- 5.2.2. Эффективность кода в режиме обнаружения ошибок
- 5.2.3. Эффективность помехоустойчивых кодов
- 5.3. Математические основы теории помехоустойчивого кодирования
- 5.3.1. Краткие сведения из теории чисел
- 5.3.2. Группы
- 5.3.3. Кольца и поля
- 5.3.4. Векторное пространство
- 5.3.5. Конечные поля
- 5.4. Линейные блочные коды
- 5.4.1. Система передачи дискретных сообщений
- 5.4.2. Параметры линейного кода
- 5.4.3. Полиномиальные циклические коды
- 5.4.4. Циклические коды и корни полиномов
- 5.4.5. Спектральное описание циклических кодов
- 5.4.6. Простейшие блочные линейные коды
- 5.5. Коды Боуза-Чоудхури-Хоквингема
- 5.5.1. Методы задания кодов БЧХ
- 5.5.2. Принципы декодирования кодов БЧХ
- 5.5.3. Методы реализации этапов декодирования кодов БЧХ
- 5.6. Коды Рида-Соломона
- 5.6.1. Основные определения
- 5.6.2. Обнаружение и исправление пакетов ошибок
- 5.7. Коды Рида-Маллера
- 5.7.1. Задание и декодирование кодов Рида-Маллера
- 5.7.2. Симплексные коды и m-последовательности
- 5.7.3. Связь между блочными кодами
- 5.8. Сверточные коды
- 5.8.1. Основные параметры
- 5.8.2. Способы задания сверточного кода
- 5.8.3. Алгоритм декодирования Витерби
- 5.9. Помехоустойчивость систем передачи дискретных сообщений
- 5.9.1. Две процедуры приема сигналов
- 5.9.2. Помехоустойчивость систем передачи информации при оптимальной процедуре приема
- 5.9.3. Помехоустойчивость систем передачи информации при посимвольном приеме сигналов
- Контрольные вопросы
- Глава 6. Сигналы с импульсной модуляцией
- 6.1. Методы импульсной модуляции
- 6.1.1. Импульсные методы передачи непрерывных сигналов
- 6.1.2. Спектральные характеристики импульсных методов модуляции
- 6.2. Помехоустойчивость непрерывных каналов связи с импульсной модуляцией
- 6.2.1. Помехоустойчивость систем передачи с импульсными методами модуляции
- 6.3. Цифровые методы передачи непрерывных сообщений
- 6.3.1. Передача сигналов с импульсно-кодовой модуляцией
- 6.3.2. Передача сигналов с дельта модуляцией
- 6.3.3. Квантование сигналов в системах с ИКМ и ДМ
- Контрольные вопросы
- Глава 7. Методы приема сигналов в сложных условиях
- 7.1. Прием сигналов в каналах с замираниями
- 7.1.1. Сущность замираний и их классификация
- 7.1.2. Принципы разнесенного приема сигналов
- 7.2. Методы борьбы с замираниями сигналов
- 7.2.1. Методы борьбы с замираниями в аналоговых системах связи
- 7.2.2. Методы борьбы с замираниями в цифровых системах связи
- 7.3. Методы борьбы с межсимвольной интерференцией
- 7.3.1. Причины возникновения и сущность межсимвольной интерференции
- 7.3.2. Обработка сигналов в каналах с межсимвольной интерференцией
- 7.3.3. Помехоустойчивость в каналах с межсимвольной интерференцией
- 7.4. Прием дискретных сообщений в каналах с сосредоточенными по спектру и импульсными помехами
- 7.4.1. Общая характеристика сосредоточенных по спектру и импульсных помех
- 7.4.2. Борьба с сосредоточенными и импульсными помехами
- 7.5. Компенсация помех и искажений в канале
- 7.5.1. Принцип работы радиолинии с ФМ ПСС (ФМ ШПС)
- 7.5.2. Помехоустойчивость радиолинии с ФМ ПСС
- 7.5.3. Принципы работы радиолиний с ППРЧ
- 7.5.4. Помехоустойчивость радиолиний с ППРЧ
- Контрольные вопросы
- Глава 8. Многоканальная связь и распределение информации
- 8.1. Методы распределения ресурса общего канала
- 8.1.1. Классификация систем передачи информации, использующих единый ресурс
- 8.1.2. Постановка задачи объединения и разделения сигналов
- 8.1.3. Энергетическая и спектральная цена уплотнения
- 8.2. Частотное разделение каналов
- 8.2.1. Принцип частотного объединения и разделения каналов
- 8.2.2. Групповой сигнал, его структура и характеристики
- 8.3. Временное разделение каналов
- 8.3.1. Принцип временного разделения каналов
- 8.3.2. Характеристики группового сигнала систем с ВРК
- 8.4. Разделение сигналов по форме
- Контрольные вопросы
- Глава 9. Эффективность систем связи
- 9.1. Оценка эффективности систем связи
- 9.1.1. Подходы к оценке эффективности
- 9.1.2. Критерии эффективности
- 9.1.3. Эффективность аналоговых и цифровых систем
- 9.2. Выбор сигналов и помехоустойчивых кодов
- 9.2.1. Многопозиционные сигналы
- 9.2.2. Корректирующие коды
- 9.3. Оптимизация систем связи
- 9.3.1. Согласование методов модуляции и кодирования
- 9.3.2. Классификация сигнально – кодовых конструкций
- 9.4. Характеристики основных типов СКК
- 9.4.1. Согласование канала кодом Грея
- 9.4.2. Согласование на основе разбиения ансамбля на вложенные подансамбли
- 9.5. Алгоритмы цифровой обработки сигналов
- 9.5.1. Дискретные сигналы и их спектры
- 9.5.2. Алгоритмы дискретного и быстрого преобразований Фурье
- Контрольные вопросы
- Глава 10. Теоретико-информационные основы криптозащиты сообщений в телекоммуникационных системах
- 10.1. Классификация криптографических систем
- 10.1.2. Классификация криптографических систем защиты информации
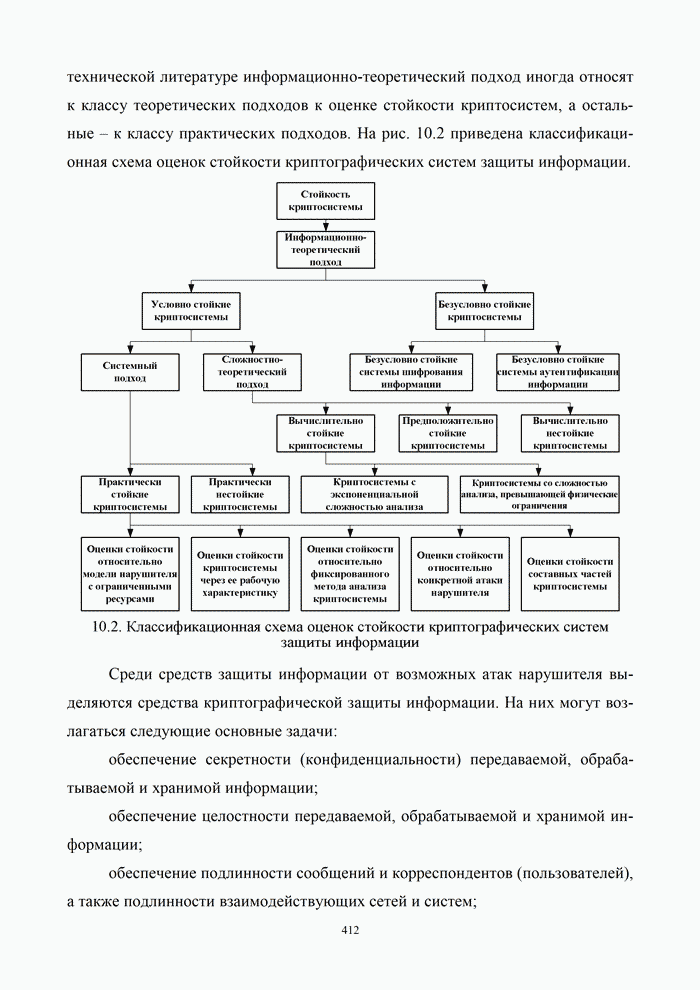
- 10.1.3. Оценка стойкости криптосистем
- 10.2. Функции, используемые в криптографических системах
- 10.2.1. Общее описание функций, используемых в криптографических системах
- 10.2.2. Однонаправленные функции
- 10.2.3. Криптографические хэш-функции
- 10.3. Модели криптографических систем
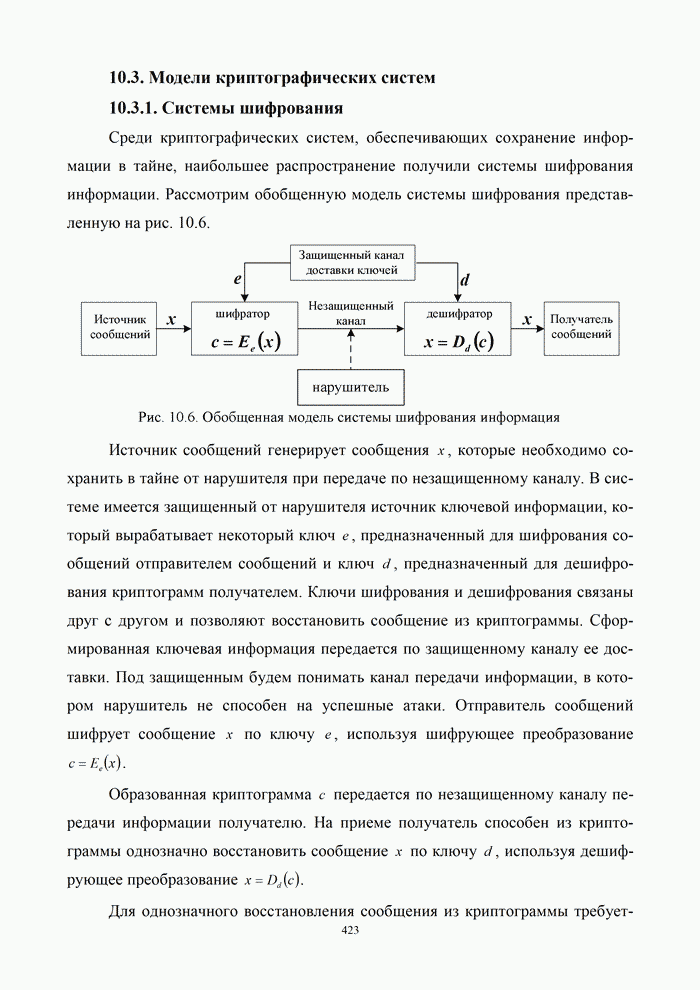
- 10.3.1. Системы шифрования
- 10.3.2. Традиционные симметричные криптосистемы
- 10.4. Алгоритмы криптографической защиты
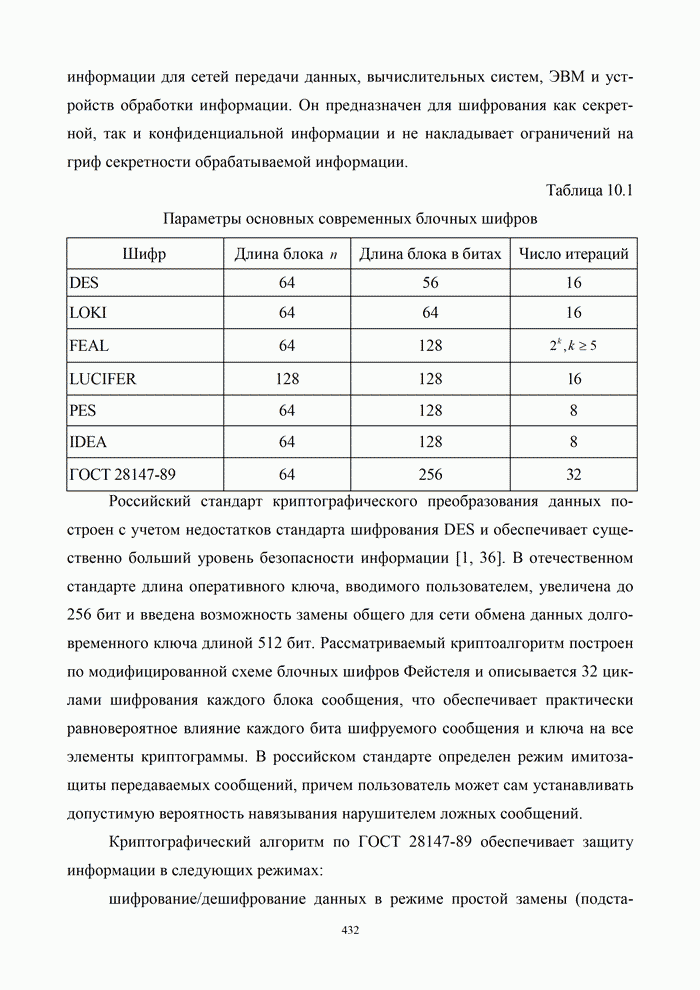
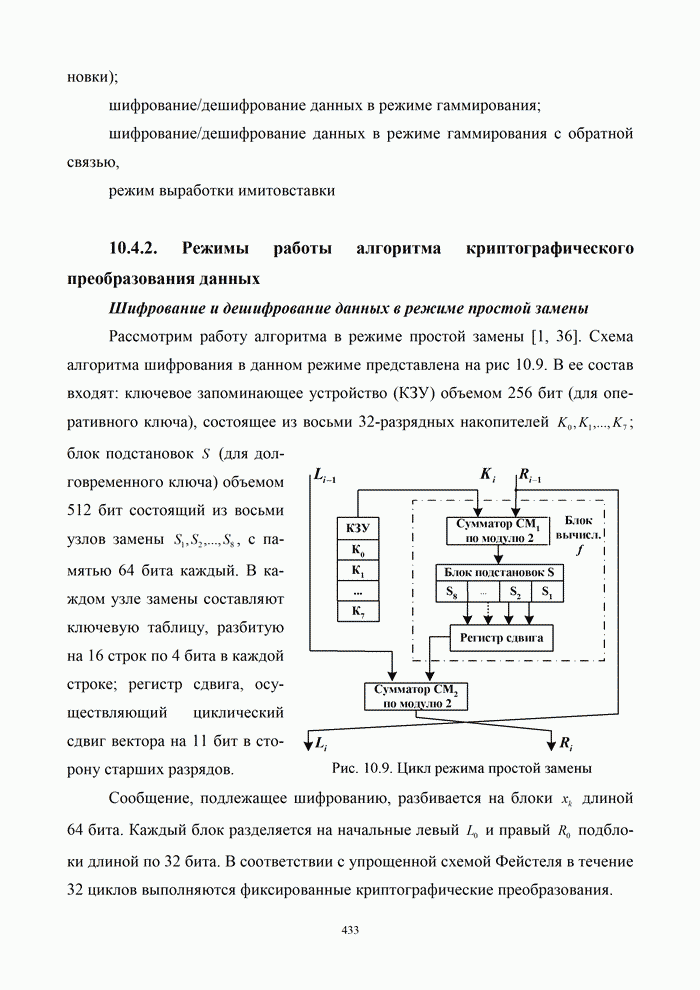
- 10.4.1. Алгоритм криптографической защиты информации согласно ГОСТ 28147-89
- Контрольные вопросы
- Заключение
- Список литературы



















































































































































































































































































































































































 .
.
 ,
,
