| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Условия равновесия сходящихся сил
Сходящиеся силы находятся в равновесии, если их равнодействующая равна нулю. В математической форме это условие выражается векторным равенством

называемым векторным условием равновесия сходящихся сил. Это условие можно выразить в геометрической форме (в терминах силового многоугольника) и в аналитической форме (через проекции сил на координатные оси).
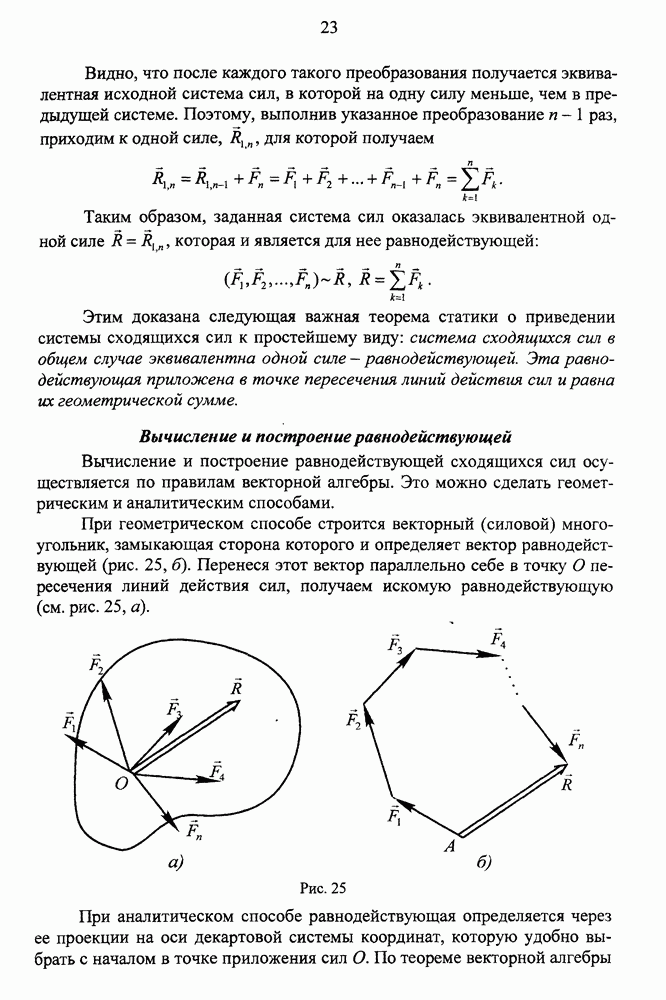
Применительно к силовому многоугольнику равенство (1) означает, что длина замыкающей стороны силового многоугольника равна нулю. Следовательно, в силовом многоугольнике конец вектора последней силы  совпадает с началом вектора первой силы
совпадает с началом вектора первой силы  . Такой силовой многоугольник называется замкнутым. Отсюда вытекает следующее геометрическое условие равновесия сходящихся сил: чтобы сходящиеся силы находилисъ в равновесии, необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил, был замкнутым.
. Такой силовой многоугольник называется замкнутым. Отсюда вытекает следующее геометрическое условие равновесия сходящихся сил: чтобы сходящиеся силы находилисъ в равновесии, необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил, был замкнутым.
Аналитические условия равновесия представляют собой покоординатную запись векторного равенства (1):

Из равенств (2) следует, что для равновесия сходящихся сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на координатные оси были равны нулю.
Если сходящиеся силы расположены в одной плоскости, то имеем плоскую систему сходящихся сил. Воспользуемся произволом в выборе координатных осей и выберем их так, чтобы координатные оси  оказались в одной плоскости с заданными силами. Тогда третье условие в (2) будет выполняться тождественно (всегда, при любых силах). Следовательно, для плоской системы сходящихся сил имеют место только два аналитических условия равновесия:
оказались в одной плоскости с заданными силами. Тогда третье условие в (2) будет выполняться тождественно (всегда, при любых силах). Следовательно, для плоской системы сходящихся сил имеют место только два аналитических условия равновесия:

Два условия равновесия плоской системы сходящихся сил остаются и при произвольном выборе осей. Кажущаяся возможность составить в этом случае также и третье условие оказывается несостоятельной: третье условие будет простым следствием первых двух, то есть не будет являться независимым.
Если среди сил, удовлетворяющих условиям равновесия, имеются неизвестные силы, тогда условия равновесия служат для определения этих сил и называются уравнениями равновесия. Такими неизвестными обычно являются реакции связей: заранее мы можем указать только направления реакций, а численные значения реакций определяются в результате составления и решения уравнений равновесия.
Пример 1.
Определить давление однородного шара на гладкую стенку и натяжение нити, если шар находится в равновесии (рис. 27, а). Вес шара Р=20 Н, угол наклона нити к вертикали  .
.
Мысленно освободим шар от наложенных связей. Для этого связи отбросим, а их действие на шар заменяем реакциями. Реакция стенки N направлена перпендикулярно стенке (от точки касания С к центру шара О), реакция нити Т - вдоль нити от точки А к точке В. Тем самым выявляется полная система сил, приложенных к покоящемуся шару. Это система сил, сходящихся в центре О шара, и состоящая из веса шара Р (активная сила), реакции стенки N и реакции нити Т (рис. 27, б). Реакции N и Т по величине неизвестны.
Для их определения следует воспользоваться условиями равновесия (в той или иной форме - геометрической, аналитической).

При геометрическом способе решения строится замкнутый многоугольник сил и используются соотношения школьной геометрии (теорема синусов, теорема косинусов, теорема Пифагора и т.д.). В данном случае это замкнутый силовой треугольник (рис. 27, в), из которого получаем:

или, после подстановки числовых значений:

При аналитическом способе решения выбирается подходящая система координат, и уравнения равновесия составляются в форме (2) или  . Выбирая оси, как показано на рис. 27, б, составляем для данной плоской системы сходящих сил два уравнения равновесия:
. Выбирая оси, как показано на рис. 27, б, составляем для данной плоской системы сходящих сил два уравнения равновесия:

Решая эти уравнения, приходим к тем же значениям для неизвестных сил:  ,
,  .
.
Отметим, что реакция N - это сила, с которой стенка действует на шар. Давление шара на стенку суть сила N, приложенная от шара к стенке. Она равна по модулю силе N, но направлена в противоположную сторону - от шара к стенке (показана штрихами на рис. 27, а).
Пример 2.
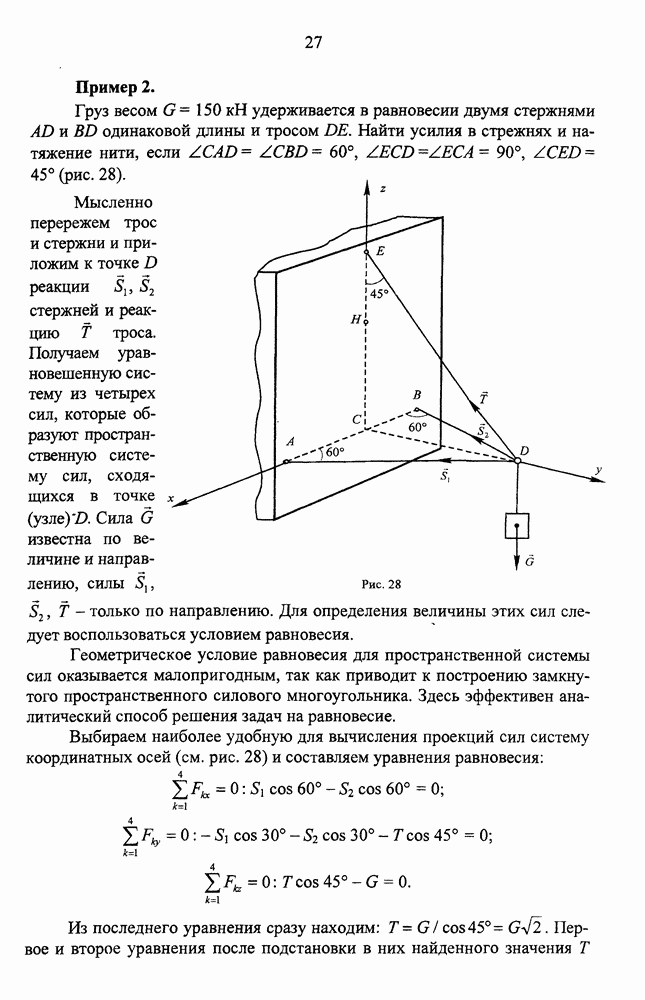
Груз весом  удерживается в равновесии двумя стержнями AD и BD одинаковой длины и тросом DE. Найти усилия в стрежнях и натяжение нити, если
удерживается в равновесии двумя стержнями AD и BD одинаковой длины и тросом DE. Найти усилия в стрежнях и натяжение нити, если  . (рис. 28).
. (рис. 28).
Мысленно перережем трос и стержни и приложим к точке D реакции  стержней и реакцию Т троса.
стержней и реакцию Т троса.
Получаем уравновешенную систему из четырех сил, которые образуют пространственную систему сил, сходящихся в точке  . Сила G известна по величине и направлению, силы
. Сила G известна по величине и направлению, силы  - только по направлению. Для определения величины этих сил следует воспользоваться условием равновесия.
- только по направлению. Для определения величины этих сил следует воспользоваться условием равновесия.
Геометрическое условие равновесия для пространственной системы сил оказывается малопригодным, так как приводит к построению замкнутого пространственного силового многоугольника. Здесь эффективен аналитический способ решения задач на равновесие.
Выбираем наиболее удобную для вычисления проекций сил систему координатных осей (см. рис. 28) и составляем уравнения равновесия;

Из последнего уравнения сразу находим:  . Первое и второе уравнения после подстановки в них найденного значения Т образуют систему для определения неизвестных
. Первое и второе уравнения после подстановки в них найденного значения Т образуют систему для определения неизвестных  и
и  .
.

Рис. 28.
Выражая из первого уравнения неизвестное  и подставляя во второе уравнение, приходим к уравнению с одним неизвестным
и подставляя во второе уравнение, приходим к уравнению с одним неизвестным  :
:

Из него находим:

Теперь легко определяется и оставшееся неизвестное (52):

После подстановки значения  , находим численные значения реакций:
, находим численные значения реакций:  .
.
Отрицательные знаки у реакций  указывают на то, что эти силы имеют направления, противоположные указанным на рис. 28. Можно было бы сразу указать точное направление этих сил, так как видно, что стержни испытывают сжатие. Мы не сделали этого только потому, что избранный вариант зрительно более удобен для вычисления проекций сил на оси.
указывают на то, что эти силы имеют направления, противоположные указанным на рис. 28. Можно было бы сразу указать точное направление этих сил, так как видно, что стержни испытывают сжатие. Мы не сделали этого только потому, что избранный вариант зрительно более удобен для вычисления проекций сил на оси.
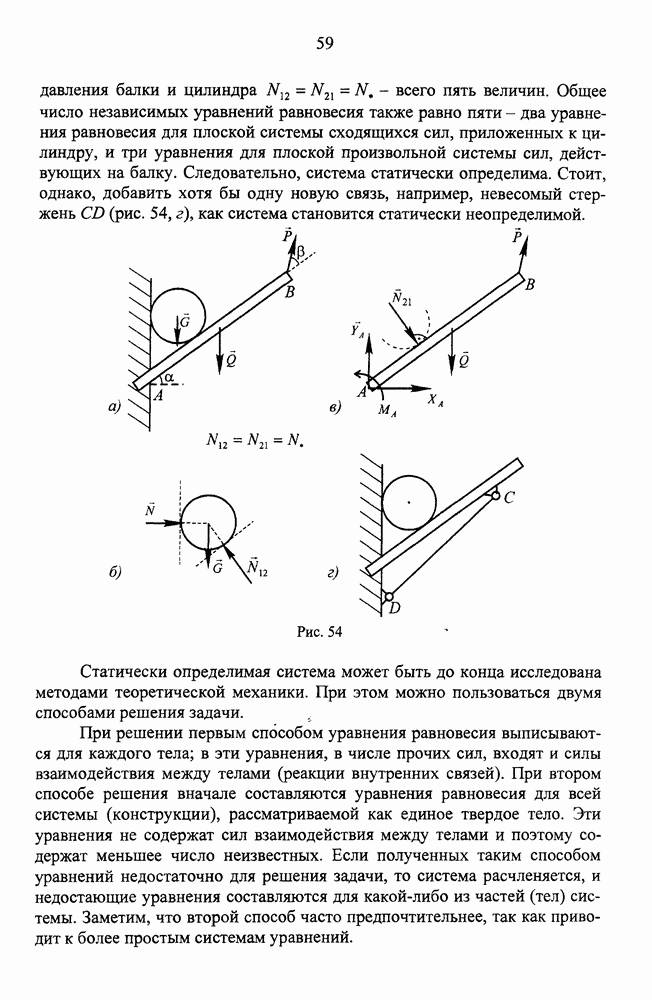
Представим себе, что груз G в приведенном примере поддерживался бы еще одной или несколькими связями - еще одним стержнем (например, вдоль  ), еще одним тросом (например, протянутым из точки D в точку Н). Тогда в уравнения равновесия вошли бы и реакции этих дополнительных связей, и мы имели бы не три, а четыре, пять и более неизвестных. Однако число уравнений равновесия остается при этом неизменным - три независимых уравнения для пространственной системы сходящихся сил и два - для плоской. Следовательно, не всякая задача на равновесие может быть решена при помощи уравнений статики. В статике могут быть однозначно решены лишь задачи, в которых количество неизвестных совпадает с числом независимых уравнений равновесия. Такие задачи называются статически определенными. Если количество неизвестных превышает число независимых уравнений статики, то задача не может быть однозначно решена методами статики и называется статически неопределенной. Методы решения статически неопределенных задач рассматриваются в курсе сопротивления материалов.
), еще одним тросом (например, протянутым из точки D в точку Н). Тогда в уравнения равновесия вошли бы и реакции этих дополнительных связей, и мы имели бы не три, а четыре, пять и более неизвестных. Однако число уравнений равновесия остается при этом неизменным - три независимых уравнения для пространственной системы сходящихся сил и два - для плоской. Следовательно, не всякая задача на равновесие может быть решена при помощи уравнений статики. В статике могут быть однозначно решены лишь задачи, в которых количество неизвестных совпадает с числом независимых уравнений равновесия. Такие задачи называются статически определенными. Если количество неизвестных превышает число независимых уравнений статики, то задача не может быть однозначно решена методами статики и называется статически неопределенной. Методы решения статически неопределенных задач рассматриваются в курсе сопротивления материалов.
В заключение раздела о сходящихся силах приведем две теоремы, весьма полезные при решении задач.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ. ПРЕДМЕТ И ОСНОВНЫЕ ПОНЯТИЯ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ
- СТАТИКА. ЛЕКЦИЯ 1. ЗАДАЧИ СТАТИКИ, АКСИОМЫ СТАТИКИ. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
- Момент силы относительно точки
- Алгебраический момент силы
- Основные типы связей и их реакции
- Упражнения
- ЛЕКЦИЯ 2. СХОДЯЩИЕСЯ СИЛЫ И ПАРЫ СИЛ
- Сходящиеся силы. Приведение сходящихся сил к простейшему виду
- Вычисление и построение равнодействующей
- Условия равновесия сходящихся сил
- Теорема о трех силах
- Теорема Вариньона
- Пара сил и ее момент
- Приведение системы пар сил к простейшему виду или сложение пар сил
- Упражнения
- ЛЕКЦИЯ 3. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ
- Момент силы относительно оси
- Аналитический способ вычисления момента
- Геометрический способ вычисления момента
- Преобразование пространственной произвольной системы сил
- Приведение пространственной произвольной системы сил к данному центру. Главный вектор и главный момент. Основная теорема статики
- Вычисление и построение главного вектора и главного момента
- Перемена центра приведения
- ЛЕКЦИЯ 4. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ (продолжение). ЧАСТНЫЕ СЛУЧАИ СИСТЕМЫ СИЛ
- Случаи приведения к простейшему виду
- Условия (уравнения) равновесия пространственной произвольной системы сил
- Частные случаи системы сил
- Плоская система сил
- Система параллельных сил
- Равновесие системы тел
- Вопросы для самопроверки
- ЛЕКЦИЯ 5. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ И ЦЕНТР ТЯЖЕСТИ
- Центр параллельных сил
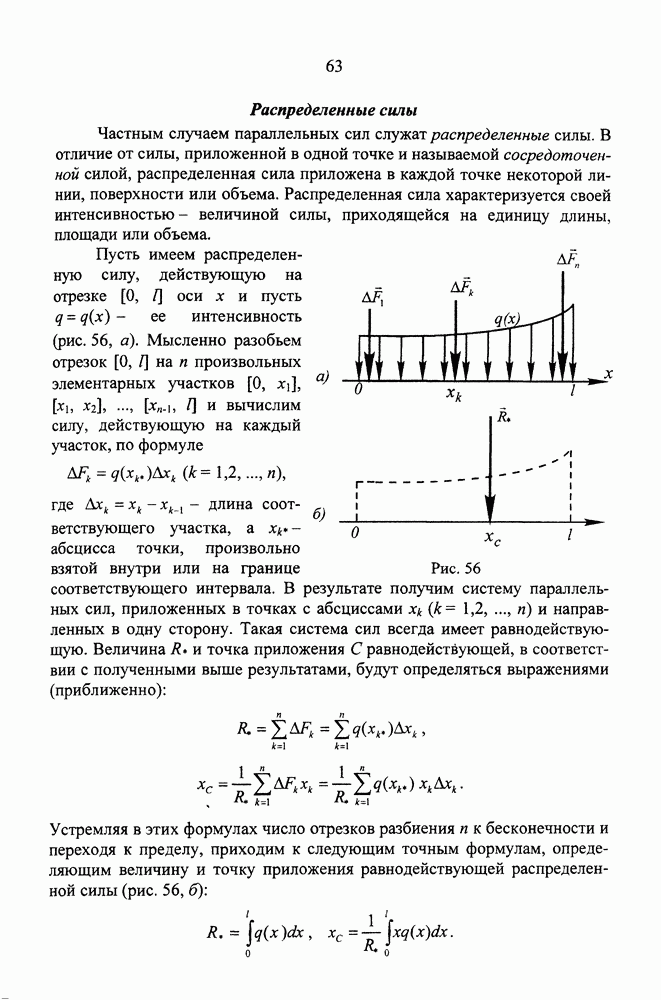
- Распределенные силы
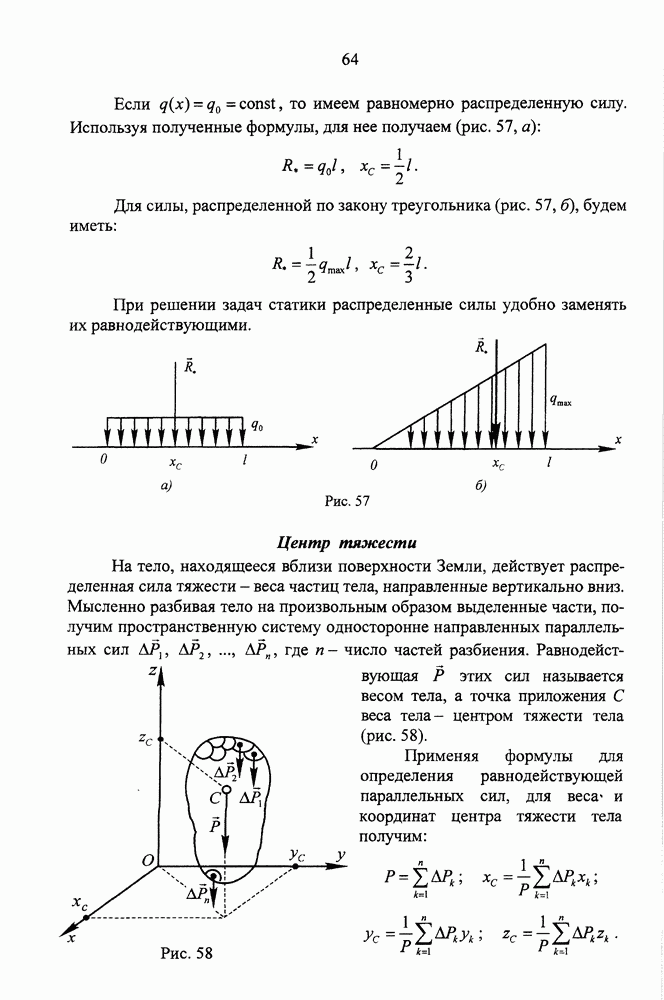
- Центр тяжести
- Интегральные формулы для координат центра тяжести
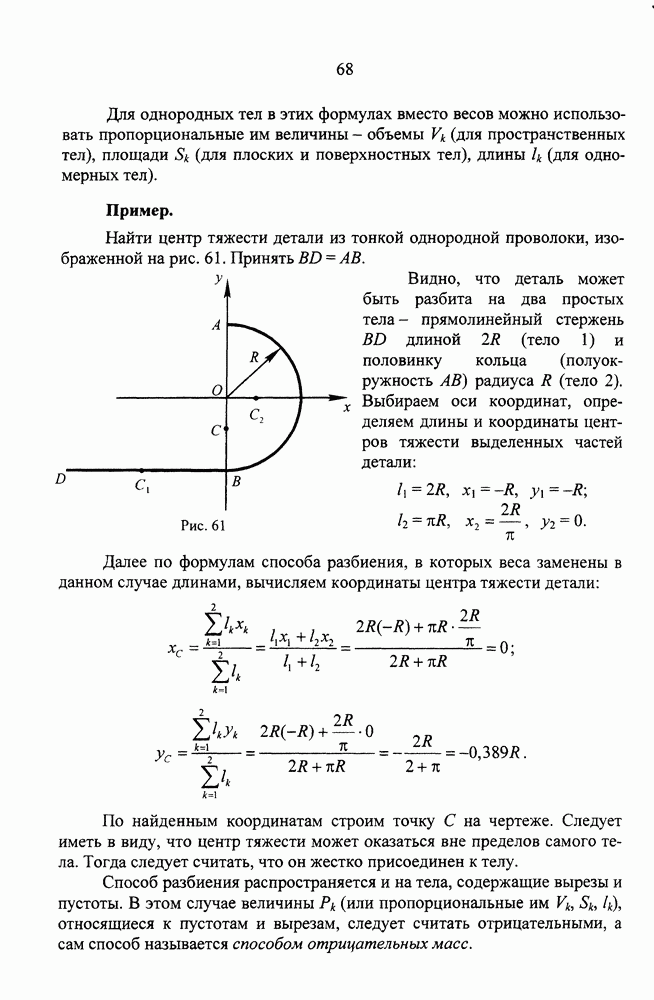
- Метод разбиения
- Вопросы для самопроверки
- ЛЕКЦИЯ 6. ТРЕНИЕ ТВЕРДЫХ ТЕЛ
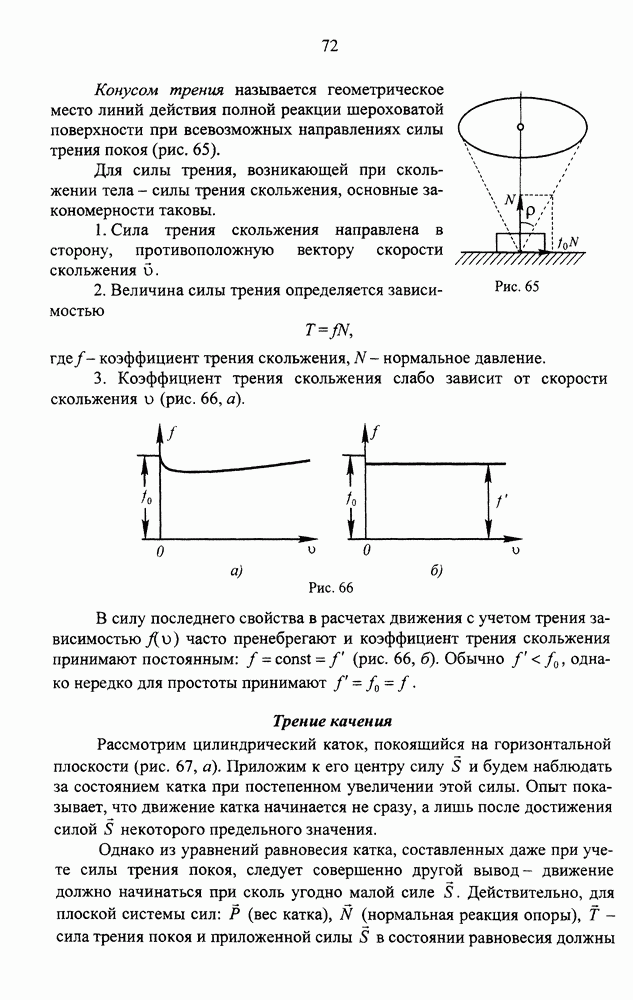
- Трение покоя и трение скольжения
- Трение качения
- Решение задач статики при учете сил трения
- Заклинивание
- Упражнения
- КИНЕМАТИКА
- ЛЕКЦИЯ 7. КИНЕМАТИКА ТОЧКИ
- Способы задания движения точки
- Определение траектории, скорости и ускорения точки при векторном способе задания движения
- Определение траектории, скорости и ускорения точки при координатном способе задания движения
- Определение скорости и ускорения точки при естественном способе задания движения
- Естественные координатные оси и их орты
- Определение скорости
- Определение ускорения
- Вопросы для самопроверки
- ЛЕКЦИЯ 8. ПРОСТЕЙШИЕ ДРИЖЕНИЯ ТВЕРДОГО ТЕЛА
- Поступательное движение
- Вращательное движение
- Уравнение вращательного движения. Угловая скорость и угловое ускорение тела
- Траектории, скорости и ускорения точек тела
- Векторы угловой скорости и углового ускорения тела
- Векторные формулы для линейной скорости, касательного и нормального ускорений точки тела
- Вопросы для самопроверки
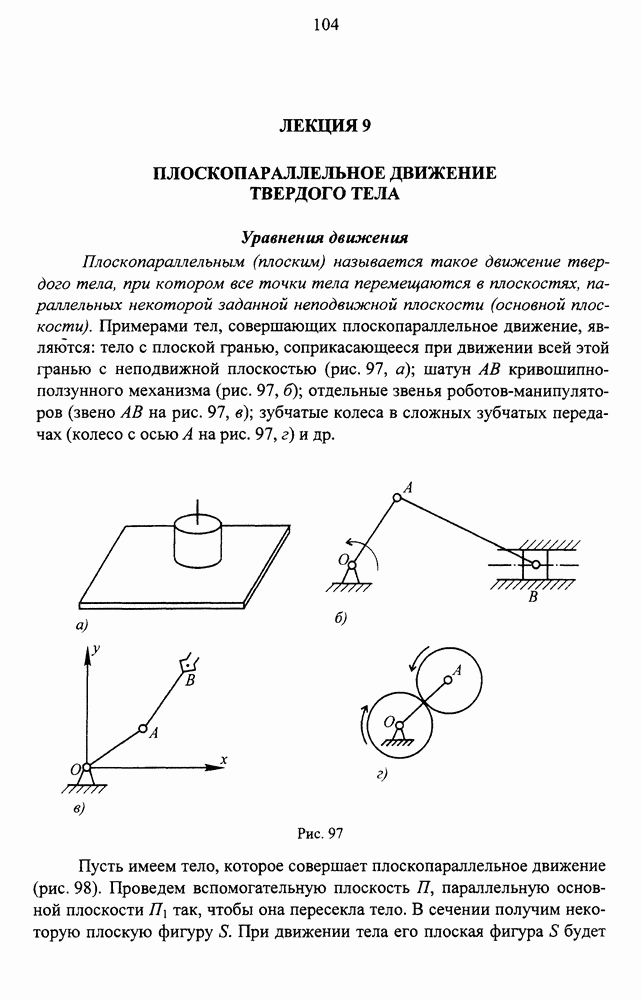
- ЛЕКЦИЯ 9. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- Уравнения движения
- Угловая скорость и угловое ускорение тела при плоскопараллельном движении
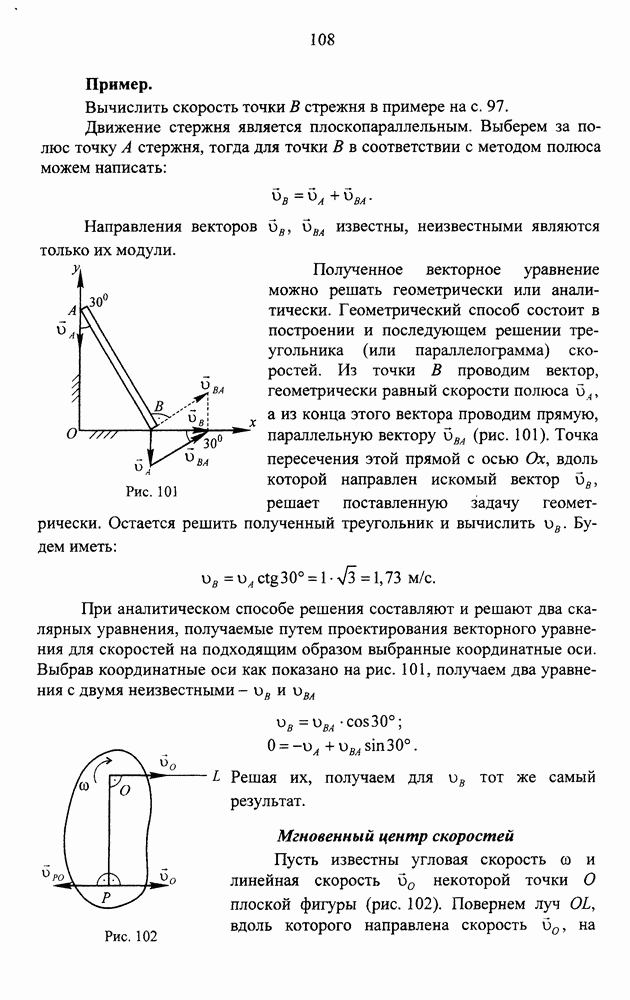
- Определение скоростей точек тела. Метод полюса
- Мгновенный центр скоростей
- Определение скоростей точек плоской фигуры через мгновенный центр скоростей
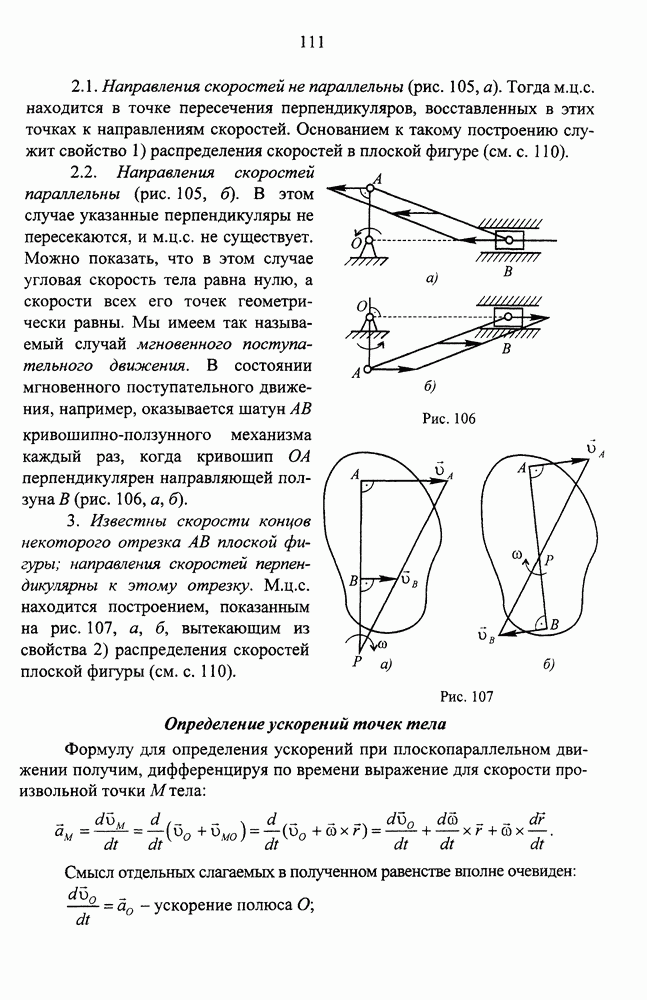
- Различные случаи определения положения мгновенного центра скоростей
- Определение ускорений точек тела
- Вопросы для самопроверки
- ЛЕКЦИЯ 10. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
- Теорема сложения скоростей
- Теорема сложения ускорений
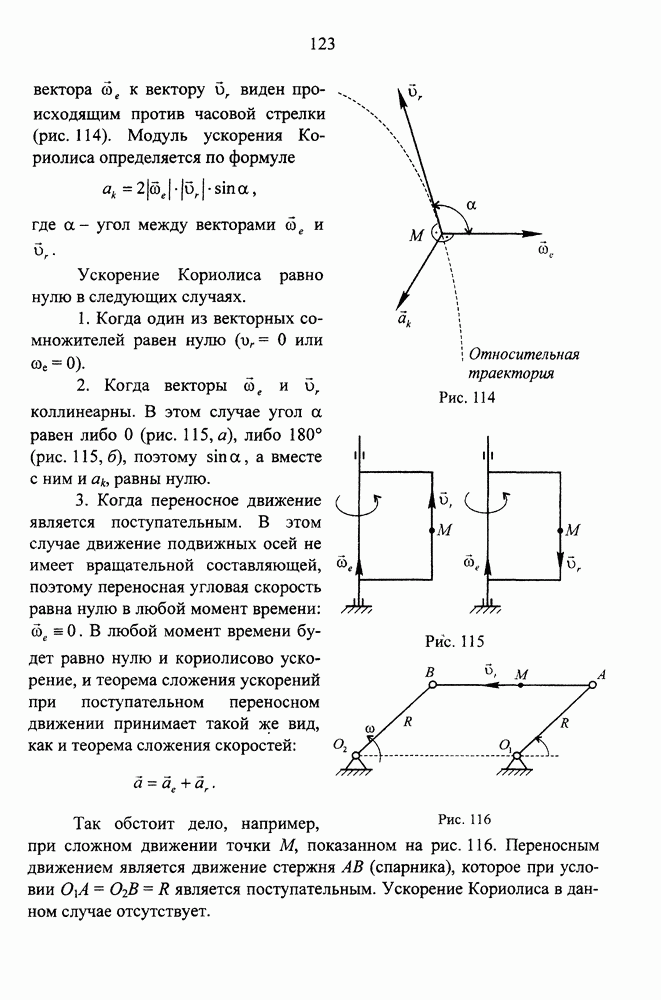
- Причины появления ускорения Кориолиса
- Вычисление и построение ускорения Кориолиса
- Вопросы для самопроверки
- ДОБАВЛЕНИЕ. КИНЕМАТИКА ПРОЦЕССА ФУГОВАНИЯ ДРЕВЕСИНЫ
- Схема и расчетная модель процесса фугования
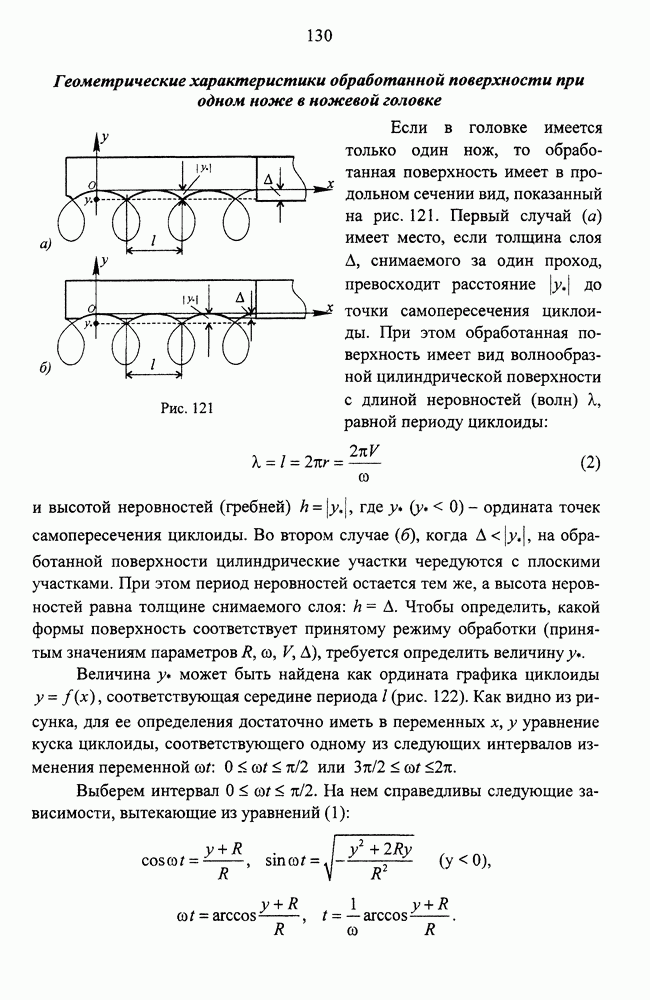
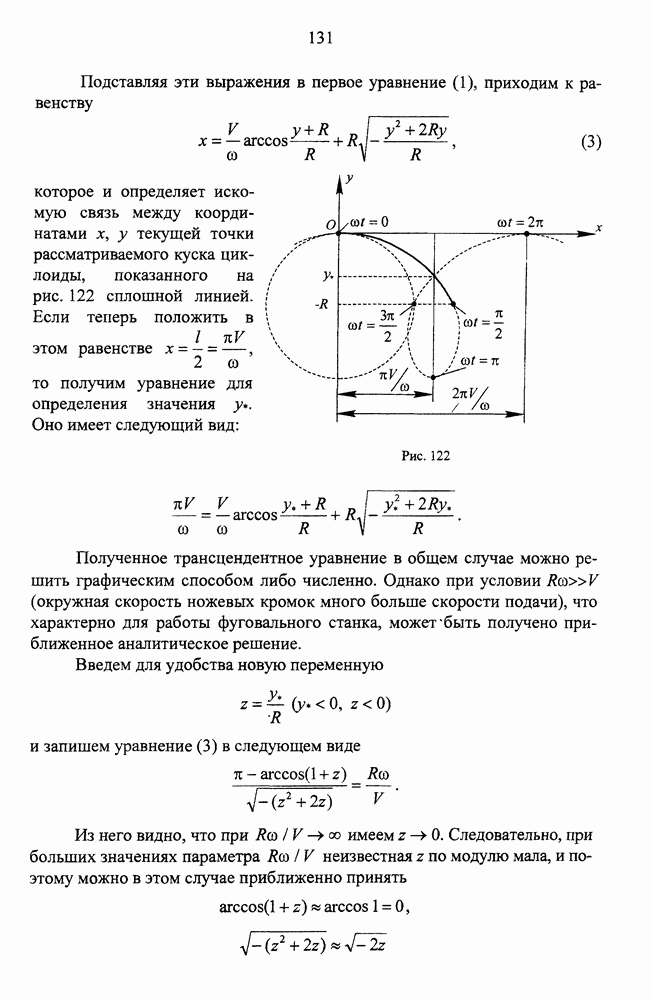
- Геометрические характеристики обработанной поверхности при одном ноже в ножевой головке
- Геометрические характеристики поверхности в случае многоножевой головки
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА