| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Геометрический способ вычисления момента
Пусть даны сила F и ось  (рис. 44). Проведем плоскость Н, перпендикулярную оси
(рис. 44). Проведем плоскость Н, перпендикулярную оси  , и отметим точку О пересечения оси с этой плоскостью. Из начала и конца вектора силы опустим перпендикуляры на плоскость Н. Вектор
, и отметим точку О пересечения оси с этой плоскостью. Из начала и конца вектора силы опустим перпендикуляры на плоскость Н. Вектор  называется проекцией силы F на плоскость Н. В отличие от проекции силы на ось, являющейся алгебраической величиной, проекция силы на плоскость является вектором, и с ней можно обращаться как с обычной силой — проектировать на оси, вычислять векторный и алгебраически моменты.
называется проекцией силы F на плоскость Н. В отличие от проекции силы на ось, являющейся алгебраической величиной, проекция силы на плоскость является вектором, и с ней можно обращаться как с обычной силой — проектировать на оси, вычислять векторный и алгебраически моменты.

Рис. 44.
Так, алгебраический момент проекции  относительно точки О имеет значение
относительно точки О имеет значение

где К - плечо этой проекции относительно точки О.
Изобразим момент силы F относительно точки О и заметим для дальнейшего, что для модуля момента справедливо равенство

устанавливающее, что модуль момента  равен удвоенной площади треугольника ОАВ (доказать самостоятельно). Вычисляя теперь момент силы относительно оси в соответствии с определением, последовательно находим
равен удвоенной площади треугольника ОАВ (доказать самостоятельно). Вычисляя теперь момент силы относительно оси в соответствии с определением, последовательно находим

В третьем из написанной цепочки равенств использована теорема геометрии о том, что площадь проекции плоской фигуры на некоторую плоскость (в нашем случае площадь треугольника ОАВ) равна площади проектируемой фигуры (треугольника ОАВ), умноженной на косинус угла между плоской фигурой и ее проекцией. Знак плюс соответствует острому углу между  и осью
и осью  , знак
, знак  тупому углу между ними (на рис. 44 изображен первый случай).
тупому углу между ними (на рис. 44 изображен первый случай).
Отбрасывая в полученной цепочке равенств промежуточные значения, получаем:

Этим равенством устанавливается следующее правило для вычисления момента силы относительно оси. Момент силы относительно оси равен алгебраическому моменту проекции этой силы на плоскость, перпендикулярную оси, вычисленному относительно точки пересечения оси с плоскостью. При этом правило для определения знака алгебраического момента остается прежним, если на силу  и точку О смотреть с положительной стороны оси
и точку О смотреть с положительной стороны оси  .
.
Из полученного правила ясно видны случаи, когда момент силы относительно оси равен нулю. Это имеет место в двух случаях:
1) когда сила параллельна оси (в этом случае имеем  );
);
2) когда сила пересекает ось (в этом случае  ).
).
Заметим, что данный (геометрический) способ вычисления момента силы относительно оси находит преимущественное использование при решении задач статики.
Пример.
Вычислить моменты относительно координатных осей силы F, действующей по диагонали грани DEKL параллелепипеда. Угол наклона силы к основанию параллелепипеда равен  , длины ребер составляют:
, длины ребер составляют:  (рис. 45).
(рис. 45).

Рис. 45.
Воспользуемся сначала более употребительным геометрическим способом. Для определения момента относительно осих силу F следует спроектировать на какую-либо плоскость, перпендикулярную оси  . На рис. 45 уже имеются две такие плоскости - плоскость
. На рис. 45 уже имеются две такие плоскости - плоскость  и плоскость грани ABDK. Выбираем эту последнюю за плоскость Н, находим проекцию
и плоскость грани ABDK. Выбираем эту последнюю за плоскость Н, находим проекцию  силы F на эту плоскость
силы F на эту плоскость  , отмечаем точку А пересечения выбранной плоскости с осью х. Далее, вычисляя алгебраический момент силы
, отмечаем точку А пересечения выбранной плоскости с осью х. Далее, вычисляя алгебраический момент силы  относительно точки А, находим момент силы F относительно оси
относительно точки А, находим момент силы F относительно оси  :
:

При вычислении момента относительно оси у замечаем, что сила F уже лежит в плоскости, перпендикулярной  и пересекающейся с этой осью в точке L. В этом случае проекция
и пересекающейся с этой осью в точке L. В этом случае проекция  равна самой силе F, и момент силы F относительно оси у совпадает с алгебраическим моментом силы F относительно точки
равна самой силе F, и момент силы F относительно оси у совпадает с алгебраическим моментом силы F относительно точки  :
:

Для определения момента относительно оси  в качестве плоскости Н удобно принять координатную плоскость
в качестве плоскости Н удобно принять координатную плоскость  . Проекция силы F на эту плоскость равна вектору
. Проекция силы F на эту плоскость равна вектору  с модулем
с модулем  . Вычисляя алгебраический момент этой проекции относительно точки О, находим:
. Вычисляя алгебраический момент этой проекции относительно точки О, находим:

При аналитическом способе вычисления осевых моментов прежде всего определяем проекции силы на координатные оси и проекции радиуса-вектора точки приложения силы (координаты точки К):

Применяя теперь аналитические выражения для моментов силы относительно координатных осей, находим:

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ. ПРЕДМЕТ И ОСНОВНЫЕ ПОНЯТИЯ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ
- СТАТИКА. ЛЕКЦИЯ 1. ЗАДАЧИ СТАТИКИ, АКСИОМЫ СТАТИКИ. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
- Момент силы относительно точки
- Алгебраический момент силы
- Основные типы связей и их реакции
- Упражнения
- ЛЕКЦИЯ 2. СХОДЯЩИЕСЯ СИЛЫ И ПАРЫ СИЛ
- Сходящиеся силы. Приведение сходящихся сил к простейшему виду
- Вычисление и построение равнодействующей
- Условия равновесия сходящихся сил
- Теорема о трех силах
- Теорема Вариньона
- Пара сил и ее момент
- Приведение системы пар сил к простейшему виду или сложение пар сил
- Упражнения
- ЛЕКЦИЯ 3. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ
- Момент силы относительно оси
- Аналитический способ вычисления момента
- Геометрический способ вычисления момента
- Преобразование пространственной произвольной системы сил
- Приведение пространственной произвольной системы сил к данному центру. Главный вектор и главный момент. Основная теорема статики
- Вычисление и построение главного вектора и главного момента
- Перемена центра приведения
- ЛЕКЦИЯ 4. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ (продолжение). ЧАСТНЫЕ СЛУЧАИ СИСТЕМЫ СИЛ
- Случаи приведения к простейшему виду
- Условия (уравнения) равновесия пространственной произвольной системы сил
- Частные случаи системы сил
- Плоская система сил
- Система параллельных сил
- Равновесие системы тел
- Вопросы для самопроверки
- ЛЕКЦИЯ 5. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ И ЦЕНТР ТЯЖЕСТИ
- Центр параллельных сил
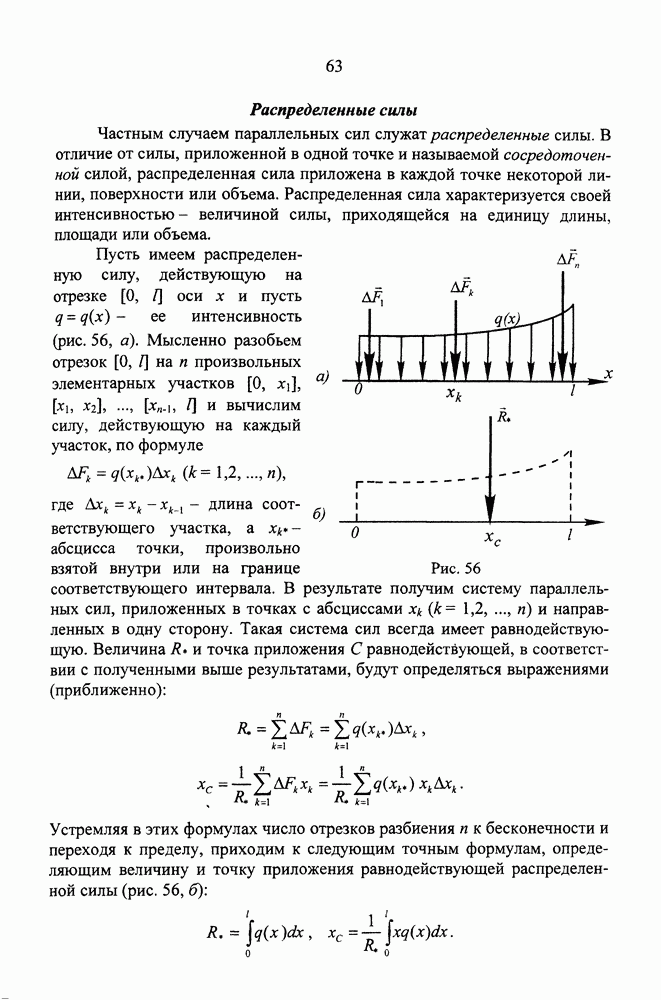
- Распределенные силы
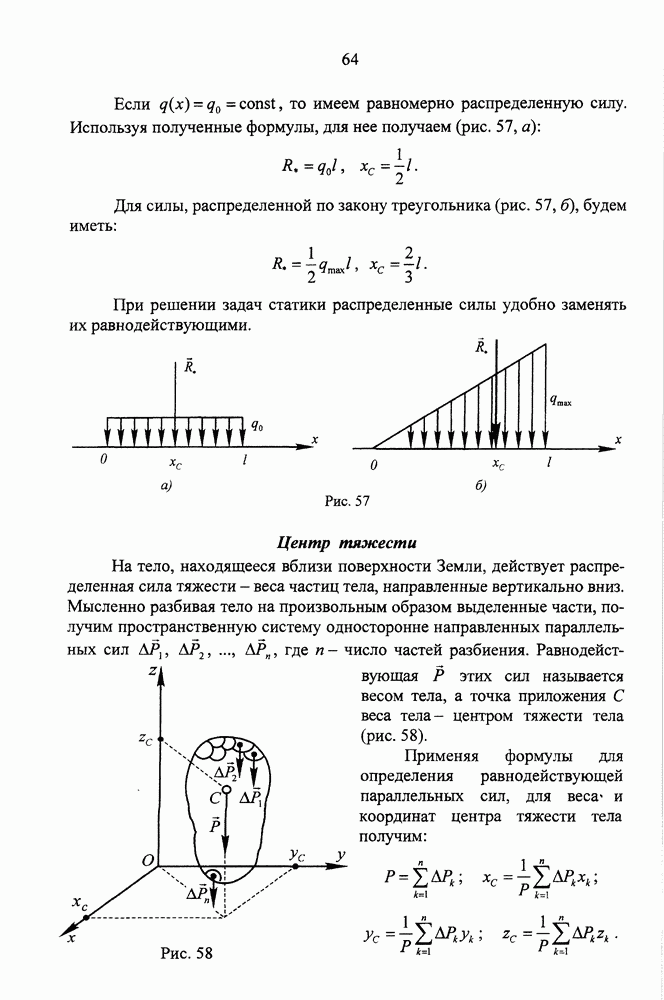
- Центр тяжести
- Интегральные формулы для координат центра тяжести
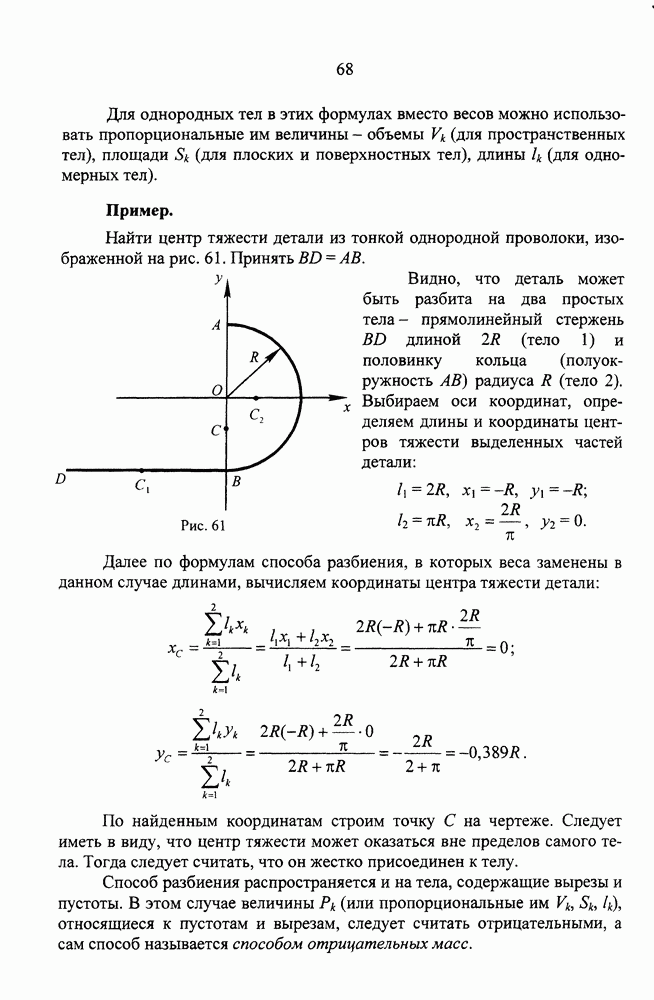
- Метод разбиения
- Вопросы для самопроверки
- ЛЕКЦИЯ 6. ТРЕНИЕ ТВЕРДЫХ ТЕЛ
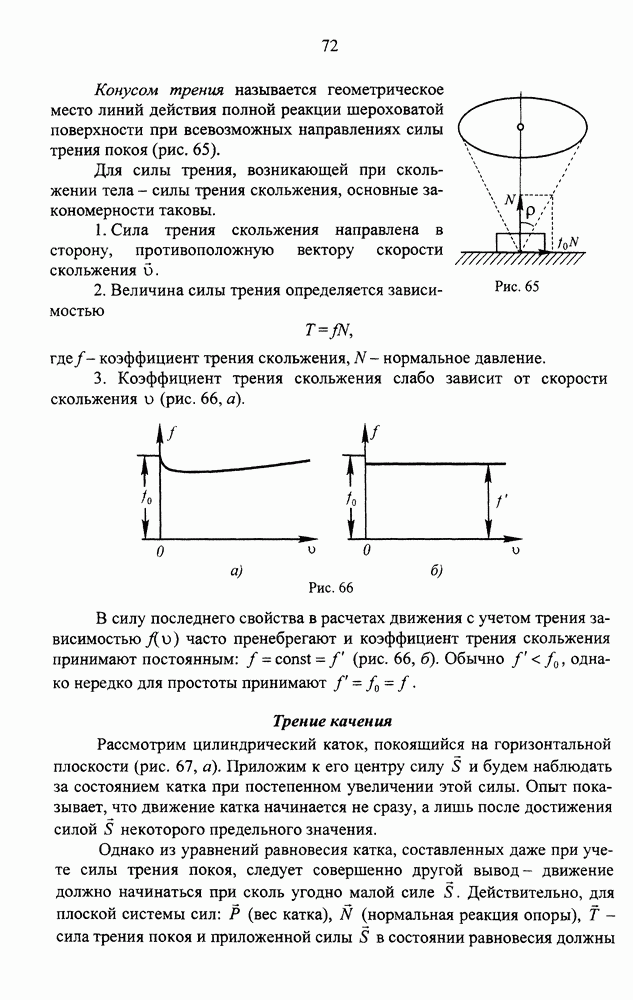
- Трение покоя и трение скольжения
- Трение качения
- Решение задач статики при учете сил трения
- Заклинивание
- Упражнения
- КИНЕМАТИКА
- ЛЕКЦИЯ 7. КИНЕМАТИКА ТОЧКИ
- Способы задания движения точки
- Определение траектории, скорости и ускорения точки при векторном способе задания движения
- Определение траектории, скорости и ускорения точки при координатном способе задания движения
- Определение скорости и ускорения точки при естественном способе задания движения
- Естественные координатные оси и их орты
- Определение скорости
- Определение ускорения
- Вопросы для самопроверки
- ЛЕКЦИЯ 8. ПРОСТЕЙШИЕ ДРИЖЕНИЯ ТВЕРДОГО ТЕЛА
- Поступательное движение
- Вращательное движение
- Уравнение вращательного движения. Угловая скорость и угловое ускорение тела
- Траектории, скорости и ускорения точек тела
- Векторы угловой скорости и углового ускорения тела
- Векторные формулы для линейной скорости, касательного и нормального ускорений точки тела
- Вопросы для самопроверки
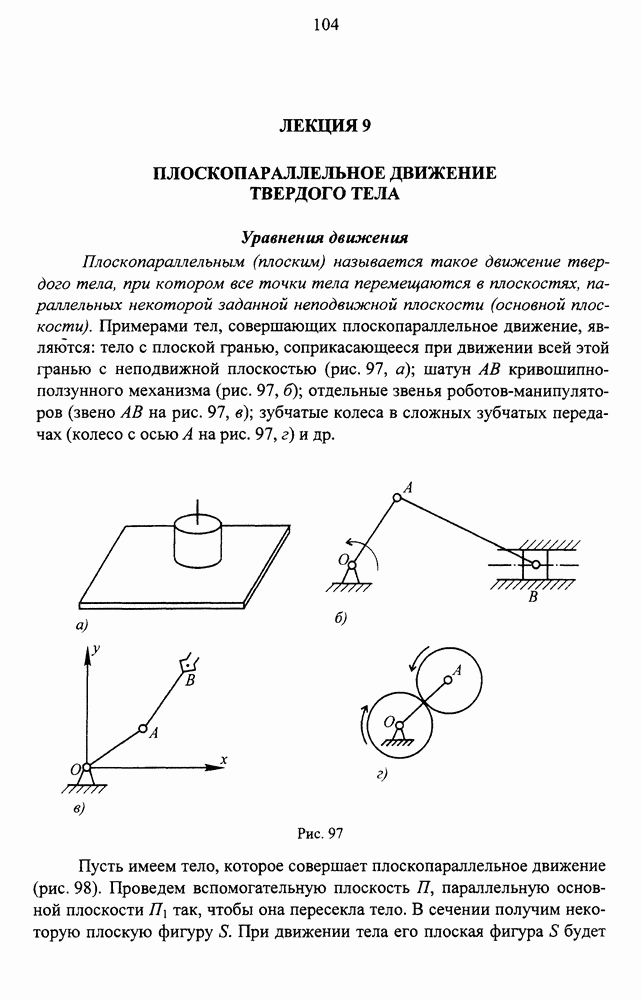
- ЛЕКЦИЯ 9. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- Уравнения движения
- Угловая скорость и угловое ускорение тела при плоскопараллельном движении
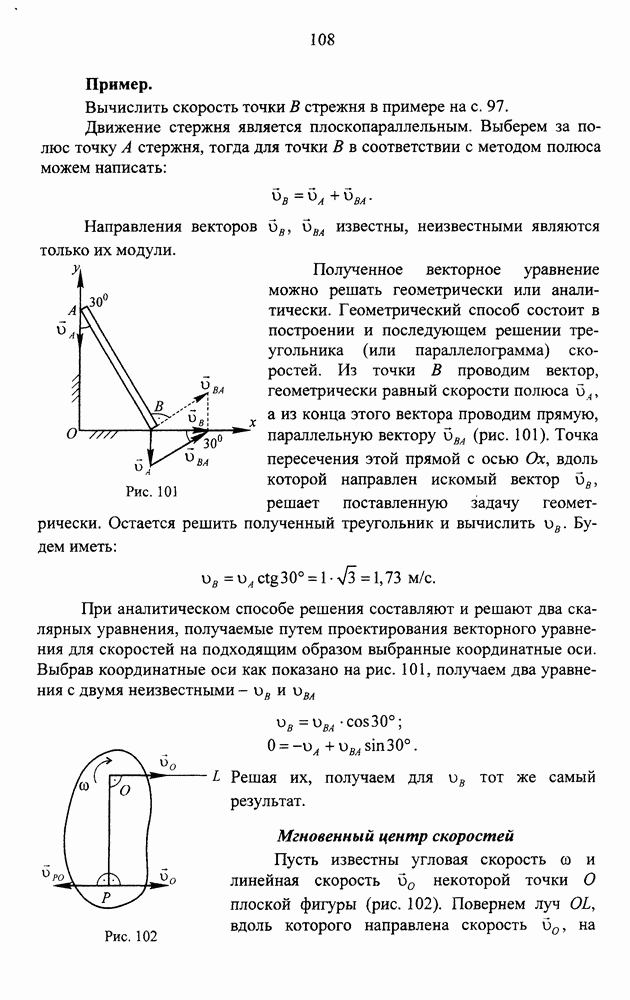
- Определение скоростей точек тела. Метод полюса
- Мгновенный центр скоростей
- Определение скоростей точек плоской фигуры через мгновенный центр скоростей
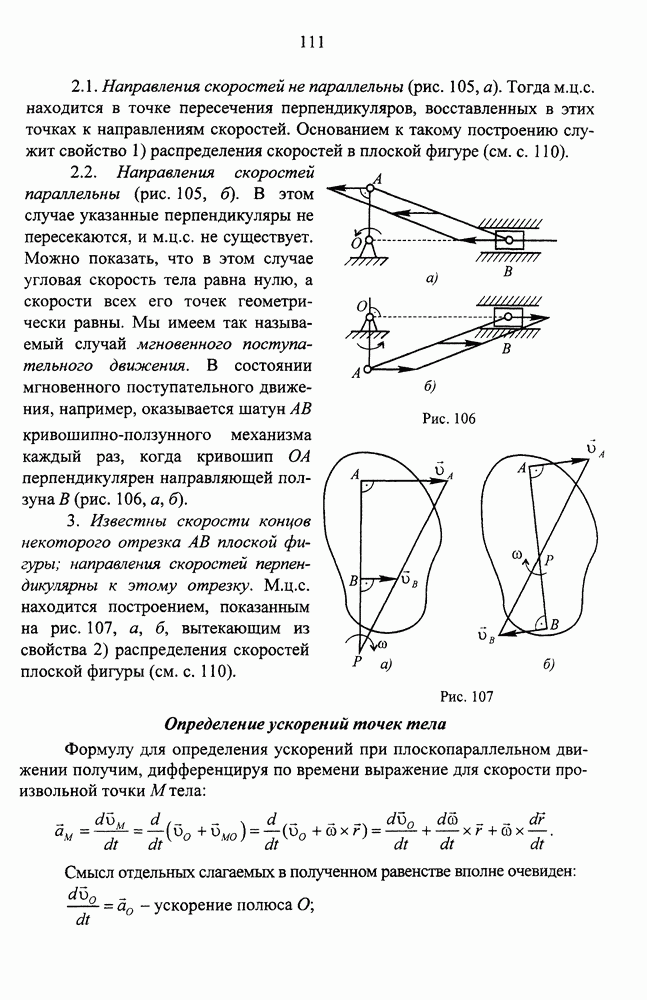
- Различные случаи определения положения мгновенного центра скоростей
- Определение ускорений точек тела
- Вопросы для самопроверки
- ЛЕКЦИЯ 10. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
- Теорема сложения скоростей
- Теорема сложения ускорений
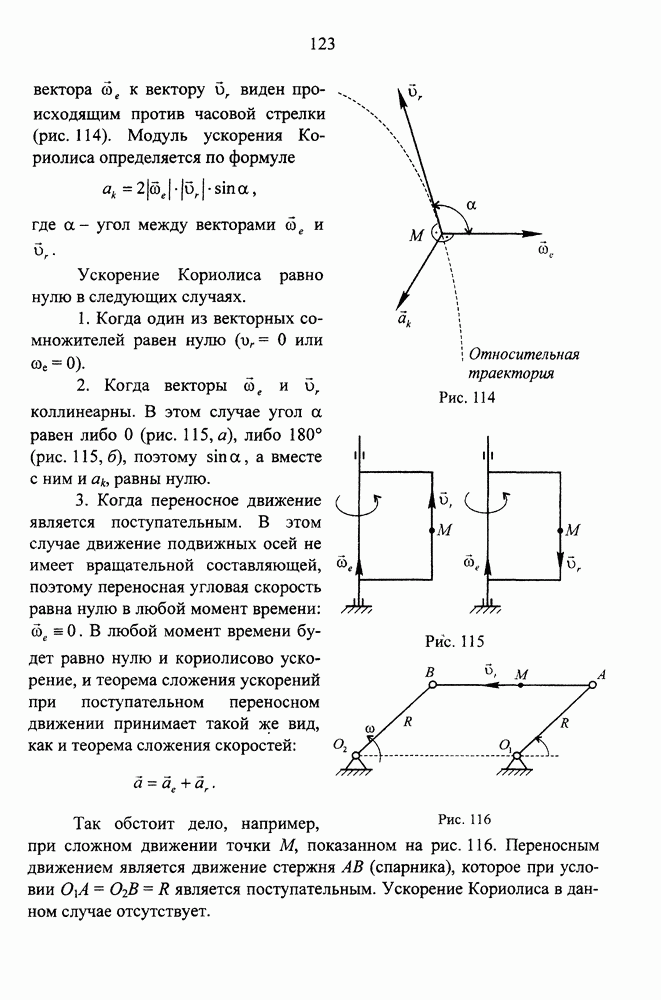
- Причины появления ускорения Кориолиса
- Вычисление и построение ускорения Кориолиса
- Вопросы для самопроверки
- ДОБАВЛЕНИЕ. КИНЕМАТИКА ПРОЦЕССА ФУГОВАНИЯ ДРЕВЕСИНЫ
- Схема и расчетная модель процесса фугования
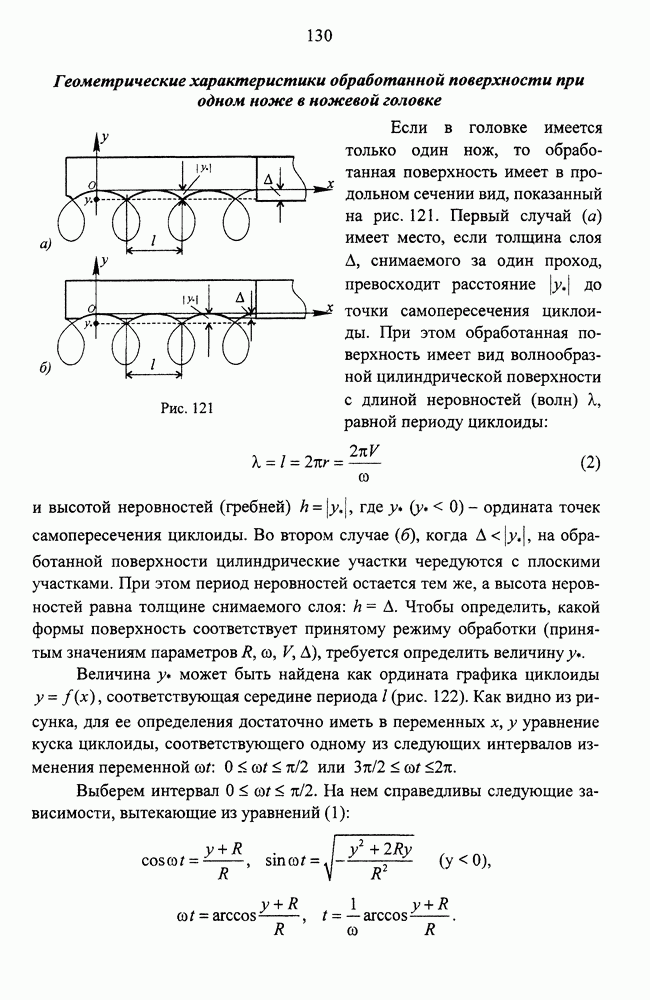
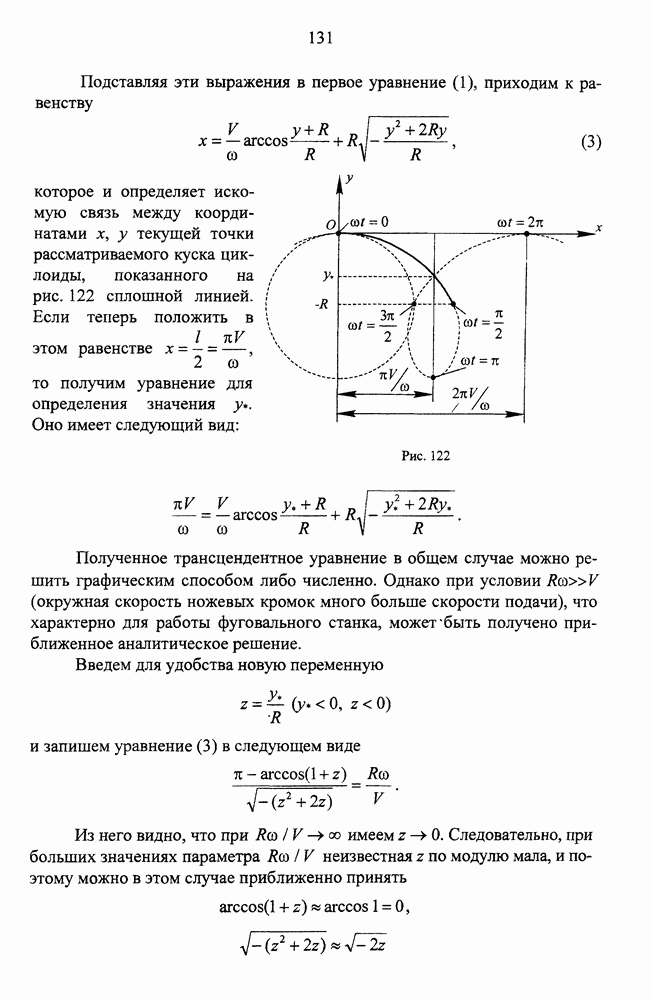
- Геометрические характеристики обработанной поверхности при одном ноже в ножевой головке
- Геометрические характеристики поверхности в случае многоножевой головки
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА