| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ЛЕКЦИЯ 4. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ (продолжение). ЧАСТНЫЕ СЛУЧАИ СИСТЕМЫ СИЛ
Случаи приведения к простейшему виду
Приведение к паре
Пусть в результате приведения сил  к центру О оказалось, что главный вектор равен нулю, а главный момент отличен от нуля:
к центру О оказалось, что главный вектор равен нулю, а главный момент отличен от нуля:  . Тогда в силу основной теоремы статики можем написать
. Тогда в силу основной теоремы статики можем написать

Это означает, что исходная система сил в этом случае эквивалентна паре сил с моментом  .
.
Момент пары не зависит от того, какая точка выбрана в качестве центра моментов при вычислении момента пары. Следовательно, в данном случае главный момент не должен зависеть от выбора центра приведения. Но именно к этому выводу и приводит соотношение

связывающее главные моменты относительно двух различных центров. При  добавочный член также равен нулю, и мы получаем
добавочный член также равен нулю, и мы получаем

Приведение к равнодействующей
Пусть теперь главный вектор не равен нулю, а главный момент равен нулю:  . В силу основной теоремы статики имеем
. В силу основной теоремы статики имеем

то есть система сил оказывается эквивалентной одной силе - главному вектору. Следовательно, в этом случае исходная система сил приводится к равнодействующей, и эта равнодействующая совпадает с главным вектором, приложенным в центре приведения:  .
.
Система сил приводится к равнодействующей и в том случае, когда главный вектор и главный момент оба не равны нулю, но взаимно перпендикулярны:  . Доказательство осуществляется при помощи следующей последовательности действий.
. Доказательство осуществляется при помощи следующей последовательности действий.
Через центр приведения О проводим плоскость, перпендикулярную главному моменту  (рис. 50, а). На рисунке эта плоскость совмещена с плоскостью чертежа, в ней же расположен главный вектор
(рис. 50, а). На рисунке эта плоскость совмещена с плоскостью чертежа, в ней же расположен главный вектор  . В этой плоскости строим пару с моментом
. В этой плоскости строим пару с моментом  , причем силы пары выберем равными по модулю главному вектору
, причем силы пары выберем равными по модулю главному вектору  ; тогда плечо пары будет равно
; тогда плечо пары будет равно  . Далее переместим пару в ее плоскости таким образом, чтобы одна из сил пары оказалась приложенной в центре приведения О противоположно главному
. Далее переместим пару в ее плоскости таким образом, чтобы одна из сил пары оказалась приложенной в центре приведения О противоположно главному  ; вторая сила пары будет приложена в точке С, отстоящей от центра О в нужную сторону, определяемую направлением
; вторая сила пары будет приложена в точке С, отстоящей от центра О в нужную сторону, определяемую направлением  , на расстоянии ОС, равном плечу пары h (рис. 50, б). Отбрасывая теперь уравновешенные силы R и —
, на расстоянии ОС, равном плечу пары h (рис. 50, б). Отбрасывая теперь уравновешенные силы R и —  , приложенные в точке О, приходим к одной силе
, приложенные в точке О, приходим к одной силе  , приложенной в точке С (рис. 50, в). Она и будет служить равнодействующей данной системы сил
, приложенной в точке С (рис. 50, в). Она и будет служить равнодействующей данной системы сил  .
.

Рис. 50.
Видно, что равйодействующая  по-прежнему равна главному вектору
по-прежнему равна главному вектору  , однако отличается от главного вектора своей точкой приложения. Если главный вектор приложен в центре приведения О, то равнодействующая
, однако отличается от главного вектора своей точкой приложения. Если главный вектор приложен в центре приведения О, то равнодействующая  - в точке С, положение которой требует специального определения. Геометрический способ нахождения точки С виден из проделанного выше построения.
- в точке С, положение которой требует специального определения. Геометрический способ нахождения точки С виден из проделанного выше построения.
Для момента равнодействующей относительно центра приведения О можно написать (см. рис. 50):

или, опуская промежуточные значения:

Если спроектировать это векторное равенство на какую-либо ось  , проходящую через точку О, получаем соответствующее равенство в проекциях:
, проходящую через точку О, получаем соответствующее равенство в проекциях:

Вспоминая, что проекция момента силы относительно точки на ось, проходящую через эту точку, является моментом силы относительно оси, перепишем этой равенство так:

Полученные равенства выражают теорему Вариньона в ее общем виде (в лекции 2 теорема была сформулирована только для сходящихся сил): если система сил имеет равнодействующую, то момент этой равнодействующей (относительно точки, относительно оси) равен сумме моментов всех заданных сил - составляющих (относительно той же точки, той же оси). Понятно, что в случае точки суммирование моментов векторное, в случае оси - алгебраическое.
Приведение к динаме
Динамой или динамическим винтом называется совокупность пары сил и силы, направленной перпендикулярно плоскости действия пары. Можно показать, что в общем случае приведения, когда  и
и  не перпендикулярен
не перпендикулярен  , исходная система сил эквивалентна некоторой динаме.
, исходная система сил эквивалентна некоторой динаме.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ. ПРЕДМЕТ И ОСНОВНЫЕ ПОНЯТИЯ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ
- СТАТИКА. ЛЕКЦИЯ 1. ЗАДАЧИ СТАТИКИ, АКСИОМЫ СТАТИКИ. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
- Момент силы относительно точки
- Алгебраический момент силы
- Основные типы связей и их реакции
- Упражнения
- ЛЕКЦИЯ 2. СХОДЯЩИЕСЯ СИЛЫ И ПАРЫ СИЛ
- Сходящиеся силы. Приведение сходящихся сил к простейшему виду
- Вычисление и построение равнодействующей
- Условия равновесия сходящихся сил
- Теорема о трех силах
- Теорема Вариньона
- Пара сил и ее момент
- Приведение системы пар сил к простейшему виду или сложение пар сил
- Упражнения
- ЛЕКЦИЯ 3. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ
- Момент силы относительно оси
- Аналитический способ вычисления момента
- Геометрический способ вычисления момента
- Преобразование пространственной произвольной системы сил
- Приведение пространственной произвольной системы сил к данному центру. Главный вектор и главный момент. Основная теорема статики
- Вычисление и построение главного вектора и главного момента
- Перемена центра приведения
- ЛЕКЦИЯ 4. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ (продолжение). ЧАСТНЫЕ СЛУЧАИ СИСТЕМЫ СИЛ
- Случаи приведения к простейшему виду
- Условия (уравнения) равновесия пространственной произвольной системы сил
- Частные случаи системы сил
- Плоская система сил
- Система параллельных сил
- Равновесие системы тел
- Вопросы для самопроверки
- ЛЕКЦИЯ 5. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ И ЦЕНТР ТЯЖЕСТИ
- Центр параллельных сил
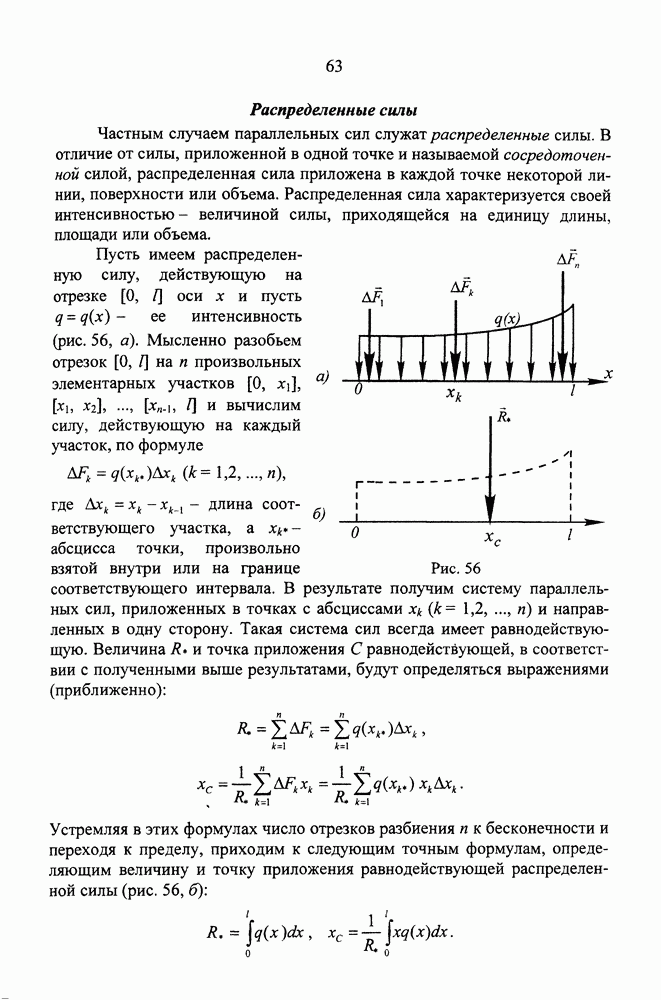
- Распределенные силы
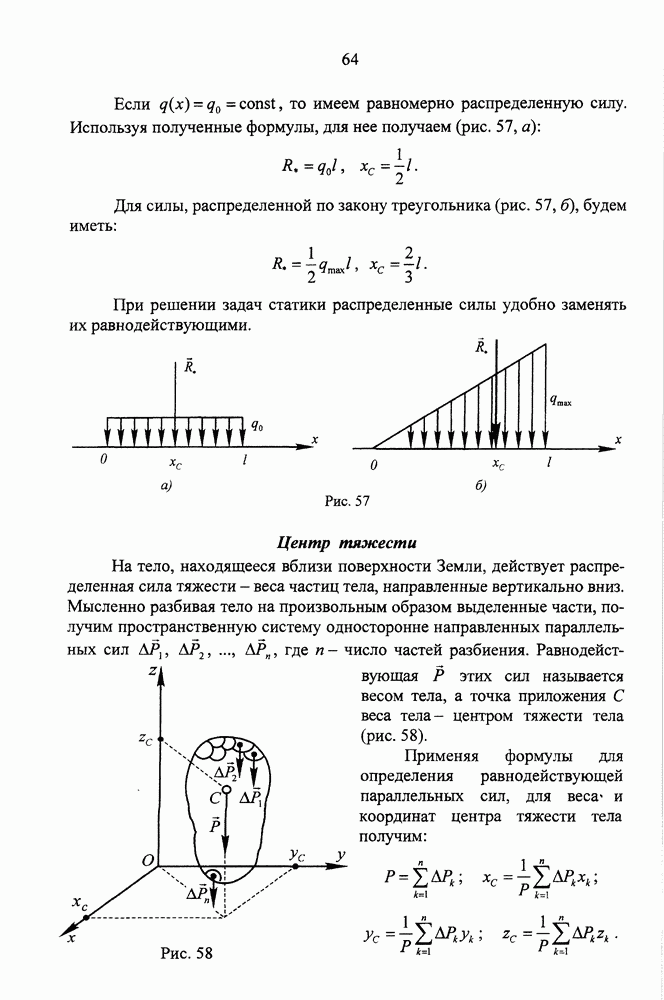
- Центр тяжести
- Интегральные формулы для координат центра тяжести
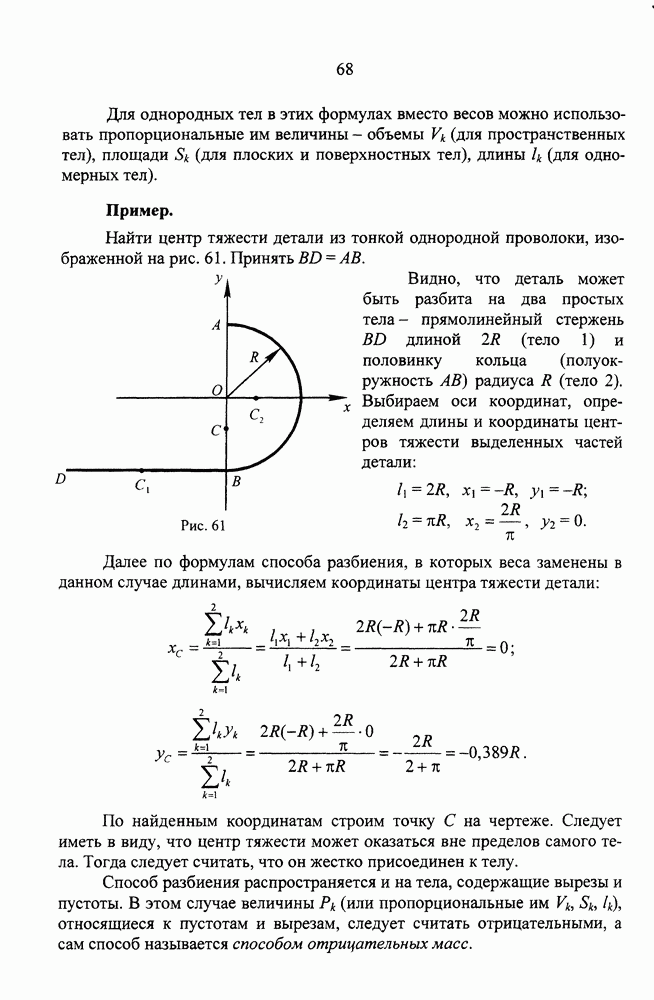
- Метод разбиения
- Вопросы для самопроверки
- ЛЕКЦИЯ 6. ТРЕНИЕ ТВЕРДЫХ ТЕЛ
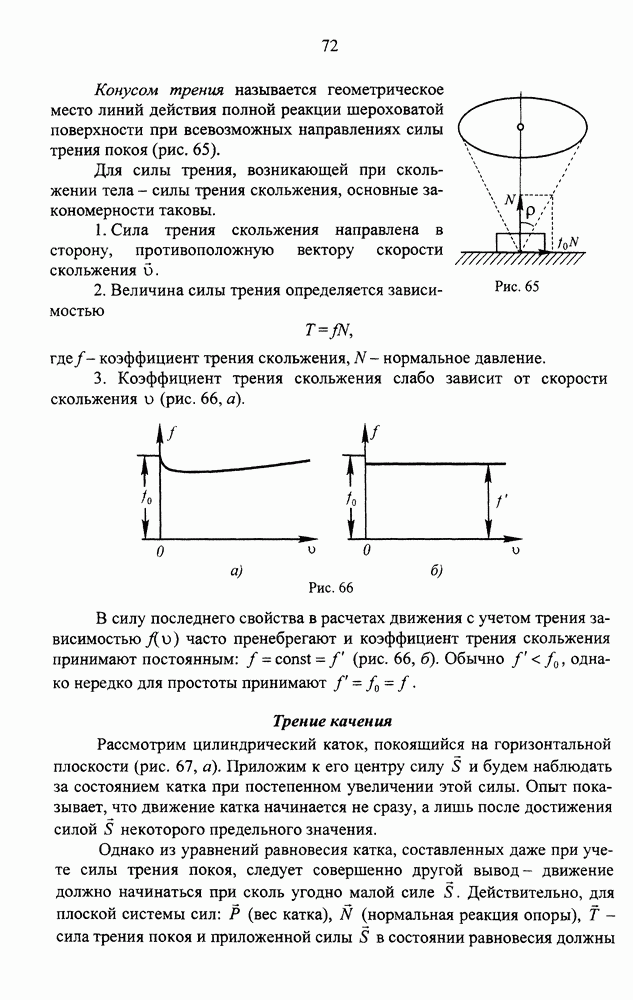
- Трение покоя и трение скольжения
- Трение качения
- Решение задач статики при учете сил трения
- Заклинивание
- Упражнения
- КИНЕМАТИКА
- ЛЕКЦИЯ 7. КИНЕМАТИКА ТОЧКИ
- Способы задания движения точки
- Определение траектории, скорости и ускорения точки при векторном способе задания движения
- Определение траектории, скорости и ускорения точки при координатном способе задания движения
- Определение скорости и ускорения точки при естественном способе задания движения
- Естественные координатные оси и их орты
- Определение скорости
- Определение ускорения
- Вопросы для самопроверки
- ЛЕКЦИЯ 8. ПРОСТЕЙШИЕ ДРИЖЕНИЯ ТВЕРДОГО ТЕЛА
- Поступательное движение
- Вращательное движение
- Уравнение вращательного движения. Угловая скорость и угловое ускорение тела
- Траектории, скорости и ускорения точек тела
- Векторы угловой скорости и углового ускорения тела
- Векторные формулы для линейной скорости, касательного и нормального ускорений точки тела
- Вопросы для самопроверки
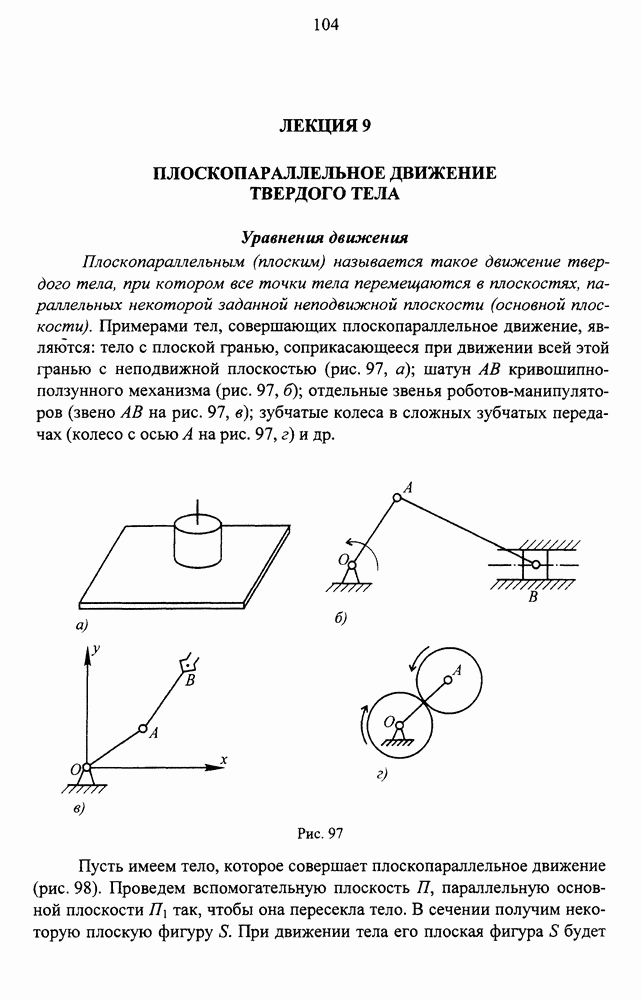
- ЛЕКЦИЯ 9. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- Уравнения движения
- Угловая скорость и угловое ускорение тела при плоскопараллельном движении
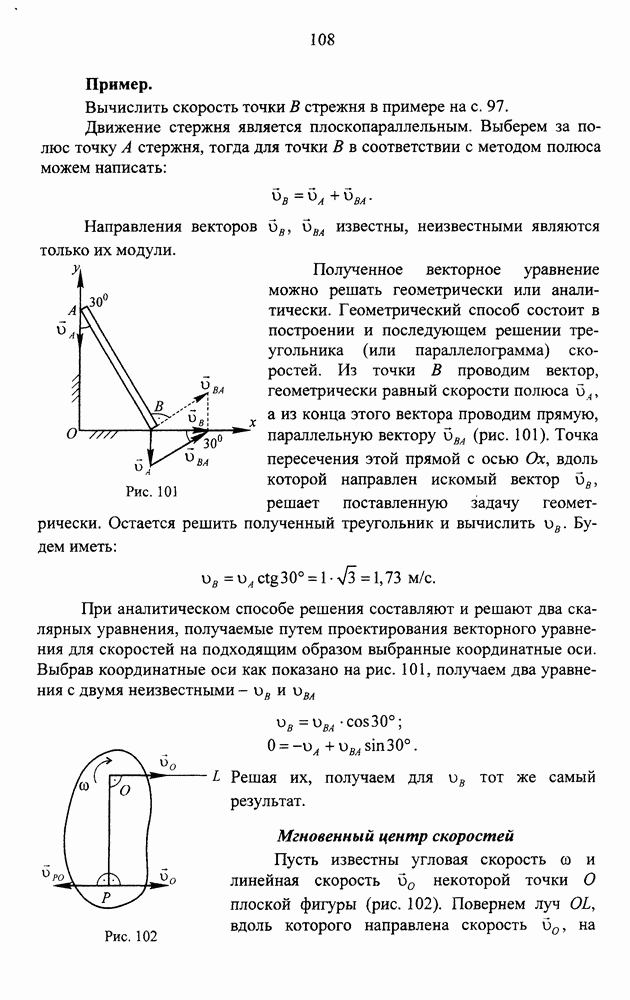
- Определение скоростей точек тела. Метод полюса
- Мгновенный центр скоростей
- Определение скоростей точек плоской фигуры через мгновенный центр скоростей
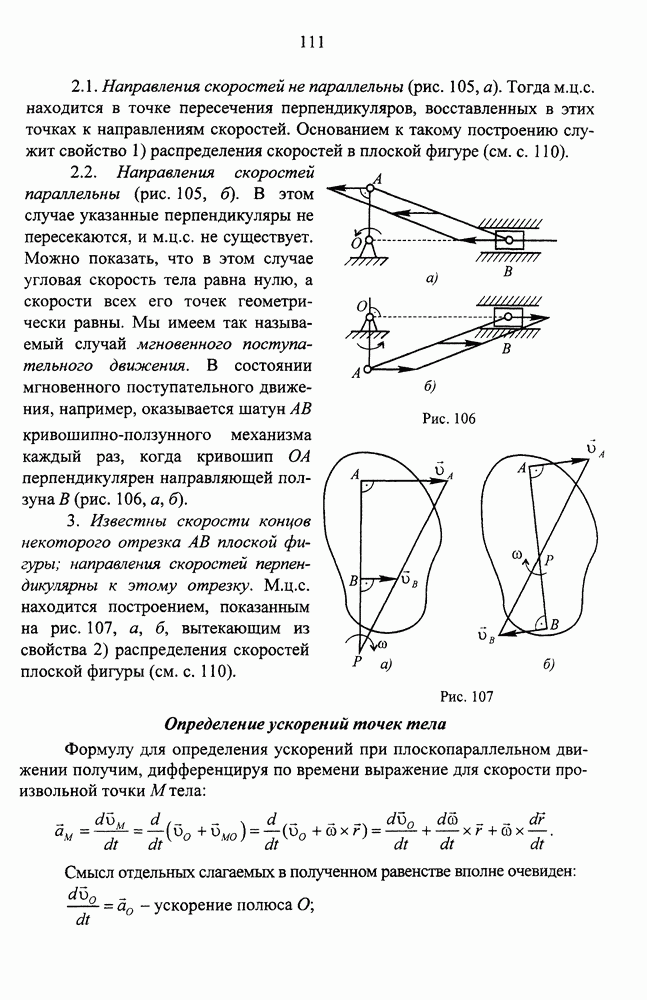
- Различные случаи определения положения мгновенного центра скоростей
- Определение ускорений точек тела
- Вопросы для самопроверки
- ЛЕКЦИЯ 10. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
- Теорема сложения скоростей
- Теорема сложения ускорений
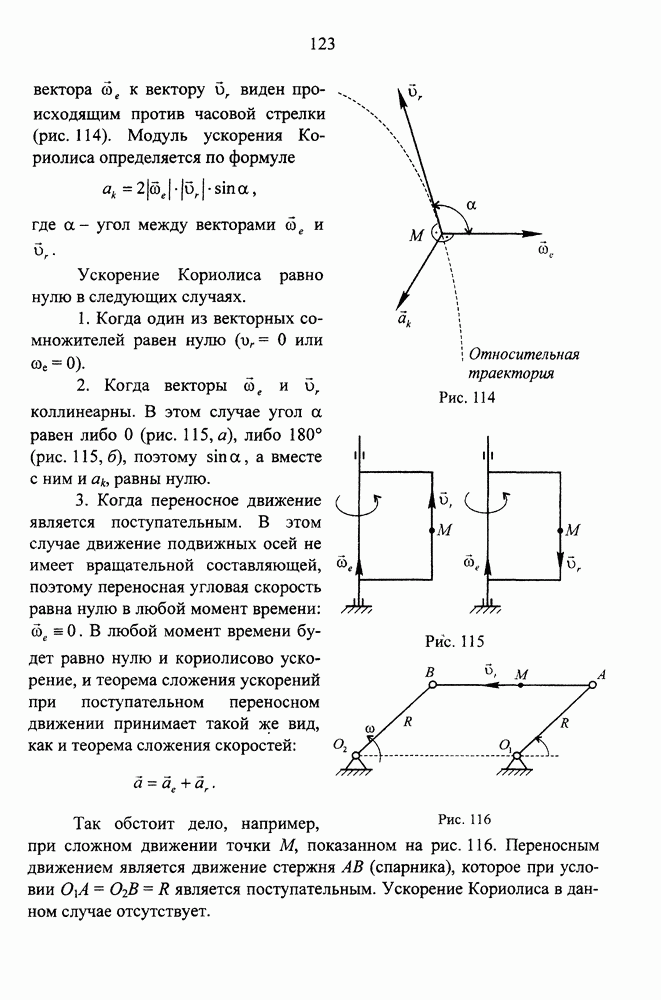
- Причины появления ускорения Кориолиса
- Вычисление и построение ускорения Кориолиса
- Вопросы для самопроверки
- ДОБАВЛЕНИЕ. КИНЕМАТИКА ПРОЦЕССА ФУГОВАНИЯ ДРЕВЕСИНЫ
- Схема и расчетная модель процесса фугования
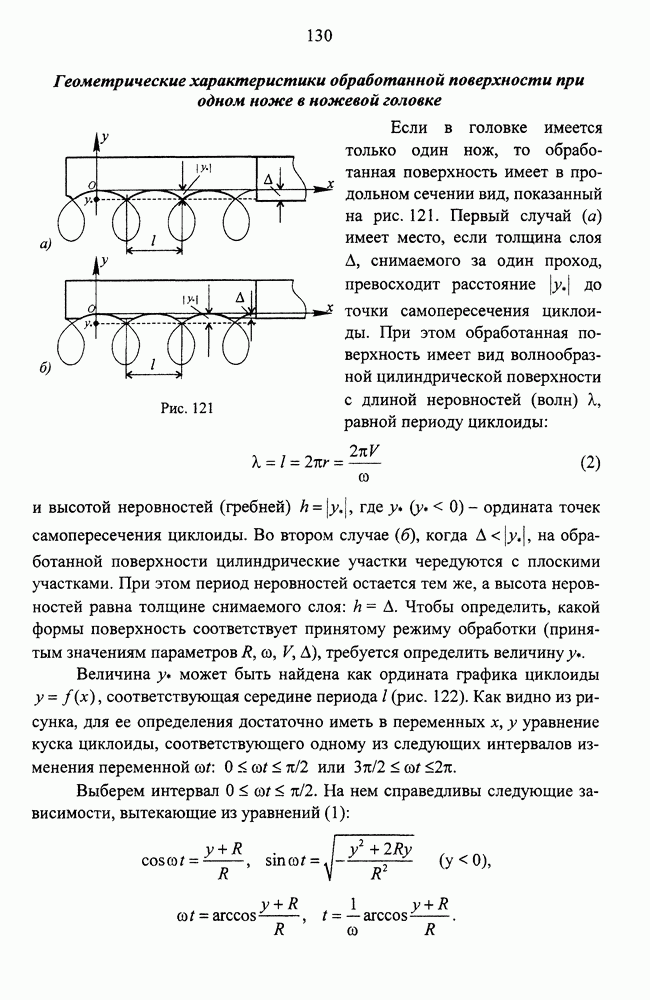
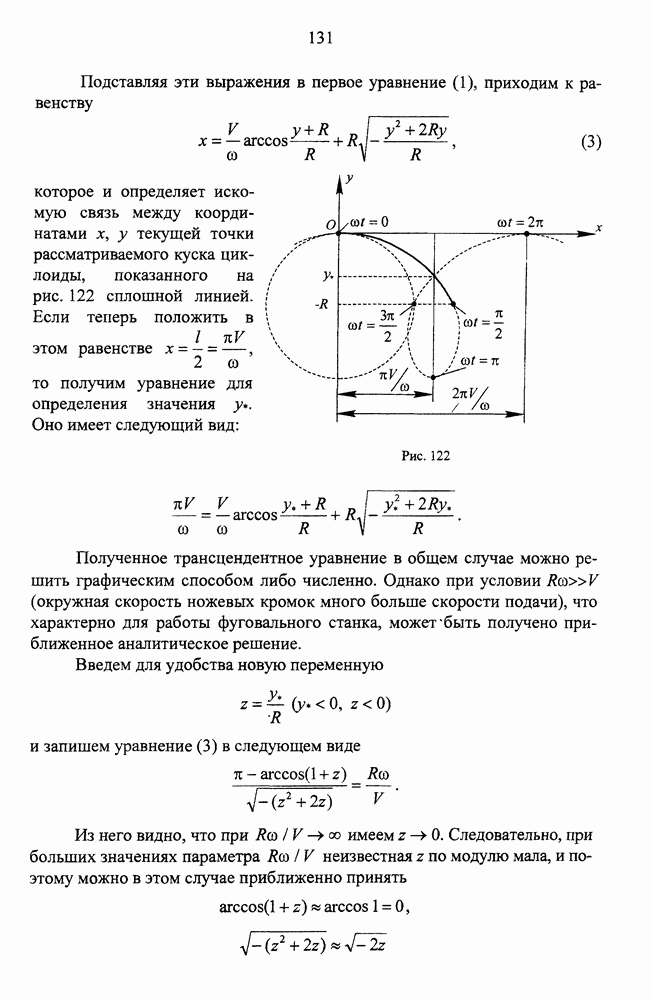
- Геометрические характеристики обработанной поверхности при одном ноже в ножевой головке
- Геометрические характеристики поверхности в случае многоножевой головки
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА