| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Определение ускорения
Будем исходить из общей формулы для ускорения

Пусть, для определенности, точка движется в положительную сторону отсчета дуг, тогда вектор скорости выражается формулой

где  - модуль скорости,
- модуль скорости,  - орт касательной. В общем случае криволинейного движения переменны оба сомножителя в этой формуле; последний- вследствие изменения направления касательной. Поэтому орт
- орт касательной. В общем случае криволинейного движения переменны оба сомножителя в этой формуле; последний- вследствие изменения направления касательной. Поэтому орт  имеет производную по времени, которая выражается формулой
имеет производную по времени, которая выражается формулой

где  и
и  - соответственно орт главной нормали и радиус кривизны траектории в рассматриваемом положении движущейся точки.
- соответственно орт главной нормали и радиус кривизны траектории в рассматриваемом положении движущейся точки.
Дифференцируя по времени выражение для скорости, получим

Формула выражает ускорение точки в виде суммы составляющих по осям естественной системы координат. Из нее следует, что ускорение имеет на эти оси проекции

Первая из них есть проекция ускорения а на касательную и называется касательным ускорением. Вектор касательного ускорения

направлен в сторону скорости, если движение ускоренное  , и против скорости, если движение замедленное
, и против скорости, если движение замедленное  .
.
Проекция ускорения на главную нормаль называется нормальным ускорением. Модуль  и вектор
и вектор  нормального ускорения выражаются формулами
нормального ускорения выражаются формулами

Так как величина  положительна, нормальное ускорение всегда направлено в сторону орта
положительна, нормальное ускорение всегда направлено в сторону орта  , то есть по главной нормали в сторону вогнутости траектории.
, то есть по главной нормали в сторону вогнутости траектории.
Проекция ускорения на бинормаль  равна нулю, что означает, что вектор ускорения лежит в соприкасающейся плоскости. Таким образом, ускорение при естественном способе задания движения точки определяется как сумма касательного и нормального ускорений:
равна нулю, что означает, что вектор ускорения лежит в соприкасающейся плоскости. Таким образом, ускорение при естественном способе задания движения точки определяется как сумма касательного и нормального ускорений:

Это правило дополнительно проиллюстрировано на рис. 87, где случай а) соответствует ускоренному движению точки, а случай 6) - замедленному движению. Модуль ускорения в обоих случаях определяется по теореме Пифагора:


Рис. 87.
Если точка движется прямолинейно, то нормальное ускорение не возникает  , и ускорение состоит только из касательного:
, и ускорение состоит только из касательного:  .
.
При равномерном криволинейном движении ( ), наоборот, отсутствует касательное ускорение
), наоборот, отсутствует касательное ускорение  , и полное ускорение точки равно ее нормальному ускорению:
, и полное ускорение точки равно ее нормальному ускорению:  .
.
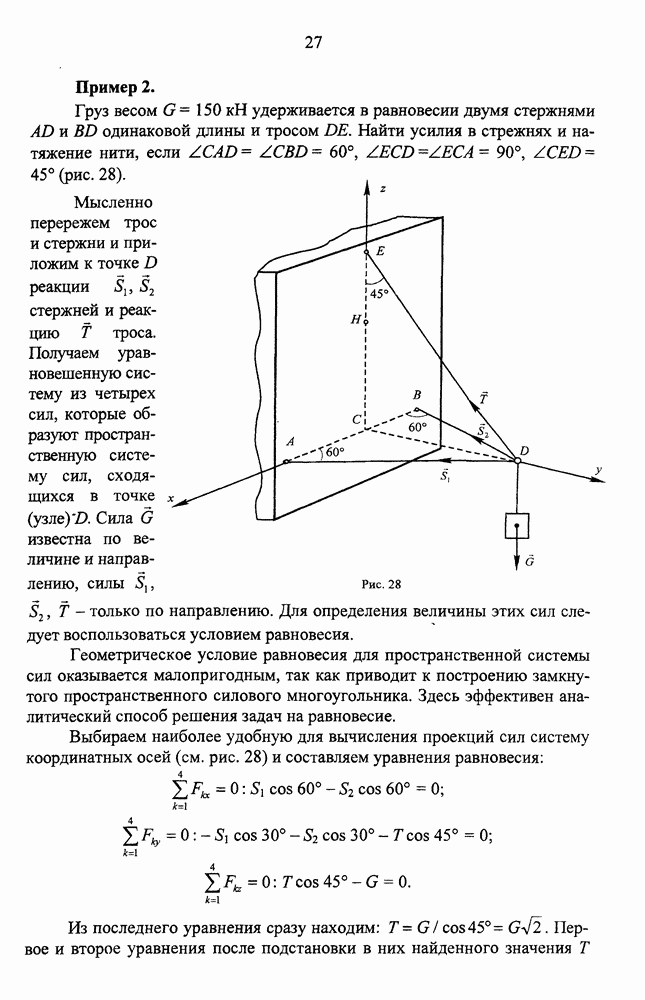
Пример.
Точка движется по окружности радиуса  согласно закону
согласно закону  . Вычислить и построить скорость и ускорение точки в момент
. Вычислить и построить скорость и ускорение точки в момент  , когда она пройдет половину окружности.
, когда она пройдет половину окружности.
В момент  дуговая координата точки
дуговая координата точки  равна половине длины окружности:
равна половине длины окружности:  , откуда находим
, откуда находим

Определяем скорость точки в момент  расчетный момент
расчетный момент  :
:

Определяем касательное ускорение

Видно, что оно не изменяется с течением времени - точка движется равноускоренно. Это же значение касательное ускорение имеет и в расчетный момент:

Определяем нормальное ускорение

Определяем полное ускорение в момент  :
:

На рис. 88 показаны положения точки в текущий (М) и расчетный  моменты времени, а также векторы скорости и ускорений точки в момент
моменты времени, а также векторы скорости и ускорений точки в момент  .
.
В заключение заметим, что от одного способа задания движения можно перейти к другим способам. Например, при определении скорости в случае координатного способа описания движения был предварительно сделан переход к векторному способу в виде


Рис. 88.
Чтобы перейти от координатного способа к естественному, прежде всего требуется найти уравнение траектории. Как было показано выше, это делается исключением из уравнений движения времени t. Закон движения по траектории можно получить на основе равенств определяющих скорость точки при естественном и координатном способах задания движения.

Приравняв правые части равенств, разрешая полученное соотношение относительно  и интегрируя, находим
и интегрируя, находим

Это выражение определяет закон движения по траектории в общем виде.
Если отсчет дуговой координаты вести от начального положения точки в сторону движения, то  радикал положителен, и закон движения примет вид
радикал положителен, и закон движения примет вид

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ. ПРЕДМЕТ И ОСНОВНЫЕ ПОНЯТИЯ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ
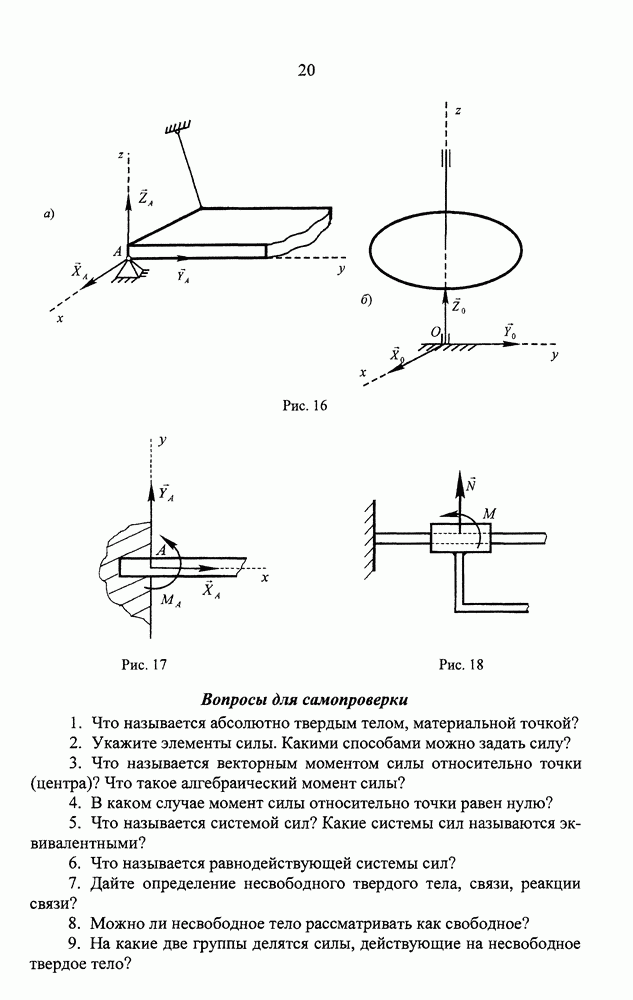
- СТАТИКА. ЛЕКЦИЯ 1. ЗАДАЧИ СТАТИКИ, АКСИОМЫ СТАТИКИ. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
- Момент силы относительно точки
- Алгебраический момент силы
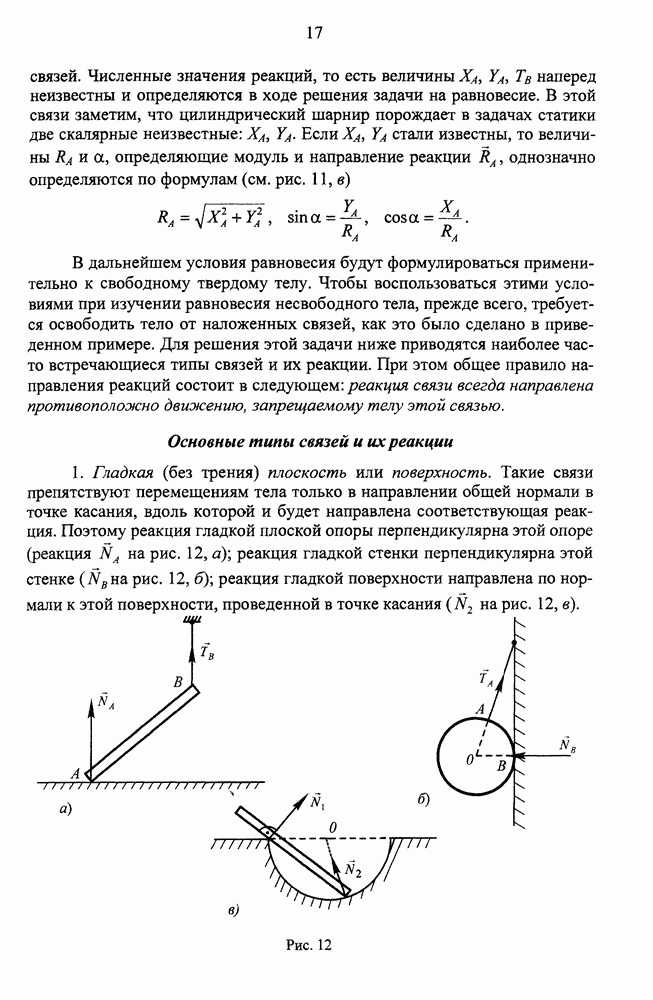
- Основные типы связей и их реакции
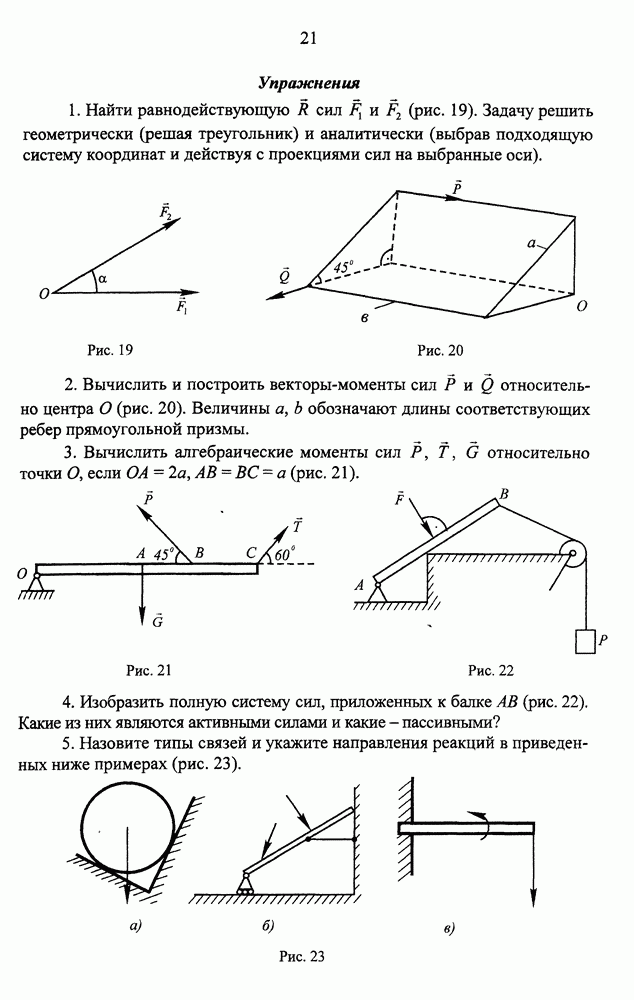
- Упражнения
- ЛЕКЦИЯ 2. СХОДЯЩИЕСЯ СИЛЫ И ПАРЫ СИЛ
- Сходящиеся силы. Приведение сходящихся сил к простейшему виду
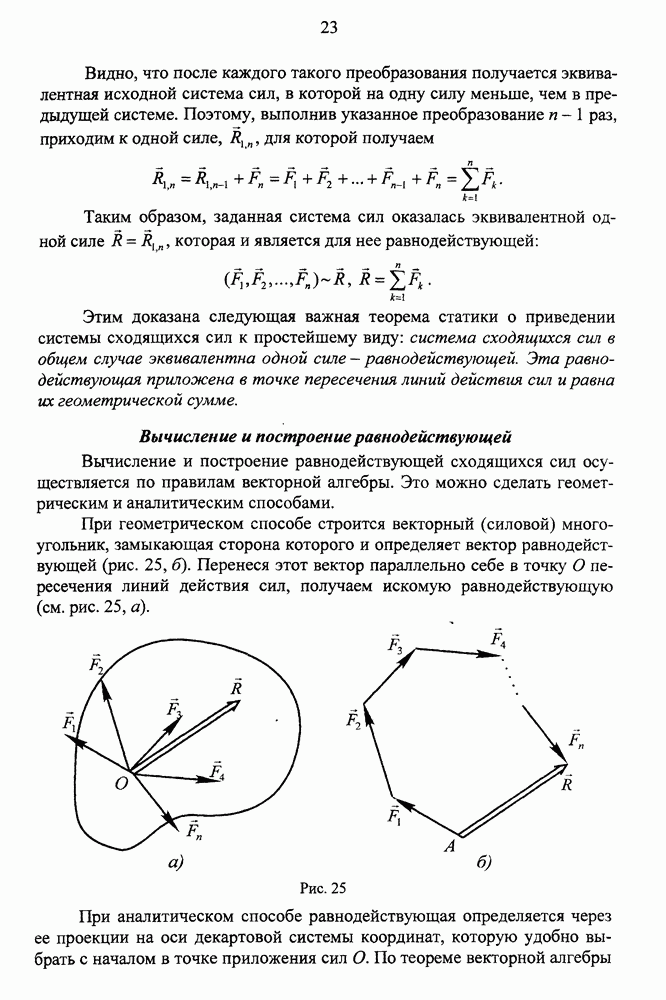
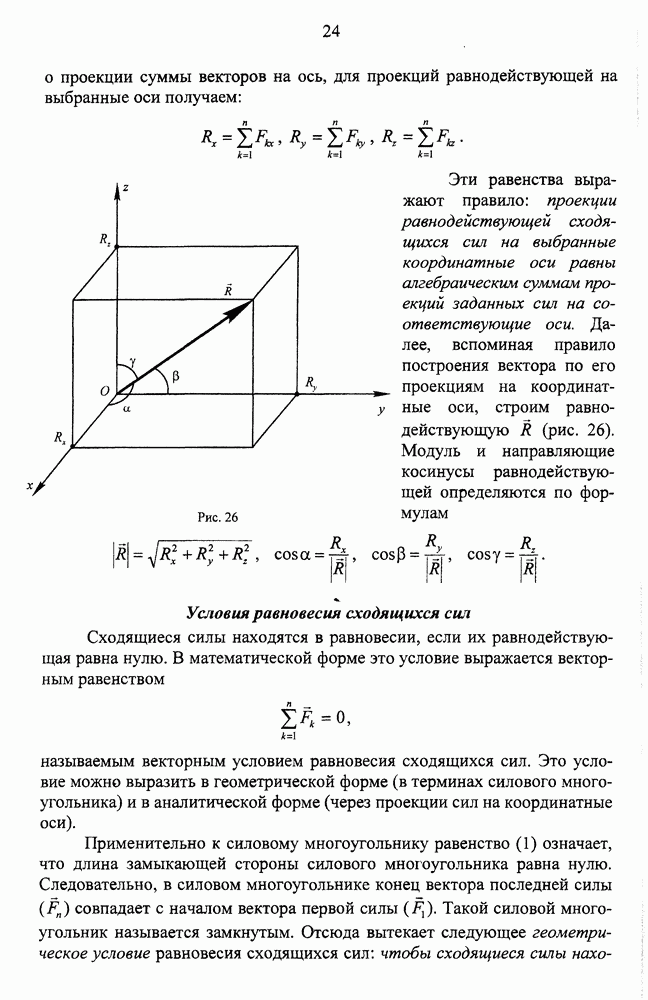
- Вычисление и построение равнодействующей
- Условия равновесия сходящихся сил
- Теорема о трех силах
- Теорема Вариньона
- Пара сил и ее момент
- Приведение системы пар сил к простейшему виду или сложение пар сил
- Упражнения
- ЛЕКЦИЯ 3. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ
- Момент силы относительно оси
- Аналитический способ вычисления момента
- Геометрический способ вычисления момента
- Преобразование пространственной произвольной системы сил
- Приведение пространственной произвольной системы сил к данному центру. Главный вектор и главный момент. Основная теорема статики
- Вычисление и построение главного вектора и главного момента
- Перемена центра приведения
- ЛЕКЦИЯ 4. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ (продолжение). ЧАСТНЫЕ СЛУЧАИ СИСТЕМЫ СИЛ
- Случаи приведения к простейшему виду
- Условия (уравнения) равновесия пространственной произвольной системы сил
- Частные случаи системы сил
- Плоская система сил
- Система параллельных сил
- Равновесие системы тел
- Вопросы для самопроверки
- ЛЕКЦИЯ 5. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ И ЦЕНТР ТЯЖЕСТИ
- Центр параллельных сил
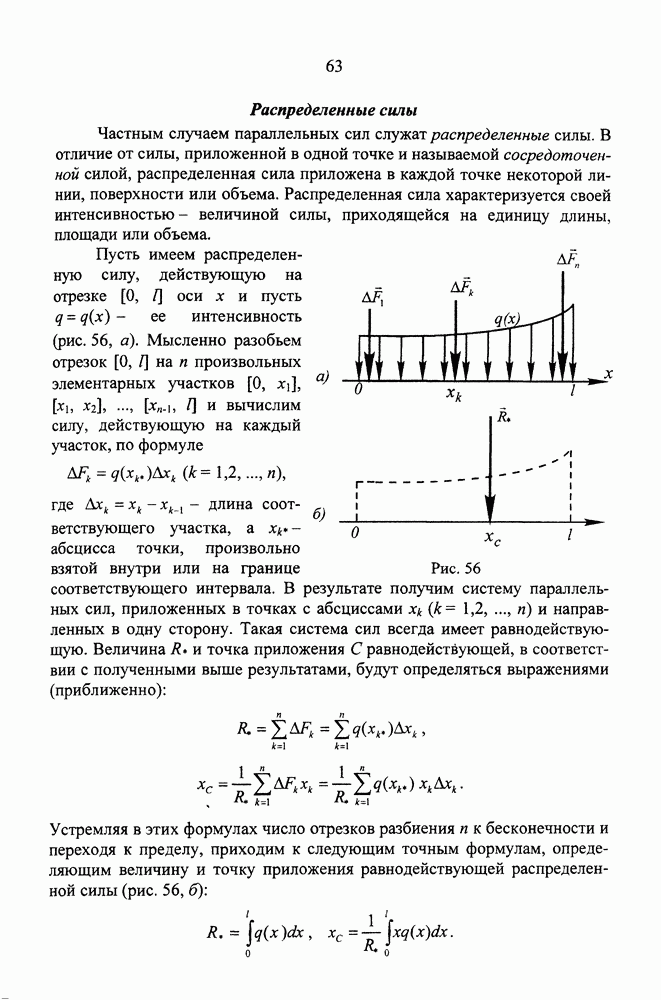
- Распределенные силы
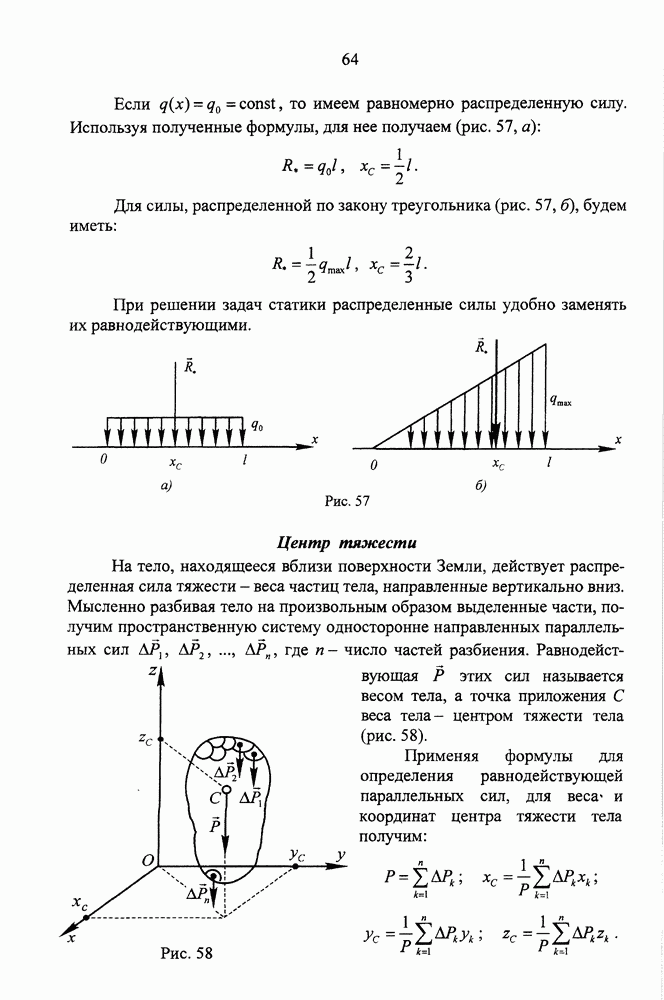
- Центр тяжести
- Интегральные формулы для координат центра тяжести
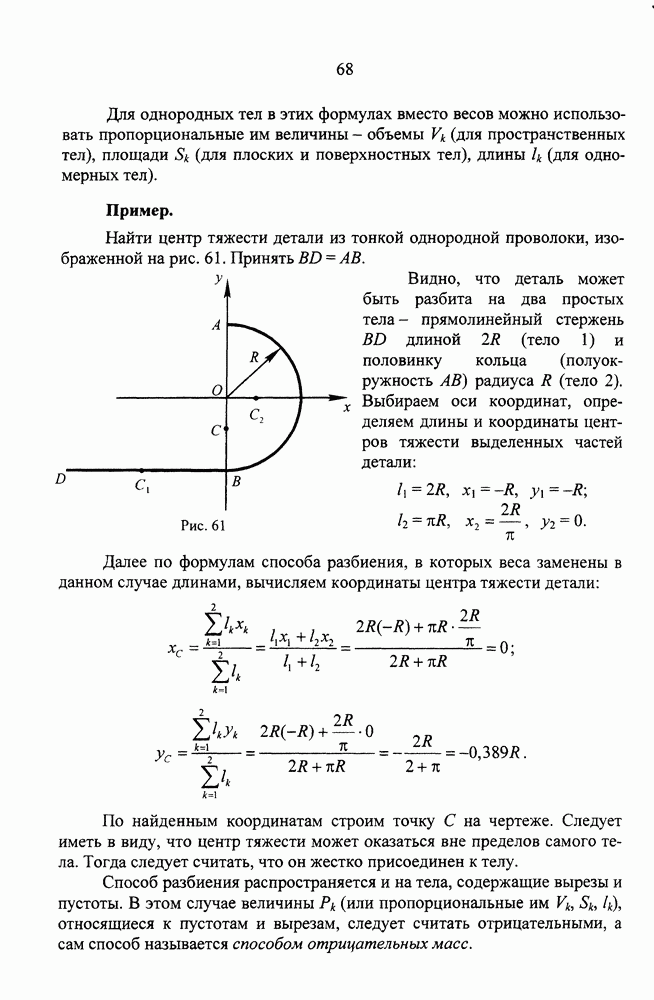
- Метод разбиения
- Вопросы для самопроверки
- ЛЕКЦИЯ 6. ТРЕНИЕ ТВЕРДЫХ ТЕЛ
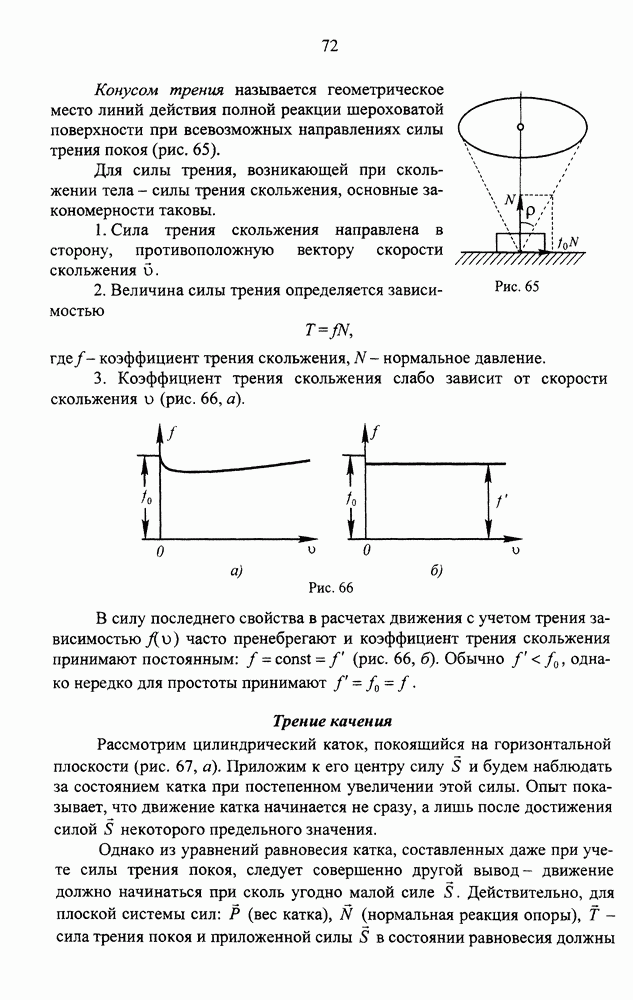
- Трение покоя и трение скольжения
- Трение качения
- Решение задач статики при учете сил трения
- Заклинивание
- Упражнения
- КИНЕМАТИКА
- ЛЕКЦИЯ 7. КИНЕМАТИКА ТОЧКИ
- Способы задания движения точки
- Определение траектории, скорости и ускорения точки при векторном способе задания движения
- Определение траектории, скорости и ускорения точки при координатном способе задания движения
- Определение скорости и ускорения точки при естественном способе задания движения
- Естественные координатные оси и их орты
- Определение скорости
- Определение ускорения
- Вопросы для самопроверки
- ЛЕКЦИЯ 8. ПРОСТЕЙШИЕ ДРИЖЕНИЯ ТВЕРДОГО ТЕЛА
- Поступательное движение
- Вращательное движение
- Уравнение вращательного движения. Угловая скорость и угловое ускорение тела
- Траектории, скорости и ускорения точек тела
- Векторы угловой скорости и углового ускорения тела
- Векторные формулы для линейной скорости, касательного и нормального ускорений точки тела
- Вопросы для самопроверки
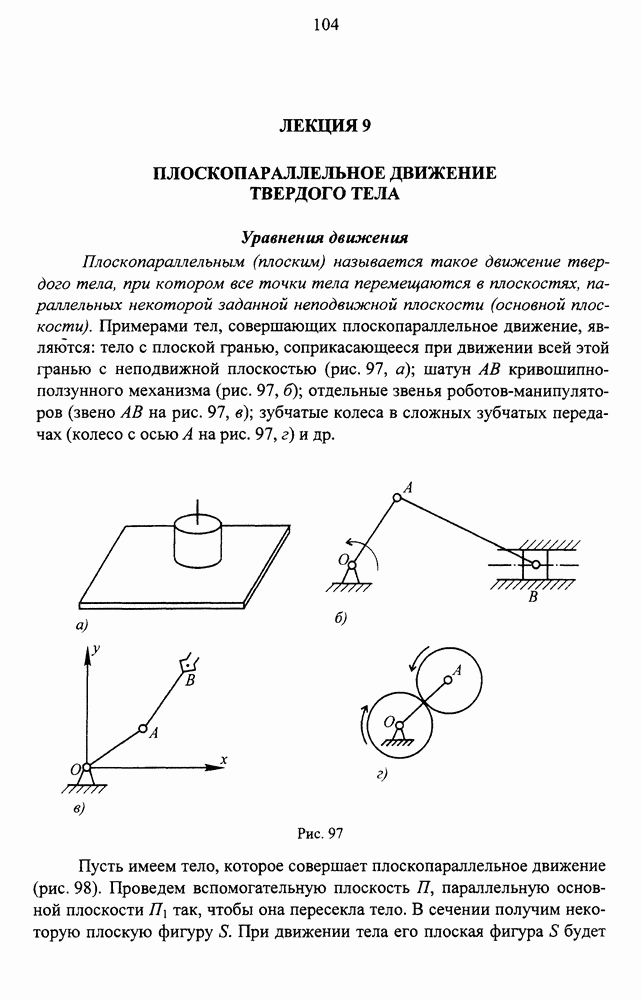
- ЛЕКЦИЯ 9. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- Уравнения движения
- Угловая скорость и угловое ускорение тела при плоскопараллельном движении
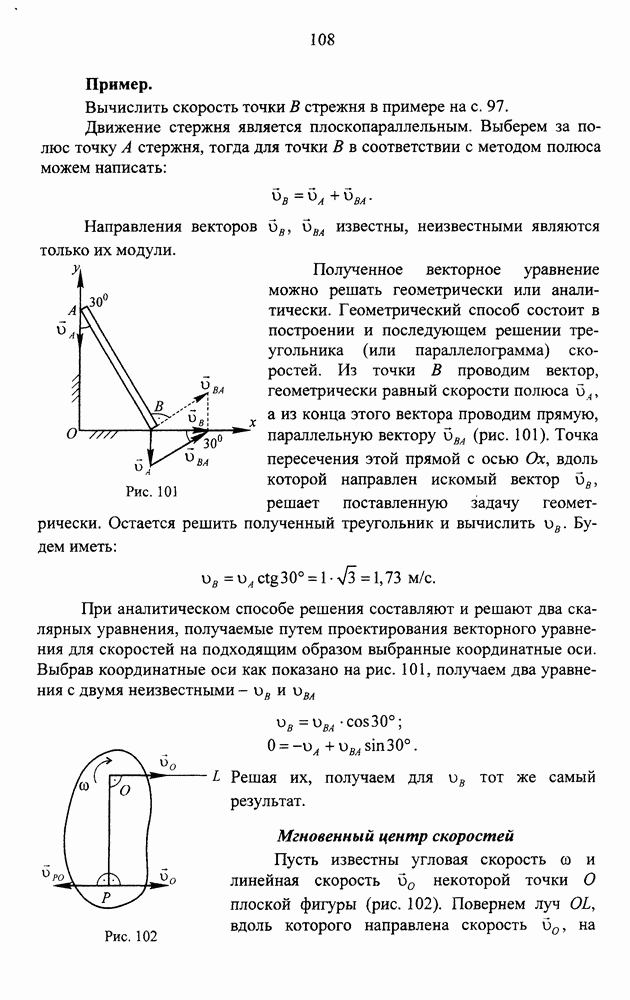
- Определение скоростей точек тела. Метод полюса
- Мгновенный центр скоростей
- Определение скоростей точек плоской фигуры через мгновенный центр скоростей
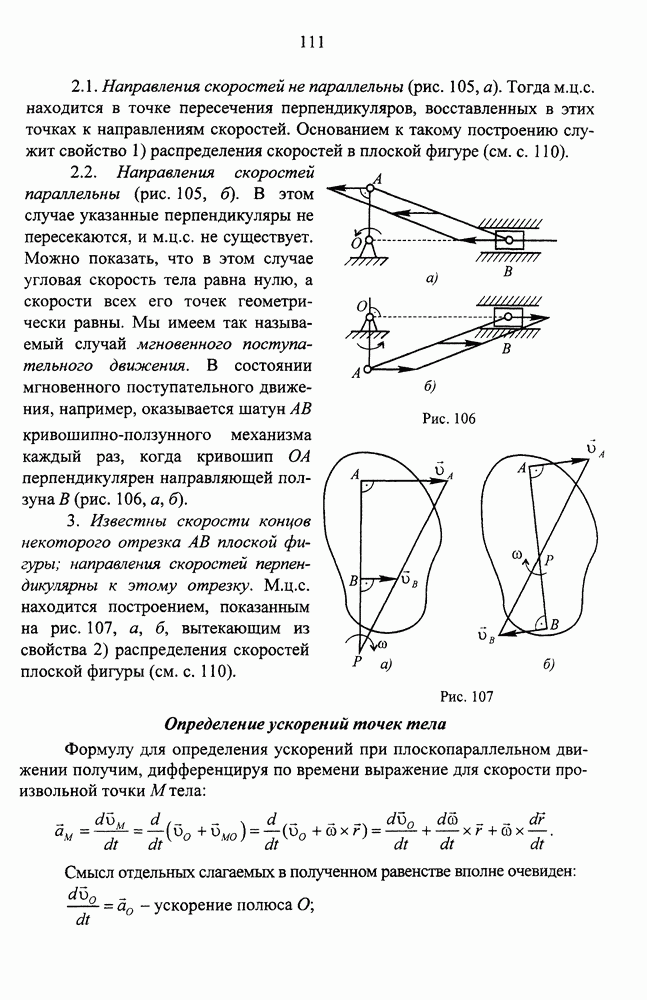
- Различные случаи определения положения мгновенного центра скоростей
- Определение ускорений точек тела
- Вопросы для самопроверки
- ЛЕКЦИЯ 10. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
- Теорема сложения скоростей
- Теорема сложения ускорений
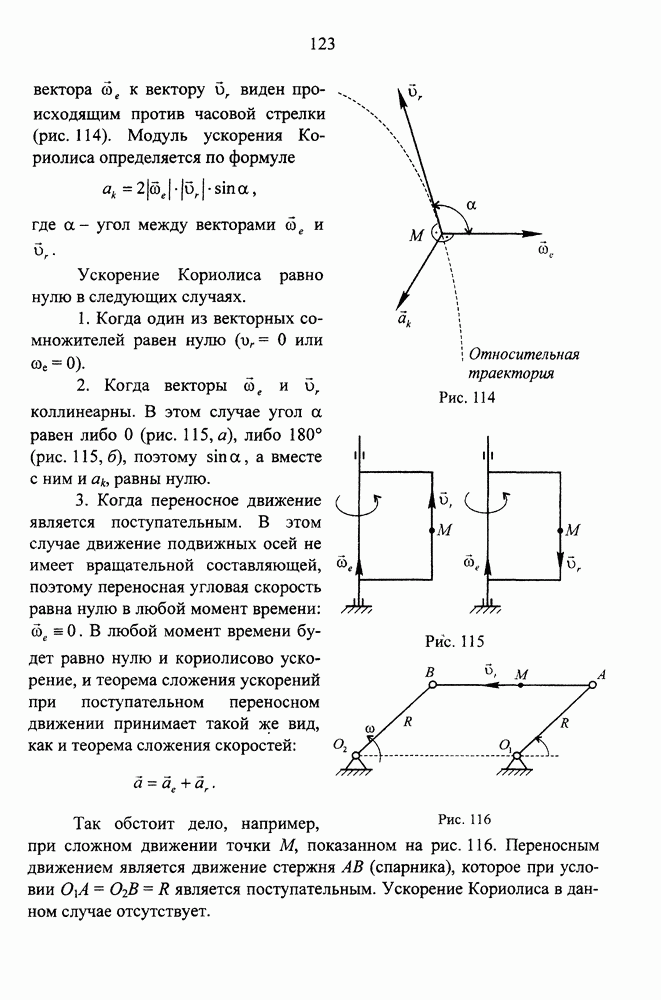
- Причины появления ускорения Кориолиса
- Вычисление и построение ускорения Кориолиса
- Вопросы для самопроверки
- ДОБАВЛЕНИЕ. КИНЕМАТИКА ПРОЦЕССА ФУГОВАНИЯ ДРЕВЕСИНЫ
- Схема и расчетная модель процесса фугования
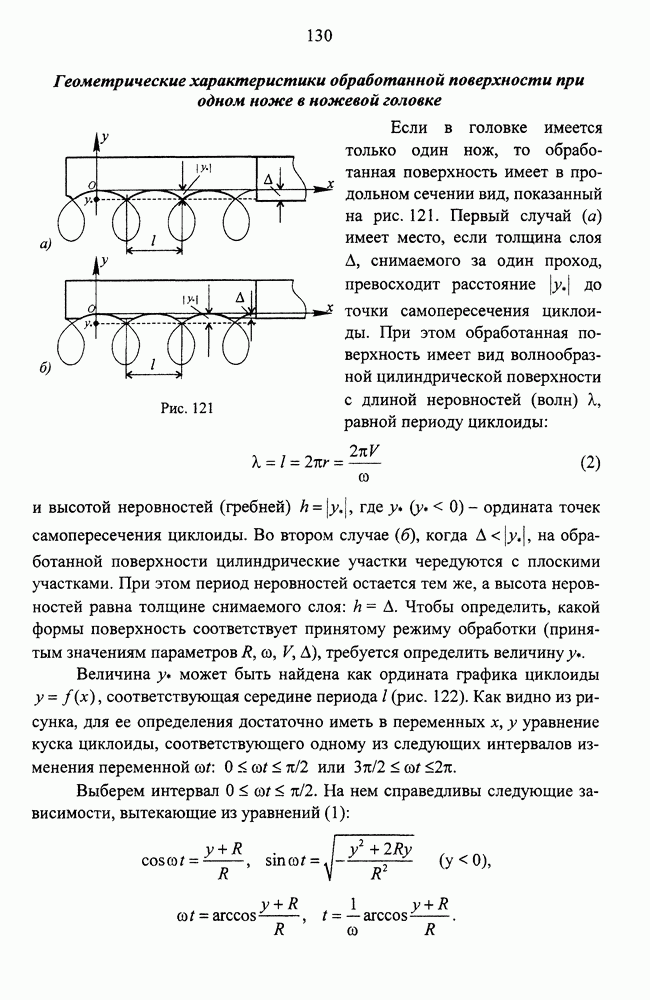
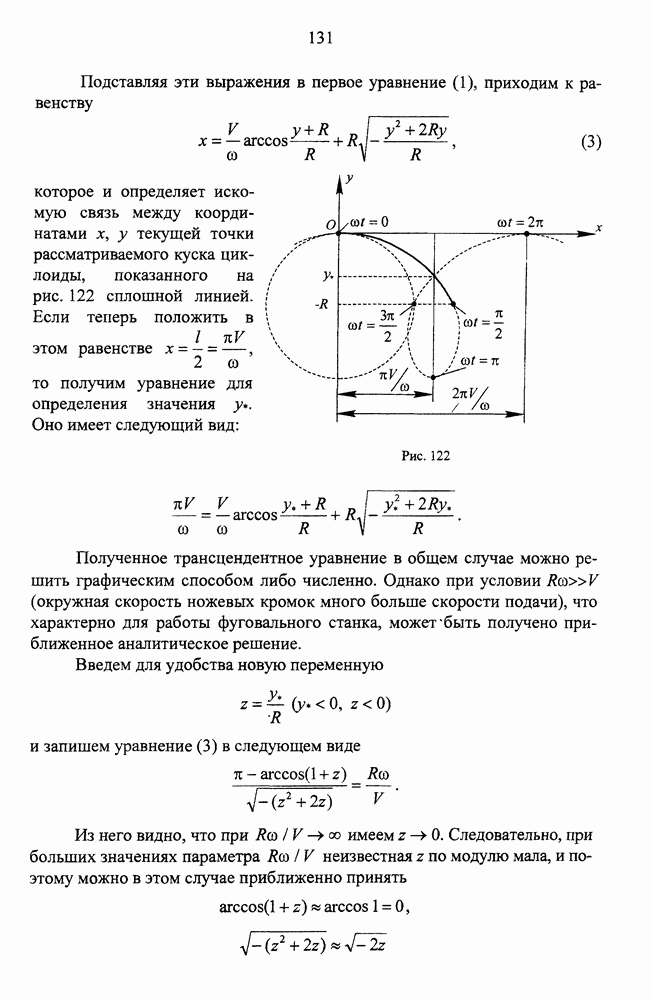
- Геометрические характеристики обработанной поверхности при одном ноже в ножевой головке
- Геометрические характеристики поверхности в случае многоножевой головки
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА