| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Интегральные формулы для координат центра тяжести
Для сплошных тел полученные приводятся к интегральному виду.
Тело называется сплошным, если вещество в теле распределено непрерывно. В сплошном теле можно неограниченно уменьшать размеры выделенных материальных элементов и осуществлять предельные переходы. Пусть  массы и объемы элементов, выделенных в сплошном теле,
массы и объемы элементов, выделенных в сплошном теле,  - точки внутри этих элементов. Отношение
- точки внутри этих элементов. Отношение  называется средней плотностью тела в точке
называется средней плотностью тела в точке  . Предел, к которому стремится средняя плотность при неограниченном уменьшении объема
. Предел, к которому стремится средняя плотность при неограниченном уменьшении объема  , называется плотностью тела в точке
, называется плотностью тела в точке  :
:

Тело называется однородным, если его плотность одинакова во всех точках:  .
.
Для сплошных однородных тел, полагая  ,
,  (
( - ускорение силы тяжести) и переходя в формулах для координат центра тяжести к пределу при
- ускорение силы тяжести) и переходя в формулах для координат центра тяжести к пределу при  , получим:
, получим:

В этих формулах  объем тела,
объем тела,  объем выделенного элемента интегрирования, х, у, z — декартовы координаты какой-либо точки внутри или на границе элемента. Знак
объем выделенного элемента интегрирования, х, у, z — декартовы координаты какой-либо точки внутри или на границе элемента. Знак  обозначает интегрирование по всему объему тела.
обозначает интегрирование по всему объему тела.
Для однородных поверхностных тел (мембраны, оболочки) и материальных линий (стержни, нити) эти формулы преобразуются к следующему виду:
для поверхностных тел

для материальных линий

В этих формулах S - площадь поверхности тела,  -площадь выделенного на ней элемента интегрирования,
-площадь выделенного на ней элемента интегрирования,  - длина линии,
- длина линии,  - длина ее элемента, х, у, z - декартовы координаты какой-либо точки, принадлежащей элементу интегрирования,
- длина ее элемента, х, у, z - декартовы координаты какой-либо точки, принадлежащей элементу интегрирования,  - декартовы координаты центра тяжести данного поверхностного тела или материальной линии.
- декартовы координаты центра тяжести данного поверхностного тела или материальной линии.
Пример 1.
Найти центр тяжести однородного полушара радиуса  .
.
Выберем начало координат в центре основания полушара, проведем координатные оси (рис. 59). Полушар симметричен относительно оси  , поэтому его центр тяжести С лежит на этой оси:
, поэтому его центр тяжести С лежит на этой оси:  . Остается определить величину
. Остается определить величину  .
.
В качестве элемента интегрирования выбираем в полушаре слой толщиной  и круглым основанием радиуса
и круглым основанием радиуса  . Далее находим (с точностью до величин первого порядка малости относительно
. Далее находим (с точностью до величин первого порядка малости относительно  ):
):

Подставляя найденные значения в интегральную формулу для координаты  , вычисляем
, вычисляем

Таким образом, центр тяжести однородного полушара находится на его оси симметрии на расстоянии  над центром основания.
над центром основания.
Пример 2.
Найти центр тяжести дуги АВ окружности с радиусом R и центральным углом  (рис. 60).
(рис. 60).
Поместим начало координат в центр соответствующей окружности, ось  проведем через середину дуги, оси
проведем через середину дуги, оси  - перпендикулярно к ней. По теореме о положении центра тяжести симметричного тела будем иметь
- перпендикулярно к ней. По теореме о положении центра тяжести симметричного тела будем иметь  Координату
Координату  вычисляем по соответствующей формуле для координат центра тяжести материальной линии.
вычисляем по соответствующей формуле для координат центра тяжести материальной линии.

Рис. 59.
Примем за элемент интегрирования бесконечно малый участок дуги, определяемый конечным углом  и бесконечно малым углом
и бесконечно малым углом  . Будем иметь:
. Будем иметь:  (
( длина дуги АВ). Далее вычисляем
длина дуги АВ). Далее вычисляем  :
:


Рис. 60.
В этой формуле a выражается в радианах.
Придавая углу  значение
значение  найдем абсциссу центра тяжести полуокружности:
найдем абсциссу центра тяжести полуокружности:

Аналогичным образом могут быть найдены центры тяжести других тел простой геометрической формы - отрезка прямой, площади треугольника, площади кругового сектора, объема конуса и т.д. А как быть в более сложных случаях? Из вычислительных способов (существуют еще экспериментальные способы) часто можно воспользоваться методом разбиения.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ. ПРЕДМЕТ И ОСНОВНЫЕ ПОНЯТИЯ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ
- СТАТИКА. ЛЕКЦИЯ 1. ЗАДАЧИ СТАТИКИ, АКСИОМЫ СТАТИКИ. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
- Момент силы относительно точки
- Алгебраический момент силы
- Основные типы связей и их реакции
- Упражнения
- ЛЕКЦИЯ 2. СХОДЯЩИЕСЯ СИЛЫ И ПАРЫ СИЛ
- Сходящиеся силы. Приведение сходящихся сил к простейшему виду
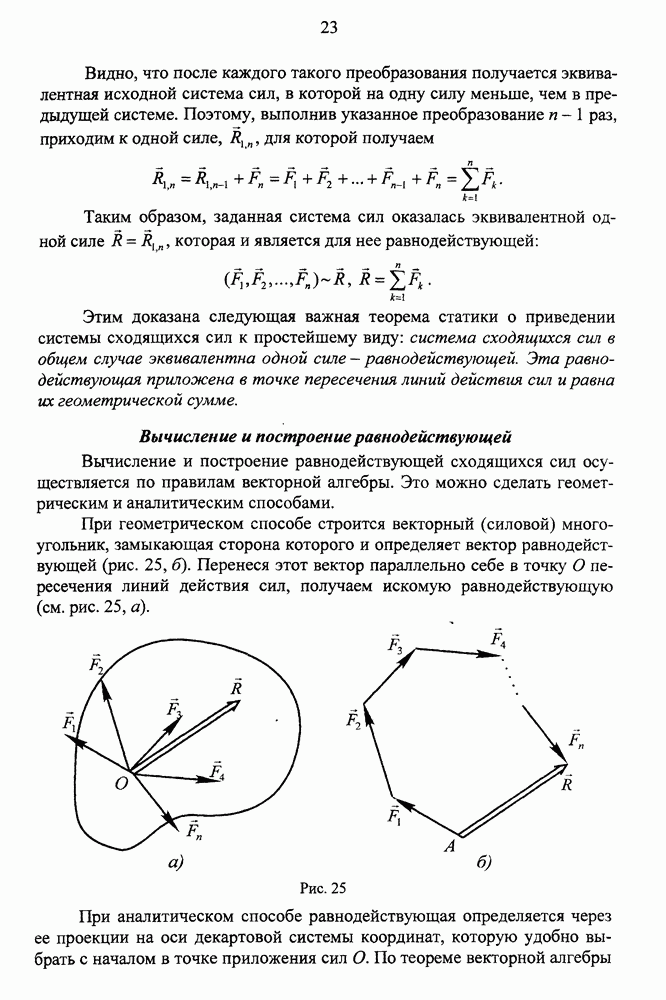
- Вычисление и построение равнодействующей
- Условия равновесия сходящихся сил
- Теорема о трех силах
- Теорема Вариньона
- Пара сил и ее момент
- Приведение системы пар сил к простейшему виду или сложение пар сил
- Упражнения
- ЛЕКЦИЯ 3. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ
- Момент силы относительно оси
- Аналитический способ вычисления момента
- Геометрический способ вычисления момента
- Преобразование пространственной произвольной системы сил
- Приведение пространственной произвольной системы сил к данному центру. Главный вектор и главный момент. Основная теорема статики
- Вычисление и построение главного вектора и главного момента
- Перемена центра приведения
- ЛЕКЦИЯ 4. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ (продолжение). ЧАСТНЫЕ СЛУЧАИ СИСТЕМЫ СИЛ
- Случаи приведения к простейшему виду
- Условия (уравнения) равновесия пространственной произвольной системы сил
- Частные случаи системы сил
- Плоская система сил
- Система параллельных сил
- Равновесие системы тел
- Вопросы для самопроверки
- ЛЕКЦИЯ 5. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ И ЦЕНТР ТЯЖЕСТИ
- Центр параллельных сил
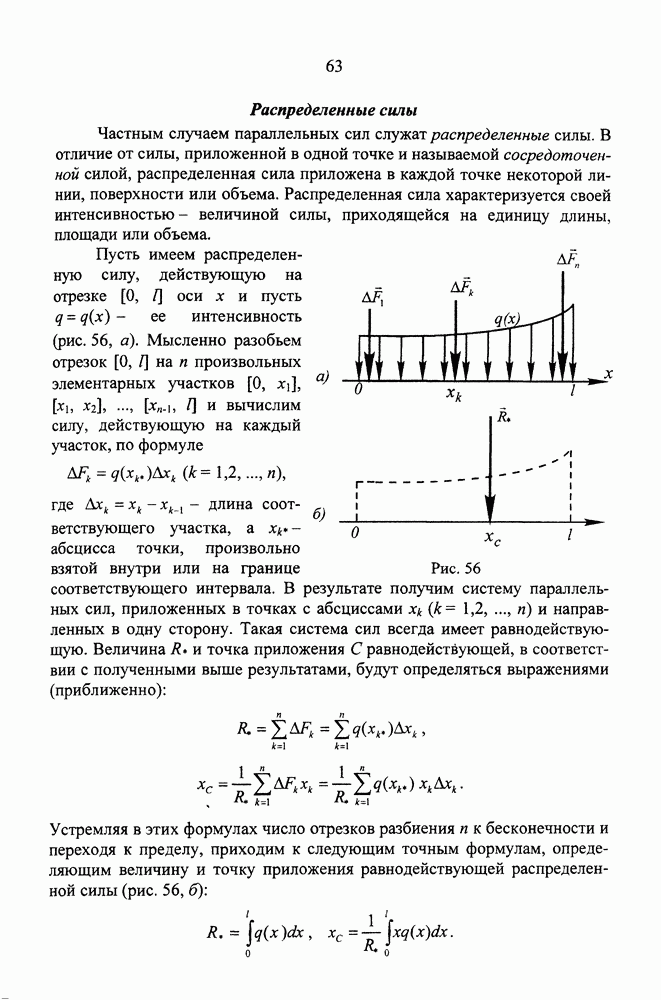
- Распределенные силы
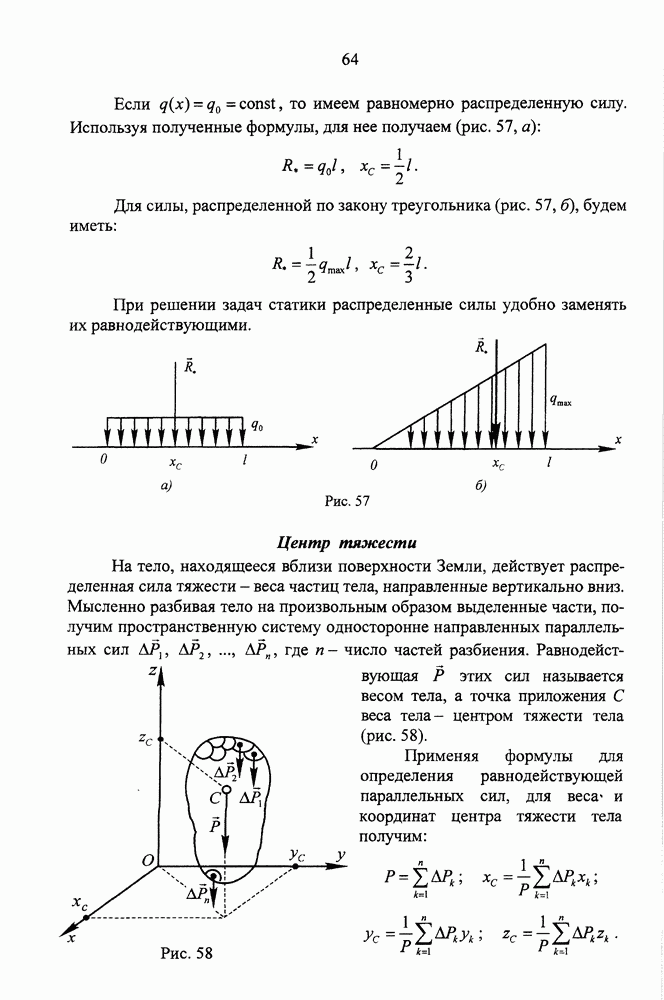
- Центр тяжести
- Интегральные формулы для координат центра тяжести
- Метод разбиения
- Вопросы для самопроверки
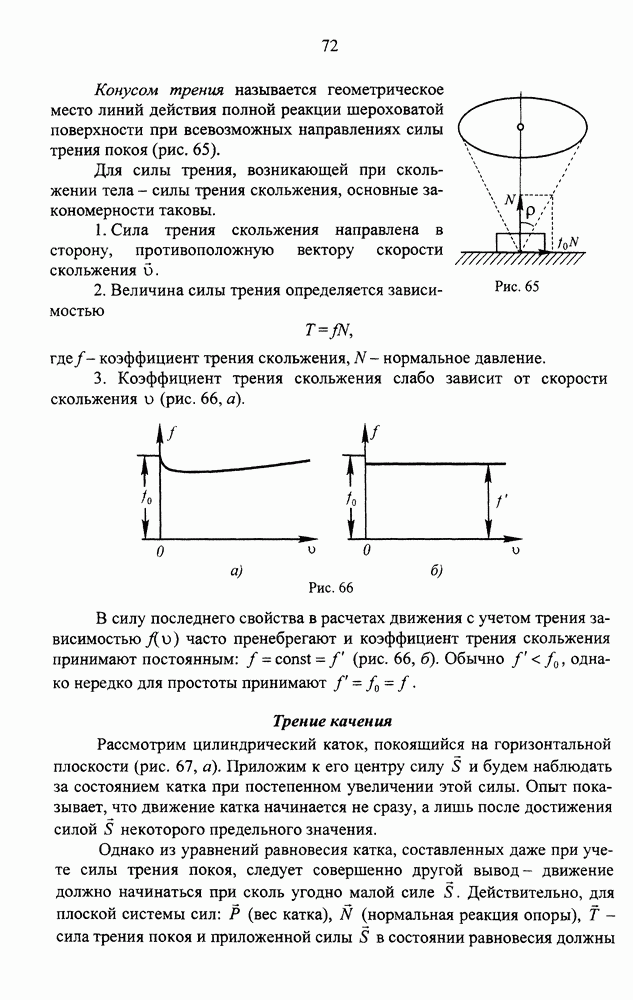
- ЛЕКЦИЯ 6. ТРЕНИЕ ТВЕРДЫХ ТЕЛ
- Трение покоя и трение скольжения
- Трение качения
- Решение задач статики при учете сил трения
- Заклинивание
- Упражнения
- КИНЕМАТИКА
- ЛЕКЦИЯ 7. КИНЕМАТИКА ТОЧКИ
- Способы задания движения точки
- Определение траектории, скорости и ускорения точки при векторном способе задания движения
- Определение траектории, скорости и ускорения точки при координатном способе задания движения
- Определение скорости и ускорения точки при естественном способе задания движения
- Естественные координатные оси и их орты
- Определение скорости
- Определение ускорения
- Вопросы для самопроверки
- ЛЕКЦИЯ 8. ПРОСТЕЙШИЕ ДРИЖЕНИЯ ТВЕРДОГО ТЕЛА
- Поступательное движение
- Вращательное движение
- Уравнение вращательного движения. Угловая скорость и угловое ускорение тела
- Траектории, скорости и ускорения точек тела
- Векторы угловой скорости и углового ускорения тела
- Векторные формулы для линейной скорости, касательного и нормального ускорений точки тела
- Вопросы для самопроверки
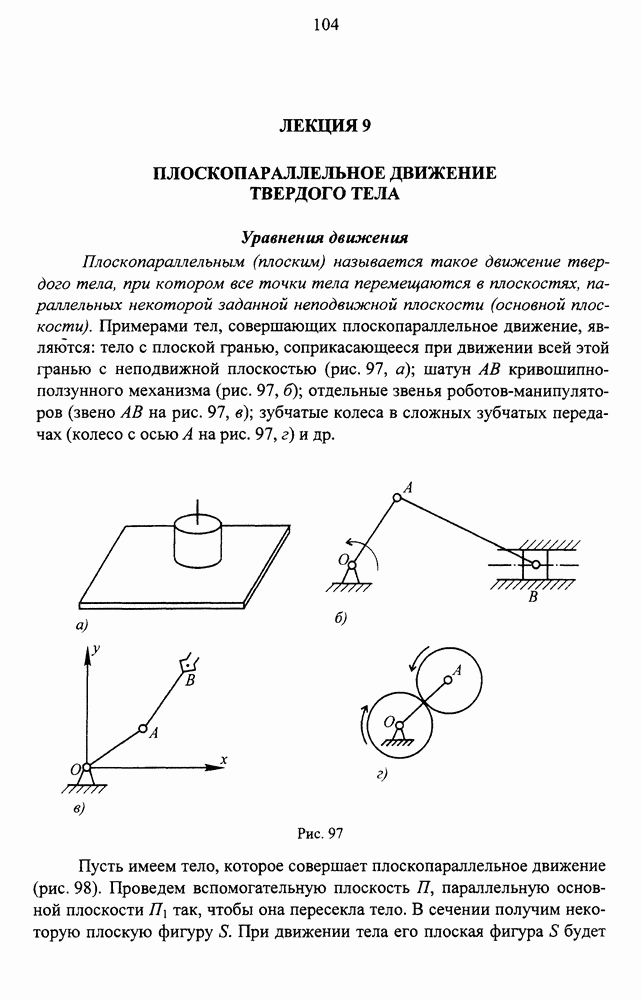
- ЛЕКЦИЯ 9. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- Уравнения движения
- Угловая скорость и угловое ускорение тела при плоскопараллельном движении
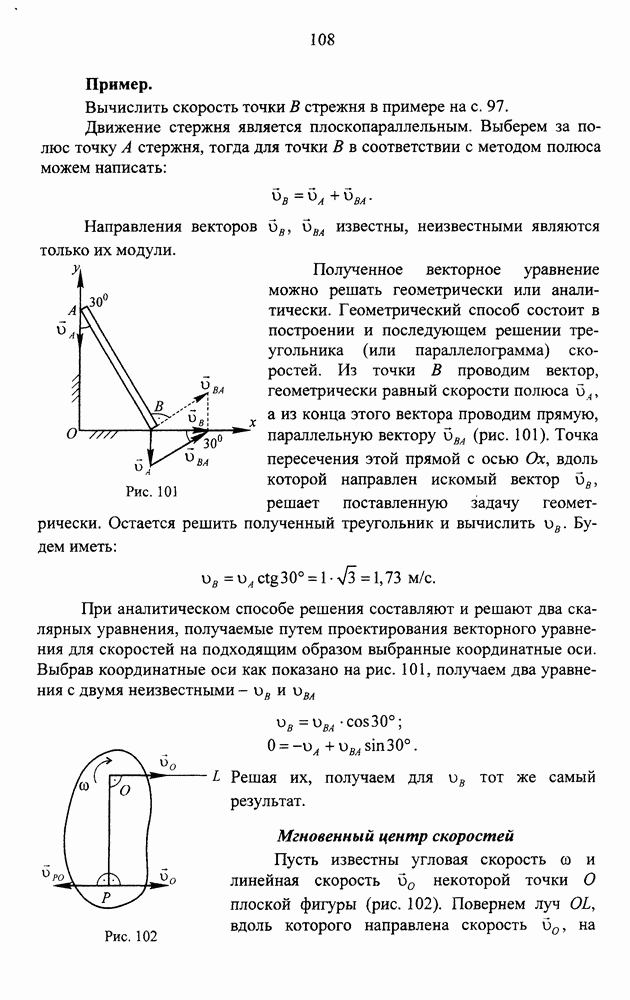
- Определение скоростей точек тела. Метод полюса
- Мгновенный центр скоростей
- Определение скоростей точек плоской фигуры через мгновенный центр скоростей
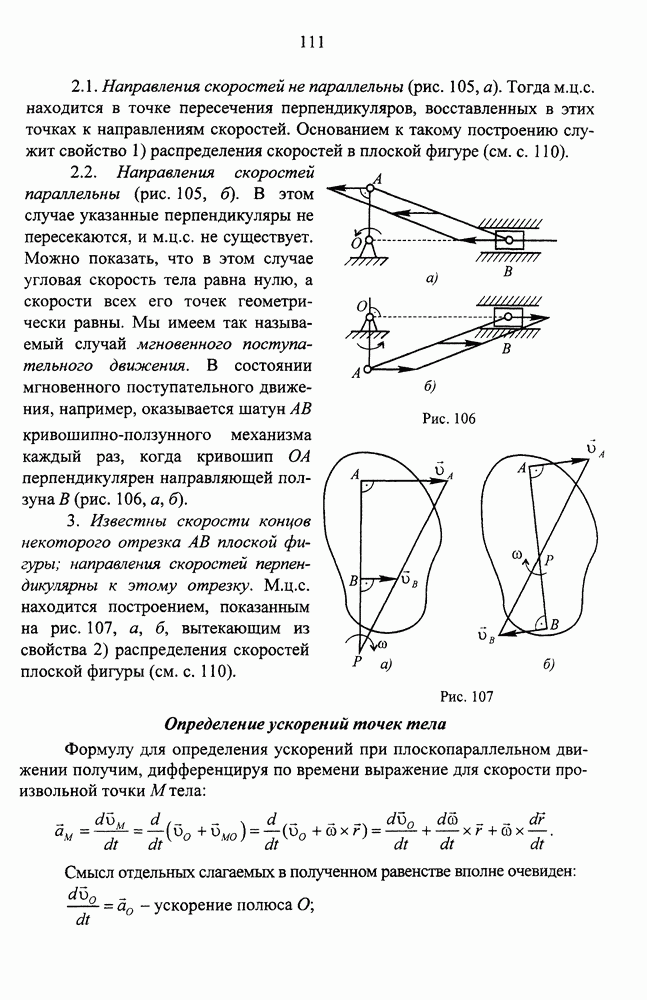
- Различные случаи определения положения мгновенного центра скоростей
- Определение ускорений точек тела
- Вопросы для самопроверки
- ЛЕКЦИЯ 10. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
- Теорема сложения скоростей
- Теорема сложения ускорений
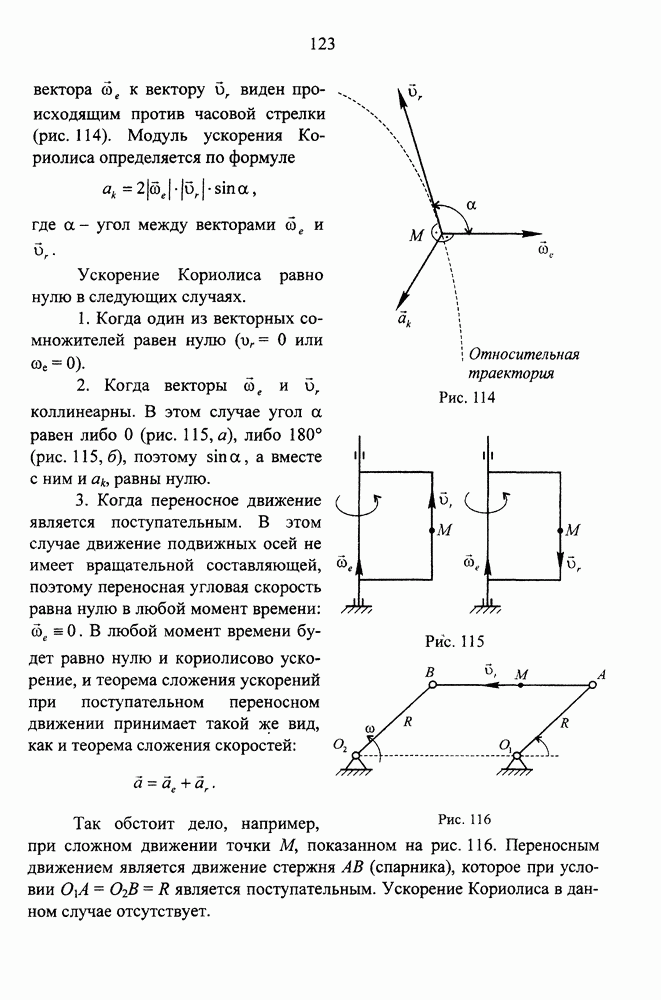
- Причины появления ускорения Кориолиса
- Вычисление и построение ускорения Кориолиса
- Вопросы для самопроверки
- ДОБАВЛЕНИЕ. КИНЕМАТИКА ПРОЦЕССА ФУГОВАНИЯ ДРЕВЕСИНЫ
- Схема и расчетная модель процесса фугования
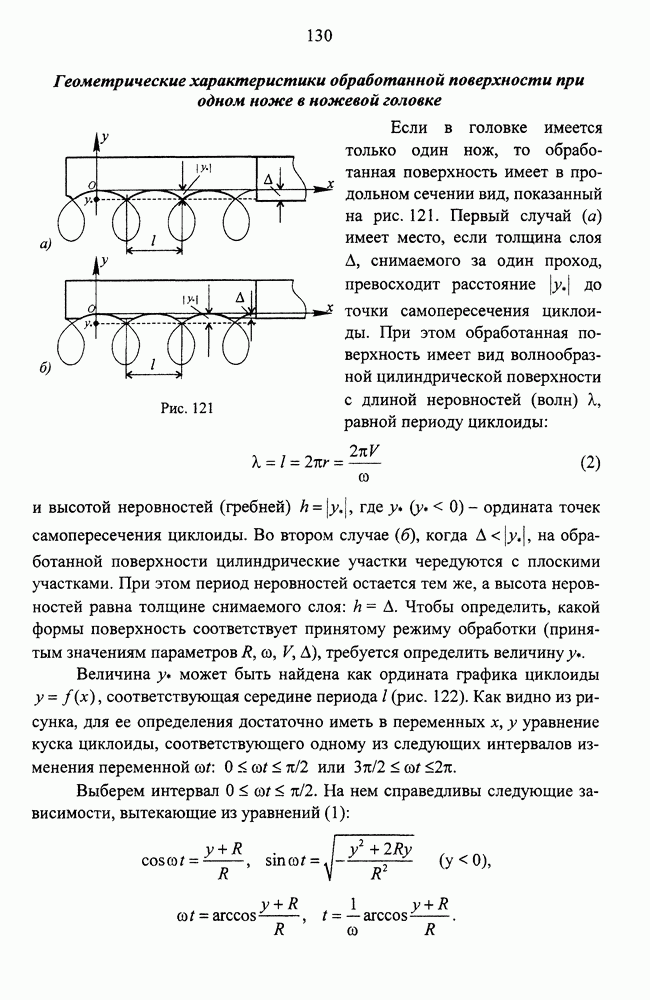
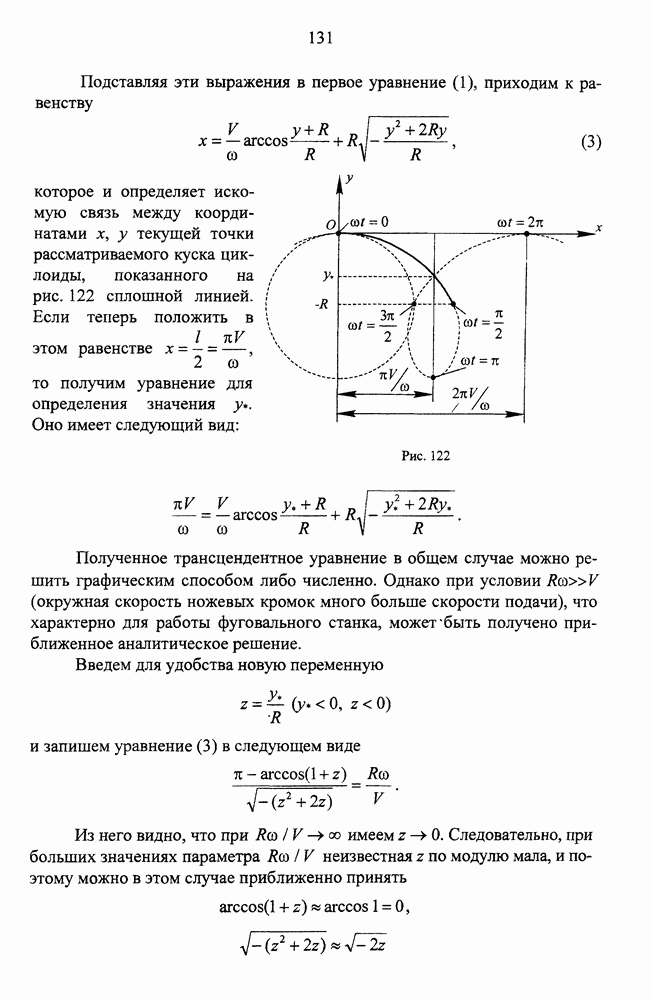
- Геометрические характеристики обработанной поверхности при одном ноже в ножевой головке
- Геометрические характеристики поверхности в случае многоножевой головки
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА