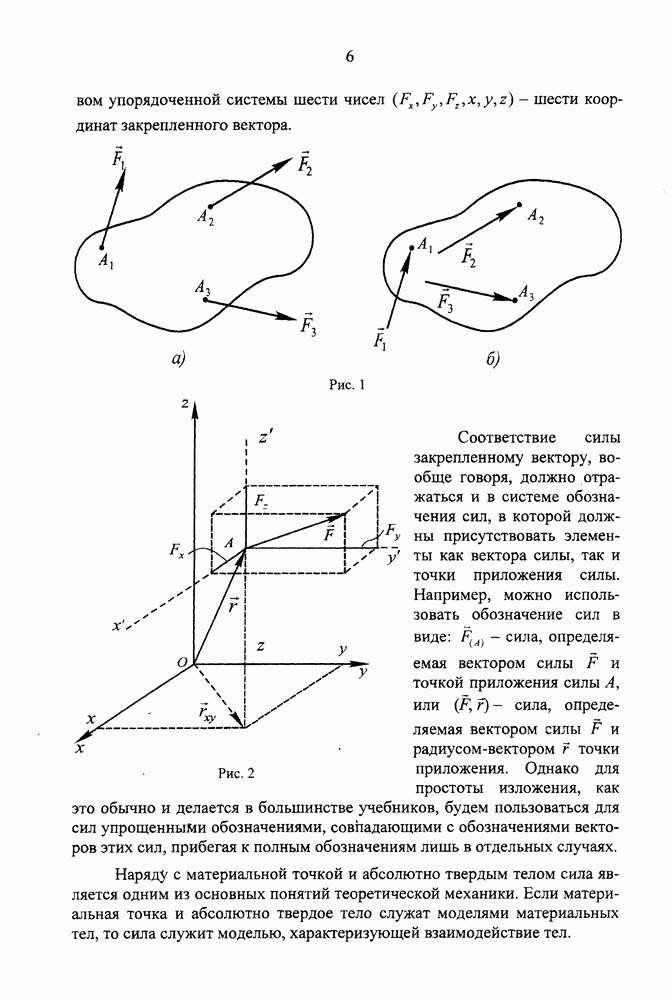
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
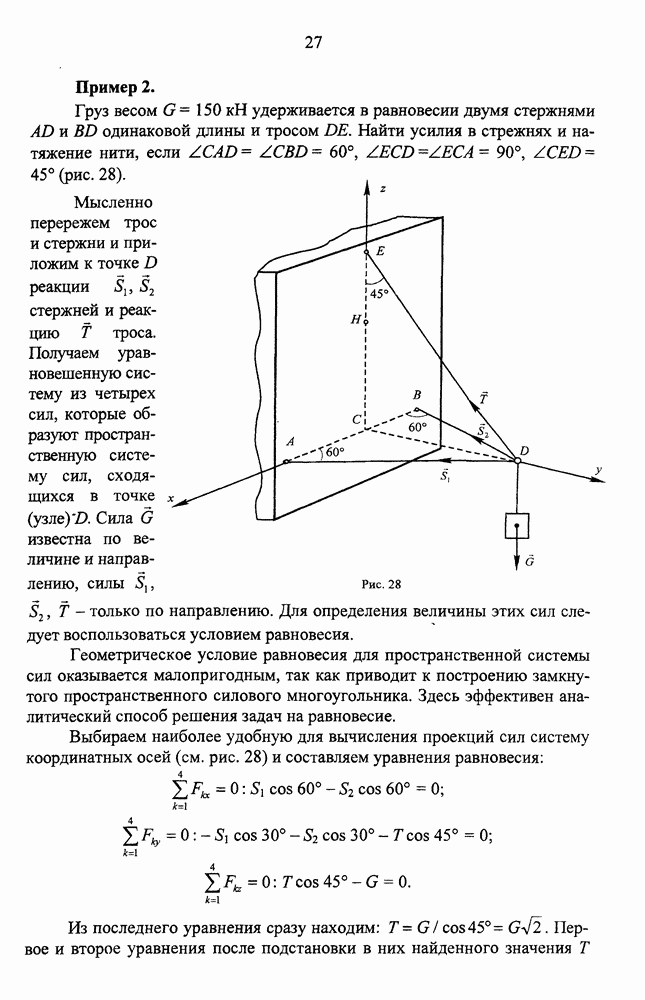
Определение скорости и ускорения точки при естественном способе задания движения
Естественные координатные оси и их орты
Пусть заданы траектория точки, начало и направление отсчета дуг. Выберем на траектории произвольным образом точку М и проведем касательную  . Плоскость, проходящая через точку М перпендикулярно к касательной
. Плоскость, проходящая через точку М перпендикулярно к касательной  , называется нормальной плоскостью траектории в точке М (рис. 84).
, называется нормальной плоскостью траектории в точке М (рис. 84).
Придадим дуговой координате s приращение  и отметим точку
и отметим точку  с координатой
с координатой  . Пусть
. Пусть  - касательная к траектории в точке
- касательная к траектории в точке  . В общем случае траектория точки - пространственная кривая, поэтому касательные
. В общем случае траектория точки - пространственная кривая, поэтому касательные  и
и  суть скрещивающиеся прямые.
суть скрещивающиеся прямые.

Рис. 83.

Рис. 84.
Проведем прямую  , параллельную касательной
, параллельную касательной  . Прямые
. Прямые  и
и  образуют плоскость
образуют плоскость  . Предельное положение плоскости
. Предельное положение плоскости  , когда точка
, когда точка  неограниченно приближается к точке М, называется соприкасающейся плоскостью траектории в точке М Соприкасающаяся плоскость представляет собой ту из бесконечного множества плоскостей, проходящих через касательную
неограниченно приближается к точке М, называется соприкасающейся плоскостью траектории в точке М Соприкасающаяся плоскость представляет собой ту из бесконечного множества плоскостей, проходящих через касательную  , которая наиболее тесно примыкает к траектории в окрестности точки М. В случае плоской траектории соприкасающаяся плоскость совпадает с плоскостью траектории.
, которая наиболее тесно примыкает к траектории в окрестности точки М. В случае плоской траектории соприкасающаяся плоскость совпадает с плоскостью траектории.
Нормальная и соприкасающаяся плоскости взаимно перпендикулярны. Проведем через точку М третью плоскость, перпендикулярную к обеим указанным плоскостям - так называемую спрямляющую плоскость. В итоге получаем прямой трехгранный угол с вершиной в точке М, называемый естественным трехгранником траектории в этой точке. Ребрами естественного трехгранника являются касательная  , главная нормаль
, главная нормаль  - линия пересечения нормальной и соприкасающейся плоскостей и бинормаль (вторая нормаль)
- линия пересечения нормальной и соприкасающейся плоскостей и бинормаль (вторая нормаль)  - линия пересечения нормальной и спрямляющей плоскостей (рис. 85).
- линия пересечения нормальной и спрямляющей плоскостей (рис. 85).
Касательная, главная нормаль и бинормаль взаимно перпендикулярны и после установления на них направлений образуют естественную систему координатных осей. Положительное направление касательной выбирается в сторону возрастания дуговой координаты s и задается ортом касательной  . Положительное направление главной нормали задается ортом
. Положительное направление главной нормали задается ортом  , который направляют от точки М в сторону вогнутости траектории.
, который направляют от точки М в сторону вогнутости траектории.  бинормали выбирают согласно правилу
бинормали выбирают согласно правилу  , чем обеспечивается правосторонность естественного координатного базиса
, чем обеспечивается правосторонность естественного координатного базиса  (см. рис. 85).
(см. рис. 85).

Рис. 85
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ. ПРЕДМЕТ И ОСНОВНЫЕ ПОНЯТИЯ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ
- СТАТИКА. ЛЕКЦИЯ 1. ЗАДАЧИ СТАТИКИ, АКСИОМЫ СТАТИКИ. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
- Момент силы относительно точки
- Алгебраический момент силы
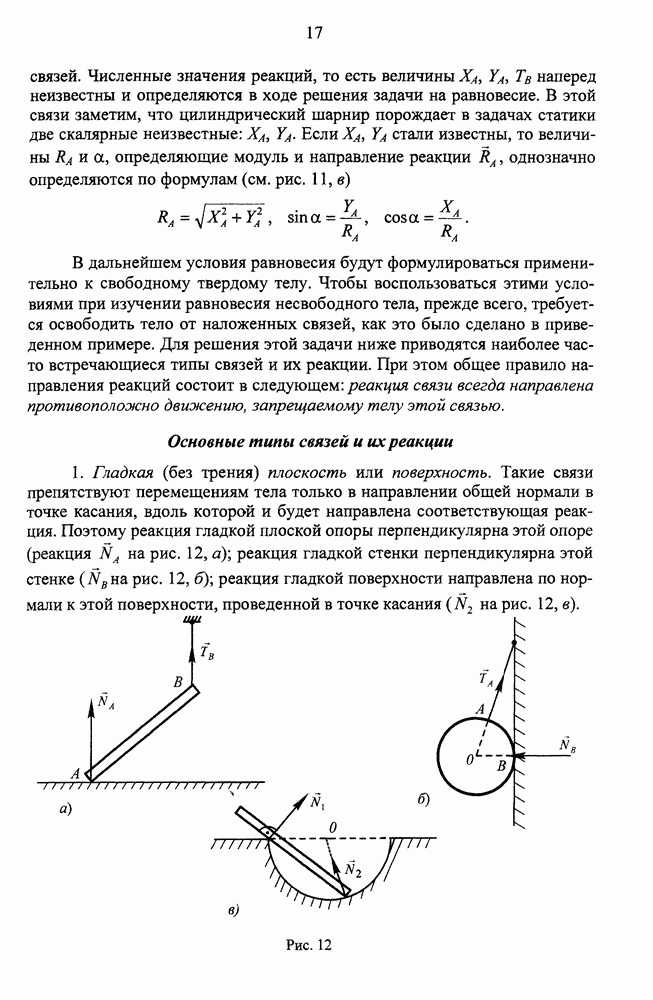
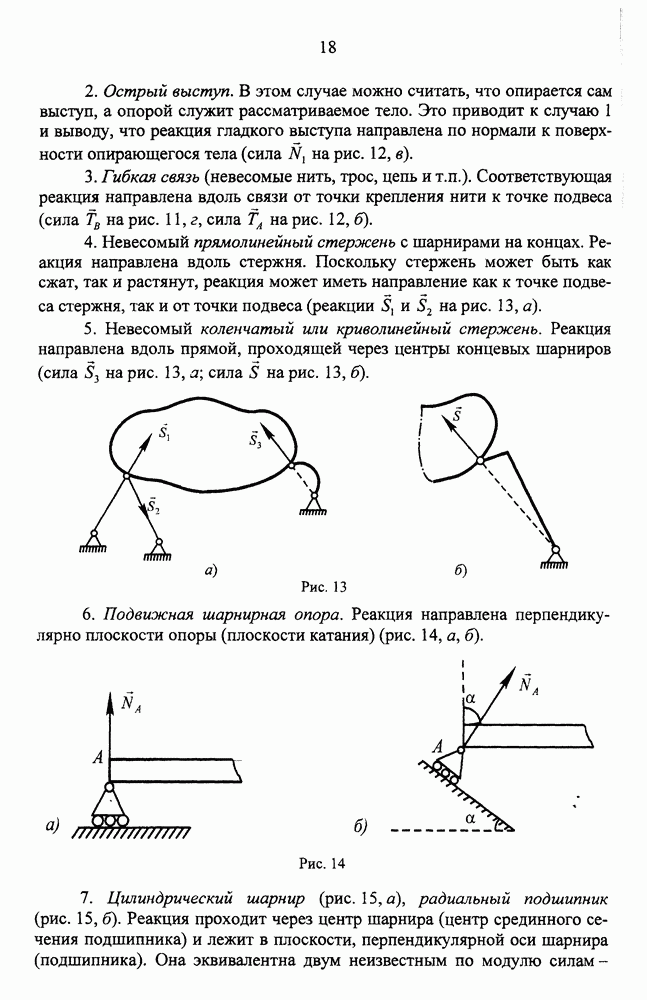
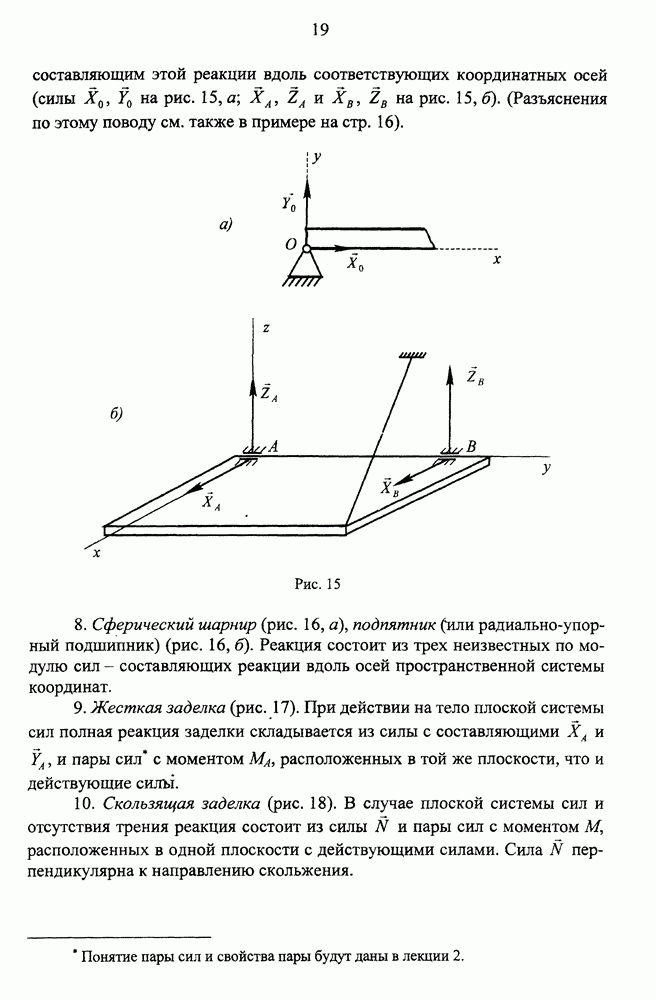
- Основные типы связей и их реакции
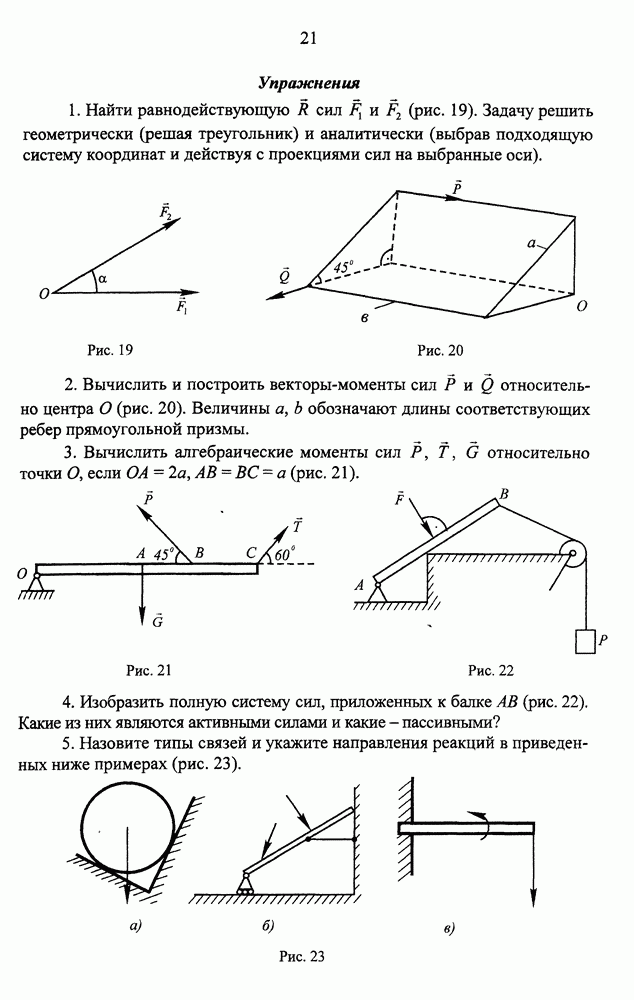
- Упражнения
- ЛЕКЦИЯ 2. СХОДЯЩИЕСЯ СИЛЫ И ПАРЫ СИЛ
- Сходящиеся силы. Приведение сходящихся сил к простейшему виду
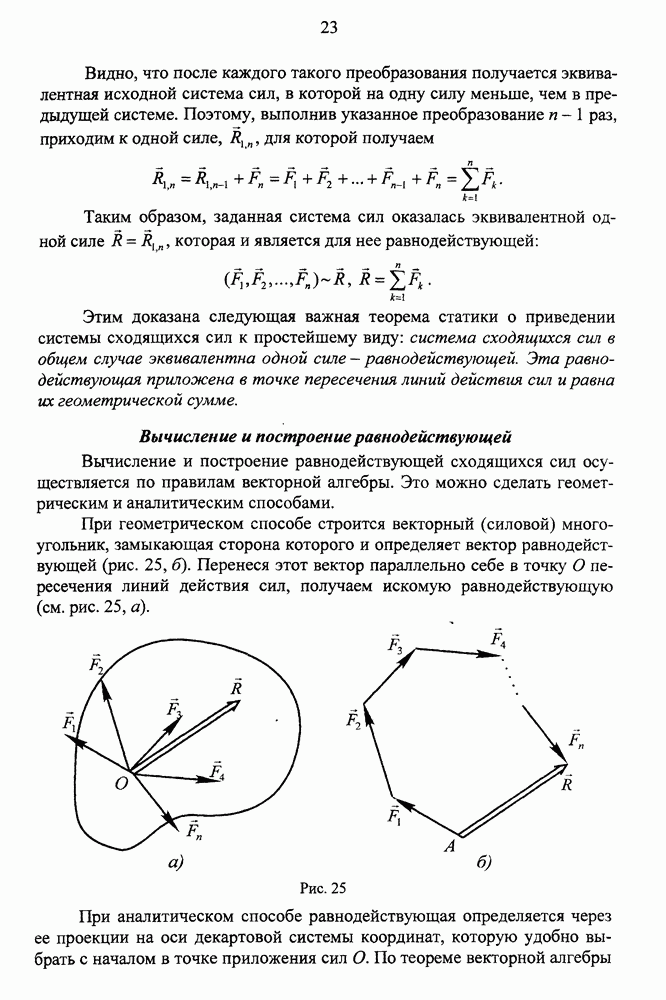
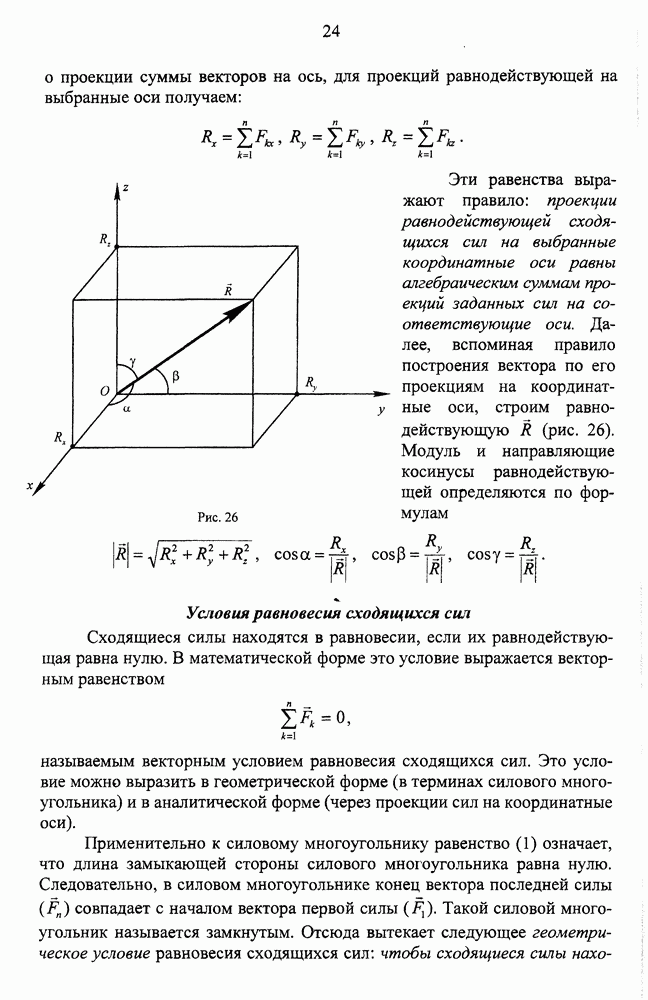
- Вычисление и построение равнодействующей
- Условия равновесия сходящихся сил
- Теорема о трех силах
- Теорема Вариньона
- Пара сил и ее момент
- Приведение системы пар сил к простейшему виду или сложение пар сил
- Упражнения
- ЛЕКЦИЯ 3. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ
- Момент силы относительно оси
- Аналитический способ вычисления момента
- Геометрический способ вычисления момента
- Преобразование пространственной произвольной системы сил
- Приведение пространственной произвольной системы сил к данному центру. Главный вектор и главный момент. Основная теорема статики
- Вычисление и построение главного вектора и главного момента
- Перемена центра приведения
- ЛЕКЦИЯ 4. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ (продолжение). ЧАСТНЫЕ СЛУЧАИ СИСТЕМЫ СИЛ
- Случаи приведения к простейшему виду
- Условия (уравнения) равновесия пространственной произвольной системы сил
- Частные случаи системы сил
- Плоская система сил
- Система параллельных сил
- Равновесие системы тел
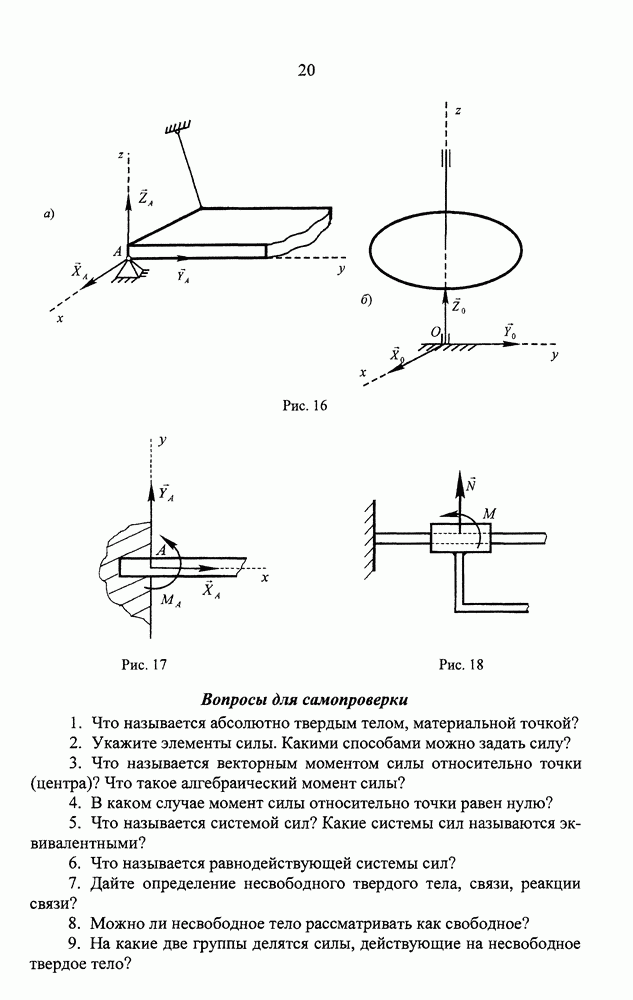
- Вопросы для самопроверки
- ЛЕКЦИЯ 5. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ И ЦЕНТР ТЯЖЕСТИ
- Центр параллельных сил
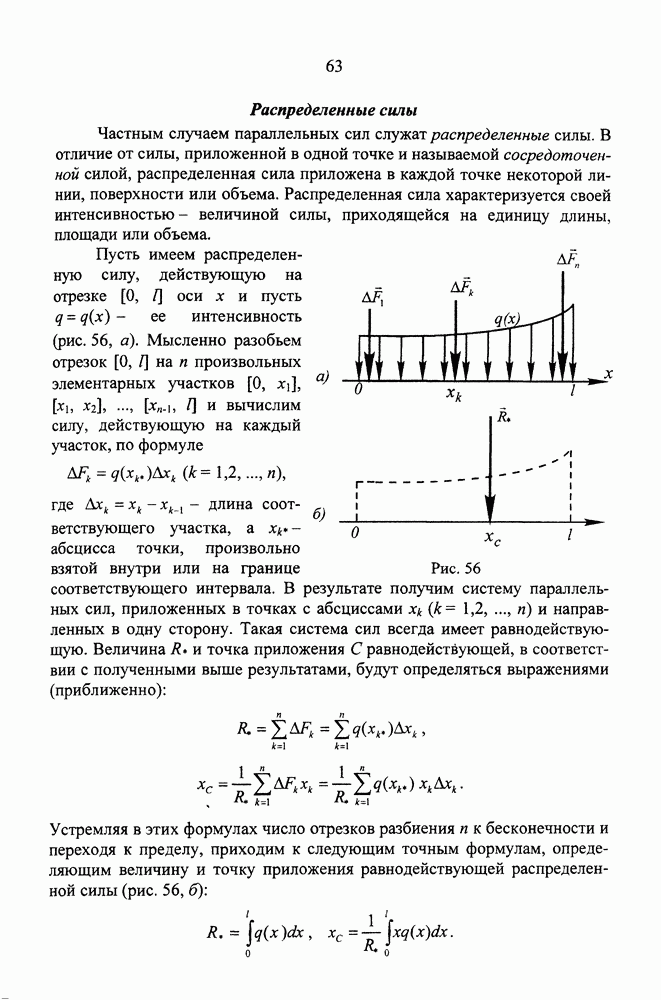
- Распределенные силы
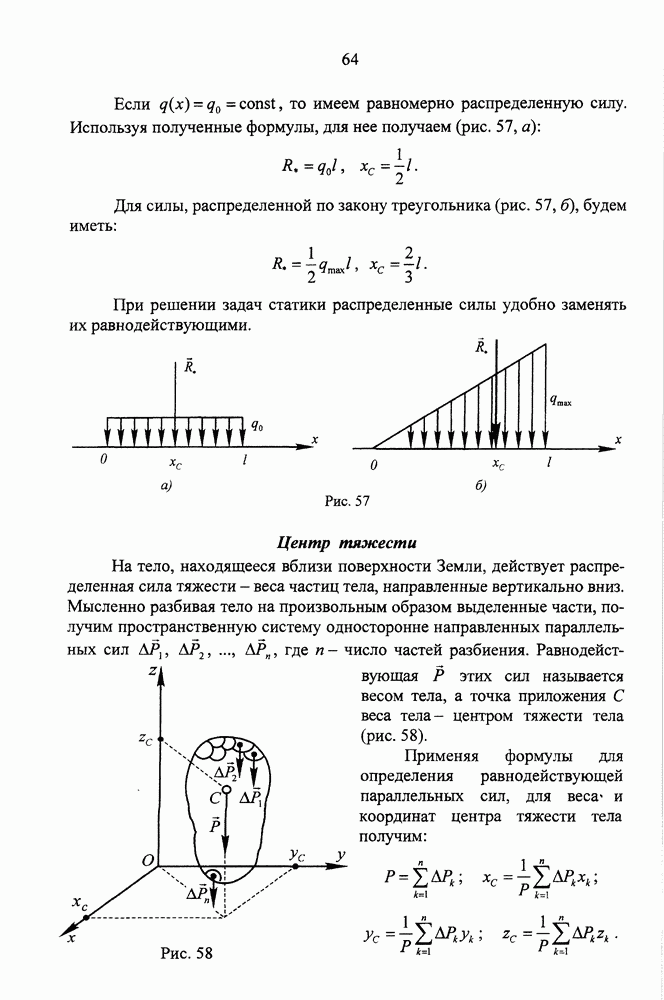
- Центр тяжести
- Интегральные формулы для координат центра тяжести
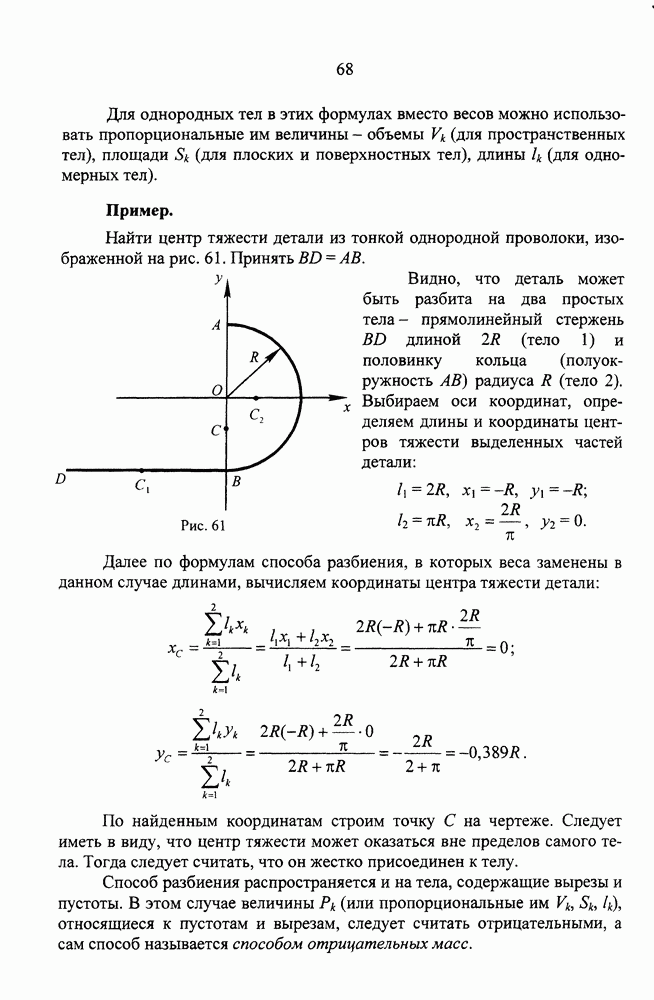
- Метод разбиения
- Вопросы для самопроверки
- ЛЕКЦИЯ 6. ТРЕНИЕ ТВЕРДЫХ ТЕЛ
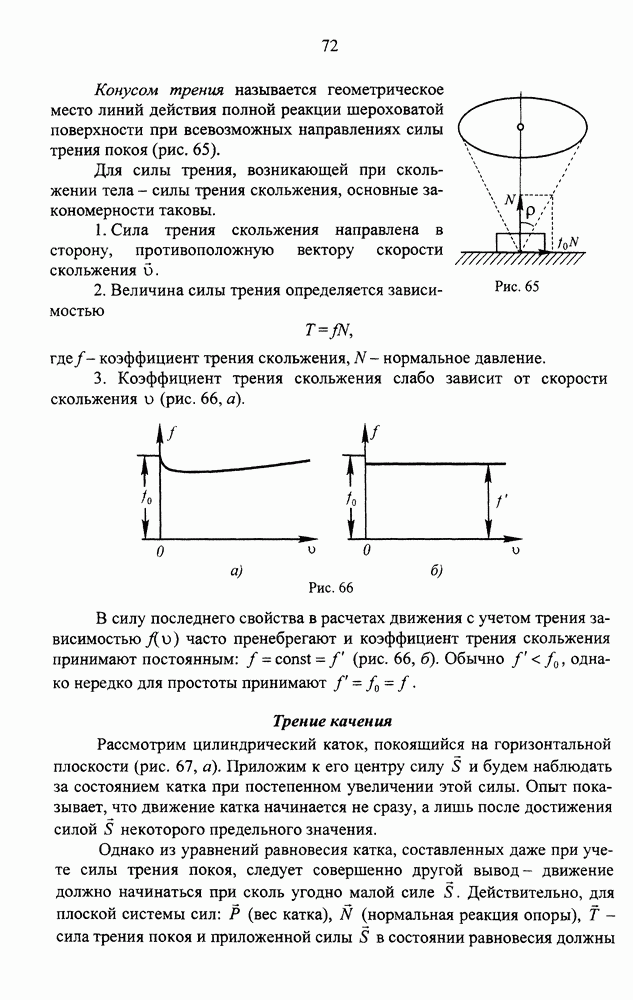
- Трение покоя и трение скольжения
- Трение качения
- Решение задач статики при учете сил трения
- Заклинивание
- Упражнения
- КИНЕМАТИКА
- ЛЕКЦИЯ 7. КИНЕМАТИКА ТОЧКИ
- Способы задания движения точки
- Определение траектории, скорости и ускорения точки при векторном способе задания движения
- Определение траектории, скорости и ускорения точки при координатном способе задания движения
- Определение скорости и ускорения точки при естественном способе задания движения
- Естественные координатные оси и их орты
- Определение скорости
- Определение ускорения
- Вопросы для самопроверки
- ЛЕКЦИЯ 8. ПРОСТЕЙШИЕ ДРИЖЕНИЯ ТВЕРДОГО ТЕЛА
- Поступательное движение
- Вращательное движение
- Уравнение вращательного движения. Угловая скорость и угловое ускорение тела
- Траектории, скорости и ускорения точек тела
- Векторы угловой скорости и углового ускорения тела
- Векторные формулы для линейной скорости, касательного и нормального ускорений точки тела
- Вопросы для самопроверки
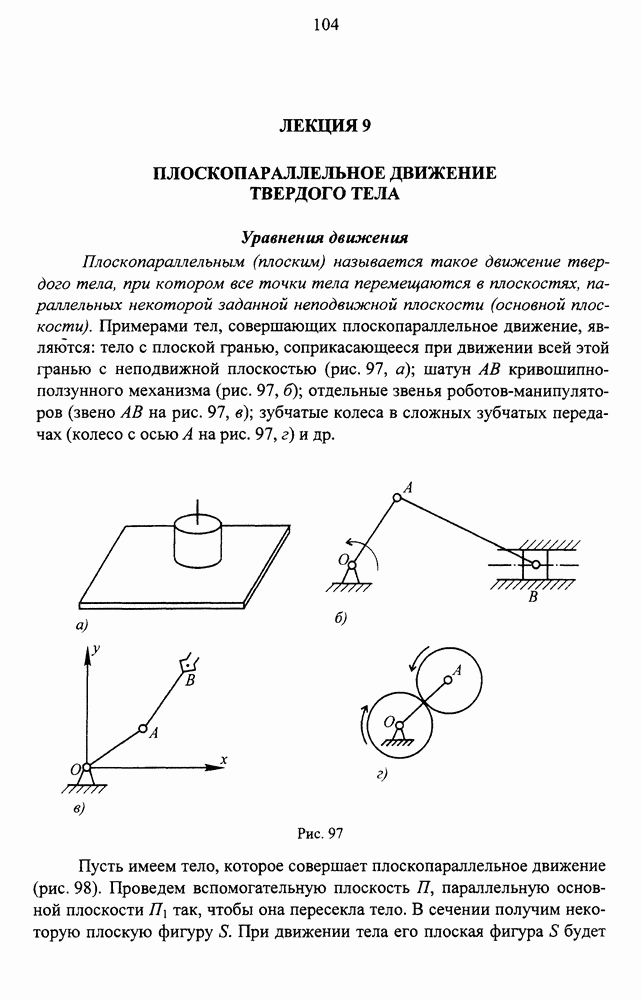
- ЛЕКЦИЯ 9. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- Уравнения движения
- Угловая скорость и угловое ускорение тела при плоскопараллельном движении
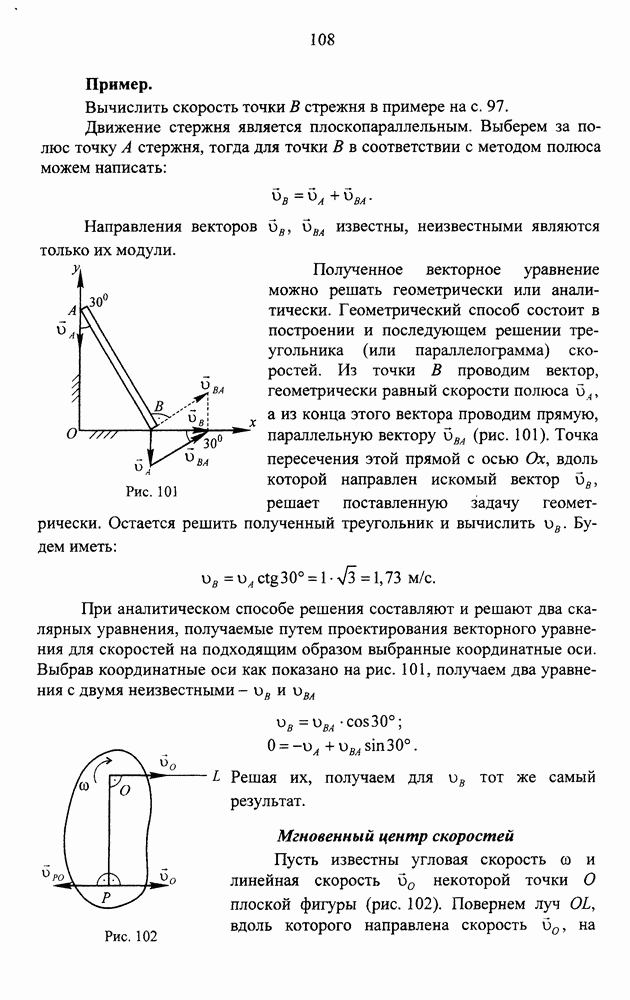
- Определение скоростей точек тела. Метод полюса
- Мгновенный центр скоростей
- Определение скоростей точек плоской фигуры через мгновенный центр скоростей
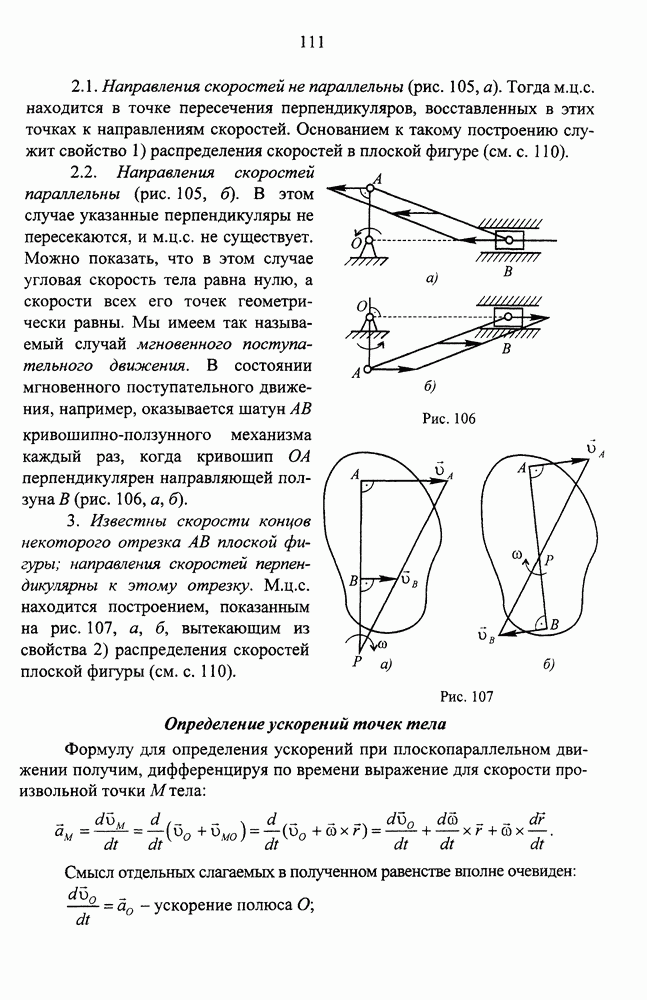
- Различные случаи определения положения мгновенного центра скоростей
- Определение ускорений точек тела
- Вопросы для самопроверки
- ЛЕКЦИЯ 10. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
- Теорема сложения скоростей
- Теорема сложения ускорений
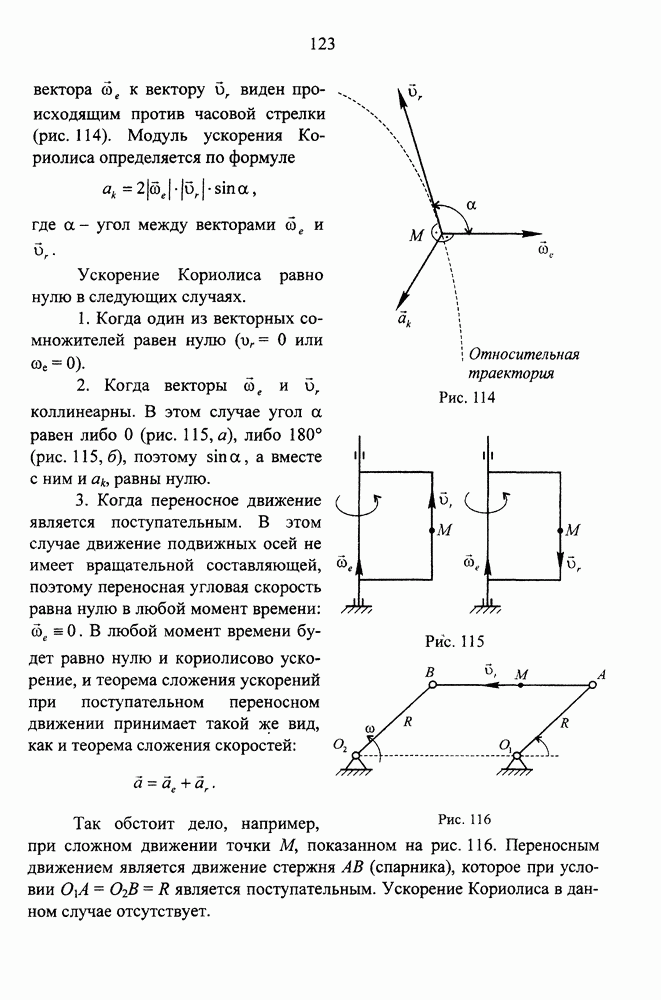
- Причины появления ускорения Кориолиса
- Вычисление и построение ускорения Кориолиса
- Вопросы для самопроверки
- ДОБАВЛЕНИЕ. КИНЕМАТИКА ПРОЦЕССА ФУГОВАНИЯ ДРЕВЕСИНЫ
- Схема и расчетная модель процесса фугования
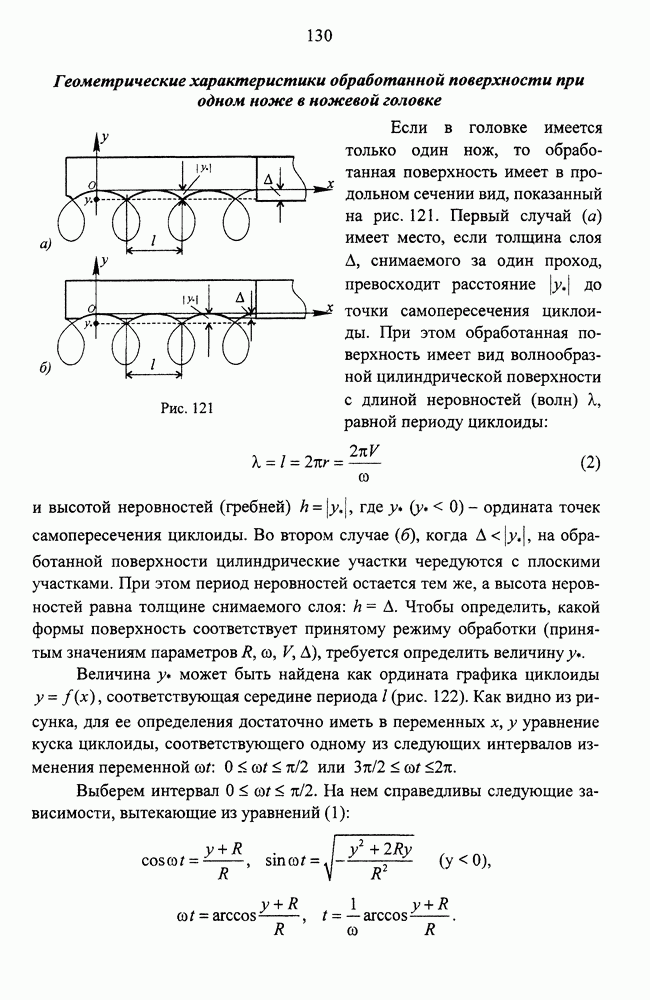
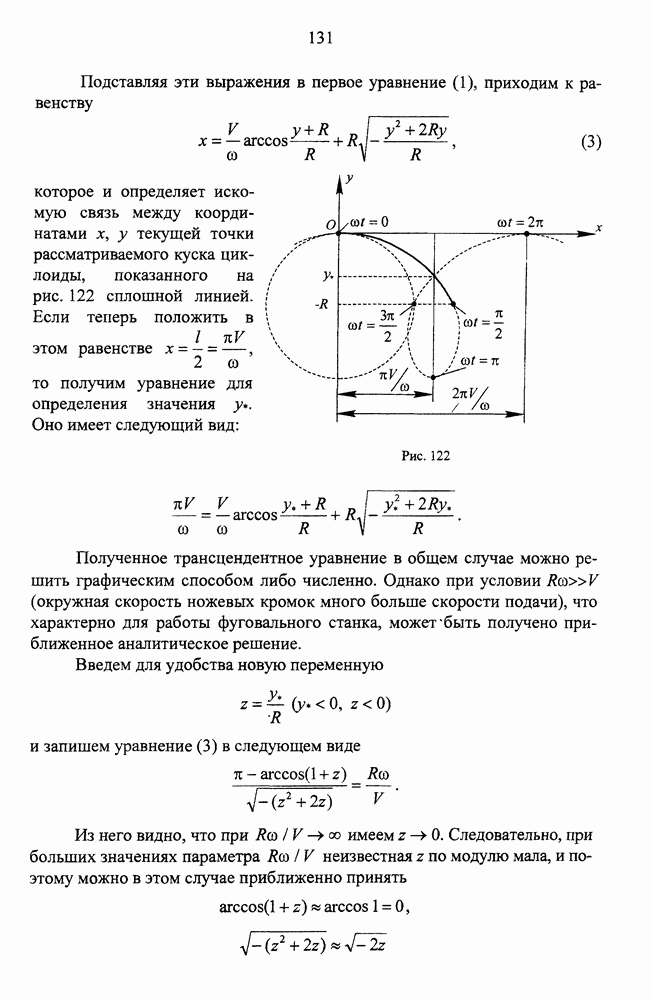
- Геометрические характеристики обработанной поверхности при одном ноже в ножевой головке
- Геометрические характеристики поверхности в случае многоножевой головки
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА