| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Определение траектории, скорости и ускорения точки при векторном способе задания движения
Пусть движение точки М задано векторным способом, то есть задан радиус-вектор точки как функция времени

Линия, описываемая концом переменного вектора, начало которого находится в заданной неподвижной точке, называется годографом этого вектора. Отсюда и из определения траектории следует правило: траектория точки есть годограф ее радиуса-вектора.
Пусть в некоторый момент t точка занимает положение М и имеет радиус-вектор  , а в момент
, а в момент  - положение
- положение  и радиус-вектор
и радиус-вектор  (рис. 78).
(рис. 78).
Вектор  , соединяющий последовательные положения точки в указанные
, соединяющий последовательные положения точки в указанные

Рис. 78.
моменты, называется вектором перемещения точки за время  . Вектор перемещения следующим образом выражается через значения вектор-функции (5):
. Вектор перемещения следующим образом выражается через значения вектор-функции (5):

Если вектор перемещения поделить на величину промежутка  , получим вектор средней скорости точки за время
, получим вектор средней скорости точки за время 

Будем теперь уменьшать промежуток  , устремляя его к нулю. Предел, к которому стремится вектор средней скорости
, устремляя его к нулю. Предел, к которому стремится вектор средней скорости  при неограниченном уменьшении промежутка
при неограниченном уменьшении промежутка  , называется скоростью точки в момент t или просто скоростью точки 0. В соответствии со сказанным для скорости получаем:
, называется скоростью точки в момент t или просто скоростью точки 0. В соответствии со сказанным для скорости получаем:

Итак, вектор скорости точки равен производной по времени от ее радиуса-вектора:

Поскольку секущая  в пределе (при
в пределе (при  ) переходит в касательную
) переходит в касательную  , приходим к выводу, что вектор скорости
, приходим к выводу, что вектор скорости  направлен по касательной к траектории в сторону движения точки.
направлен по касательной к траектории в сторону движения точки.
В общем случае скорость точки также переменна, и можно интересоваться быстротой изменения скорости. Скорость изменения скорости называется ускорением точки.
Для определения ускорения а выберем какую-либо неподвижную точку А и будем откладывать из нее вектор скорости и в различные моменты времени.
Линия, которую опишет конец N вектора скорости, представляет собой годограф скорости (рис. 79). Изменение вектора скорости выражается в том, что геометрическая точка N движется по годографу скорости, а скорость этого движения служит, по определению, ускорением точки М.

Рис. 79.
Применив для переменного вектора  все те рассуждения, которые были использованы выше для переменного вектора
все те рассуждения, которые были использованы выше для переменного вектора  , для ускорения
, для ускорения  получаем:
получаем:

или, при обозначении производной по времени точкой:

Формулы (6) - (8) являются наиболее общими формулами кинематики для определения скорости и ускорения.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ. ПРЕДМЕТ И ОСНОВНЫЕ ПОНЯТИЯ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ
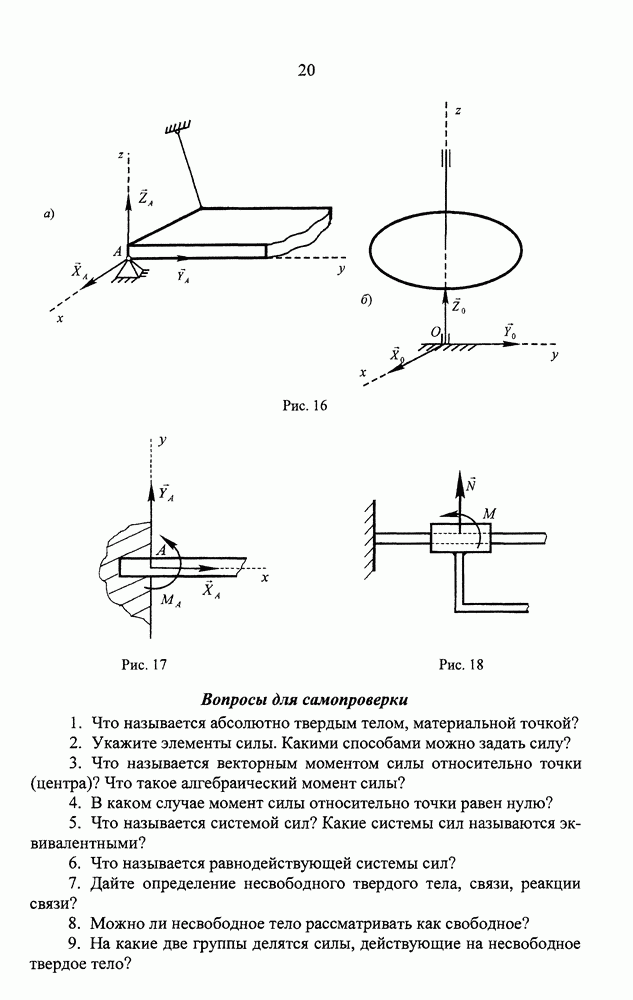
- СТАТИКА. ЛЕКЦИЯ 1. ЗАДАЧИ СТАТИКИ, АКСИОМЫ СТАТИКИ. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
- Момент силы относительно точки
- Алгебраический момент силы
- Основные типы связей и их реакции
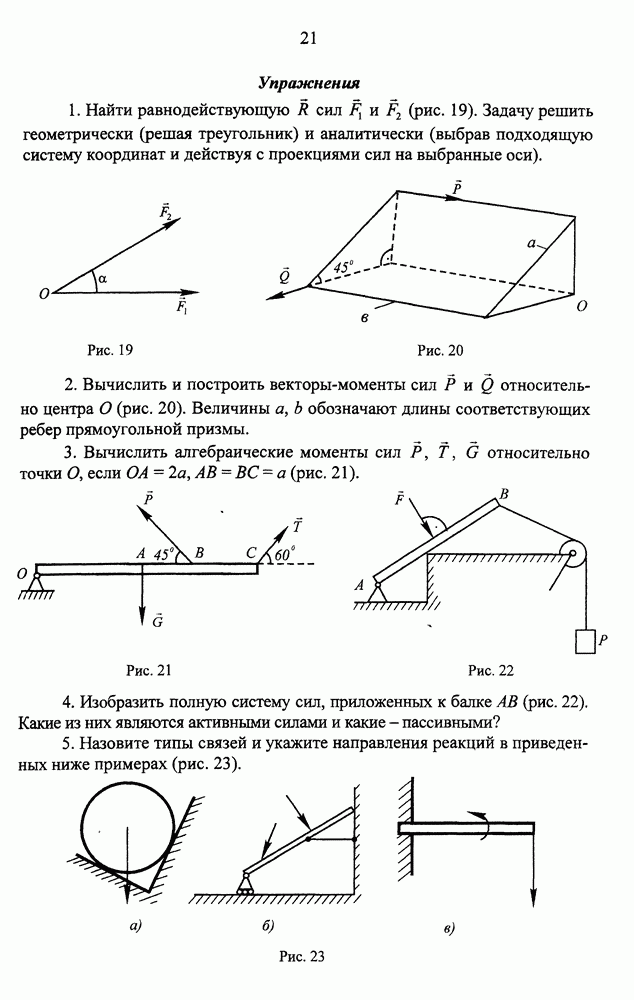
- Упражнения
- ЛЕКЦИЯ 2. СХОДЯЩИЕСЯ СИЛЫ И ПАРЫ СИЛ
- Сходящиеся силы. Приведение сходящихся сил к простейшему виду
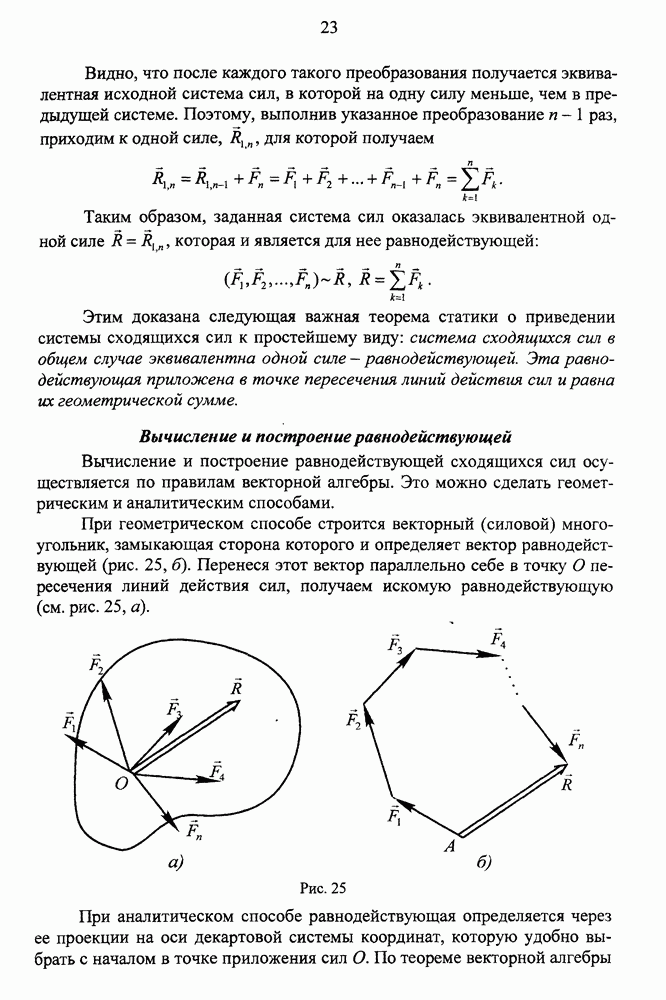
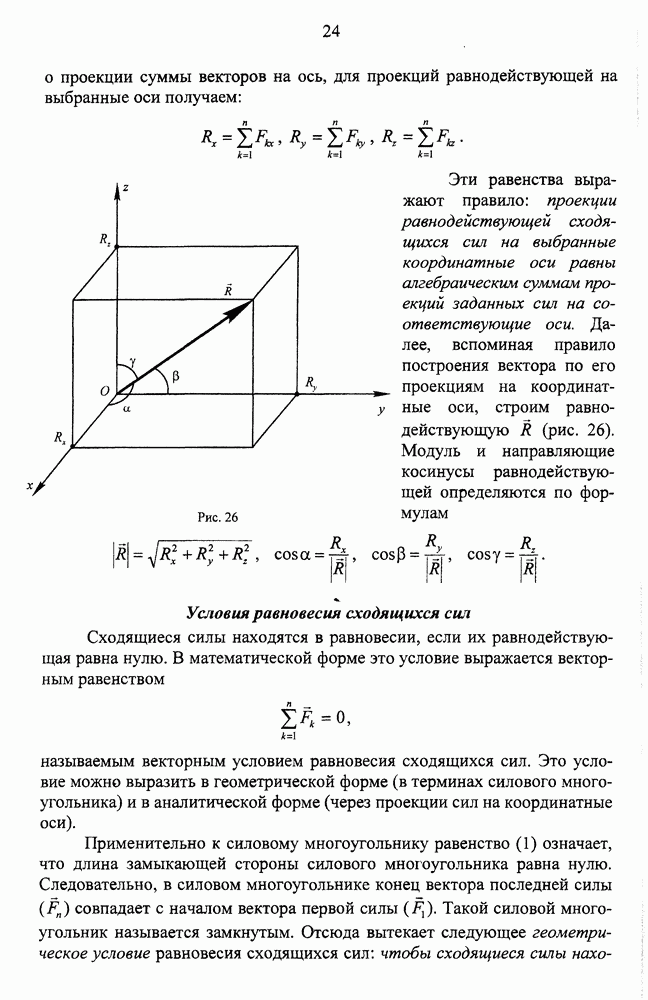
- Вычисление и построение равнодействующей
- Условия равновесия сходящихся сил
- Теорема о трех силах
- Теорема Вариньона
- Пара сил и ее момент
- Приведение системы пар сил к простейшему виду или сложение пар сил
- Упражнения
- ЛЕКЦИЯ 3. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ
- Момент силы относительно оси
- Аналитический способ вычисления момента
- Геометрический способ вычисления момента
- Преобразование пространственной произвольной системы сил
- Приведение пространственной произвольной системы сил к данному центру. Главный вектор и главный момент. Основная теорема статики
- Вычисление и построение главного вектора и главного момента
- Перемена центра приведения
- ЛЕКЦИЯ 4. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ (продолжение). ЧАСТНЫЕ СЛУЧАИ СИСТЕМЫ СИЛ
- Случаи приведения к простейшему виду
- Условия (уравнения) равновесия пространственной произвольной системы сил
- Частные случаи системы сил
- Плоская система сил
- Система параллельных сил
- Равновесие системы тел
- Вопросы для самопроверки
- ЛЕКЦИЯ 5. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ И ЦЕНТР ТЯЖЕСТИ
- Центр параллельных сил
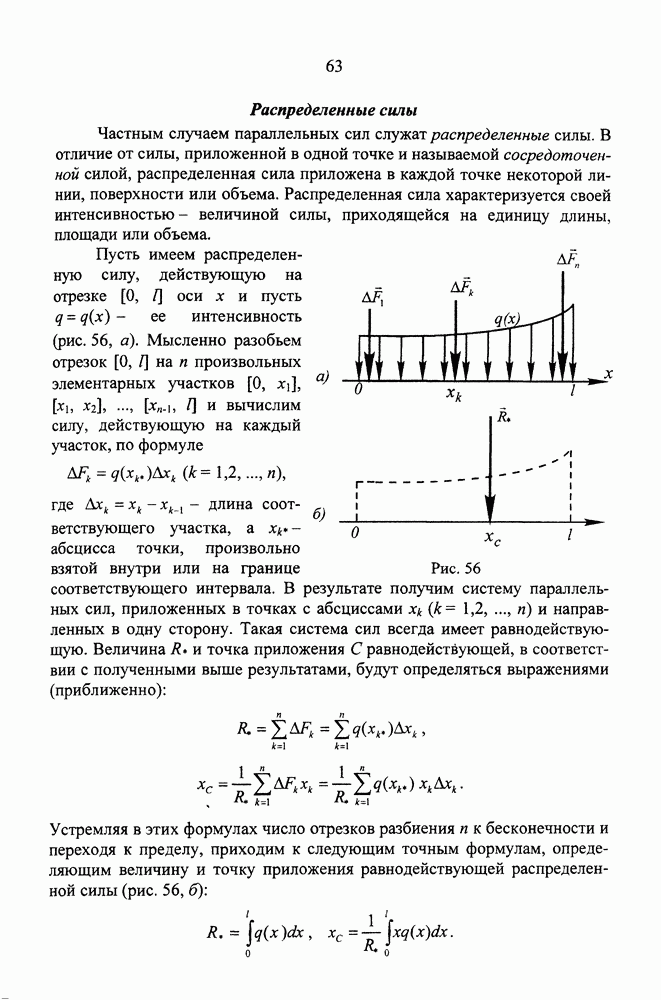
- Распределенные силы
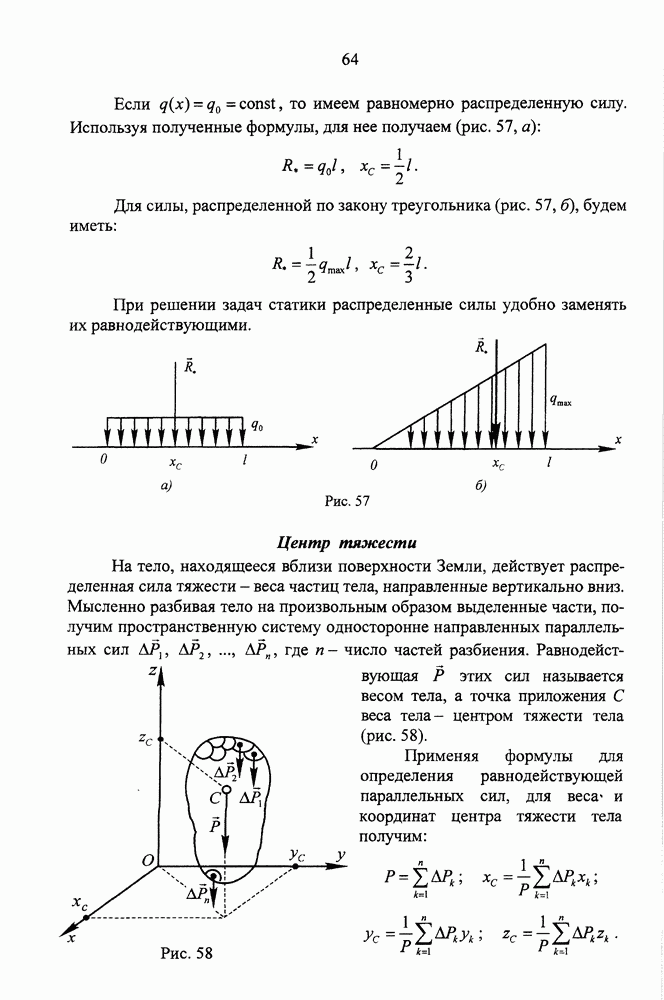
- Центр тяжести
- Интегральные формулы для координат центра тяжести
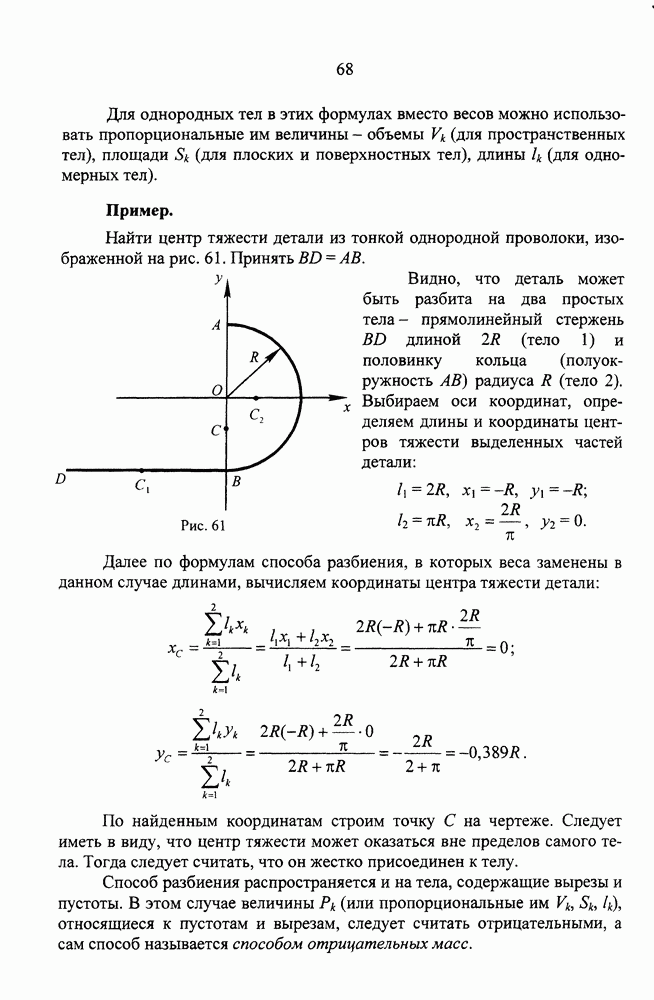
- Метод разбиения
- Вопросы для самопроверки
- ЛЕКЦИЯ 6. ТРЕНИЕ ТВЕРДЫХ ТЕЛ
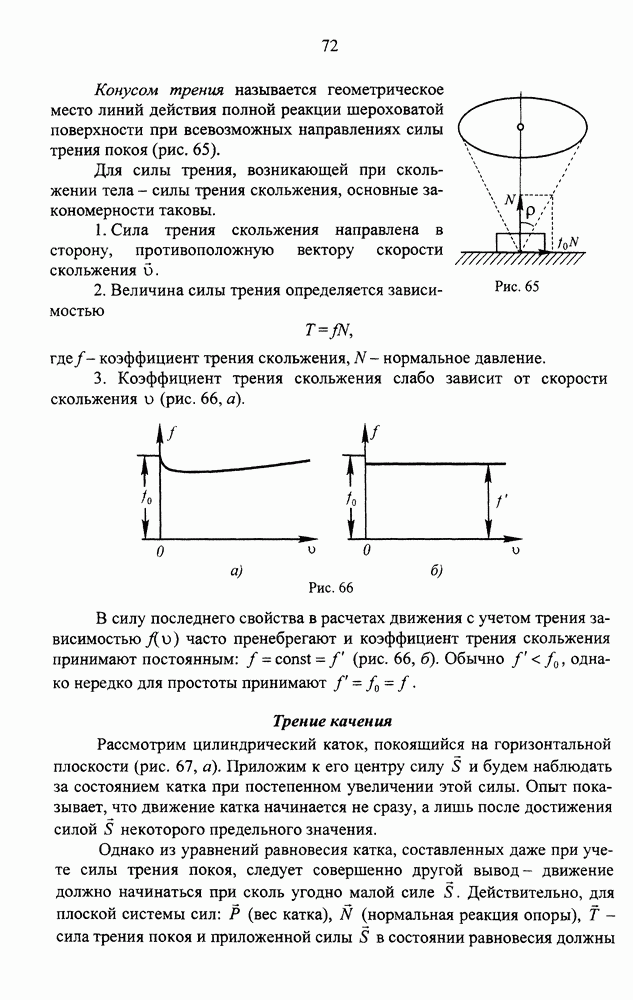
- Трение покоя и трение скольжения
- Трение качения
- Решение задач статики при учете сил трения
- Заклинивание
- Упражнения
- КИНЕМАТИКА
- ЛЕКЦИЯ 7. КИНЕМАТИКА ТОЧКИ
- Способы задания движения точки
- Определение траектории, скорости и ускорения точки при векторном способе задания движения
- Определение траектории, скорости и ускорения точки при координатном способе задания движения
- Определение скорости и ускорения точки при естественном способе задания движения
- Естественные координатные оси и их орты
- Определение скорости
- Определение ускорения
- Вопросы для самопроверки
- ЛЕКЦИЯ 8. ПРОСТЕЙШИЕ ДРИЖЕНИЯ ТВЕРДОГО ТЕЛА
- Поступательное движение
- Вращательное движение
- Уравнение вращательного движения. Угловая скорость и угловое ускорение тела
- Траектории, скорости и ускорения точек тела
- Векторы угловой скорости и углового ускорения тела
- Векторные формулы для линейной скорости, касательного и нормального ускорений точки тела
- Вопросы для самопроверки
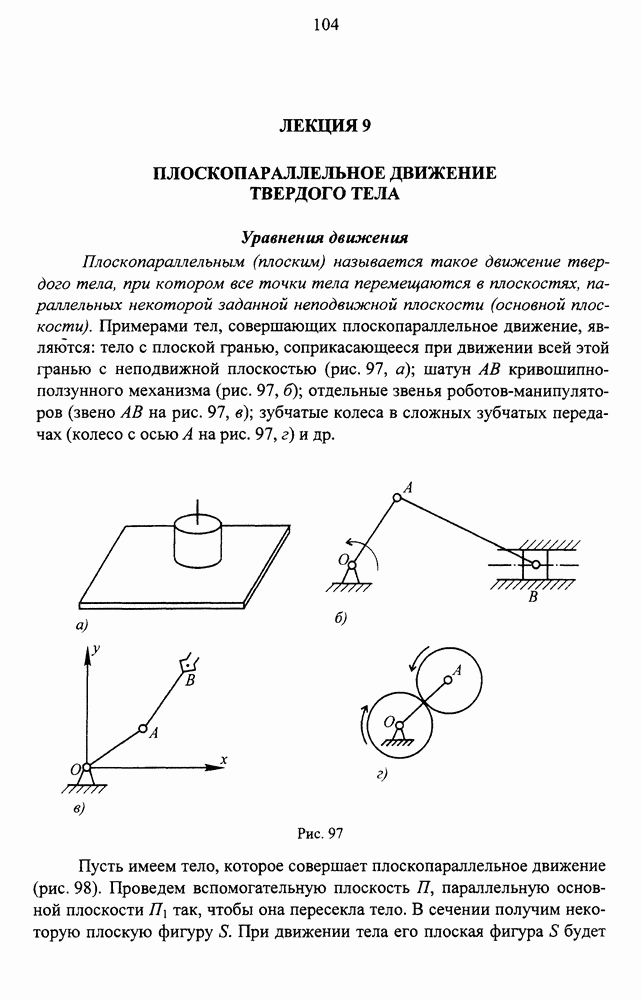
- ЛЕКЦИЯ 9. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- Уравнения движения
- Угловая скорость и угловое ускорение тела при плоскопараллельном движении
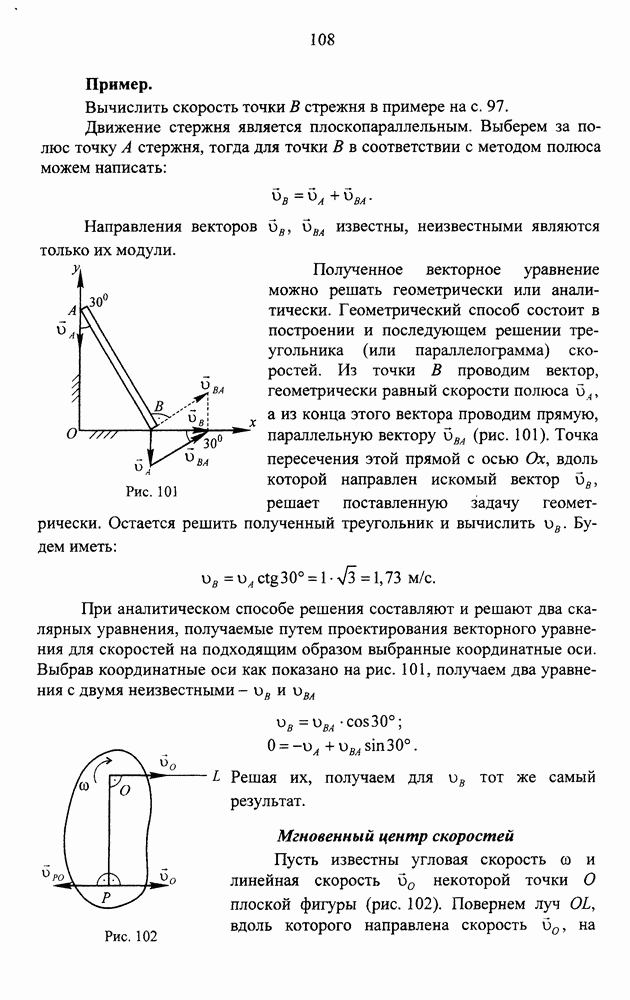
- Определение скоростей точек тела. Метод полюса
- Мгновенный центр скоростей
- Определение скоростей точек плоской фигуры через мгновенный центр скоростей
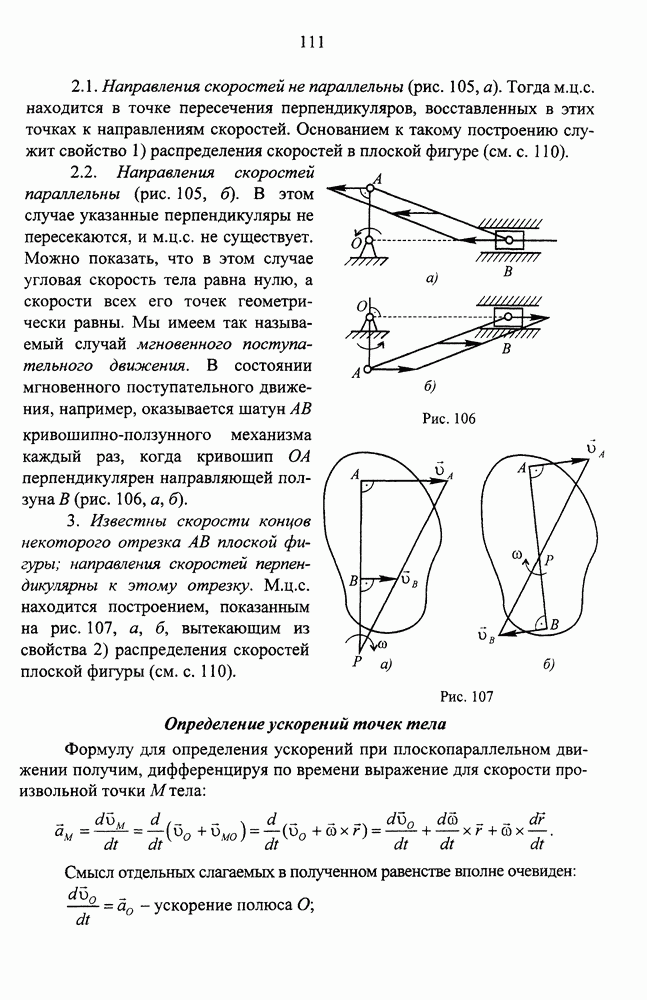
- Различные случаи определения положения мгновенного центра скоростей
- Определение ускорений точек тела
- Вопросы для самопроверки
- ЛЕКЦИЯ 10. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
- Теорема сложения скоростей
- Теорема сложения ускорений
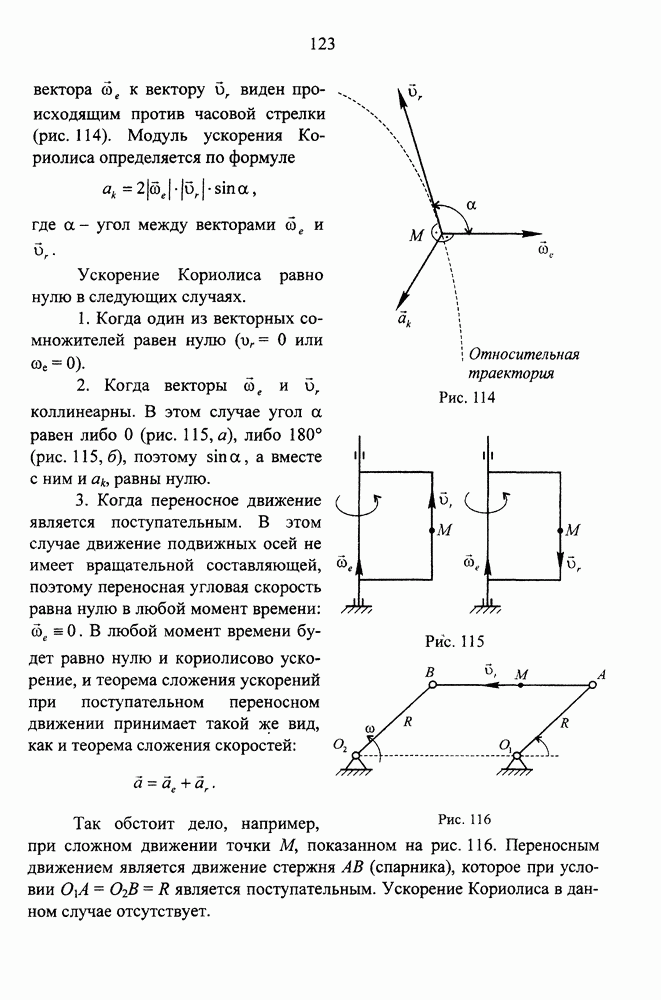
- Причины появления ускорения Кориолиса
- Вычисление и построение ускорения Кориолиса
- Вопросы для самопроверки
- ДОБАВЛЕНИЕ. КИНЕМАТИКА ПРОЦЕССА ФУГОВАНИЯ ДРЕВЕСИНЫ
- Схема и расчетная модель процесса фугования
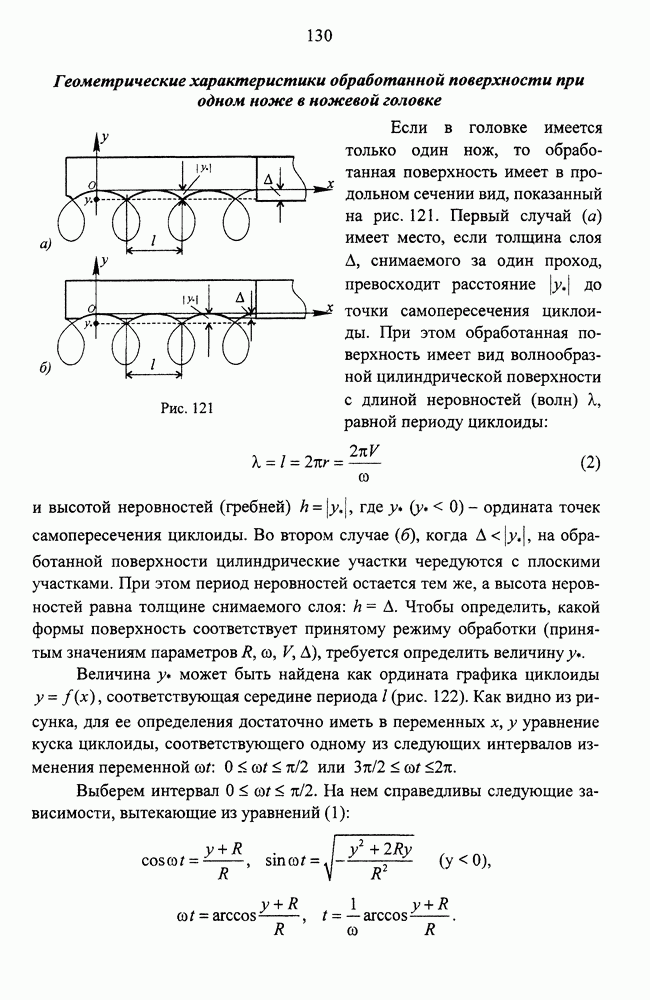
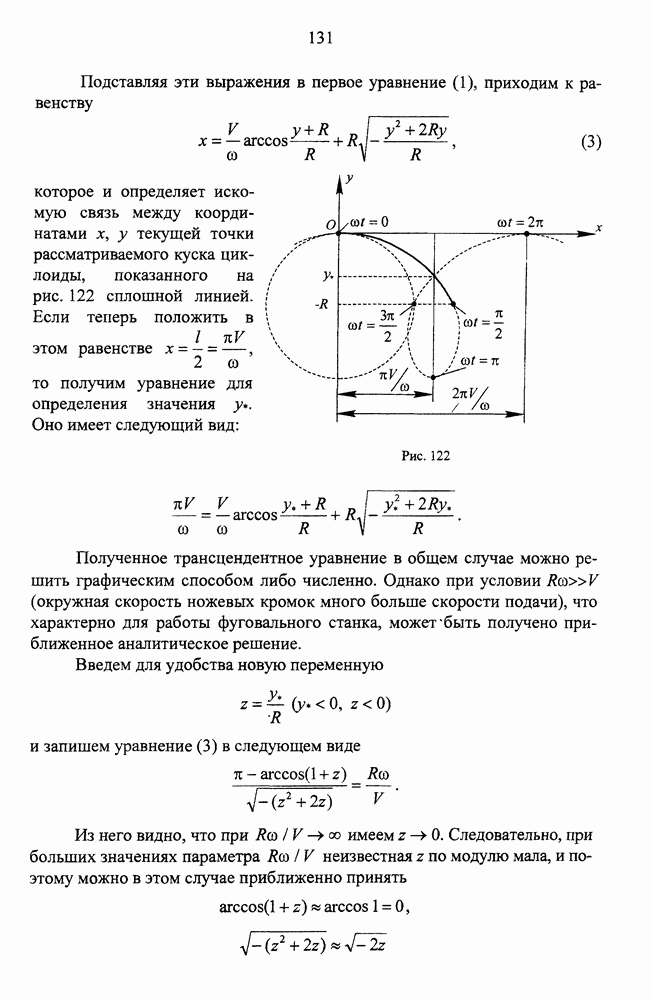
- Геометрические характеристики обработанной поверхности при одном ноже в ножевой головке
- Геометрические характеристики поверхности в случае многоножевой головки
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА