| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Решение задач статики при учете сил трения
Общие правила решения задач на равновесие с учетом сил трения остаются теми же самыми, что и при отсутствии трения. Некоторое отличие состоит только в том, что в уравнения равновесия будут входить, наряду с нормальными реакциями, также и силы трения шероховатых связей. Это увеличивает общее число неизвестных, так как силы трения покоя заранее неизвестны. В результате задача статики, будучи статически определенной при гладких связях, может оказаться при учете трения статически неопределенной.
Если рассматривать не произвольное, а предельное состояние равновесия системы с трением, то число неизвестных уменьшается - в этом случае все или некоторые силы трения принимают свои максимальные значения и могут быть выражены при помощи закона Кулона:

Здесь  - число всех связей (контактов) с трением,
- число всех связей (контактов) с трением,  - число связей в состоянии предельного равновесия,
- число связей в состоянии предельного равновесия,  — соответствующие коэффициенты трения и нормальные реакции. В задачах с трением качения то же самое можно сказать относительно моментов трения качения.
— соответствующие коэффициенты трения и нормальные реакции. В задачах с трением качения то же самое можно сказать относительно моментов трения качения.
При определении направления сил трения и моментов трения руководствуются физическими соображениями.
Пример.
Исследовать равновесие стержня АВ весом Р, удерживаемого силами трения под углом  к вертикали (рис. 68). Стержень однородный, коэффициент трения покоя между стержнем и стенкой
к вертикали (рис. 68). Стержень однородный, коэффициент трения покоя между стержнем и стенкой  между стержнем и полом
между стержнем и полом  .
.
Прикладываем к стержню действующие силы - вес Р, нормальные реакции связей  , силы трения
, силы трения  ,
,  . Это плоская произвольная система сил, следовательно, мы можем составить для стержня три независимых уравнения равновесия.
. Это плоская произвольная система сил, следовательно, мы можем составить для стержня три независимых уравнения равновесия.

Рис. 68.
Обозначив для удобства длину стержня  , запишем эти уравнения в следующем виде:
, запишем эти уравнения в следующем виде:

При произвольном а в этих уравнениях содержатся четыре неизвестные -  . Следовательно, задача не имеет однозначного решения (является статически неопределенной).
. Следовательно, задача не имеет однозначного решения (является статически неопределенной).
Ситуация меняется, если рассматривать значение  , соответствующее предельному равновесию. В этом случае для сил трения справедливы равенства
, соответствующее предельному равновесию. В этом случае для сил трения справедливы равенства

Подставляя их и значение  в написанные уравнения равновесия и разделив все члены третьего уравнения на
в написанные уравнения равновесия и разделив все члены третьего уравнения на  , приходим к следующим уравнениям предельного равновесия стержня:
, приходим к следующим уравнениям предельного равновесия стержня:

В этой системе три уравнения и три неизвестные -  , что открывает возможность для получения однозначного решения.
, что открывает возможность для получения однозначного решения.
Из первого уравнения имеем

Подставляя это значение во второе уравнение, получим

После этого определяется и реакция  :
:

Подставляя найденные значения реакций в третье уравнение, находим  :
:

При углах наклона, больших  , равновесие невозможно - стержень соскальзывает под действием силы тяжести.
, равновесие невозможно - стержень соскальзывает под действием силы тяжести.
При  стержень находится в равновесии. Однако положения равновесия при
стержень находится в равновесии. Однако положения равновесия при  уже не будут предельными, и найденные значения реакций на эти положения не распространяются. В этих положениях задача остается статически неопределенной.
уже не будут предельными, и найденные значения реакций на эти положения не распространяются. В этих положениях задача остается статически неопределенной.
Таким образом, стержень имеет бесконечное множество непрерывно расположенных положений равновесия. Соответствующий им интервал  значений угла
значений угла  определяет область равновесия.
определяет область равновесия.
Если трения нет  область равновесия стягивается в точку
область равновесия стягивается в точку  - покой становится возможным только для вертикально поставленного стержня. Эта ситуация сохраняется и в случае
- покой становится возможным только для вертикально поставленного стержня. Эта ситуация сохраняется и в случае  . Поэтому поддержание равновесия в наклонном положении за счет шероховатости стенки невозможно (даже при очень больших значениях
. Поэтому поддержание равновесия в наклонном положении за счет шероховатости стенки невозможно (даже при очень больших значениях  ).
).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ. ПРЕДМЕТ И ОСНОВНЫЕ ПОНЯТИЯ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ
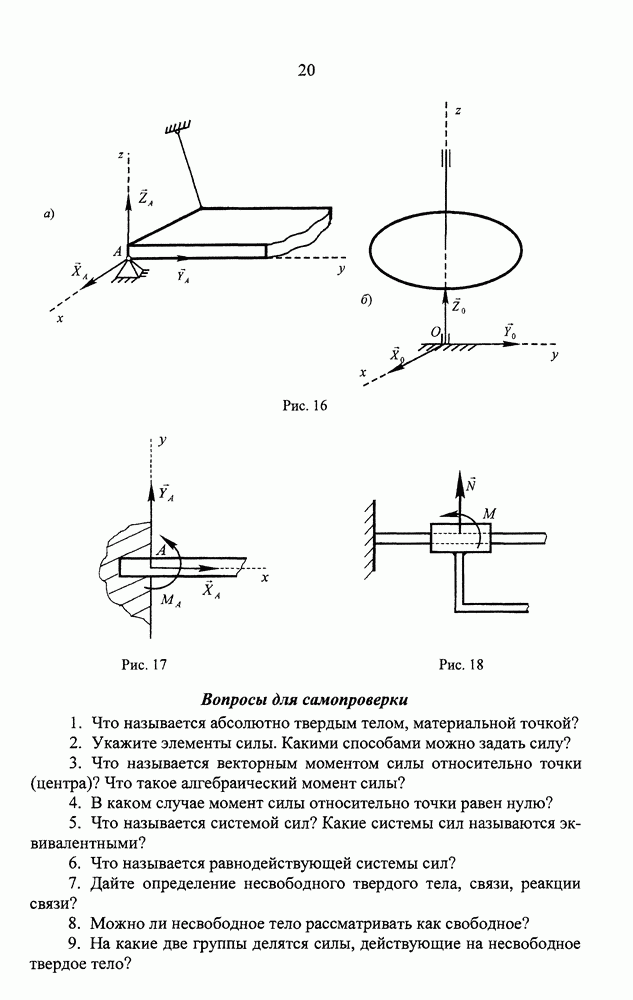
- СТАТИКА. ЛЕКЦИЯ 1. ЗАДАЧИ СТАТИКИ, АКСИОМЫ СТАТИКИ. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
- Момент силы относительно точки
- Алгебраический момент силы
- Основные типы связей и их реакции
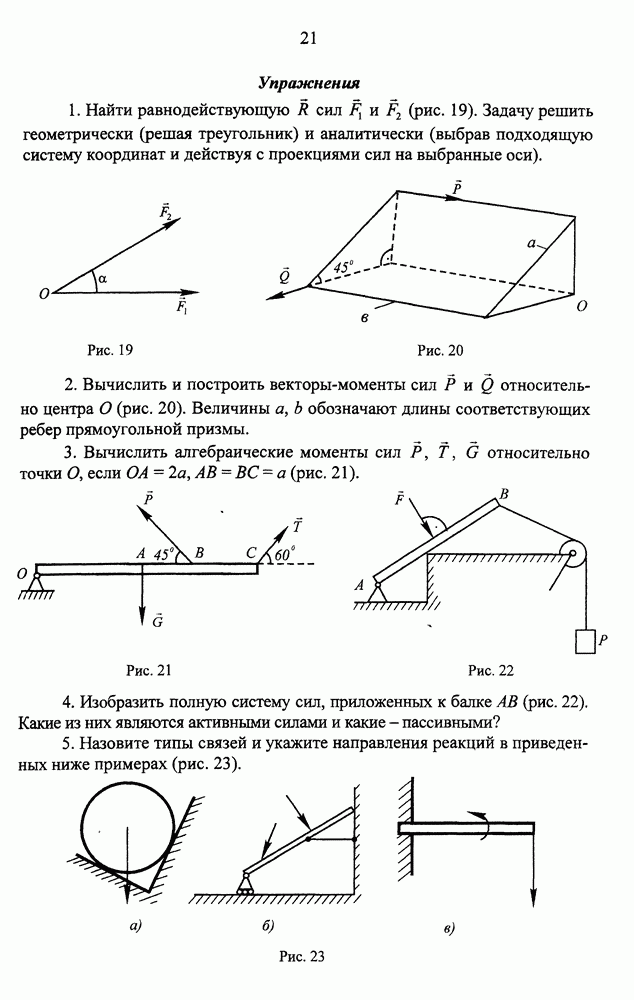
- Упражнения
- ЛЕКЦИЯ 2. СХОДЯЩИЕСЯ СИЛЫ И ПАРЫ СИЛ
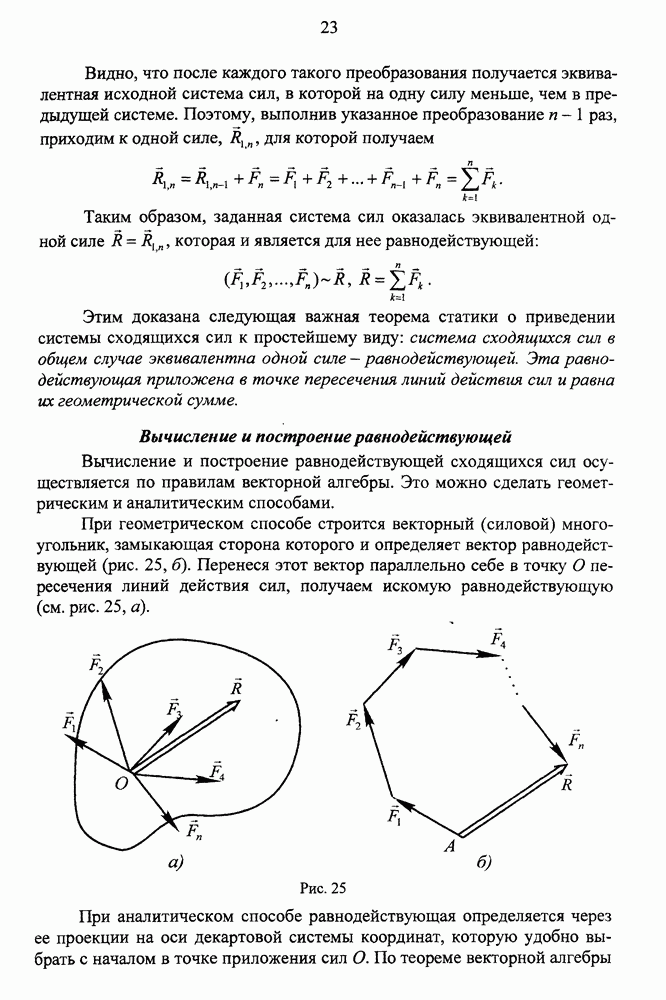
- Сходящиеся силы. Приведение сходящихся сил к простейшему виду
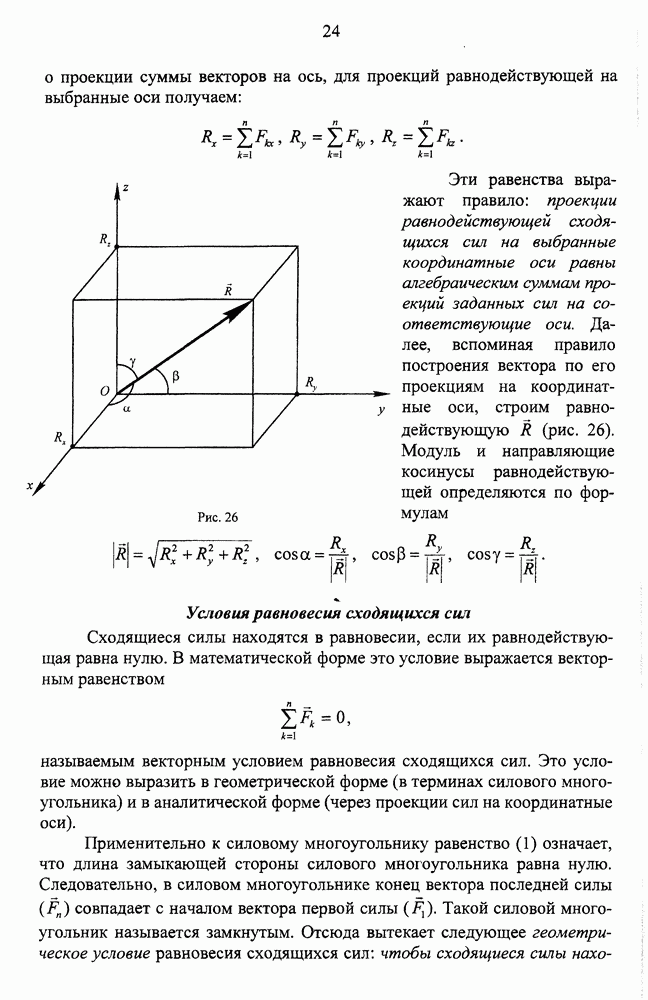
- Вычисление и построение равнодействующей
- Условия равновесия сходящихся сил
- Теорема о трех силах
- Теорема Вариньона
- Пара сил и ее момент
- Приведение системы пар сил к простейшему виду или сложение пар сил
- Упражнения
- ЛЕКЦИЯ 3. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ
- Момент силы относительно оси
- Аналитический способ вычисления момента
- Геометрический способ вычисления момента
- Преобразование пространственной произвольной системы сил
- Приведение пространственной произвольной системы сил к данному центру. Главный вектор и главный момент. Основная теорема статики
- Вычисление и построение главного вектора и главного момента
- Перемена центра приведения
- ЛЕКЦИЯ 4. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ (продолжение). ЧАСТНЫЕ СЛУЧАИ СИСТЕМЫ СИЛ
- Случаи приведения к простейшему виду
- Условия (уравнения) равновесия пространственной произвольной системы сил
- Частные случаи системы сил
- Плоская система сил
- Система параллельных сил
- Равновесие системы тел
- Вопросы для самопроверки
- ЛЕКЦИЯ 5. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ И ЦЕНТР ТЯЖЕСТИ
- Центр параллельных сил
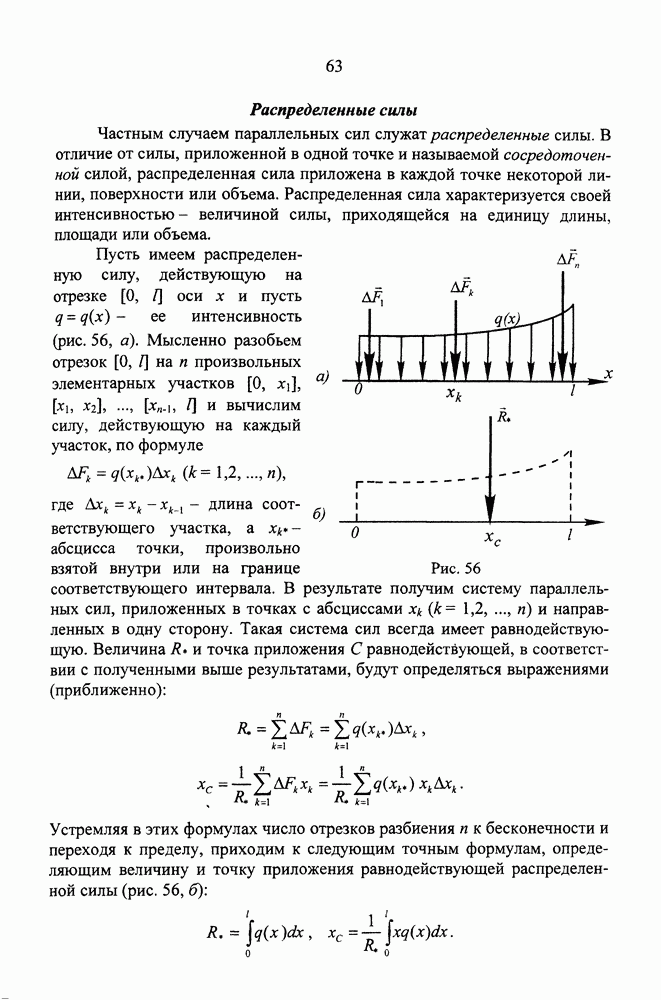
- Распределенные силы
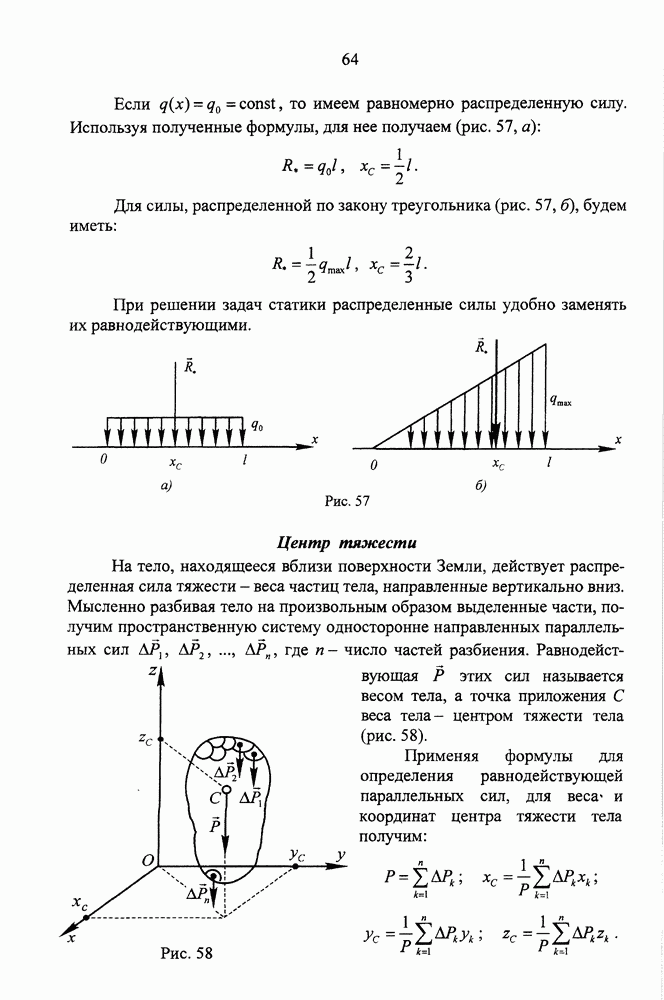
- Центр тяжести
- Интегральные формулы для координат центра тяжести
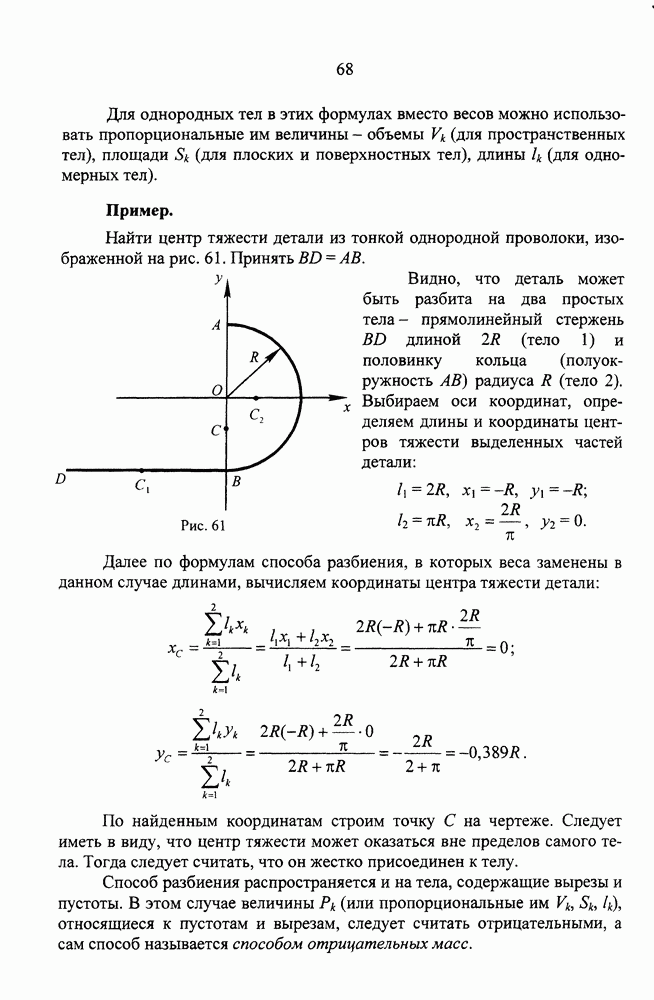
- Метод разбиения
- Вопросы для самопроверки
- ЛЕКЦИЯ 6. ТРЕНИЕ ТВЕРДЫХ ТЕЛ
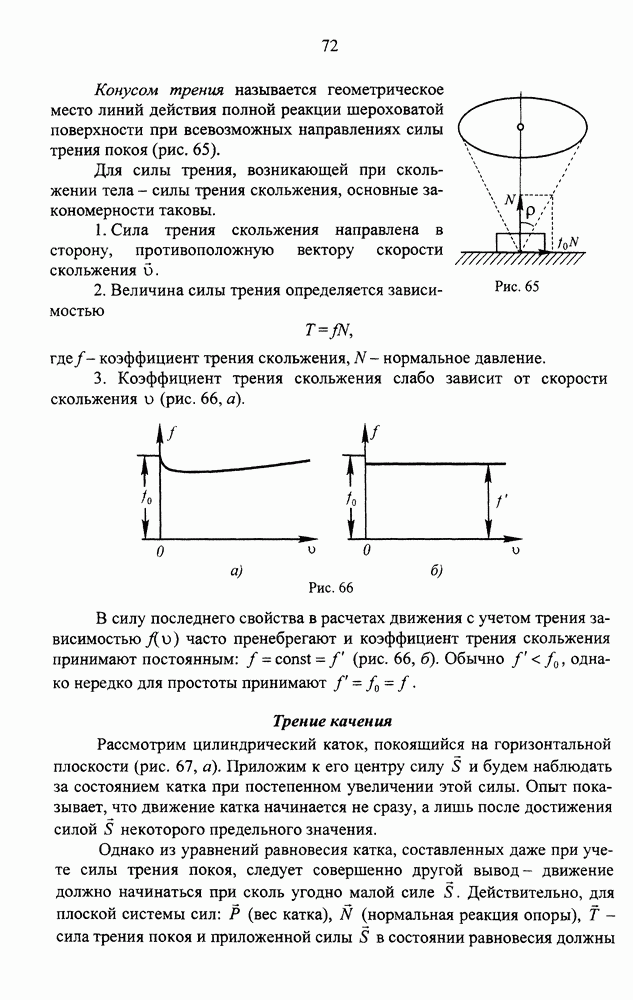
- Трение покоя и трение скольжения
- Трение качения
- Решение задач статики при учете сил трения
- Заклинивание
- Упражнения
- КИНЕМАТИКА
- ЛЕКЦИЯ 7. КИНЕМАТИКА ТОЧКИ
- Способы задания движения точки
- Определение траектории, скорости и ускорения точки при векторном способе задания движения
- Определение траектории, скорости и ускорения точки при координатном способе задания движения
- Определение скорости и ускорения точки при естественном способе задания движения
- Естественные координатные оси и их орты
- Определение скорости
- Определение ускорения
- Вопросы для самопроверки
- ЛЕКЦИЯ 8. ПРОСТЕЙШИЕ ДРИЖЕНИЯ ТВЕРДОГО ТЕЛА
- Поступательное движение
- Вращательное движение
- Уравнение вращательного движения. Угловая скорость и угловое ускорение тела
- Траектории, скорости и ускорения точек тела
- Векторы угловой скорости и углового ускорения тела
- Векторные формулы для линейной скорости, касательного и нормального ускорений точки тела
- Вопросы для самопроверки
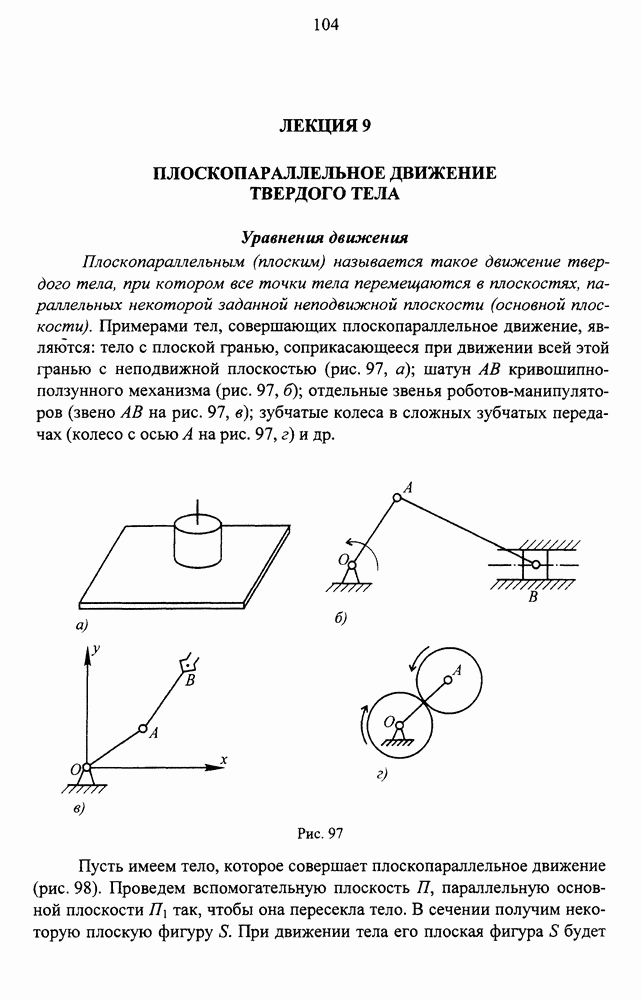
- ЛЕКЦИЯ 9. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- Уравнения движения
- Угловая скорость и угловое ускорение тела при плоскопараллельном движении
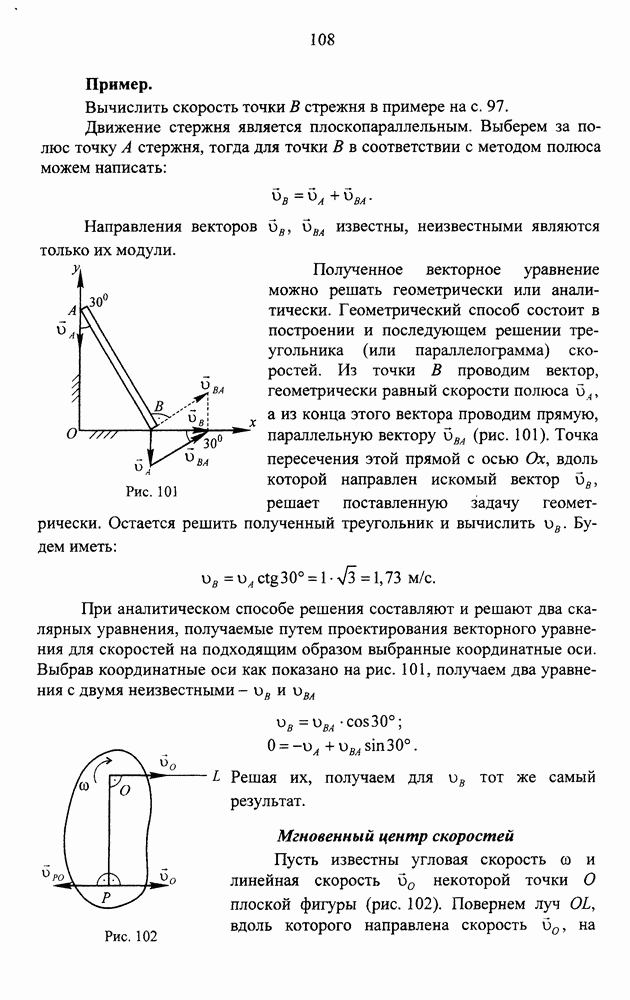
- Определение скоростей точек тела. Метод полюса
- Мгновенный центр скоростей
- Определение скоростей точек плоской фигуры через мгновенный центр скоростей
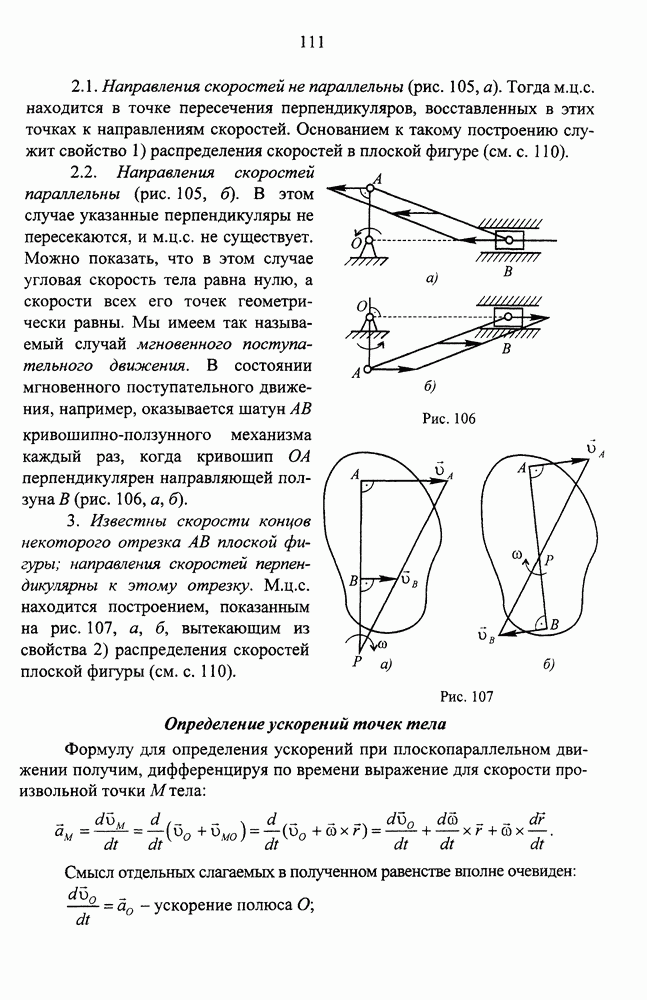
- Различные случаи определения положения мгновенного центра скоростей
- Определение ускорений точек тела
- Вопросы для самопроверки
- ЛЕКЦИЯ 10. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
- Теорема сложения скоростей
- Теорема сложения ускорений
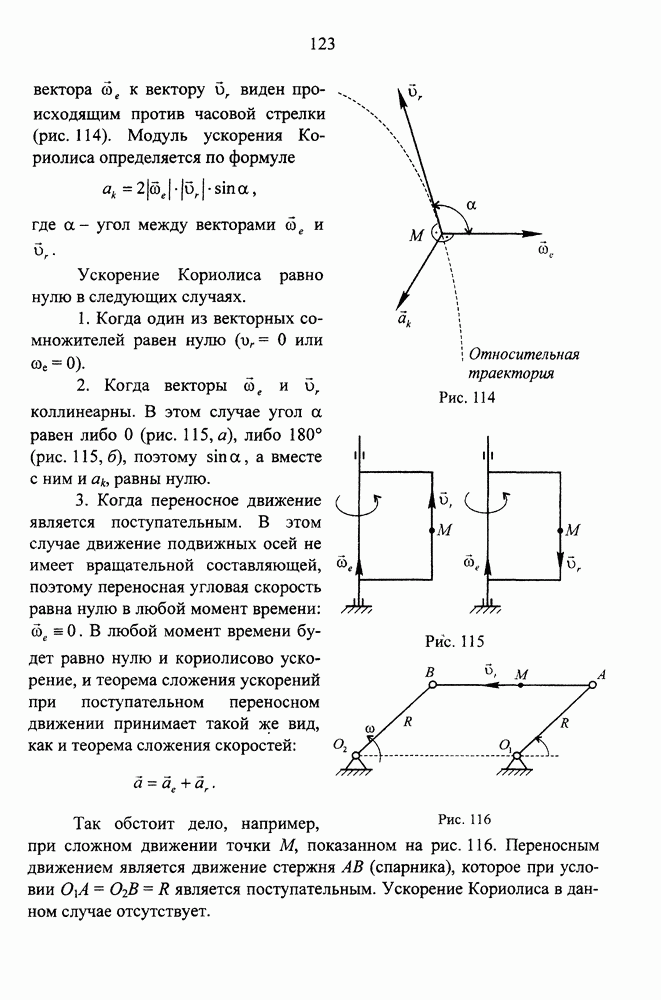
- Причины появления ускорения Кориолиса
- Вычисление и построение ускорения Кориолиса
- Вопросы для самопроверки
- ДОБАВЛЕНИЕ. КИНЕМАТИКА ПРОЦЕССА ФУГОВАНИЯ ДРЕВЕСИНЫ
- Схема и расчетная модель процесса фугования
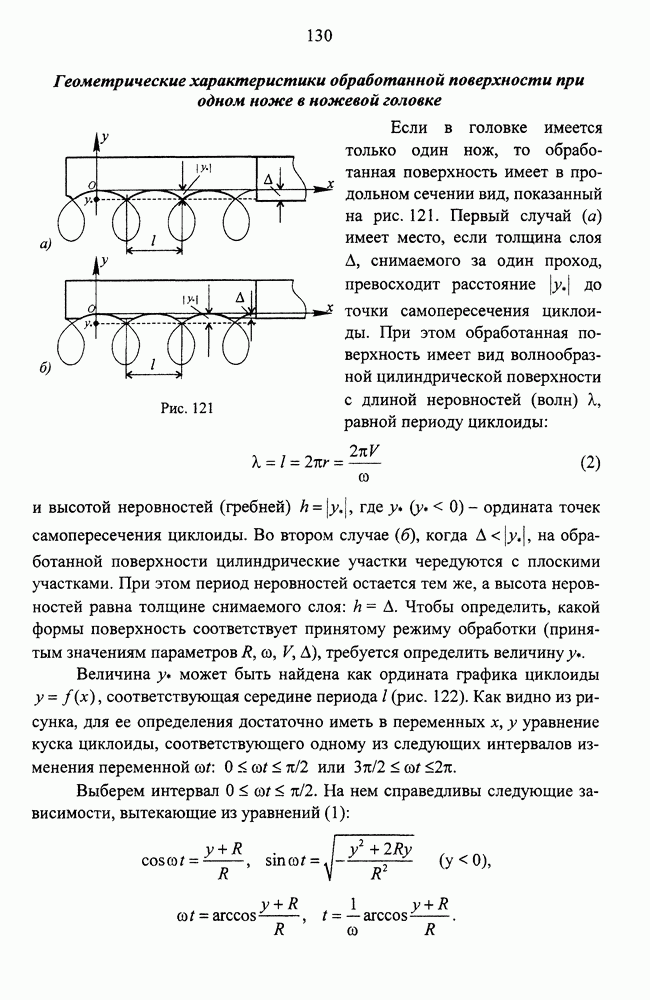
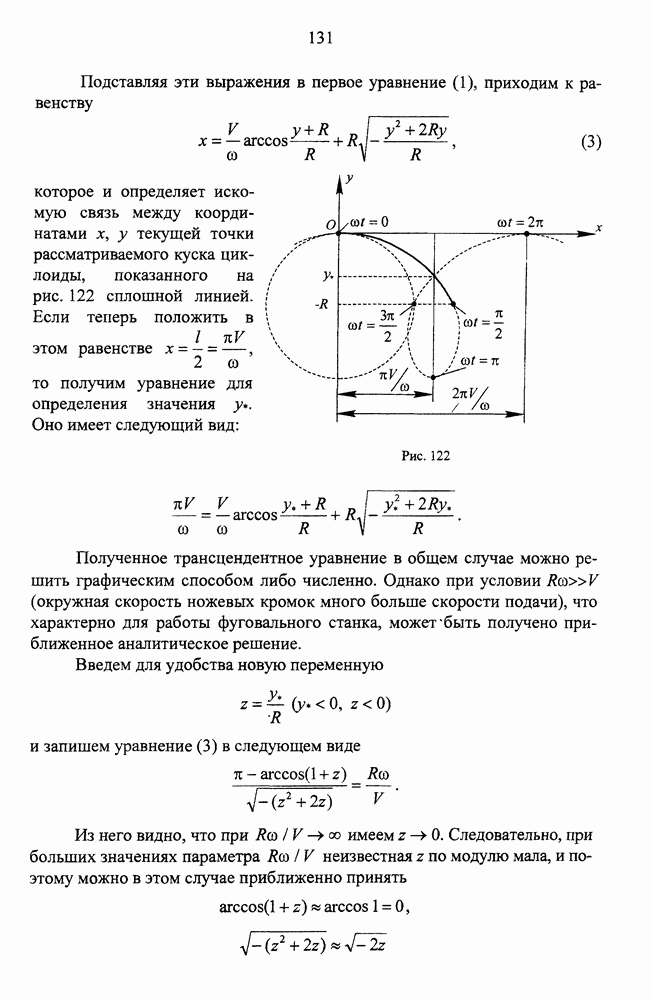
- Геометрические характеристики обработанной поверхности при одном ноже в ножевой головке
- Геометрические характеристики поверхности в случае многоножевой головки
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА