| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Метод разбиения
Он состоит в том, что рассматриваемое тело мысленно разбивается на части, центры тяжести которых известны либо легко могут быть определены, после чего применяются формулы для определения координат центра системы параллельных сил

В этих формулах  и
и  - веса и координаты центров тяжести
- веса и координаты центров тяжести  выделенных частей тела.
выделенных частей тела.
Для однородных тел в этих формулах вместо весов можно использовать пропорциональные им величины - объемы  (для пространственных тел), площади
(для пространственных тел), площади  (для плоских и поверхностных тел), длины
(для плоских и поверхностных тел), длины  (для одномерных тел).
(для одномерных тел).
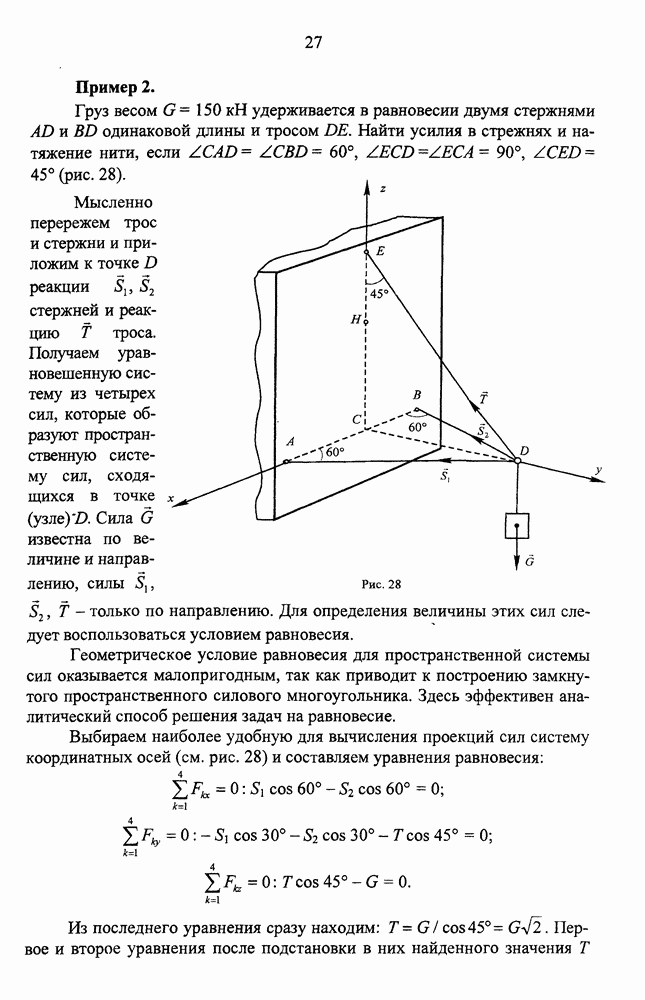
Пример.
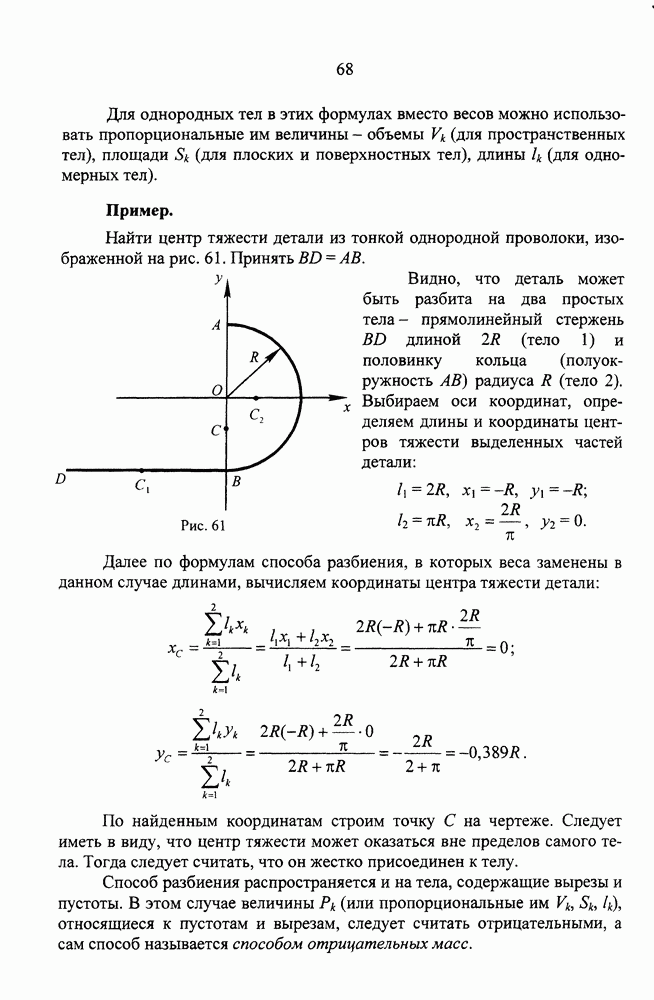
Найти центр тяжести детали из тонкой однородной проволоки, изображенной на рис. 61. Принять BD=АВ.
Видно, что деталь может быть разбита на два простых тела - прямолинейный стержень BD длиной 2R (тело 1) и половинку кольца (полуокружность АВ) радиуса R (тело 2). Выбираем оси координат, определяем длины и координаты центров тяжести выделенных частей детали:

Далее по формулам способа разбиения, в которых веса заменены в данном случае длинами, вычисляем координаты центра тяжести детали:

По найденным координатам строим точку С на чертеже. Следует иметь в виду, что центр тяжести может оказаться вне пределов самого тела. Тогда следует считать, что он жестко присоединен к телу.
Способ разбиения распространяется и на тела, содержащие вырезы и пустоты. В этом случае величины  (или пропорциональные им
(или пропорциональные им  ), относящиеся к пустотам и вырезам, следует считать отрицательными, а сам способ называется способом отрицательных масс.
), относящиеся к пустотам и вырезам, следует считать отрицательными, а сам способ называется способом отрицательных масс.

Рис. 61.
Пример.
Определить положение центра тяжести плоской шайбы с прямоугольным вырезом (рис. 62).
Тело симметрично относительно оси  , откуда сразу следует, что
, откуда сразу следует, что  . Для определения
. Для определения  шайбу считаем состоящей из двух тел - сплошного круга радиуса R с центром в начале координат (тело 1) и прямоугольника со сторонами 2а, 2b и отрицательной площадью (тело 2). Вычисляем нужные величины:
шайбу считаем состоящей из двух тел - сплошного круга радиуса R с центром в начале координат (тело 1) и прямоугольника со сторонами 2а, 2b и отрицательной площадью (тело 2). Вычисляем нужные величины:

и определяем абсциссу центра тяжести шайбы:


Рис. 62.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ. ПРЕДМЕТ И ОСНОВНЫЕ ПОНЯТИЯ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ
- СТАТИКА. ЛЕКЦИЯ 1. ЗАДАЧИ СТАТИКИ, АКСИОМЫ СТАТИКИ. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
- Момент силы относительно точки
- Алгебраический момент силы
- Основные типы связей и их реакции
- Упражнения
- ЛЕКЦИЯ 2. СХОДЯЩИЕСЯ СИЛЫ И ПАРЫ СИЛ
- Сходящиеся силы. Приведение сходящихся сил к простейшему виду
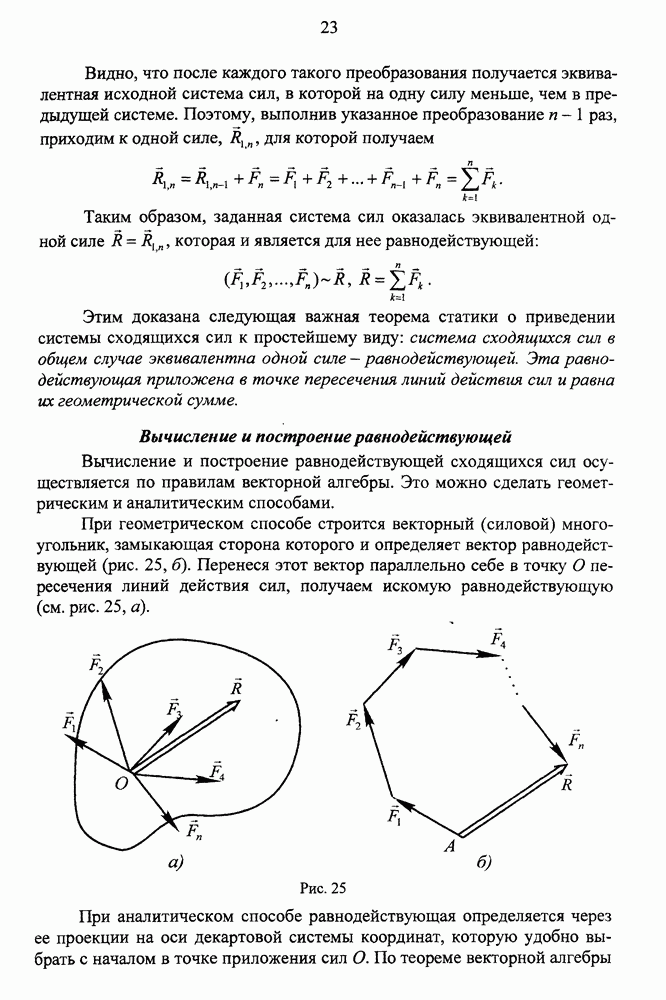
- Вычисление и построение равнодействующей
- Условия равновесия сходящихся сил
- Теорема о трех силах
- Теорема Вариньона
- Пара сил и ее момент
- Приведение системы пар сил к простейшему виду или сложение пар сил
- Упражнения
- ЛЕКЦИЯ 3. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ
- Момент силы относительно оси
- Аналитический способ вычисления момента
- Геометрический способ вычисления момента
- Преобразование пространственной произвольной системы сил
- Приведение пространственной произвольной системы сил к данному центру. Главный вектор и главный момент. Основная теорема статики
- Вычисление и построение главного вектора и главного момента
- Перемена центра приведения
- ЛЕКЦИЯ 4. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ (продолжение). ЧАСТНЫЕ СЛУЧАИ СИСТЕМЫ СИЛ
- Случаи приведения к простейшему виду
- Условия (уравнения) равновесия пространственной произвольной системы сил
- Частные случаи системы сил
- Плоская система сил
- Система параллельных сил
- Равновесие системы тел
- Вопросы для самопроверки
- ЛЕКЦИЯ 5. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ И ЦЕНТР ТЯЖЕСТИ
- Центр параллельных сил
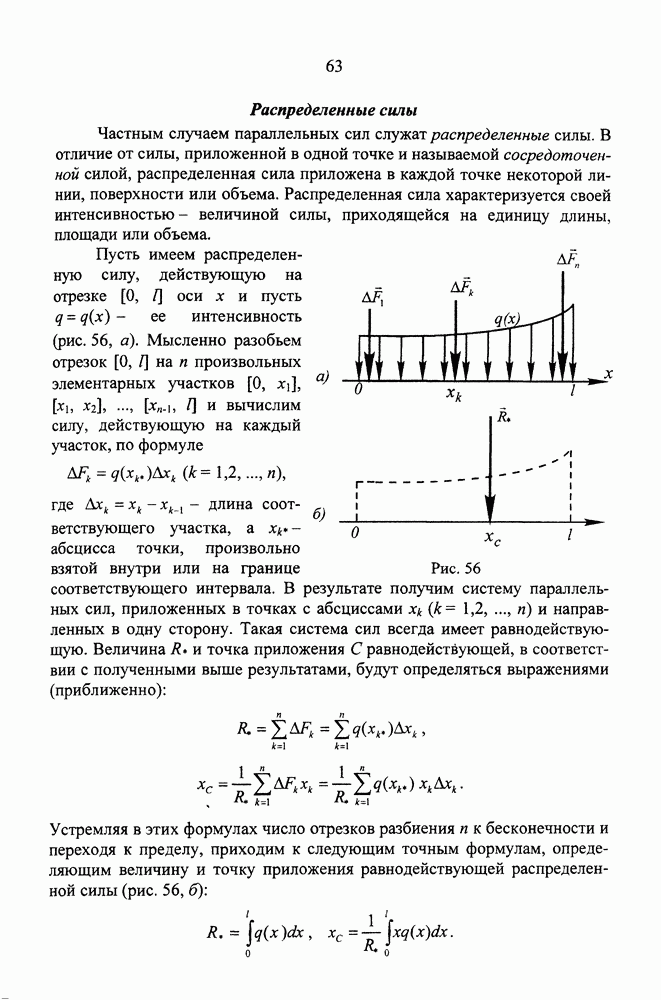
- Распределенные силы
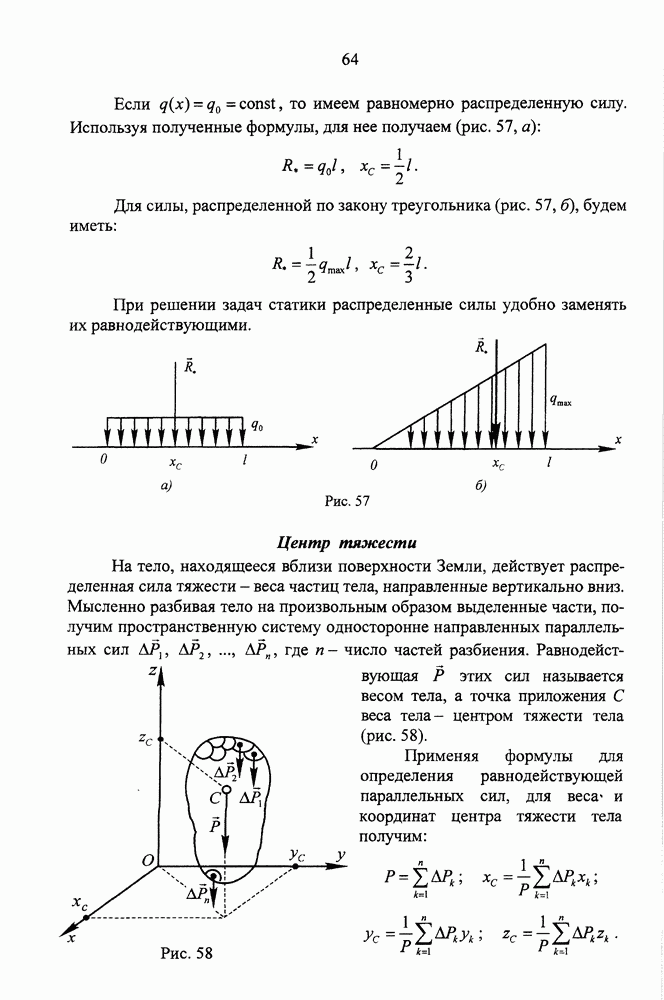
- Центр тяжести
- Интегральные формулы для координат центра тяжести
- Метод разбиения
- Вопросы для самопроверки
- ЛЕКЦИЯ 6. ТРЕНИЕ ТВЕРДЫХ ТЕЛ
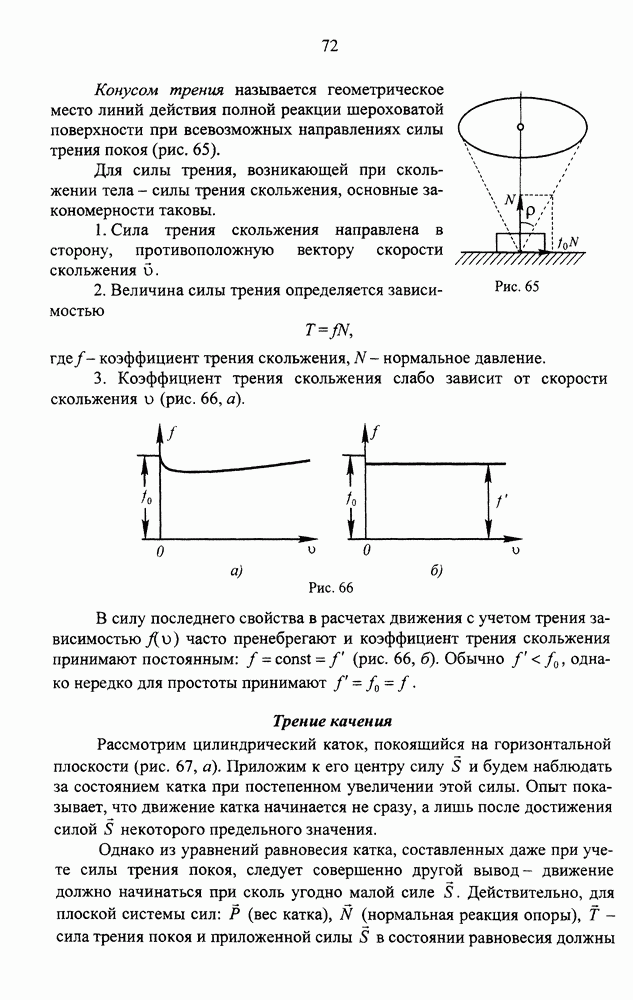
- Трение покоя и трение скольжения
- Трение качения
- Решение задач статики при учете сил трения
- Заклинивание
- Упражнения
- КИНЕМАТИКА
- ЛЕКЦИЯ 7. КИНЕМАТИКА ТОЧКИ
- Способы задания движения точки
- Определение траектории, скорости и ускорения точки при векторном способе задания движения
- Определение траектории, скорости и ускорения точки при координатном способе задания движения
- Определение скорости и ускорения точки при естественном способе задания движения
- Естественные координатные оси и их орты
- Определение скорости
- Определение ускорения
- Вопросы для самопроверки
- ЛЕКЦИЯ 8. ПРОСТЕЙШИЕ ДРИЖЕНИЯ ТВЕРДОГО ТЕЛА
- Поступательное движение
- Вращательное движение
- Уравнение вращательного движения. Угловая скорость и угловое ускорение тела
- Траектории, скорости и ускорения точек тела
- Векторы угловой скорости и углового ускорения тела
- Векторные формулы для линейной скорости, касательного и нормального ускорений точки тела
- Вопросы для самопроверки
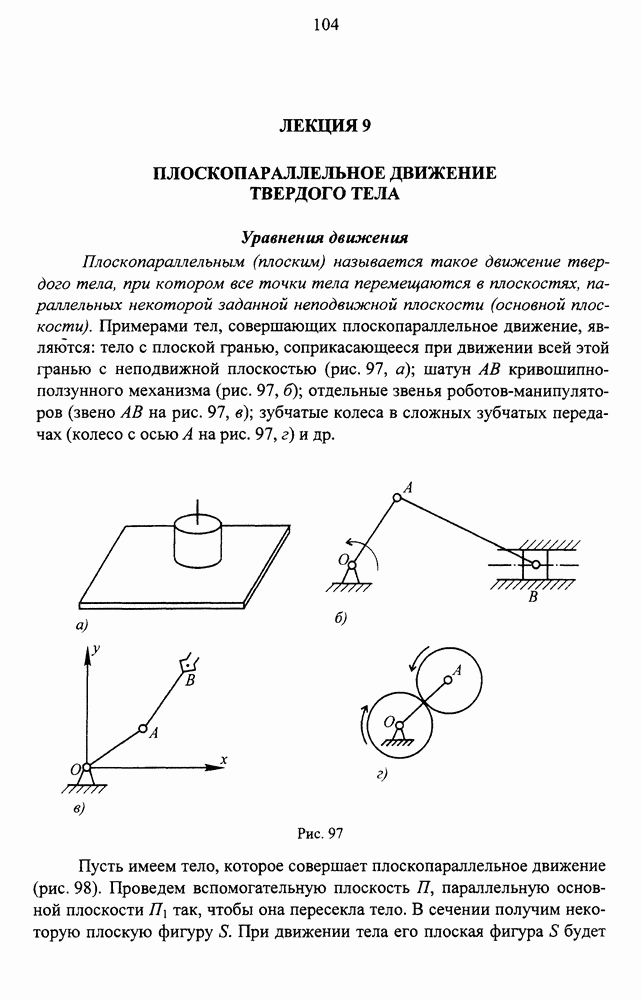
- ЛЕКЦИЯ 9. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- Уравнения движения
- Угловая скорость и угловое ускорение тела при плоскопараллельном движении
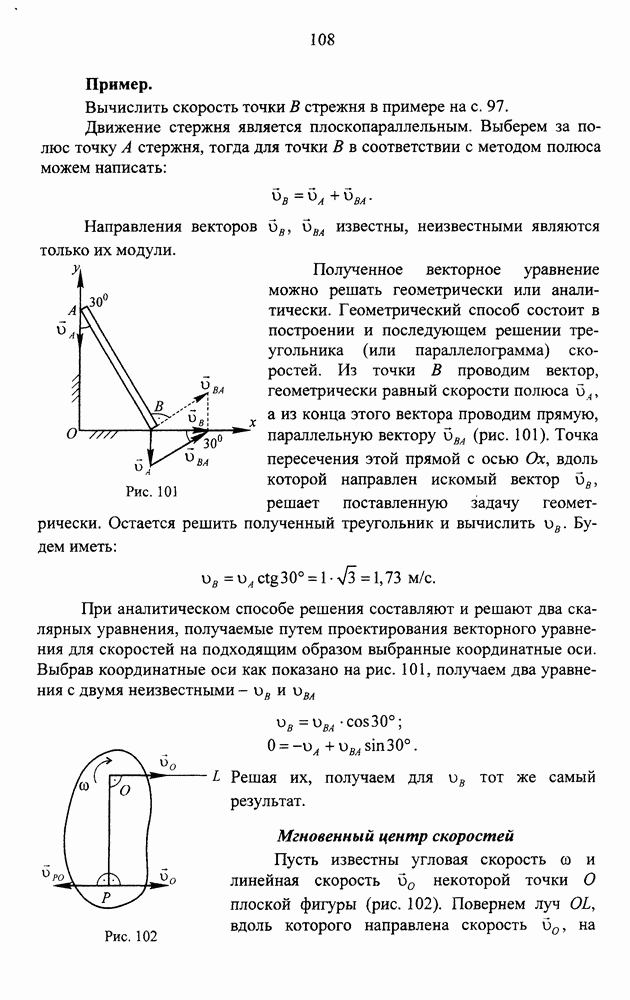
- Определение скоростей точек тела. Метод полюса
- Мгновенный центр скоростей
- Определение скоростей точек плоской фигуры через мгновенный центр скоростей
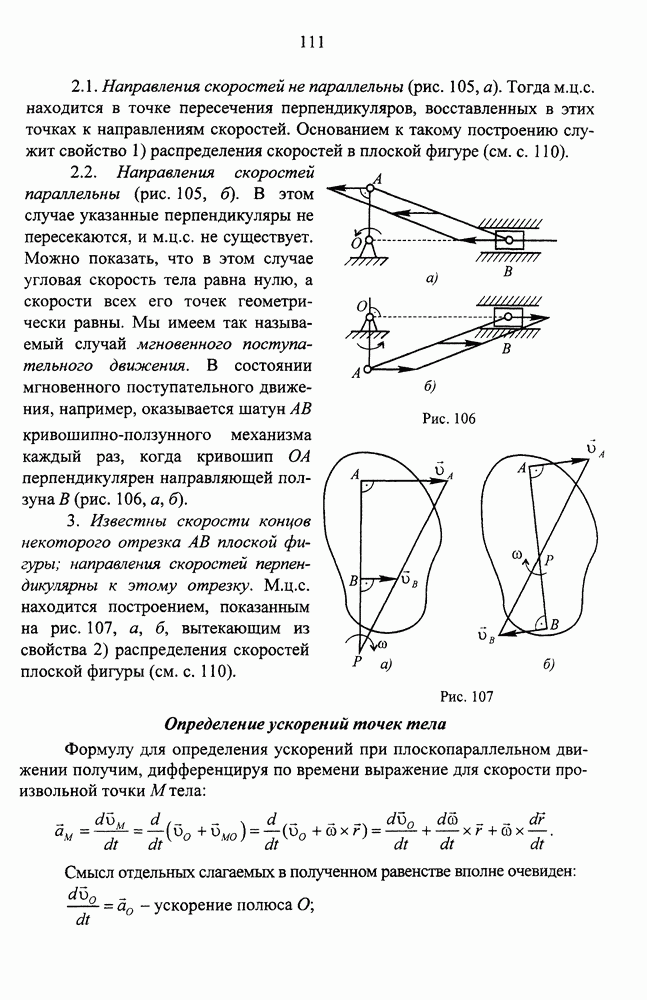
- Различные случаи определения положения мгновенного центра скоростей
- Определение ускорений точек тела
- Вопросы для самопроверки
- ЛЕКЦИЯ 10. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
- Теорема сложения скоростей
- Теорема сложения ускорений
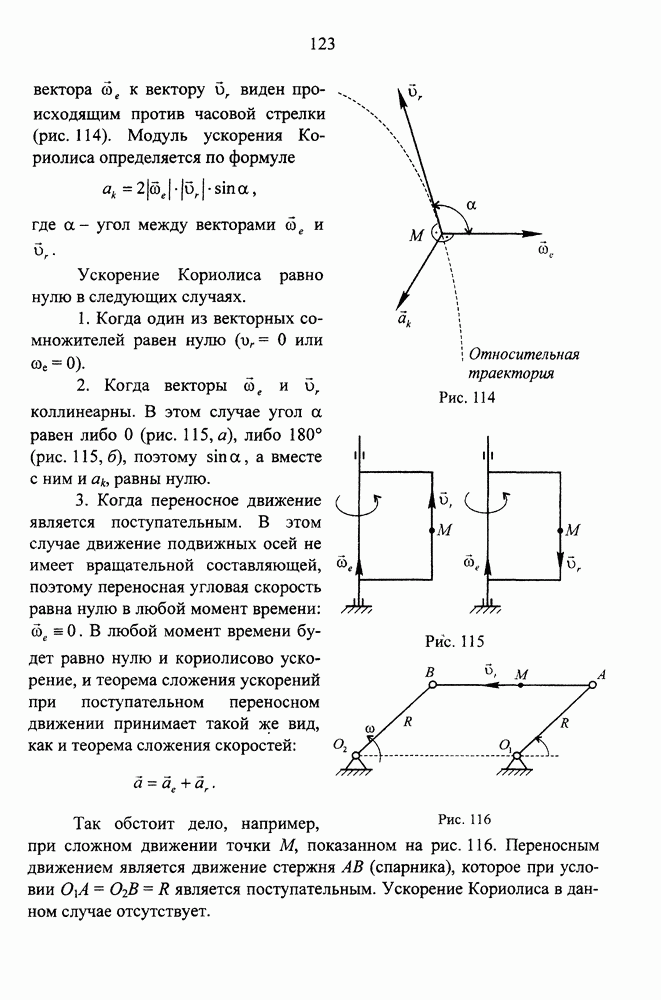
- Причины появления ускорения Кориолиса
- Вычисление и построение ускорения Кориолиса
- Вопросы для самопроверки
- ДОБАВЛЕНИЕ. КИНЕМАТИКА ПРОЦЕССА ФУГОВАНИЯ ДРЕВЕСИНЫ
- Схема и расчетная модель процесса фугования
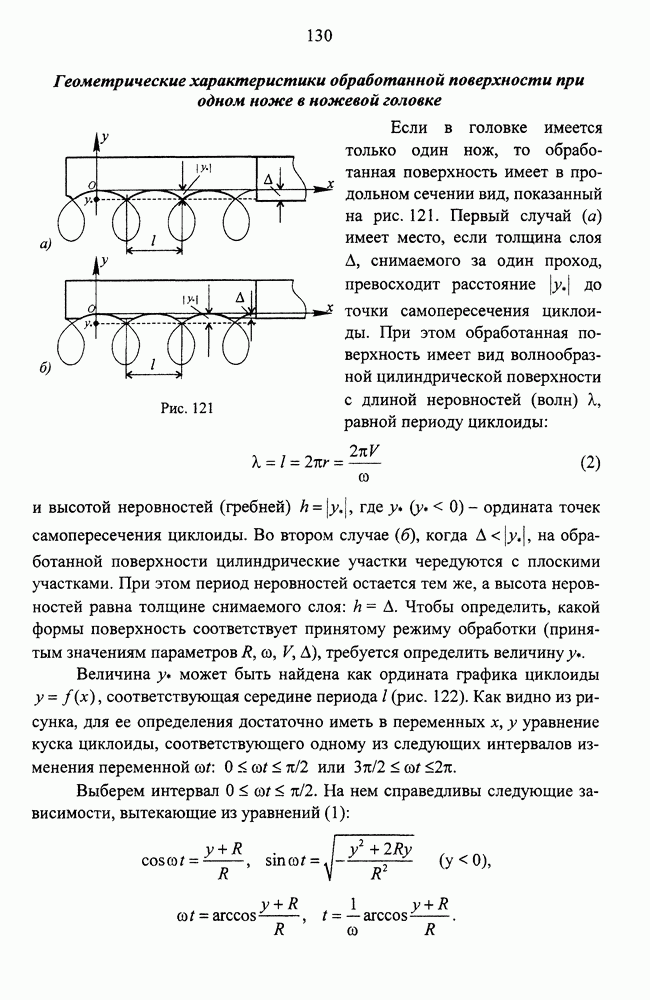
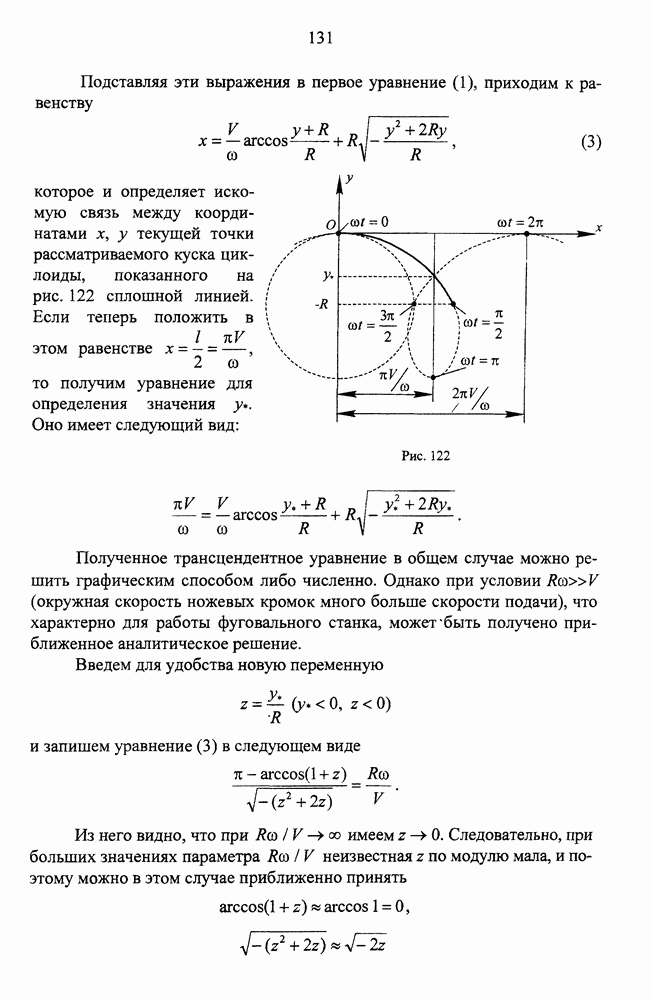
- Геометрические характеристики обработанной поверхности при одном ноже в ножевой головке
- Геометрические характеристики поверхности в случае многоножевой головки
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА