| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Частные случаи системы сил
Плоская система сил
Совокупность  , расположенных в одной плоскости, называется плоской системой
, расположенных в одной плоскости, называется плоской системой  . Выберем центр приведения О и координатные оси
. Выберем центр приведения О и координатные оси  в той же плоскости, ось z направим перпендикулярно к ней Для проекции главного вектора и главного момента на эти оси будем иметь:
в той же плоскости, ось z направим перпендикулярно к ней Для проекции главного вектора и главного момента на эти оси будем иметь:  .
.
Величины  равны нулю
равны нулю  , а значащие проекции определяются по формулам:
, а значащие проекции определяются по формулам:

Заметим, что моменты сил относительно оси z в данном случае совпадают с алгебраическими моментами сил относительно точки О, что и учтено в формуле для  .
.
Видно, что скалярное произведение  поэтому главный вектор и главный момент, если не равны нулю, то взаимно перпендикулярны. Отсюда следует, что для плоской системы сил возможны только два случая приведения к простейшему виду - к паре сил (если
поэтому главный вектор и главный момент, если не равны нулю, то взаимно перпендикулярны. Отсюда следует, что для плоской системы сил возможны только два случая приведения к простейшему виду - к паре сил (если  и к равнодействующей (если
и к равнодействующей (если  ).
).
Условия равновесия, представляющие собой координатную запись векторных равенств  , запишутся так:
, запишутся так:

Следовательно, для плоской произвольной системы сил имеются три независимых условия (уравнения) равновесия - должны равняться нулю алгебраические суммы проекций сил на две координатные оси и сумма алгебраических моментов сил относительно произвольной точки, взятой в плоскости действия сил.
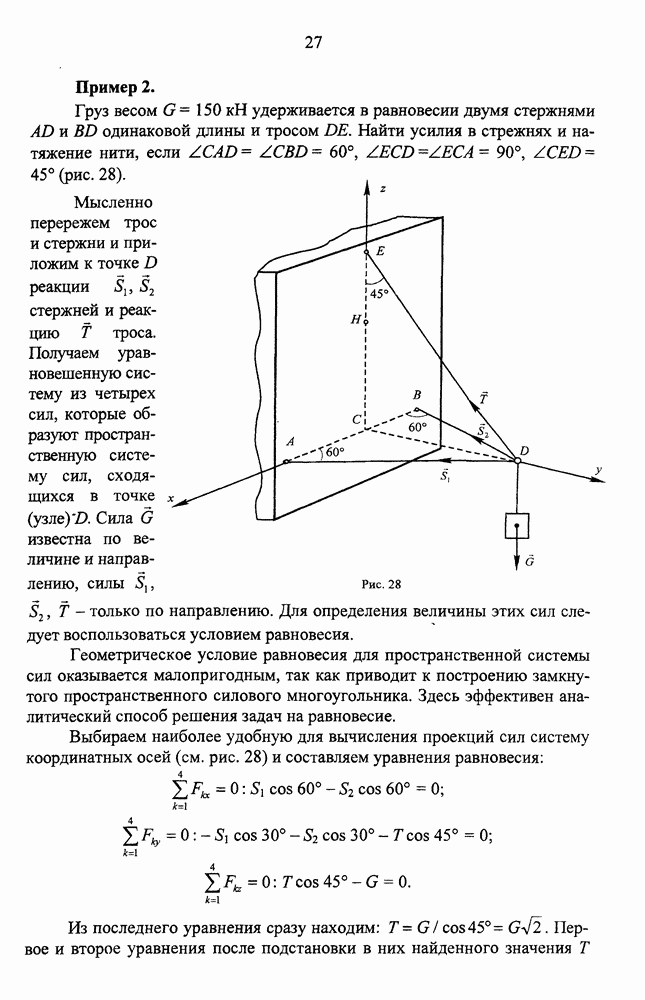
Пример.
Найти реакцию цилиндрического шарнира  и натяжения ветвей троса, удерживающих в равновесии ступенчатую балку АВС (рис. 52, а). К балке приложены пара сил с моментом
и натяжения ветвей троса, удерживающих в равновесии ступенчатую балку АВС (рис. 52, а). К балке приложены пара сил с моментом  , сосредоточенная сила
, сосредоточенная сила  и равномерно распределенная сила интенсивностью
и равномерно распределенная сила интенсивностью  , действующие в одной плоскости. Принять
, действующие в одной плоскости. Принять  ,
,  , блок считать идеальным.
, блок считать идеальным.
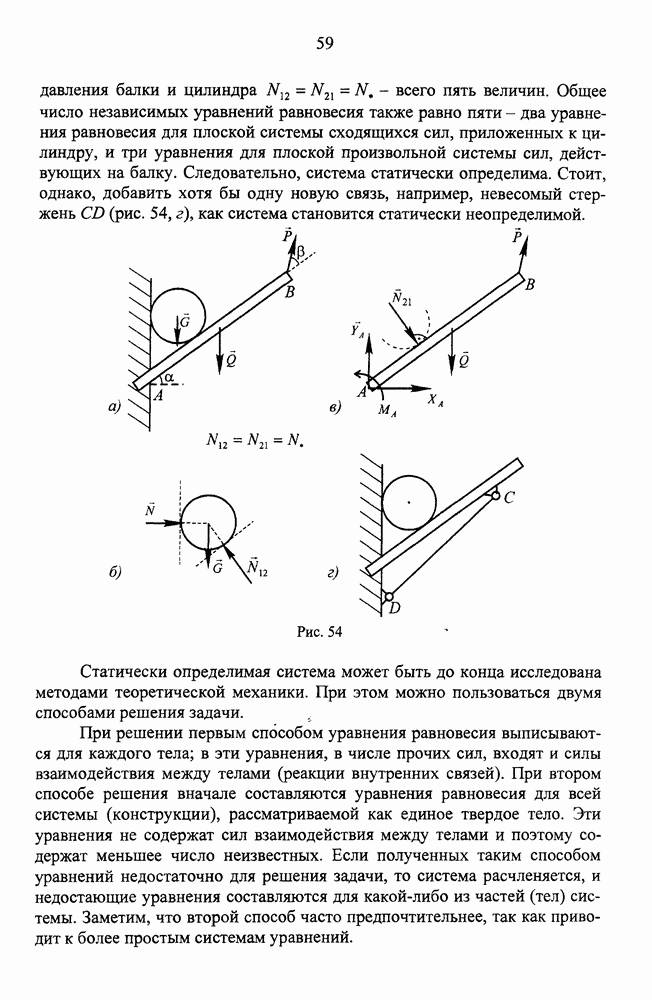
Распределенную силу, представляющую собой плоскую систему параллельных сил, заменяем равнодействующей - сосредоточенной силой Q, приложенной посередине участка ВС балки и равной по модулю  .
.

Рис. 52.
Мысленно отбрасываем связи, заменяя их действие реакциями- силами  . Вследствие идеальности блока (отсутствия трения в оси блока) натяжения ветвей троса по величине одинаковы:
. Вследствие идеальности блока (отсутствия трения в оси блока) натяжения ветвей троса по величине одинаковы:  .
.
В полученной плоской системе сил (рис. 52, б) неизвестными являются силы  ,
,  и величина Т сил
и величина Т сил  и
и  . Для их определения воспользуемся условиями равновесия плоской произвольной системы сил. Выбираем координатные оси и составляем уравнения равновесия:
. Для их определения воспользуемся условиями равновесия плоской произвольной системы сил. Выбираем координатные оси и составляем уравнения равновесия:

Для удобства определения момента сила P разложена на составляющие вдоль координатных осей (на рис. 52, б показаны штриховыми линиями), после чего применена теорема Вариньона.
Из последнего уравнения, содержащего одну неизвестную  ), находим
), находим  . После подстановки значений
. После подстановки значений  в первое и второе уравнения определяем остальные неизвестные:
в первое и второе уравнения определяем остальные неизвестные:  ,
,  . Отрицательный знак величины
. Отрицательный знак величины  означает, что реакция
означает, что реакция  направлена в противоположную сторону.
направлена в противоположную сторону.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ. ПРЕДМЕТ И ОСНОВНЫЕ ПОНЯТИЯ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ
- СТАТИКА. ЛЕКЦИЯ 1. ЗАДАЧИ СТАТИКИ, АКСИОМЫ СТАТИКИ. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
- Момент силы относительно точки
- Алгебраический момент силы
- Основные типы связей и их реакции
- Упражнения
- ЛЕКЦИЯ 2. СХОДЯЩИЕСЯ СИЛЫ И ПАРЫ СИЛ
- Сходящиеся силы. Приведение сходящихся сил к простейшему виду
- Вычисление и построение равнодействующей
- Условия равновесия сходящихся сил
- Теорема о трех силах
- Теорема Вариньона
- Пара сил и ее момент
- Приведение системы пар сил к простейшему виду или сложение пар сил
- Упражнения
- ЛЕКЦИЯ 3. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ
- Момент силы относительно оси
- Аналитический способ вычисления момента
- Геометрический способ вычисления момента
- Преобразование пространственной произвольной системы сил
- Приведение пространственной произвольной системы сил к данному центру. Главный вектор и главный момент. Основная теорема статики
- Вычисление и построение главного вектора и главного момента
- Перемена центра приведения
- ЛЕКЦИЯ 4. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ (продолжение). ЧАСТНЫЕ СЛУЧАИ СИСТЕМЫ СИЛ
- Случаи приведения к простейшему виду
- Условия (уравнения) равновесия пространственной произвольной системы сил
- Частные случаи системы сил
- Плоская система сил
- Система параллельных сил
- Равновесие системы тел
- Вопросы для самопроверки
- ЛЕКЦИЯ 5. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ И ЦЕНТР ТЯЖЕСТИ
- Центр параллельных сил
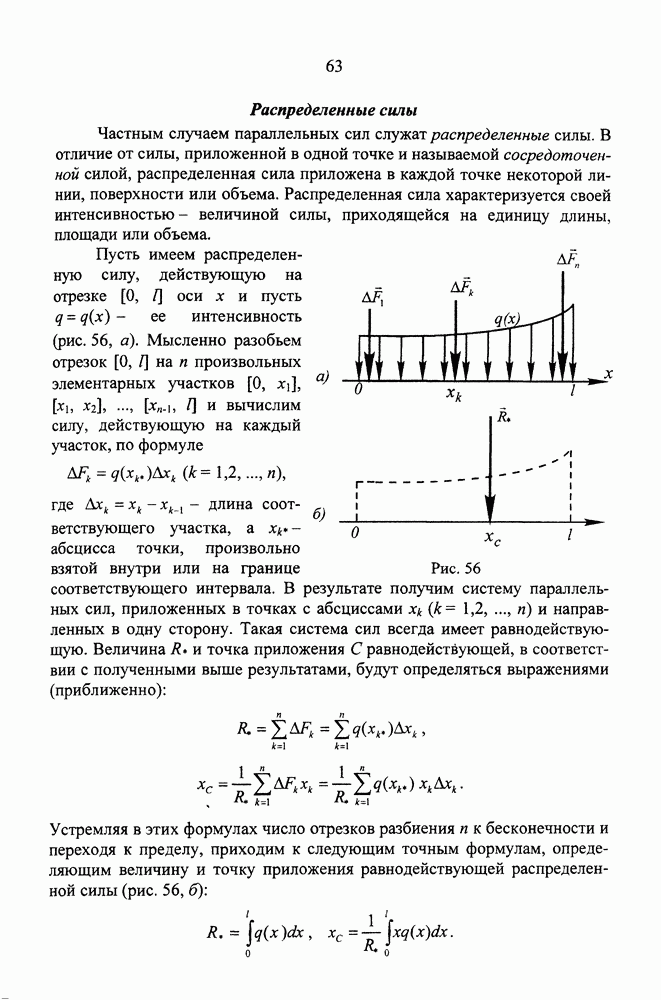
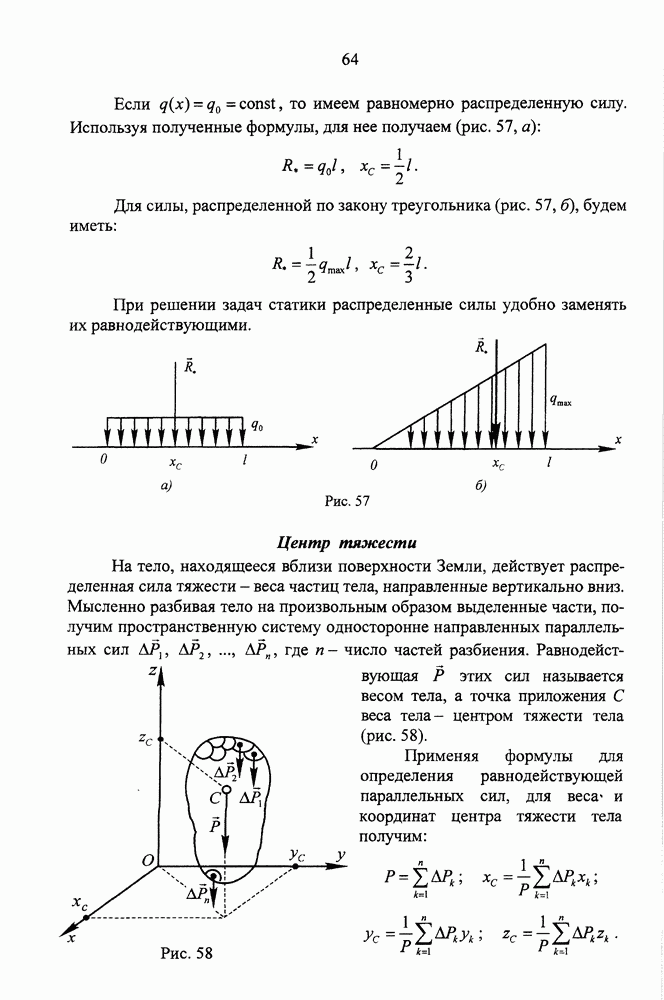
- Распределенные силы
- Центр тяжести
- Интегральные формулы для координат центра тяжести
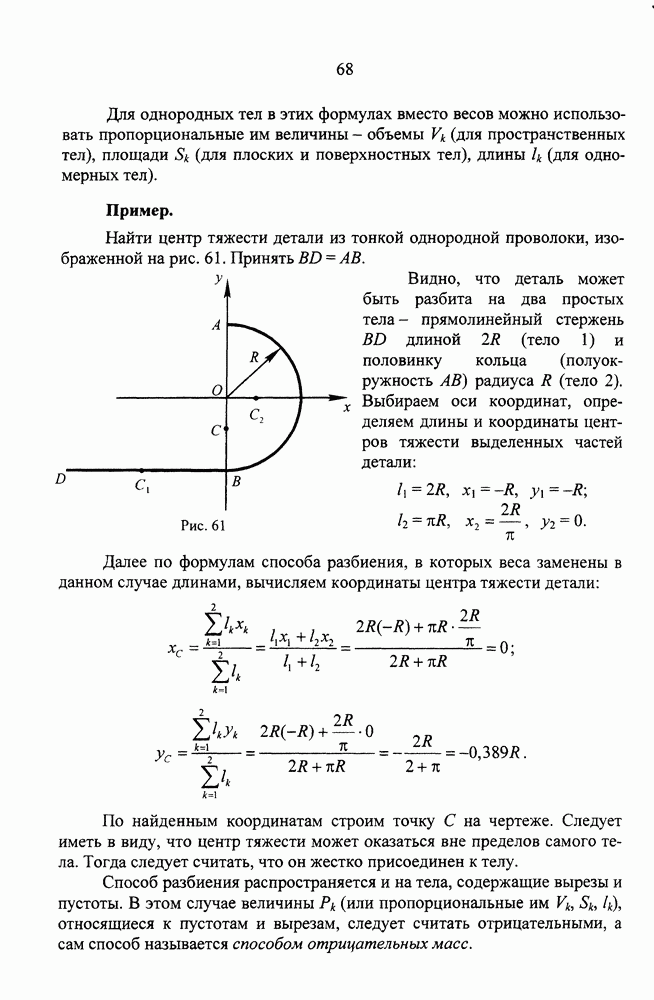
- Метод разбиения
- Вопросы для самопроверки
- ЛЕКЦИЯ 6. ТРЕНИЕ ТВЕРДЫХ ТЕЛ
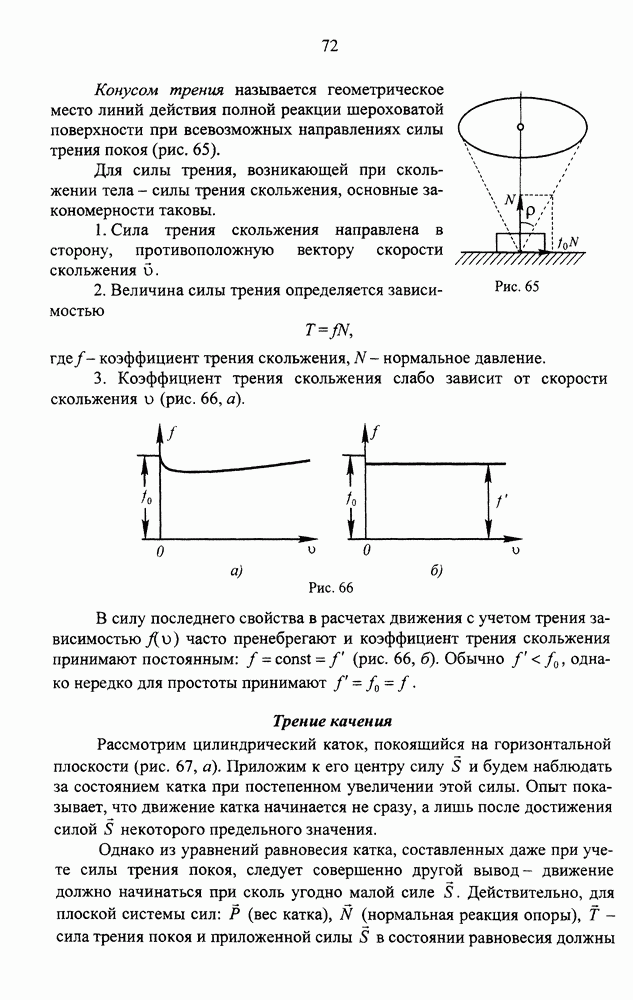
- Трение покоя и трение скольжения
- Трение качения
- Решение задач статики при учете сил трения
- Заклинивание
- Упражнения
- КИНЕМАТИКА
- ЛЕКЦИЯ 7. КИНЕМАТИКА ТОЧКИ
- Способы задания движения точки
- Определение траектории, скорости и ускорения точки при векторном способе задания движения
- Определение траектории, скорости и ускорения точки при координатном способе задания движения
- Определение скорости и ускорения точки при естественном способе задания движения
- Естественные координатные оси и их орты
- Определение скорости
- Определение ускорения
- Вопросы для самопроверки
- ЛЕКЦИЯ 8. ПРОСТЕЙШИЕ ДРИЖЕНИЯ ТВЕРДОГО ТЕЛА
- Поступательное движение
- Вращательное движение
- Уравнение вращательного движения. Угловая скорость и угловое ускорение тела
- Траектории, скорости и ускорения точек тела
- Векторы угловой скорости и углового ускорения тела
- Векторные формулы для линейной скорости, касательного и нормального ускорений точки тела
- Вопросы для самопроверки
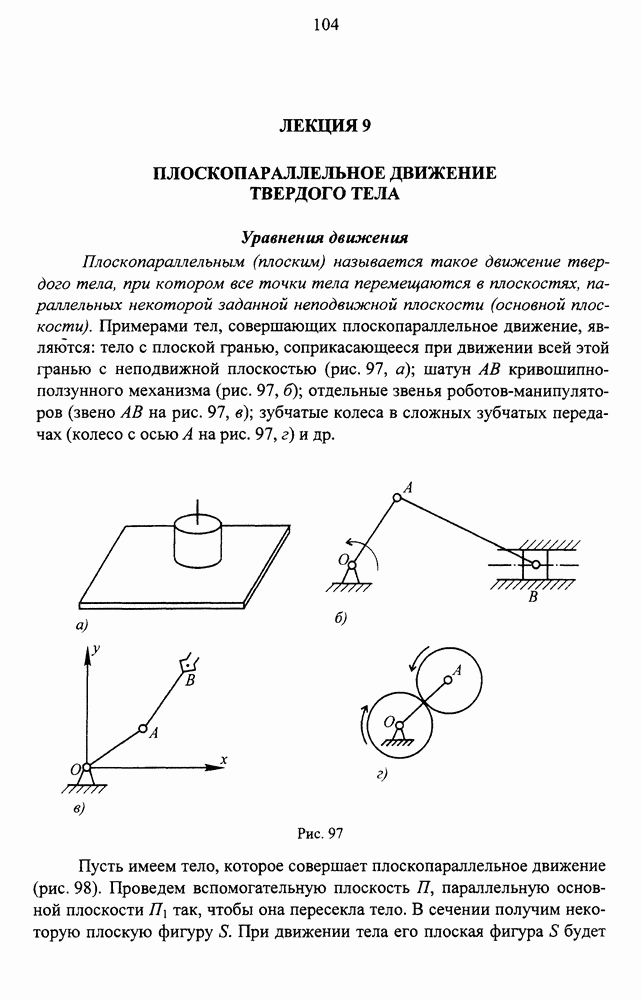
- ЛЕКЦИЯ 9. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- Уравнения движения
- Угловая скорость и угловое ускорение тела при плоскопараллельном движении
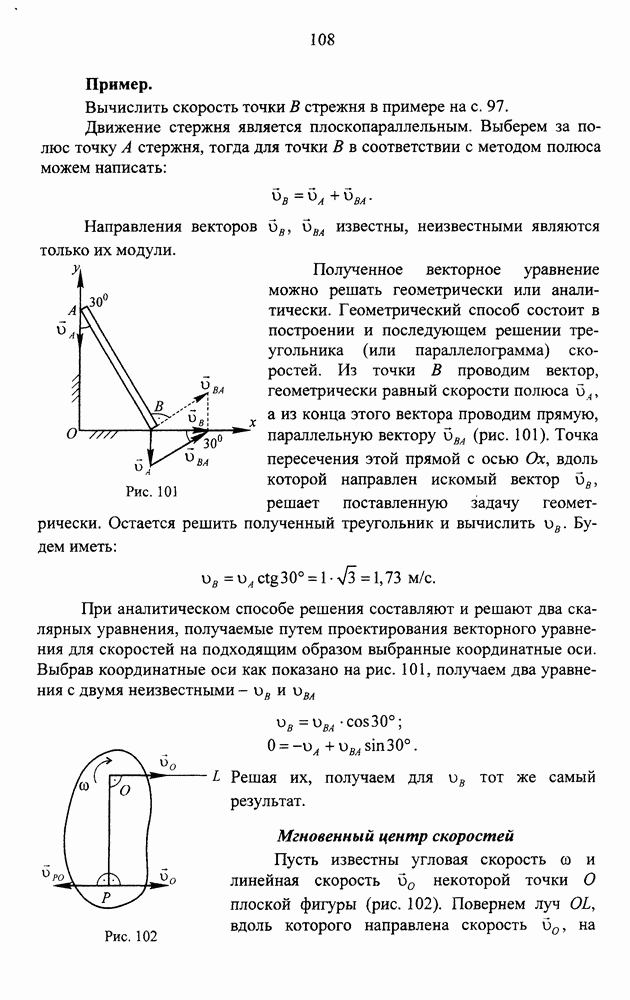
- Определение скоростей точек тела. Метод полюса
- Мгновенный центр скоростей
- Определение скоростей точек плоской фигуры через мгновенный центр скоростей
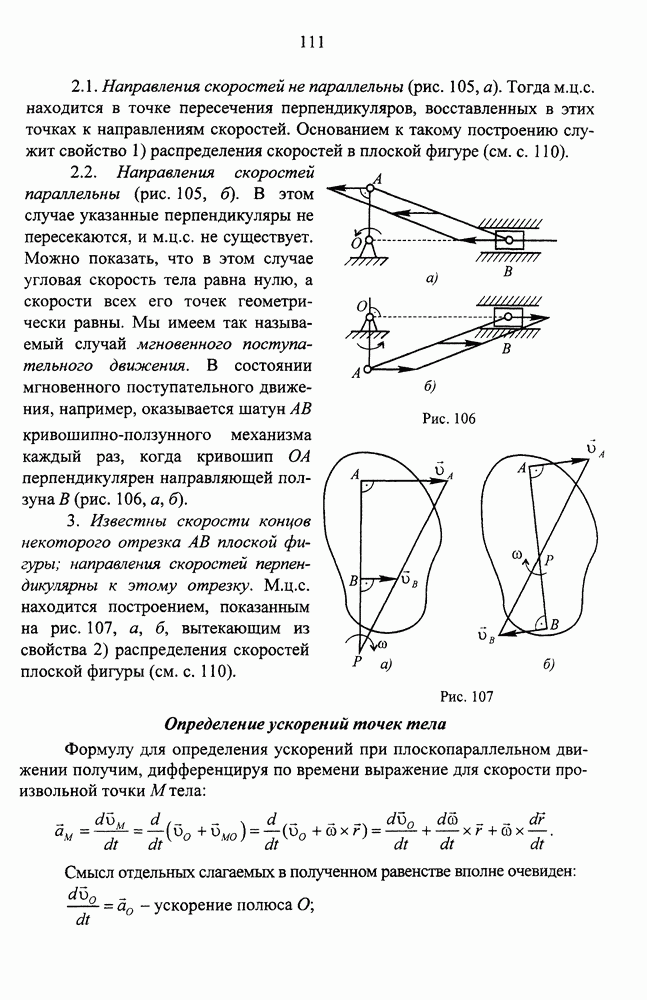
- Различные случаи определения положения мгновенного центра скоростей
- Определение ускорений точек тела
- Вопросы для самопроверки
- ЛЕКЦИЯ 10. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
- Теорема сложения скоростей
- Теорема сложения ускорений
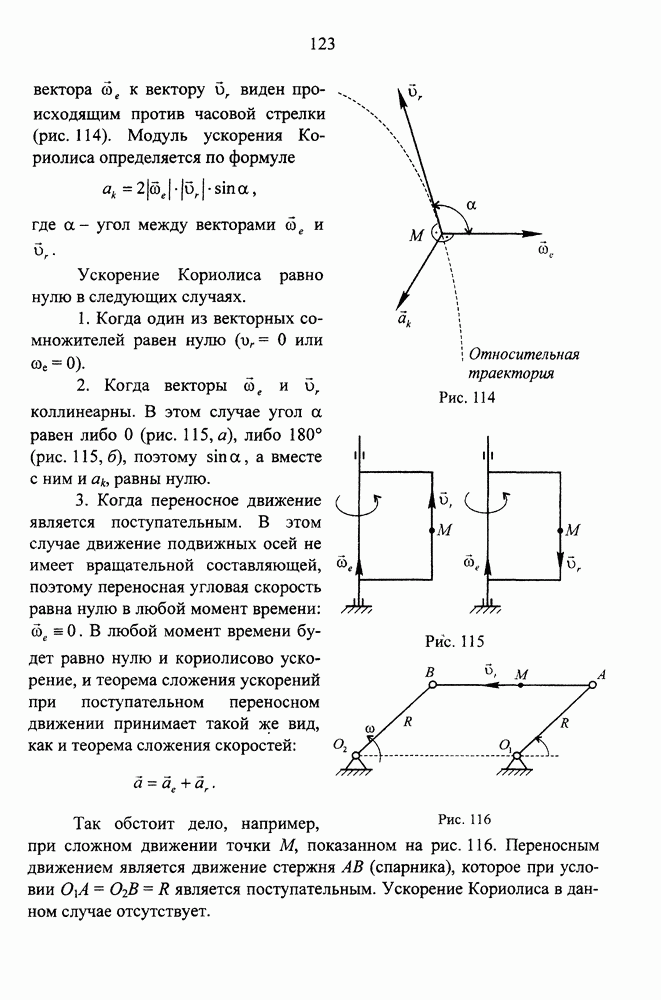
- Причины появления ускорения Кориолиса
- Вычисление и построение ускорения Кориолиса
- Вопросы для самопроверки
- ДОБАВЛЕНИЕ. КИНЕМАТИКА ПРОЦЕССА ФУГОВАНИЯ ДРЕВЕСИНЫ
- Схема и расчетная модель процесса фугования
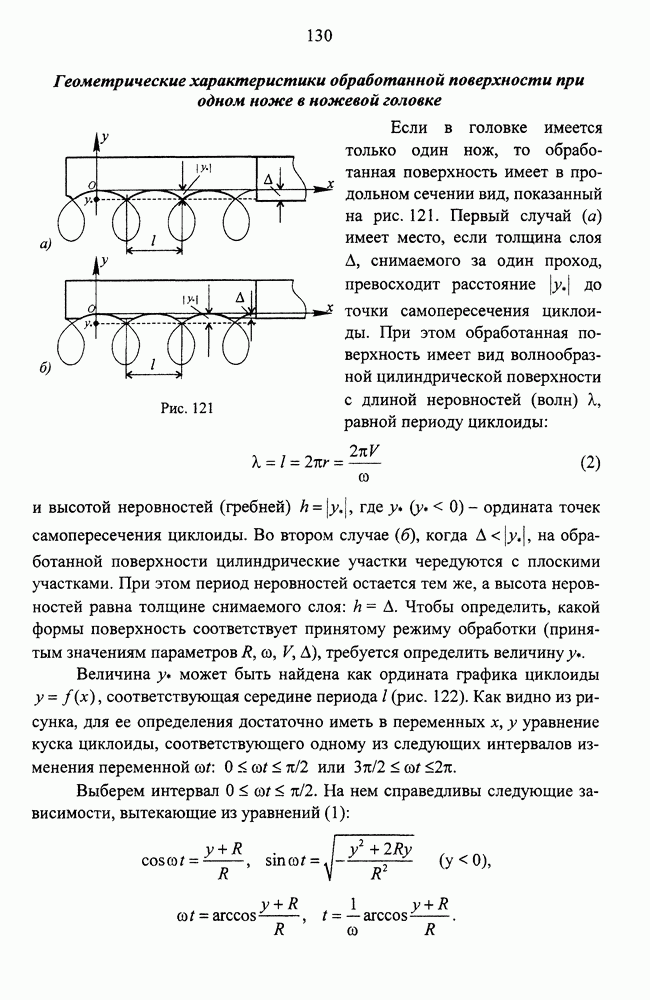
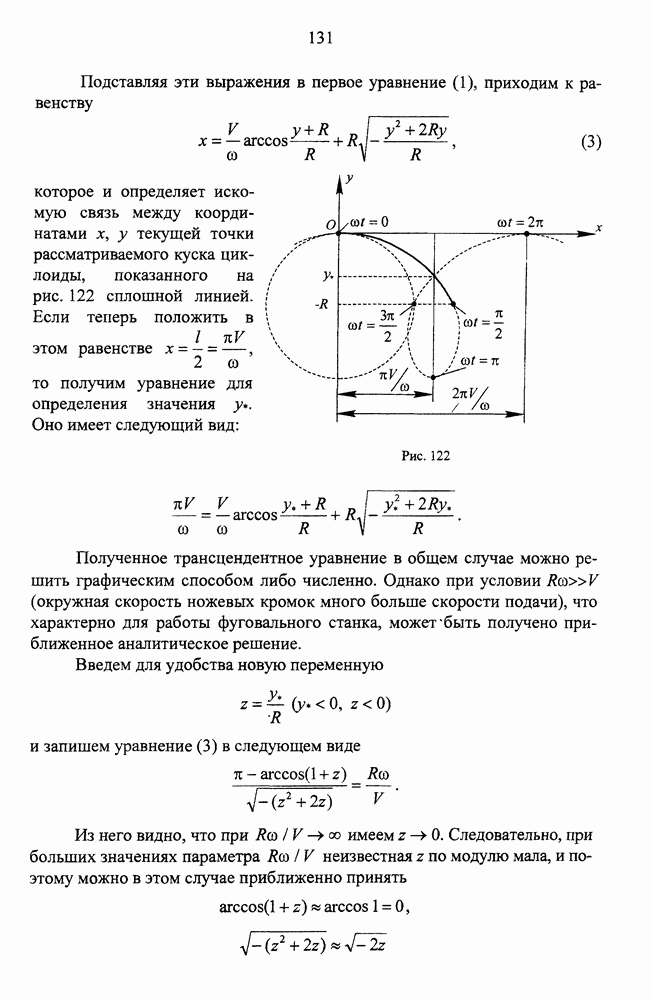
- Геометрические характеристики обработанной поверхности при одном ноже в ножевой головке
- Геометрические характеристики поверхности в случае многоножевой головки
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА