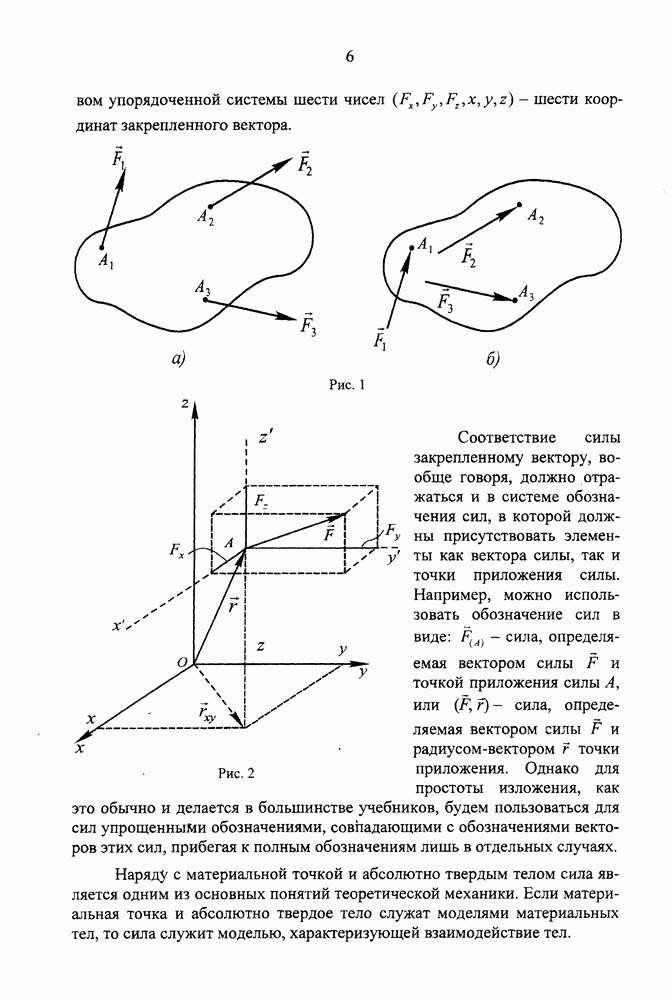
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Приведение системы пар сил к простейшему виду или сложение пар сил
Пусть к твердому телу приложены одновременно несколько пар сил с моментами  , действующих в различных плоскостях. Можно ли эту систему пар привести к более простому виду? Оказывается, что можно, и ответ подсказывается следующей теоремой о сложении двух пар.
, действующих в различных плоскостях. Можно ли эту систему пар привести к более простому виду? Оказывается, что можно, и ответ подсказывается следующей теоремой о сложении двух пар.
Теорема. Две пары сил, действующие в разных плоскостях, эквивалентны одной паре сил с моментом, равным геометрической сумме моментов заданных пар.

Рис. 36
Пусть пары заданы своими моментами  и
и  (рис. 36,а). Построим две плоскости, перпендикулярные этим векторам (плоскости действия пар) и, выбрав некоторый отрезок АВ на линии пересечения плоскостей за плечо, общее для обеих пар, построим соответствующие пары:
(рис. 36,а). Построим две плоскости, перпендикулярные этим векторам (плоскости действия пар) и, выбрав некоторый отрезок АВ на линии пересечения плоскостей за плечо, общее для обеих пар, построим соответствующие пары:  (рис. 36, б).
(рис. 36, б).
В соответствии с определением момента пары можем написать

В точках А и В имеем сходящиеся силы. Применяя правило параллелограмма сил (аксиома 3), будем иметь:

Заданные пары оказываются эквивалентными двум силам  , также образующим пару. Тем самым первая часть теоремы доказана. Вторая часть теоремы доказывается прямым вычислением момента результирующей пары:
, также образующим пару. Тем самым первая часть теоремы доказана. Вторая часть теоремы доказывается прямым вычислением момента результирующей пары:

Если число пар  то, попарно складывая их в соответствии с этой теоремой, можно любое число пар привести к одной паре. В результате приходим к следующему выводу: совокупность (систему) пар сил, приложенных к абсолютно твердому телу, можно привести к одной паре с моментом, равным геометрической сумме моментов всех заданных пар.
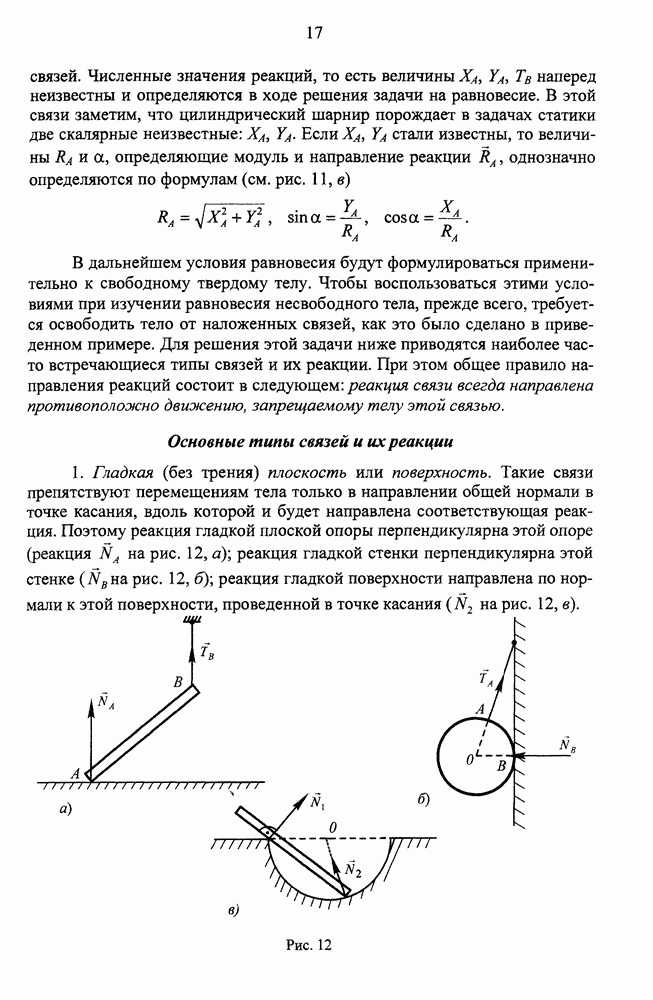
то, попарно складывая их в соответствии с этой теоремой, можно любое число пар привести к одной паре. В результате приходим к следующему выводу: совокупность (систему) пар сил, приложенных к абсолютно твердому телу, можно привести к одной паре с моментом, равным геометрической сумме моментов всех заданных пар.
Математически это можно записать следующим образом:

На рис. 37 дается геометрическая иллюстрация полученного вывода.
Для равновесия пар сил требуется, чтобы момент результирующей пары был равен нулю, что приводит к равенству


Рис. 37.
Это условие можно выразить в геометрической и аналитической форме. Геометрическое условие равновесия пар сил: чтобы система пар сил находилась в равновесии, необходимо и достаточно, чтобы векторный многоугольник, построенный из моментов всех пар, был замкнутым.
Аналитическое условие равновесия пар сил: чтобы система пар сил находилась в равновесии, необходимо и достаточно, чтобы алгебраические суммы проекций векторов-моментов всех пар на произвольно выбранные координатные оси Oxyz были равны нулю:

Если все пары лежат в одной плоскости, то есть образуют плоскую систему пар, получается лишь одно аналитическое условие равновесия-сумма алгебраических моментов пар равна нулю.
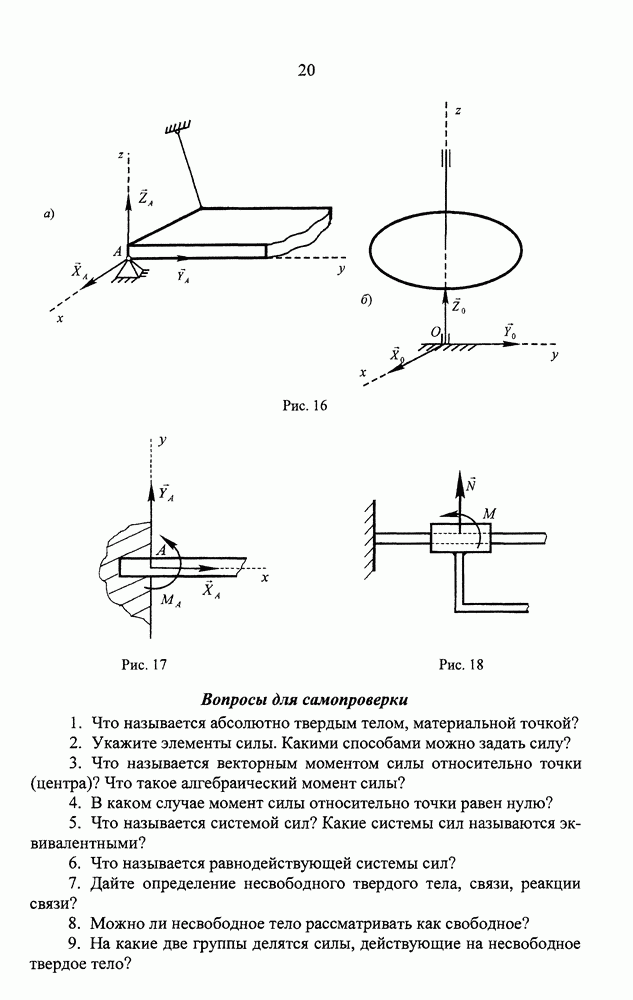
Вопросы для самопроверки
1. В чем состоит правило силового многоугольника? Для чего служит силовой многоугольник?
2. Как найти равнодействующую сходящихся сил аналитическим способом?
3. В чем состоит геометрическое условие равновесия сходящихся сил? Как формулируется это же условие аналитически?
4. Сформулируйте теорему о трех силах.
5. Какие задачи статики называются статически определенными и какие - статически неопределенными? Приведите пример статически неопределенной задачи.
6. Что называется парой сил?
7. Что называется моментом (вектором-моментом) пары сил? Каковы направление, модуль и точка приложения момента?
8. Что называется алгебраическим моментом пары?
9. Сформулируйте правило сложения пар, произвольным образом расположенных в пространстве.
10. В чем заключаются векторное, геометрическое и аналитическое условия равновесия системы пар сил?
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ. ПРЕДМЕТ И ОСНОВНЫЕ ПОНЯТИЯ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ
- СТАТИКА. ЛЕКЦИЯ 1. ЗАДАЧИ СТАТИКИ, АКСИОМЫ СТАТИКИ. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
- Момент силы относительно точки
- Алгебраический момент силы
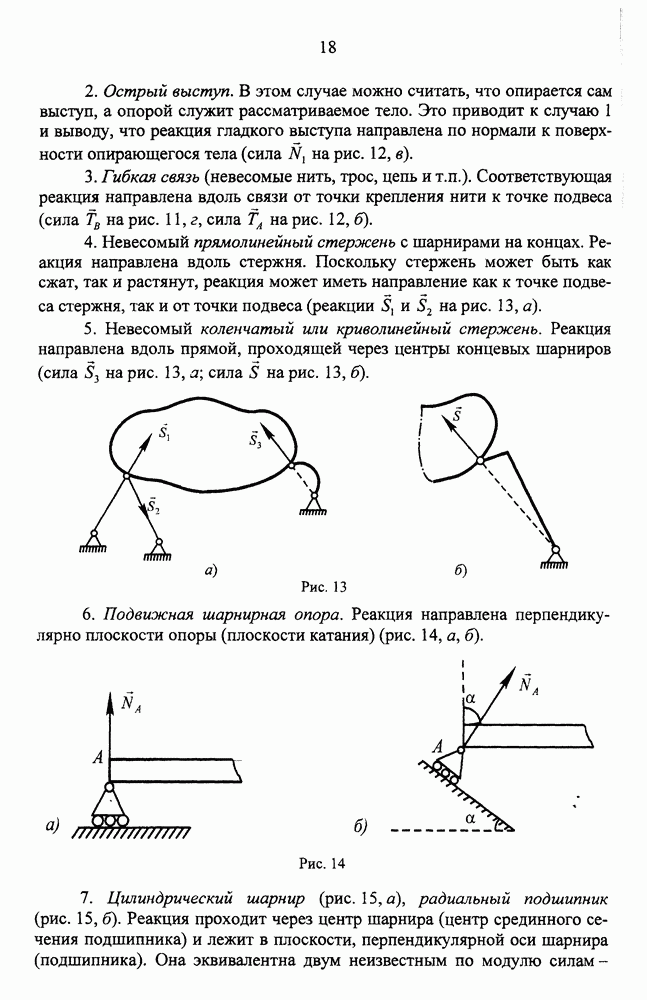
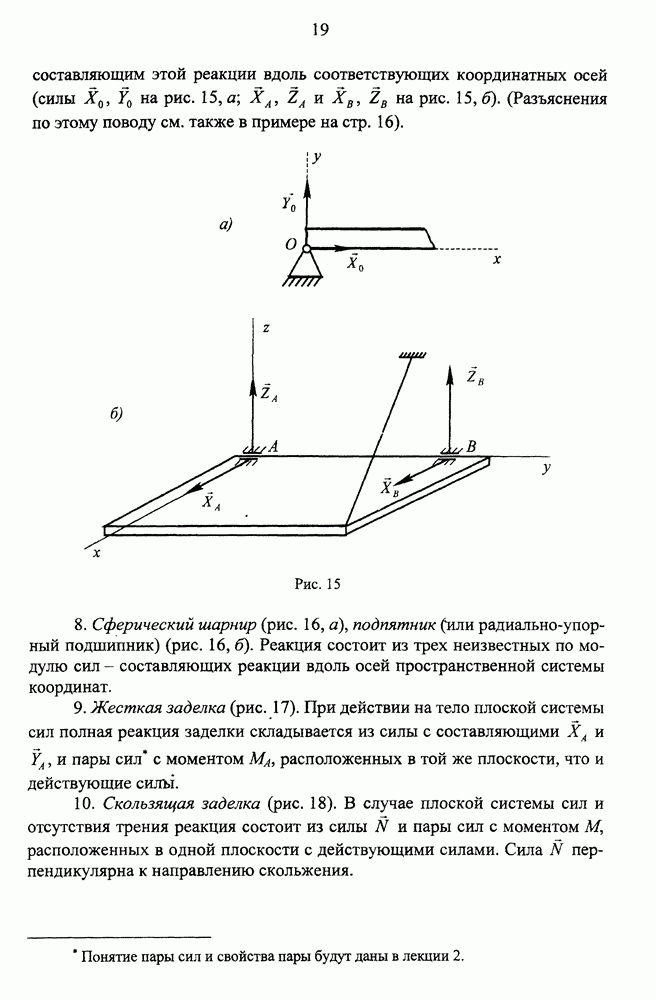
- Основные типы связей и их реакции
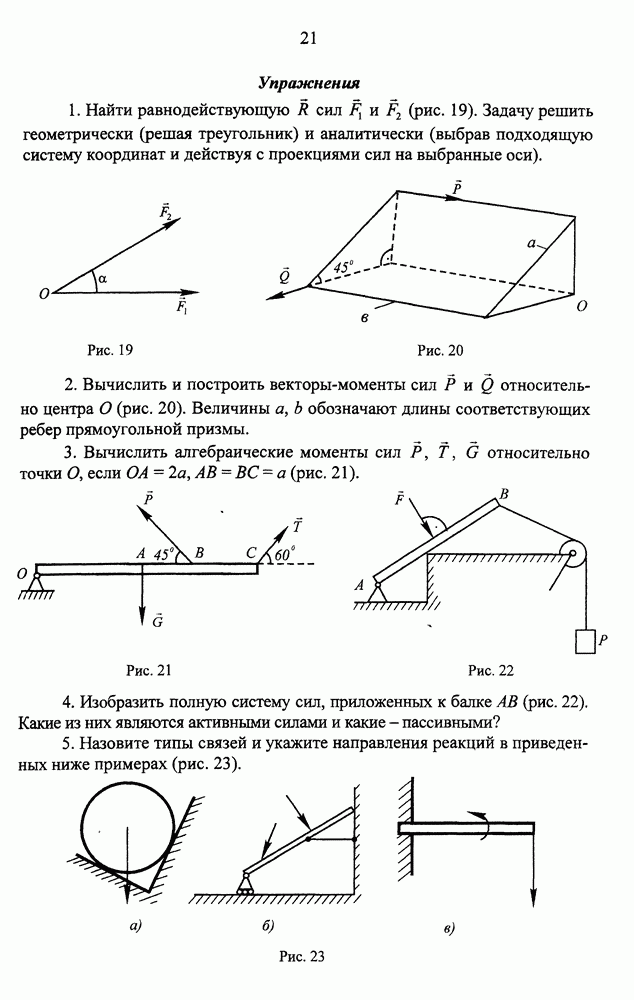
- Упражнения
- ЛЕКЦИЯ 2. СХОДЯЩИЕСЯ СИЛЫ И ПАРЫ СИЛ
- Сходящиеся силы. Приведение сходящихся сил к простейшему виду
- Вычисление и построение равнодействующей
- Условия равновесия сходящихся сил
- Теорема о трех силах
- Теорема Вариньона
- Пара сил и ее момент
- Приведение системы пар сил к простейшему виду или сложение пар сил
- Упражнения
- ЛЕКЦИЯ 3. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ
- Момент силы относительно оси
- Аналитический способ вычисления момента
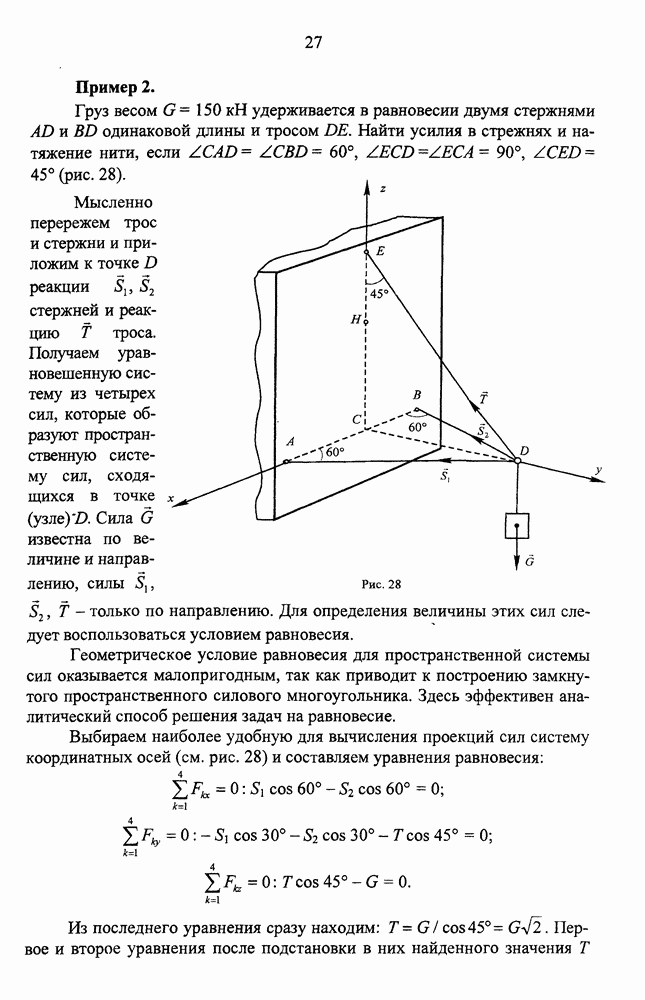
- Геометрический способ вычисления момента
- Преобразование пространственной произвольной системы сил
- Приведение пространственной произвольной системы сил к данному центру. Главный вектор и главный момент. Основная теорема статики
- Вычисление и построение главного вектора и главного момента
- Перемена центра приведения
- ЛЕКЦИЯ 4. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ (продолжение). ЧАСТНЫЕ СЛУЧАИ СИСТЕМЫ СИЛ
- Случаи приведения к простейшему виду
- Условия (уравнения) равновесия пространственной произвольной системы сил
- Частные случаи системы сил
- Плоская система сил
- Система параллельных сил
- Равновесие системы тел
- Вопросы для самопроверки
- ЛЕКЦИЯ 5. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ И ЦЕНТР ТЯЖЕСТИ
- Центр параллельных сил
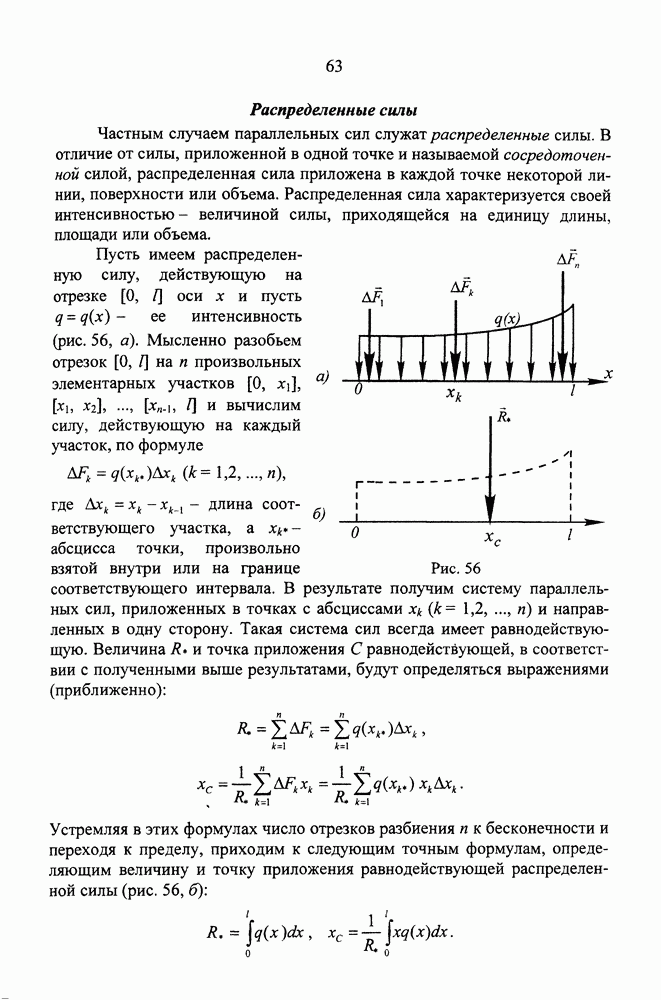
- Распределенные силы
- Центр тяжести
- Интегральные формулы для координат центра тяжести
- Метод разбиения
- Вопросы для самопроверки
- ЛЕКЦИЯ 6. ТРЕНИЕ ТВЕРДЫХ ТЕЛ
- Трение покоя и трение скольжения
- Трение качения
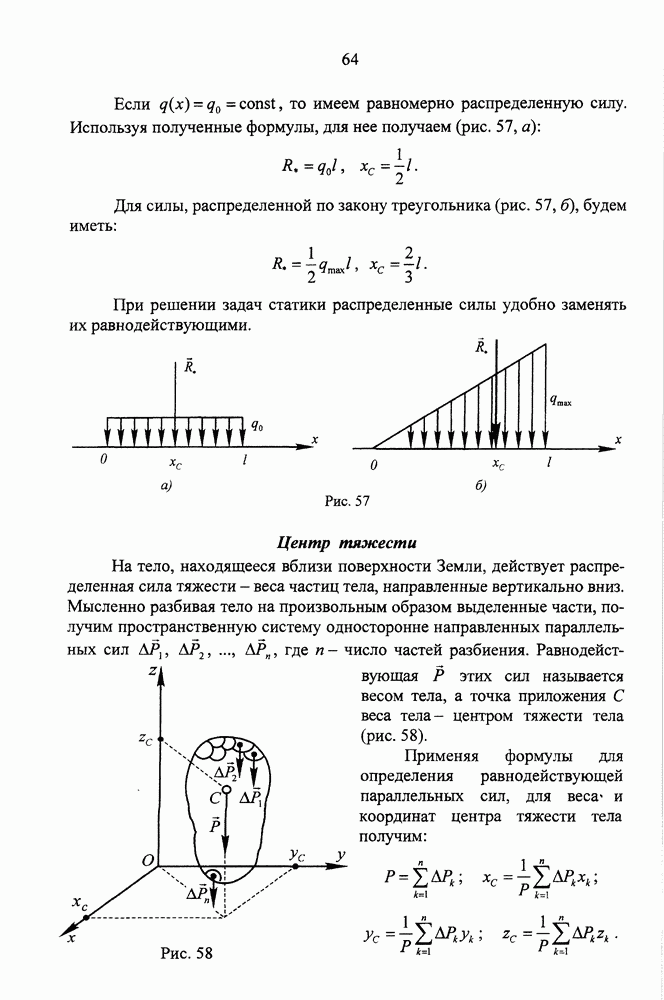
- Решение задач статики при учете сил трения
- Заклинивание
- Упражнения
- КИНЕМАТИКА
- ЛЕКЦИЯ 7. КИНЕМАТИКА ТОЧКИ
- Способы задания движения точки
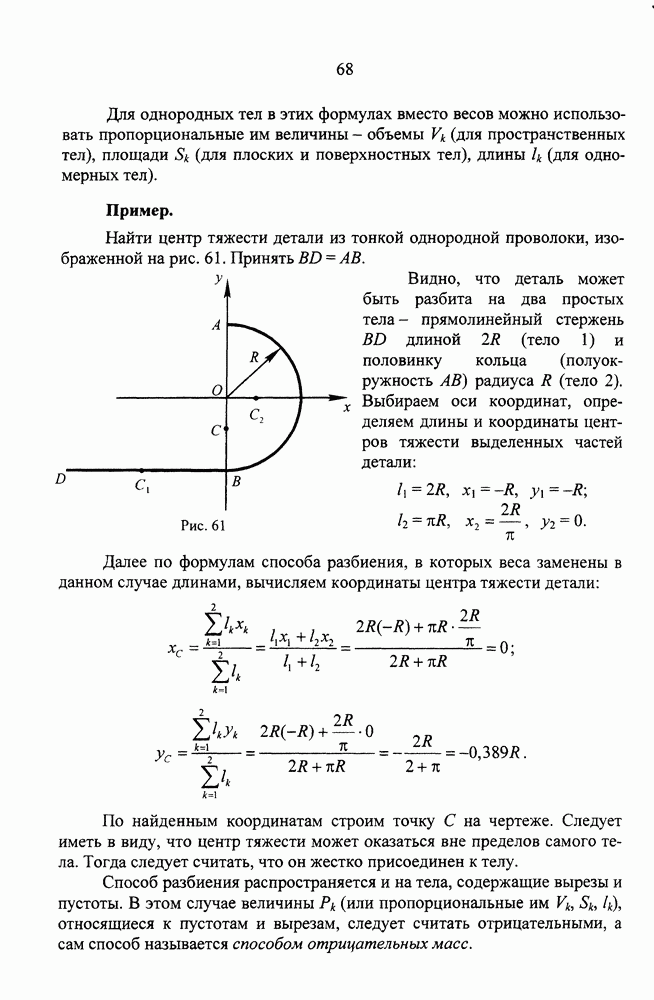
- Определение траектории, скорости и ускорения точки при векторном способе задания движения
- Определение траектории, скорости и ускорения точки при координатном способе задания движения
- Определение скорости и ускорения точки при естественном способе задания движения
- Естественные координатные оси и их орты
- Определение скорости
- Определение ускорения
- Вопросы для самопроверки
- ЛЕКЦИЯ 8. ПРОСТЕЙШИЕ ДРИЖЕНИЯ ТВЕРДОГО ТЕЛА
- Поступательное движение
- Вращательное движение
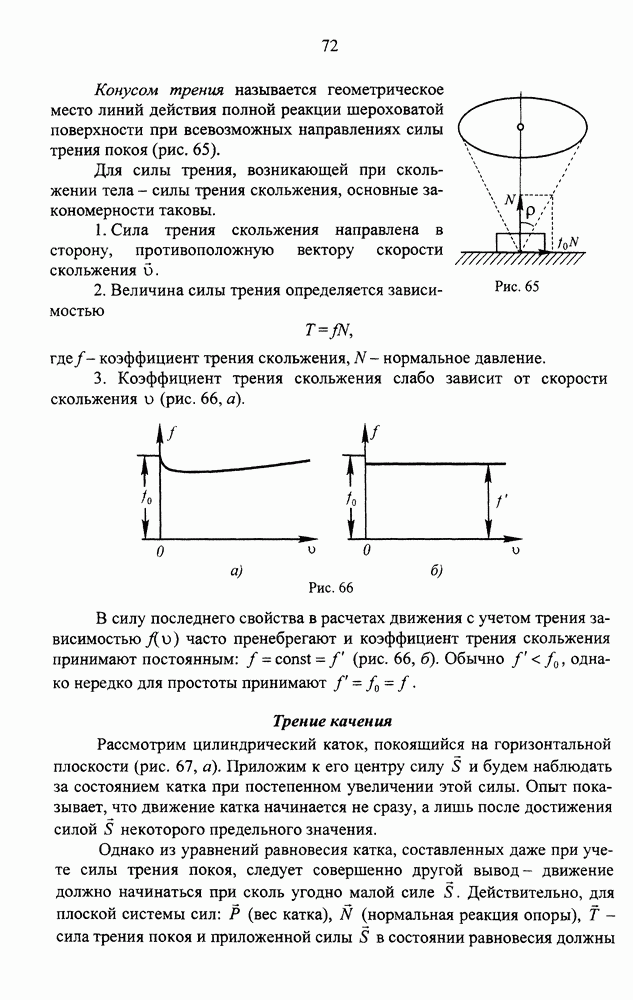
- Уравнение вращательного движения. Угловая скорость и угловое ускорение тела
- Траектории, скорости и ускорения точек тела
- Векторы угловой скорости и углового ускорения тела
- Векторные формулы для линейной скорости, касательного и нормального ускорений точки тела
- Вопросы для самопроверки
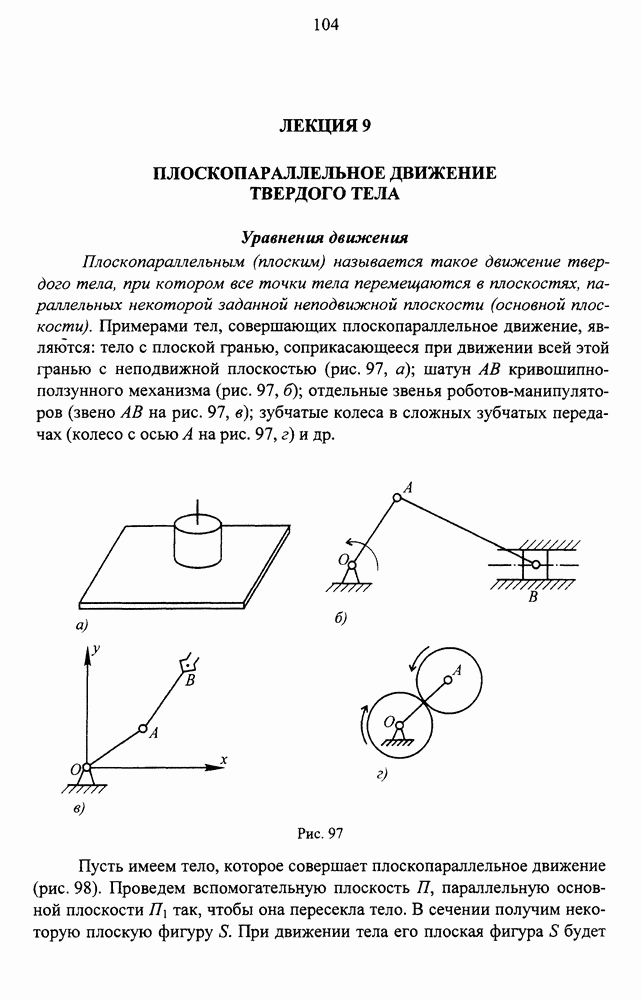
- ЛЕКЦИЯ 9. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- Уравнения движения
- Угловая скорость и угловое ускорение тела при плоскопараллельном движении
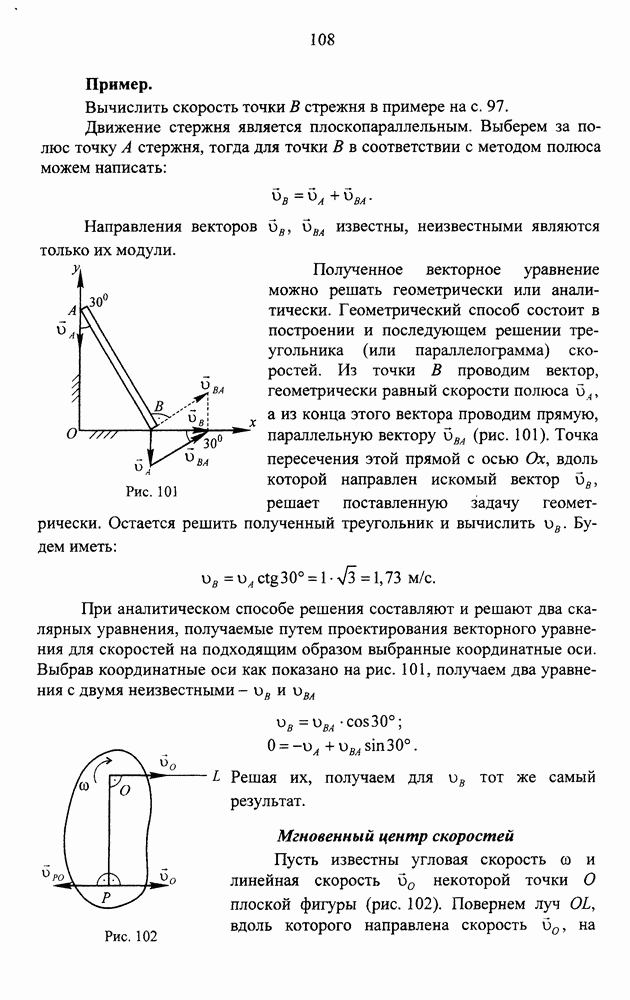
- Определение скоростей точек тела. Метод полюса
- Мгновенный центр скоростей
- Определение скоростей точек плоской фигуры через мгновенный центр скоростей
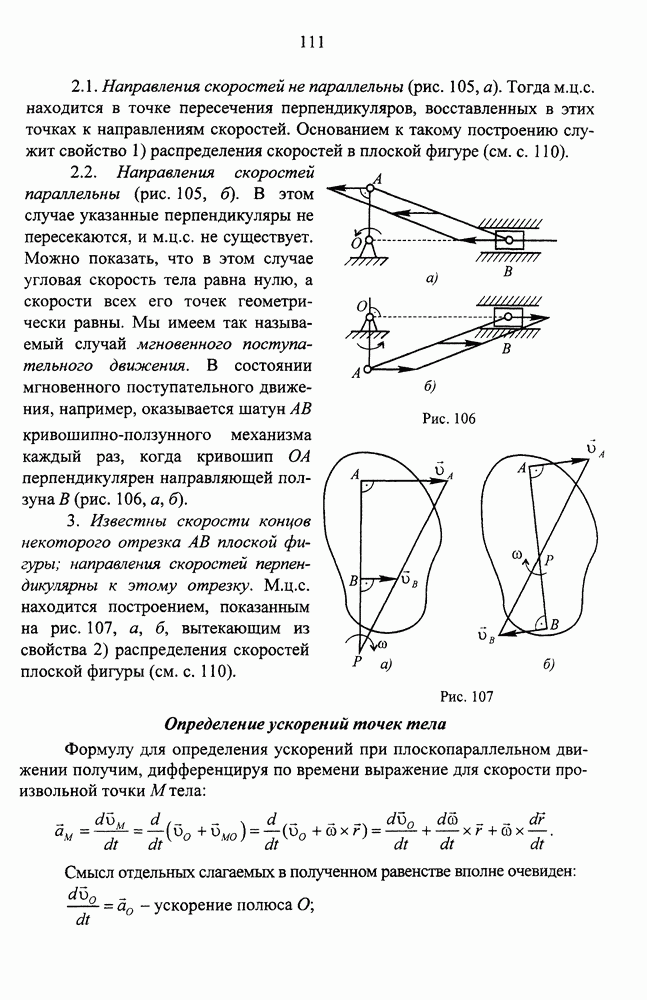
- Различные случаи определения положения мгновенного центра скоростей
- Определение ускорений точек тела
- Вопросы для самопроверки
- ЛЕКЦИЯ 10. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
- Теорема сложения скоростей
- Теорема сложения ускорений
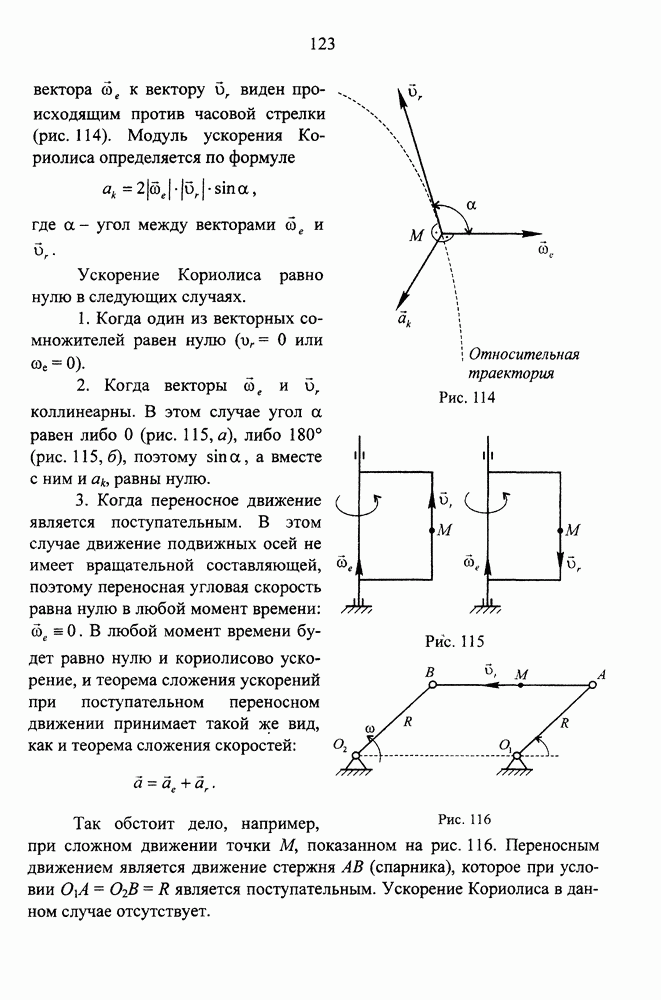
- Причины появления ускорения Кориолиса
- Вычисление и построение ускорения Кориолиса
- Вопросы для самопроверки
- ДОБАВЛЕНИЕ. КИНЕМАТИКА ПРОЦЕССА ФУГОВАНИЯ ДРЕВЕСИНЫ
- Схема и расчетная модель процесса фугования
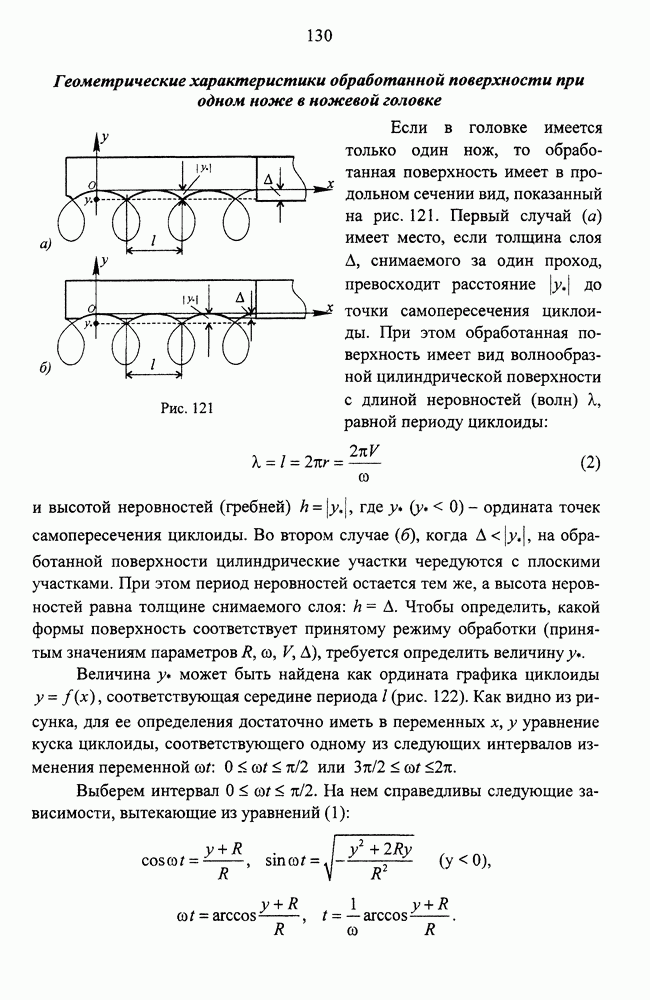
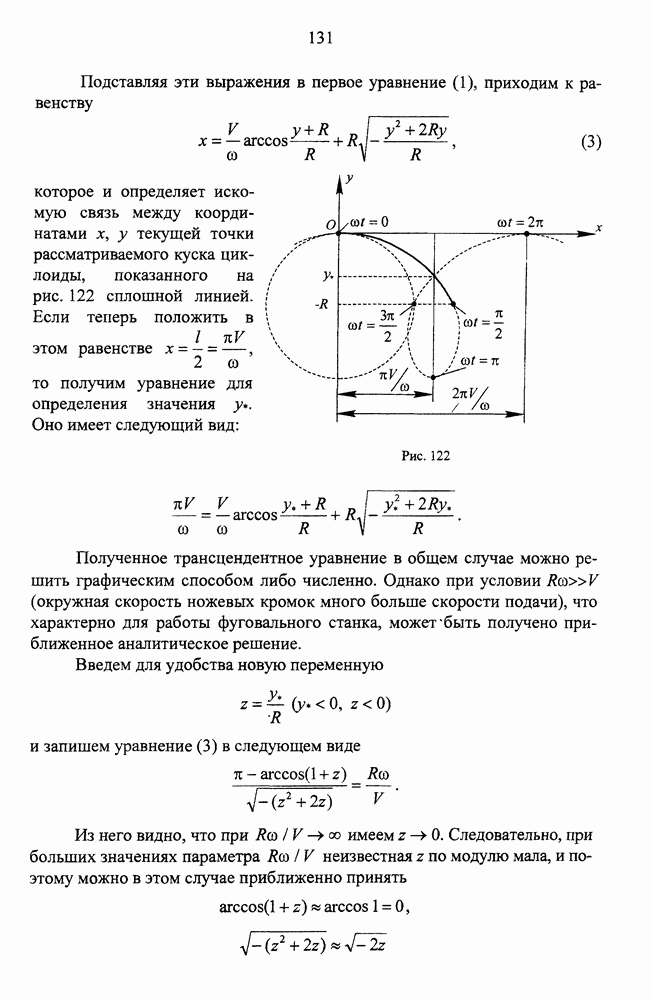
- Геометрические характеристики обработанной поверхности при одном ноже в ножевой головке
- Геометрические характеристики поверхности в случае многоножевой головки
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА