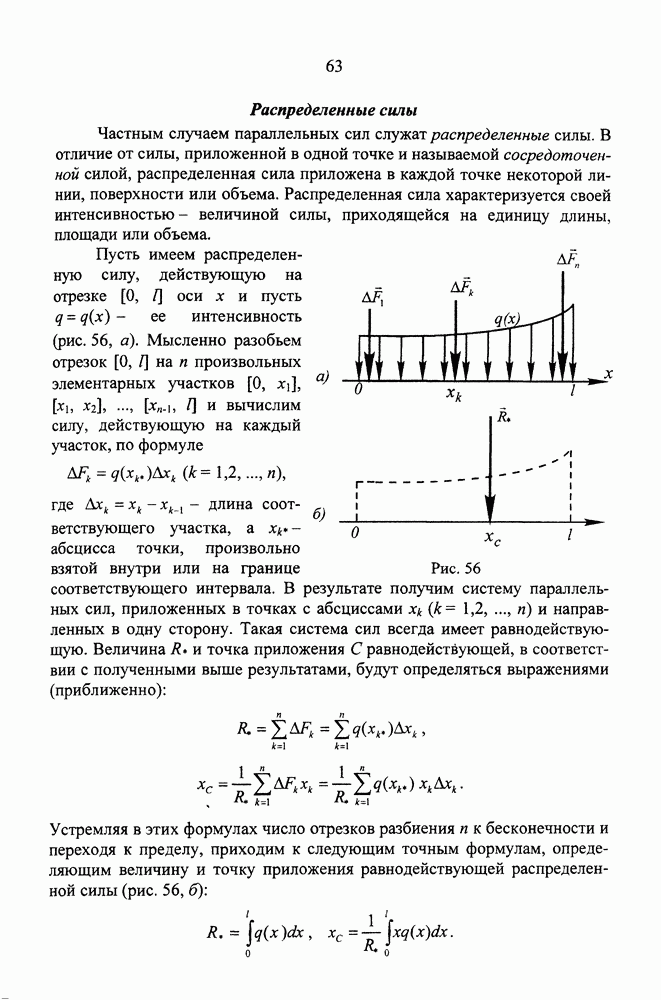
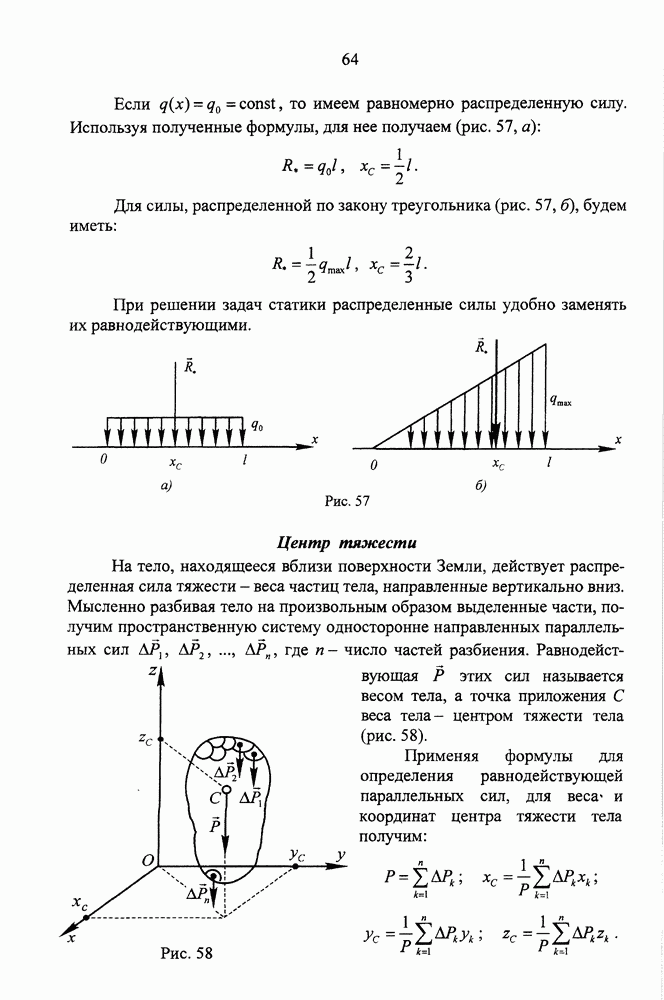
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ЛЕКЦИЯ 7. КИНЕМАТИКА ТОЧКИ
Поскольку в кинематике действие сил не рассматривается, то остаются в стороне также и инертные свойства тел. В частности, остается без всякого применения мера инертности материальной точки - ее масса. По этой причине понятия материальной точки и геометрической точки в кинематике не различаются, можно говорить просто о точке. С вопросов движения этого самого простого объекта мы и начнем изложение кинематики.
Способы задания движения точки
Различают векторный, координатный и естественный (натуральный) способы задания движения.
Векторный способ задания движения состоит в следующем.
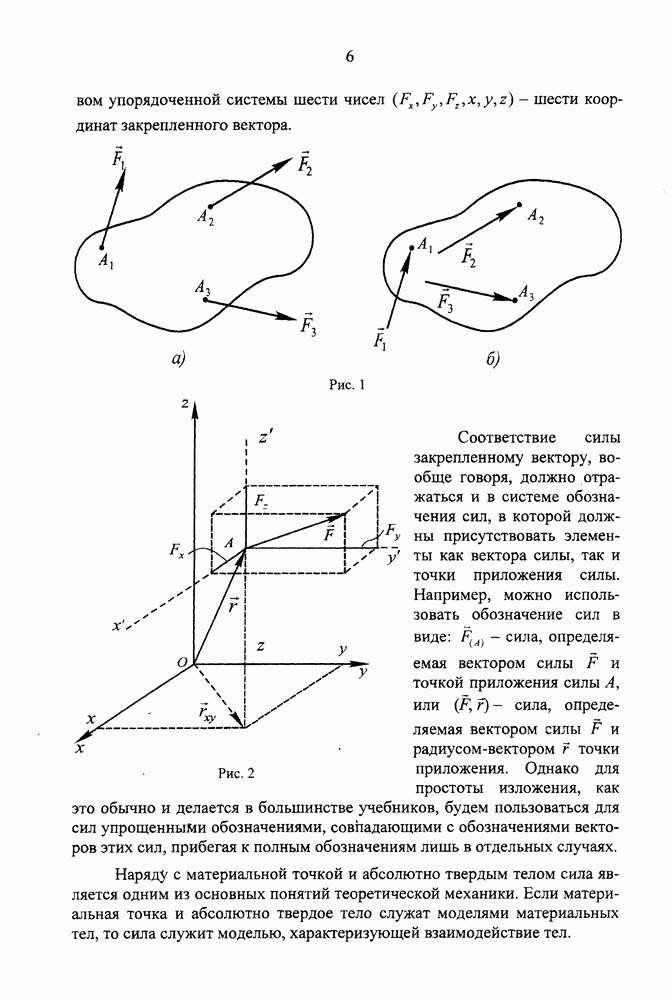
Пусть М - движущаяся точка, А - тело отсчета (рис. 72). Выберем в теле А произвольную точку О - точку отсчета, построим вектор  . Этот вектор, начало которого совпадает с точкой отсчета О, а конец - с точкой М называется радиусом-вектором точки М. При движении точки М радиус-вектор
. Этот вектор, начало которого совпадает с точкой отсчета О, а конец - с точкой М называется радиусом-вектором точки М. При движении точки М радиус-вектор  непрерывно изменяется во времени, поэтому существует некоторая вектор-функция времени
непрерывно изменяется во времени, поэтому существует некоторая вектор-функция времени

Если эта функция известна, то для каждого момента времени t может быть построен вектор  и тем самым найдено положение движущейся точки в этот момент.
и тем самым найдено положение движущейся точки в этот момент.
Функция (1) называется векторным законом (векторным уравнением) движения точки М.
При координатном способе задания движения с телом отсчета связывается какая-либо, например декартова прямоугольная, система координат (рис. 73).
Движение точки будет задано, если ее координаты будут известны как функции времени Рис. 72


Рис. 72.

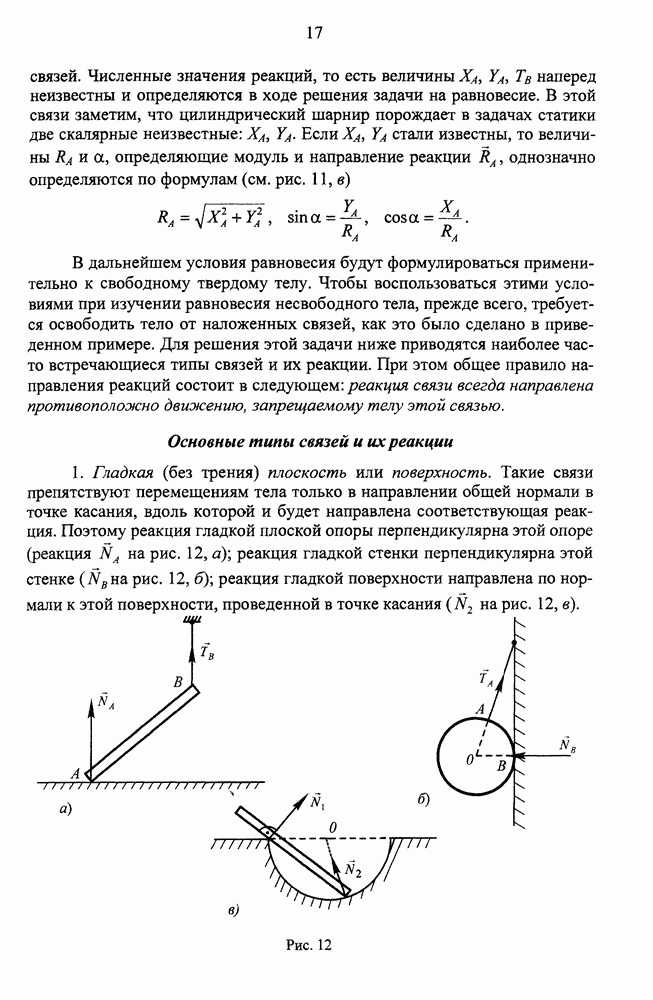
Рис. 73.

Рис. 74.
Зависимости (2), выражающие текущие координаты движущейся точки в виде функций времени, называются уравнениями движения точки в декартовых координатах.
Если точка движется, оставаясь все время в одной плоскости, то оси  можно расположить в той же плоскости и ограничиться двумя уравнениями движения
можно расположить в той же плоскости и ограничиться двумя уравнениями движения

При движении в плоскости часто удобно пользоваться полярной системой координат, задавая положение точки ее полярным углом  и полярным радиусом
и полярным радиусом  (рис. 74). В этом случае уравнения движения точки имеют вид
(рис. 74). В этом случае уравнения движения точки имеют вид

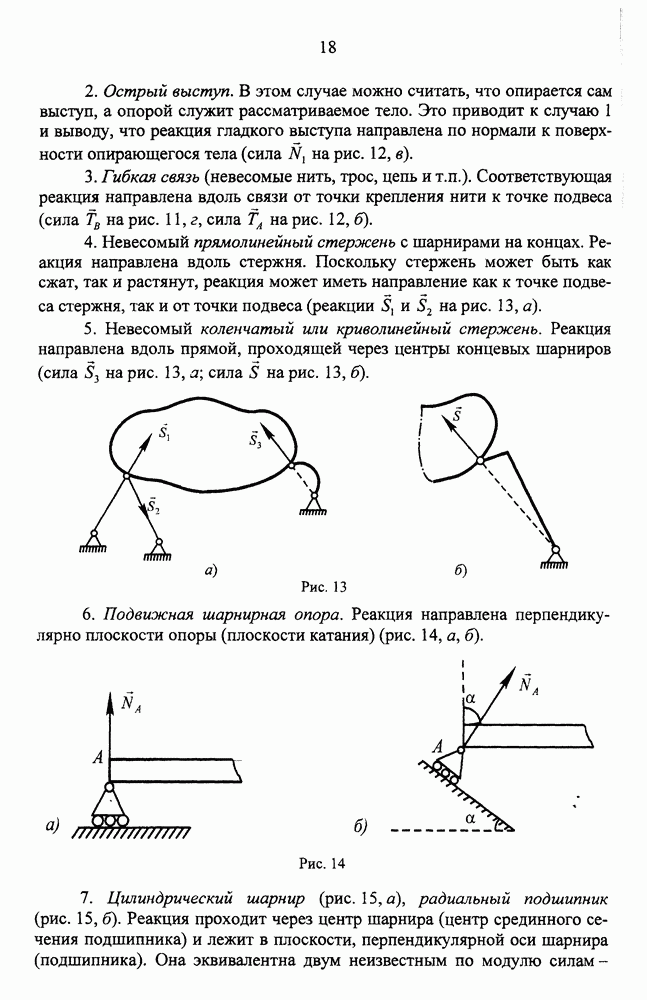
Линия, описываемая движущейся точкой в пространстве, называется траекторией точки. Естественный способ задания движения состоит в задании траектории точки и закона движения по траектории.
 Пусть траектория точки М суть заданная кривая, М - положение точки на ней (рис. 75). Будем рассматривать траекторию как криволинейную координатную ось, для чего выберем на ней начало отсчета
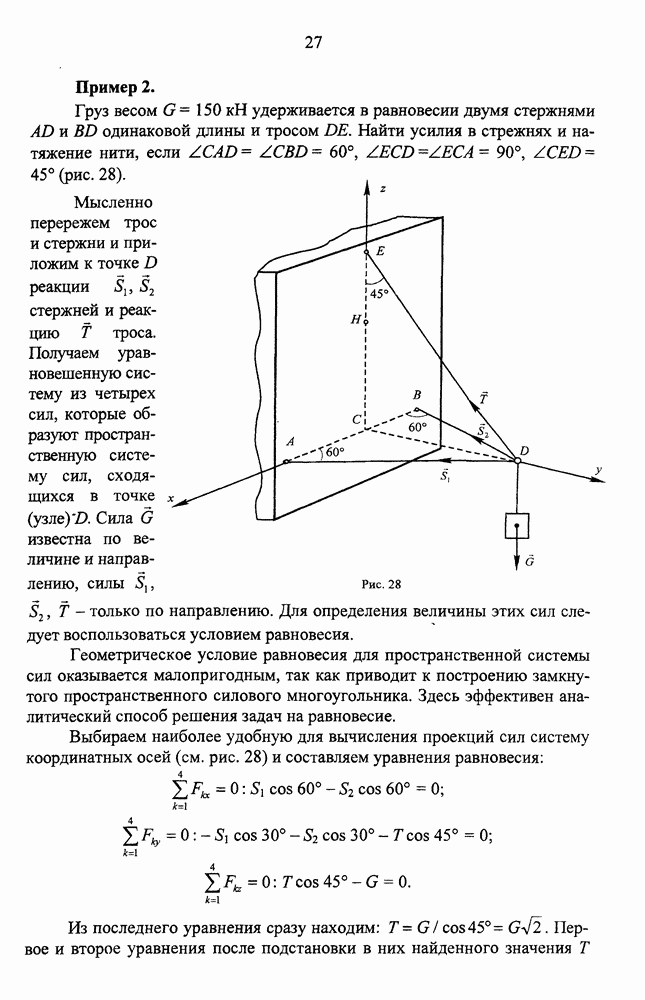
Пусть траектория точки М суть заданная кривая, М - положение точки на ней (рис. 75). Будем рассматривать траекторию как криволинейную координатную ось, для чего выберем на ней начало отсчета  (точку
(точку  ) и направление отсчета дуг (на рис. 75 направление отсчета
) и направление отсчета дуг (на рис. 75 направление отсчета  выбрано вправо от точки
выбрано вправо от точки  ). Длина дуги
). Длина дуги  , взятая со знаком плюс или минус в зависимости от положения точки М относительно начала отсчета
, взятая со знаком плюс или минус в зависимости от положения точки М относительно начала отсчета  , вполне определяет положение точки в пространстве и называется дуговой координатой точки. Движение точки будет задано, если ее дуговая координата 5 будет выражена в виде функции времени
, вполне определяет положение точки в пространстве и называется дуговой координатой точки. Движение точки будет задано, если ее дуговая координата 5 будет выражена в виде функции времени

Зависимость (4) называется законом движения точки по траектории или, что то же самое, законом движения точки в естественной форме.

Рис. 75.
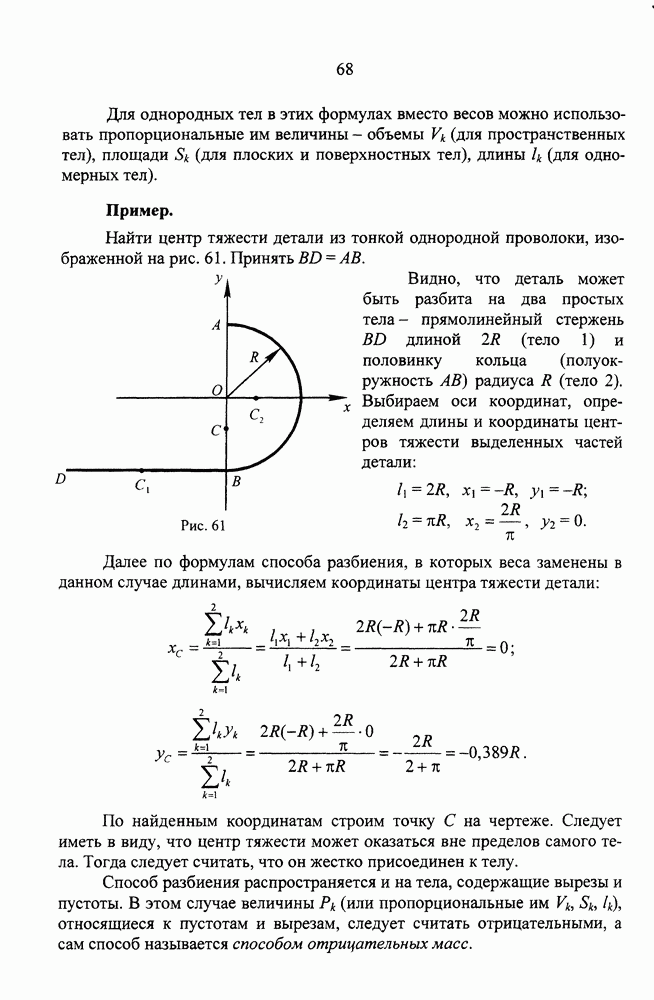
Пример.
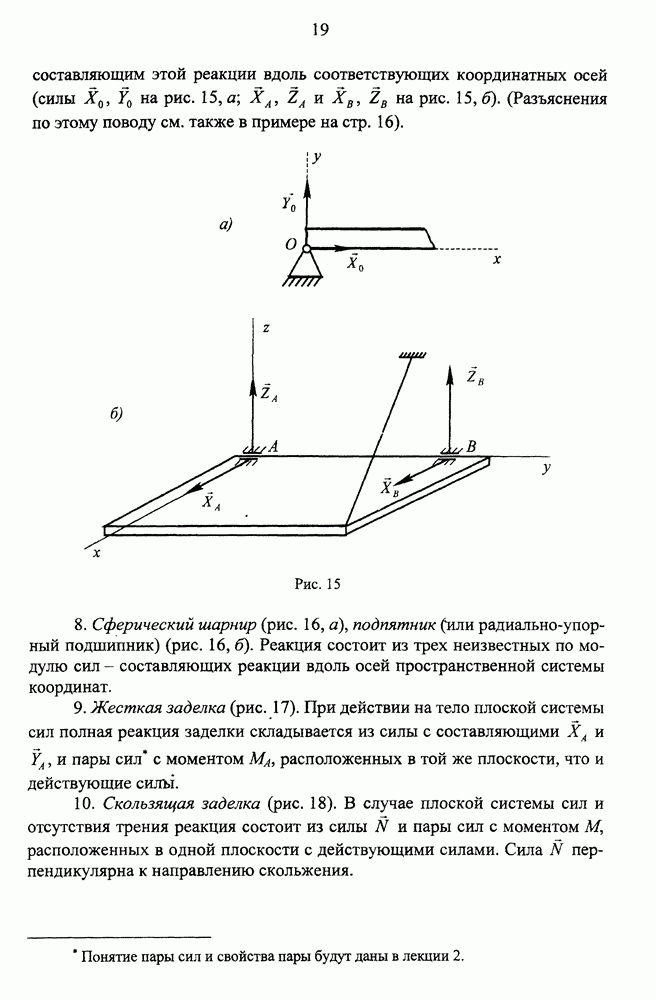
Написать уравнения движения точки, движущейся равномерно по окружности радиуса R и делающей n оборотов за одну минуту.
Начнем с естественного способа описания движения. Изображаем траекторию- окружность радиуса R с центром в точке О (рис. 76). Начало отсчета дуг  совместим с положением точки в момент начала наблюдения, то есть при
совместим с положением точки в момент начала наблюдения, то есть при  ; за положительное направление отсчета выберем направление в сторону движения точки.
; за положительное направление отсчета выберем направление в сторону движения точки.
Пусть М положение движущейся точки в текущий момент времени  . Для центрального угла
. Для центрального угла  , который будем отсчитывать в сторону движения точки, согласно условию, можем написать
, который будем отсчитывать в сторону движения точки, согласно условию, можем написать

Здесь  измеряется в радианах, t - в секундах.
измеряется в радианах, t - в секундах.
Длина s дуги  , радиус окружности R и центральный угол
, радиус окружности R и центральный угол  связаны геометрическим соотношением
связаны геометрическим соотношением

Подставляя сюда найденное значение  , получаем
, получаем

Это и есть закон естественной форме.
Для описания движения в координатной форме прежде всего следует выбрать подходящую систему координат, например, изображенную на рис. 77. Далее строят координатные отрезки и определяют соответствующие переменные расстояния. В нашем случае будем иметь:

Подставляя сюда угол  как функцию времени, получаем уравнения движения в координатной форме
как функцию времени, получаем уравнения движения в координатной форме


Рис. 76.
движения точки в

Рис. 77.
Пусть  - координатные орты. Тогда для радиуса-вектора точки
- координатные орты. Тогда для радиуса-вектора точки  будем иметь:
будем иметь:

Полученное равенство, выражающее радиус-вектор точки М как функцию времени, служит векторным уравнением ее движения.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ. ПРЕДМЕТ И ОСНОВНЫЕ ПОНЯТИЯ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ
- СТАТИКА. ЛЕКЦИЯ 1. ЗАДАЧИ СТАТИКИ, АКСИОМЫ СТАТИКИ. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
- Момент силы относительно точки
- Алгебраический момент силы
- Основные типы связей и их реакции
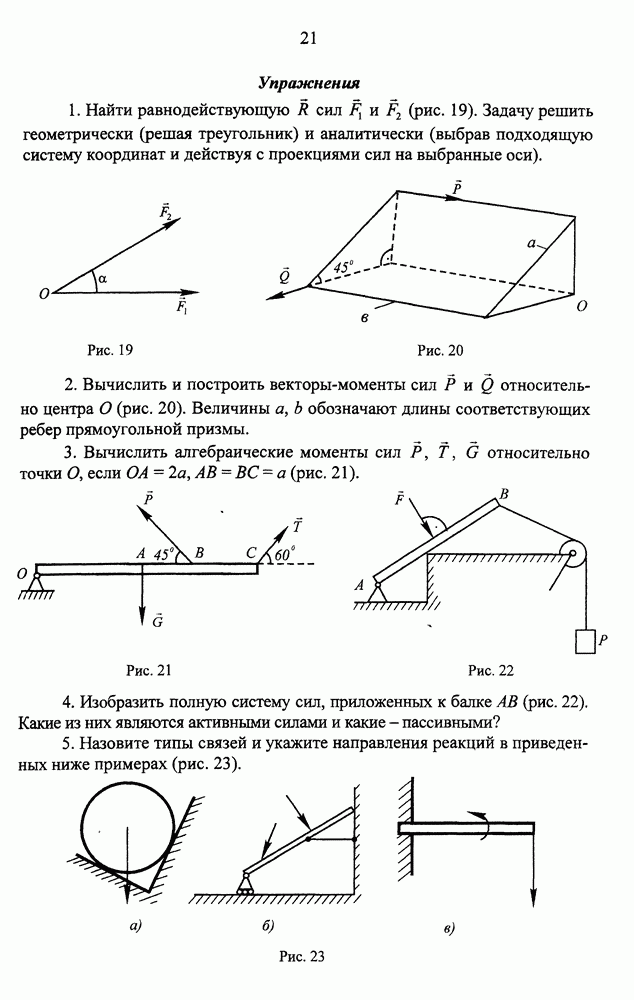
- Упражнения
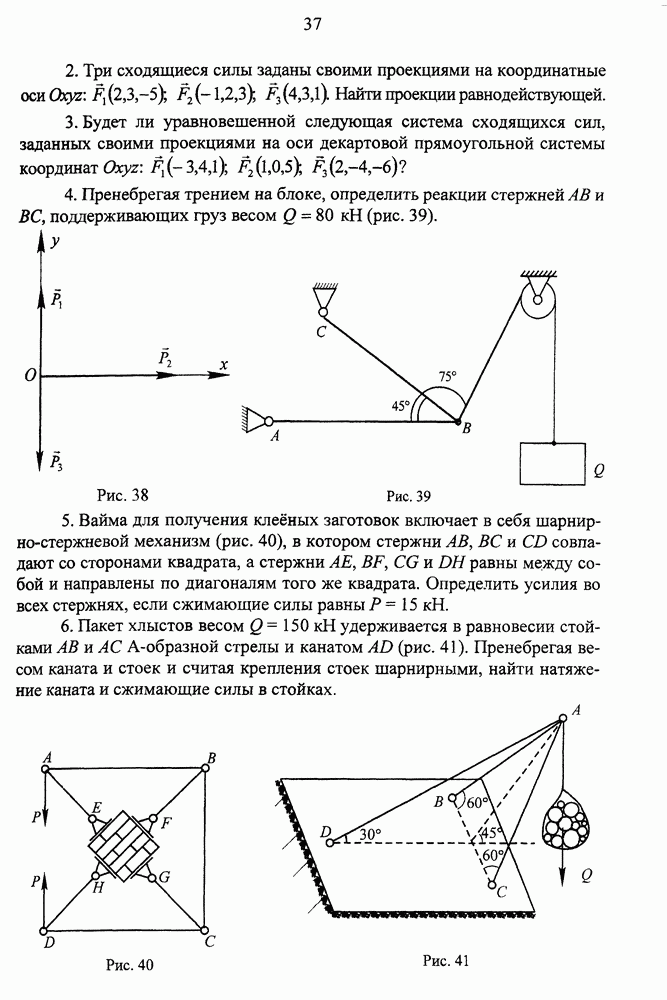
- ЛЕКЦИЯ 2. СХОДЯЩИЕСЯ СИЛЫ И ПАРЫ СИЛ
- Сходящиеся силы. Приведение сходящихся сил к простейшему виду
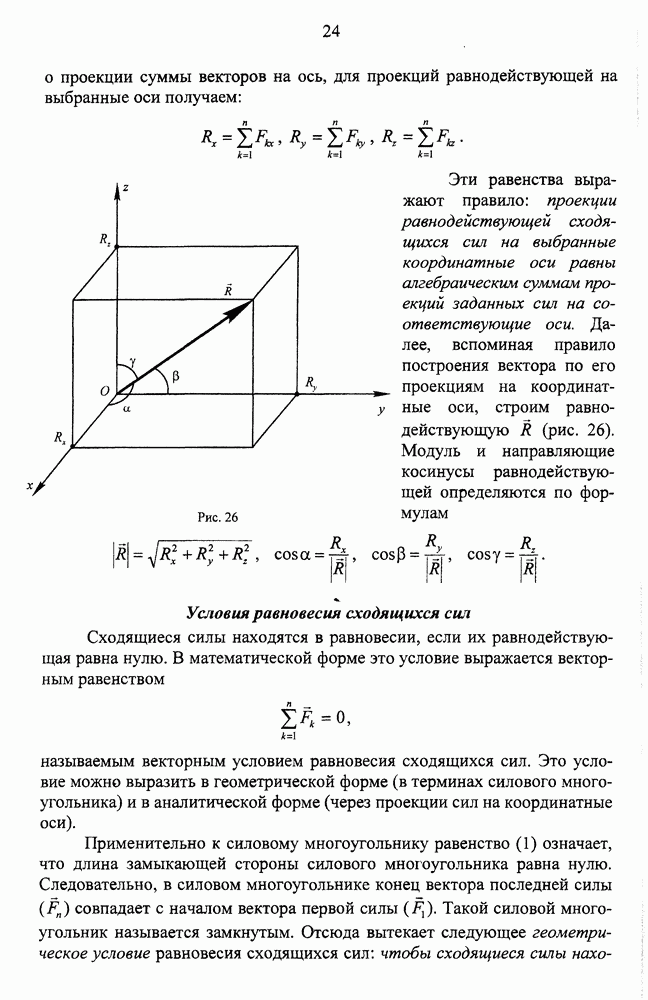
- Вычисление и построение равнодействующей
- Условия равновесия сходящихся сил
- Теорема о трех силах
- Теорема Вариньона
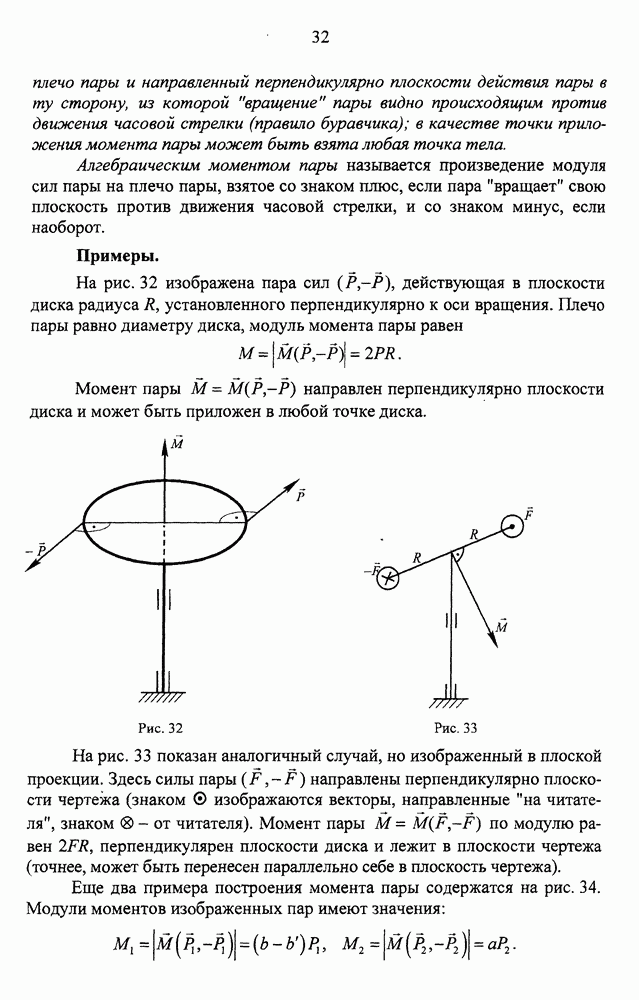
- Пара сил и ее момент
- Приведение системы пар сил к простейшему виду или сложение пар сил
- Упражнения
- ЛЕКЦИЯ 3. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ
- Момент силы относительно оси
- Аналитический способ вычисления момента
- Геометрический способ вычисления момента
- Преобразование пространственной произвольной системы сил
- Приведение пространственной произвольной системы сил к данному центру. Главный вектор и главный момент. Основная теорема статики
- Вычисление и построение главного вектора и главного момента
- Перемена центра приведения
- ЛЕКЦИЯ 4. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ (продолжение). ЧАСТНЫЕ СЛУЧАИ СИСТЕМЫ СИЛ
- Случаи приведения к простейшему виду
- Условия (уравнения) равновесия пространственной произвольной системы сил
- Частные случаи системы сил
- Плоская система сил
- Система параллельных сил
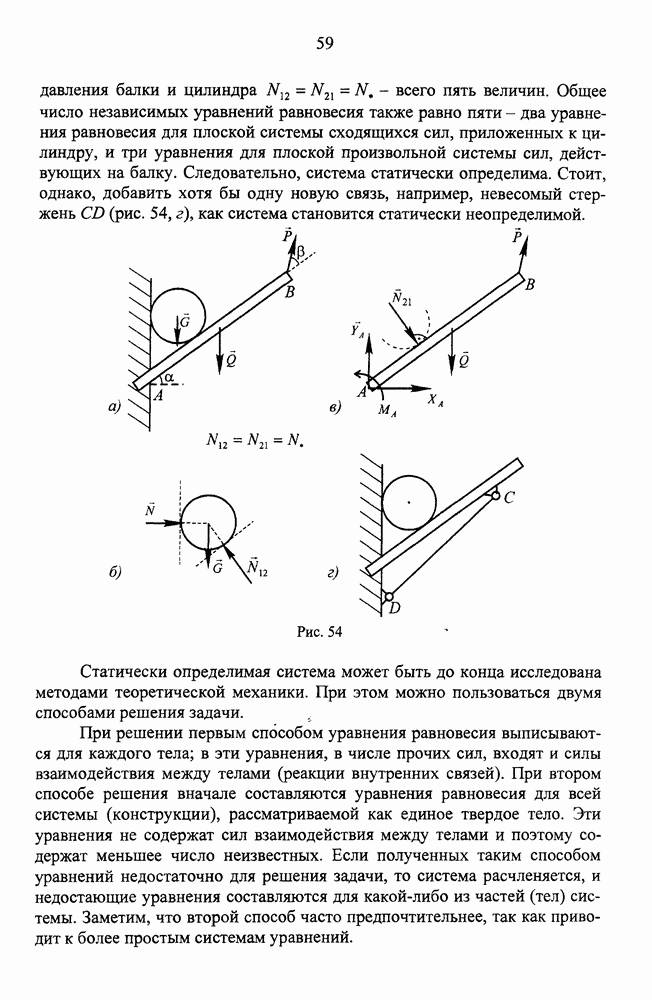
- Равновесие системы тел
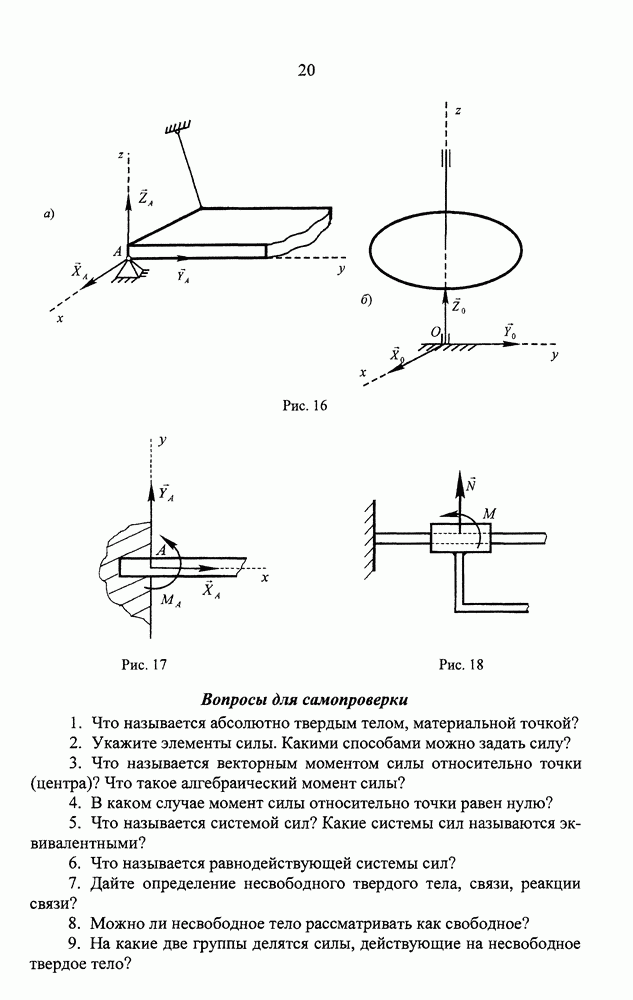
- Вопросы для самопроверки
- ЛЕКЦИЯ 5. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ И ЦЕНТР ТЯЖЕСТИ
- Центр параллельных сил
- Распределенные силы
- Центр тяжести
- Интегральные формулы для координат центра тяжести
- Метод разбиения
- Вопросы для самопроверки
- ЛЕКЦИЯ 6. ТРЕНИЕ ТВЕРДЫХ ТЕЛ
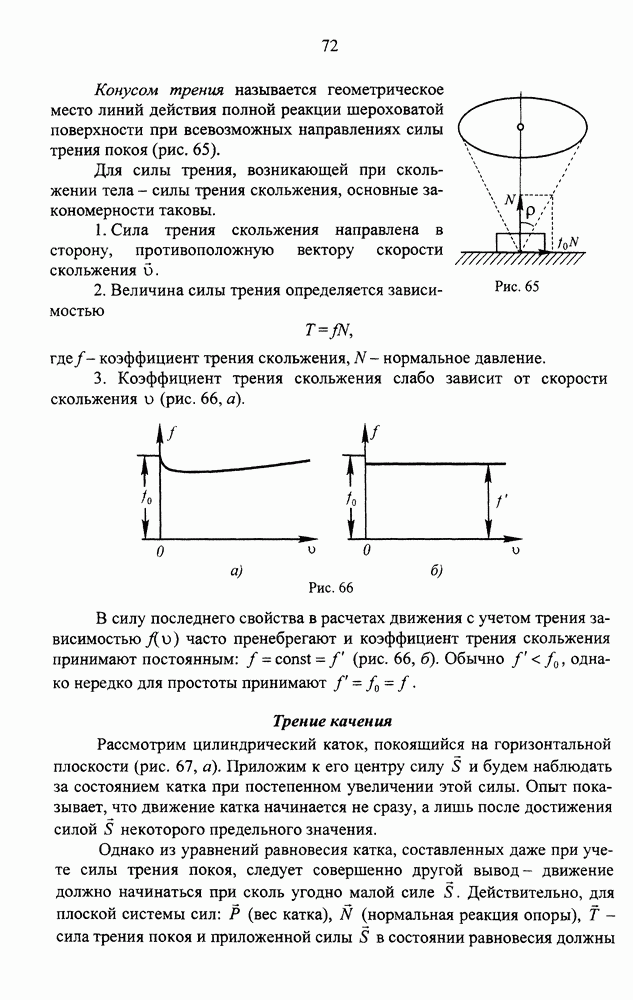
- Трение покоя и трение скольжения
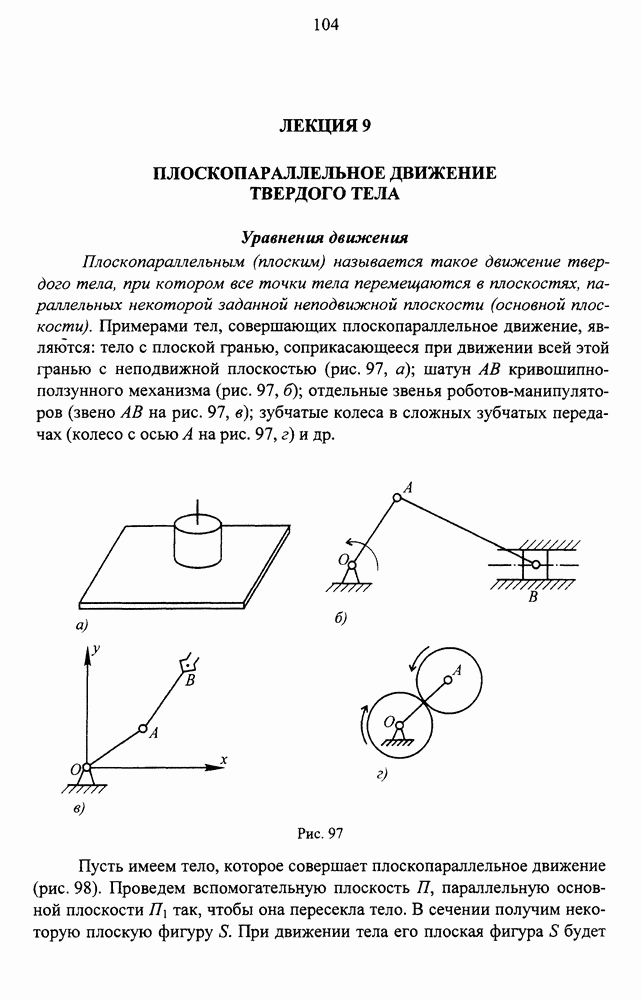
- Трение качения
- Решение задач статики при учете сил трения
- Заклинивание
- Упражнения
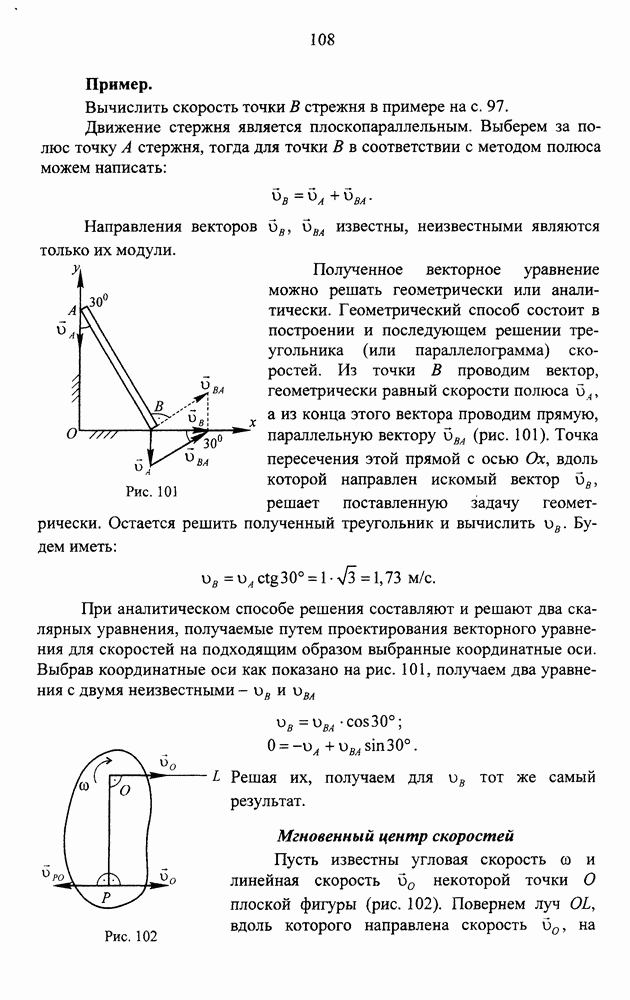
- КИНЕМАТИКА
- ЛЕКЦИЯ 7. КИНЕМАТИКА ТОЧКИ
- Способы задания движения точки
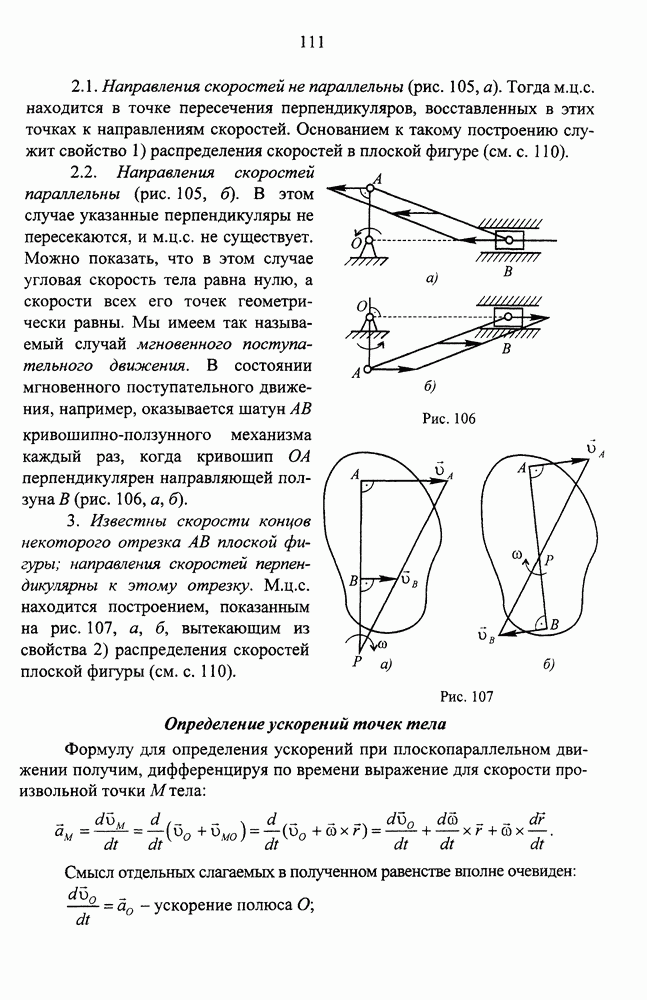
- Определение траектории, скорости и ускорения точки при векторном способе задания движения
- Определение траектории, скорости и ускорения точки при координатном способе задания движения
- Определение скорости и ускорения точки при естественном способе задания движения
- Естественные координатные оси и их орты
- Определение скорости
- Определение ускорения
- Вопросы для самопроверки
- ЛЕКЦИЯ 8. ПРОСТЕЙШИЕ ДРИЖЕНИЯ ТВЕРДОГО ТЕЛА
- Поступательное движение
- Вращательное движение
- Уравнение вращательного движения. Угловая скорость и угловое ускорение тела
- Траектории, скорости и ускорения точек тела
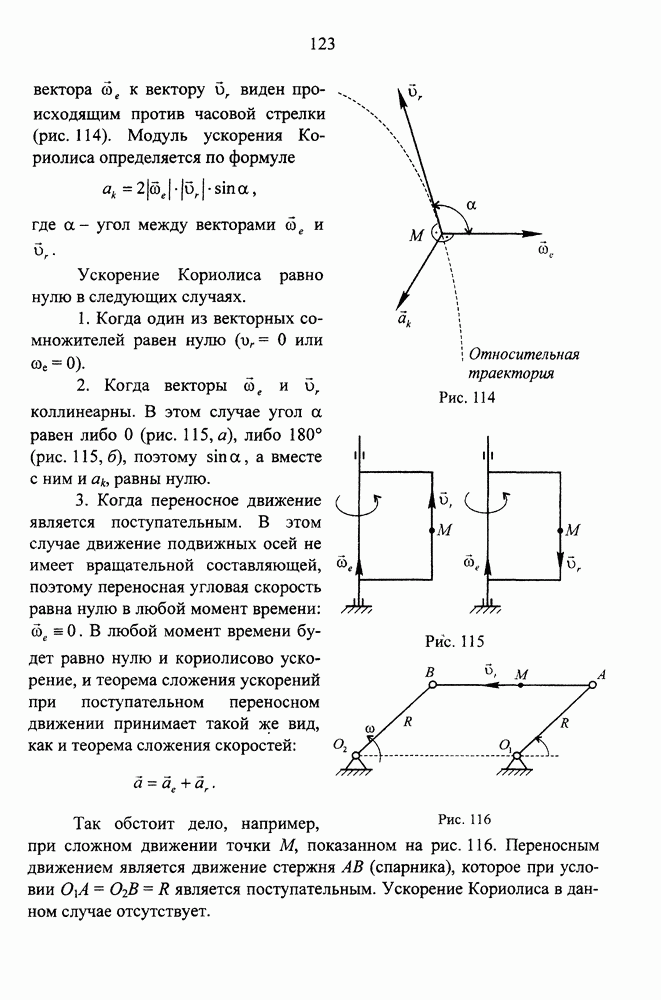
- Векторы угловой скорости и углового ускорения тела
- Векторные формулы для линейной скорости, касательного и нормального ускорений точки тела
- Вопросы для самопроверки
- ЛЕКЦИЯ 9. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- Уравнения движения
- Угловая скорость и угловое ускорение тела при плоскопараллельном движении
- Определение скоростей точек тела. Метод полюса
- Мгновенный центр скоростей
- Определение скоростей точек плоской фигуры через мгновенный центр скоростей
- Различные случаи определения положения мгновенного центра скоростей
- Определение ускорений точек тела
- Вопросы для самопроверки
- ЛЕКЦИЯ 10. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
- Теорема сложения скоростей
- Теорема сложения ускорений
- Причины появления ускорения Кориолиса
- Вычисление и построение ускорения Кориолиса
- Вопросы для самопроверки
- ДОБАВЛЕНИЕ. КИНЕМАТИКА ПРОЦЕССА ФУГОВАНИЯ ДРЕВЕСИНЫ
- Схема и расчетная модель процесса фугования
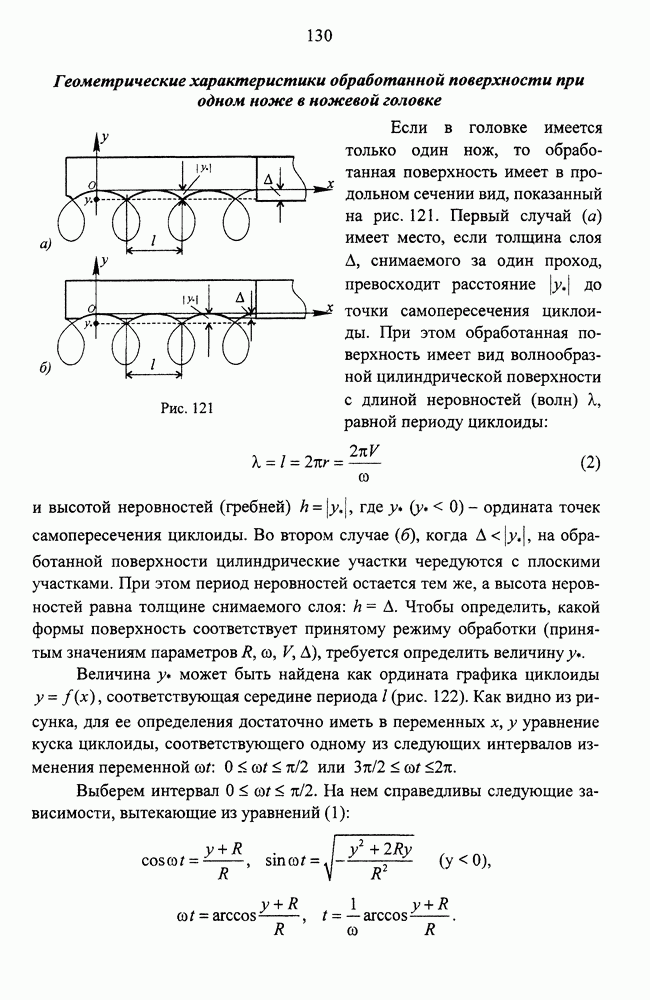
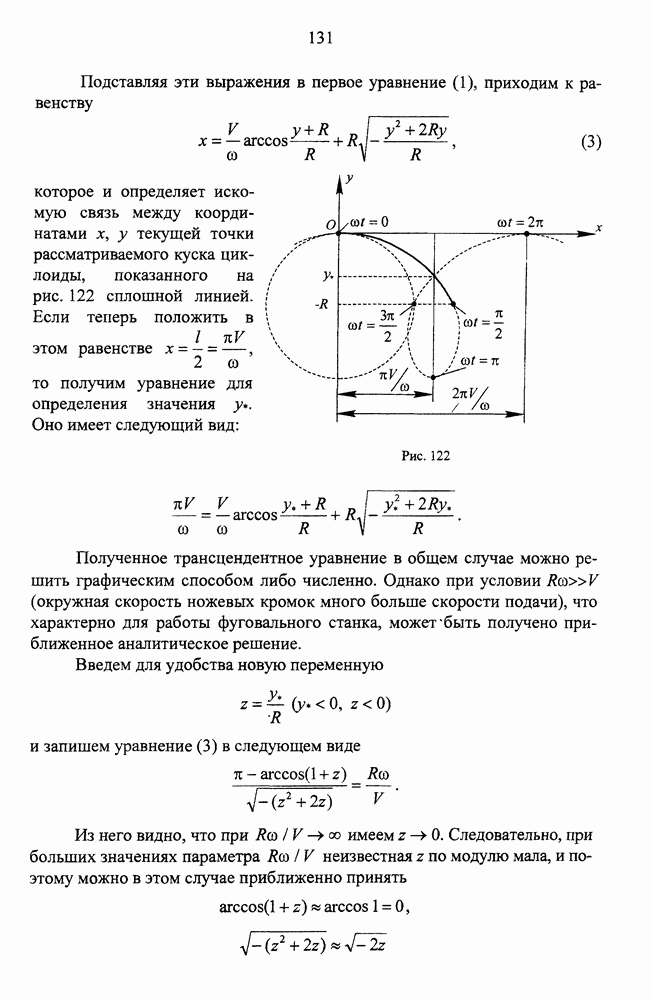
- Геометрические характеристики обработанной поверхности при одном ноже в ножевой головке
- Геометрические характеристики поверхности в случае многоножевой головки
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА