| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Определение траектории, скорости и ускорения точки при координатном способе задания движения
Пусть движение точки задано уравнениями движения в декартовых координатах:  .
.
Для каждого момента времени t по этим уравнениям можно определить координаты точки в этот момент и указать ее положение в пространстве. Придавая t всевозможные значения, получим множество положений движущейся точки в пространстве — ее траекторию. Следовательно, уравнения движения одновременно являются уравнениями траектории точки в параметрической форме, причем параметром служит время t.
Чтобы получить уравнение траектории в виде зависимости между координатами точки, достаточно из уравнений движения исключить время.
Пример 1.
Движение точки задано уравнениями  , у (х, у - в сантиметрах, t - в секундах). Найти уравнение траектории точки в координатной форме.
, у (х, у - в сантиметрах, t - в секундах). Найти уравнение траектории точки в координатной форме.
Для определения уравнения траектории из уравнений движения исключаем время t. Для этого из первого уравнения выражаем

и подставляем это значение во второе уравнение, преобразованное к функциям одинарного угла:

Опуская промежуточные выражения, получаем уравнение траектории

Уравнение определяет параболу, расположенную симметрично относительно оси у, с вершиной в точке (0,4). Траекторией служит кусок этой параболы, заключенный между точками с координатами  и
и  (рис. 80).
(рис. 80).
Пример 2.
Определить уравнение траектории, если точка движется согласно уравнениям ( в сантиметрах, t - в секундах):
в сантиметрах, t - в секундах):

Для исключения времени t из уравнений движения выразим из этих уравнений  и
и  :
:

Возводя эти равенства в квадрат и почленно складывая, получаем уравнение траектории в координатной форме:

Это уравнение эллипса с центром в точке А (2,3) и с полуосями  ,
,  (рис. 81). Траекторией служит вся кривая эллипса.
(рис. 81). Траекторией служит вся кривая эллипса.

Рис. 80.

Рис. 81.

Рис. 82
Займемся теперь определением скорости и ускорения.
Зная уравнения движения точки, можно выразить в функции времени радиус-вектор точки (рис. 82):

Теперь находим скорость, дифференцируя радиус-вектор по времени:

При дифференцировании учитывается, что оси Oxyz неподвижны, поэтому координатные орты являются постоянными векторами, и их производные равны нулю.
Полученная формула определяет скорость точки в виде разложения по координатному базису  . Так как коэффициенты при ортах равны проекциям скорости на соответствующие координатные оси, отсюда следуют формулы
. Так как коэффициенты при ортах равны проекциям скорости на соответствующие координатные оси, отсюда следуют формулы

По известным проекциям находим модуль и направляющие косинусы скорости:

Аналогичным образом определяется и ускорение. Дифференцируя выражение для вектора скорости, получаем:

Откуда для проекций ускорения следуют формулы

Проекции ускорения можно выразить также через проекции скорости:

Модуль и направляющие косинусы ускорения выражаются равенствами

Пример.
Точка движется в плоскости  согласно уравнениям
согласно уравнениям

где  заданы в сантиметрах, время
заданы в сантиметрах, время  в секундах, а величины
в секундах, а величины  - заданные постоянные. Найти скорость и ускорение точки в момент, когда она впервые после начала движения пересекает ось х.
- заданные постоянные. Найти скорость и ускорение точки в момент, когда она впервые после начала движения пересекает ось х.
Скорость и ускорение находим, вычисляя их проекции на координатные оси. Сначала это сделаем для произвольного момента  :
:

Когда точка находится на оси х, выполняется равенство  . Подставляя это значение во второе уравнение движения и решая полученное уравнение относительно
. Подставляя это значение во второе уравнение движения и решая полученное уравнение относительно  находим
находим

Момент  соответствует началу движения, а первое после начала движения пересечение оси
соответствует началу движения, а первое после начала движения пересечение оси  происходит при
происходит при  . Подставляя это значение в предыдущие формулы, найдем
. Подставляя это значение в предыдущие формулы, найдем

Таким образом, в расчетный момент времени  скорость
скорость  и ускорение
и ускорение  имеют модули
имеют модули

и направляющие косинусы

На рис. 83 показана геометрическая картина движения. Траекторией точки служит окружность радиуса  с центром в точке С (1,0). Подставляя в уравнения движения
с центром в точке С (1,0). Подставляя в уравнения движения  находим, что в начальный момент точка находится в положении
находим, что в начальный момент точка находится в положении  .
.
Придавая времени t малое положительное значение  и определяя знаки координат х, у, получаем
и определяя знаки координат х, у, получаем  из чего следует, что точка движется из положения
из чего следует, что точка движется из положения  против хода часовой стрелки. В расчетный момент
против хода часовой стрелки. В расчетный момент  она находится в начале координат, имея скорость
она находится в начале координат, имея скорость  и ускорение
и ускорение  .
.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ. ПРЕДМЕТ И ОСНОВНЫЕ ПОНЯТИЯ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ
- СТАТИКА. ЛЕКЦИЯ 1. ЗАДАЧИ СТАТИКИ, АКСИОМЫ СТАТИКИ. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
- Момент силы относительно точки
- Алгебраический момент силы
- Основные типы связей и их реакции
- Упражнения
- ЛЕКЦИЯ 2. СХОДЯЩИЕСЯ СИЛЫ И ПАРЫ СИЛ
- Сходящиеся силы. Приведение сходящихся сил к простейшему виду
- Вычисление и построение равнодействующей
- Условия равновесия сходящихся сил
- Теорема о трех силах
- Теорема Вариньона
- Пара сил и ее момент
- Приведение системы пар сил к простейшему виду или сложение пар сил
- Упражнения
- ЛЕКЦИЯ 3. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ
- Момент силы относительно оси
- Аналитический способ вычисления момента
- Геометрический способ вычисления момента
- Преобразование пространственной произвольной системы сил
- Приведение пространственной произвольной системы сил к данному центру. Главный вектор и главный момент. Основная теорема статики
- Вычисление и построение главного вектора и главного момента
- Перемена центра приведения
- ЛЕКЦИЯ 4. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ (продолжение). ЧАСТНЫЕ СЛУЧАИ СИСТЕМЫ СИЛ
- Случаи приведения к простейшему виду
- Условия (уравнения) равновесия пространственной произвольной системы сил
- Частные случаи системы сил
- Плоская система сил
- Система параллельных сил
- Равновесие системы тел
- Вопросы для самопроверки
- ЛЕКЦИЯ 5. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ И ЦЕНТР ТЯЖЕСТИ
- Центр параллельных сил
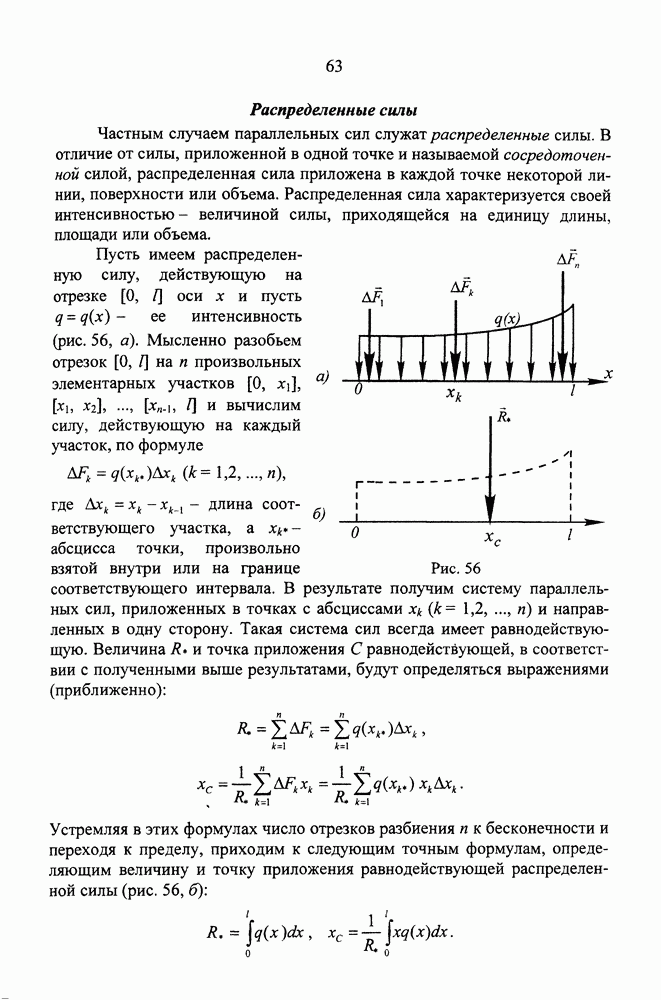
- Распределенные силы
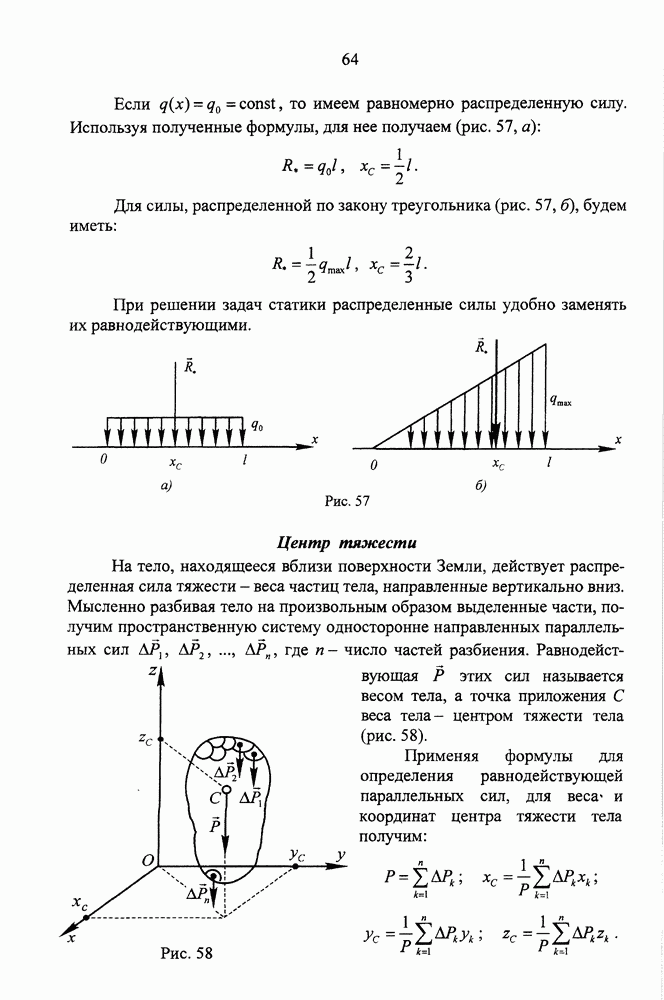
- Центр тяжести
- Интегральные формулы для координат центра тяжести
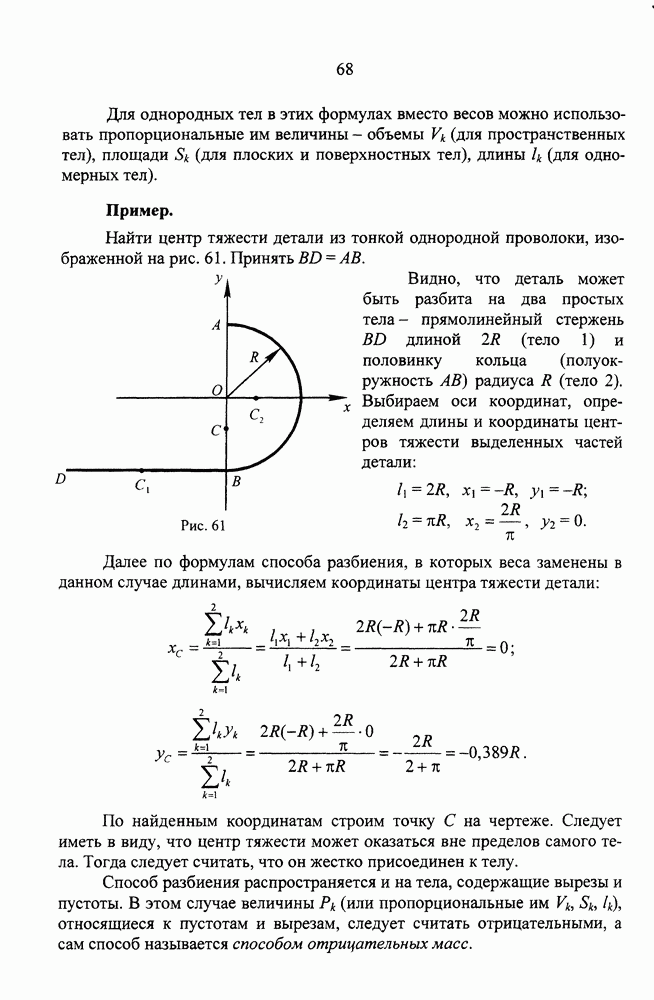
- Метод разбиения
- Вопросы для самопроверки
- ЛЕКЦИЯ 6. ТРЕНИЕ ТВЕРДЫХ ТЕЛ
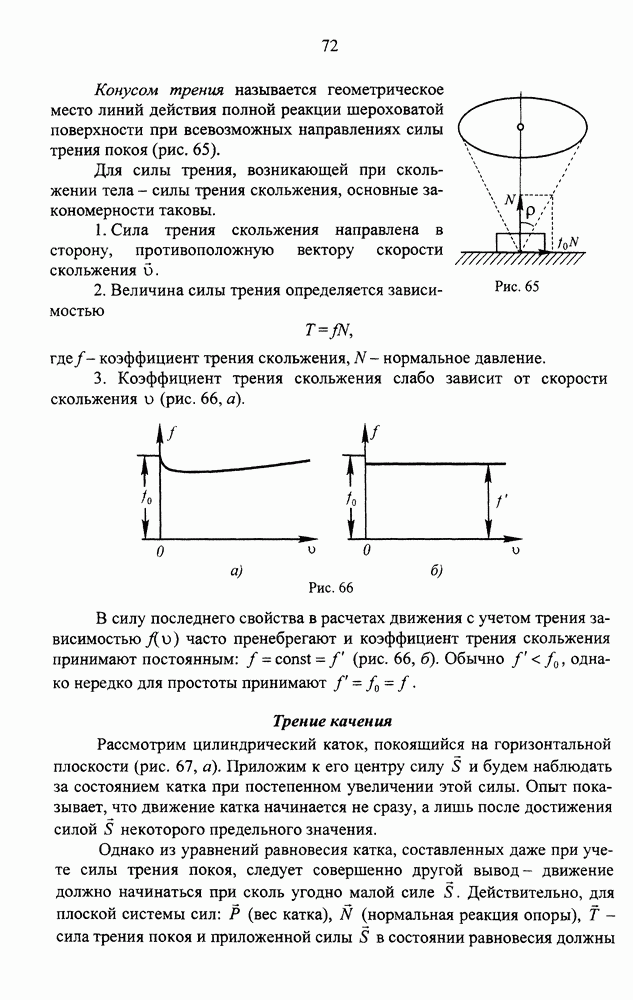
- Трение покоя и трение скольжения
- Трение качения
- Решение задач статики при учете сил трения
- Заклинивание
- Упражнения
- КИНЕМАТИКА
- ЛЕКЦИЯ 7. КИНЕМАТИКА ТОЧКИ
- Способы задания движения точки
- Определение траектории, скорости и ускорения точки при векторном способе задания движения
- Определение траектории, скорости и ускорения точки при координатном способе задания движения
- Определение скорости и ускорения точки при естественном способе задания движения
- Естественные координатные оси и их орты
- Определение скорости
- Определение ускорения
- Вопросы для самопроверки
- ЛЕКЦИЯ 8. ПРОСТЕЙШИЕ ДРИЖЕНИЯ ТВЕРДОГО ТЕЛА
- Поступательное движение
- Вращательное движение
- Уравнение вращательного движения. Угловая скорость и угловое ускорение тела
- Траектории, скорости и ускорения точек тела
- Векторы угловой скорости и углового ускорения тела
- Векторные формулы для линейной скорости, касательного и нормального ускорений точки тела
- Вопросы для самопроверки
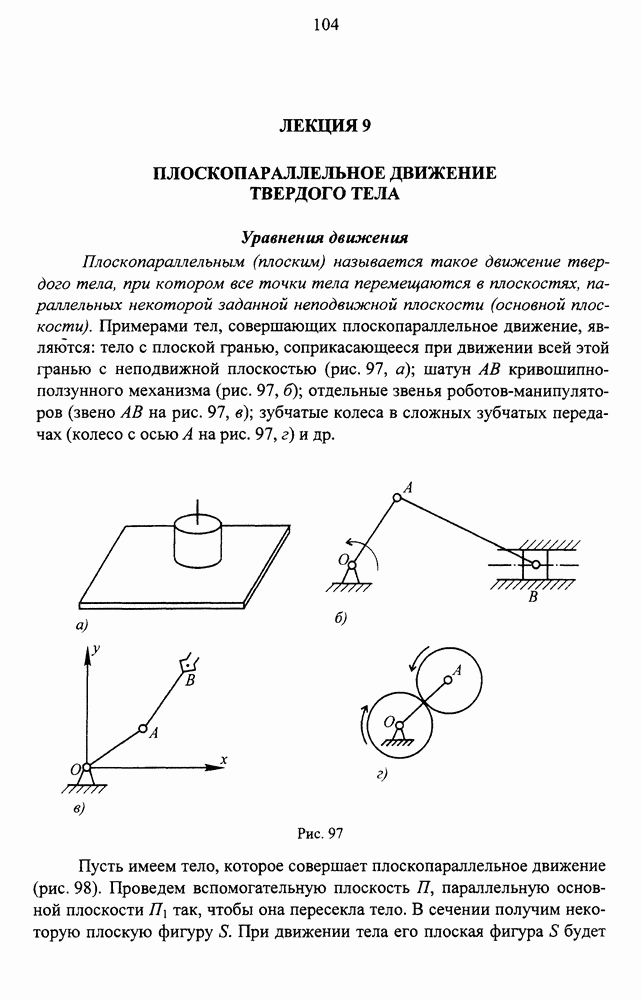
- ЛЕКЦИЯ 9. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- Уравнения движения
- Угловая скорость и угловое ускорение тела при плоскопараллельном движении
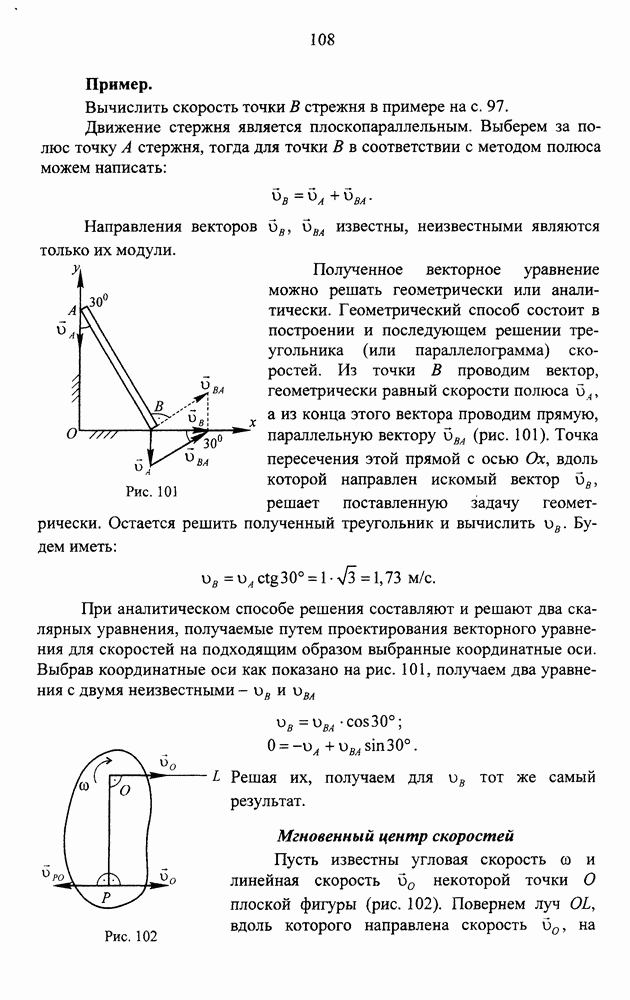
- Определение скоростей точек тела. Метод полюса
- Мгновенный центр скоростей
- Определение скоростей точек плоской фигуры через мгновенный центр скоростей
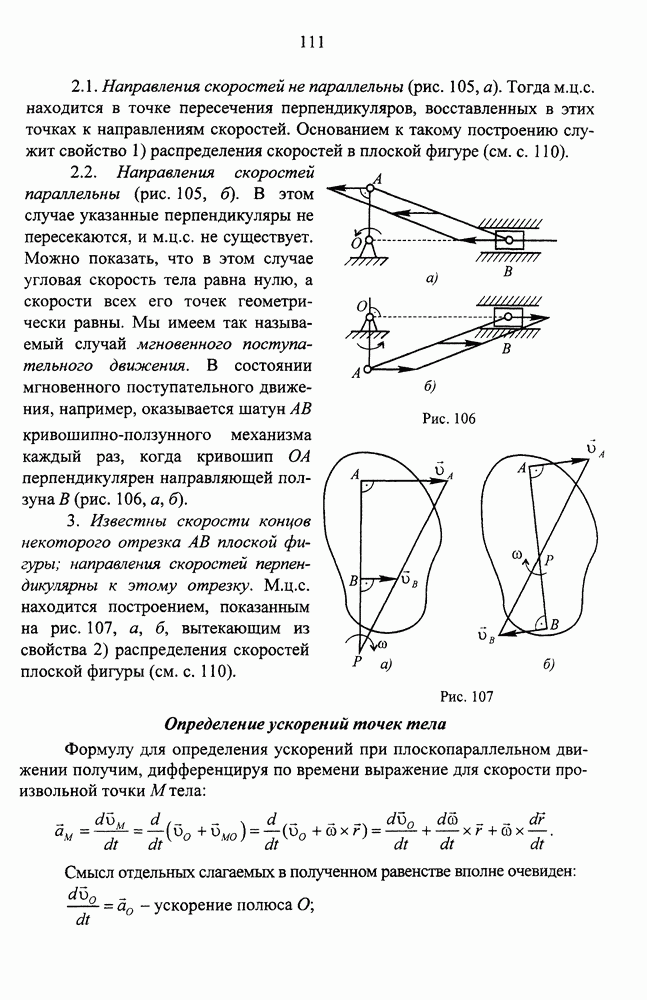
- Различные случаи определения положения мгновенного центра скоростей
- Определение ускорений точек тела
- Вопросы для самопроверки
- ЛЕКЦИЯ 10. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
- Теорема сложения скоростей
- Теорема сложения ускорений
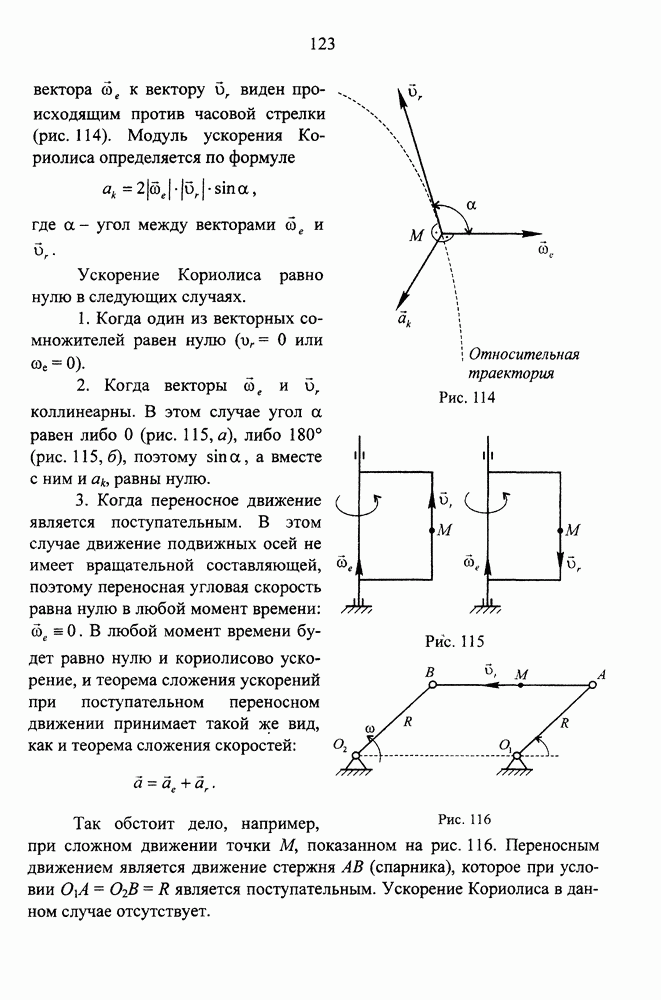
- Причины появления ускорения Кориолиса
- Вычисление и построение ускорения Кориолиса
- Вопросы для самопроверки
- ДОБАВЛЕНИЕ. КИНЕМАТИКА ПРОЦЕССА ФУГОВАНИЯ ДРЕВЕСИНЫ
- Схема и расчетная модель процесса фугования
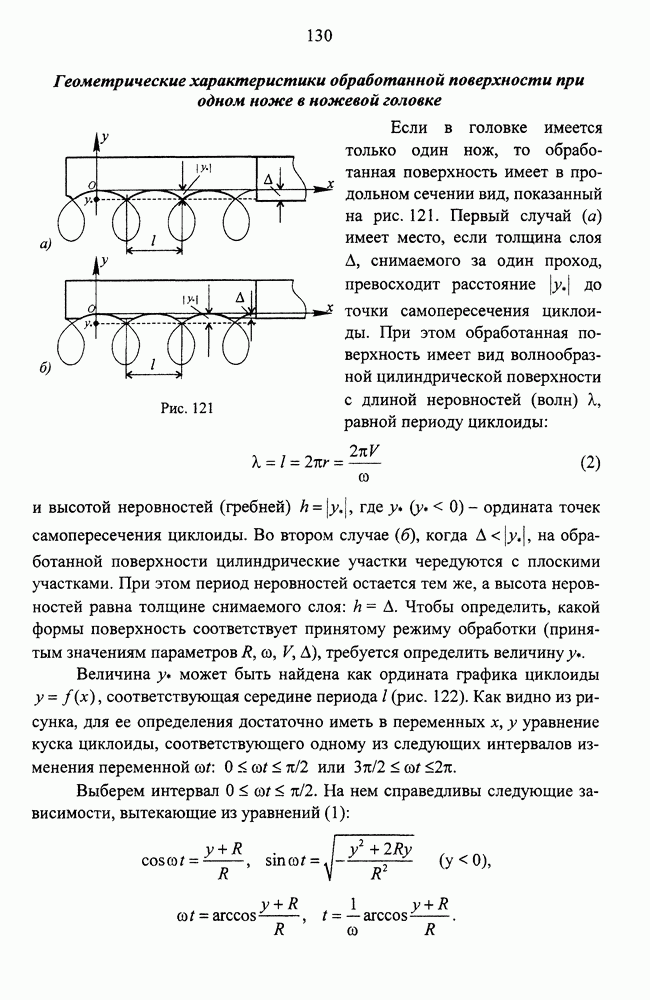
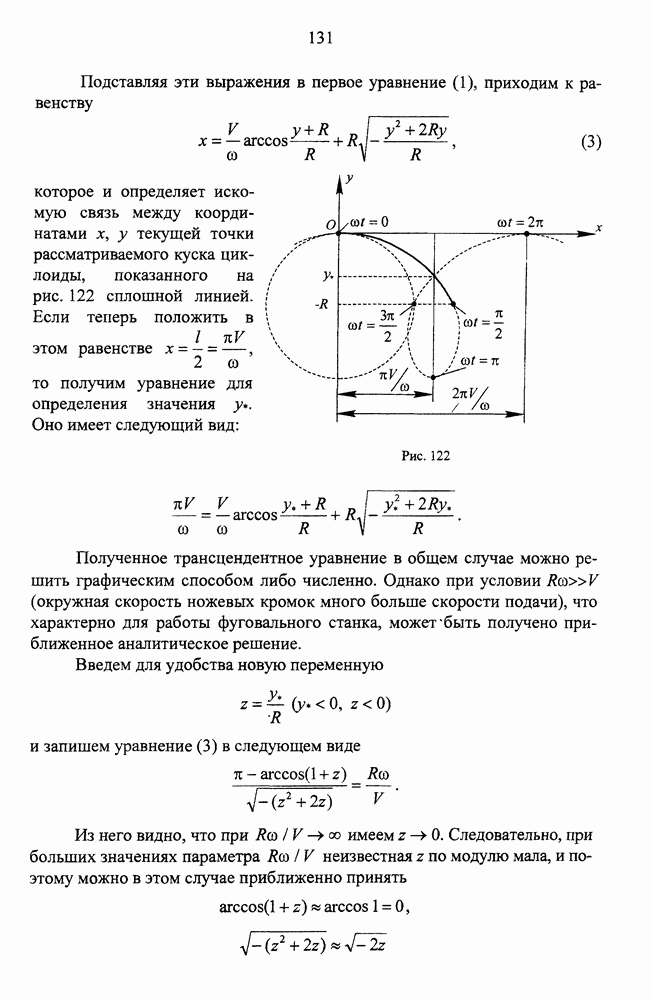
- Геометрические характеристики обработанной поверхности при одном ноже в ножевой головке
- Геометрические характеристики поверхности в случае многоножевой головки
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА