| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
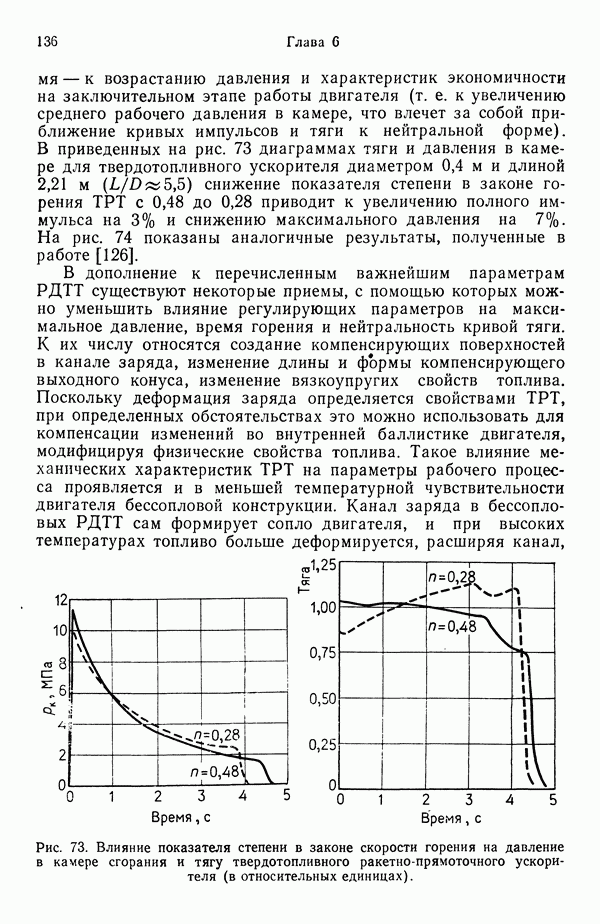
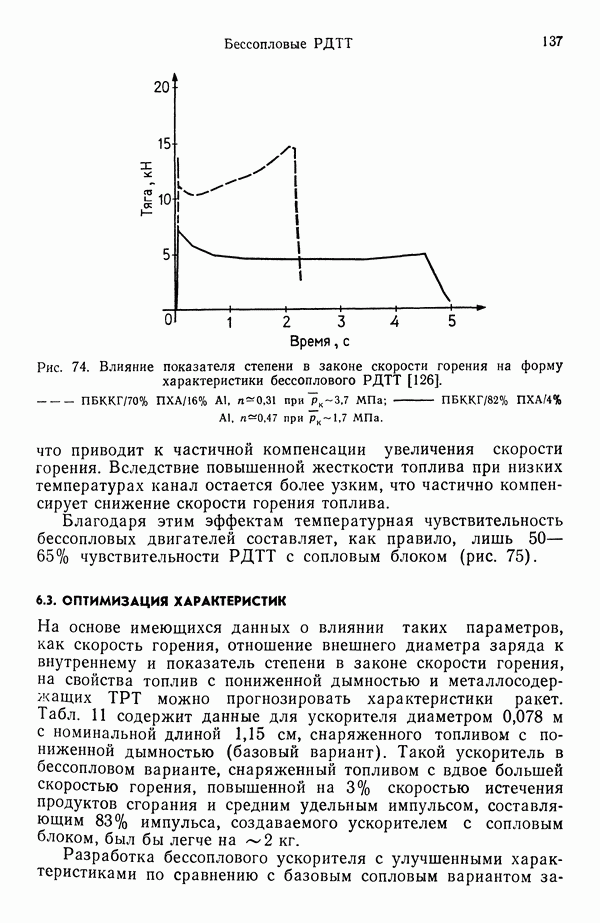
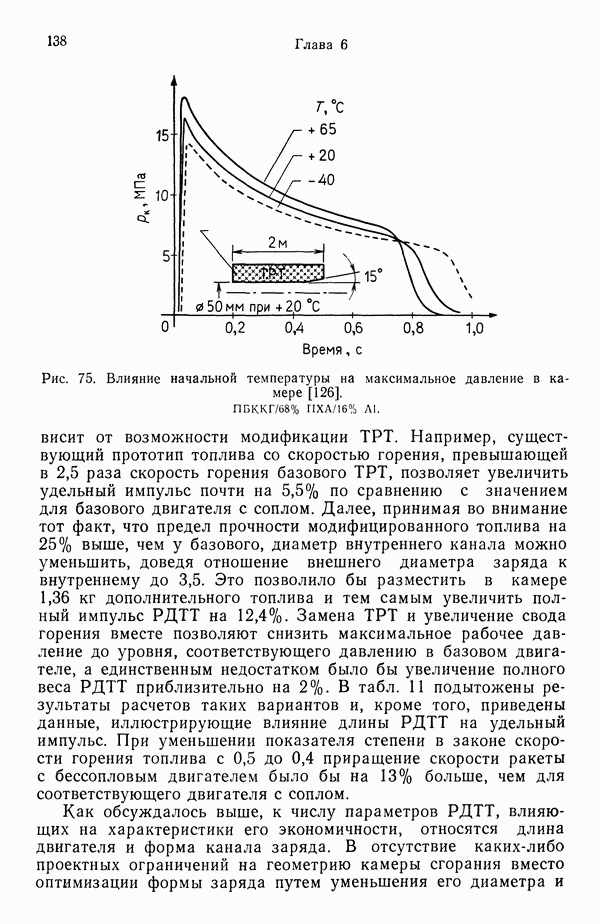
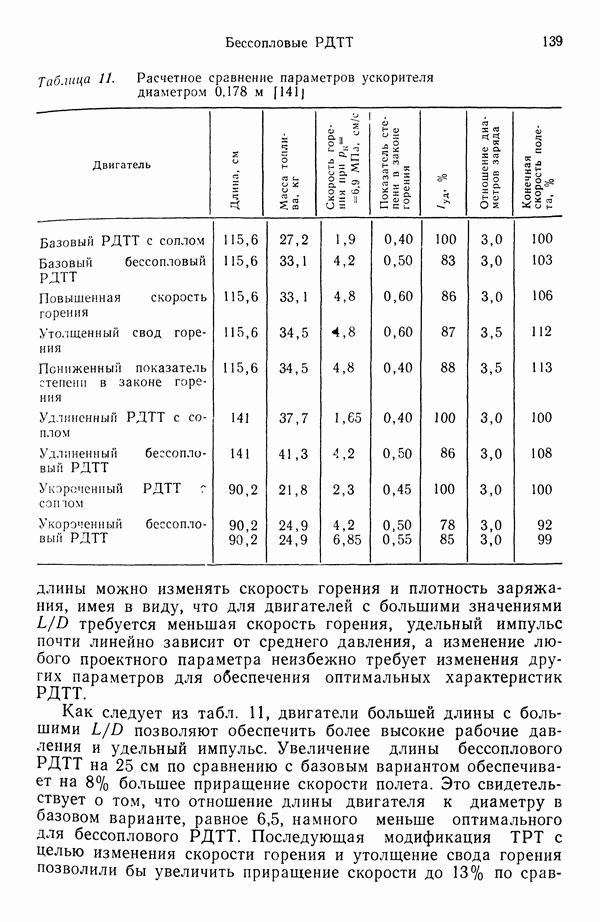
3.5.4. УРАВНЕНИЯ СОХРАНЕНИЯ В ГАЗОВОЙ ФАЗЕ
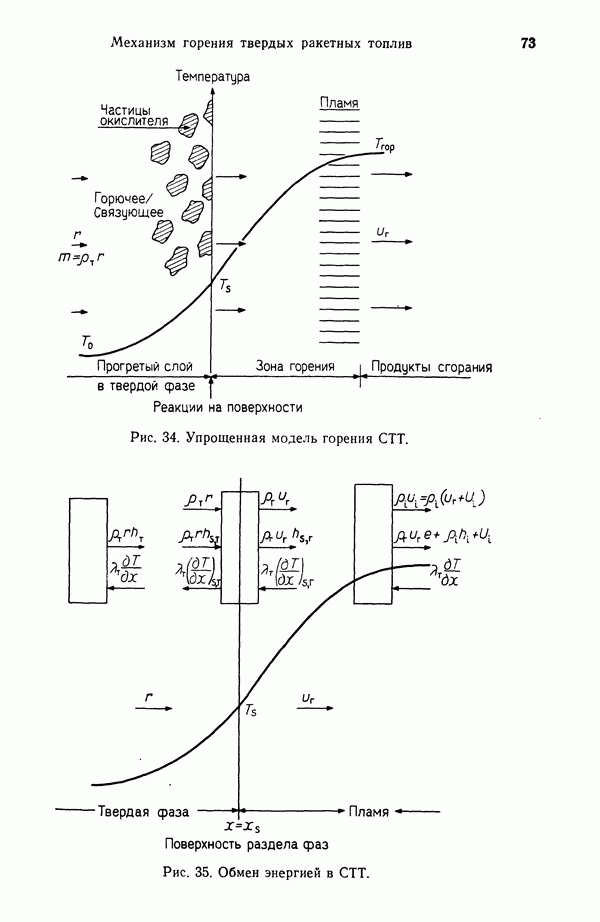
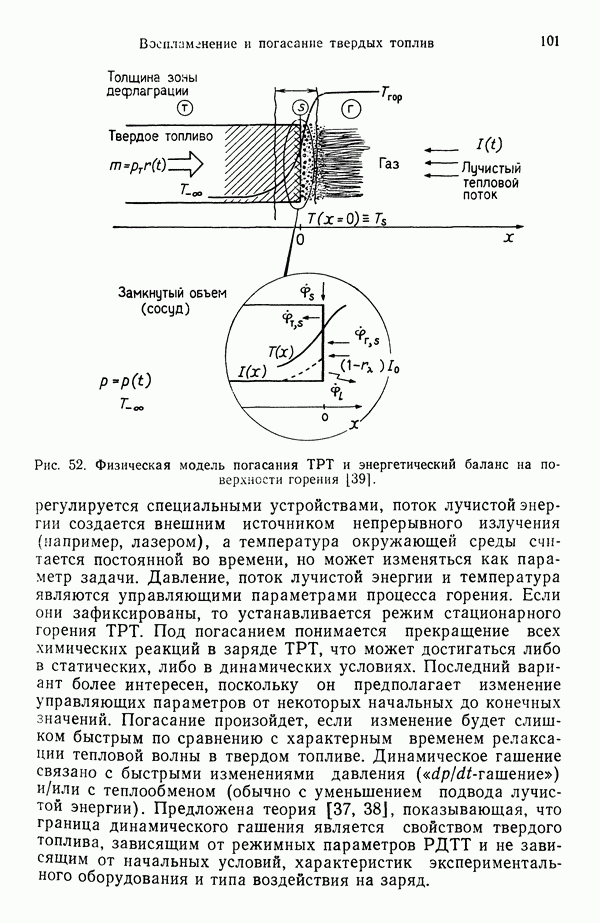
Возвращаясь к рис. 35, запишем уравнения неразрывности и сохранения компонент:

Здесь  скорость образования
скорость образования  компоненты в химической реакции. Вводя массовую долю
компоненты в химической реакции. Вводя массовую долю  получим
получим

Скорость  компоненты
компоненты  можно записать в виде суммы средней скорости газа
можно записать в виде суммы средней скорости газа  и скорости диффузии
и скорости диффузии  компоненты
компоненты  относительно средней скорости:
относительно средней скорости:  Используя это определение, получим
Используя это определение, получим

так как по  Если предположить, что выполняется закон Фика и, более того, что все компоненты имеют одинаковые коэффициенты диффузии
Если предположить, что выполняется закон Фика и, более того, что все компоненты имеют одинаковые коэффициенты диффузии  т. е.
т. е.

то получим уравнение сохранения для  компоненты в окончательном виде:
компоненты в окончательном виде:

Обозначая через  полную внутреннюю энергию (тепловую и кинетическую), включая работу
полную внутреннюю энергию (тепловую и кинетическую), включая работу  совершаемую силами давления, и учитывая, что каждая компонента переносит свою энтальпию со скоростью
совершаемую силами давления, и учитывая, что каждая компонента переносит свою энтальпию со скоростью  [последнее равенство следует из
[последнее равенство следует из  запишем уравнение сохранения энергии в виде
запишем уравнение сохранения энергии в виде

Поскольку  возможна альтернативная запись:
возможна альтернативная запись:

Используя (3.28), последнее уравнение можно переписать в виде

Теперь, положив  получим для левой части
получим для левой части
уравнения:

Здесь использовано уравнение (3.31) и соотношение 

Полагая  и учитывая, что теплоемкость газа определяется как
и учитывая, что теплоемкость газа определяется как  где
где  тепловой эффект,
тепловой эффект,  скорость реакции, получим для правой части:
скорость реакции, получим для правой части:

Из (3.32в, д) окончательно имеем

Предположив, что все газы имеют одинаковую теплоемкость, это уравнение можно упростить, так как

и, следовательно,

Для стационарного течения последнее уравнение принимает вид

Это уравнение можно решить, если предположить, что химическая реакция протекает в очень узком слое на расстоянии  от поверхности раздела твердой и газовой фаз, т. е.
от поверхности раздела твердой и газовой фаз, т. е.  где
где  а
а  -функция, как обычно, удовлетворяет условию
-функция, как обычно, удовлетворяет условию  при
при  и
и

Таким образом, для  получаем уравнение
получаем уравнение

которое при граничных условиях  при
при  имеет решение
имеет решение

При  имеем
имеем  следовательно,
следовательно,

где  поток массы. Поскольку тепловой эффект реакции удовлетворяет соотношению
поток массы. Поскольку тепловой эффект реакции удовлетворяет соотношению

то

С другой стороны, тепло, поступающее на поверхность раздела, определяется выражением

так что расстояние от поверхности до фронта пламени  можно рассчитать по формуле
можно рассчитать по формуле

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ АВТОРА К РУССКОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- 1. ХАРАКТЕРИСТИКИ РАКЕТНЫХ ДВИГАТЕЛЕЙ НА ХИМИЧЕСКОМ ТОПЛИВЕ
- 1.2. ТЕРМОХИМИЯ ПРОЦЕССА В КАМЕРЕ СГОРАНИЯ
- 1.3. РАСШИРЕНИЕ ГАЗА В СОПЛЕ
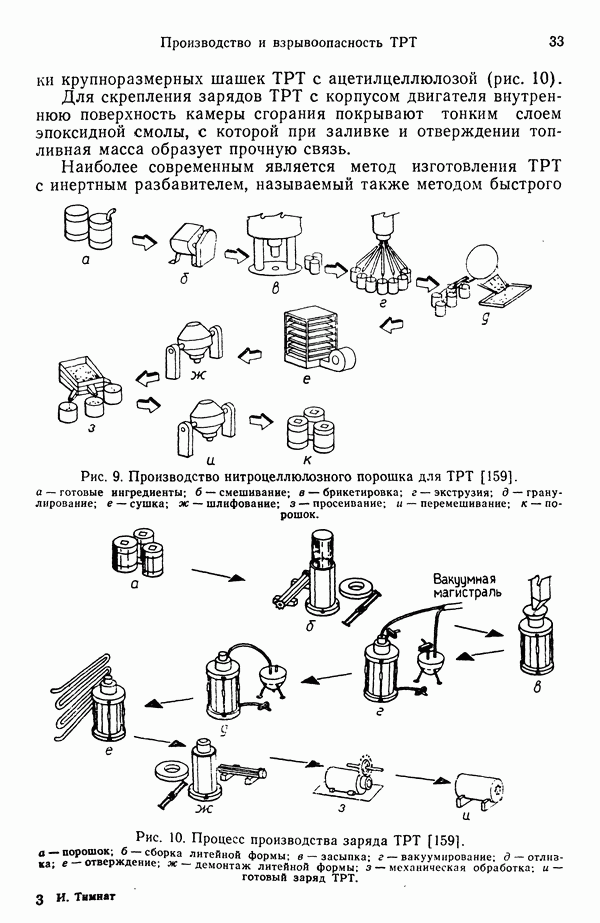
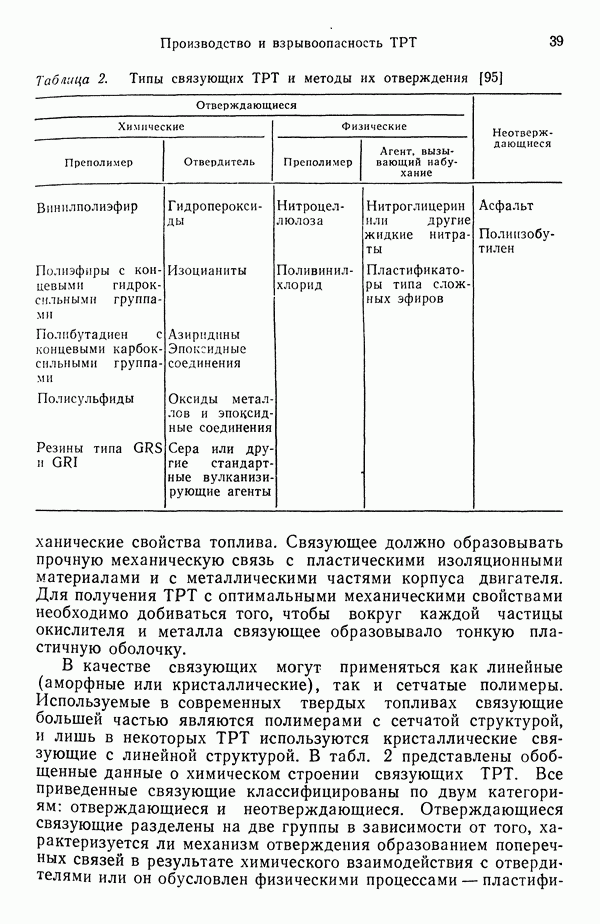
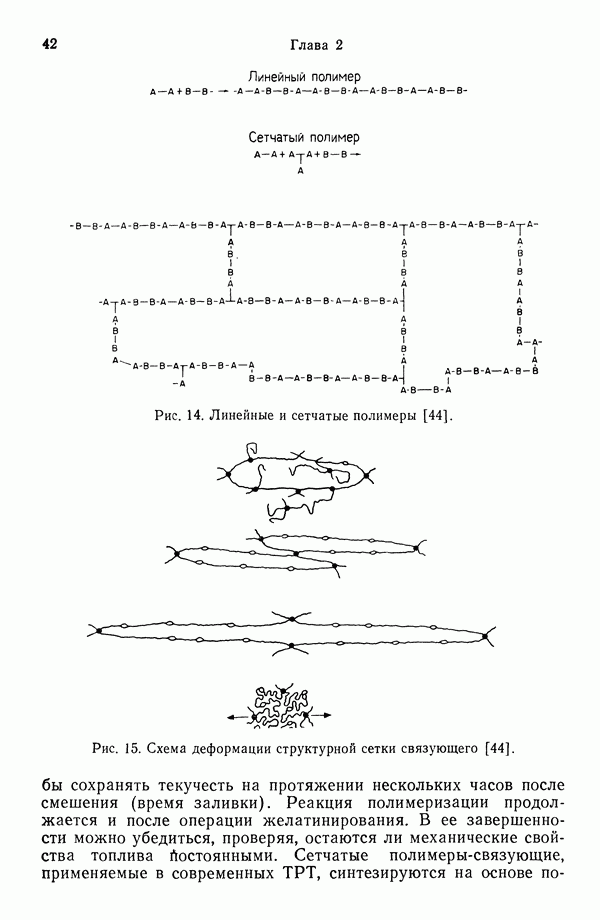
- 2. СВОЙСТВА, ПРОИЗВОДСТВО И ВЗРЫВООПАСНОСТЬ ТВЕРДЫХ РАКЕТНЫХ ТОПЛИВ
- 2.2. ГОМОГЕННЫЕ ТОПЛИВА
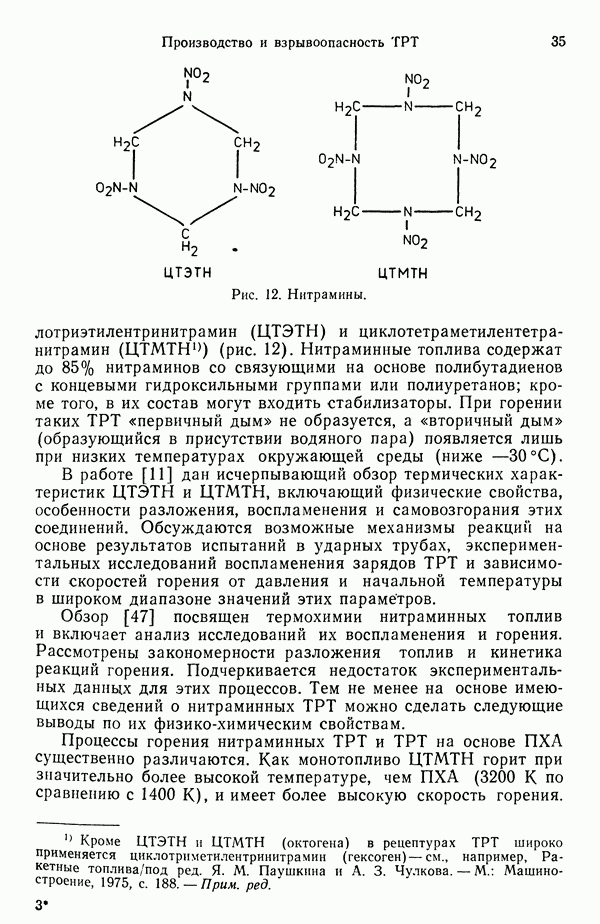
- 2.3. НИТРАМИННЫЕ ТОПЛИВА
- 2.4. ГЕТЕРОГЕННЫЕ ТОПЛИВА
- 2.5. МЕХАНИЧЕСКИЕ ИСПЫТАНИЯ, КРИТЕРИИ РАЗРУШЕНИЯ И СТАРЕНИЕ
- 2.6. ВЗРЫВООПАСНОСТЬ
- 3. МЕХАНИЗМ ГОРЕНИЯ ТВЕРДЫХ РАКЕТНЫХ ТОПЛИВ
- 3.2. СТАЦИОНАРНОЕ ГОРЕНИЕ ГОМОГЕННЫХ ТОПЛИВ
- 3.2.1. РАЗЛОЖЕНИЕ ТОПЛИВА
- 3.2.2. МЕХАНИЗМ ГОРЕНИЯ В ГАЗОВОЙ ФАЗЕ
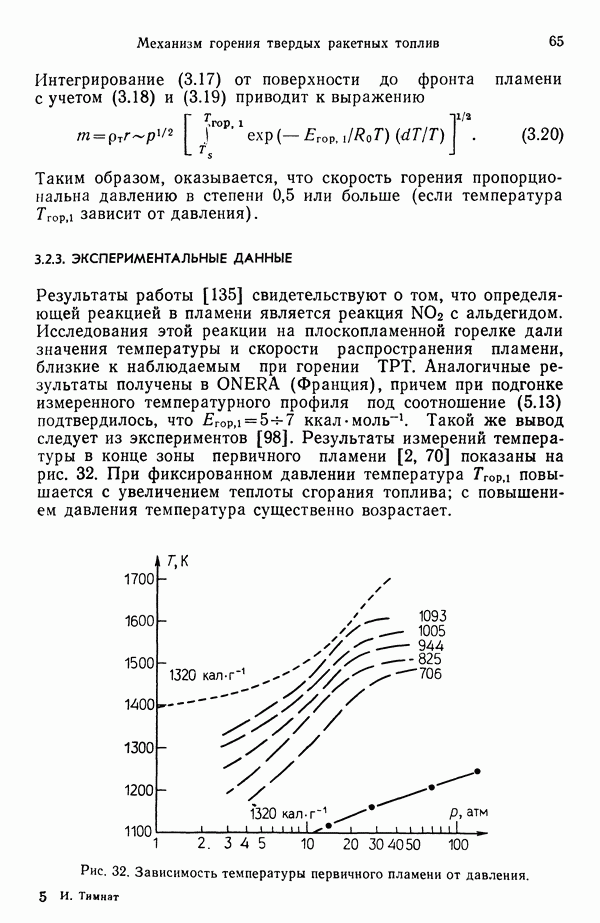
- 3.2.3. ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ
- 3.3. СТАЦИОНАРНОЕ ГОРЕНИЕ НИТРАМИННЫХ ТОПЛИВ
- 3.4. СТАЦИОНАРНОЕ ГОРЕНИЕ СМЕСЕВЫХ ТОПЛИВ
- 3.4.2. ГОРЕНИЕ СВЯЗУЮЩЕГО
- 3.4.3. ГОРЕНИЕ СМЕСЕВЫХ ТВЕРДЫХ ТОПЛИВ
- 3.5. ОСНОВНЫЕ УРАВНЕНИЯ МОДЕЛИ ГОРЕНИЯ СМЕСЕВОГО ТОПЛИВА
- 3.5.2. УРАВНЕНИЯ СОХРАНЕНИЯ В ТВЕРДОЙ ФАЗЕ
- 3.5.3. УСЛОВИЯ НА ПОВЕРХНОСТИ РАЗДЕЛА ТВЕРДАЯ ФАЗА — ГАЗ
- 3.5.4. УРАВНЕНИЯ СОХРАНЕНИЯ В ГАЗОВОЙ ФАЗЕ
- 3.5.5. ХАРАКТЕРИСТИЧЕСКИЕ ПАРАМЕТРЫ ПРОЦЕССА ГОРЕНИЯ
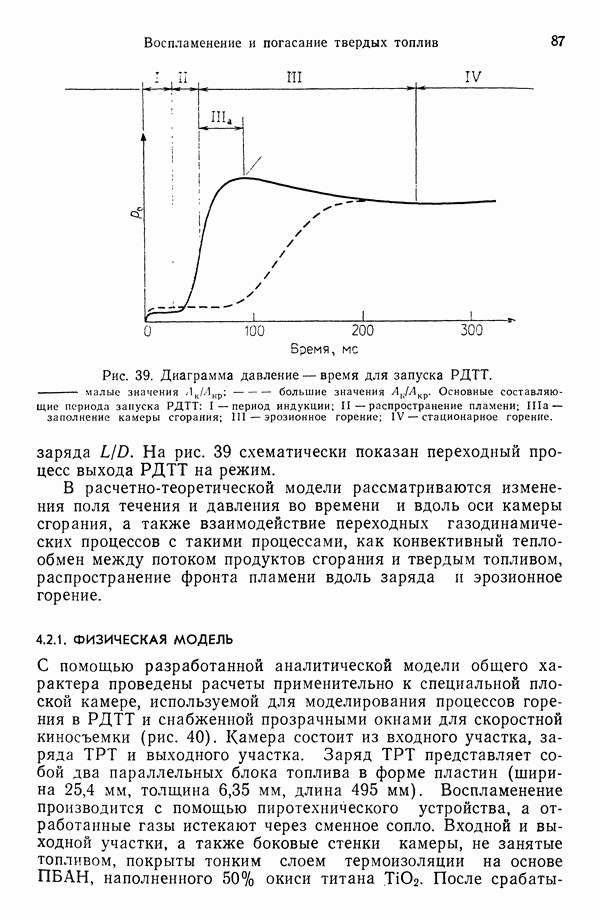
- 4. ВОСПЛАМЕНЕНИЕ И ПОГАСАНИЕ ТВЕРДЫХ ТОПЛИВ
- 4.2. ВОСПЛАМЕНЕНИЕ ТВЕРДЫХ ТОПЛИВ
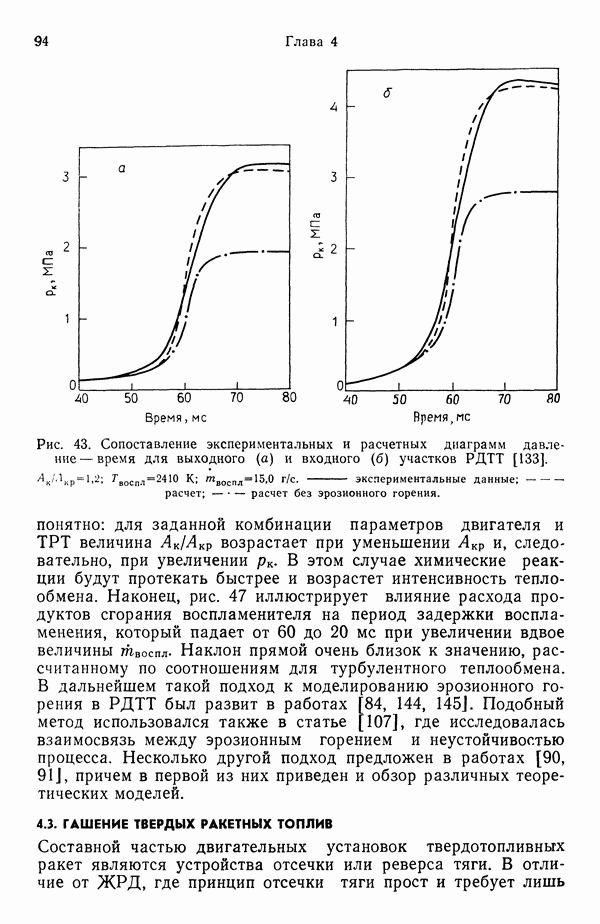
- 4.3. ГАШЕНИЕ ТВЕРДЫХ РАКЕТНЫХ ТОПЛИВ
- 5. ПРОГНОЗИРОВАНИЕ ХАРАКТЕРИСТИК ГОРЕНИЯ ТВЕРДЫХ РАКЕТНЫХ ТОПЛИВ
- 5.2. МОДЕЛЬ ТЕЧЕНИЯ В КАМЕРЕ РДТТ
- 5.3. РАСПРОСТРАНЕНИЕ ФРОНТА ГОРЕНИЯ В ТВЕРДОМ ТОПЛИВЕ
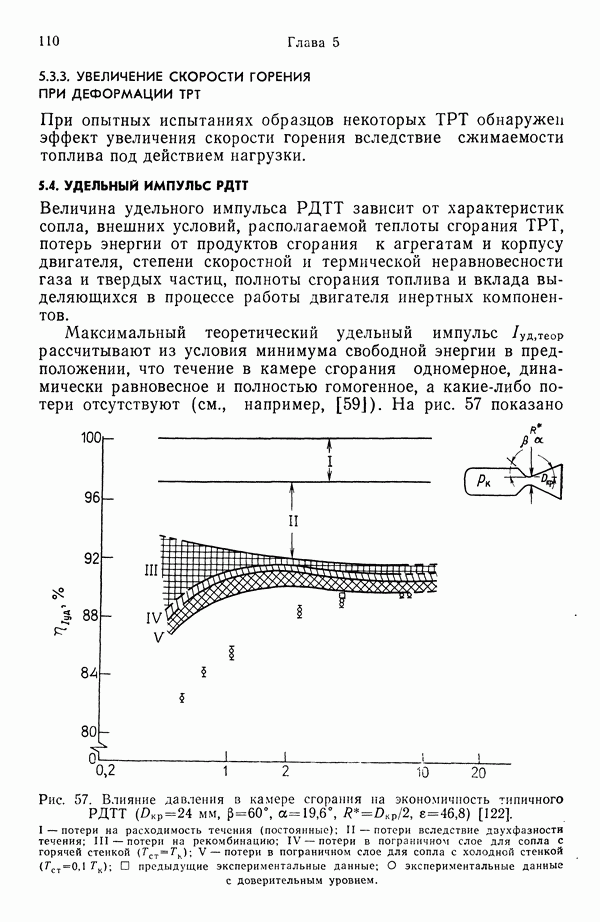
- 5.4. УДЕЛЬНЫЙ ИМПУЛЬС РДТТ
- 5.5. ХАРАКТЕРИСТИКИ СОПЛА
- 5.6. НЕУСТОЙЧИВОСТЬ ГОРЕНИЯ В РДТТ
- 5.6.2. ИЗМЕРЕНИЯ ЧУВСТВИТЕЛЬНОСТИ ГОРЕНИЯ
- 5.6.3. ДЕМПФИРУЮЩАЯ РОЛЬ ЧАСТИЦ КОНДЕНСИРОВАННОЙ ФАЗЫ
- 5.6.4. ДРУГИЕ ИСТОЧНИКИ УСИЛЕНИЯ И ДЕМПФИРОВАНИЯ КОЛЕБАНИЙ
- 5.6.5. ВИДЫ НЕУСТОЙЧИВОСТЕЙ В РДТТ
- 6. БЕССОПЛОВЫЕ РДТТ
- 6.2. ВНУТРЕННЯЯ БАЛЛИСТИКА
- 6.3. ОПТИМИЗАЦИЯ ХАРАКТЕРИСТИК
- 7. МЕХАНИЗМ ГОРЕНИЯ ЖИДКИХ ТОПЛИВ
- 7.2. ГОРЕНИЕ ОДИНОЧНОЙ КАПЛИ
- 7.3. ОБЩАЯ МОДЕЛЬ ГОРЕНИЯ
- 7.4. ИСПОЛЬЗОВАНИЕ МОДЕЛИ
- 7.4.2. ПРОГРАММА РАСПРЕДЕЛЕНИЯ ЖИДКОСТНЫХ СТРУЙ
- 7.4.3. МОДЕЛЬ ЗОНЫ ГОРЕНИЯ 3-D COMBUST
- 7.4.4. МОДЕЛЬ ДОГОРАНИЯ В ТРУБКАХ ТОКА STRMTB
- 7.4.5. ПРИМЕР РАСЧЕТА
- 8. ЭКОНОМИЧНОСТЬ, УСТОЙЧИВОСТЬ И РЛБОТОСПОСОБНОСЬ ЖРД
- 8.2. ЭКОНОМИЧНОСТЬ
- 8.3. НЕУСТОЙЧИВОСТЬ РАБОЧЕГО ПРОЦЕССА
- 8.4. РАБОТОСПОСОБНОСТЬ КАМЕРЫ
- 8.5. ВЗАИМОСВЯЗЬ ЭКОНОМИЧНОСТИ, УСТОЙЧИВОСТИ И РАБОТОСПОСОБНОСТИ ЖРД
- 9. НОВЫЕ СХЕМЫ ЖРД
- 9.2. ЖРД С КОЛЬЦЕВОЙ КАМЕРОЙ СГОРАНИЯ И ЦЕНТРАЛЬНЫМ ТЕЛОМ
- 9.2.1. КОНСТРУКЦИЯ КАМЕРЫ СГОРАНИЯ
- 9.2.2. ИСПЫТАНИЯ
- 9.3. ЖРД, РАБОТАЮЩИЕ НА ДВУХ ГОРЮЧИХ
- 9.4. ЖРД С СОПЛОМ ДВОЙНОГО РАСШИРЕНИЯ
- 10. УПРАВЛЕНИЕ ВЕКТОРОМ И ВЕЛИЧИНОЙ ТЯГИ
- 10.2. УПРАВЛЕНИЕ ВЕКТОРОМ ТЯГИ В ЖРД
- 10.3. УПРАВЛЕНИЕ ВЕКТОРОМ ТЯГИ В РДТТ
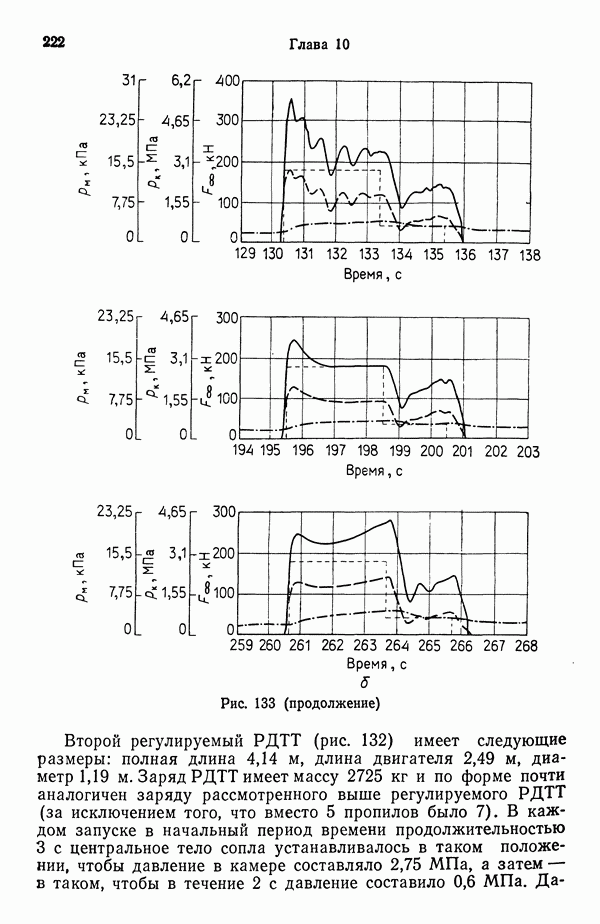
- 10.4. РЕГУЛИРОВАНИЕ ВЕЛИЧИНЫ ТЯГИ
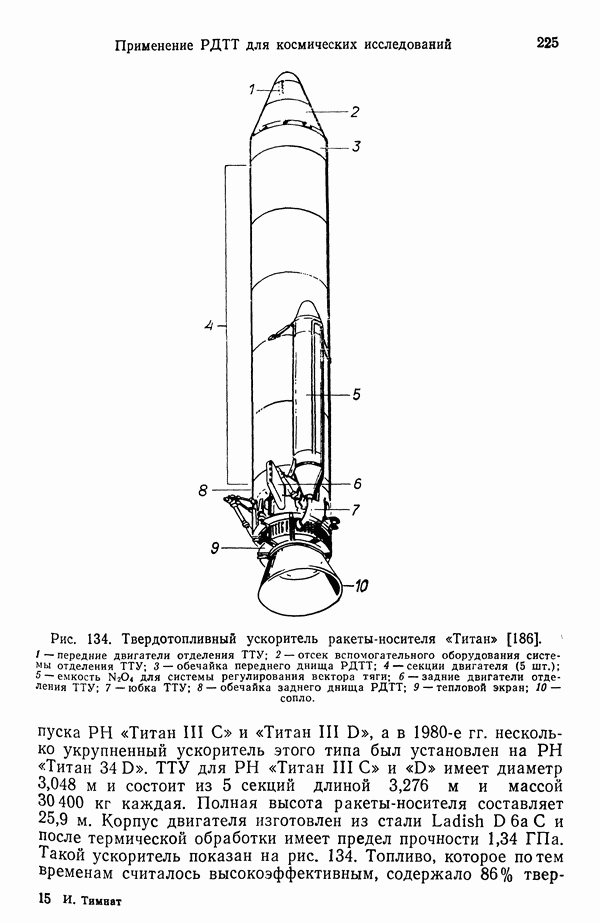
- 11. ПРИМЕНЕНИЕ РДТТ ДЛЯ КОСМИЧЕСКИХ ИССЛЕДОВАНИЙ
- 11.2. УСКОРИТЕЛИ РАКЕТЫ-НОСИТЕЛЯ «ТИТАН»
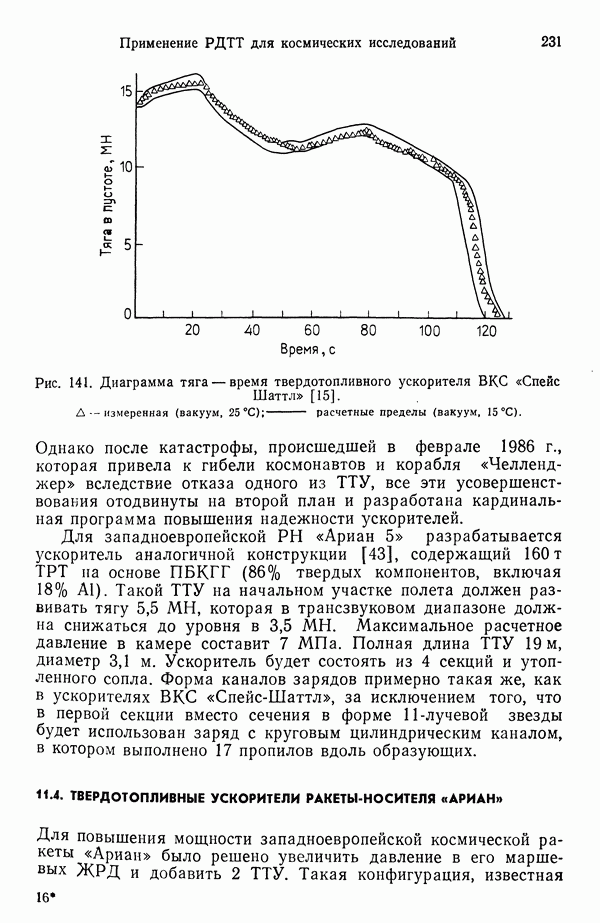
- 11.3. ТВЕРДОТОПЛИВНЫЙ УСКОРИТЕЛЬ ВКС «СПЕЙС ШАТТЛ»
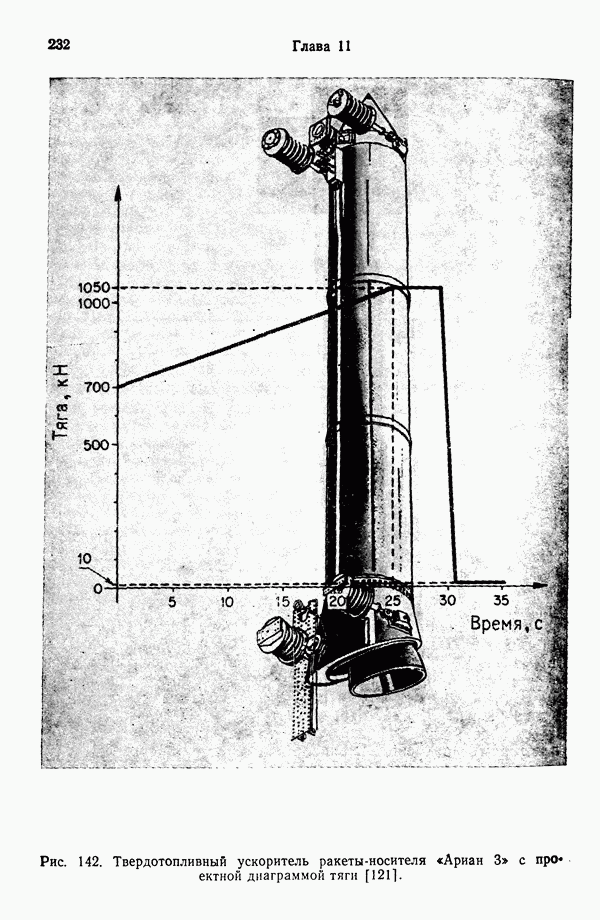
- 11.4. ТВЕРДОТОПЛИВНЫЕ УСКОРИТЕЛИ РАКЕТЫ-НОСИТЕЛЯ «АРИАН»
- 11.5. ТВЕРДОТОПЛИВНЫЕ ДВИГАТЕЛИ ДЛЯ ПОСЛЕДНИХ СТУПЕНЕЙ РАКЕТ-НОСИТЕЛЕЙ
- 12. ПРИМЕНЕНИЕ ЖРД ДЛЯ КОСМИЧЕСКИХ ИССЛЕДОВАНИЙ
- 12.2. КИСЛОРОДО-ВОДОРОДНЫЕ ЖРД RL-10, НМ-7 И LE-5
- 12.3. МАРШЕВЫЙ ДВИГАТЕЛЬ ВКС «СПЕЙС ШАТТЛ»
- 12.4. СРАВНЕНИЕ РАЗЛИЧНЫХ КИСЛОРОДО-ВОДОРОДНЫЙ ЖРД
- 12.5. ЖРД ДЛЯ МАНЕВРИРОВАНИЯ И ИЗМЕНЕНИЯ ОРБИТЫ
- 12.6. ВСПОМОГАТЕЛЬНЫЕ ДВИГАТЕЛЬНЫЕ УСТАНОВКИ С ЖРД
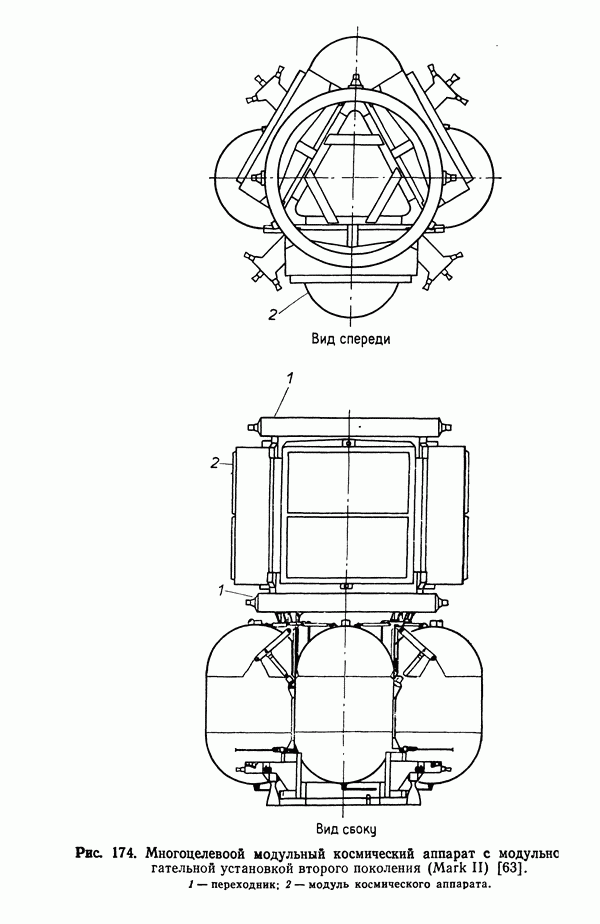
- 12.6.2. МОДУЛЬНАЯ ДВИГАТЕЛЬНАЯ УСТАНОВКА ВТОРОГО ПОКОЛЕНИЯ
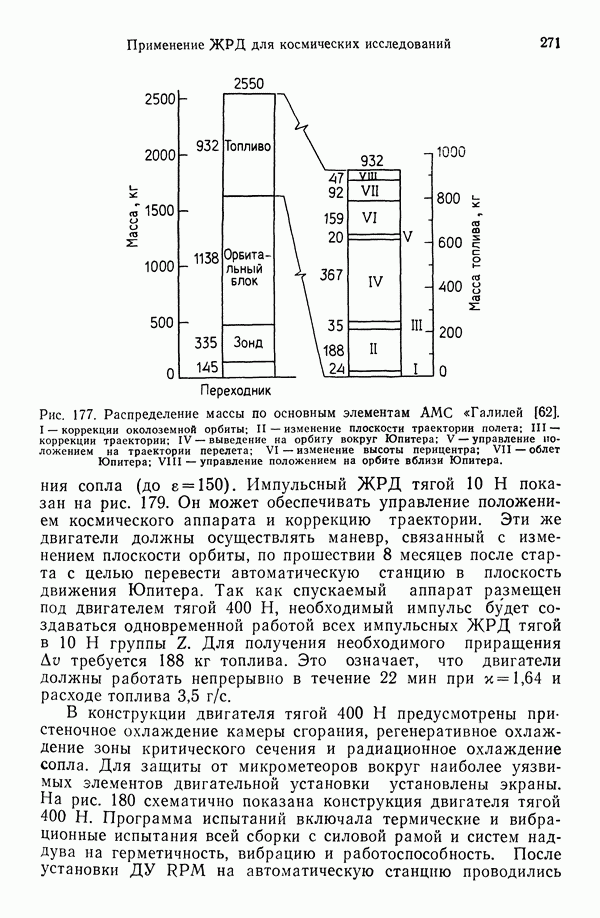
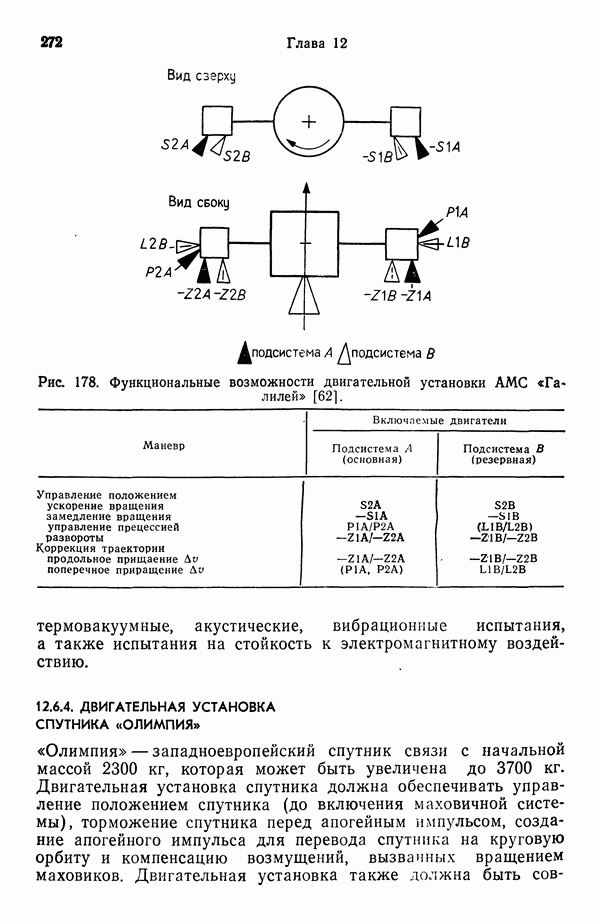
- 12.6.3. ДВУХКОМПОНЕНТНАЯ ДВИГАТЕЛЬНАЯ УСТАНОВКА АВТОМАТИЧЕСКОЙ МЕЖПЛАНЕТНОЙ СТАНЦИИ «ГАЛИЛЕЙ»
- 12.6.4. ДВИГАТЕЛЬНАЯ УСТАНОВКА СПУТНИКА «ОЛИМПИЯ»
- 12.6.5. СИСТЕМА РЕАКТИВНОГО УПРАВЛЕНИЯ С ИМПУЛЬСНЫМИ ОДНОКОМПОНЕНТНЫМИ ЖРД
- 12.6.6. ВСПОМОГАТЕЛЬНАЯ ДВИГАТЕЛЬНАЯ УСТАНОВКА КОСМИЧЕСКОЙ СТАНЦИИ