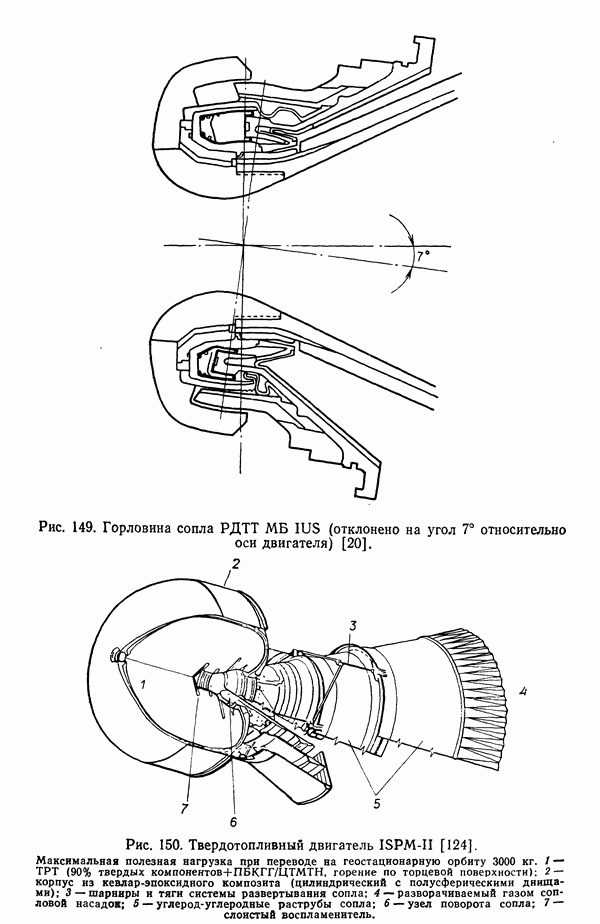
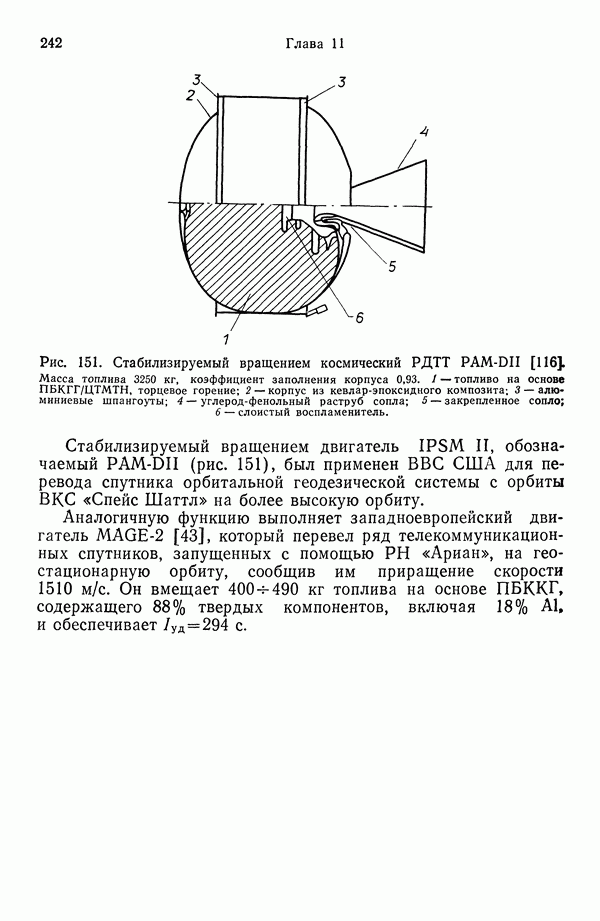
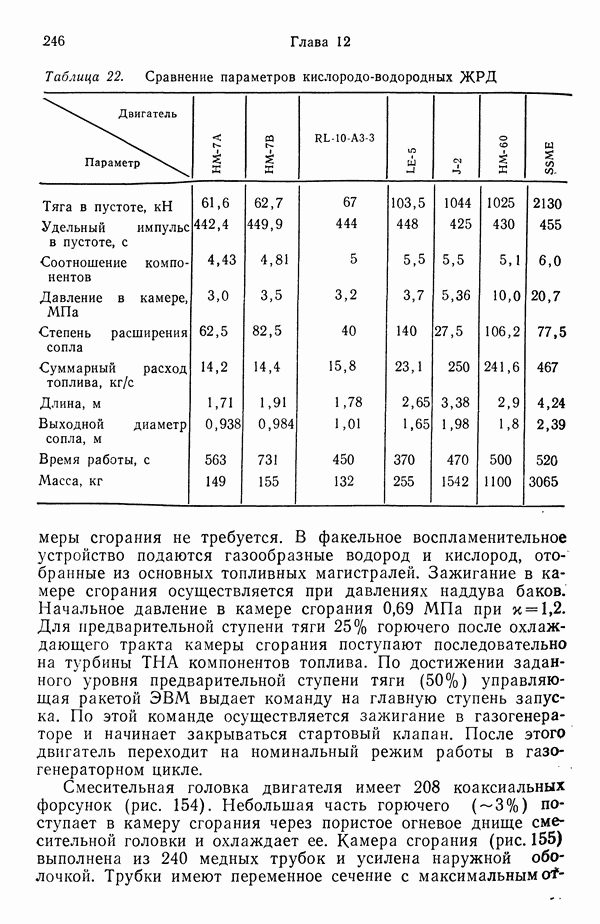
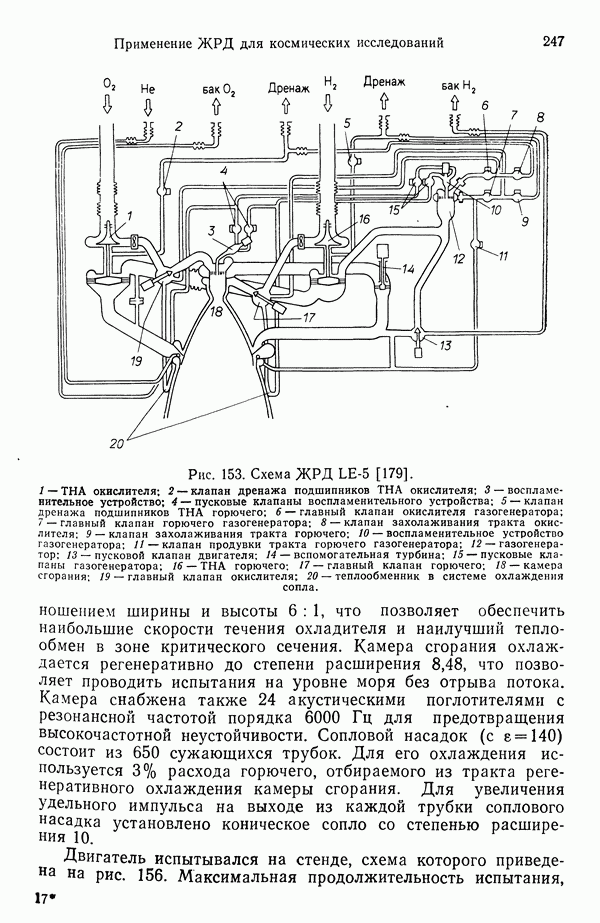
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
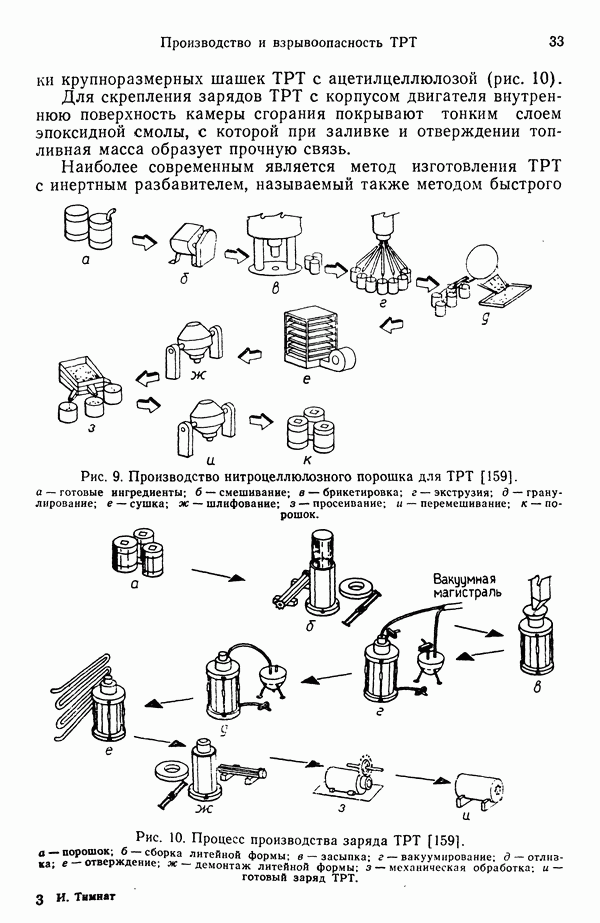
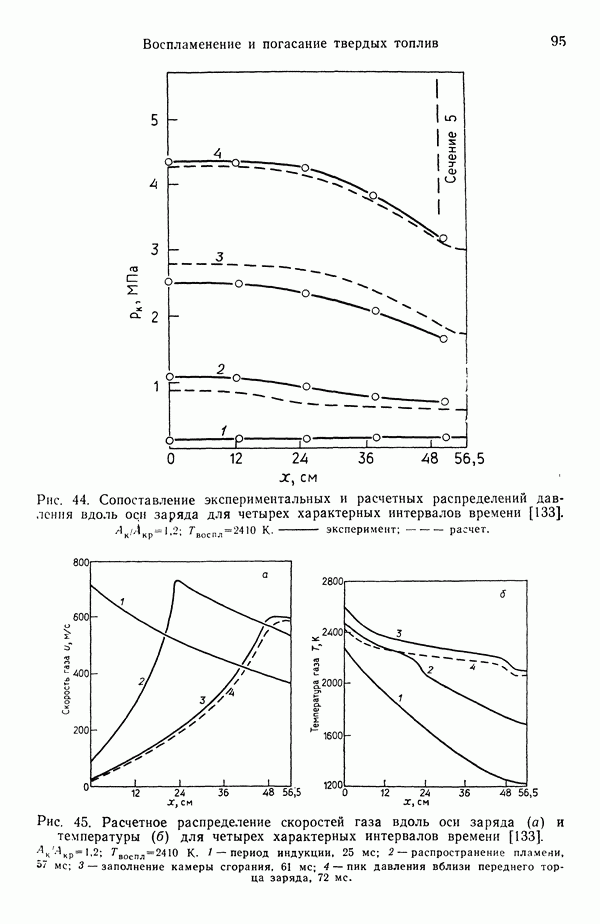
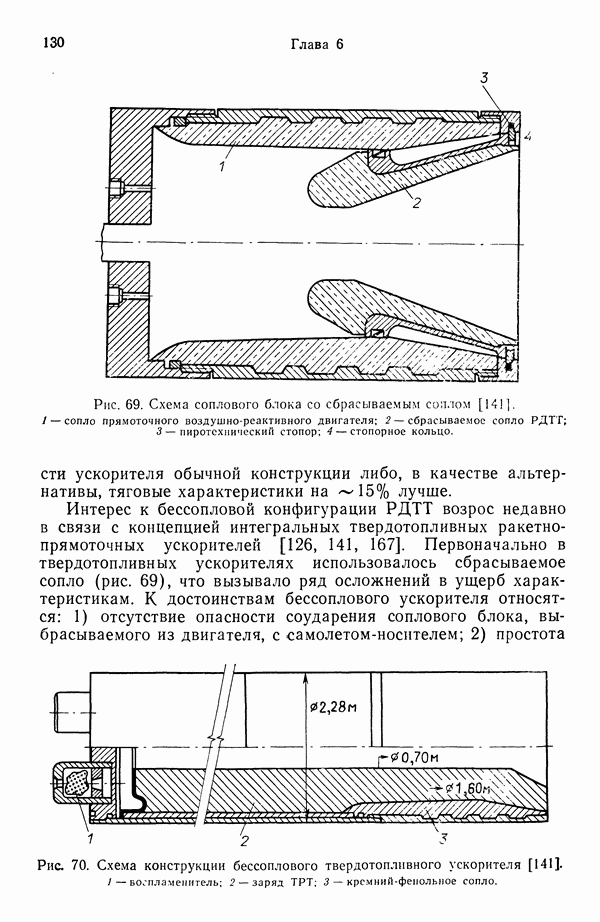
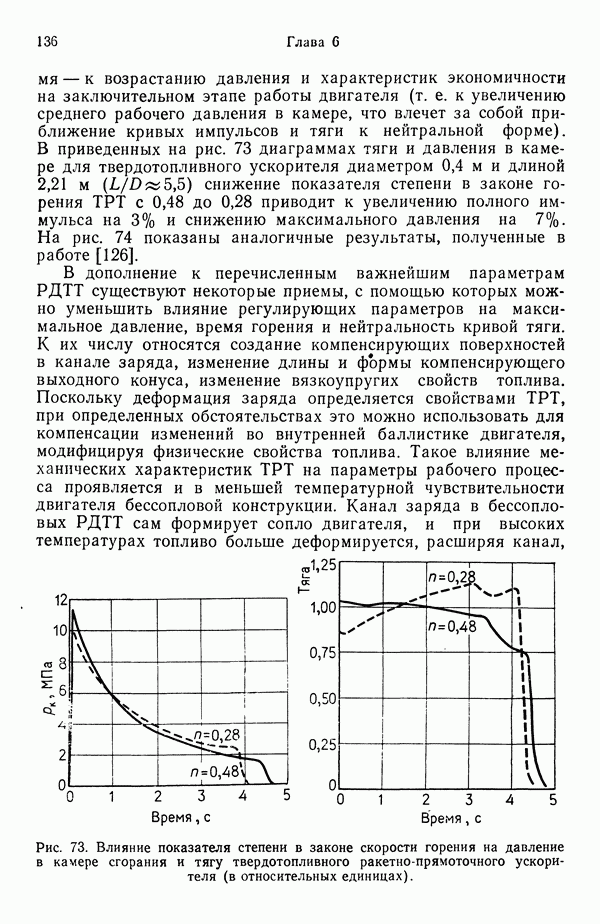
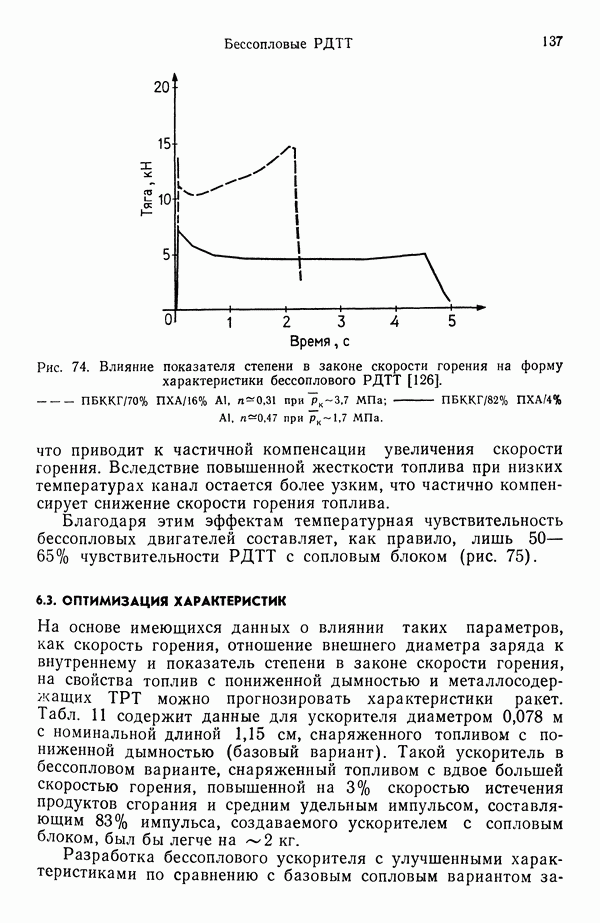
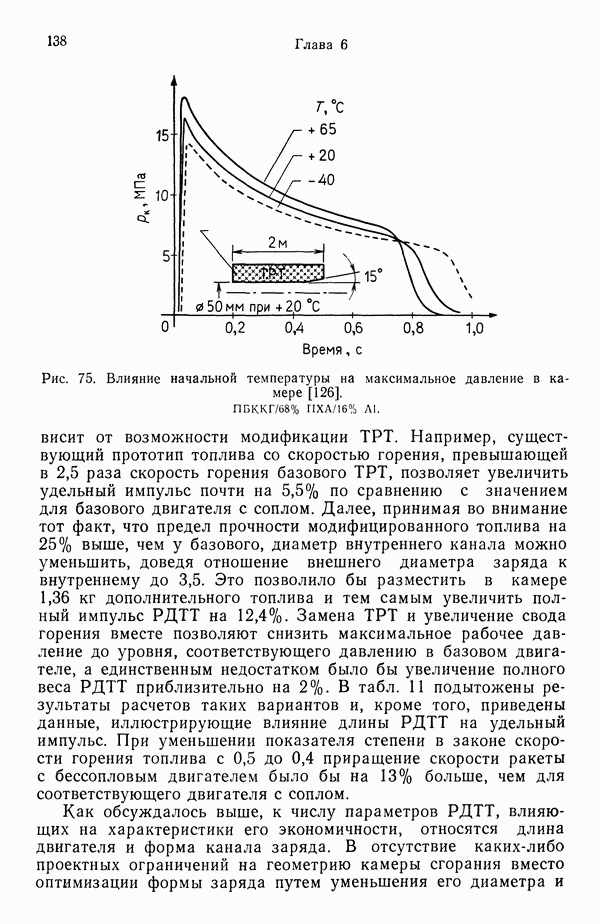
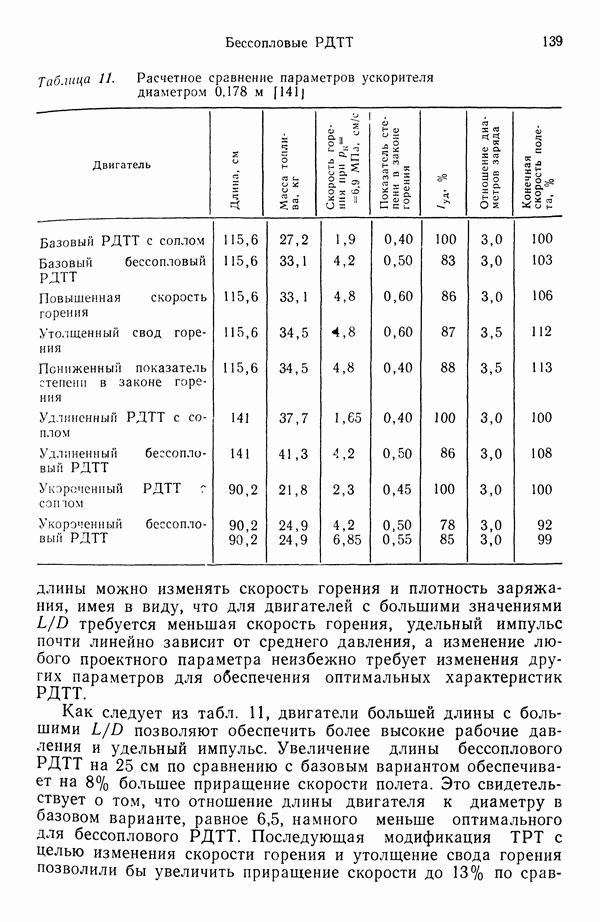
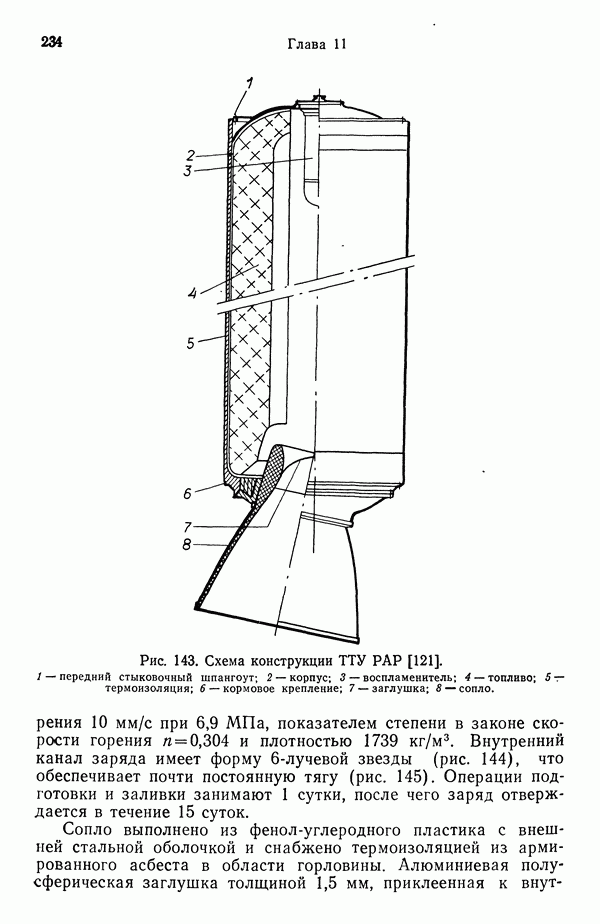
7.2. ГОРЕНИЕ ОДИНОЧНОЙ КАПЛИ
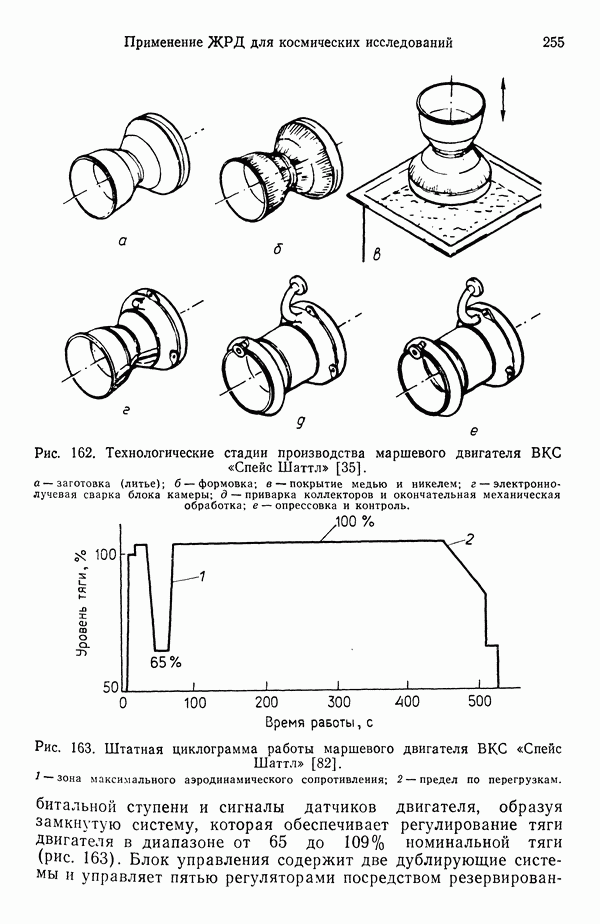
Это явление изучено достаточно глубоко, так как служит отправной точкой для понимания горения распыленного топлива, характерного для камер сгорания жидкостных ракетных двигателей (а также топок паровых и водогрейных котлов). Процесс горения одиночной капли теоретически обоснован, накоплен также богатый экспериментальный материал. Существуют два типа горения капель:
1) капли горючего горят в атмосфере окислителя; в этом случае горючее является источником пара и, так как горючее и окислитель поступают независимо, имеет место диффузионное горение;
2) капли монотоплива (к примеру гидразина), которые могут разлагаться без наличия окислителя; этот случай аналогичен гомогенному горению предварительно смешанных газов и рассматриваться не будет.
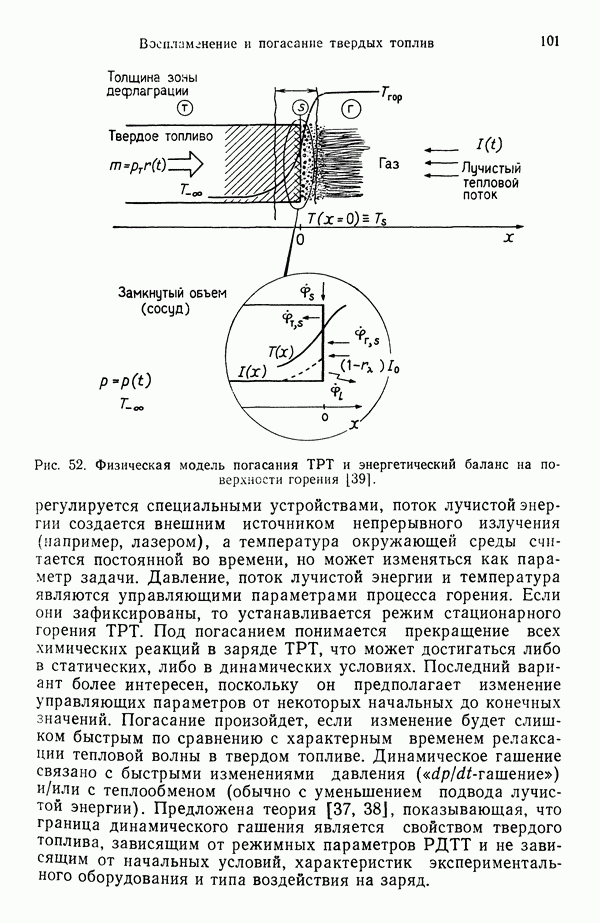
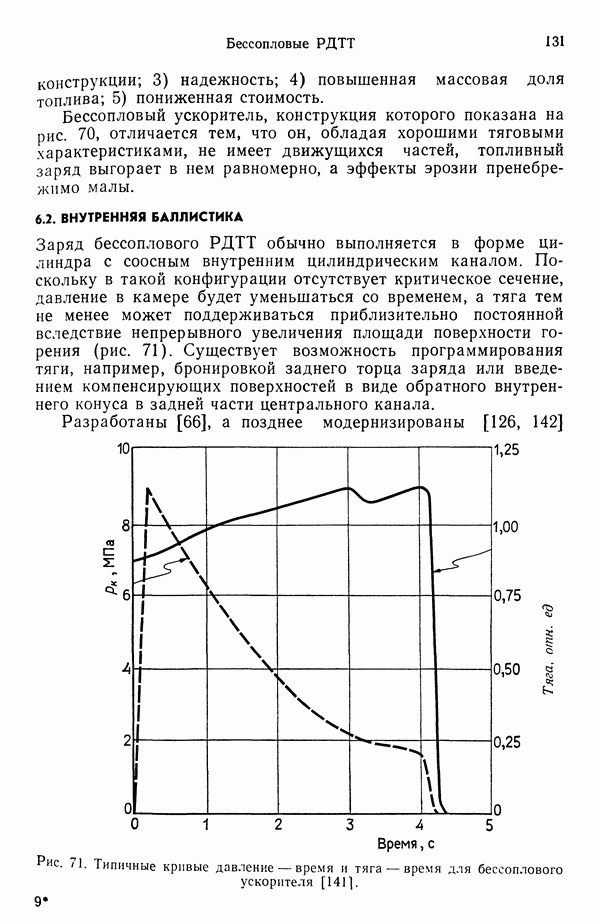
Теория, объясняющая физико-химические процессы, происходящие в горящей капле [57, 58, 158], хорошо согласуется, с экспериментом. Она разработана в начале 1950-х гг. В модели, представленной на рис. 77, рассматривается сферическая капля при следующих допущениях.
1. Капля состоит из одного химического элемента (т. е. модель верна для водорода, но не для керосина).
2. Система обладает сферической симметрией, и тепло, поступающее из зоны горения к капле, идет на испарение (при наличии конвекции симметрия нарушается).
3. После воспламенения процесс считается квазиустановившимся, т. е. количество прореагировавшего горючего равно испарившемуся из капли.

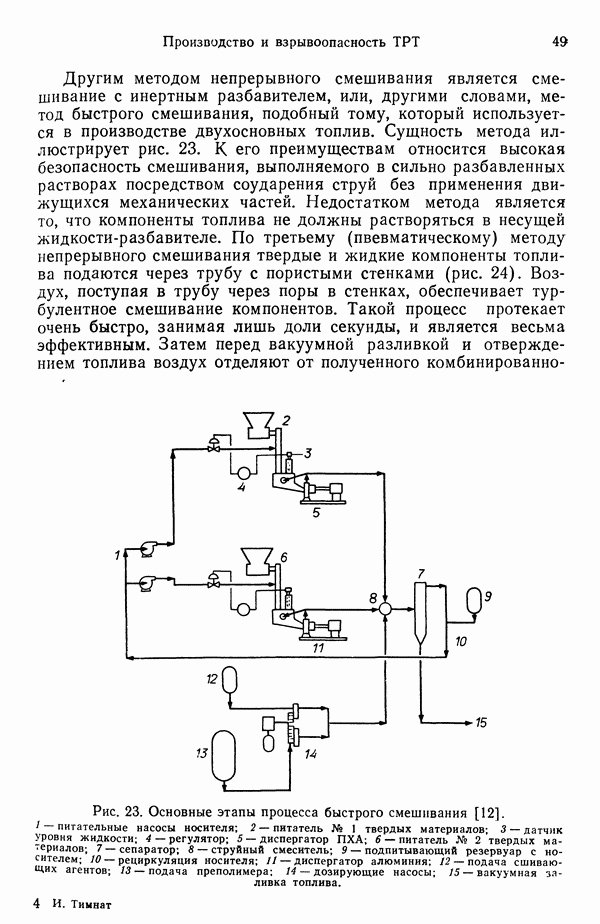
Рис. 77. Модель горения одиночной сферической капли [176].
4. Температура капли постоянна и равна температуре кипения жидкости.
5. Излучение и тепловая диффузия не учитываются.
6. Давление принимается постоянным (для малой скорости распространения пламени и низкой вязкости это допущение справедливо).
Исходя из закона сохранения массы, имеем

или

или

Последнее уравнение подтверждено экспериментально: массовый расход  пропорционален радиусу капли
пропорционален радиусу капли  здесь К — константа испарения (горения). Для того чтобы определить ее значение, запишем уравнения сохранения. Уравнение неразрывности дает
здесь К — константа испарения (горения). Для того чтобы определить ее значение, запишем уравнения сохранения. Уравнение неразрывности дает

Из уравнения сохранения для составляющей смеси имеем

Здесь  массовая доля
массовая доля  компоненты смеси в полном массовом расходе
компоненты смеси в полном массовом расходе  Величина
Величина  сумма конвекционной и диффузионной составляющих:
сумма конвекционной и диффузионной составляющих:

где  массовая доля конвективного потока и
массовая доля конвективного потока и  коэффициент диффузии.
коэффициент диффузии.
Уравнение сохранения энергии дает

Граничные условия, определяющие, что ни в жидкой фазе, ни на бесконечности реакция не происходит, выглядят следующим образом:

Для того чтобы получить аналитическое решение, необходимо сделать дополнительное допущение, состоящее в том, что химическая реакция идет по схеме

и протекает мгновенно (константа скорости реакции бесконечно велика). Вследствие этого пламя ограничено поверхностью, куда горючее и окислитель поступают в стехиометрическом соотношении, т. е. толщина зоны горения бесконечно мала.
Для постоянных (или средних) теплоемкости и теплопроводности получается следующее решение:

Параметр вдува В, называемый также числом Сполдинга, равен

где k — стехиометрическое соотношение  массовая доля окислителя в окружающей среде.
массовая доля окислителя в окружающей среде.
Часто допускается, что число Льюиса  равно единице.
равно единице.
Тогда  можно заменить отношением
можно заменить отношением  и из (7.2) и (7.6) получить
и из (7.2) и (7.6) получить

Анализ дает также численное значение температуры горения  отношение радиусов
отношение радиусов  и массовую долю горючего в газовой фазе у поверхности капли,
и массовую долю горючего в газовой фазе у поверхности капли, 


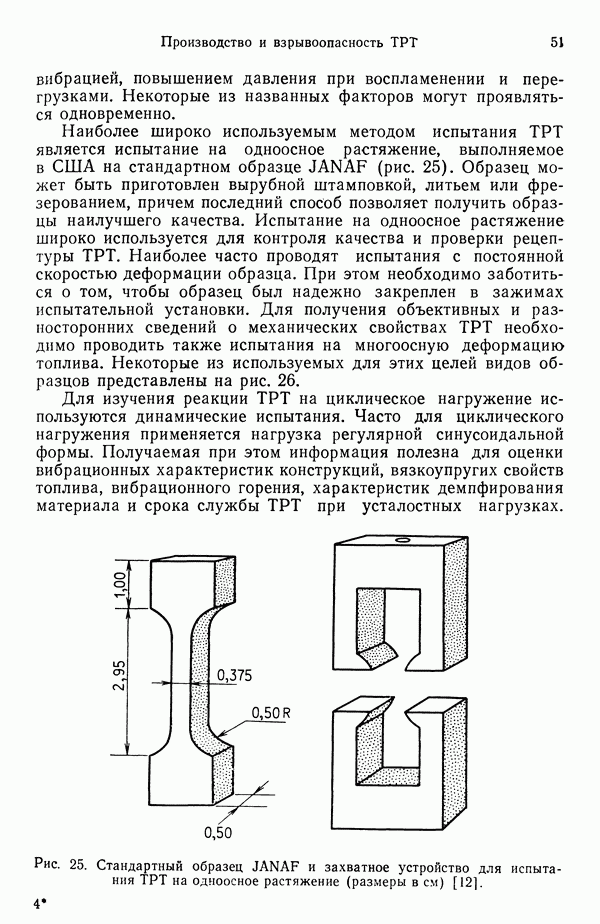
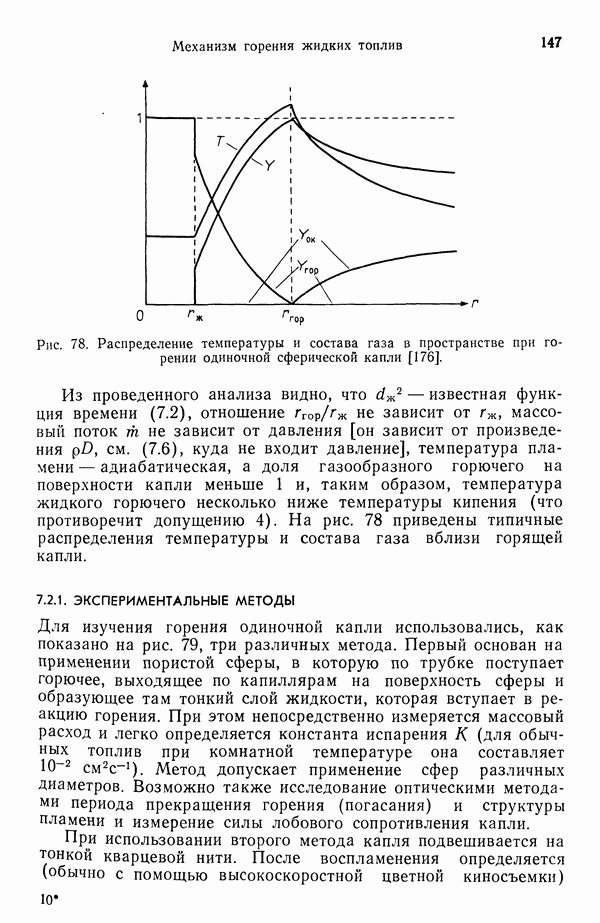
Рис. 78. Распределение температуры и состава газа в пространстве при горении одиночной сферической капли [176].
Из проведенного анализа видно, что  известная функция времени (7.2), отношение
известная функция времени (7.2), отношение  не зависит от
не зависит от  массовый поток
массовый поток  не зависит от давления [он зависит от произведения
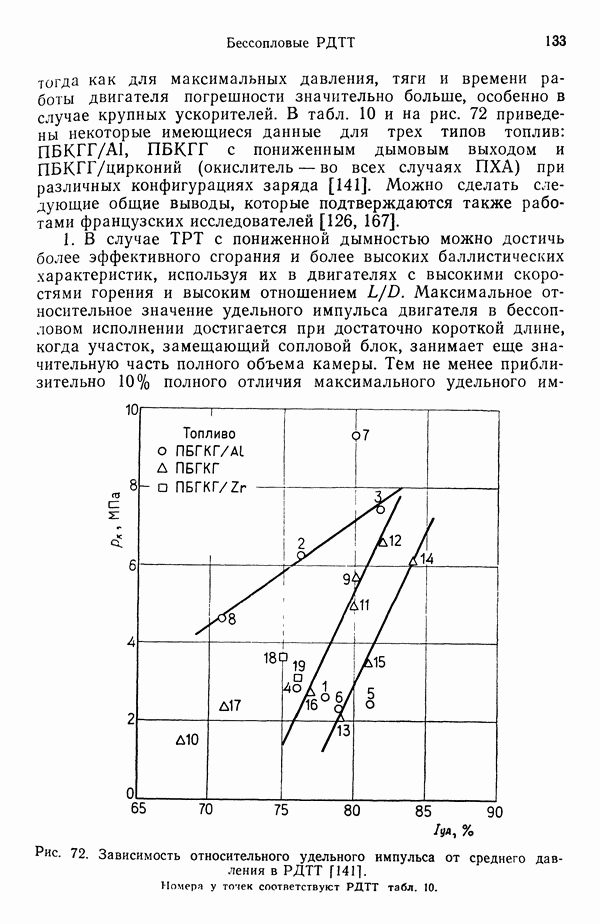
не зависит от давления [он зависит от произведения  см. (7.6), куда не входит давление], температура пламени — адиабатическая, а доля газообразного горючего на поверхности капли меньше 1 и, таким образом, температура жидкого горючего несколько ниже температуры кипения (что противоречит допущению 4). На рис. 78 приведены типичные распределения температуры и состава газа вблизи горящей капли.
см. (7.6), куда не входит давление], температура пламени — адиабатическая, а доля газообразного горючего на поверхности капли меньше 1 и, таким образом, температура жидкого горючего несколько ниже температуры кипения (что противоречит допущению 4). На рис. 78 приведены типичные распределения температуры и состава газа вблизи горящей капли.
7.2.1. ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ
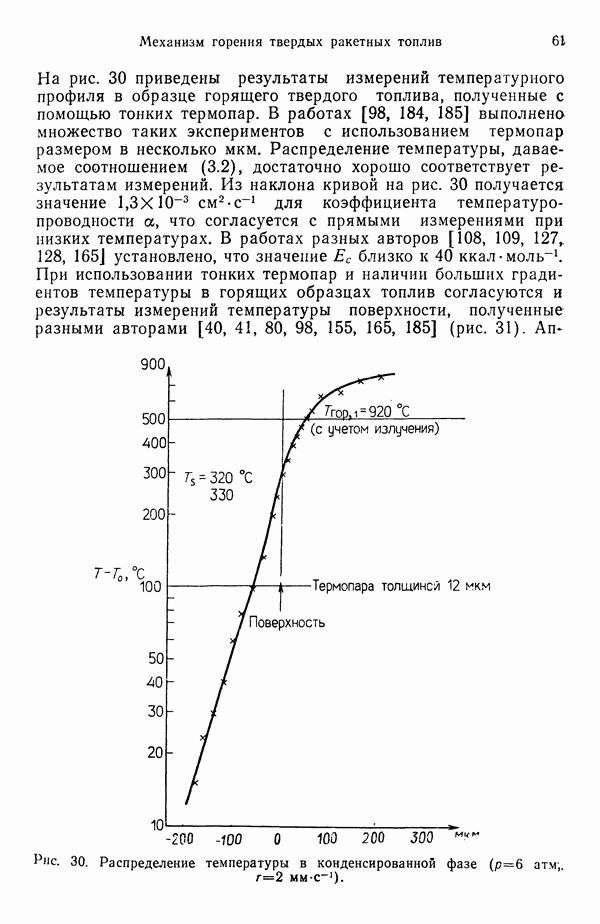
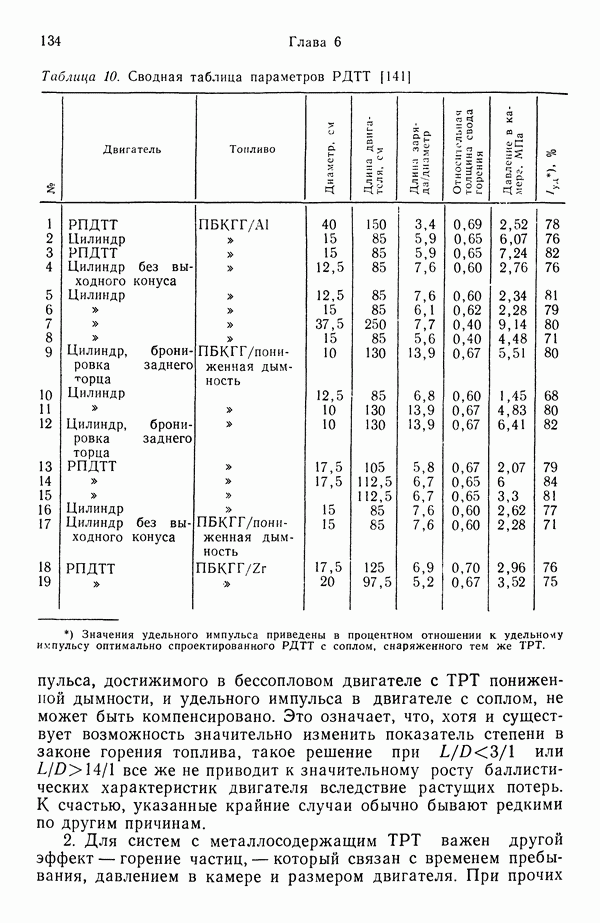
Для изучения горения одиночной капли использовались, как показано на рис. 79, три различных метода. Первый основан на применении пористой сферы, в которую по трубке поступает горючее, выходящее по капиллярам на поверхность сферы и образующее там тонкий слой жидкости, которая вступает в реакцию горения. При этом непосредственно измеряется массовый расход и легко определяется константа испарения К (для обычных топлив при комнатной температуре она составляет  Метод допускает применение сфер различных диаметров. Возможно также исследование оптическими методами периода прекращения горения (погасания) и структуры пламени и измерение силы лобового сопротивления капли.
Метод допускает применение сфер различных диаметров. Возможно также исследование оптическими методами периода прекращения горения (погасания) и структуры пламени и измерение силы лобового сопротивления капли.
При использовании второго метода капля подвешивается на тонкой кварцевой нити. После воспламенения определяется (обычно с помощью высокоскоростной цветной киносъемки)

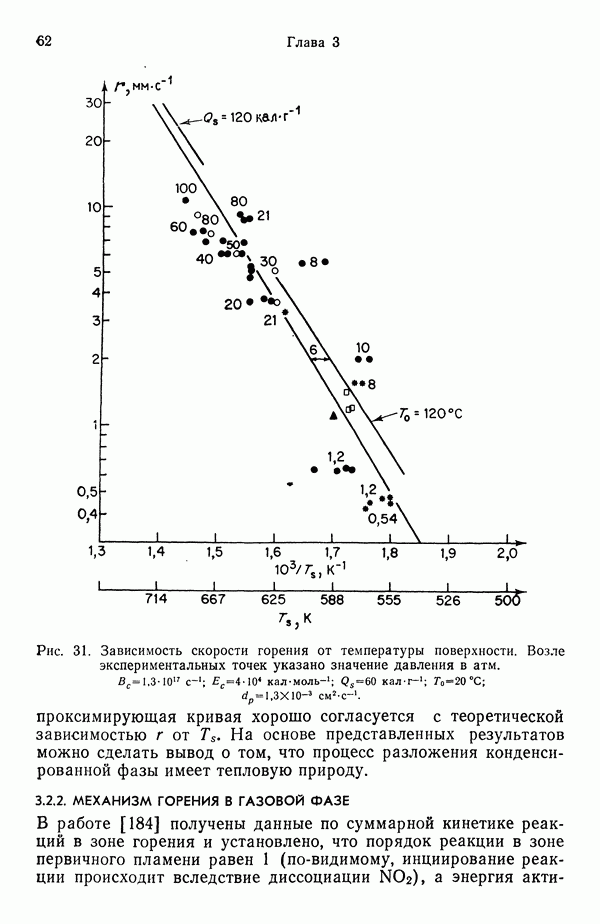
Рис. 79. Методы исследования горения капли горючего в атмосфере окислителя [176]. а — пористая сфера; б - капля, подвешенная на кварцевой нити; в — падающая капля; 1 — пламя; 2— пористая сфера; 3 — кварцевая нить; 4 — подвешенная капля;  свободная капля.
свободная капля.
скорость уменьшения диаметра (также может применяться теневая киносъемка). Для этого уравнение (7.2) удобно использовать в форме  Метод позволяет определять постоянную К и сравнивать полученные данные с результатами теоретических расчетов. При этом, однако, необходимо вносить поправку на отклонение формы капли от сферы. Преимущество описанного метода состоит в том, что экспериментальное устройство можно поместить в замкнутую полость; это позволяет изучать влияние различных температур и давлений. Если же реализовать условия свободного падения всего контейнера (к примеру в башне создания невесомости), то можно изучать влияние изменения силы тяжести на горение капли. Этот метод позволяет исследовать взаимовлияние капель, расположенных в непосредственной близости друг от друга. Недостатки метода состоят в том, что нить отводит тепло и не удается получить каплю диаметром меньше 100 мкм. Для капель меньших размеров используется третий метод, заключающийся в том, что капля свободно падает в топке или пролетает сквозь плоское пламя. Способы измерения при этом аналогичны упомянутым выше.
Метод позволяет определять постоянную К и сравнивать полученные данные с результатами теоретических расчетов. При этом, однако, необходимо вносить поправку на отклонение формы капли от сферы. Преимущество описанного метода состоит в том, что экспериментальное устройство можно поместить в замкнутую полость; это позволяет изучать влияние различных температур и давлений. Если же реализовать условия свободного падения всего контейнера (к примеру в башне создания невесомости), то можно изучать влияние изменения силы тяжести на горение капли. Этот метод позволяет исследовать взаимовлияние капель, расположенных в непосредственной близости друг от друга. Недостатки метода состоят в том, что нить отводит тепло и не удается получить каплю диаметром меньше 100 мкм. Для капель меньших размеров используется третий метод, заключающийся в том, что капля свободно падает в топке или пролетает сквозь плоское пламя. Способы измерения при этом аналогичны упомянутым выше.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ АВТОРА К РУССКОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- 1. ХАРАКТЕРИСТИКИ РАКЕТНЫХ ДВИГАТЕЛЕЙ НА ХИМИЧЕСКОМ ТОПЛИВЕ
- 1.2. ТЕРМОХИМИЯ ПРОЦЕССА В КАМЕРЕ СГОРАНИЯ
- 1.3. РАСШИРЕНИЕ ГАЗА В СОПЛЕ
- 2. СВОЙСТВА, ПРОИЗВОДСТВО И ВЗРЫВООПАСНОСТЬ ТВЕРДЫХ РАКЕТНЫХ ТОПЛИВ
- 2.2. ГОМОГЕННЫЕ ТОПЛИВА
- 2.3. НИТРАМИННЫЕ ТОПЛИВА
- 2.4. ГЕТЕРОГЕННЫЕ ТОПЛИВА
- 2.5. МЕХАНИЧЕСКИЕ ИСПЫТАНИЯ, КРИТЕРИИ РАЗРУШЕНИЯ И СТАРЕНИЕ
- 2.6. ВЗРЫВООПАСНОСТЬ
- 3. МЕХАНИЗМ ГОРЕНИЯ ТВЕРДЫХ РАКЕТНЫХ ТОПЛИВ
- 3.2. СТАЦИОНАРНОЕ ГОРЕНИЕ ГОМОГЕННЫХ ТОПЛИВ
- 3.2.1. РАЗЛОЖЕНИЕ ТОПЛИВА
- 3.2.2. МЕХАНИЗМ ГОРЕНИЯ В ГАЗОВОЙ ФАЗЕ
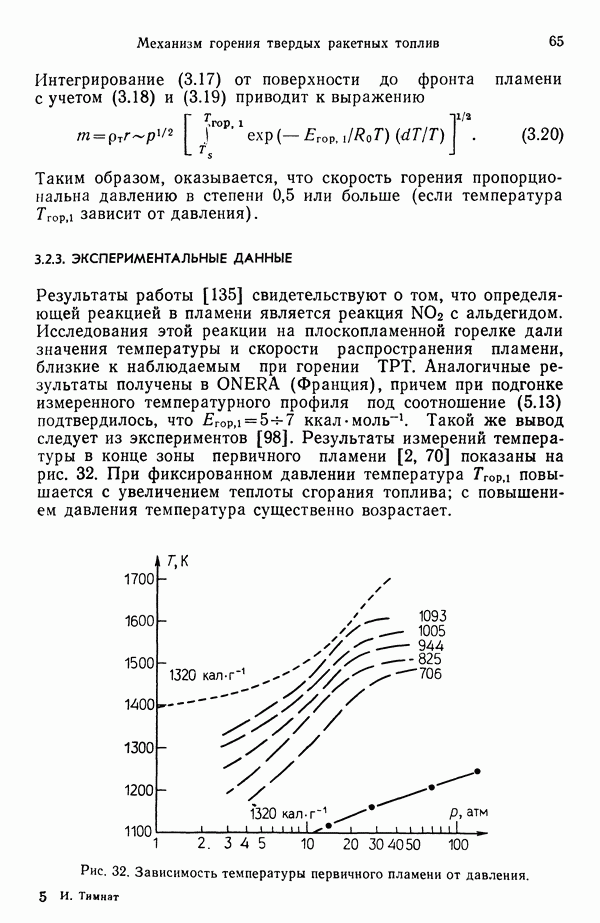
- 3.2.3. ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ
- 3.3. СТАЦИОНАРНОЕ ГОРЕНИЕ НИТРАМИННЫХ ТОПЛИВ
- 3.4. СТАЦИОНАРНОЕ ГОРЕНИЕ СМЕСЕВЫХ ТОПЛИВ
- 3.4.2. ГОРЕНИЕ СВЯЗУЮЩЕГО
- 3.4.3. ГОРЕНИЕ СМЕСЕВЫХ ТВЕРДЫХ ТОПЛИВ
- 3.5. ОСНОВНЫЕ УРАВНЕНИЯ МОДЕЛИ ГОРЕНИЯ СМЕСЕВОГО ТОПЛИВА
- 3.5.2. УРАВНЕНИЯ СОХРАНЕНИЯ В ТВЕРДОЙ ФАЗЕ
- 3.5.3. УСЛОВИЯ НА ПОВЕРХНОСТИ РАЗДЕЛА ТВЕРДАЯ ФАЗА — ГАЗ
- 3.5.4. УРАВНЕНИЯ СОХРАНЕНИЯ В ГАЗОВОЙ ФАЗЕ
- 3.5.5. ХАРАКТЕРИСТИЧЕСКИЕ ПАРАМЕТРЫ ПРОЦЕССА ГОРЕНИЯ
- 4. ВОСПЛАМЕНЕНИЕ И ПОГАСАНИЕ ТВЕРДЫХ ТОПЛИВ
- 4.2. ВОСПЛАМЕНЕНИЕ ТВЕРДЫХ ТОПЛИВ
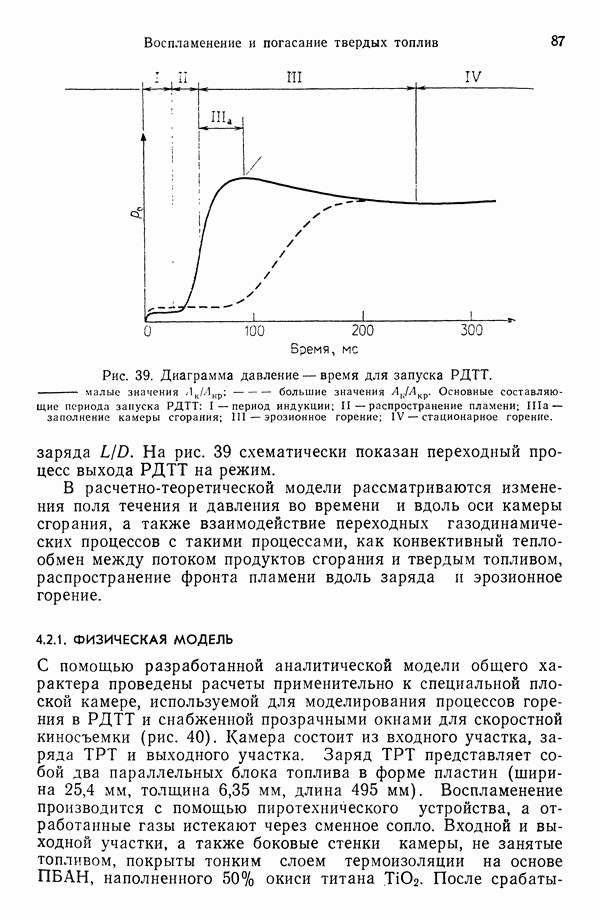
- 4.3. ГАШЕНИЕ ТВЕРДЫХ РАКЕТНЫХ ТОПЛИВ
- 5. ПРОГНОЗИРОВАНИЕ ХАРАКТЕРИСТИК ГОРЕНИЯ ТВЕРДЫХ РАКЕТНЫХ ТОПЛИВ
- 5.2. МОДЕЛЬ ТЕЧЕНИЯ В КАМЕРЕ РДТТ
- 5.3. РАСПРОСТРАНЕНИЕ ФРОНТА ГОРЕНИЯ В ТВЕРДОМ ТОПЛИВЕ
- 5.4. УДЕЛЬНЫЙ ИМПУЛЬС РДТТ
- 5.5. ХАРАКТЕРИСТИКИ СОПЛА
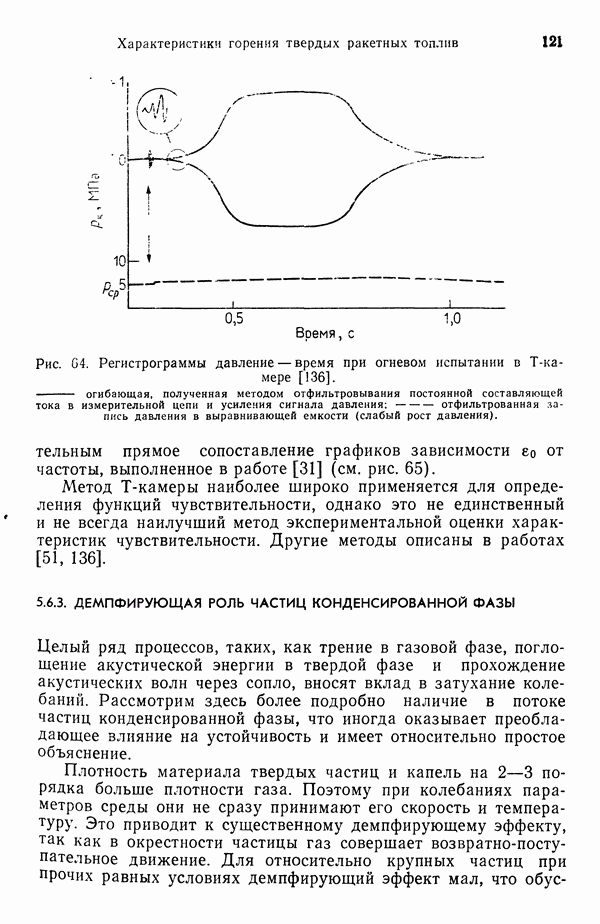
- 5.6. НЕУСТОЙЧИВОСТЬ ГОРЕНИЯ В РДТТ
- 5.6.2. ИЗМЕРЕНИЯ ЧУВСТВИТЕЛЬНОСТИ ГОРЕНИЯ
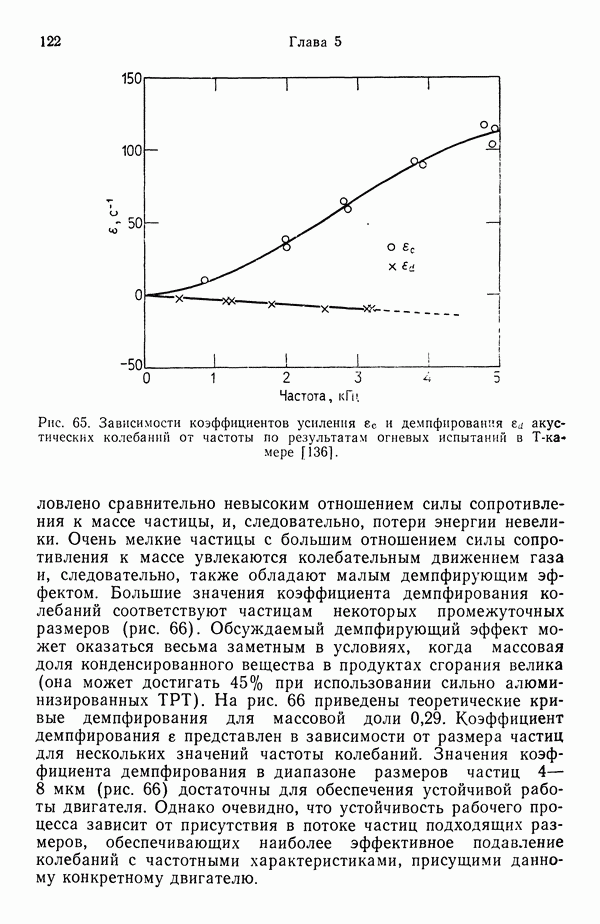
- 5.6.3. ДЕМПФИРУЮЩАЯ РОЛЬ ЧАСТИЦ КОНДЕНСИРОВАННОЙ ФАЗЫ
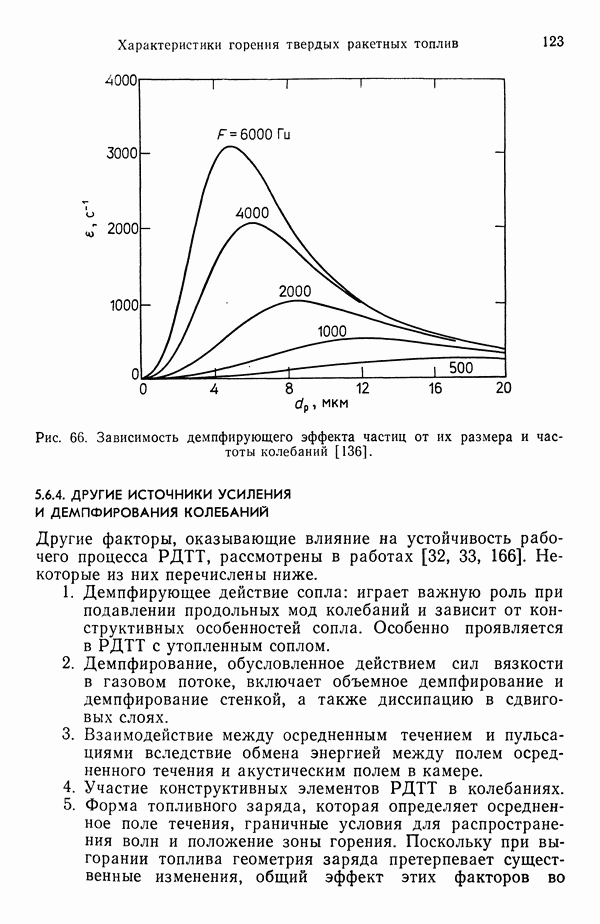
- 5.6.4. ДРУГИЕ ИСТОЧНИКИ УСИЛЕНИЯ И ДЕМПФИРОВАНИЯ КОЛЕБАНИЙ
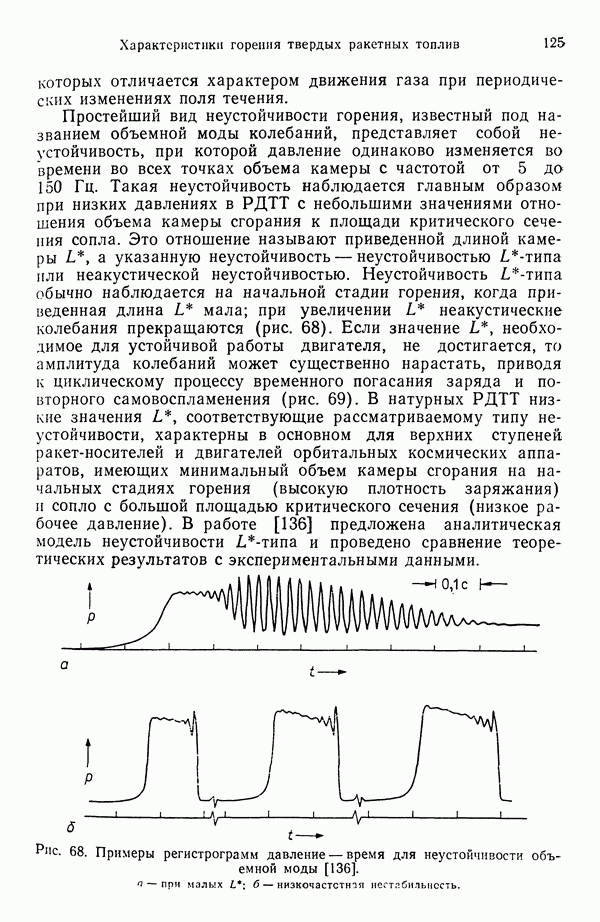
- 5.6.5. ВИДЫ НЕУСТОЙЧИВОСТЕЙ В РДТТ
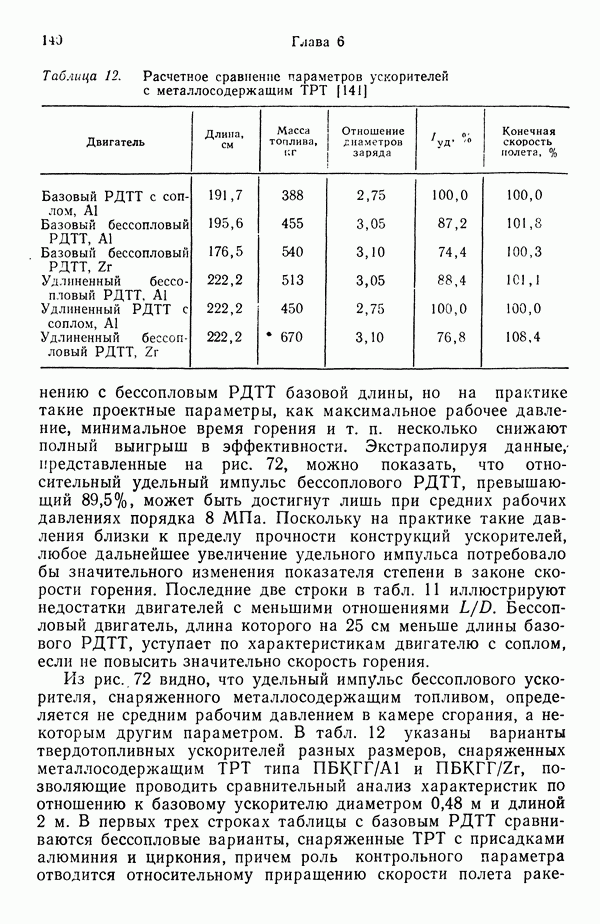
- 6. БЕССОПЛОВЫЕ РДТТ
- 6.2. ВНУТРЕННЯЯ БАЛЛИСТИКА
- 6.3. ОПТИМИЗАЦИЯ ХАРАКТЕРИСТИК
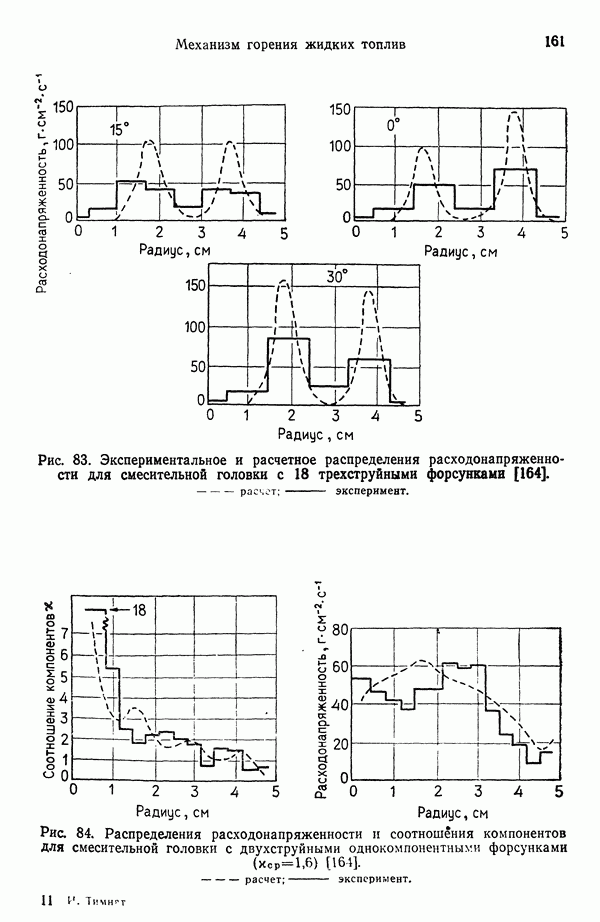
- 7. МЕХАНИЗМ ГОРЕНИЯ ЖИДКИХ ТОПЛИВ
- 7.2. ГОРЕНИЕ ОДИНОЧНОЙ КАПЛИ
- 7.3. ОБЩАЯ МОДЕЛЬ ГОРЕНИЯ
- 7.4. ИСПОЛЬЗОВАНИЕ МОДЕЛИ
- 7.4.2. ПРОГРАММА РАСПРЕДЕЛЕНИЯ ЖИДКОСТНЫХ СТРУЙ
- 7.4.3. МОДЕЛЬ ЗОНЫ ГОРЕНИЯ 3-D COMBUST
- 7.4.4. МОДЕЛЬ ДОГОРАНИЯ В ТРУБКАХ ТОКА STRMTB
- 7.4.5. ПРИМЕР РАСЧЕТА
- 8. ЭКОНОМИЧНОСТЬ, УСТОЙЧИВОСТЬ И РЛБОТОСПОСОБНОСЬ ЖРД
- 8.2. ЭКОНОМИЧНОСТЬ
- 8.3. НЕУСТОЙЧИВОСТЬ РАБОЧЕГО ПРОЦЕССА
- 8.4. РАБОТОСПОСОБНОСТЬ КАМЕРЫ
- 8.5. ВЗАИМОСВЯЗЬ ЭКОНОМИЧНОСТИ, УСТОЙЧИВОСТИ И РАБОТОСПОСОБНОСТИ ЖРД
- 9. НОВЫЕ СХЕМЫ ЖРД
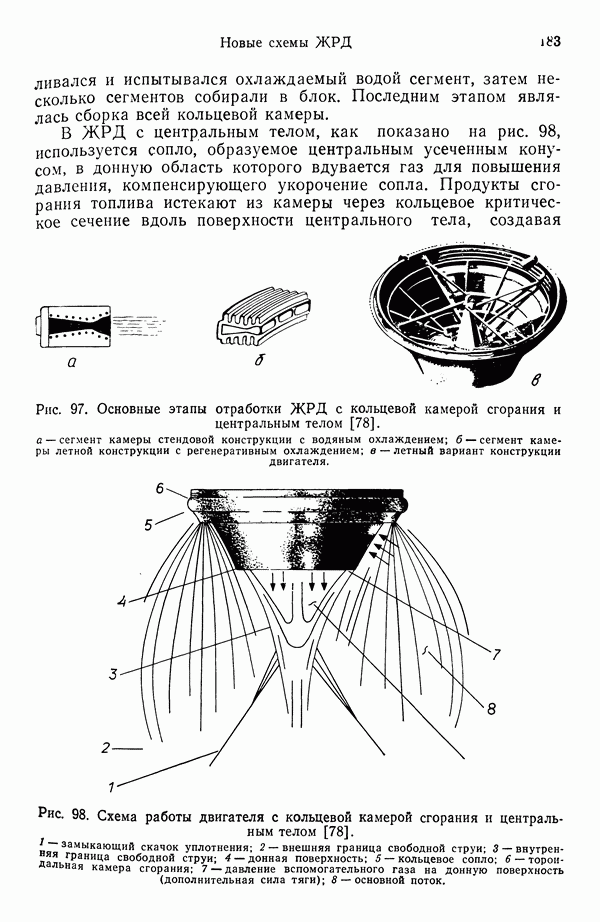
- 9.2. ЖРД С КОЛЬЦЕВОЙ КАМЕРОЙ СГОРАНИЯ И ЦЕНТРАЛЬНЫМ ТЕЛОМ
- 9.2.1. КОНСТРУКЦИЯ КАМЕРЫ СГОРАНИЯ
- 9.2.2. ИСПЫТАНИЯ
- 9.3. ЖРД, РАБОТАЮЩИЕ НА ДВУХ ГОРЮЧИХ
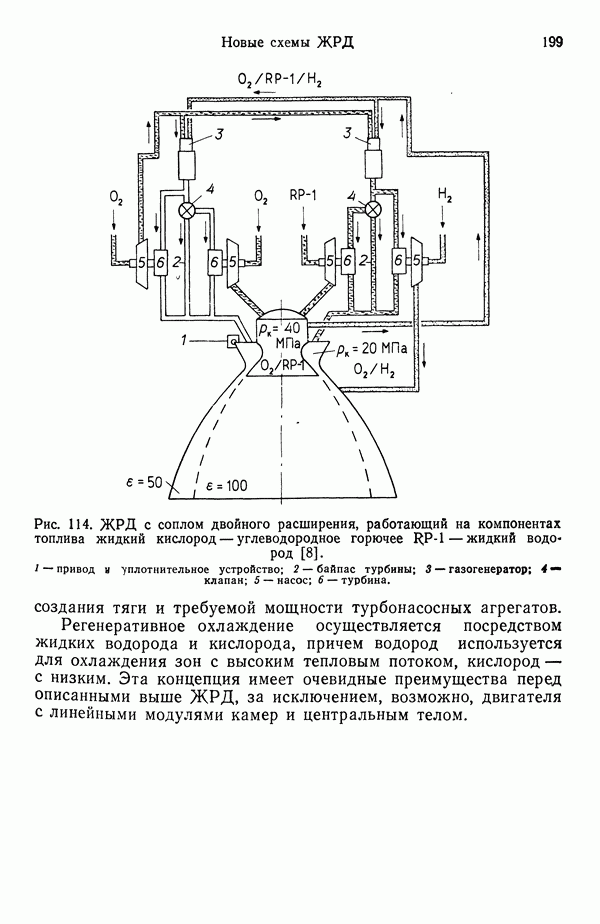
- 9.4. ЖРД С СОПЛОМ ДВОЙНОГО РАСШИРЕНИЯ
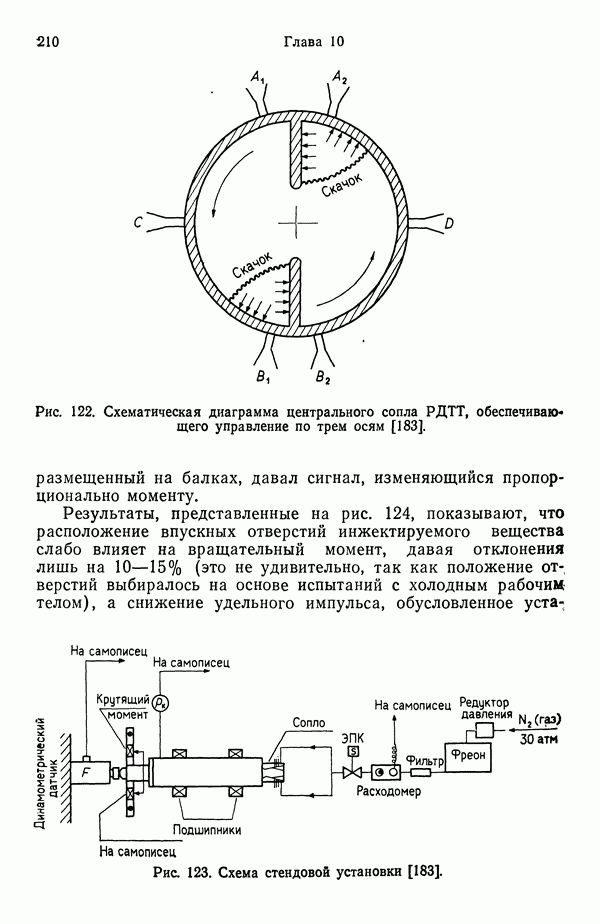
- 10. УПРАВЛЕНИЕ ВЕКТОРОМ И ВЕЛИЧИНОЙ ТЯГИ
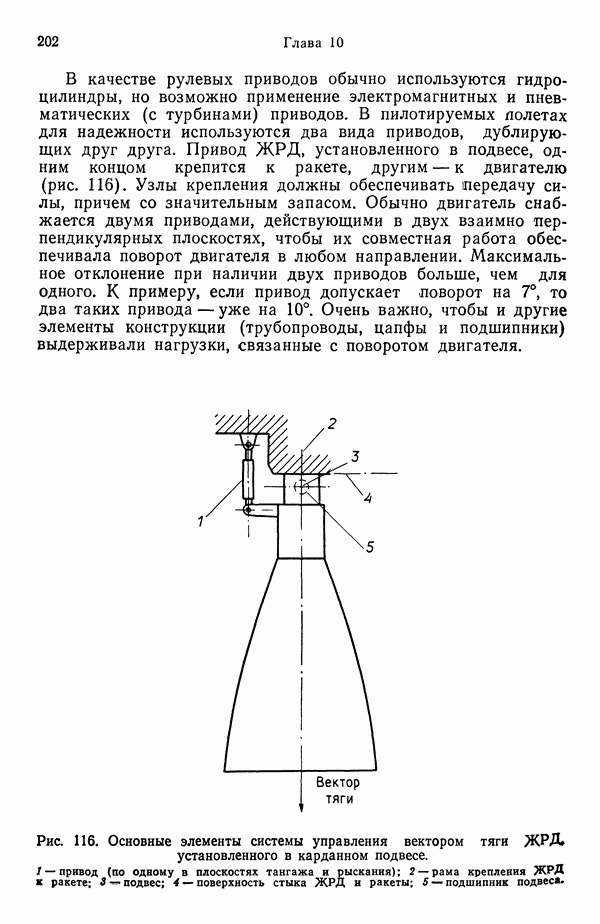
- 10.2. УПРАВЛЕНИЕ ВЕКТОРОМ ТЯГИ В ЖРД
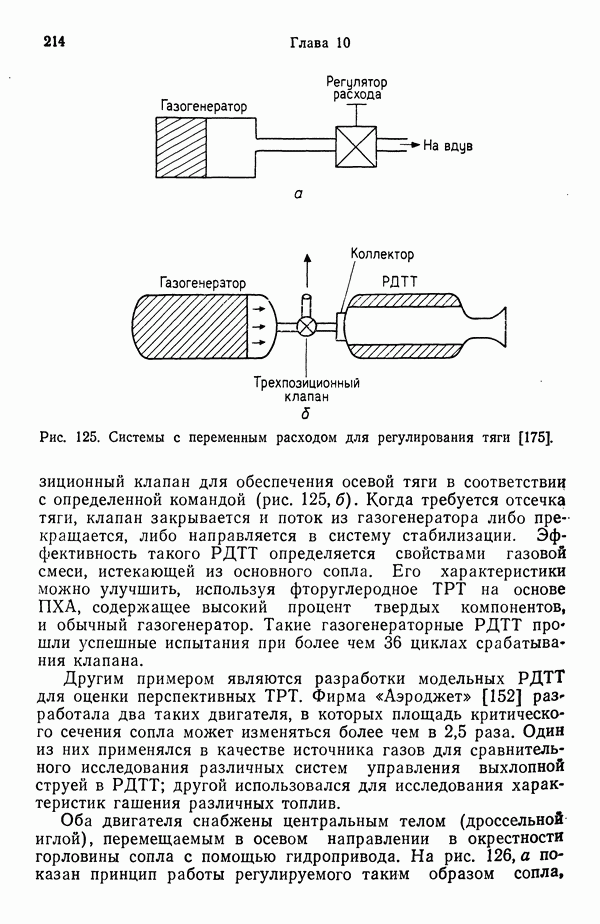
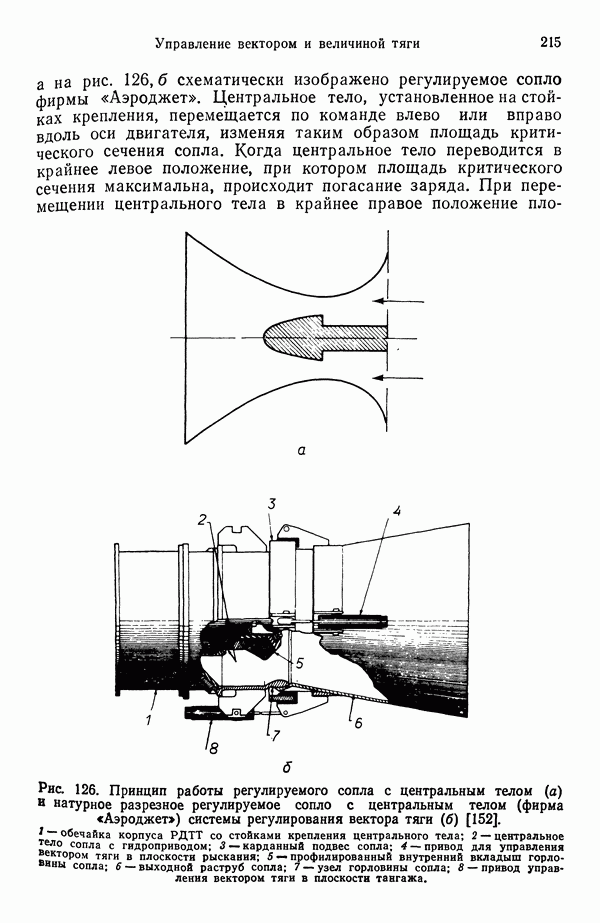
- 10.3. УПРАВЛЕНИЕ ВЕКТОРОМ ТЯГИ В РДТТ
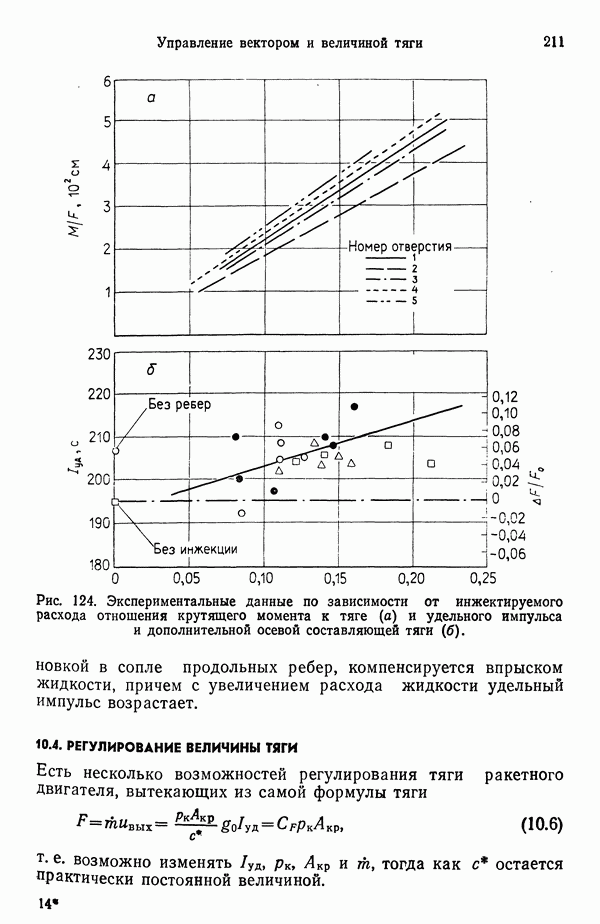
- 10.4. РЕГУЛИРОВАНИЕ ВЕЛИЧИНЫ ТЯГИ
- 11. ПРИМЕНЕНИЕ РДТТ ДЛЯ КОСМИЧЕСКИХ ИССЛЕДОВАНИЙ
- 11.2. УСКОРИТЕЛИ РАКЕТЫ-НОСИТЕЛЯ «ТИТАН»
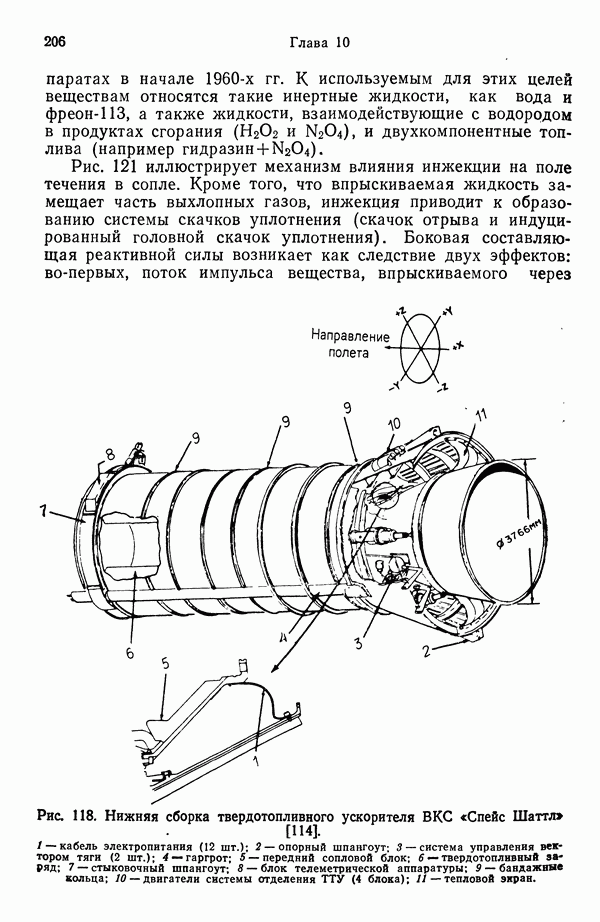
- 11.3. ТВЕРДОТОПЛИВНЫЙ УСКОРИТЕЛЬ ВКС «СПЕЙС ШАТТЛ»
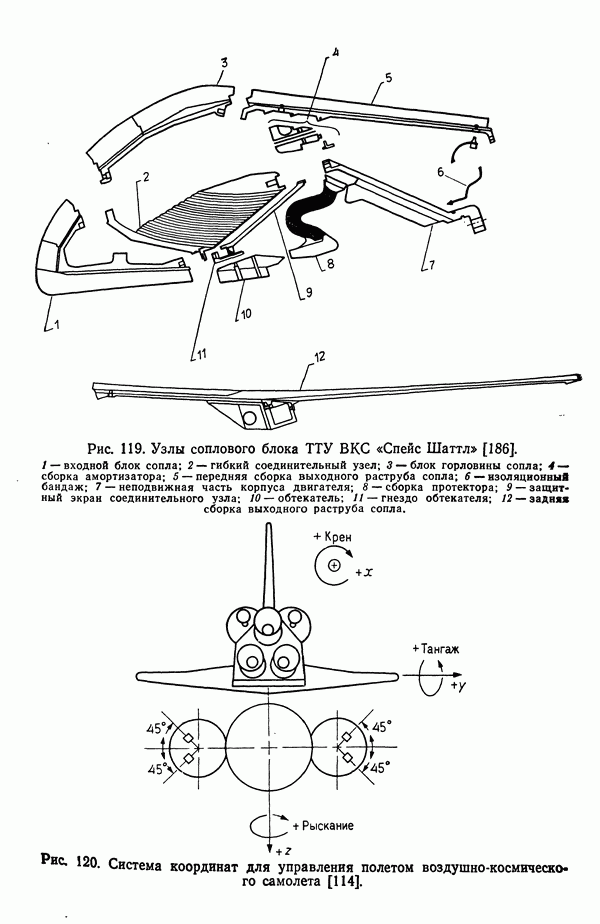
- 11.4. ТВЕРДОТОПЛИВНЫЕ УСКОРИТЕЛИ РАКЕТЫ-НОСИТЕЛЯ «АРИАН»
- 11.5. ТВЕРДОТОПЛИВНЫЕ ДВИГАТЕЛИ ДЛЯ ПОСЛЕДНИХ СТУПЕНЕЙ РАКЕТ-НОСИТЕЛЕЙ
- 12. ПРИМЕНЕНИЕ ЖРД ДЛЯ КОСМИЧЕСКИХ ИССЛЕДОВАНИЙ
- 12.2. КИСЛОРОДО-ВОДОРОДНЫЕ ЖРД RL-10, НМ-7 И LE-5
- 12.3. МАРШЕВЫЙ ДВИГАТЕЛЬ ВКС «СПЕЙС ШАТТЛ»
- 12.4. СРАВНЕНИЕ РАЗЛИЧНЫХ КИСЛОРОДО-ВОДОРОДНЫЙ ЖРД
- 12.5. ЖРД ДЛЯ МАНЕВРИРОВАНИЯ И ИЗМЕНЕНИЯ ОРБИТЫ
- 12.6. ВСПОМОГАТЕЛЬНЫЕ ДВИГАТЕЛЬНЫЕ УСТАНОВКИ С ЖРД
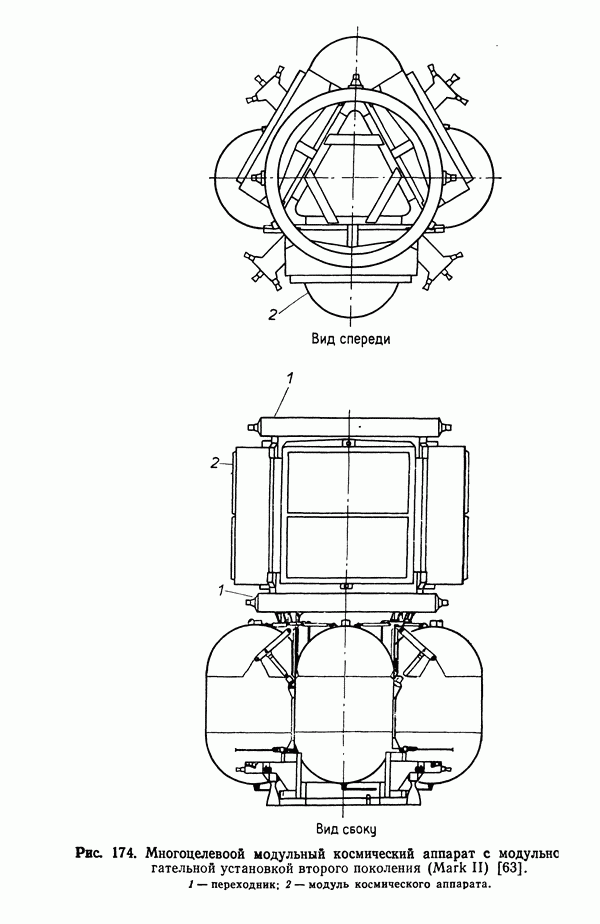
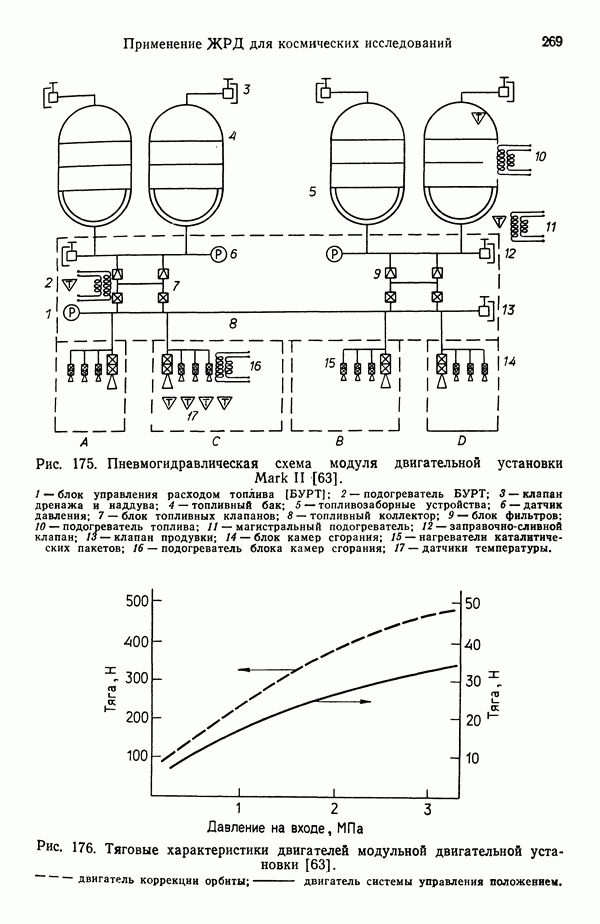
- 12.6.2. МОДУЛЬНАЯ ДВИГАТЕЛЬНАЯ УСТАНОВКА ВТОРОГО ПОКОЛЕНИЯ
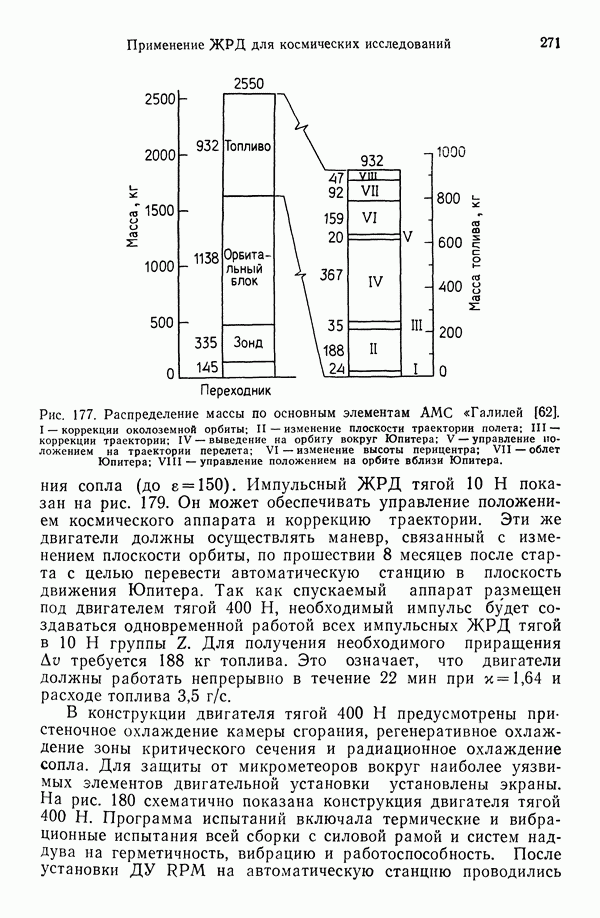
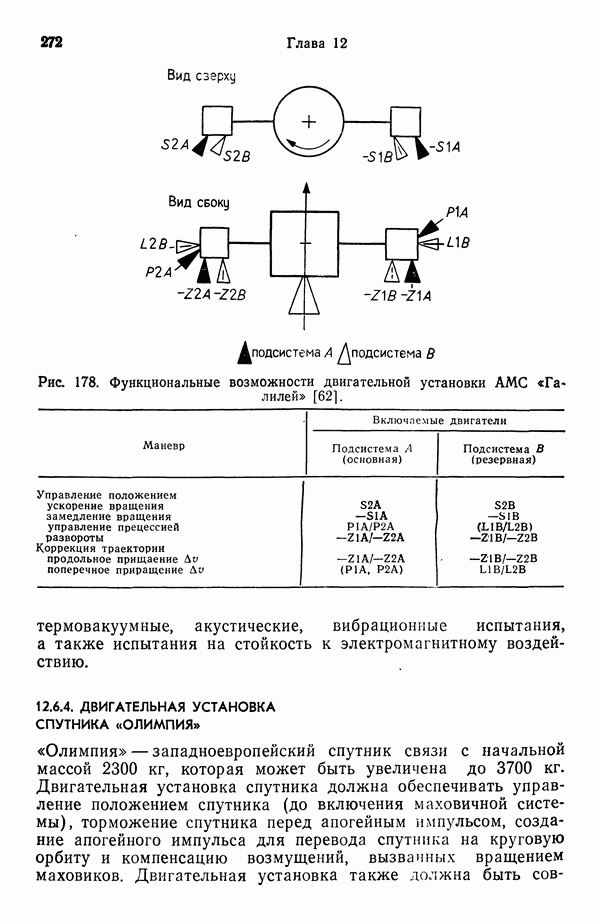
- 12.6.3. ДВУХКОМПОНЕНТНАЯ ДВИГАТЕЛЬНАЯ УСТАНОВКА АВТОМАТИЧЕСКОЙ МЕЖПЛАНЕТНОЙ СТАНЦИИ «ГАЛИЛЕЙ»
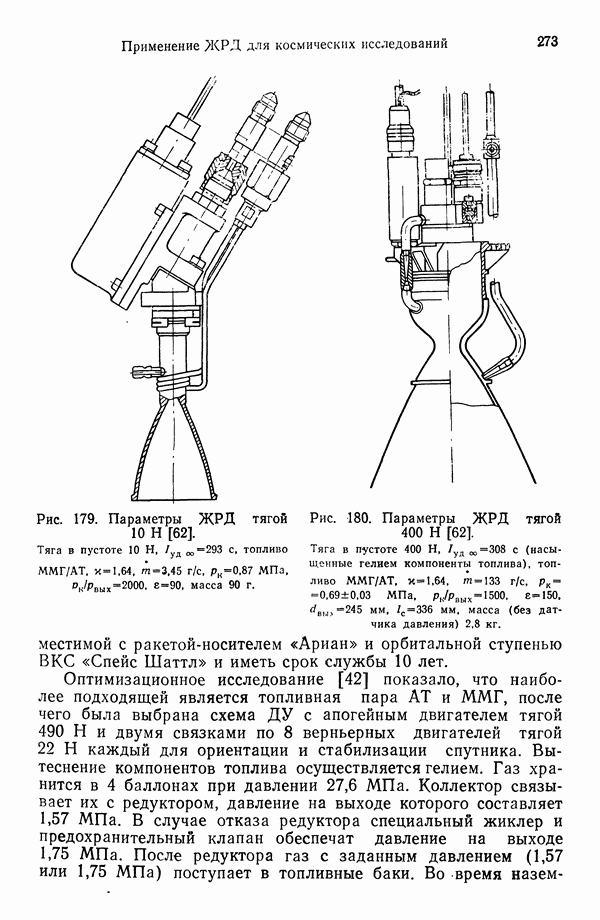
- 12.6.4. ДВИГАТЕЛЬНАЯ УСТАНОВКА СПУТНИКА «ОЛИМПИЯ»
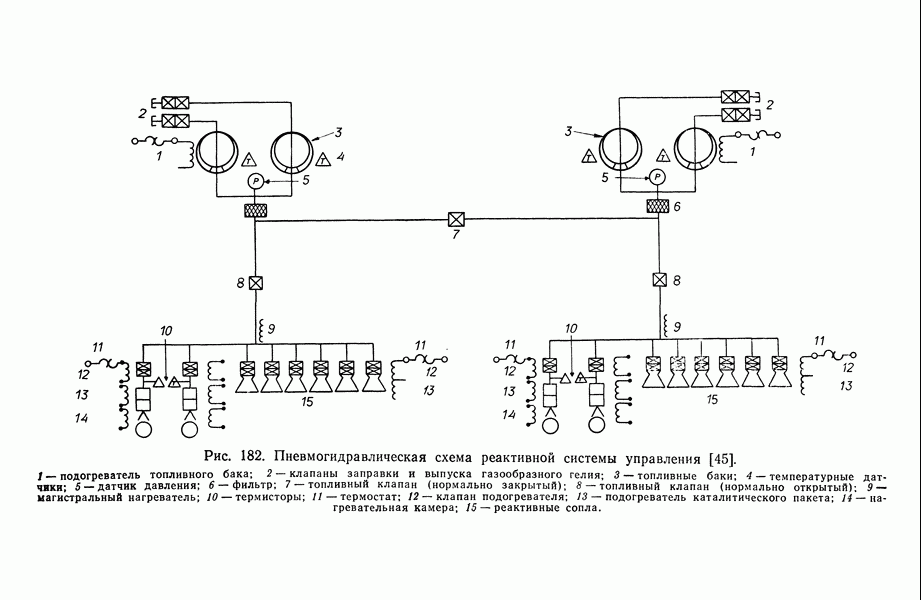
- 12.6.5. СИСТЕМА РЕАКТИВНОГО УПРАВЛЕНИЯ С ИМПУЛЬСНЫМИ ОДНОКОМПОНЕНТНЫМИ ЖРД
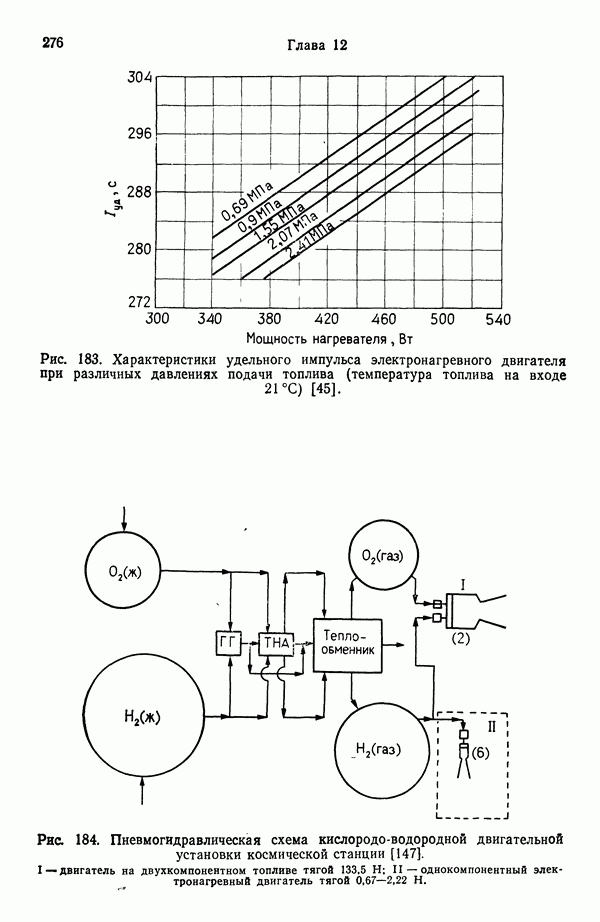
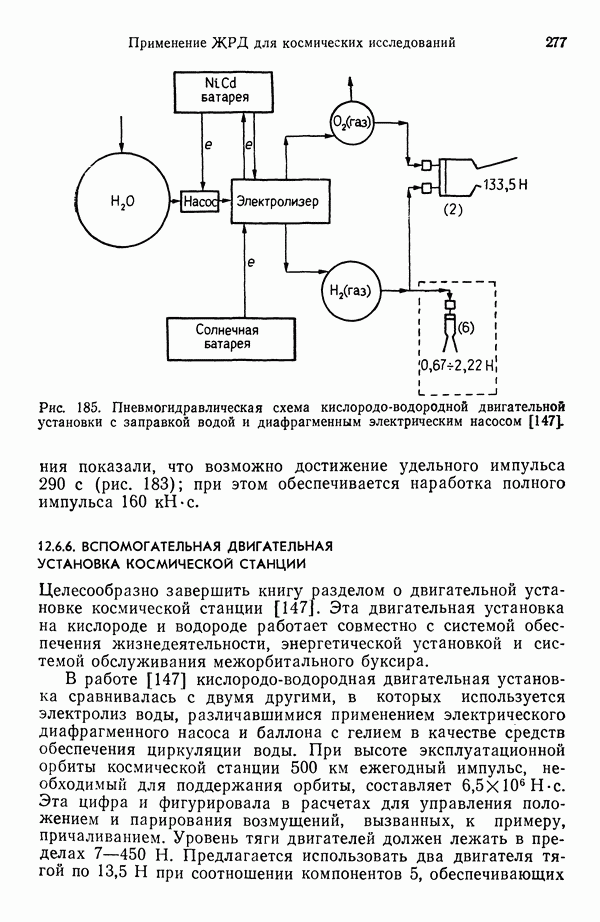
- 12.6.6. ВСПОМОГАТЕЛЬНАЯ ДВИГАТЕЛЬНАЯ УСТАНОВКА КОСМИЧЕСКОЙ СТАНЦИИ