| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
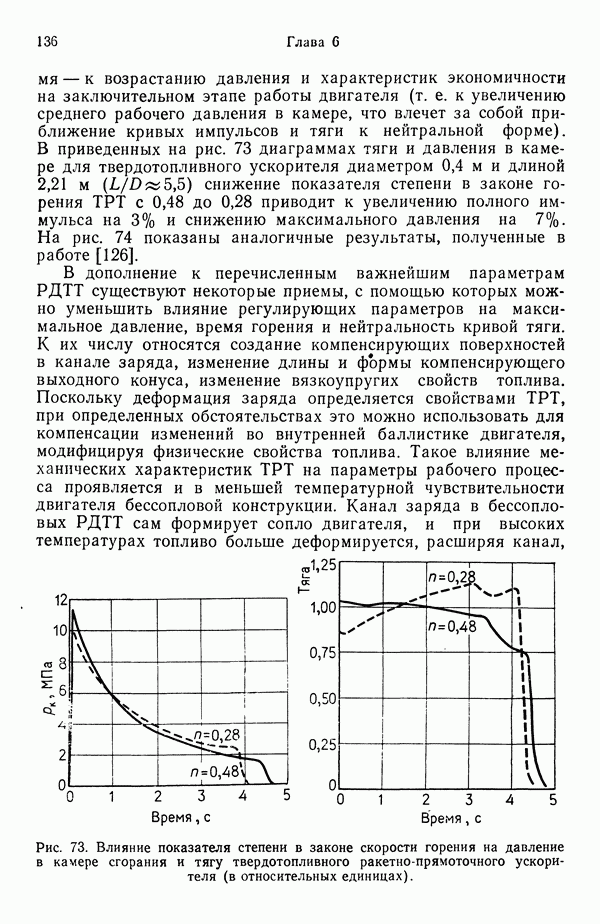
1.3. РАСШИРЕНИЕ ГАЗА В СОПЛЕ
В предыдущем разделе приведен метод расчета температуры адиабатического горения и состава продуктов в камере сгорания. Рассмотрим теперь более детально процесс расширения продуктов сгорания в сопле. Для того чтобы выявить важные особенности протекания химических реакций, пренебрежем диссипативными потерями, связанными с трением и теплопередачей, и будем считать, что на входе в сопло газы имеют нулевую скорость, а их температура и состав найдены по описанной выше процедуре.
Известно, что энтальпия торможения продуктов сгорания высока и распределена по различным степеням свободы молекул в виде поступательного, вращательного и колебательного движений, а также энергии диссоциации молекул (энергию электронного возбуждения и ионизации можно не рассматривать, так как температуры в камере сгорания не настолько высоки).
Поскольку при расширении газов в сопле значительная часть энтальпии преобразуется в кинетическую энергию, возникает вопрос, какие из степеней свободы могут запаздывать в процессе такого преобразования. Равновесие по поступательным и вращательным степеням свободы достигается очень быстро, тогда как релаксация колебательной энергии к новому равновесному состоянию для молекул  при температуре
при температуре
Тк происходит за времена порядка  Время релаксации колебательной энергии уменьшается с повышением температуры пропорционально
Время релаксации колебательной энергии уменьшается с повышением температуры пропорционально  Что же касается процесса релаксации к равновесию по диссоциации, то он может оказаться существенным при временах расширения порядка
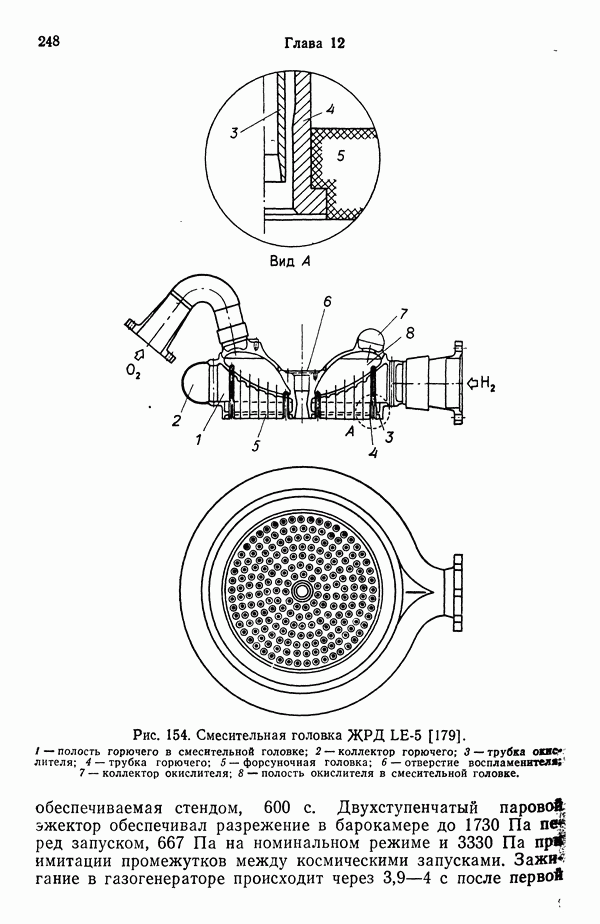
Что же касается процесса релаксации к равновесию по диссоциации, то он может оказаться существенным при временах расширения порядка  с и меньше, что характерно для малоразмерных двигателей (с тягой ~250 Н и длиной сопла менее 5 см). Для двигателей тягой ~500 Н и выше эти эффекты, как правило, несущественны, хотя для двигателей на высокоэнергетических топливах и камер с низкими значениями
с и меньше, что характерно для малоразмерных двигателей (с тягой ~250 Н и длиной сопла менее 5 см). Для двигателей тягой ~500 Н и выше эти эффекты, как правило, несущественны, хотя для двигателей на высокоэнергетических топливах и камер с низкими значениями  их все же надо рассматривать.
их все же надо рассматривать.
Если характерные времена реакции много меньше характерного времени расширения газа в сопле, то устанавливается химическое равновесие и о таком течении говорят как о равновесном. Если же расширение происходит настолько быстро, что химические реакции в сопле не успевают произойти, то говорят о замороженном течении. Эти два случая являются предельными и соответствуют бесконечной и нулевой скоростям реакции. В общем случае химические реакции развиваются с некоторой конечной скоростью. В прошлом при расчете характеристик ракетных двигателей течение полагали либо равновесным, либо замороженным [59]; к настоящему же времени появилась возможность расчета рабочего процесса с учетом точных конечных скоростей химических реакций для все более расширяющегося класса ракетных топлив. Существует, однако, и несколько полезных приближенных подходов, в которых используется метод Брэя [16, 17] для сверхзвукового сопла. Отметим, что два указанных выше предельных процесса являются изоэнтропическими, тогда как при конечной скорости реакции энтропия возрастает.
Изоэнтропичность равновесного и замороженного течений можно проверить следующим образом. Из закона сохранения энергии следует:

а если пренебречь диссипативными потерями, то

Обобщенное уравнение с учетом химических реакций имеет вид

Здесь  химический потенциал компоненты
химический потенциал компоненты  ее массовая концентрация. Из уравнений (1.27) и (1.28) следует
ее массовая концентрация. Из уравнений (1.27) и (1.28) следует

В случае когда химический состав заморожен,  имеем
имеем  Это означает, что замороженное течение является изоэнтропическим.
Это означает, что замороженное течение является изоэнтропическим.
Для одноступенчатой обратимой химической реакции скорость образования компоненты  можно записать в следующем виде:
можно записать в следующем виде:

где  стехиометрические коэффициенты. Если за время
стехиометрические коэффициенты. Если за время  степень развития некоторой реакции
степень развития некоторой реакции  незначительна, то
незначительна, то

Здесь величина  содержит все входящие в уравнение реакции члены, которые могут изменяться по мере расширения газа в сопле. Полное изменение величины
содержит все входящие в уравнение реакции члены, которые могут изменяться по мере расширения газа в сопле. Полное изменение величины  можно записать следующим образом:
можно записать следующим образом:

Подставляя это соотношение в (1.29), получим 

или, после изменения порядка суммирования,

Но член с суммированием  есть не что иное, как изменение свободной энергии за время
есть не что иное, как изменение свободной энергии за время  Записав
Записав

окончательно получим

Если  т.е. константа скорости реакции стремится к нулю, мы вновь приходим к уравнению (1.29). При равновесном течении
т.е. константа скорости реакции стремится к нулю, мы вновь приходим к уравнению (1.29). При равновесном течении  поскольку это и есть условие химического равновесия.
поскольку это и есть условие химического равновесия.
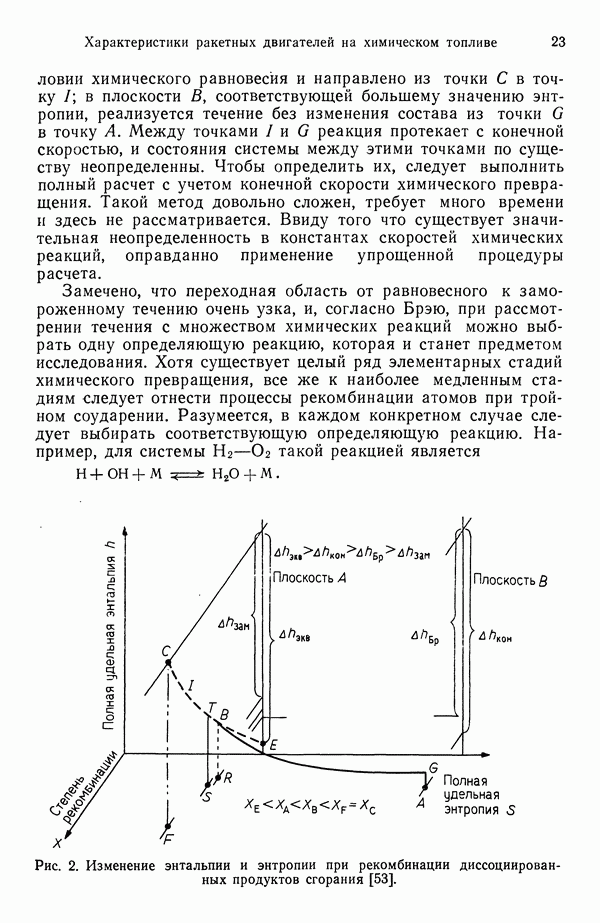
На рис. 2 приведена трехмерная диаграмма состояния химически реагирующей системы в координатах энтальпия — энтропия — состав. Для простоты здесь рассмотрена координата лишь одной реакции. На диаграмме показаны две плоскости постоянной энтропии: в плоскости А течение происходит при
условии химического равновесия и направлено из точки С в точку  в плоскости В, соответствующей большему значению энтропии, реализуется течение без изменения состава из точки
в плоскости В, соответствующей большему значению энтропии, реализуется течение без изменения состава из точки  в точку А. Между точками
в точку А. Между точками  реакция протекает с конечной скоростью, и состояния системы между этими точками по существу неопределенны. Чтобы определить их, следует выполнить полный расчет с учетом конечной скорости химического превращения. Такой метод довольно сложен, требует много времени и здесь не рассматривается. Ввиду того что существует значительная неопределенность в константах скоростей химических реакций, оправданно применение упрощенной процедуры расчета.
реакция протекает с конечной скоростью, и состояния системы между этими точками по существу неопределенны. Чтобы определить их, следует выполнить полный расчет с учетом конечной скорости химического превращения. Такой метод довольно сложен, требует много времени и здесь не рассматривается. Ввиду того что существует значительная неопределенность в константах скоростей химических реакций, оправданно применение упрощенной процедуры расчета.
Замечено, что переходная область от равновесного к замороженному течению очень узка, и, согласно Брэю, при рассмотрении течения с множеством химических реакций можно выбрать одну определяющую реакцию, которая и станет предметом исследования. Хотя существует целый ряд элементарных стадий химического превращения, все же к наиболее медленным стадиям следует отнести процессы рекомбинации атомов при тройном соударении. Разумеется, в каждом конкретном случае следует выбирать соответствующую определяющую реакцию. Например, для системы  такой реакцией является
такой реакцией является


Рис. 2. Изменение энтальпии и энтропии при рекомбинации диссоциированных продуктов сгорания [53].

Рис. 3. Изменение химического состава продуктов сгорания вдоль сопла с переходом от равновесного к замороженному течению [53].
Чтобы определить состояние системы, в котором выбранная реакция «замораживается», Брэй оценивает порядок различных членов уравнения реакции:

где  скорости прямой и обратной реакций соответственно. Проанализируем три возможных случая.
скорости прямой и обратной реакций соответственно. Проанализируем три возможных случая.
1. Если течение близко к равновесному, как и в начале расширения, то

Тогда

2. В переходной области все параметры:  одного порядка.
одного порядка.
3. Если течение близко к замороженному, то либо  либо
либо  и величина
и величина  имеет тот же порядок, что и большая из двух скоростей реакций:
имеет тот же порядок, что и большая из двух скоростей реакций:

На рис. 3 эта ситуация показана графически. Поскольку переходная область очень мала, то условие замораживания примет вид

Положив, что в точке, определяемой одним из этих уравнений, происходит замораживание реакции, можно оценить входящие в них величины, рассмотрев течение, близкое к равновесному:

Чтобы выполнить расчет, следует сначала определить по всей длине сопла состав, давление, температуру, скорость и т.д. для равновесного течения, а затем рассчитать соответствующие значения  и сравнить их со значениями величины
и сравнить их со значениями величины  Практически всегда замораживание происходит за критическим сечением сопла, поэтому такое сравнение можно проводить, начиная с критического сечения. Когда условие (1.39) удовлетворяется, расчет продолжается в приближении замороженного течения. Разумеется, оба расчета изоэнтропические. Окончательное значение разности энтальпий определяют, рассчитав разности энтальпий для равновесного и замороженного течений и просуммировав их. Тогда
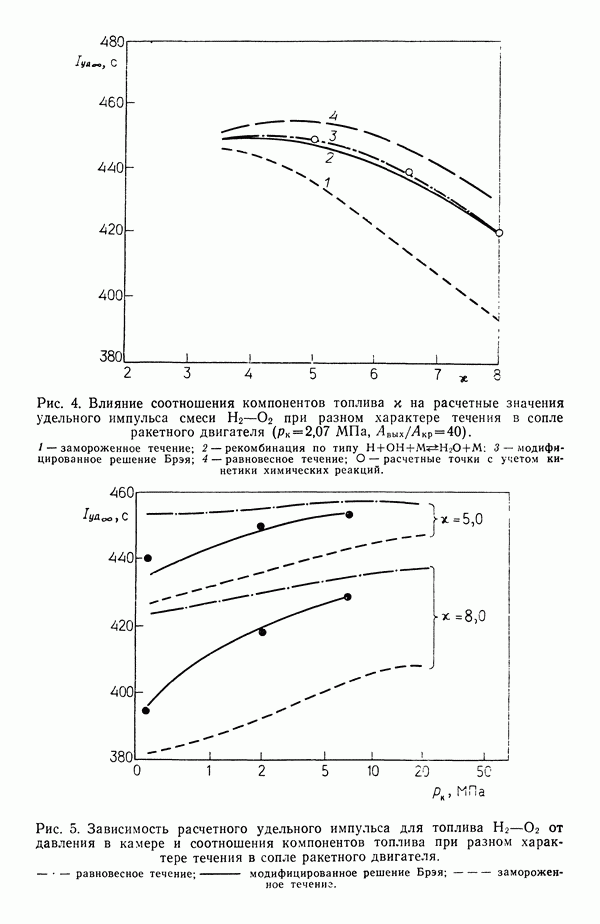
Практически всегда замораживание происходит за критическим сечением сопла, поэтому такое сравнение можно проводить, начиная с критического сечения. Когда условие (1.39) удовлетворяется, расчет продолжается в приближении замороженного течения. Разумеется, оба расчета изоэнтропические. Окончательное значение разности энтальпий определяют, рассчитав разности энтальпий для равновесного и замороженного течений и просуммировав их. Тогда  На рис. 4 приведены результаты расчетов удельного импульса для топлива
На рис. 4 приведены результаты расчетов удельного импульса для топлива  при
при  и степени расширения сопла, равной 40, в виде зависимости от отношения массы окислителя к массе горючего. На рис. 5 показано изменение величины
и степени расширения сопла, равной 40, в виде зависимости от отношения массы окислителя к массе горючего. На рис. 5 показано изменение величины  в зависимости от давления в камере
в зависимости от давления в камере  для двух значений отношения и. Видно, что при увеличении давления результаты кинетических расчетов приближаются к равновесному решению, а при очень низких
для двух значений отношения и. Видно, что при увеличении давления результаты кинетических расчетов приближаются к равновесному решению, а при очень низких  они близки к «замороженному» решению. Эта особенность является одной из причин того, что для достижения высоких
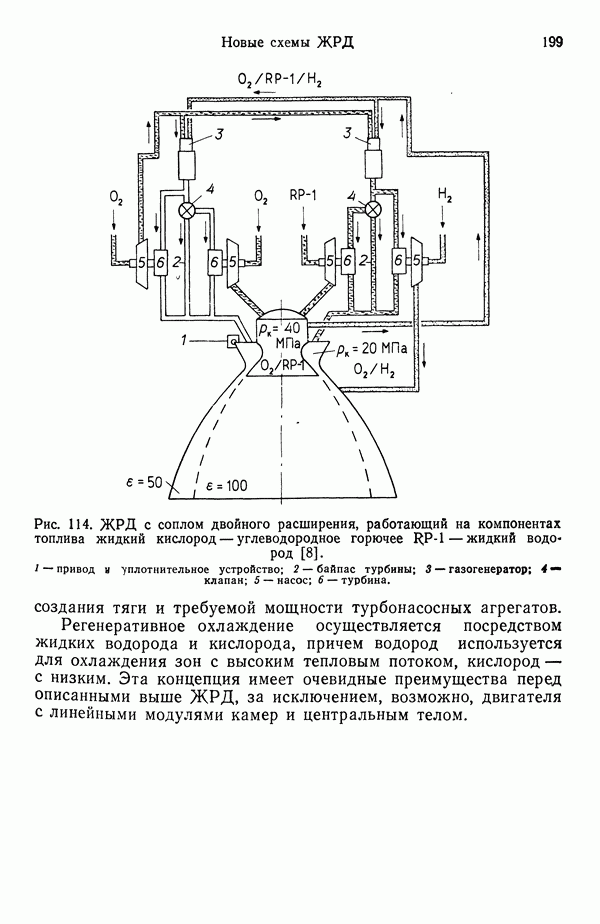
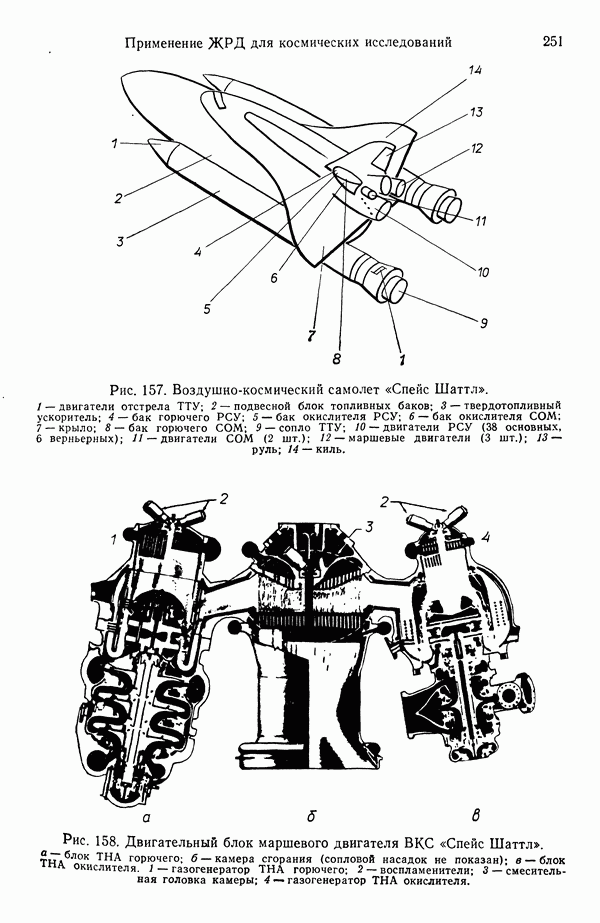
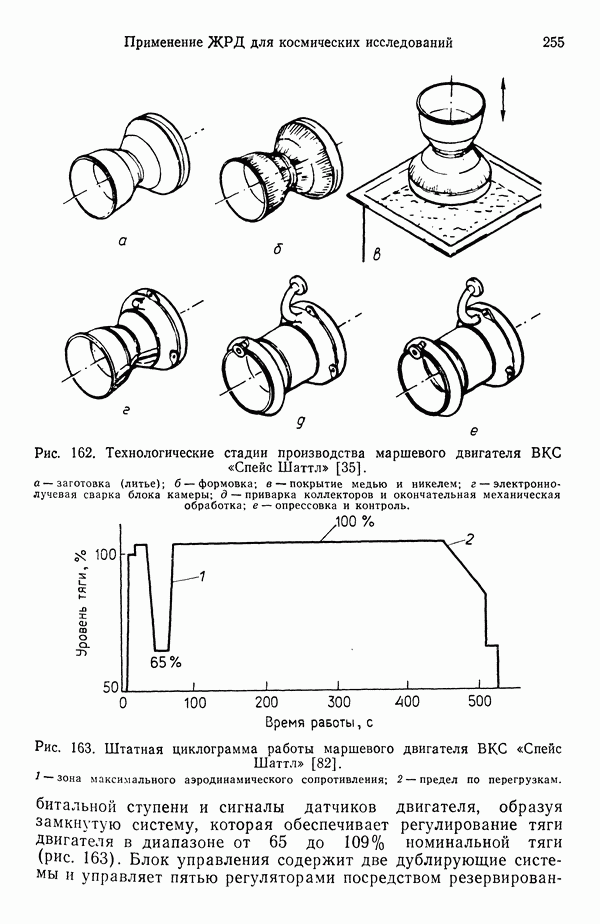
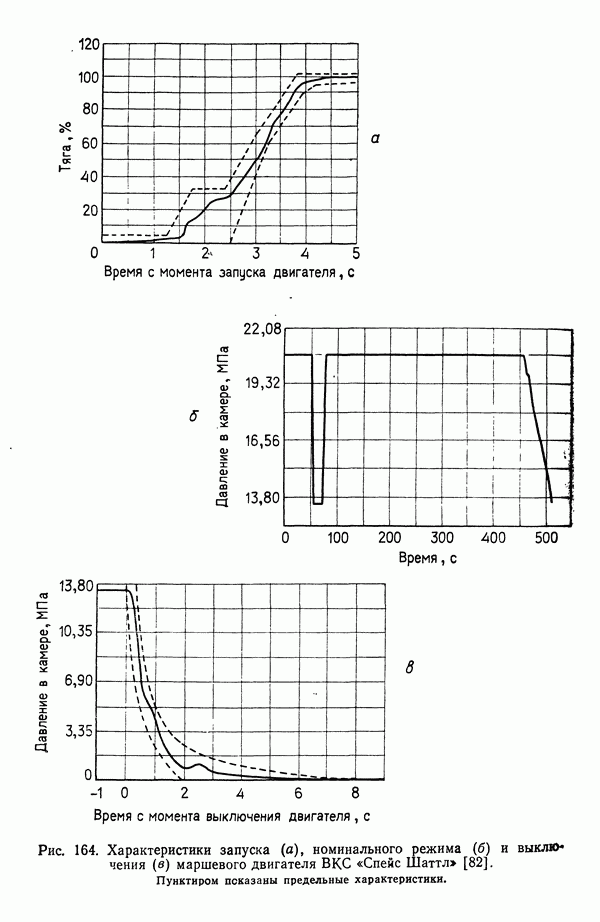
они близки к «замороженному» решению. Эта особенность является одной из причин того, что для достижения высоких  на новых ЖРД типа маршевого двигателя ВКС «Спейс Шаттл» используются очень высокие давления в камере сгорания.
на новых ЖРД типа маршевого двигателя ВКС «Спейс Шаттл» используются очень высокие давления в камере сгорания.
Процедура расчета характеристик камеры показана на рис. 2. Модифицированный процесс Брэя изображается следующим образом: течение начинается из точки С, соответствующей условиям в камере сгорания, и происходит вдоль равновесной кривой до точки замораживания В, расположенной сразу за горловиной сопла. Поскольку между точками  течение предполагается равновесным, процесс на этом участке считается изоэнтропическим. Далее процесс развивается из точки В в точку
течение предполагается равновесным, процесс на этом участке считается изоэнтропическим. Далее процесс развивается из точки В в точку  оставаясь замороженным.
оставаясь замороженным.
Легко получить оценку, допустив, что до критического сечения течение равновесное, а после него — замороженное. Такой процесс также происходит в плоскости А и изображен линией  на рис. 2. На рис. 2 показаны также соответствующие изменения энтропии: полностью равновесное течение представлено линией
на рис. 2. На рис. 2 показаны также соответствующие изменения энтропии: полностью равновесное течение представлено линией  полностью замороженное —
полностью замороженное —  течение с конечными скоростями реакций —
течение с конечными скоростями реакций —  , модифицированное приближенное решение Брэя —
, модифицированное приближенное решение Брэя —  и приближенное решение Брэя —
и приближенное решение Брэя — 
Наконец, интересно отметить, что в недавней работе Глика и Акри [55] показана приемлемость одномерного расчета для РДТТ. Как станет ясно из дальнейшего изложения, для ЖРД этот вывод несправедлив.

(кликните для просмотра скана)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ АВТОРА К РУССКОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- 1. ХАРАКТЕРИСТИКИ РАКЕТНЫХ ДВИГАТЕЛЕЙ НА ХИМИЧЕСКОМ ТОПЛИВЕ
- 1.2. ТЕРМОХИМИЯ ПРОЦЕССА В КАМЕРЕ СГОРАНИЯ
- 1.3. РАСШИРЕНИЕ ГАЗА В СОПЛЕ
- 2. СВОЙСТВА, ПРОИЗВОДСТВО И ВЗРЫВООПАСНОСТЬ ТВЕРДЫХ РАКЕТНЫХ ТОПЛИВ
- 2.2. ГОМОГЕННЫЕ ТОПЛИВА
- 2.3. НИТРАМИННЫЕ ТОПЛИВА
- 2.4. ГЕТЕРОГЕННЫЕ ТОПЛИВА
- 2.5. МЕХАНИЧЕСКИЕ ИСПЫТАНИЯ, КРИТЕРИИ РАЗРУШЕНИЯ И СТАРЕНИЕ
- 2.6. ВЗРЫВООПАСНОСТЬ
- 3. МЕХАНИЗМ ГОРЕНИЯ ТВЕРДЫХ РАКЕТНЫХ ТОПЛИВ
- 3.2. СТАЦИОНАРНОЕ ГОРЕНИЕ ГОМОГЕННЫХ ТОПЛИВ
- 3.2.1. РАЗЛОЖЕНИЕ ТОПЛИВА
- 3.2.2. МЕХАНИЗМ ГОРЕНИЯ В ГАЗОВОЙ ФАЗЕ
- 3.2.3. ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ
- 3.3. СТАЦИОНАРНОЕ ГОРЕНИЕ НИТРАМИННЫХ ТОПЛИВ
- 3.4. СТАЦИОНАРНОЕ ГОРЕНИЕ СМЕСЕВЫХ ТОПЛИВ
- 3.4.2. ГОРЕНИЕ СВЯЗУЮЩЕГО
- 3.4.3. ГОРЕНИЕ СМЕСЕВЫХ ТВЕРДЫХ ТОПЛИВ
- 3.5. ОСНОВНЫЕ УРАВНЕНИЯ МОДЕЛИ ГОРЕНИЯ СМЕСЕВОГО ТОПЛИВА
- 3.5.2. УРАВНЕНИЯ СОХРАНЕНИЯ В ТВЕРДОЙ ФАЗЕ
- 3.5.3. УСЛОВИЯ НА ПОВЕРХНОСТИ РАЗДЕЛА ТВЕРДАЯ ФАЗА — ГАЗ
- 3.5.4. УРАВНЕНИЯ СОХРАНЕНИЯ В ГАЗОВОЙ ФАЗЕ
- 3.5.5. ХАРАКТЕРИСТИЧЕСКИЕ ПАРАМЕТРЫ ПРОЦЕССА ГОРЕНИЯ
- 4. ВОСПЛАМЕНЕНИЕ И ПОГАСАНИЕ ТВЕРДЫХ ТОПЛИВ
- 4.2. ВОСПЛАМЕНЕНИЕ ТВЕРДЫХ ТОПЛИВ
- 4.3. ГАШЕНИЕ ТВЕРДЫХ РАКЕТНЫХ ТОПЛИВ
- 5. ПРОГНОЗИРОВАНИЕ ХАРАКТЕРИСТИК ГОРЕНИЯ ТВЕРДЫХ РАКЕТНЫХ ТОПЛИВ
- 5.2. МОДЕЛЬ ТЕЧЕНИЯ В КАМЕРЕ РДТТ
- 5.3. РАСПРОСТРАНЕНИЕ ФРОНТА ГОРЕНИЯ В ТВЕРДОМ ТОПЛИВЕ
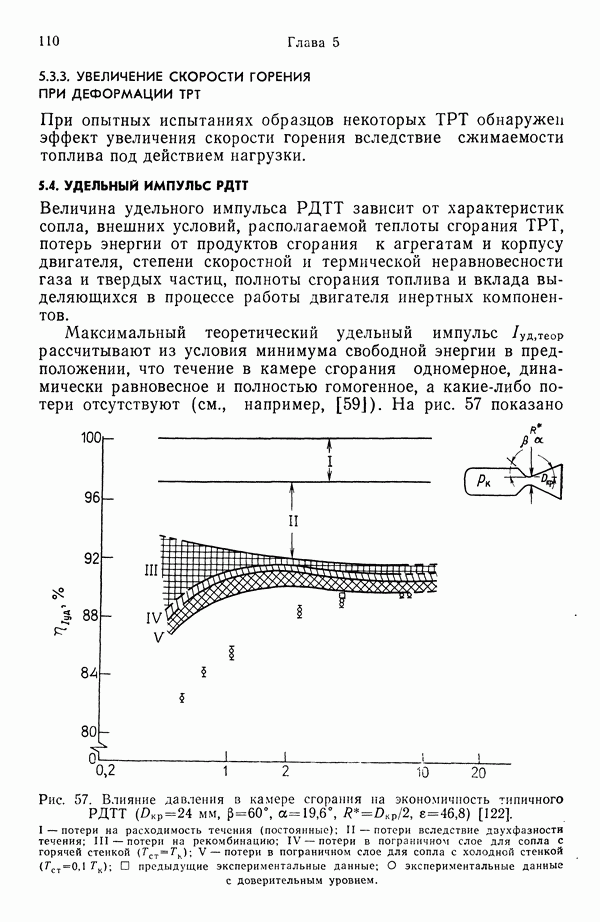
- 5.4. УДЕЛЬНЫЙ ИМПУЛЬС РДТТ
- 5.5. ХАРАКТЕРИСТИКИ СОПЛА
- 5.6. НЕУСТОЙЧИВОСТЬ ГОРЕНИЯ В РДТТ
- 5.6.2. ИЗМЕРЕНИЯ ЧУВСТВИТЕЛЬНОСТИ ГОРЕНИЯ
- 5.6.3. ДЕМПФИРУЮЩАЯ РОЛЬ ЧАСТИЦ КОНДЕНСИРОВАННОЙ ФАЗЫ
- 5.6.4. ДРУГИЕ ИСТОЧНИКИ УСИЛЕНИЯ И ДЕМПФИРОВАНИЯ КОЛЕБАНИЙ
- 5.6.5. ВИДЫ НЕУСТОЙЧИВОСТЕЙ В РДТТ
- 6. БЕССОПЛОВЫЕ РДТТ
- 6.2. ВНУТРЕННЯЯ БАЛЛИСТИКА
- 6.3. ОПТИМИЗАЦИЯ ХАРАКТЕРИСТИК
- 7. МЕХАНИЗМ ГОРЕНИЯ ЖИДКИХ ТОПЛИВ
- 7.2. ГОРЕНИЕ ОДИНОЧНОЙ КАПЛИ
- 7.3. ОБЩАЯ МОДЕЛЬ ГОРЕНИЯ
- 7.4. ИСПОЛЬЗОВАНИЕ МОДЕЛИ
- 7.4.2. ПРОГРАММА РАСПРЕДЕЛЕНИЯ ЖИДКОСТНЫХ СТРУЙ
- 7.4.3. МОДЕЛЬ ЗОНЫ ГОРЕНИЯ 3-D COMBUST
- 7.4.4. МОДЕЛЬ ДОГОРАНИЯ В ТРУБКАХ ТОКА STRMTB
- 7.4.5. ПРИМЕР РАСЧЕТА
- 8. ЭКОНОМИЧНОСТЬ, УСТОЙЧИВОСТЬ И РЛБОТОСПОСОБНОСЬ ЖРД
- 8.2. ЭКОНОМИЧНОСТЬ
- 8.3. НЕУСТОЙЧИВОСТЬ РАБОЧЕГО ПРОЦЕССА
- 8.4. РАБОТОСПОСОБНОСТЬ КАМЕРЫ
- 8.5. ВЗАИМОСВЯЗЬ ЭКОНОМИЧНОСТИ, УСТОЙЧИВОСТИ И РАБОТОСПОСОБНОСТИ ЖРД
- 9. НОВЫЕ СХЕМЫ ЖРД
- 9.2. ЖРД С КОЛЬЦЕВОЙ КАМЕРОЙ СГОРАНИЯ И ЦЕНТРАЛЬНЫМ ТЕЛОМ
- 9.2.1. КОНСТРУКЦИЯ КАМЕРЫ СГОРАНИЯ
- 9.2.2. ИСПЫТАНИЯ
- 9.3. ЖРД, РАБОТАЮЩИЕ НА ДВУХ ГОРЮЧИХ
- 9.4. ЖРД С СОПЛОМ ДВОЙНОГО РАСШИРЕНИЯ
- 10. УПРАВЛЕНИЕ ВЕКТОРОМ И ВЕЛИЧИНОЙ ТЯГИ
- 10.2. УПРАВЛЕНИЕ ВЕКТОРОМ ТЯГИ В ЖРД
- 10.3. УПРАВЛЕНИЕ ВЕКТОРОМ ТЯГИ В РДТТ
- 10.4. РЕГУЛИРОВАНИЕ ВЕЛИЧИНЫ ТЯГИ
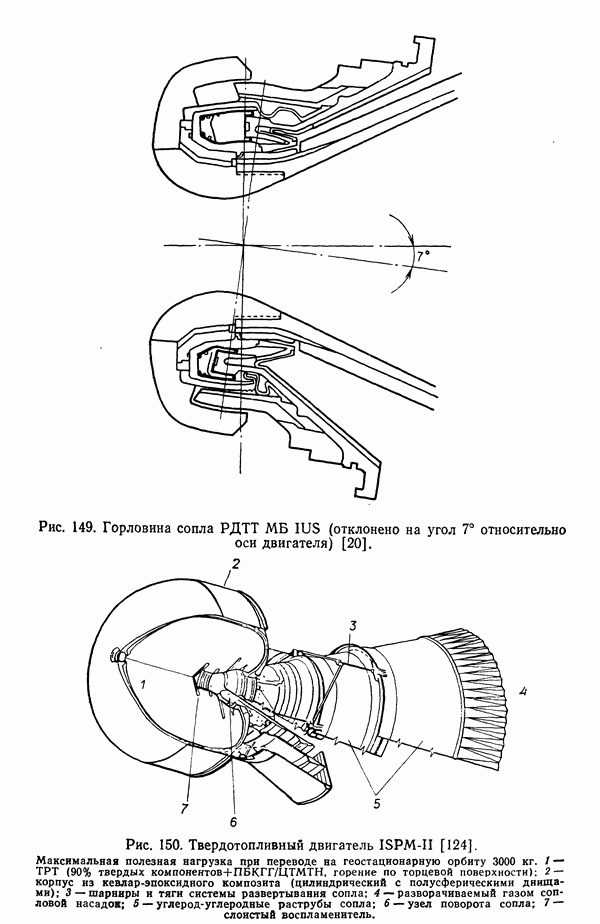
- 11. ПРИМЕНЕНИЕ РДТТ ДЛЯ КОСМИЧЕСКИХ ИССЛЕДОВАНИЙ
- 11.2. УСКОРИТЕЛИ РАКЕТЫ-НОСИТЕЛЯ «ТИТАН»
- 11.3. ТВЕРДОТОПЛИВНЫЙ УСКОРИТЕЛЬ ВКС «СПЕЙС ШАТТЛ»
- 11.4. ТВЕРДОТОПЛИВНЫЕ УСКОРИТЕЛИ РАКЕТЫ-НОСИТЕЛЯ «АРИАН»
- 11.5. ТВЕРДОТОПЛИВНЫЕ ДВИГАТЕЛИ ДЛЯ ПОСЛЕДНИХ СТУПЕНЕЙ РАКЕТ-НОСИТЕЛЕЙ
- 12. ПРИМЕНЕНИЕ ЖРД ДЛЯ КОСМИЧЕСКИХ ИССЛЕДОВАНИЙ
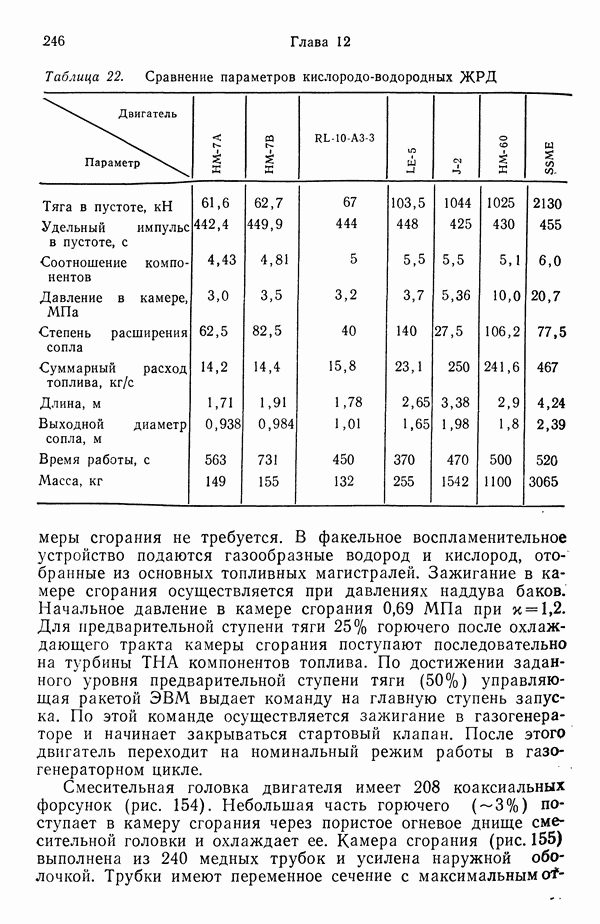
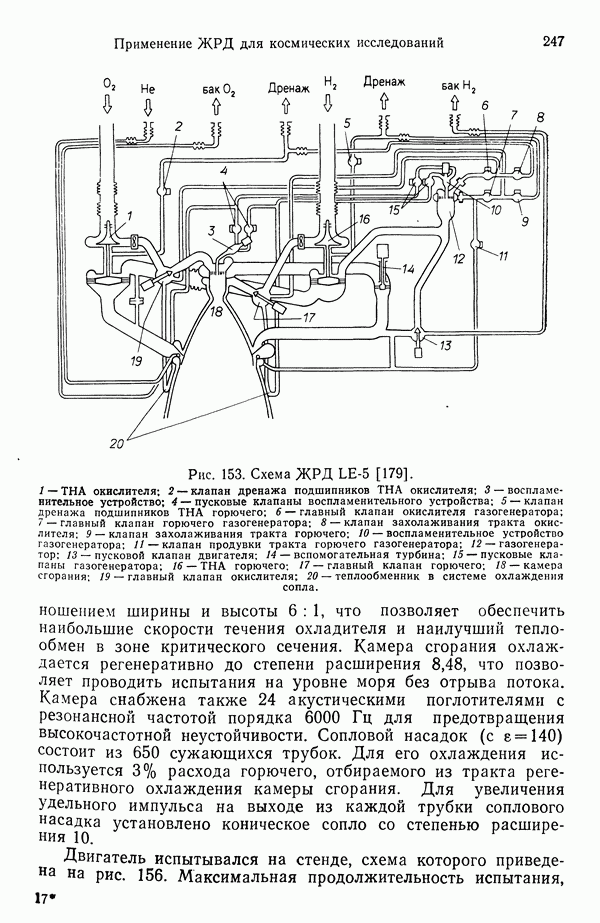
- 12.2. КИСЛОРОДО-ВОДОРОДНЫЕ ЖРД RL-10, НМ-7 И LE-5
- 12.3. МАРШЕВЫЙ ДВИГАТЕЛЬ ВКС «СПЕЙС ШАТТЛ»
- 12.4. СРАВНЕНИЕ РАЗЛИЧНЫХ КИСЛОРОДО-ВОДОРОДНЫЙ ЖРД
- 12.5. ЖРД ДЛЯ МАНЕВРИРОВАНИЯ И ИЗМЕНЕНИЯ ОРБИТЫ
- 12.6. ВСПОМОГАТЕЛЬНЫЕ ДВИГАТЕЛЬНЫЕ УСТАНОВКИ С ЖРД
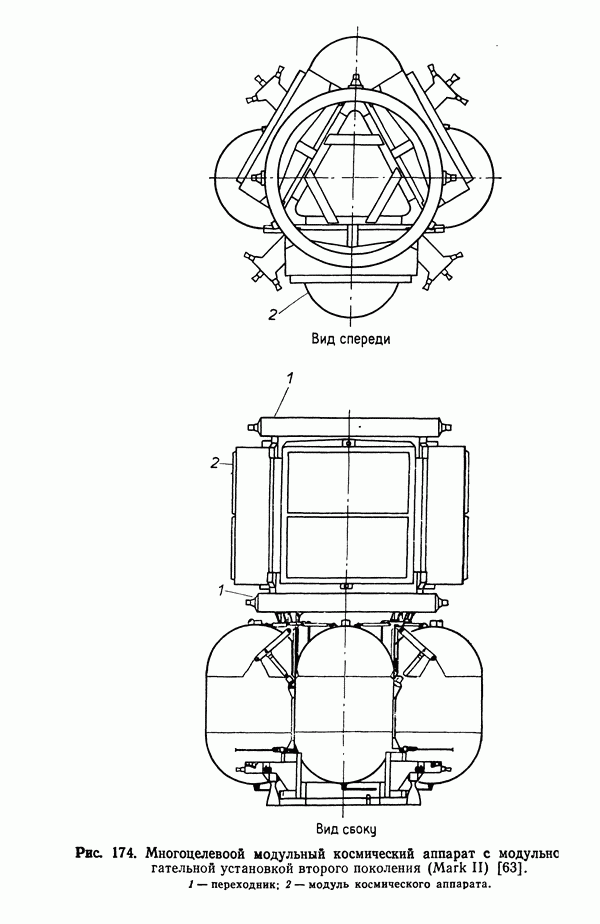
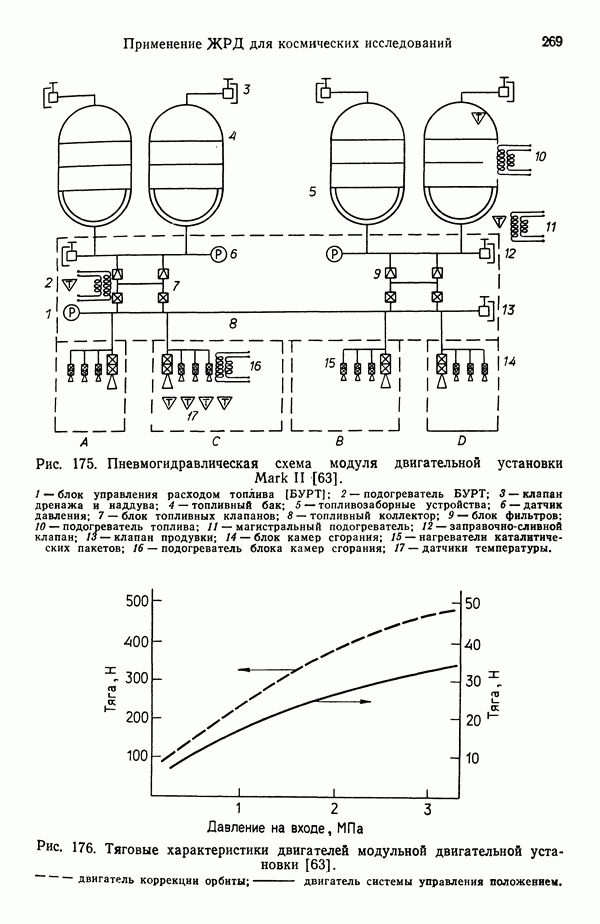
- 12.6.2. МОДУЛЬНАЯ ДВИГАТЕЛЬНАЯ УСТАНОВКА ВТОРОГО ПОКОЛЕНИЯ
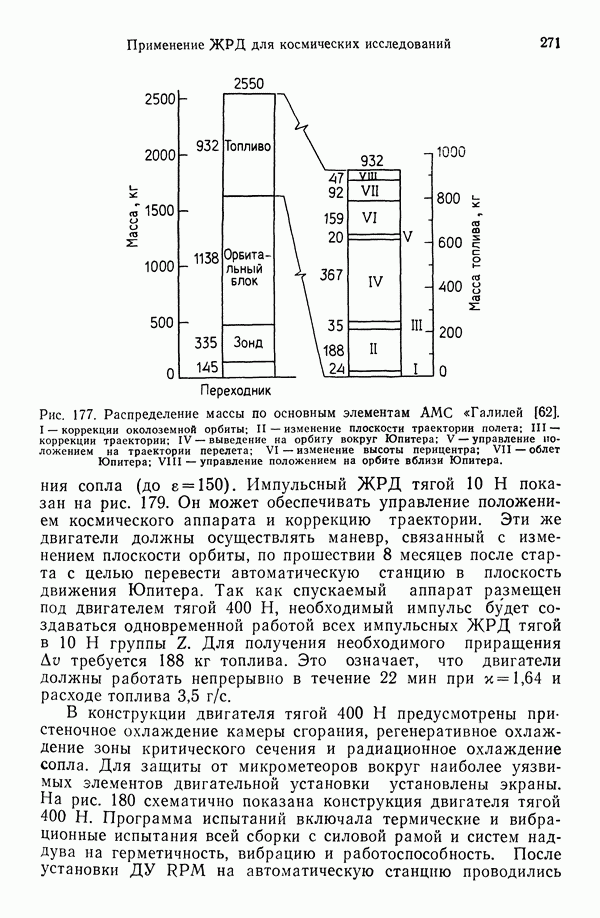
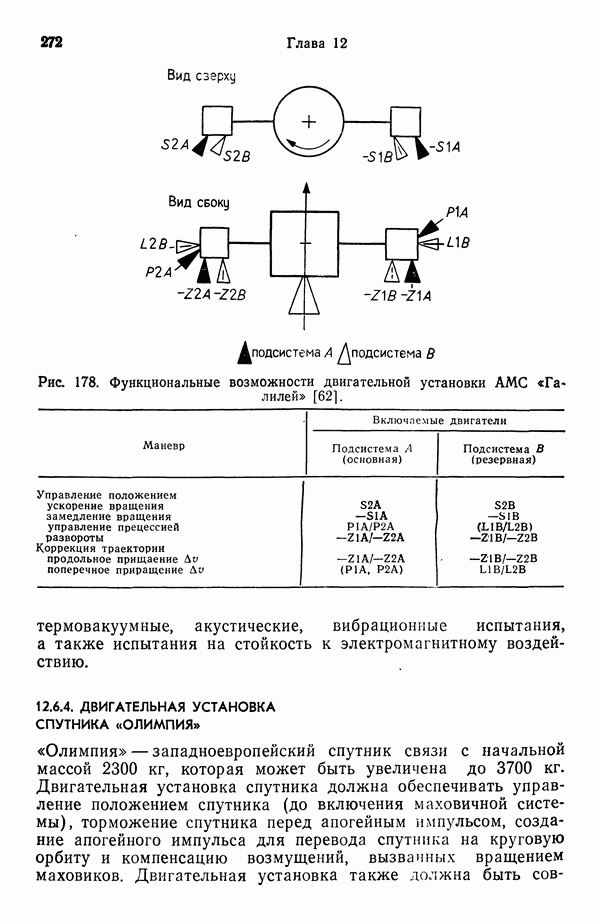
- 12.6.3. ДВУХКОМПОНЕНТНАЯ ДВИГАТЕЛЬНАЯ УСТАНОВКА АВТОМАТИЧЕСКОЙ МЕЖПЛАНЕТНОЙ СТАНЦИИ «ГАЛИЛЕЙ»
- 12.6.4. ДВИГАТЕЛЬНАЯ УСТАНОВКА СПУТНИКА «ОЛИМПИЯ»
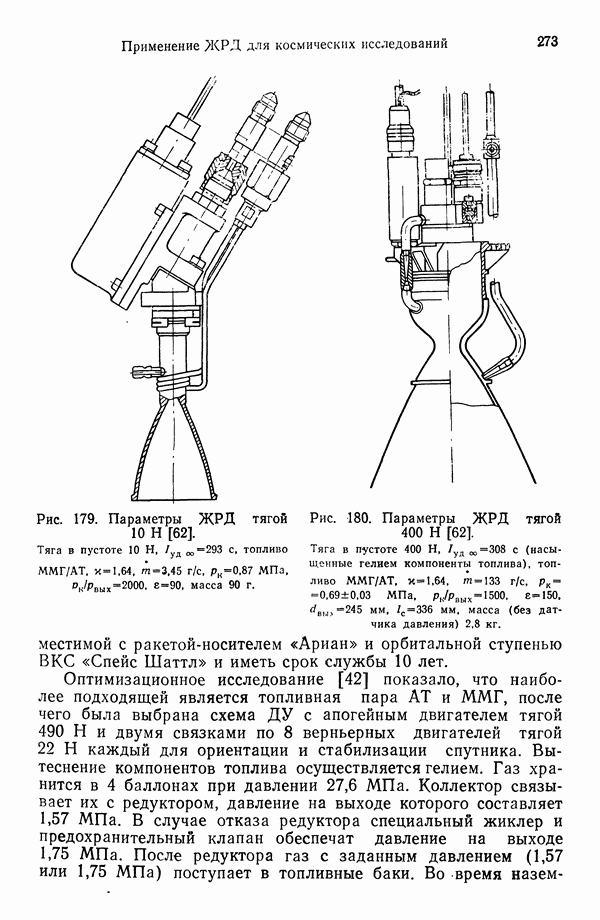
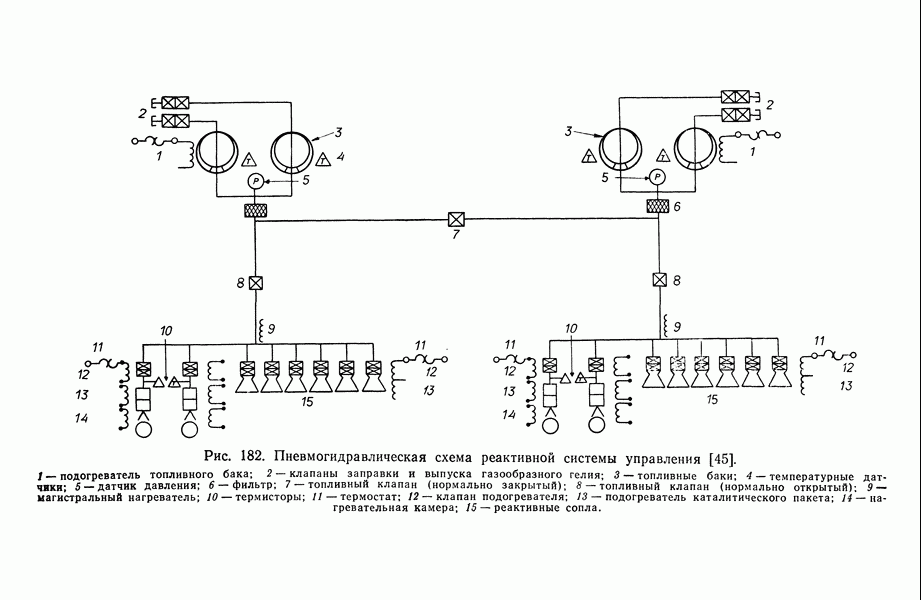
- 12.6.5. СИСТЕМА РЕАКТИВНОГО УПРАВЛЕНИЯ С ИМПУЛЬСНЫМИ ОДНОКОМПОНЕНТНЫМИ ЖРД
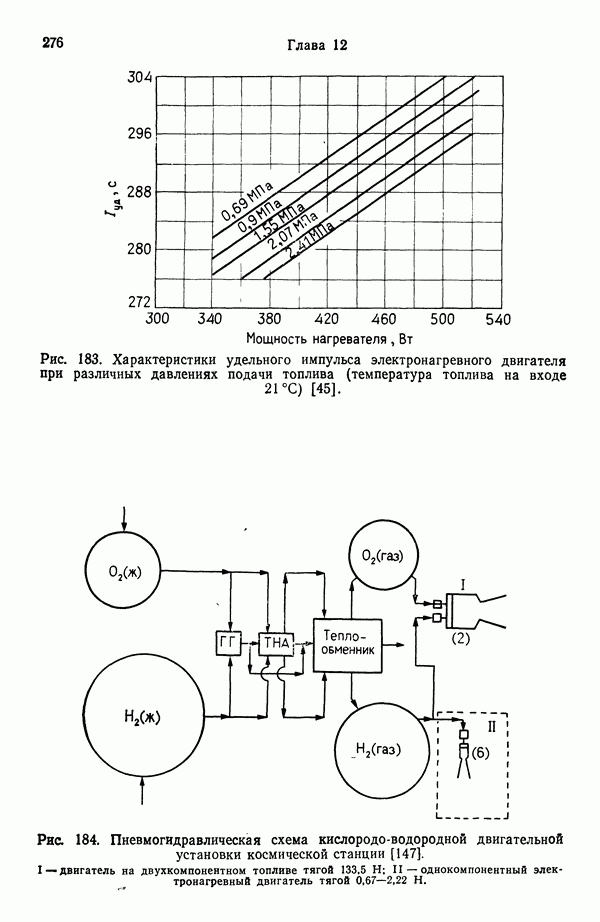
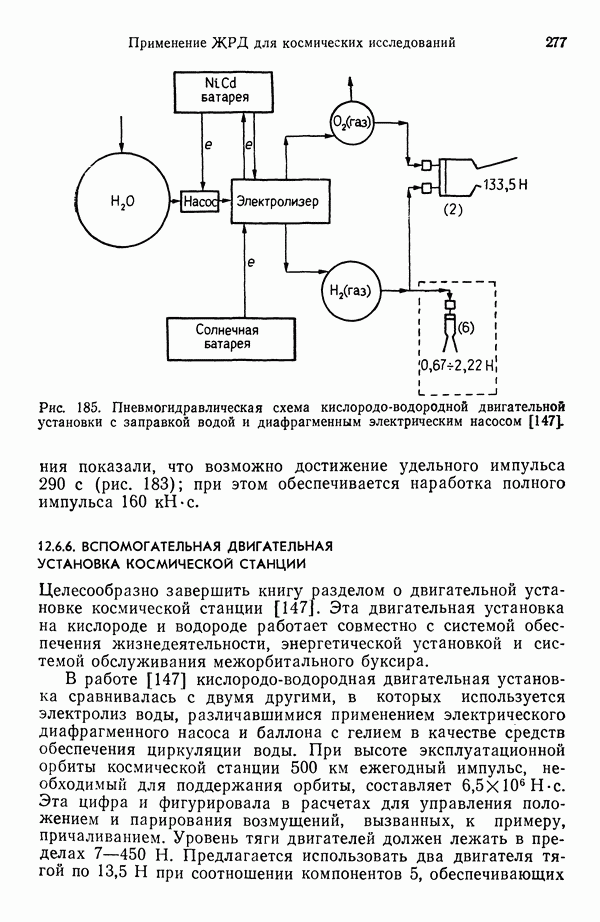
- 12.6.6. ВСПОМОГАТЕЛЬНАЯ ДВИГАТЕЛЬНАЯ УСТАНОВКА КОСМИЧЕСКОЙ СТАНЦИИ