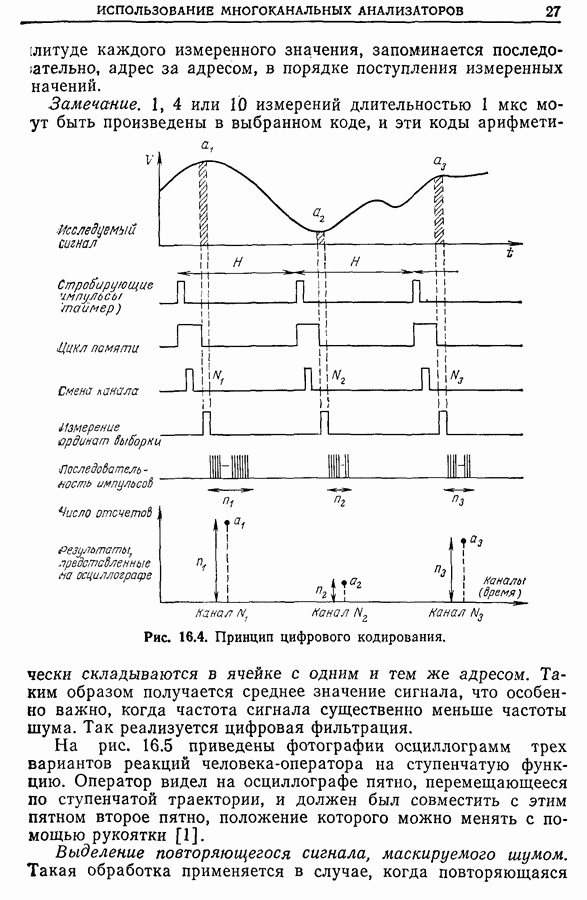
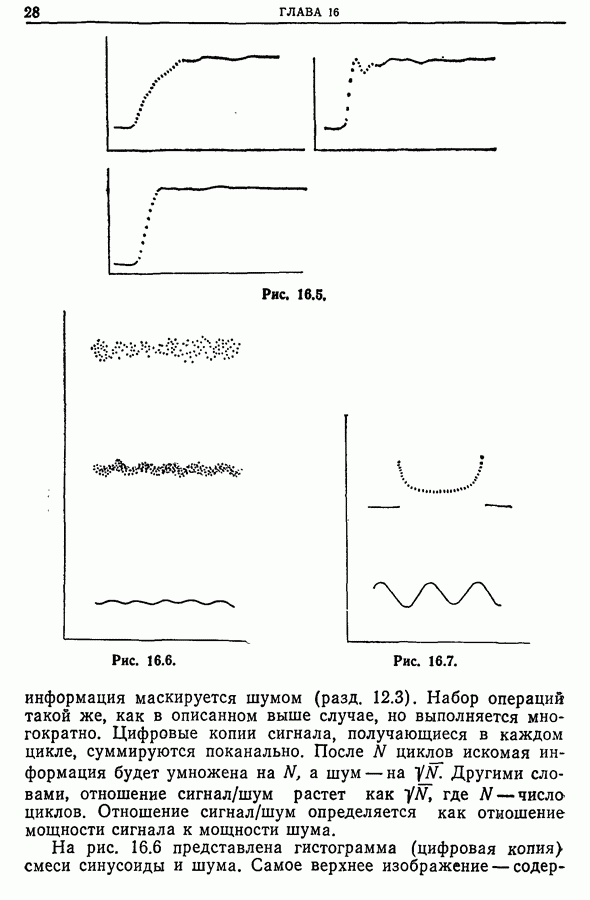
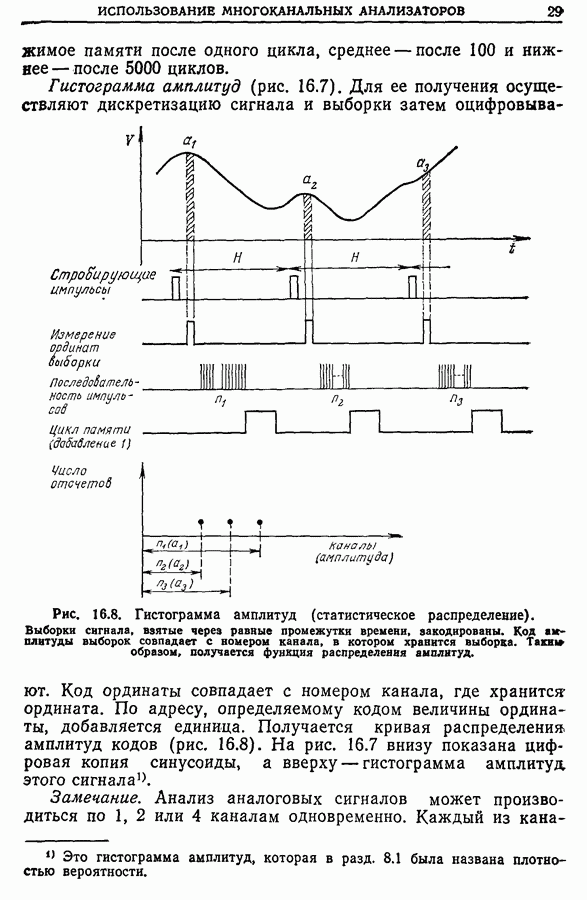
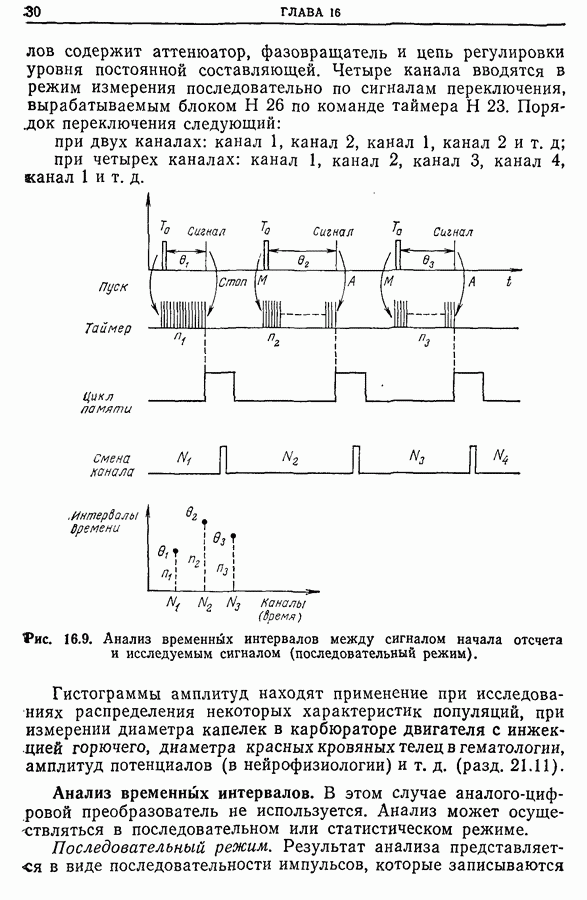
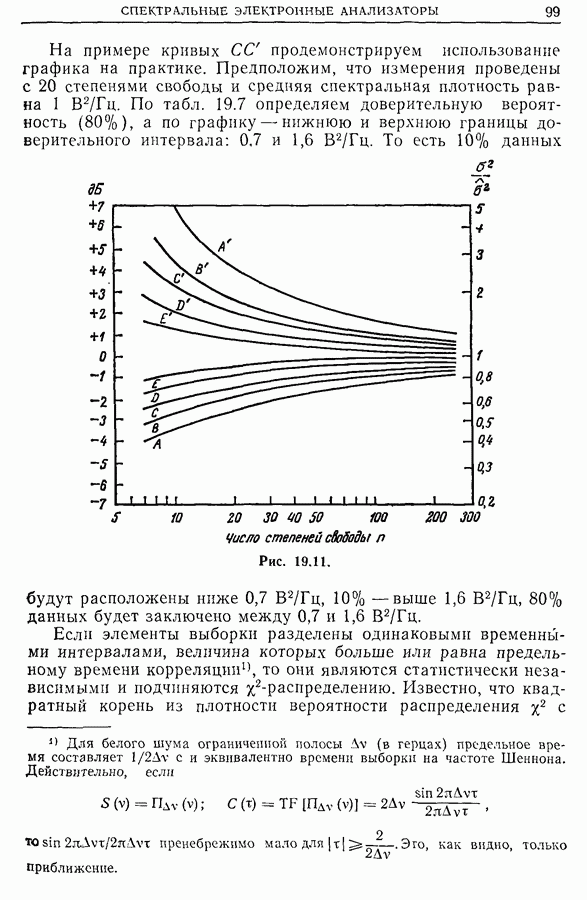
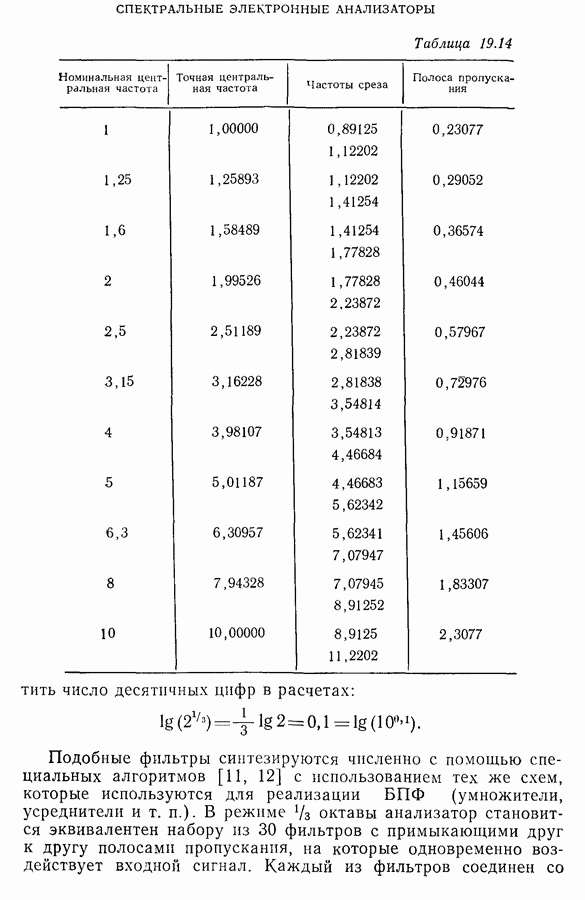
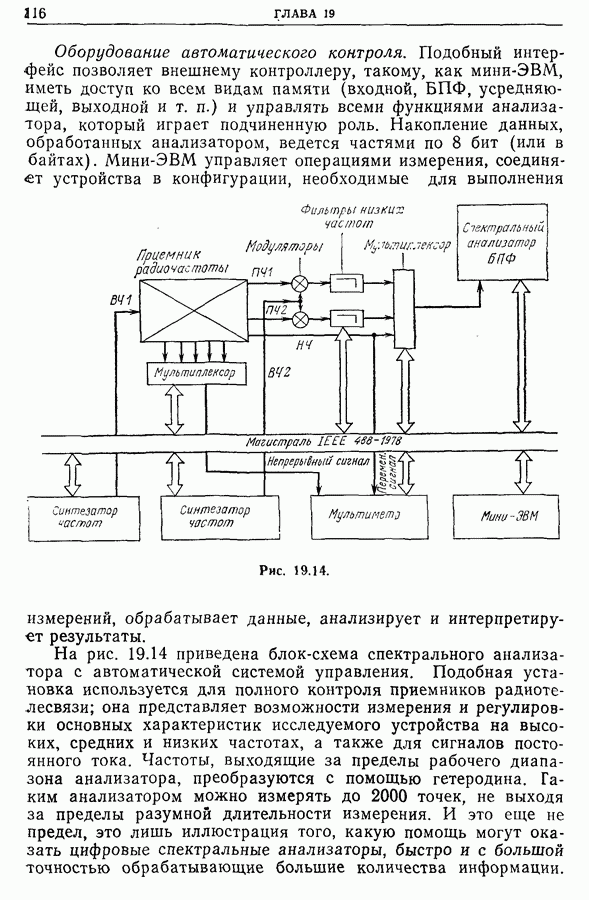
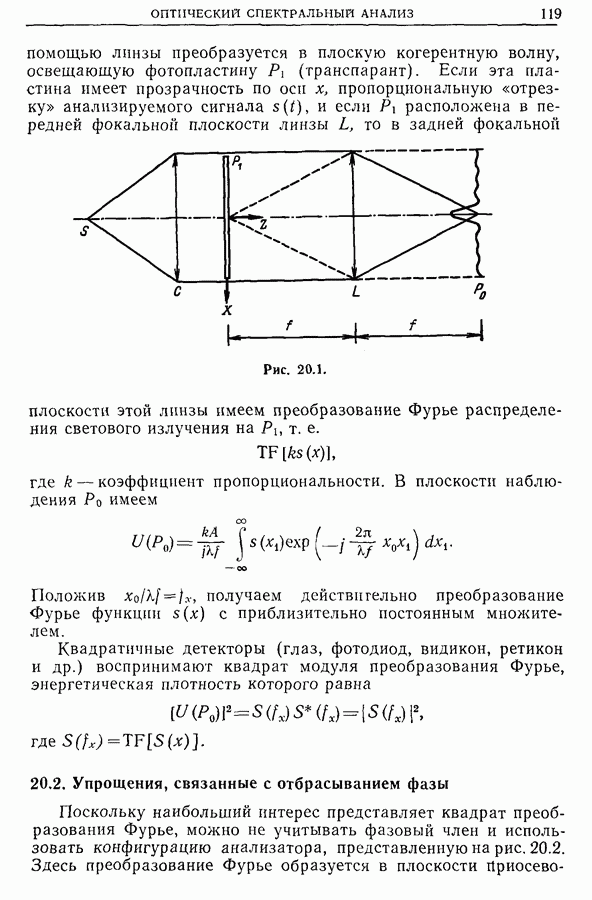
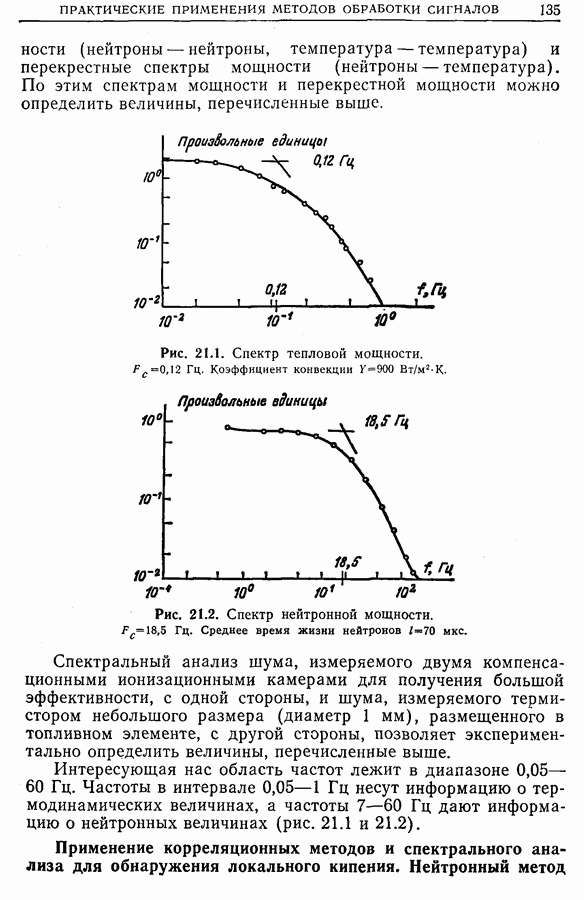
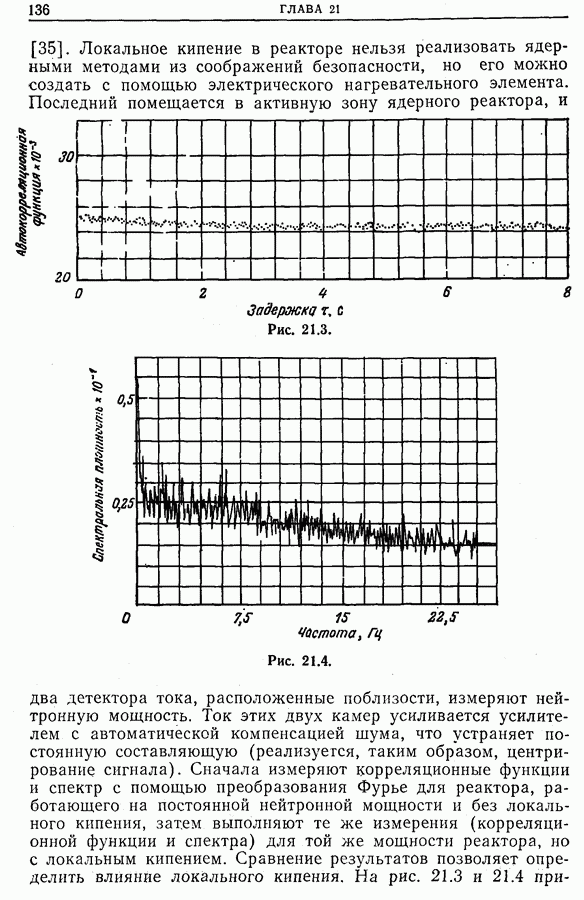
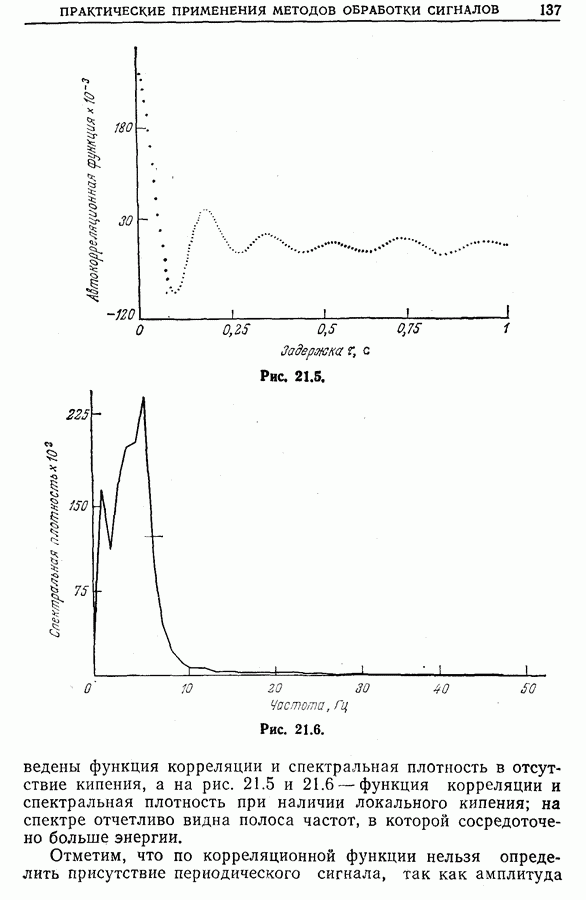
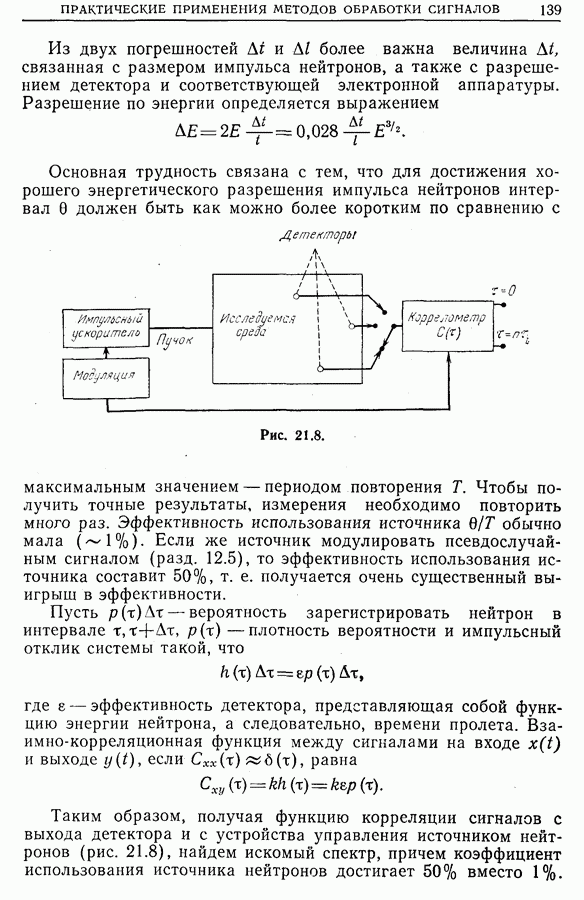
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
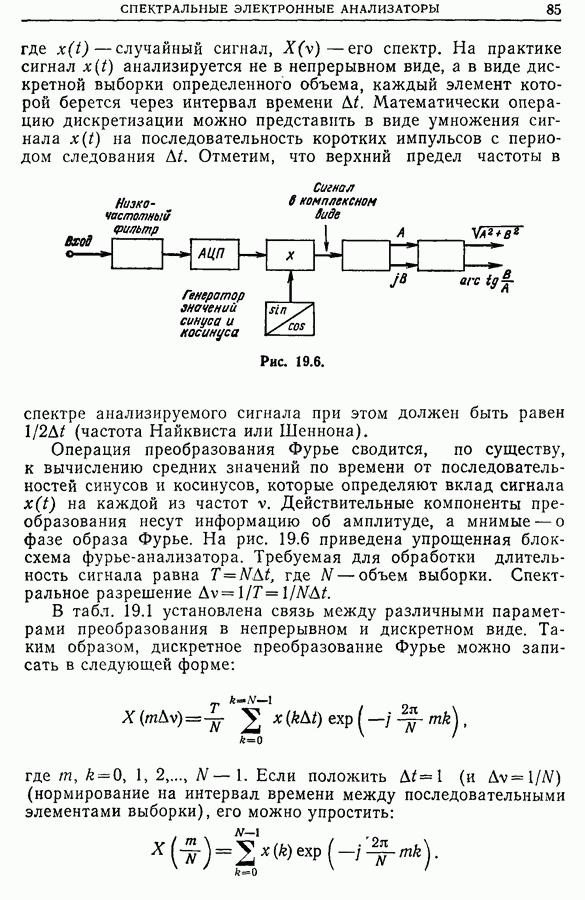
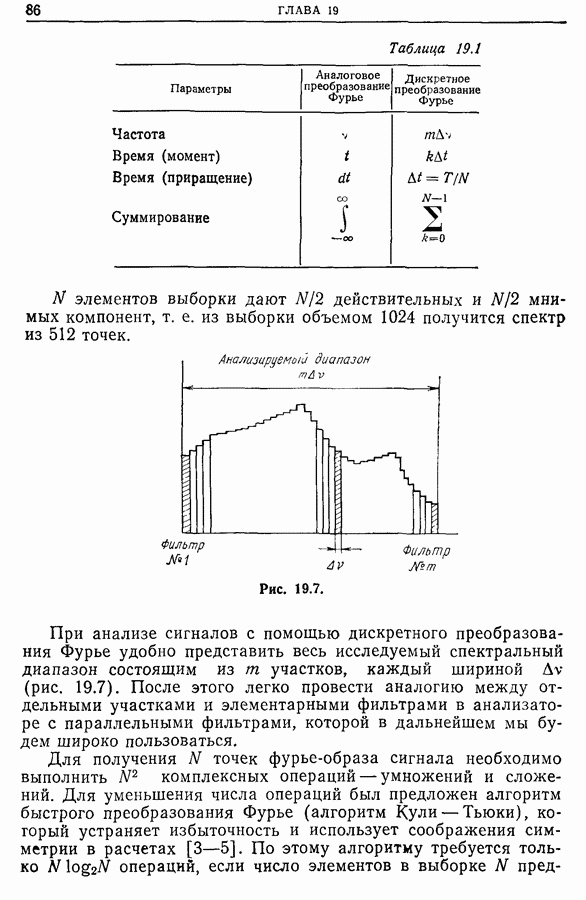
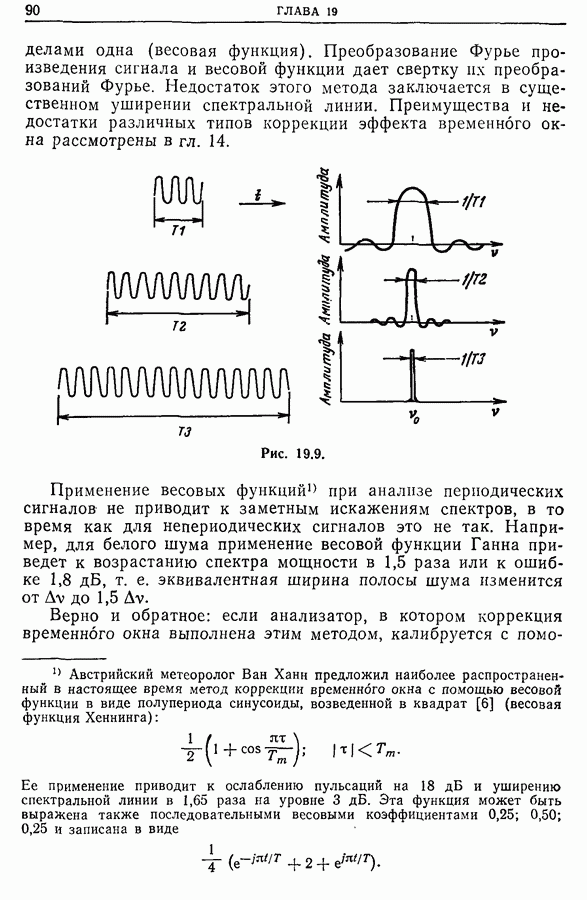
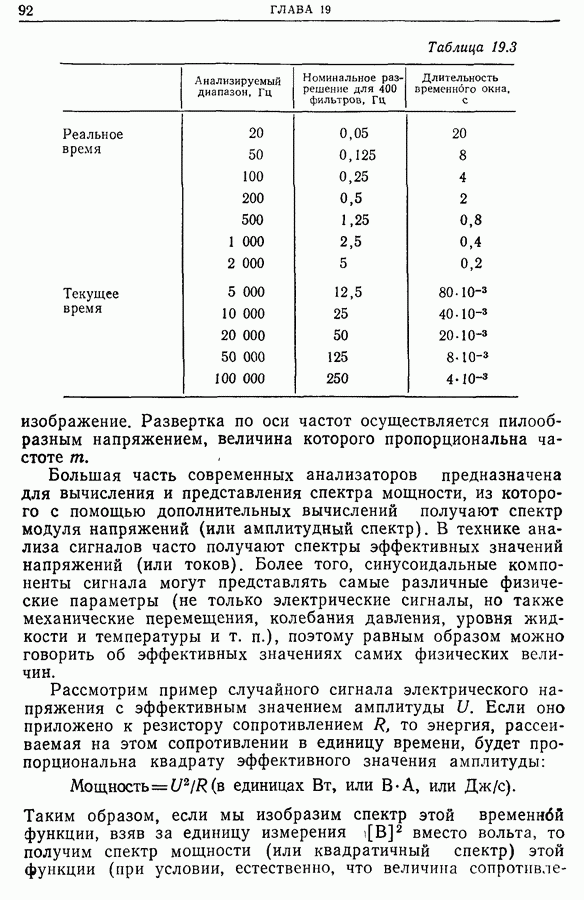
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Глава 17. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ
17.1. Оптимальная фильтрация
Пусть  — известный импульсный сигнал конечной длительности Т. Предположим, что на
— известный импульсный сигнал конечной длительности Т. Предположим, что на  наложен шум
наложен шум  который считается не зависящим от
который считается не зависящим от  и стационарным
и стационарным  порядка. Представим сигнал
порядка. Представим сигнал  в виде
в виде

Часто встречающаяся проблема состоит в следующем: определить с помощью линейного фильтра (т. е. посредством временного разложения или частотного фильтра) тот момент, когда появляется  Эта задача такая же, как задача обнаружения сигнала на фоне шума. Критерием, которым пользуются при выборе фильтра, является отношение сигнала к максимальному шуму.
Эта задача такая же, как задача обнаружения сигнала на фоне шума. Критерием, которым пользуются при выборе фильтра, является отношение сигнала к максимальному шуму.
Мы предположим (для упрощения последующих вычислений), что сигнал  появляется в момент
появляется в момент  и длится от 0 до Т; так как шум считается стационарным, такое предположение относительно момента появления сигнала не может повлиять на результаты. Требуется отыскать фильтр, обеспечивающий в момент Т максимум отношения сигнал/шум. Это отношение определяется как отношение энергии сигнала к энергии шума на интервале длительностью Т.
и длится от 0 до Т; так как шум считается стационарным, такое предположение относительно момента появления сигнала не может повлиять на результаты. Требуется отыскать фильтр, обеспечивающий в момент Т максимум отношения сигнал/шум. Это отношение определяется как отношение энергии сигнала к энергии шума на интервале длительностью Т.
Пусть  — импульсная функция отклика фильтра; если на вход подан сигнал
— импульсная функция отклика фильтра; если на вход подан сигнал  то на выходе этого фильтра в момент Т имеем
то на выходе этого фильтра в момент Т имеем

На выходе фильтра при воздействии шума 

Оценим квадрат модуля 

Оценка представляет собой мощность сигнала  в момент
в момент  . Квадрат модуля
. Квадрат модуля  равен
равен 

и средняя мощность шума в момент 

Отношение сигнал/шум в момент Т определяется тогда выражением

Это отношение остается неизменным, если вместо импульсного отклика  брать
брать  Следовательно, можно ввести нормировку в виде условия
Следовательно, можно ввести нормировку в виде условия  т. е.
т. е.

Необходимо найти  при котором
при котором  достигает максимума
достигает максимума 
Используя выражение (17.5), найдем, что величина

отрицательна или равна нулю; она равна нулю для  Вычислим
Вычислим  с помощью метода вариации.
с помощью метода вариации.
Приравняем нулю первую вариацию К по 

Что дает

Принимая во внимание условие (17.6), запишем

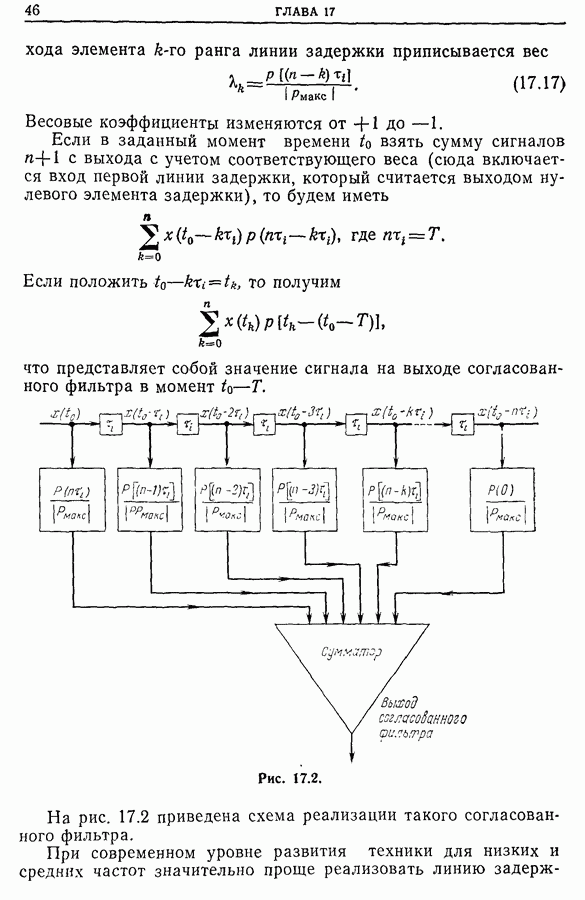
где

Последнее выражение представляет собой уравнение для оптимального фильтра.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
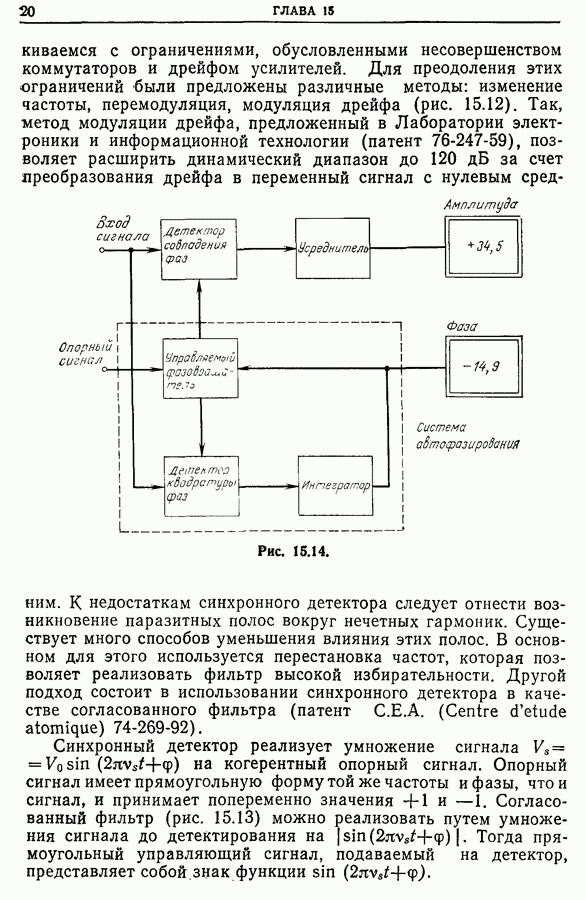
- Глава 15. СИНХРОННОЕ ДЕТЕКТИРОВАНИЕ
- 15.2. Схема метода
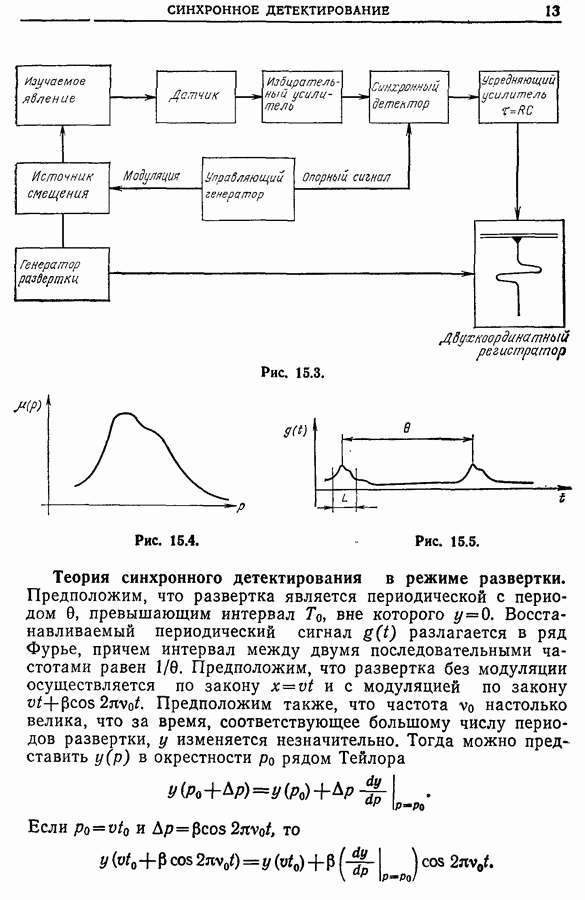
- 15.3. Теория синхронного детектирования
- 15.4. Синхронное детектирование в режиме развертки
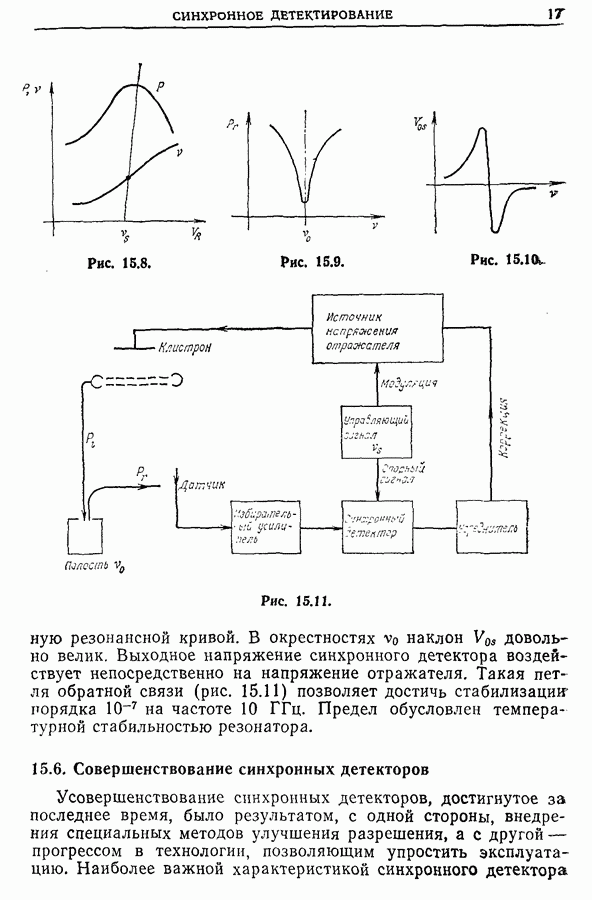
- 15.5. Примеры применения синхронных детекторов
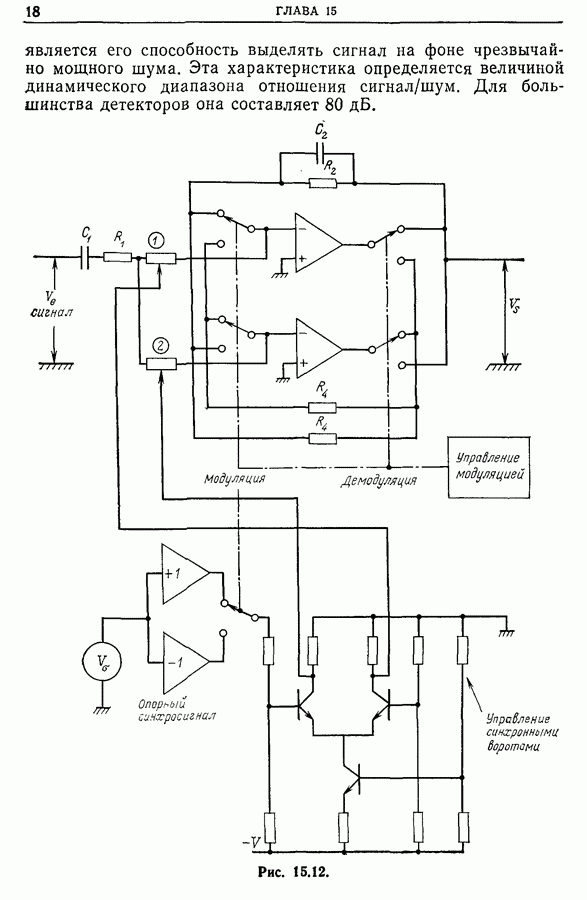
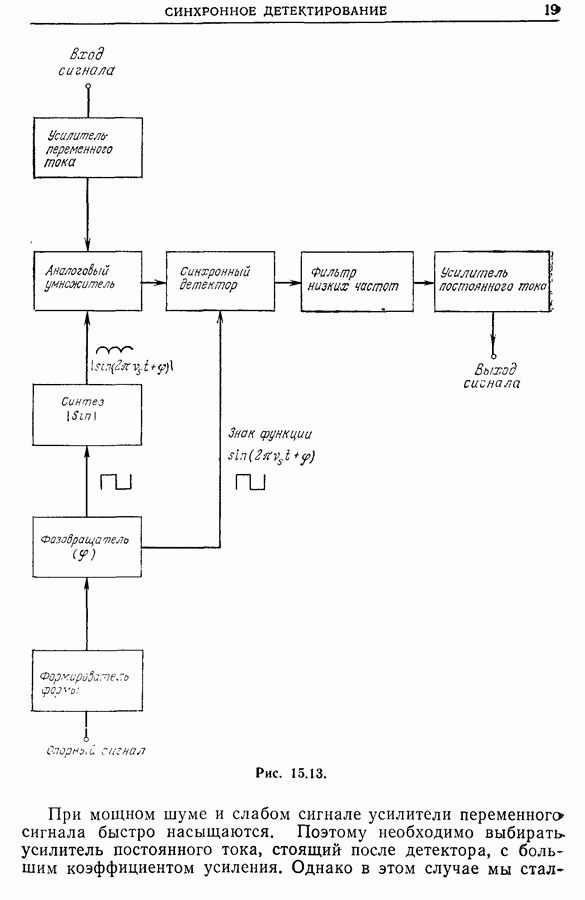
- 15.6. Совершенствование синхронных детекторов
- Глава 16. ИСПОЛЬЗОВАНИЕ МНОГОКАНАЛЬНЫХ АНАЛИЗАТОРОВ ПРИ СТАТИЧЕСКОЙ ОБРАБОТКЕ ИЗМЕРЕНИЙ
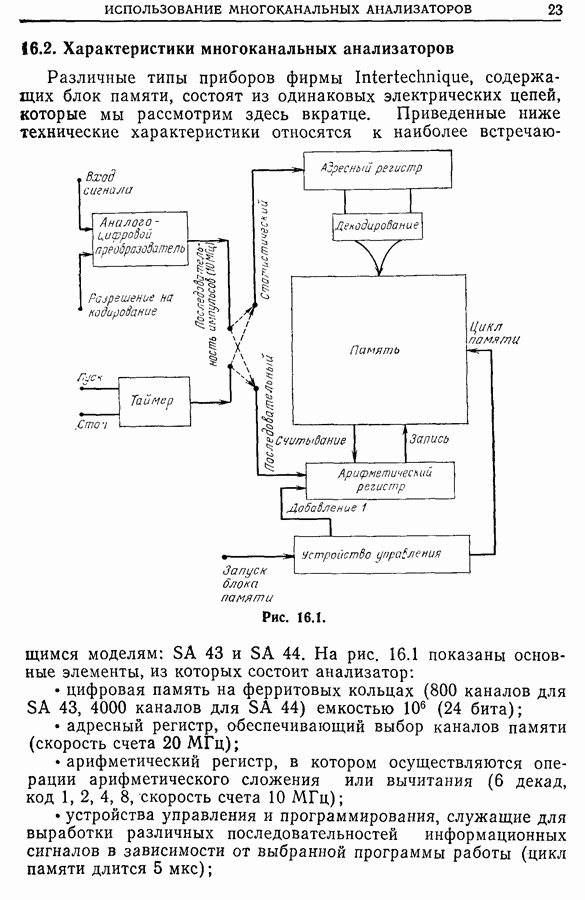
- 16.2. Характеристики многоканальных анализаторов
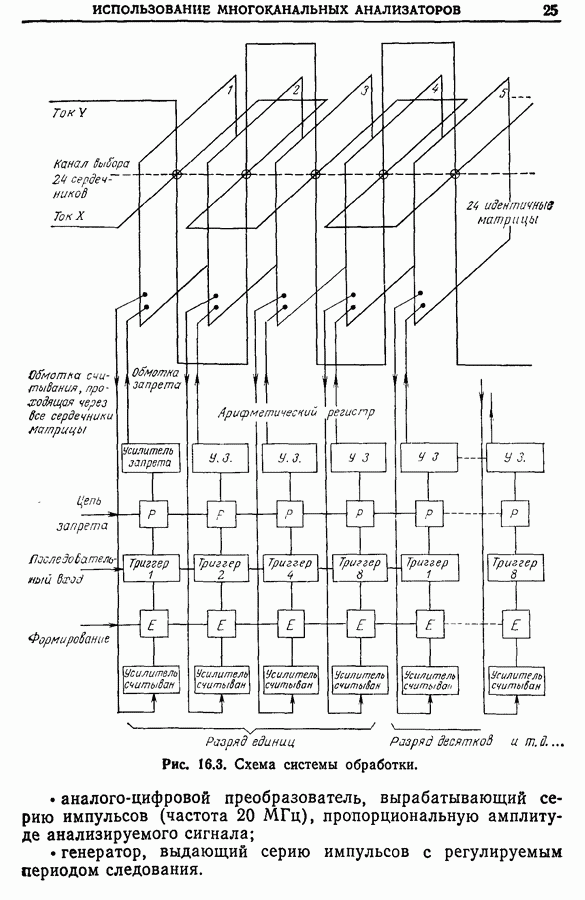
- 16.3. Схема системы обработки
- 16.4. Примеры применения
- Глава 17. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ
- 17.2. Частный случай белого шума. Согласованный фильтр
- 17.3. Согласованная фильтрация и корреляция Корреляция.
- 17.4. Реализация согласованных фильтров методом «взвешивания»
- 17.5. Рекурсивная согласованная фильтрация [7]
- 17.6. Применения метода согласованной фильтрации
- Глава 18. ОСНОВНЫЕ ТИПЫ ЭЛЕКТРОННЫХ КОРРЕЛОМЕТРОВ
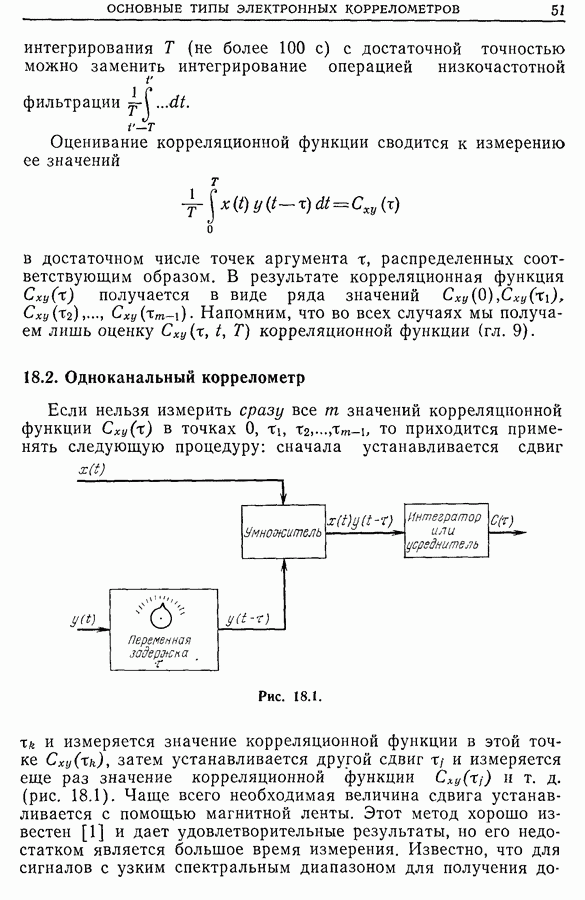
- 18.2. Одноканальный коррелометр
- 18.3. Автоматические коррелометры
- 18.4. Автоматические коррелометры на линии с исследуемым сигналом
- 18.5. Автоматические коррелометры реального времени (или мультикоррелометры)
- 18.6. Коррелометры на больших интегральных схемах
- 18.7. Коррелометры реального времени для высокочастотных сигналов
- 18.8 Развитие коррелометров
- 18.9. Приборы с зарядовой связью [11]
- Глава 19. СПЕКТРАЛЬНЫЕ ЭЛЕКТРОННЫЕ АНАЛИЗАТОРЫ
- 19.2. Спектральные анализаторы, основанные на методе непосредственного преобразования Фурье
- 19.3. Применения анализаторов на основе метода БПФ
- Глава 20. ОПТИЧЕСКИЙ СПЕКТРАЛЬНЫЙ АНАЛИЗ
- 20.2. Упрощения, связанные с отбрасыванием фазы
- 20.3. Эффект виньетирования
- 20.4. Двумерный анализ
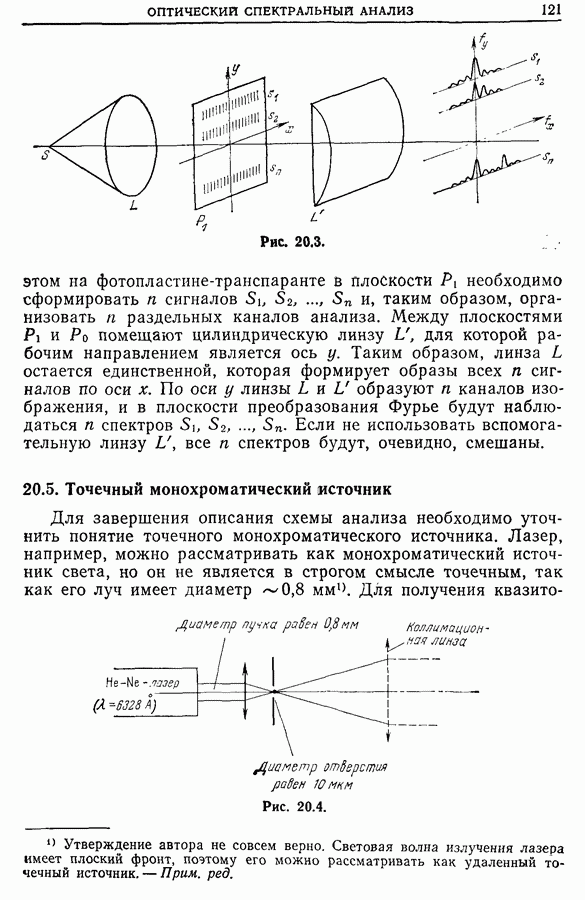
- 20.5. Точечный монохроматический источник
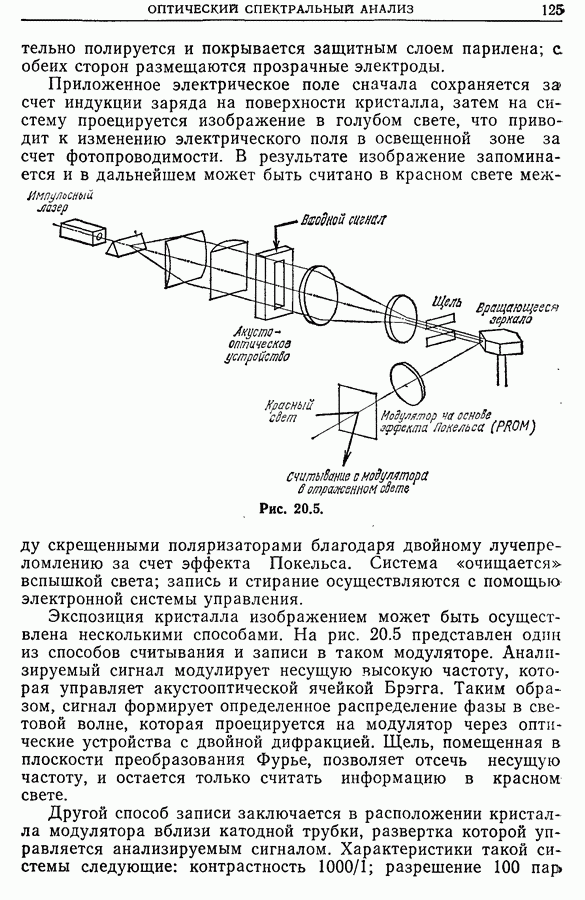
- 20.6. Электрооптическое преобразование сигнала
- 20.7. Устройства отображения на жидких кристаллах
- 20.8. Ограничения устройств отображения
- 20.9. Модулятор на основе эффекта Покельса (PROM)
- 20.10. Трубки Титус и Фототитус
- 20.11. Другие электрооптические кристаллы
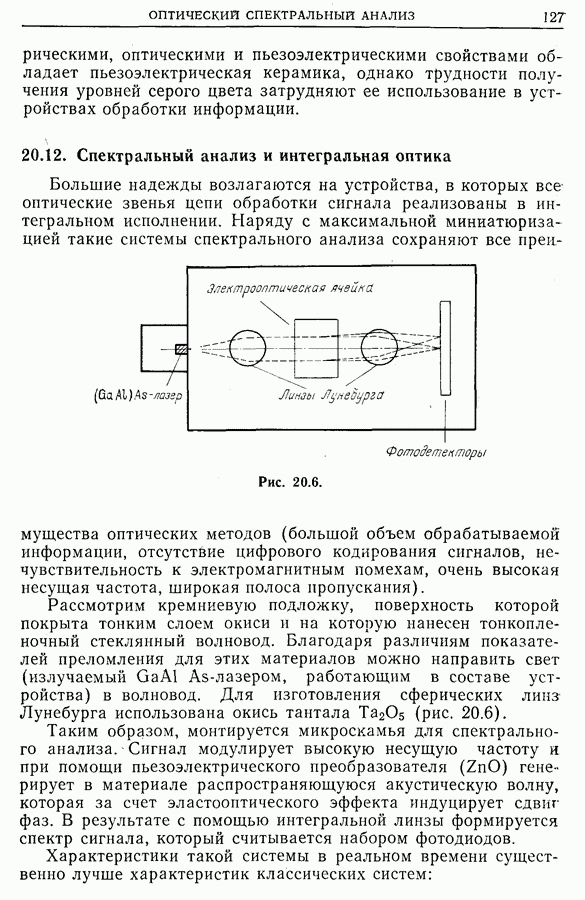
- 20.12. Спектральный анализ и интегральная оптика
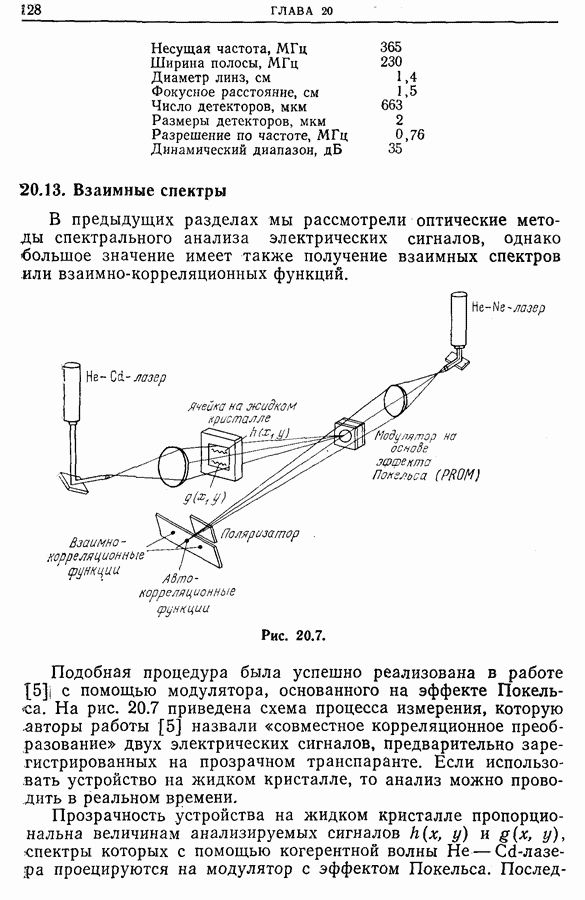
- 20.13. Взаимные спектры
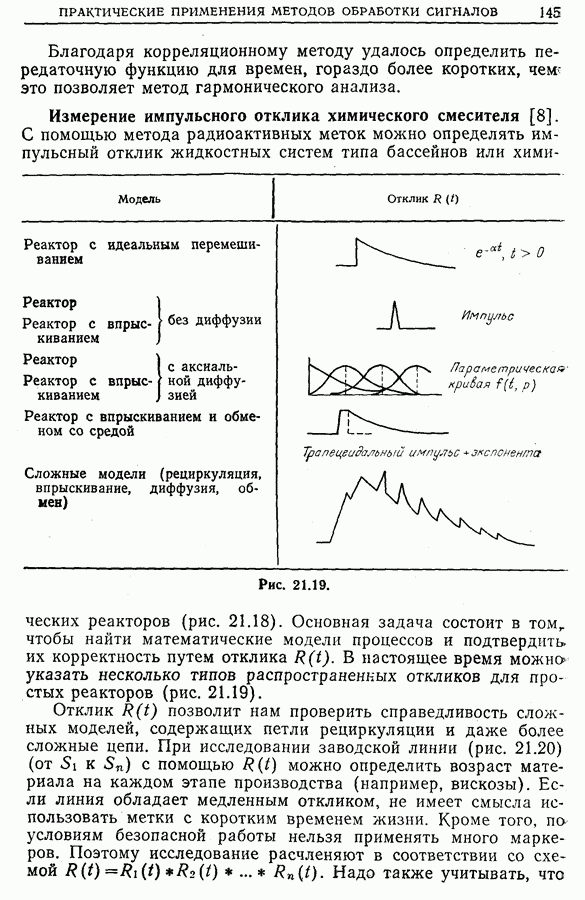
- Глава 21. НЕКОТОРЫЕ ПРАКТИЧЕСКИЕ ПРИМЕНЕНИЯ МЕТОДОВ ОБРАБОТКИ СИГНАЛОВ
- 21.2. Исследование ядерных сред
- 21.3. Ядерный магнитный резонанс (ЯМР) с возбуждением случайным сигналом
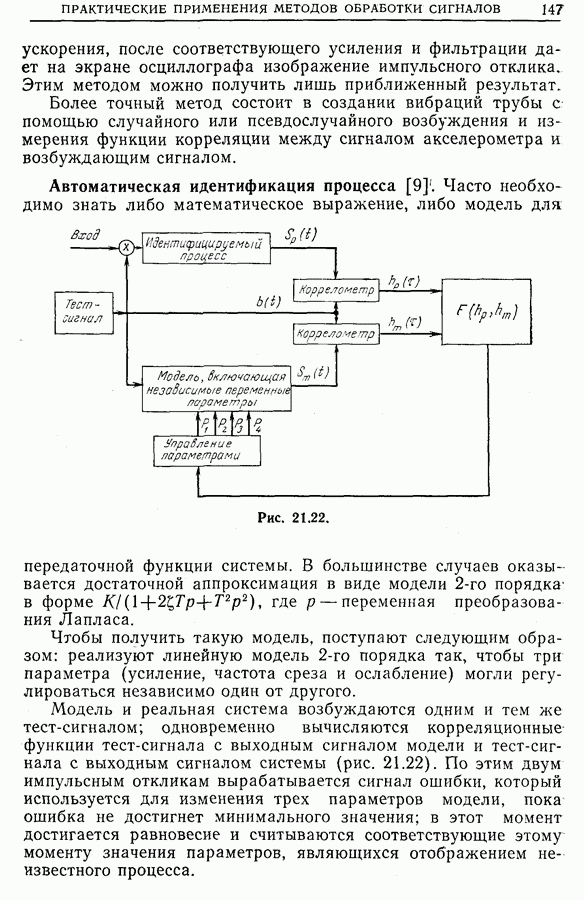
- 21.4. Идентификация процессов. Измерение импульсных откликов и передаточных функций
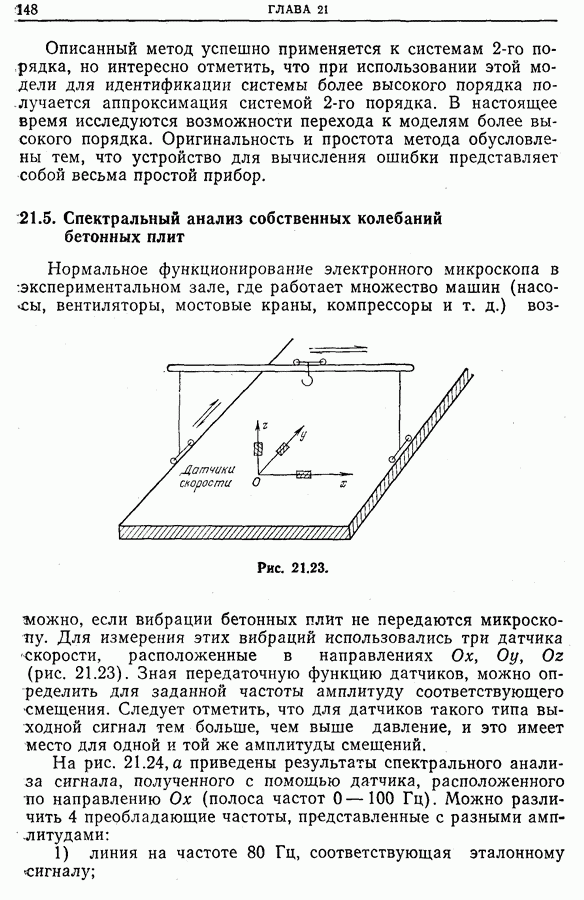
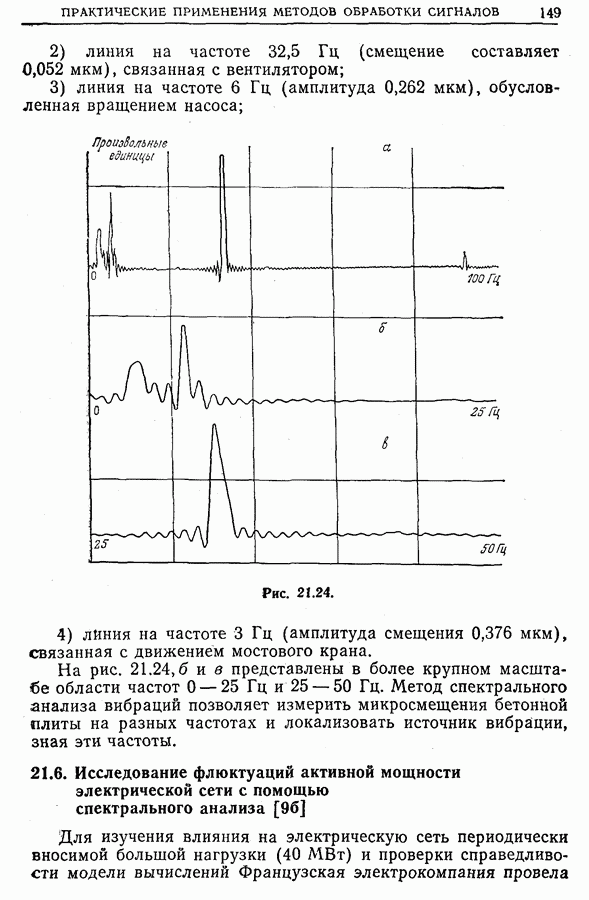
- 21.5. Спектральный анализ собственных колебаний бетонных плит
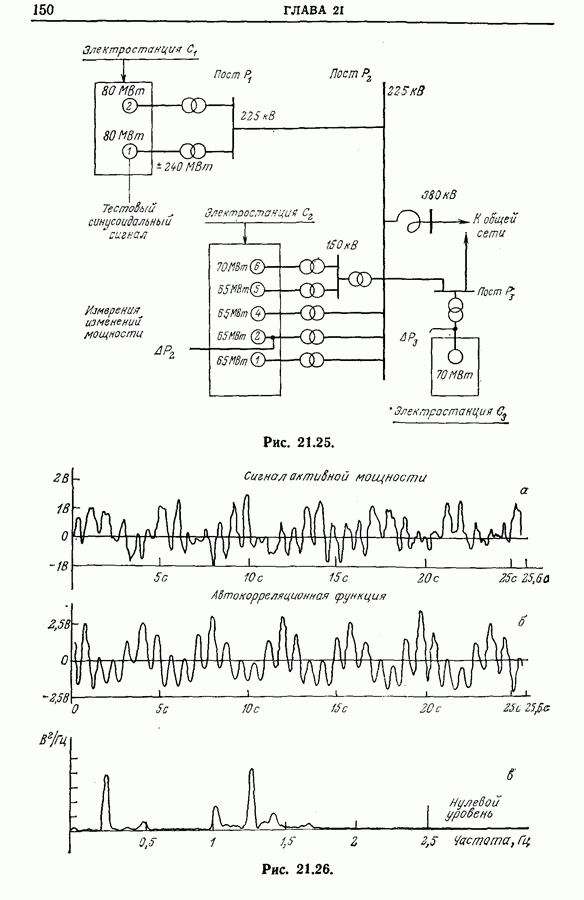
- 21.6. Исследование флюктуаций активной мощности электрической сети с помощью спектрального анализа
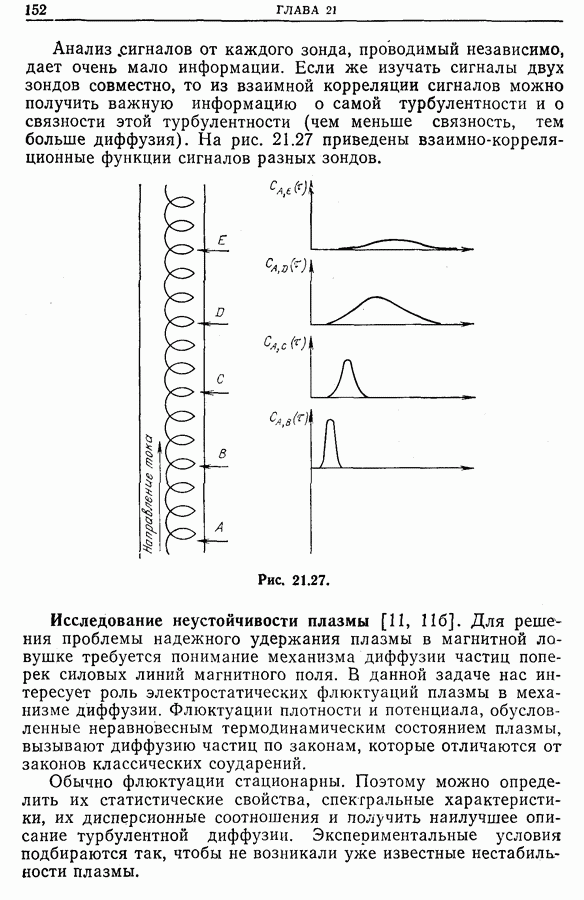
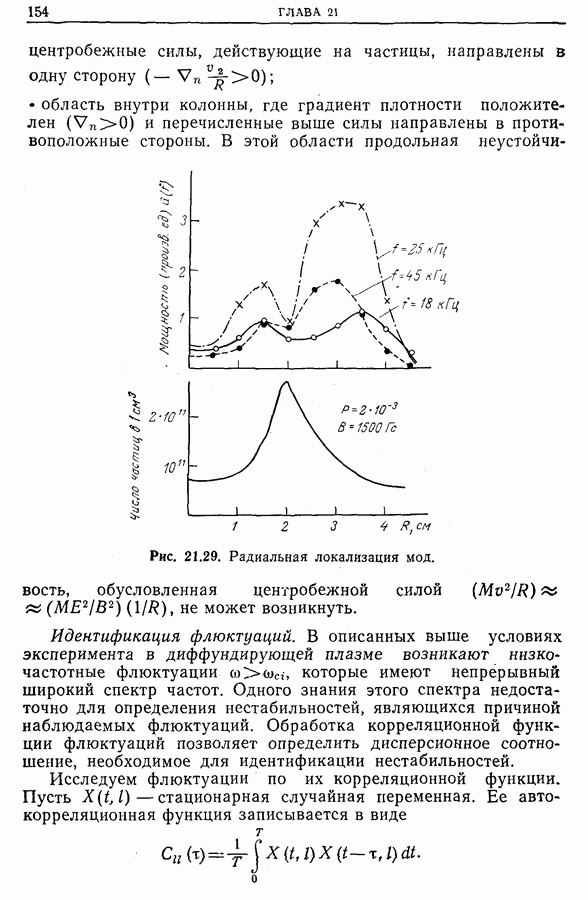
- 21.7. Изучение турбулентности
- 21.8. Применения в геофизике
- 21.9. Применения в астрофизике
- 21.10. Применения в астрономии и радиоастрономии
- 21.11. Применения в биологии и медицине
- 21.12. Применения в акустике
- 21.13. Исследование процессов намагничивания ферромагнетиков
- 21.14. Применения новых методов обработки сигналов
- 21.15. Заключение
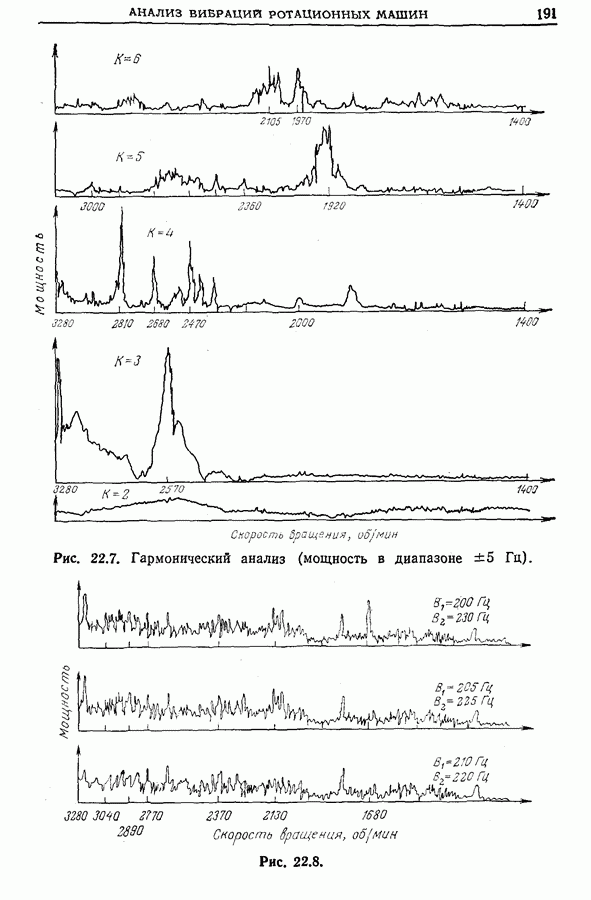
- Глава 22. ПРИМЕНЕНИЕ МЕТОДОВ ОБРАБОТКИ СИГНАЛОВ ДЛЯ АНАЛИЗА ВИБРАЦИЙ РОТАЦИОННЫХ МАШИНА
- 22.2. Анализ поведения системы «ротационная машина — конструкция»
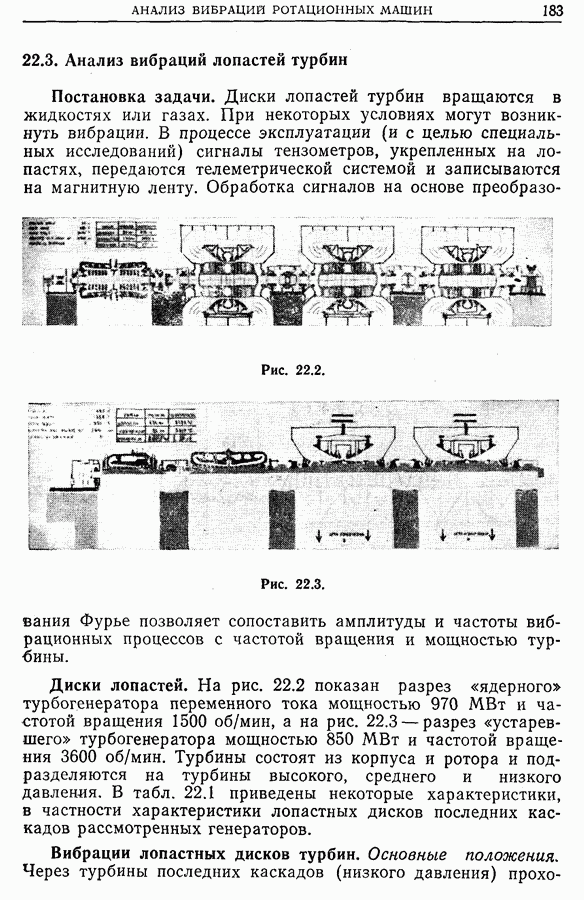
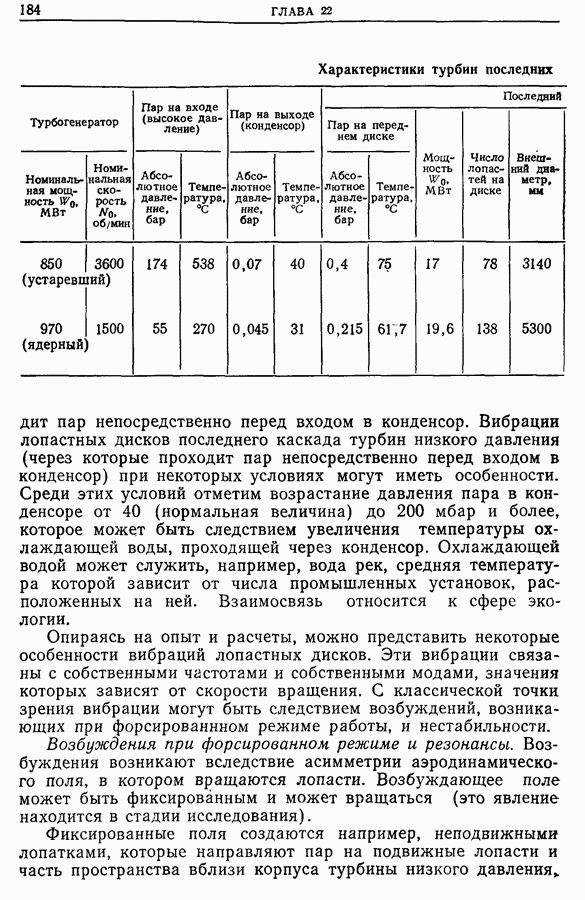
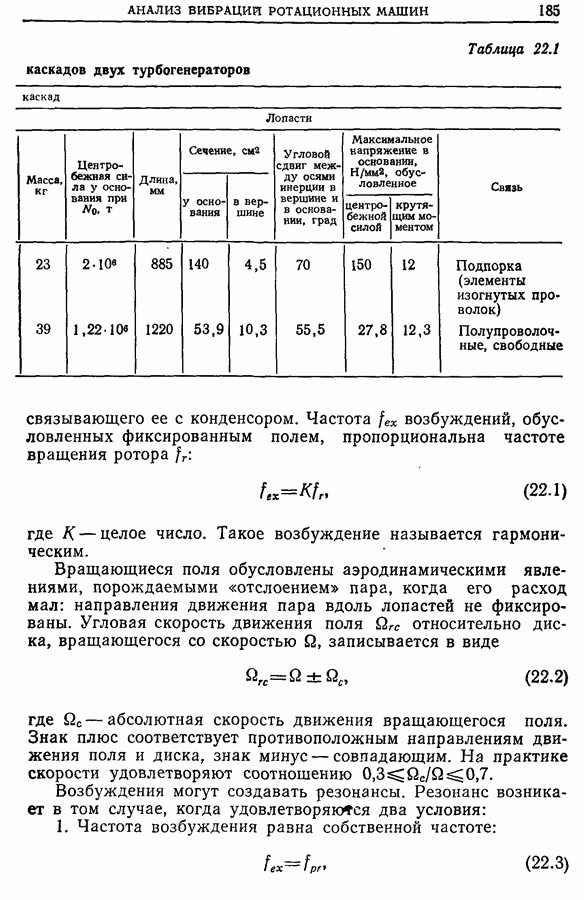
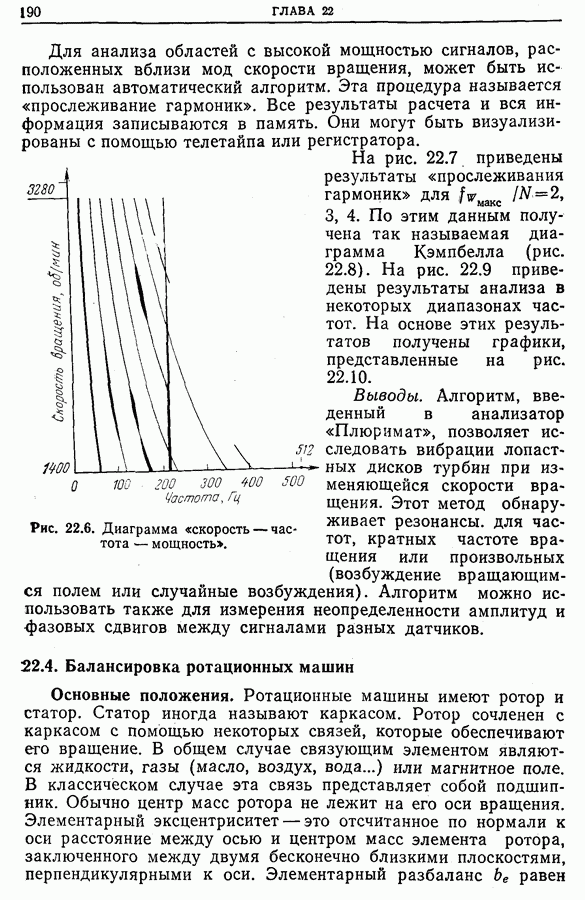
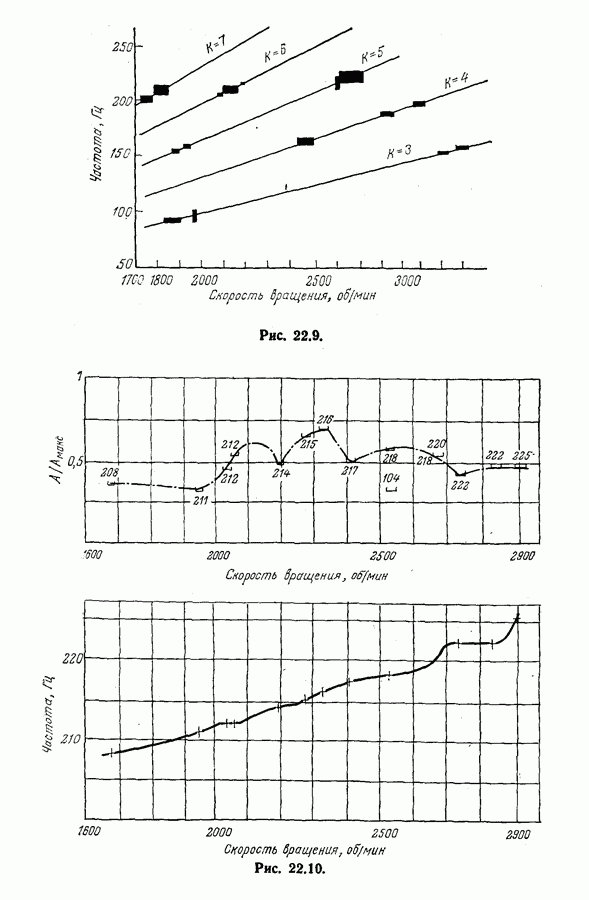
- 22.3. Анализ вибраций лопастей турбин
- 22.4. Балансировка ротационных машин
- Глава 23. ФУНКЦИЯ НЕОПРЕДЕЛЕННОСТИ
- 23.2. Временная корреляция. Временной сдвиг
- 23.3. Частотная корреляция. Частотный сдвиг
- 23.4. Временной и частотный сдвиги. Функция неопределенности
- 23.5. Функция неопределенности Вудворда
- 23.6. Взаимная функция неопределенности
- 23.7. Некоторые свойства функции неопределенности
- 23.8. Представление функций неопределенности
- 23.9. Примеры функций неопределенности
- 23.10. Применение функции неопределенности
- 23.11. Применение функций неопределенности для описания линейных неоднородных во времени систем. Обобщение понятия передаточной функции. Функция диффузии (функция рассеивания)
- 23.12. Генерация тестового сигнала
- 23.13. Прибор для измерения функции неопределенности в режиме реального времени
- Глава 24. ПОНЯТИЕ МГНОВЕННОГО СПЕКТРА ИЛИ ЧАСТОТНО-ВРЕМЕННОГО ПРЕДСТАВЛЕНИЯ В АНАЛИЗЕ И СИНТЕЗЕ СИГНАЛОВ
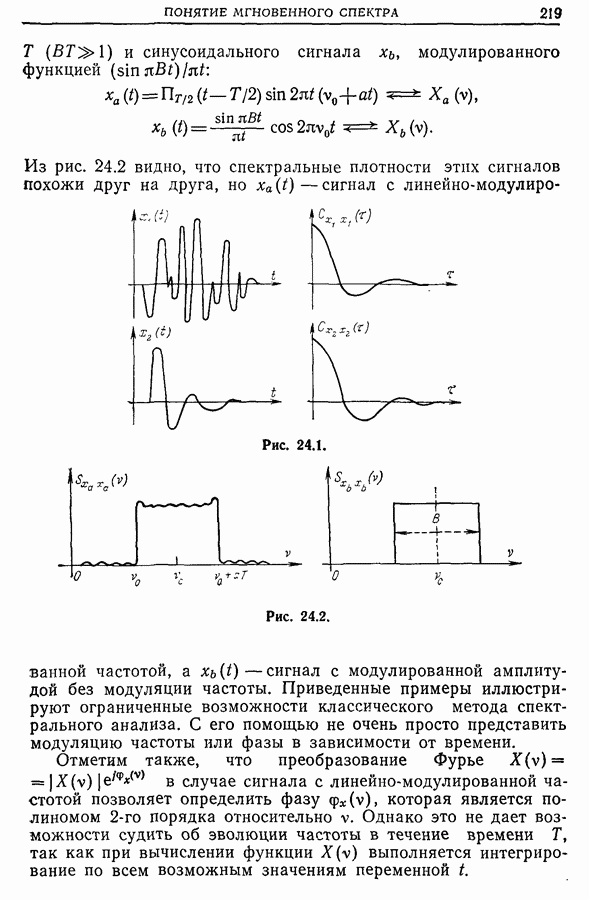
- 24.2. Примеры спектрального анализа модулированных и немодулированных сигналов
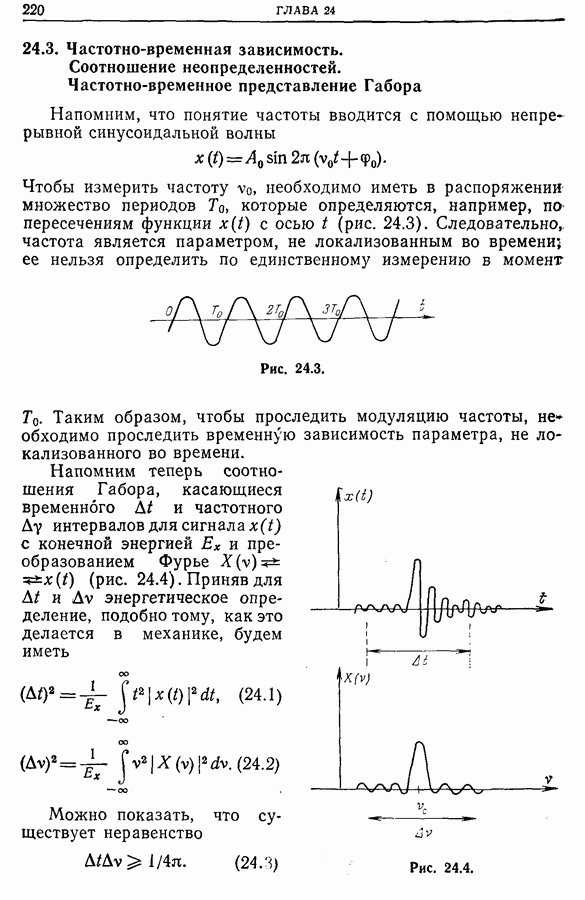
- 24.3. Частотно-временная зависимость. Соотношение неопределенностей. Частотно-временное представление Габора
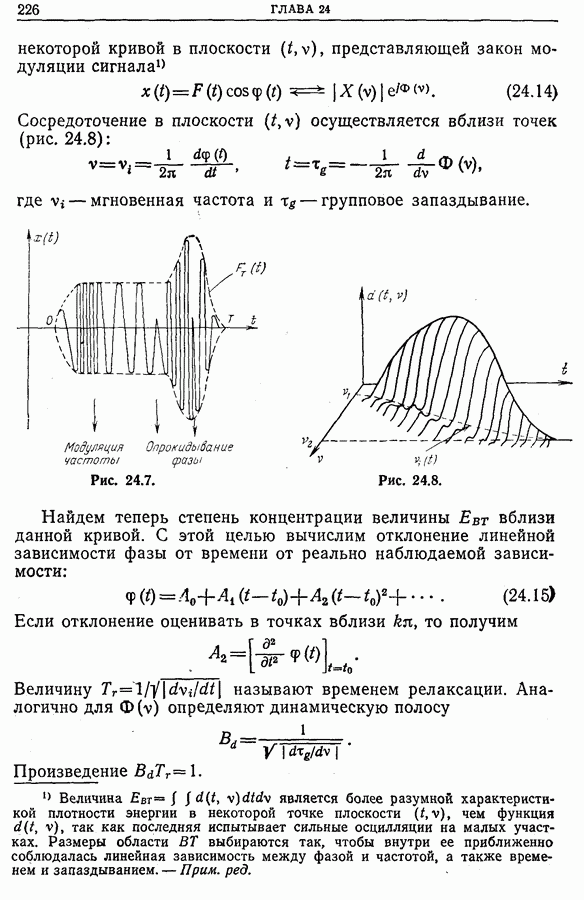
- 24.4. Представление [t, v] по Бонне. Мгновенный спектр мощности по Биллю. Функция неопределенности
- 24.5. Другие определения частотно-временного представления
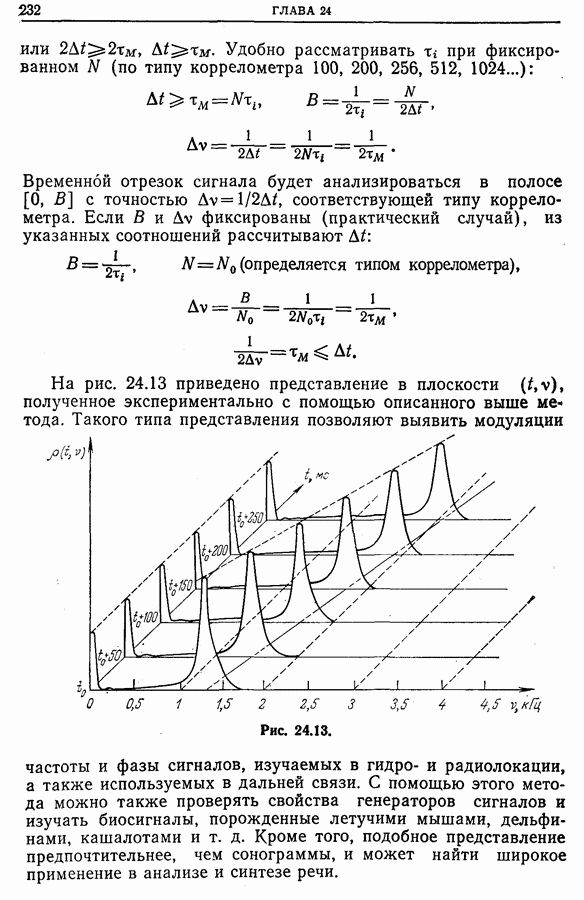
- 24.6. Измерение мгновенных спектров
- 24.7. Обобщение понятия мгновенного спектра мощности на случайные локально-стационарные сигналы. Функция структуры. Функция диффузии
- 24.8 Восстановление сигнала x(t) по известной функции
- 24.9. Заключение
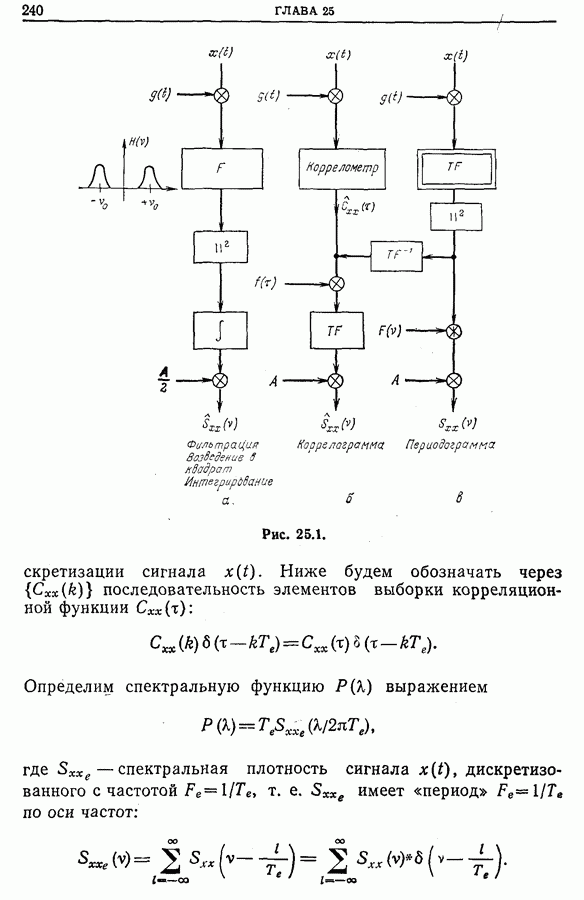
- Глава 25. НОВЫЕ МЕТОДЫ СПЕКТРАЛЬНОГО АНАЛИЗА
- 25.2. Проблемы, обусловленные дискретизацией корреляционной функции
- 25.3. Постановка проблемы получения спектральной функции из конечного числа значений автокорреляционной функции
- 25.4. Классический метод, основанный на преобразовании Фурье корреляционной функции
- 25.5. Метод максимума энтропии или метод авторегрессионной модели
- 25.6. Метод Писаренко
- 25.7. Смешанные методы
- 25.8. Заключение