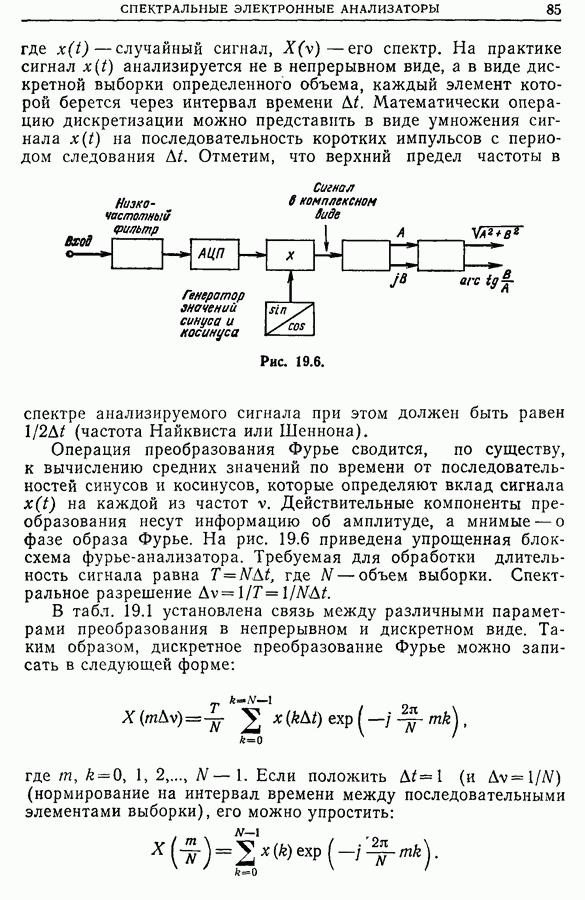
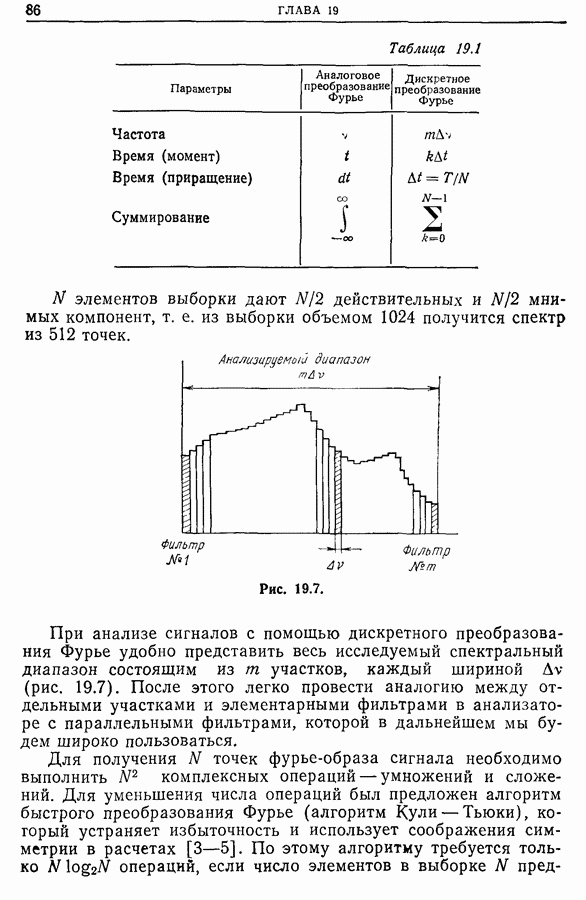
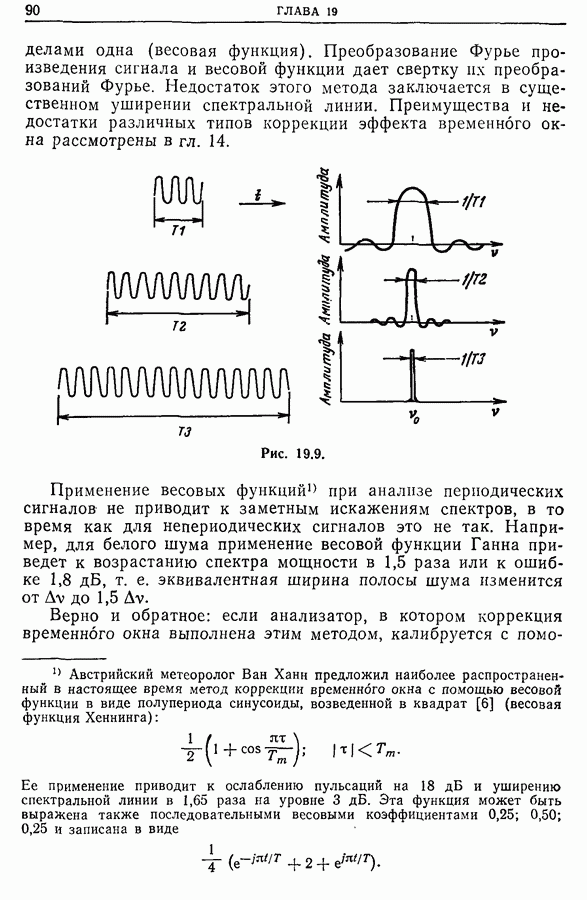
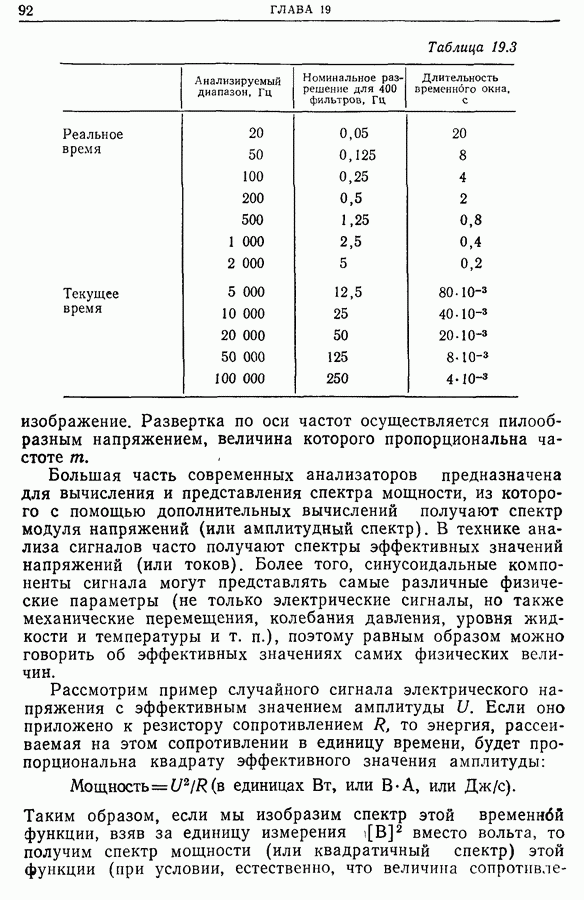
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
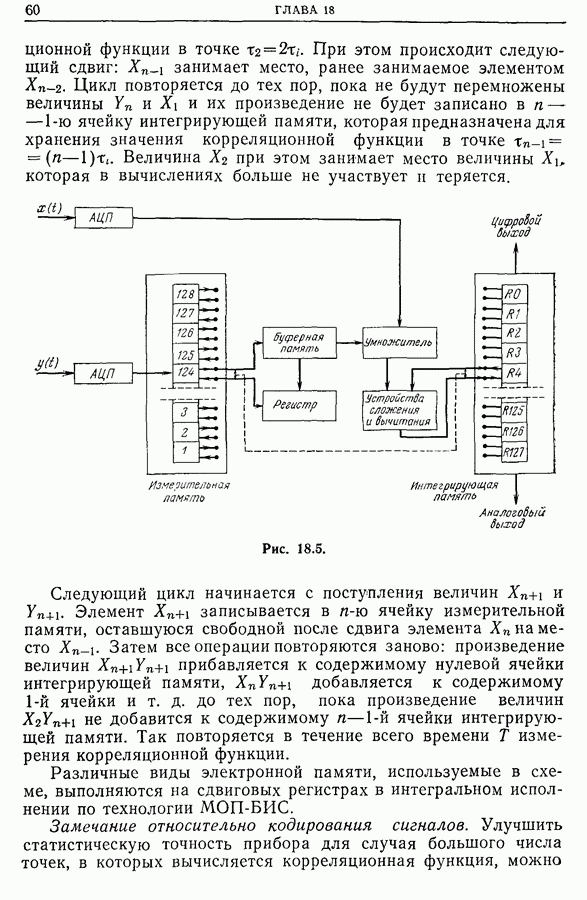
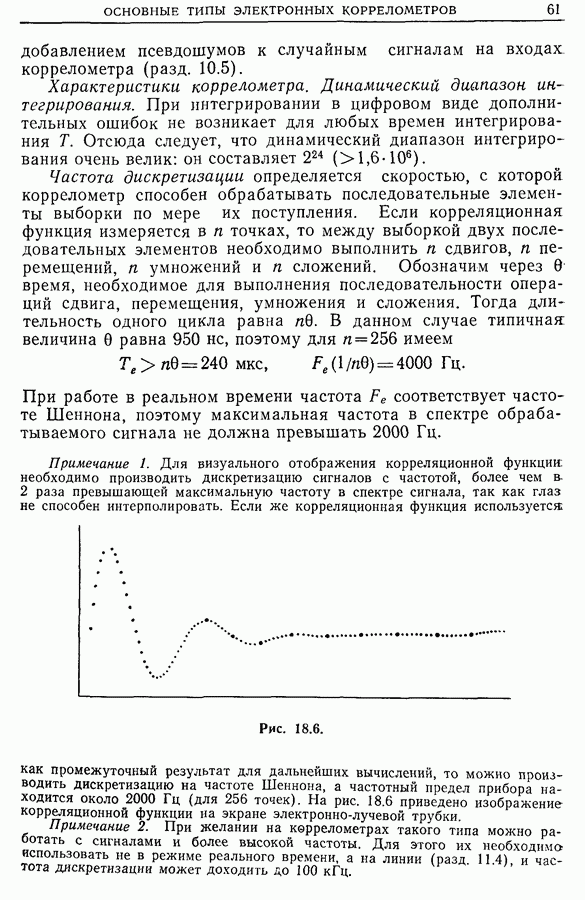
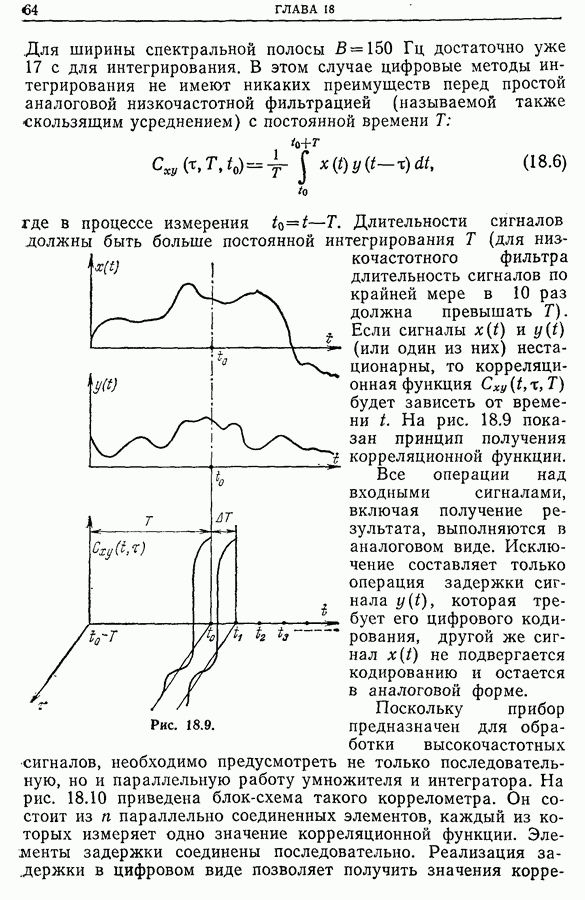
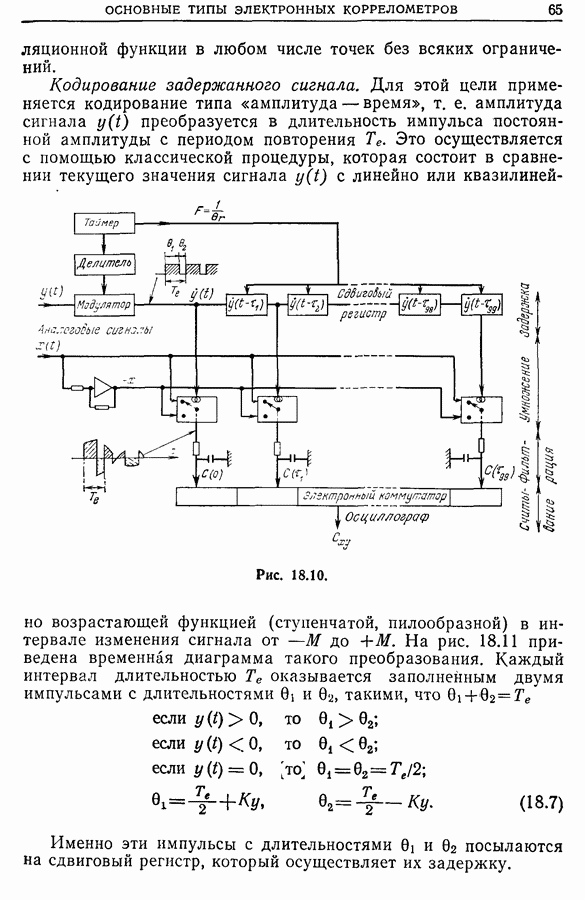
23.4. Временной и частотный сдвиги. Функция неопределенности
Ничто не мешает нам рассмотреть сигнал, который бы одновременно подвергался и частотной, и временной трансляции. Для сигнала  будем иметь
будем иметь

Среднеквадратичное отклонение между  будет равно
будет равно

где  представляет собой энергию
представляет собой энергию  сигнала.
сигнала.
Если время  мало по сравнению с длительностью сигнала
мало по сравнению с длительностью сигнала  и частота
и частота  мала по сравнению с центральной частотой, то
мала по сравнению с центральной частотой, то

Отсюда

Скалярное произведение в этом выражении называют функцией неопределенности и обозначают греческой буквой 

Функция  имеет два выражения в зависимости от того, какое представление сигнала X рассматривается — временное или частотное:
имеет два выражения в зависимости от того, какое представление сигнала X рассматривается — временное или частотное:


Рассмотрим выражение (23.12) и положим  . Тогда
. Тогда

Аналогично

Таким образом, видно, что функция неопределенности обобщает понятие корреляционной функции в случае двух трансляций — одной по времени, другой по частоте.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Глава 15. СИНХРОННОЕ ДЕТЕКТИРОВАНИЕ
- 15.2. Схема метода
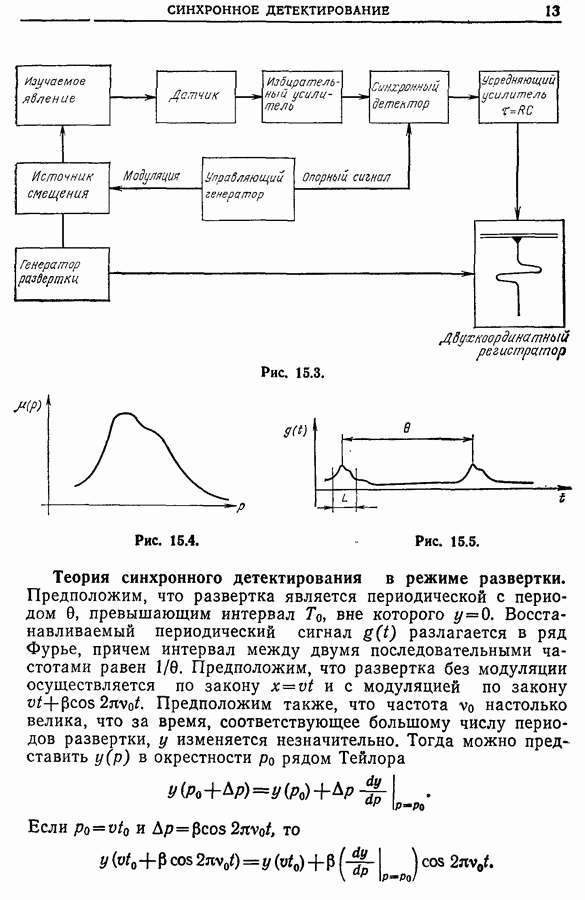
- 15.3. Теория синхронного детектирования
- 15.4. Синхронное детектирование в режиме развертки
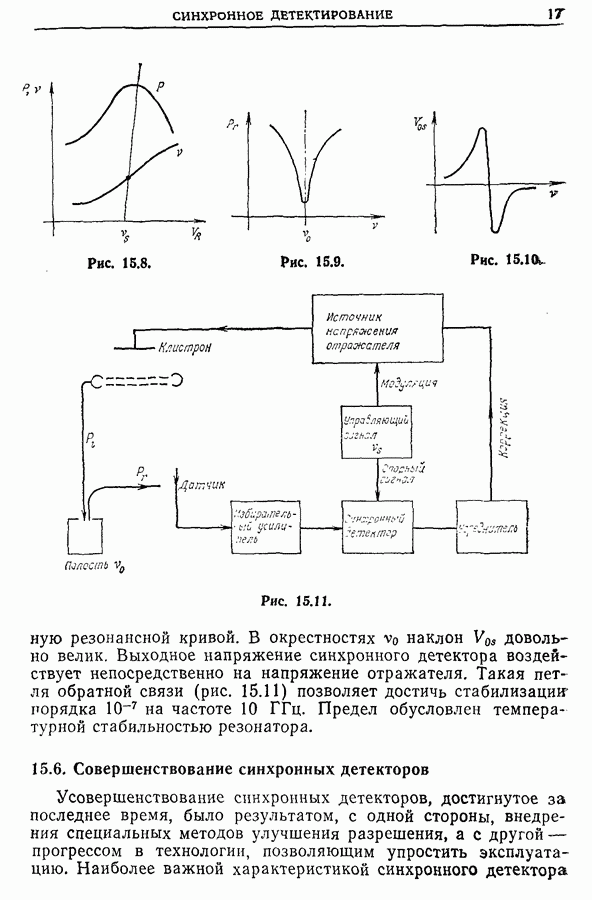
- 15.5. Примеры применения синхронных детекторов
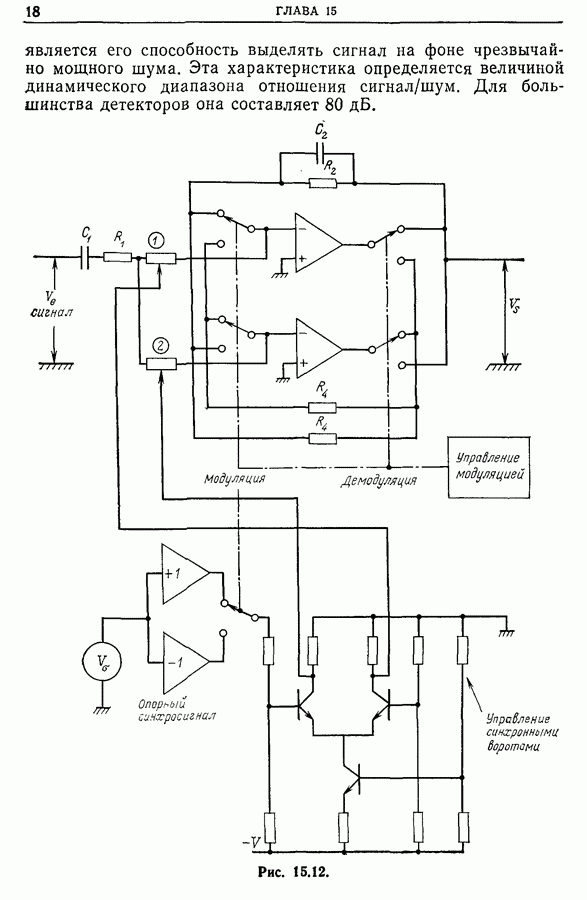
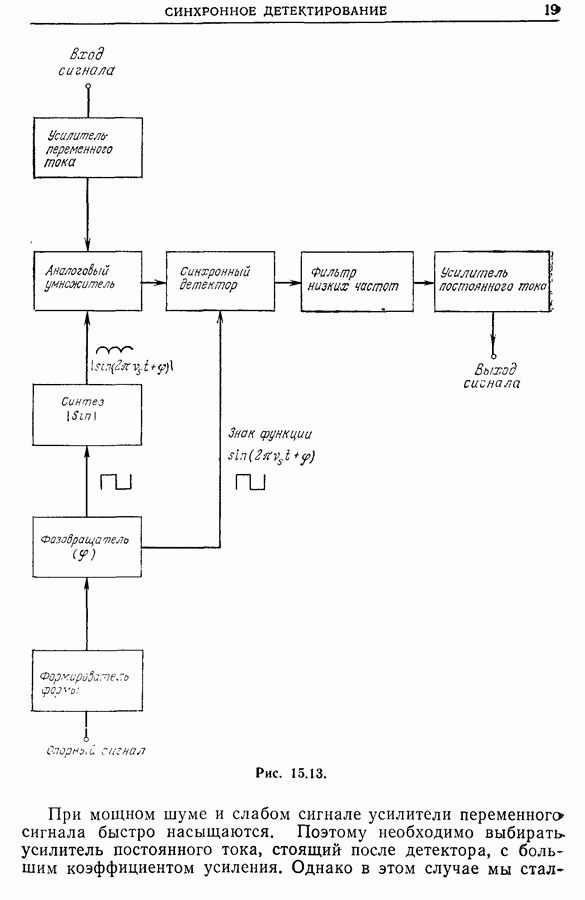
- 15.6. Совершенствование синхронных детекторов
- Глава 16. ИСПОЛЬЗОВАНИЕ МНОГОКАНАЛЬНЫХ АНАЛИЗАТОРОВ ПРИ СТАТИЧЕСКОЙ ОБРАБОТКЕ ИЗМЕРЕНИЙ
- 16.2. Характеристики многоканальных анализаторов
- 16.3. Схема системы обработки
- 16.4. Примеры применения
- Глава 17. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ
- 17.2. Частный случай белого шума. Согласованный фильтр
- 17.3. Согласованная фильтрация и корреляция Корреляция.
- 17.4. Реализация согласованных фильтров методом «взвешивания»
- 17.5. Рекурсивная согласованная фильтрация [7]
- 17.6. Применения метода согласованной фильтрации
- Глава 18. ОСНОВНЫЕ ТИПЫ ЭЛЕКТРОННЫХ КОРРЕЛОМЕТРОВ
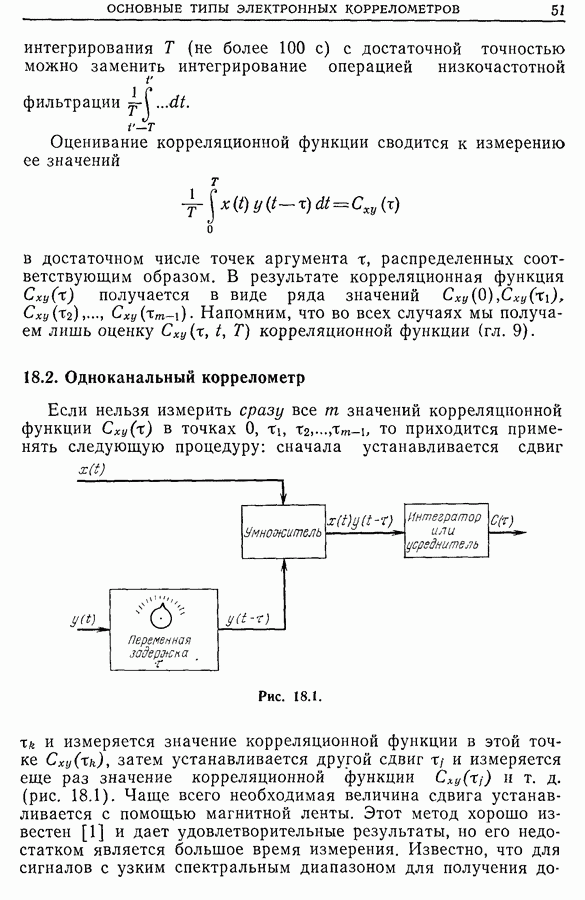
- 18.2. Одноканальный коррелометр
- 18.3. Автоматические коррелометры
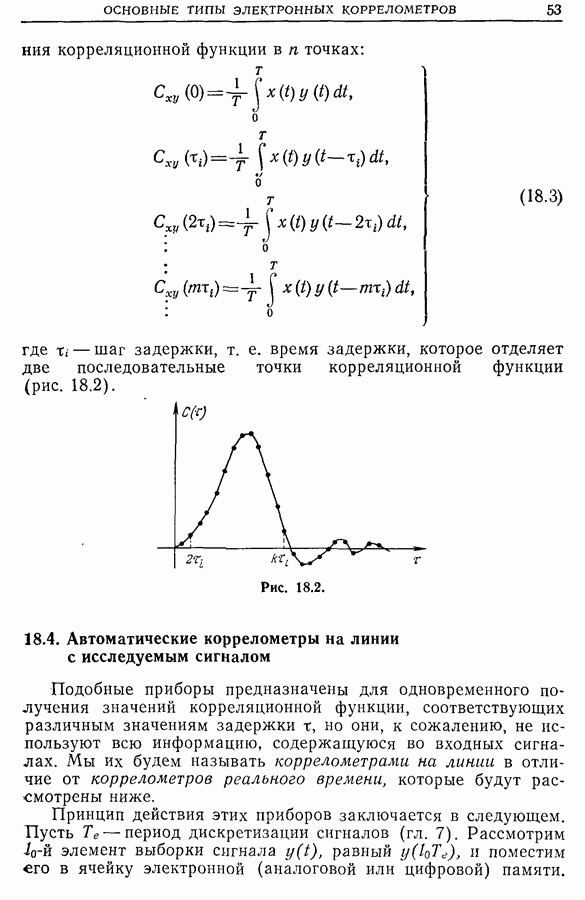
- 18.4. Автоматические коррелометры на линии с исследуемым сигналом
- 18.5. Автоматические коррелометры реального времени (или мультикоррелометры)
- 18.6. Коррелометры на больших интегральных схемах
- 18.7. Коррелометры реального времени для высокочастотных сигналов
- 18.8 Развитие коррелометров
- 18.9. Приборы с зарядовой связью [11]
- Глава 19. СПЕКТРАЛЬНЫЕ ЭЛЕКТРОННЫЕ АНАЛИЗАТОРЫ
- 19.2. Спектральные анализаторы, основанные на методе непосредственного преобразования Фурье
- 19.3. Применения анализаторов на основе метода БПФ
- Глава 20. ОПТИЧЕСКИЙ СПЕКТРАЛЬНЫЙ АНАЛИЗ
- 20.2. Упрощения, связанные с отбрасыванием фазы
- 20.3. Эффект виньетирования
- 20.4. Двумерный анализ
- 20.5. Точечный монохроматический источник
- 20.6. Электрооптическое преобразование сигнала
- 20.7. Устройства отображения на жидких кристаллах
- 20.8. Ограничения устройств отображения
- 20.9. Модулятор на основе эффекта Покельса (PROM)
- 20.10. Трубки Титус и Фототитус
- 20.11. Другие электрооптические кристаллы
- 20.12. Спектральный анализ и интегральная оптика
- 20.13. Взаимные спектры
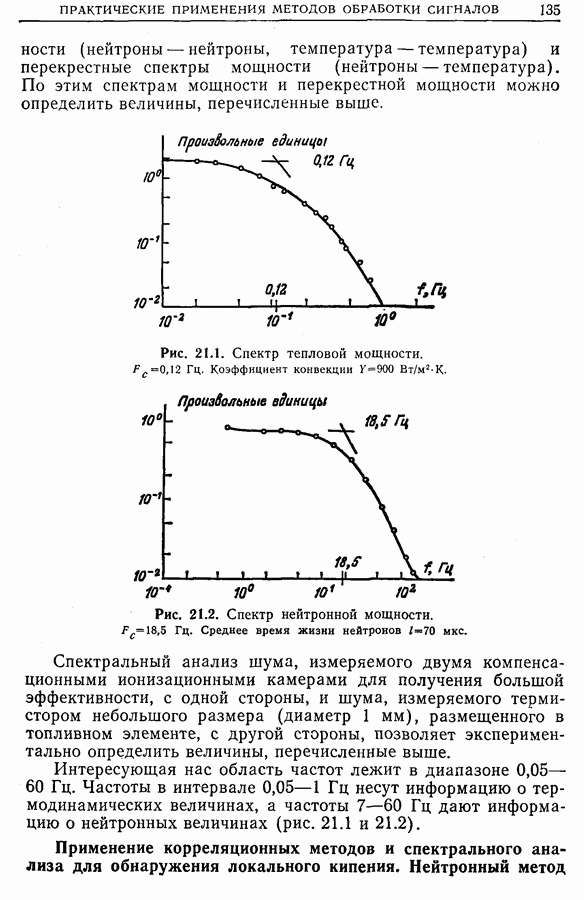
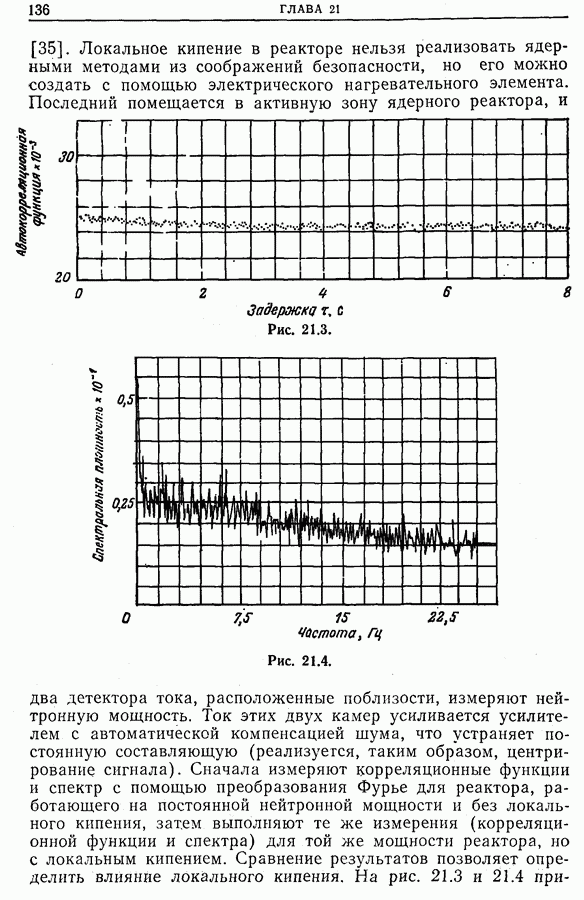
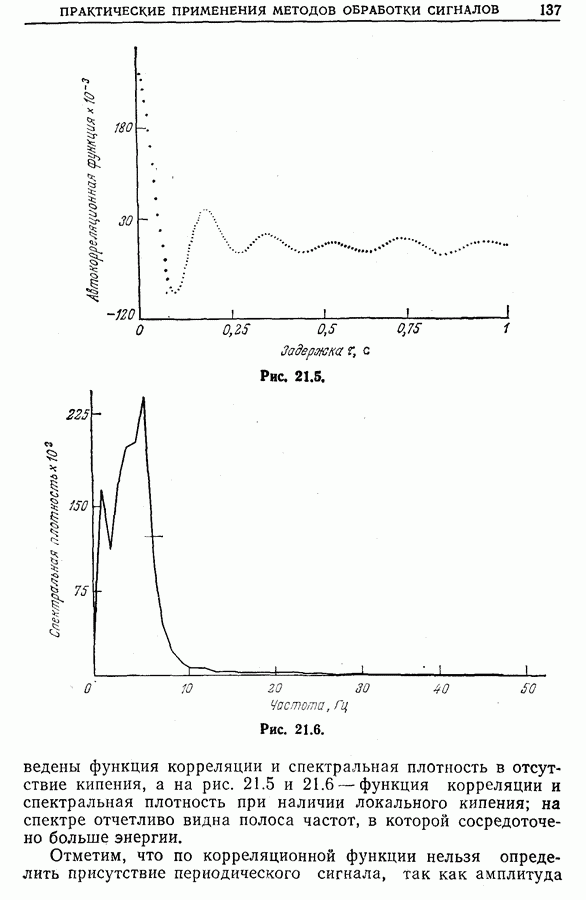
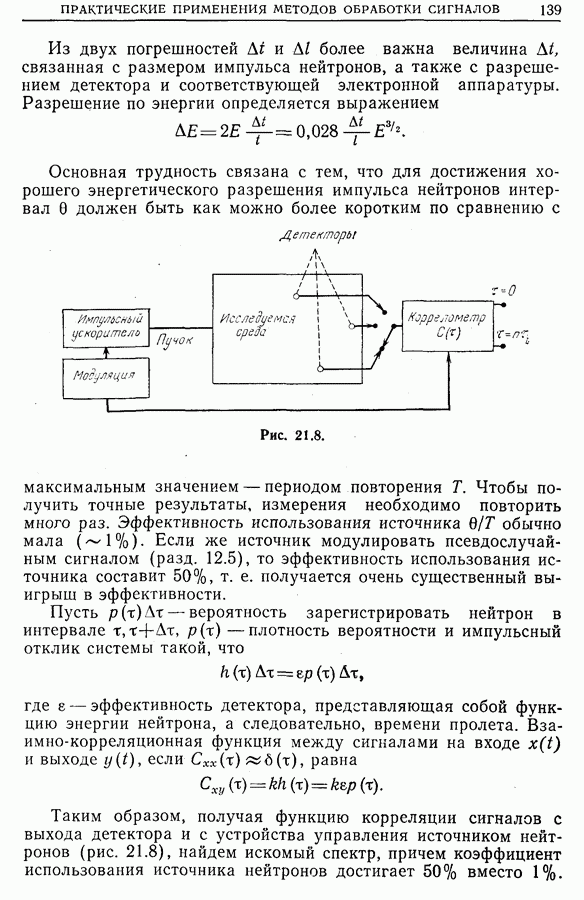
- Глава 21. НЕКОТОРЫЕ ПРАКТИЧЕСКИЕ ПРИМЕНЕНИЯ МЕТОДОВ ОБРАБОТКИ СИГНАЛОВ
- 21.2. Исследование ядерных сред
- 21.3. Ядерный магнитный резонанс (ЯМР) с возбуждением случайным сигналом
- 21.4. Идентификация процессов. Измерение импульсных откликов и передаточных функций
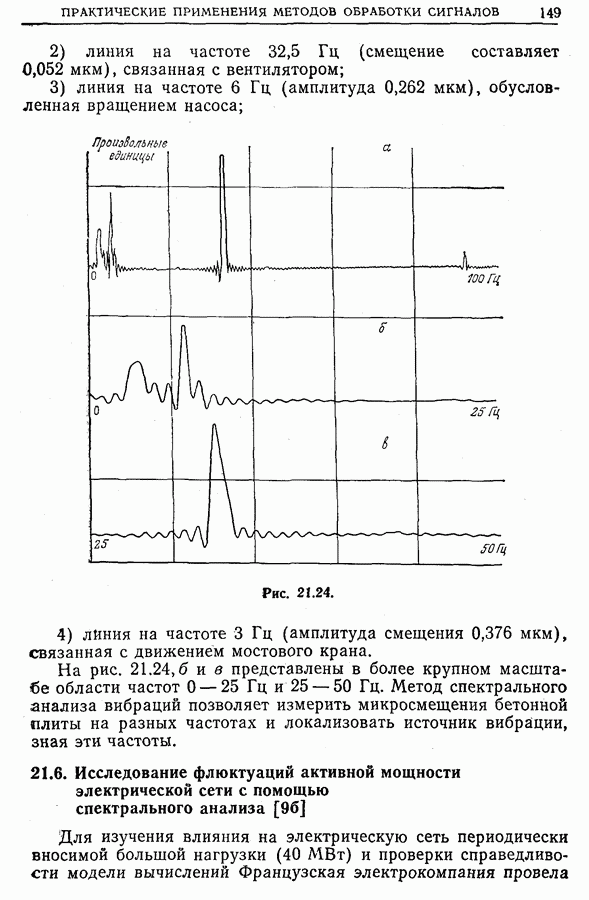
- 21.5. Спектральный анализ собственных колебаний бетонных плит
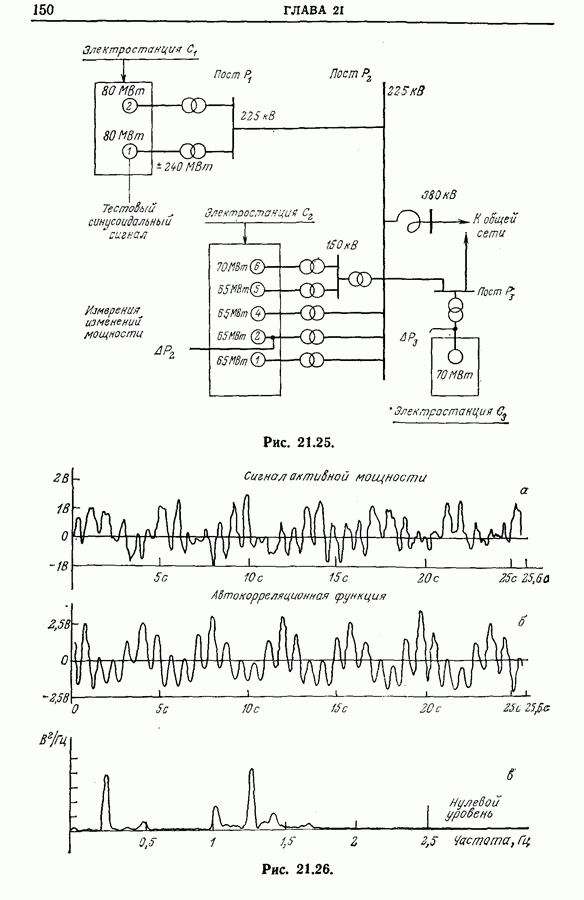
- 21.6. Исследование флюктуаций активной мощности электрической сети с помощью спектрального анализа
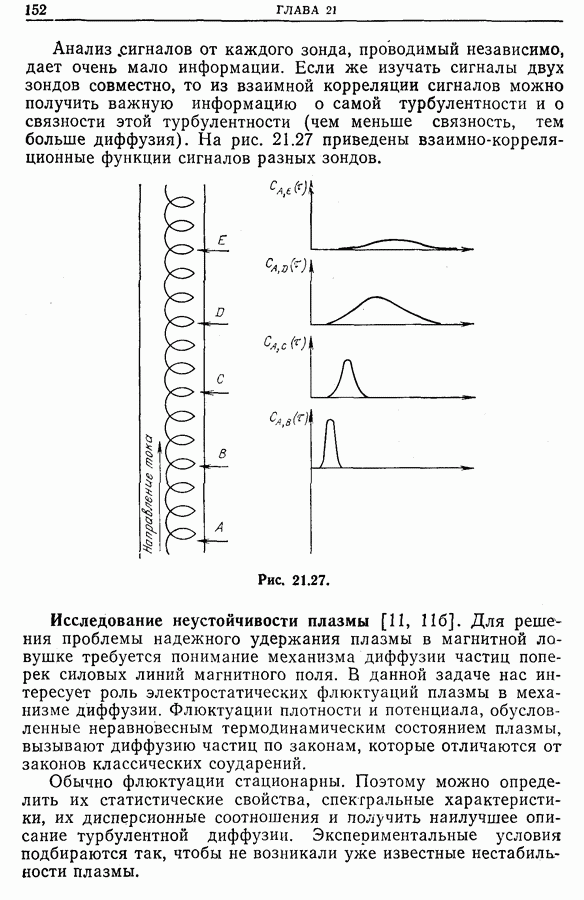
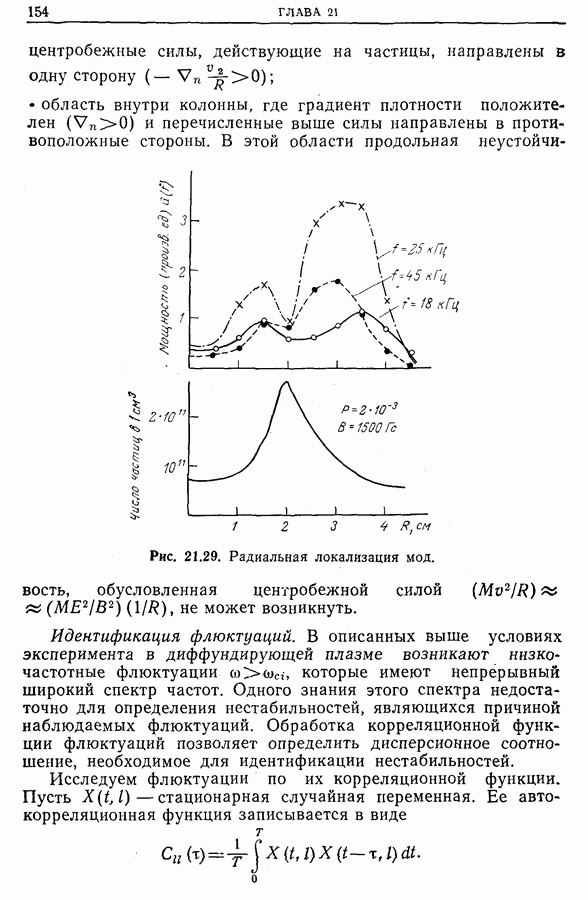
- 21.7. Изучение турбулентности
- 21.8. Применения в геофизике
- 21.9. Применения в астрофизике
- 21.10. Применения в астрономии и радиоастрономии
- 21.11. Применения в биологии и медицине
- 21.12. Применения в акустике
- 21.13. Исследование процессов намагничивания ферромагнетиков
- 21.14. Применения новых методов обработки сигналов
- 21.15. Заключение
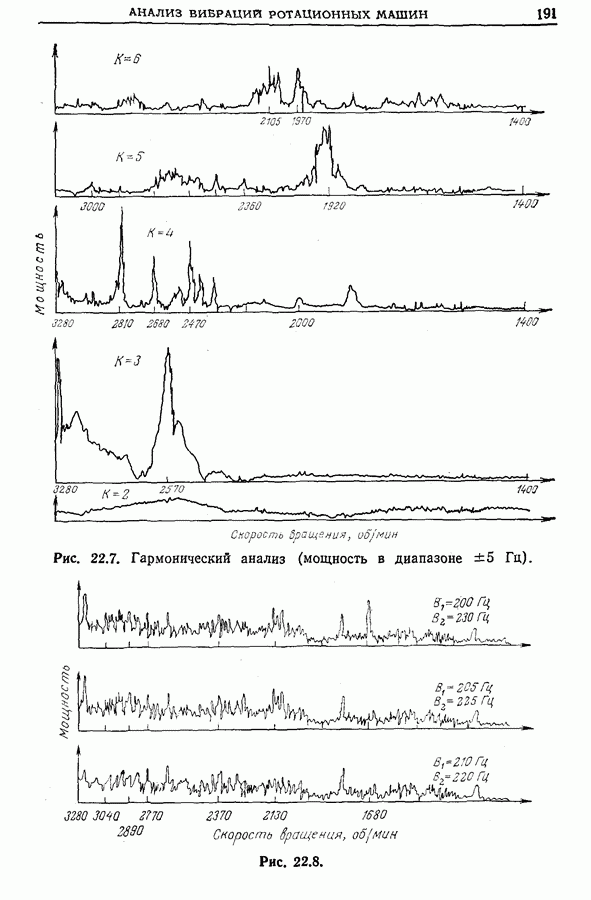
- Глава 22. ПРИМЕНЕНИЕ МЕТОДОВ ОБРАБОТКИ СИГНАЛОВ ДЛЯ АНАЛИЗА ВИБРАЦИЙ РОТАЦИОННЫХ МАШИНА
- 22.2. Анализ поведения системы «ротационная машина — конструкция»
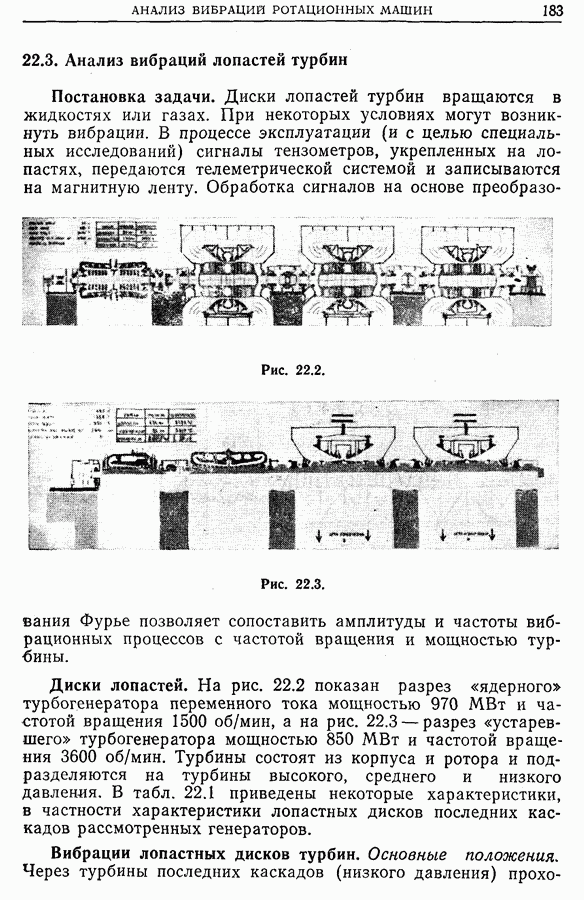
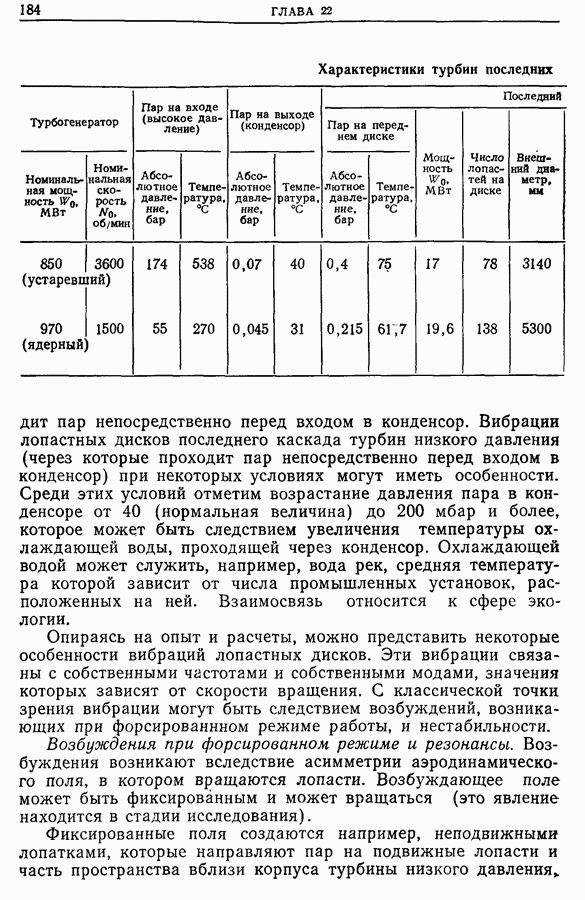
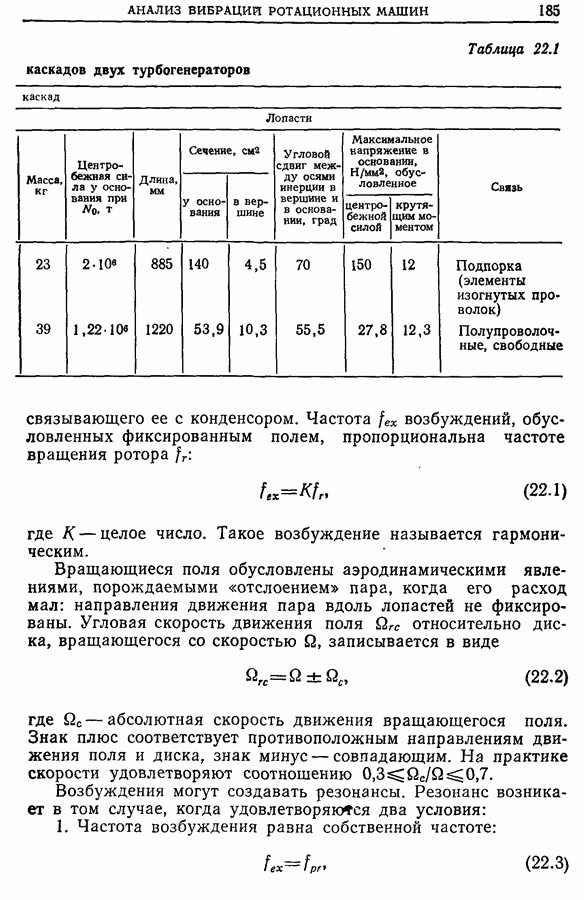
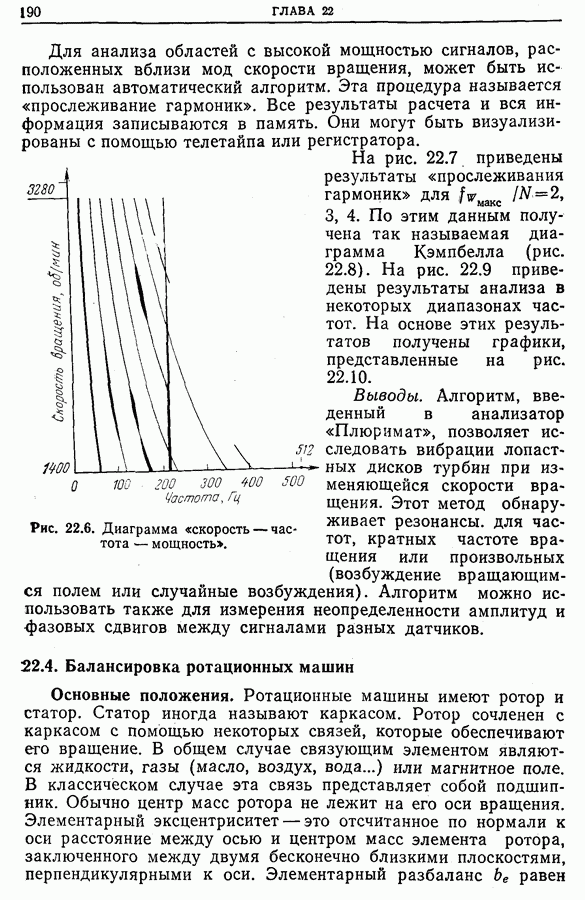
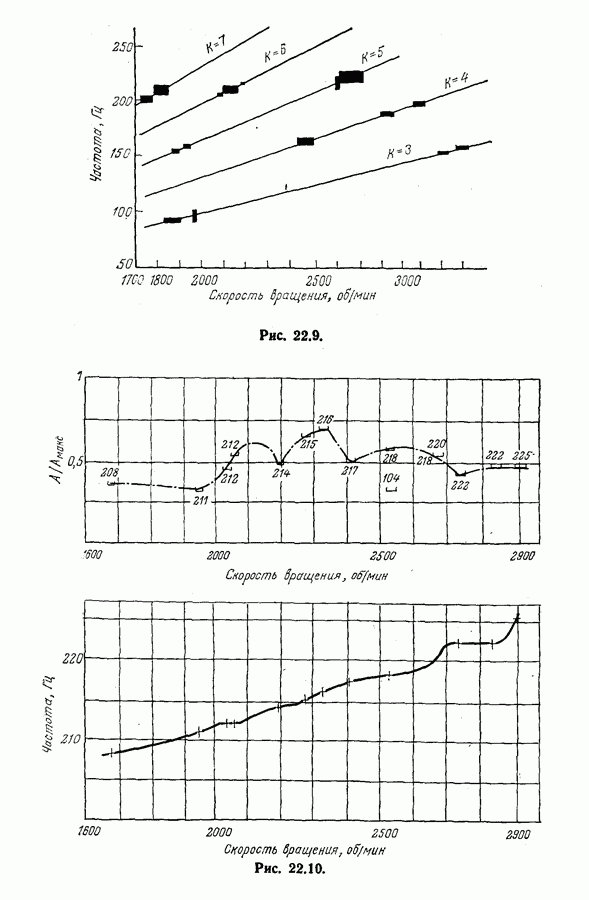
- 22.3. Анализ вибраций лопастей турбин
- 22.4. Балансировка ротационных машин
- Глава 23. ФУНКЦИЯ НЕОПРЕДЕЛЕННОСТИ
- 23.2. Временная корреляция. Временной сдвиг
- 23.3. Частотная корреляция. Частотный сдвиг
- 23.4. Временной и частотный сдвиги. Функция неопределенности
- 23.5. Функция неопределенности Вудворда
- 23.6. Взаимная функция неопределенности
- 23.7. Некоторые свойства функции неопределенности
- 23.8. Представление функций неопределенности
- 23.9. Примеры функций неопределенности
- 23.10. Применение функции неопределенности
- 23.11. Применение функций неопределенности для описания линейных неоднородных во времени систем. Обобщение понятия передаточной функции. Функция диффузии (функция рассеивания)
- 23.12. Генерация тестового сигнала
- 23.13. Прибор для измерения функции неопределенности в режиме реального времени
- Глава 24. ПОНЯТИЕ МГНОВЕННОГО СПЕКТРА ИЛИ ЧАСТОТНО-ВРЕМЕННОГО ПРЕДСТАВЛЕНИЯ В АНАЛИЗЕ И СИНТЕЗЕ СИГНАЛОВ
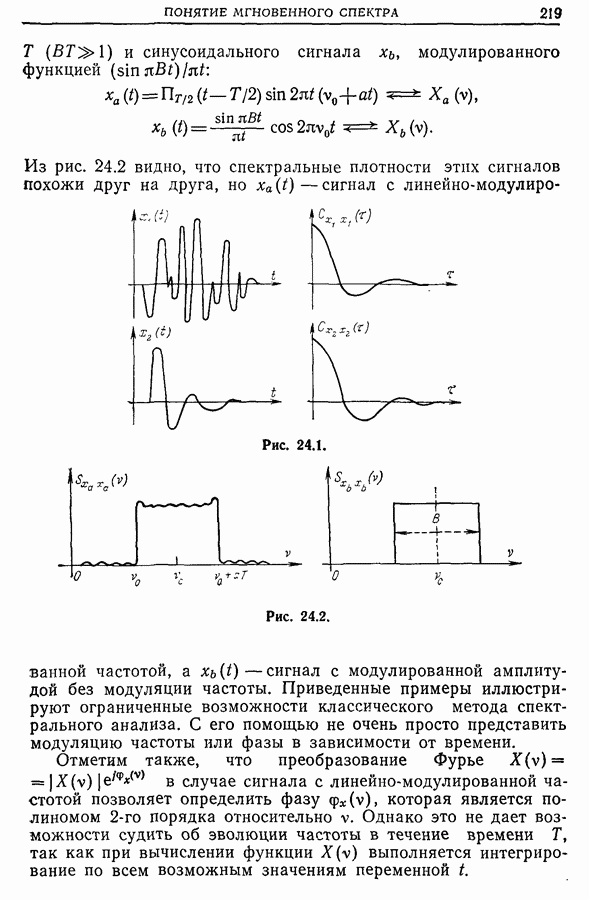
- 24.2. Примеры спектрального анализа модулированных и немодулированных сигналов
- 24.3. Частотно-временная зависимость. Соотношение неопределенностей. Частотно-временное представление Габора
- 24.4. Представление [t, v] по Бонне. Мгновенный спектр мощности по Биллю. Функция неопределенности
- 24.5. Другие определения частотно-временного представления
- 24.6. Измерение мгновенных спектров
- 24.7. Обобщение понятия мгновенного спектра мощности на случайные локально-стационарные сигналы. Функция структуры. Функция диффузии
- 24.8 Восстановление сигнала x(t) по известной функции
- 24.9. Заключение
- Глава 25. НОВЫЕ МЕТОДЫ СПЕКТРАЛЬНОГО АНАЛИЗА
- 25.2. Проблемы, обусловленные дискретизацией корреляционной функции
- 25.3. Постановка проблемы получения спектральной функции из конечного числа значений автокорреляционной функции
- 25.4. Классический метод, основанный на преобразовании Фурье корреляционной функции
- 25.5. Метод максимума энтропии или метод авторегрессионной модели
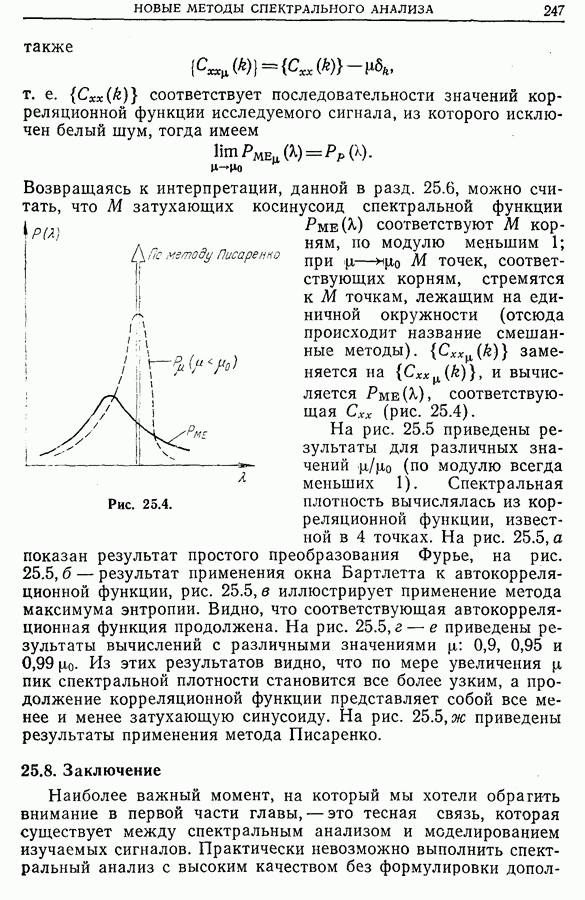
- 25.6. Метод Писаренко
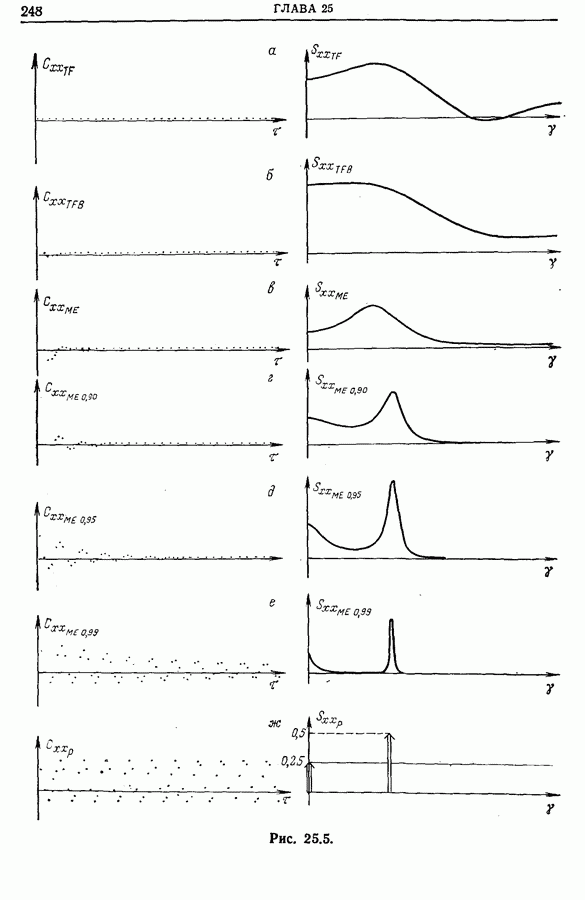
- 25.7. Смешанные методы
- 25.8. Заключение