| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
19.3. Применения анализаторов на основе метода БПФ
Измеряемые величины.
Мощность и спектральная плотность мощности. Проводя аналогию между анализатором на основе метода БПФ и совокупностью элементарных фильтров с примыкающими друг к другу прямоугольными спектральными характеристиками одинаковой ширины  можно сделать два вывода.
можно сделать два вывода.
Определение мощности, независимое от величины  строго говоря, справедливо только для периодических сигналов, но оно легко может быть обобщено на произвольные случайные сигналы. Действительно, величина мощности на выходе любого элементарного фильтра равна квадрату показаний вольтметра, измеряющего эффективное напряжение на выходе фильтра (на нагрузке 1 Ом). Для идеально прямоугольной спектральной характеристики фильтра измеренная мощность зависит от природы сигнала, т. е. измерение синусоидального сигнала с эффективным напряжением 1 В, частота которого расположена в
строго говоря, справедливо только для периодических сигналов, но оно легко может быть обобщено на произвольные случайные сигналы. Действительно, величина мощности на выходе любого элементарного фильтра равна квадрату показаний вольтметра, измеряющего эффективное напряжение на выходе фильтра (на нагрузке 1 Ом). Для идеально прямоугольной спектральной характеристики фильтра измеренная мощность зависит от природы сигнала, т. е. измерение синусоидального сигнала с эффективным напряжением 1 В, частота которого расположена в
полосе пропускания фильтра, и измерение белого шума с тем же эффективным напряжением в полосе дадут одинаковый результат. Мощность сигнала с широкой спектральной полосой получается суммированием индивидуальных вкладов элементарных фильтров, спектральные характеристики которых перекрывают спектр сигнала.
Определение спектральной плотности мощности справедливо только для случайных стационарных сигналов [8] и представляет ее как зависимость мощности в единичной полосе (1 Гц) от частоты. Такое представление позволяет просто сравнивать значения, полученные с помощью фильтров с различной шириной полосы. Рассмотрим это определение на следующем примере.
Предположим, что случайный сигнал, представляющий собой белый шум, поступает на анализатор, эквивалентный 400 элементарным фильтрам с  таким образом, анализируемый спектральный диапазон простирается от 0 до
таким образом, анализируемый спектральный диапазон простирается от 0 до  При этом на каждый фильтр поступает белый шум одинаковой средней мощности, равной, например,
При этом на каждый фильтр поступает белый шум одинаковой средней мощности, равной, например,  (отнесенной к 1 Ом). Если теперь взять ширину полосы элементарного фильтра
(отнесенной к 1 Ом). Если теперь взять ширину полосы элементарного фильтра  а границу диапазона анализатора соответственно уменьшить до
а границу диапазона анализатора соответственно уменьшить до  то мощность, поступающая на каждый фильтр, уменьшится в 2 раза и составит
то мощность, поступающая на каждый фильтр, уменьшится в 2 раза и составит  Нормируя, получим, что спектральная плотность мощности одинакова в обоих случаях и равна
Нормируя, получим, что спектральная плотность мощности одинакова в обоих случаях и равна 
Однако существенно то, что нельзя измерять спектральную плотность мощности сигналов, имеющих линейчатый спектр. Рассмотрим, что произойдет, если синусоидальный сигнал определенной амплитуды (и, следовательно, определенной мощности) измеряется двумя фильтрами, один из которых имеет ширину полосы  , а другой
, а другой  . Наблюдаемая мощность в обоих случаях будет одинакова, а плотность мощности будет различаться в 2 раза, что лишено смысла.
. Наблюдаемая мощность в обоих случаях будет одинакова, а плотность мощности будет различаться в 2 раза, что лишено смысла.
Приведенные рассуждения позволяют нам лучше понять трудности, возникающие при интерпретации результатов анализа сложных сигналов. Действительно, предположим, что мы должны измерить спектр шумов. Измеряемый спектр будет неоднородным в том смысле, что содержит непрерывную составляющую (в общем случае зависящую от частоты) и дискретные линии. Мощность, поступающая на элементарный фильтр от периодического сигнала, постоянна для любой полосы фильтра, а поступающая от шума растет с увеличением ширины полосы фильтра. Мы приходим к выводу, что результаты измерения зависят от свойств анализатора. Таким образом, результат отражает не только свойства самого сигнала и не может быть правильно интерпретирован, если не известны характеристики используемого анализатора.
Поэтому важно различать ширину спектральной линии, которая является единственным свойством сигнала, и элементарную ширину полосы анализатора, которая является существенной характеристикой последнего.
Наконец, следует отметить, что измерение средней мощности спектра неэквивалентно вычислению квадрата среднего значения амплитудного спектра (напряжения). Действительно, во втором случае появляется дополнительный член, который в зависимости от природы сигнала и шума может достигать 1 дБ. Для синусоидального сигнала и гауссова шума отношение сигнал/шум уменьшается в  раза.
раза.
Анализ переходных процессов. Для анализа переходных процессов длительность временного окна необходимо выбирать равной длительности процесса. В этом случае наибольшая скорость повторения переходного процесса, допустимая для анализатора, будет определяться полосой частот в реальном времени.
Действительно, при анализе переходных процессов можно считать, что анализ осуществляется в реальном времени, если временное окно имеет по крайней мере такую же длительность, как и полная длительность переходного процесса, и если в случае повторения процесса ни одна его часть не теряется.
Учитывая, что данные поступают только в период нестационарности, единственным критерием правильности анализа является полный и точный охват сигнала временным окном. Другими словами, чем более коротким окном мы полностью захватим переходной участок, тем лучше будет точность измерений и большее количество информации будет содержаться в полученном спектре.
Рассмотренный ниже пример поможет нам пояснить это требование. Предположим, что собственный шум анализатора не зависит от выбранного для анализа спектрального диапазона, и рассмотрим регистрацию участка синусоиды частотой  имеющего длительность
имеющего длительность  Проведем измерения 2 раза с помощью анализатора, эквивалентного 400 элементарным фильтрам, сначала в диапазоне
Проведем измерения 2 раза с помощью анализатора, эквивалентного 400 элементарным фильтрам, сначала в диапазоне  а затем в диапазоне
а затем в диапазоне  . В диапазоне
. В диапазоне  разрешение равно 50 Гц, и мы получим узкий пик. В диапазоне
разрешение равно 50 Гц, и мы получим узкий пик. В диапазоне  разрешение равно 5 Гц, и мы получим широкий пик, растянутый на 10 фильтров. Поскольку полная энергия сигнала одинакова в обоих случаях, пик во втором случае будет иметь амплитуду примерно на 10 дБ меньше, чем в первом случае, т. е. динамический диапазон амплитуд будет лучше в случае более широкого диапазона. Разрешение при этом не ухудшается, поскольку оно зависит от объема выборки данных.
разрешение равно 5 Гц, и мы получим широкий пик, растянутый на 10 фильтров. Поскольку полная энергия сигнала одинакова в обоих случаях, пик во втором случае будет иметь амплитуду примерно на 10 дБ меньше, чем в первом случае, т. е. динамический диапазон амплитуд будет лучше в случае более широкого диапазона. Разрешение при этом не ухудшается, поскольку оно зависит от объема выборки данных.
Отметим, что на практике при измерении спектральной плотности мощности сигналов с линейчатыми спектрами обычно выбирают ширину полосы элементарного фильтра, равной четверти ширины линии спектральной мощности, что дает ошибку около 3%.
Ошибки оценок.
Вопросы статистической точности спектральных измерений требуют особого внимания, так как результаты зависят не только от свойств исследуемого сигнала, но и от характеристик анализатора и часто искажаются сопутствующими шумами. Обычно различают мгновенный и средний спектры. Строго говоря, понятие мгновенного спектра, так же как и изменение спектра во времени, не имеет смысла с классической точки зрения, согласно которой интеграл Фурье определен на всей действительной оси. На практике из-за конечного времени измерения можно говорить о мгновенных спектрах, а также с их помощью следить за изменением спектрального состава исследуемых сигналов во времени (гл. 24). Средний спектр получается путем усреднения большого количества мгновенных спектров.
Проблемы, связанные с ошибками оценок, подробно изложены в гл. 9. Здесь мы ограничимся некоторыми практическими выводами.
Напомним, что если ошибка измерения находится в пределах 20%, то среднеквадратичное отклонение усредненного значения спектральной плотности мощности  при 68%-ной доверительной вероятности составляет
при 68%-ной доверительной вероятности составляет

где  — ширина полосы элементарного фильтра анализатора, Т — эквивалентная длительность усреднения.
— ширина полосы элементарного фильтра анализатора, Т — эквивалентная длительность усреднения.
В табл. 19.4 приведены значения доверительных интервалов от 68% и выше и соответствующие им относительные увеличения ошибок, а в табл. 19.5 значения произведений  для получения заданной точности для тех же доверительных интервалов.
для получения заданной точности для тех же доверительных интервалов.
Число степеней свободы. Рассмотрим условие взаимной независимости элементов выборки случайного сигнала. Известно, что если случайный стационарный сигнал поступает на фильтр с шириной полосы  то для устранения корреляций (из-за
то для устранения корреляций (из-за
Таблица 19.4

Таблица 19.5

влияния частотной характеристики фильтра) необходимо выбирать величину интервала между элементами выборки так, чтобы она была не меньше  Таким способом учитываются статистически независимые элементы выборки. Число степеней свободы определяется как число независимых элементов выборки, на основе которых вычисляется оценка. Это число определяет статистическую устойчивость оценки измерения [6].
Таким способом учитываются статистически независимые элементы выборки. Число степеней свободы определяется как число независимых элементов выборки, на основе которых вычисляется оценка. Это число определяет статистическую устойчивость оценки измерения [6].
Из соотношения  следует, что статистическая ошибка нормируется делением на
следует, что статистическая ошибка нормируется делением на  По мере того как
По мере того как  возрастает, дисперсия амплитуды уменьшается, поскольку
возрастает, дисперсия амплитуды уменьшается, поскольку

По мере увеличения  случайные изменения амплитуды уменьшаются, улучшается статистическая точность без потери спектрального разрешения, но за счет увеличения длительности измерения. Достаточная статистическая точность получается со 128 степенями свободы. При
случайные изменения амплитуды уменьшаются, улучшается статистическая точность без потери спектрального разрешения, но за счет увеличения длительности измерения. Достаточная статистическая точность получается со 128 степенями свободы. При  Гц,
Гц,  с 68% данных укладываются в диапазон ±0,6 дБ. В табл. 19.6 приведены необходимые значения времени усреднения для достижения такой же статистической точности при различных значениях ширины полос элементарных фильтров.
с 68% данных укладываются в диапазон ±0,6 дБ. В табл. 19.6 приведены необходимые значения времени усреднения для достижения такой же статистической точности при различных значениях ширины полос элементарных фильтров.
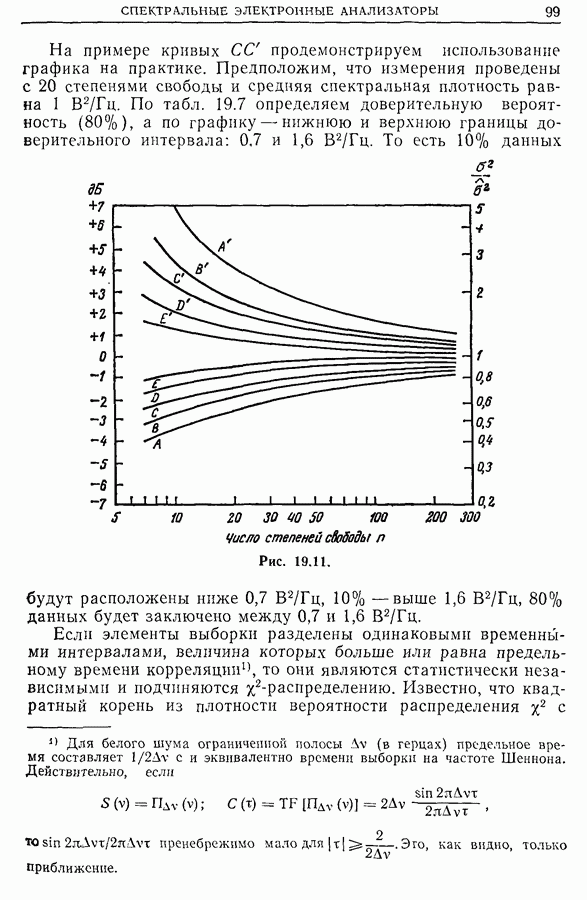
Статистическая точность измерений. На рис. 19.11 приведены кривые, показывающие воспроизводимость или стабильность результатов измерения стационарного центрированного гауссова шума в зависимости от числа степеней свободы. Парные кривые соответствуют верхней и нижней границам значений ошибки в относительных единицах. По оси ординат отложено отношение истинной и наблюдаемой дисперсий.
Таблица 19.6

На примере кривых С С продемонстрируем использование графика на практике. Предположим, что измерения проведены с 20 степенями свободы и средняя спектральная плотность равна  По табл. 19.7 определяем доверительную вероятность
По табл. 19.7 определяем доверительную вероятность  а по графику — нижнюю и верхнюю границы доверительного интервала: 0,7 и
а по графику — нижнюю и верхнюю границы доверительного интервала: 0,7 и  То есть 10% данных будут расположены ниже
То есть 10% данных будут расположены ниже  — выше
— выше  данных будет заключено между 0,7 и
данных будет заключено между 0,7 и 

Рис. 19.11.
Если элементы выборки разделены одинаковыми временными интервалами, величина которых больше или равна предельному времени корреляции, то они являются статистически независимыми и подчиняются  -распределению. Известно, что квадратный корень из плотности вероятности распределения
-распределению. Известно, что квадратный корень из плотности вероятности распределения  с
с
Таблица 19.7 (см. скан)
двумя степенями свободы является распределением Рэлея, которому подчиняется плотность вероятности пиковых значений гауссова сигнала, прошедшего через фильтр с очень узкой полосой пропускания. Для трех степеней свободы оно представляет собой распределение Максвелла. Отметим, что  -распределение стремится к нормальному распределению при увеличении числа степеней свободы. В частности, начиная с
-распределение стремится к нормальному распределению при увеличении числа степеней свободы. В частности, начиная с  можно считать, что величина
можно считать, что величина  распределена практически нормально со средним значением
распределена практически нормально со средним значением  и дисперсией
и дисперсией 
Таблица 19.8 (см. скан)
Таблица 19.9 (см. скан)
Таблица 19.10 (см. скан)
Например, для измерения со 120 степенями свободы (60 последовательных сложений в памяти анализатора) точное значение величины лежит в пределах 0,79-1,31 от измеренного с доверительной вероятностью 95% и в пределах  с доверительной вероятностью 80%. Если число сложений уменьшить до 15, то для интервала
с доверительной вероятностью 80%. Если число сложений уменьшить до 15, то для интервала  доверительная вероятность окажется очень малой — 30%.
доверительная вероятность окажется очень малой — 30%.
В табл. 19.8 приведены верхний и нижний пределы разброса истинного значения, выраженного в децибелах, для различного числа сложений при доверительной вероятности 95,46% (средняя ошибка составляет  ). Если уменьшить число сложений и допустить меньшие доверительные вероятности, то разброс увеличивается, как показано в табл. 19.9, составленной для доверительной вероятности 90%.
). Если уменьшить число сложений и допустить меньшие доверительные вероятности, то разброс увеличивается, как показано в табл. 19.9, составленной для доверительной вероятности 90%.
В табл. 19.10 дано в более общем виде число степеней свободы, которое необходимо иметь для получения определенного разброса. Например, если с доверительной вероятностью 90% необходимо получить разброс 5 дБ, необходимо иметь по крайней мере 18 степеней свободы.
В заключение отметим, что можно улучшить статистическую точность за счет точности анализа, но без увеличения длительности последнего, усредняя результаты измерений по нескольким соседним элементарным фильтрам. Этого же можно добиться заменой элементарных фильтров с узкой полосой на фильтры с более широкой полосой (на 1/3 октавы, например).
Линейное усреднение. Статистическую точность можно увеличить также путем усреднения определенного числа измеренных спектров. Обычно среднее значение вычисляется через
усредненные величины по следующей формуле:

где М — число спектров, по которым производится усреднение; его выбирают в виде степени числа 2 (не более 1024).
Среднеквадратичное отклонение а зависит от числа усредняемых спектров:  Для 100 спектров получается значение
Для 100 спектров получается значение  дБ.
дБ.
Линейным называется такое усреднение, при котором элементы выборки складываются с равными весами. Примером устройства, производящего линейное усреднение, может служить идеальный интегратор. Алгоритм суммирования записывается в рекуррентном виде

где  — текущее среднее,
— текущее среднее,  — предыдущее среднее,
— предыдущее среднее,  — текущее значение, М — полное число усредняемых спектров. Усреднение завершается, когда
— текущее значение, М — полное число усредняемых спектров. Усреднение завершается, когда 
Предыдущее выражение можно записать в виде

Тогда итерационный процесс осуществляется следующим образом:

В разд. 9.5 было показано, что линейное среднее является несмещенной оценкой с дисперсией, пропорциональной 
Экспоненциальное усреднение. Алгоритм вычисления экспоненциального среднего отличается от алгоритма вычисления линейного тем, что вычисления в первом не прекращаются при  и наиболее ранние элементы выборки дают наименьший вклад в результат. Экспоненциальное среднее еще называют «скользящим» средним
и наиболее ранние элементы выборки дают наименьший вклад в результат. Экспоненциальное среднее еще называют «скользящим» средним

или

Здесь также для удобства выбирается  Итерационный процесс приводит к выражению
Итерационный процесс приводит к выражению

или

Для больших значений М коэффициент  стремится к
стремится к  (отсюда происходит название метода «экспоненциальное» усреднение).
(отсюда происходит название метода «экспоненциальное» усреднение).
Вычислим смещение этой оценки; для этого определим сначала ее математическое ожидание

Положим  тогда
тогда

Преобразуем сумму

и получаем окончательно

Отсюда смещение

Вычислим дисперсию  :
:

Положим, как в разд. 9.5,

Предположим, что  некоррелированы, т. e.
некоррелированы, т. e.

тогда

так как

Для дисперсии получаем выражение

Если положить  то
то

Сумму в этом выражении можно преобразовать:

Окончательно получаем дисперсию в виде

Отсюда видно, что при неограниченном увеличении  дисперсия стремится к
дисперсия стремится к 
Таким образом, при неограниченном увеличении объема выборки  дисперсия не стремится к нулю. Для фиксированного объема выборки
дисперсия не стремится к нулю. Для фиксированного объема выборки  если положить
если положить  получим дисперсию скользящего (или экспоненциального) усреднения
получим дисперсию скользящего (или экспоненциального) усреднения

тогда как для линейного усреднения дисперсия была равна  Но это достигнуто ценой смещения оценки, относительная величина которого составляет
Но это достигнуто ценой смещения оценки, относительная величина которого составляет  и стремится к
и стремится к  при неограниченном увеличении
при неограниченном увеличении  Этим смещением нельзя пренебречь, так как оно изменяется от 0,349 до 0,368 при изменении
Этим смещением нельзя пренебречь, так как оно изменяется от 0,349 до 0,368 при изменении  от 8 до 4096.
от 8 до 4096.
Итак, для выборки объемом  скользящее усреднение оптимально с точки зрения получения минимальной дисперсии, относительная величина которой близка к II
скользящее усреднение оптимально с точки зрения получения минимальной дисперсии, относительная величина которой близка к II  но дает смещение — 0,37, в то время как линейное усреднение дает нулевое смещение и относительную дисперсию
но дает смещение — 0,37, в то время как линейное усреднение дает нулевое смещение и относительную дисперсию  Скользящее усреднение экспоненциального типа ведет себя как интегрирующая
Скользящее усреднение экспоненциального типа ведет себя как интегрирующая  -цепь с постоянной времени
-цепь с постоянной времени  , где
, где  — интервал времени между элементами выборки спектра [9]. Преимуществом экспоненциального усреднения перед линейным является также возможность постоянного наблюдения за изменениями спектра. Некоторые анализаторы на начальном участке производят линейное усреднение, а затем переходят на скользящее.
— интервал времени между элементами выборки спектра [9]. Преимуществом экспоненциального усреднения перед линейным является также возможность постоянного наблюдения за изменениями спектра. Некоторые анализаторы на начальном участке производят линейное усреднение, а затем переходят на скользящее.
Распределение максимальных значений. Спектральные анализаторы, основанные на методе БПФ, обладают третьей возможностью обработки спектров: усреднением пиковых значений. Это название неудачно, так как в действительности речь идет о размещении в памяти максимумов.
При усреднении пиковых значений сравниваются между собой последовательно поступающие на анализатор спектры и сохраняется только максимальная величина амплитуды, достигаемая для каждой частоты. В результате обработки величины, размещенные в памяти, представляют собой максимальные амплитуды на каждой частоте для обработанной совокупности спектров.
Такой тип обработки полезен в механике при измерении параметров структур в состоянии вибрации и в акустике при измерении экстремальных уровней. Он используется, например, Для обнаружения критических моментов разбалансированной ротационной машины.
Сравнение спектров.
Спектральные цифровые анализаторы, основанные на методе БПФ, обычно дают возможность сравнения
двух спектров, полученных в разных условиях. Этого можно добиться одновременным выводом на экран двух спектров, но относительно простые дополнительные вычисления, выполненные в самом приборе или в дополнительном вычислительном устройстве, позволяют также получать разность или отношение двух спектров. Наконец, может оказаться полезным изменить схему вычислений и выполнить фурье-анализ с различными значениями ширины полосы элементарного фильтра.
Одновременный вывод на экран двух спектров. Спектр сигнала, записанный в памяти анализатора, может быть в любой момент использован для сравнения с любым другим мгновенным спектром. Для облегчения визуального сравнения двух спектров, выведенных на экран прибора, обычно используется курсор (или светящаяся метка). Таким образом, можно одновременно представлять совмещенные или раздвинутые по экрану мгновенный и усредненный спектры для определения частотных компонент с наибольшей дисперсией, амплитуды которых для обоих спектров будут сильно различаться. После нескольких усреднений мгновенного спектра это различие будет исчезать.
Можно сравнивать два спектра, полученных усреднением различного числа мгновенных спектров, например при определении числа усреднений для получения заданной точности при М=32 и 128.
Для лучшей интерпретации природы исследуемого сигнала сравнивают результаты линейного и экспоненциального усреднений, а для определения эффективности преобразования — два усредненных спектра, полученных с помощью различной предварительной фильтрации.
Разность двух спектров. Разность двух спектров получается вычитанием по точкам одного спектра из другого. Одно из наиболее частых применений этого метода состоит в вычитании шума из смеси сигнала с шумом. Для этого необходимо сначала измерить спектр сигнала вместе с шумом, затем спектр только шума. После вычитания получится чистый спектр сигнала.
Этот метод применяется при изучении дефектов ротационных машин, где фоновый шум создается внешними факторами. Измерения проводят сначала с работающим механизмом (например, турбогенератором переменного тока), затем при выключенном механизме регистрируют окружающий шум и вычитают второй спектр из первого.
Отношение двух спектров. Отношение двух спектров вычисляется поточечным делением значений одного спектра на другой.
Рассмотрим систему, на вход которой поступает белый гауссов шум. Измеряя отношение спектральной плотности мощности
на выходе этой системы  к спектральной плотности на входе
к спектральной плотности на входе  можно получить модуль передаточной функции рассматриваемой системы в определенном диапазоне частот:
можно получить модуль передаточной функции рассматриваемой системы в определенном диапазоне частот:

Этот метод предполагает отсутствие шумов; с его помощью нельзя определить изменение фазы, вносимое системой. Тем не менее он широко применяется для схем, частотная характеристика которых лежит в известных пределах. Известно, например, что наладка остро настроенных фильтров очень трудна классическими методами, так как для получения графика спектральной характеристики методом развертки требуется большое время, тем большее, чем более высока добротность  исследуемого фильтра. Эту процедуру можно упростить, используя фурье-анализатор, в памяти которого предварительно записана спектральная характеристика фильтра-образца. После этого достаточно наложить на экране характеристики фильтра-образца и исследуемого фильтра и осуществить необходимую регулировку. Операция занимает мало времени, в особенности если используется экспоненциальный тип усреднения, позволяющий быстрее реагировать на изменения.
исследуемого фильтра. Эту процедуру можно упростить, используя фурье-анализатор, в памяти которого предварительно записана спектральная характеристика фильтра-образца. После этого достаточно наложить на экране характеристики фильтра-образца и исследуемого фильтра и осуществить необходимую регулировку. Операция занимает мало времени, в особенности если используется экспоненциальный тип усреднения, позволяющий быстрее реагировать на изменения.
Измерение когерентности. Для определения передаточной функции системы используют взаимные спектры мощности (или функции плотности взаимных спектров), с помощью которых удается избежать искажений, вызванных паразитными шумами, и получить фазовые соотношения для используемой системы. Для измерения когерентности используются анализаторы с двумя входами в отличие от рассмотренных ранее фурье-анализаторов с одним входом, т. е. не приспособленных к одновременному вычислению двух преобразований Фурье.
Взаимные спектры были рассмотрены в гл. 10 и 13. Напомним, что функция взаимной спектральной плотности  характеризует подобие двух сигналов на каждой из частот, которое соответствует условной вероятности появления частот в обоих сигналах. Она является комплексной функцией, действительная часть которой характеризует совпадение амплитуд, а мнимая — соотношение фаз. Модуль функции равен произведению амплитудных спектров, а аргумент представляет собой разность их фаз.
характеризует подобие двух сигналов на каждой из частот, которое соответствует условной вероятности появления частот в обоих сигналах. Она является комплексной функцией, действительная часть которой характеризует совпадение амплитуд, а мнимая — соотношение фаз. Модуль функции равен произведению амплитудных спектров, а аргумент представляет собой разность их фаз.
Если на вход какой-либо системы поступает только один сигнал, то в общем случае анализ входного и выходного сигналов может не дать информации о причинной связи между ними, так как невозможно понять, с чем связаны параметры
выходного сигнала: с усилением системы, уровнем входного сигнала или с влиянием на сигнал возмущений в системе. Мы увидим, что функция когерентности, вычисленная из взаимных спектров, позволяет определить связь между входным и выходным сигналами: она определяет доверительный уровень при измерении передаточной функции.
Функция взаимной спектральной плотности является прямым преобразованием Фурье взаимно-корреляционной функции

Функция спектральной плотности представляет собой спектр автокорреляционной функции  Это действительная, всегда положительная функция, которая получается умножением амплитудного спектра на свое комплексно-сопряженное значение:
Это действительная, всегда положительная функция, которая получается умножением амплитудного спектра на свое комплексно-сопряженное значение:  Она является прямым преобразованием Фурье автокорреляционной функции
Она является прямым преобразованием Фурье автокорреляционной функции 
Передаточная функция системы тогда определяется выражением

Функция когерентности может приближенно рассматриваться как эквивалент в области частот нормированной корреляционной функции (коэффициент корреляции). Преимущество когерентности перед корреляцией заключается в возможности распознавания сходных частотных компонент в исследуемых сигналах, даже если общее сходство является очень слабым. Когерентность определяется как отношение квадрата модуля среднего взаимного спектра к произведению средних входного и выходного спектров [10]:

Это выражение показывает, какая часть выходной мощности изучаемой системы эффективно связана с входной; в знаменателе стоит величина, зависящая от внешних шумов, а числитель от них не зависит.
Если предыдущее выражение записать в виде

то можно сделать вывод, что для каждой анализируемой частоты величина когерентности соответствует той части выходной мощности, которую дает только входной сигнал. Таким образом, для каждой частоты когерентность будет коэффициентом, изменяющимся в пределах  Максимальное значение (1) показывает полную когерентность (передача всей мощности с
Максимальное значение (1) показывает полную когерентность (передача всей мощности с
входа на выход), тогда как значение 0 показывает, что мощность, измеряемая на выходе, не имеет никакого отношения к входной.
Как и при обработке спектров, статистическая точность измерения когерентности зависит от числа М усредняемых членов. В табл. 19.11 приведены предельные значения разброса когерентности  для М = 16, 32, 64, 128, 256 с доверительной вероятностью 90%. Точность определения модуля и фазы передаточной функции из спектров автокорреляционной и взаимно-корреляционной функции также связана с числом усреднений и с измеренным значением когерентной функции.
для М = 16, 32, 64, 128, 256 с доверительной вероятностью 90%. Точность определения модуля и фазы передаточной функции из спектров автокорреляционной и взаимно-корреляционной функции также связана с числом усреднений и с измеренным значением когерентной функции.
Таблица 19.11 (см. скан)
В табл. 19.12 и 19.13 приведены границы доверительных интервалов для 90% доверительной вероятности в зависимости от числа усредняемых членов соответственно для модуля (в децибелах) и для фазы (в градусах).
Отношение сигнала к шуму на выходе системы выражается через функцию когерентности как 
Таблица 19.12 (см. скан)
Таблица 19.13 (см. скан)
Действительно, мощность сигнала на выходе есть  а мощность шума
а мощность шума 
Анализ с помощью фильтров с шириной спектральной полосы 1 октава и  октавы. Отметим еще одну возможность, предоставляемую цифровыми спектральными анализаторами для обработки сигналов. Она заключается в представлении анализатора в виде набора эквивалентных элементарных фильтров с постоянным отношением ширины полос соседних фильтров, равным, например,
октавы. Отметим еще одну возможность, предоставляемую цифровыми спектральными анализаторами для обработки сигналов. Она заключается в представлении анализатора в виде набора эквивалентных элементарных фильтров с постоянным отношением ширины полос соседних фильтров, равным, например,  октавы (или 1 октаве). Такие фильтры традиционно используются в акустике (инфразвук, слышимый диапазон и ультразвук) для измерения энергии звука, нормированной на ширину полосы.
октавы (или 1 октаве). Такие фильтры традиционно используются в акустике (инфразвук, слышимый диапазон и ультразвук) для измерения энергии звука, нормированной на ширину полосы.
До сих пор мы предполагали, что ширина спектральных полос всех элементарных фильтров постоянна во всем диапазоне изучаемых частот. В этом случае говорят, что анализ осуществлен с постоянной шириной полосы  Теперь рассмотрим случай, когда ширина полосы растет пропорционально частоте, т. е. анализ идет при постоянном отношении
Теперь рассмотрим случай, когда ширина полосы растет пропорционально частоте, т. е. анализ идет при постоянном отношении  где через
где через  обозначается центр полосы пропускания фильтра. В этом случае анализатор работает в логарифмическом масштабе по частоте: если знаменатель прогрессии частот
обозначается центр полосы пропускания фильтра. В этом случае анализатор работает в логарифмическом масштабе по частоте: если знаменатель прогрессии частот  равен
равен  то говорят, что используются фильтры шириной
то говорят, что используются фильтры шириной  октав. В частности, при
октав. В частности, при  ширина полосы фильтра составляет
ширина полосы фильтра составляет  октавы, расстояние между центрами полос фильтров также
октавы, расстояние между центрами полос фильтров также  октавы (или
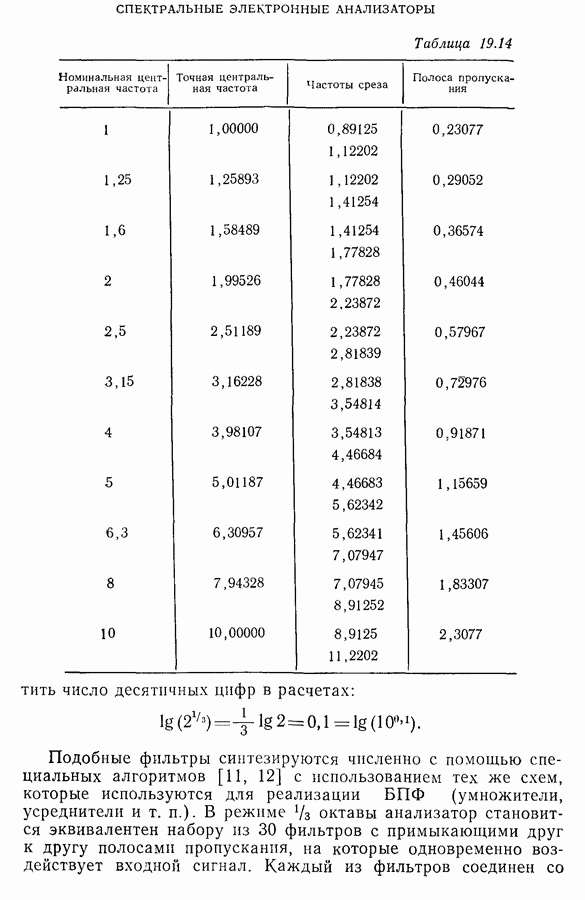
октавы (или  ). В табл. 19.14 приведены основные данные полос пропускания таких фильтров.
). В табл. 19.14 приведены основные данные полос пропускания таких фильтров.
Постоянное отношение ширины к положению центра спектральной полосы для фильтров в  октавы составляет
октавы составляет

Точное значение этой величины равно 0,23156, вычисленной в предложении, что  На практике предпочитают пользоваться округленным значением
На практике предпочитают пользоваться округленным значением  что позволяет
что позволяет
Таблица 19.14 (см. скан)
сократить число десятичных цифр в расчетах:

Подобные фильтры синтезируются численно с помощью специальных алгоритмов [11, 12] с использованием тех же схем, которые используются для реализации БПФ (умножители, усреднители и т. п.). В режиме  октавы анализатор становится эквивалентен набору из 30 фильтров с примыкающими друг к другу полосами пропускания, на которые одновременно воздействует входной сигнал. Каждый из фильтров соединен со
октавы анализатор становится эквивалентен набору из 30 фильтров с примыкающими друг к другу полосами пропускания, на которые одновременно воздействует входной сигнал. Каждый из фильтров соединен со
схемой возведения в квадрат, а затем со схемой усреднения. Центральные частоты полос пропускания фильтров расположены между 25 Гд и 20 кГц. Анализ с помощью фильтров с шириной полосы, равной 1 октаве, проводят, группируя сконструированные ранее фильтры по 3. При этом общее число фильтров уменьшается до 10.
Как и при анализе с постоянной шириной полосы пропускания фильтров  наилучшей точности измерений можно добиться путем последовательных усреднений измеряемых спектров.
наилучшей точности измерений можно добиться путем последовательных усреднений измеряемых спектров.
Системы с встроенными спектральными анализаторами.
Спектральный анализ широко применяется в самых различных областях науки и техники.
Рис. 19.12. (см. скан)
Очень часто анализаторы используются в качестве измерительных устройств, которые связаны с другим, более специфическим оборудованием. Применение стандартных интерфейсов облегчает их использование в системах автоматического управления. На рис. 19.12 приведена полная схема системы измерения фазовых шумов частотного синтезатора.
Большая часть цифровых спектральных анализаторов, основанных на методе БПФ, предназначена для сопряжения с двумя типами интерфейсов, ставших уже классическими:
• стандарт IEEE 488-1978 общего назначения (относительно! медленный);
• магистраль обмена, совместимая с мини-ЭВМ, которая: позволяет осуществлять гораздо более быстрый обмен и эффективнее использовать рабочее время как анализатора, так и ЭВМ.
Выбор интерфейса зависит от области применения и часто» определяется имеющимся периферийным оборудованием.
В памяти анализатора хранятся данные, информация с» командах оператора и содержимое регистра состояния системы. Данными, находящимися в распоряжении системы, являются мгновенные и усредненные спектры мощности, комплексный спектр в виде действительной и мнимой частей, а также входной сигнал как функция от времени. Доступ к данным, определение содержимого регистра состояния, управление системой сводятся к обращению по соответствующим адресам памяти в надлежащие моменты времени.
Одни типы передачи информации, такие, например, как считывание спектра из памяти анализатора, могут происходить в любой момент: они асинхронны по отношению к обработке, осуществляемой анализатором. Другие типы передачи, такие, как подача цифровых данных на вход анализатора, должны осуществляться в строго определенные моменты цикла обработки, по отношению к которой они синхронны. Для осуществления-синхронной передачи внешнее управляющее устройство должно остановить блок внутренней обработки в определенной точке программы, выполнить необходимую передачу информации и, наконец, передать управление анализатору для продолжения обработки спектра.
Стандартный интерфейс IEEE 488-1978.1) Благодаря все большему распространению мини-ЭВМ пользователи могут автоматизировать свои измерительные комплексы простыми средствами, даже если отдельные приборы выполняют очень сложные функции. Цифровой интерфейс для программируемых устройств IEEE 488-1978 в таких случаях служит для соединения стандартными кабелями и разъемами различных электронных устройств независимо от их назначения. С его помощью непосредственно с анализатором можно связать генератор сигналов, программируемые фильтры, мультиметры (универсальные измерители), регистраторы нестационарных процессов, калибровочные источники напряжения, тока, сопротивления и т. д.
Каждое из устройств, соединяемых с помощью этого интерфейса, играет по крайней мере одну из трех ролей — источника,
приемника и контроллера, функции которых состоят в следующем:
• источник направляет данные к другому устройству по магистрали интерфейса;
• приемник получает данные от другого устройства;
• контроллер управляет обменом данных по магистрали, выделяя устройства, которые должны выдавать и получать данные в процессе измерения. Он может также приостанавливать определенные устройства и завершать выполняемые ими действия.

Рис. 19.13.  — интерфейс свободен,
— интерфейс свободен,  — внимание,
— внимание,  — запрос на обслуживание,
— запрос на обслуживание,  — дистанционное управление,
— дистанционное управление,  — конец передачи,
— конец передачи,  — данные на магистрали,
— данные на магистрали,  — неготовность к приему данных,
— неготовность к приему данных,  — данные не приняты.
— данные не приняты.
Многие устройства могут одновременно служить и источниками, и приемниками. Например, мультиметр работает как приемник, когда получает программные инструкции, и как источник, когда передает результаты измерений другим приборам системы, таким, как спектральный анализатор или печатающее устройство. Роль приемников могут одновременно выполнять многие устройства в системе, но во избежание недоразумений источником в каждый момент может быть только одно устройство.
Кроме мини-ЭВМ, которая управляет измерительным комплексом, к магистрали можно присоединить еще до 14 устройств. Длина соединительного кабеля равна  на устройство, полная длина должна быть в пределах
на устройство, полная длина должна быть в пределах  Адаптеры параллельной (IEEE) и последовательной (RS232C или
Адаптеры параллельной (IEEE) и последовательной (RS232C или  передачи позволяют передавать данные на расстояние до 1 км, но с уменьшенной скоростью (не более 20 кбит/с). Магистраль
передачи позволяют передавать данные на расстояние до 1 км, но с уменьшенной скоростью (не более 20 кбит/с). Магистраль
обмена состоит из 16 шин и организована следующим образом, (рис. 19.13):
• Передача данных. Для передачи данных отводится 8 шин, по которым параллельным кодом передается  -разрядное слово в коде ASCIII). Шины данных двунаправленные и могут передавать либо адрес, либо данные. Обмен данными осуществляется по асинхронному принципу для обеспечения максимальной совместимости устройств различного типа.
-разрядное слово в коде ASCIII). Шины данных двунаправленные и могут передавать либо адрес, либо данные. Обмен данными осуществляется по асинхронному принципу для обеспечения максимальной совместимости устройств различного типа.
• Управление. Обмен информацией между различными устройствами происходит под контролем шин управления (именно они определяют тип информации на шинах данных). Всего шин управления 5. Шина «Внимание», обозначаемая  позволяет узнать, является ли информация на шинах данных адресом или данными. Шина
позволяет узнать, является ли информация на шинах данных адресом или данными. Шина  служит для передачи сигнала требования на обмен данными, который устройство может выработать в любой момент. Этот сигнал служит только для привлечения внимания контроллера, который решает, можно ли разрешить обмен. На шину
служит для передачи сигнала требования на обмен данными, который устройство может выработать в любой момент. Этот сигнал служит только для привлечения внимания контроллера, который решает, можно ли разрешить обмен. На шину  источник подает сигнал отметки конца передачи после обмена определенным количеством информации по шинам данных. Шина «Интерфейс свободен», обозначаемая
источник подает сигнал отметки конца передачи после обмена определенным количеством информации по шинам данных. Шина «Интерфейс свободен», обозначаемая  может быть использована только контроллером для прекращения всех передач по шинам данных, в том числе и адресов устройств. Шина
может быть использована только контроллером для прекращения всех передач по шинам данных, в том числе и адресов устройств. Шина  переключает управление устройствами, подключенными к магистрали с местного на дистанционное и наоборот.
переключает управление устройствами, подключенными к магистрали с местного на дистанционное и наоборот.
• Команды передачи. Шины команд передачи (их всего 3) позволяют обмениваться информацией устройствам, работающим с разной скоростью. Когда источник готов к передаче данных, он сообщает об этом сигналом на шине  Как только все адресуемые приемники готовы получить информацию, выставленную на шинах данных, они об этом сообщают по шине
Как только все адресуемые приемники готовы получить информацию, выставленную на шинах данных, они об этом сообщают по шине  Когда приемники получают информацию, находящуюся на шинах данных, они сообщают об этом сигналом по шине
Когда приемники получают информацию, находящуюся на шинах данных, они сообщают об этом сигналом по шине  Таким образом, две шины
Таким образом, две шины  и
и  позволяют отрегулировать скорость передачи данных по наиболее медленному устройству. Максимальная скорость передачи составляет
позволяют отрегулировать скорость передачи данных по наиболее медленному устройству. Максимальная скорость передачи составляет  Сигналы магистрали IEEE совместимы с отрицательной логикой ТТЛ:
Сигналы магистрали IEEE совместимы с отрицательной логикой ТТЛ:

Оборудование автоматического контроля. Подобный интерфейс позволяет внешнему контроллеру, такому, как мини-ЭВМ, иметь доступ ко всем видам памяти (входной, БПФ, усредняющей, выходной и т. п.) и управлять всеми функциями анализатора, который играет подчиненную роль. Накопление данных, обработанных анализатором, ведется частями по 8 бит (или в байтах). Мини-ЭВМ управляет операциями измерения, соединяет устройства в конфигурации, необходимые для выполнения измерений, обрабатывает данные, анализирует и интерпретирует результаты.
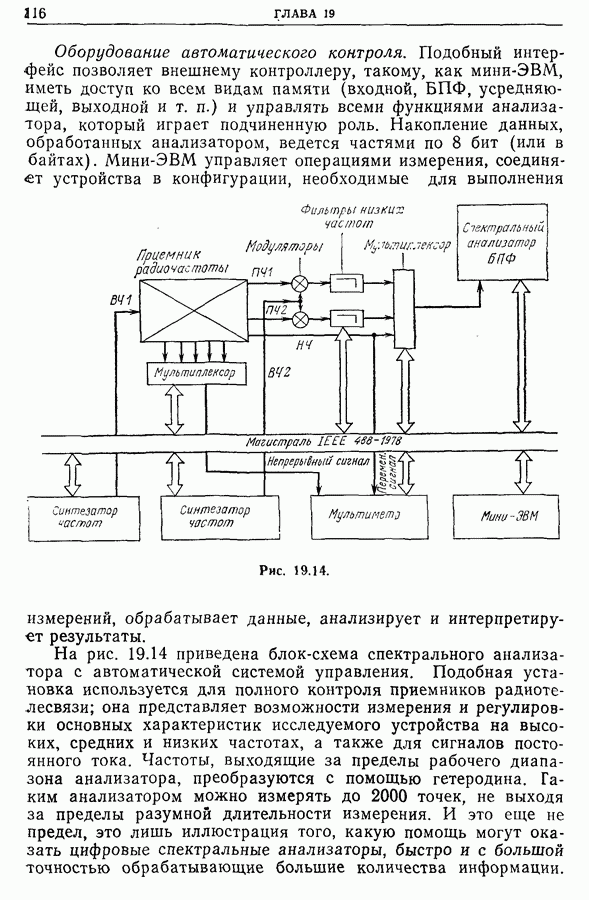
Рис. 19.14. (см. скан)
На рис. 19.14 приведена блок-схема спектрального анализатора с автоматической системой управления. Подобная установка используется для полного контроля приемников радиотелесвязи; она представляет возможности измерения и регулировки основных характеристик исследуемого устройства на высоких, средних и низких частотах, а также для сигналов постоянного тока. Частоты, выходящие за пределы рабочего диапазона анализатора, преобразуются с помощью гетеродина. Таким анализатором можно измерять до 2000 точек, не выходя за пределы разумной длительности измерения. И это еще не предел, это лишь иллюстрация того, какую помощь могут оказать цифровые спектральные анализаторы, быстро и с большой точностью обрабатывающие большие количества информации.
ЛИТЕРАТУРА
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- Глава 15. СИНХРОННОЕ ДЕТЕКТИРОВАНИЕ
- 15.2. Схема метода
- 15.3. Теория синхронного детектирования
- 15.4. Синхронное детектирование в режиме развертки
- 15.5. Примеры применения синхронных детекторов
- 15.6. Совершенствование синхронных детекторов
- Глава 16. ИСПОЛЬЗОВАНИЕ МНОГОКАНАЛЬНЫХ АНАЛИЗАТОРОВ ПРИ СТАТИЧЕСКОЙ ОБРАБОТКЕ ИЗМЕРЕНИЙ
- 16.2. Характеристики многоканальных анализаторов
- 16.3. Схема системы обработки
- 16.4. Примеры применения
- Глава 17. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ
- 17.2. Частный случай белого шума. Согласованный фильтр
- 17.3. Согласованная фильтрация и корреляция Корреляция.
- 17.4. Реализация согласованных фильтров методом «взвешивания»
- 17.5. Рекурсивная согласованная фильтрация [7]
- 17.6. Применения метода согласованной фильтрации
- Глава 18. ОСНОВНЫЕ ТИПЫ ЭЛЕКТРОННЫХ КОРРЕЛОМЕТРОВ
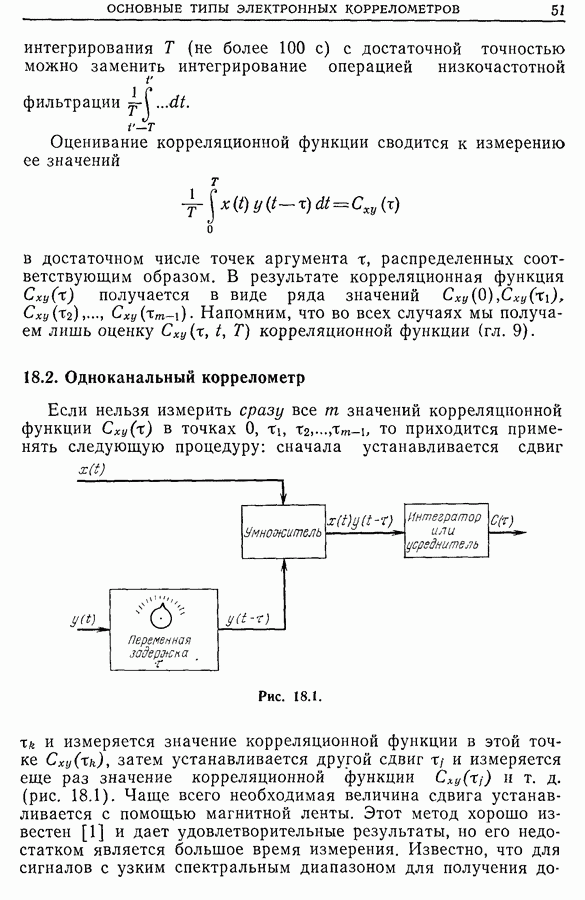
- 18.2. Одноканальный коррелометр
- 18.3. Автоматические коррелометры
- 18.4. Автоматические коррелометры на линии с исследуемым сигналом
- 18.5. Автоматические коррелометры реального времени (или мультикоррелометры)
- 18.6. Коррелометры на больших интегральных схемах
- 18.7. Коррелометры реального времени для высокочастотных сигналов
- 18.8 Развитие коррелометров
- 18.9. Приборы с зарядовой связью [11]
- Глава 19. СПЕКТРАЛЬНЫЕ ЭЛЕКТРОННЫЕ АНАЛИЗАТОРЫ
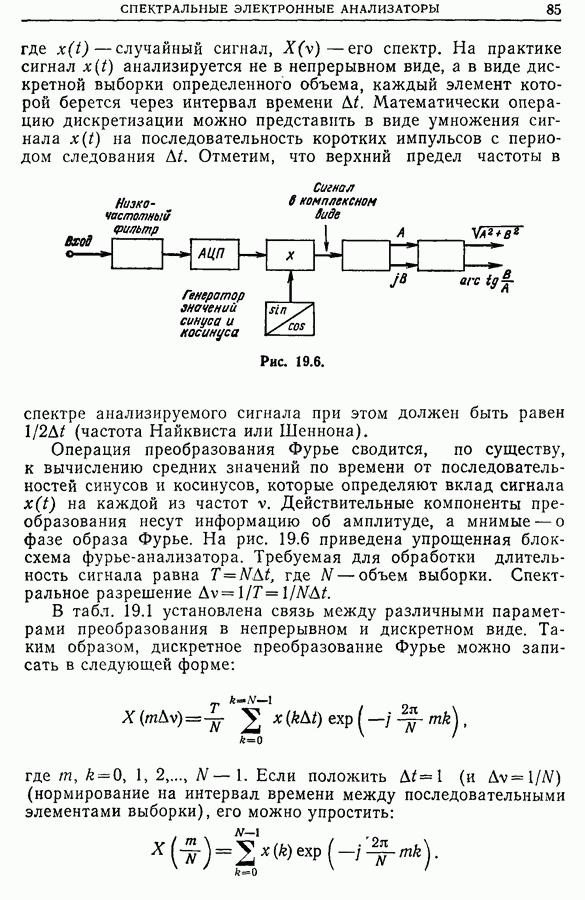
- 19.2. Спектральные анализаторы, основанные на методе непосредственного преобразования Фурье
- 19.3. Применения анализаторов на основе метода БПФ
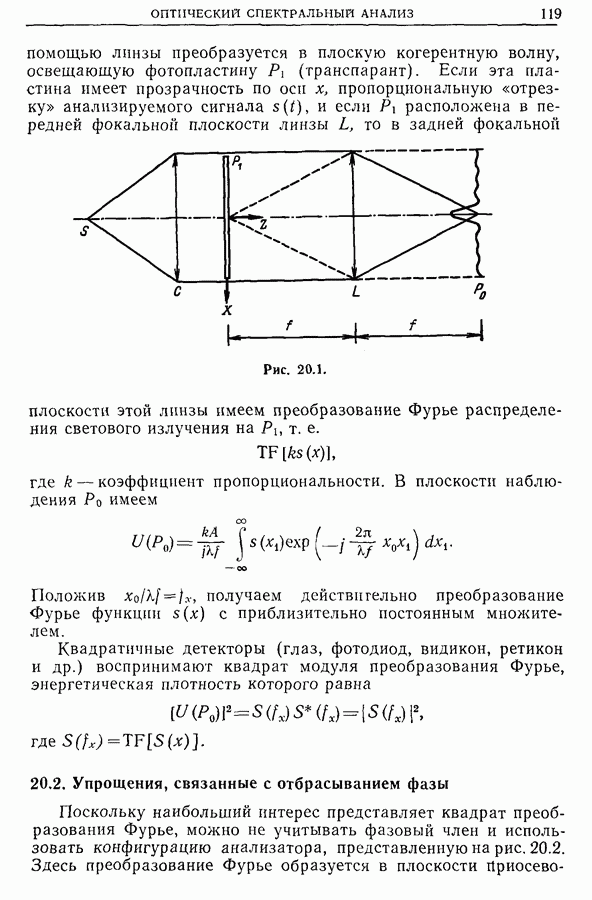
- Глава 20. ОПТИЧЕСКИЙ СПЕКТРАЛЬНЫЙ АНАЛИЗ
- 20.2. Упрощения, связанные с отбрасыванием фазы
- 20.3. Эффект виньетирования
- 20.4. Двумерный анализ
- 20.5. Точечный монохроматический источник
- 20.6. Электрооптическое преобразование сигнала
- 20.7. Устройства отображения на жидких кристаллах
- 20.8. Ограничения устройств отображения
- 20.9. Модулятор на основе эффекта Покельса (PROM)
- 20.10. Трубки Титус и Фототитус
- 20.11. Другие электрооптические кристаллы
- 20.12. Спектральный анализ и интегральная оптика
- 20.13. Взаимные спектры
- Глава 21. НЕКОТОРЫЕ ПРАКТИЧЕСКИЕ ПРИМЕНЕНИЯ МЕТОДОВ ОБРАБОТКИ СИГНАЛОВ
- 21.2. Исследование ядерных сред
- 21.3. Ядерный магнитный резонанс (ЯМР) с возбуждением случайным сигналом
- 21.4. Идентификация процессов. Измерение импульсных откликов и передаточных функций
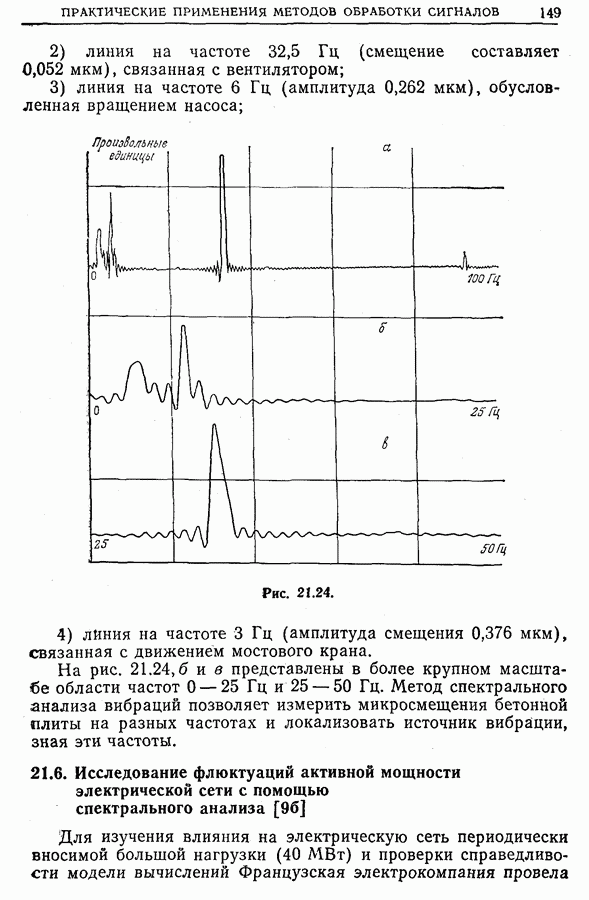
- 21.5. Спектральный анализ собственных колебаний бетонных плит
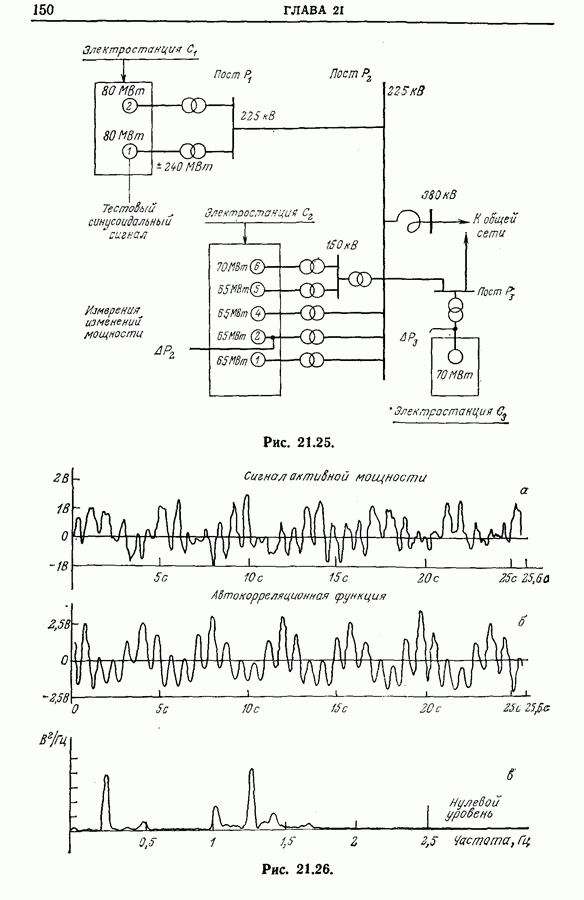
- 21.6. Исследование флюктуаций активной мощности электрической сети с помощью спектрального анализа
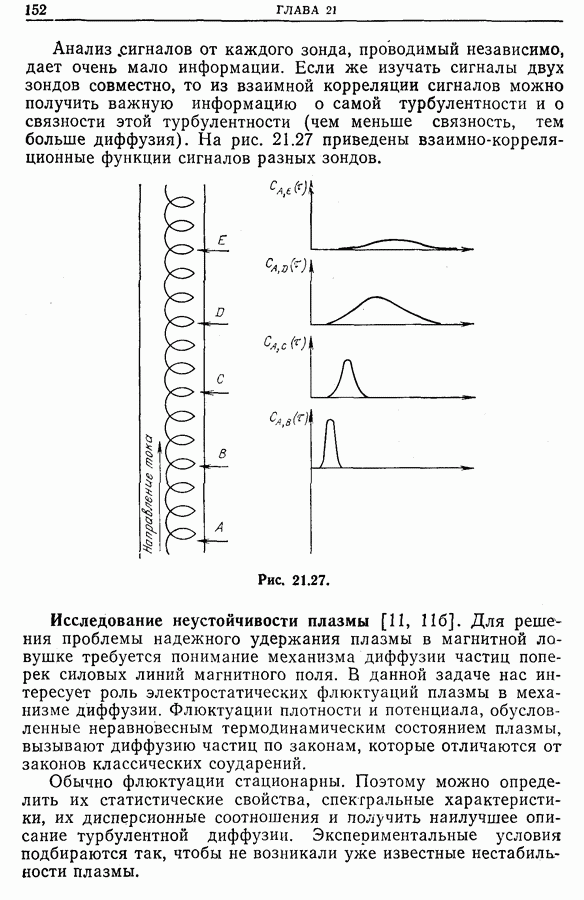
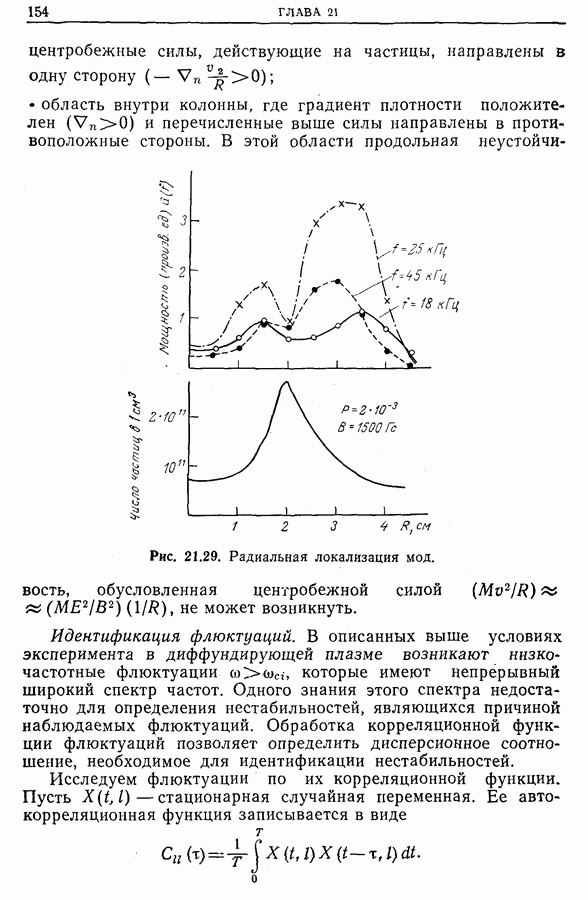
- 21.7. Изучение турбулентности
- 21.8. Применения в геофизике
- 21.9. Применения в астрофизике
- 21.10. Применения в астрономии и радиоастрономии
- 21.11. Применения в биологии и медицине
- 21.12. Применения в акустике
- 21.13. Исследование процессов намагничивания ферромагнетиков
- 21.14. Применения новых методов обработки сигналов
- 21.15. Заключение
- Глава 22. ПРИМЕНЕНИЕ МЕТОДОВ ОБРАБОТКИ СИГНАЛОВ ДЛЯ АНАЛИЗА ВИБРАЦИЙ РОТАЦИОННЫХ МАШИНА
- 22.2. Анализ поведения системы «ротационная машина — конструкция»
- 22.3. Анализ вибраций лопастей турбин
- 22.4. Балансировка ротационных машин
- Глава 23. ФУНКЦИЯ НЕОПРЕДЕЛЕННОСТИ
- 23.2. Временная корреляция. Временной сдвиг
- 23.3. Частотная корреляция. Частотный сдвиг
- 23.4. Временной и частотный сдвиги. Функция неопределенности
- 23.5. Функция неопределенности Вудворда
- 23.6. Взаимная функция неопределенности
- 23.7. Некоторые свойства функции неопределенности
- 23.8. Представление функций неопределенности
- 23.9. Примеры функций неопределенности
- 23.10. Применение функции неопределенности
- 23.11. Применение функций неопределенности для описания линейных неоднородных во времени систем. Обобщение понятия передаточной функции. Функция диффузии (функция рассеивания)
- 23.12. Генерация тестового сигнала
- 23.13. Прибор для измерения функции неопределенности в режиме реального времени
- Глава 24. ПОНЯТИЕ МГНОВЕННОГО СПЕКТРА ИЛИ ЧАСТОТНО-ВРЕМЕННОГО ПРЕДСТАВЛЕНИЯ В АНАЛИЗЕ И СИНТЕЗЕ СИГНАЛОВ
- 24.2. Примеры спектрального анализа модулированных и немодулированных сигналов
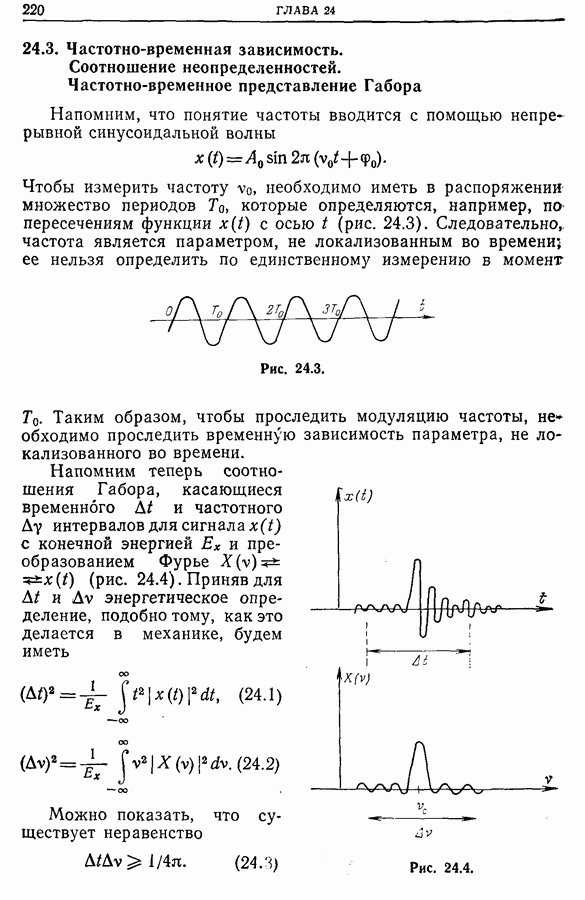
- 24.3. Частотно-временная зависимость. Соотношение неопределенностей. Частотно-временное представление Габора
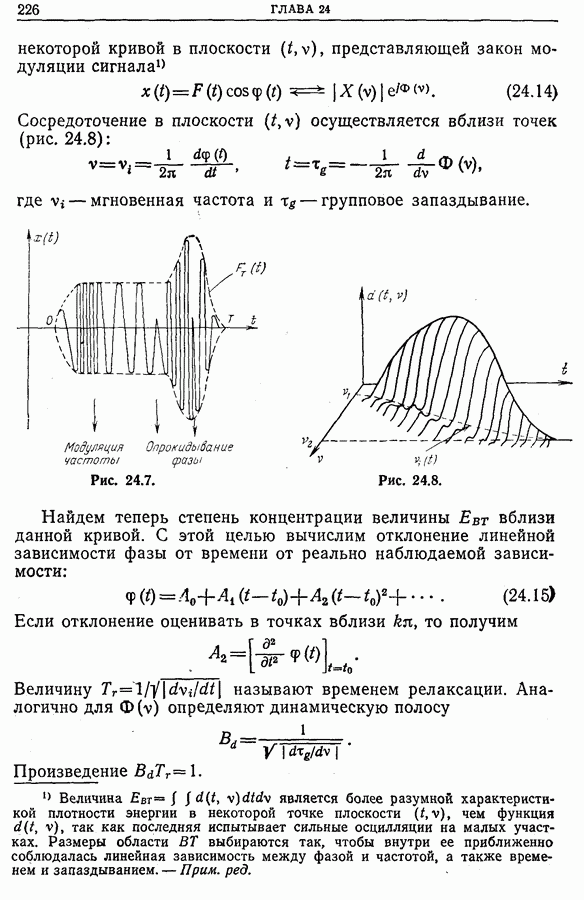
- 24.4. Представление [t, v] по Бонне. Мгновенный спектр мощности по Биллю. Функция неопределенности
- 24.5. Другие определения частотно-временного представления
- 24.6. Измерение мгновенных спектров
- 24.7. Обобщение понятия мгновенного спектра мощности на случайные локально-стационарные сигналы. Функция структуры. Функция диффузии
- 24.8 Восстановление сигнала x(t) по известной функции
- 24.9. Заключение
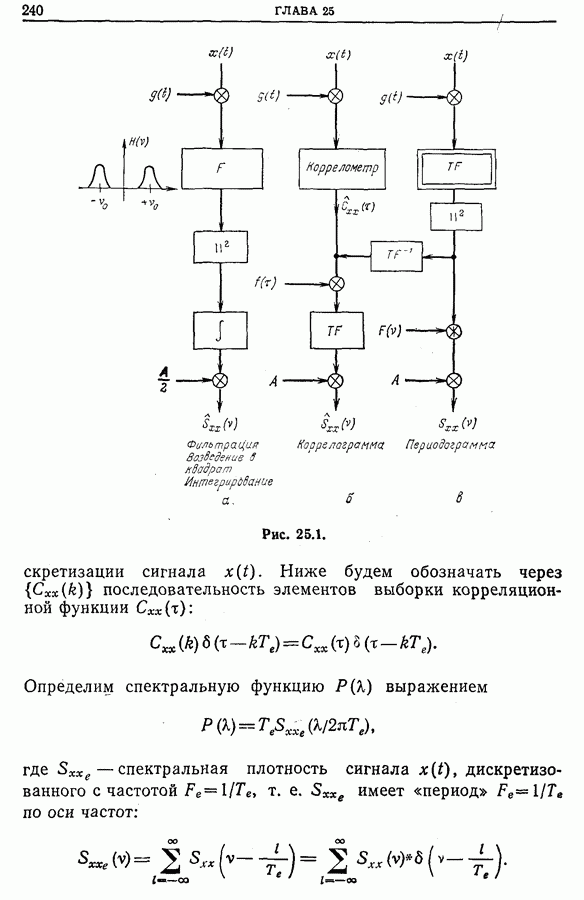
- Глава 25. НОВЫЕ МЕТОДЫ СПЕКТРАЛЬНОГО АНАЛИЗА
- 25.2. Проблемы, обусловленные дискретизацией корреляционной функции
- 25.3. Постановка проблемы получения спектральной функции из конечного числа значений автокорреляционной функции
- 25.4. Классический метод, основанный на преобразовании Фурье корреляционной функции
- 25.5. Метод максимума энтропии или метод авторегрессионной модели
- 25.6. Метод Писаренко
- 25.7. Смешанные методы
- 25.8. Заключение