| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
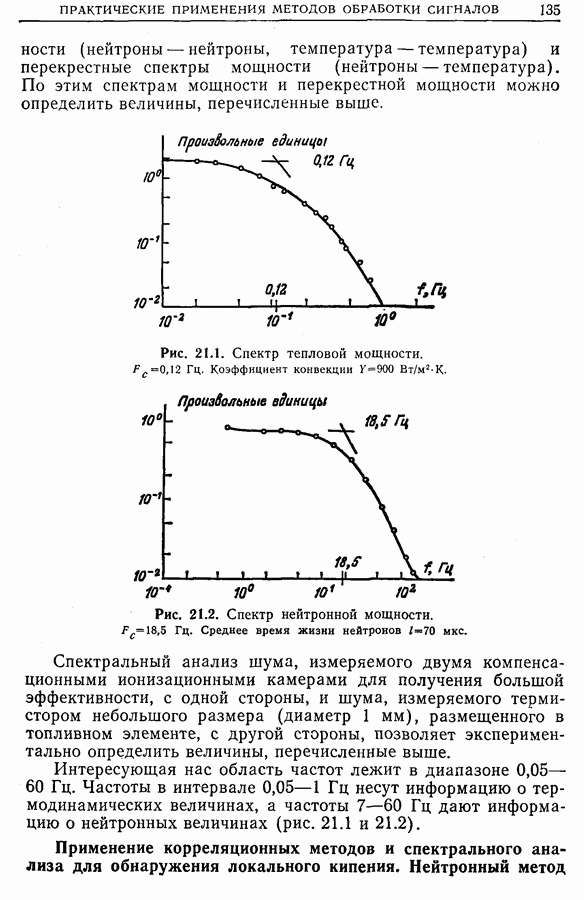
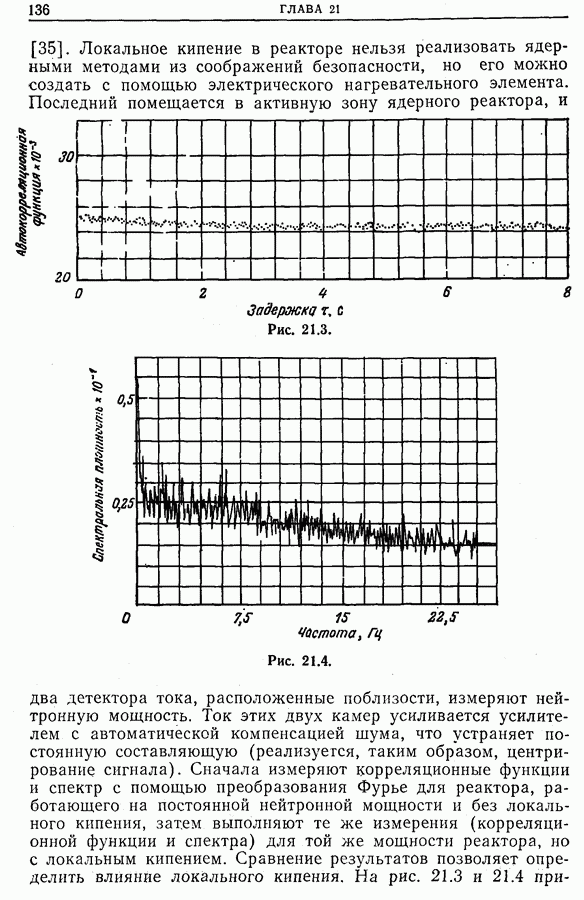
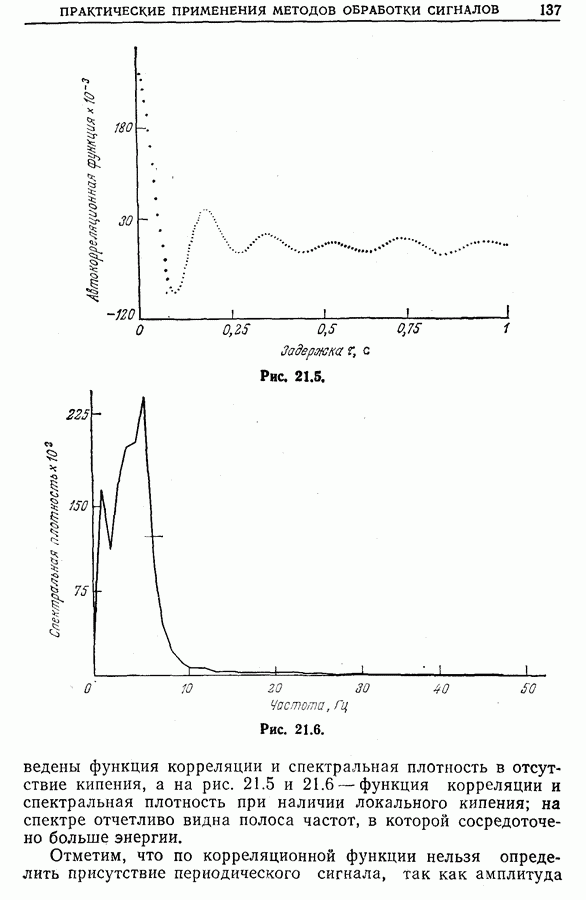
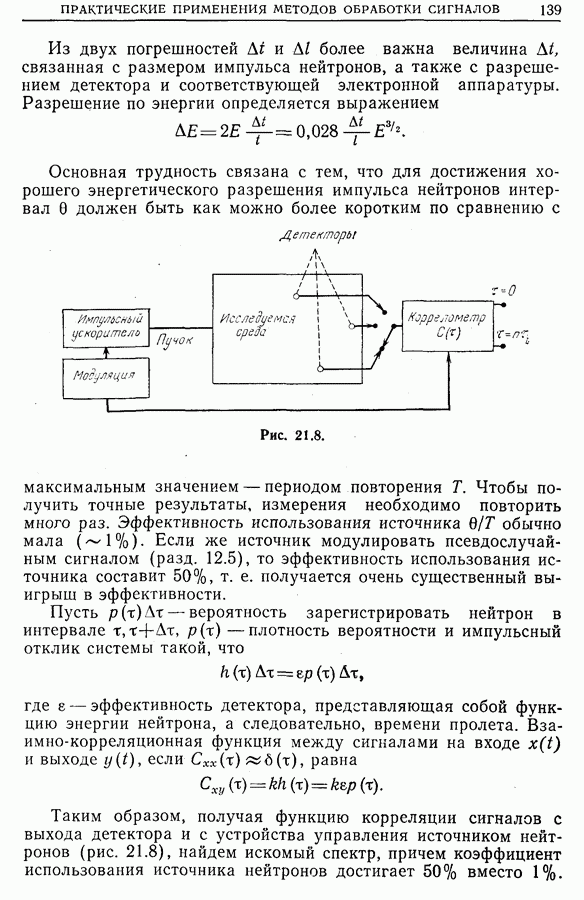
23.10. Применение функции неопределенности
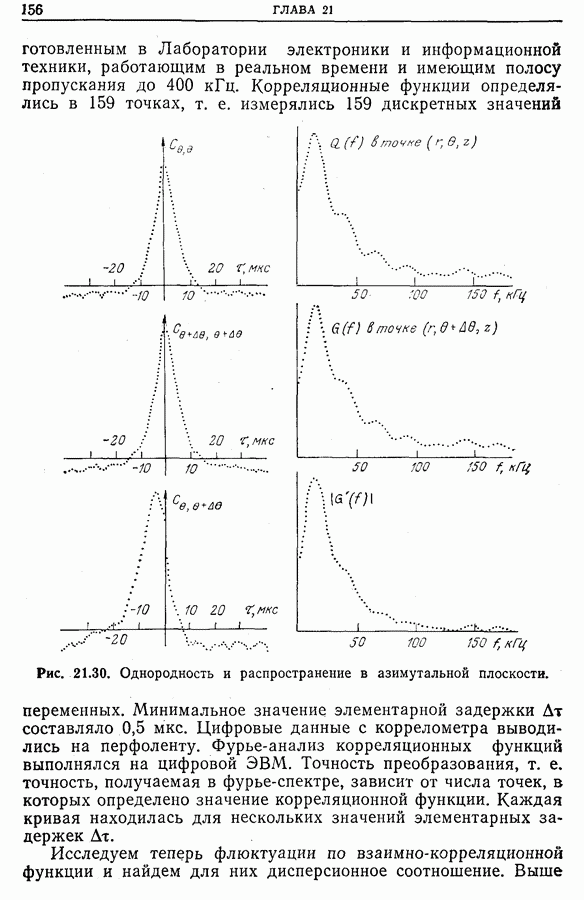
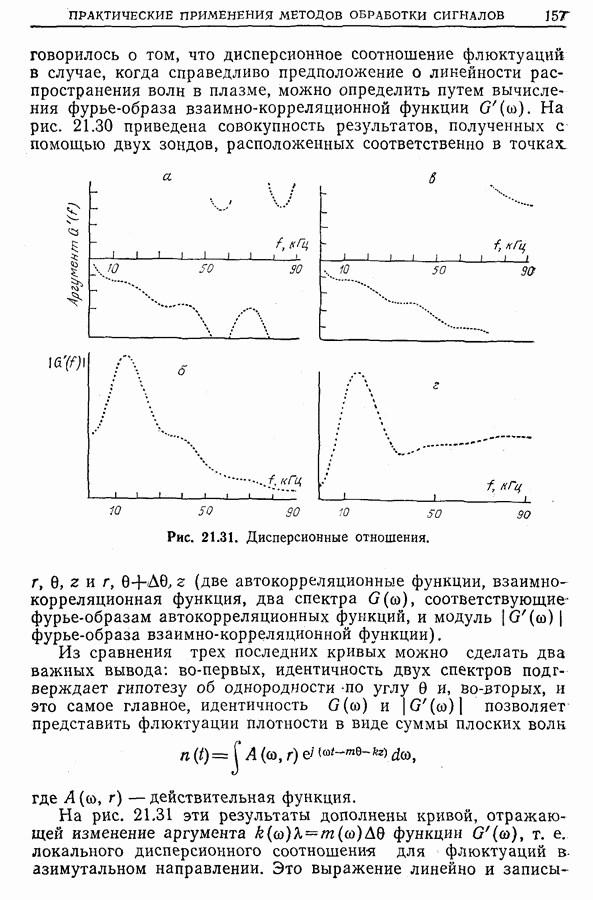
С функцией неопределенности имеют дело всякий раз, когда желают оценить одновременно временной и частотный сдвиги для двух сигналов. В радиолокации и гидролокации временной сдвиг  между отраженным и излученным сигналами связан с расстоянием до объекта, а частотный сдвиг
между отраженным и излученным сигналами связан с расстоянием до объекта, а частотный сдвиг  обусловлен радиальной скоростью объекта. Если значение
обусловлен радиальной скоростью объекта. Если значение  велико, особых трудностей не возникает, так как функция неопределенности
велико, особых трудностей не возникает, так как функция неопределенности
стремится к нулю при возрастании т. То же справедливо и для  Следовательно, если объект далеко и движется быстро, измерение
Следовательно, если объект далеко и движется быстро, измерение  не приводит к большим ошибкам. Однако при малых значениях
не приводит к большим ошибкам. Однако при малых значениях  мы приближаемся к центральному пику функции неопределенности и ошибка может быть большой.
мы приближаемся к центральному пику функции неопределенности и ошибка может быть большой.
Важной проблемой является обнаружение двух близких объектов (разрешение двух целей). Пусть две цели находятся на расстоянии  Если выполнить предыдущие расчеты, то обнаружится, что в расчетах появляется интервал времени
Если выполнить предыдущие расчеты, то обнаружится, что в расчетах появляется интервал времени  Следовательно, необходимо определить наименьшее значение интервала
Следовательно, необходимо определить наименьшее значение интервала  поддающееся измерению. Для уменьшения интервала необходимо, чтобы функция неопределенности спадала как можно быстрее при увеличении Дт. Если же требуется определить скорости двух целей, необходимо, чтобы функция
поддающееся измерению. Для уменьшения интервала необходимо, чтобы функция неопределенности спадала как можно быстрее при увеличении Дт. Если же требуется определить скорости двух целей, необходимо, чтобы функция  резко спадала с увеличением
резко спадала с увеличением  Поскольку объем под поверхностью
Поскольку объем под поверхностью  является постоянным, очевидно невозможно иметь одновременно хорошее разрешение для
является постоянным, очевидно невозможно иметь одновременно хорошее разрешение для  Отсюда следует справедливость названия «функция неопределенности», так как сигнал, оптимальный с точки зрения разрешения скоростей, нельзя использовать для получения хорошего разрешения расстояний и, наоборот, сигнал, позволяющий получить хорошее разрешение расстояний, не обеспечивает высокого разрешения скоростей.
Отсюда следует справедливость названия «функция неопределенности», так как сигнал, оптимальный с точки зрения разрешения скоростей, нельзя использовать для получения хорошего разрешения расстояний и, наоборот, сигнал, позволяющий получить хорошее разрешение расстояний, не обеспечивает высокого разрешения скоростей.
Можно, однако, повысить разрешение, если учесть, что функция неопределенности имеет боковые выбросы. Проблема будет заключаться в подборе сигналов, которые имеют требуемую функцию неопределенности. Вид этой функции зависит от целей применения сигналов [8, 6]. В работах [4, 16, 17] показано, что летучая мышь использует для своего локатора попеременно два сигнала, о которых мы только что говорили: моночастотный сигнал и сигнал, линейно-модулированный по частоте.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Глава 15. СИНХРОННОЕ ДЕТЕКТИРОВАНИЕ
- 15.2. Схема метода
- 15.3. Теория синхронного детектирования
- 15.4. Синхронное детектирование в режиме развертки
- 15.5. Примеры применения синхронных детекторов
- 15.6. Совершенствование синхронных детекторов
- Глава 16. ИСПОЛЬЗОВАНИЕ МНОГОКАНАЛЬНЫХ АНАЛИЗАТОРОВ ПРИ СТАТИЧЕСКОЙ ОБРАБОТКЕ ИЗМЕРЕНИЙ
- 16.2. Характеристики многоканальных анализаторов
- 16.3. Схема системы обработки
- 16.4. Примеры применения
- Глава 17. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ
- 17.2. Частный случай белого шума. Согласованный фильтр
- 17.3. Согласованная фильтрация и корреляция Корреляция.
- 17.4. Реализация согласованных фильтров методом «взвешивания»
- 17.5. Рекурсивная согласованная фильтрация [7]
- 17.6. Применения метода согласованной фильтрации
- Глава 18. ОСНОВНЫЕ ТИПЫ ЭЛЕКТРОННЫХ КОРРЕЛОМЕТРОВ
- 18.2. Одноканальный коррелометр
- 18.3. Автоматические коррелометры
- 18.4. Автоматические коррелометры на линии с исследуемым сигналом
- 18.5. Автоматические коррелометры реального времени (или мультикоррелометры)
- 18.6. Коррелометры на больших интегральных схемах
- 18.7. Коррелометры реального времени для высокочастотных сигналов
- 18.8 Развитие коррелометров
- 18.9. Приборы с зарядовой связью [11]
- Глава 19. СПЕКТРАЛЬНЫЕ ЭЛЕКТРОННЫЕ АНАЛИЗАТОРЫ
- 19.2. Спектральные анализаторы, основанные на методе непосредственного преобразования Фурье
- 19.3. Применения анализаторов на основе метода БПФ
- Глава 20. ОПТИЧЕСКИЙ СПЕКТРАЛЬНЫЙ АНАЛИЗ
- 20.2. Упрощения, связанные с отбрасыванием фазы
- 20.3. Эффект виньетирования
- 20.4. Двумерный анализ
- 20.5. Точечный монохроматический источник
- 20.6. Электрооптическое преобразование сигнала
- 20.7. Устройства отображения на жидких кристаллах
- 20.8. Ограничения устройств отображения
- 20.9. Модулятор на основе эффекта Покельса (PROM)
- 20.10. Трубки Титус и Фототитус
- 20.11. Другие электрооптические кристаллы
- 20.12. Спектральный анализ и интегральная оптика
- 20.13. Взаимные спектры
- Глава 21. НЕКОТОРЫЕ ПРАКТИЧЕСКИЕ ПРИМЕНЕНИЯ МЕТОДОВ ОБРАБОТКИ СИГНАЛОВ
- 21.2. Исследование ядерных сред
- 21.3. Ядерный магнитный резонанс (ЯМР) с возбуждением случайным сигналом
- 21.4. Идентификация процессов. Измерение импульсных откликов и передаточных функций
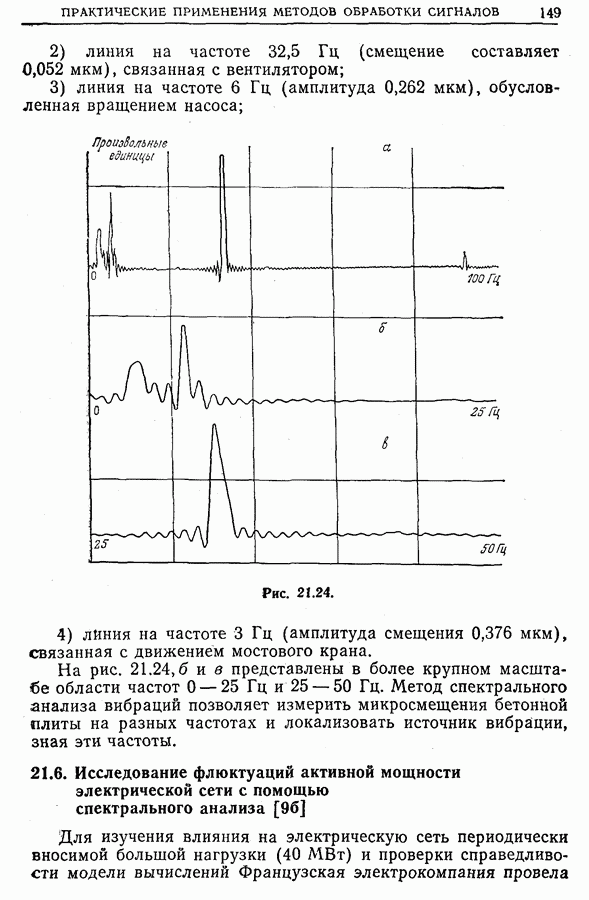
- 21.5. Спектральный анализ собственных колебаний бетонных плит
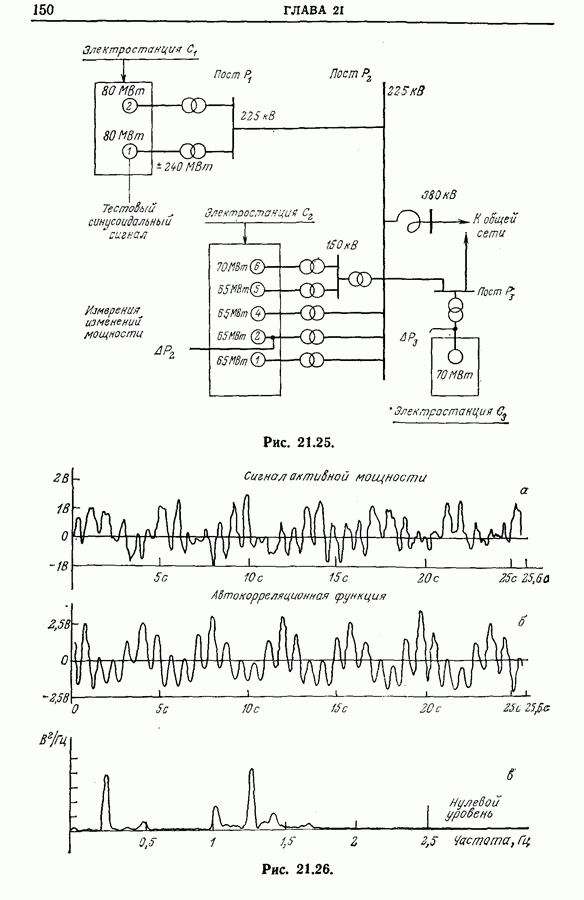
- 21.6. Исследование флюктуаций активной мощности электрической сети с помощью спектрального анализа
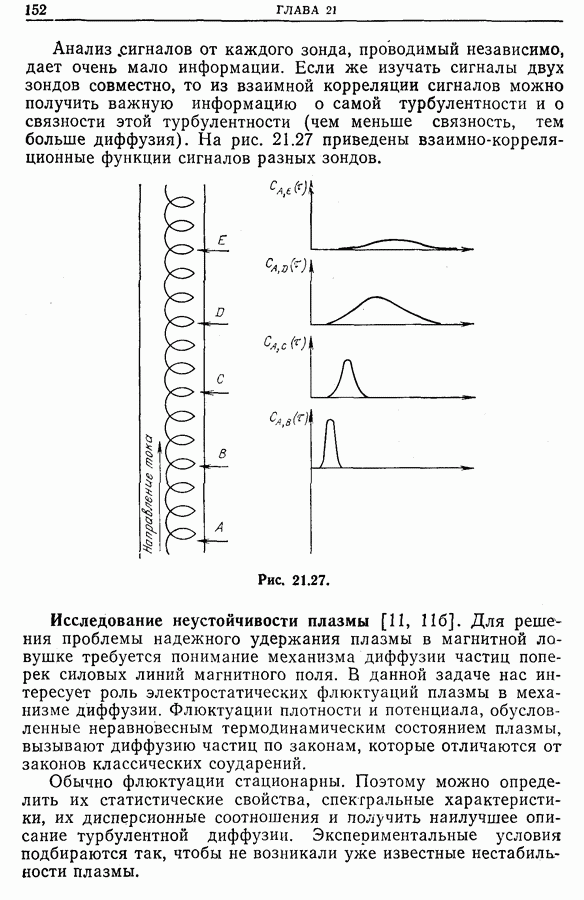
- 21.7. Изучение турбулентности
- 21.8. Применения в геофизике
- 21.9. Применения в астрофизике
- 21.10. Применения в астрономии и радиоастрономии
- 21.11. Применения в биологии и медицине
- 21.12. Применения в акустике
- 21.13. Исследование процессов намагничивания ферромагнетиков
- 21.14. Применения новых методов обработки сигналов
- 21.15. Заключение
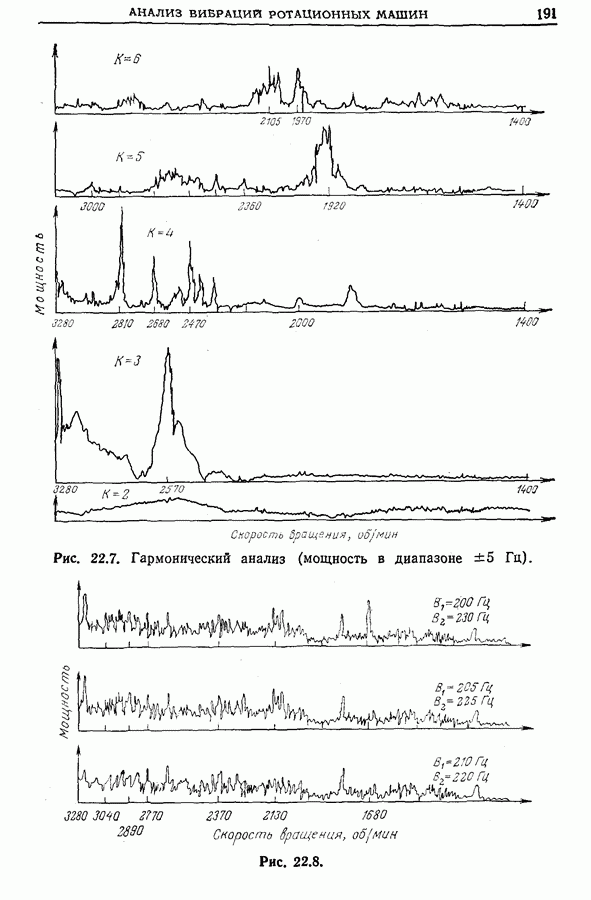
- Глава 22. ПРИМЕНЕНИЕ МЕТОДОВ ОБРАБОТКИ СИГНАЛОВ ДЛЯ АНАЛИЗА ВИБРАЦИЙ РОТАЦИОННЫХ МАШИНА
- 22.2. Анализ поведения системы «ротационная машина — конструкция»
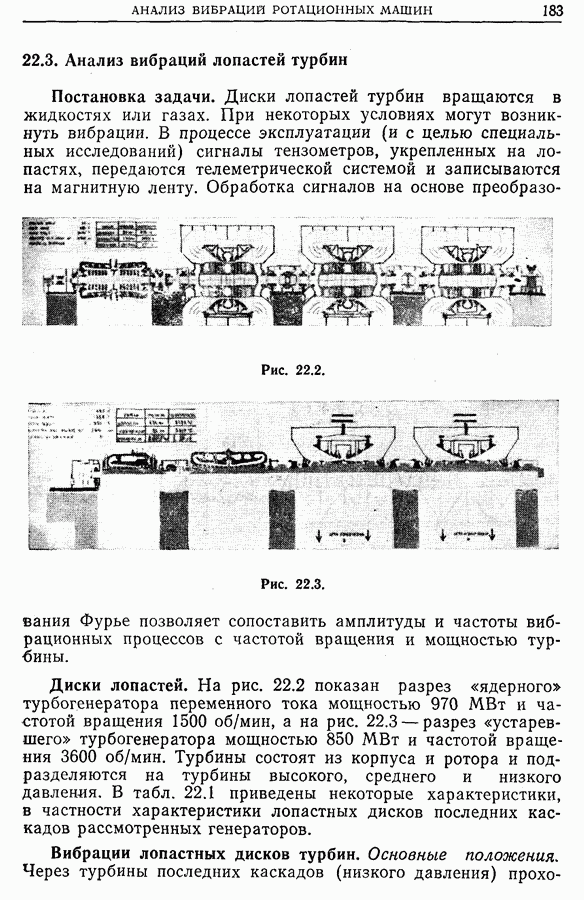
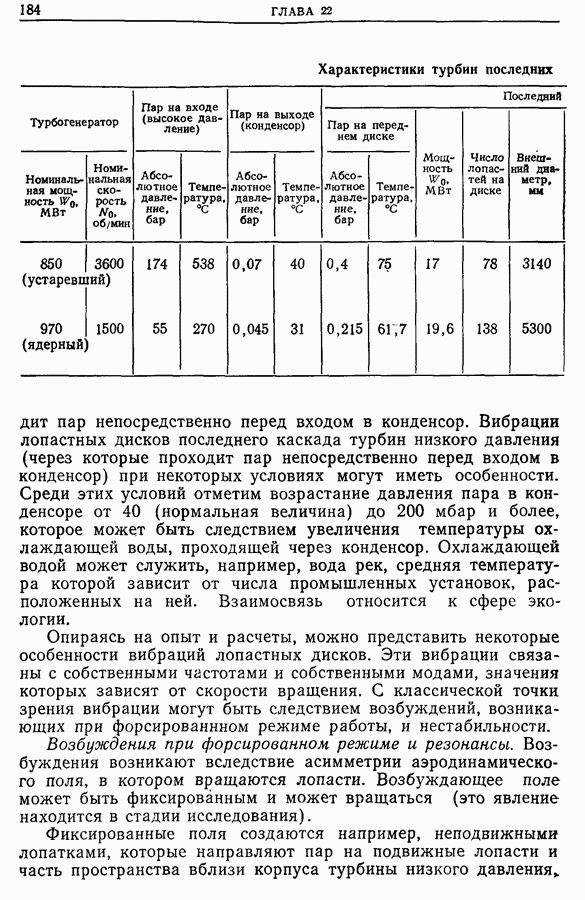
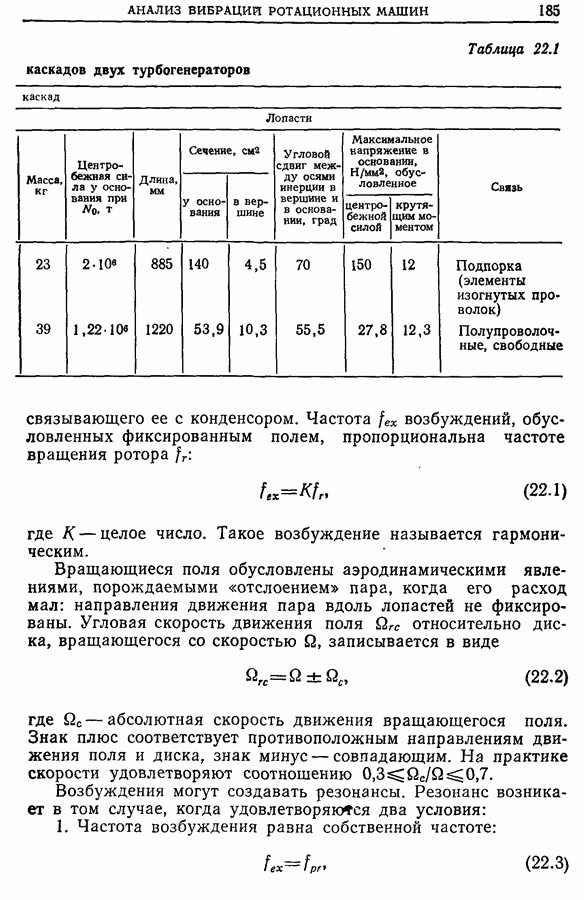
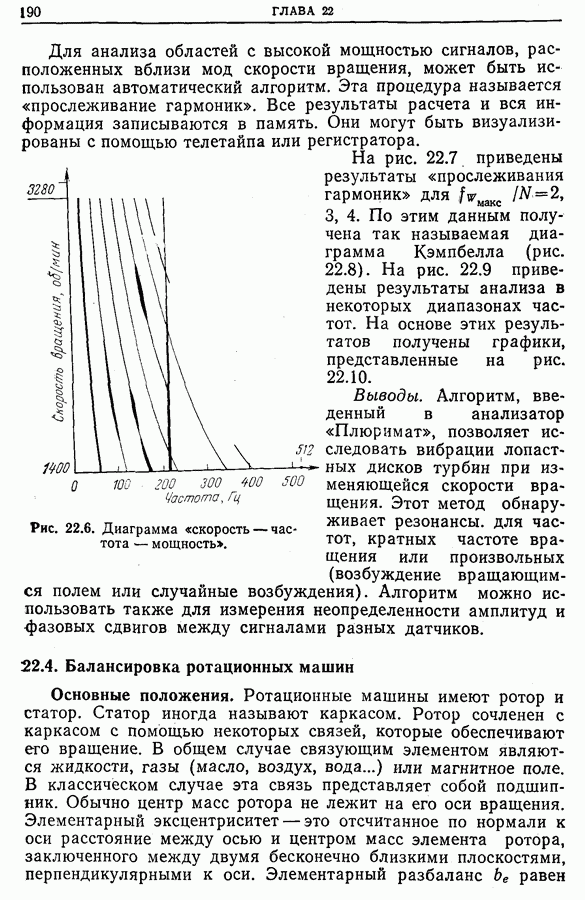
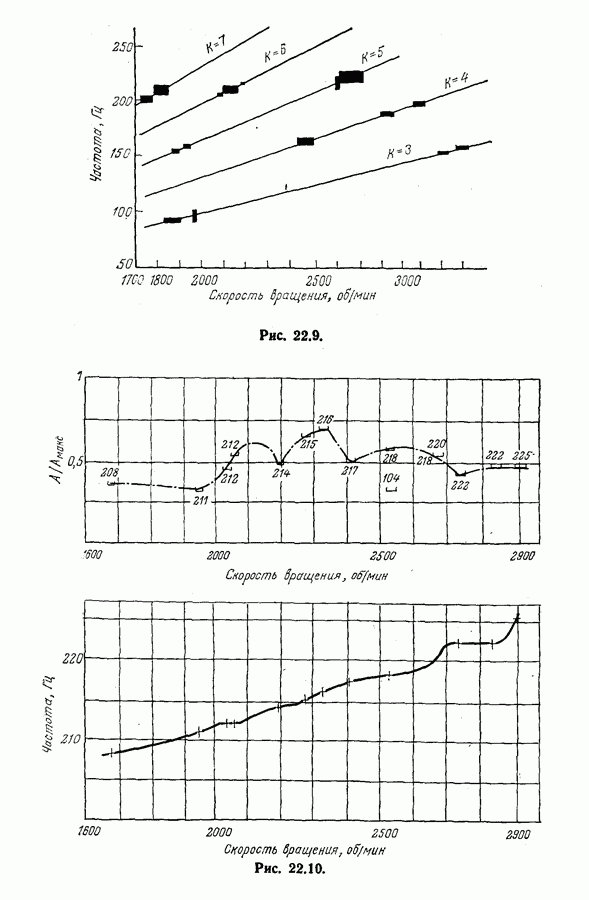
- 22.3. Анализ вибраций лопастей турбин
- 22.4. Балансировка ротационных машин
- Глава 23. ФУНКЦИЯ НЕОПРЕДЕЛЕННОСТИ
- 23.2. Временная корреляция. Временной сдвиг
- 23.3. Частотная корреляция. Частотный сдвиг
- 23.4. Временной и частотный сдвиги. Функция неопределенности
- 23.5. Функция неопределенности Вудворда
- 23.6. Взаимная функция неопределенности
- 23.7. Некоторые свойства функции неопределенности
- 23.8. Представление функций неопределенности
- 23.9. Примеры функций неопределенности
- 23.10. Применение функции неопределенности
- 23.11. Применение функций неопределенности для описания линейных неоднородных во времени систем. Обобщение понятия передаточной функции. Функция диффузии (функция рассеивания)
- 23.12. Генерация тестового сигнала
- 23.13. Прибор для измерения функции неопределенности в режиме реального времени
- Глава 24. ПОНЯТИЕ МГНОВЕННОГО СПЕКТРА ИЛИ ЧАСТОТНО-ВРЕМЕННОГО ПРЕДСТАВЛЕНИЯ В АНАЛИЗЕ И СИНТЕЗЕ СИГНАЛОВ
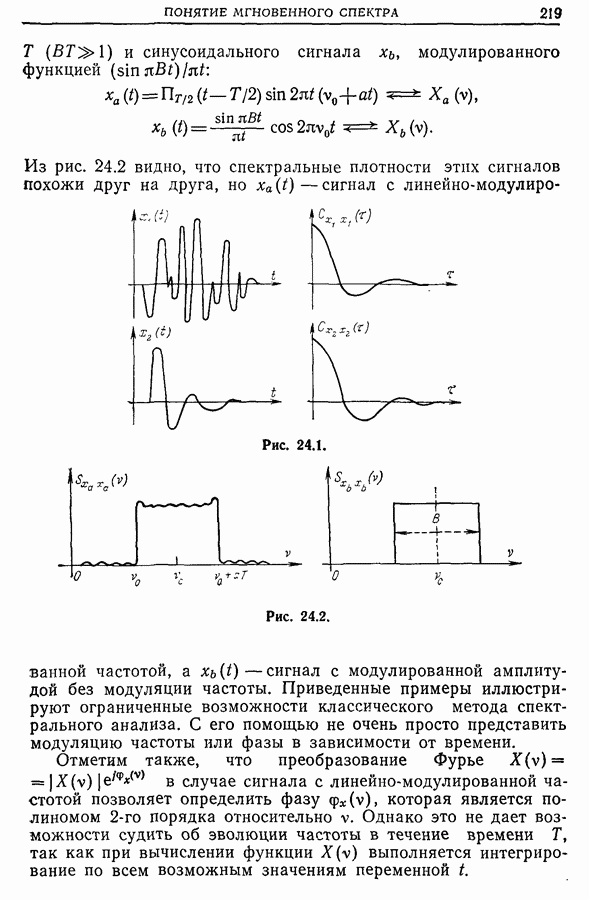
- 24.2. Примеры спектрального анализа модулированных и немодулированных сигналов
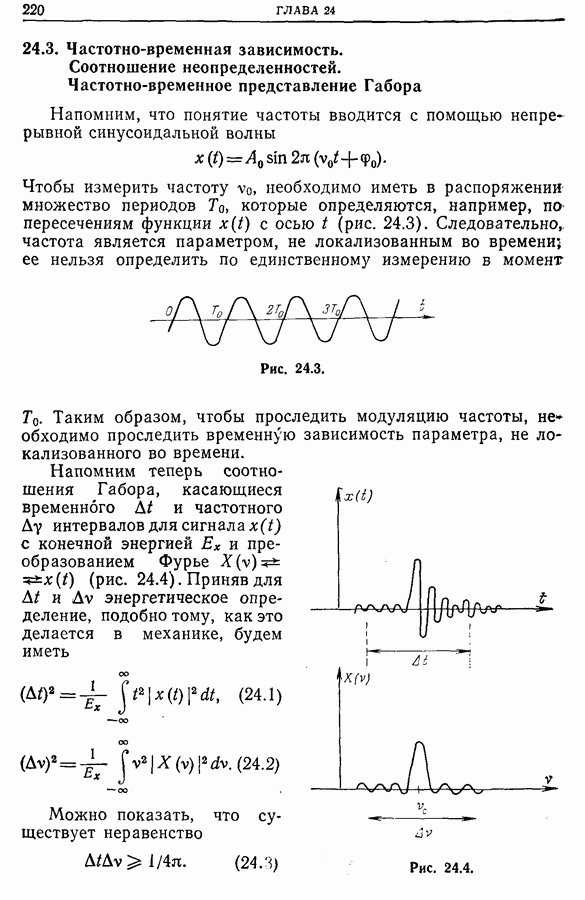
- 24.3. Частотно-временная зависимость. Соотношение неопределенностей. Частотно-временное представление Габора
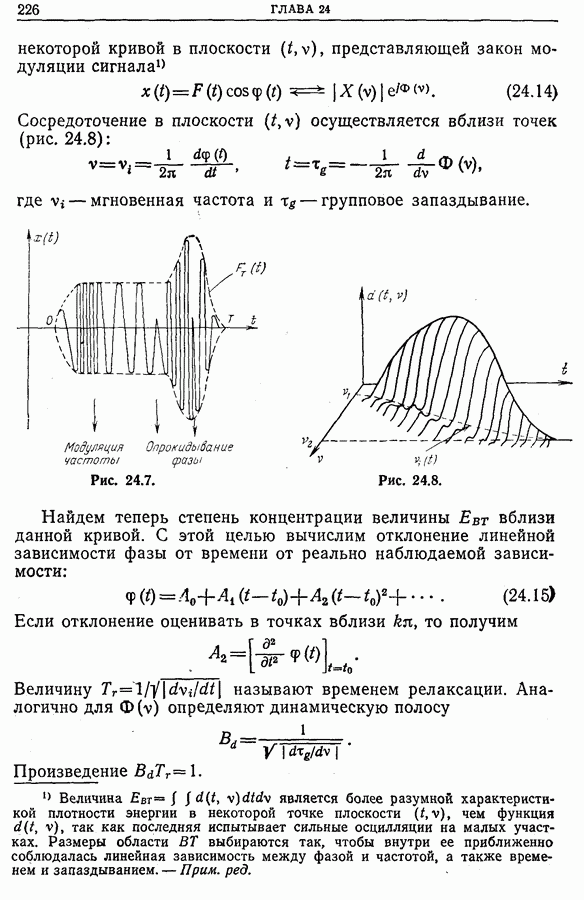
- 24.4. Представление [t, v] по Бонне. Мгновенный спектр мощности по Биллю. Функция неопределенности
- 24.5. Другие определения частотно-временного представления
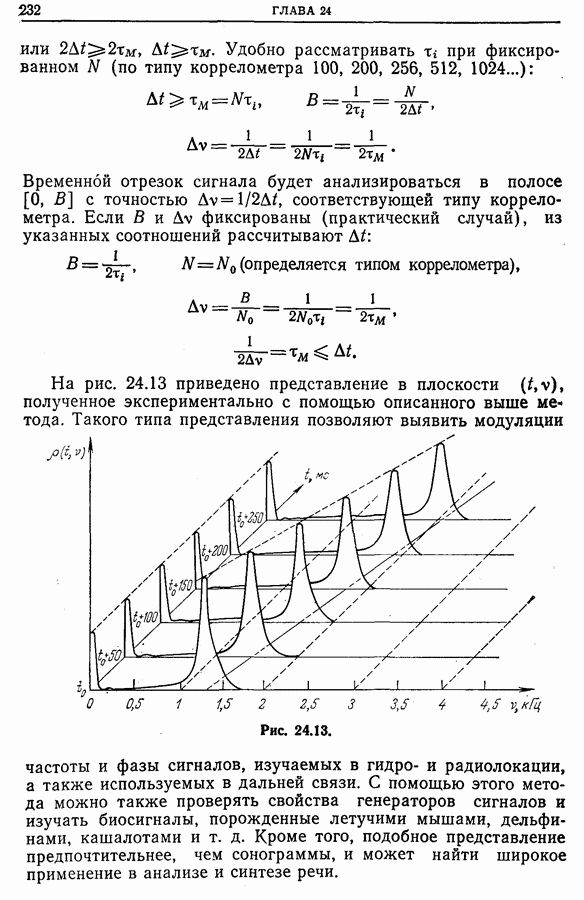
- 24.6. Измерение мгновенных спектров
- 24.7. Обобщение понятия мгновенного спектра мощности на случайные локально-стационарные сигналы. Функция структуры. Функция диффузии
- 24.8 Восстановление сигнала x(t) по известной функции
- 24.9. Заключение
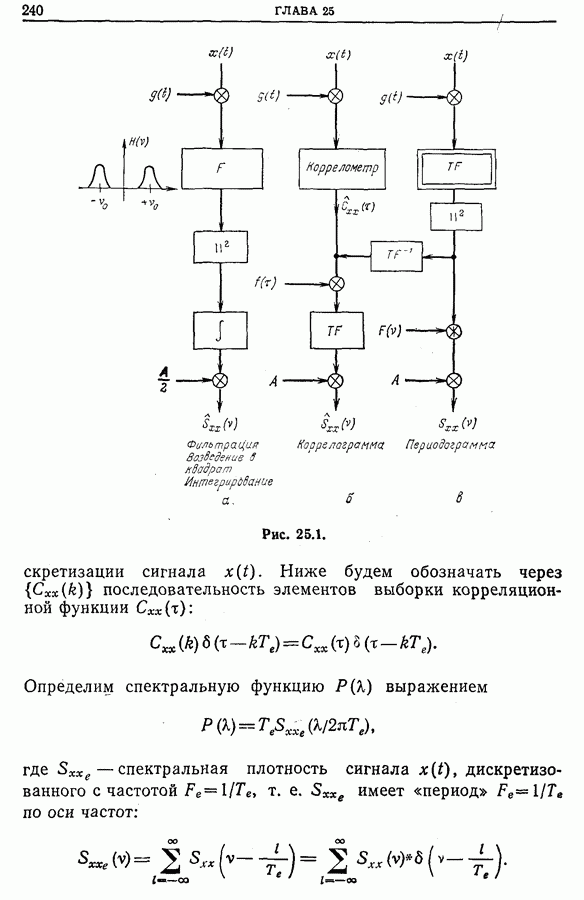
- Глава 25. НОВЫЕ МЕТОДЫ СПЕКТРАЛЬНОГО АНАЛИЗА
- 25.2. Проблемы, обусловленные дискретизацией корреляционной функции
- 25.3. Постановка проблемы получения спектральной функции из конечного числа значений автокорреляционной функции
- 25.4. Классический метод, основанный на преобразовании Фурье корреляционной функции
- 25.5. Метод максимума энтропии или метод авторегрессионной модели
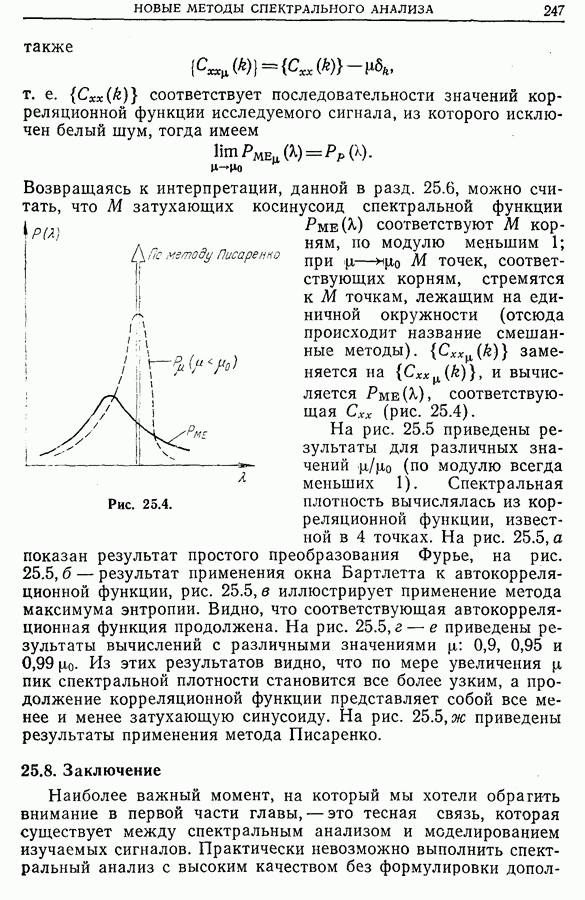
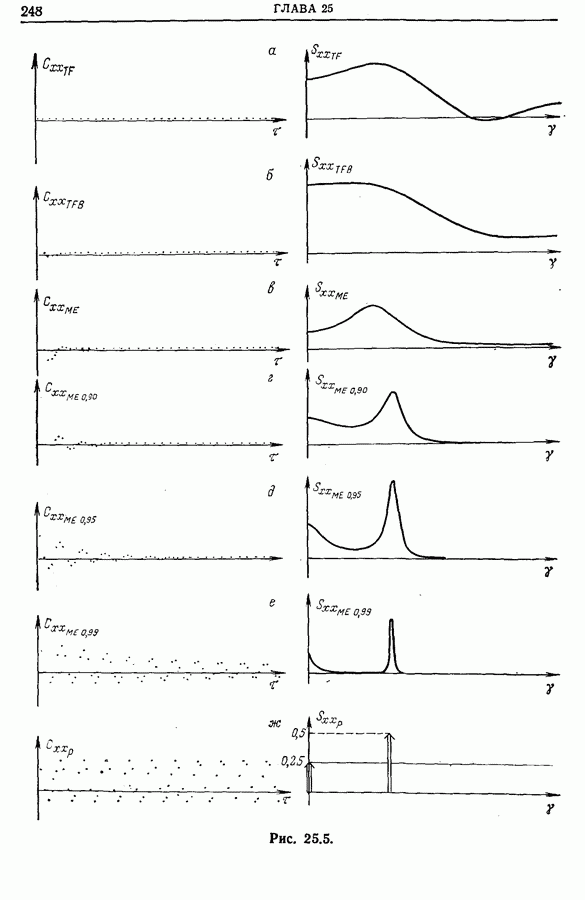
- 25.6. Метод Писаренко
- 25.7. Смешанные методы
- 25.8. Заключение