| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
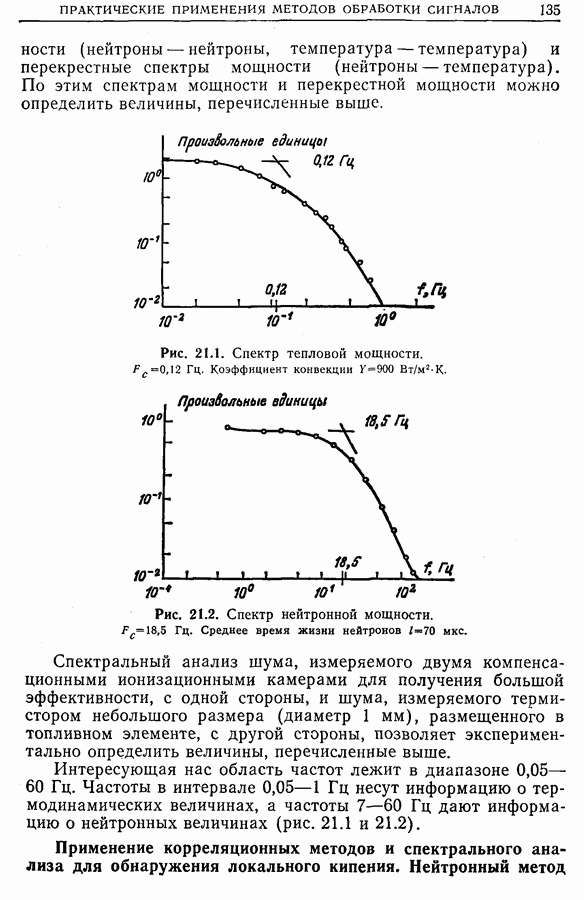
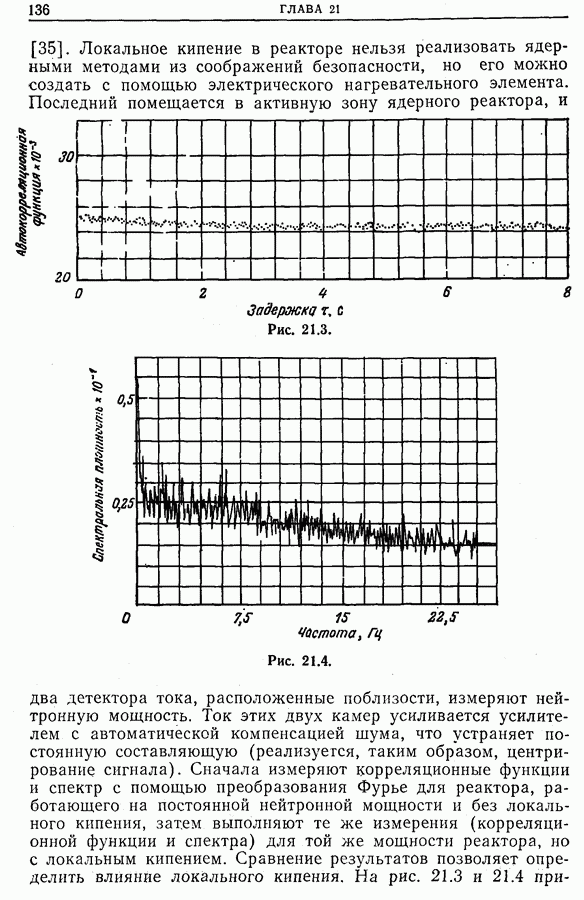
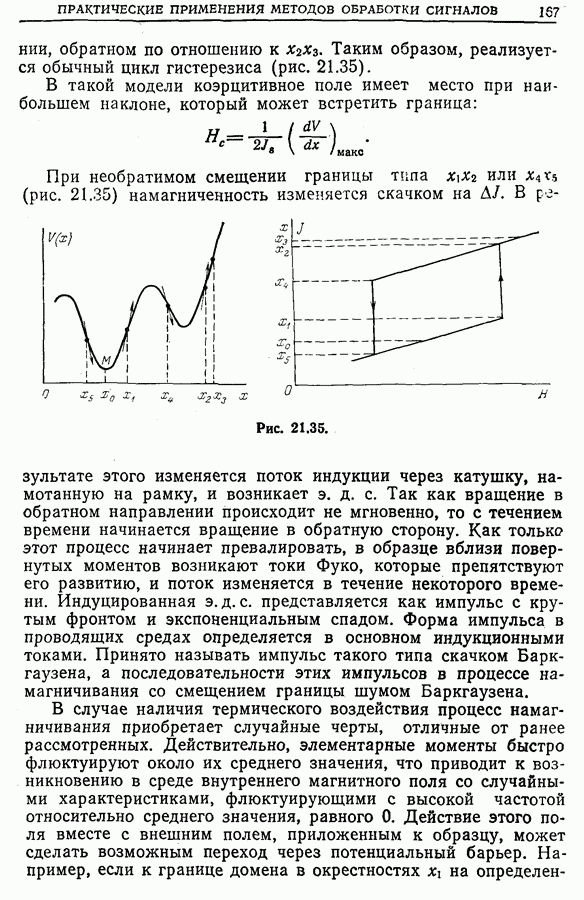
21.7. Изучение турбулентности
Общие замечания.
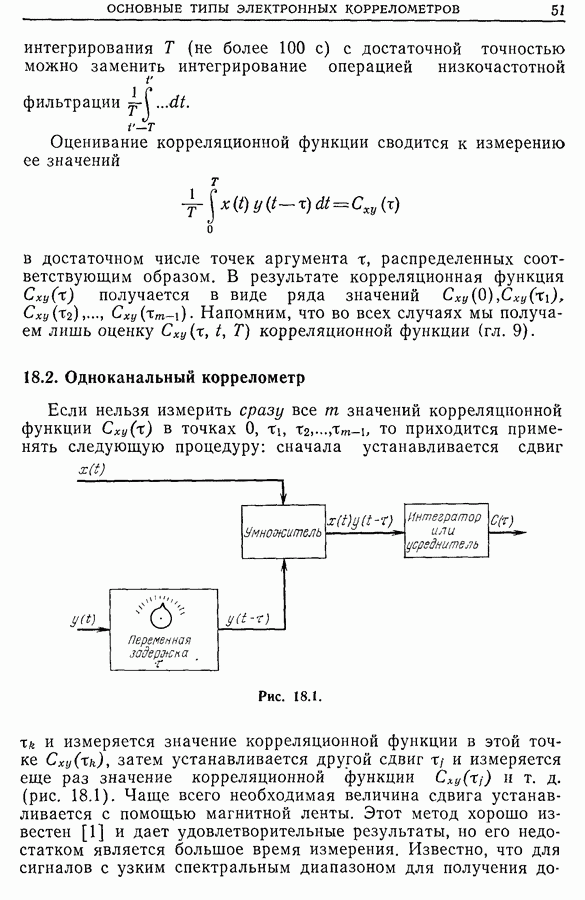
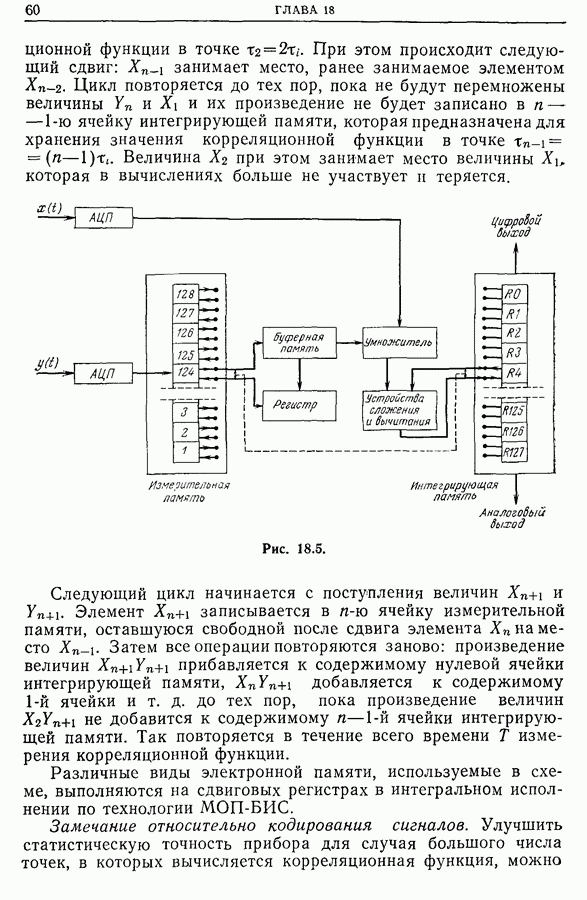
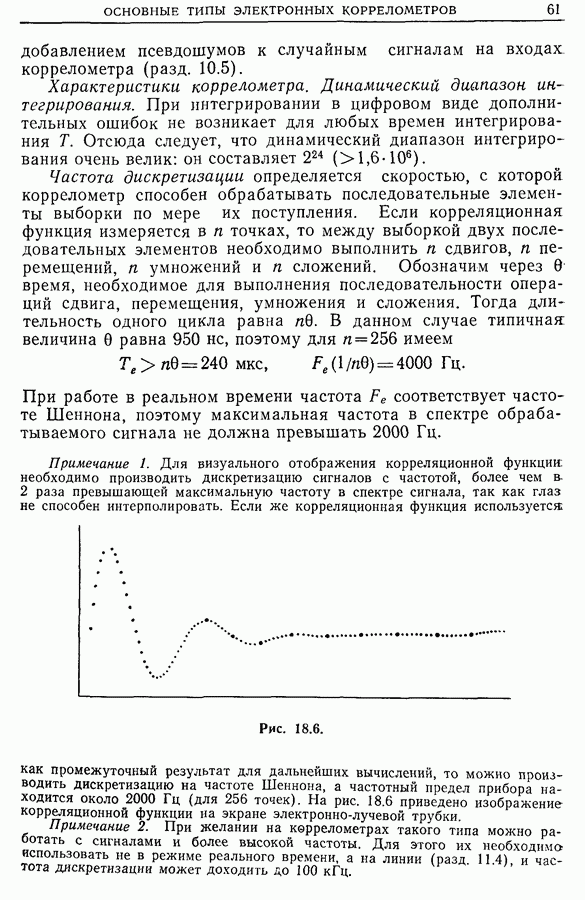
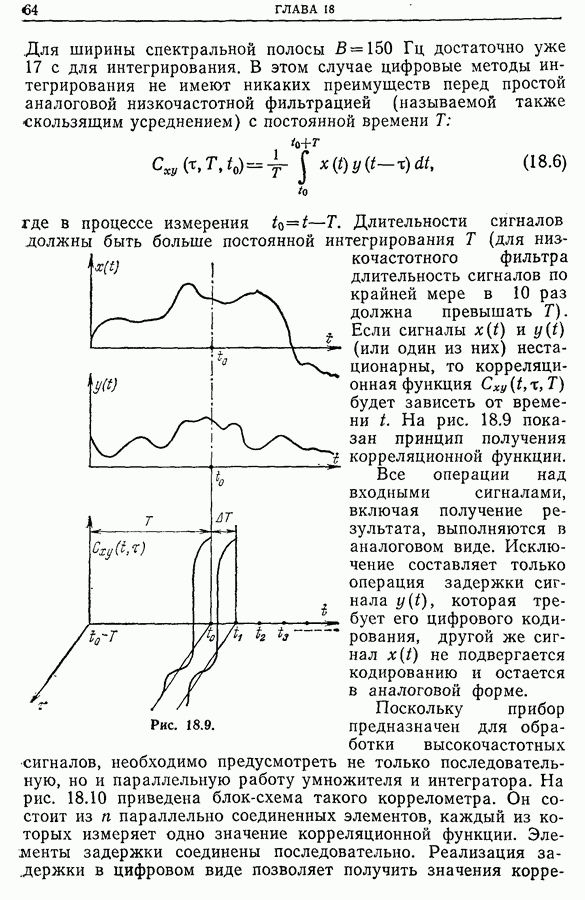
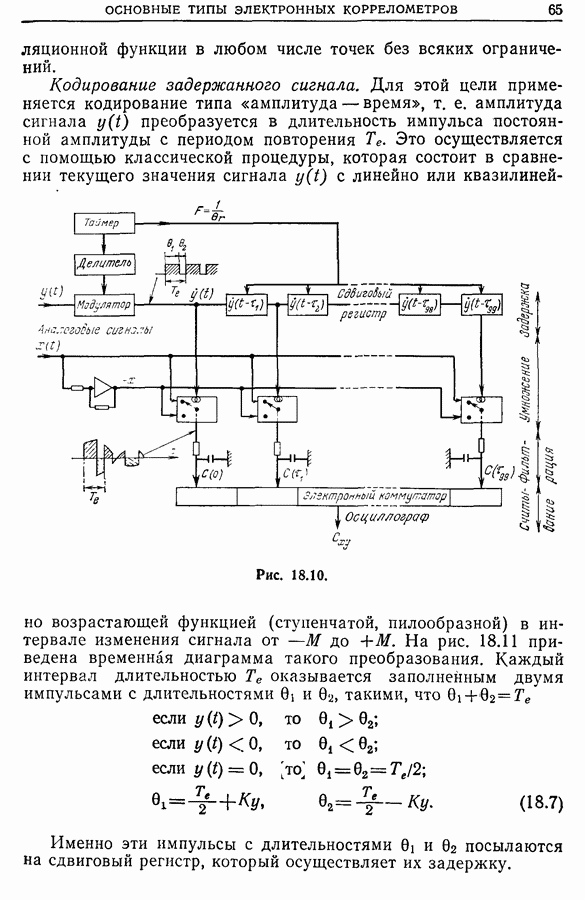
К задачам, рассмотренным в предыдущем разделе, весьма близки задачи турбулентности. Последние касаются исследования нерегулярностей, паразитных токов в течении жидкостей, газов или смесей. Исследование выполняется с помощью зондов с быстрым откликом, помещаемых в разных точках на входе потока (например, анемометр с нагреваемой нитью в случае газового потока).
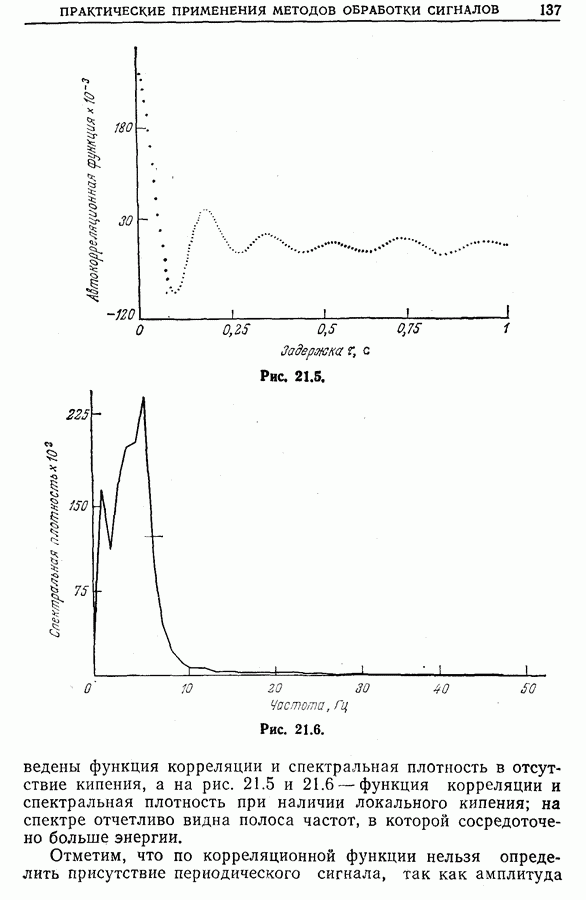
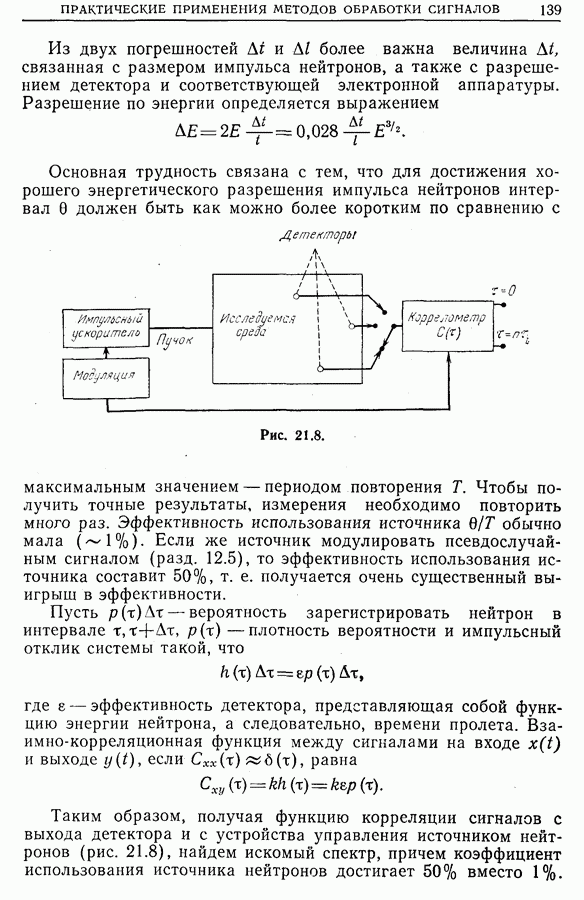
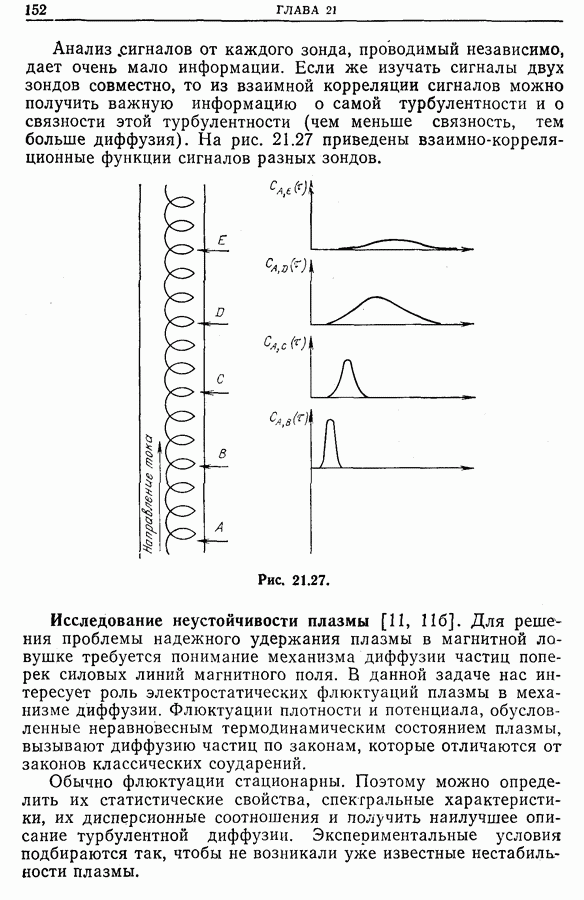
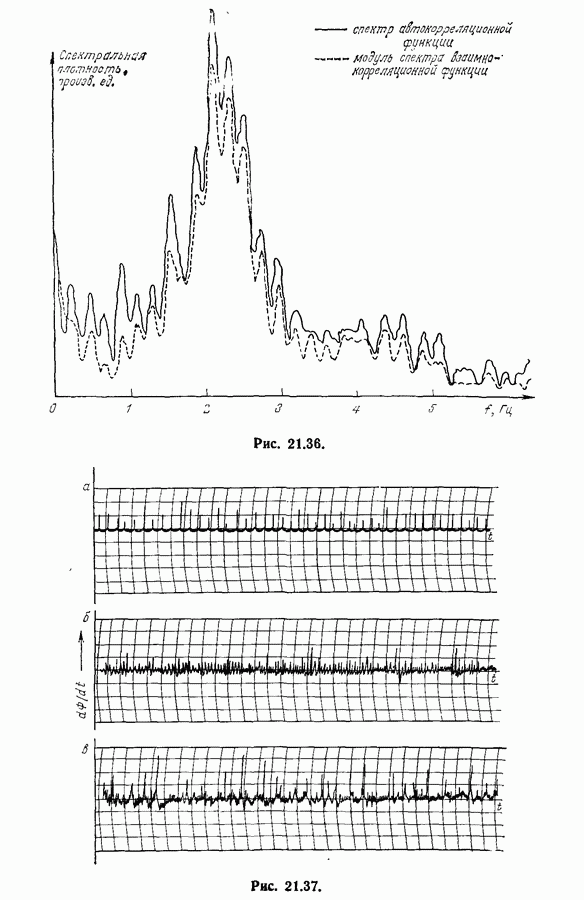
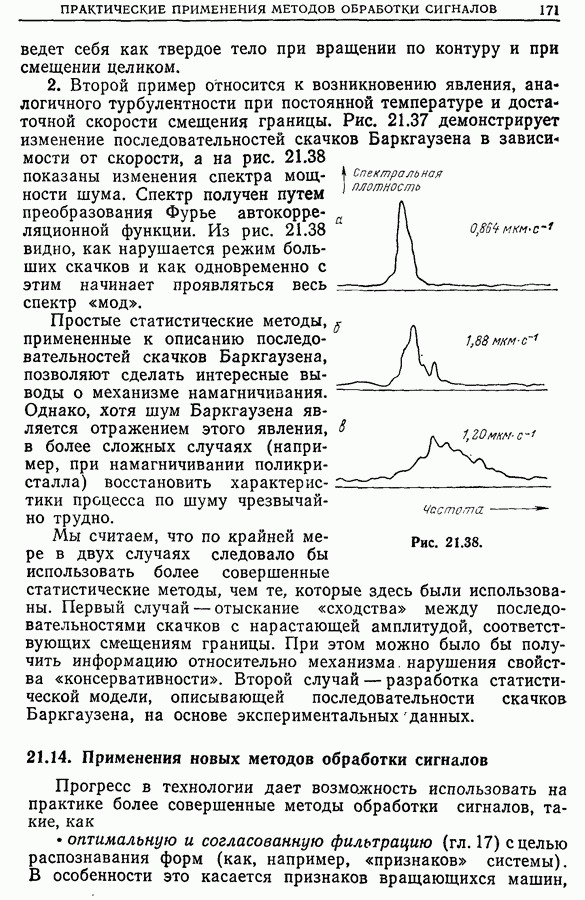
Анализ сигналов от каждого зонда, проводимый независимо, дает очень мало информации. Если же изучать сигналы двух зондов совместно, то из взаимной корреляции сигналов можно получить важную информацию о самой турбулентности и о связности этой турбулентности (чем меньше связность, тем больше диффузия). На рис. 21.27 приведены взаимно-корреляционные функции сигналов разных зондов.
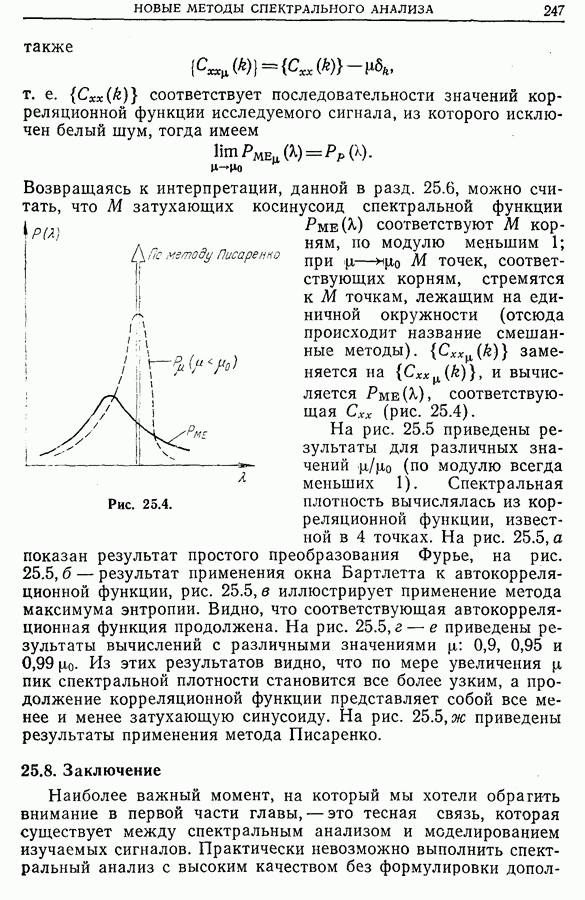
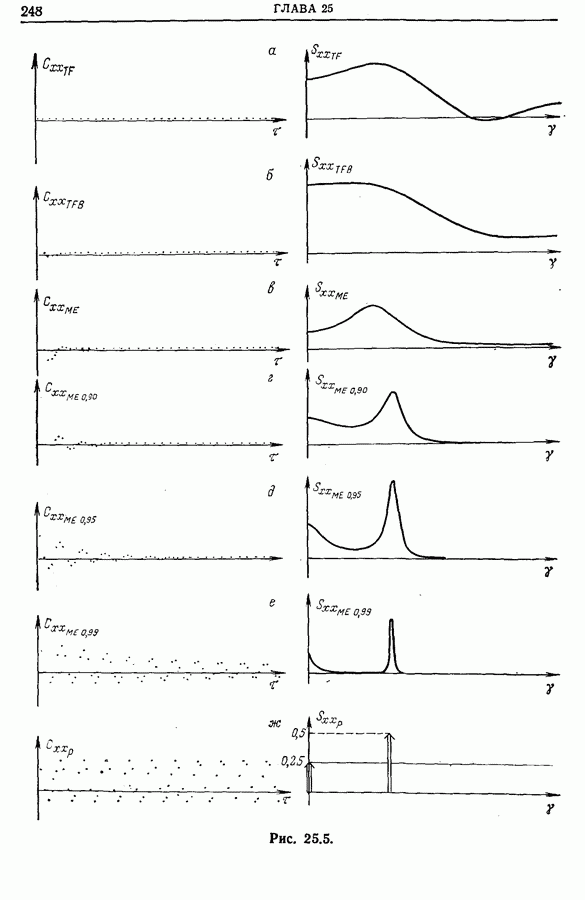
Рис. 21.27. (см. скан)
Исследование неустойчивости плазмы [11, 11б].
Для решения проблемы надежного удержания плазмы в магнитной ловушке требуется понимание механизма диффузии частиц поперек силовых линий магнитного поля. В данной задаче нас интересует роль электростатических флюктуаций плазмы в механизме диффузии. Флюктуации плотности и потенциала, обусловленные неравновесным термодинамическим состоянием плазмы, вызывают диффузию частиц по законам, которые отличаются от законов классических соударений.
Обычно флюктуации стационарны. Поэтому можно определить их статистические свойства, спектральные характеристики, их дисперсионные соотношения и получить наилучшее описание турбулентной диффузии. Экспериментальные условия подбираются так, чтобы не возникали уже известные нестабильности плазмы.
Приведем здесь описание эксперимента «Дафнис» (рис. 21.28). В начальный момент времени нейтральный газ вводится в коаксиальный источник со стороны нагреваемого катода, где газ ионизируется. Образованная таким образом водородная плазма диффундирует вдоль силовых линий магнитного поля В и рекомбинирует на противоположном конце камеры. Пока плазма диффундирует, макроскопический ток вдоль силовых линий поля равен нулю, что позволяет избежать нестабильностей, обусловленных наличием тока, параллельного полю В.

Рис. 21.28. Принципиальная схема эксперимента.
Рабочее давление  ; напряженность однородного магнитного поля
; напряженность однородного магнитного поля  плотность
плотность 
Магнитное поле однородно по всему объему для уменьшения эффектов, связанных с изгибом силовых линий (приводящим к появлению нестабильностей потока) и с потерей частиц из-за конвекции. Условия, при которых ионизируется нейтральный газ в источнике, поддерживаются с большой тщательностью с тем, чтобы получить однородную плазму и минимальное количество быстрых электронов в области диффузии. Измерения выполняются на расстоянии  от источника с помощью зондов, которые расположены на стенке камеры и которые можно перемещать в трех направлениях
от источника с помощью зондов, которые расположены на стенке камеры и которые можно перемещать в трех направлениях 
Рассмотрим характеристики диффундирующей плазмы. В описанных выше условиях нормального функционирования получены следующие характеристики плазмы:

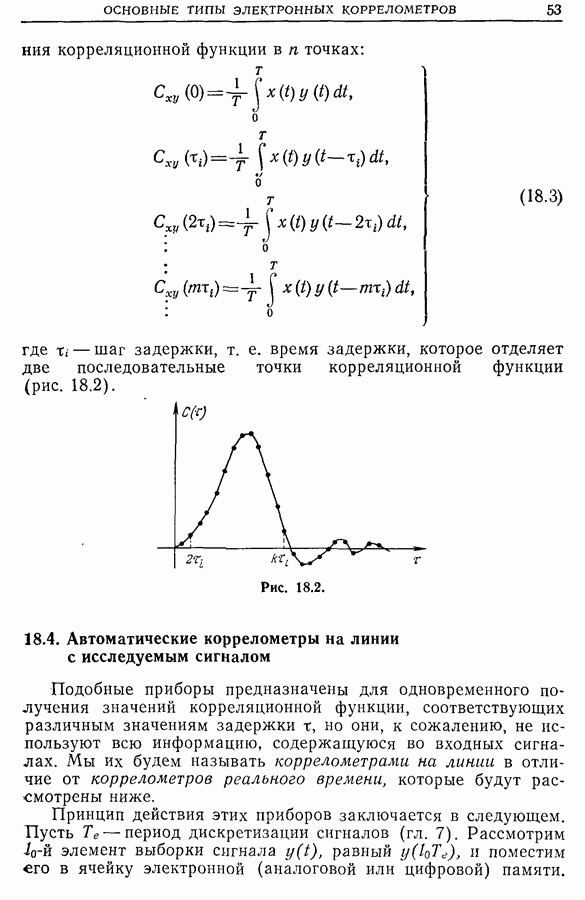
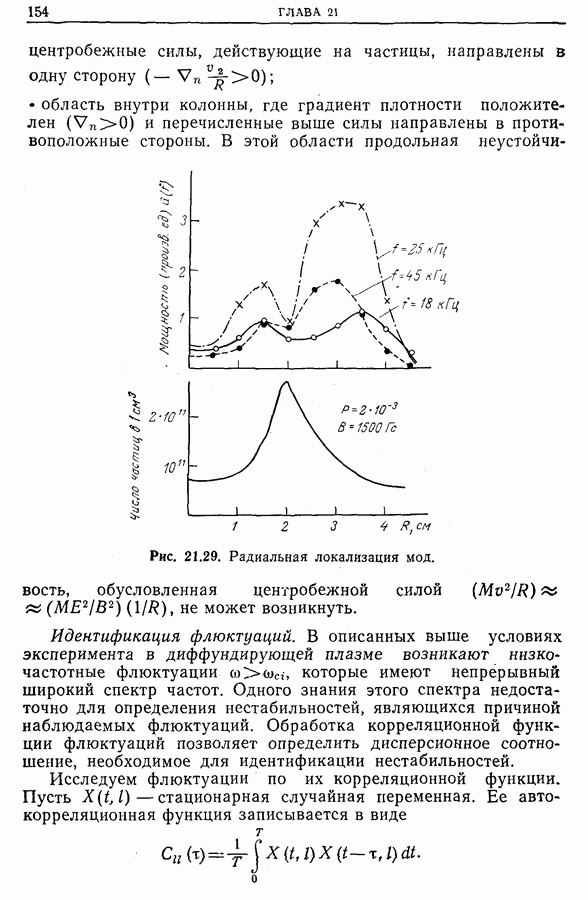
На рис. 21.29 приведена типичная зависимость плотности плазмы от радиуса. Радиальное положение максимума плотности определяется диаметром коаксиальных электродов источника. Этот регулируемый геометрический параметр весьма важен, так как позволяет определить две области в плазме:
• область, внешнюю по отношению к колонне, где градиент плотности отрицателен  и в которой силы давления и
и в которой силы давления и
центробежные силы, действующие на частицы, направлены в одну сторону  ;
;
• область внутри колонны, где градиент плотности положителен  и перечисленные выше силы направлены в противоположные стороны.
и перечисленные выше силы направлены в противоположные стороны.
Рис. 21.29. Радиальная локализация мод. (см. скан)
В этой области продольная неустойчивость, обусловленная центробежной силой  не может возникнуть.
не может возникнуть.
Идентификация флюктуаций. В описанных выше условиях эксперимента в диффундирующей плазме возникают низкочастотные флюктуации  которые имеют непрерывный широкий спектр частот. Одного знания этого спектра недостаточно для определения нестабильностей, являющихся причиной наблюдаемых флюктуаций. Обработка корреляционной функции флюктуаций позволяет определить дисперсионное соотношение, необходимое для идентификации нестабильностей.
которые имеют непрерывный широкий спектр частот. Одного знания этого спектра недостаточно для определения нестабильностей, являющихся причиной наблюдаемых флюктуаций. Обработка корреляционной функции флюктуаций позволяет определить дисперсионное соотношение, необходимое для идентификации нестабильностей.
Исследуем флюктуации по их корреляционной функции. Пусть  - стационарная случайная переменная. Ее автокорреляционная функция записывается в виде
- стационарная случайная переменная. Ее автокорреляционная функция записывается в виде

Автокорреляционная функция  имеет в качестве образа Фурье функцию
имеет в качестве образа Фурье функцию  являющуюся спектральной плотностью энергии (теорема Винера — Хинчина):
являющуюся спектральной плотностью энергии (теорема Винера — Хинчина):

Отсюда следует точный экспериментальный метод для определения спектра мощности флюктуаций  по измеренной автокорреляционной функции и ее образу Фурье. Приведенное выражение основано только на предположении о стационарности.
по измеренной автокорреляционной функции и ее образу Фурье. Приведенное выражение основано только на предположении о стационарности.
Взаимно-корреляционная функция  сигналов, измеренных в двух точках, отстоящих на Н, и ее фурье-образ
сигналов, измеренных в двух точках, отстоящих на Н, и ее фурье-образ  записываются в виде
записываются в виде

Представим переменную  в виде суммы плоских волн, распространяющихся в плазме:
в виде суммы плоских волн, распространяющихся в плазме:

В этом случае  имеет вид
имеет вид

Из последнего выражения можно заключить, что  имеет в качестве модуля ранее определенный энергетический спектр, а в качестве аргумента функцию
имеет в качестве модуля ранее определенный энергетический спектр, а в качестве аргумента функцию  На практике измерение взаимно-корреляционной функции
На практике измерение взаимно-корреляционной функции  и вычисление ее фурье-образа дают возможность
и вычисление ее фурье-образа дают возможность
• проверить предположения относительно распространения, если  ;
;
• найти функцию  , т. е. определить дисперсионное соотношение
, т. е. определить дисперсионное соотношение 
Величины, подверженные флюктуациям, измерялись с помощью электростатических зондов, перемещаемых в трех направлениях  . Автокорреляционная и взаимно-корреляционная функции измерялись многоканальным коррелометром,
. Автокорреляционная и взаимно-корреляционная функции измерялись многоканальным коррелометром,
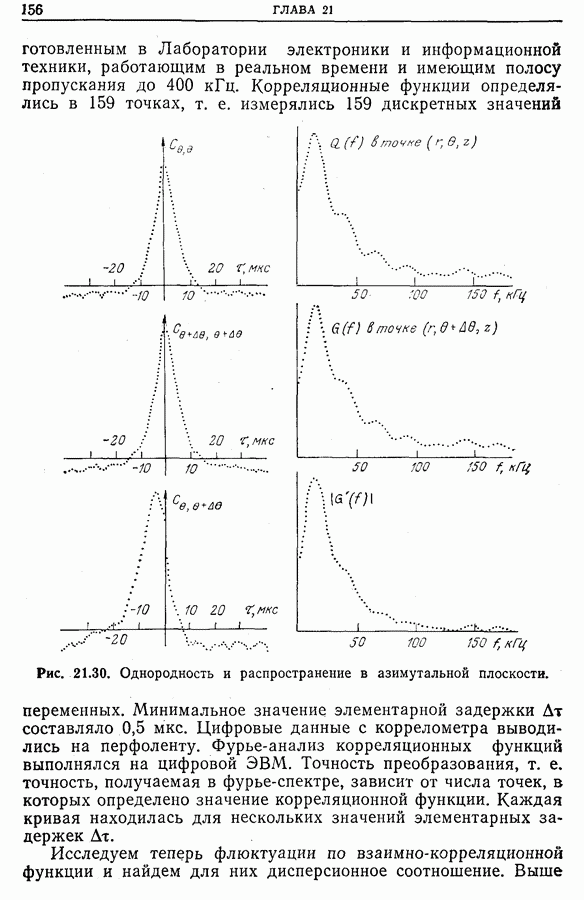
изготовленным в Лаборатории электроники и информационной техники, работающим в реальном времени и имеющим полосу пропускания до 400 кГц. Корреляционные функции определялись в 159 точках, т. е. измерялись 159 дискретных значений переменных.
Рис. 21.30. Однородность и распространение в азимутальной плоскости. (см. скан)
Минимальное значение элементарной задержки  составляло 0,5 мкс. Цифровые данные с коррелометра выводились на перфоленту. Фурье-анализ корреляционных функций выполнялся на цифровой ЭВМ. Точность преобразования, т. е. точность, получаемая в фурье-спектре, зависит от числа точек, в которых определено значение корреляционной функции. Каждая кривая находилась для нескольких значений элементарных задержек Дт.
составляло 0,5 мкс. Цифровые данные с коррелометра выводились на перфоленту. Фурье-анализ корреляционных функций выполнялся на цифровой ЭВМ. Точность преобразования, т. е. точность, получаемая в фурье-спектре, зависит от числа точек, в которых определено значение корреляционной функции. Каждая кривая находилась для нескольких значений элементарных задержек Дт.
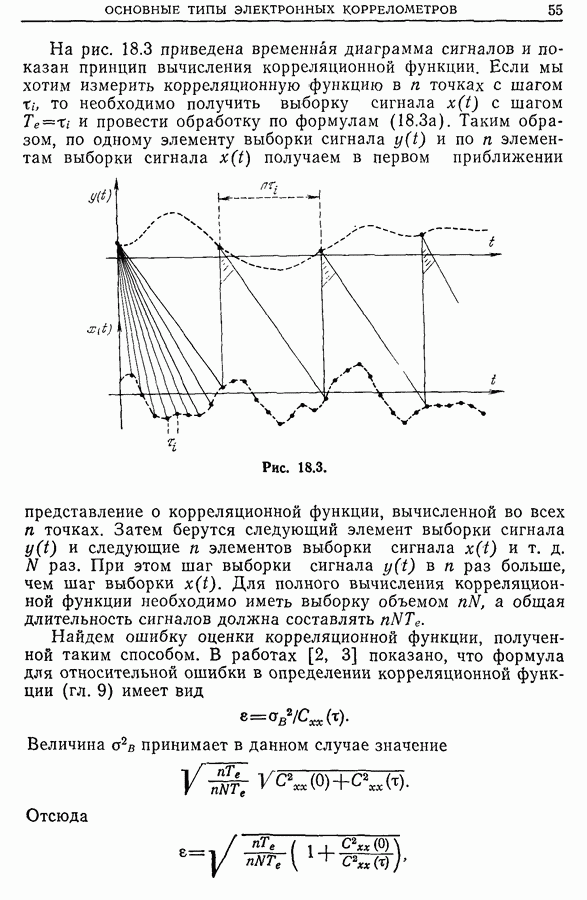
Исследуем теперь флюктуации по взаимно-корреляционной функции и найдем для них дисперсионное соотношение. Выше
говорилось о том, что дисперсионное соотношение флюктуаций в случае, когда справедливо предположение о линейности распространения волн в плазме, можно определить путем вычисления фурье-образа взаимно-корреляционной функции  . На рис. 21.30 приведена совокупность результатов, полученных с помощью двух зондов, расположенных соответственно в точках
. На рис. 21.30 приведена совокупность результатов, полученных с помощью двух зондов, расположенных соответственно в точках  (две автокорреляционные функции, взаимнокорреляционная функция, два спектра
(две автокорреляционные функции, взаимнокорреляционная функция, два спектра  соответствующие фурье-образам автокорреляционных функций, и модуль
соответствующие фурье-образам автокорреляционных функций, и модуль  фурье-образа взаимно-корреляционной функции).
фурье-образа взаимно-корреляционной функции).
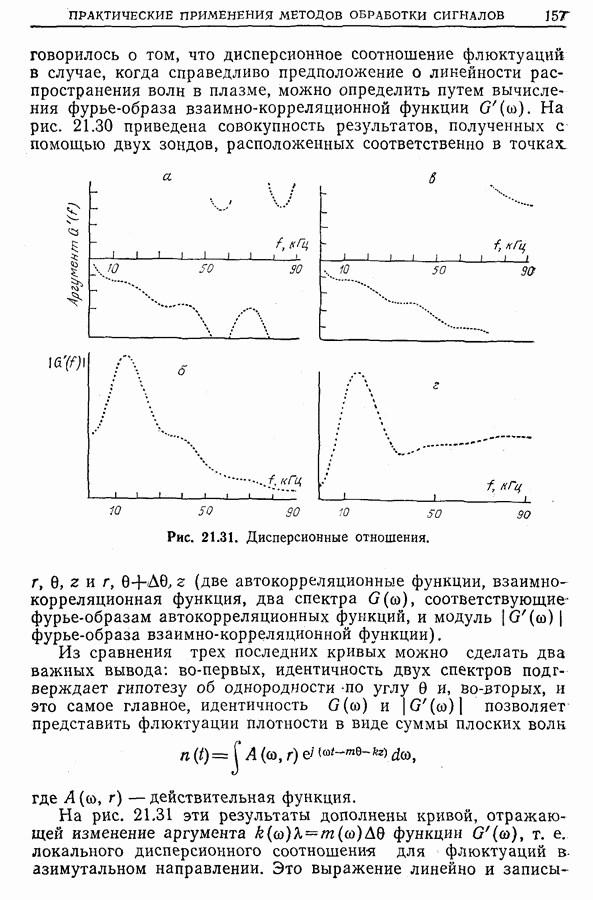
Рис. 21.31. Дисперсионные отношения. (см. скан)
Из сравнения трех последних кривых можно сделать два важных вывода: во-первых, идентичность двух спектров подтверждает гипотезу об однородности -по углу 0 и, во-вторых, и это самое главное, идентичность  позволяет представить флюктуации плотности в виде суммы плоских волк
позволяет представить флюктуации плотности в виде суммы плоских волк

где  — действительная функция.
— действительная функция.
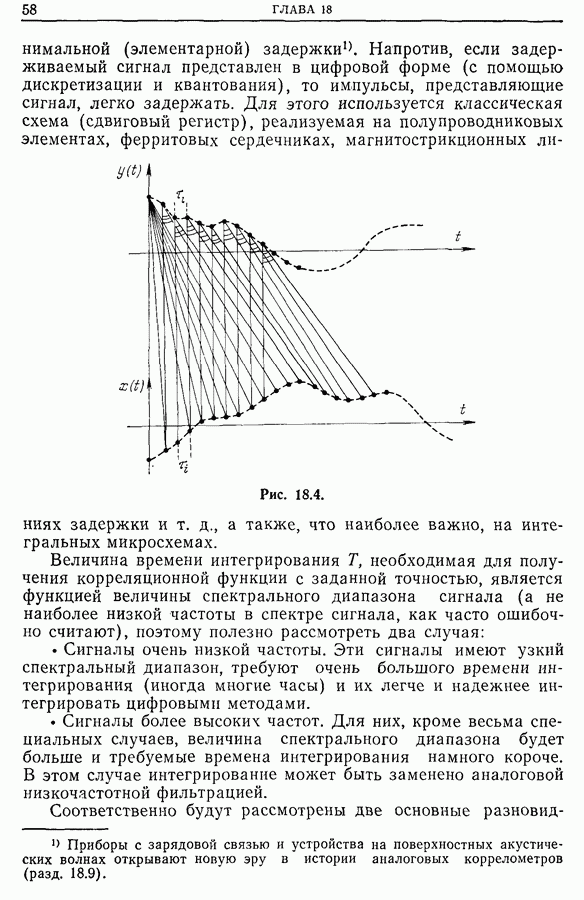
На рис. 21.31 эти результаты дополнены кривой, отражающей изменение аргумента  функции
функции  т. е. локального дисперсионного соотношения для флюктуаций в азимутальном направлении. Это выражение линейно и
т. е. локального дисперсионного соотношения для флюктуаций в азимутальном направлении. Это выражение линейно и
записывается как функция расстояния до точки измерения  в виде
в виде

где  скорость распространения флюктуаций.
скорость распространения флюктуаций.
Кривая на рис. 21.31, г построена для внешней области плазмы  см) и соответствует фазовой скорости флюктуаций
см) и соответствует фазовой скорости флюктуаций 
По кривой на рис. 21.31,б, построенной для внутренней области плазмы  см), скорость
см), скорость  оценивается равной
оценивается равной 
В результате проведенных измерений было установлено, что, с одной стороны, флюктуации имеют одинаковую природу внутри и вне плазменной колонны. Их дисперсионное соотношение всегда приблизительно линейно. С другой стороны, флюктуации распространяются в одном и том же направлении независимо от знака градиента. Это говорит о важной роли радиального электрического поля в определении скорости их распространения.
Итак, нестабильности, на которые влияют характеристики рассмотренных флюктуаций, должны возбуждаться независимо от знака градиента плотности  быть локализованы в области, где
быть локализованы в области, где  имеет большое значение, и обладать линейным дисперсионным соотношением с фазовой скоростью, имеющей большее значение вне колонны.
имеет большое значение, и обладать линейным дисперсионным соотношением с фазовой скоростью, имеющей большее значение вне колонны.
Полученные результаты хорошо описывают свойства классических неустойчивостей плазмы, называемых неустойчивостями резистивного дрейфа. Последние развиваются в плазме под действием сил, вызываемых градиентом плотности в направлении, перпендикулярном силовым линиям магнитного поля. Из этого примера следует, что для физики плазмы большой интерес представляет информация, получаемая обработкой авто- и взаимно-корреляционных функций шума разряда.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 15. СИНХРОННОЕ ДЕТЕКТИРОВАНИЕ
- 15.2. Схема метода
- 15.3. Теория синхронного детектирования
- 15.4. Синхронное детектирование в режиме развертки
- 15.5. Примеры применения синхронных детекторов
- 15.6. Совершенствование синхронных детекторов
- Глава 16. ИСПОЛЬЗОВАНИЕ МНОГОКАНАЛЬНЫХ АНАЛИЗАТОРОВ ПРИ СТАТИЧЕСКОЙ ОБРАБОТКЕ ИЗМЕРЕНИЙ
- 16.2. Характеристики многоканальных анализаторов
- 16.3. Схема системы обработки
- 16.4. Примеры применения
- Глава 17. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ
- 17.2. Частный случай белого шума. Согласованный фильтр
- 17.3. Согласованная фильтрация и корреляция Корреляция.
- 17.4. Реализация согласованных фильтров методом «взвешивания»
- 17.5. Рекурсивная согласованная фильтрация [7]
- 17.6. Применения метода согласованной фильтрации
- Глава 18. ОСНОВНЫЕ ТИПЫ ЭЛЕКТРОННЫХ КОРРЕЛОМЕТРОВ
- 18.2. Одноканальный коррелометр
- 18.3. Автоматические коррелометры
- 18.4. Автоматические коррелометры на линии с исследуемым сигналом
- 18.5. Автоматические коррелометры реального времени (или мультикоррелометры)
- 18.6. Коррелометры на больших интегральных схемах
- 18.7. Коррелометры реального времени для высокочастотных сигналов
- 18.8 Развитие коррелометров
- 18.9. Приборы с зарядовой связью [11]
- Глава 19. СПЕКТРАЛЬНЫЕ ЭЛЕКТРОННЫЕ АНАЛИЗАТОРЫ
- 19.2. Спектральные анализаторы, основанные на методе непосредственного преобразования Фурье
- 19.3. Применения анализаторов на основе метода БПФ
- Глава 20. ОПТИЧЕСКИЙ СПЕКТРАЛЬНЫЙ АНАЛИЗ
- 20.2. Упрощения, связанные с отбрасыванием фазы
- 20.3. Эффект виньетирования
- 20.4. Двумерный анализ
- 20.5. Точечный монохроматический источник
- 20.6. Электрооптическое преобразование сигнала
- 20.7. Устройства отображения на жидких кристаллах
- 20.8. Ограничения устройств отображения
- 20.9. Модулятор на основе эффекта Покельса (PROM)
- 20.10. Трубки Титус и Фототитус
- 20.11. Другие электрооптические кристаллы
- 20.12. Спектральный анализ и интегральная оптика
- 20.13. Взаимные спектры
- Глава 21. НЕКОТОРЫЕ ПРАКТИЧЕСКИЕ ПРИМЕНЕНИЯ МЕТОДОВ ОБРАБОТКИ СИГНАЛОВ
- 21.2. Исследование ядерных сред
- 21.3. Ядерный магнитный резонанс (ЯМР) с возбуждением случайным сигналом
- 21.4. Идентификация процессов. Измерение импульсных откликов и передаточных функций
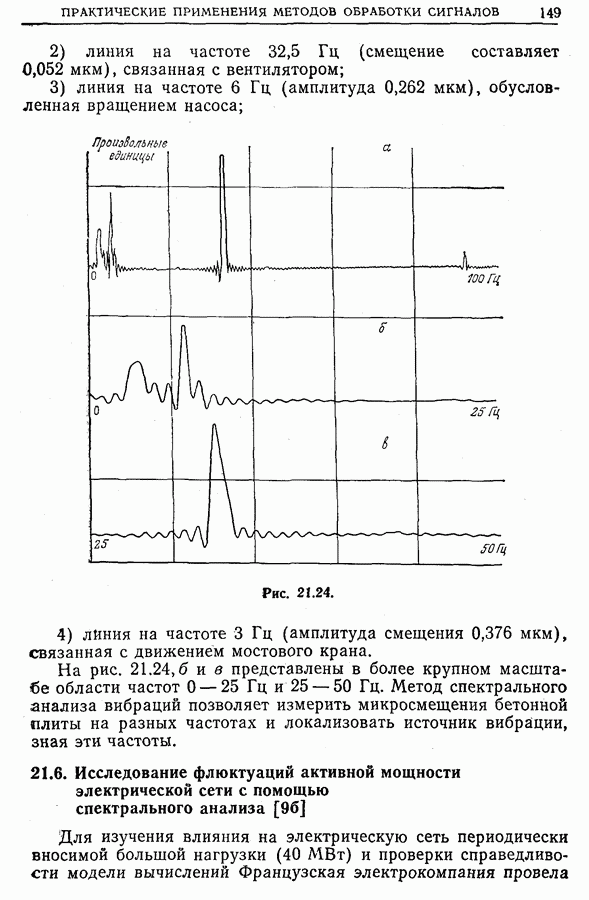
- 21.5. Спектральный анализ собственных колебаний бетонных плит
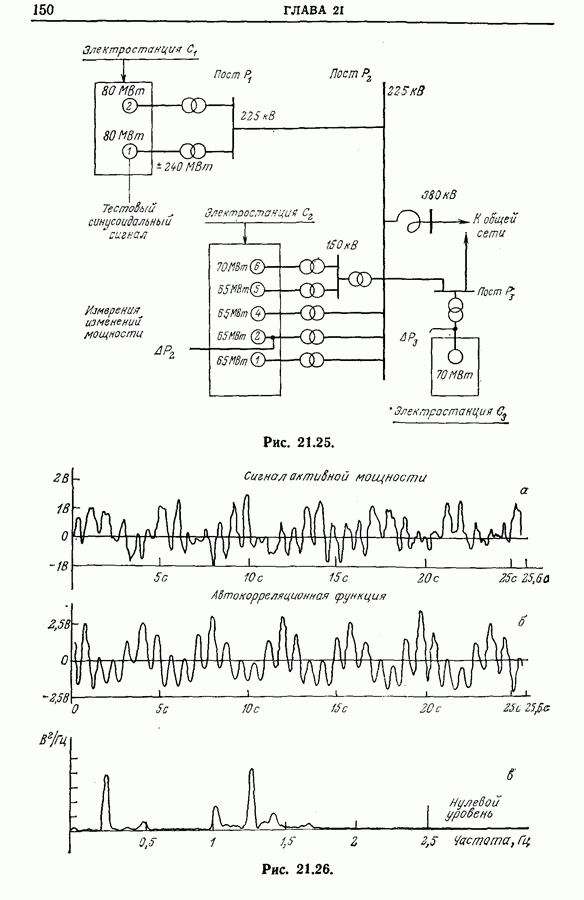
- 21.6. Исследование флюктуаций активной мощности электрической сети с помощью спектрального анализа
- 21.7. Изучение турбулентности
- 21.8. Применения в геофизике
- 21.9. Применения в астрофизике
- 21.10. Применения в астрономии и радиоастрономии
- 21.11. Применения в биологии и медицине
- 21.12. Применения в акустике
- 21.13. Исследование процессов намагничивания ферромагнетиков
- 21.14. Применения новых методов обработки сигналов
- 21.15. Заключение
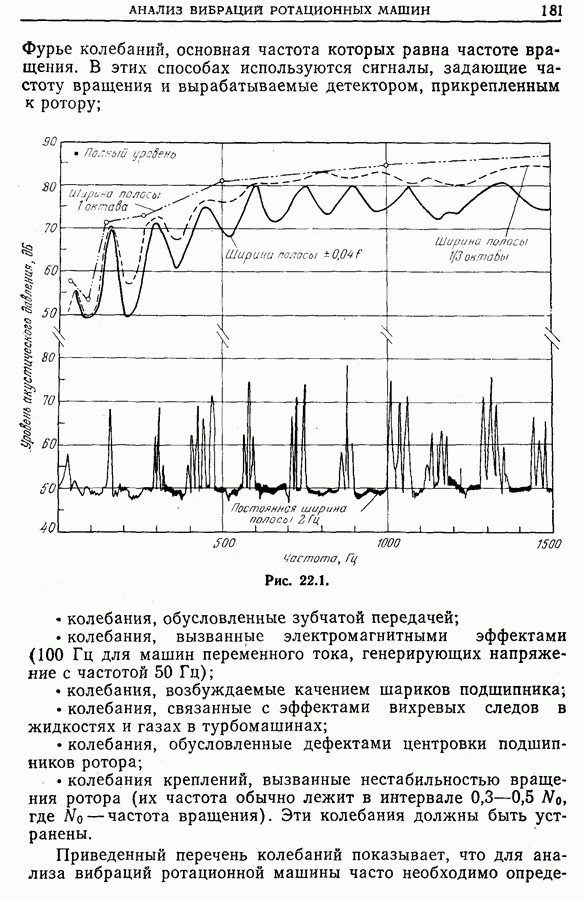
- Глава 22. ПРИМЕНЕНИЕ МЕТОДОВ ОБРАБОТКИ СИГНАЛОВ ДЛЯ АНАЛИЗА ВИБРАЦИЙ РОТАЦИОННЫХ МАШИНА
- 22.2. Анализ поведения системы «ротационная машина — конструкция»
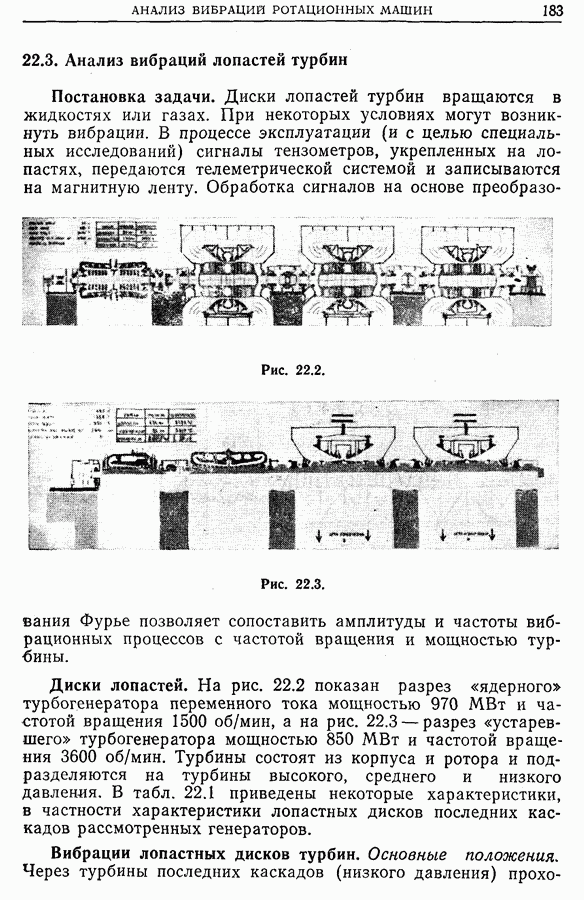
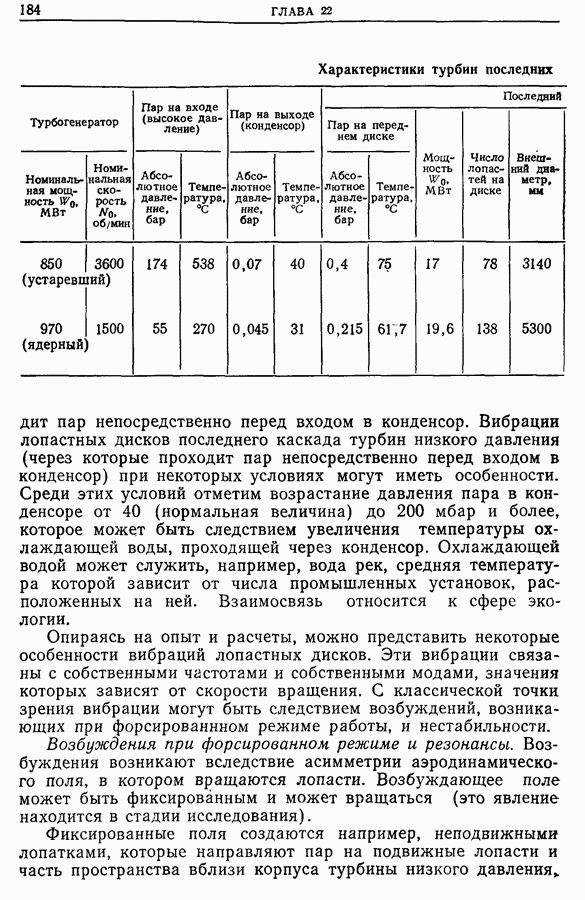
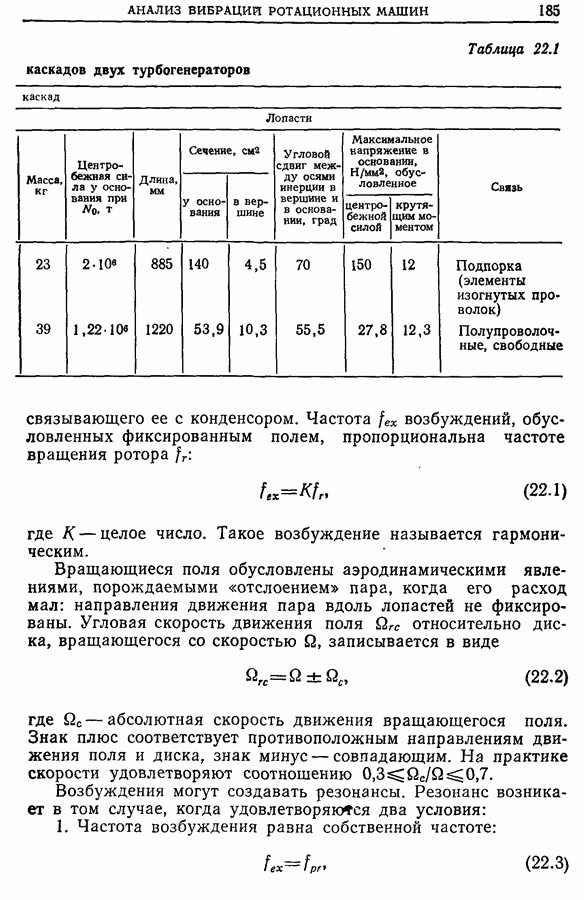
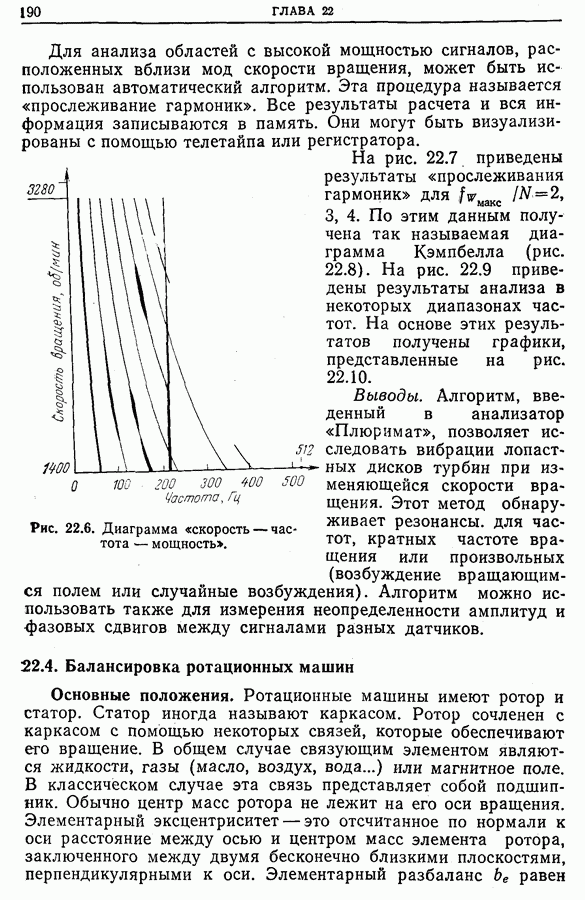
- 22.3. Анализ вибраций лопастей турбин
- 22.4. Балансировка ротационных машин
- Глава 23. ФУНКЦИЯ НЕОПРЕДЕЛЕННОСТИ
- 23.2. Временная корреляция. Временной сдвиг
- 23.3. Частотная корреляция. Частотный сдвиг
- 23.4. Временной и частотный сдвиги. Функция неопределенности
- 23.5. Функция неопределенности Вудворда
- 23.6. Взаимная функция неопределенности
- 23.7. Некоторые свойства функции неопределенности
- 23.8. Представление функций неопределенности
- 23.9. Примеры функций неопределенности
- 23.10. Применение функции неопределенности
- 23.11. Применение функций неопределенности для описания линейных неоднородных во времени систем. Обобщение понятия передаточной функции. Функция диффузии (функция рассеивания)
- 23.12. Генерация тестового сигнала
- 23.13. Прибор для измерения функции неопределенности в режиме реального времени
- Глава 24. ПОНЯТИЕ МГНОВЕННОГО СПЕКТРА ИЛИ ЧАСТОТНО-ВРЕМЕННОГО ПРЕДСТАВЛЕНИЯ В АНАЛИЗЕ И СИНТЕЗЕ СИГНАЛОВ
- 24.2. Примеры спектрального анализа модулированных и немодулированных сигналов
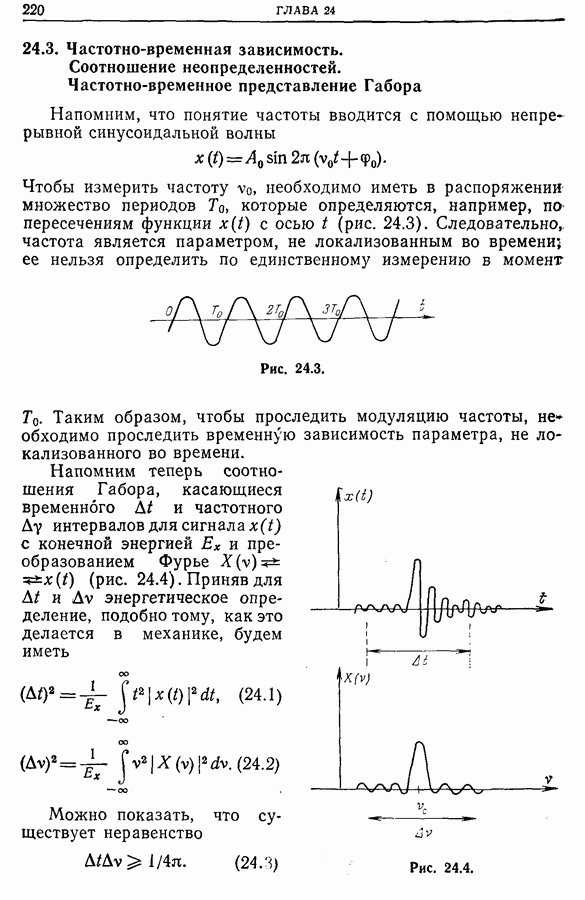
- 24.3. Частотно-временная зависимость. Соотношение неопределенностей. Частотно-временное представление Габора
- 24.4. Представление [t, v] по Бонне. Мгновенный спектр мощности по Биллю. Функция неопределенности
- 24.5. Другие определения частотно-временного представления
- 24.6. Измерение мгновенных спектров
- 24.7. Обобщение понятия мгновенного спектра мощности на случайные локально-стационарные сигналы. Функция структуры. Функция диффузии
- 24.8 Восстановление сигнала x(t) по известной функции
- 24.9. Заключение
- Глава 25. НОВЫЕ МЕТОДЫ СПЕКТРАЛЬНОГО АНАЛИЗА
- 25.2. Проблемы, обусловленные дискретизацией корреляционной функции
- 25.3. Постановка проблемы получения спектральной функции из конечного числа значений автокорреляционной функции
- 25.4. Классический метод, основанный на преобразовании Фурье корреляционной функции
- 25.5. Метод максимума энтропии или метод авторегрессионной модели
- 25.6. Метод Писаренко
- 25.7. Смешанные методы
- 25.8. Заключение