| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
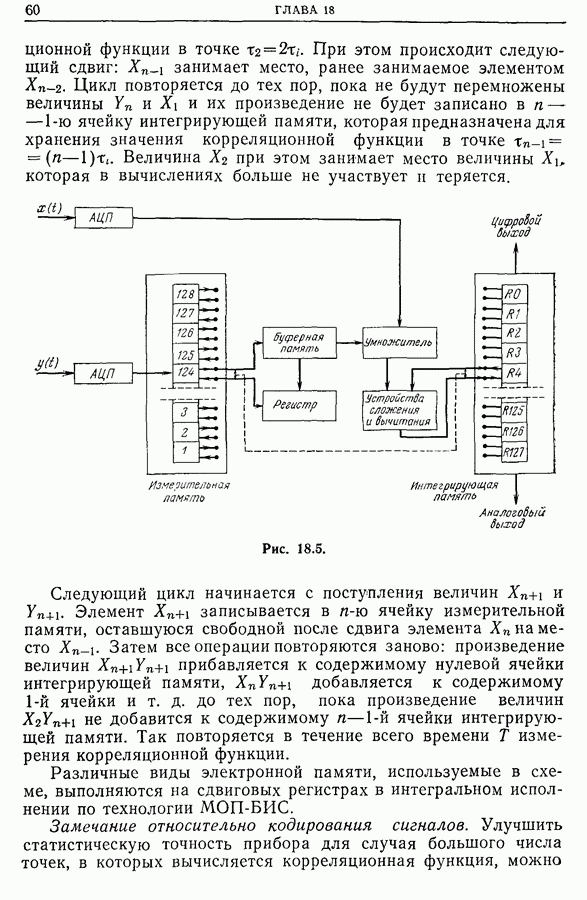
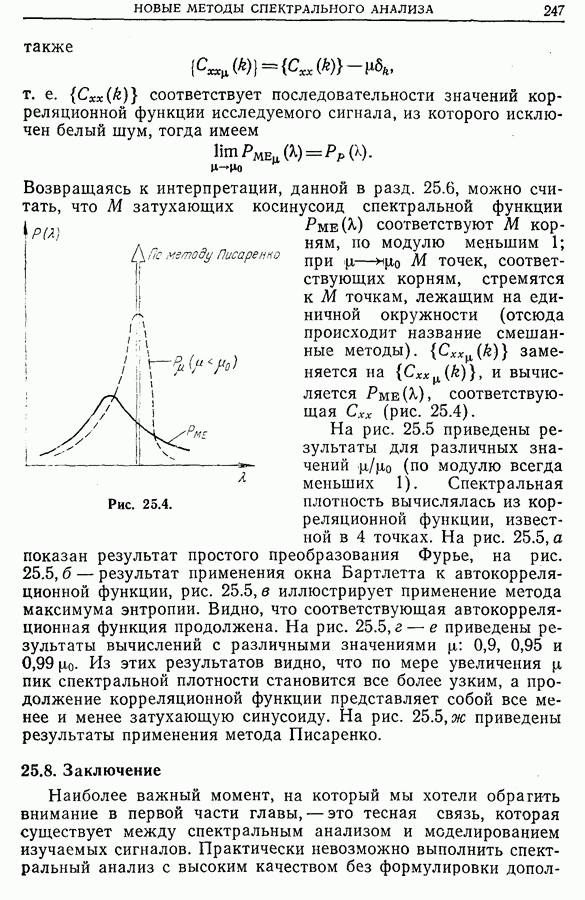
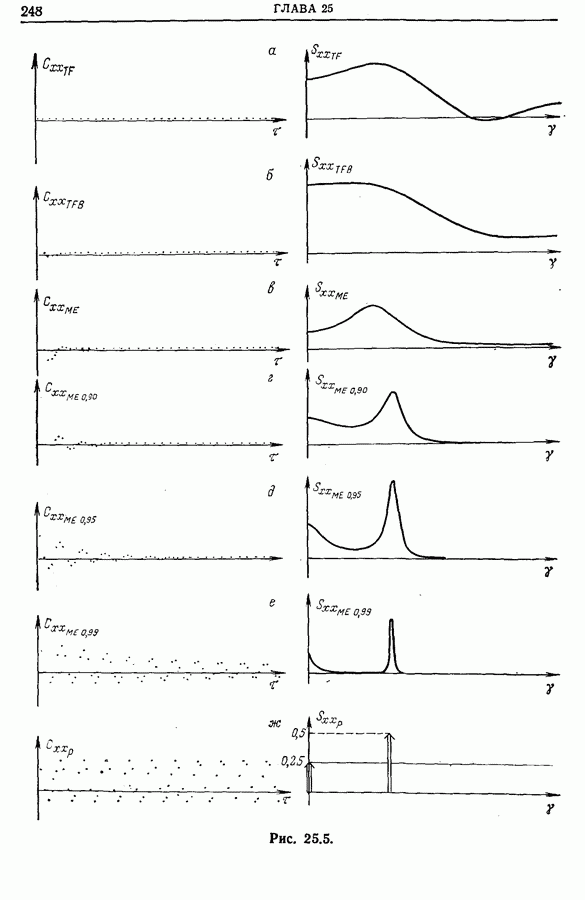
18.4. Автоматические коррелометры на линии с исследуемым сигналом
Подобные приборы предназначены для одновременного получения значений корреляционной функции, соответствующих различным значениям задержки  но они, к сожалению, не используют всю информацию, содержащуюся во входных сигналах. Мы их будем называть коррелометрами на линии в отличие от коррелометров реального времени, которые будут рассмотрены ниже.
но они, к сожалению, не используют всю информацию, содержащуюся во входных сигналах. Мы их будем называть коррелометрами на линии в отличие от коррелометров реального времени, которые будут рассмотрены ниже.
Принцип действия этих приборов заключается в следующем. Пусть  — период дискретизации сигналов (гл. 7). Рассмотрим
— период дискретизации сигналов (гл. 7). Рассмотрим  элемент выборки сигнала
элемент выборки сигнала  равный
равный  и поместим его в ячейку электронной (аналоговой или цифровой) памяти.
и поместим его в ячейку электронной (аналоговой или цифровой) памяти.
Затем умножим величину  на последовательные элементы выборки сигнала
на последовательные элементы выборки сигнала 

в результате чего получим  произведений:
произведений:

Если положить

то произведения приводятся к виду

Все произведения также расположим в  последовательных ячейках памяти в соответствии с их временем задержки. Когда все указанные операции завершены, выборка повторяется для значений случайных сигналов
последовательных ячейках памяти в соответствии с их временем задержки. Когда все указанные операции завершены, выборка повторяется для значений случайных сигналов

Произведение, соответствующее задержке 

добавляется к содержимому ячейки памяти, в которой содержится произведение, соответствующее такой же величине задержки от предыдущей выборки, и т. д.
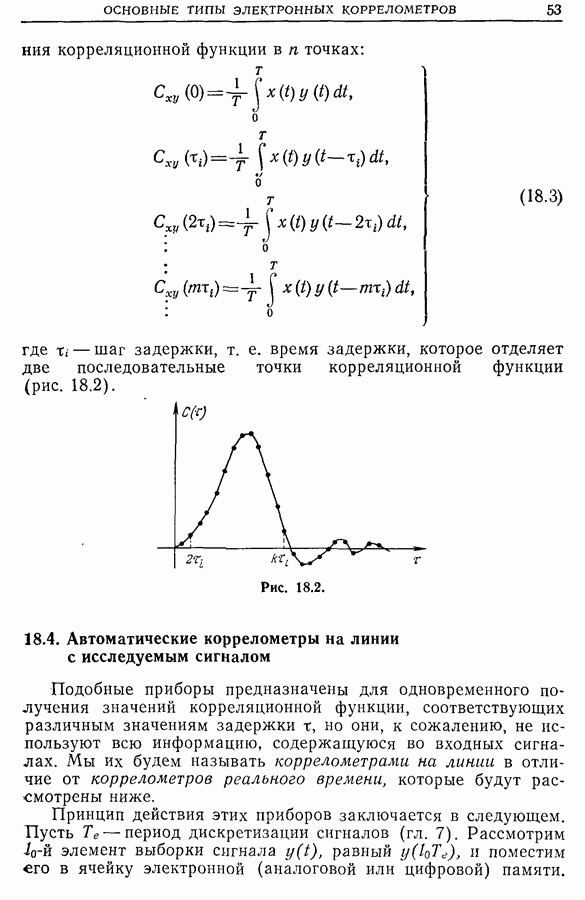
Примечание. Дискретизация корреляционных функций. Из описания работы коррелометра следует, что корреляционная функция  определяется в дискретных точках с шагом, равным периоду дискретизации Те, и выборка ее значений может быть представлена в виде
определяется в дискретных точках с шагом, равным периоду дискретизации Те, и выборка ее значений может быть представлена в виде

В разумности принятия шага дискретизации Те корреляционной функции  равным шагу дискретизации исходного случайного сигнала, можно убедиться путем следующих рассуждений. Применение теоремы Шеннона (гл. 7), с одной стороны, к случайному сигналу, а с другой — к его автокорреляционной функции даст одну и ту же граничную частоту дискретизации, поскольку в обоих случаях речь идет об одной и той же спектральной плотности. То же самое можно сказать и о взаимно-корреляционной функции.
равным шагу дискретизации исходного случайного сигнала, можно убедиться путем следующих рассуждений. Применение теоремы Шеннона (гл. 7), с одной стороны, к случайному сигналу, а с другой — к его автокорреляционной функции даст одну и ту же граничную частоту дискретизации, поскольку в обоих случаях речь идет об одной и той же спектральной плотности. То же самое можно сказать и о взаимно-корреляционной функции.
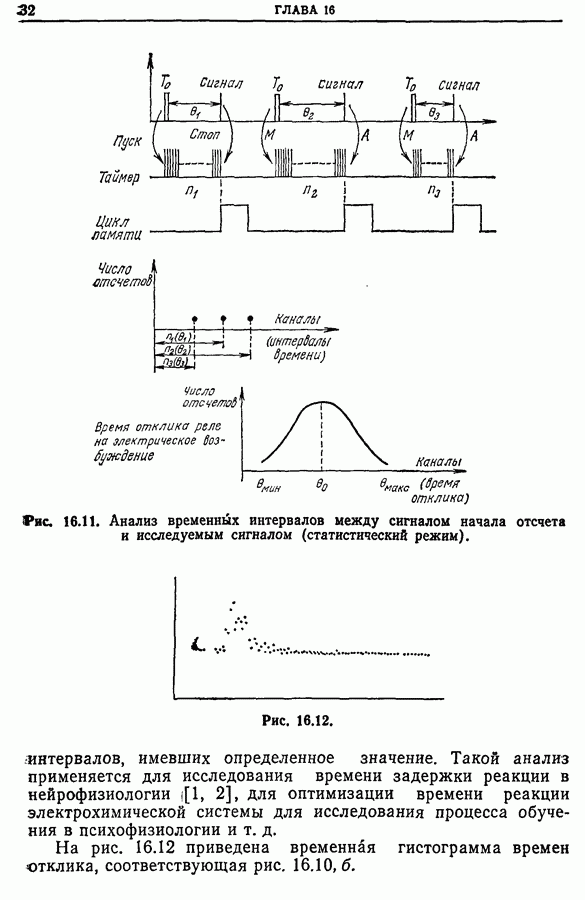
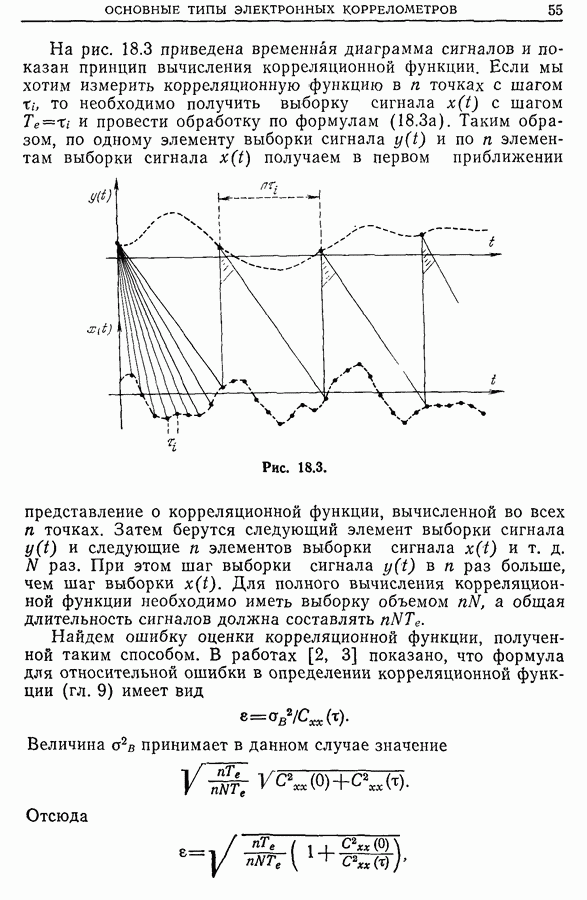
На рис. 18.3 приведена временная диаграмма сигналов и показан принцип вычисления корреляционной функции. Если мы хотим измерить корреляционную функцию в  точках с шагом
точках с шагом  то необходимо получить выборку сигнала
то необходимо получить выборку сигнала  с шагом
с шагом  и провести обработку по формулам (18.3а). Таким образом, по одному элементу выборки сигнала
и провести обработку по формулам (18.3а). Таким образом, по одному элементу выборки сигнала  и по
и по  элементам выборки сигнала
элементам выборки сигнала  получаем в первом приближении представление о корреляционной функции, вычисленной во всех
получаем в первом приближении представление о корреляционной функции, вычисленной во всех  точках.
точках.

Рис. 18.3.
Затем берутся следующий элемент выборки сигнала  и следующие
и следующие  элементов выборки сигнала
элементов выборки сигнала  раз. При этом шаг выборки сигнала
раз. При этом шаг выборки сигнала  раз больше, чем шаг выборки
раз больше, чем шаг выборки  Для полного вычисления корреляционной функции необходимо иметь выборку объемом
Для полного вычисления корреляционной функции необходимо иметь выборку объемом  а общая длительность сигналов должна составлять
а общая длительность сигналов должна составлять 
Найдем ошибку оценки корреляционной функции, полученной таким способом. В работах [2, 3] показано, что формула для относительной ошибки в определении корреляционной функции (гл. 9) имеет вид

Величина  принимает в данном случае значение
принимает в данном случае значение

Отсюда

и ошибка при  равна
равна

Пропорциональность относительной ошибки величине  можно было ожидать заранее, так как каждая точка корреляционной функции вычисляется как сумма
можно было ожидать заранее, так как каждая точка корреляционной функции вычисляется как сумма  произведений, полученных из независимых элементов выборки. Независимость соответствующих элементов выборки, которые следуют друг за другом через интервал времени
произведений, полученных из независимых элементов выборки. Независимость соответствующих элементов выборки, которые следуют друг за другом через интервал времени  будет выполняться при таком выборе интервала времени
будет выполняться при таком выборе интервала времени  что
что

Вернемся к формуле  . Поскольку Те есть период выборки, то можно записать
. Поскольку Те есть период выборки, то можно записать  где В — ширина спектральной полосы рассматриваемого сигнала, а — коэффициент, показывающий во сколько раз частота выборки превосходит частоту Шеннона (гл. 7). Таким образом, имеем
где В — ширина спектральной полосы рассматриваемого сигнала, а — коэффициент, показывающий во сколько раз частота выборки превосходит частоту Шеннона (гл. 7). Таким образом, имеем

Если для идеального коррелометра (т. е. без учета погрешности выборки) ошибка составляет  , то в рассматриваемом случае она будет в
, то в рассматриваемом случае она будет в  раз больше. Во столько же раз больше будет и время измерения для достижения одинаковой точности.
раз больше. Во столько же раз больше будет и время измерения для достижения одинаковой точности.
Для представления корреляционной функции на экране электронно-лучевой трубки необходимо использовать дискретизацию с частотой, существенно превышающей частоту Шеннона (коэффициент  невелико). В частности, для гауссова шума с шириной спектральной полосы В можно принять, что для задержки
невелико). В частности, для гауссова шума с шириной спектральной полосы В можно принять, что для задержки  корреляционная функция принимает пренебрежимо малые значения
корреляционная функция принимает пренебрежимо малые значения  Коэффициент
Коэффициент  и точность только в 3 раза хуже, чем для идеального коррелометра.
и точность только в 3 раза хуже, чем для идеального коррелометра.
Если же необходимо получить корреляционную функцию для применения ее в последующих расчетах, например для вычисления спектральной плотности, то используют частоту дискретизации, близкую к частоте Шеннона, в пределе с коэффициентом  . В этом случае ошибка по сравнению с идеальным коррелометром будет больше примерно в
. В этом случае ошибка по сравнению с идеальным коррелометром будет больше примерно в  раз. Это необходимо принимать во внимание, когда случайный сигнал имеет ограниченную длительность. В этом случае регистрация на коррелометре сигнала с длительностью Т с точки зрения ошибки эквивалентна регистрации на идеальном коррелометре сигнала с длительностью Т, немного превышающей
раз. Это необходимо принимать во внимание, когда случайный сигнал имеет ограниченную длительность. В этом случае регистрация на коррелометре сигнала с длительностью Т с точки зрения ошибки эквивалентна регистрации на идеальном коррелометре сигнала с длительностью Т, немного превышающей 
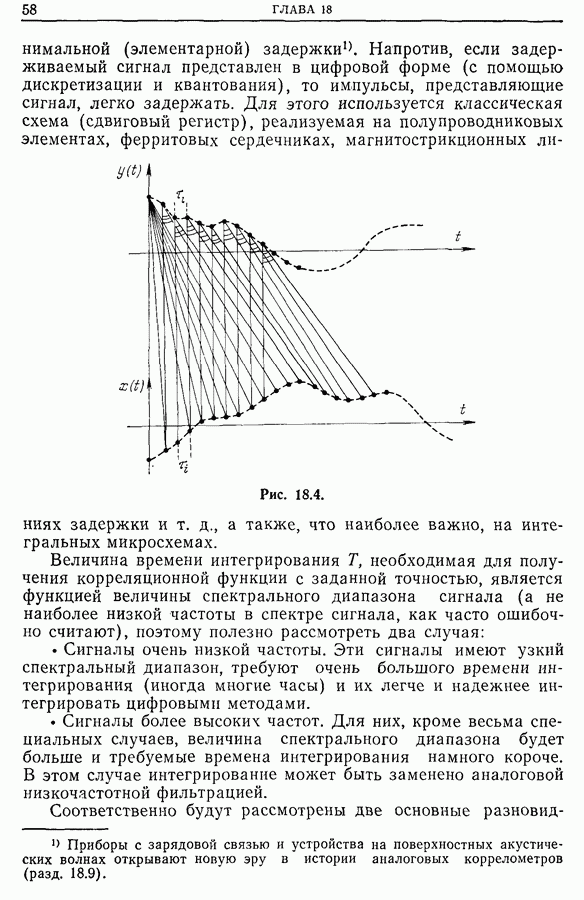
Назовем автоматическим коррелометром реального времени прибор, который с максимальной эффективностью использует всю информацию, содержащуюся во входных сигналах. Этот тип коррелометра иногда путают с автоматическим коррелометром на линии из-за того, что в теоретическом аспекте эти приборы одинаково используют определение корреляционной функции:

Однако существенное отличие заключается в том, как функция  стремится к своему пределу. Автоматические коррелометры реального времени позволяют добиться такой же точности измерения корреляционной функции, которую можно получить с помощью коррелометров на линии, используя входные сигналы в
стремится к своему пределу. Автоматические коррелометры реального времени позволяют добиться такой же точности измерения корреляционной функции, которую можно получить с помощью коррелометров на линии, используя входные сигналы в  раз большей длительности, что часто на практике оказывается неприемлемым.
раз большей длительности, что часто на практике оказывается неприемлемым.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 15. СИНХРОННОЕ ДЕТЕКТИРОВАНИЕ
- 15.2. Схема метода
- 15.3. Теория синхронного детектирования
- 15.4. Синхронное детектирование в режиме развертки
- 15.5. Примеры применения синхронных детекторов
- 15.6. Совершенствование синхронных детекторов
- Глава 16. ИСПОЛЬЗОВАНИЕ МНОГОКАНАЛЬНЫХ АНАЛИЗАТОРОВ ПРИ СТАТИЧЕСКОЙ ОБРАБОТКЕ ИЗМЕРЕНИЙ
- 16.2. Характеристики многоканальных анализаторов
- 16.3. Схема системы обработки
- 16.4. Примеры применения
- Глава 17. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ
- 17.2. Частный случай белого шума. Согласованный фильтр
- 17.3. Согласованная фильтрация и корреляция Корреляция.
- 17.4. Реализация согласованных фильтров методом «взвешивания»
- 17.5. Рекурсивная согласованная фильтрация [7]
- 17.6. Применения метода согласованной фильтрации
- Глава 18. ОСНОВНЫЕ ТИПЫ ЭЛЕКТРОННЫХ КОРРЕЛОМЕТРОВ
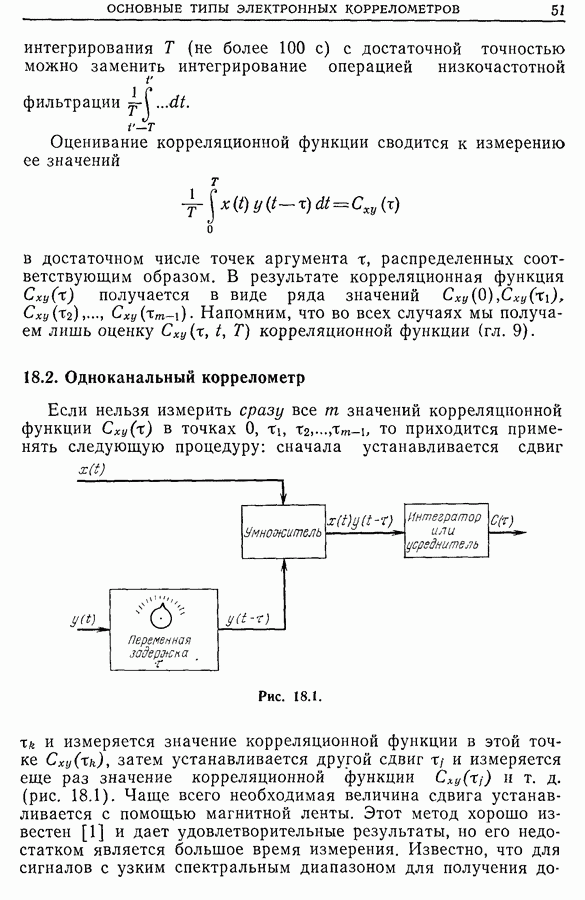
- 18.2. Одноканальный коррелометр
- 18.3. Автоматические коррелометры
- 18.4. Автоматические коррелометры на линии с исследуемым сигналом
- 18.5. Автоматические коррелометры реального времени (или мультикоррелометры)
- 18.6. Коррелометры на больших интегральных схемах
- 18.7. Коррелометры реального времени для высокочастотных сигналов
- 18.8 Развитие коррелометров
- 18.9. Приборы с зарядовой связью [11]
- Глава 19. СПЕКТРАЛЬНЫЕ ЭЛЕКТРОННЫЕ АНАЛИЗАТОРЫ
- 19.2. Спектральные анализаторы, основанные на методе непосредственного преобразования Фурье
- 19.3. Применения анализаторов на основе метода БПФ
- Глава 20. ОПТИЧЕСКИЙ СПЕКТРАЛЬНЫЙ АНАЛИЗ
- 20.2. Упрощения, связанные с отбрасыванием фазы
- 20.3. Эффект виньетирования
- 20.4. Двумерный анализ
- 20.5. Точечный монохроматический источник
- 20.6. Электрооптическое преобразование сигнала
- 20.7. Устройства отображения на жидких кристаллах
- 20.8. Ограничения устройств отображения
- 20.9. Модулятор на основе эффекта Покельса (PROM)
- 20.10. Трубки Титус и Фототитус
- 20.11. Другие электрооптические кристаллы
- 20.12. Спектральный анализ и интегральная оптика
- 20.13. Взаимные спектры
- Глава 21. НЕКОТОРЫЕ ПРАКТИЧЕСКИЕ ПРИМЕНЕНИЯ МЕТОДОВ ОБРАБОТКИ СИГНАЛОВ
- 21.2. Исследование ядерных сред
- 21.3. Ядерный магнитный резонанс (ЯМР) с возбуждением случайным сигналом
- 21.4. Идентификация процессов. Измерение импульсных откликов и передаточных функций
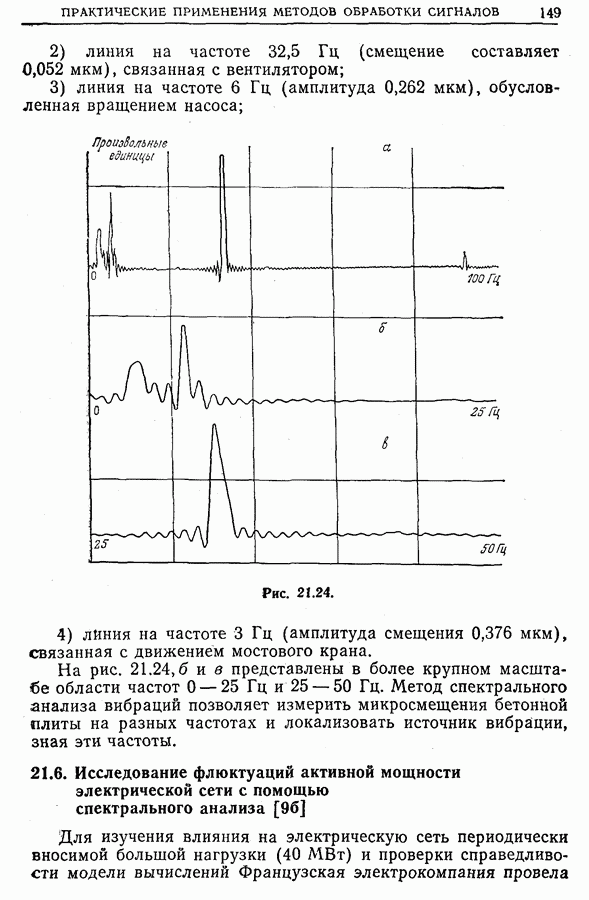
- 21.5. Спектральный анализ собственных колебаний бетонных плит
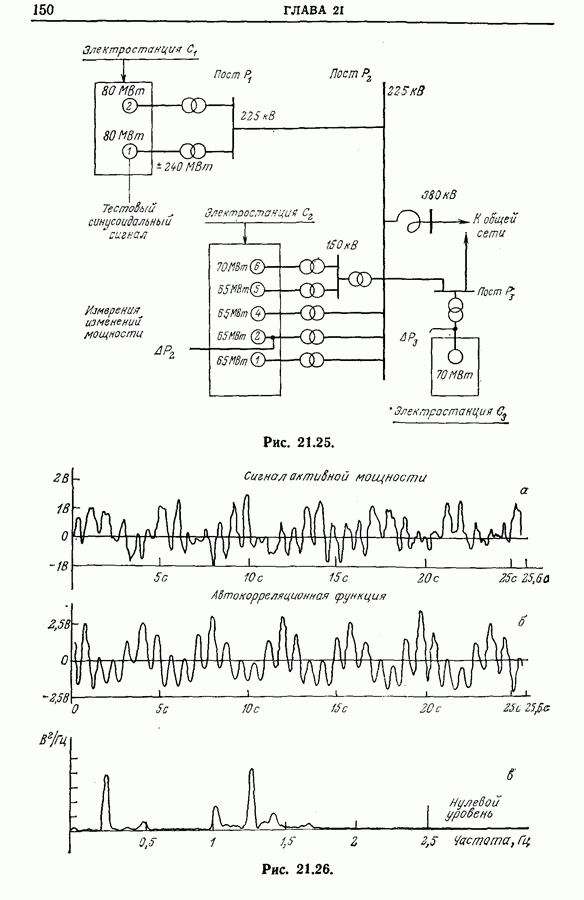
- 21.6. Исследование флюктуаций активной мощности электрической сети с помощью спектрального анализа
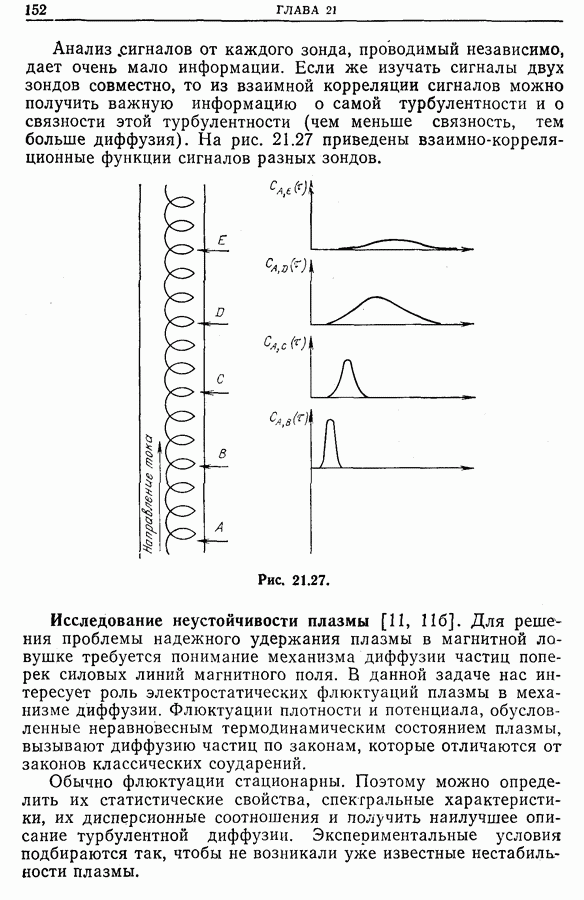
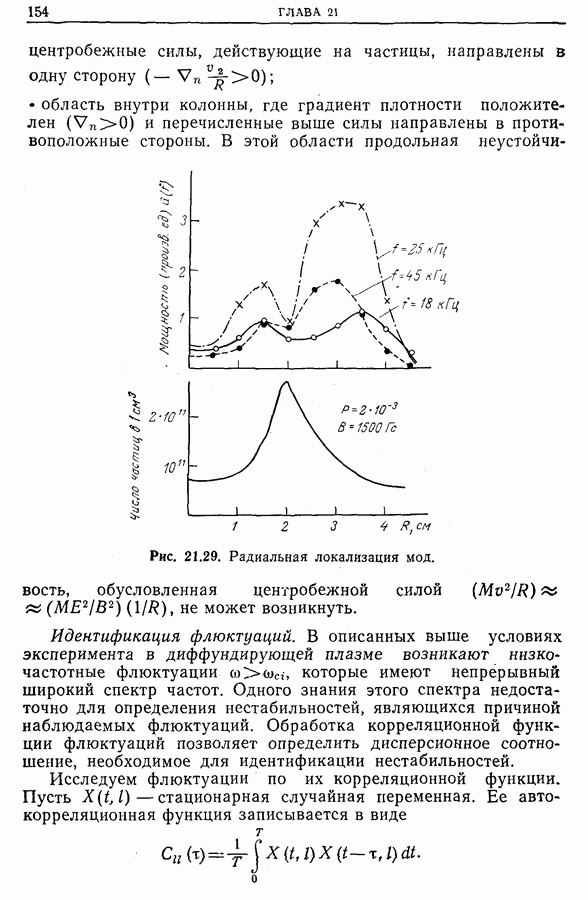
- 21.7. Изучение турбулентности
- 21.8. Применения в геофизике
- 21.9. Применения в астрофизике
- 21.10. Применения в астрономии и радиоастрономии
- 21.11. Применения в биологии и медицине
- 21.12. Применения в акустике
- 21.13. Исследование процессов намагничивания ферромагнетиков
- 21.14. Применения новых методов обработки сигналов
- 21.15. Заключение
- Глава 22. ПРИМЕНЕНИЕ МЕТОДОВ ОБРАБОТКИ СИГНАЛОВ ДЛЯ АНАЛИЗА ВИБРАЦИЙ РОТАЦИОННЫХ МАШИНА
- 22.2. Анализ поведения системы «ротационная машина — конструкция»
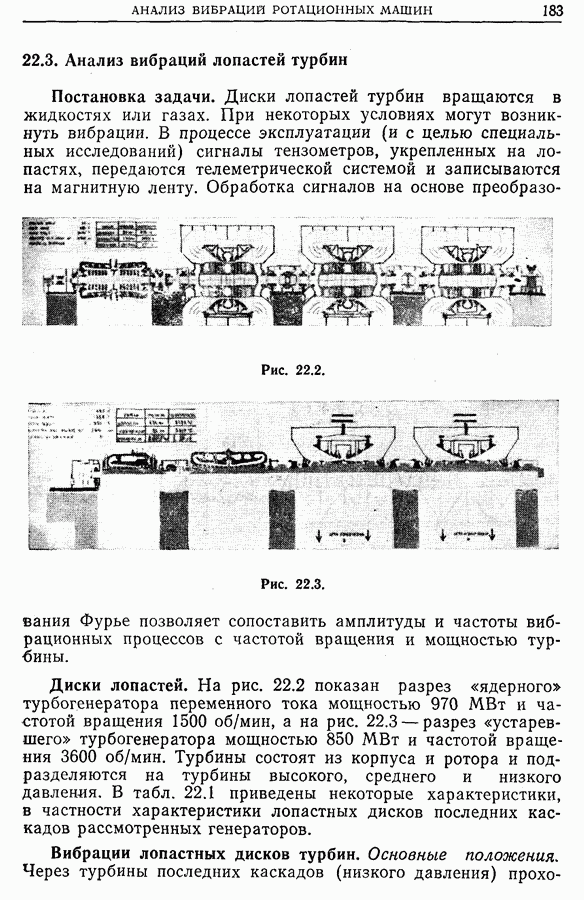
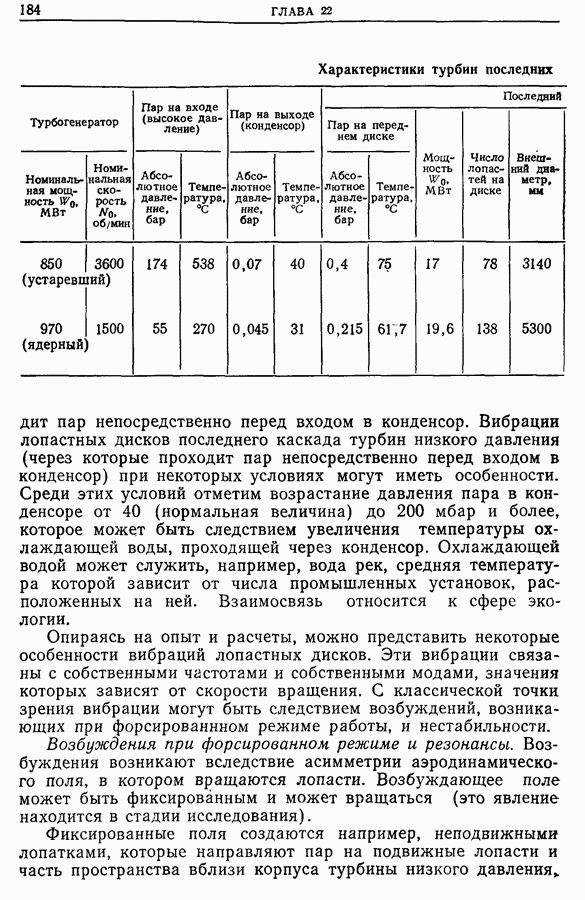
- 22.3. Анализ вибраций лопастей турбин
- 22.4. Балансировка ротационных машин
- Глава 23. ФУНКЦИЯ НЕОПРЕДЕЛЕННОСТИ
- 23.2. Временная корреляция. Временной сдвиг
- 23.3. Частотная корреляция. Частотный сдвиг
- 23.4. Временной и частотный сдвиги. Функция неопределенности
- 23.5. Функция неопределенности Вудворда
- 23.6. Взаимная функция неопределенности
- 23.7. Некоторые свойства функции неопределенности
- 23.8. Представление функций неопределенности
- 23.9. Примеры функций неопределенности
- 23.10. Применение функции неопределенности
- 23.11. Применение функций неопределенности для описания линейных неоднородных во времени систем. Обобщение понятия передаточной функции. Функция диффузии (функция рассеивания)
- 23.12. Генерация тестового сигнала
- 23.13. Прибор для измерения функции неопределенности в режиме реального времени
- Глава 24. ПОНЯТИЕ МГНОВЕННОГО СПЕКТРА ИЛИ ЧАСТОТНО-ВРЕМЕННОГО ПРЕДСТАВЛЕНИЯ В АНАЛИЗЕ И СИНТЕЗЕ СИГНАЛОВ
- 24.2. Примеры спектрального анализа модулированных и немодулированных сигналов
- 24.3. Частотно-временная зависимость. Соотношение неопределенностей. Частотно-временное представление Габора
- 24.4. Представление [t, v] по Бонне. Мгновенный спектр мощности по Биллю. Функция неопределенности
- 24.5. Другие определения частотно-временного представления
- 24.6. Измерение мгновенных спектров
- 24.7. Обобщение понятия мгновенного спектра мощности на случайные локально-стационарные сигналы. Функция структуры. Функция диффузии
- 24.8 Восстановление сигнала x(t) по известной функции
- 24.9. Заключение
- Глава 25. НОВЫЕ МЕТОДЫ СПЕКТРАЛЬНОГО АНАЛИЗА
- 25.2. Проблемы, обусловленные дискретизацией корреляционной функции
- 25.3. Постановка проблемы получения спектральной функции из конечного числа значений автокорреляционной функции
- 25.4. Классический метод, основанный на преобразовании Фурье корреляционной функции
- 25.5. Метод максимума энтропии или метод авторегрессионной модели
- 25.6. Метод Писаренко
- 25.7. Смешанные методы
- 25.8. Заключение