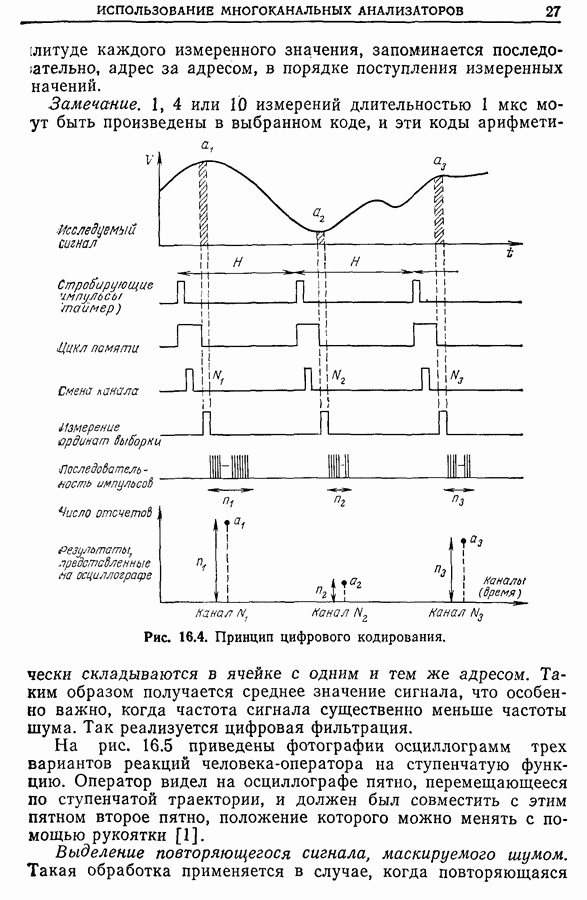
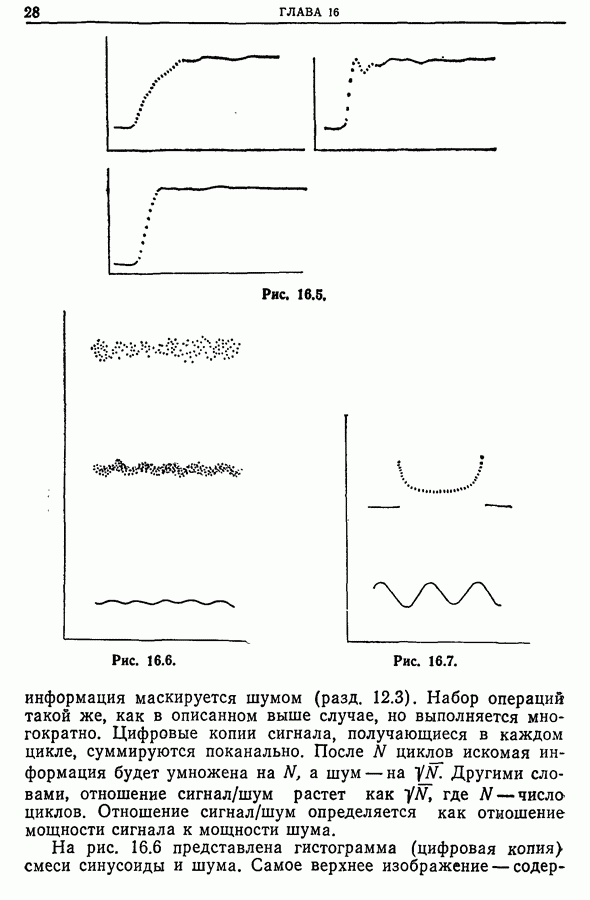
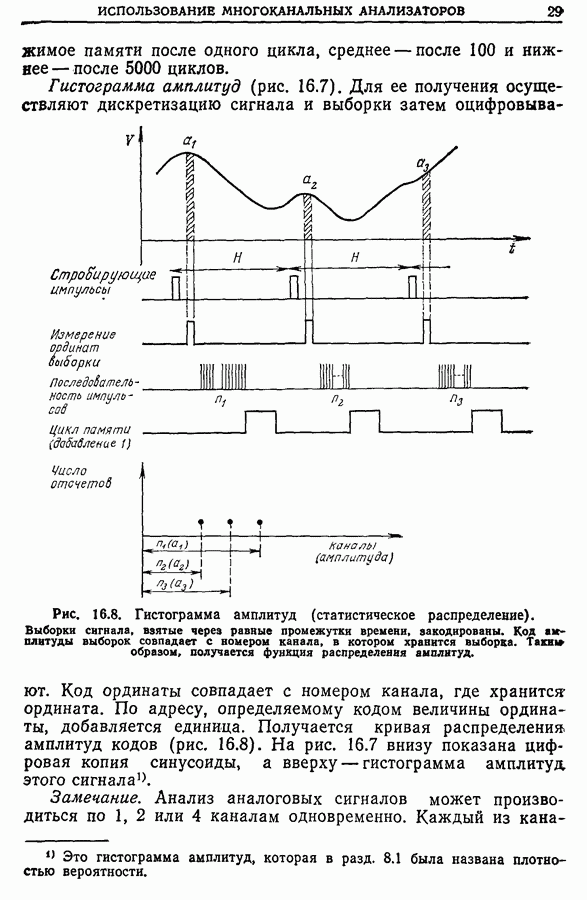
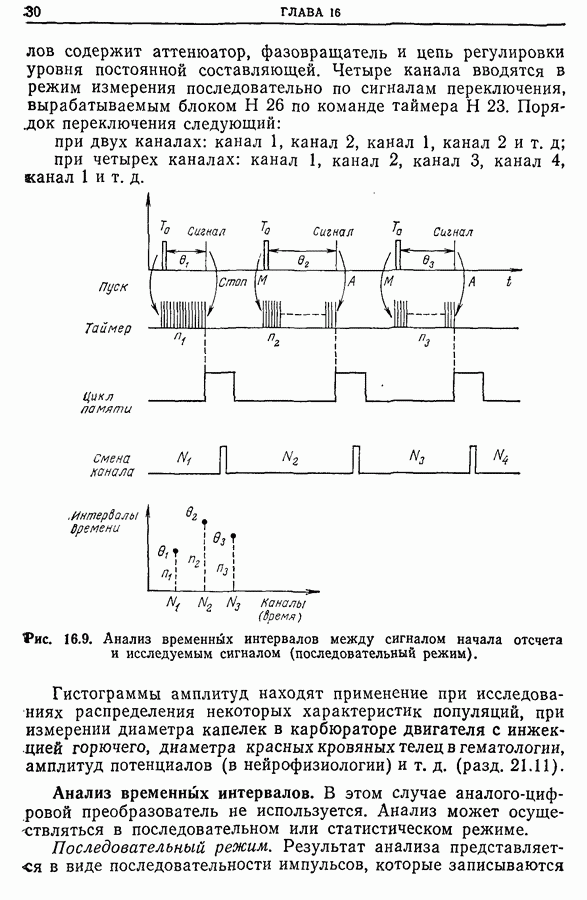
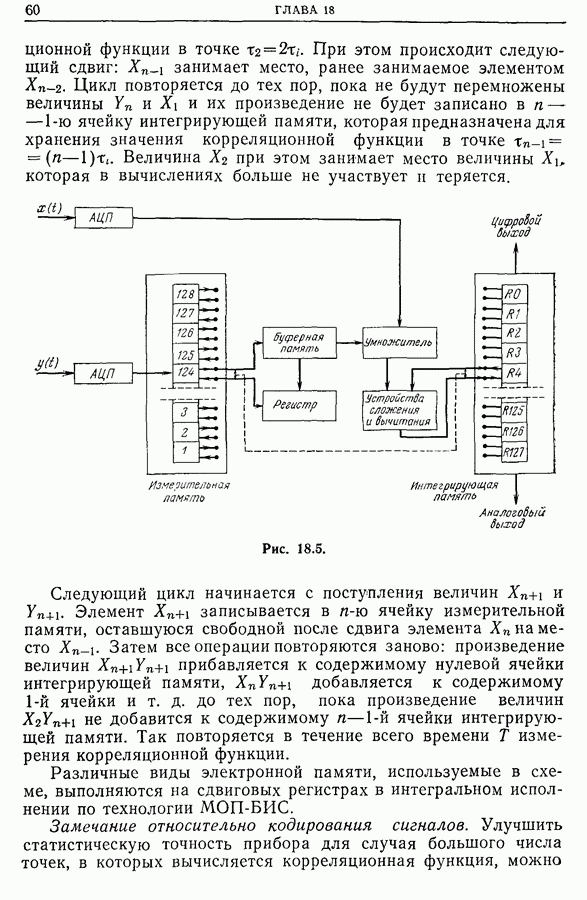
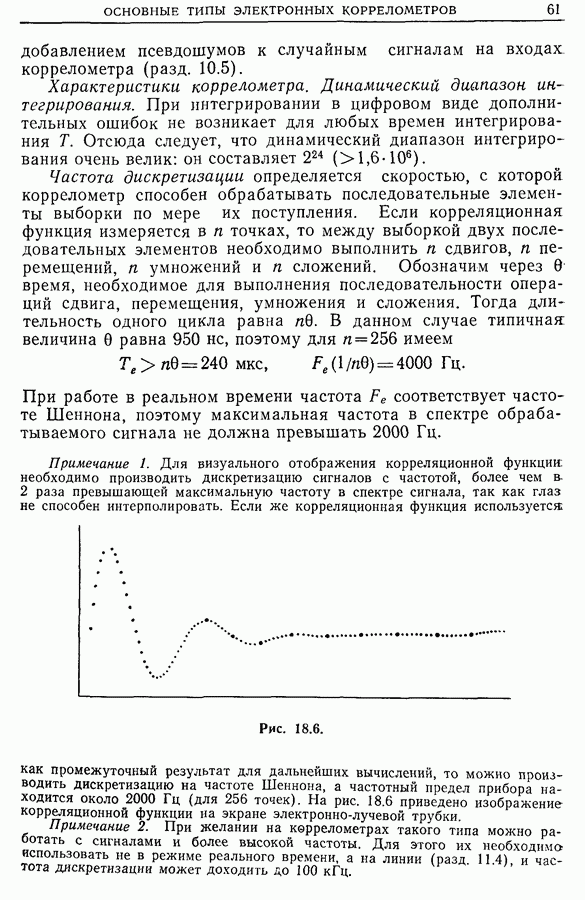
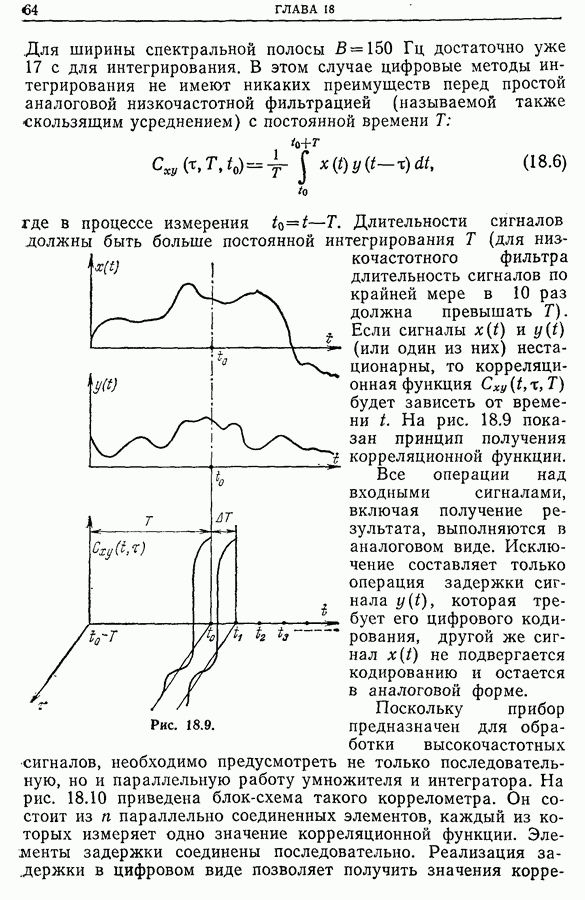
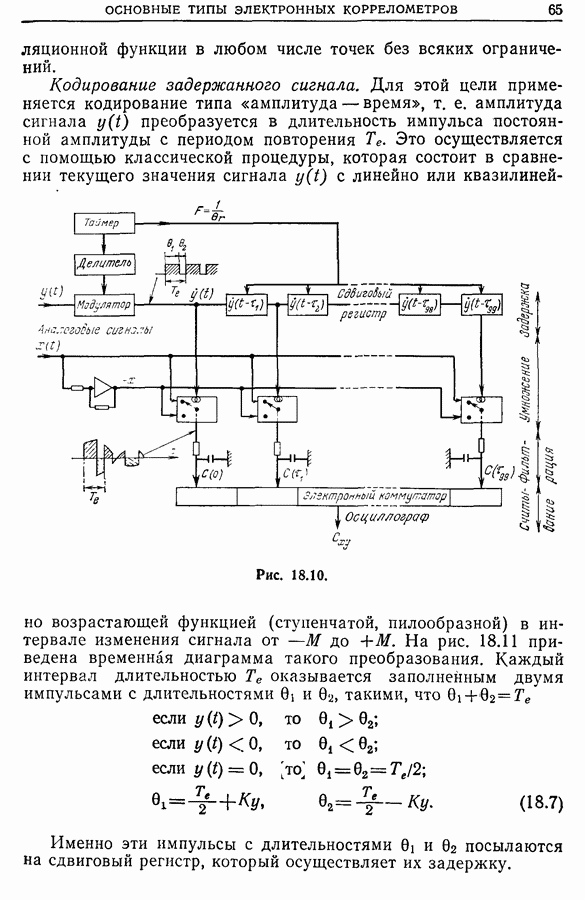
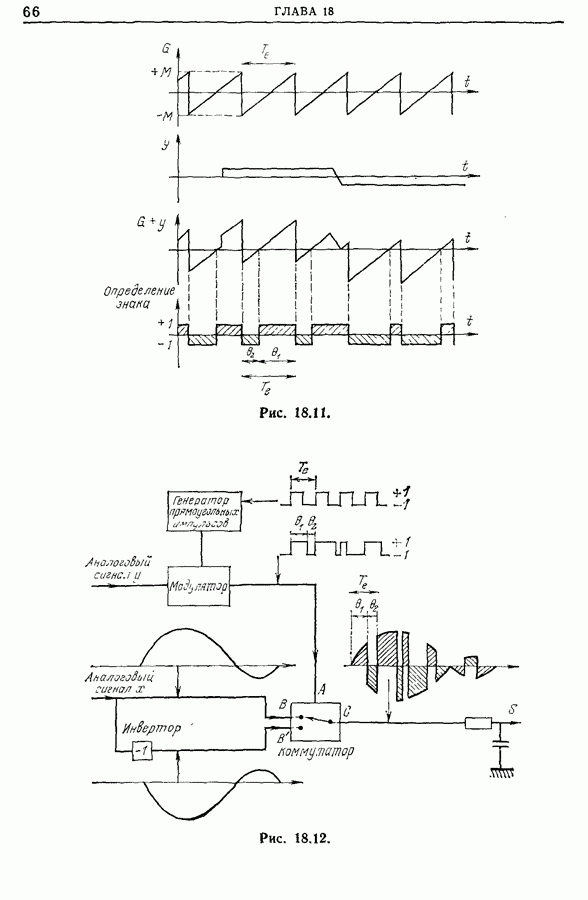
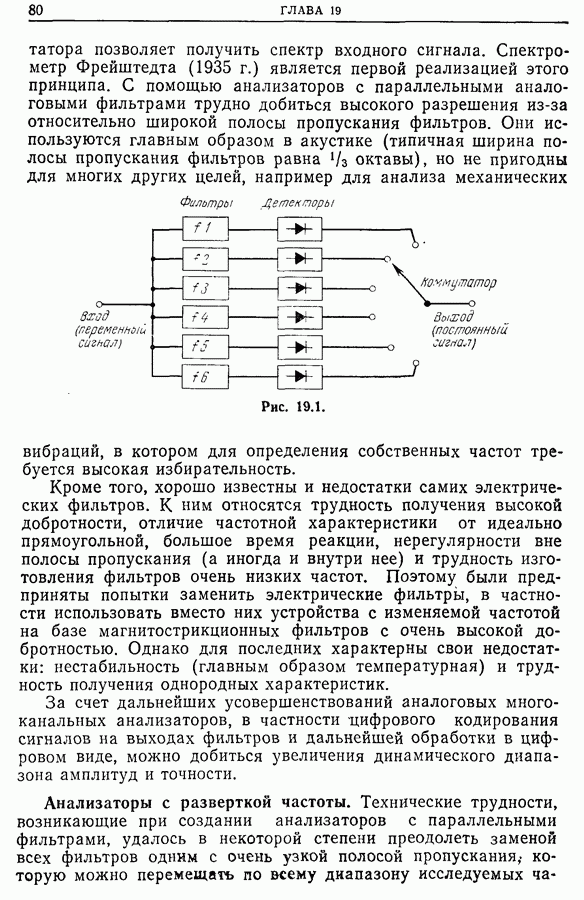
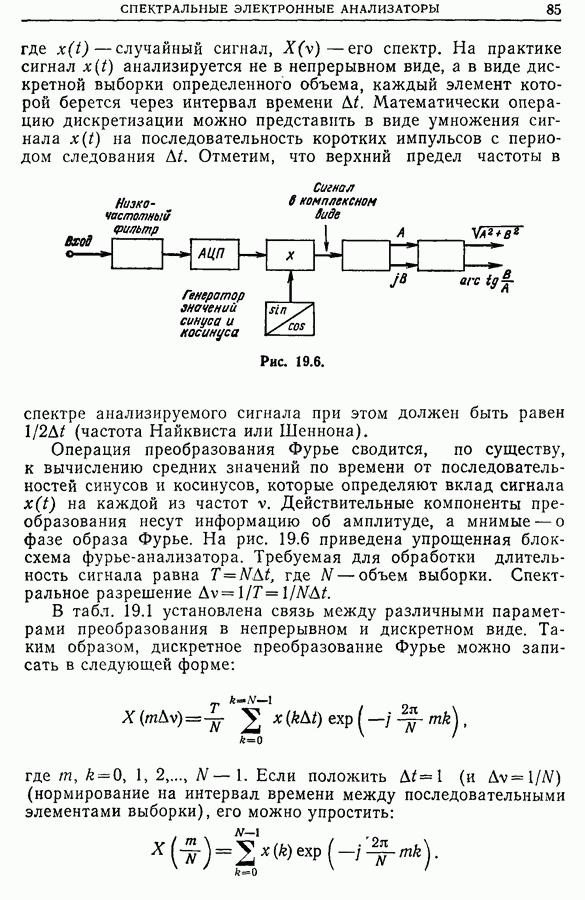
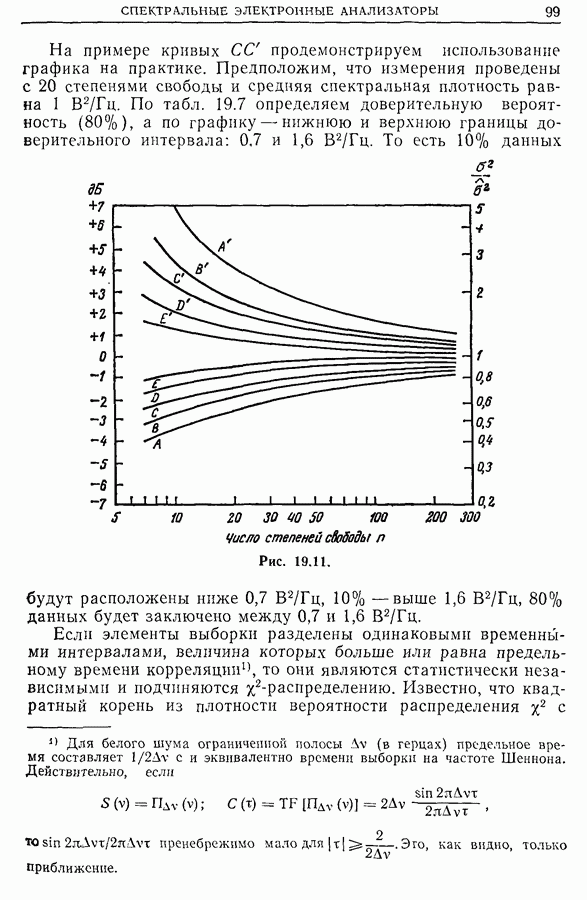
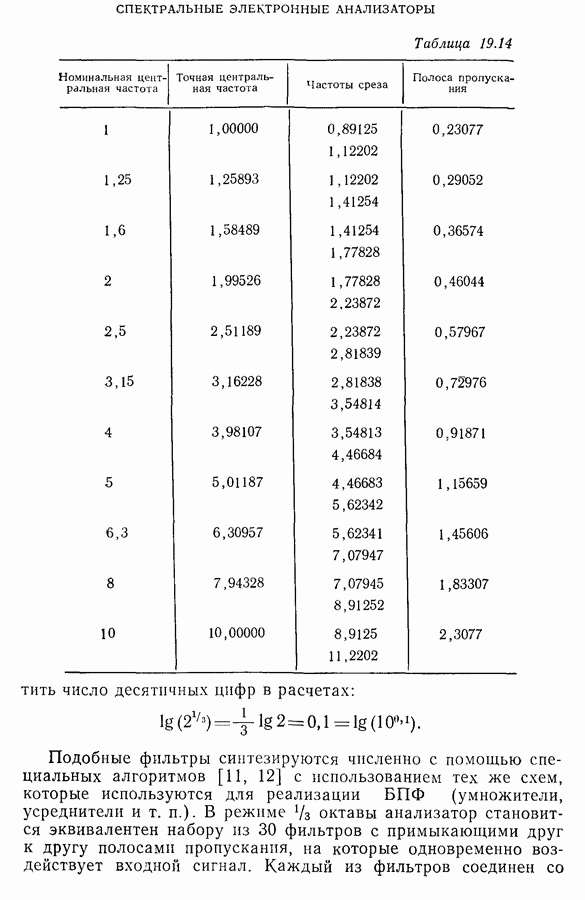
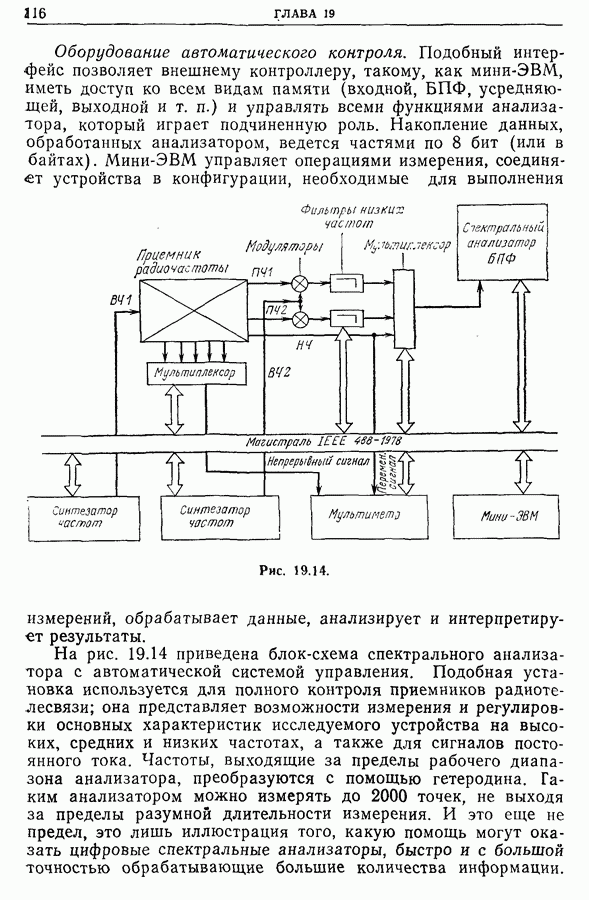
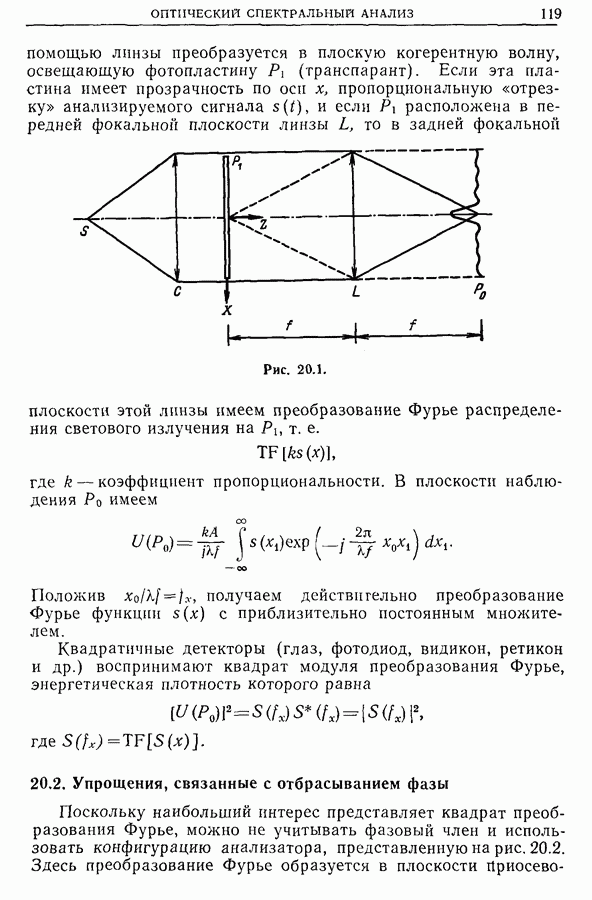
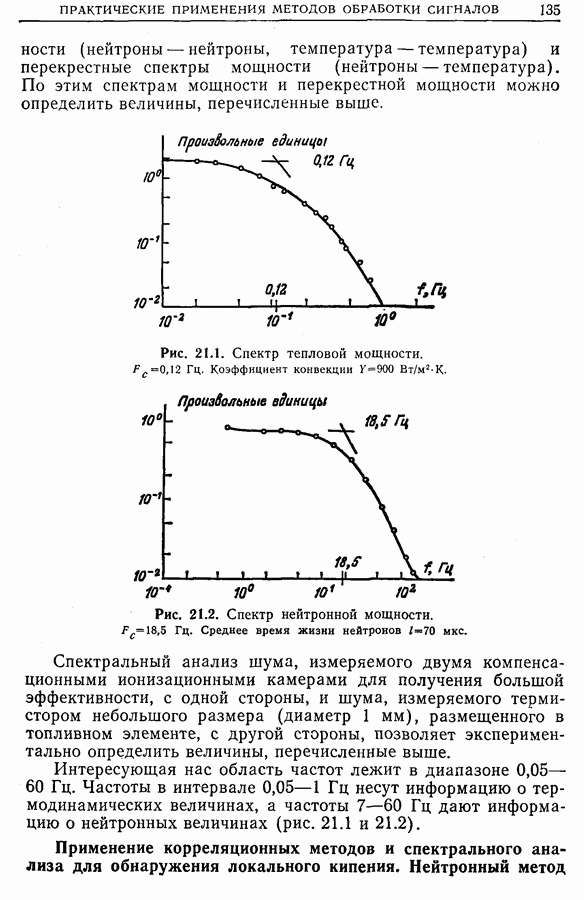
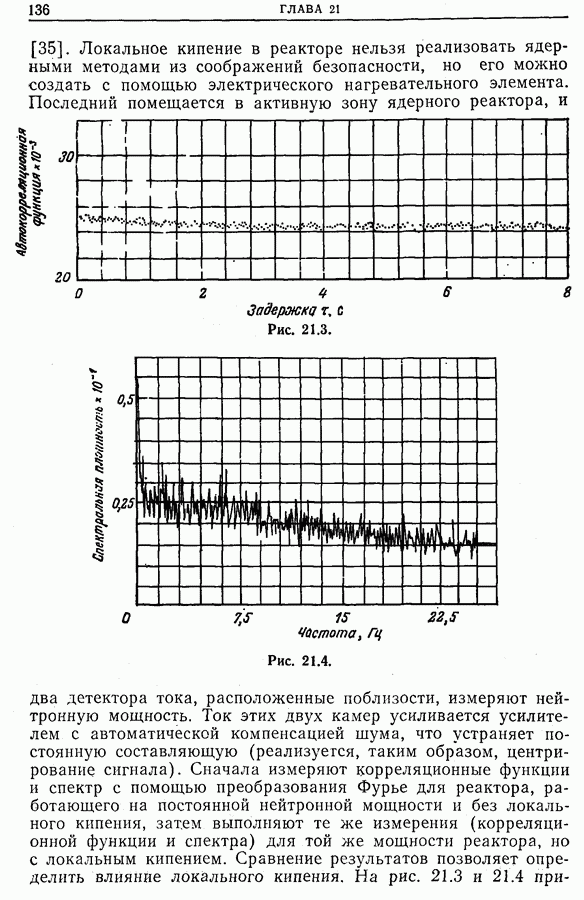
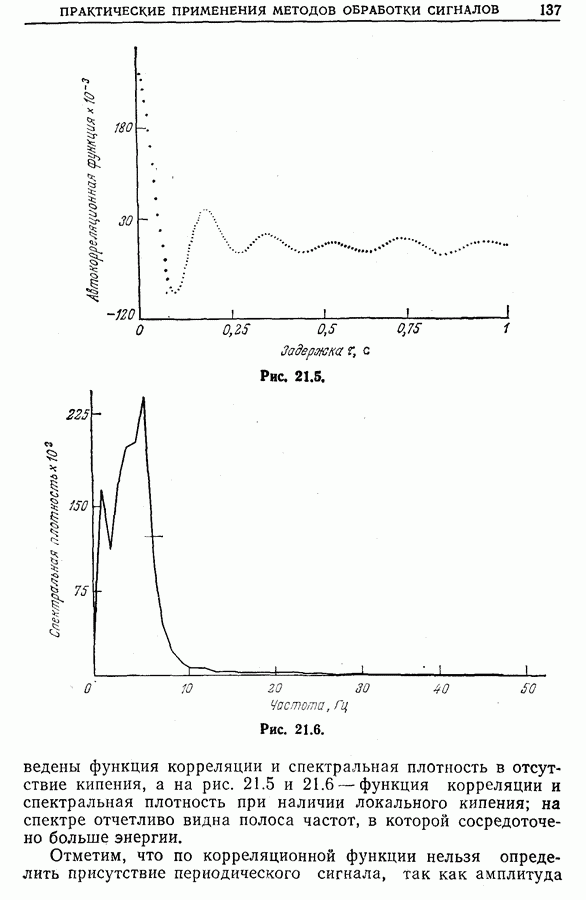
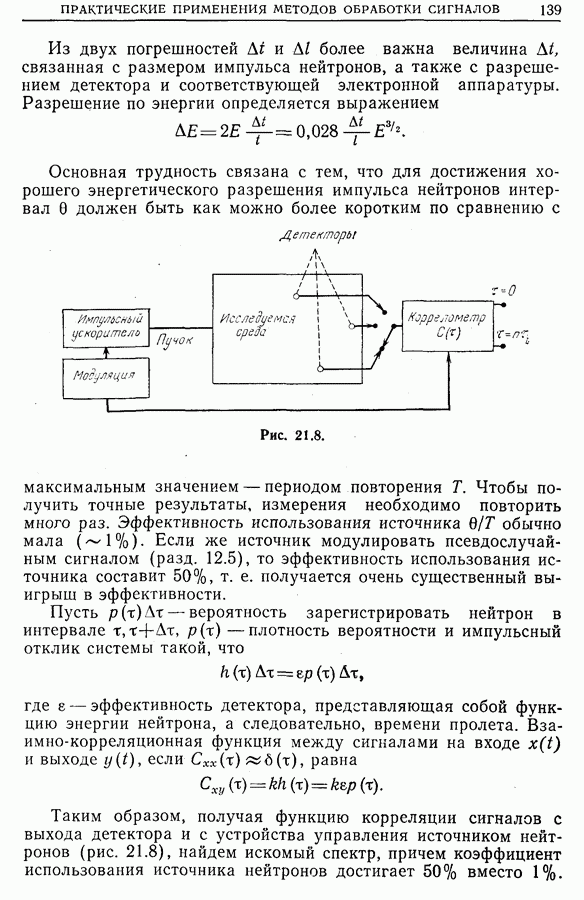
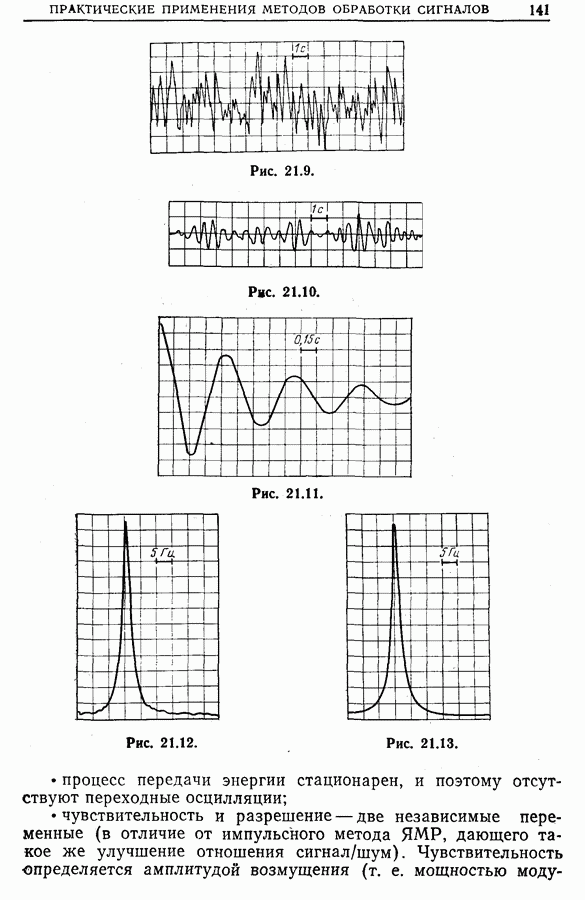
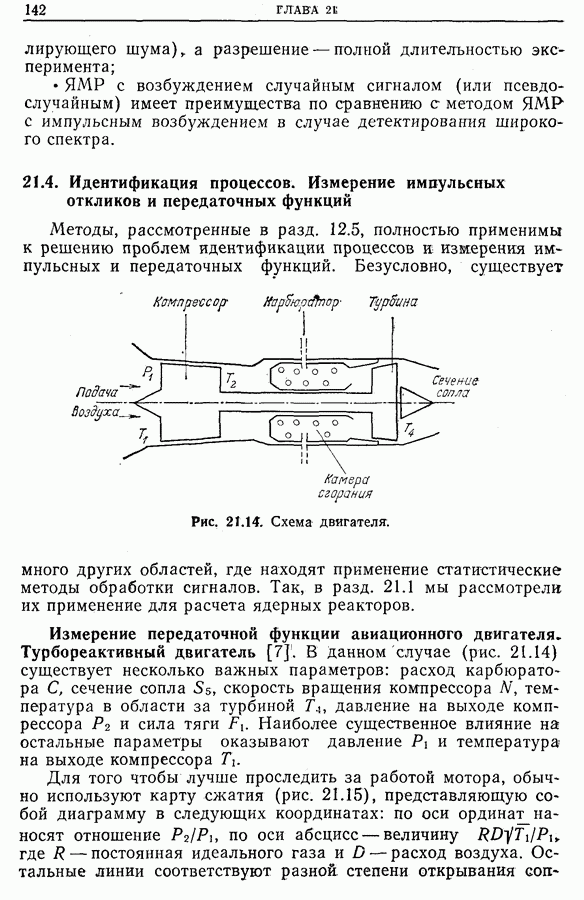
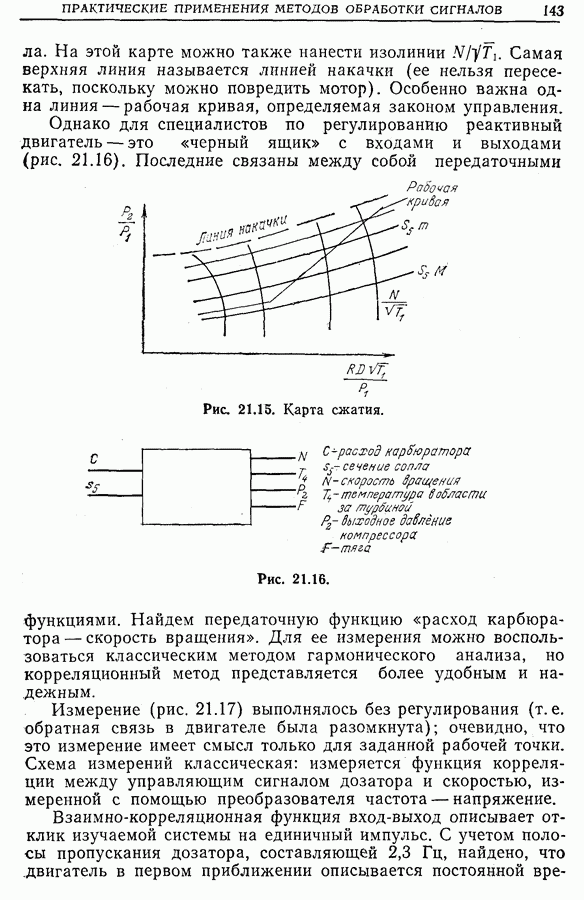
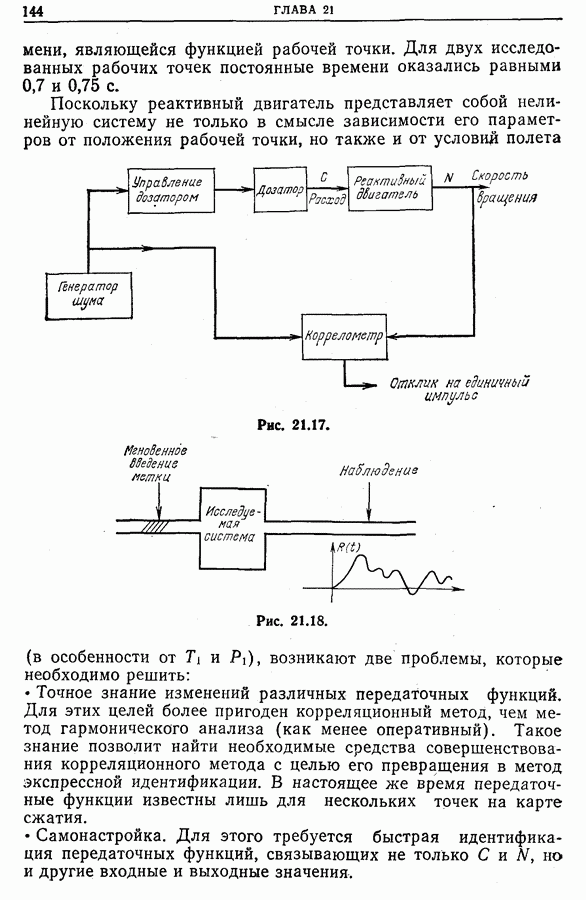
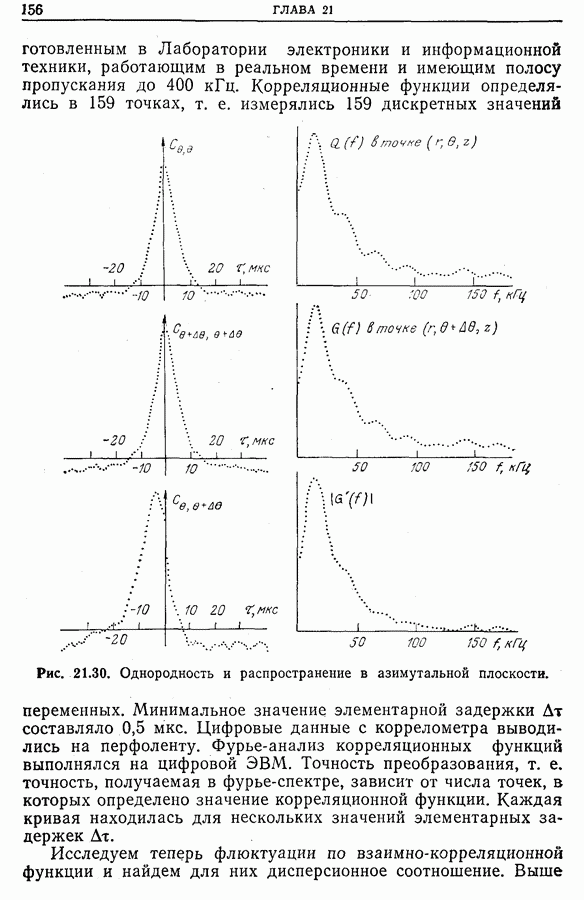
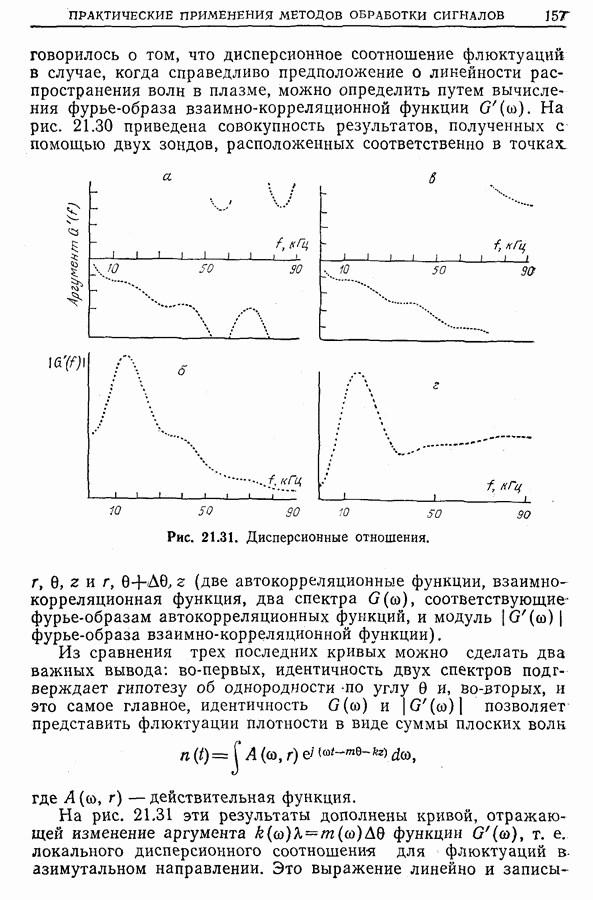
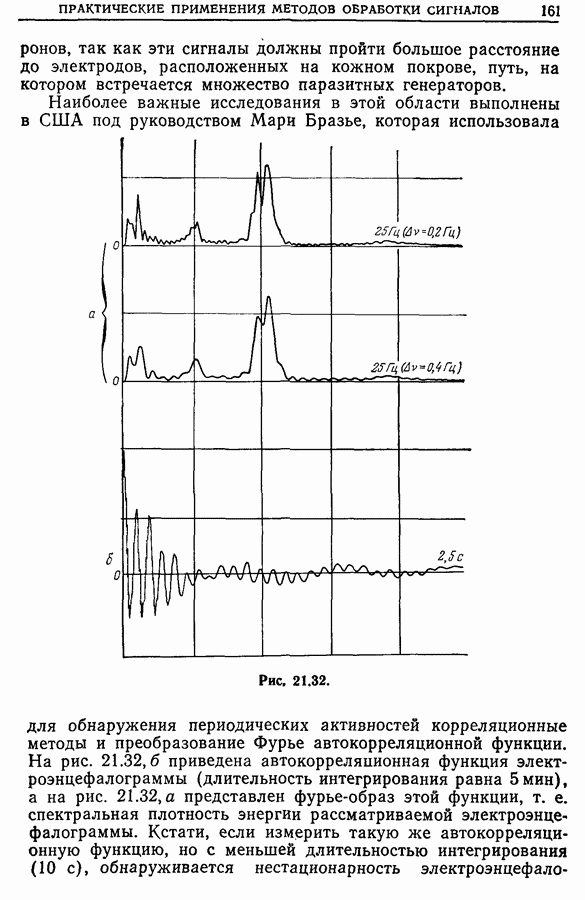
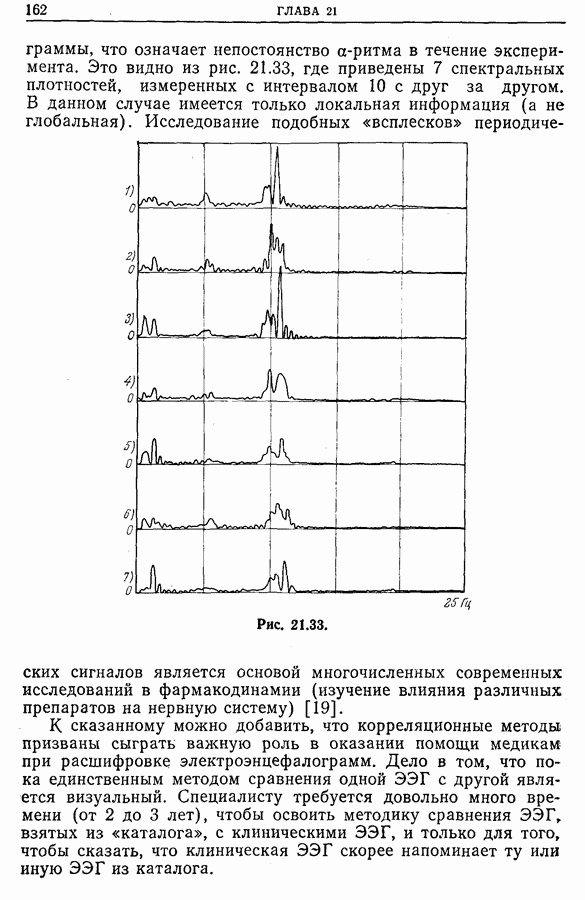
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
23.11. Применение функций неопределенности для описания линейных неоднородных во времени систем. Обобщение понятия передаточной функции. Функция диффузии (функция рассеивания)
Линейные системы.
Система называется линейной, если ее входной и выходной сигналы связаны линейным интегродифференциальным уравнением.
Линейные и однородные (или инвариантные) во времени системы.
Для такой линейной системы коэффициенты интегро-дифференциального уравнения не зависят от времени. Она полностью характеризуется импульсным откликом  преобразованием Фурье которого является комплексный коэффициент передачи
преобразованием Фурье которого является комплексный коэффициент передачи  или передаточной функции
или передаточной функции 
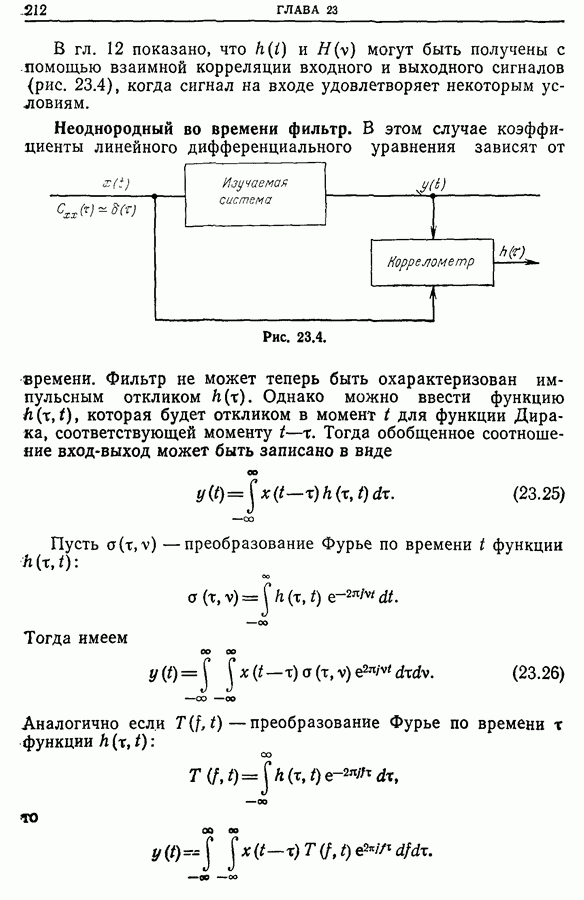
В гл. 12 показано, что  могут быть получены с помощью взаимной корреляции входного и выходного сигналов (рис. 23.4), когда сигнал на входе удовлетворяет некоторым условиям.
могут быть получены с помощью взаимной корреляции входного и выходного сигналов (рис. 23.4), когда сигнал на входе удовлетворяет некоторым условиям.
Неоднородный во времени фильтр.
В этом случае коэффициенты линейного дифференциального уравнения зависят от времени.

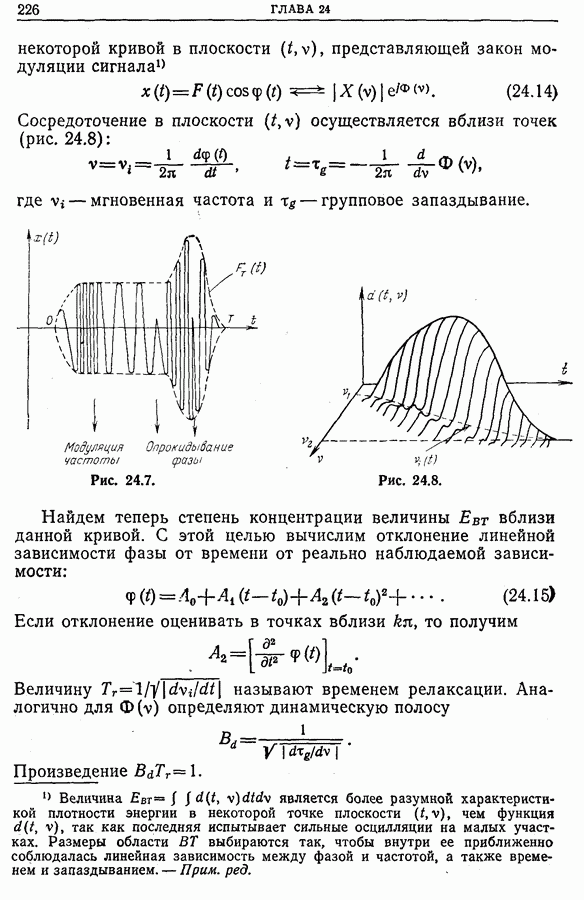
Рис. 23.4.
Фильтр не может теперь быть охарактеризован импульсным откликом  Однако можно ввести функцию
Однако можно ввести функцию  которая будет откликом в момент
которая будет откликом в момент  для функции Дирака, соответствующей моменту
для функции Дирака, соответствующей моменту  . Тогда обобщенное соотношение вход-выход может быть записано в виде
. Тогда обобщенное соотношение вход-выход может быть записано в виде

Пусть  — преобразование Фурье по времени
— преобразование Фурье по времени  функции
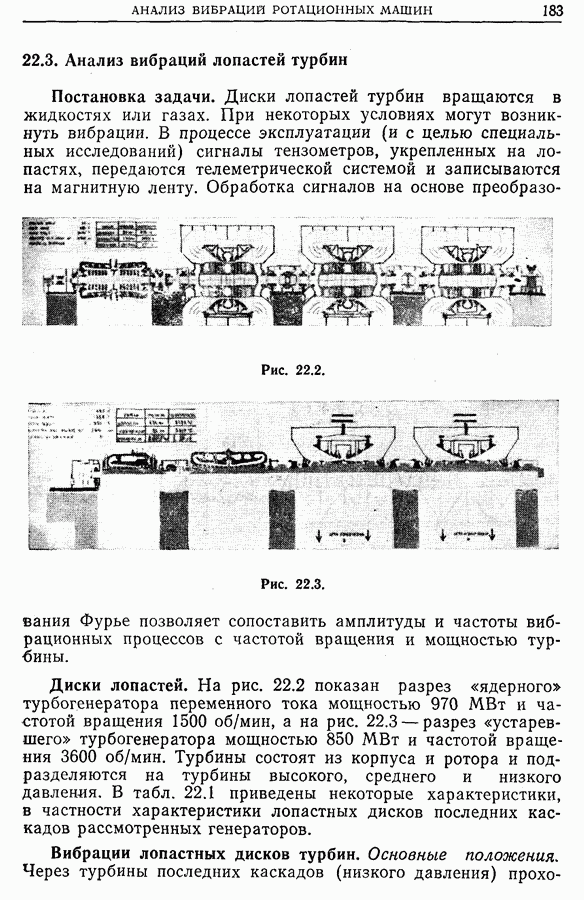
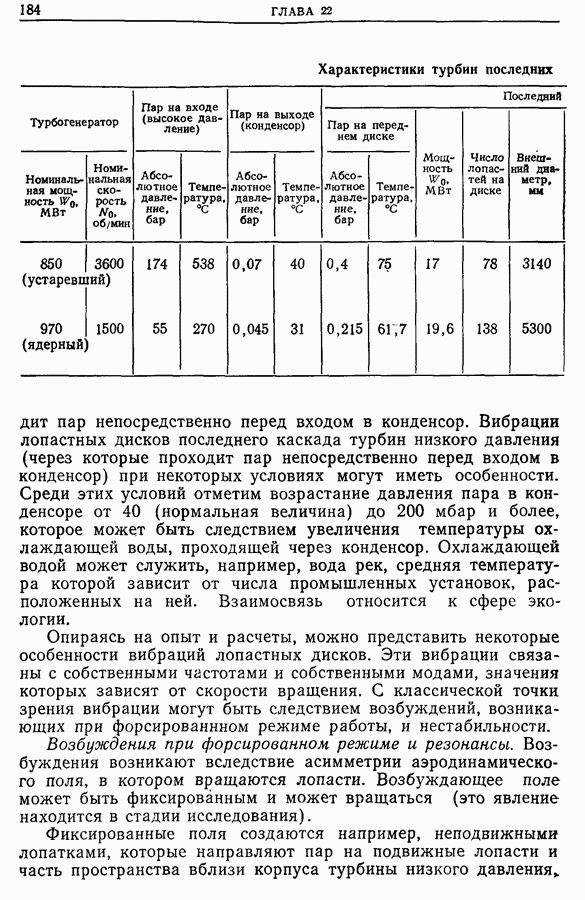
функции 

Тогда имеем

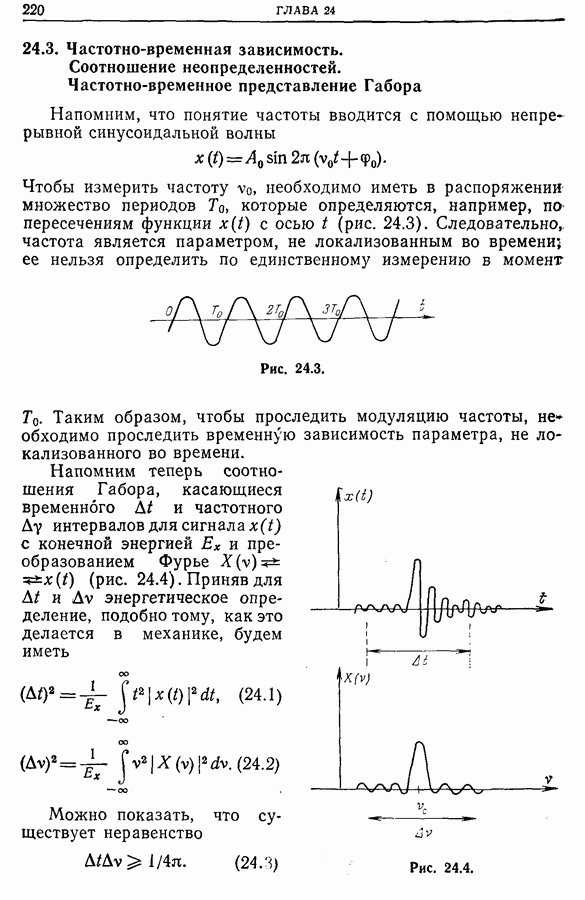
Аналогично если  — преобразование Фурье по времени
— преобразование Фурье по времени  функции
функции 

то

Последнее выражение можно записать в виде

или

Если  — двухчастотный отклик фильтра,
— двухчастотный отклик фильтра,

или

то (23.28)

Таким образом, линейный неоднородный во времени фильтр характеризуется одной из четырех передаточных функций: 
Идентификация с помощью взаимной функции неопределенности.
Напомним, что по определению функция неопределенности сигнала  записывается следующим образом:
записывается следующим образом:

Аналогично можно определить взаимную функцию неопределенности для двух сигналов 

Рис. 23.5.
Пусть неоднородный фильтр характеризуется одной из передаточных функций — функцией  (рис. 23.5). Найдем взаимную функцию неопределенности для входного
(рис. 23.5). Найдем взаимную функцию неопределенности для входного  и выходного
и выходного  сигналов
сигналов

Используя выражение (23.26), получим

Положим  Тогда
Тогда

Так как

то окончательно получим

Предположим теперь, что можно сконструировать такой тестовый сигнал  функция неопределенности которого представляет собой произведение функций Дирака
функция неопределенности которого представляет собой произведение функций Дирака  Тогда
Тогда

Отсюда

Таким образом, вводя в систему соответствующим образом подобранный тестовый сигнал, можно получить одну из передаточных характеристик фильтра с помощью расчета взаимной функции неопределенности для входного и выходного сигналов. Этот вывод представляет собой обобщение результата, полученного в разд. 12.5.
Случайные фильтры.
Прежде чем обобщать предыдущие результаты на случайные фильтры, дадим следующие определения:
1. Пусть  — случайная функция. На основе некоторых гипотез [9] мы можем определить математическое ожидание функции неопределенности
— случайная функция. На основе некоторых гипотез [9] мы можем определить математическое ожидание функции неопределенности

2. Если фильтр является случайным, то передаточная функция  будет также случайной функцией.
будет также случайной функцией.
Предположим существование моментов до второго порядка включительно, и пусть  - среднее значение, а
- среднее значение, а  — момент второго порядка.
— момент второго порядка.
Очевидно, что функцию  можно определить так же, как это описано в предыдущем разделе, рассматривая математическое ожидание обеих частей уравнения (23.31).
можно определить так же, как это описано в предыдущем разделе, рассматривая математическое ожидание обеих частей уравнения (23.31).
Ниже мы будем интересоваться в основном случайными флюктуациями вида

Их свойства второго порядка содержатся в корреляционной функции

Для упрощения задачи можно рассмотреть различные гипотезы (подробно эти вопросы изучены в работе [3]). Мы предположим, что рассматриваемая система является стационарной и удовлетворяет условию микроскопической корреляции. Тогда

Таким образом, флюктуации характеризуются функцией  которая называется «функцией диффузии» системы.
которая называется «функцией диффузии» системы.
Если теперь вычислить  используя уравнение (23.31), то получим
используя уравнение (23.31), то получим

С учетом выражения (23.32) это соотношение преобразуется к виду

Вводя в систему рассмотренный выше тестовый сигнал  получим
получим

Следует помнить, что этот простой результат получен при очень большом числе предположений, сделанных в процессе расчета. Тем не менее соотношение (23.32) показывает, каким образом расчет функции взаимной неопределенности позволяет определить основные характеристики неоднородных детерминированных или случайных систем.
Измерение функции неопределенности.
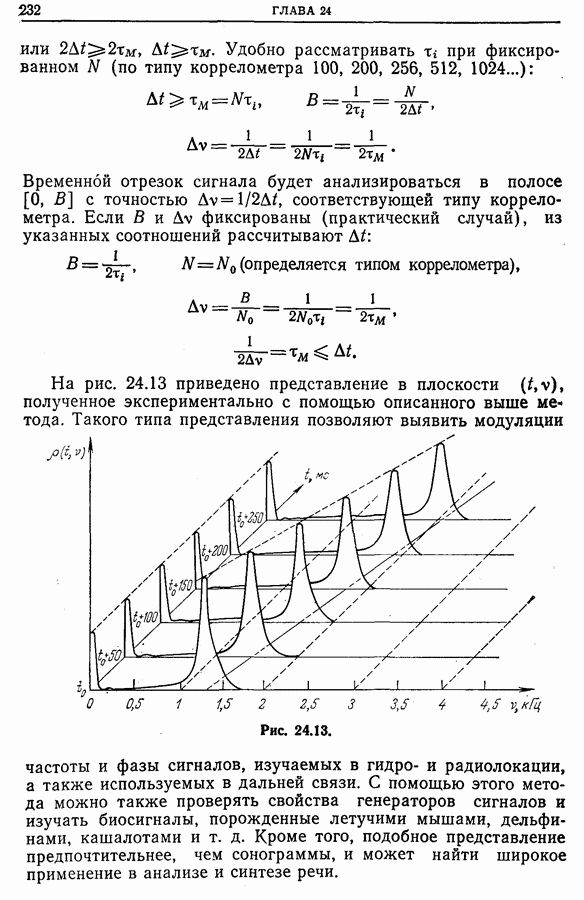
Вернемся к наиболее простому случаю, рассмотренному в разд. 23.4. Схема метода, реализующего идентификацию фильтра, приведена на рис. 23.6.

Рис. 23.6.
При реализации этого метода возникают два вопроса:
1) Можно ли создать такой тестовый сигнал, функцией неопределенности которого было бы произведение 
2) Можно ли реализовать расчет функции взаимной неопределенности в режиме реального времени?
| << Предыдущий параграф | Следующий параграф >> |
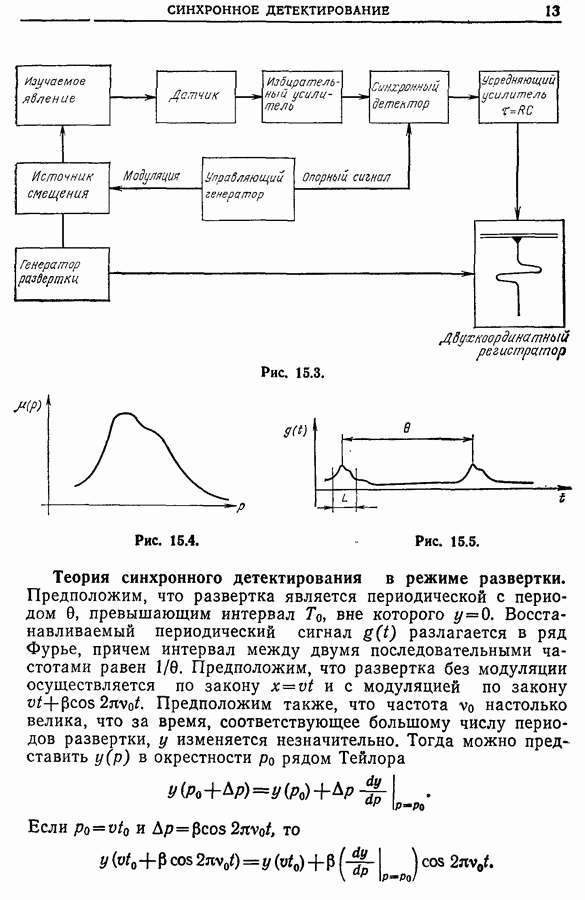
- Глава 15. СИНХРОННОЕ ДЕТЕКТИРОВАНИЕ
- 15.2. Схема метода
- 15.3. Теория синхронного детектирования
- 15.4. Синхронное детектирование в режиме развертки
- 15.5. Примеры применения синхронных детекторов
- 15.6. Совершенствование синхронных детекторов
- Глава 16. ИСПОЛЬЗОВАНИЕ МНОГОКАНАЛЬНЫХ АНАЛИЗАТОРОВ ПРИ СТАТИЧЕСКОЙ ОБРАБОТКЕ ИЗМЕРЕНИЙ
- 16.2. Характеристики многоканальных анализаторов
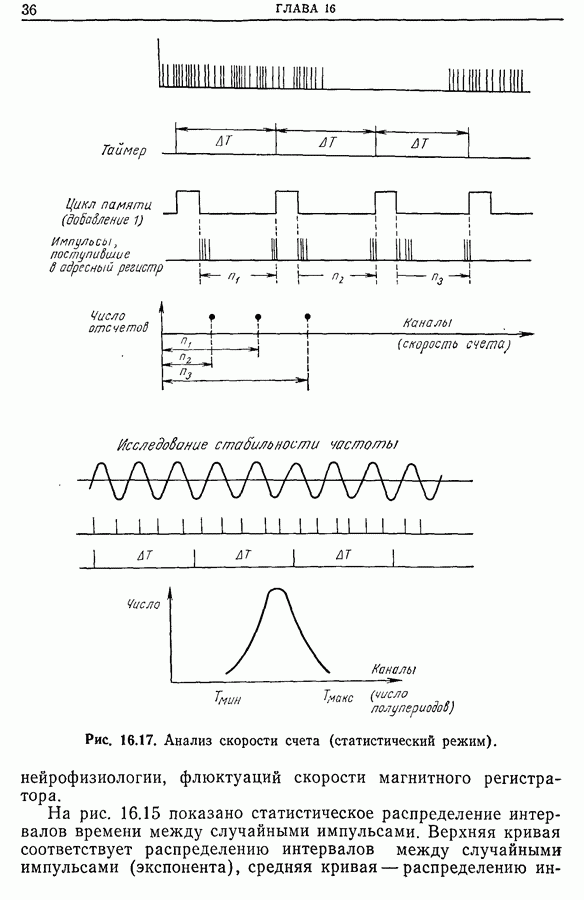
- 16.3. Схема системы обработки
- 16.4. Примеры применения
- Глава 17. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ
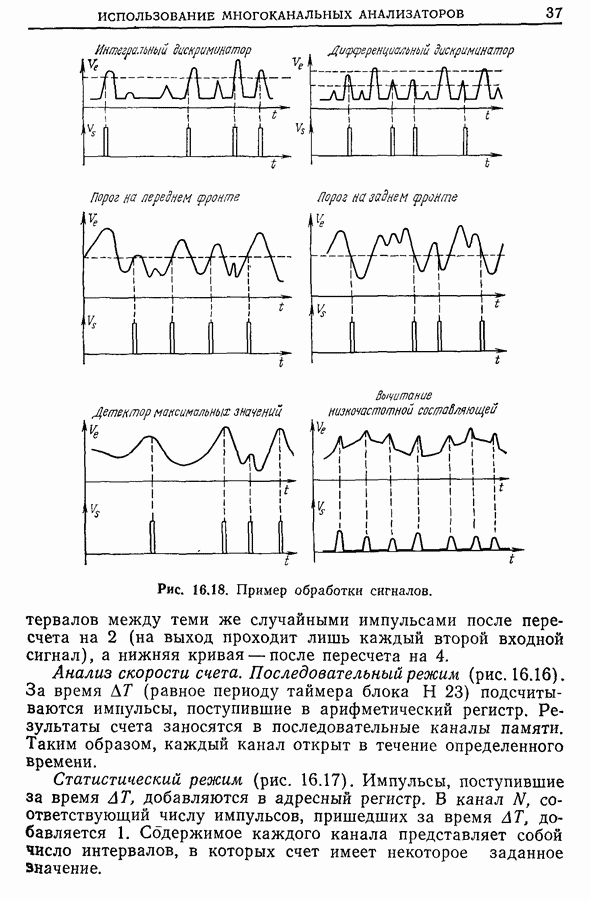
- 17.2. Частный случай белого шума. Согласованный фильтр
- 17.3. Согласованная фильтрация и корреляция Корреляция.
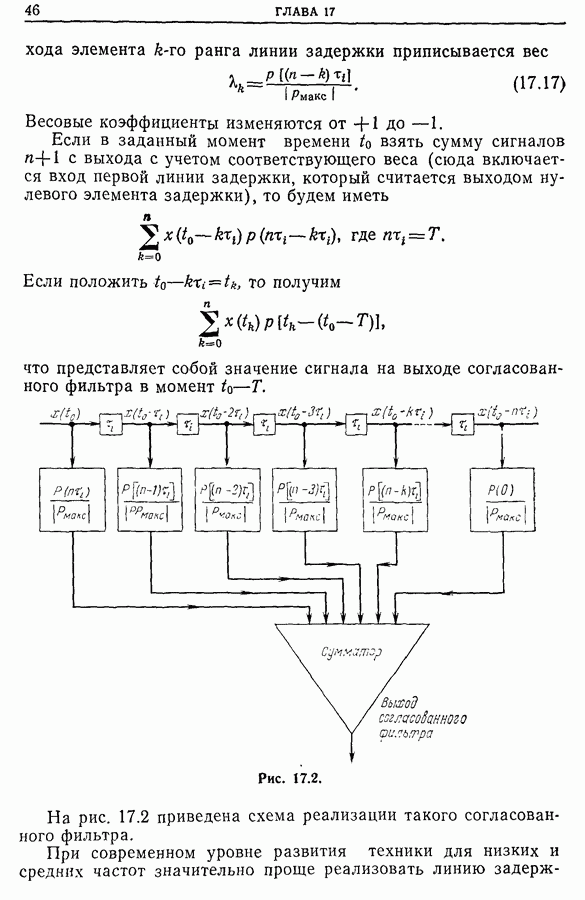
- 17.4. Реализация согласованных фильтров методом «взвешивания»
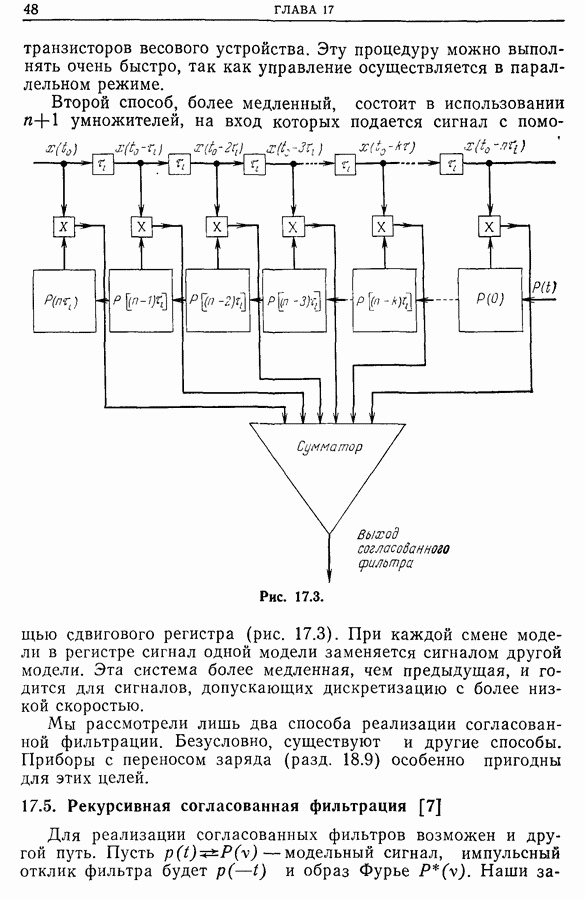
- 17.5. Рекурсивная согласованная фильтрация [7]
- 17.6. Применения метода согласованной фильтрации
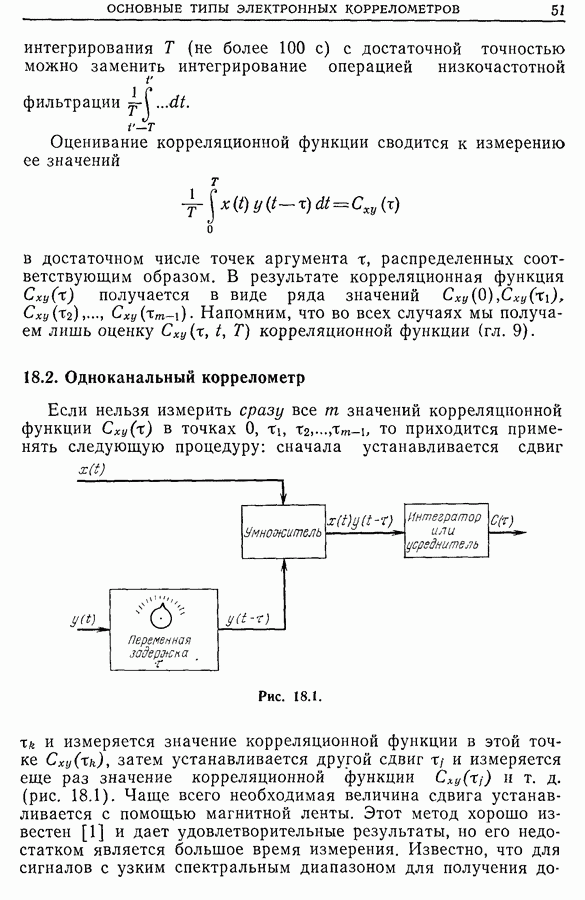
- Глава 18. ОСНОВНЫЕ ТИПЫ ЭЛЕКТРОННЫХ КОРРЕЛОМЕТРОВ
- 18.2. Одноканальный коррелометр
- 18.3. Автоматические коррелометры
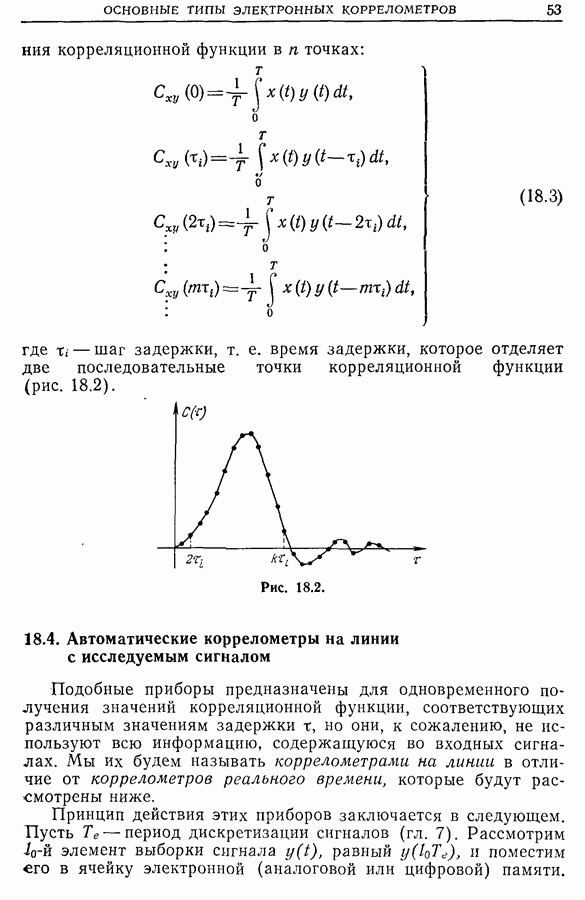
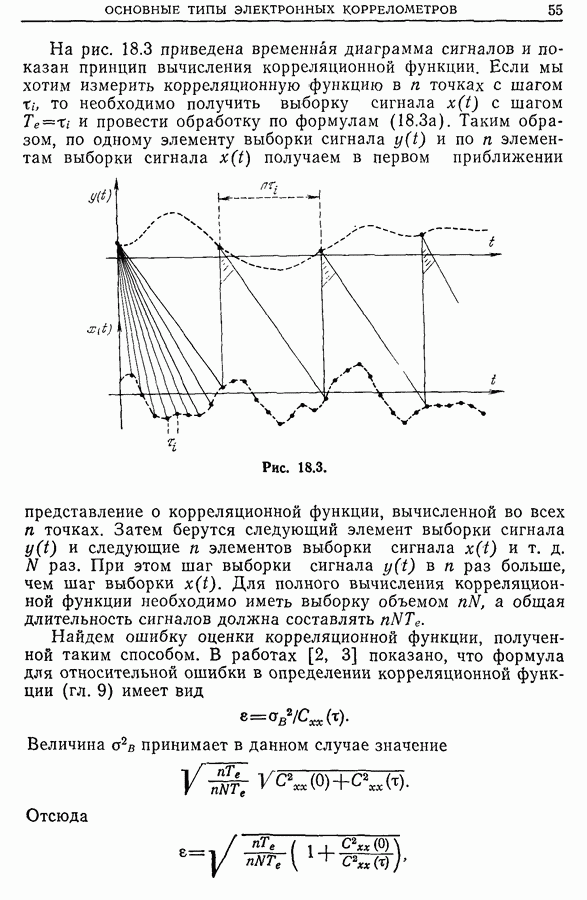
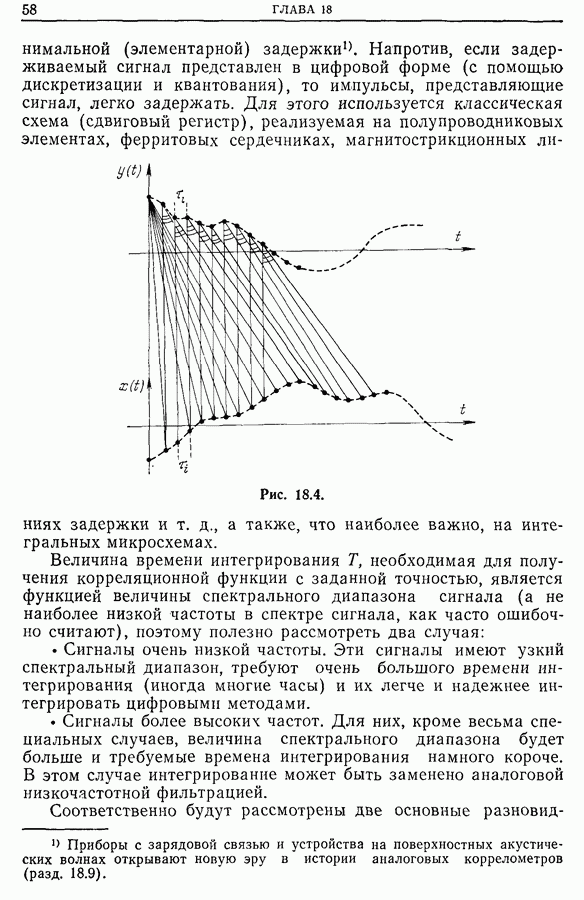
- 18.4. Автоматические коррелометры на линии с исследуемым сигналом
- 18.5. Автоматические коррелометры реального времени (или мультикоррелометры)
- 18.6. Коррелометры на больших интегральных схемах
- 18.7. Коррелометры реального времени для высокочастотных сигналов
- 18.8 Развитие коррелометров
- 18.9. Приборы с зарядовой связью [11]
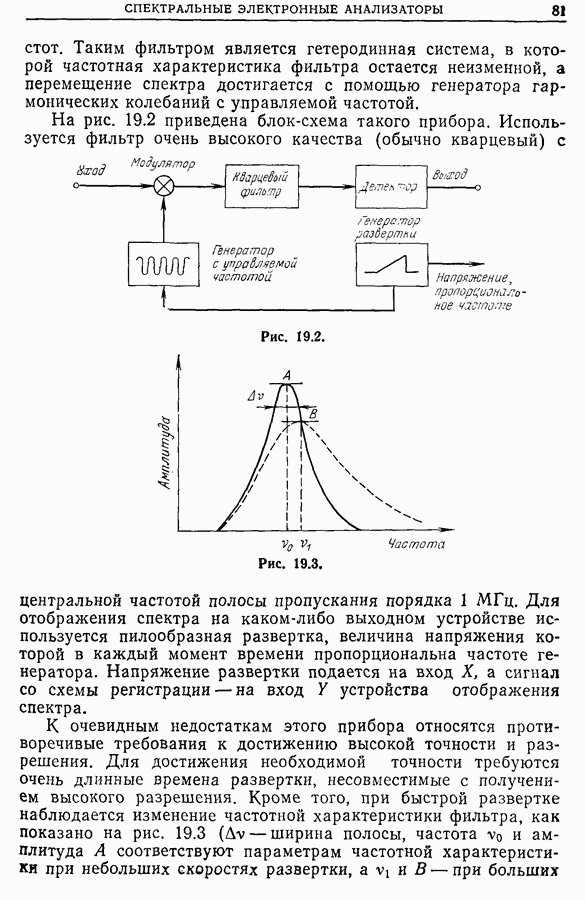
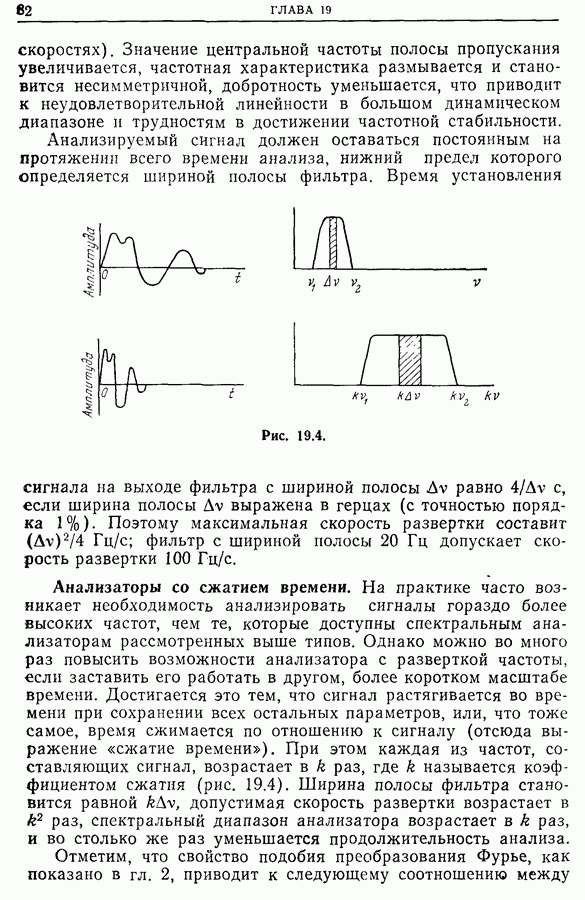
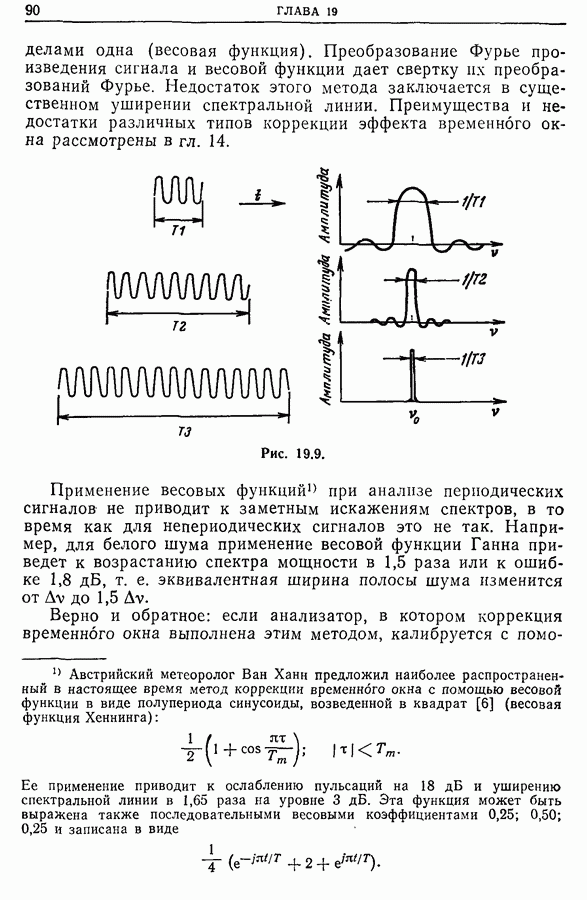
- Глава 19. СПЕКТРАЛЬНЫЕ ЭЛЕКТРОННЫЕ АНАЛИЗАТОРЫ
- 19.2. Спектральные анализаторы, основанные на методе непосредственного преобразования Фурье
- 19.3. Применения анализаторов на основе метода БПФ
- Глава 20. ОПТИЧЕСКИЙ СПЕКТРАЛЬНЫЙ АНАЛИЗ
- 20.2. Упрощения, связанные с отбрасыванием фазы
- 20.3. Эффект виньетирования
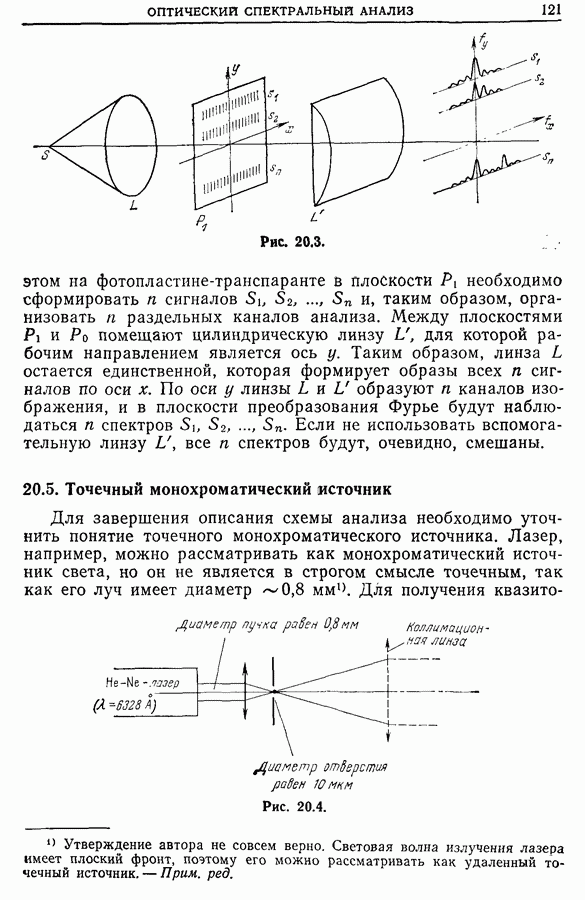
- 20.4. Двумерный анализ
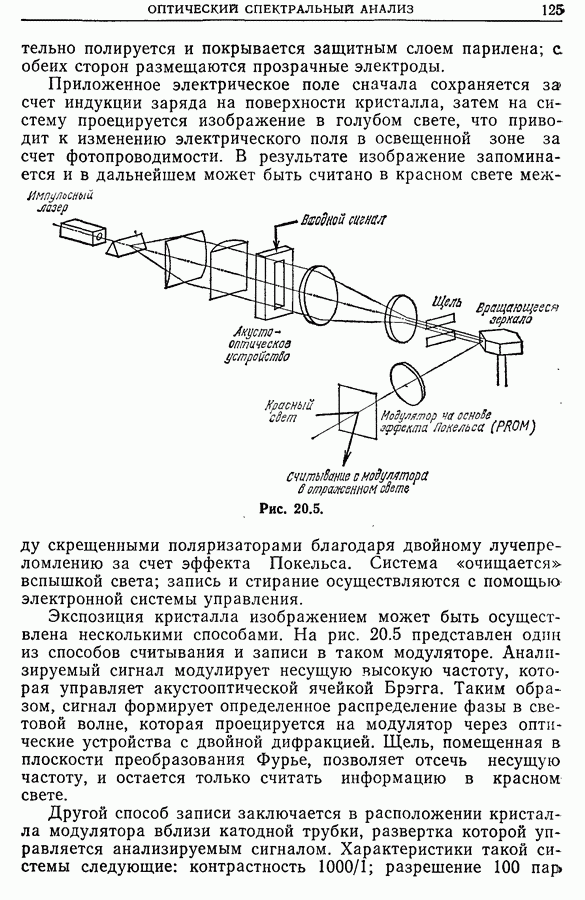
- 20.5. Точечный монохроматический источник
- 20.6. Электрооптическое преобразование сигнала
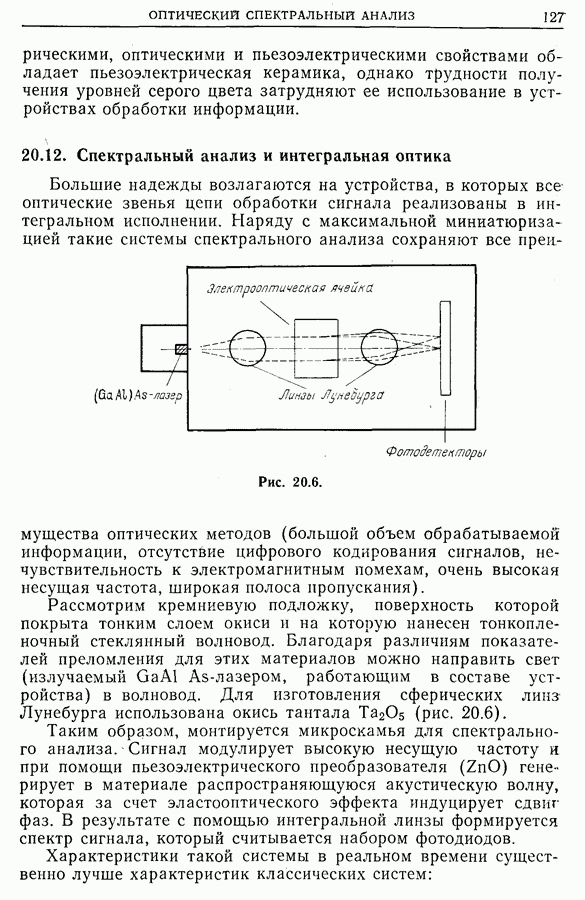
- 20.7. Устройства отображения на жидких кристаллах
- 20.8. Ограничения устройств отображения
- 20.9. Модулятор на основе эффекта Покельса (PROM)
- 20.10. Трубки Титус и Фототитус
- 20.11. Другие электрооптические кристаллы
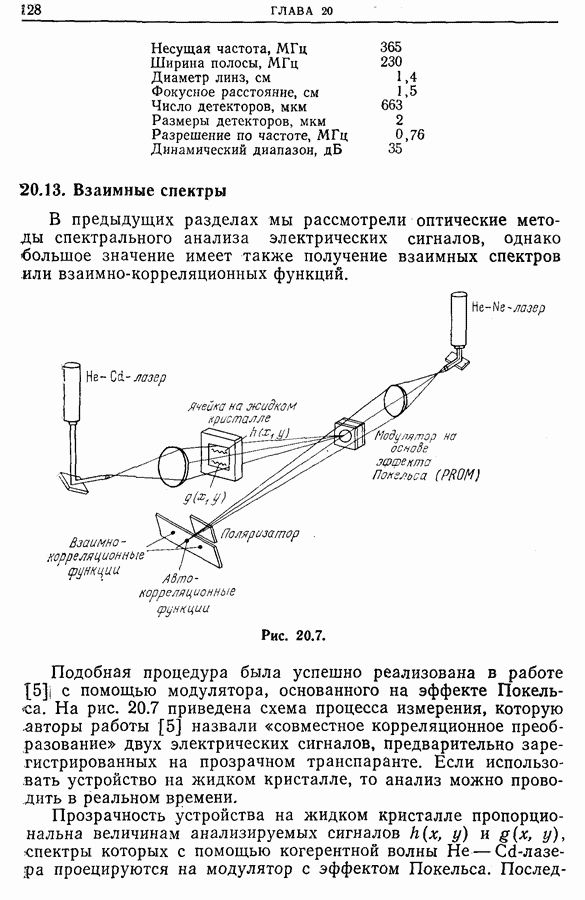
- 20.12. Спектральный анализ и интегральная оптика
- 20.13. Взаимные спектры
- Глава 21. НЕКОТОРЫЕ ПРАКТИЧЕСКИЕ ПРИМЕНЕНИЯ МЕТОДОВ ОБРАБОТКИ СИГНАЛОВ
- 21.2. Исследование ядерных сред
- 21.3. Ядерный магнитный резонанс (ЯМР) с возбуждением случайным сигналом
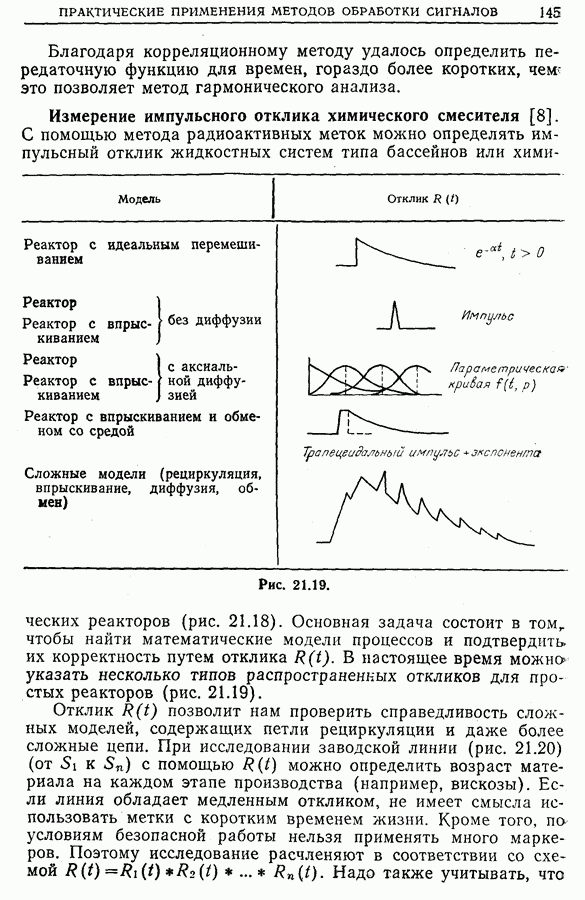
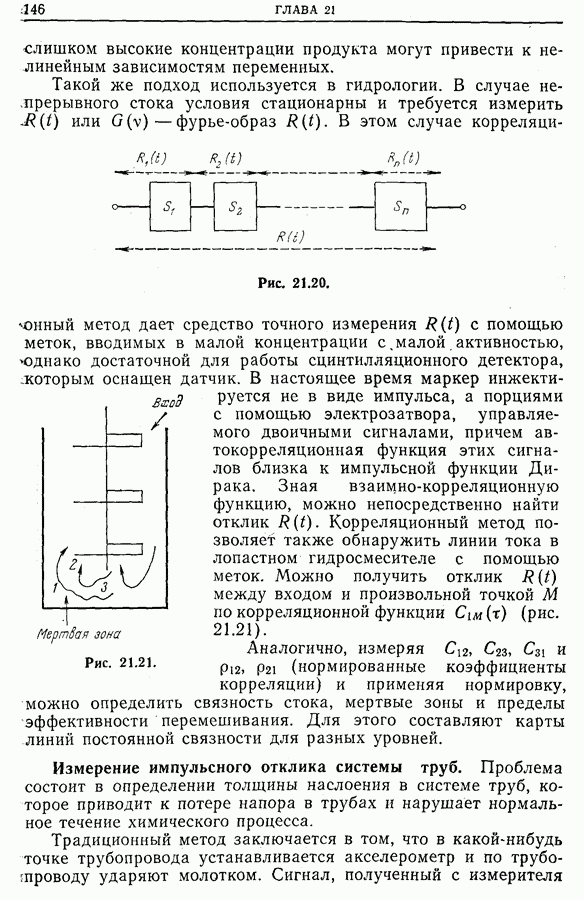
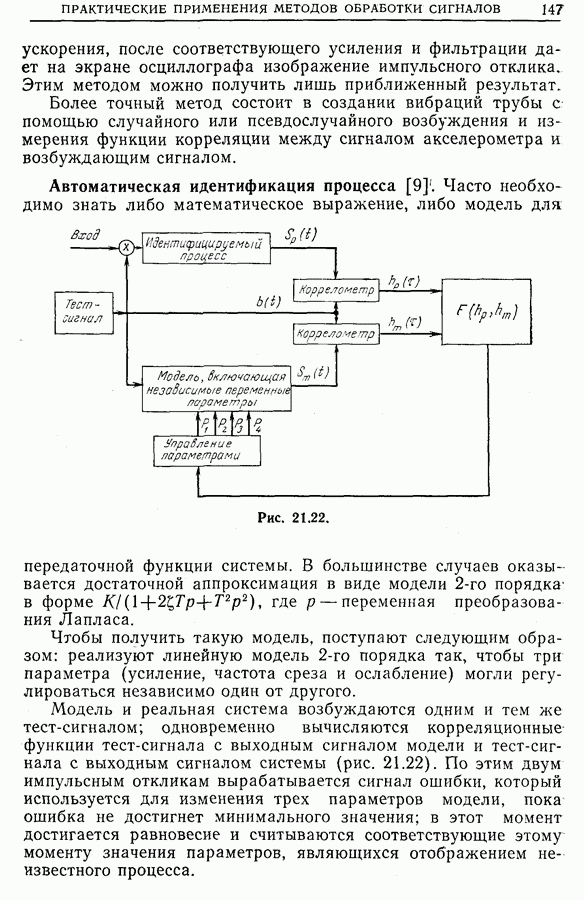
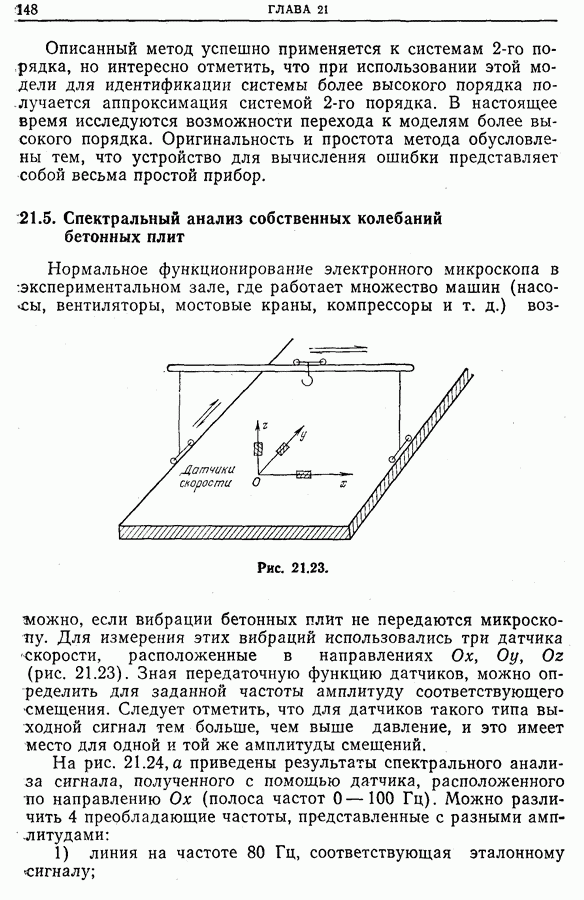
- 21.4. Идентификация процессов. Измерение импульсных откликов и передаточных функций
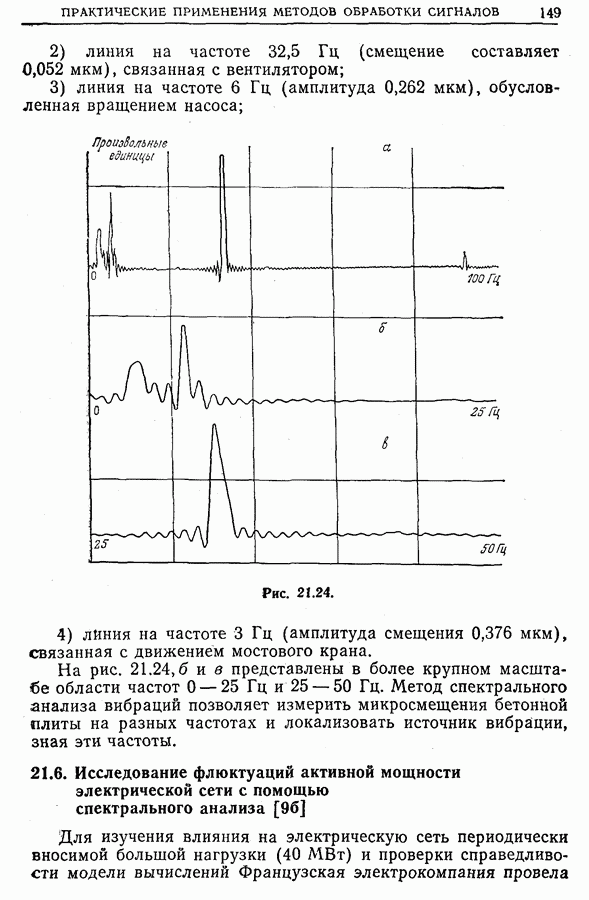
- 21.5. Спектральный анализ собственных колебаний бетонных плит
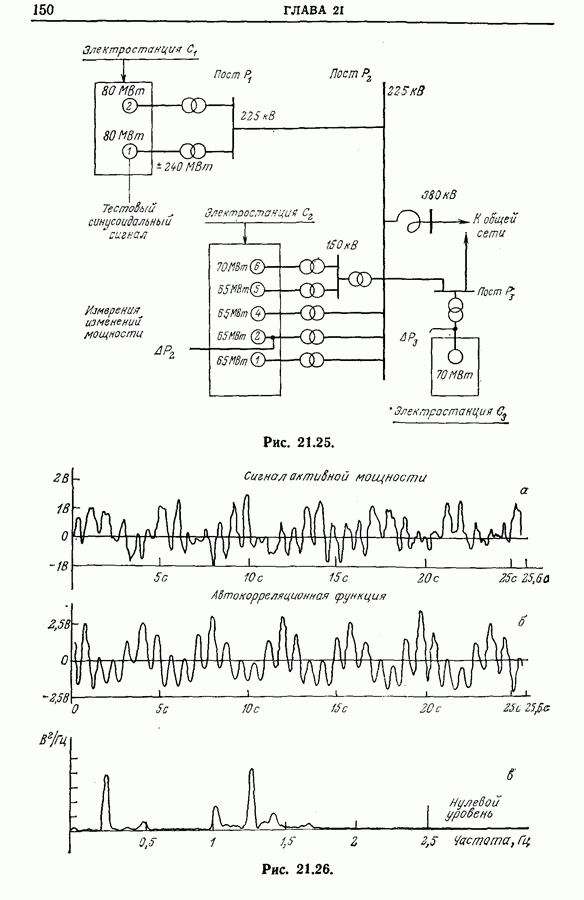
- 21.6. Исследование флюктуаций активной мощности электрической сети с помощью спектрального анализа
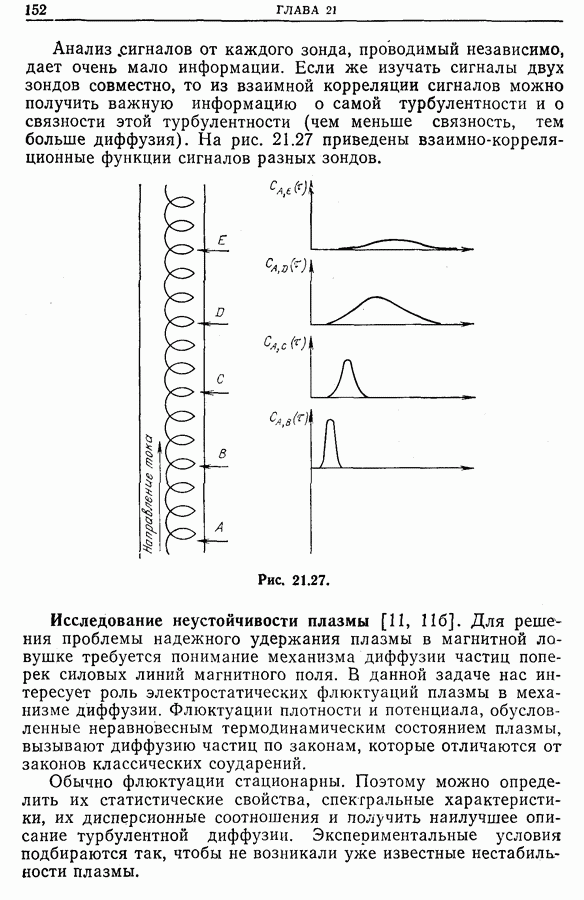
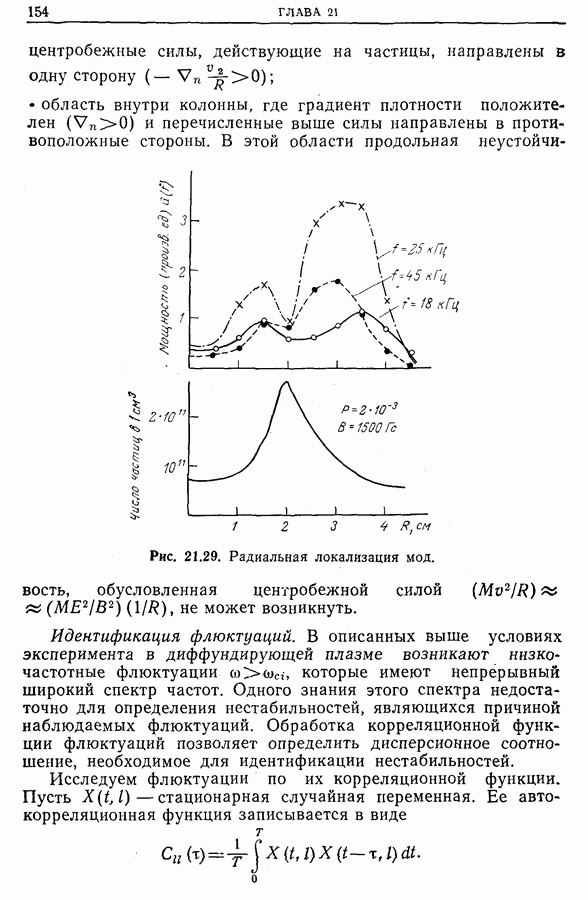
- 21.7. Изучение турбулентности
- 21.8. Применения в геофизике
- 21.9. Применения в астрофизике
- 21.10. Применения в астрономии и радиоастрономии
- 21.11. Применения в биологии и медицине
- 21.12. Применения в акустике
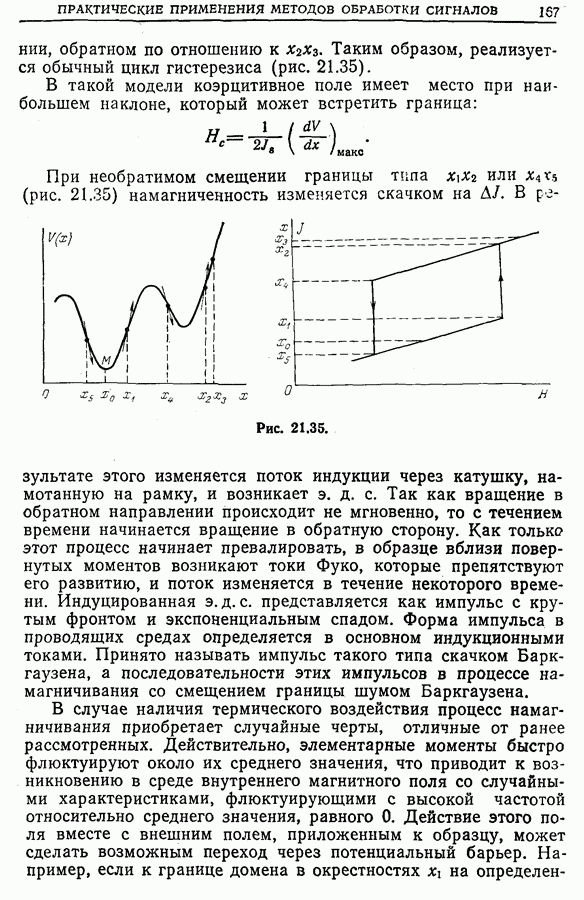
- 21.13. Исследование процессов намагничивания ферромагнетиков
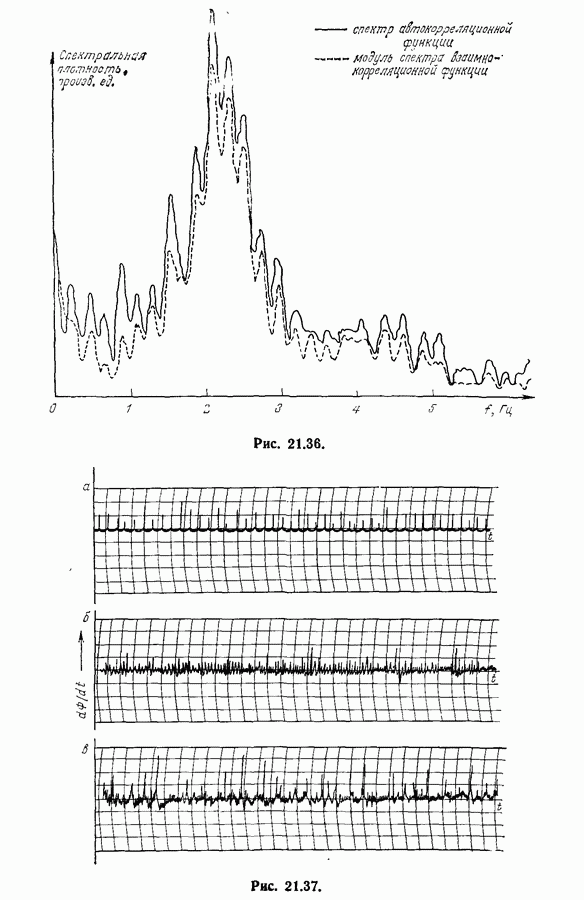
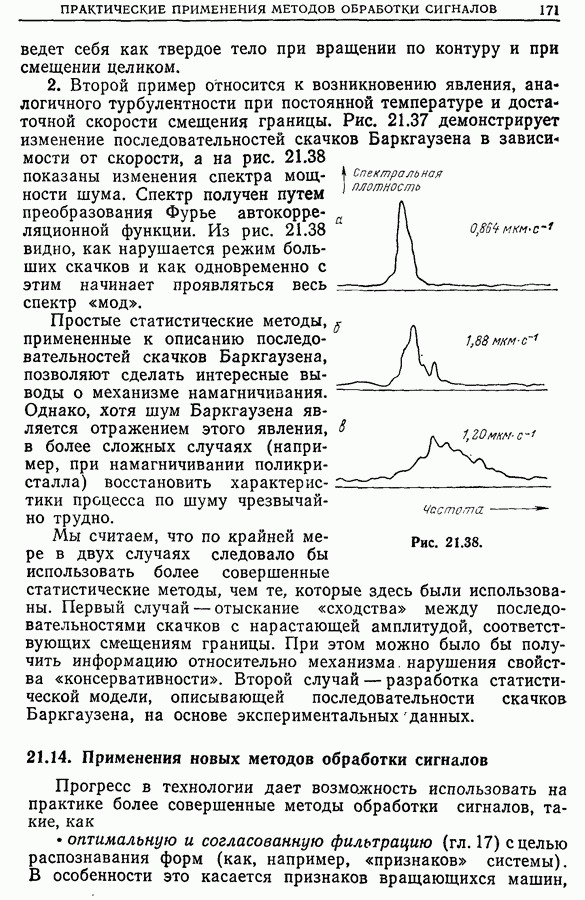
- 21.14. Применения новых методов обработки сигналов
- 21.15. Заключение
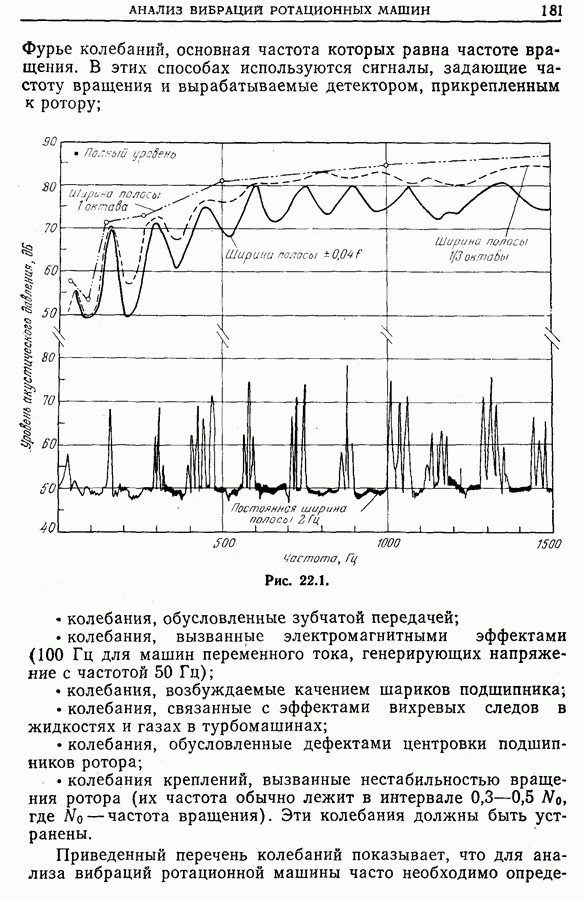
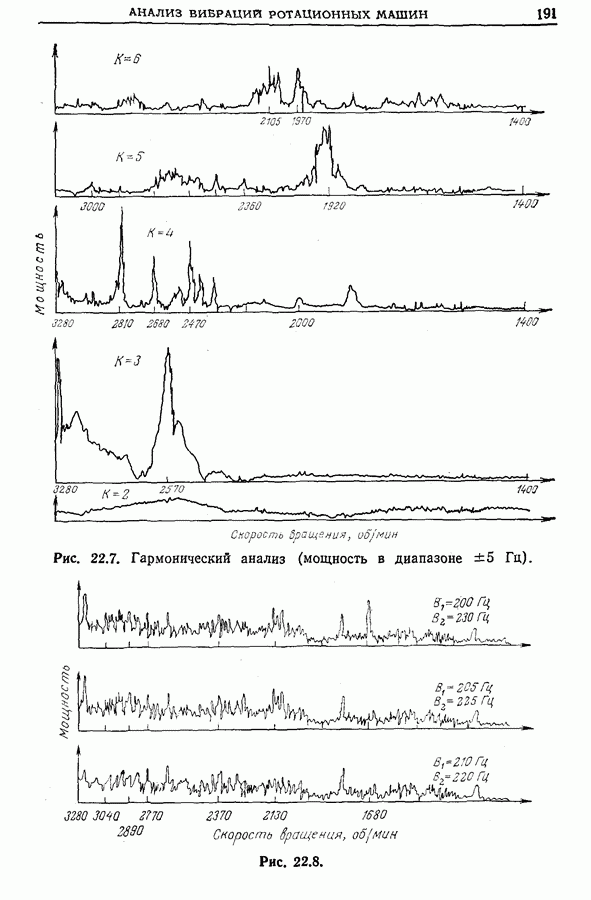
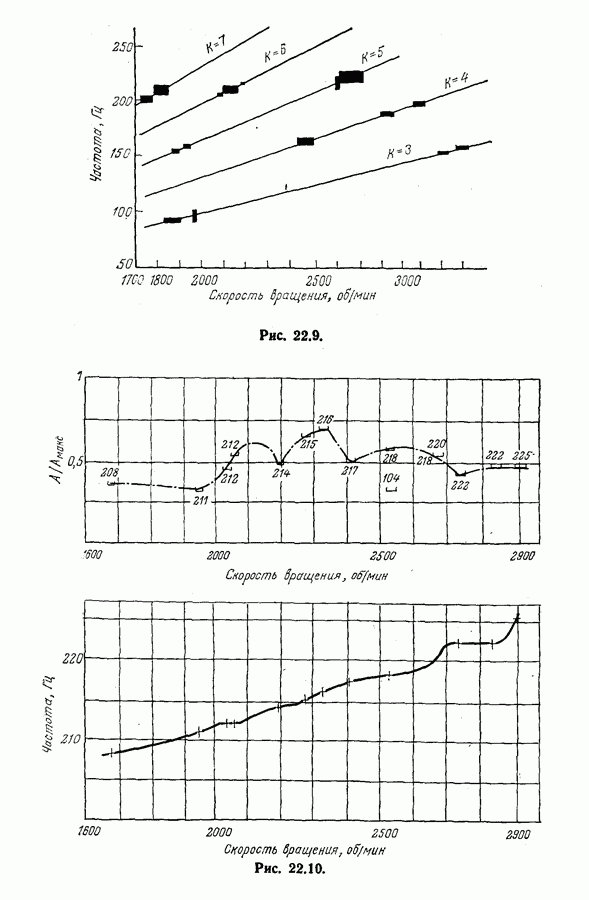
- Глава 22. ПРИМЕНЕНИЕ МЕТОДОВ ОБРАБОТКИ СИГНАЛОВ ДЛЯ АНАЛИЗА ВИБРАЦИЙ РОТАЦИОННЫХ МАШИНА
- 22.2. Анализ поведения системы «ротационная машина — конструкция»
- 22.3. Анализ вибраций лопастей турбин
- 22.4. Балансировка ротационных машин
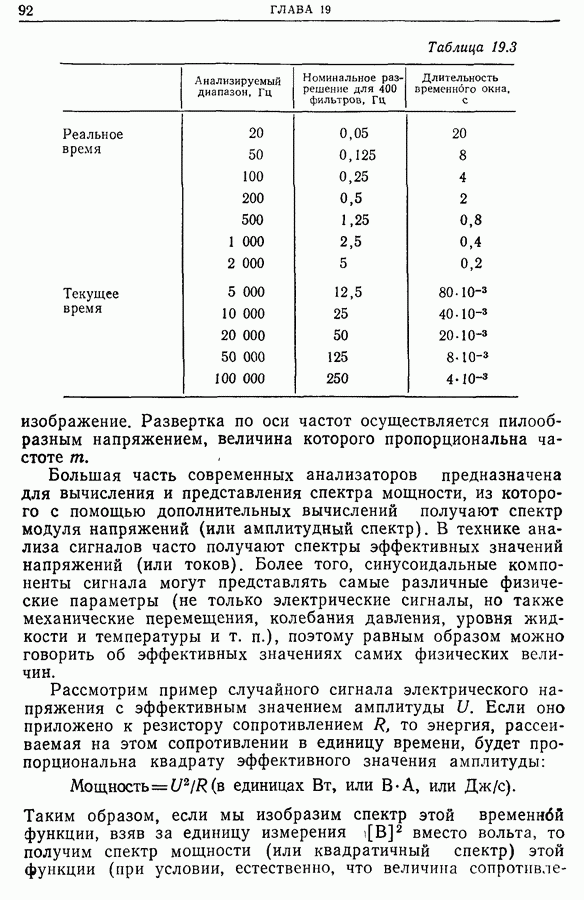
- Глава 23. ФУНКЦИЯ НЕОПРЕДЕЛЕННОСТИ
- 23.2. Временная корреляция. Временной сдвиг
- 23.3. Частотная корреляция. Частотный сдвиг
- 23.4. Временной и частотный сдвиги. Функция неопределенности
- 23.5. Функция неопределенности Вудворда
- 23.6. Взаимная функция неопределенности
- 23.7. Некоторые свойства функции неопределенности
- 23.8. Представление функций неопределенности
- 23.9. Примеры функций неопределенности
- 23.10. Применение функции неопределенности
- 23.11. Применение функций неопределенности для описания линейных неоднородных во времени систем. Обобщение понятия передаточной функции. Функция диффузии (функция рассеивания)
- 23.12. Генерация тестового сигнала
- 23.13. Прибор для измерения функции неопределенности в режиме реального времени
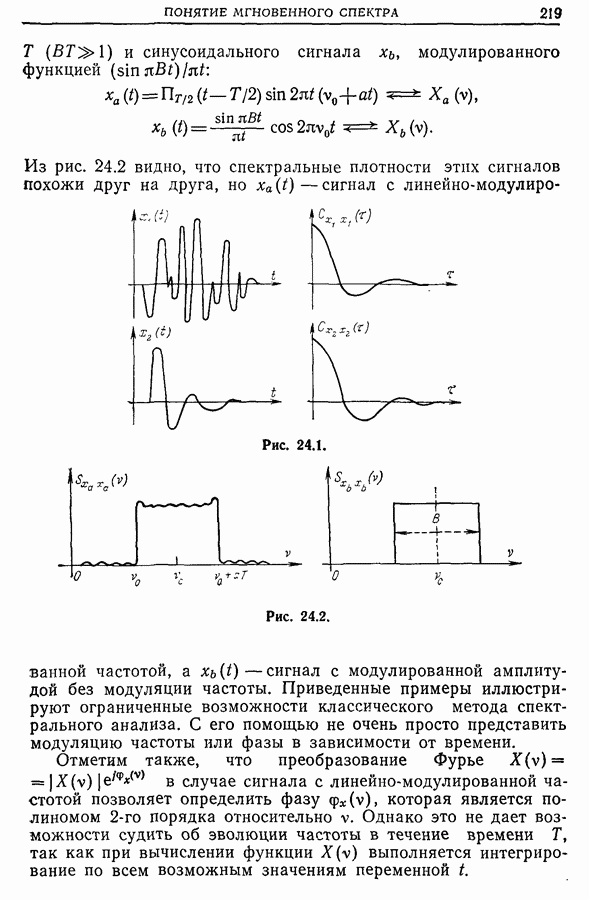
- Глава 24. ПОНЯТИЕ МГНОВЕННОГО СПЕКТРА ИЛИ ЧАСТОТНО-ВРЕМЕННОГО ПРЕДСТАВЛЕНИЯ В АНАЛИЗЕ И СИНТЕЗЕ СИГНАЛОВ
- 24.2. Примеры спектрального анализа модулированных и немодулированных сигналов
- 24.3. Частотно-временная зависимость. Соотношение неопределенностей. Частотно-временное представление Габора
- 24.4. Представление [t, v] по Бонне. Мгновенный спектр мощности по Биллю. Функция неопределенности
- 24.5. Другие определения частотно-временного представления
- 24.6. Измерение мгновенных спектров
- 24.7. Обобщение понятия мгновенного спектра мощности на случайные локально-стационарные сигналы. Функция структуры. Функция диффузии
- 24.8 Восстановление сигнала x(t) по известной функции
- 24.9. Заключение
- Глава 25. НОВЫЕ МЕТОДЫ СПЕКТРАЛЬНОГО АНАЛИЗА
- 25.2. Проблемы, обусловленные дискретизацией корреляционной функции
- 25.3. Постановка проблемы получения спектральной функции из конечного числа значений автокорреляционной функции
- 25.4. Классический метод, основанный на преобразовании Фурье корреляционной функции
- 25.5. Метод максимума энтропии или метод авторегрессионной модели
- 25.6. Метод Писаренко
- 25.7. Смешанные методы
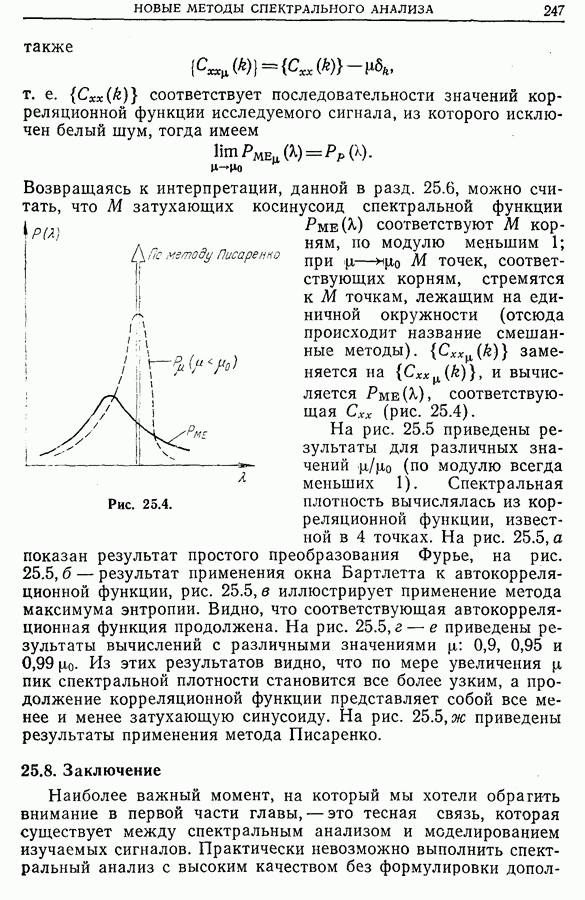
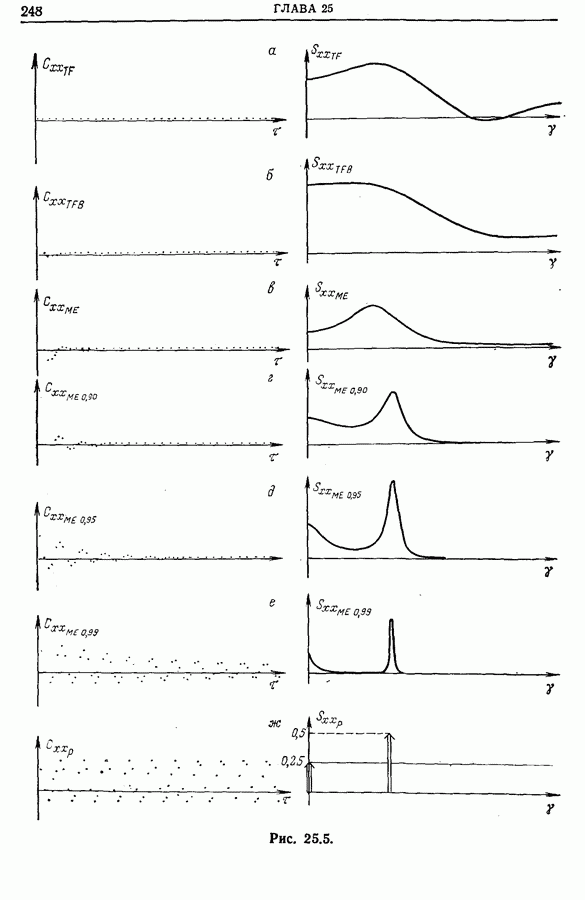
- 25.8. Заключение