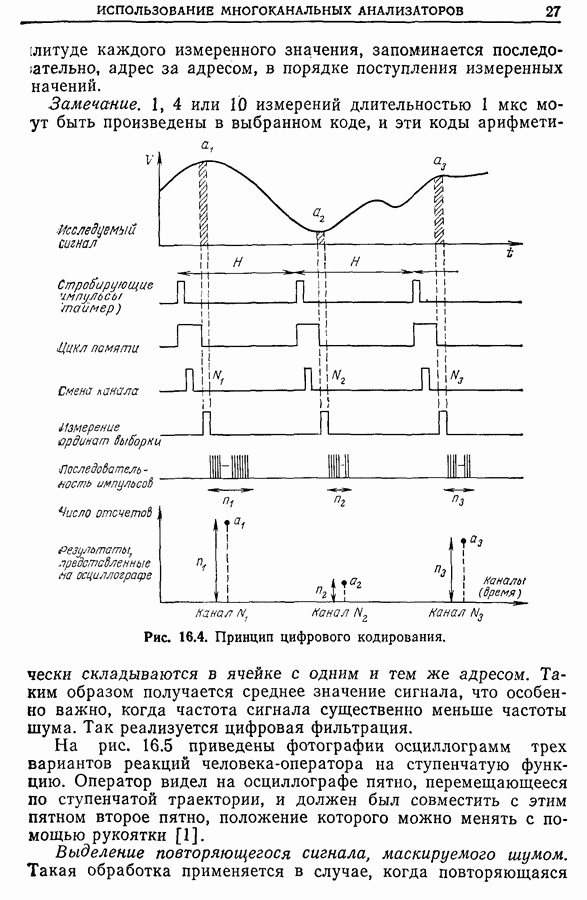
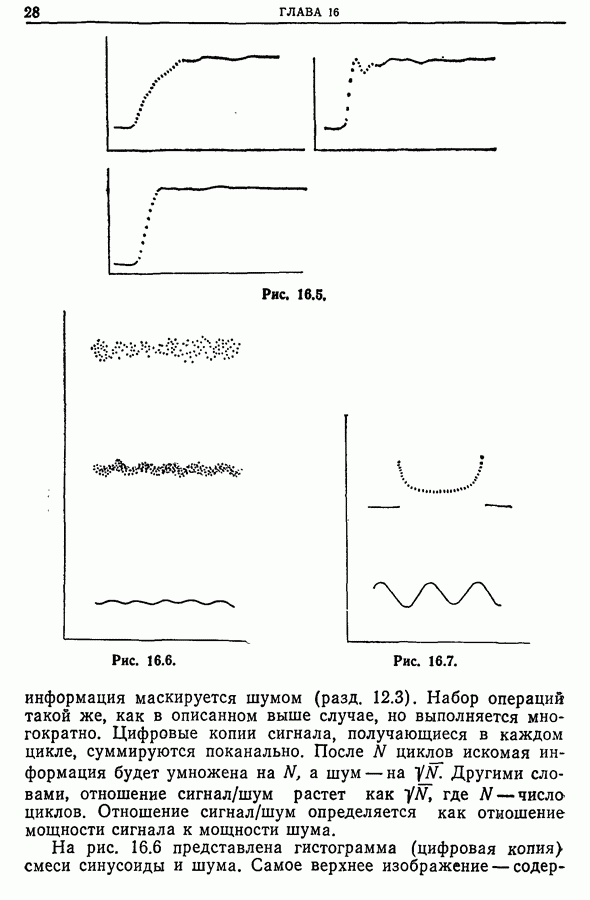
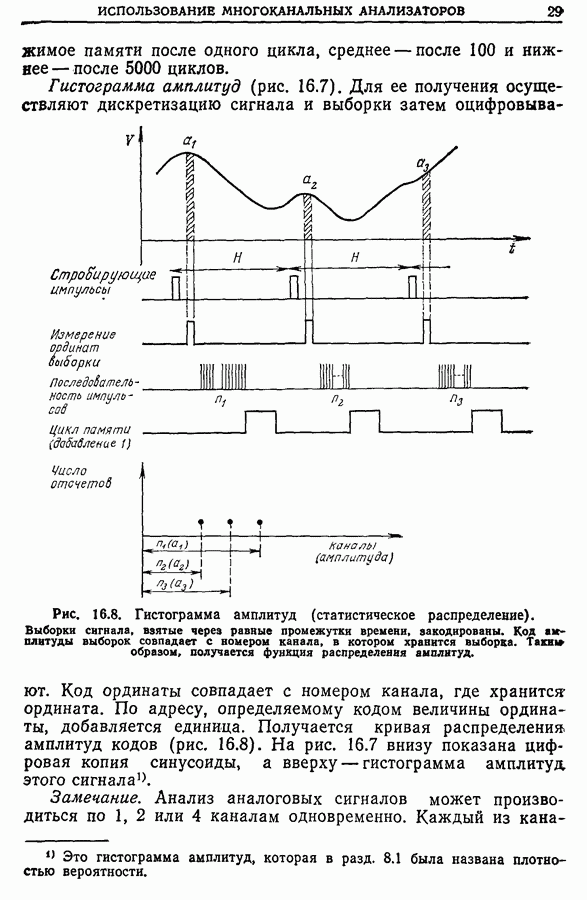
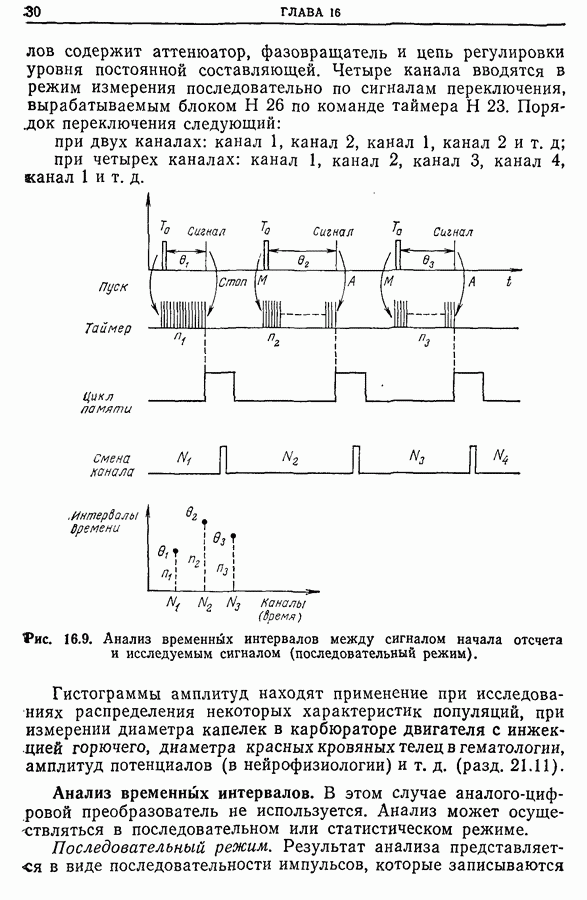
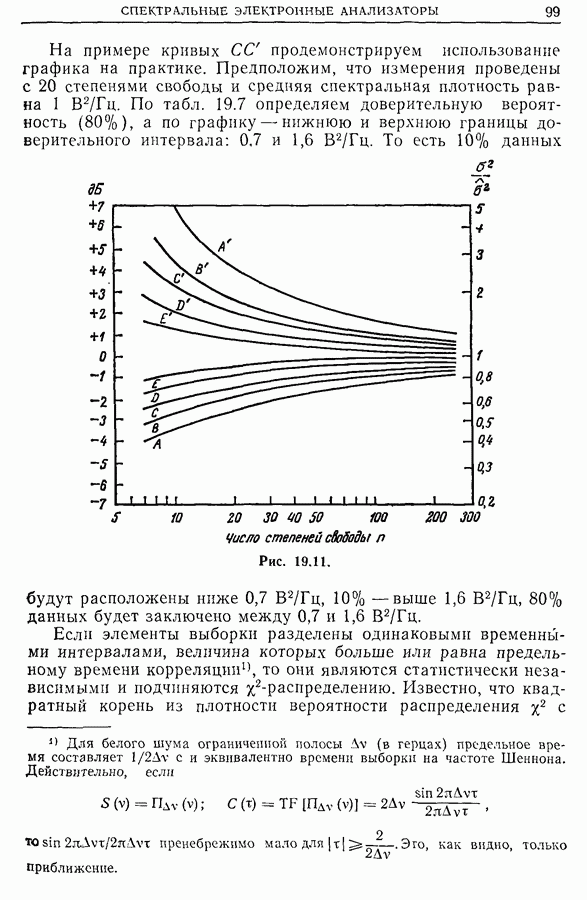
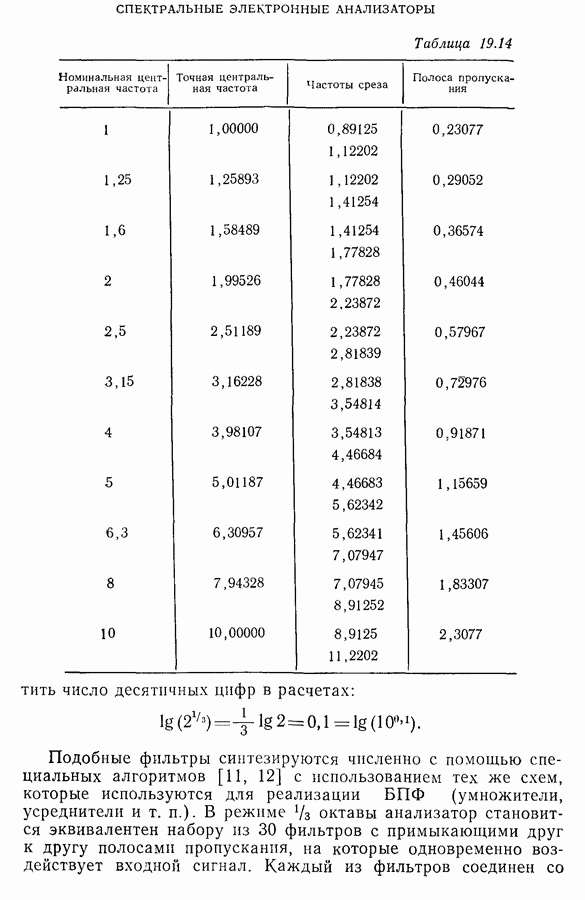
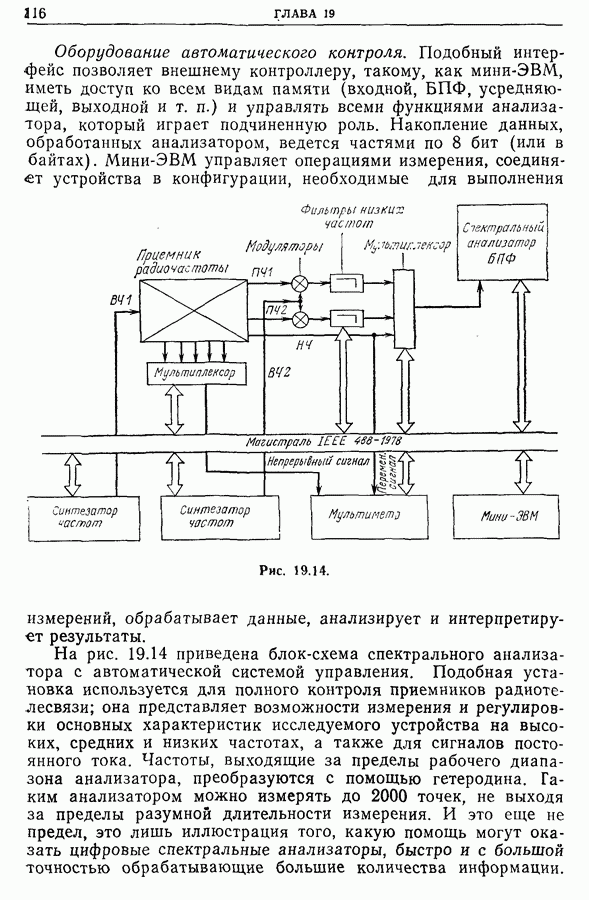
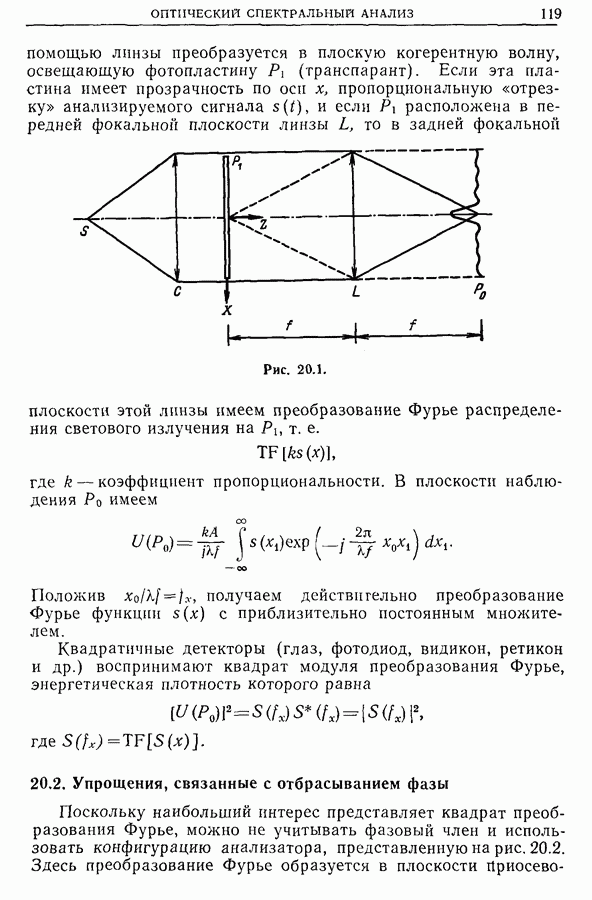
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
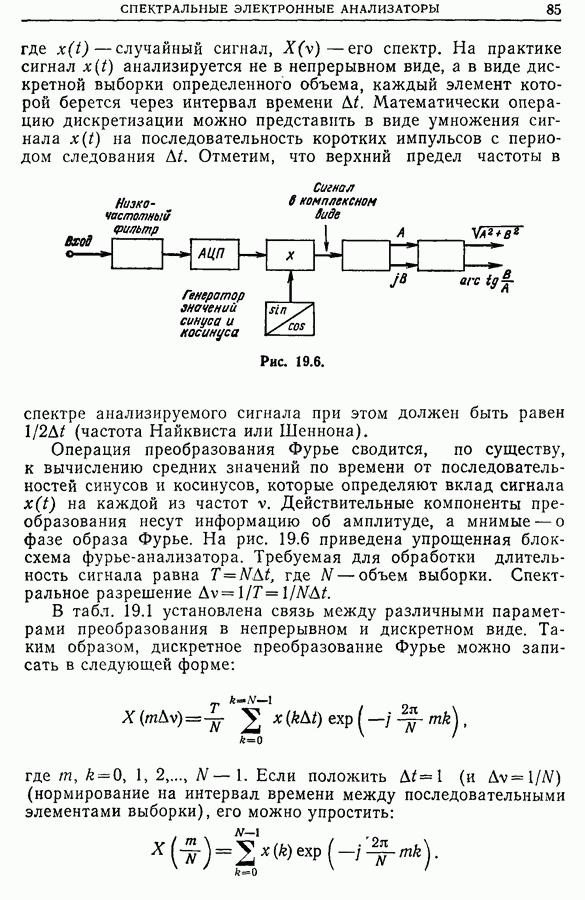
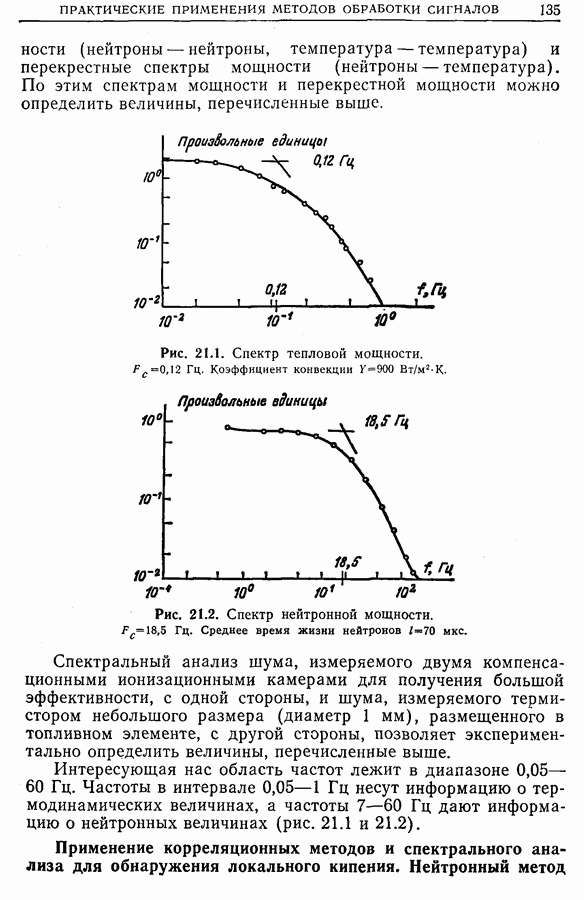
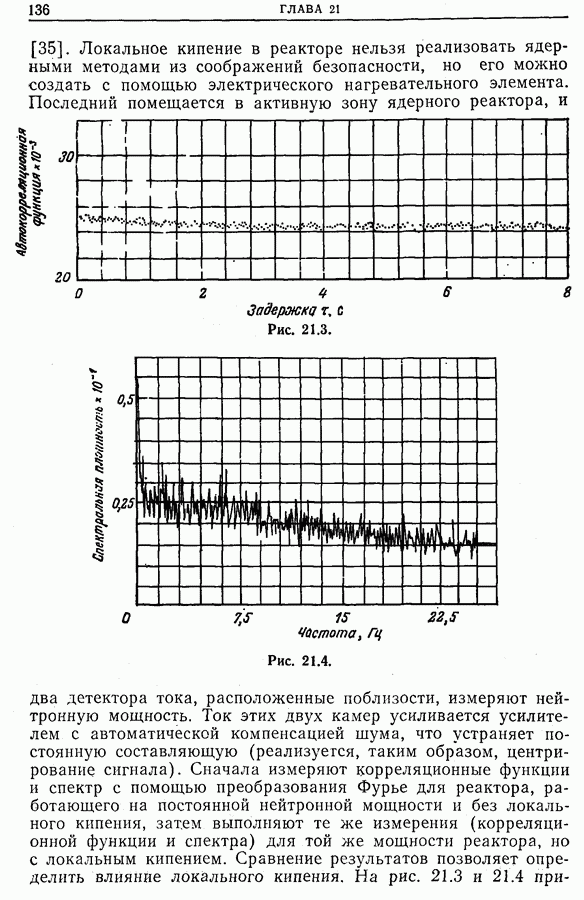
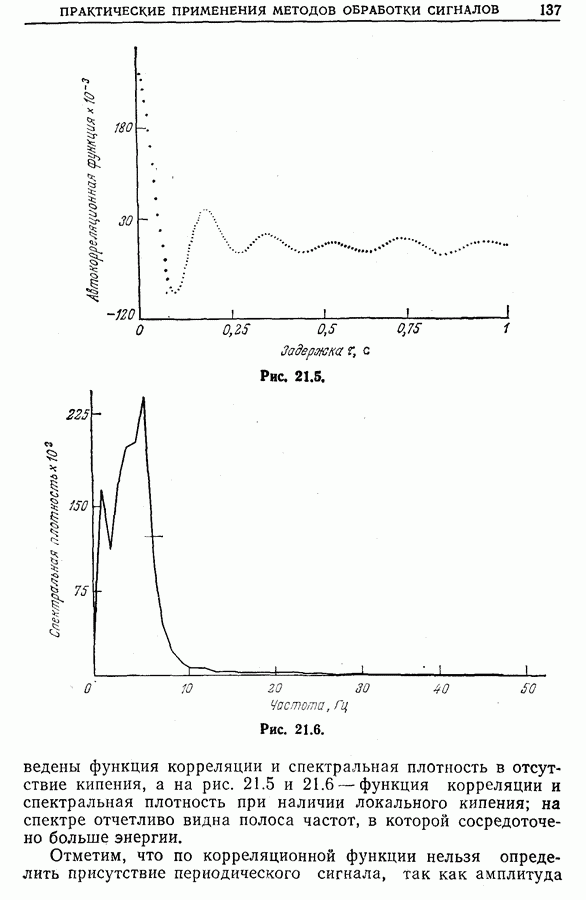
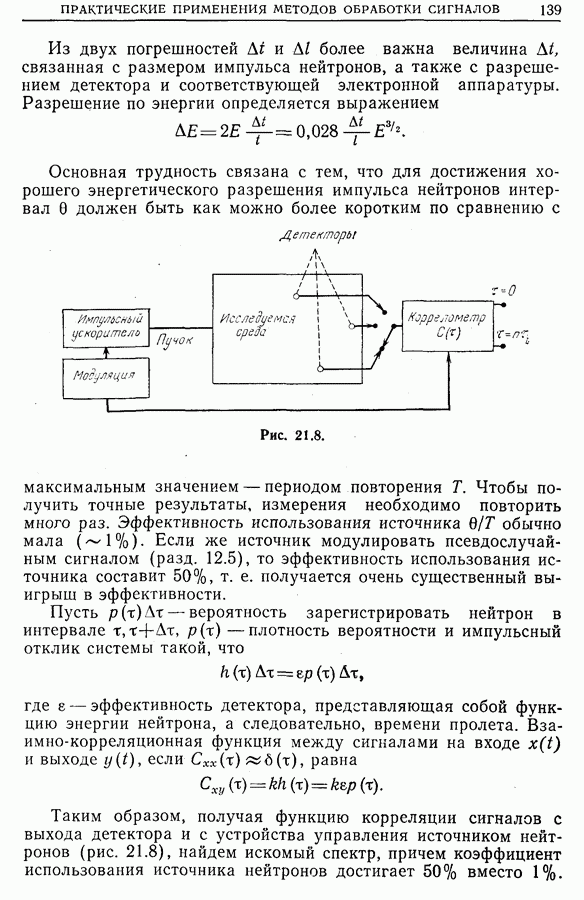
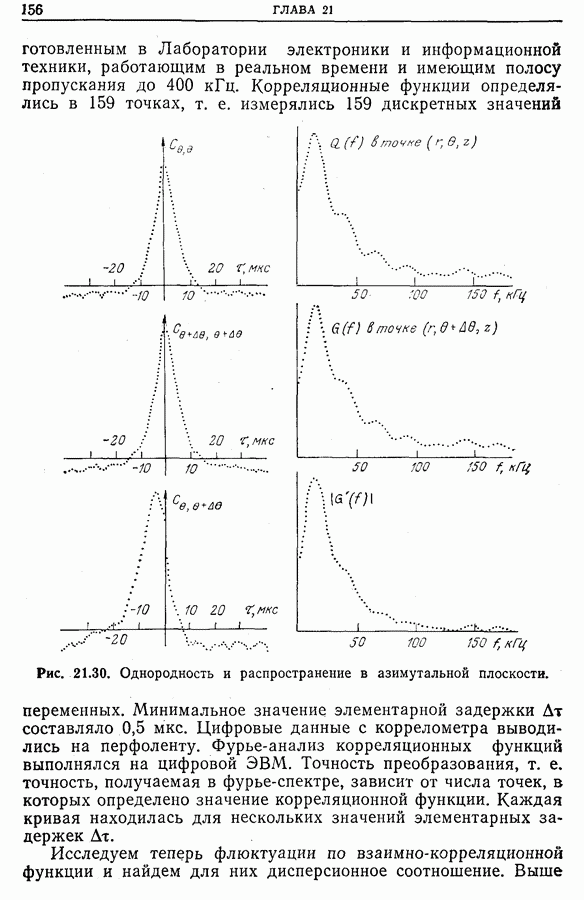
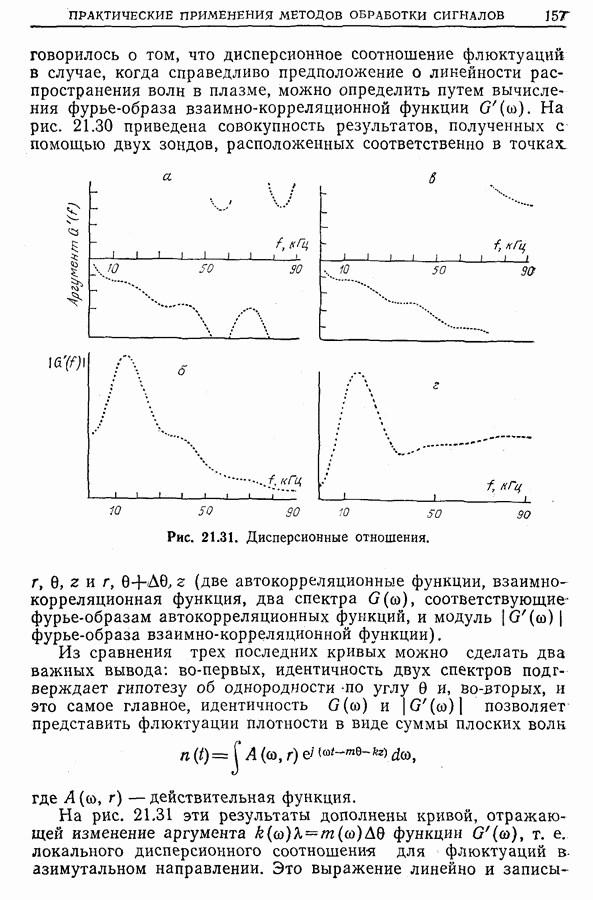
21.14. Применения новых методов обработки сигналов
Прогресс в технологии дает возможность использовать на практике более совершенные методы обработки сигналов, такие, как
• оптимальную и согласованную фильтрацию (гл. 17) с целью распознавания форм (как, например, «признаков» системы). В особенности это касается признаков вращающихся машин,
полученных по их вибрациям, и признаков магнитных масс (морские суда, самолеты, подводные лодки, мины и т. д.) по локальному возмущению, вносимому ими в магнитное поле Земли;
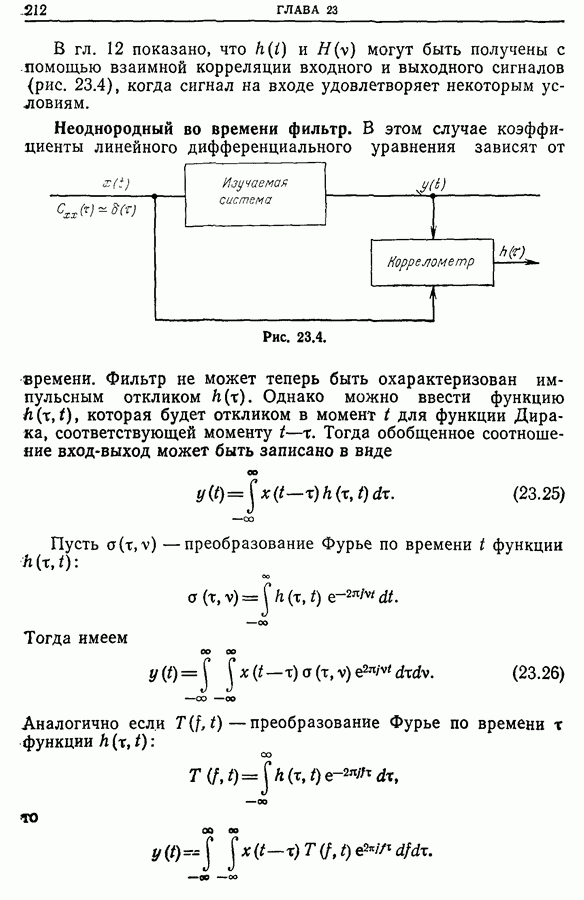
• функцию неопределенности (гл. 23) для синтеза сигналов радаров или гидролокаторов, более удобных для использования в частных случаях, а также для описания линейных систем, неоднородных во времени (т. е. систем, параметры которых зависят от времени);
• мгновенный спектр (гл. 24) для описания нестационарных систем (например, электроэнцефалограммы [33], шумы самолетов [34]);
• новые методы спектрального анализа (гл. 25), позволяющие за счет усреднения ряда априорных гипотез достичь наилучшего разрешения по частоте [35].
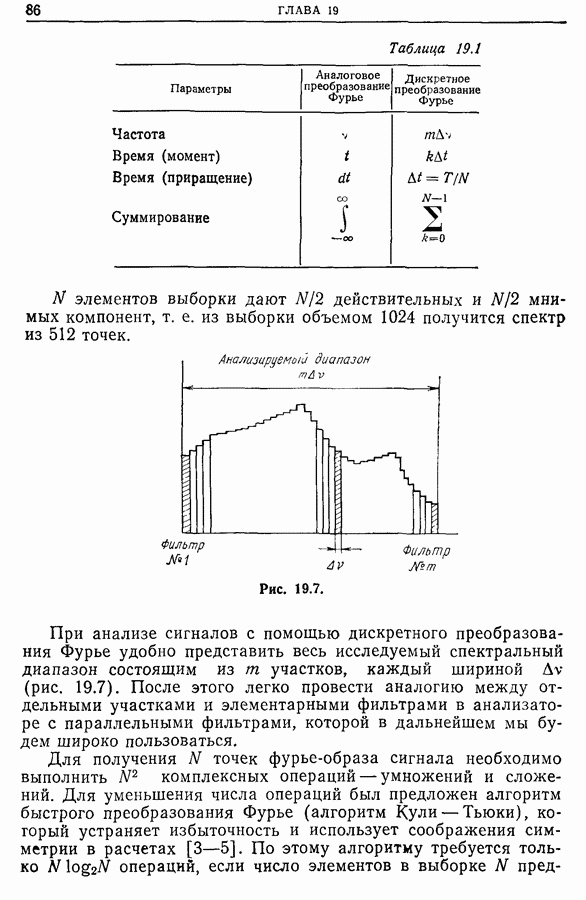
Следует, наконец, отметить, что существует множество способов, пригодных для обработки сигналов в частных случаях. Приведем несколько примеров.
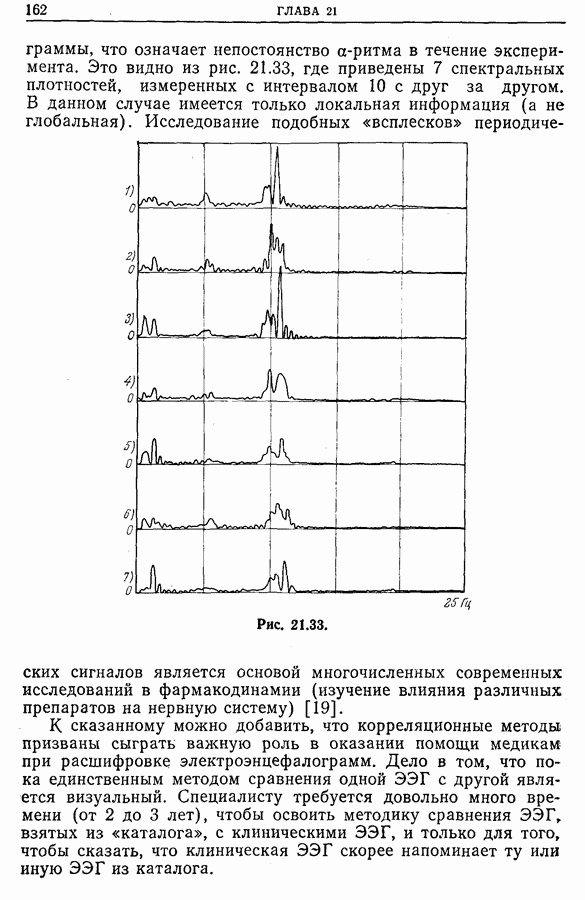
Для анализа электроэнцефалограмм можно использовать параметры, введенные в работе [36]. К ним относятся:

или во временном представлении

Активность есть средняя мощность сигнала на заданном интервале Т. Подвижность (мобильность) дает интервальную оценку производной сигнала, деленную на интервальную оценку амплитуды; в частотном представлении подвижность соответствует центру тяжести спектральной плотности, т. е. средней частоте сигнала. Сложность представляет собой общую оценку наиболее важных деталей, которыми сигнал отличается от синусоиды, принимаемой за эталон сложности. Сложность, так же как и подвижность, тем больше, чем больше длина спектрального интервала сигнала.
Поскольку электроэнцефалограммы часто напоминают синусоиду, промодулированную  -ритмом, перечисленные параметры представляют большой интерес, так как, используя их для модулированного синусоидального сигнала, например для импульсного отклика фильтра второго порядка в области резонанса (или автокорреляционной функции такого фильтра, возбужденного белым шумом), можно найти характеристики фильтра.
-ритмом, перечисленные параметры представляют большой интерес, так как, используя их для модулированного синусоидального сигнала, например для импульсного отклика фильтра второго порядка в области резонанса (или автокорреляционной функции такого фильтра, возбужденного белым шумом), можно найти характеристики фильтра.
Пусть  -передаточная функция фильтра. Тогда импульсный отклик запишется в виде
-передаточная функция фильтра. Тогда импульсный отклик запишется в виде

Введенные выше параметры дают: активность  отсюда
отсюда  подвижность
подвижность  отсюда
отсюда  сложность
сложность  отсюда
отсюда 
По-видимому, этот метод можно было бы применить для анализа вибраций, так как последние чаще всего сходны с модулированной синусоидой, но, насколько нам известно, подобные попытки пока не предпринимались.
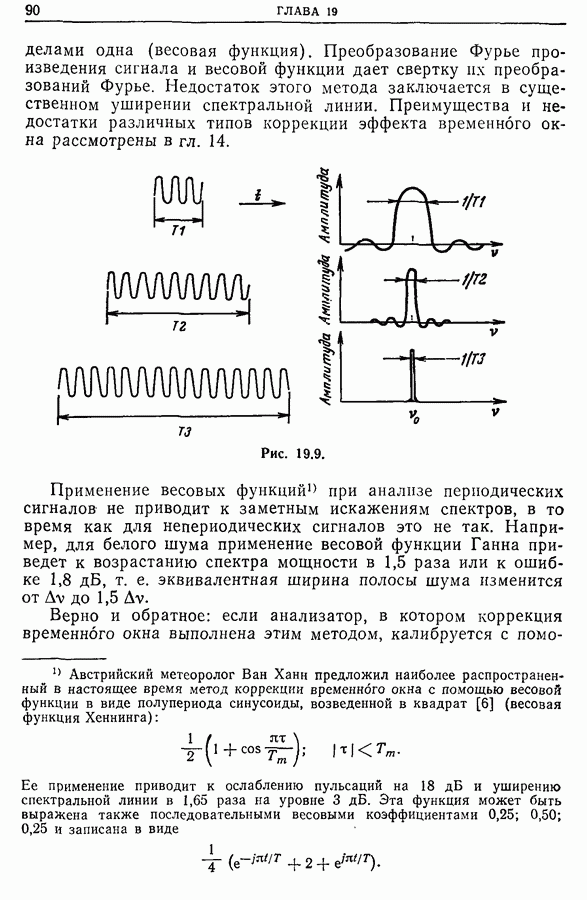
Интересно отметить, что еще до введения этих параметров мы использовали метод, основанный на том же принципе, для решения задач борьбы с загрязнением, не предполагая, какой широкий круг задач можно решать с его помощью [37].
Сепстр. Сепстральный анализ [39].
Сепстр — образ Фурье от логарифма спектральной плотности:

Этот оператор (известный также под названием гомоморфное преобразование или фильтрация) с успехом применяется для обработки зашумленных сигналов, образованных не только суммированием сигналов с шумом (линейная система), но и сверткой с шумом или умножением.
Среди многочисленных применений сепстрального анализа наиболее важными являются следующие:
• анализ речи [40];
• обработка изображений [38] ;
• анализ сейсмических сигналов [41];
• оценка интервала времени между двумя сигналами [42].
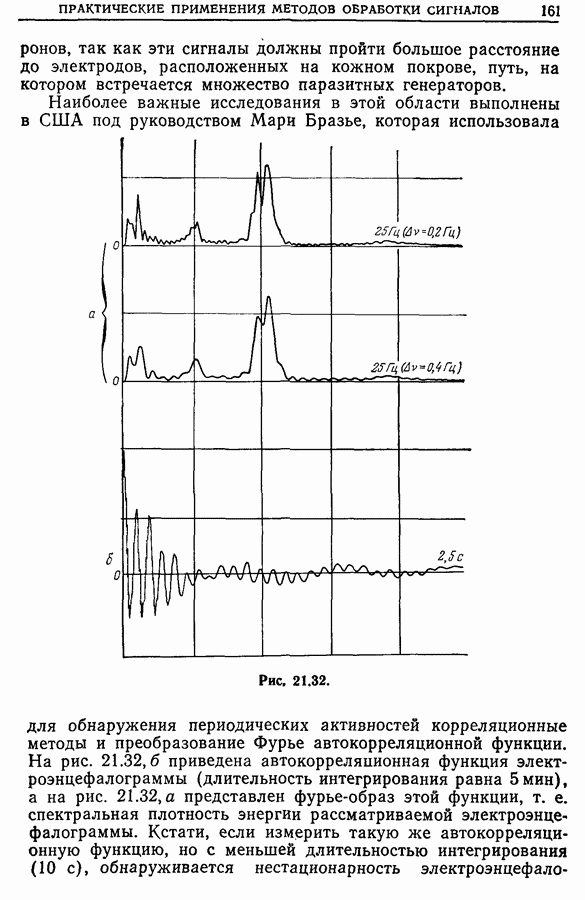
Система нистагмолаб [43, 47]. Специальные методы обработки сигналов применялись для обработки электронистагмо графических сигналов (нистагм — непроизвольные быстрые ритмические движения глазных яблок, дающие важную информацию о вестибулярном аппарате и центральной нервной системе). Система нистагмолаб обнаруживает и устраняет искажения в электронистагмографических кривых; она определяет по этим кривым характеристические параметры и восстанавливает данные, которые отсутствуют на классических кривых, например совмещенные движения глазного яблока.
Реосанс. Лилиан Костич [48] применила для измерения скорости потока жидкостей фурье-образ функции когерентности между сигналами, полученными с помощью двух зондов. Этот фурье-образ называется реосансом:

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
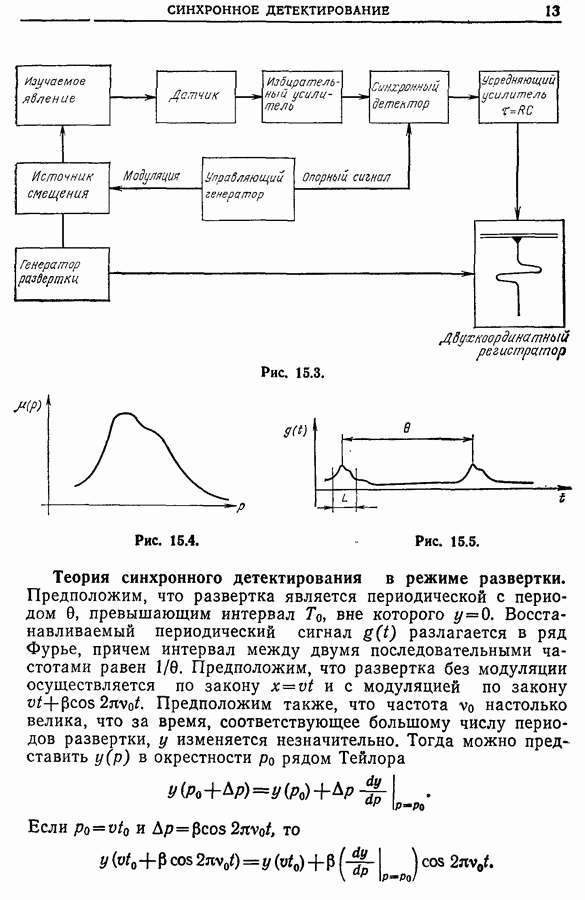
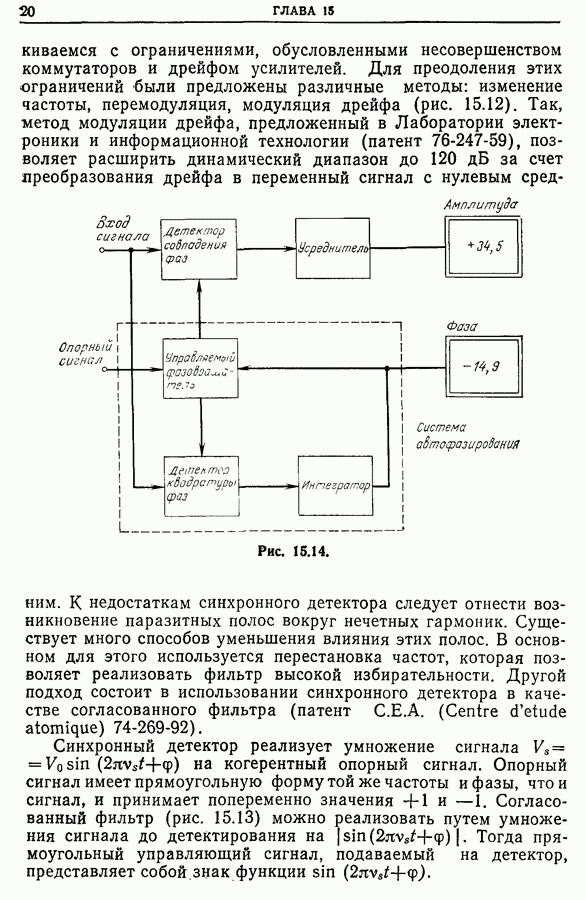
- Глава 15. СИНХРОННОЕ ДЕТЕКТИРОВАНИЕ
- 15.2. Схема метода
- 15.3. Теория синхронного детектирования
- 15.4. Синхронное детектирование в режиме развертки
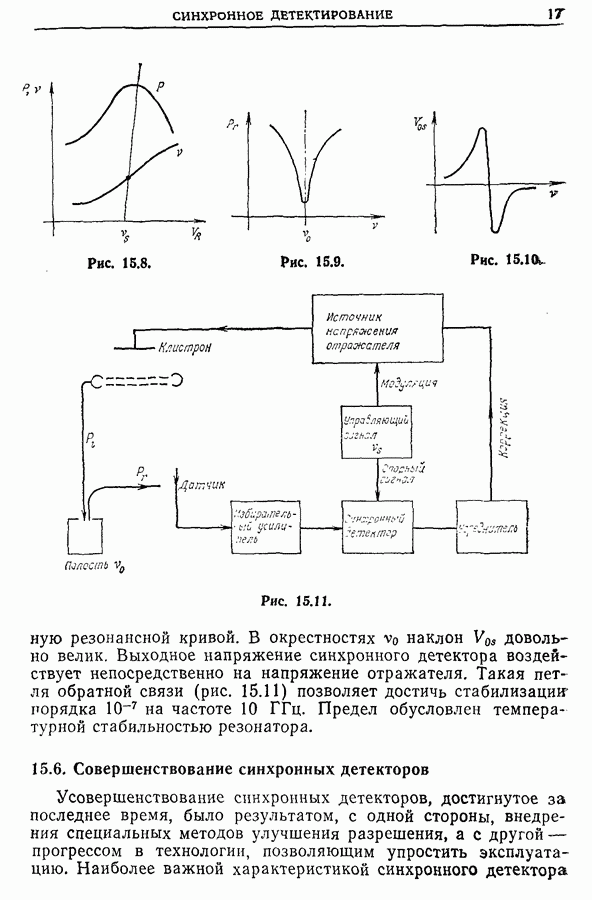
- 15.5. Примеры применения синхронных детекторов
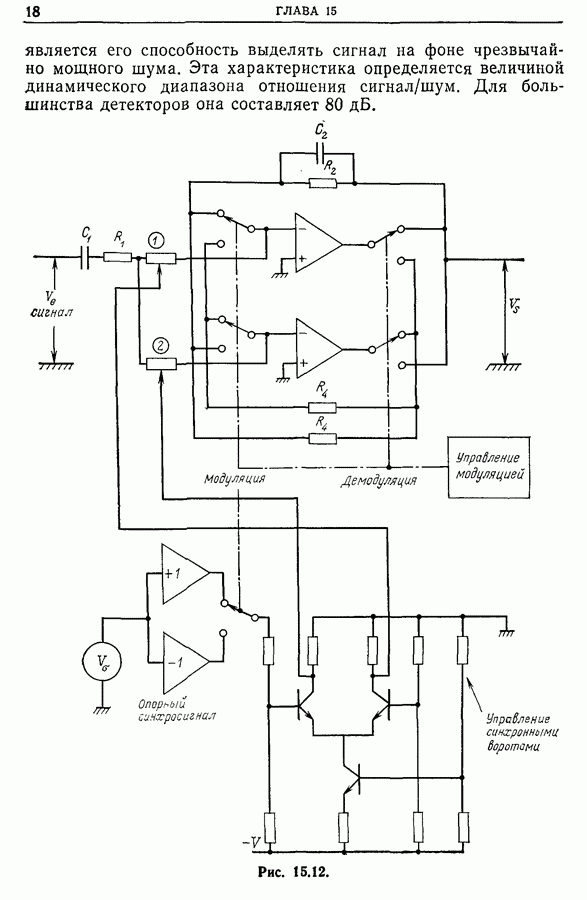
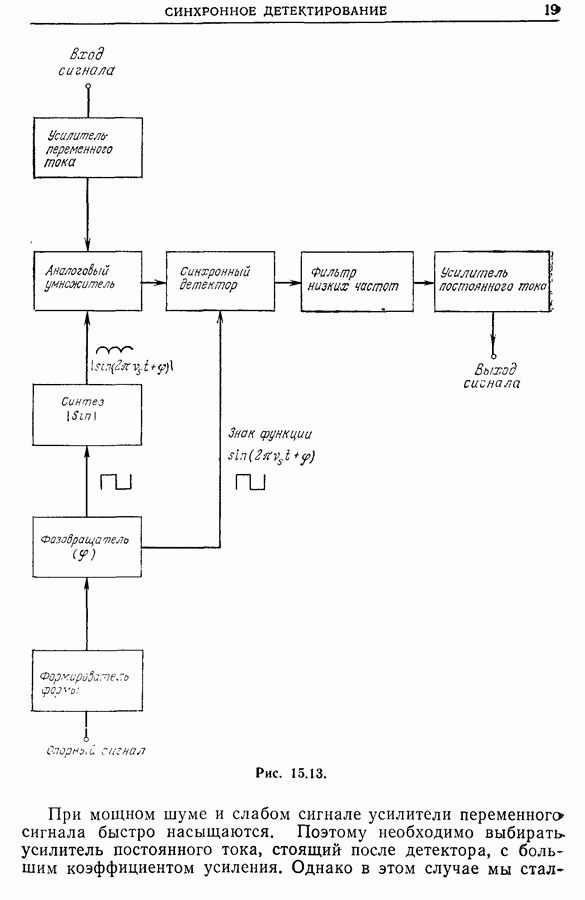
- 15.6. Совершенствование синхронных детекторов
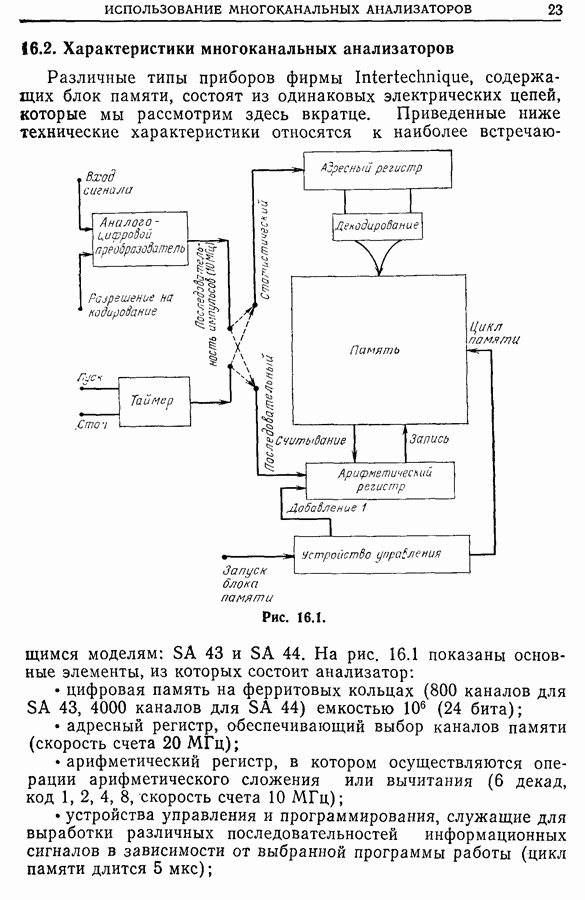
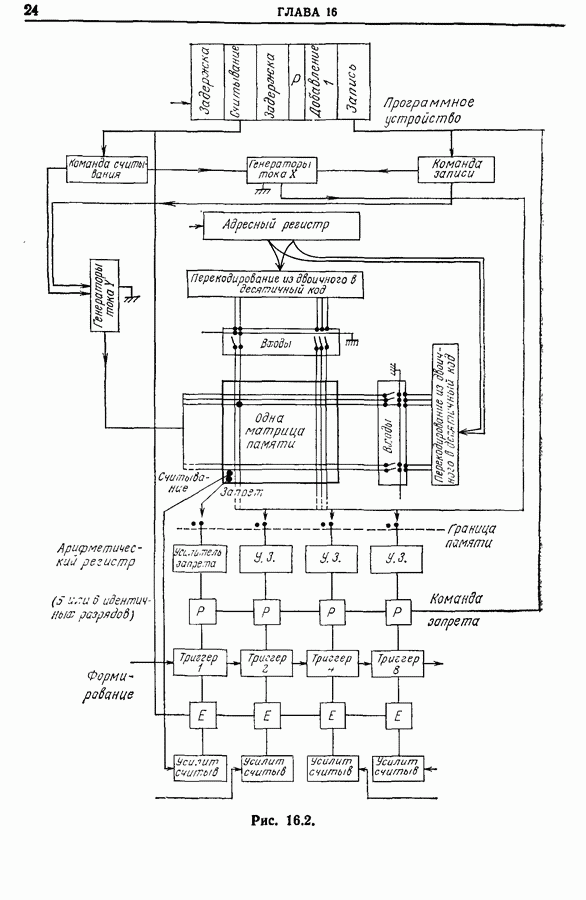
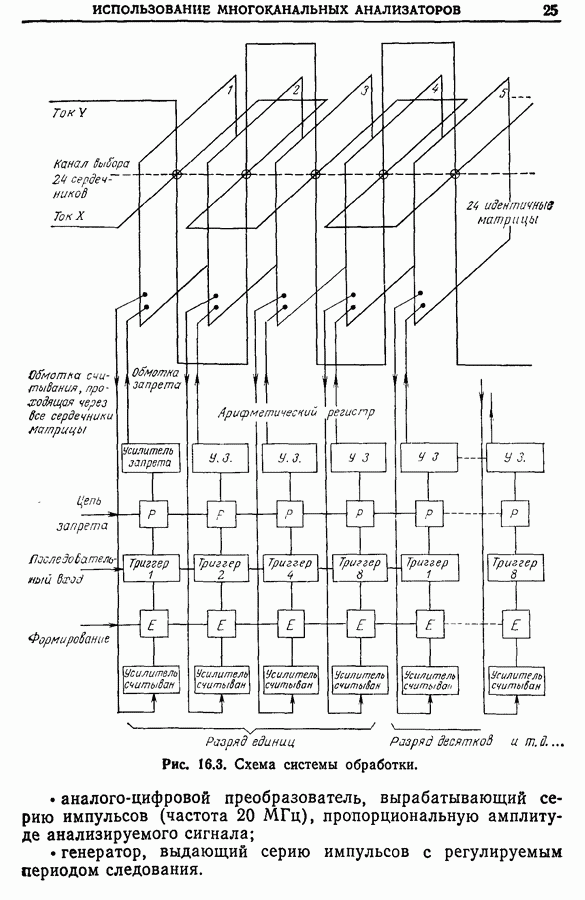
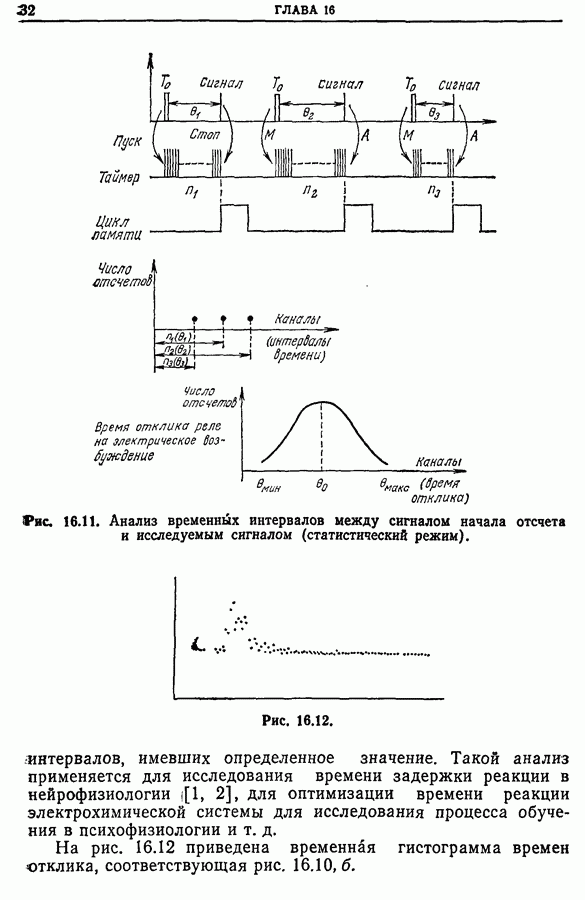
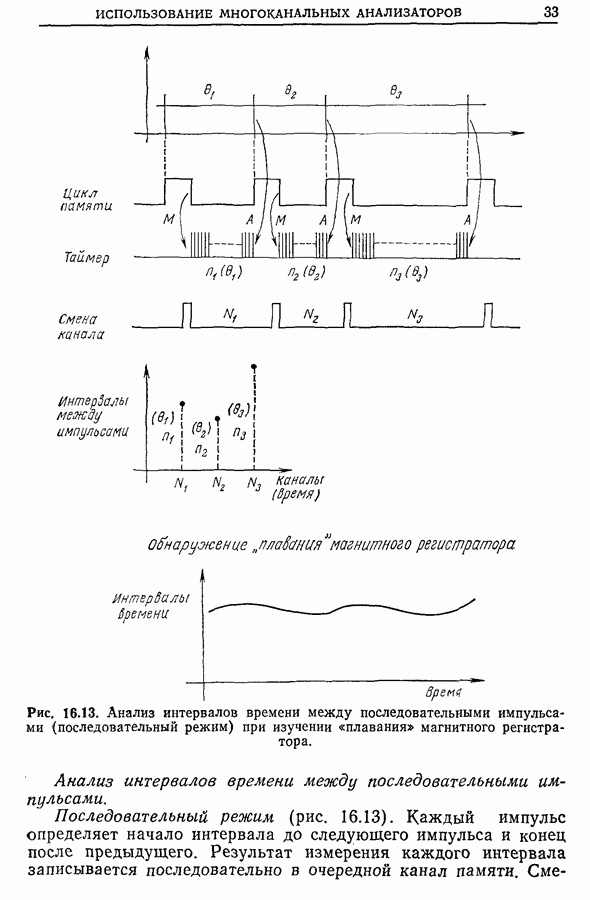
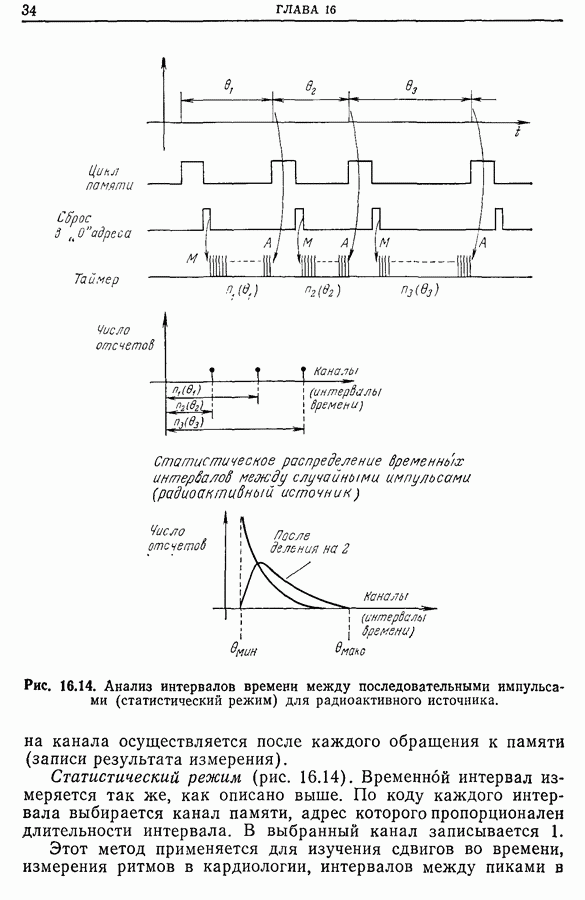
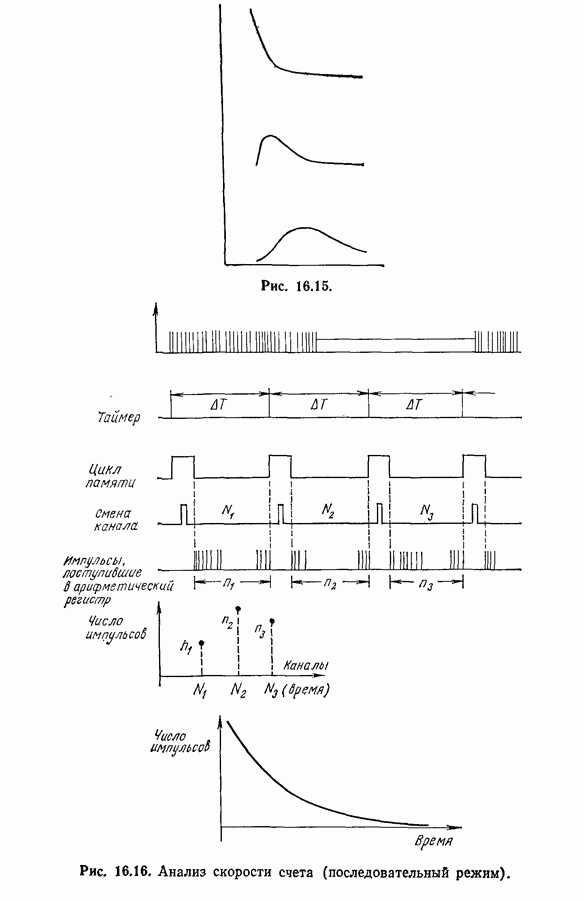
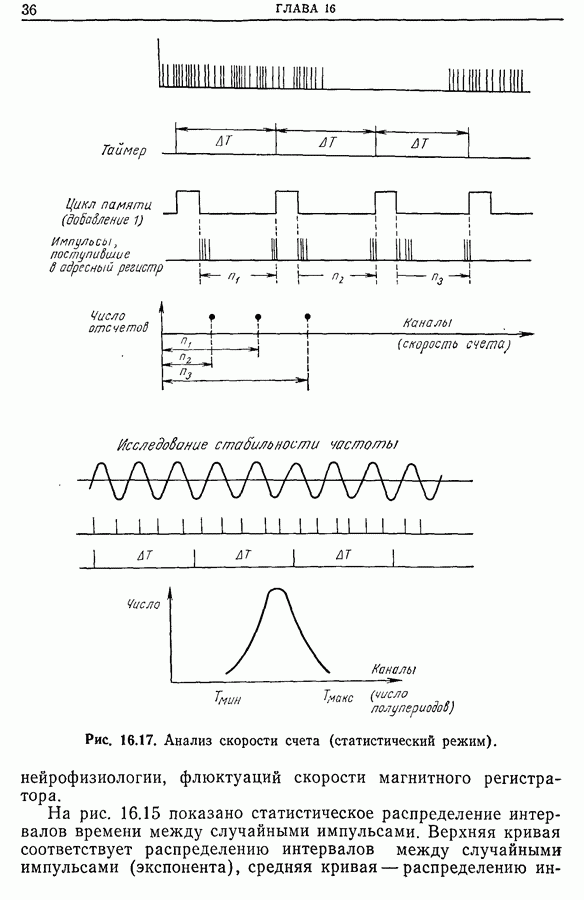
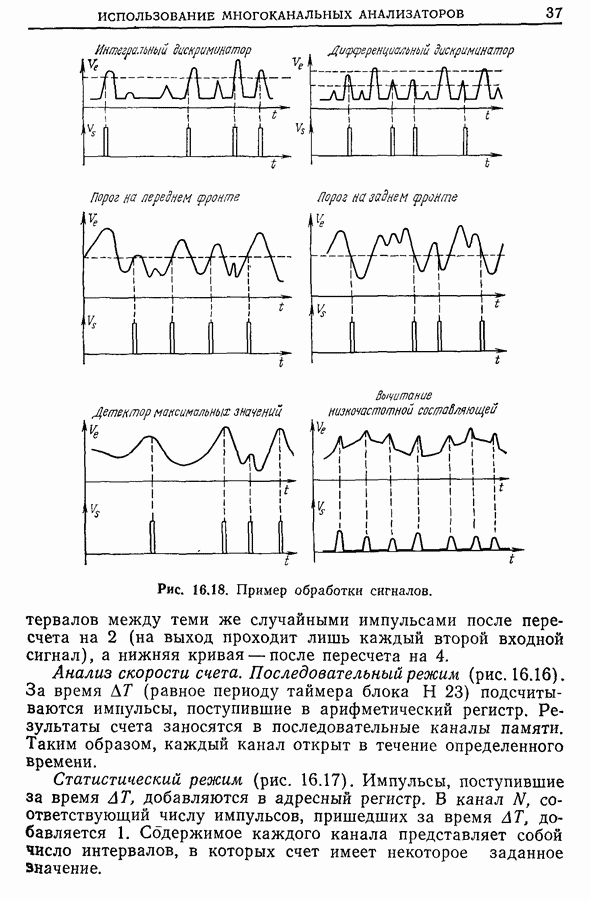
- Глава 16. ИСПОЛЬЗОВАНИЕ МНОГОКАНАЛЬНЫХ АНАЛИЗАТОРОВ ПРИ СТАТИЧЕСКОЙ ОБРАБОТКЕ ИЗМЕРЕНИЙ
- 16.2. Характеристики многоканальных анализаторов
- 16.3. Схема системы обработки
- 16.4. Примеры применения
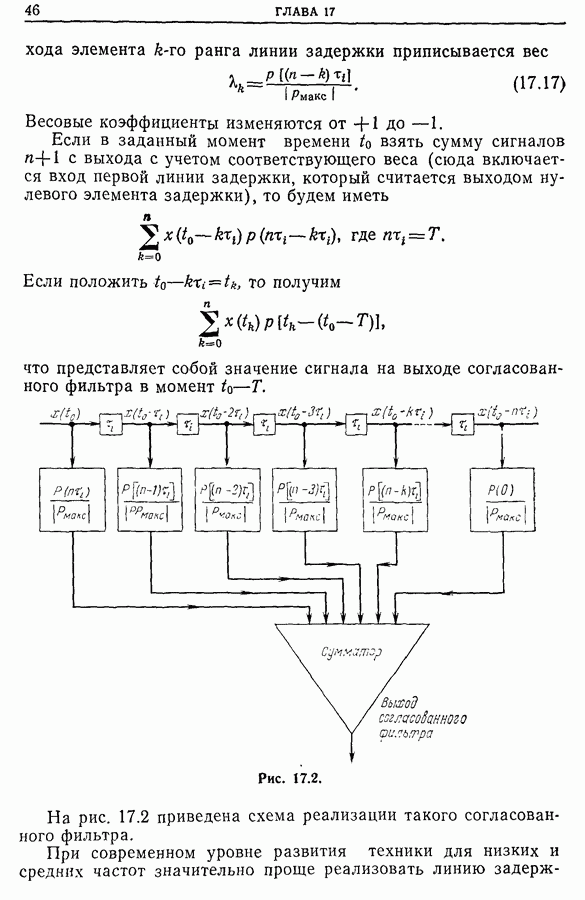
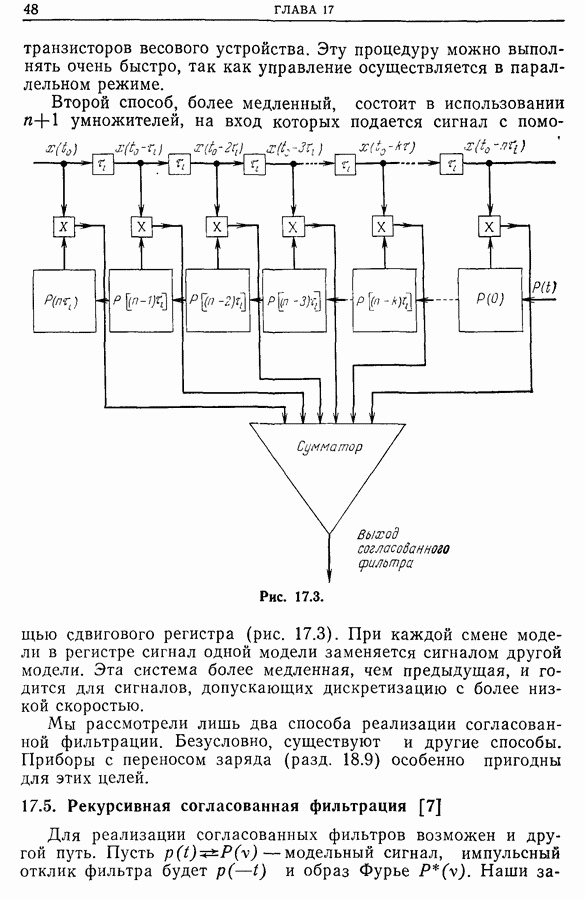
- Глава 17. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ
- 17.2. Частный случай белого шума. Согласованный фильтр
- 17.3. Согласованная фильтрация и корреляция Корреляция.
- 17.4. Реализация согласованных фильтров методом «взвешивания»
- 17.5. Рекурсивная согласованная фильтрация [7]
- 17.6. Применения метода согласованной фильтрации
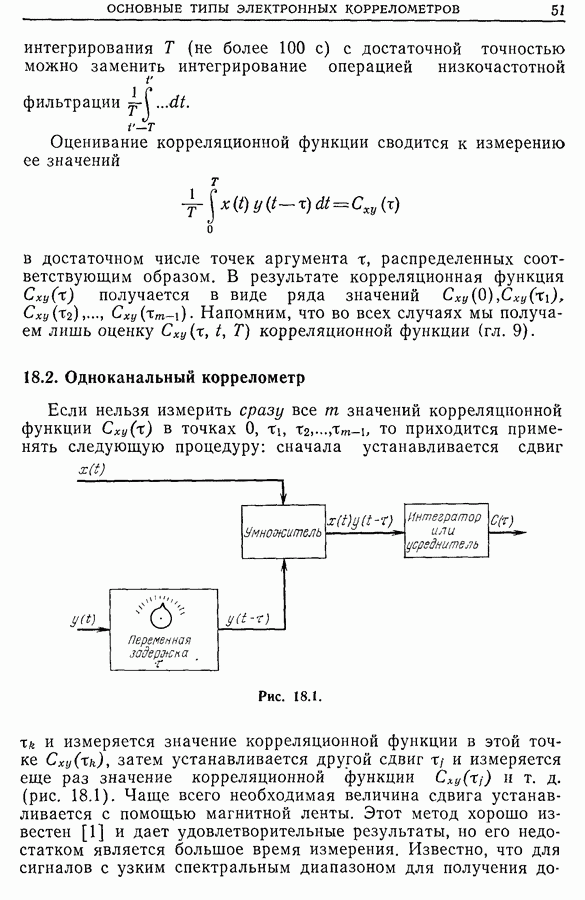
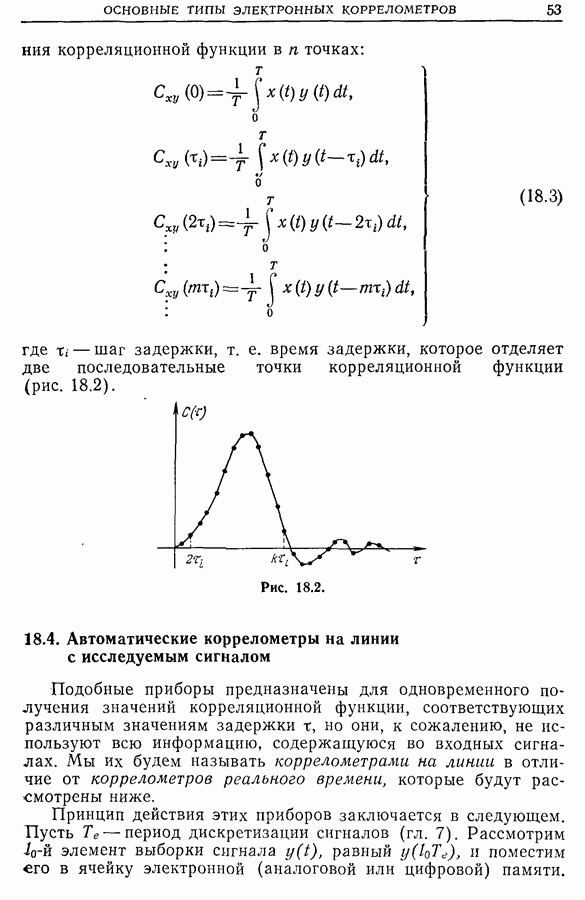
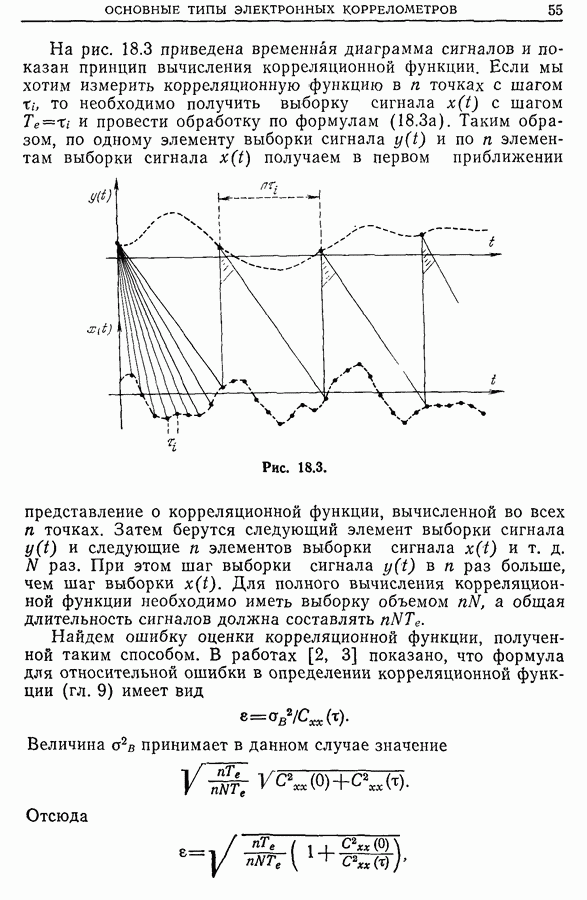
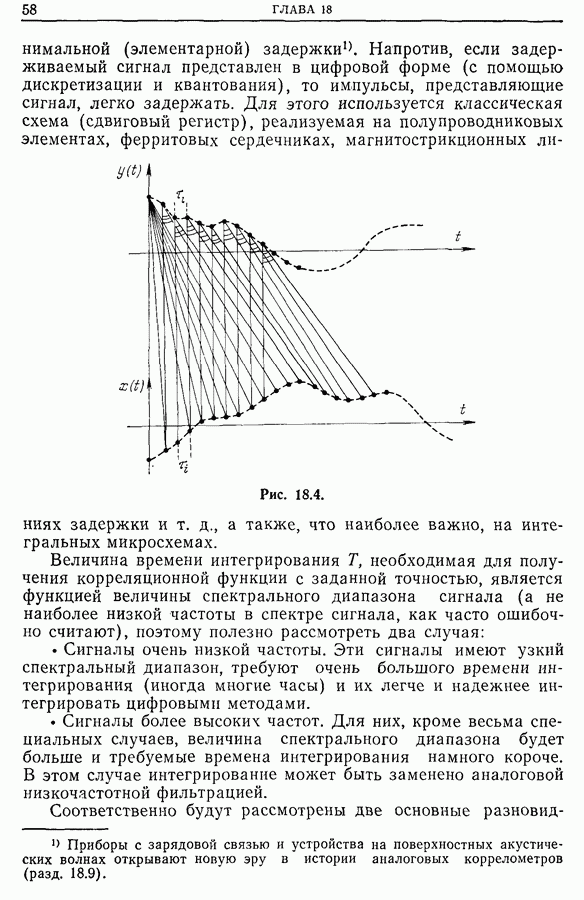
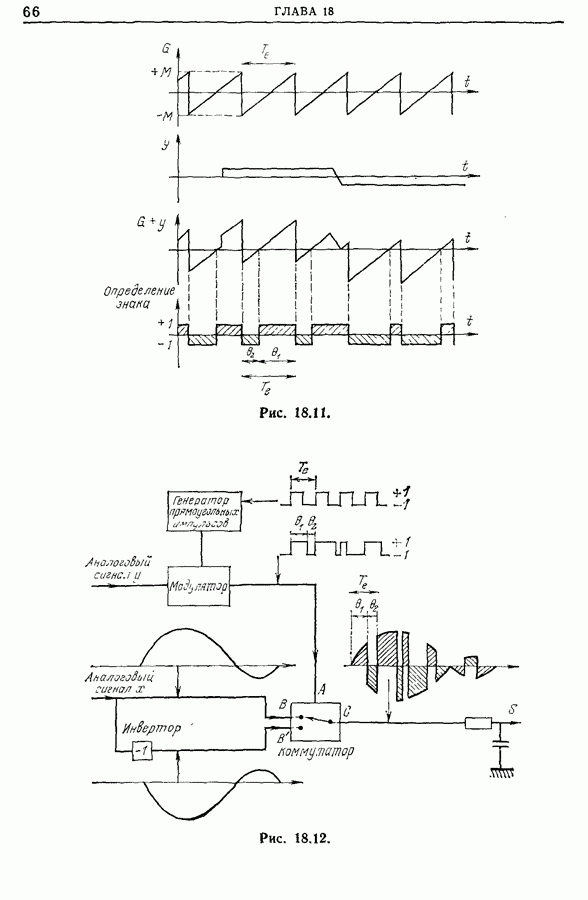
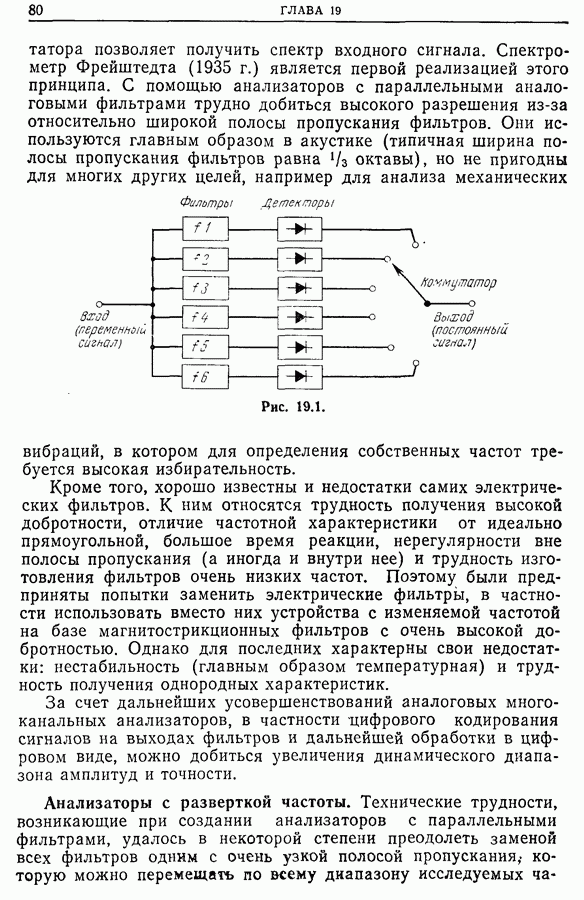
- Глава 18. ОСНОВНЫЕ ТИПЫ ЭЛЕКТРОННЫХ КОРРЕЛОМЕТРОВ
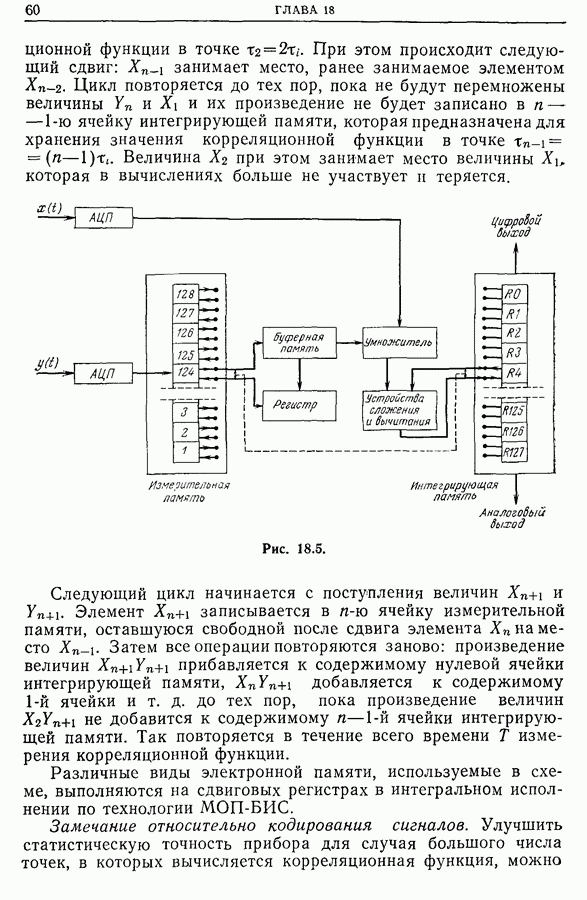
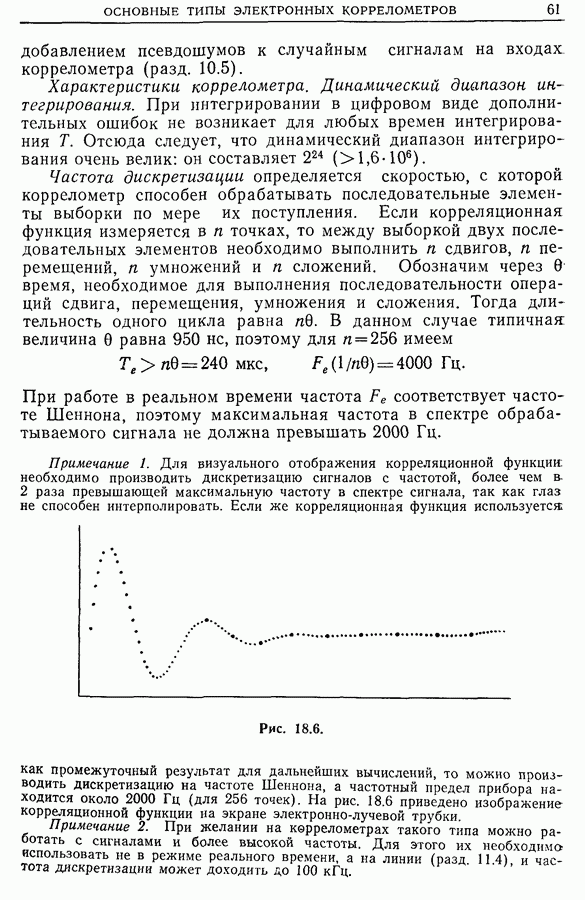
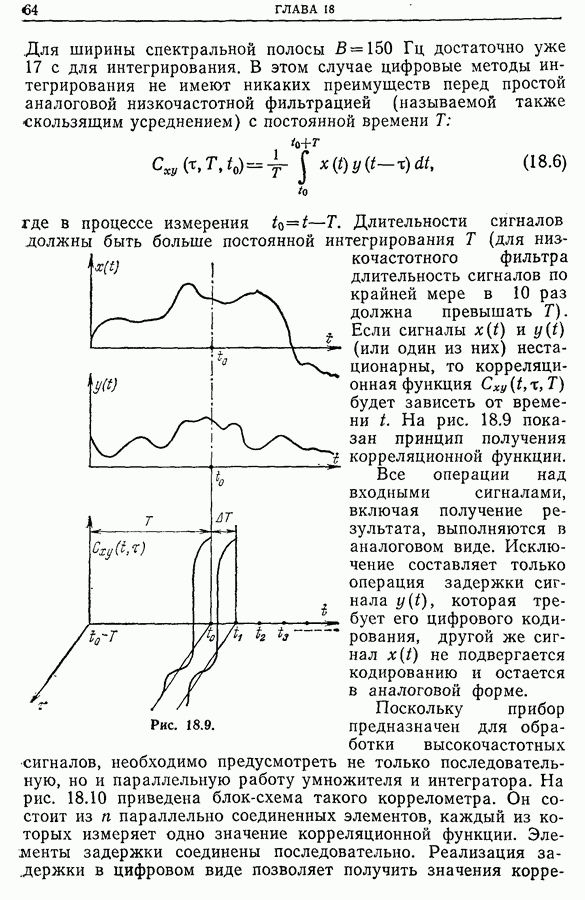
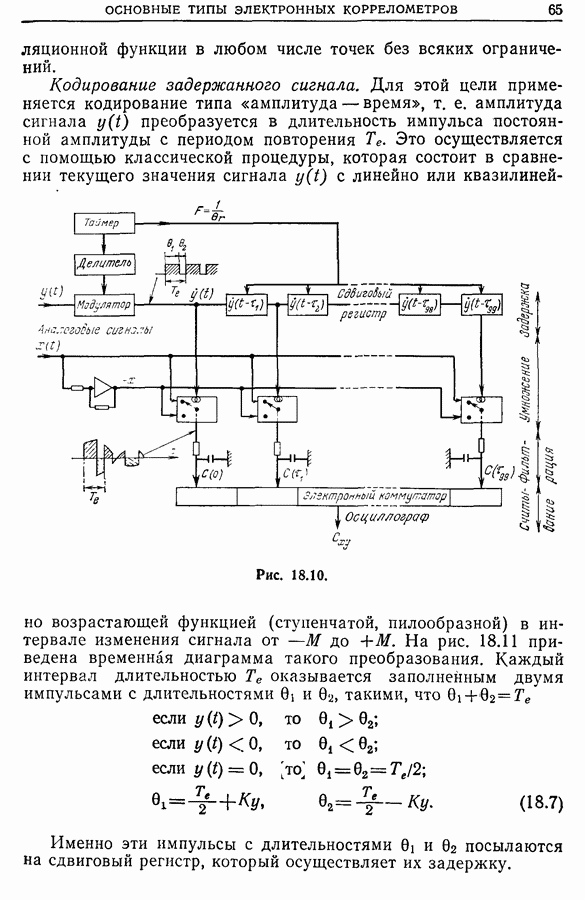
- 18.2. Одноканальный коррелометр
- 18.3. Автоматические коррелометры
- 18.4. Автоматические коррелометры на линии с исследуемым сигналом
- 18.5. Автоматические коррелометры реального времени (или мультикоррелометры)
- 18.6. Коррелометры на больших интегральных схемах
- 18.7. Коррелометры реального времени для высокочастотных сигналов
- 18.8 Развитие коррелометров
- 18.9. Приборы с зарядовой связью [11]
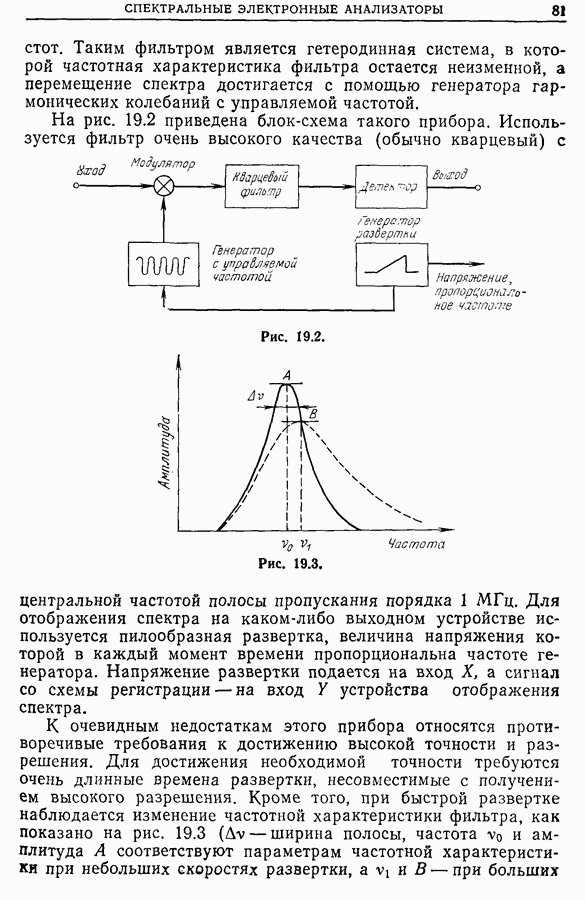
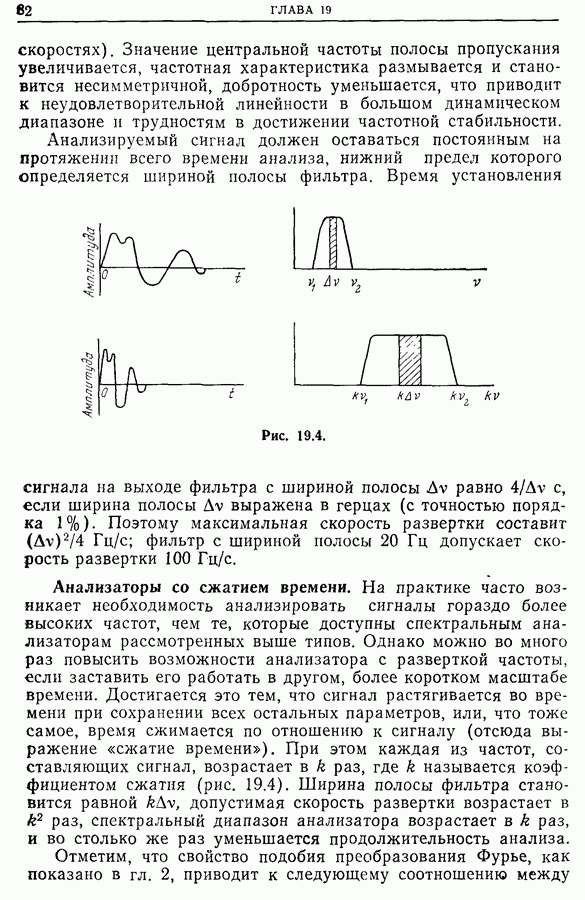
- Глава 19. СПЕКТРАЛЬНЫЕ ЭЛЕКТРОННЫЕ АНАЛИЗАТОРЫ
- 19.2. Спектральные анализаторы, основанные на методе непосредственного преобразования Фурье
- 19.3. Применения анализаторов на основе метода БПФ
- Глава 20. ОПТИЧЕСКИЙ СПЕКТРАЛЬНЫЙ АНАЛИЗ
- 20.2. Упрощения, связанные с отбрасыванием фазы
- 20.3. Эффект виньетирования
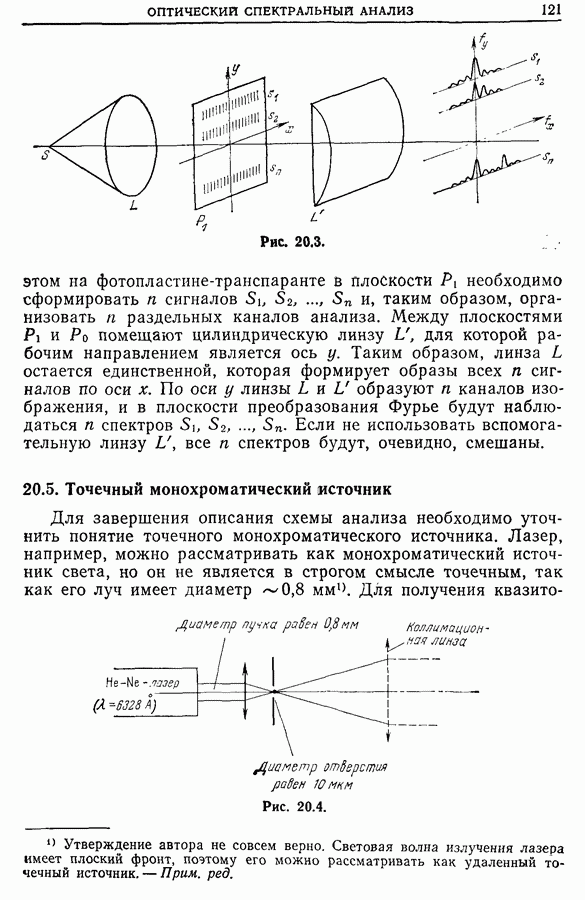
- 20.4. Двумерный анализ
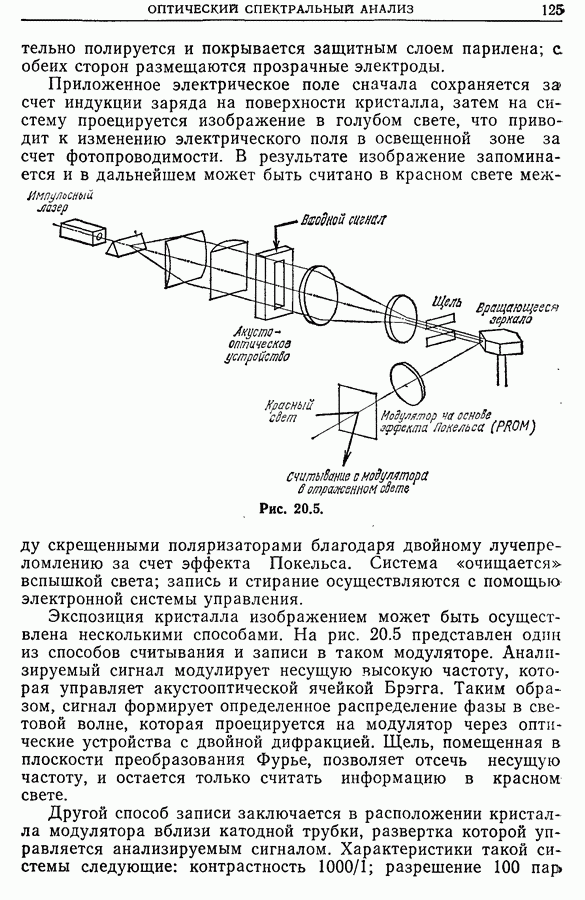
- 20.5. Точечный монохроматический источник
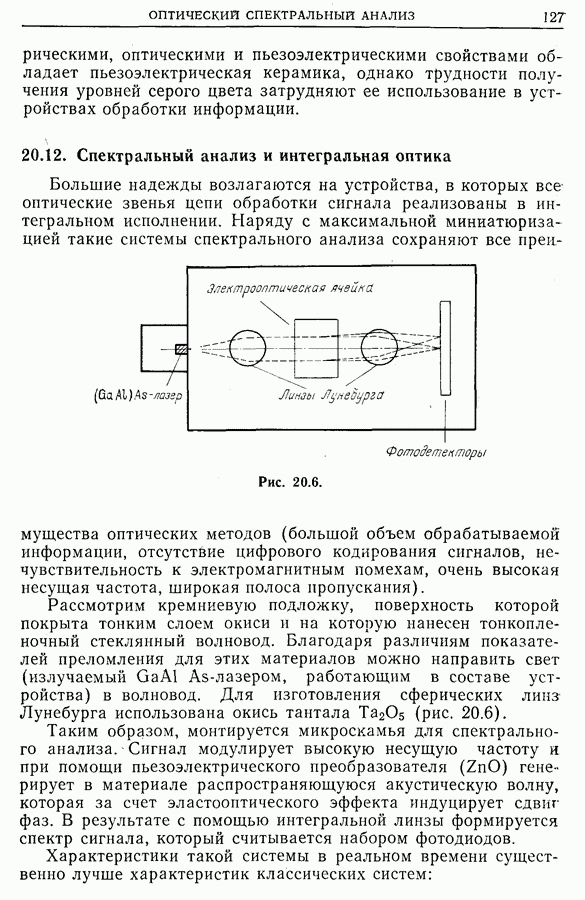
- 20.6. Электрооптическое преобразование сигнала
- 20.7. Устройства отображения на жидких кристаллах
- 20.8. Ограничения устройств отображения
- 20.9. Модулятор на основе эффекта Покельса (PROM)
- 20.10. Трубки Титус и Фототитус
- 20.11. Другие электрооптические кристаллы
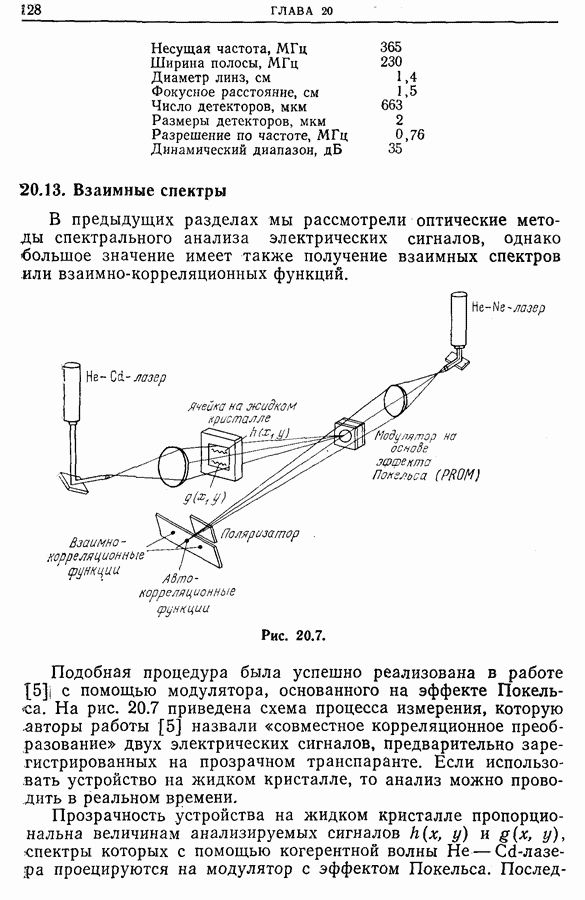
- 20.12. Спектральный анализ и интегральная оптика
- 20.13. Взаимные спектры
- Глава 21. НЕКОТОРЫЕ ПРАКТИЧЕСКИЕ ПРИМЕНЕНИЯ МЕТОДОВ ОБРАБОТКИ СИГНАЛОВ
- 21.2. Исследование ядерных сред
- 21.3. Ядерный магнитный резонанс (ЯМР) с возбуждением случайным сигналом
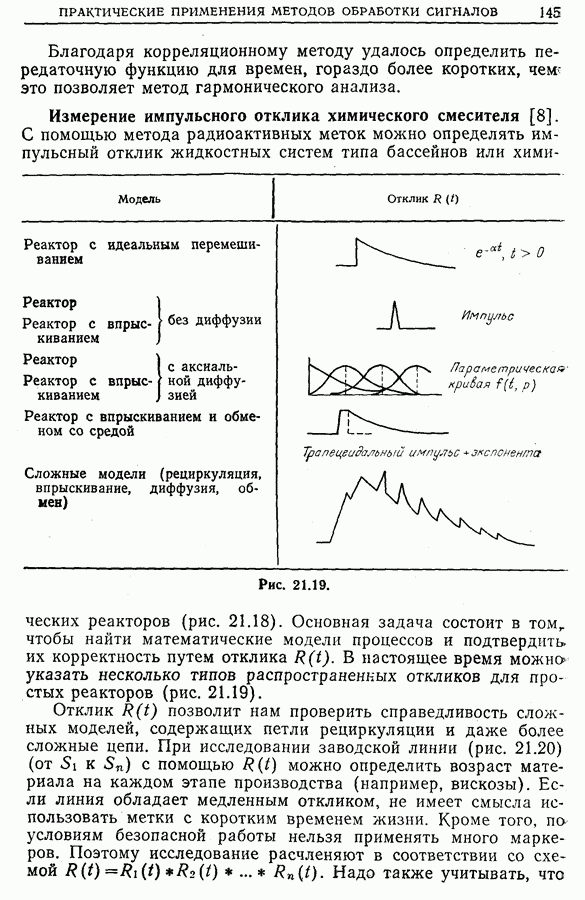
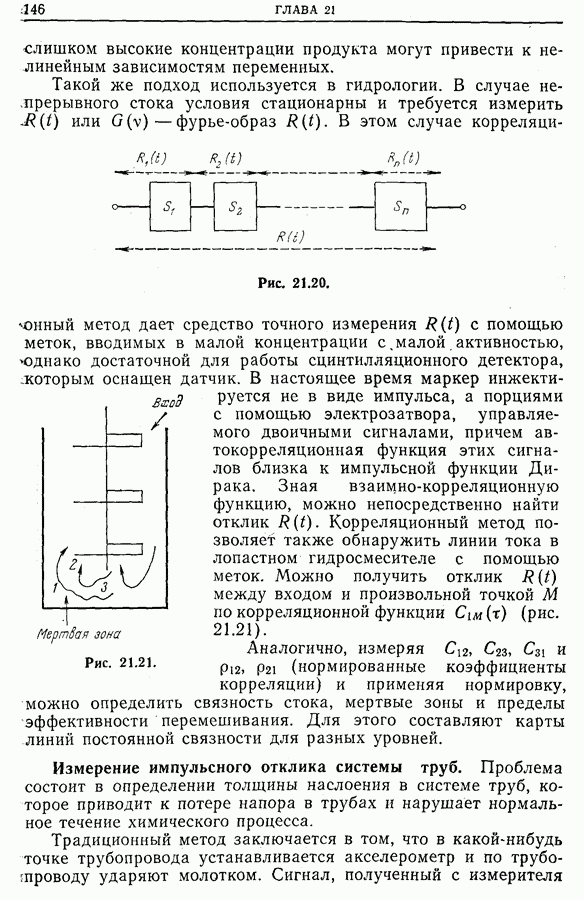
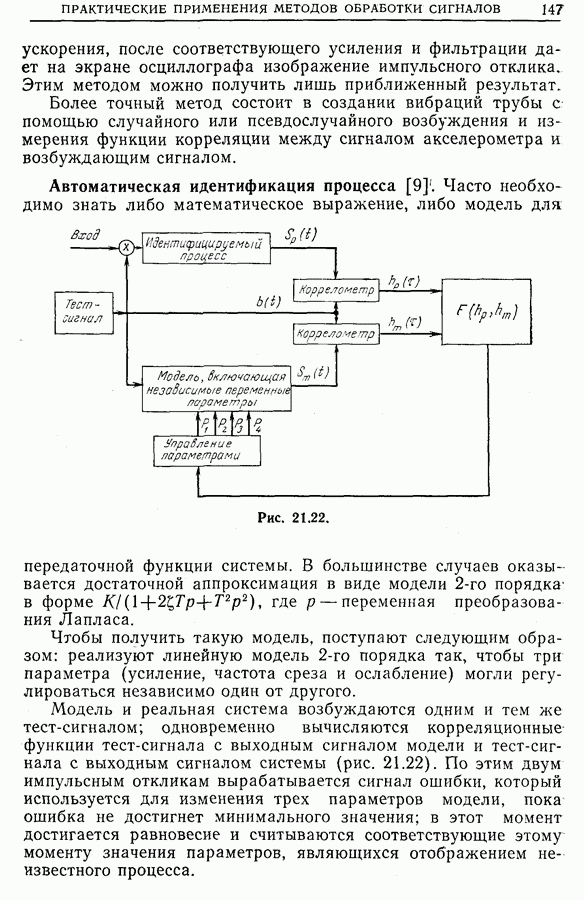
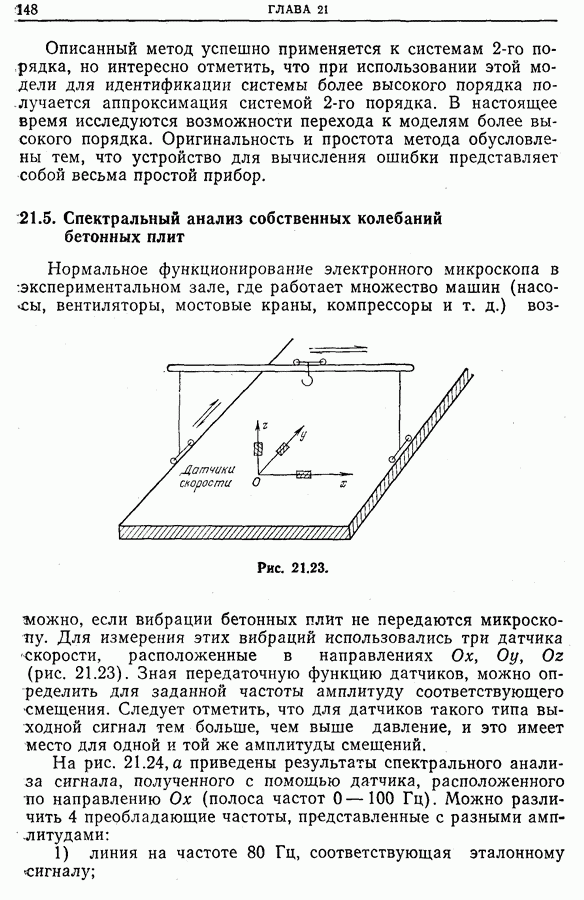
- 21.4. Идентификация процессов. Измерение импульсных откликов и передаточных функций
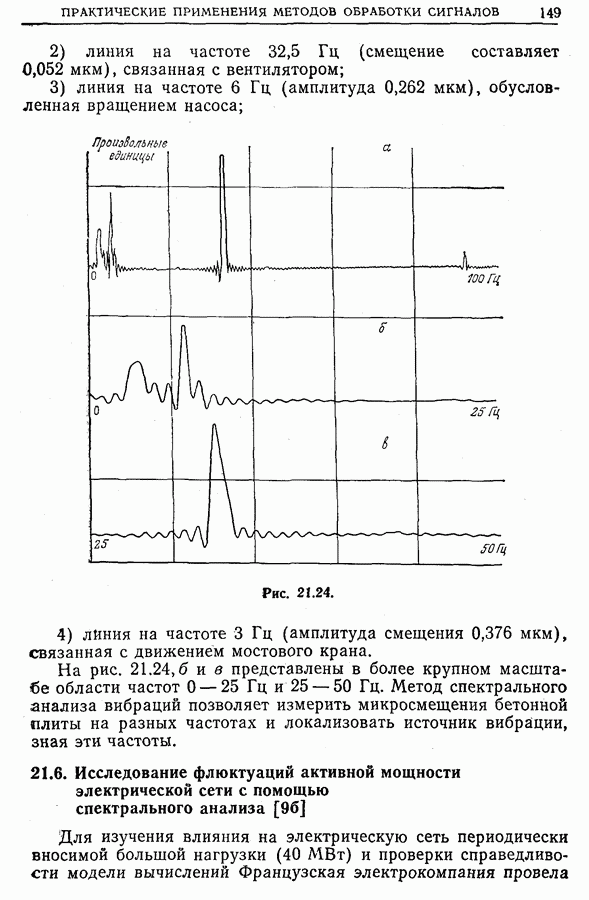
- 21.5. Спектральный анализ собственных колебаний бетонных плит
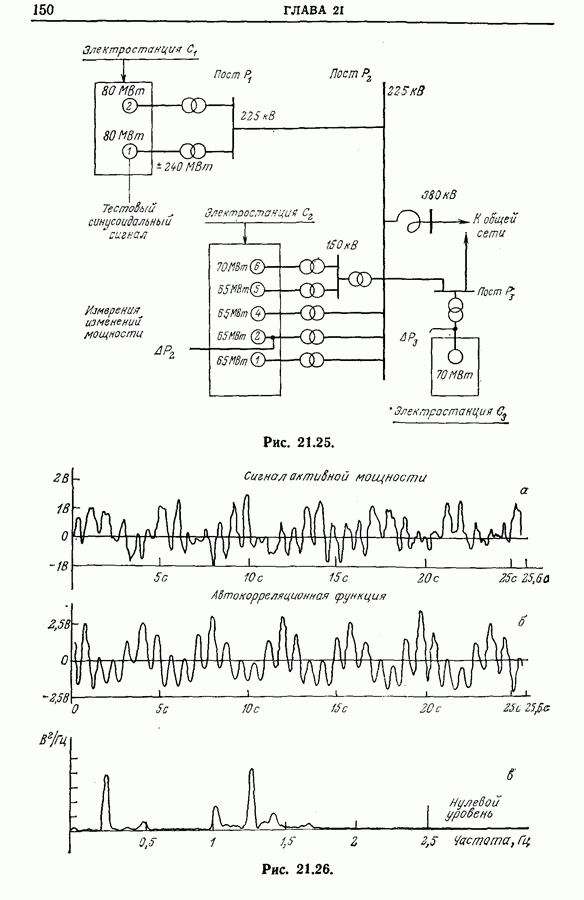
- 21.6. Исследование флюктуаций активной мощности электрической сети с помощью спектрального анализа
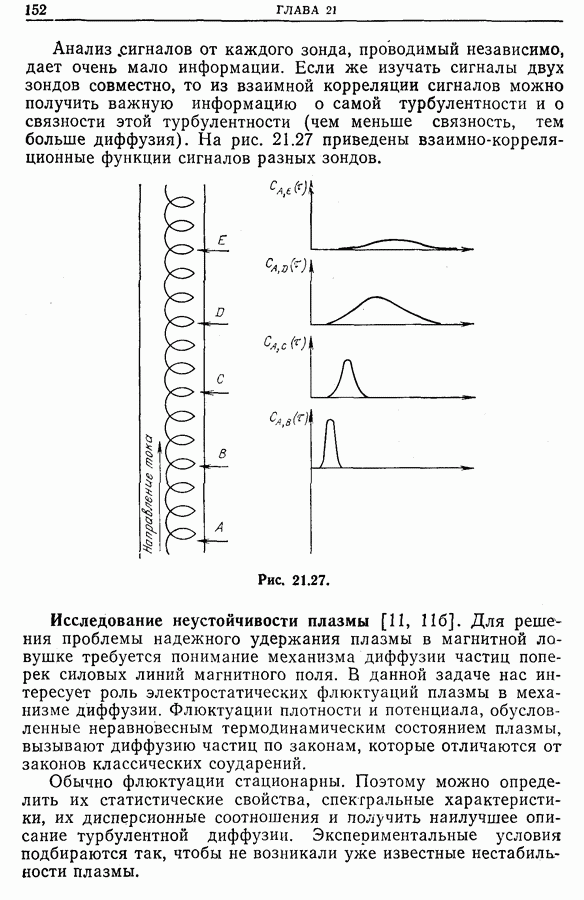
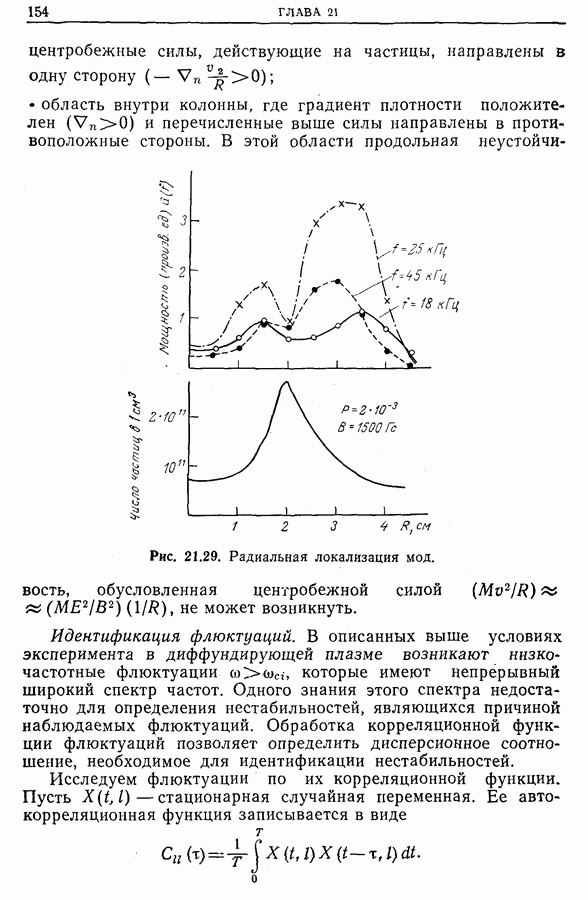
- 21.7. Изучение турбулентности
- 21.8. Применения в геофизике
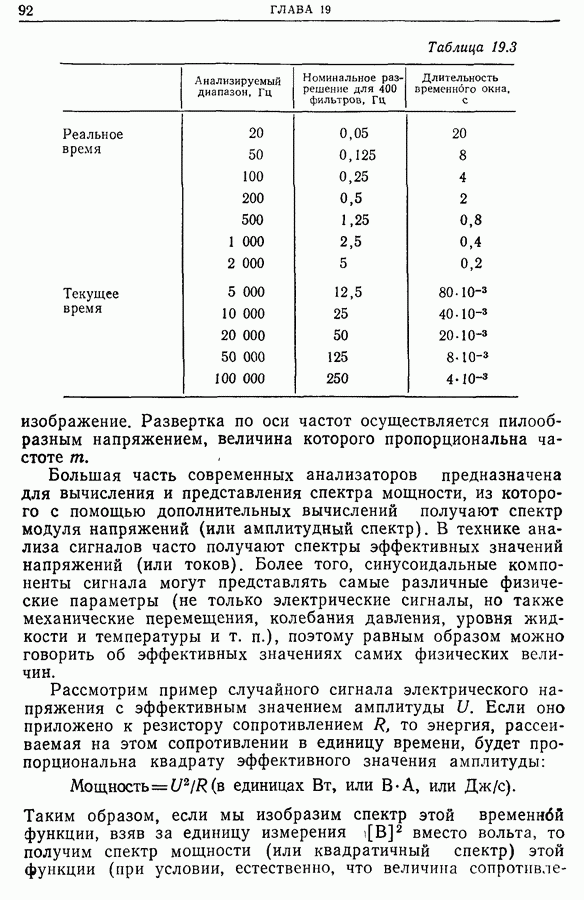
- 21.9. Применения в астрофизике
- 21.10. Применения в астрономии и радиоастрономии
- 21.11. Применения в биологии и медицине
- 21.12. Применения в акустике
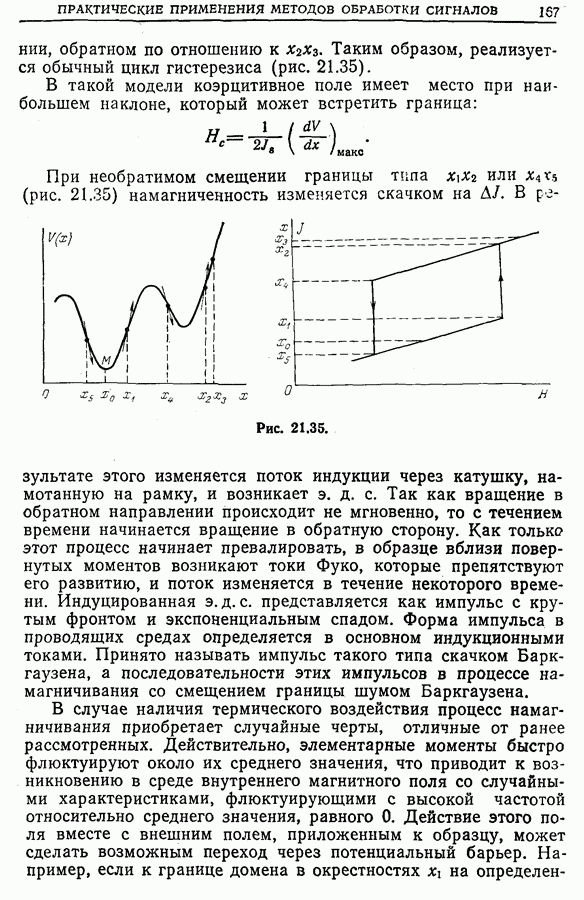
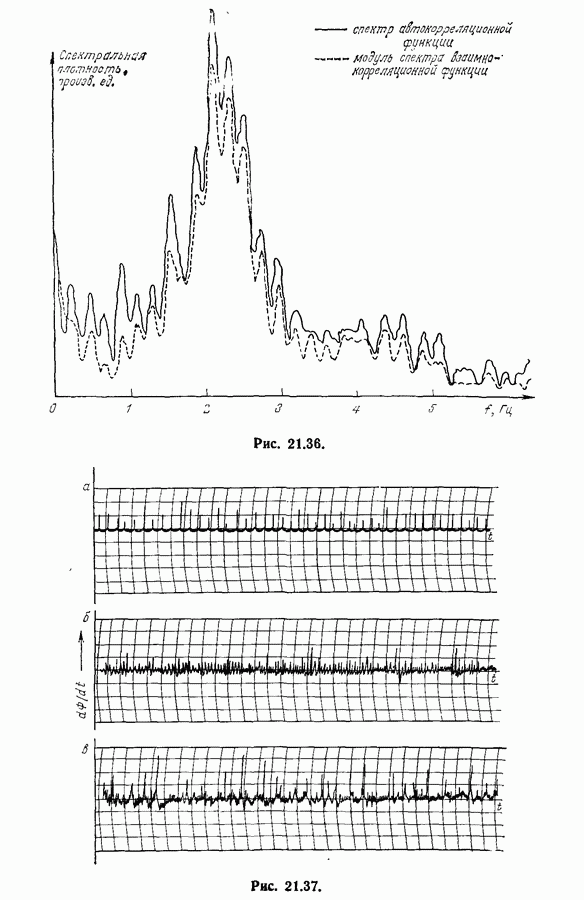
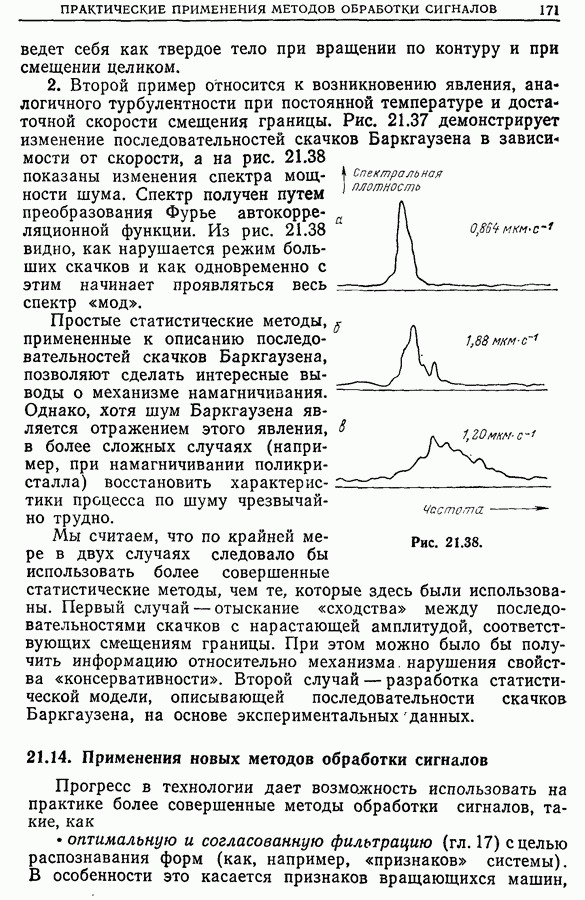
- 21.13. Исследование процессов намагничивания ферромагнетиков
- 21.14. Применения новых методов обработки сигналов
- 21.15. Заключение
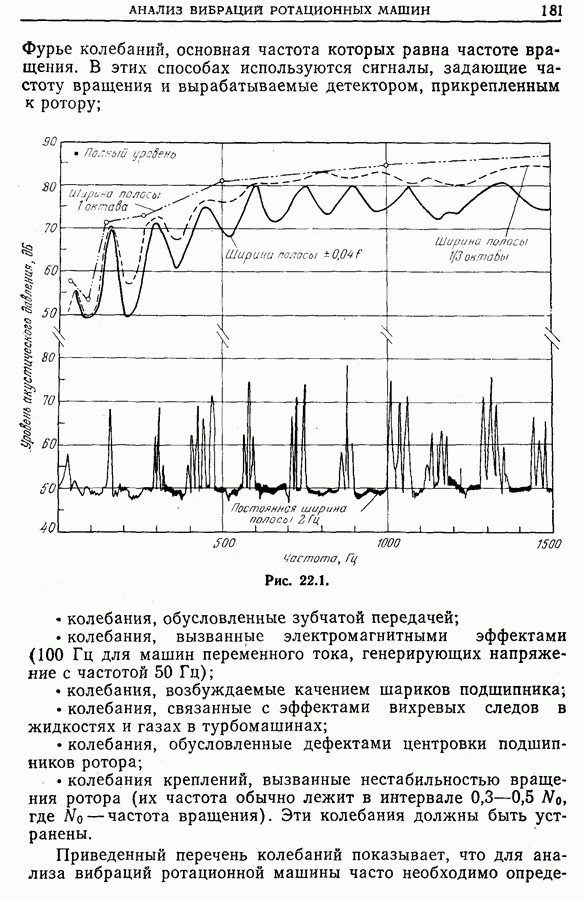
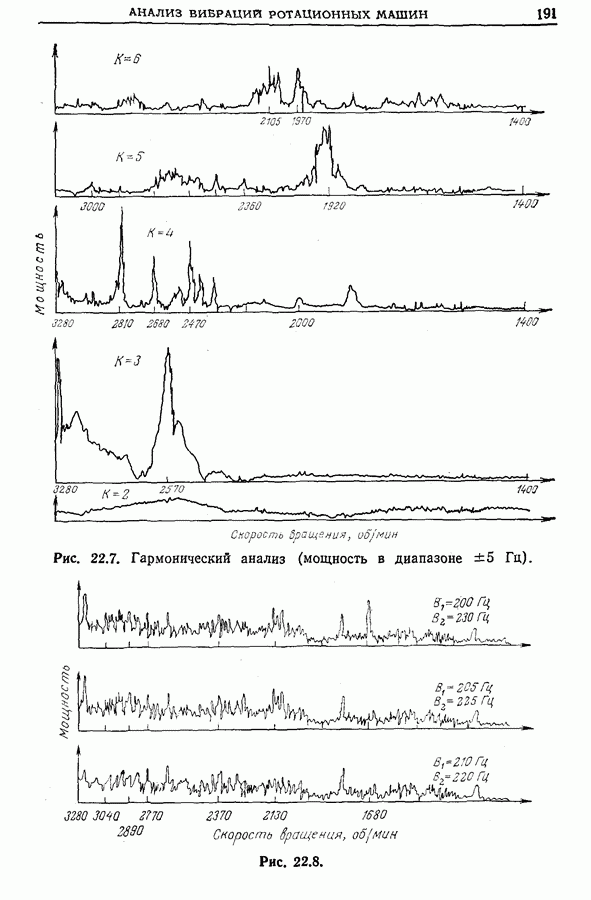
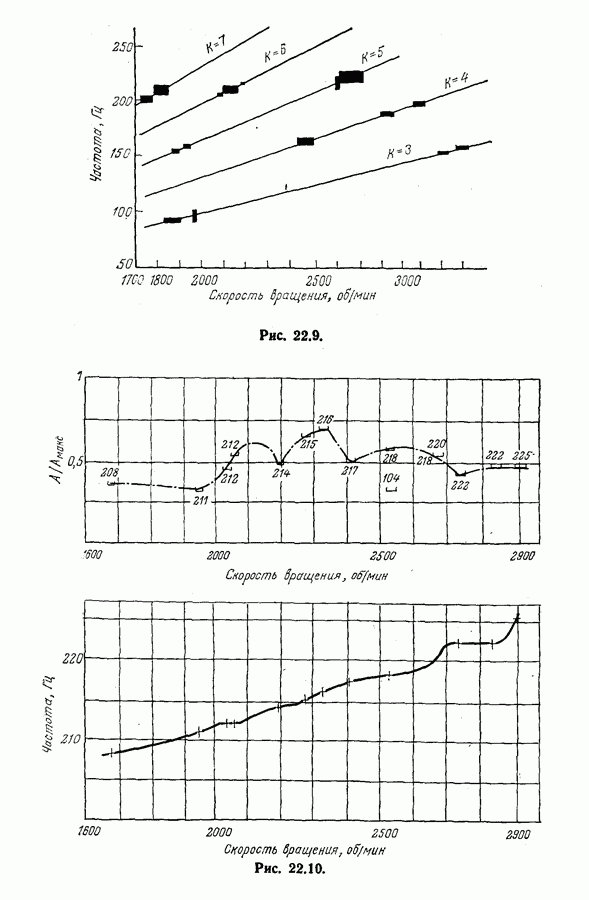
- Глава 22. ПРИМЕНЕНИЕ МЕТОДОВ ОБРАБОТКИ СИГНАЛОВ ДЛЯ АНАЛИЗА ВИБРАЦИЙ РОТАЦИОННЫХ МАШИНА
- 22.2. Анализ поведения системы «ротационная машина — конструкция»
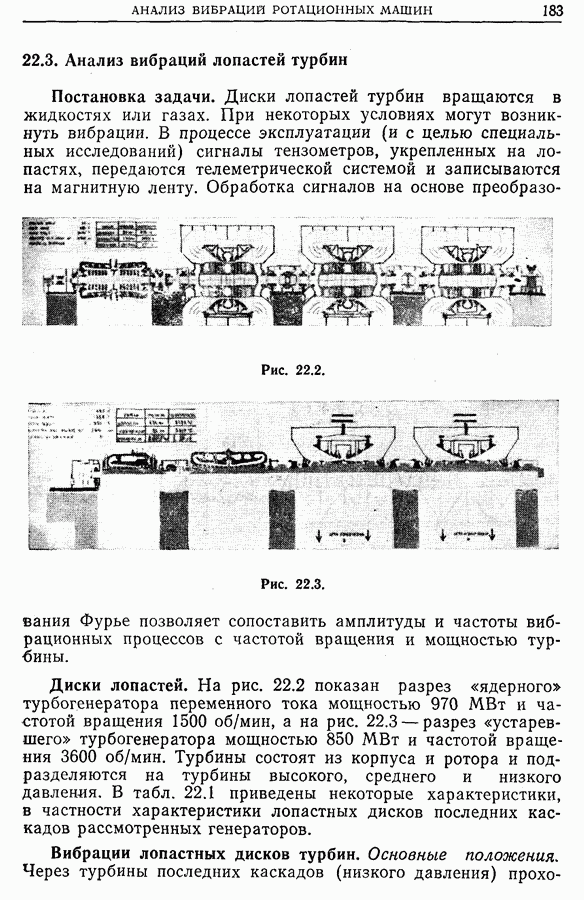
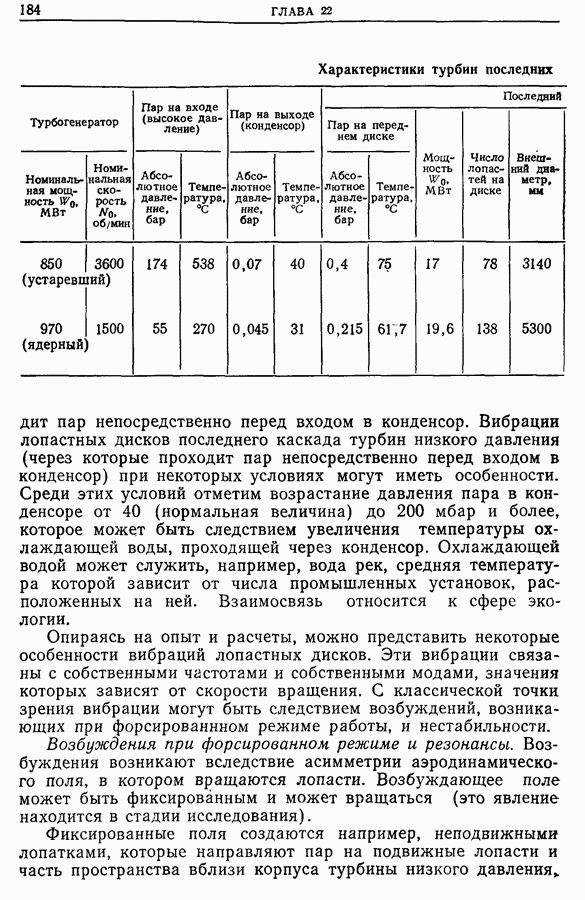
- 22.3. Анализ вибраций лопастей турбин
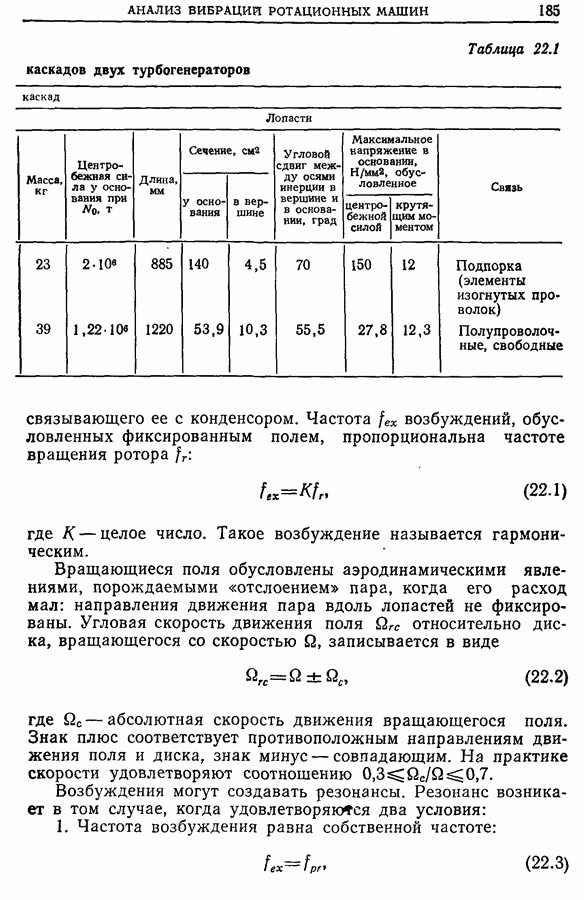
- 22.4. Балансировка ротационных машин
- Глава 23. ФУНКЦИЯ НЕОПРЕДЕЛЕННОСТИ
- 23.2. Временная корреляция. Временной сдвиг
- 23.3. Частотная корреляция. Частотный сдвиг
- 23.4. Временной и частотный сдвиги. Функция неопределенности
- 23.5. Функция неопределенности Вудворда
- 23.6. Взаимная функция неопределенности
- 23.7. Некоторые свойства функции неопределенности
- 23.8. Представление функций неопределенности
- 23.9. Примеры функций неопределенности
- 23.10. Применение функции неопределенности
- 23.11. Применение функций неопределенности для описания линейных неоднородных во времени систем. Обобщение понятия передаточной функции. Функция диффузии (функция рассеивания)
- 23.12. Генерация тестового сигнала
- 23.13. Прибор для измерения функции неопределенности в режиме реального времени
- Глава 24. ПОНЯТИЕ МГНОВЕННОГО СПЕКТРА ИЛИ ЧАСТОТНО-ВРЕМЕННОГО ПРЕДСТАВЛЕНИЯ В АНАЛИЗЕ И СИНТЕЗЕ СИГНАЛОВ
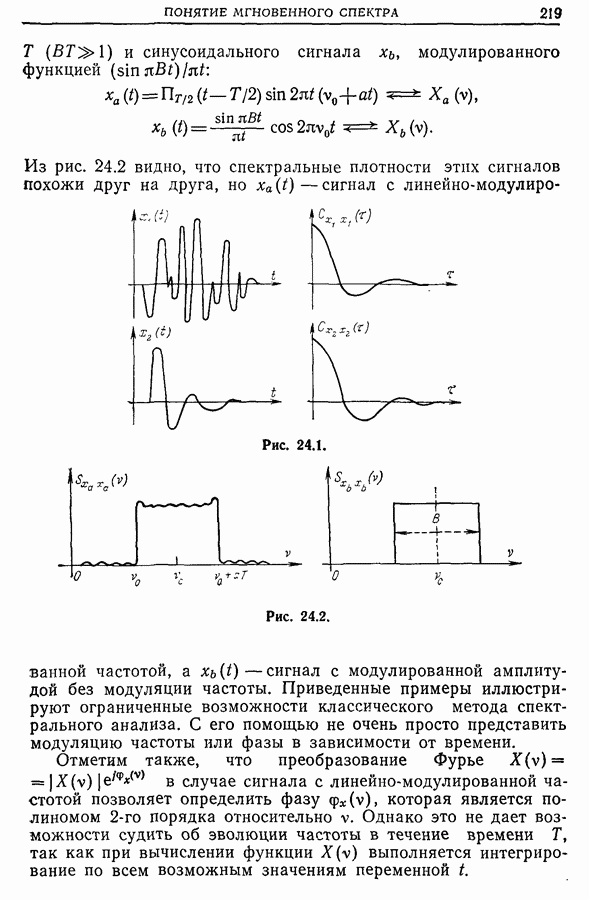
- 24.2. Примеры спектрального анализа модулированных и немодулированных сигналов
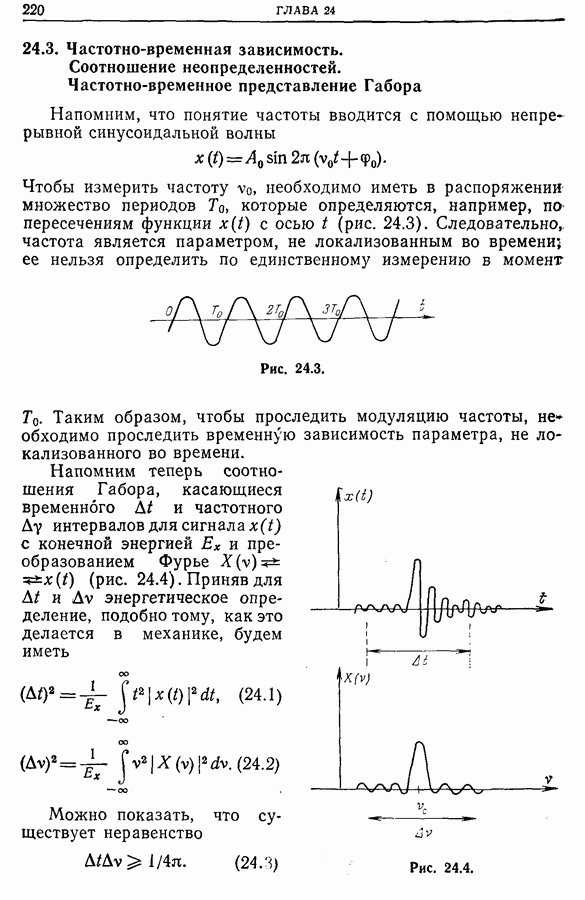
- 24.3. Частотно-временная зависимость. Соотношение неопределенностей. Частотно-временное представление Габора
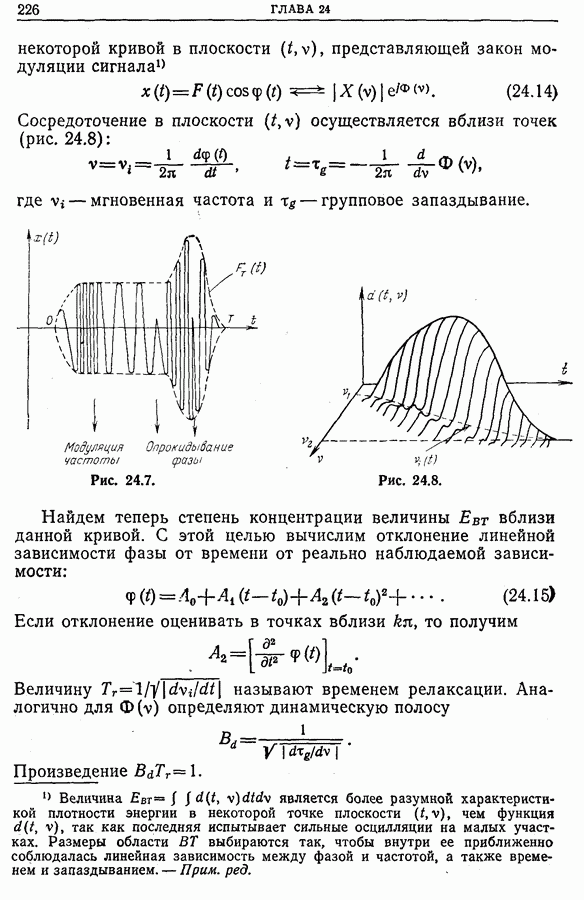
- 24.4. Представление [t, v] по Бонне. Мгновенный спектр мощности по Биллю. Функция неопределенности
- 24.5. Другие определения частотно-временного представления
- 24.6. Измерение мгновенных спектров
- 24.7. Обобщение понятия мгновенного спектра мощности на случайные локально-стационарные сигналы. Функция структуры. Функция диффузии
- 24.8 Восстановление сигнала x(t) по известной функции
- 24.9. Заключение
- Глава 25. НОВЫЕ МЕТОДЫ СПЕКТРАЛЬНОГО АНАЛИЗА
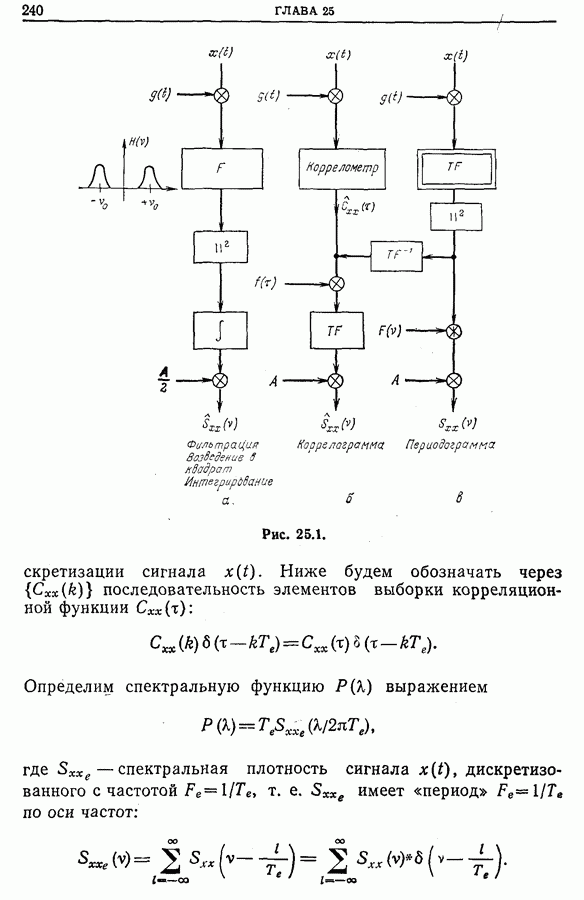
- 25.2. Проблемы, обусловленные дискретизацией корреляционной функции
- 25.3. Постановка проблемы получения спектральной функции из конечного числа значений автокорреляционной функции
- 25.4. Классический метод, основанный на преобразовании Фурье корреляционной функции
- 25.5. Метод максимума энтропии или метод авторегрессионной модели
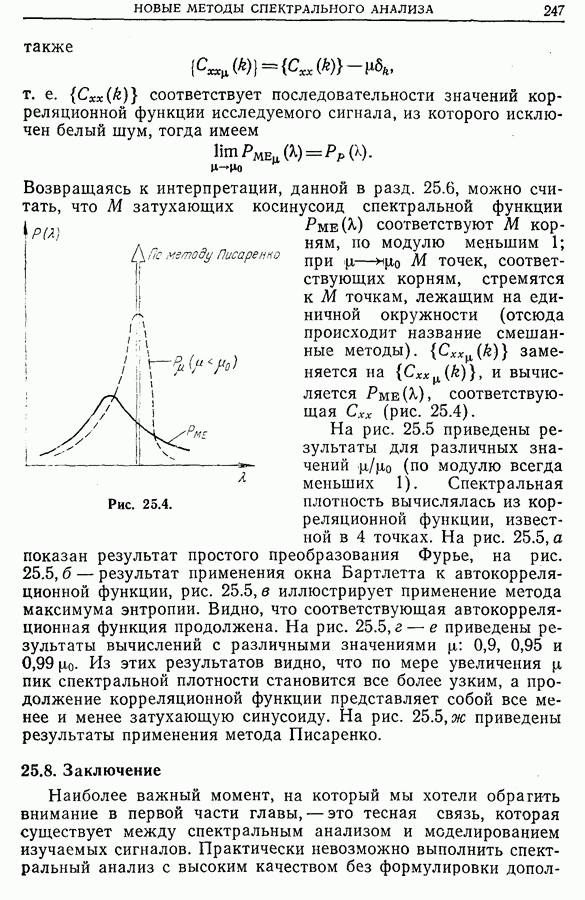
- 25.6. Метод Писаренко
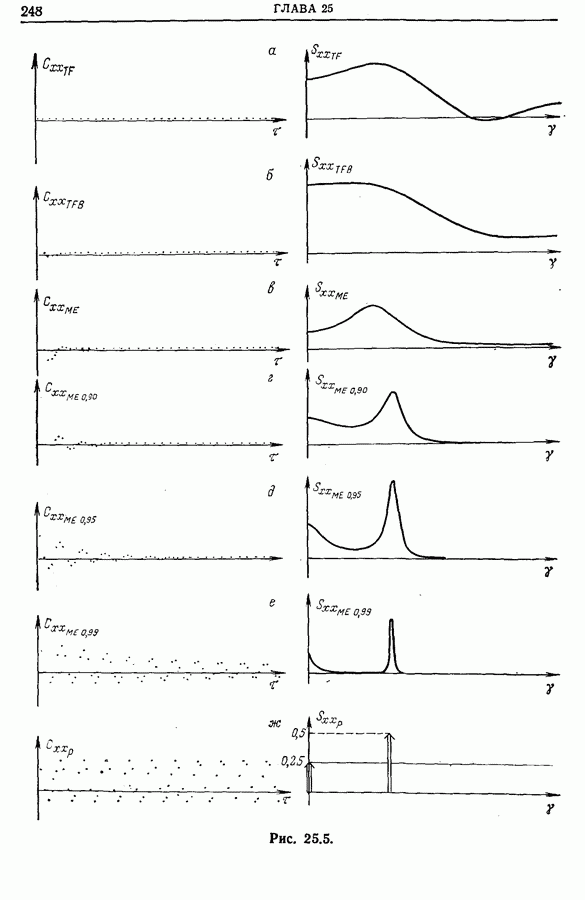
- 25.7. Смешанные методы
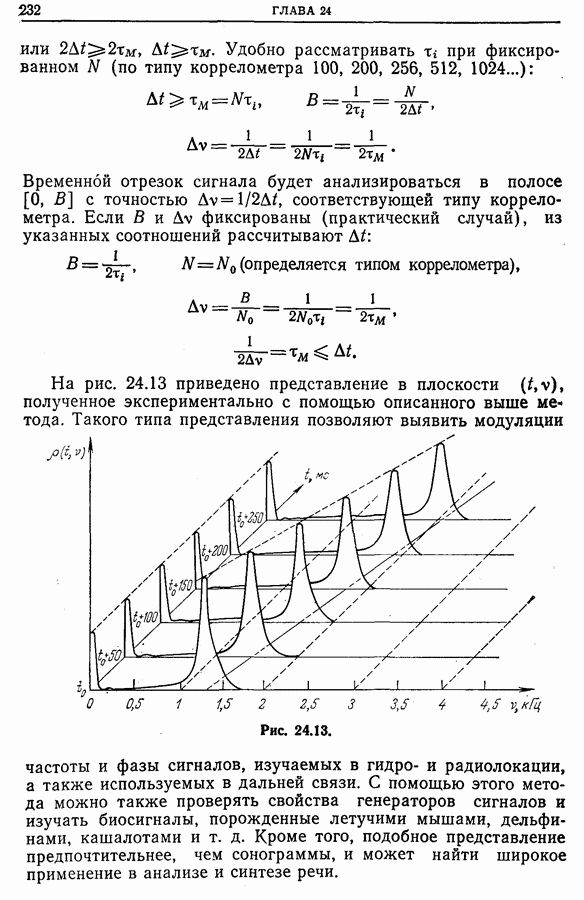
- 25.8. Заключение