| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
24.5. Другие определения частотно-временного представления
Определение по Рихачеку.
Приведем вкратце результаты Рихачека [12], используя применяемые на практике вещественные сигналы. Имея выражение взаимно-корреляционной функции двух сигналов  [выражение (11.37)]:
[выражение (11.37)]:

введем определение .энергии взаимодействия х и у с помощью соотношения

Рассмотрим теперь  как сигнал на выходе фильтра
как сигнал на выходе фильтра  с полосой пропускания
с полосой пропускания  вблизи частоты
вблизи частоты  — сигнал на входе). Тогда
— сигнал на входе). Тогда

Величина  представляющая собой энергию взаимодействия сигнала
представляющая собой энергию взаимодействия сигнала  и его отклика на выходе фильтра в интервале
и его отклика на выходе фильтра в интервале  и полосе
и полосе  отражает модуляцию частоты и фазы сигнала
отражает модуляцию частоты и фазы сигнала 
Рихачек [12] показал, что в пределе  можно получить функцию
можно получить функцию  которая представляет собой плотность энергии в плоскости
которая представляет собой плотность энергии в плоскости 

Следовательно, согласно выражению (23.20),

и

Таким образом, функция  позволяет определить представление в плоскости «время — частота».
позволяет определить представление в плоскости «время — частота».
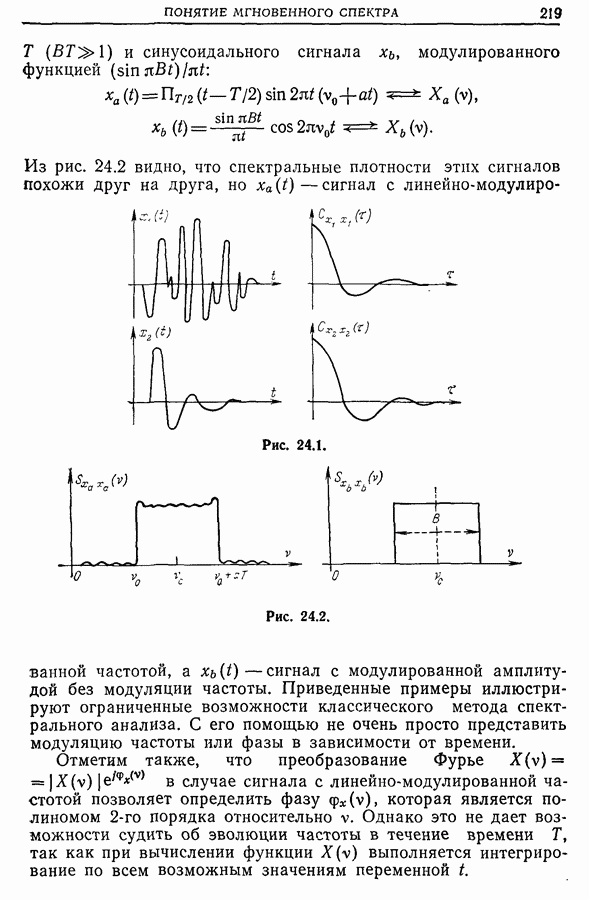
Новая функция  представляет интерес для изучения широкополосных или сильно модулированных сигналов типа
представляет интерес для изучения широкополосных или сильно модулированных сигналов типа

где  — действительная функция (рис. 24.7). Если произведение ВТ (В — спектральная полоса, Т — длительность сигнала) велико по сравнению с 1, величина
— действительная функция (рис. 24.7). Если произведение ВТ (В — спектральная полоса, Т — длительность сигнала) велико по сравнению с 1, величина  сосредоточена вблизи
сосредоточена вблизи
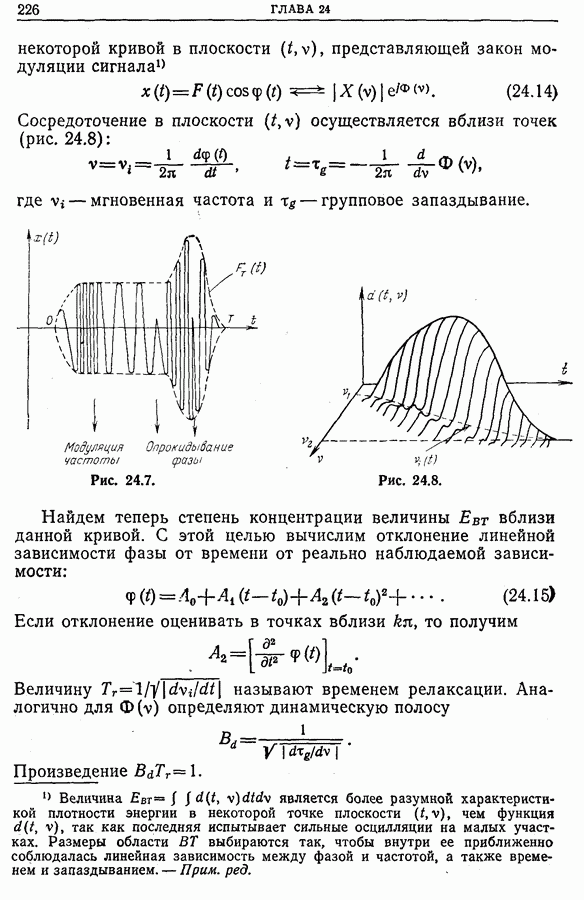
некоторой кривой в плоскости  представляющей закон модуляции сигнала
представляющей закон модуляции сигнала

Сосредоточение в плоскости  осуществляется вблизи точек (рис. 24.8):
осуществляется вблизи точек (рис. 24.8):

где  — мгновенная частота и
— мгновенная частота и  — групповое запаздывание.
— групповое запаздывание.

Рис. 24.7.

Рис. 24.8.
Найдем теперь степень концентрации величины  вблизи данной кривой. С этой целью вычислим отклонение линейной зависимости фазы от времени от реально наблюдаемой зависимости:
вблизи данной кривой. С этой целью вычислим отклонение линейной зависимости фазы от времени от реально наблюдаемой зависимости:

Если отклонение оценивать в точках вблизи  то получим
то получим

Величину  называют временем релаксации. Аналогично для
называют временем релаксации. Аналогично для  определяют динамическую полосу
определяют динамическую полосу

Произведение 
Последнее выражение находится в согласии с соотношением неопределенностей в плоскости  Учитывая, что
Учитывая, что  -динамическая полоса (связанная с наклоном кривой модуляции), а
-динамическая полоса (связанная с наклоном кривой модуляции), а  время релаксации, в плоскости
время релаксации, в плоскости  можно изобразить ячейки
можно изобразить ячейки  Рассмотренный случай представляет собой гиперболическую модуляцию частоты (рис. 24.9), где
Рассмотренный случай представляет собой гиперболическую модуляцию частоты (рис. 24.9), где  -некоторая огибающая, определенная на отрезке
-некоторая огибающая, определенная на отрезке  фаза, модулированная по времени.
фаза, модулированная по времени.

Рис. 24.9.
Определение по Пейджу [15].
Пейдж определил представление в плоскости  рассматривая сигнал
рассматривая сигнал  в интервале времени
в интервале времени  Он обнаружил, что с точки зрения акустики именно короткий временной отрезок передает информацию такому приемнику, как наше ухо. Чтобы определить
Он обнаружил, что с точки зрения акустики именно короткий временной отрезок передает информацию такому приемнику, как наше ухо. Чтобы определить  Пейдж использовал оператор сечения
Пейдж использовал оператор сечения  для момента
для момента  где
где

Отсюда

Величина  является мгновенной автокорреляционной функцией, определенной Фано [14]. Имеем
является мгновенной автокорреляционной функцией, определенной Фано [14]. Имеем

Функцию  можно представить в следующем виде:
можно представить в следующем виде:

Двумерное преобразование Фурье функции  можно представить с помощью функции неопределенности сигнала
можно представить с помощью функции неопределенности сигнала  в виде
в виде

Итак, несмотря на множество определений, можно выделить один существенный момент: энергетическое представление в плоскости «время — частота» связано с функцией неопределенности с помощью преобразования Фурье. Существуют также другие определения, в основе которых лежит определение Пейджа и которые используют понятие оператора сечения [8].
Итак, если назвать  фазой или аргументом косинуса и если по аналогии с классическим случаем постоянной частоты положить
фазой или аргументом косинуса и если по аналогии с классическим случаем постоянной частоты положить

где  - мгновенная частота», то
- мгновенная частота», то

В случае сигнала типа

величину  можно определить либо так, как это указано выше, либо по точкам пересечения 4 функции
можно определить либо так, как это указано выше, либо по точкам пересечения 4 функции  с осью времени:
с осью времени:

Для синусоидального сигнала два определения функции  не соответствуют друг другу [8]. Это показывает их относительный характер, обусловленный сопряженностью параметров
не соответствуют друг другу [8]. Это показывает их относительный характер, обусловленный сопряженностью параметров  и
и  связанных соотношением неопределенностей. Однако независимо от определения физический смысл функции
связанных соотношением неопределенностей. Однако независимо от определения физический смысл функции  состоит в том, что последняя отражает спектральный и временной вклады в процесс на отрезке
состоит в том, что последняя отражает спектральный и временной вклады в процесс на отрезке  в полосе
в полосе  Показано, что в случае сигнала с модулированной частотой или фазой при
Показано, что в случае сигнала с модулированной частотой или фазой при  можно проследить изменение
можно проследить изменение  со временем.
со временем.
Отметим, что были также введены другие понятия, которые связаны с функцией неопределенности. Эта функция дает возможность выразить квадратичное отклонение между  (с точностью до
(с точностью до  если х — вещественный сигнал. С ее помощью можно получить закон модуляции частоты через параметры
если х — вещественный сигнал. С ее помощью можно получить закон модуляции частоты через параметры  в более удобной форме, чем с помощью функции
в более удобной форме, чем с помощью функции  зависящей лишь от одного параметра
зависящей лишь от одного параметра  . Бонне и Гарампон определили понятия мгновенного спектра и частотно-временного представления с помощью мощного
. Бонне и Гарампон определили понятия мгновенного спектра и частотно-временного представления с помощью мощного
формализма и получили простые соотношения с функцией неопределенности без каких бы то ни было предположений о спектральной природе сигнала  Кроме того, функция неопределенности дает нам метод представления модуляций фазы к частоты сигнала по оценкам характеристик отфильтрованного сигнала. Этим объясняется возрастающее значение функции неопределенности в анализе и синтезе сигналов.
Кроме того, функция неопределенности дает нам метод представления модуляций фазы к частоты сигнала по оценкам характеристик отфильтрованного сигнала. Этим объясняется возрастающее значение функции неопределенности в анализе и синтезе сигналов.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 15. СИНХРОННОЕ ДЕТЕКТИРОВАНИЕ
- 15.2. Схема метода
- 15.3. Теория синхронного детектирования
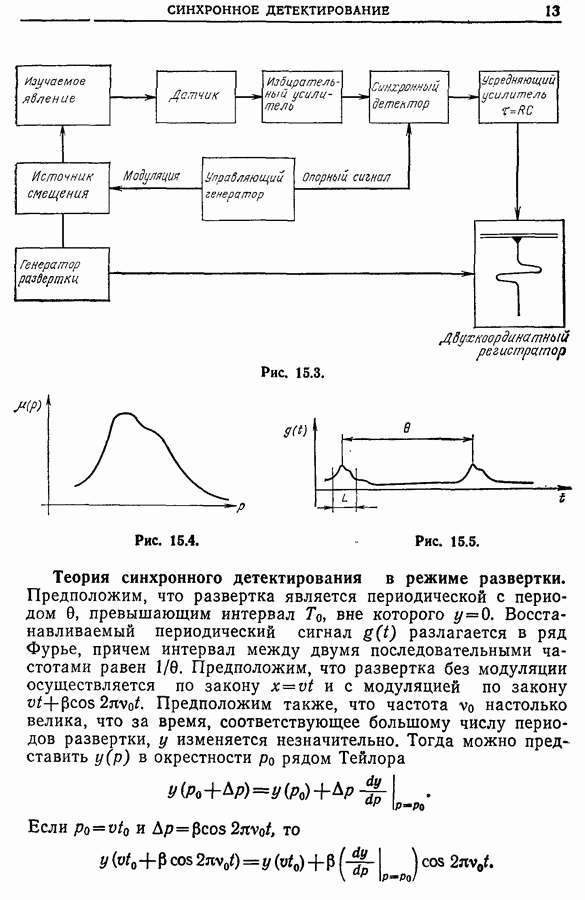
- 15.4. Синхронное детектирование в режиме развертки
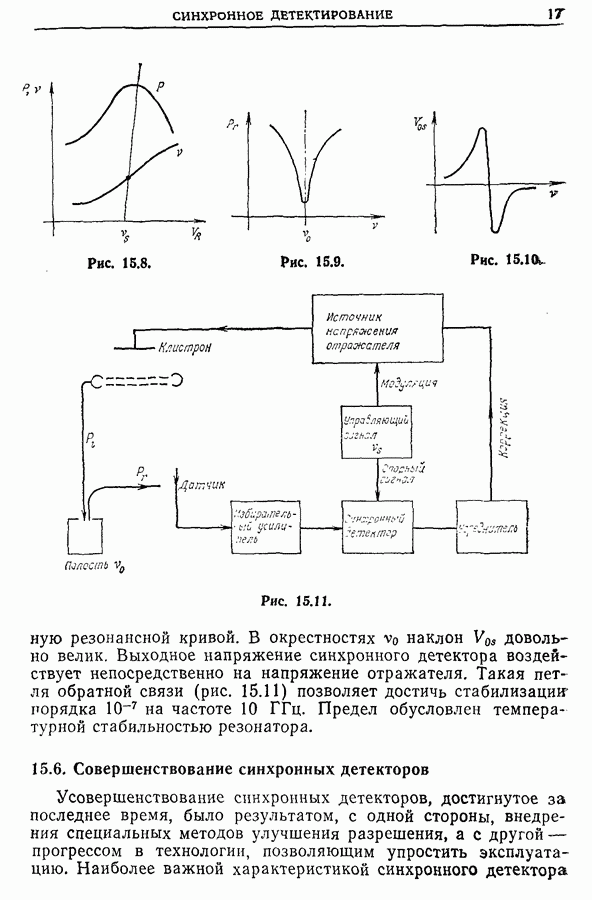
- 15.5. Примеры применения синхронных детекторов
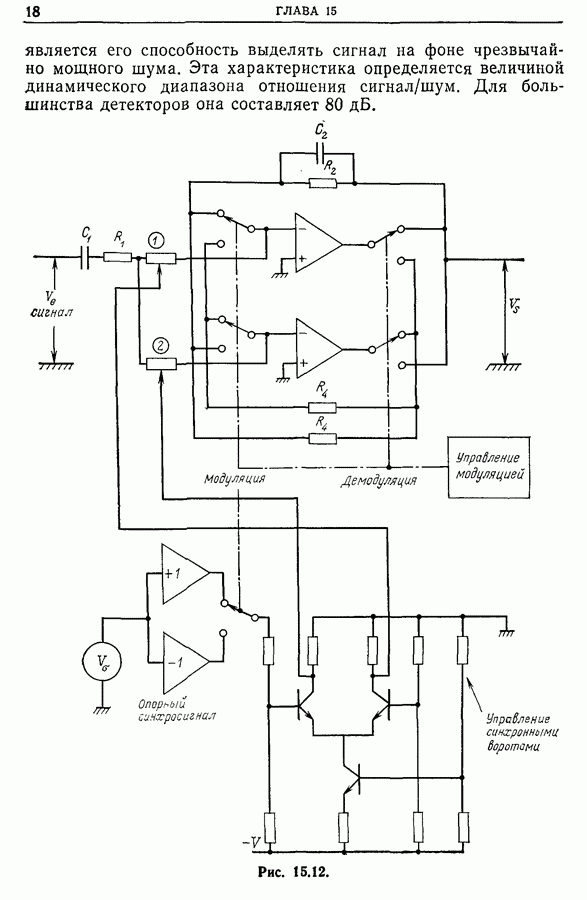
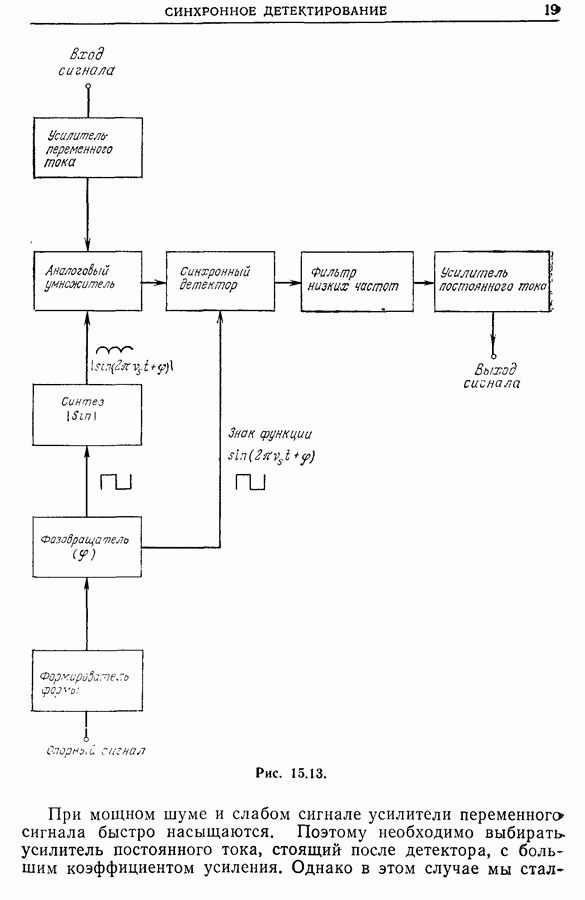
- 15.6. Совершенствование синхронных детекторов
- Глава 16. ИСПОЛЬЗОВАНИЕ МНОГОКАНАЛЬНЫХ АНАЛИЗАТОРОВ ПРИ СТАТИЧЕСКОЙ ОБРАБОТКЕ ИЗМЕРЕНИЙ
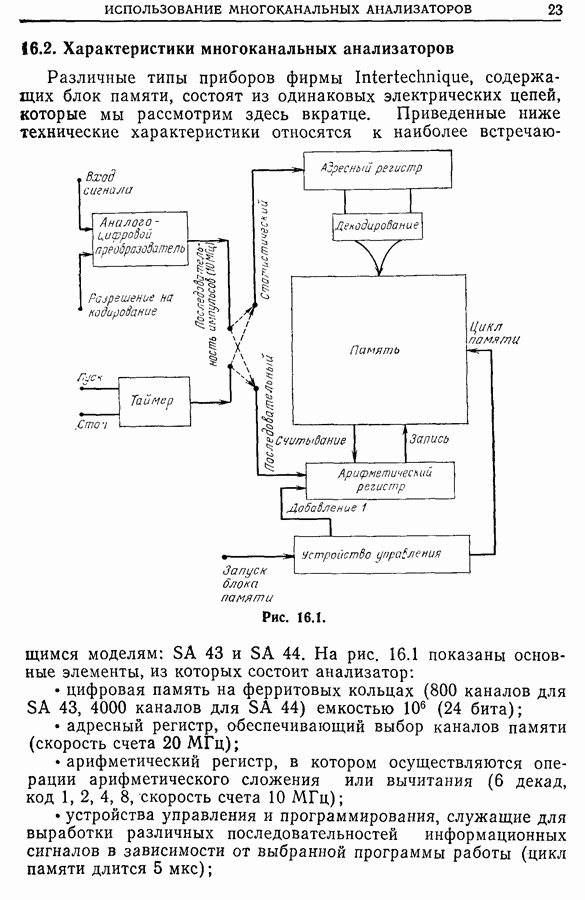
- 16.2. Характеристики многоканальных анализаторов
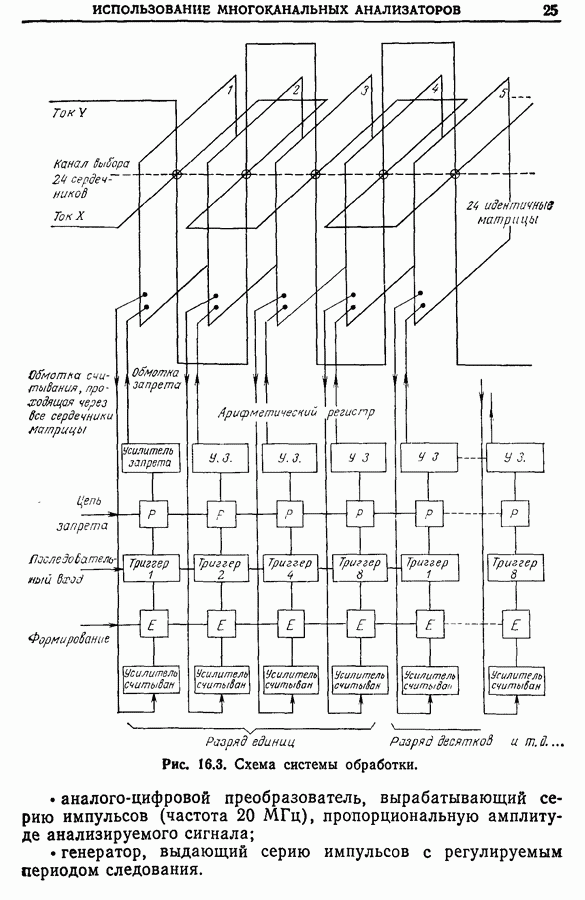
- 16.3. Схема системы обработки
- 16.4. Примеры применения
- Глава 17. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ
- 17.2. Частный случай белого шума. Согласованный фильтр
- 17.3. Согласованная фильтрация и корреляция Корреляция.
- 17.4. Реализация согласованных фильтров методом «взвешивания»
- 17.5. Рекурсивная согласованная фильтрация [7]
- 17.6. Применения метода согласованной фильтрации
- Глава 18. ОСНОВНЫЕ ТИПЫ ЭЛЕКТРОННЫХ КОРРЕЛОМЕТРОВ
- 18.2. Одноканальный коррелометр
- 18.3. Автоматические коррелометры
- 18.4. Автоматические коррелометры на линии с исследуемым сигналом
- 18.5. Автоматические коррелометры реального времени (или мультикоррелометры)
- 18.6. Коррелометры на больших интегральных схемах
- 18.7. Коррелометры реального времени для высокочастотных сигналов
- 18.8 Развитие коррелометров
- 18.9. Приборы с зарядовой связью [11]
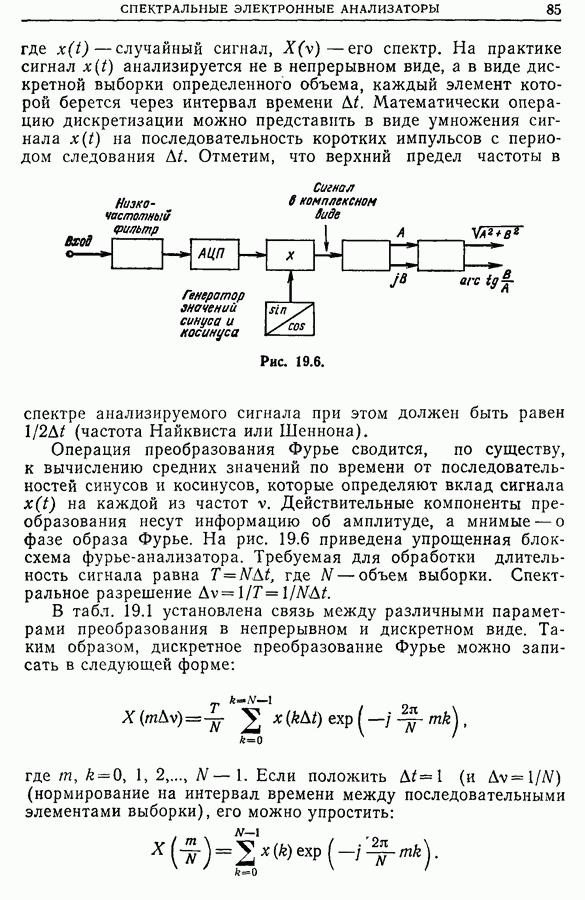
- Глава 19. СПЕКТРАЛЬНЫЕ ЭЛЕКТРОННЫЕ АНАЛИЗАТОРЫ
- 19.2. Спектральные анализаторы, основанные на методе непосредственного преобразования Фурье
- 19.3. Применения анализаторов на основе метода БПФ
- Глава 20. ОПТИЧЕСКИЙ СПЕКТРАЛЬНЫЙ АНАЛИЗ
- 20.2. Упрощения, связанные с отбрасыванием фазы
- 20.3. Эффект виньетирования
- 20.4. Двумерный анализ
- 20.5. Точечный монохроматический источник
- 20.6. Электрооптическое преобразование сигнала
- 20.7. Устройства отображения на жидких кристаллах
- 20.8. Ограничения устройств отображения
- 20.9. Модулятор на основе эффекта Покельса (PROM)
- 20.10. Трубки Титус и Фототитус
- 20.11. Другие электрооптические кристаллы
- 20.12. Спектральный анализ и интегральная оптика
- 20.13. Взаимные спектры
- Глава 21. НЕКОТОРЫЕ ПРАКТИЧЕСКИЕ ПРИМЕНЕНИЯ МЕТОДОВ ОБРАБОТКИ СИГНАЛОВ
- 21.2. Исследование ядерных сред
- 21.3. Ядерный магнитный резонанс (ЯМР) с возбуждением случайным сигналом
- 21.4. Идентификация процессов. Измерение импульсных откликов и передаточных функций
- 21.5. Спектральный анализ собственных колебаний бетонных плит
- 21.6. Исследование флюктуаций активной мощности электрической сети с помощью спектрального анализа
- 21.7. Изучение турбулентности
- 21.8. Применения в геофизике
- 21.9. Применения в астрофизике
- 21.10. Применения в астрономии и радиоастрономии
- 21.11. Применения в биологии и медицине
- 21.12. Применения в акустике
- 21.13. Исследование процессов намагничивания ферромагнетиков
- 21.14. Применения новых методов обработки сигналов
- 21.15. Заключение
- Глава 22. ПРИМЕНЕНИЕ МЕТОДОВ ОБРАБОТКИ СИГНАЛОВ ДЛЯ АНАЛИЗА ВИБРАЦИЙ РОТАЦИОННЫХ МАШИНА
- 22.2. Анализ поведения системы «ротационная машина — конструкция»
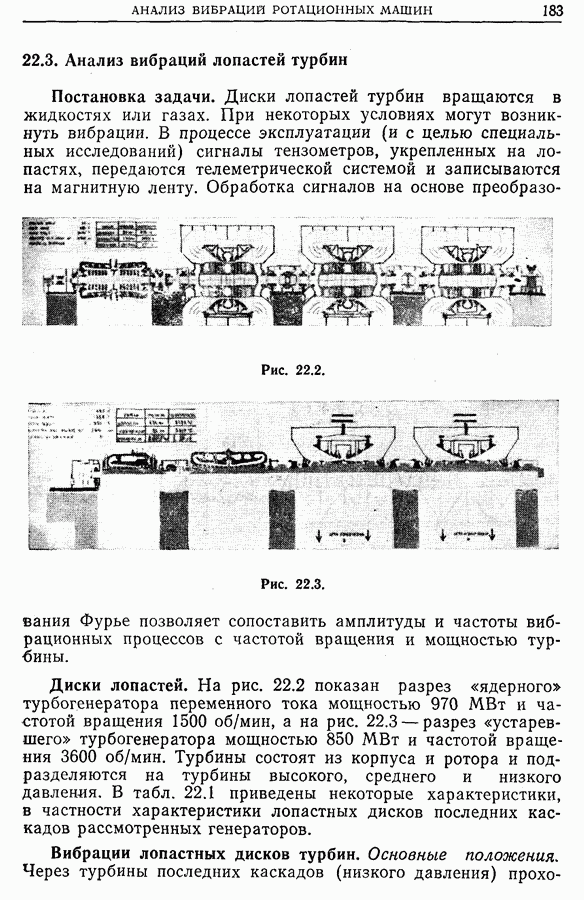
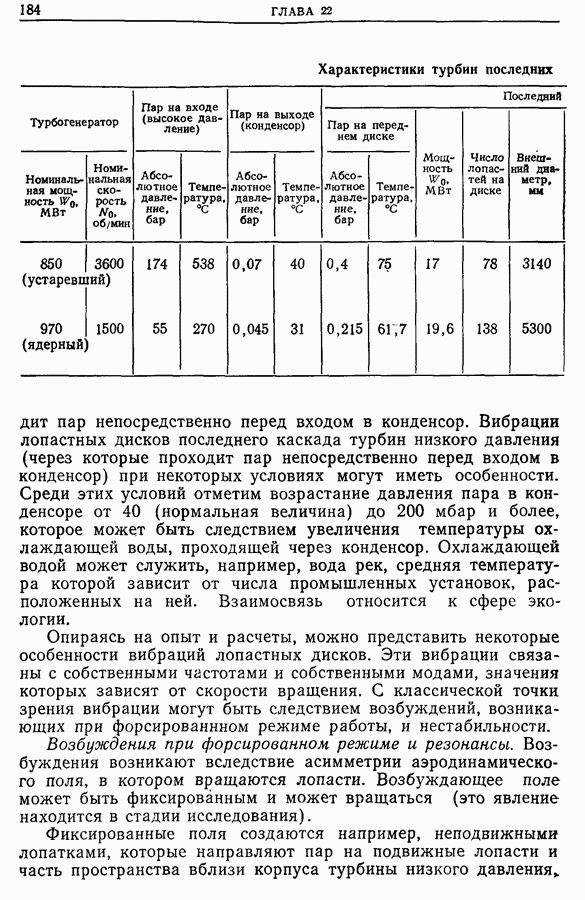
- 22.3. Анализ вибраций лопастей турбин
- 22.4. Балансировка ротационных машин
- Глава 23. ФУНКЦИЯ НЕОПРЕДЕЛЕННОСТИ
- 23.2. Временная корреляция. Временной сдвиг
- 23.3. Частотная корреляция. Частотный сдвиг
- 23.4. Временной и частотный сдвиги. Функция неопределенности
- 23.5. Функция неопределенности Вудворда
- 23.6. Взаимная функция неопределенности
- 23.7. Некоторые свойства функции неопределенности
- 23.8. Представление функций неопределенности
- 23.9. Примеры функций неопределенности
- 23.10. Применение функции неопределенности
- 23.11. Применение функций неопределенности для описания линейных неоднородных во времени систем. Обобщение понятия передаточной функции. Функция диффузии (функция рассеивания)
- 23.12. Генерация тестового сигнала
- 23.13. Прибор для измерения функции неопределенности в режиме реального времени
- Глава 24. ПОНЯТИЕ МГНОВЕННОГО СПЕКТРА ИЛИ ЧАСТОТНО-ВРЕМЕННОГО ПРЕДСТАВЛЕНИЯ В АНАЛИЗЕ И СИНТЕЗЕ СИГНАЛОВ
- 24.2. Примеры спектрального анализа модулированных и немодулированных сигналов
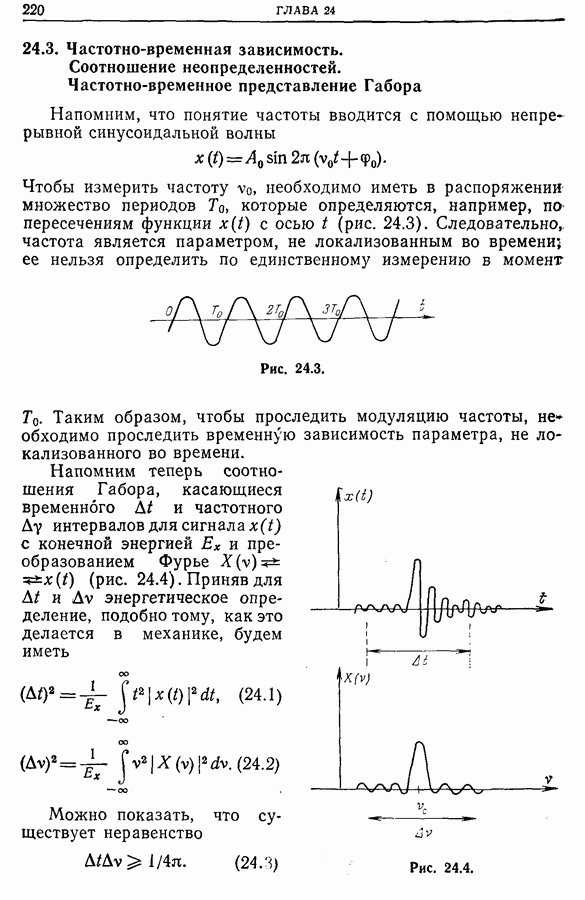
- 24.3. Частотно-временная зависимость. Соотношение неопределенностей. Частотно-временное представление Габора
- 24.4. Представление [t, v] по Бонне. Мгновенный спектр мощности по Биллю. Функция неопределенности
- 24.5. Другие определения частотно-временного представления
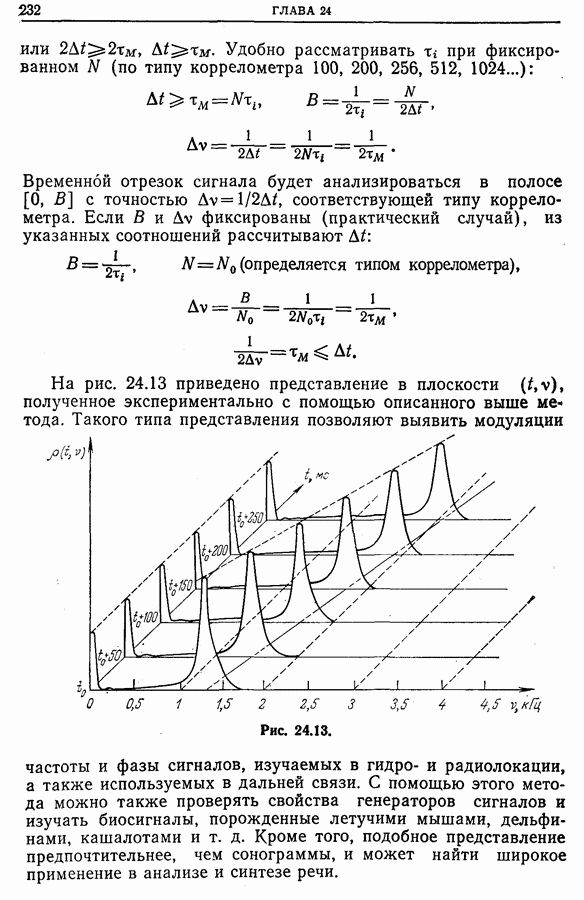
- 24.6. Измерение мгновенных спектров
- 24.7. Обобщение понятия мгновенного спектра мощности на случайные локально-стационарные сигналы. Функция структуры. Функция диффузии
- 24.8 Восстановление сигнала x(t) по известной функции
- 24.9. Заключение
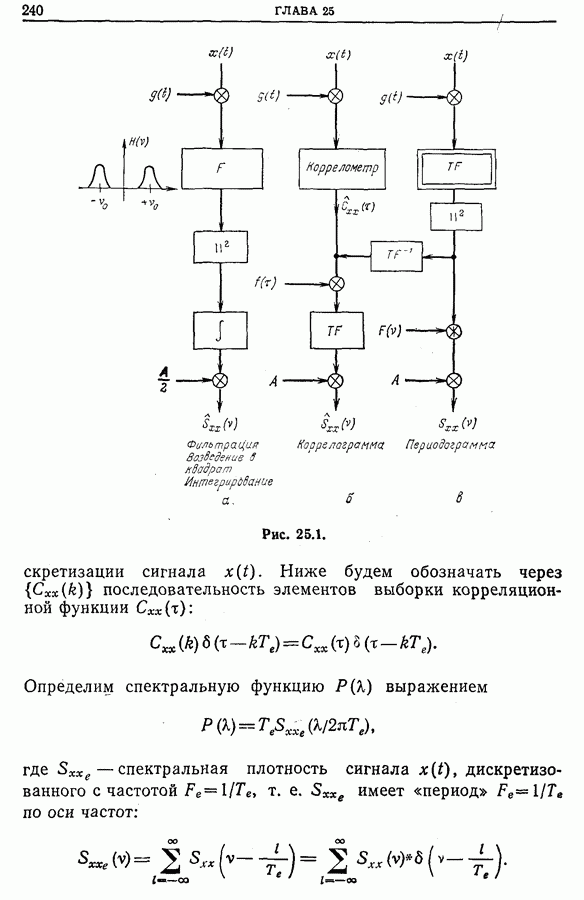
- Глава 25. НОВЫЕ МЕТОДЫ СПЕКТРАЛЬНОГО АНАЛИЗА
- 25.2. Проблемы, обусловленные дискретизацией корреляционной функции
- 25.3. Постановка проблемы получения спектральной функции из конечного числа значений автокорреляционной функции
- 25.4. Классический метод, основанный на преобразовании Фурье корреляционной функции
- 25.5. Метод максимума энтропии или метод авторегрессионной модели
- 25.6. Метод Писаренко
- 25.7. Смешанные методы
- 25.8. Заключение