| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.2.2. Сложение двух когерентных волн
Обобщим теперь предыдущее рассмотрение на случай, который является более реальным, т. е. экспериментально реализуемым. Для этого скажем несколько слов о том, как распространяется свет. Оптическое поле  распространяется в соответствии с волновым уравнением
распространяется в соответствии с волновым уравнением

где  вторая частная производная по пространственным координатам, а с — скорость света. В случае когерентного света можно воспользоваться выражением (4); подставляя его в уравнение (17а), мы получим волновое уравнение (уравнение Гельмгольца), описывающее распространение комплексной амплитуды:
вторая частная производная по пространственным координатам, а с — скорость света. В случае когерентного света можно воспользоваться выражением (4); подставляя его в уравнение (17а), мы получим волновое уравнение (уравнение Гельмгольца), описывающее распространение комплексной амплитуды:

где  длина волны света. Существенную роль играют следующие решения этого волнового уравнения:
длина волны света. Существенную роль играют следующие решения этого волнового уравнения:
1) плоская волна, распространяющаяся вдоль оси 

где А — постоянная;
2) сходящаяся (отрицательная экспонента) и расходящаяся (положительная экспонента) сферические волны

где  радиус сферической волны.
радиус сферической волны.
Идеальный точечный источник излучает расходящуюся сферическую волну; расположенный на бесконечности, он будет давать плоскую волну. В качестве первого примера рассмотрим сложение двух плоских волн.
2.2.2.1. Сложение двух плоских волн
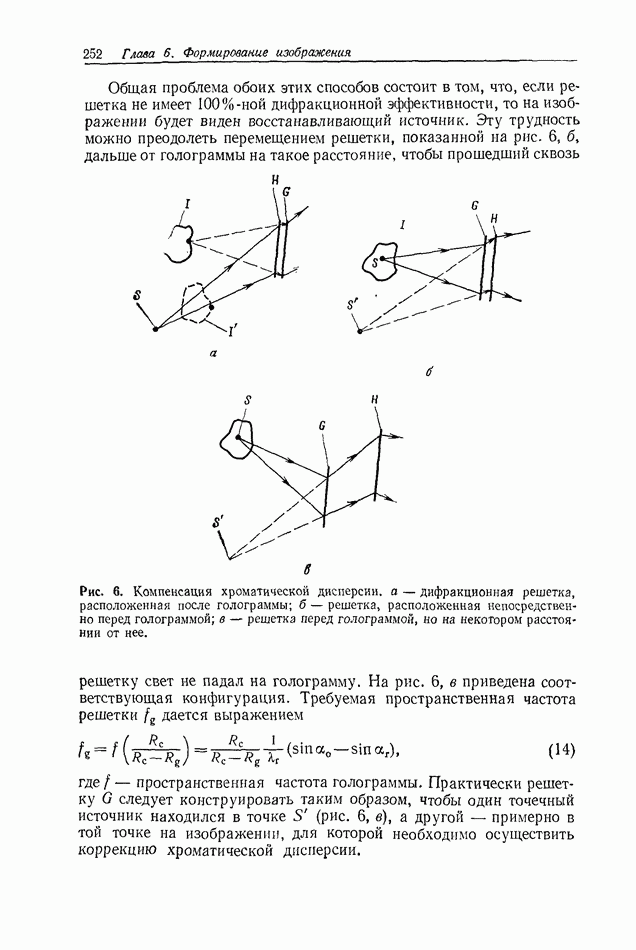
Мы будем рассматривать два идеальных точечных источника одинаковой интенсивности, расположенных на бесконечности и создающих две плоские волны, сходящиеся под углом 20 друг к другу. Иными словами, два плоских волновых фронта образуют углы ±0 относительно плоскости, в которой мы будем записывать интенсивность, создаваемую в результате их взаимодействия (рис. 1).

Рис. 1. Сложение двух плоских волн, расположенных симметрично относительно оптической оси.
Будем предполагать, что в точке  обе эти волны имеют одинаковые фазы. Тогда результирующая комплексная амплитуда запишется в виде [см. выражение (14)]
обе эти волны имеют одинаковые фазы. Тогда результирующая комплексная амплитуда запишется в виде [см. выражение (14)]

а интенсивность  если угол
если угол  мал
мал  дается выражением
дается выражением

где  — постоянная интенсивность, связанная с каждой отдельной плоской волной. Наконец, заметим, что
— постоянная интенсивность, связанная с каждой отдельной плоской волной. Наконец, заметим, что

Для голографических исследований выражение (21) полезно записать в виде выражения (15):

Если делается фотографическая запись интенсивности  и затем негатив освещается когерентной волной
и затем негатив освещается когерентной волной  то второй и третий члены выражения (23) воссоздадут первоначальную и сопряженную ей волну.
то второй и третий члены выражения (23) воссоздадут первоначальную и сопряженную ей волну.
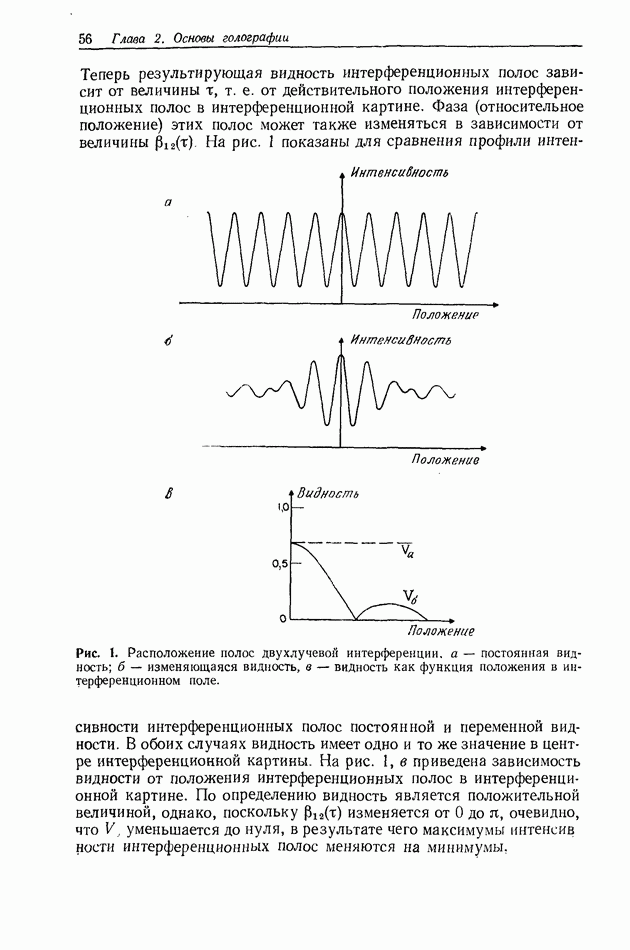
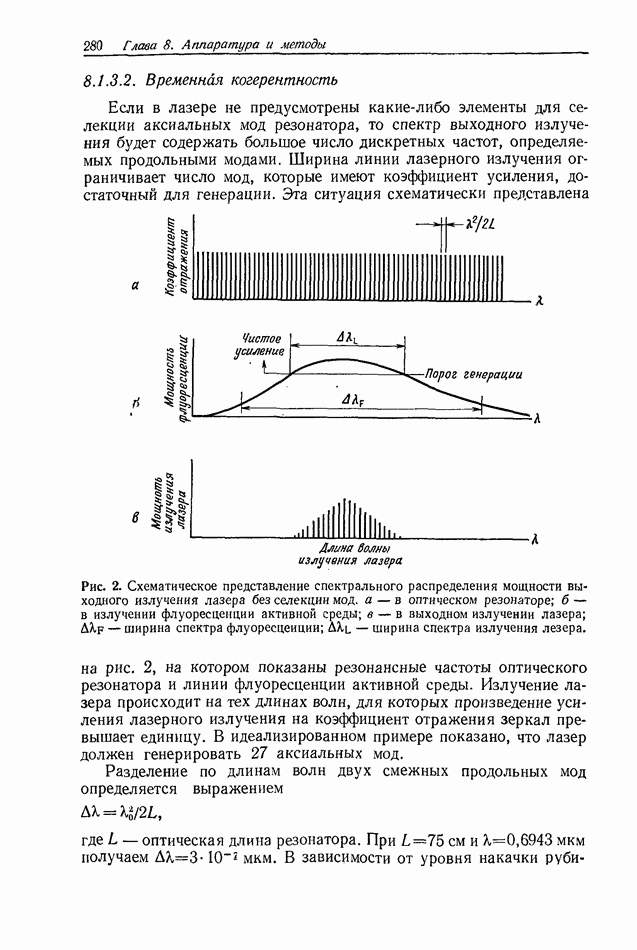
В соответствии с (22) результирующая интенсивность представляет собой серию интерференционных полос с профилем в виде квадрата косинуса, что иллюстрируется на рис. 2, б. Естественно, что в случае, когда две волны некогерентны, складываются их интенсивности, что и дает результирующую интенсивность, равную 21 (рис. 2, а). Наконец, рис. 2, в иллюстрирует частично-когерентное сложение двух пучков (см. разд. 2.3.2, в котором обсуждается этот результат).

Рис. 2. Суммарная нормализованная интенсивность, образуемая двумя волнами, которые складываются некогерентно (а), когерентно (б) и частично-когерентно (в),
2.2.2.2. Сложение цилиндрической (или сферической) и плоской волн
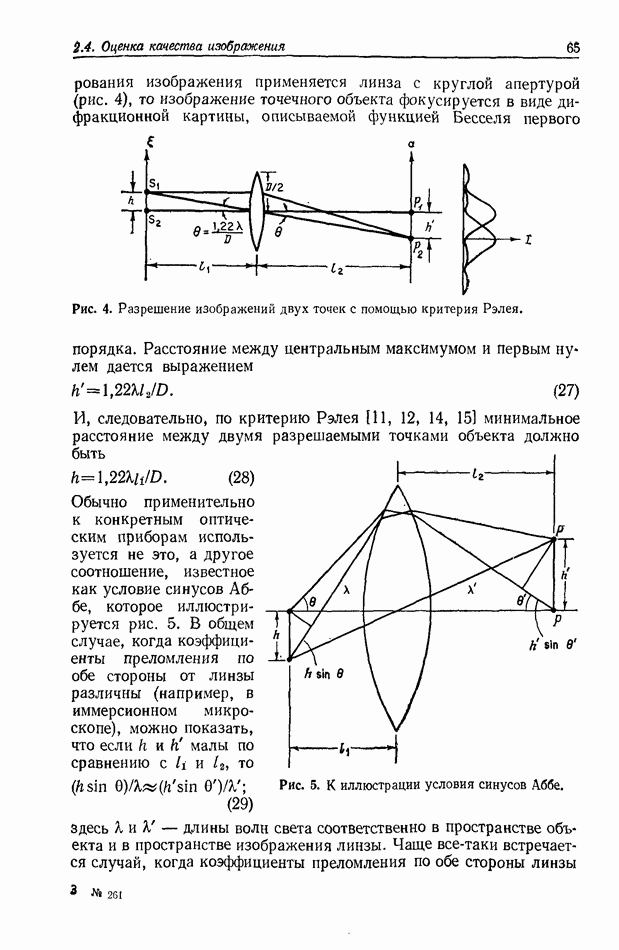
Будем предполагать, что плоская волна распространяется вдоль оптической оси системы (рис. 3) и что в точке  разность хода (а следовательно, и разность фаз) плоской и цилиндрической волн равна нулю. Тогда в предположении малых углов разность хода между этими двумя волнами равна
разность хода (а следовательно, и разность фаз) плоской и цилиндрической волн равна нулю. Тогда в предположении малых углов разность хода между этими двумя волнами равна  где
где  радиус сферической волны. Следовательно, разность фаз равна
радиус сферической волны. Следовательно, разность фаз равна  При этом результирующая амплитуда в плоскости х запишется в виде
При этом результирующая амплитуда в плоскости х запишется в виде

а результирующая интенсивность

или


Рис. 3. Сложение плоской и цилиндрической волн.
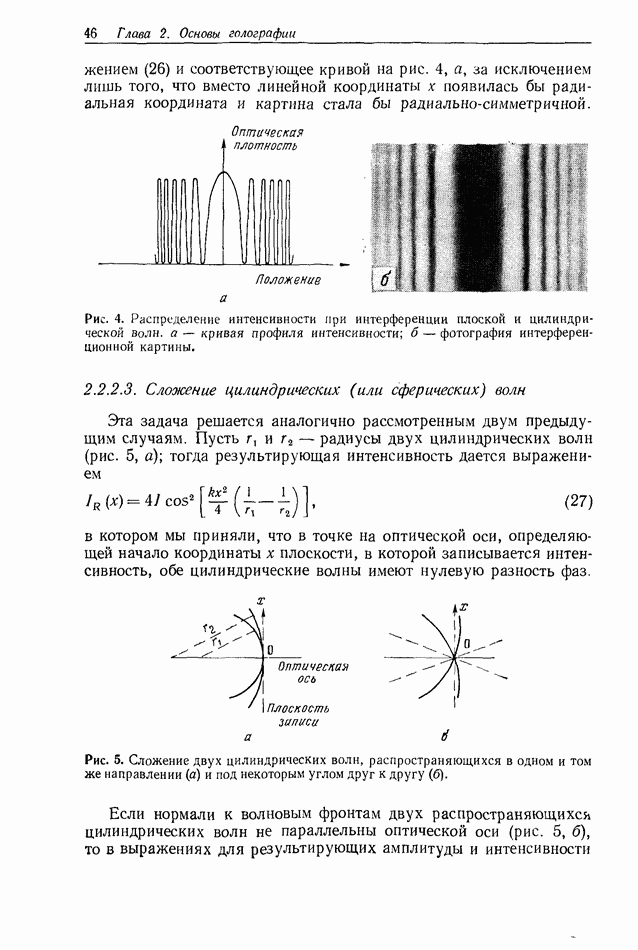
Профиль результирующей интенсивности имеет вид  и представляет собой серию интерференционных полос, причем аргумент косинуса зависит от квадрата пространственной координаты. Это иллюстрируется на рис. 4. Если бы задача решалась для сферической и плоской волн, то мы имели бы решение, описываемое
и представляет собой серию интерференционных полос, причем аргумент косинуса зависит от квадрата пространственной координаты. Это иллюстрируется на рис. 4. Если бы задача решалась для сферической и плоской волн, то мы имели бы решение, описываемое
выражением (26) и соответствующее кривой на рис. 4, а, за исключением лишь того, что вместо линейной координаты  появилась бы радиальная координата и картина стала бы радиально-симметричной.
появилась бы радиальная координата и картина стала бы радиально-симметричной.

Рис. 4. Распределение интенсивности при интерференции плоской и цилиндрической волн, а — кривая профиля интенсивности; б - фотография интерференционной картины.
2.2.2.3. Сложение цилиндрических (или сферических) волн
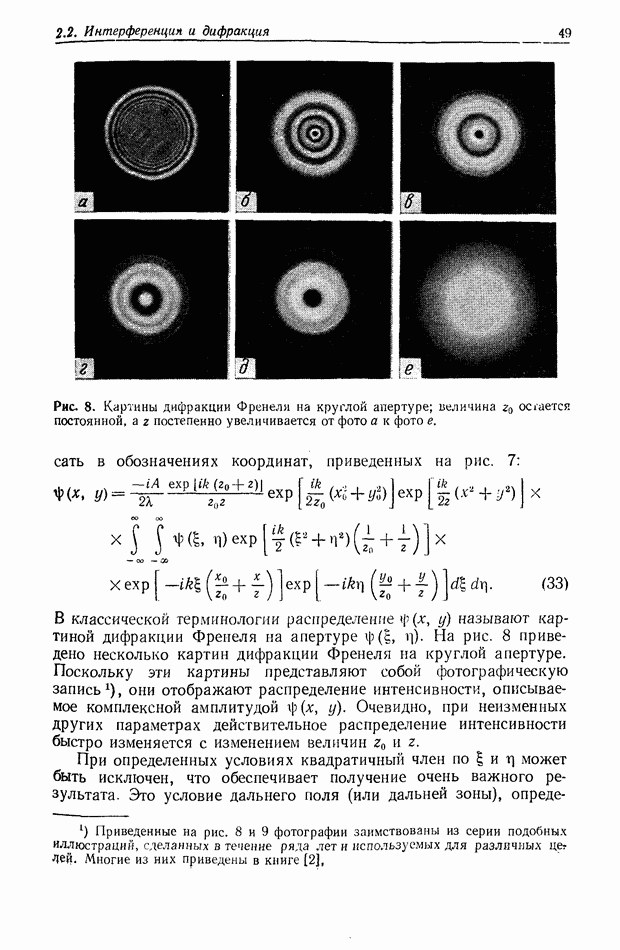
Эта задача решается аналогично рассмотренным двум предыдущим случаям. Пусть  радиусы двух цилиндрических волн (рис. 5, а); тогда результирующая интенсивность дается выражением
радиусы двух цилиндрических волн (рис. 5, а); тогда результирующая интенсивность дается выражением

в котором мы приняли, что в точке на оптической оси, определяющей начало координаты х плоскости, в которой записывается интенсивность, обе цилиндрические волны имеют нулевую разность фаз.

Рис. 5. Сложение двух цилиндрических волн, распространяющихся в одном и том же направлении (а) и под некоторым углом друг к другу 
Если нормали к волновым фронтам двух распространяющихся цилиндрических волн не параллельны оптической оси (рис. 5, б), то в выражениях для результирующих амплитуды и интенсивности
появляются линейный и квадратичный члены относительно х:

и

Последнее выражение представляет собой комбинацию выражений (22) и (27).
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие
- Глава 1. ВВЕДЕНИЕ
- Глава 2. ОСНОВЫ ГОЛОГРАФИИ
- 2.1.1. Преобразование Фурье
- 2.1.2. Преобразование Лапласа
- 2.1.3. Преобразование Фурье — Бесселя
- 2.1.4. Преобразование Френеля
- 2.1.5. Преобразование Гильберта
- 2.1.6. Преобразование Меллина
- 2.1.7. Преобразование Абеля
- 2.2. ИНТЕРФЕРЕНЦИЯ И ДИФРАКЦИЯ
- 2.2.2. Сложение двух когерентных волн
- 2.2.3. Интерференция двух пучков
- 2.2.4. Распространение когерентного света — дифракция Френеля и Фраунгофера
- 2.3. ЧАСТИЧНО-КОГЕРЕНТНЫЙ СВЕТ
- 2.3.1. Сложение двух частично-когерентных квазимонохроматических полей
- 2.3.2. Интерференция двух частично-когерентных квазимонохроматических пучков
- 2.3.3. Интерференция двух частично-когерентных полихроматических пучков
- 2.3.4. Пространственная и временная когерентность
- 2.3.5. Дифракция и интерференция частично-когерентного света
- 2.4. ОЦЕНКА КАЧЕСТВА ИЗОБРАЖЕНИЯ
- 2.4.2. Формирование изображения в когерентном и некогерентном свете
- 2.4.3. Предел разрешения
- 2.4.4. Аберрации
- 2.4.5. Голографические изображения
- 2.4.6. Голографические аберрации
- 2.4.7. Отношение сигнал/шум
- 2.4.8. Заключение
- 2.5. ТЕОРИЯ СВЯЗИ
- 2.5.2. Теорема выборки (или теорема отсчетов)
- 2.5.3. Статистическое описание случайных сигналов
- 2.5.4. Выводы
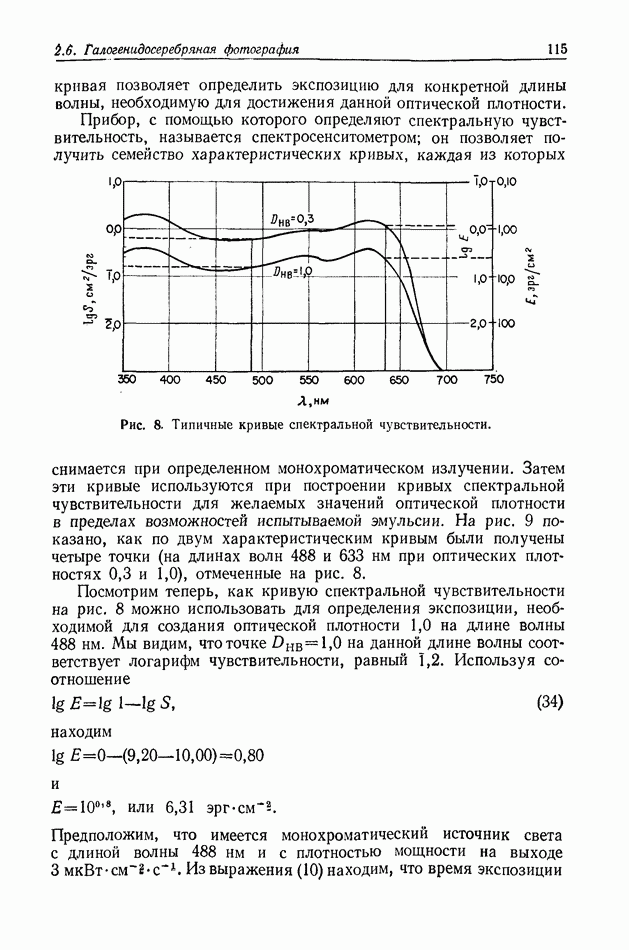
- 2.6. ГАЛОГЕНИДОСЕРЕБРЯНАЯ ФОТОГРАФИЯ
- 2.6.2. Галогенидосеребряный фотографический процесс
- 2.6.3. Сенситометрия
- 2.6.4. Денситометрия
- 2.6.5. Взаимозаместимость
- 2.6.6. Характеристики изображения
- 2.6.7. Влияние изменения окружающей среды на стабильность пространственных параметров слоя
- 2.6.8. Характеристики сохраняемости фотоматериалов
- 2.6.9. Словарь терминов
- Глава 3. КЛАССИФИКАЦИЯ ГОЛОГРАММ
- 3.2. РЕГИСТРИРУЮЩИЕ СРЕДЫ И ИХ ПРИМЕНЕНИЕ
- 3.3. РЕГИСТРИРУЕМЫЕ ПАРАМЕТРЫ ОБЪЕКТНОЙ ВОЛНЫ
- 3.4. МОДУЛИРУЕМЫЕ ПАРАМЕТРЫ
- 3.5. КОНФИГУРАЦИЯ
- 3.6. СВОЙСТВА ИСТОЧНИКОВ
- 3.7. ОПИСАНИЕ ГОЛОГРАММЫ
- Глава 4. ОСНОВНЫЕ ТИПЫ ГОЛОГРАММ
- 4.1. ГОЛОГРАФИЯ ФРЕНЕЛЯ
- 4.2. ГОЛОГРАММЫ ФРАУНГОФЕРА
- 4.3. ГОЛОГРАФИЯ ФУРЬЕ
- 4.3.4. Свойства голограмм Фурье
- Глава 5. РАЗЛИЧНЫЕ ВИДЫ ГОЛОГРАММ
- 5.1. ОТРАЖАТЕЛЬНЫЕ ГОЛОГРАММЫ
- 5.2. МУЛЬТИПЛЕКСНЫЕ ГОЛОГРАММЫ
- 5.3. ЦВЕТНЫЕ ГОЛОГРАММЫ
- 5.4. ПОЛЯРИЗАЦИОННЫЕ ГОЛОГРАММЫ
- 5.5. СИНТЕЗИРОВАННЫЕ ГОЛОГРАММЫ
- 5.6. ГОЛОГРАММЫ С ЛОКАЛЬНЫМ ОПОРНЫМ ПУЧКОМ
- Глава 6. ФОРМИРОВАНИЕ ИЗОБРАЖЕНИЯ
- 6.1. ФОРМИРОВАНИЕ ИЗОБРАЖЕНИЯ В КОГЕРЕНТНОМ СВЕТЕ
- 6.2. ФОРМИРОВАНИЕ ИЗОБРАЖЕНИЯ В ЧАСТИЧНО-КОГЕРЕНТНОМ СВЕТЕ
- 6.3. ОЦЕНКА ЯРКОСТИ ВОССТАНОВЛЕННОГО ИЗОБРАЖЕНИЯ
- Глава 7. КАРДИНАЛЬНЫЕ ТОЧКИ И ГЛАВНЫЕ ЛУЧИ В ГОЛОГРАФИИ
- 7.2. ГОЛОГРАФИЧЕСКИЕ УРАВНЕНИЯ ОПТИЧЕСКИХ ЛУЧЕЙ
- 7.3. ГЛАВНЫЕ ТОЧКИ ГОЛОГРАММ
- 7.4. КАРДИНАЛЬНЫЕ ТОЧКИ ГОЛОГРАММЫ
- 7.5. УРАВНЕНИЯ СОПРЯЖЕНИЯ
- 7.6. ПРИЛОЖЕНИЯ К РАЗЛИЧНЫМ ТИПАМ ГОЛОГРАММ
- Глава 8. АППАРАТУРА И МЕТОДЫ
- 8.1. ТВЕРДОТЕЛЬНЫЕ ЛАЗЕРЫ
- 8.1.2. Рубиновый и Nd:YAG-лазеры
- 8.1.3. Главные конструктивные характеристики лазеров для голографии
- 8.2. ГАЗОВЫЕ ЛАЗЕРЫ
- 8.2.2. Когерентные свойства газовых лазеров
- 8.2.3. Когерентные свойства коммерческих лазеров
- 8.2.4. Диапазон длин волн выходного излучения газовых лазеров
- 8.2.5. Диапазон мощностей выходного излучения
- 8.2.6. Срок службы и стоимость
- 8.3. РЕГИСТРИРУЮЩИЕ СРЕДЫ
- 8.3.3. Галогенидосеребряные эмульсии
- 8.3.4. Задубленная бихромированная желатина
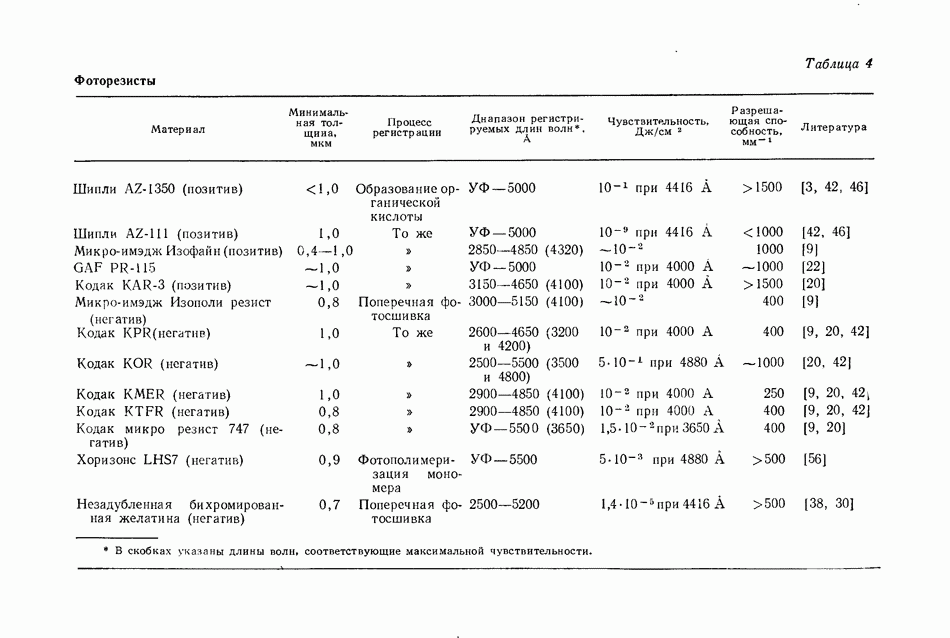
- 8.3.5. Фоторезисты
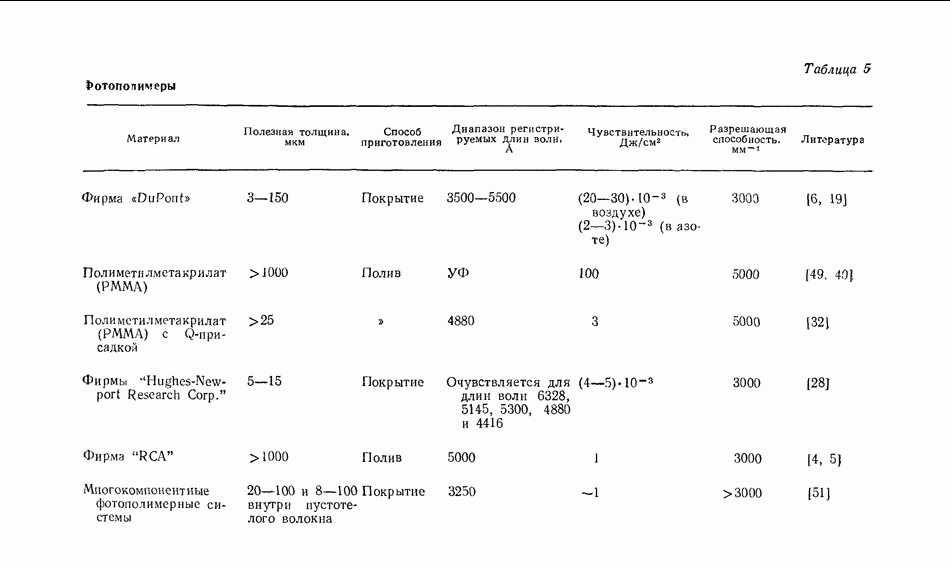
- 8.3.6. Фотополимеры
- 8.3.7. Фотопластики
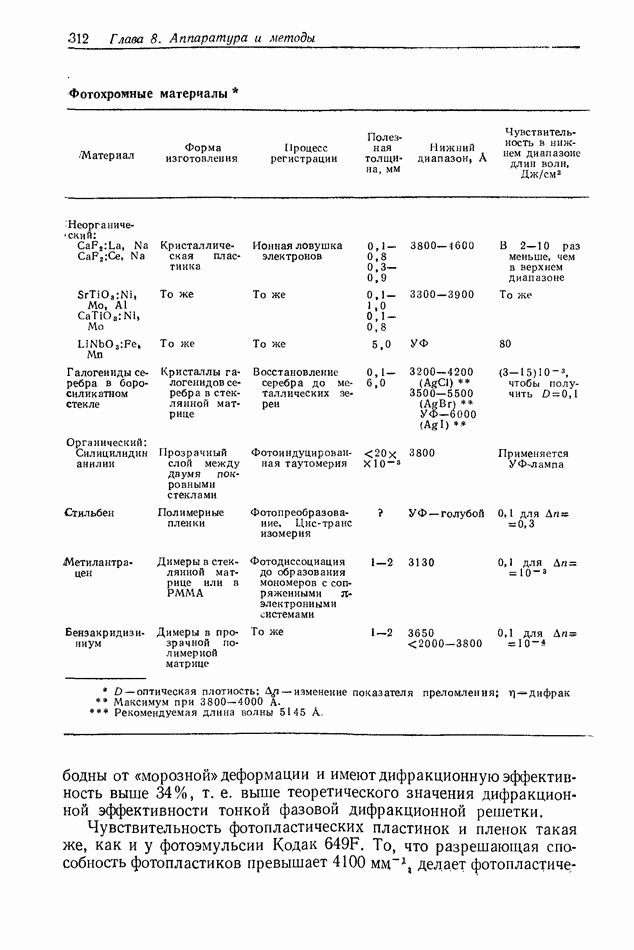
- 8.3.8. Фотохромные материалы
- 8.3.9. Прозрачные электрофотографические пленки
- 8.4. ГОЛОГРАФИЧЕСКИЕ СИСТЕМЫ
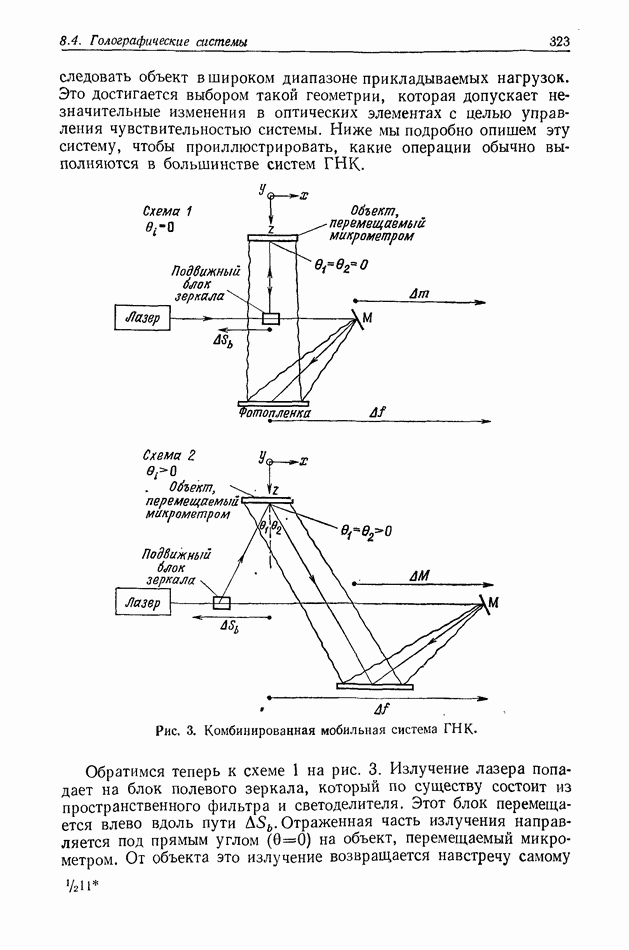
- 8.4.2. Описание комбинированной мобильной установки ГНК; система с переменной чувствительностью
- 8.4.3. Акустооптический голографический неразрушающий контроль
- 8.4.4. Неразрушающий контроль с применением голографии спеклов
- 8.4.5. Голографическая корреляция
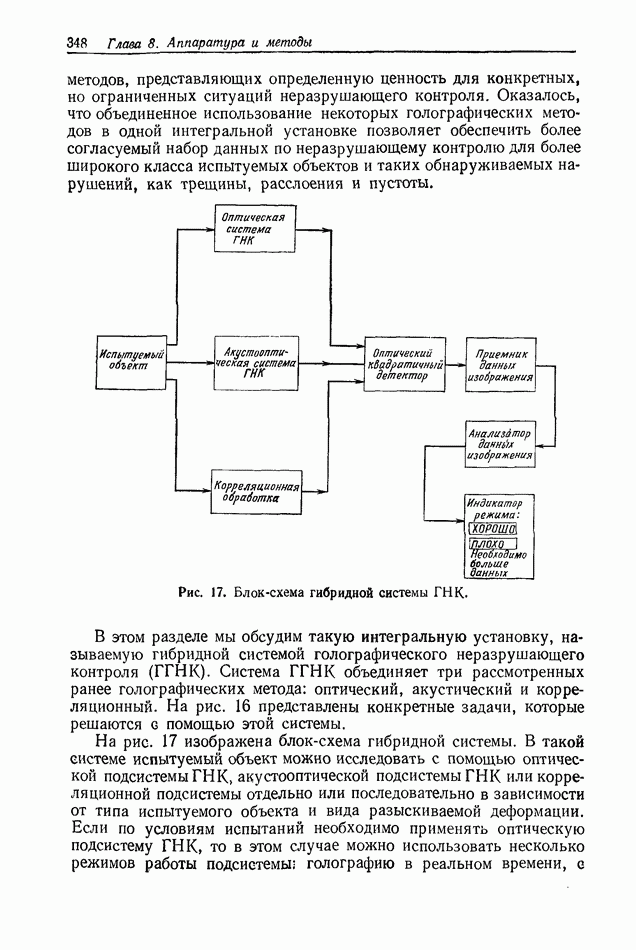
- 8.4.6. Гибридная система ГНК с автоматической обработкой данных
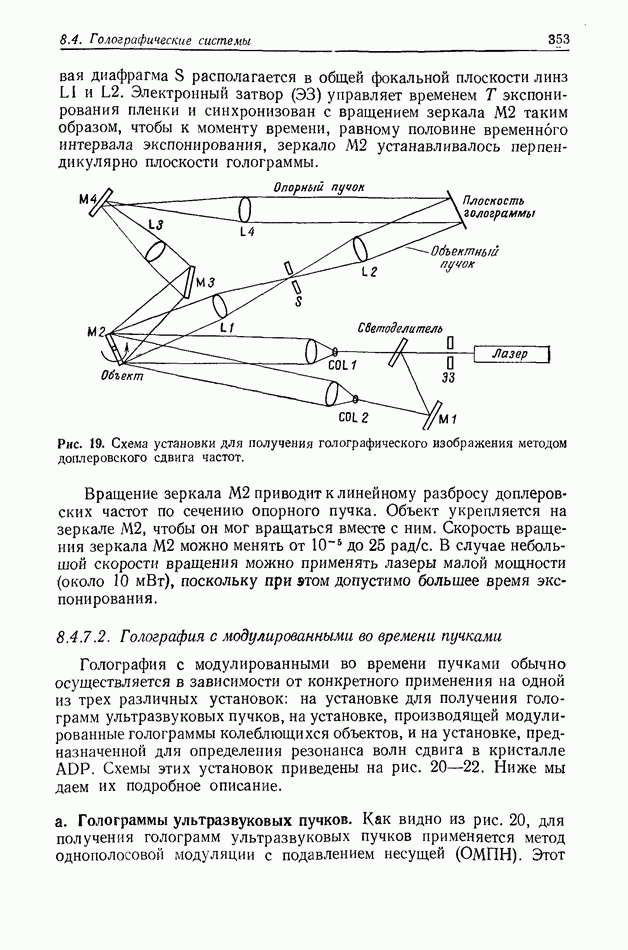
- 8.4.7. Голография движущихся объектов
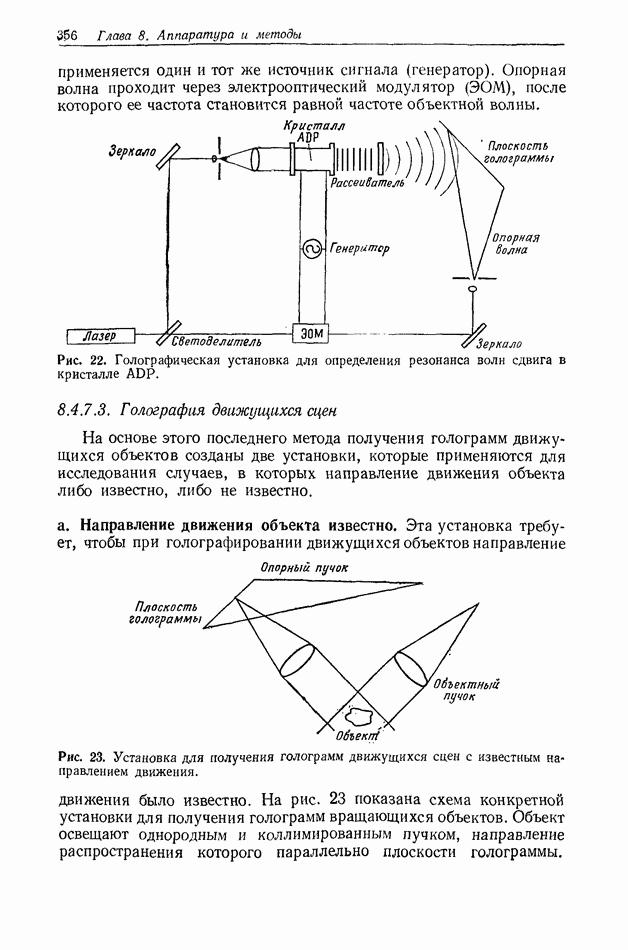
- 8.4.7.3. Голография движущихся сцен
- 8.4.8. Другие голографические системы
- 8.4.9. Заключение