| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
2.3.4. Пространственная и временная когерентность
Функция взаимной когерентности и комплексная степень когерентности зависят как от пространственных, так и от временных координат. Если свет является квазимонохроматическим, т. е.  полосы частот много меньше, чем средняя частота спектра излучения), то существенна лишь зависимость от пространственных координат. На основании экспериментальных данных условие когерентности состоит в том, чтобы максимальная величина
полосы частот много меньше, чем средняя частота спектра излучения), то существенна лишь зависимость от пространственных координат. На основании экспериментальных данных условие когерентности состоит в том, чтобы максимальная величина  была меньше, чем
была меньше, чем  следовательно, максимальная разность оптических путей меньше, чем
следовательно, максимальная разность оптических путей меньше, чем  где X — средняя длина волны света, а
где X — средняя длина волны света, а  ширина спектра. Таким образом, эмпирически даже белый свет иногда можно рассматривать как квазимонохроматический! Эти рассуждения приводят к определению временной когерентности света, которая характеризуется длиной когерентности
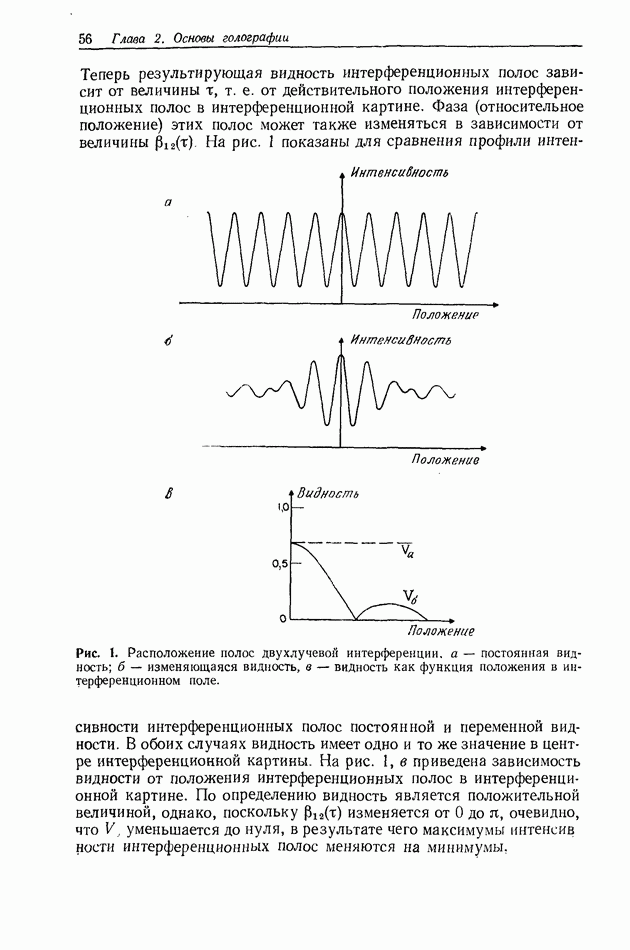
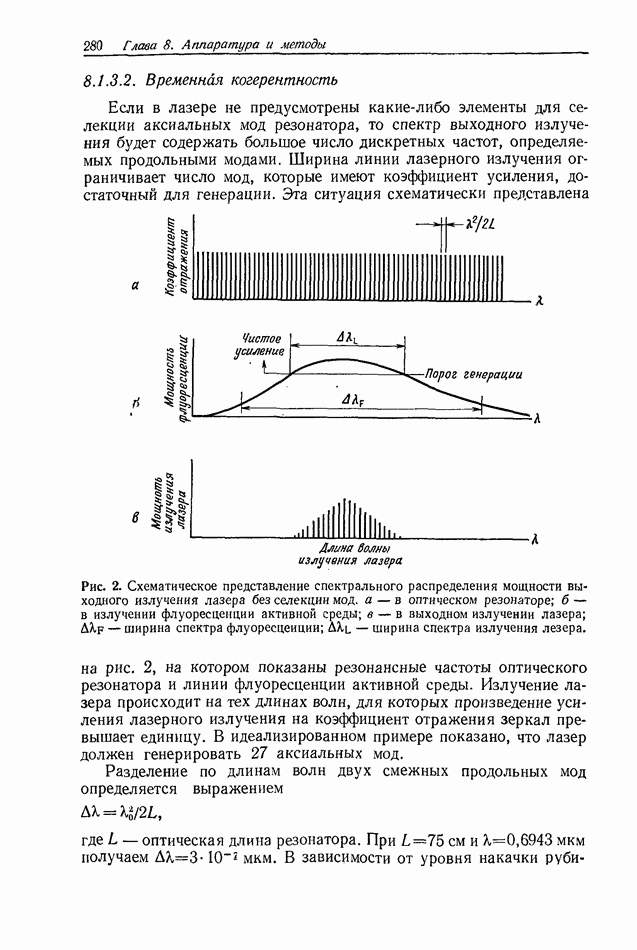
ширина спектра. Таким образом, эмпирически даже белый свет иногда можно рассматривать как квазимонохроматический! Эти рассуждения приводят к определению временной когерентности света, которая характеризуется длиной когерентности  Кривая видности на рис. 1, в, обозначенная
Кривая видности на рис. 1, в, обозначенная  в действительности является графиком временной когерентности света, проходящего через два отверстия для получения интерферирующих пучков. Временную часть комплексной степени когерентности можно получить, если положить
в действительности является графиком временной когерентности света, проходящего через два отверстия для получения интерферирующих пучков. Временную часть комплексной степени когерентности можно получить, если положить  и записать степень когерентности как
и записать степень когерентности как  Эта функция представляет собой нормализованный фурье-образ спектрального распределения света
Эта функция представляет собой нормализованный фурье-образ спектрального распределения света  Таким образом,
Таким образом,

Рассмотрим простой, хотя и не очень реальный пример: пусть спектральное распределение имеет вид прямоугольной функции. При этом временная когерентность будет иметь вид функции  где
где  ширина прямоугольного спектрального профиля.
ширина прямоугольного спектрального профиля.
Если свет действительно монохроматический, то пространственную когерентность можно рассматривать отдельно, т. е. мы имеем  В качестве примера исследуем степень когерентности поля, образованного светом от некогерентного источника. Если расстояние
В качестве примера исследуем степень когерентности поля, образованного светом от некогерентного источника. Если расстояние  от источника до плоскости, в которой исследуется поле, больше, чем размеры источника и размеры области, занимаемой интересующим нас полем, то комплексная степень когерентности дается преобразованием Фурье распределения интенсивности источника:
от источника до плоскости, в которой исследуется поле, больше, чем размеры источника и размеры области, занимаемой интересующим нас полем, то комплексная степень когерентности дается преобразованием Фурье распределения интенсивности источника:

здесь  распределение интенсивности источника. Таким образом, например, длинный и тонкий однородный некогерентный линейный источник шириной 2а создает поле, когерентность которого в направлении, перпендикулярном ширине линейного источника, дается выражением
распределение интенсивности источника. Таким образом, например, длинный и тонкий однородный некогерентный линейный источник шириной 2а создает поле, когерентность которого в направлении, перпендикулярном ширине линейного источника, дается выражением

Степень когерентности оказывается вещественной, но не везде она является положительной величиной; отрицательная величина означает, что функция когерентности имеет сдвиг по фазе, равный 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Предисловие
- Глава 1. ВВЕДЕНИЕ
- Глава 2. ОСНОВЫ ГОЛОГРАФИИ
- 2.1.1. Преобразование Фурье
- 2.1.2. Преобразование Лапласа
- 2.1.3. Преобразование Фурье — Бесселя
- 2.1.4. Преобразование Френеля
- 2.1.5. Преобразование Гильберта
- 2.1.6. Преобразование Меллина
- 2.1.7. Преобразование Абеля
- 2.2. ИНТЕРФЕРЕНЦИЯ И ДИФРАКЦИЯ
- 2.2.2. Сложение двух когерентных волн
- 2.2.3. Интерференция двух пучков
- 2.2.4. Распространение когерентного света — дифракция Френеля и Фраунгофера
- 2.3. ЧАСТИЧНО-КОГЕРЕНТНЫЙ СВЕТ
- 2.3.1. Сложение двух частично-когерентных квазимонохроматических полей
- 2.3.2. Интерференция двух частично-когерентных квазимонохроматических пучков
- 2.3.3. Интерференция двух частично-когерентных полихроматических пучков
- 2.3.4. Пространственная и временная когерентность
- 2.3.5. Дифракция и интерференция частично-когерентного света
- 2.4. ОЦЕНКА КАЧЕСТВА ИЗОБРАЖЕНИЯ
- 2.4.2. Формирование изображения в когерентном и некогерентном свете
- 2.4.3. Предел разрешения
- 2.4.4. Аберрации
- 2.4.5. Голографические изображения
- 2.4.6. Голографические аберрации
- 2.4.7. Отношение сигнал/шум
- 2.4.8. Заключение
- 2.5. ТЕОРИЯ СВЯЗИ
- 2.5.2. Теорема выборки (или теорема отсчетов)
- 2.5.3. Статистическое описание случайных сигналов
- 2.5.4. Выводы
- 2.6. ГАЛОГЕНИДОСЕРЕБРЯНАЯ ФОТОГРАФИЯ
- 2.6.2. Галогенидосеребряный фотографический процесс
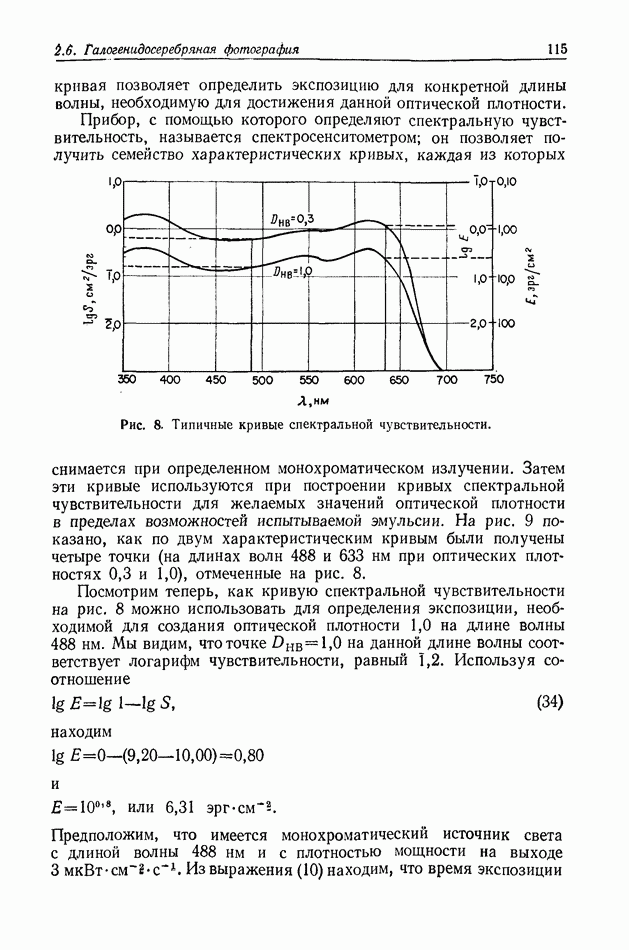
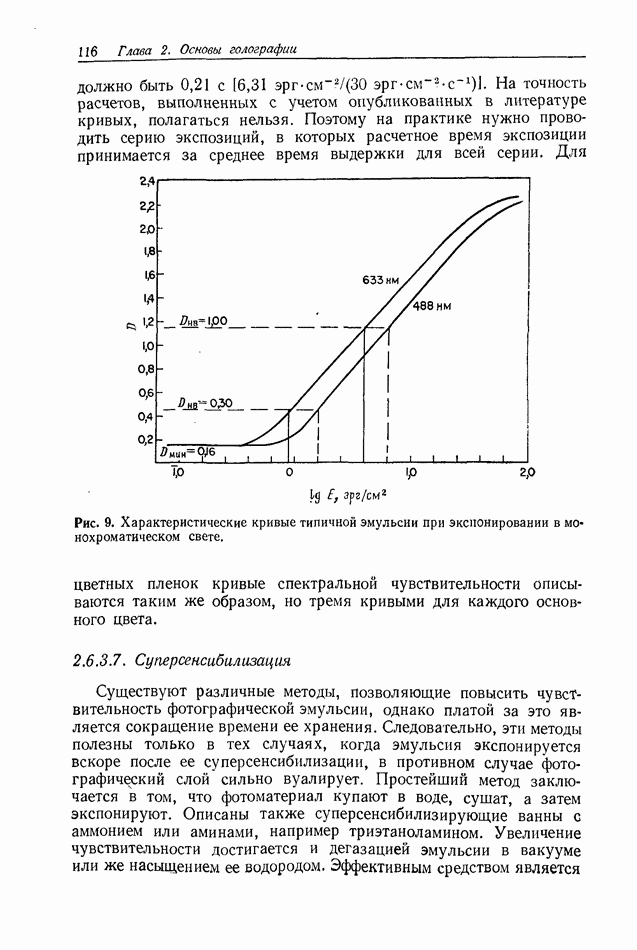
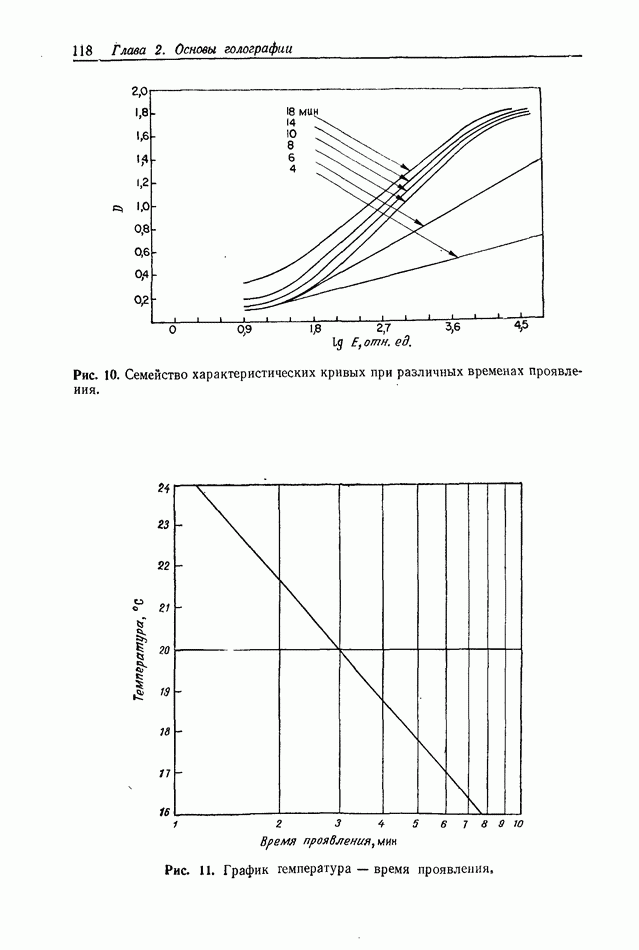
- 2.6.3. Сенситометрия
- 2.6.4. Денситометрия
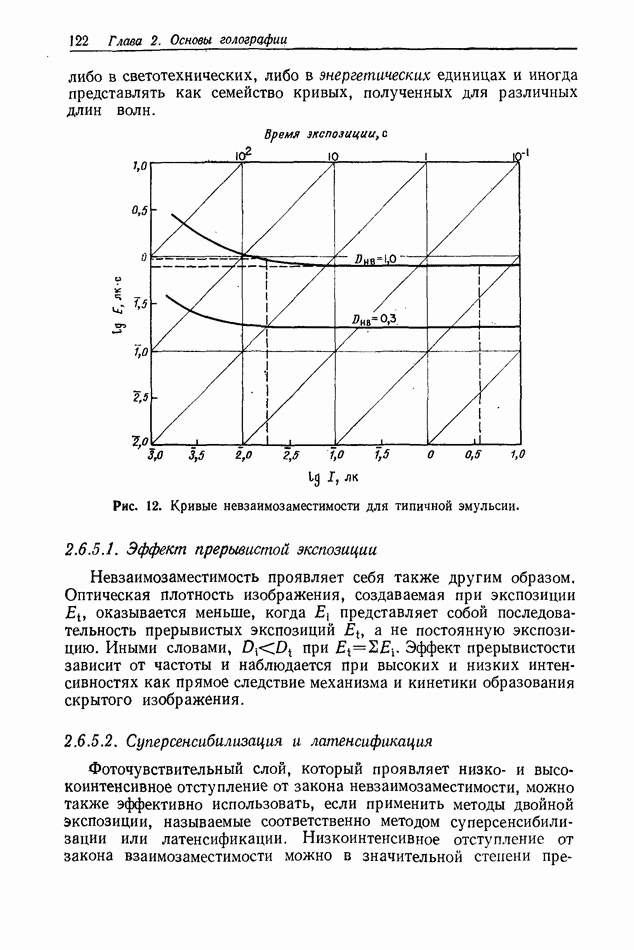
- 2.6.5. Взаимозаместимость
- 2.6.6. Характеристики изображения
- 2.6.7. Влияние изменения окружающей среды на стабильность пространственных параметров слоя
- 2.6.8. Характеристики сохраняемости фотоматериалов
- 2.6.9. Словарь терминов
- Глава 3. КЛАССИФИКАЦИЯ ГОЛОГРАММ
- 3.2. РЕГИСТРИРУЮЩИЕ СРЕДЫ И ИХ ПРИМЕНЕНИЕ
- 3.3. РЕГИСТРИРУЕМЫЕ ПАРАМЕТРЫ ОБЪЕКТНОЙ ВОЛНЫ
- 3.4. МОДУЛИРУЕМЫЕ ПАРАМЕТРЫ
- 3.5. КОНФИГУРАЦИЯ
- 3.6. СВОЙСТВА ИСТОЧНИКОВ
- 3.7. ОПИСАНИЕ ГОЛОГРАММЫ
- Глава 4. ОСНОВНЫЕ ТИПЫ ГОЛОГРАММ
- 4.1. ГОЛОГРАФИЯ ФРЕНЕЛЯ
- 4.2. ГОЛОГРАММЫ ФРАУНГОФЕРА
- 4.3. ГОЛОГРАФИЯ ФУРЬЕ
- 4.3.4. Свойства голограмм Фурье
- Глава 5. РАЗЛИЧНЫЕ ВИДЫ ГОЛОГРАММ
- 5.1. ОТРАЖАТЕЛЬНЫЕ ГОЛОГРАММЫ
- 5.2. МУЛЬТИПЛЕКСНЫЕ ГОЛОГРАММЫ
- 5.3. ЦВЕТНЫЕ ГОЛОГРАММЫ
- 5.4. ПОЛЯРИЗАЦИОННЫЕ ГОЛОГРАММЫ
- 5.5. СИНТЕЗИРОВАННЫЕ ГОЛОГРАММЫ
- 5.6. ГОЛОГРАММЫ С ЛОКАЛЬНЫМ ОПОРНЫМ ПУЧКОМ
- Глава 6. ФОРМИРОВАНИЕ ИЗОБРАЖЕНИЯ
- 6.1. ФОРМИРОВАНИЕ ИЗОБРАЖЕНИЯ В КОГЕРЕНТНОМ СВЕТЕ
- 6.2. ФОРМИРОВАНИЕ ИЗОБРАЖЕНИЯ В ЧАСТИЧНО-КОГЕРЕНТНОМ СВЕТЕ
- 6.3. ОЦЕНКА ЯРКОСТИ ВОССТАНОВЛЕННОГО ИЗОБРАЖЕНИЯ
- Глава 7. КАРДИНАЛЬНЫЕ ТОЧКИ И ГЛАВНЫЕ ЛУЧИ В ГОЛОГРАФИИ
- 7.2. ГОЛОГРАФИЧЕСКИЕ УРАВНЕНИЯ ОПТИЧЕСКИХ ЛУЧЕЙ
- 7.3. ГЛАВНЫЕ ТОЧКИ ГОЛОГРАММ
- 7.4. КАРДИНАЛЬНЫЕ ТОЧКИ ГОЛОГРАММЫ
- 7.5. УРАВНЕНИЯ СОПРЯЖЕНИЯ
- 7.6. ПРИЛОЖЕНИЯ К РАЗЛИЧНЫМ ТИПАМ ГОЛОГРАММ
- Глава 8. АППАРАТУРА И МЕТОДЫ
- 8.1. ТВЕРДОТЕЛЬНЫЕ ЛАЗЕРЫ
- 8.1.2. Рубиновый и Nd:YAG-лазеры
- 8.1.3. Главные конструктивные характеристики лазеров для голографии
- 8.2. ГАЗОВЫЕ ЛАЗЕРЫ
- 8.2.2. Когерентные свойства газовых лазеров
- 8.2.3. Когерентные свойства коммерческих лазеров
- 8.2.4. Диапазон длин волн выходного излучения газовых лазеров
- 8.2.5. Диапазон мощностей выходного излучения
- 8.2.6. Срок службы и стоимость
- 8.3. РЕГИСТРИРУЮЩИЕ СРЕДЫ
- 8.3.3. Галогенидосеребряные эмульсии
- 8.3.4. Задубленная бихромированная желатина
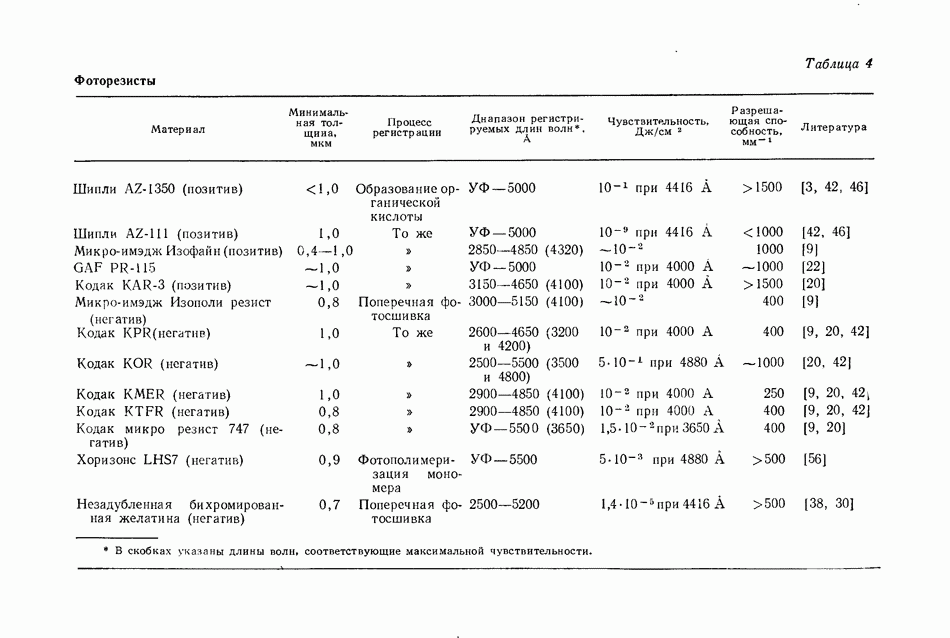
- 8.3.5. Фоторезисты
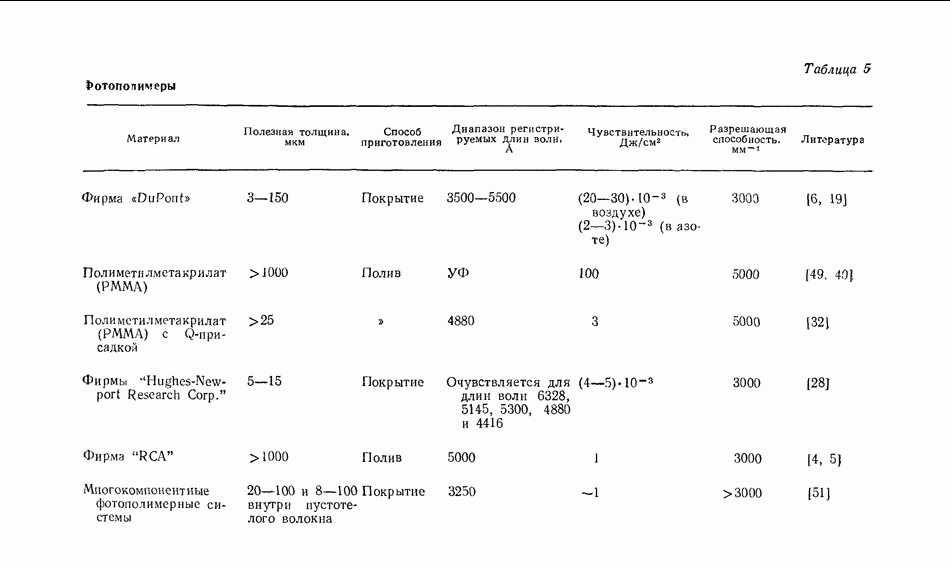
- 8.3.6. Фотополимеры
- 8.3.7. Фотопластики
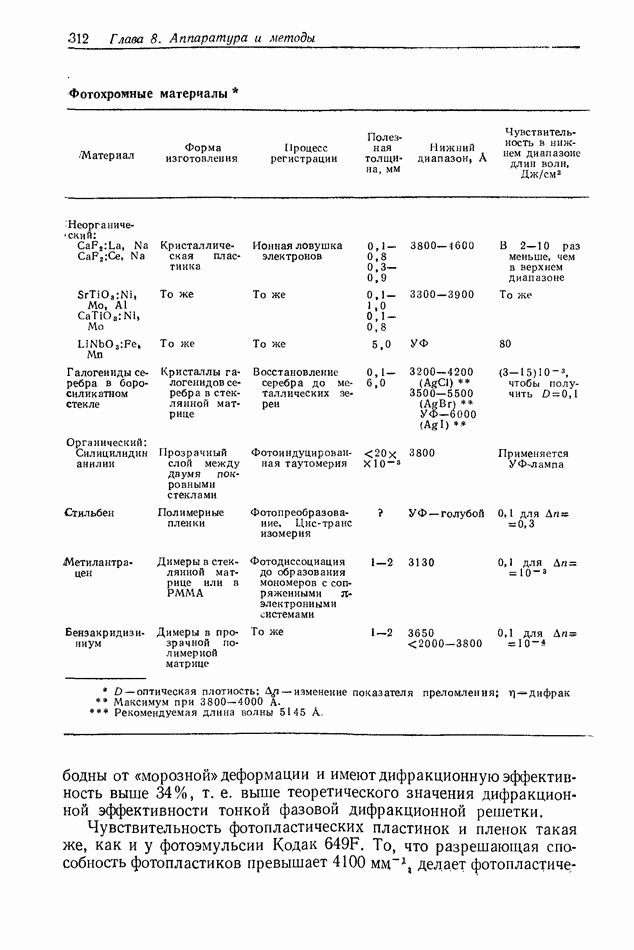
- 8.3.8. Фотохромные материалы
- 8.3.9. Прозрачные электрофотографические пленки
- 8.4. ГОЛОГРАФИЧЕСКИЕ СИСТЕМЫ
- 8.4.2. Описание комбинированной мобильной установки ГНК; система с переменной чувствительностью
- 8.4.3. Акустооптический голографический неразрушающий контроль
- 8.4.4. Неразрушающий контроль с применением голографии спеклов
- 8.4.5. Голографическая корреляция
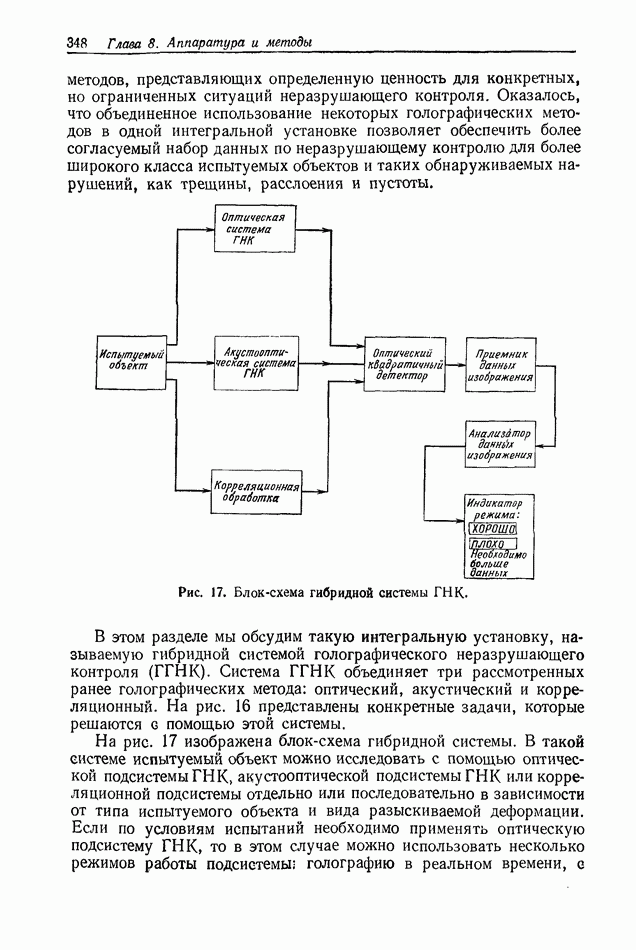
- 8.4.6. Гибридная система ГНК с автоматической обработкой данных
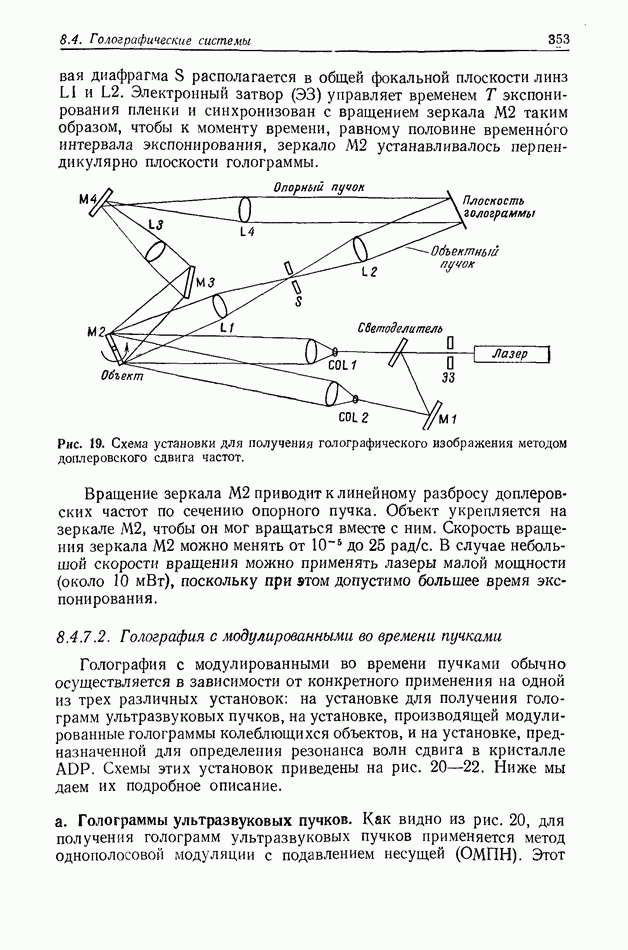
- 8.4.7. Голография движущихся объектов
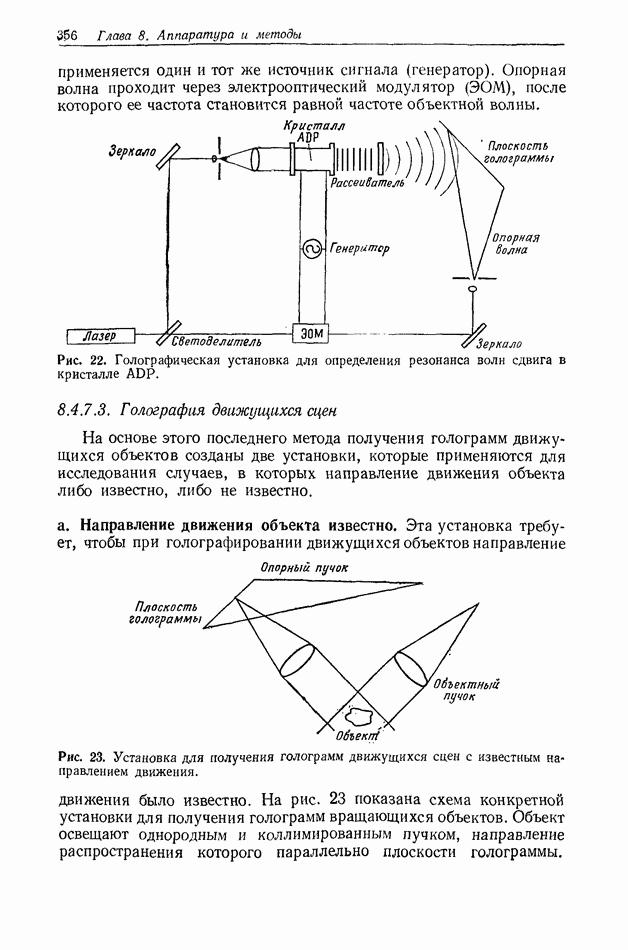
- 8.4.7.3. Голография движущихся сцен
- 8.4.8. Другие голографические системы
- 8.4.9. Заключение